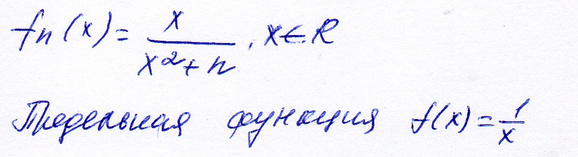Равномерная сходимость функциональных последовательностей и рядов
разделов
от теории до практики
примеров
Примеры решения задач
видео
Примеры решения задач
-
Сходимость функциональной последовательности и ряда.
Начать изучение
-
Сходимость последовательности функций.
Начать изучение
-
Сходимость функционального ряда.
Начать изучение
-
Равномерная сходимость функциональной последовательности.
Начать изучение
-
Понятие равномерной сходимости последовательности функций.
Начать изучение
-
Критерии равномерной сходимости последовательности функций.
Начать изучение
-
Неравномерная сходимость последовательности функций.
Начать изучение
-
Определение и критерий равномерной сходимости функционального ряда.
Начать изучение
-
Признаки равномерной сходимости функциональных рядов.
Начать изучение
-
Признак Вейерштрасса.
Начать изучение
-
Признак Дирихле.
Начать изучение
-
Признак Абеля.
Начать изучение
-
Свойства равномерно сходящихся функциональных последовательностей и рядов.
Начать изучение
-
Непрерывность суммы равномерно сходящегося ряда.
Начать изучение
-
Почленное интегрирование функционального ряда.
Начать изучение
-
Почленное дифференцирование функционального ряда.
Начать изучение
Сходимость функциональной последовательности и ряда.
Сходимость последовательности функций.
Пусть функции (f_{n}(x)), (n in mathbb{N}), определены на множестве (E) и пусть (x_{0} in E). Если числовая последовательность ({f_{n}(x_{0})}) сходится, то последовательность функций ({f_{n}(x)}) сходится в точке (x_{0}).
Последовательность ({f_{n}(x)}), сходящуюся в каждой точке (x in E), называют сходящейся на множестве (E). В этом случае на множестве (E) определена функция (f(x)), значение которой в любой точке (x in E) равно пределу последовательности ({f_{n}(x)}). Эту функцию называют предельной функцией последовательности ({f_{n}(x)}) на множестве (E) и пишут
$$
lim_{n rightarrow infty}f_{n}(x) = f(x), x in E,label{ref1}
$$
или
$$
f_{n}(x) rightarrow f(x), x in E,nonumber
$$
или, короче,
$$
f_{n} xrightarrow[E]{} f.nonumber
$$
По определению предела запись eqref{ref1} означает, что
$$
forall x in E forall varepsilon > 0 exists N = N_{varepsilon}(x): forall n geq N rightarrow |f_{n}(x)-f(x)| < varepsilon.nonumber
$$
Пример 1.
Найти предельную функцию (f(x)) последовательности ({f_{n}(x)}) на множестве (E), если:
- $$
f_{n}(x) = frac{n + 1}{n + x^{2}}, E = mathbb{R};nonumber
$$ - $$
f_{n}(x) = n sin frac{1}{nx}, E = (0, + infty).nonumber
$$
Решение.
- (vartriangle) Так как (f_{n}(x) = displaystylefrac{1 + displaystylefrac{1}{n}}{1 + frac{displaystyle x^{2}}{n}}), то (f(x) = 1).
- Используя асимптотическую формулу (sin t sim t) при (t rightarrow 0), получаем (displaystyle n sin frac{1}{nx} sim nfrac{1}{nx}) при (n rightarrow infty), если (x neq 0).Поэтому (f(x) = displaystylefrac{1}{x}). (blacktriangle)
Сходимость функционального ряда.
Пусть функции (u_{n}(x)), (n in mathbb{N}), определены на множестве (E) и пусть для каждого (x in E) существует конечный предел последовательности ({S_{n}(x)}), где (S_{n}(x) = displaystylesum_{k = 1}^{n}u_{k}(x)). Тогда ряд
$$
sum_{n = 1}^{infty}u_{n}(x),label{ref2}
$$
называют сходящимся на множестве (E).
Если (S(x)) — предельная функция последовательности ({S_{n}(x)}) на множестве (E), то есть
$$
lim_{n rightarrow infty}S_{n}(x) = S(x), x in E,nonumber
$$
то функцию называют (S(x)) суммой ряда eqref{ref2} и пишут
$$
sum_{n = 1}^{infty}u_{n}(x) = S(x), x in E.nonumber
$$
Например, если (u_{n}(x) = x^{n-1}), (E = (-1,1)), то (S_{n}(x) = displaystylefrac{1-x^{n}}{1-x}), (S(x) = displaystylefrac{1}{1-x}). Если в каждой точке (x in E) сходится ряд (displaystylesum_{n = 1}^{infty}|u_{n}(x)|), то ряд eqref{ref2} называют абсолютно сходящимся на множестве (E).
Равномерная сходимость функциональной последовательности.
Понятие равномерной сходимости последовательности функций.
Определение.
Последовательность функций
$$
{f_{n}(x)}nonumber
$$
называется равномерно сходящейся на множестве (E) к функции (f(x)), если
$$
forall varepsilon > 0 exists N_{varepsilon}: forall n geq N_{varepsilon} forall x in E rightarrow |f_{n}(x)-f(x)|<varepsilon.label{ref3}
$$
В этом определении существенно, что номер (N_{varepsilon}) не зависит от (x). Если справедливо утверждение eqref{ref3}, то пишут
$$
f_{n}(x) rightrightarrows f(x), x in E,nonumber
$$
или
$$
f_{n} underset{E}rightrightarrows f.nonumber
$$
Говорят, что последовательность ({f_{n}(x)}) равномерно сходится на множестве (E), если существует функция (f), удовлетворяющая условию eqref{ref3}.
Если существуют числовая последовательность ({a_{n}}) и номер (n_{0}) такие, что
$$
forall n geq n_{0} forall x in E rightarrow |f_{n}(x)-f(x)| leq a_{n},nonumber
$$
причем (displaystylelim_{n rightarrow infty}a_{n} = 0), то
$$
f_{n}(x) underset{E}rightrightarrows f(x), x in E.nonumber
$$
Пример 2.
Доказать, что последовательность ({f_{n}(x)}) равномерно сходится на множестве (E), и найти ее предельную функцию (f(x)), если:
- (displaystyle f_{n}(x) = frac{n + 1}{n + x^{2}}, E = [-1, 1];)
- (displaystyle f_{n}(x) = sqrt{x^{2} + frac{1}{n}}, E = mathbb{R};)
- (displaystyle f_{n}(x) = frac{operatorname{arctg} n^{2}x}{sqrt[3]{n + x}}, E = [0, +infty));
- (displaystyle f_{n}(x) = n sin frac{1}{nx}, E = [1, +infty)).
Решение.
- (vartriangle) В этом случае (f(x) = 1) (пример 1) и (|f_{n}(x)-f(x)| = displaystylefrac{1-x^{2}}{n + x^{2}} leq frac{1}{n}), так как (|x| leq 1). Следовательно,
$$
frac{n + 1}{n + x^{2}} rightrightarrows 1, x in [-1, 1].nonumber
$$ - Используя неравенство (x^{2} + displaystylefrac{1}{n} leq left(|x| + frac{1}{sqrt{n}}right)^{2}), получаем (0 leq displaystylesqrt{x^{2} + frac{1}{n}}-sqrt{x^{2}} leq |x| + frac{1}{sqrt{n}}-|x| = frac{1}{sqrt{n}}), откуда следует, что
$$
sqrt{x^{2} + frac{1}{n}} rightrightarrows |x|, x in mathbb{R}.nonumber
$$ - Так как (0 leq operatorname{arctg} x leq displaystylefrac{pi}{2}) и (sqrt[3]{n + x} geq sqrt[3]{n}) при (x > 0), то (0 leq f_{n}(x) leq displaystylefrac{pi}{2sqrt[3]{n}}), откуда получаем (f_{n}(x) rightrightarrows 0), (x in E).
- В этом случае (f(x) = displaystylefrac{1}{x}) (пример 1). Используя неравенство (|sin t-t| leq displaystylefrac{t^{2}}{2}, t in mathbb{R}) (пример разобран здесь), получаем
$$
|f_{n}(x)-f(x)| = n left|sin frac{1}{nx}-frac{1}{nx}right| leq frac{n}{2(nx)^{2}} leq frac{1}{2n},nonumber
$$
так как (x geq 1). Следовательно,
$$
n sin frac{1}{nx} rightrightarrows frac{1}{x}, x in [1, +infty). blacktrianglenonumber
$$
Критерии равномерной сходимости последовательности функций.
Теорема 1.
Чтобы последовательность функций ({f_{n}(x)}), определенных на множестве (E), сходилась равномерно на этом множестве к функции (f(x)), необходимо и достаточно, чтобы
$$
lim_{n rightarrow infty} sup_{x in E} |f_{n}(x)-f(x)| = 0.label{ref4}
$$
Доказательство.
(circ) Обозначим (sigma_{n} = displaystylesup_{x in E} |f_{n}(x)-f(x)|). Тогда условие eqref{ref4} означает, что
$$
forall varepsilon > 0 exists n_{varepsilon}: forall n geq n_{varepsilon} rightarrow sigma_{n} < varepsilon.label{ref5}
$$
Если (f_{n}(x) rightrightarrows f(x)), (x in E), то
$$
forall varepsilon > 0 exists N_{varepsilon}: forall n geq N_{varepsilon} rightarrow |f_{n}(x)-f(x)| < frac{varepsilon}{2},nonumber
$$
откуда следует, что (sigma_{n} leq displaystylefrac{varepsilon}{2} < varepsilon) для (n geq N_{varepsilon}). Поэтому неравенство (sigma_{n} < varepsilon) выполняется при всех (n geq N_{varepsilon}), где (n_{varepsilon} = N_{varepsilon}). Обратно, если выполняется условие eqref{ref4} или равносильное ему условие eqref{ref5}, то, используя неравенство (|f_{n}(x)-f(x)| leq sigma_{n}) для (x in E), (n in mathbb{N}), получаем (|f_{n}(x)-f(x)| < varepsilon) для (x in E), (n geq n_{varepsilon}), то есть (f_{n}(x) rightrightarrows 0), (x in E). (bullet)
Пример 3.
Доказать, что последовательность ({f_{n}(x)}) сходится равномерно на множестве (E), и найти предельную функцию (f(x)), если:
- (f_{n}(x) = displaystylefrac{2n^{2}x}{1 + n^{alpha}x^{2}}), (alpha > 4), (E = mathbb{R});
- (f_{n}(x) = displaystyle x^{n}-x^{n + 1}), (E = [0, 1]);
- (f_{n}(x) = displaystyle nx^{2}e^{-nx}), (E = [2, +infty)).
Решение.
- (vartriangle) Если (x = 0), то (f_{n}(0) = 0) для всех (n in mathbb{N}), и поэтому (displaystylelim_{n rightarrow infty}f_{n}(0) = f(0) = 0). Если (x neq 0), то (|f_{n}(x)| leq displaystylefrac{2n^{2}|x|}{n^{alpha}x^{2}} = frac{2}{|x|n^{alpha-2}}), откуда следует, что (f_{n}(x) rightarrow 0) при (n rightarrow infty), так как (alpha > 4). Таким образом, предельная функция (f(x) = 0), (x in mathbb{R}).
Так как при (x neq 0) справедливо неравенство (1 + n^{alpha}x^{2} geq 2n^{alpha/2}|x|), причем это неравенство обращается в равенство лишь в случае, когда (n^{alpha}x^{2} = 1), то есть (|x| = n^{-alpha/2}), то
$$
|f_{n}(x)-f(x)| leq frac{2n^{2}|x|}{2n^{alpha/2}|x|} = frac{1}{n^{alpha/2-2}}, x neq 0.nonumber
$$
Следовательно, (displaystylesup_{x in E} |f_{n}(x)-f(x)| = frac{1}{n^{alpha/2-2}} rightarrow 0) при (n rightarrow infty), если (alpha > 4), и поэтому (f_{n}(x) rightrightarrows 0), (x in R). - Если (x in [0, 1)), то (x^{n} rightarrow 0) при (n rightarrow infty), и поэтому (f_{n}(x) rightarrow 0) при (n rightarrow infty). Если (x = 1), то (f_{n}(1) = 0), и поэтому (f(1) = 0). Следовательно, (f(x) = 0), (x in [0, 1]).Чтобы вычислить (displaystylesup_{x in E} |f_{n}(x)-f(x)| = sup_{x in E} |f_{n}(x)|), найдем точки экстремума функции (f_{n}(x)).Уравнение (f_{n}'(x) = nx^{n-1}-(n + 1)x^{n} = x^{n-1}(n-x(n + 1)) = 0) имеет внутри отрезка [0,1] единственный корень (x_{n} = displaystylefrac{n}{n + 1}), причем (f_{n}(x_{n}) = displaystyleleft(frac{n}{n + 1}right)^{n}frac{1}{n}). Заметим, что (f_{n}'(x) > 0) при (x in (0, x_{n})) и (f_{n}'(x) < 0) при (x in (x_{n}, 1)). Поэтому (displaystylesup_{x in E} f_{n}(x) = max_{x in E} f_{n}(x) = f_{n}(x_{n} < frac{1}{n}) для всех (n in mathbb{N}) и, согласно теореме 1, (f_{n}(x) rightrightarrows 0), (x in [0, 1]).
- Учитывая, что (te^{-alpha t} rightarrow 0) при (t rightarrow +infty) (если (alpha > 0)), находим (lim_{n rightarrow infty} f_{n}(x) = f(x) = 0), (x in [0, +infty]).
- Так как (f_{n}'(x) = nxe^{-nx}(2-xn) < 0) при (x > displaystylefrac{2}{n}), то функция (f_{n}(x)) является убывающей на промежутке (displaystyleleft[frac{2}{n}, +inftyright)), и поэтому
$$
sup_{x in E} f_{n}(x) leq f_{n}left(frac{2}{n}right) = frac{4}{n}e^{-2} rightarrow 0 mbox{при} n rightarrow infty.nonumber
$$По теореме 1 последовательность ({f_{n}(x)}) равномерно сходится к (f(x) = 0) на множестве (E = [2, +infty)). (blacktriangle)
Теорема 2.
(критерий Коши равномерной сходимости последовательности)
Чтобы последовательность функций ({f_{n}(x)}) сходилась равномерно на множестве (E), необходимо и достаточно, чтобы выполнялось условие Коши
$$
forall varepsilon > 0 exists N_{varepsilon}: forall n geq N_{varepsilon} forall p in mathbb{N} forall x in E rightarrow |f_{n + p}(x)-f_{n}(x)| < varepsilon.label{ref6}
$$
Доказательство.
(circ) Необходимость. Пусть (f_{n}(x) rightrightarrows f(x)), (x in E). Тогда по определению равномерной сходимости
$$
forall varepsilon > 0 exists N_{varepsilon}: forall k geq N_{varepsilon} forall x in E rightarrow |f_{k}(x)-f(x)| < frac{varepsilon}{2}.label{ref7}
$$
В частности, eqref{ref7} выполняется при (k = n), если (n geq N_{varepsilon}), и при (k = n + p) для (p in mathbb{N}), то есть
$$
|f_{n}(x)-f_(x)| < frac{varepsilon}{2},quad |f_{n + p}(x)-f_(x)| < frac{varepsilon}{2},nonumber
$$
откуда следует, что
$$
|f_{n + p}(x)-f_{n}(x)| = |(f_{n + p}(x)-f(x))-(f_{n}(x)-f_(x))| leq\
leq |f_{n + p}(x)-f(x)| + |f_{n}(x)-f_(x)| < frac{varepsilon}{2} + frac{varepsilon}{2} = varepsilon,nonumber
$$
то есть выполняется условие eqref{ref6}.
Достаточность. Заметим, что числовая последовательность ({f_{n}(x_{0})}), где (x_{0}) — фиксированная точка множества (E), удовлетворяет условию Коши eqref{ref6} и в силу критерия Коши для числовой последовательности существует конечный
$$
lim_{n rightarrow infty}f_{n}(x_{0}).label{ref8}
$$
Так как предел eqref{ref8} существует для каждого (x_{0} in E), то на множестве (E) определена функция (обозначим ее (f(x))), которая является предельной функцией для последовательности ({f_{n}(x)}) на множестве (E).
Запишем условие Коши eqref{ref6} в виде
$$
forall varepsilon > 0 exists N_{varepsilon}: forall n geq N_{varepsilon} forall p in mathbb{N} forall x in E rightarrow |f_{n + p}(x)-f_{n}(x)| < frac{varepsilon}{2}.label{ref9}
$$
Переходя в неравенстве eqref{ref9} к пределу при (p rightarrow infty) (при каждом фиксированном (n geq N_{varepsilon}) и фиксированном (x in E)) и учитывая, что существует (displaystylelim_{p rightarrow infty}f_{n + p}(x) = f(x)), получаем неравенство
$$
|f(x)-f_{n}(x)| leq frac{varepsilon}{2} < varepsilon,nonumber
$$
справедливое при всех (n geq N_{varepsilon}) и для всех (x in E). Это означает, что
$$
f_{n}(x) rightrightarrows f(x), x in E. bulletnonumber
$$
Неравномерная сходимость последовательности функций.
Последовательность ({f_{n}(x)}) не является равномерно сходящейся на множестве (E), если условие Коши eqref{ref6} не выполняется, то есть
$$
exists varepsilon_{0} > 0: forall k in mathbb{N} exists n geq k exists p in mathbb{N} exists tilde{x} in E: |f_{n + p}(tilde{x})-f_{n}(tilde{x})| geq varepsilon_{0}.label{ref10}
$$
Пример 4.
Доказать, что последовательность ({f_{n}(x)}), где (f_{n}(x) = displaystylefrac{ln nx}{sqrt{nx}}), не является равномерно сходящейся на множестве (E = (0, 1)).
Решение.
(vartriangle) Для любого (k in mathbb{N}) возьмем (p = k = n), (tilde{x} = 1/k = 1/n). Тогда
$$
|f_{n + p}(tilde{x})-f_{n}(tilde{x})| = left|f_{2n}(frac{1}{n})-f_{n} (frac{1}{n})right| = left|frac{ln 2}{sqrt{2}}-ln 1right| = frac{ln 2}{sqrt{2}} = varepsilon_{0},nonumber
$$
то есть выполняется условие eqref{ref10}, и поэтому последовательность ({f_{n}(x)}) не является равномерно сходящейся на (E). (blacktriangle)
Если существует предельная функция (f(x)) последовательности ({f_{n}(x)}) на множестве (E), но не выполняется условие eqref{ref3}, то есть
$$
exists varepsilon_{0} > 0: forall k in mathbb{N} exists n geq k exists tilde{x} in E: |f_{n}(tilde{x})-f(tilde{x})| geq varepsilon_{0},label{ref11}
$$
то говорят, что последовательность ({f_{n}(x)}) сходится неравномерно на множестве (E) к функции (f(x)).
Пример 5.
Исследовать на сходимость и равномерную сходимость на множестве (E) последовательность ({f_{n}(x)}), если:
- (displaystyle f_{n}(x) = x^{n}-x^{2n}, E = [0, 1];)
- (displaystyle f_{n}(x) = nsin frac{1}{nx}, E = (0, 1].)
Решение.
- (vartriangle) В этом случае предельная функция (f(x) = 0), (x in E). Для любого (k in mathbb{N}) возьмем (n = k), (tilde{x} = 1/sqrt[n]{2}). Тогда (tilde{x} in E) при любом (n in mathbb{N}) и (|f_{n}(tilde{x})-f(tilde{x})| = displaystyle f_{n}left(frac{1}{n}right) = frac{1}{2}-frac{1}{4} = varepsilon_{0}), то есть выполняется условие eqref{ref11}, и поэтому последовательность ({f_{n}(x)}) сходится неравномерно на множестве (E) к (f(x) = 0).
- Здесь предельная функция (f(x) = x^{-1}) на множестве (x > 0) (пример 1). Возьмем (tilde{x} = 1/n). Тогда (|f_{n}(tilde{x})-f(tilde{x})| = |n sin 1-n| geq 1-sin 1 = varepsilon_{0}) для любого (n in mathbb{N}), и поэтому ({f_{n}(x)}) сходится неравномерно на множестве (E) к (x^{-1}). (blacktriangle)
Неравномерную сходимость последовательности можно установить, используя теорему 1. Если условие eqref{ref4} не выполняется, то есть
$$
sup_{x in E}|f_{n}(x)-f(x)| nrightarrow 0 mbox{при} n rightarrow infty,label{ref12}
$$
то ({f_{n}(x)}) сходится неравномерно на множестве (E) к (f(x)).
Пример 6.
Исследовать на сходимость и равномерную сходимость последовательность (f_{n}(x) = n^{2}x^{2}e^{-nx}), (E = (0, 2)).
Решение.
(vartriangle) Предельная функция (f(x) = 0), (x in E). Так как уравнение (f_{n}'(x) = n^{2}xe^{-nx}(2-xn)) имеет на интервале (0,2) единственный корень (x_{n} = 2/n), причем (f_{n}'(x) > 0) при (x in (0, x_{n})) и (f_{n}'(x) < 0) при (x in (x_{n}, 2)), то (displaystylesup_{x in E} f_{n}(x_{n}) = f_{n}(x_{n}) = 4e^{-1}). Таким образом, выполняется условие eqref{ref12}, и поэтому ({f_{n}(x)}) сходится неравномерно на множестве (E) к 0. (blacktriangle)
Определение и критерий равномерной сходимости функционального ряда.
Пусть функции (u_{n}(x)), (n in mathbb{N}), определены на множестве (E). Обозначим
$$
S_{n}(x) = sum_{k = 1}^{n}u_{k}(x).label{ref13}
$$
Определение.
Ряд
$$
sum_{n = 1}^{infty}u_{n}(x),label{ref14}
$$
называется равномерно сходящимся на множестве (E), если на этом множестве определена функция (S(x)) такая, что
$$
S_{n}(x) rightrightarrows S(x), x in E.label{ref15}
$$
Согласно определению равномерной сходимости последовательности функций запись eqref{ref15} означает, что
$$
forall varepsilon > 0 exists N_{varepsilon}: forall n geq N_{varepsilon} forall x in E rightarrow |S_{n}(x)-S(x)| < varepsilon.label{ref16}
$$
где (S(x)) — сумма ряда (14), a (S_{n}(x)) определяется формулой eqref{ref13}.
Пусть (r_{n}(x) = S(x)-S_{n}(x)), то есть (r_{n}(x)) — (n)-й остаток ряда eqref{ref14}. Тогда условие eqref{ref15} примет вид
$$
r_{n}(x) rightrightarrows 0,quad x in E.nonumber
$$
Это означает, что
$$
forall varepsilon > 0 exists N_{varepsilon}: forall n geq N_{varepsilon} forall x in E rightarrow |r_{n}(x)| < varepsilon.label{ref17}
$$
В силу теоремы 1 для равномерной сходимости ряда eqref{ref14} на множестве (E) необходимо и достаточно, чтобы
$$
sup_{x in E}|r_{n}(x)| rightarrow 0 mbox{при} n rightarrow infty,label{ref18}
$$
Если ряд eqref{ref14} сходится на множестве (E), но не выполняется условие eqref{ref17} или равносильное ему условие eqref{ref18}, то говорят, что ряд eqref{ref14} сходится неравномерно на множестве (E).
Следовательно, если
$$
exists varepsilon_{0} > 0: forall k in mathbb{N} exists n geq k exists tilde{x} in E: |r_{n}(tilde{x})| geq varepsilon_{0},label{ref19}
$$
или
$$
sup_{x in E}|r_{n}(x)| nrightarrow 0 mbox{при} n rightarrow infty,label{ref20}
$$
то ряд eqref{ref14} сходится неравномерно на множестве (E).
Пример 7.
Исследовать на сходимость и равномерную сходимость на указанных множествах ряд (displaystylesum_{n = 1}^{infty}u_{n}(x)), если:
- (u_{n}(x) = x^{n-1}, E_{1} = (-q, q), mbox{где} 0 < q < 1, E_{2} = (-1, 1));
- (u_{n}(x) = displaystylefrac{x}{(1 + nx)(1 + (n + 1)x)}, E_{1} = (delta, +infty), mbox{где} delta > 0, E_{2} = (0, +infty));
- (u_{n}(x) = displaystylefrac{(-1)^{n}}{sqrt{n + x}}, E = (0, +infty)).
Решение.
- (vartriangle) В этом случае (S_{n}(x) = displaystylefrac{1-x^{n}}{1-x}), (S(x) = displaystylefrac{1}{1-x}) для любого (x in E_{2}), то есть ряд сходится на множестве (E_{2}), а значит, и на (E_{1}).Для любого (x in E_{1}) выполняется неравенство (|r_{n}(x)| = displaystyleleft|frac{x^{n}}{1-x}right| leq frac{|x|^{n}}{1-|x|}), откуда следует, что (displaystylesup_{x in E}|r_{n}(x)| leq frac{q^{n}}{1-q}), и поэтому выполняется условие eqref{ref18}. Следовательно, ряд сходится равномерно на множестве (E_{1}).На множестве (E_{2}) ряд сходится неравномерно. В самом деле, возьмем (tilde{x} = displaystyle 1-frac{1}{n}). Тогда (tilde{x} in E) для любого (n in mathbb{N}) и (r_{n}(tilde{x}) = displaystyle nleft(1-frac{1}{n}right)^{n} rightarrow +infty) при (n rightarrow infty), откуда следует, что выполняется условие eqref{ref20}.
- Так как (u_{n}(x) = displaystylefrac{1}{1 + nx}-frac{1}{1 + (n + 1)x}), то (S_{n}(x) = displaystylefrac{1}{1 + x}-frac{1}{1 + (n + 1)x}). Если (x in E_{2}), то (S_{n}(x) rightarrow S(x)) при (n rightarrow infty), где (S(x) = displaystylefrac{1}{1 + x}), и поэтому (r_{n}(x) = displaystylefrac{1}{1 + (n + 1)x}).На множестве (E_{1}) ряд сходится равномерно, так как (|r_{n}(x)| leq displaystylefrac{1}{1 + (n + 1)delta}), и поэтому выполняется условие eqref{ref18}, а на множестве (E_{2}) — неравномерно, так как (displaystyle r_{n}left(frac{1}{n + 1}right) = frac{1}{2}), и поэтому выполняется условие eqref{ref20}.
- При каждом (x > 0) последовательность (displaystyleleft{frac{1}{sqrt{n + x}}right}) монотонно стремится к нулю, и поэтому по признаку Лейбница ряд (displaystylesum_{n = 1}^{infty} frac{(-1)^{n}}{sqrt{n + x}}) сходится на множестве (E), причем (|r_{n}(x)| leq |u_{n + 1}(x)| = displaystylefrac{1}{sqrt{n + 1 + x}} leq frac{1}{sqrt{n + 1}}), откуда следует, что выполняется условие eqref{ref18}. Следовательно, ряд сходится равномерно на множестве (E). (blacktriangle)
Теорема 3.
(критерий Коши равномерной сходимости ряда)
Для того чтобы ряд eqref{ref14} равномерно сходился на множестве (E), необходимо и достаточно, чтобы выполнялось условие Коши, то есть
$$
forall varepsilon > 0 exists N_{varepsilon}: forall n geq N_{varepsilon} forall p in mathbb{N} forall x in E rightarrow left|sum_{k = n + 1}^{n + p} u_{k}(x)right| < varepsilon.label{ref21}
$$
Доказательство.
(circ) По определению равномерная сходимость ряда eqref{ref14} на множестве (E) означает равномерную сходимость последовательности ({S_{n}(x)}) на (E).
Согласно теореме 2 (S_{n}(x) rightrightarrows S(x)) на (E) тогда и только тогда, когда
$$
forall varepsilon > 0 exists N_{varepsilon}: forall n geq N_{varepsilon} forall p in mathbb{N} forall x in E rightarrow |S_{n + p}(x)-S_{n}(x)| < varepsilon.label{ref22}
$$
Так как (S_{n + p}(x)-S_{n}(x) = u_{n + 1}(x) + ldots + u_{n + p}(x)), то условие eqref{ref22} равносильно условию eqref{ref21}. (bullet)
Если условие eqref{ref21} не выполняется, то есть
$$
exists varepsilon_{0} > 0: forall m in mathbb{N} exists n geq m exists p in mathbb{N} exists tilde{x} in E: left|sum_{k = n + 1}^{n + p} u_{k}(tilde{x})right| geq varepsilon_{0},label{ref23}
$$
то ряд eqref{ref14} не является равномерно сходящимся на множестве (E). В частности, если
$$
exists varepsilon_{0} > 0: forall n_{0} in mathbb{N}: forall n geq n_{0} exists x_{n} in E: |u_{n}(x_{n})| geq varepsilon_{0},label{ref24}
$$
то ряд eqref{ref14} не является равномерно сходящимся на множестве (E).
Пример 8.
Доказать, что ряд (displaystylesum_{n = 1}^{infty}u_{n}(x)) не является равномерно сходящимся на множестве (E), если:
- (u_{n}(x) = displaystylefrac{n^{2}}{x}e^{-n^{2}/x}, E = (0, +infty));
- (u_{n}(x) = displaystylefrac{n}{1 + n^{2}x^{2}}operatorname{tg} sqrt{frac{x}{n}}, E = (0, 1));
- (u_{n}(x) = displaystylefrac{sin nx}{n^{alpha}}, E = [0, 2pi], 0 < alpha leq 1).
Решение.
- (vartriangle) Пусть (x_{n} = x^{2}), тогда (u_{n}(x_{n}) = e^{-1}), то есть выполняется условие eqref{ref24}.
- Возьмем (x_{n} = displaystylefrac{1}{n}) и воспользуемся тем, что (operatorname{tg} x > x) при (0 < x < displaystylefrac{pi}{2}) (этот факт разбирали ранее). Тогда (u_{n}(x_{n}) = displaystylefrac{n}{2}operatorname{tg} frac{1}{n} > frac{1}{2}) при всех (n in mathbb{N}), то есть выполняется условие eqref{ref24}.
- Возьмем (x_{n} = displaystylefrac{pi}{4(n + 1)}); тогда (x_{n} in E) при любом (n in mathbb{N}). Если (n + 1 leq k leq 2n), то (displaystylefrac{pi}{4} leq kx_{n} leq frac{pi}{4} frac{2n}{n + 1} < frac{pi}{2}), и поэтому (displaystylesin kx_{n} geq sin frac{pi}{4} = frac{1}{sqrt{2}}) откуда следует, что
$$
sum_{k = n + 1}^{2n} frac{sin kx_{n}}{k^{alpha}} geq frac{1}{sqrt{2}} sum_{k = n + 1}^{2n} frac{1}{k^{alpha}} geq frac{1}{sqrt{2}} sum_{k = n + 1}^{2n} frac{1}{k} > frac{1}{sqrt{2}}nfrac{1}{2n} = frac{1}{2sqrt{2}},nonumber
$$
так как (0 < alpha leq 1). Следовательно, выполняется условие eqref{ref23}, и поэтому ряд не является равномерно сходящимся на множестве ([0, 2pi]) при (alpha in ()0, 1]). (blacktriangle)
Признаки равномерной сходимости функциональных рядов.
Признак Вейерштрасса.
Теорема 4.
Если для функционального ряда eqref{ref14} можно указать такой сходящийся числовой ряд (displaystylesum_{n = 1}^{infty}a_{n}), что для всех (n geq n_{0}) и для всех (x in E) выполняется условие
$$
|u_{n}(x)| leq a_{n},label{ref25}
$$
то ряд eqref{ref14} сходится абсолютно и равномерно на множестве (E).
Доказательство.
(circ) Согласно условию eqref{ref25} для любого (n geq n_{0}), любого (p in mathbb{N}) и для каждого (x in E) выполняется неравенство
$$
left|sum_{k = n + 1}^{n + p}u_{k}(x)right| leq sum_{k = n + 1}^{n + p}|u_{k}(x)| leq sum_{k = n + 1}^{n + p}a_{k}.label{ref26}
$$
Из сходимости ряда (displaystylesum_{n = 1}^{infty}a_{n}) следует (свойства сходящихся рядов можно посмотреть здесь), что для него выполняется условие Коши, то есть
$$
forall varepsilon > 0 exists N_{varepsilon}: forall n geq N_{varepsilon} forall p in mathbb{N} rightarrow sum_{k = n + 1}^{n + p}a_{k} < varepsilon,label{ref27}
$$
а из eqref{ref26} и eqref{ref27} следует, что для ряда eqref{ref14} выполняется на множестве (E) условие Коши eqref{ref21}, и в силу теоремы 3 этот ряд сходится равномерно на множестве (E).
Абсолютная сходимость ряда eqref{ref14} для каждого (x in E) следует из правого неравенства eqref{ref26}. (bullet)
Следствие.
Если сходится ряд (displaystylesum_{n = 1}^{infty}a_{n}), где (a_{n} = sup_{x in E}|u_{n}(x)|), то ряд eqref{ref14} сходится абсолютно и равномерно на множестве (E).
Пример 9.
Доказать, что ряд (displaystylesum_{n = 1}^{infty}u_{n}(x)) сходится равномерно на множестве (E), если:
- (u_{n}(x) = displaystyleln left(1 + frac{x}{nsqrt[3]{n + 1}}right), E = [0, 3]);
- (u_{n}(x) = displaystylefrac{nx}{n^{2} + x^{2}} operatorname{arctg} frac{x}{n}, E = [-1, 1]);
- (u_{n}(x) = displaystylefrac{displaystylesin frac{1}{nx}cos nx}{displaystyle4 + ln^{2}(n + 1)x}, E = [1, +infty));
- (u_{n}(x) = x^{2}e^{-nx}, E = (0, +infty)).
Решение.
- (vartriangle) Так как при (t geq 0) справедливо неравенство (ln(1 + t) leq t) (§ 17, пример 1, а)), то (|u_{n}(x)| leq displaystylefrac{x}{nsqrt[3]{n + 1}} leq frac{3}{n^{3/2}}) при всех (x in [0, 3]), и из сходимости ряда (displaystylesum_{n = 1}^{infty}frac{3}{n^{3/2}}) по теореме 4 следует равномерная сходимость ряда (displaystylesum_{n = 1}^{infty}u_{n}(x)) на множестве [0,3].
- Используя неравенство (|operatorname{arctg} t| leq t) для всех (t in mathbb{R}) (§ 17, (19)) и учитывая, что (|x| leq 1) и (n^{2} + x^{2} geq n^{2}), получаем (|u_{n}(x)| leq displaystylefrac{|nx|}{n^{2} + x^{2}} |frac{x}{n}| leq frac{1}{n^{2}}), откуда следует равномерная сходимость ряда на множестве [-1,1].
- Так как (|sin t| leq |t|) и (|cos t| leq 1) для всех (t in mathbb{R}), а (x geq 1), то (|u_{n}(x)| leq displaystylefrac{1}{nx ln^{2}(n + 1)x} leq frac{1}{n ln^{2}(n + 1)}). Из сходимости ряда (displaystylesum_{n = 1}^{infty} frac{1}{nln^{2}(n + 1)}) следует равномерная сходимость ряда (displaystylesum_{n = 1}^{infty}u_{n}(x)) на множестве ([1, +infty)).
- На промежутке ((0, +infty)) уравнение (u_{n}'(x) = xe^{-nx}(2-nx) = 0) имеет единственный корень (x = x_{n} = displaystylefrac{2}{n}), причем (u_{n}'(x) > 0) при (x in (0, x_{n})) и (u_{n}'(x) < 0) при (x > x_{n}). Поэтому (displaystylesup_{x in E}|u_{n}(x)| = u_{n}(x_{n}) = frac{4}{n^{2}}e^{-2}), и из сходимости ряда (displaystylesum_{n = 1}^{infty}frac{4}{n^{2}}e^{-2}) следует равномерная сходимость ряда (displaystylesum_{n = 1}^{infty}u_{n}(x)) на множестве ((0, +infty)). (blacktriangle)
Признак Дирихле.
Теорема 5.
Ряд
$$
sum_{k = 1}^{infty}a_{k}(x)b_{k}(x),label{ref28}
$$
сходится равномерно на множестве (E), если выполняются условия:
- последовательность ({B_{n}(x)}), где (B_{n}(x) = displaystylesum_{k = 1}^{n}b_{k}(x)) равномерно ограничена на множестве (E), то есть
$$
exists M > 0 forall x in E forall n in mathbb{N} rightarrow |B_{n}(x)| leq M;label{ref29}
$$ - последовательность ({a_{n}(x)}) монотонна на множестве (E), то есть
$$
forall x in E forall n in mathbb{N} rightarrow a_{n + 1}(x) leq a_{n}(x);label{ref30}
$$
и равномерно стремится к нулю, то есть
$$
a_{n}(x) rightrightarrows 0, qquad x in E.label{ref31}
$$
Доказательство.
(circ) Воспользуемся оценкой
$$
left|sum_{k = n + 1}^{n + p}a_{k}(x)b_{k}(x)right| leq 2M(|a_{n + 1}(x)| + |a_{n + p}(x)|),label{ref32}
$$
полученной при доказательстве признака Дирихле для числовых рядов.
Условие eqref{ref31} означает, что
$$
forall varepsilon > 0 exists N_{varepsilon}: forall k geq N_{varepsilon} forall x in E rightarrow |a_{k}(x)| < frac{varepsilon}{4M};label{ref33}
$$
Из eqref{ref29}, eqref{ref32} и eqref{ref33} следует, что для всех (n geq N_{varepsilon}), для всех (p in mathbb{N}) и для всех (x in E) выполняется неравенство (displaystyleleft|sum_{k = n + 1}^{n + p}a_{k}(x)b_{k}(x)right| leq varepsilon), и в силу критерия Коши ряд eqref{ref28} сходится равномерно на множестве (E). (bullet)
Пример 10.
Доказать, что при (alpha > 0) ряд
$$
sum_{n = 1}^{infty}frac{sin nx}{n^{alpha}},label{ref34}
$$
сходится равномерно на множестве (E = [delta, 2pi-delta]), где (0 < delta < 2pi-delta < 2pi).
Решение.
(vartriangle) Если (alpha > 1), то по признаку Вейерштрасса ряд eqref{ref34} сходится абсолютно и равномерно на (mathbb{R}), так как (|sin x| leq 1), а ряд (displaystylesum_{n = 1}^{infty}frac{1}{n^{alpha}}), где (alpha > 1), сходится.
Пусть (0 < alpha < 1). Тогда последовательность ({a_{n}}), где (a_{n} = displaystylefrac{1}{n^{alpha}}), удовлетворяет условиям eqref{ref30}, eqref{ref31}. Полагая (B_{n}(x) = displaystylesum_{k = 1}^{n}sin kx) и используя неравенство (|B_{n}(x)| leq displaystylefrac{1}{displaystyleleft|sin frac{x}{2}right|}), справедливое при (x neq pi m), (m in mathbb{Z}), получаем (|B_{n}(x)| leq displaystylefrac{1}{displaystylesin frac{delta}{2}}) для всех (x in E). По признаку Дирихле ряд eqref{ref34} сходится равномерно на множестве (E).
Заметим, что на множестве ([0, 2pi]) ряд eqref{ref34} при (alpha in (0, 1]) сходится неравномерно (пример 8, в)). (blacktriangle)
Признак Абеля.
Теорема 6.
Ряд eqref{ref28} сходится равномерно на множестве (E), если выполняются условия:
- ряд
$$
sum_{n = 1}^{infty}b_{n}(x),label{ref35}
$$
сходится равномерно на множестве (E); - последовательность ({a_{n}(x)}) монотонна на множестве (E), то есть
$$
forall n in mathbb{N} forall x in E rightarrow a_{n + 1}(x) leq a_{n}(x);label{ref36}
$$
и равномерно ограничена, то есть
$$
exists M > 0: forall n in mathbb{N} forall x in E rightarrow |a_{n}(x)| leq M;label{ref37}
$$
Доказательство.
(circ) Обозначим (B_{j}^{(n)}(x) = displaystylesum_{k = n + 1}^{n + j}b_{k}(x)). Тогда ряд eqref{ref35} в силу теоремы 3 удовлетворяет условию Коши, то есть
$$
forall varepsilon > 0 exists N_{varepsilon}: forall n geq N_{varepsilon} forall j in mathbb{N} rightarrow |B_{j}^{(n)}(x)| < frac{varepsilon}{3M}.label{ref38}
$$
Используя преобразование Абеля, преобразуем сумму:
$$
sigma = sum_{k = n + 1}^{n + p}a_{k}(x)b_{k}(x) = sum_{j = 1}^{p}a_{n + j}(x)b_{n + j}(x).nonumber
$$
Так как (b_{n + j}(x) = displaystyle B_{j}^{(n)}(x)-B_{j-1}^{(n)}(x)), где (j = overline{1, p}), (B_{0}^{(n)}(x) = 0), то
$$
sigma = sum_{j = 1}^{p-1}(a_{n + j}(x)-a_{n + j + 1}(x)) B_{j}^{(n)}(x) + a_{n + p}(x)B_{p}^{(n)}(x),nonumber
$$
откуда, используя условия eqref{ref36}-eqref{ref38}, получаем
$$
|sigma| < frac{varepsilon}{3M} sum_{j = 1}^{p-1}(a_{n + j}(x)-a_{n + j + 1}(x)) + frac{varepsilon}{3M} |a_{n + p}(x)| =\= frac{varepsilon}{3M} (a_{n + 1}(x)-a_{n + p}(x) + |a_{n + p}(x)|) leq frac{varepsilon}{3M} (2|a_{n + p}(x)| + |a_{n + 1}(x)| leq varepsilon.nonumber
$$
Таким образом,
$$
forall varepsilon > 0 exists N_{varepsilon}: forall n geq N_{varepsilon} forall p in mathbb{N} forall x in E rightarrow left|sum_{k = n + 1}^{n + p}a_{k}(x)b_{k}(x)right| < varepsilon,nonumber
$$
и по теореме 3 ряд eqref{ref28} сходится равномерно на множестве (E). (bullet)
Свойства равномерно сходящихся функциональных последовательностей и рядов.
Непрерывность суммы равномерно сходящегося ряда.
Теорема 7.
Если все члены ряда eqref{ref14} — непрерывные на отрезке ([a, b]) функции, а ряд eqref{ref14} сходится равномерно на ([a, b]), то его сумма (S(x)) также непрерывна на отрезке ([a, b]).
Доказательство.
(circ) Пусть (x_{0}) — произвольная точка отрезка ([a, b]). Для определенности будем считать, что (x_{0} in (a, b)).
Нужно доказать, что функция
$$
S(x) = sum_{n = 1}^{infty}u_{n}(x)nonumber
$$
непрерывна в точке (x_{0}), то есть
$$
forall varepsilon > 0 exists delta = delta (varepsilon) > 0: forall x in U_{delta}(x_{0}) rightarrow |S(x)-S(x_{0})| < varepsilon,label{ref39}
$$
где (U_{delta}(x_{0}) = (x_{0}-delta, x_{0} + delta) subset [a, b]).
По условию (S_{n}(x) rightrightarrows S(x)), (x in [a, b]), где (S_{n}(x) = displaystylesum_{k = 1}^{n}u_{k}(x)), то есть
$$
forall varepsilon > 0 exists N_{varepsilon}: forall n geq N_{varepsilon} forall x in [a, b] rightarrow |S(x)-S_{n}(x)| < frac{varepsilon}{3}.label{ref40}
$$
Фиксируем номер (n_{0} geq N_{varepsilon}). Тогда из eqref{ref40} при (n = n_{0}) получаем
$$
|S(x)-S_{n_{0}}(x)| < frac{varepsilon}{3}label{ref41}
$$
и, в частности, при (x = x_{0}) находим
$$
|S(x_{0})-S_{n_{0}}(x_{0})| < frac{varepsilon}{3}.label{ref42}
$$
Функция (S_{n_{0}}(x)) непрерывна в точке (x_{0}) как сумма конечного числа непрерывных функций (u_{k}(x)), (k = overline{1, n_{0}}). По определению непрерывности
$$
forall varepsilon > 0 exists delta = delta (varepsilon) > 0: forall x in U_{delta}(x_{0}) subset [a, b] rightarrow |S_{n_{0}}(x)-S_{n_{0}}(x_{0})| < frac{varepsilon}{3}.label{ref43}
$$
Воспользуемся равенством
$$
S(x)-S(x_{0}) =\= (S(x)-S_{n_{0}}(x)) + (S_{n_{0}}(x)-S_{n_{0}}(x_{0})) + (S_{n_{0}}(x_{0})-S(x_{0})).nonumber
$$
Из этого равенства, используя оценки eqref{ref41}—eqref{ref43}, получаем
$$
|S(x)-S(x_{0})| leq\leq |S(x)-S_{n_{0}}(x)| + |S_{n_{0}}(x)-S_{n_{0}}(x_{0})| + |S_{n_{0}}(x_{0})-S(x_{0})| < varepsilon
$$
для любого (x in U_{delta}(x_{0}) subset [a, b]), то есть справедливо утверждение eqref{ref39}.
Так как (x_{0}) — произвольная точка отрезка ([a, b]), то функция S(x) непрерывна на отрезке ([a, b]). (bullet)
Замечание 1.
Согласно теореме 7
$$
lim_{x rightarrow x_{0}} sum_{n = 1}^{infty}u_{n}(x) = sum_{n = 1}^{infty} lim_{x rightarrow x_{0}} u_{n}(x)
$$
то есть при условиях теоремы 7 возможен почленный предельный переход.
Теорема 8.
Если последовательность ({S_{n}(x)}) непрерывных на отрезке ([a, b]) функций равномерно сходится на ([a, b]), то ее предельная функция (S(x)) также непрерывна на отрезке ([a, b]).
Доказательство.
(circ) Доказательство этого утверждения следует из теоремы 7. (bullet)
Почленное интегрирование функционального ряда.
Теорема 9.
Если все члены ряда eqref{ref14} — непрерывные на отрезке ([a, b]) функции, а ряд eqref{ref14} сходится равномерно на ([a, b]), то ряд
$$
sum_{n = 1}^{infty}intlimits_a^x u_{n}(t) dt,label{ref44}
$$
также равномерно сходится на ([a, b]), и если
$$
S(x) = sum_{n = 1}^{infty}u_{n}(x),label{ref45}
$$
то
$$
intlimits_a^x S(t) dt = sum_{n = 1}^{infty}intlimits_a^x u_{n}(t) dt,quad x in [a, b],label{ref46}
$$
то есть ряд eqref{ref45} можно почленно интегрировать.
Доказательство.
(circ) По условию ряд eqref{ref45} сходится равномерно к (S(x)) на отрезке ([a, b]), то есть (S_{n}(x) = displaystylesum_{k = 1}^{n}u_{k}(x) rightrightarrows S(x)), (x in [a, b]). Это означает, что
$$
forall varepsilon > 0 exists N_{varepsilon}: forall n in N_{varepsilon} forall t in [a, b] rightarrow |S(t)-S_{n}(t)| < frac{varepsilon}{b-a}.label{ref47}
$$
Пусть (sigma(x) = displaystyleintlimits_a^x S(t) dt), а (sigma_{n}(x) = displaystylesum_{k = 1}^{n} intlimits_a^x u_{k}(t) dt) — (n)-я частичная сумма ряда eqref{ref44}.
Функции (u_{k}(x)), (k in mathbb{N}), по условию непрерывны на отрезке ([a, b]) и поэтому они интегрируемы на ([a, b]). Функция (S(x)) также интегрируема на ([a, b]), так как она непрерывна на этом отрезке (теорема 7). Используя свойства интеграла, получаем
$$
sigma_{n}(x) = intlimits_a^x sum_{k = 1}^{n}u_{k}(t) dt = intlimits_a^x S_{n}(t) dt.nonumber
$$
Следовательно
$$
sigma(x)-sigma_{n}(x) = intlimits_a^x (S(t)-S_{n}(t)) dt,nonumber
$$
откуда в силу условия eqref{ref47} получаем
$$
|sigma(x)-sigma_{n}(x)| < frac{varepsilon}{b-a} intlimits_a^x dt = frac{varepsilon}{b-a} (x-a) leq varepsilon,nonumber
$$
причем это неравенство выполняется для всех (n geq N_{varepsilon}) и для всех (x in [a, b]). Это означает, что ряд eqref{ref44} сходится равномерно на отрезке ([a, b]), и выполняется равенство eqref{ref46}. (bullet)
Замечание 2.
Равенство eqref{ref46} остается в силе, если заменить (a) на (c), (x) на (d), где (a leq c leq d leq b), то есть ряд eqref{ref45} можно при условиях теоремы 9 почленно интегрировать на любом отрезке ([c, d] subset [a, b]).
Теорема 10.
Если (S_{n}(t) rightrightarrows S(t)), (x in [a, b]), а каждая из функций (S_{n}(t)) непрерывна на отрезке ([a, b]), то
$$
intlimits_{x_{0}}^x S_{n}(t) dt rightrightarrows intlimits_{x_{0}}^x S(t) dt,quad x in [a, b],nonumber
$$
для любой точки (x_{0} in [a, b]).
Доказательство.
(circ) Доказательство этого утверждения получено при доказательстве теоремы 9. (bullet)
Почленное дифференцирование функционального ряда.
Теорема 11.
Если функции (u_{n}(x)), (n in mathbb{N}), имеют непрерывные производные на отрезке ([a, b]), ряд
$$
sum_{n = 1}^{infty}u_{n}'(x),label{ref48}
$$
сходится равномерно на отрезке ([a, b]), а ряд
$$
sum_{n = 1}^{infty}u_{n}(x),label{ref49}
$$
сходится хотя бы в одной точке (x in [a, b]), то есть сходится ряд
$$
sum_{n = 1}^{infty}u_{n}(x_{0}),label{ref50}
$$
то ряд eqref{ref49} сходится равномерно на отрезке ([a, b]), и его можно почленно дифференцировать, то есть
$$
S'(x) = sum_{n = 1}^{infty}u_{n}'(x),label{ref51}
$$
где
$$
S(x) = sum_{n = 1}^{infty}u_{n}(x),label{ref52}
$$
Доказательство.
(circ) Обозначим через (tau(x)) сумму ряда eqref{ref48}, то есть
$$
tau(x) = sum_{n = 1}^{infty}u_{n}'(x),label{ref53}
$$
По теореме 9 ряд eqref{ref53} можно почленно интегрировать, то есть
$$
intlimits_{x_{0}}^x tau(t) dt = sum_{n = 1}^{infty}intlimits_{x_{0}}^x u_{n}'(t) dt,label{ref54}
$$
где (x_{0}, x in [a, b]), причем ряд eqref{ref54} сходится равномерно на отрезке ([a, b]). Так как (displaystyleintlimits_{x_{0}}^x u_{n}'(t) dt = u_{n}(x)-u_{n}(x_{0})), то равенство eqref{ref54} можно записать в виде
$$
intlimits_{x_{0}}^x tau(t) dt = sum_{n = 1}^{infty}v_{n}(x),label{ref55}
$$
где
$$
v_{n}(x) = u_{n}(x)-u_{n}(x_{0}).label{ref56}
$$
Ряд eqref{ref55} сходится равномерно, а ряд eqref{ref50} сходится (а значит, и равномерно сходится на отрезке ([a, b])). Поэтому ряд eqref{ref49} сходится равномерно на ([a, b]) как разность равномерно сходящихся рядов.
Из равенств eqref{ref55}, eqref{ref56} и eqref{ref52} следует, что
$$
intlimits_{x_{0}}^x tau(t) dt = S(x)-S(x_{0}).label{ref57}
$$
Так как функция (tau(t)) непрерывна на отрезке ([a, b]) по теореме 7, то в силу свойств интеграла с переменным верхним пределом левая часть равенства eqref{ref57} имеет производную, которая равна (tau(x)). Следовательно, правая часть eqref{ref57} — дифференцируемая функция, а ее производная равна (S'(x)). Итак, доказано, что (tau(x) = S'(x)), то есть справедливо равенство eqref{ref51} для всех (x in [a, b]). (bullet)
Замечание 3.
При условиях теоремы 11 функция (S'(x)) непрерывна на отрезке ([a, b]), то есть (S(x)) — непрерывно дифференцируемая на ([a, b]) функция.
Теорема 12.
Если последовательность ({S_{n}(x)}) непрерывно дифференцируемых на ([a, b]) функций сходится хотя бы в одной точке (x_{0} in [a, b]), а последовательность ({S_{n}'(x)}) сходится равномерно на ([a, b]), то последовательность ({S_{n}(x)}) также сходится равномерно на ([a, b]) к некоторой функции (S(x)) и
$$
S'(x) = lim_{n rightarrow infty}S_{n}'(x),quad x in [a, b].nonumber
$$
Доказательство.
(circ) Доказательство этого утверждения получено при доказательстве теоремы 11. (bullet)
Содержание:
- Равномерная сходимость функциональных последовательностей и рядов.
- Сходимость функциональной последовательности и ряда
- Равномерная сходимость функциональной последовательности
- Признаки равномерной сходимости функциональных рядов.
Равномерная сходимость функциональных последовательностей и рядов.
Сходимость функциональной последовательности и ряда
а) Сходимость последовательности функций. Пусть функции  определены на множестве
определены на множестве  и пусть
и пусть  Если числовая последовательность
Если числовая последовательность  сходится, то говорят, что последовательность функций
сходится, то говорят, что последовательность функций  сходится в точке
сходится в точке 
Последовательность  сходящуюся в каждой точке
сходящуюся в каждой точке  называют сходящейся на множестве
называют сходящейся на множестве  В этом случае на множестве
В этом случае на множестве  определена функция
определена функция  значение которой в любой точке
значение которой в любой точке  равно пределу последовательности
равно пределу последовательности  Эту Функцию называют предельной функцией последовательности
Эту Функцию называют предельной функцией последовательности  на множестве
на множестве  и пишут
и пишут

или

или, короче,

По определению предела запись (1) означает, что


По этой ссылке вы найдёте полный курс лекций по высшей математике:
Примеры с решением
Пример 1.
Найти предельную функцию  последовательности
последовательности  на множестве
на множестве  если:
если:

Так как 
б) Используя асимптотическую формулу  при
при  , получаем
, получаем  при
при  если
если 
Поэтому 
б) Сходимость функционального ряда. Пусть функции  определены на множестве
определены на множестве  и пусть для каждого
и пусть для каждого  существует
существует
конечный предел последовательности  где
где 
Тогда ряд 
называют сходящимся на множестве 
Если  — предельная функция последовательности
— предельная функция последовательности  на множестве
на множестве  т. е.
т. е.

то функцию называют  суммой ряда (2) и пишут
суммой ряда (2) и пишут

Например, если  то
то 

Если в каждой точке  сходится ряд
сходится ряд  то ряд (2) называют абсолютно сходящимся на множестве
то ряд (2) называют абсолютно сходящимся на множестве 
Равномерная сходимость функциональной последовательности
а) Понятие равномерной сходимости последовательности функций.
Возможно вам будут полезны данные страницы:
Определение. Последовательность функций

называется равномерно сходящейся на множестве  к функции
к функции  если
если

В этом определении существенно, что номер  не зависит от
не зависит от  Если справедливо утверждение (3), то пишут
Если справедливо утверждение (3), то пишут

или

Говорят, что последовательность  равномерно сходится на множестве
равномерно сходится на множестве  если существует функция
если существует функция  удовлетворяющая условию (3).
удовлетворяющая условию (3).
Если существуют числовая последовательность  и номер
и номер  такие, что
такие, что

причем  то
то

Пример 2.
Доказать, что последовательность  равномерно сходится на множестве
равномерно сходится на множестве  и найти ее предельную функцию
и найти ее предельную функцию  если:
если:

В этом случае  (пример 1.а) и
(пример 1.а) и 
 так как
так как  Следовательно
Следовательно

б) Используя неравенство  получаем
получаем 

откуда следует, что 
в) Так как  при
при  то
то 

откуда получаем 
г) В этом случае  (пример 1, б)). Используя неравенство
(пример 1, б)). Используя неравенство
 (§ 18, пример 1, а)), получаем
(§ 18, пример 1, а)), получаем

так как  Следовательно,
Следовательно,

б) Критерии равномерной сходимости последовательности функций.
Теорема 1. Для того чтобы последовательность функций  определенных на множестве
определенных на множестве  сходилась равномерно на этом множестве к функции
сходилась равномерно на этом множестве к функции  необходимо и достаточно, чтобы
необходимо и достаточно, чтобы

Обозначим  Тогда условие (4) означает, что
Тогда условие (4) означает, что

Если  то
то

откуда следует, что  для
для  Поэтому неравенство
Поэтому неравенство 
выполняется при всех  где
где  Обратно, если выполняется условие (4) или равносильное ему условие (5), то, используя неравенство
Обратно, если выполняется условие (4) или равносильное ему условие (5), то, используя неравенство  для
для  получаем для
получаем для  т.е.
т.е.
Пример 3.
Доказать, что последовательность сходится равномерно на множестве и найти предельную функцию если:

Если  то
то  для всех
для всех  и поэтому
и поэтому 

Если  то
то  откуда следует,
откуда следует,
что  при
при  так как
так как  Таким образом, предельная функция
Таким образом, предельная функция 
Так как при  справедливо неравенство
справедливо неравенство  причем это неравенство обращается в равенство лишь в случае, когда
причем это неравенство обращается в равенство лишь в случае, когда  то
то

Следовательно,  при
при  если
если 
и поэтому 
б) Если  то
то  при
при  и поэтому
и поэтому  при
при  Если
Если  то
то  и поэтому
и поэтому  Следовательно,
Следовательно, 
Чтобы вычислить  найдем точки экстремума функции
найдем точки экстремума функции 
Уравнение  имеет внутри отрезка
имеет внутри отрезка  единственный корень причем
единственный корень причем
 Заметим, что
Заметим, что  при
при 
при  Поэтому
Поэтому  для всех
для всех 
и, согласно теореме 
в) Учитывая, что  при
при  (если
(если  находим
находим

Так как  при
при  то функция
то функция 
является убывающей на промежутке  и поэтому
и поэтому
 при
при 
По теореме 1 последовательность  равномерно сходится к
равномерно сходится к  на множестве
на множестве 
Теорема 2 (критерий Коши равномерной сходимости последовательности). Для того чтобы последовательность функций  сходилась равномерно на множестве
сходилась равномерно на множестве  необходимо и достаточно, чтобы выполнялось условие Коши
необходимо и достаточно, чтобы выполнялось условие Коши

Необходимость. Пусть  Тогда по определению равномерной сходимости
Тогда по определению равномерной сходимости

В частности, (7) выполняется при  если
если  и при
и при  для
для 

откуда следует, что

т. е. выполняется условие (6).
Достаточность. Заметим, что числовая последовательность  где
где  — фиксированная точка множества
— фиксированная точка множества  удовлетворяет условию Коши (6) и в силу критерия Коши для числовой последовательности (§ 8) существует конечный
удовлетворяет условию Коши (6) и в силу критерия Коши для числовой последовательности (§ 8) существует конечный

Так как предел (8) существует для каждого  то на множестве
то на множестве  определена функция (обозначим ее
определена функция (обозначим ее  которая является предельной функцией для последовательности
которая является предельной функцией для последовательности  на множестве
на множестве  Запишем условие Коши (6) в виде
Запишем условие Коши (6) в виде

Переходя в неравенстве (9) к пределу при  (при каждом фиксированном
(при каждом фиксированном  и фиксированном
и фиксированном  и учитывая, что существует
и учитывая, что существует  получаем неравенство
получаем неравенство

справедливое при всех  и для всех
и для всех  Это означает, что
Это означает, что

в) Неравномерная сходимость последовательности функций. Последовательность  не является равномерно сходящейся на множестве
не является равномерно сходящейся на множестве  если условие Коши (6) не выполняется, т. е
если условие Коши (6) не выполняется, т. е

Ряд функций – это серия, где каждый член является функцией, а не числом, в отличие от ряда чисел
Пример 4.
Доказать, что последовательность  где
где 
 не является равномерно сходящейся на множестве
не является равномерно сходящейся на множестве 
Для любого  возьмем
возьмем  Тогда
Тогда

т. е. выполняется условие (10), и поэтому последовательность  не является равномерно сходящейся на
не является равномерно сходящейся на 
Если существует предельная функция  последовательности
последовательности  на множестве
на множестве  но не выполняется условие (3), т. е.
но не выполняется условие (3), т. е.

то говорят, что последовательность  сходится неравномерно на множестве
сходится неравномерно на множестве  к функции
к функции 
Пример 5.
Исследовать на сходимость и равномерную сходимость на множестве  последовательность
последовательность  если:
если:


а) В этом случае предельная функция  Для любого
Для любого  возьмем
возьмем  Тогда
Тогда  при любом п
при любом п  и
и  т. е. выполняется условие (11), и поэтому последовательность
т. е. выполняется условие (11), и поэтому последовательность  сходится неравномерно на множестве
сходится неравномерно на множестве 
б) Здесь предельная функция  на множестве
на множестве  (пример 1,
(пример 1,  )). Возьмем
)). Возьмем  Тогда
Тогда 

для любого  и поэтому
и поэтому  сходится неравномерно на множестве
сходится неравномерно на множестве 
Неравномерную сходимость последовательности можно установить, используя теорему 1. Если условие (4) не выполняется, т. е.
 при
при 
то  сходится неравномерно на множестве
сходится неравномерно на множестве 
Пример 6.
Исследовать на сходимость и равномерную сходимость последовательность 
Предельная функция  Так как уравнение
Так как уравнение 
 имеет на интервале (0,2) единственный корень
имеет на интервале (0,2) единственный корень  причем
причем  при
при  и
и  при
при  то
то 
Таким образом, выполняется условие (12), и поэтому  сходится неравномерно на множестве
сходится неравномерно на множестве 
3. Определение и критерий равномерной сходимости функционального ряда. Пусть функции  определены на множестве
определены на множестве  Обозначим
Обозначим

Определение. Ряд

называется равномерно сходящимся на множестве  если на этом множестве определена функция
если на этом множестве определена функция  такая, что
такая, что

Согласно определению равномерной сходимости последовательности функций запись (15) означает, что

где  — сумма ряда (14), а
— сумма ряда (14), а  определяется формулой (13).
определяется формулой (13).
Пусть  т.е.
т.е.  остаток ряда (14). Тогда условие (15) примет вид
остаток ряда (14). Тогда условие (15) примет вид

Это означает, что

В силу теоремы 1 для равномерной сходимости ряда (14) на множестве  необходимо и достаточно, чтобы
необходимо и достаточно, чтобы

Если ряд (14) сходится на множестве  но не выполняется условие (17) или равносильное ему условие (18), то говорят, что ряд (14) сходится неравномерно на множестве
но не выполняется условие (17) или равносильное ему условие (18), то говорят, что ряд (14) сходится неравномерно на множестве  Следовательно, если
Следовательно, если

или

то ряд (14) сходится неравномерно на множестве 
Пример 7.
Исследовать на сходимость и равномерную сходимость на указанных множествах ряд  если:
если:

а) В этом случае  для любого
для любого 
т. е. ряд сходится на множестве  а значит, и на
а значит, и на  Для любого
Для любого  выполняется неравенство
выполняется неравенство 

откуда следует, что  и поэтому выполняется условие (18). Следовательно, ряд сходится равномерно на множестве
и поэтому выполняется условие (18). Следовательно, ряд сходится равномерно на множестве 
На множестве  ряд сходится неравномерно. В самом деле, возьмем
ряд сходится неравномерно. В самом деле, возьмем  Тогда
Тогда  для любого
для любого 

при  откуда следует, что выполняется условие (20).
откуда следует, что выполняется условие (20).
б) Так как 

Если  при
при  где
где 

и поэтому 
На множестве  ряд сходится равномерно, так как
ряд сходится равномерно, так как 

и поэтому выполняется условие (18), а на множестве  неравномерно, и поэтому выполняется
неравномерно, и поэтому выполняется
условие (20).
в) При каждом  последовательность
последовательность  монотонно стремится к нулю, и поэтому по признаку Лейбница (§ 41, теорема 1)
монотонно стремится к нулю, и поэтому по признаку Лейбница (§ 41, теорема 1)
ряд  сходится на множестве
сходится на множестве  причем
причем 

откуда следует, что выполняется условие (18).
Следовательно, ряд сходится равномерно на множестве 
Теорема 3 (критерий Коши равномерной сходимости ряда). Для того чтобы ряд (14) равномерно сходился на множестве  необходимо и достаточно, чтобы выполнялось условие Коши, т. е.
необходимо и достаточно, чтобы выполнялось условие Коши, т. е.

По определению равномерная сходимость ряда (14) на множестве  означает равномерную сходимость последовательности
означает равномерную сходимость последовательности  на
на 
Согласно теореме 2 на
на  тогда и только тогда, когда
тогда и только тогда, когда

Так как  то условие (22) равносильно условию (21). •
то условие (22) равносильно условию (21). •
Если условие (21) не выполняется, т. е.

то ряд (14) не является равномерно сходящимся на множестве  В частности, если
В частности, если

то ряд (14) не является равномерно сходящимся на множестве 
Пример 8.
Доказать, что ряд  не является равномерно
не является равномерно
сходящимся на множестве  если:
если:

а) Пусть  тогда
тогда  т. е. выполняется условие (24).
т. е. выполняется условие (24).
б) Возьмем  и воспользуемся тем, что
и воспользуемся тем, что  при
при 
(§ 12, (3)). Тогда  при всех
при всех  т. е. выполняется условие (24).
т. е. выполняется условие (24).
в) Возьмем  тогда
тогда  при любом
при любом  Если
Если

 и поэтому
и поэтому 
откуда следует, что

так как  Следовательно, выполняется условие (23), и поэтому ряд не является равномерно сходящимся на множестве
Следовательно, выполняется условие (23), и поэтому ряд не является равномерно сходящимся на множестве  при
при 
Признаки равномерной сходимости функциональных рядов.
а) Признак Вейерштрасса.
Теорема 4. Если для функционального ряда (14) можно указать такой сходящийся числовой ряд  что для всех
что для всех  и для всех
и для всех
 выполняется условие
выполняется условие 
то ряд (14) сходится абсолютно и равномерно на множестве 
Согласно условию (25) для любого  любого и для каждого выполняется неравенство
любого и для каждого выполняется неравенство
Из сходимости ряда следует (§ 39), что для него выполняется
условие Коши, т. е.
а из (26) и (27) следует, что для ряда (14) выполняется на множестве Е условие Коши (21), и в силу теоремы 3 этот ряд сходится равномерно на множестве Е.
Абсолютная сходимость ряда (14) для каждого следует из правого неравенства (26).
Следствие. Если сходится ряд  то ряд (14) сходится абсолютно и равномерно на множестве
то ряд (14) сходится абсолютно и равномерно на множестве 
Пример 9.
Доказать, что ряд  сходится равномерно на множестве
сходится равномерно на множестве  если:
если:

а) Так как при  справедливо неравенство
справедливо неравенство  пример
пример  то
то  при всех
при всех  и из сходимости ряда
и из сходимости ряда  по теореме 4 следует равномерная сходимость
по теореме 4 следует равномерная сходимость  ряда на множестве
ряда на множестве 
б) Используя неравенство  для всех
для всех  и учитывая, что
и учитывая, что  получаем
получаем 
 откуда следует равномерная сходимость ряда на множестве
откуда следует равномерная сходимость ряда на множестве 
в) Так как  для всех
для всех 

Из сходимости ряда  следует равномерная сходимость ряда
следует равномерная сходимость ряда  на множестве
на множестве 
г) На промежутке  уравнение
уравнение 
имеет единственный корень  причем
причем  при
при 

Поэтому  и из сходимости ряда
и из сходимости ряда  следует равномерная сходимость ряда
следует равномерная сходимость ряда  на множестве
на множестве 


Лекции:
- Производная второго порядка
- Метод Жордана Гаусса
- Некоторые простые неявные функции
- Рациональные числа
- Предел числовой последовательности
- Каноническое уравнение гиперболы
- Метод интервалов
- Обратная матрица примеры решения
- Дифференцирование функций, заданных неявно и параметрически
- Полярная система координат: примеры решения
Дана функциональная последовательность $%f_n(x)$% на множестве $%E$%. Найти предельную функцию последовательности.
$%f_n(x)=x^n−3x^{n+2}+2x^{n+3}, E = [0, 1].$%
Нашла такой алгоритм(не знаю точно правильный ли он)
- Найти поточечный предел последовательности.
- Для каждого члена последовательности найти супремум (максимум) модуля разности этого члена и поточечного предела. Получится последовательность супремумов.
- Равномерная сходимость равносильна сходимости к 0 этой последовательности супремумов (максимумов).
1) $%lim_{n rightarrow infty } (x^n−3x^{n+2}+2x^{n+3})=infty -infty+infty$% подскажите пожалуйста
2)Найдём супремум (максимум) модуля разности
$%mid f_n(x)-f(x)mid=mid x^n−3x^{n+2}+2x^{n+3} mid$%
Стационарные точки
$%(x^n−3x^{n+2}+2x^{n+3})’=nx^{n-1}−3(n+2)x^{n+1}+2(n+3)x^{n+2}$%
Поэтому максимум модуля достигается в точках x= подскажите пожалуйста как это найти
1.Найти
предельную функцию
![]()
для последовательности
![]()
на
![]()
1.1
![]() ,
,
![]() ;
;
1.2
![]() ,
,
![]() ;
;
1.3
![]()
![]() ;
;
1.4
![]() ,
,![]() ;
;
1.5
![]() ,
,
![]() ;
;
1.6
![]() ,
,
![]() ;
;
1.7
![]() ,
,![]() ;
;
1.8
![]() ,
,![]() ;
;
1.9
![]() ,
,
![]() ;
;
1.10
![]() ,
,![]() ;
;
1.11
![]() ,
,![]() ;
;
1.12
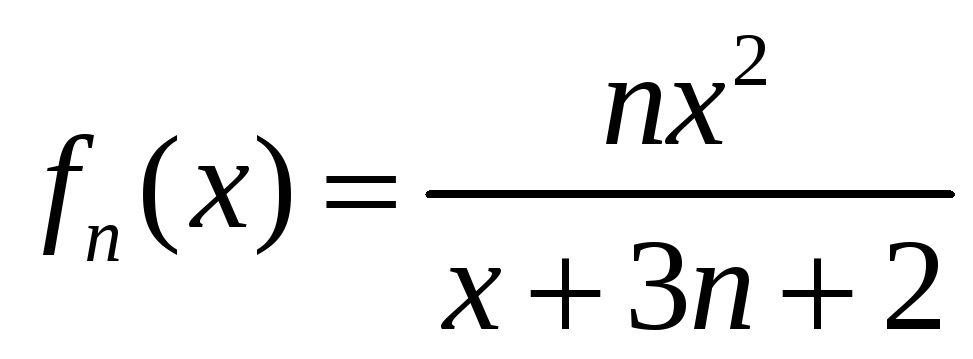 ,
,
![]() .
.
2.
Исследовать сходимость и равномерную
сходимость
![]()
на множестве![]()
2.1 а)
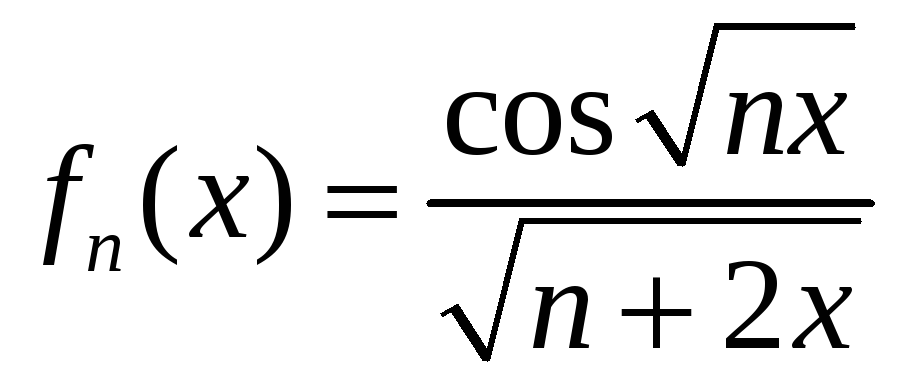 ,
,![]() ; б)
; б)
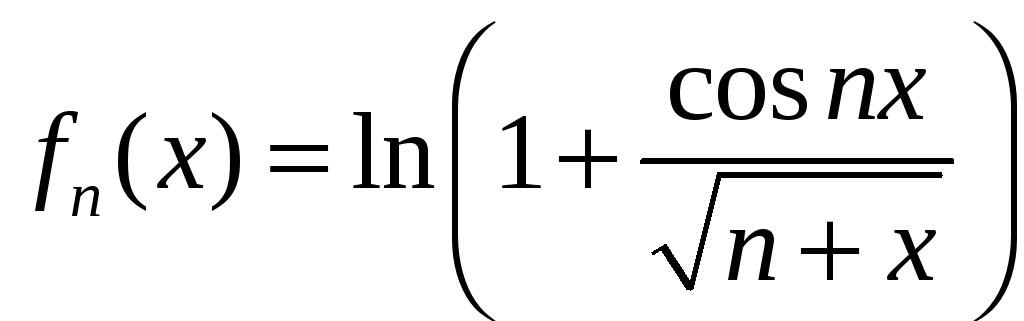 ,
,![]() ;
;
2.2
а)
![]() ,
,![]() ; б)
; б)
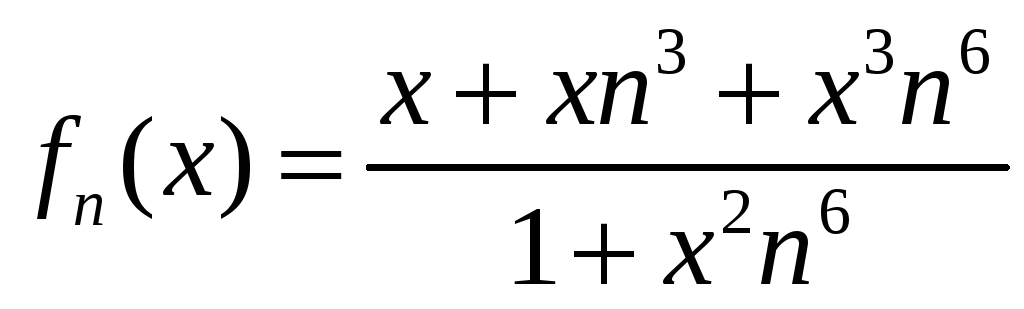 ,
,![]() ;
;
2.3
а)
![]()
![]() ; б)
; б)![]() ,
,![]() ;
;
2.4
а)
![]() ,
,
![]() ; б)
; б)
![]() ,
,
![]() ;
;
2.5
а)
![]() ,
,![]() ; б)
; б)
![]()
![]() ;
;
2.6
а)
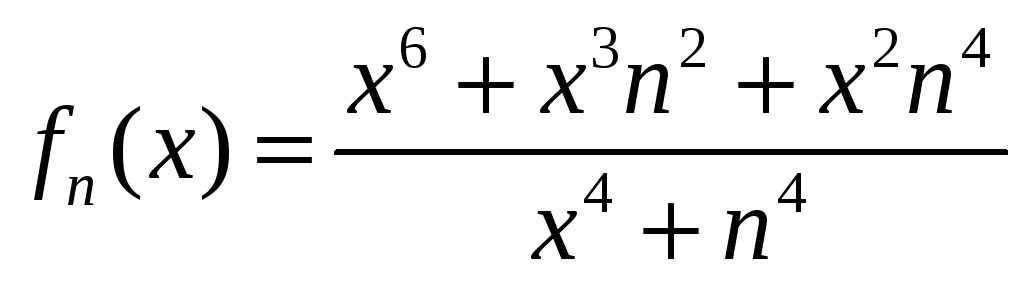 ,
,![]() ; б)
; б)
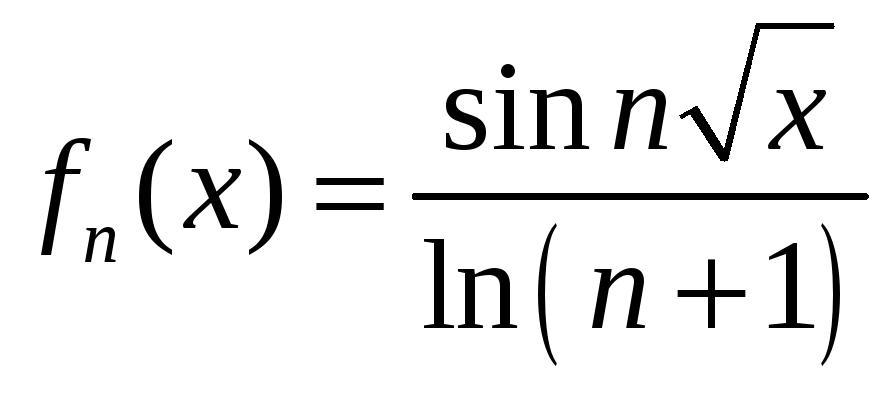
![]() ;
;
2.7 а)
![]()
![]() ; б)
; б)
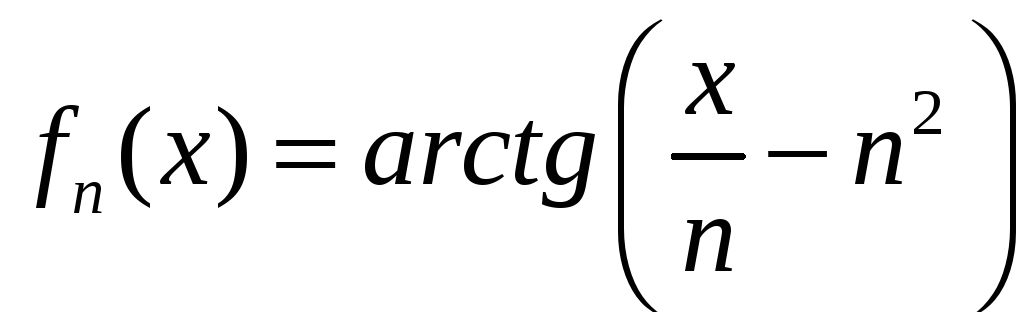 ,
,![]() ;
;
2.8 а)
![]() ,
,![]() ; б)
; б)
![]() ,
,![]() ;
;
2.9 а)
![]() ,
,![]() ; б)
; б)
![]()
![]() ;
;
2.10 а)
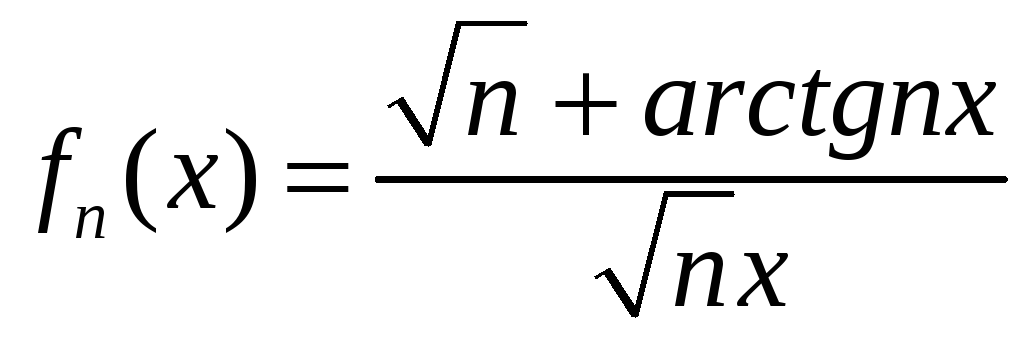 ,
,![]() ; б)
; б)
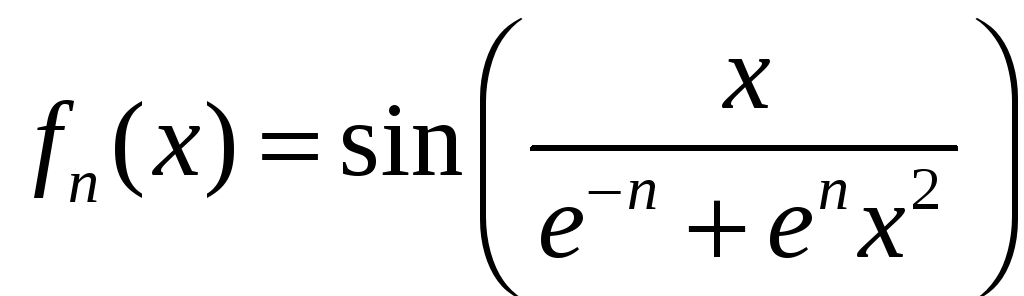 ,
,![]() ;
;
2.11 а)
![]() ,
,![]() ; б)
; б)
![]() ,
,![]() ;
;
2.12 а)
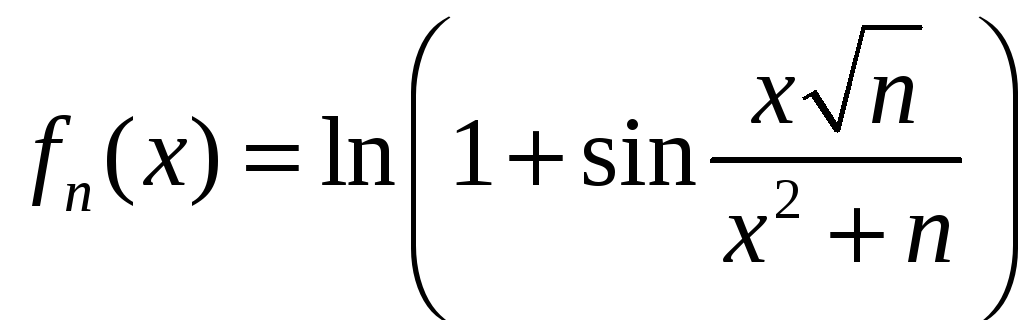 ,
,![]() ; б)
; б)
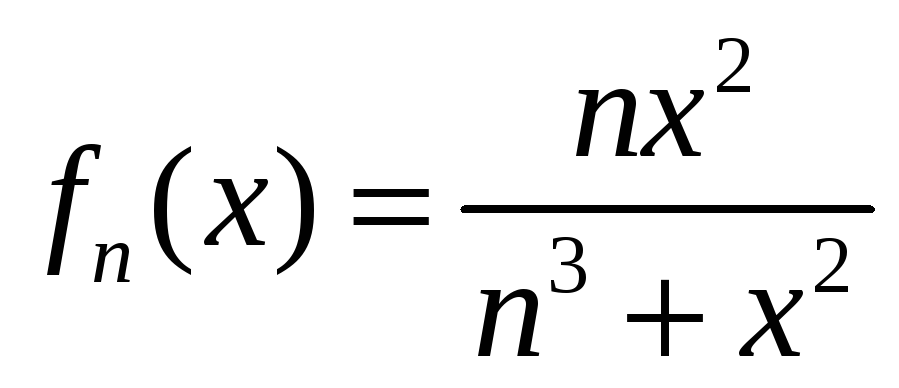
![]() .
.
3.Доказать:
3.1
Если последовательности
![]()
и
![]()
равномерно сходятся на множестве![]() ,
,
то
![]()
последовательность
![]()
равномерно сходится на множестве![]() .
.
3.2
Если последовательность
![]()
равномерно сходится на множестве![]() и
и
функция
![]()
ограничена на![]() ,
,
то последовательность
![]()
равномерно сходится на этом множестве.
3.3
Если
![]() –
–
произвольная функция на
![]() ,
,
то последовательность
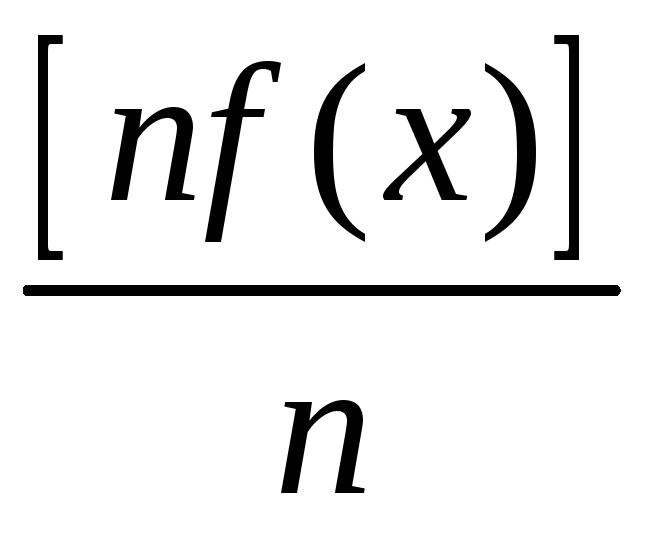
сходится равномерно к
![]()
на
![]() .
.
3.4
Если
![]()
имеет непрерывную производную на
![]() ,
,
то последовательность
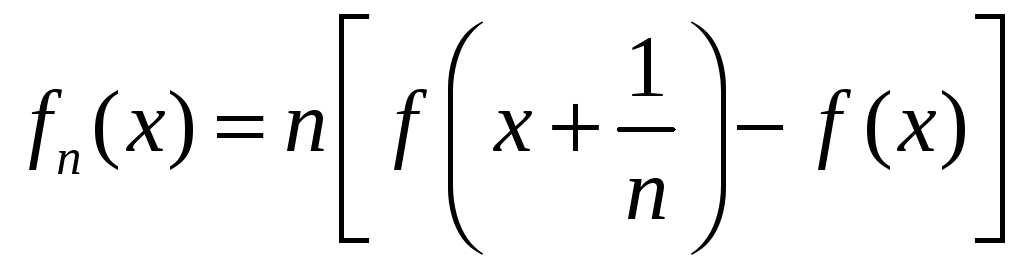
сходится равномерно к
![]()
на
![]() ,
,
где
![]() .
.
3.5
Если последовательность многочленов
степени не выше
![]()
равномерно сходится на
![]() ,
,
то предельная функция этой последовательности
– многочлен степени не выше
![]() .
.
3.6
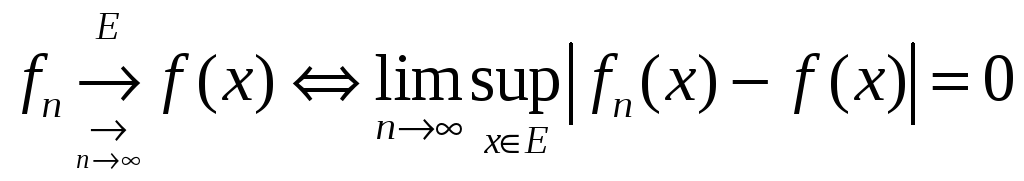
3.8
Если последовательности
![]()
и
![]()
поточечно сходятся на множестве
![]() ,
,
то
![]()
последовательность
![]()
поточечно сходится на множестве![]()
3.9
Если последовательности
![]()
и
![]()
поточечно сходятся на множестве
![]() ,
,
то последовательность
![]()
поточечно сходится на множестве![]() .
.
3.10 Если
последовательность
![]()
равномерно сходится на множестве![]() и
и
функция
![]()
равномерно непрерывна на![]() при
при
каждом
![]() ,
,
то функция
![]()
равномерно непрерывна на этом множестве.
Лабораторная работа 4 функциональные ряды
1.Найти
область сходимости и абсолютной
сходимости ряда:
1.1
а)
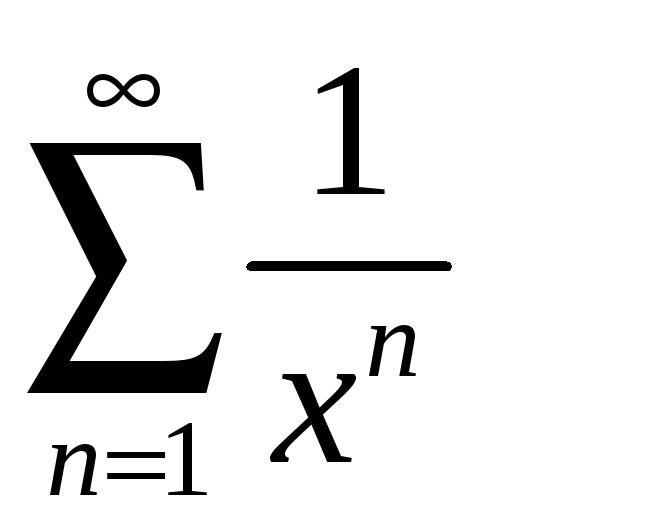 ;
;
б)
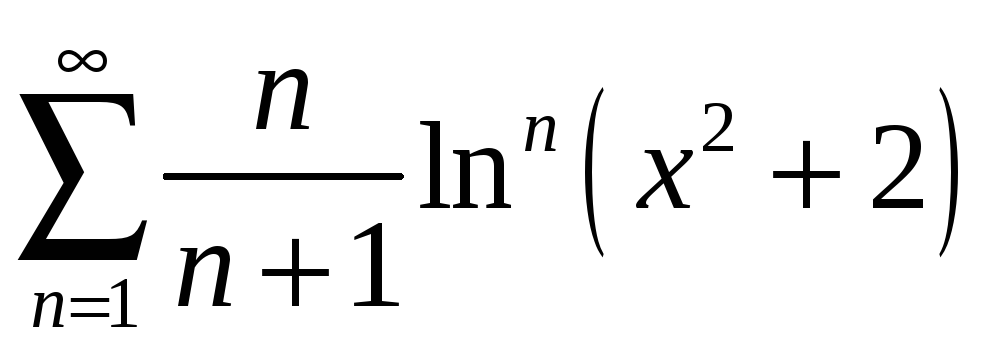 ;
;
1.2
а)
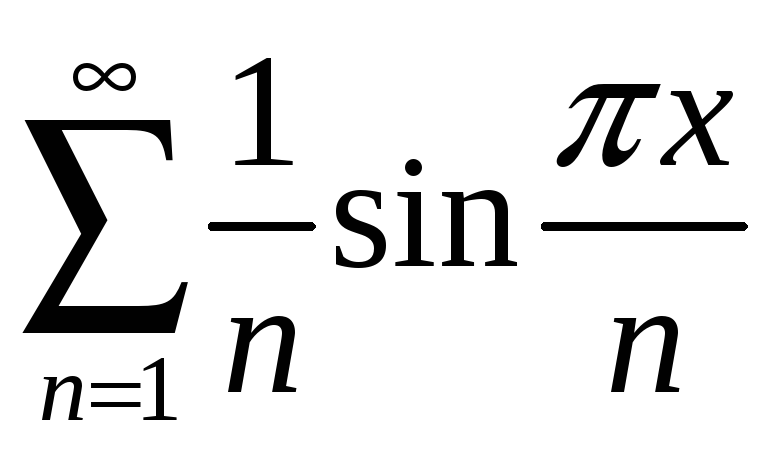 ;
;
б)
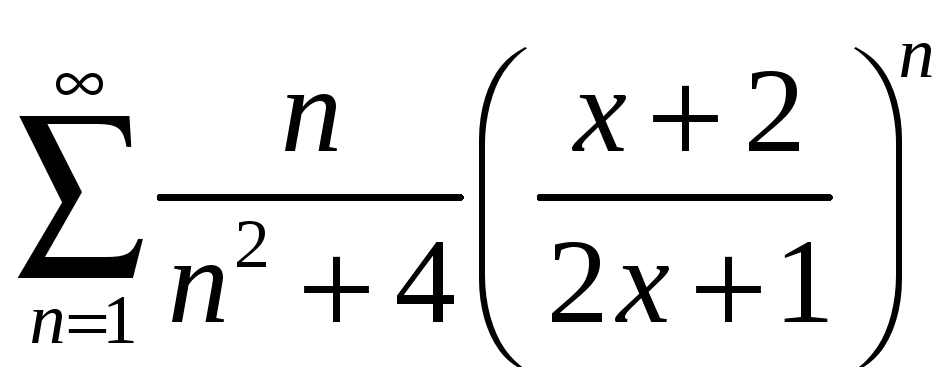 ;
;
1.3
а)
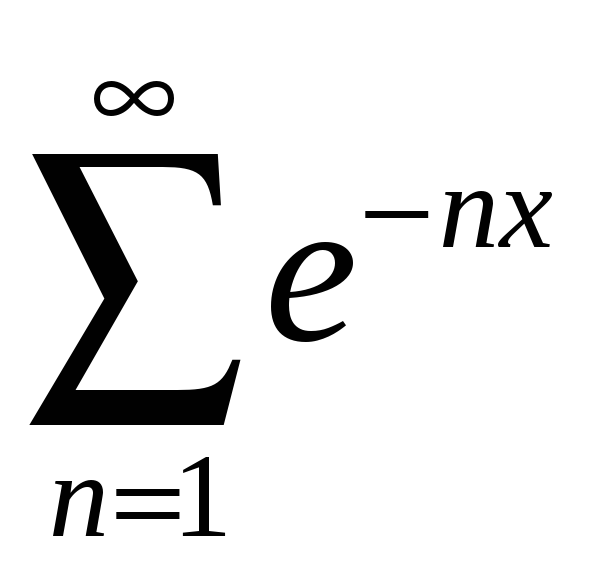 ;
;
б)
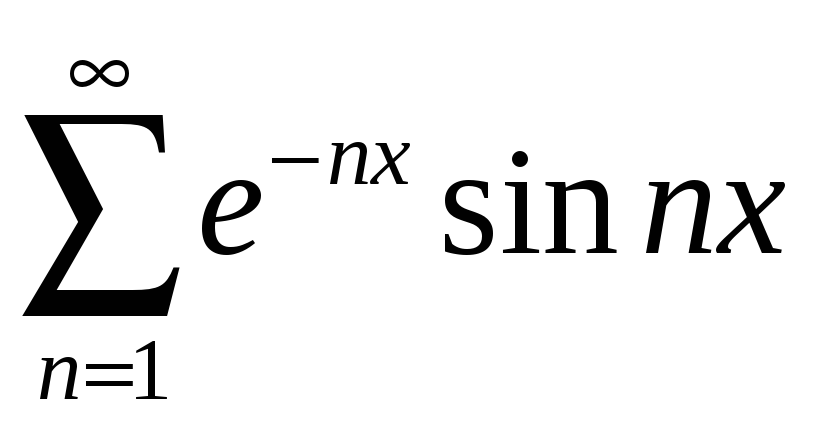 ;
;
1.4
а)
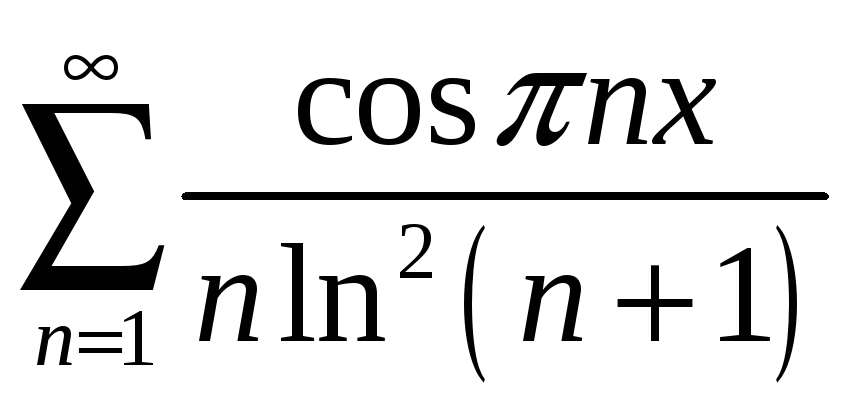 ;
;
б)
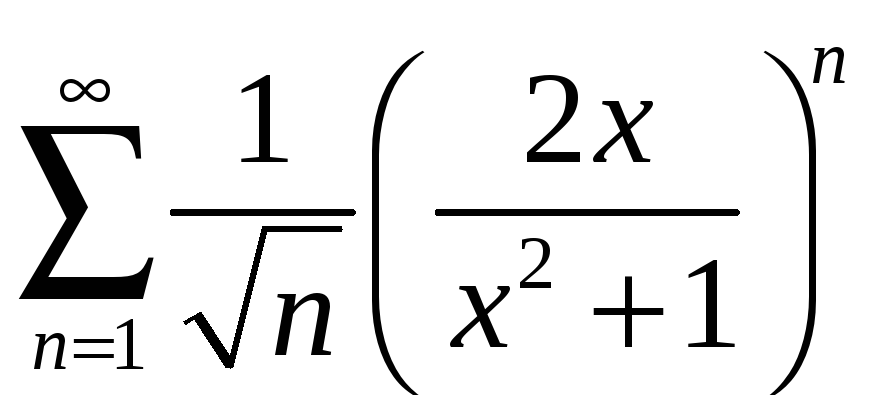 ;
;
1.5
а)
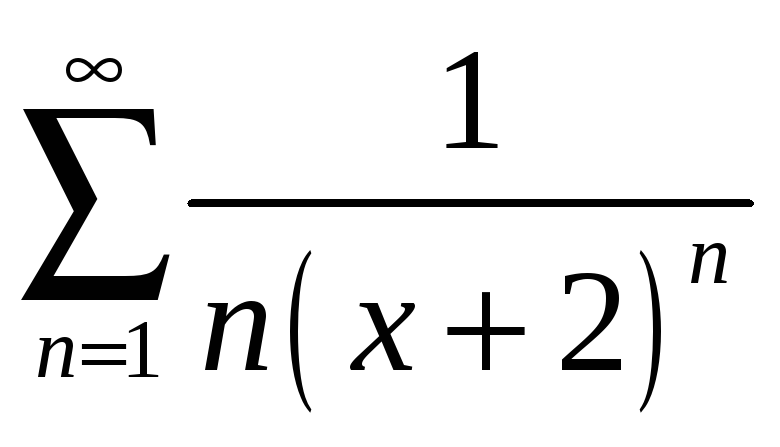 ;
;
б)
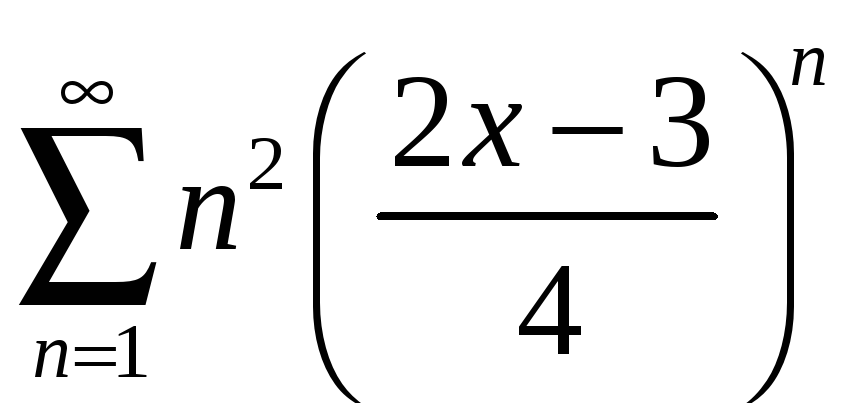 ;
;
1.6
а)
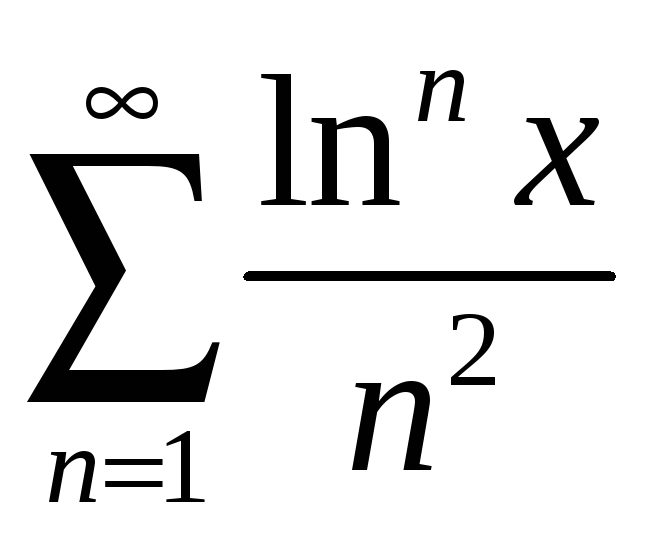 ;
;
б)
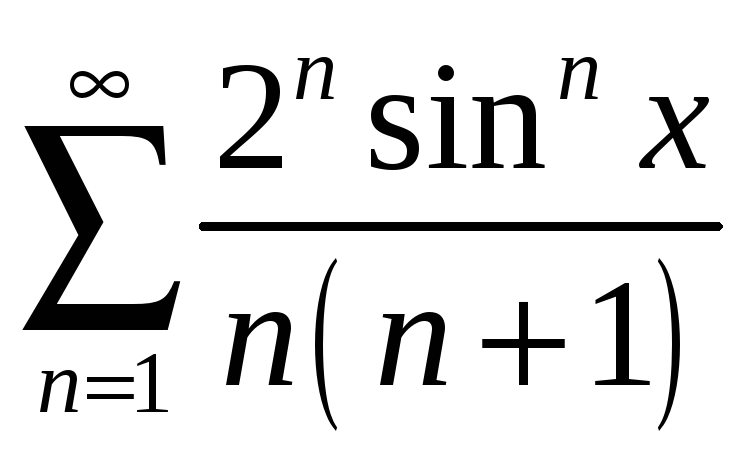 ;
;
1.7
а)
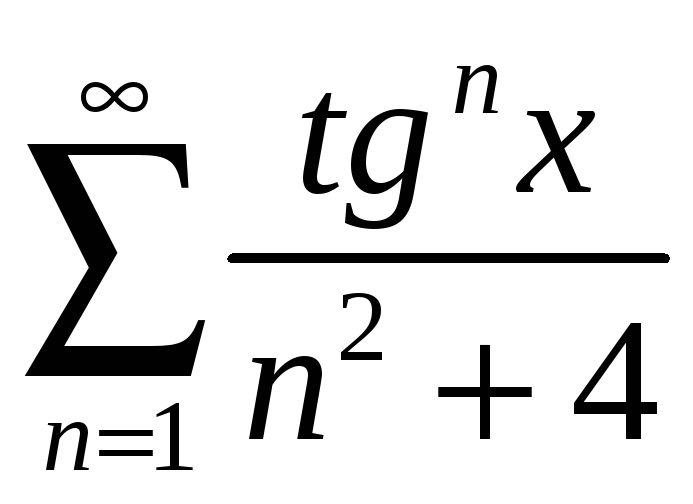 ;
;
б)
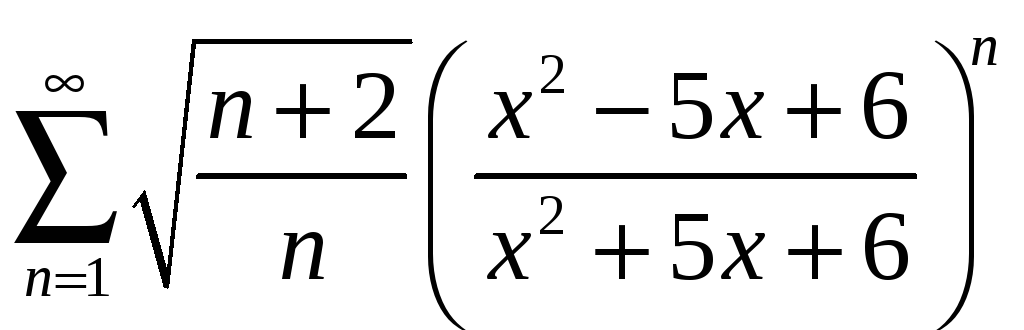 ;
;
1.8
а)
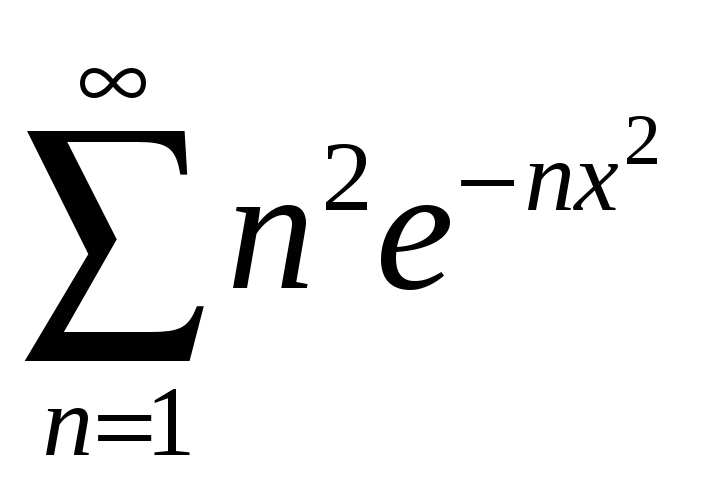 ;
;
б)
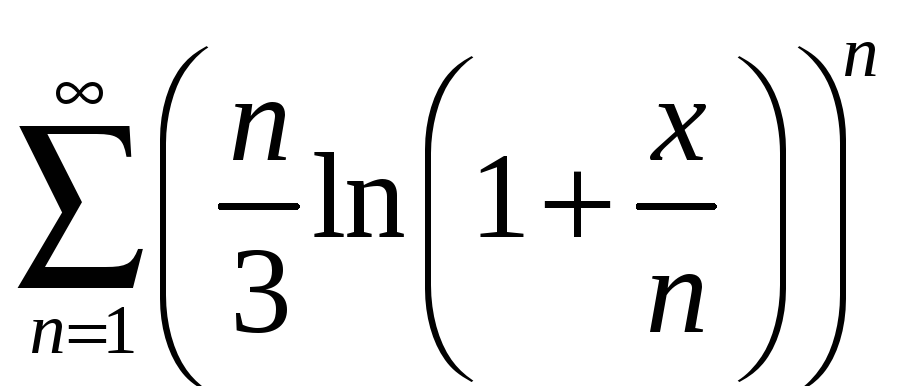 ;
;
1.9
а)
![]() ;
;
б)
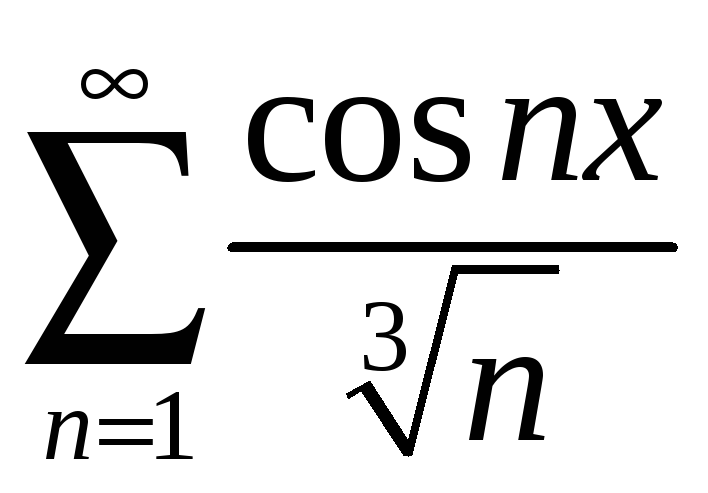 ;
;
1.10
а)
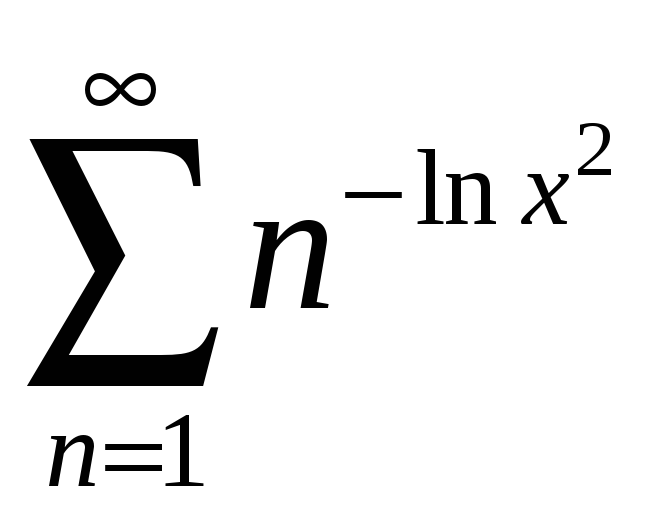 ;
;
б)
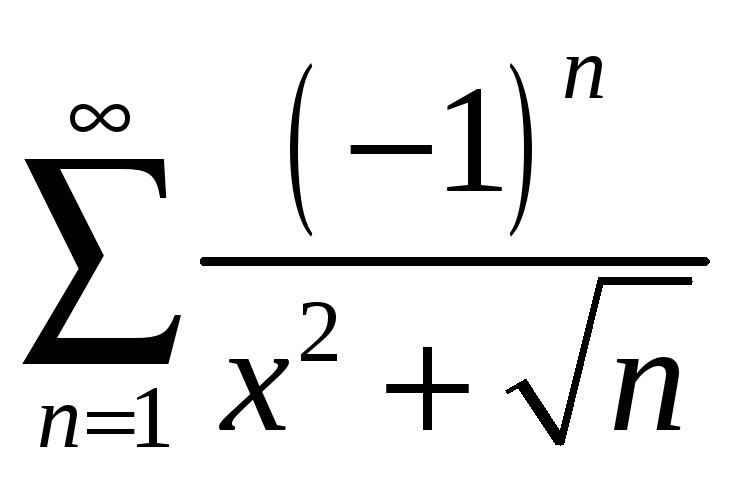 ;
;
1.11 а)
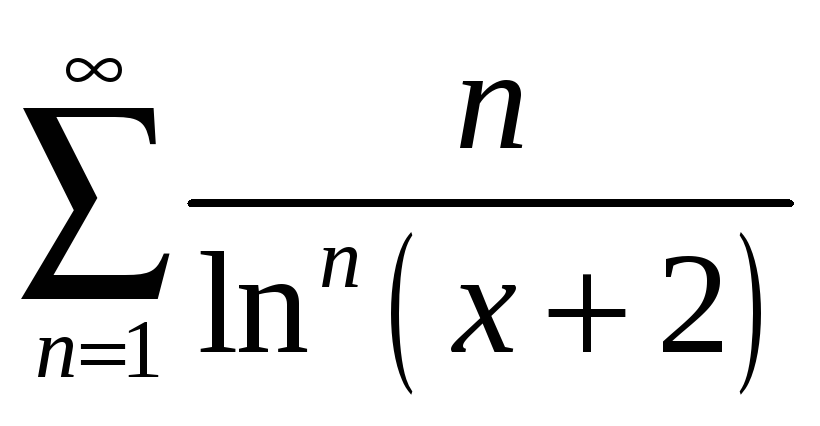 ;
;
б)
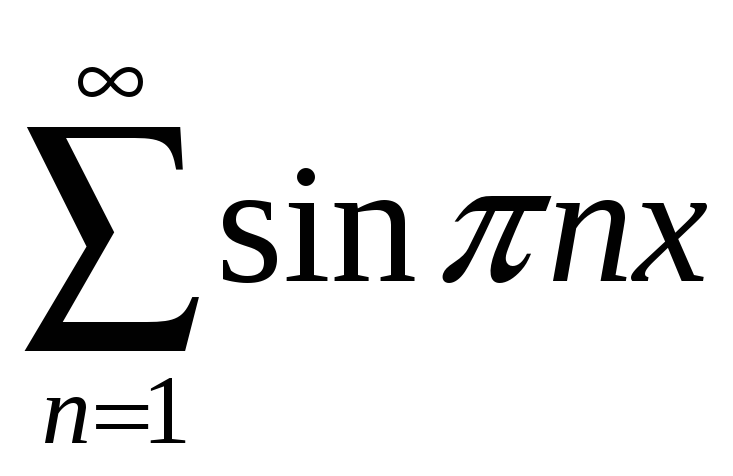 ;
;
1.12
а)
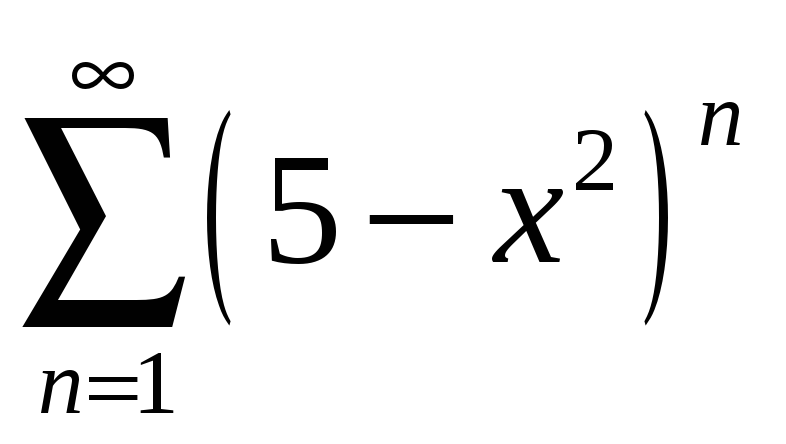 ;
;
б)
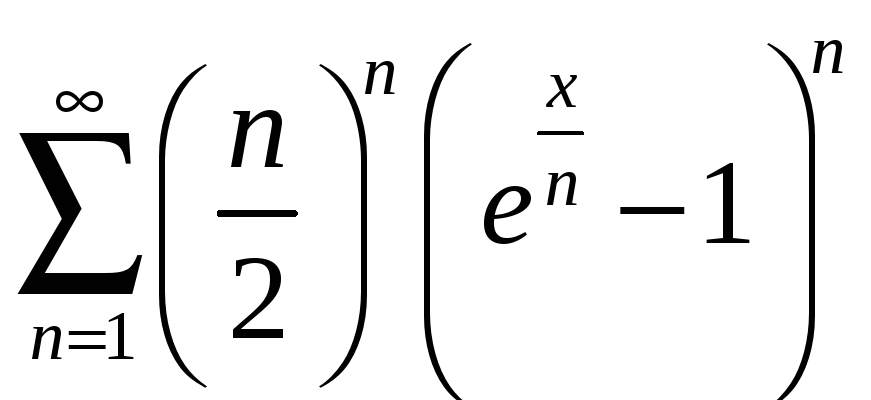 .
.
2.Исходя
из определения равномерной сходимости,
доказать равномерную сходимость ряда
на указанном промежутке
2.1
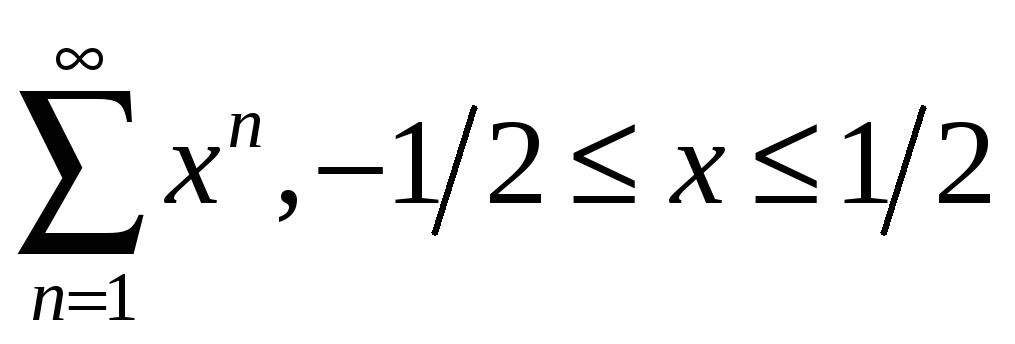 ;
;
2.6
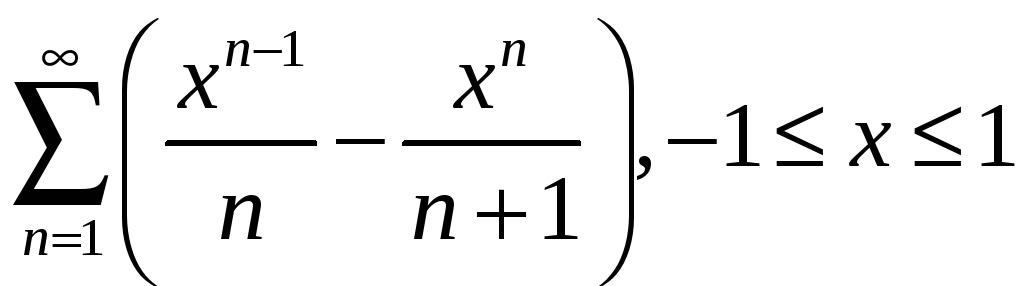 ;
;
2.2
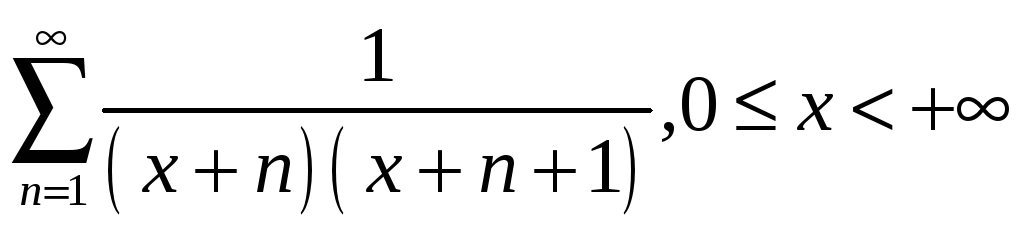 ;
;
2.7
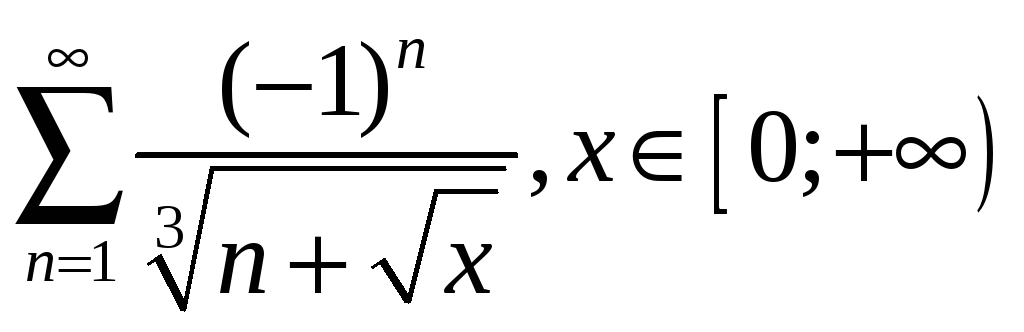 ;
;
2.3
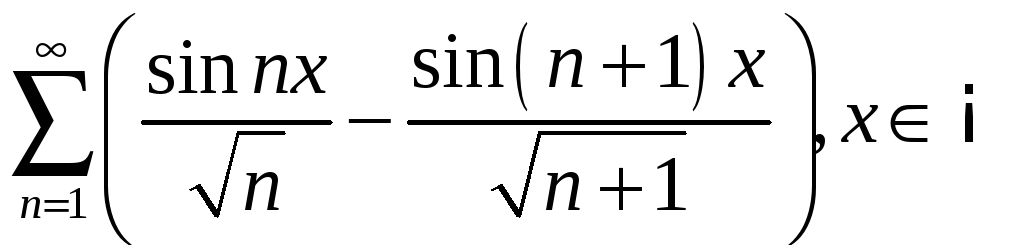 ;
;
2.8
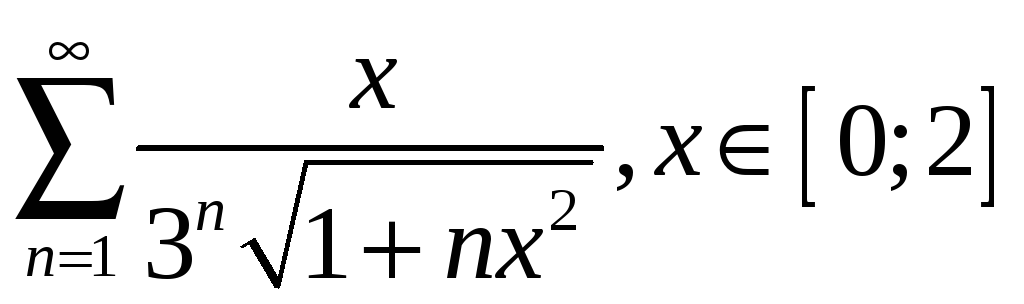 ;
;
2.4
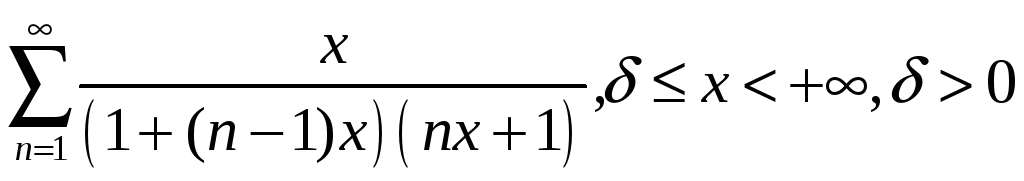 ;
;
2.9
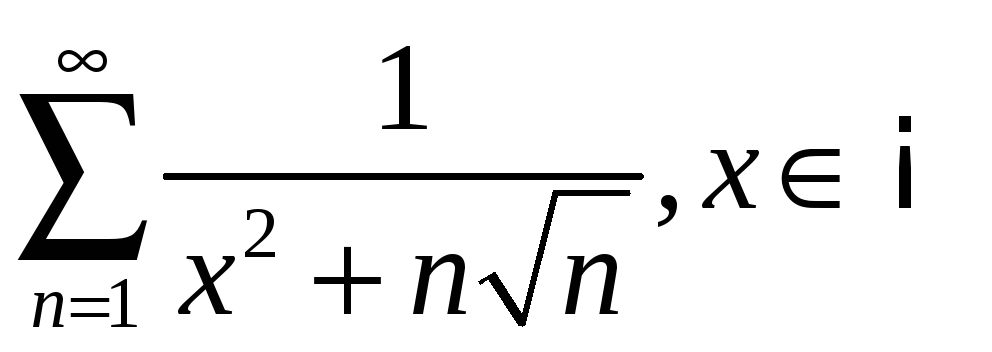 ;
;
2.5
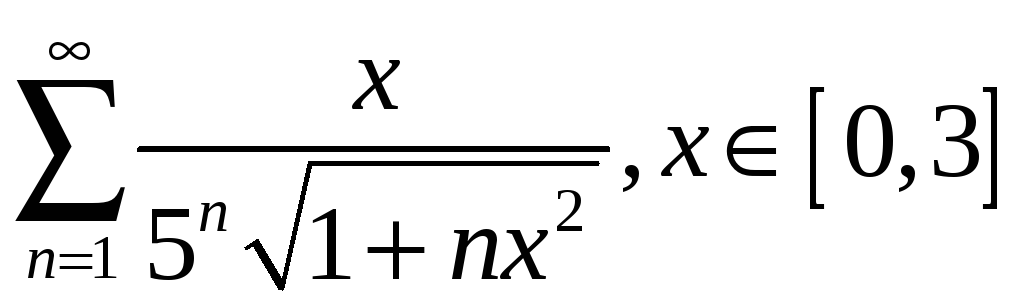 ;
;
2.10
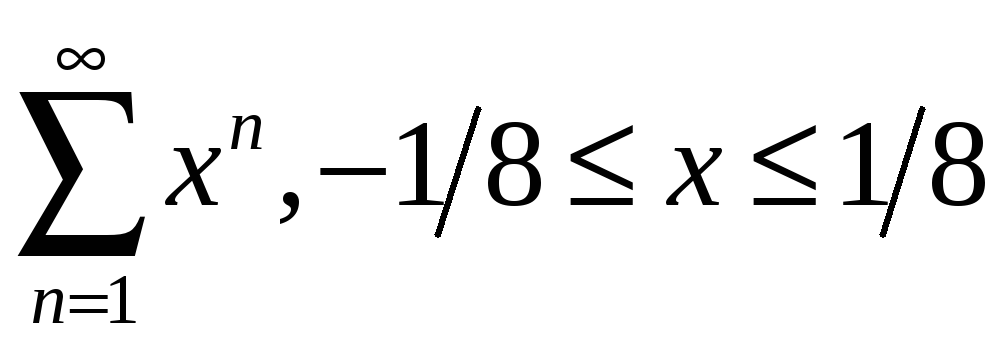 .
.
3
Пользуясь признаком Вейерштрасса,
доказать равномерную сходимость ряда.
3.1
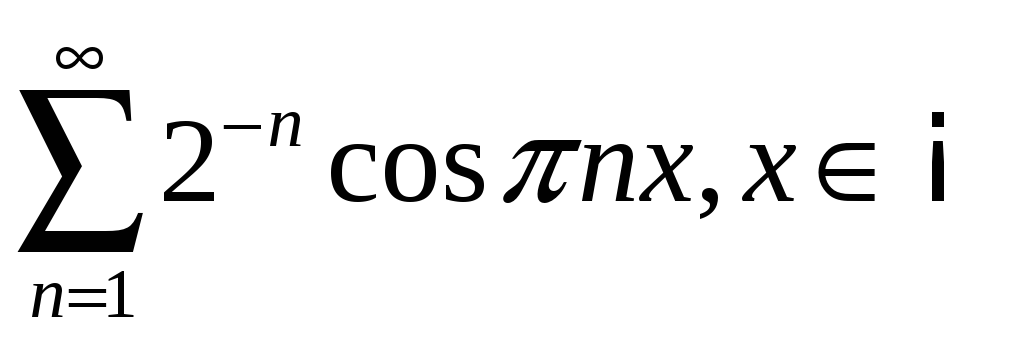 ;
;
3.7
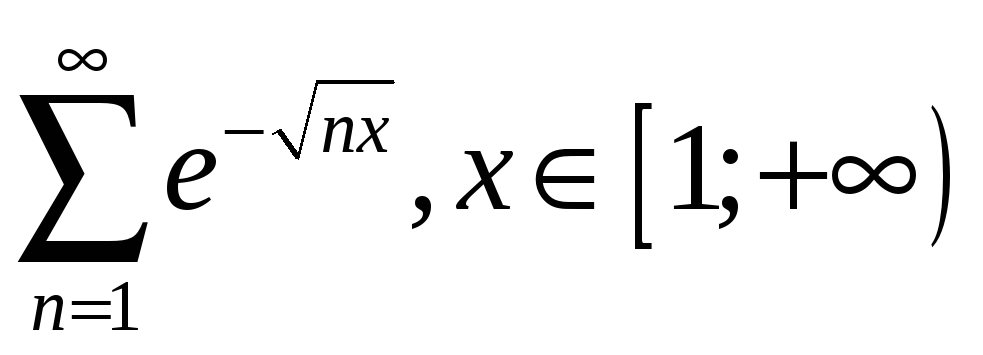 ;
;
3.2
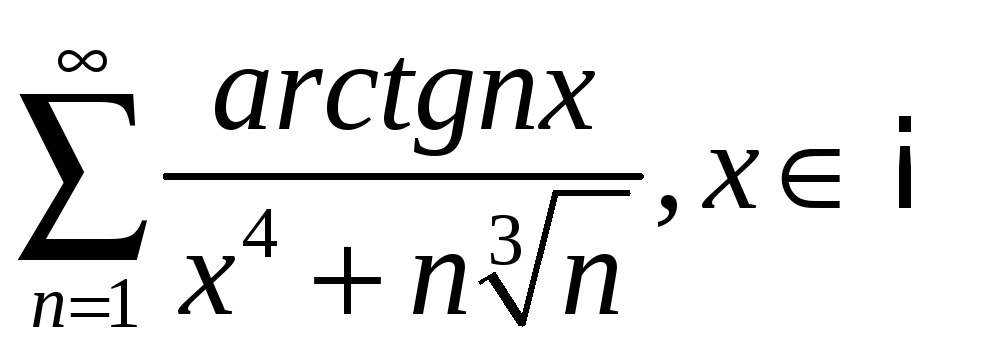 ;
;
3.8
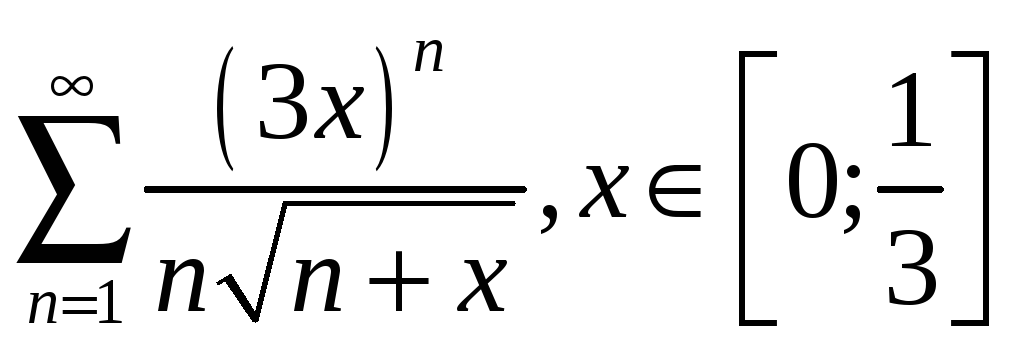 ;
;
3.3
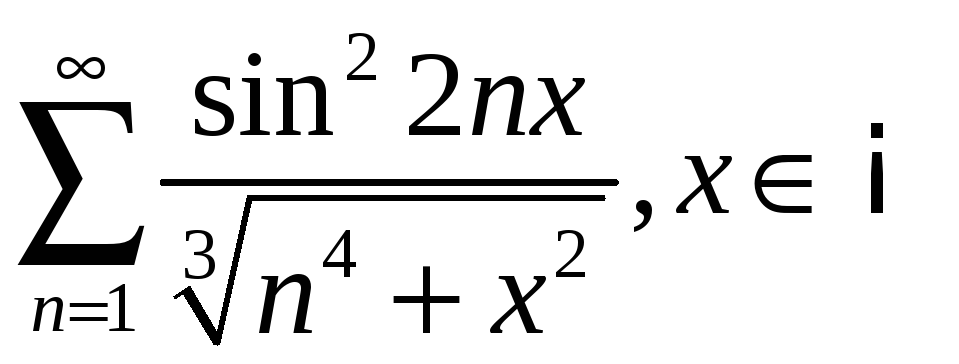 ;
;
3.9
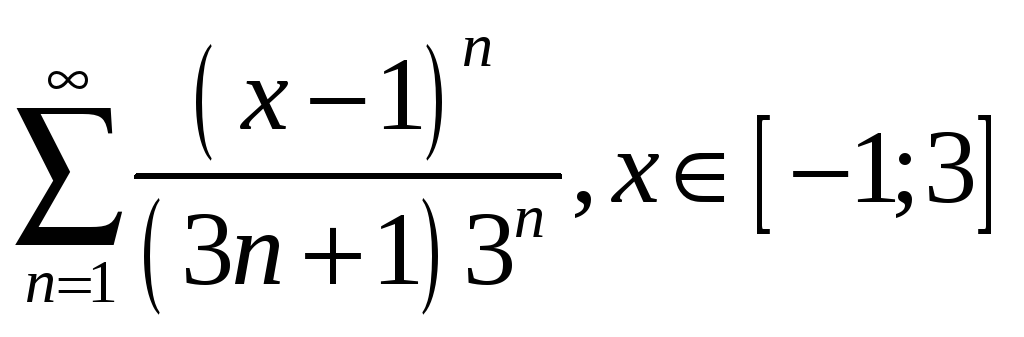 ;
;
3.4
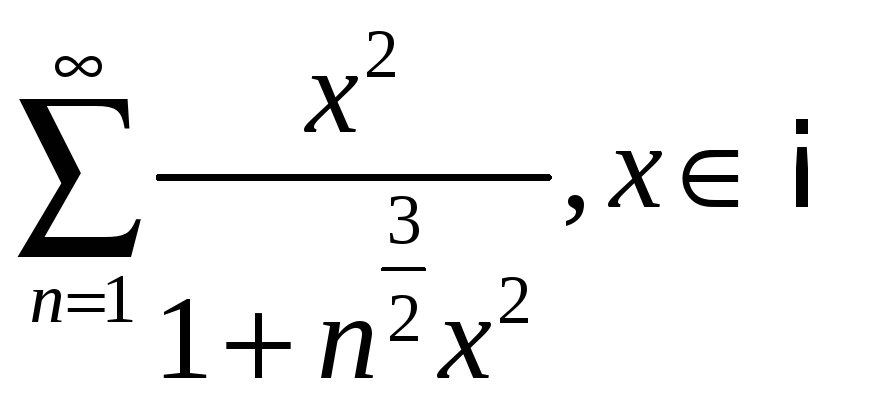 ;
;
3.10
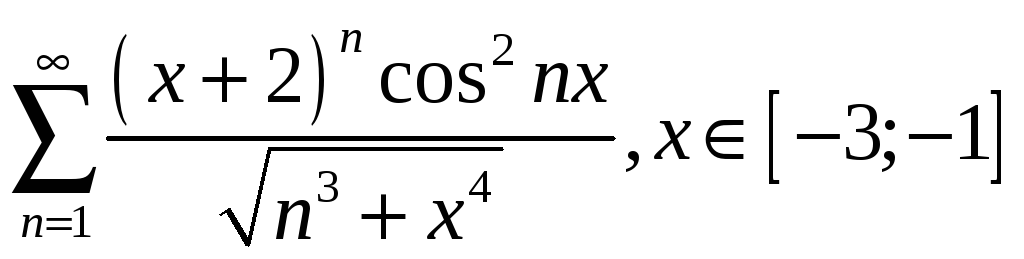 ;
;
3.5
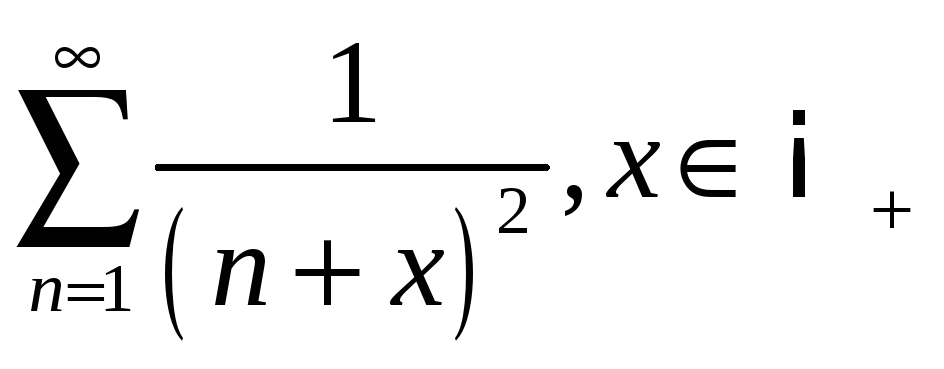 ;
;
3.11
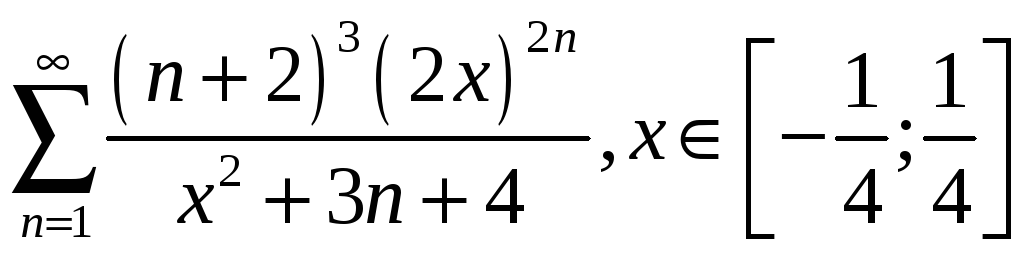
3.6
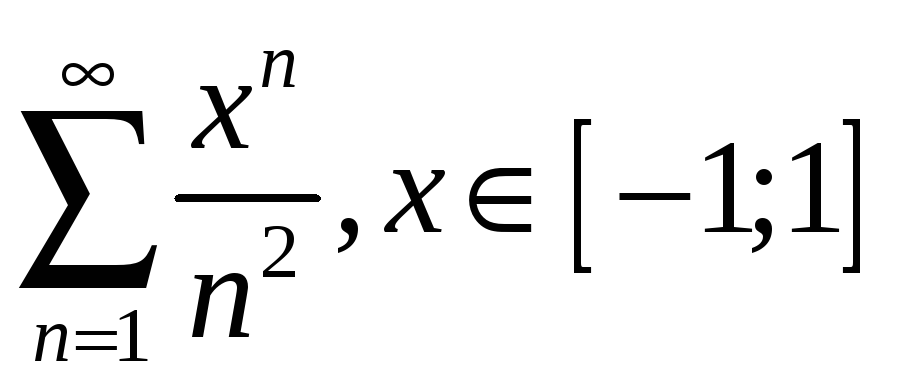 ;
;
3.12
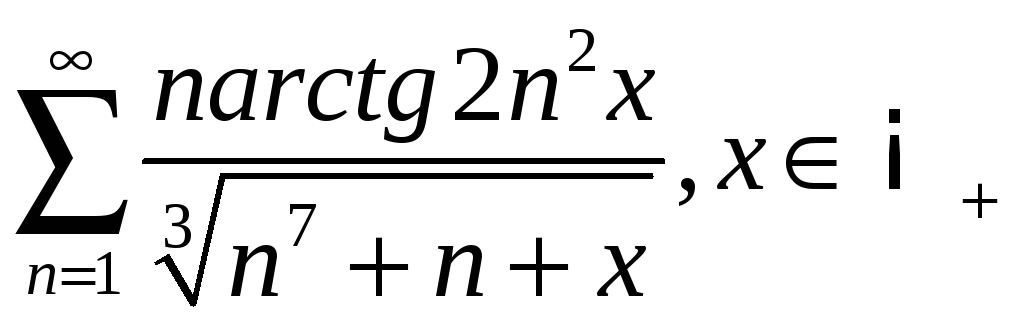 .
.
4.Исследовать
сходимость и равномерную сходимость
ряда.
4.1
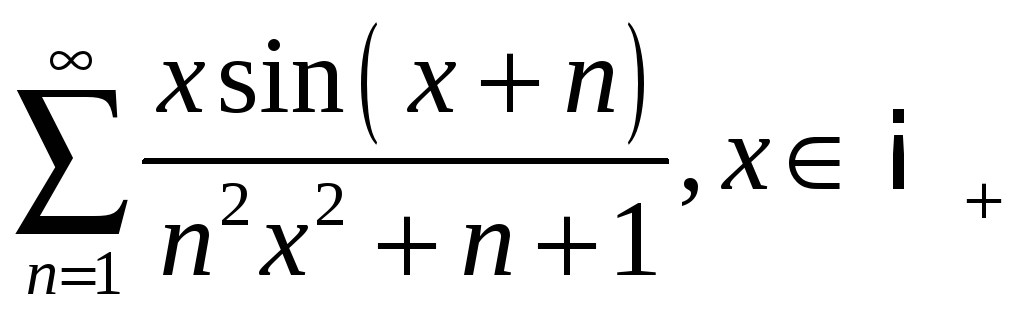 ;
;
4.6
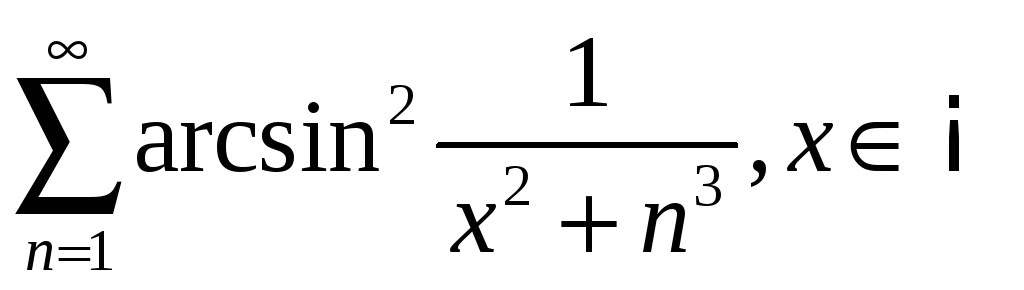 ;
;
4.2
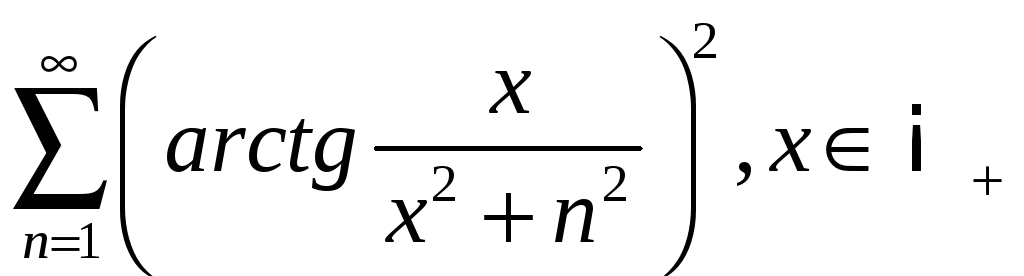 ;
;
4.7
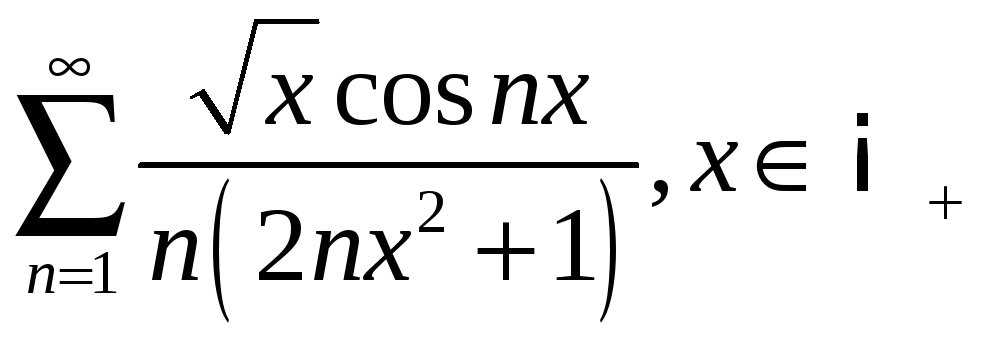 ;
;
4.3
![]() ;
;
4.8
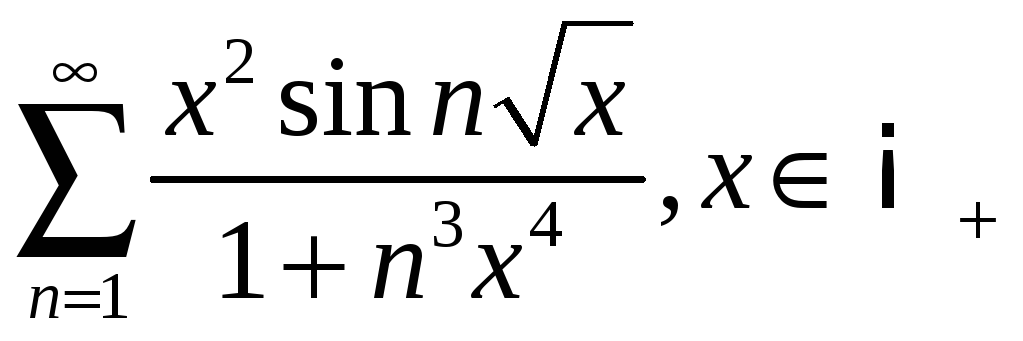 ;
;
4.4
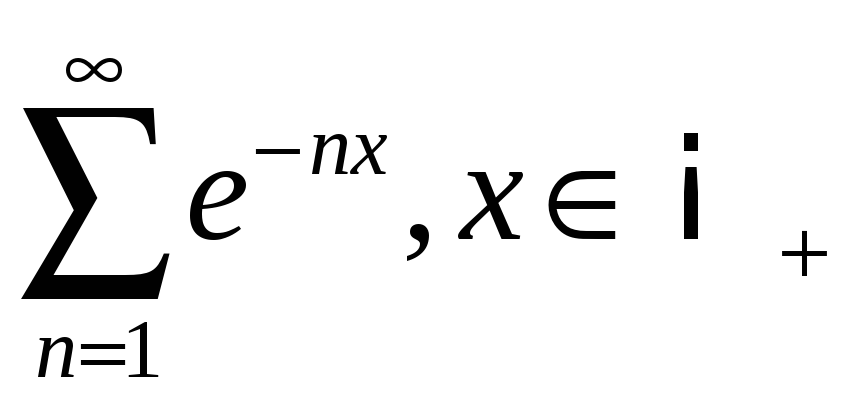 ;
;
4.9
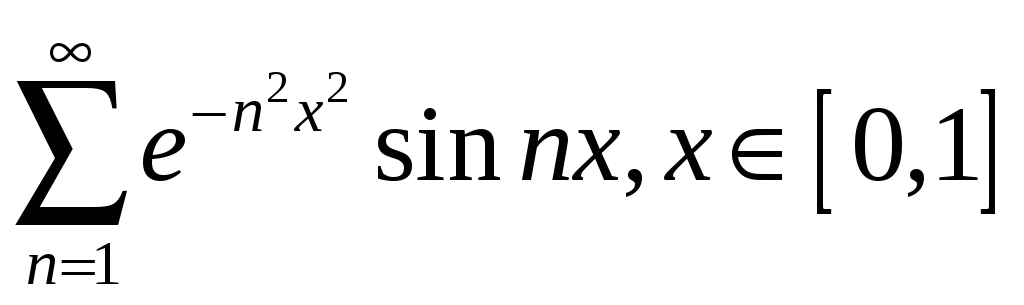 ;
;
4.5
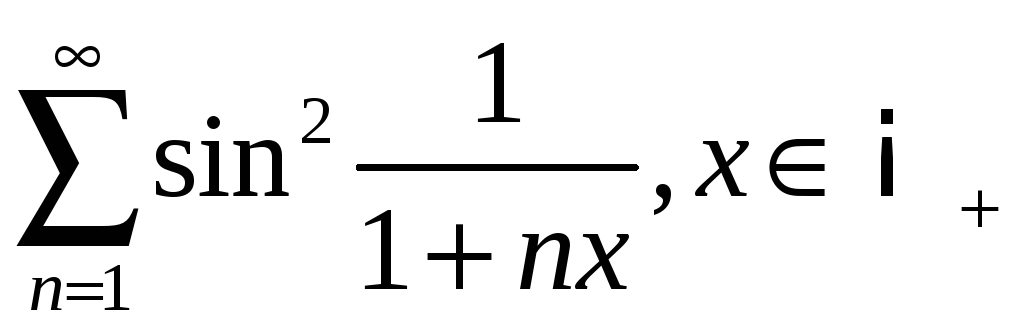 ;
;
4.10
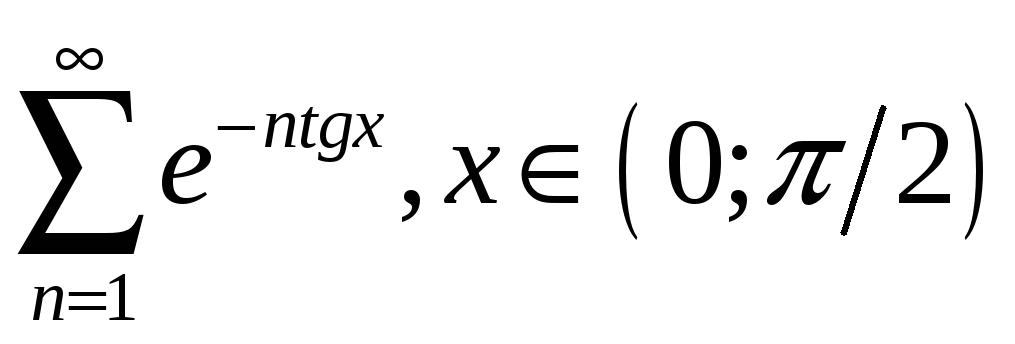 .
.
Соседние файлы в папке лаб.раб. ряды
- #
- #
| Автор | Сообщение | ||
|---|---|---|---|
|
Заголовок сообщения: Нахождение предельной функции(равномерная сходимость)
|
|||
|
Здравствуйте! объясните мне как получается эта предельная функция! может кто расписать вот эти два примера. как из Fn(x) получить Fx! Не догоняю. уже весь интернет перелопатил. и везде показывается сразу результат. последовательно нигде не расписано. Последний раз редактировалось azotklas 15 янв 2015, 18:16, всего редактировалось 2 раз(а). |
||
| Вернуться к началу |
|
||
|
azotklas |
Заголовок сообщения: Re: Нахождение предельной функции(равномерная сходимость)
|
|
|
|
| Вернуться к началу |
|
|
azotklas |
Заголовок сообщения: Re: Нахождение предельной функции(равномерная сходимость)
|
|
как я понимаю нужно найти предел fn(x) но меня сбивают иксы. не знаю как с ними находить предел
|
|
| Вернуться к началу |
|