Если мы подбросим камень в воздух – он упадет на Землю. Если у самолета на высоте 10 километром отключаться двигатели – он тоже упадет на Землю. Но спутники и космические корабли, что мы запускаем в космос, не падают. Почему?
Все дело в том, с какой скоростью тот или иной объект удаляется от планеты. Хватит ли этому объекту энергии преодолеть притяжение планеты.
Телеграмм-канал Космос нас ждет – больше космоса и красоты. Подписывайтесь!
Первая космическая скорость
Это та самая минимальная скорость для выхода корабля или спутника на круговую орбиту, равную радиуса планеты, без учета вращения планеты и сопротивления ее атмосферы.
Если скорость будет превышать первую, но не достигнет второй космической скорости, то траектория тела из круговой начнет переходить в эллиптическую.
Впервые такую скорость смог достичь первый искусственный спутник Земли «Спутник-1» СССР 4 октября 1957 года.
Расчет
Вторая космическая скорость
Это минимальная скорость, которую следует придать телу для того, чтобы оно покинуло замкнутую орбиту и смогло улететь от небесного тела за пределы его гравитационного поля.
Иными словами, для Земли, это та скорость, с которой должны двигаться космические аппараты (КА) для полетов к другим объектам Солнечной системы: Луны, Марса и т.д.
Движение тела на второй космической скорости происходит по параболической траектории.
Впервые такую скорость развил Советский космический аппарат Луна-1 2 января 1959 года, чтобы преодолеть расстояние от Земли до Луны и изучить наш естественный спутник.
Расчет
Третья космическая скорость
Такую скорость необходимо придать телу, чтобы оно смогло покинуть Солнечную систему. Так как 99,8% массы Солнечной системы приходится на Солнце, то можно сказать, что КА надо преодолеть гравитационное притяжение Солнца.
Расчет
Для Солнечной системы это величина равна 16,650 км/с.
Самое выгодное расположение космодрома для подобного запуска – максимально близко к экватору, так как на экваторе самая большая скорость собственного вращения Земли вокруг своей оси и направление движения в сторону вращения Земли и в сторону орбитального движения Земли по орбите.
КА “Новые горизонты” покинул атмосферу Земли со скоростью близкой к третьей космической – 16,26 км /с. Относительно Солнца он имел скорость 45 км/с. Такой скорости недостаточно, чтобы покинуть Солнечную систему. Но благодаря гравитационному маневру у Юпитера, “Новые горизонты” добавил еще 4 км/с, что позволило ему покинуть Солнечную системы, предварительно показав нам карликовую планету Плутон.
Четвертая космическая скорость
Эта та скорость, которая позволит покинуть галактику в данной точке.
Четвертая космическая в основном не зависит от месторасположения Земли в Млечном пути. Она зависит от расположения и плотности звездного вещества в окрестностях Солнечной системы. А эти данные пока мало изучены.
Для нашей части галактики четвертая космическая скорость примерно равна 550 км/с.
Пятая космическая скорость
Эта скорость редко применима и является больше «фантазией», так как такую скорость необходимо развить для путешествия на другую планету в другую звездную систему, независимо от их взаимного расположения, с траекторией перпендикулярно плоскости эклиптики.
Для Земли эта скорость будет равна 43,6 км/с.
Почему спутники не падают на Землю
Этот вопрос поднимался в самом начале статьи. Теперь давайте на него ответим.
На спутник на орбите действует сила тяжести со стороны Земли. И под действием этой силы спутнику логичнее упасть.
Но, он летит вокруг Земли с первой космической скоростью – 7,9 км/с. Вспомните, чем больше скорость – тем сложнее затормозить. Вот и здесь, спутник и хотел бы упасть, но он не может затормозить и просто пролетает мимо Земли по инерции, тем самым продолжая бесконечное падение.
То есть, спутники падают, но промахиваются и не попадают в Землю.
Еще больше космоса и интересных фактов в телеграмм-канале.
Если Вам понравилась статья:

Содержание
- Первая космическая скорость
- Вторая космическая скорость
- Третья космическая скорость
- Четвёртая и пятая космическая скорости
Любой предмет, будучи подброшенным вверх, рано или поздно оказывается на земной поверхности, будь то камень, лист бумаги или простое перышко. В то же время, спутник, запущенный в космос полвека назад, космическая станция или Луна продолжают вращаться по своим орбитам, словно на них вовсе не действует сила притяжения нашей планеты. Почему так происходит?
На нашей Земле всемирное тяготение воздействует на любое материальное тело. Тогда логично будет предположить, что есть некая сила, нейтрализующая действие гравитации. Эту силу принято называть центробежной.
Центробежную силу легко ощутить привязав на один конец нитки небольшой груз и раскрутив его по окружности. При этом чем больше скорость вращения тем сильнее натяжение нити, а чем медленнее вращаем мы груз тем больше вероятность, что он упадет вниз.
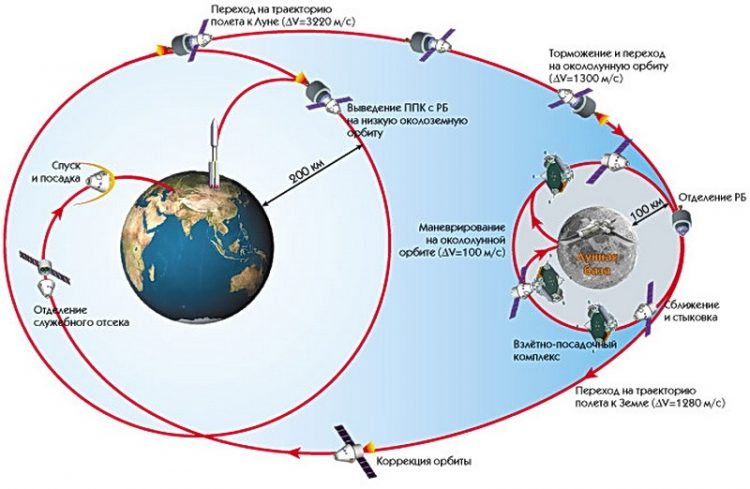
Траектория полета космических кораблей
Таким образом мы вплотную приблизились к понятию «космическая скорость». Простыми словами — это скорость, позволяющая любому объекту преодолеть тяготение небесного тела и их системы. Космические скорости используются для характеристики типа движения космического аппарата в сфере действия небесных тел: Солнца, Земли и Луны, других планет и их естественных спутников, а также астероидов и комет.
Это также значит, что космическая скорость есть у каждого объекта, который движется по орбите. Размер и форма орбиты космического объекта зависят от величины и направления скорости, которую данный объект получил на момент выключения двигателей, и высоты, на которой произошло данное событие.
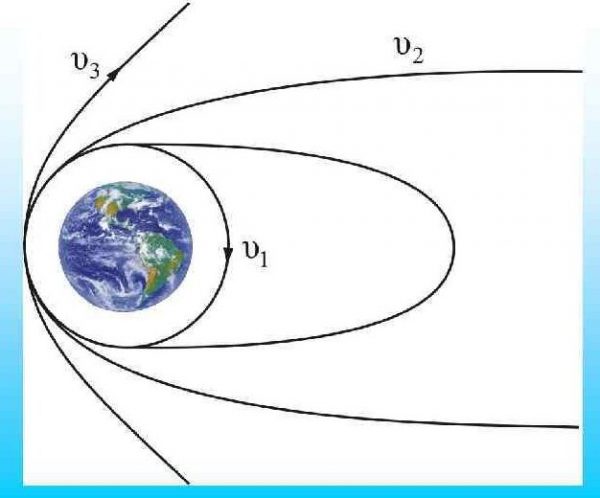
Космическая скорость (первая v1, вторая v2, третья v3 и четвёртая v4) — это минимальная скорость, при которой какое-либо тело в свободном движении сможет:
- v1 — стать спутником небесного тела (то есть способность вращаться по орбите вокруг небесного тела и не падать на его поверхность);
- v2 — преодолеть гравитационное притяжение небесного тела и начать двигаться по параболической орбите;
- v3 — покинуть при запуске планету, преодолев притяжение Звезды;
- v4 — при запуске из планетной системы объект покинул Галактику.
Космические скорости могут быть рассчитаны для любого удаления от центра Земли. Однако в космонавтике часто используются величины, рассчитанные конкретно для поверхности шаровой однородной модели Земли радиусом 6371 км.
Первая космическая скорость

Первая космическая скорость или Круговая скорость V1 — скорость, которую необходимо придать объекту без двигателя, пренебрегая сопротивлением атмосферы и вращением планеты, чтобы вывести его на круговую орбиту с радиусом, равным радиусу планеты.
Иными словами, первая космическая скорость — это минимальная скорость, при которой тело, движущееся горизонтально над поверхностью планеты, не упадёт на неё, а будет двигаться по круговой орбите.
Формула

где G — гравитационная постоянная (6,67259·10−11 м³·кг−1·с−2), — первая космическая скорость. Подставляя численные значения (для Земли M = 5,97·1024 кг, R = 6 378 км), найдем
7,9 км/с
Первую космическую скорость можно определить через ускорение свободного падения —
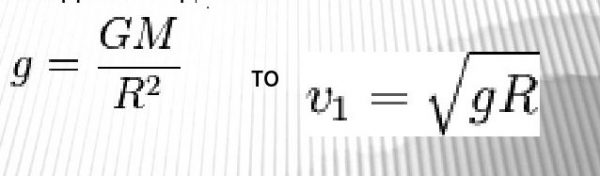
Вторая космическая скорость
Вторая космическая скорость (параболическая скорость, скорость убегания) — наименьшая скорость, которую необходимо придать объекту (например, космическому аппарату), масса которого пренебрежимо мала относительно массы небесного тела (например, планеты), для преодоления гравитационного притяжения этого небесного тела.
Предполагается, что после приобретения телом этой скорости оно не получает негравитационного ускорения (двигатель выключен, атмосфера отсутствует).
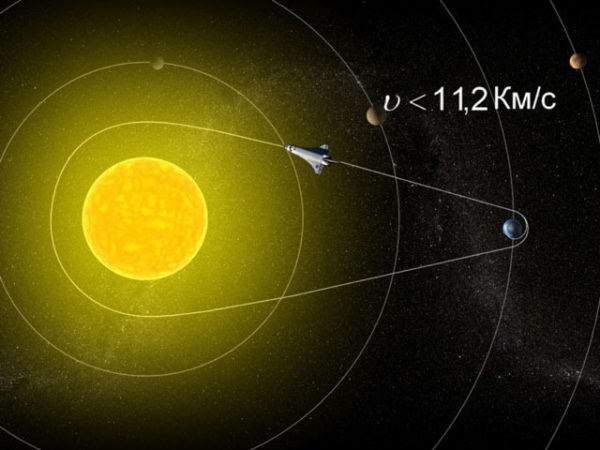
Вторая космическая скорость определяется радиусом и массой небесного тела, поэтому она своя для каждого небесного тела (для каждой планеты) и является его характеристикой:
- для Земли вторая космическая скорость равна 11,2 км/с. Тело, имеющее около Земли такую скорость, покидает окрестности Земли и становится спутником Солнца.
- для Солнца вторая космическая скорость составляет 617,7 км/с.
- для Луны скорость убегания равна 2,4 км/с, несмотря на то, что в действительности для удаления тела на бесконечность с поверхности Луны необходимо преодолеть притяжение Земли, Солнца и Галактики.
Параболической вторая космическая скорость называется потому, что тела, имеющие вторую космическую скорость, движутся по параболе.
Формула
Для получения формулы второй космической скорости удобно обратить задачу — спросить, какую скорость получит тело на поверхности планеты, если будет падать на неё из бесконечности. Очевидно, что это именно та скорость, которую надо придать телу на поверхности планеты, чтобы вывести его за пределы её гравитационного влияния .
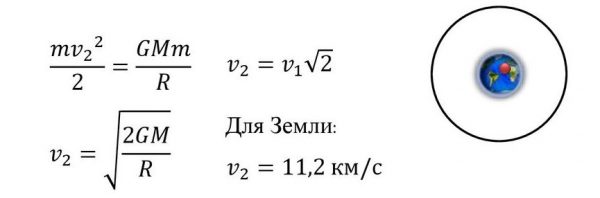
Третья космическая скорость
Третья космическая скорость — минимально необходимая скорость тела без двигателя, позволяющая преодолеть притяжение Солнца и в результате уйти за пределы Солнечной системы.

Только на космических кораблях, которым доступны такие скорости, принципиально могут быть осуществлены пилотируемые межзвёздные перелёты к планетным системам других звёзд.
Взлетая с поверхности Земли и наилучшим образом используя орбитальное движение планеты космический аппарат может достичь третей космической скорости уже при 16,6 км/с относительно Земли, а при старте с Земли в самом неблагоприятном направлении его необходимо разогнать до 72,8 км/с.
Здесь для расчёта предполагается, что космический аппарат приобретает эту скорость сразу на поверхности Земли и после этого не получает негравитационного ускорения (двигатели выключены и сопротивление атмосферы отсутствует). Если к тому же учесть притяжение других планет, которое может как ускорить, так и притормозить аппарат, то диапазон возможных значений 3-й космической скорости станет еще больше.
При наиболее энергетически выгодном старте скорость объекта должна быть сонаправлена скорости орбитального движения Земли вокруг Солнца. Орбита такого аппарата в Солнечной системе представляет собой параболу.
Четвёртая и пятая космическая скорости
Четвёртая космическая скорость — минимально необходимая скорость тела без двигателя, позволяющая преодолеть притяжение галактики Млечный Путь. Она используется довольно редко.
Четвёртая космическая скорость не постоянна для всех точек Галактики, а зависит от расстояния до центральной массы.
Для нашей галактики таковой является объект Стрелец A*, сверхмассивная чёрная дыра.
По грубым предварительным расчётам в районе нашего Солнца четвёртая космическая скорость составляет около 550 км/с. Значение сильно зависит не только (и не столько) от расстояния до центра галактики, а от распределения масс вещества по Галактике, о которых пока нет точных данных, ввиду того что видимая материя составляет лишь малую часть общей гравитирующей массы, а все остальное — скрытая масса.
Ещё реже в некоторых источниках встречается понятие «пятая космическая скорость». Это скорость, позволяющая добраться до иной планеты звездной системы вне зависимости от разности плоскостей эклиптики планет. Например, для Солнечной системы и, конкретно, для Земли, чтобы орбита межпланетного перелета была перпендикулярной к земной орбите, нужна скорость запуска 43,6 километра в секунду.
Видео
Источники
- https://ru.wikipedia.org/wiki/Космическая_скорость
https://mirznanii.com/a/9233/kosmicheskie-skorosti
http://www.astronet.ru/db/msg/1162252
https://fb.ru/article/54389/kosmicheskaya-skorost
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 19 июля 2021 года; проверки требуют 10 правок.
Файл:Скорость небесного тела
Скорость кеплеровского движения небесного тела вокруг Солнца, а также её радиальная и поперечная компоненты (анимация).
Орбитальная скорость тела (обычно планеты, естественного или искусственного спутника, кратной звезды) — скорость, с которой оно вращается вокруг барицентра системы, как правило вокруг более массивного тела.
Определение[править | править код]
В полярных координатах выражение для орбитальной скорости 
где:
— гравитационный параметр, равный G(M + m) — в общей задаче двух тел, или GM — в ограниченной, где G — гравитационная постоянная, M — масса центрального тела, m — масса вращающегося тела;
— фокальный параметр конического сечения (расстояние от фокуса до директрисы для параболы, отношение
— для эллипса и гиперболы);
— эксцентриситет (
для эллипса,
для параболы,
— для гиперболы);
— истинная аномалия, угол между направлением из центра, расположенного в фокусе, на ближайшую к нему точку орбиты и радиусом-вектором вращающегося тела.
Орбитальная скорость также может вычисляться по общей формуле
где
— гравитационный параметр,
— расстояние между вращающимся телом и центральным телом,
— удельная орбитальная энергия,
— длина большой полуоси (или вещественной оси).
При этом
Орбиты Земли[править | править код]
| Орбита | Расстояние между центрами масс, км | Высота над поверхностью Земли, км |
Орбитальная скорость, км/с | Орбитальный период | Удельная орбитальная энергия, МДж/кг |
|---|---|---|---|---|---|
| Поверхность Земли, для сравнения | 6 400 | 0 | 7,89 | — | −62,6 |
| Низкая околоземная орбита | 6 600—8 400 | 200—2 000 | круговая: 7,8—6,9 эллиптическая: 6,5—8,2 |
89—128 мин | −29,8 |
| Высокоэллиптическая орбита спутников Молния | 6 900—46 300 | 500—39 900 | 1,5—10,0 | 11 ч 58 мин | −4,7 |
| Геостационарная орбита | 42 000 | 35 786 | 3,1 | 23 ч 56 мин | −4,6 |
| Орбита Луны | 363 000—406 000 | 357 000—399 000 | 0,97—1,08 | 27,3 дня | −0,5 |
Солнечная система[править | править код]
| Планета (другое тело) |
Орбитальная скорость, км/с |
|---|---|
| Меркурий | 47,36 |
| Венера | 35,02 |
| Земля | 29,78 |
| Марс | 24,13 |
| Церера | 17,88 |
| Юпитер | 13,07 |
| Сатурн | 9,69 |
| Уран | 6,81 |
| Нептун | 5,43 |
| Плутон | 4,66 |
| Хаумеа | 4,48 |
| Макемаке | 4,41 |
| Эрида | 3,43 |
| Луна | 1,02 |
Примечания[править | править код]
- ↑ Балк М. Б. Скорость спутника и её компоненты // Элементы динамики космического полета. — М.: Наука, 1965. — С. 61—62. — 340 с. — (Механика космического полета).
Здесь приведены формулы и примеры расчета первой и второй космической скорости для небесных тел произвольной массы и радиуса.
Для быстрого расчета можно воспользоваться онлайн-калькулятором.
Первая космическая скорость
Первая космическая скорость – это скорость, которую нужно придать телу, масса которого пренебрежительно мала по сравнению с массой планеты,
чтобы это тело стало спутником планеты и вращалось вокруг нее по круговой траектории. Примечание: если скорость будет выше заданной (но меньше второй космической), то траектория орбиты будет
не круговой, а эллипсоидной.
Формула первой космической скорости:
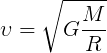
где
G – гравитационная постоянная (постоянная Ньютона), равная 6,6743015·10-11 м3/(кг*с2), или Н*м2/кг2
R – радиус небесного тела
M – масса небесного тела
Вторая космическая скорость
Вторая космическая скорость – это минимальная скорость, которой должно обладать тело, чтобы преодолеть гравитационное притяжение планеты и покинуть замкнутую орбиту вокруг нее.
Формула второй космической скорости:
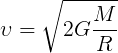
где
G – гравитационная постоянная
R – радиус небесного тела
M – масса небесного тела
Пример:
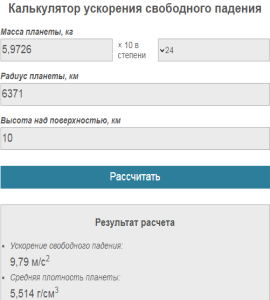
Масса планеты Земля составляет 5,9726*1024 кг, средний радиус – 6371 км (или 6371000 м). Подставив эти значения в формулы первой и второй
космических скоростей, мы получим значение соответственно 7 910 м/с и 11 187 м/с.
Теперь рассчитаем значение космических скоростей для планеты Нептун. Масса Нептуна – 1,0243*1026 кг. средний радиус – 24 622 км (24 622 000 м).
В итоге получим значения – 16 663 м/с и 23 565 м/с.
Значения для Марса (6,4171*1023 кг и 3389,5 км) будет 3 555 м/с и 5 027 м/с.
Для Венеры (4,8675*1024 кг и 6051,8 км) – 7 327 м/с и 10 362 м/с соответственно.
Калькулятор космических скоростей
Другие формулы
Скорости движения космических аппаратов на орбитах разного типа
Движению космических
аппаратов по эллиптическим траекториям
соответствуют так называемые эллиптические
скорости, определяемые соотношением
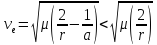 ,
,
частным случаем которых являетсякруговая,
илипервая
космическаяскорость.
Параболической
траектории соответствует параболическая
скорость
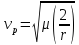 ,
,
называемая такжевторой
космической скоростью.
Гиперболические
скорости
 соответствуют движению по гиперболическим
соответствуют движению по гиперболическим
траекториям.
Здесь μ–гравитационный
параметр, равный ,
,
гдеG—гравитационная
постоянная,M– масса центрального
тела,m– масса вращающегося тела; – расстояние между вращающимся телом
– расстояние между вращающимся телом
и центральным телом;a
–длинабольшой
полуоси(для эллипса).
Космическая скорость
Космическая
скорость
(первая v1,
вторая v2,
третья v3
и четвёртая v4)
– это минимальная скорость, при которой
какое-либо тело в свободном движении с
поверхности небесного тела сможет:
-
v1
(круговая скорость) – стать спутником
небесного тела (то есть вращаться по
круговой орбите вокруг НТ на нулевой
или пренебрежимо малой высоте относительно
поверхности); -
v2
(параболическая скорость, скорость
убегания) – преодолеть гравитационное
притяжение небесного тела и уйти на
бесконечность; -
v3
– покинуть звёздную систему, преодолев
притяжение звезды; -
v4
– покинуть
галактику.
Первая космическая
скорость (круговая скорость) –
минимальная скорость, которую необходимо
придать объекту, чтобы вывести его на
геоцентрическую орбиту. Иными словами,
первая космическая скорость – это
минимальная скорость, при которой тело,
движущееся горизонтально над поверхностью
планеты, не упадёт на неё, а будет
двигаться по круговой орбите.
В инерциальной
системе отсчётана объект, движущийся
по круговой орбите вокруг Земли, будет
действовать только одна сила – сила
тяготения Земли. При этом движение
объекта не будет ни равномерным, ни
равноускоренным. Происходит это потому,
что скорость и ускорение (величины не
скалярные, а векторные) в данном случае
не удовлетворяют условиям
равномерности/равноускоренности
движения – то есть движения с постоянной
(по величине и направлению)
скоростью/ускорением. Действительно –
вектор скорости будет постоянно направлен
по касательной к поверхности Земли, а
вектор ускорения – перпендикулярно
ему к центру Земли, при этом по мере
движения по орбите эти векторы постоянно
будут менять свое направление. Поэтому
в инерциальной системе отсчета такое
движение часто называют «движение по
круговой орбите с постоянной по модулю
скоростью».
Часто для удобства
вычисления первой космической скорости
переходят к рассмотрению этого движения
в неинерциальной системе отсчета –
относительно Земли. В этом случае объект
на орбите будет находиться в состоянии
покоя, так как на него будут действовать
уже две силы: центробежная сила и сила
тяготения. Соответственно, для вычисления
первой космической скорости необходимо
рассмотреть равенство этих сил.
Точнее, на тело
действует одна сила – сила тяготения,
она же – центростремительная. Центробежная
сила действует на Землю. Центростремительная
сила, вычисляемая из условия вращательного
движения равна силе тяготения. Отсюда,
приравниванием этих формул, вычисляется
скорость.


где m – масса
объекта, M – масса планеты, G – гравитационная
постоянная, v1 – первая космическая
скорость, R – радиус планеты. Подставляя
численные значения (дляЗемлиM = 5,97·1024 кг, R = 6371 км), найдем
 7,9 км/с.
7,9 км/с.
Первую космическую
скорость можно определить через ускорение
свободного падения. Поскольку

то
 .
.
Вторая космическая
скорость (параболическая скорость,
скорость освобождения, скорость убегания)
– наименьшая
скорость,
которую необходимо придать объекту
(например,космическому
аппарату), масса которого пренебрежимо
мала по сравнению с массойнебесного
тела(например, планеты), для преодолениягравитационного
притяженияэтого небесного тела и
покиданиязамкнутой
орбитывокруг него. Предполагается,
что после приобретения телом этой
скорости оно более не получает
негравитационного ускорения (двигатель
выключен, атмосфера отсутствует).
Вторая космическая
скорость определяется радиусом и массой
небесного тела, поэтому она своя для
каждого небесного тела (для каждой
планеты) и является его характеристикой.
Для Земли вторая космическая скорость
равна 11,2 км/с. Тело, имеющее около Земли
такую скорость, покидает окрестности
Земли и становится спутникомСолнца. Для Солнца вторая космическая
скорость составляет 617,7 км/с.
Параболической
вторая космическая скорость называется
потому, что тела, имеющие при старте
скорость, в точности равную второй
космической, движутся по дуге параболыотносительно небесного тела. Однако,
если энергии телу придано чуть больше,
его траектория перестает быть параболой
и становится гиперболой; если чуть
меньше, то она превращается вэллипс.
В общем случае все они являютсяконическими
сечениями.
Для получения
формулы второй космической скорости
удобно обратить задачу – спросить,
какую скорость получит тело на поверхности
планеты,
если будет падать на неё избесконечности.
Очевидно, что это именно та скорость,
которую надо придать телу на поверхности
планеты, чтобы вывести его за пределы
её гравитационного влияния.
Запишем затем
закон
сохранения энергии

где слева стоят
кинетическаяипотенциальнаяэнергии на поверхности планеты
(потенциальная энергия отрицательна,
так как точка отсчета взята на
бесконечности), справа то же, но на
бесконечности (покоящееся тело на
границе гравитационного влияния –
энергия равна нулю). Здесь m – масса
пробного тела, M – масса планеты, R –
радиус планеты, G –гравитационная
постоянная, v2 — вторая космическая
скорость.
Решая это уравнение
относительно v2,
получим
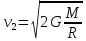 .
.
Между первойи второй космическими скоростями
существует простое соотношение:

Квадрат скорости
убегания равен удвоенному ньютоновскому
потенциалув данной точке (например,
на поверхности небесного тела):
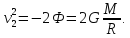
Вторая космическая
скорость обычно определяется в
предположении отсутствия каких-либо
других небесных тел (например, для Луны
скорость убегания равна 2,4 км/с, несмотря
на то, что в действительности для удаления
тела на бесконечность с поверхности
Луны необходимо преодолеть притяжение
Земли, Солнца и Галактики). Величины
первой и второй космических скоростей
для планет солнечной системы приведены
в табл. 5.
Таблица 5
Соседние файлы в папке 02-12-2014_07-07-59
- #
- #


