Нахождение проекций точек на поверхности конуса
Для нахождения недостающих проекций точек на поверхности конуса могут применяться следующие линии, принадлежащие поверхности конуса: окружность — параллель конуса (рис. 2.7, а), прямая — образующая конуса (рис. 2.7, б). Рассмотрим оба способа.
Пример 2.1. На поверхности конуса заданы проекции А2 и В, (см. рис. 2.7). Найдите недостающие проекции точек Ли В на поверхности конуса.

Рис. 2.7. Нахождение проекций точек на поверхности конуса
Способ 1. На рис. 2.7, а точка А задана проекцией А. Для нахождения недостающих проекций точки А воспользуемся вышеизложенным алгоритмом.
- 1. Через заданную проекцию точки Аг проводим линию, принадлежащую поверхности конуса — параллель.
- 2. Строим проекции параллели на других изображениях конуса. Па виде сверху она представляет собой окружность радиусом Rvна виде слева — отрезок.
- 3. На проекциях линии находим соответствующие проекции точек.
- 4. На пересечении окружности радиусом Л., с вертикальной линией связи, опущенной из А2, отмечаем проекцию Л,.
- 5. На виде сверху измеряем координату от проекции А, до горизонтальной оси и откладываем ее на проведенной линии связи на виде слева — получаем проекцию Л3.
- 6. Отмечаем проекцию А.л как невидимую. Проекция А., задана как видимая, следовательно, точка лежит в той части конической поверхности, которая обращена к наблюдателю (на виде сверху это часть, расположенная ниже горизонтальной оси). Таким образом, на виде слева ее проекция не видна.
Способ 2. Па рис. 2.7, 6 точка В задана проекцией В,. Построение недостающих проекций аналогично построению проекций точки А, за исключением того, что вместо окружности используется образующая конуса, пересекающая его основание в точке 1.
Коническая поверхность вращения
Коническая поверхность вращения — это линейчатая поверхность, образованная вращением прямолинейной образующей, которая пересекает криво-линейную направляющую (окружность) и проходит через неподвижную точку оси вращения, называемую вершиной.
Конусом называют геометрическое тело, ограниченное конической поверхностью и плоскостью основания, пересекающего все его образующие.
Конус называют прямым, если ось вращения перпендикулярна его основанию. Конус называют круговым, так как направляющей является окружность Конус с двумя параллельными основаниями, т.е. конус со срезанной вершиной, называют усеченным.
Построение проекций прямого кругового конуса
На рис. 4.71 показан пример построения проекций прямою кругового конуса с горизонтально-проецирующей осью вращения 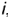 , заданной высотой
, заданной высотой  и основанием радиусом
и основанием радиусом  .
.
Для построения проекций конуса требуется выполнить графо-аналитические действия в следующем порядке:
1-е действие. По заданному условию построить горизонтальную проекцию очерка прямого кругового конуса, которая представляет собой окружность заданного радиуса  с вершиной
с вершиной  , совпадающей с осью вращения
, совпадающей с осью вращения 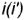 .
.
2-е действие. Выполнить графический анализ построенной горизонтальной проекции конуса:
- Круг радиуса
 является невидимой проекцией основания конуса.
является невидимой проекцией основания конуса. - Круг радиуса
 с вершиной конуса
с вершиной конуса  является видимой проекцией боковой поверхности конуса.
является видимой проекцией боковой поверхности конуса. - Обозначить на горизонтальной проекции характерные образующие конуса
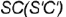 и
и 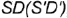 которые будут определять очерки фронтальной и профильной проекций конуса.
которые будут определять очерки фронтальной и профильной проекций конуса.
3-е действие. Построить фронтальную проекцию (очерк) конуса, которая представляет собой треугольник 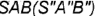 заданной высоты
заданной высоты 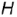 , ограниченный:
, ограниченный:
4-е действие. Построить профильную проекцию (очерк) конуса:
- ‘Задать на окружности горизонтальной проекции конуса положение базовой линии (б.о.), совпадающей с горизонтальной линией оси этой окружности.
- Выбрать положение базовой оси
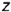 (б.о.), которая будет совпадать с вертикальной осью
(б.о.), которая будет совпадать с вертикальной осью 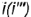 вращения на профильной проекции конуса.
вращения на профильной проекции конуса. - Профильная проекция конуса представляет собой треугольник
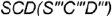 ограниченный:
ограниченный:
слева и справа очерковыми образующими 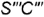 и
и 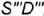 построенными по координате
построенными по координате 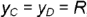 :
:
вершиной  , лежащей на базовой оси
, лежащей на базовой оси 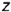 ; горизонтальным отрезком проекцией основания;
; горизонтальным отрезком проекцией основания;
профильными проекциями характерных образующих 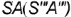 и
и 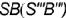 , которые совпадают с осью вращения конуса
, которые совпадают с осью вращения конуса 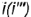 .
.
. Запомните характерные признаки очерков прямого круговою конуса на чертеже — окружность основания и два треугольника.
. Характерные признаки очерков прямого кругового усеченного конуса окружность основания и две равнобокие трапеции.
Построение проекции точек, лежащих на поверхности конуса
Принадлежность точки поверхности конуса определяется ее принадлежностью образующей поверхности и принадлежностью круговым параллелям (окружностям), по которой точка вращается вокруг оси конуса. Следовательно, проекции точки можно строить либо по принадлежности образующей, либо по принадлежности круговой параллели.
На рис. 4.71 показан пример построения горизонтальных и профильных проекций точек 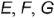 и
и  , заданных фронтальными проекциям
, заданных фронтальными проекциям 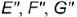 и
и 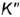 но их принадлежности круговым параллелям.
но их принадлежности круговым параллелям.
Посфоение горизонтальных проекций заданных точек:
горизонтальные проекции точек 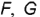 и
и 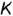 построены на вспомогательных круговых параллелях, проведенных через заданные фронтальные проекции точек.
построены на вспомогательных круговых параллелях, проведенных через заданные фронтальные проекции точек.
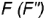
Рассмотрим графический алгоритм для построения горизонтальных проекции точек, лежащих на боковой поверхности конуса (на примере заданной точки , по их при надежности круговым параллелям:
Графический алгоритм I:
1-е действие. Провести фронтальную проекцию вспомогательной круговой параллели 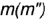 через заданную фронтальную проекцию точки
через заданную фронтальную проекцию точки 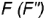 : проекция параллели — это прямая, перпендикулярная оси конуса и параллельная его основанию.
: проекция параллели — это прямая, перпендикулярная оси конуса и параллельная его основанию.
2-е действие. Провести окружность горизонтальной проекции параллели 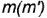 полученным радиусом
полученным радиусом 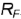 .
.
3-е действие. Построить по вертикальной линии связи горизонтальную проекцию точки 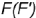 на горизонтальной проекции параллели
на горизонтальной проекции параллели 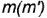
Повторить действия графического алгоритма 1 и построить аналогично горизонтальные проекции 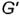 и
и 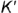 точек
точек 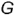 и
и 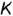 .
.
Построение профильных проекций заданных точек. Точки 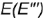 и
и 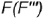 построены по принадлежности характерным образующим:
построены по принадлежности характерным образующим:
точка 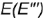 лежит на видимой характерной образующей
лежит на видимой характерной образующей 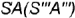 , совпадающей с осью конуса;
, совпадающей с осью конуса;
На рис. 4.72 показан пример построения горизонтальной и профильной проекции точки 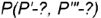 по ее принадлежности образующей
по ее принадлежности образующей 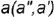 .
.
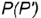
- Построение горизонтальной проекции точки по принадлежности образующей выполняется по графическому алгоритму II:
1-е действие. Провести через вершину конуса 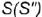 и заданную невидимую фронтальную проекцию точки
и заданную невидимую фронтальную проекцию точки 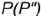 вспомогательную образующую
вспомогательную образующую 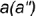
2-е действие. Построить горизонтальную проекцию образующей 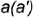 проходящей через вершину конуса
проходящей через вершину конуса 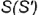 и вспомогательную точку
и вспомогательную точку 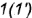 , лежащую на основании конуса.
, лежащую на основании конуса.
3-е действие. Построить по вертикальной линии связи горизонтальную проекцию точки 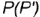 по ее принадлежности образующей
по ее принадлежности образующей 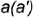 .
.
- Построение профильной проекции невидимой точки
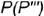 выполняется по принадлежности образующей
выполняется по принадлежности образующей 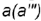 , построенной но координате
, построенной но координате 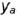 .
.
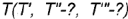
На рис. 4.72 показано построение фронтальной и профильной проекции точки по ее заданной горизонтальной проекции. Построение выполнено по приведенным алгоритмам I и II, но в обратном порядке:
1-е действие. Провести на горизонтальной проекции конуса радиусом 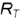 окружность вспомогательной параллели
окружность вспомогательной параллели 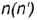 или вспомогательную образующую
или вспомогательную образующую 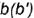 , на которых лежит горизонтальная проекция точки
, на которых лежит горизонтальная проекция точки 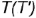 .
.
2-е действие. Построить фронтальные проекции вспомогательной параллели 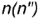 или вспомогательной образующей
или вспомогательной образующей 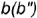 :
:
параллель 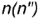 провести через вспомогательную точку
провести через вспомогательную точку 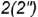 на образующей
на образующей 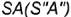 параллельно основанию конуса;
параллельно основанию конуса;
образующую 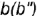 провести через вспомогательную точку
провести через вспомогательную точку 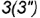 на основании конуса и вершину конуса
на основании конуса и вершину конуса 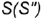
3-е действие. Построить по вертикальной линии связи фронтальную проекцию точки 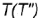 по ее принадлежности либо параллели
по ее принадлежности либо параллели 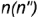 , либо образующей
, либо образующей 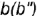 .
.
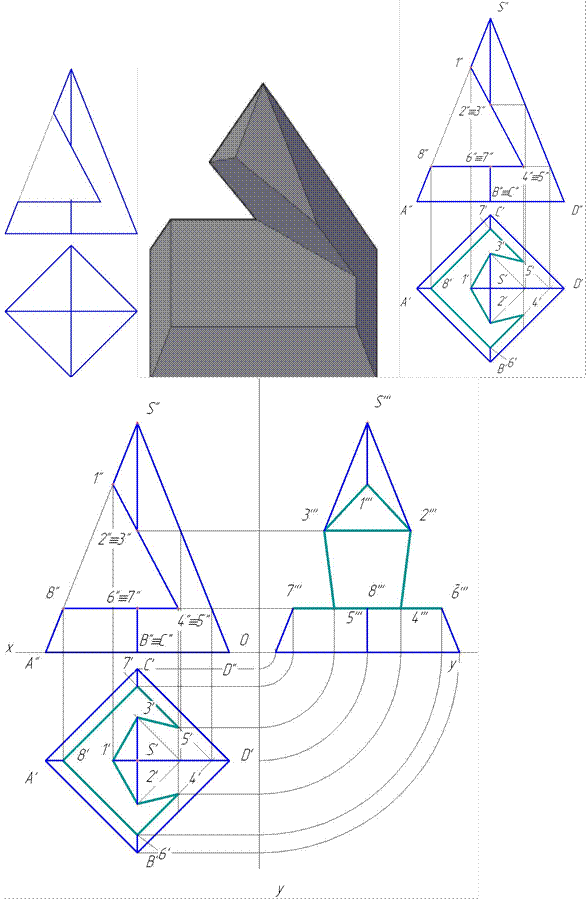
Конические сечения
Рассмотрим пять возможных случаев расположения секущей плоскости относительно оси конуса и его образующих, определяющих форму линии ее пересечения с поверхностью конуса (математические доказательства не приводятся):
1-й случаи. Гели секущая плоскость проходит через вершину конуса, то эта плоскость пересекает коническую поверхность по двум образующим  (фронтально-проецирующая плоскость
(фронтально-проецирующая плоскость  , рис. 4.73).
, рис. 4.73).

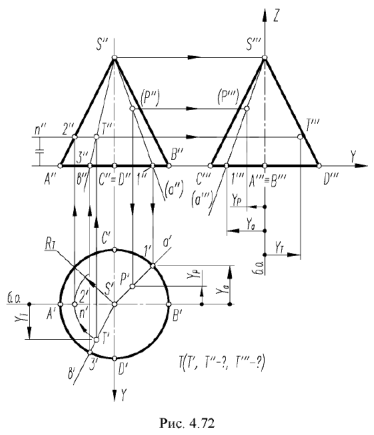
2-й случай. Если секущая плоскость расположена перпендикулярно оси конуса, то эта плоскость пересекает коническую поверхность но окружности (горизонтальная плоскость рис. 4.73).
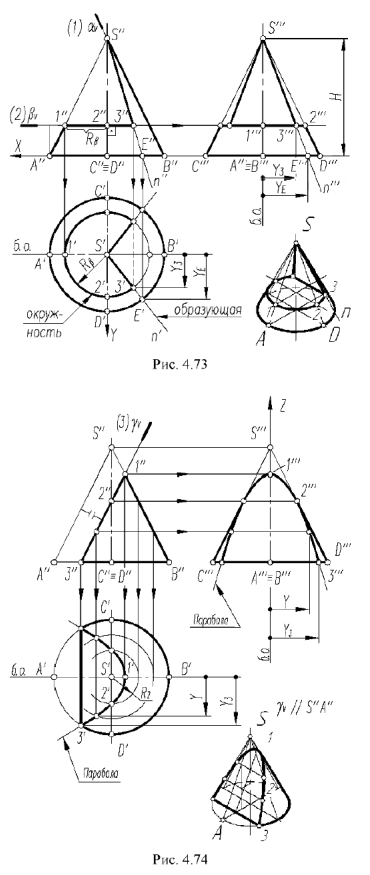
3-й случай. Если секущая плоскость расположена параллельно одной образующей конуса, то эта плоскость пересекает коническую поверхность по параболе (фронтально-проецирующая плоскость 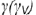 параллельна одной образующей
параллельна одной образующей  , рис.4.74).
, рис.4.74).
4-и случай. Если секущая плоскость расположена параллельно двум образующим конуса, то эта плоскость пересекает коническую поверхность по гиперболе (фронтальная плоскость 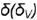 параллельна двум образующим —
параллельна двум образующим —  и
и 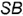 , рис.4.75).
, рис.4.75).
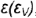
5-й случай. Если плоскость пересекает все образующие конуса под углом, отличным от прямого (или иначе, не параллельна ни одной образующей конуса), то эта плоскость пересекает коническую поверхность по эллипсу (фронтально-проецирующая плоскость ), рис 4.76).
Рассмотрим построение на проекциях конуса линии пересечения для всех пяти случаев сечений.
1-й и 2-й случаи. На рис. 4.73 показано построение проекций прямого кругового конуса с вырезом, образованным сечениями конической поверхности фронтально-проецирующей плоскостью  , проходящей через вершину конуса (1-й случай), и горизонтальной плоскостью
, проходящей через вершину конуса (1-й случай), и горизонтальной плоскостью  , расположенной перпендикулярно оси конуса (2-й случай).
, расположенной перпендикулярно оси конуса (2-й случай).
Плоскость  пересекает поверхность конуса по образующим
пересекает поверхность конуса по образующим  , горизонтальные и профильные проекции которых строятся с помощью вспомогательной точки
, горизонтальные и профильные проекции которых строятся с помощью вспомогательной точки 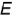 лежащей на основании конуса.
лежащей на основании конуса.

Плоскость пересекает поверхность конуса по окружности радиуса ограниченной линией 3-3 пересечения плоскостей выреза.
Построение горизонтальной и профильной проекций конуса с вырезом и оформление очерков этих проекций видно из чертежа.
3-й случай. На рис. 4.74 показано построение проекций конуса со срезом фронтально-проецирующей плоскостью 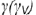 , расположенной параллельно одной образующей конуса
, расположенной параллельно одной образующей конуса  .
.
Плоскость пересекает поверхность конуса по параболе, горизонтальная и профильная проекции которой строятся по отмеченным характерным точкам 1, 2 и 3 и промежуточной точке (не обозначена)
Построение проекций этих точек выполнено по их принадлежности:
- проекции промежуточной точки построены по ее принадлежности соответствующей параллели (профильные проекции — по координате
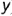 ).
).
Оформление очерков проекций видно из чертежа.
4-й случай. На рис. 4.75 показано построение проекций конуса со срезом фронтальной плоскостью 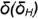 , расположенной параллельно двум образующим конуса
, расположенной параллельно двум образующим конуса  и
и  .
.
Плоскость 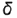 пересекает поверхность конуса по гиперболе, фронтальная проекция которой строится по отмеченным точкам 1. 2 и 3 по их принадлежности параллелям (обратный алгоритм I), а профильная проекция гиперболы проецируется в вертикальную линию и совпадает с вырожденной проекцией плоскости среза
пересекает поверхность конуса по гиперболе, фронтальная проекция которой строится по отмеченным точкам 1. 2 и 3 по их принадлежности параллелям (обратный алгоритм I), а профильная проекция гиперболы проецируется в вертикальную линию и совпадает с вырожденной проекцией плоскости среза 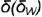
Оформление очерков проекций видно из чертежа.
На рис 4 75 на профильной проекции конуса показано положение секущей плоскости  под углом
под углом 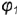 к оси конуса. При
к оси конуса. При 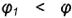 плоскость пересекает поверхность конуса также по гиперболе.
плоскость пересекает поверхность конуса также по гиперболе.
5-й ыучай. На рис. 4.76 показано построение проекции конуса со срезом фронтально-проецирующей плоскостью 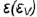 пересекающей все образующие конуса под углом
пересекающей все образующие конуса под углом 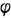 к оси, отличным от прямого.
к оси, отличным от прямого.
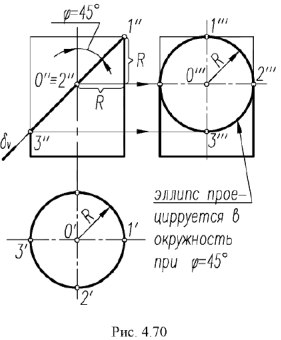
Плоскость 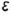 пересекает поверхность конуса по эллипсу, горизонтальная и профильная проекции которого построены по проекциям отмеченных характерных точек 1, 2, 4 и про-межуточных точек 3, взятых на середине отрезка 1-4, который является совпадающей проекцией эллипса и его большой оси. Почки 3 определяют проекции малой оси эллипса и построены на горизонтальной проекции конуса по радиусу параллели, а на профильной проекции но координате
пересекает поверхность конуса по эллипсу, горизонтальная и профильная проекции которого построены по проекциям отмеченных характерных точек 1, 2, 4 и про-межуточных точек 3, взятых на середине отрезка 1-4, который является совпадающей проекцией эллипса и его большой оси. Почки 3 определяют проекции малой оси эллипса и построены на горизонтальной проекции конуса по радиусу параллели, а на профильной проекции но координате  (алгоритм I).
(алгоритм I).
Оформление очерков проекций видно из чертежа.
. Количество взятых промежуточных точек должно быть минимальным, но достаточным, чтобы построить на проекциях конуса формы кривых второго порядка (параболы, гиперболы и эллипса), которые выполняют на чертеже по построенным характерным и промежуточным точкам с помощью лекала.
Построении проекции прямого конуса со срезами плоскостями частного положения
На рис. 4.77 показан пример построения проекций прямого круговою конуса со срезами фронтально-проецирующей плоскостью  и профильной плоскостью
и профильной плоскостью  .
.
Для построения проекций конуса со срезами следует выполнить графический алгоритм, определяющий порядок действий при решении всех подобных задач.
1-е действие. Построить на чертеже тонкими линиями по заданному радиусу основания  и высоте
и высоте 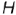 фронтальную, горизонтальную и профильную проекции конуса без срезов, а затем выполнить на его фронтальной проекции заданные срезы фронтально-проецирующей плоскостью
фронтальную, горизонтальную и профильную проекции конуса без срезов, а затем выполнить на его фронтальной проекции заданные срезы фронтально-проецирующей плоскостью  и профильной плоскостью
и профильной плоскостью  ;
;
2-е действие. Обозначить на фронтальной проекции характерные точки пересечения плоскостей срезов с образующими и основанием конуса и выпол-иить графический анализ сечений:
1. Фронтально-проецирующая плоскость  параллельна одной образующей конуса
параллельна одной образующей конуса 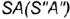 и пересекает его поверхность по участку параболы
и пересекает его поверхность по участку параболы 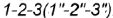 , которая проецируется в отрезок и ограничена вырожденной в точку фронтально-проецирующей линией пересечения
, которая проецируется в отрезок и ограничена вырожденной в точку фронтально-проецирующей линией пересечения 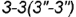 плоскостей срезов
плоскостей срезов  и
и  .
.
- Профильная плоскость
 параллельна двум образующим конуса
параллельна двум образующим конуса 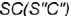 и
и 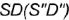 и пересекает его поверхность по участку гиперболы
и пересекает его поверхность по участку гиперболы 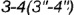 , которая проецируется в отрезок и ограничена вырожденными в точки фронтально-проецирующими линиями пересечения плоскостей срезов
, которая проецируется в отрезок и ограничена вырожденными в точки фронтально-проецирующими линиями пересечения плоскостей срезов  и
и 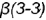 и плоскости
и плоскости  с основанием конуса (4-4).
с основанием конуса (4-4).
3-е действие. Достроить горизонтальную проекцию конуса со срезами, построив проекции плоскостей срезов по горизонтальным проекциям обозначенных точек и определить видимость плоскостей срезов:
1. Плоскость среза 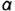 определяет видимая горизонтальная проекция участка параболы
определяет видимая горизонтальная проекция участка параболы 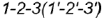 построенной по горизонтальным проекциям обозначенных точек:
построенной по горизонтальным проекциям обозначенных точек:
- Плоскость среза
 определяет вертикальный видимый отрезок
определяет вертикальный видимый отрезок  вырожденной в линию проекции профильной плоскости, точки
вырожденной в линию проекции профильной плоскости, точки 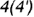 которой лежат на очерковой окружности основания конуса.
которой лежат на очерковой окружности основания конуса.
. Поскольку горизонтальная проекция имеет вертикальную симметрию, точки обозначены на одной ее половине (нижней).
4-е действие. Выполнить графический анализ построенной горизонтальной проекции конуса для определения ее очерка и внутреннего контура:
- Горизонтальный очерк определяют участок окружности и отрезок
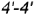 .
. - Внутренний контур определяет видимый участок параболы
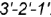 .
.
5-е действие. Достроить профильную проекцию конуса со срезами, пост-роив проекции плоскостей срезов по профильным проекциям обозначенных точек, и определить видимость плоскостей срезов:
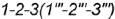
1. Плоскость среза а определяет видимый участок параболы , построенный по профильным проекциям обозначенных точек:
- Плоскость среза
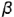 определяют видимые участки гиперболы
определяют видимые участки гиперболы 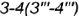 , ограниченные видимым отрезком
, ограниченные видимым отрезком 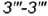 (построен) и видимым отрезком
(построен) и видимым отрезком 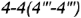 . точки которого построены но координате
. точки которого построены но координате  .
.
6-е действие. Выполнить графический анализ построенной профильной проекции конуса для определения ее очерка и внутреннего контура.
- Профильный очерк определяют:
- Внутренний контур определяют:
7-е действие. Оформить чертеж конуса, выполнив толстыми сплошными линиями очерки и видимый внутренний контур каждой его проекции (оставить сплошными тонкими линиями полные очерки проекций и линии построения).
Эта теория взята со страницы задач по начертательной геометрии:
Возможно эти страницы вам будут полезны:





















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
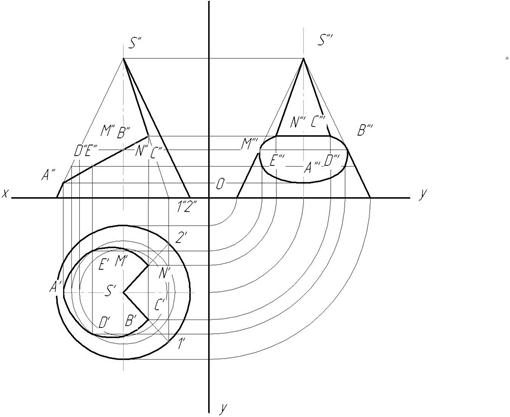
Сечение поверхности конуса плоскостью общего положения
При пересечении прямого кругового конуса с плоскостью могут образовываться следующие кривые второго порядка: окружность, эллипс, гипербола и парабола. Вид этих кривых зависит от угла наклона секущей плоскости к оси конической поверхности.
Ниже мы рассмотрим задачу, в которой требуется построить проекции и натуральную величину сечения конуса ω плоскостью α . Начальные данные представлены на рисунке ниже.

Определение высшей и низшей точки сечения. Границы видимости
Построение линии пересечения следует начинать с нахождения её характерных точек. Они определяют границы сечения и его видимость по отношению к наблюдателю.
Через ось конической поверхности проведем вспомогательную плоскость γ, параллельную П2. Она пересекает конус ω по двум образующим, а плоскость α по фронтали fγ. Точки 1 и 2 пересечения fγ с образующими являются граничными точками. Они делят сечение на видимую и невидимую части.

Определим высшую и низшую точки линии пересечения. Для этого через ось конуса перпендикулярно h0α введем дополнительную секущую плоскость β. Она пересекает коническую поверхность по образующим SL и SK, а плоскость α по прямой MN. Искомые точки 3 = SL ∩ MN и 4 = SK ∩ MN определяют большую ось эллипса. Его центр находится в точке O, которая делит отрезок 3–4 пополам.
Определение промежуточных точек и построение проекций эллипса
Чтобы построить проекции сечения наиболее точно, найдем ряд дополнительных точек. В случае с эллипсом целесообразно определить величину его малого диаметра. Для этого через центр O проводим вспомогательную горизонтальную плоскость δ. Она пересекает коническую поверхность по окружности диаметром AB, а плоскость α – по горизонтали hδ. Строим горизонтальные проекции окружности и прямой hδ. Их пересечение определяет точки 5′ и 6′ малого диаметра эллипса.
Для построения промежуточных точек 7 и 8 вводим вспомогательную горизонтальную плоскость ε. Проекции 7′ и 8′ определяются аналогично 5′ и 6′, как это показано на рисунке.

Соединив найденные точки плавной кривой, мы получили контур эллиптического сечения. На рисунке он обозначен красным цветом. Фронтальная проекция контура меняет свою видимость в точках 1 и 2, как это было отмечено выше.
Построение натуральной величины сечения методом совмещения
Чтобы найти натуральную величину сечения, повернем плоскость α до совмещения её с горизонтальной плоскостью. В качестве оси вращения будем использовать след h0α. Его положение в процессе преобразований останется неизменным.

Построение начинается с определения направления фронтального следа f1α. На прямой f0α возьмем произвольную точку E и определим её проекцию E’. Из E’ опустим перпендикуляр к h0α. Пересечение данного перпендикуляра с окружностью радиусом XαE» определяет положение точки E’1. Через Xα и E’1 проводим f1α.
Строим проекцию горизонтали h’1δ ∥ h0α, как это показано на рисунке. Точки O’1 и 5′1, 6′1 лежат на пересечении h’1δ с прямыми, проведенными перпендикулярно h0α из O’ и 5′, 6′. Аналогично на горизонтали h’1ε находим 7′1 и 8′1.
Строим проекции фронталей f’1γ ∥ f1α, f’3 ∥ f1α и f’4 ∥ f1α. Точки 1′1, 2′1, 3′1 и 4′1 лежат на пересечении этих фронталей с перпендикулярами, восстановленными к h0α из 1′, 2′, 3′ и 4′ соответственно.
Точка принадлежит
поверхности конуса, если она принадлежит
линии этой поверхности.
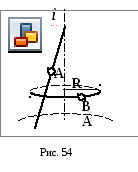
В качестве
линии берется либо образующая конуса
(для точки А), либо параллель, проходящая
через данную точку (для точки В). Радиус
параллели R
замеряют от оси вращения до образующей
конуса (рис.54).

Дано:
– прямой круговой конус 1,2,3,4
Построить:
11
,21
, 31,
41 -?
.



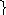

1.
Постройте горизонтальную проекцию
точки 1.
Эта точка является
опорной точкой, так как принадлежит
очерку поверхности – главному фронтальному
меридиану.
Очерковая
образующая проецируется на горизонтальную
плоскость проекций в виде отрезка
прямой, проходящей через горизонтальную
осевую.
Спроецируйте
точку 1 на горизонтальную проекцию
очерковой образующей.


2.
Постройте горизонтальную проекцию
точки 2.
Точка 2 является
опорной точкой, так как принадлежит
очерку поверхности – экватору.
Экватор
проецируется на горизонтальную плоскость
проекций в виде окружности.



3.
Спроецируйте
точку 2 на горизонтальную проекцию
экватора.
Так как
вертикальная линия связи дважды
пересекает горизонтальную проекцию
экватора, получают две проекции 21
и 21I.
Точка 2 – видимая,
а 2I
– невидимая.

4.
Постройте горизонтальную проекцию
точки 3.
Для построения
недостающей проекции точки воспользуйтесь
вспомогательной линией – образующей
конуса.



5.
Постройте
горизонтальную проекцию образующей
конуса (задача имеет два решения).



6.
Спроецируйте
точку 3 на горизонтальные проекции
вспомогательных образующих. Для этого
проведите из фронтальной проекции
точки 32
вертикальную линию связи до пересечения
с горизонтальными проекциями
вспомогательных образующих. Получится
две проекции 31
и 31I.

7.
Постройте горизонтальную проекцию
точки 4.



Для построения
недостающей проекции точки воспользуйтесь
вспомогательной линией – параллелью.
8.
Через
фронтальную проекцию точки 42
проведите параллель (фронтальная
проекция параллели – отрезок прямой).
9. Замерьте радиус
параллели R.
10. Горизонтальную
проекцию параллели проведите радиусом
R
11. Спроецируйте
точку 4 на горизонтальную проекцию
параллели. Получится две проекции 41
и 41I.

7.4 Цилиндр
Цилиндр
– геометрическое тело, ограниченное
цилиндрической поверхностью и двумя
плоскостями.
Цилиндрическая
поверхность
образуется при вращении прямой линии
(образующей) вокруг неподвижной оси i,
параллельной образующей (рис.55).



1.Спроецируйте
нижнее основание цилиндра
на горизонтальную плоскость проекций.
Получится окружность, а на фронтальной
и профильной проекции – отрезок прямой,
равный диаметру окружности. Аналогично
спроецируйте верхнее основание.
2.Спроецируйте
контурные образующие на
фронтальную и профильную плоскости
проекций в виде прямых, перпендикулярных
к проекции основания и равных высоте
цилиндра. На П1
образующие проецируются в точки.
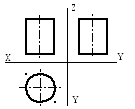
3.Постройте
комплексный чертеж цилиндра.


Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

Коническая поверхность вращения
Прямой круговой конус
Коническая поверхность вращения — это линейчатая поверхность, образованная вращением прямолинейной образующей, которая пересекает криво-линейную направляющую (окружность) и проходит через неподвижную точку оси вращения, называемую вершиной.
Конусом называют геометрическое тело, ограниченное конической поверхностью и плоскостью основания, пересекающего все его образующие.

Конус называют прямым, если ось вращения перпендикулярна его основанию. Конус называют круговым, так как направляющей является окружность Конус с двумя параллельными основаниями, т.е. конус со срезанной вершиной, называют усеченным.
Построение проекций прямого кругового конуса
На рис. 4.71 показан пример построения проекций прямою кругового конуса с горизонтально-проецирующей осью вращения  , заданной высотой
, заданной высотой 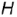 и основанием радиусом
и основанием радиусом  .
.
Для построения проекций конуса требуется выполнить графо-аналитические действия в следующем порядке:
1-е действие. По заданному условию построить горизонтальную проекцию очерка прямого кругового конуса, которая представляет собой окружность заданного радиуса  с вершиной
с вершиной 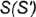 , совпадающей с осью вращения
, совпадающей с осью вращения 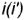 .
.

2-е действие. Выполнить графический анализ построенной горизонтальной проекции конуса:
- Круг радиуса
 является невидимой проекцией основания конуса.
является невидимой проекцией основания конуса. - Круг радиуса
 с вершиной конуса
с вершиной конуса 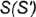 является видимой проекцией боковой поверхности конуса.
является видимой проекцией боковой поверхности конуса. - Обозначить на горизонтальной проекции характерные образующие конуса
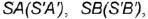
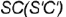 и
и 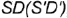 которые будут определять очерки фронтальной и профильной проекций конуса.
которые будут определять очерки фронтальной и профильной проекций конуса.
3-е действие. Построить фронтальную проекцию (очерк) конуса, которая представляет собой треугольник 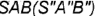 заданной высоты
заданной высоты 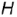 , ограниченный:
, ограниченный:
4-е действие. Построить профильную проекцию (очерк) конуса:
- ‘Задать на окружности горизонтальной проекции конуса положение базовой линии (б.о.), совпадающей с горизонтальной линией оси этой окружности.
- Выбрать положение базовой оси
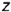 (б.о.), которая будет совпадать с вертикальной осью
(б.о.), которая будет совпадать с вертикальной осью 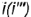 вращения на профильной проекции конуса.
вращения на профильной проекции конуса. - Профильная проекция конуса представляет собой треугольник
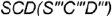 ограниченный:
ограниченный:
слева и справа очерковыми образующими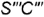 и
и 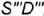 построенными по координате
построенными по координате 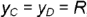 :
:
вершиной  , лежащей на базовой оси
, лежащей на базовой оси  ; горизонтальным отрезком проекцией основания;
; горизонтальным отрезком проекцией основания;
профильными проекциями характерных образующих 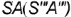 и
и 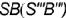 , которые совпадают с осью вращения конуса
, которые совпадают с осью вращения конуса 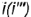 .
.
!!! Запомните характерные признаки очерков прямого круговою конуса на чертеже — окружность основания и два треугольника.
!!! Характерные признаки очерков прямого кругового усеченного конуса окружность основания и две равнобокие трапеции.
Построение проекции точек, лежащих на поверхности конуса
Принадлежность точки поверхности конуса определяется ее принадлежностью образующей поверхности и принадлежностью круговым параллелям (окружностям), по которой точка вращается вокруг оси конуса. Следовательно, проекции точки можно строить либо по принадлежности образующей, либо по принадлежности круговой параллели.
На рис. 4.71 показан пример построения горизонтальных и профильных проекций точек 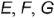 и
и 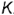 , заданных фронтальными проекциям
, заданных фронтальными проекциям 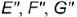 и
и 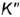 но их принадлежности круговым параллелям.
но их принадлежности круговым параллелям.
Посфоение горизонтальных проекций заданных точек:
горизонтальные проекции точек 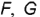 и
и 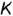 построены на вспомогательных круговых параллелях, проведенных через заданные фронтальные проекции точек.
построены на вспомогательных круговых параллелях, проведенных через заданные фронтальные проекции точек.
Рассмотрим графический алгоритм для построения горизонтальных проекции точек, лежащих на боковой поверхности конуса (на примере заданной точки 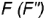 , по их при надежности круговым параллелям:
, по их при надежности круговым параллелям:
Графический алгоритм I:
1-е действие. Провести фронтальную проекцию вспомогательной круговой параллели 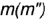 через заданную фронтальную проекцию точки
через заданную фронтальную проекцию точки 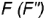 : проекция параллели — это прямая, перпендикулярная оси конуса и параллельная его основанию.
: проекция параллели — это прямая, перпендикулярная оси конуса и параллельная его основанию.
2-е действие. Провести окружность горизонтальной проекции параллели 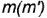 полученным радиусом
полученным радиусом 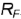 .
.
3-е действие. Построить по вертикальной линии связи горизонтальную проекцию точки 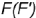 на горизонтальной проекции параллели
на горизонтальной проекции параллели 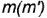
Повторить действия графического алгоритма 1 и построить аналогично горизонтальные проекции 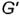 и
и 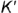 точек
точек 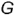 и
и 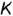 .
.
Построение профильных проекций заданных точек. Точки 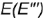 и
и 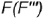 построены по принадлежности характерным образующим:
построены по принадлежности характерным образующим:
точка 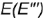 лежит на видимой характерной образующей
лежит на видимой характерной образующей 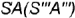 , совпадающей с осью конуса;
, совпадающей с осью конуса;
На рис. 4.72 показан пример построения горизонтальной и профильной проекции точки 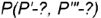 по ее принадлежности образующей
по ее принадлежности образующей 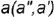 .
.
- Построение горизонтальной проекции точки
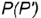 по принадлежности образующей выполняется по графическому алгоритму II:
по принадлежности образующей выполняется по графическому алгоритму II:
1-е действие. Провести через вершину конуса 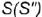 и заданную невидимую фронтальную проекцию точки
и заданную невидимую фронтальную проекцию точки 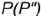 вспомогательную образующую
вспомогательную образующую 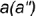
2-е действие. Построить горизонтальную проекцию образующей 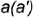 проходящей через вершину конуса
проходящей через вершину конуса 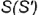 и вспомогательную точку
и вспомогательную точку 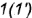 , лежащую на основании конуса.
, лежащую на основании конуса.
3-е действие. Построить по вертикальной линии связи горизонтальную проекцию точки 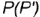 по ее принадлежности образующей
по ее принадлежности образующей 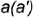 .
.
- Построение профильной проекции невидимой точки
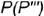 выполняется по принадлежности образующей
выполняется по принадлежности образующей 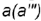 , построенной но координате
, построенной но координате 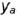 .
.
На рис. 4.72 показано построение фронтальной и профильной проекции точки 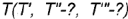 по ее заданной горизонтальной проекции. Построение выполнено по приведенным алгоритмам I и II, но в обратном порядке:
по ее заданной горизонтальной проекции. Построение выполнено по приведенным алгоритмам I и II, но в обратном порядке:
1-е действие. Провести на горизонтальной проекции конуса радиусом 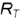 окружность вспомогательной параллели
окружность вспомогательной параллели 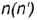 или вспомогательную образующую
или вспомогательную образующую 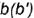 , на которых лежит горизонтальная проекция точки
, на которых лежит горизонтальная проекция точки 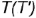 .
.
2-е действие. Построить фронтальные проекции вспомогательной параллели 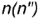 или вспомогательной образующей
или вспомогательной образующей 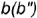 :
:
параллель 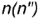 провести через вспомогательную точку
провести через вспомогательную точку 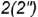 на образующей
на образующей 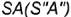 параллельно основанию конуса;
параллельно основанию конуса;
образующую 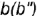 провести через вспомогательную точку
провести через вспомогательную точку 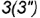 на основании конуса и вершину конуса
на основании конуса и вершину конуса 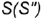
3-е действие. Построить по вертикальной линии связи фронтальную проекцию точки 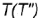 по ее принадлежности либо параллели
по ее принадлежности либо параллели 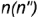 , либо образующей
, либо образующей 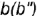 .
.

Конические сечения
Рассмотрим пять возможных случаев расположения секущей плоскости относительно оси конуса и его образующих, определяющих форму линии ее пересечения с поверхностью конуса (математические доказательства не приводятся):

1-й случаи. Гели секущая плоскость проходит через вершину конуса, то эта плоскость пересекает коническую поверхность по двум образующим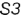 (фронтально-проецирующая плоскость
(фронтально-проецирующая плоскость  , рис. 4.73).
, рис. 4.73).
2-й случай. Если секущая плоскость расположена перпендикулярно оси конуса, то эта плоскость пересекает коническую поверхность но окружности (горизонтальная плоскость  рис. 4.73).
рис. 4.73).
3-й случай. Если секущая плоскость расположена параллельно одной образующей конуса, то эта плоскость пересекает коническую поверхность по параболе (фронтально-проецирующая плоскость 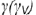 параллельна одной образующей
параллельна одной образующей  , рис.4.74).
, рис.4.74).
4-и случай. Если секущая плоскость расположена параллельно двум образующим конуса, то эта плоскость пересекает коническую поверхность по гиперболе (фронтальная плоскость 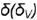 параллельна двум образующим —
параллельна двум образующим —  и
и 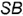 , рис.4.75).
, рис.4.75).
5-й случай. Если плоскость пересекает все образующие конуса под углом, отличным от прямого (или иначе, не параллельна ни одной образующей конуса), то эта плоскость пересекает коническую поверхность по эллипсу (фронтально-проецирующая плоскость 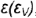 ), рис 4.76).
), рис 4.76).
Рассмотрим построение на проекциях конуса линии пересечения для всех пяти случаев сечений.
1-й и 2-й случаи. На рис. 4.73 показано построение проекций прямого кругового конуса с вырезом, образованным сечениями конической поверхности фронтально-проецирующей плоскостью  , проходящей через вершину конуса (1-й случай), и горизонтальной плоскостью
, проходящей через вершину конуса (1-й случай), и горизонтальной плоскостью  , расположенной перпендикулярно оси конуса (2-й случай).
, расположенной перпендикулярно оси конуса (2-й случай).
Плоскость  пересекает поверхность конуса по образующим
пересекает поверхность конуса по образующим  , горизонтальные и профильные проекции которых строятся с помощью вспомогательной точки
, горизонтальные и профильные проекции которых строятся с помощью вспомогательной точки 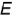 лежащей на основании конуса.
лежащей на основании конуса.
Плоскость  пересекает поверхность конуса по окружности радиуса ограниченной линией 3-3 пересечения плоскостей выреза.
пересекает поверхность конуса по окружности радиуса ограниченной линией 3-3 пересечения плоскостей выреза.
Построение горизонтальной и профильной проекций конуса с вырезом и оформление очерков этих проекций видно из чертежа.
3-й случай. На рис. 4.74 показано построение проекций конуса со срезом фронтально-проецирующей плоскостью 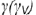 , расположенной параллельно одной образующей конуса
, расположенной параллельно одной образующей конуса  .
.
Плоскость пересекает поверхность конуса по параболе, горизонтальная и профильная проекции которой строятся по отмеченным характерным точкам 1, 2 и 3 и промежуточной точке (не обозначена)
Построение проекций этих точек выполнено по их принадлежности:
- проекции промежуточной точки построены по ее принадлежности соответствующей параллели (профильные проекции — по координате
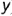 ).
).
Оформление очерков проекций видно из чертежа.
4-й случай. На рис. 4.75 показано построение проекций конуса со срезом фронтальной плоскостью 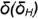 , расположенной параллельно двум образующим конуса
, расположенной параллельно двум образующим конуса  и
и  .
.
Плоскость 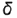 пересекает поверхность конуса по гиперболе, фронтальная проекция которой строится по отмеченным точкам 1. 2 и 3 по их принадлежности параллелям (обратный алгоритм I), а профильная проекция гиперболы проецируется в вертикальную линию и совпадает с вырожденной проекцией плоскости среза
пересекает поверхность конуса по гиперболе, фронтальная проекция которой строится по отмеченным точкам 1. 2 и 3 по их принадлежности параллелям (обратный алгоритм I), а профильная проекция гиперболы проецируется в вертикальную линию и совпадает с вырожденной проекцией плоскости среза 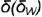
Оформление очерков проекций видно из чертежа.

На рис 4 75 на профильной проекции конуса показано положение секущей плоскости 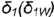 под углом
под углом 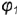 к оси конуса. При
к оси конуса. При 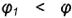 плоскость пересекает поверхность конуса также по гиперболе.
плоскость пересекает поверхность конуса также по гиперболе.
5-й ыучай. На рис. 4.76 показано построение проекции конуса со срезом фронтально-проецирующей плоскостью 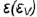 пересекающей все образующие конуса под углом
пересекающей все образующие конуса под углом 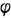 к оси, отличным от прямого.
к оси, отличным от прямого.
Плоскость 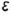 пересекает поверхность конуса по эллипсу, горизонтальная и профильная проекции которого построены по проекциям отмеченных характерных точек 1, 2, 4 и про-межуточных точек 3, взятых на середине отрезка 1-4, который является совпадающей проекцией эллипса и его большой оси. Почки 3 определяют проекции малой оси эллипса и построены на горизонтальной проекции конуса по радиусу параллели, а на профильной проекции но координате
пересекает поверхность конуса по эллипсу, горизонтальная и профильная проекции которого построены по проекциям отмеченных характерных точек 1, 2, 4 и про-межуточных точек 3, взятых на середине отрезка 1-4, который является совпадающей проекцией эллипса и его большой оси. Почки 3 определяют проекции малой оси эллипса и построены на горизонтальной проекции конуса по радиусу параллели, а на профильной проекции но координате 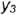 (алгоритм I).
(алгоритм I).
Оформление очерков проекций видно из чертежа.
!!! Количество взятых промежуточных точек должно быть минимальным, но достаточным, чтобы построить на проекциях конуса формы кривых второго порядка (параболы, гиперболы и эллипса), которые выполняют на чертеже по построенным характерным и промежуточным точкам с помощью лекала.
Построении проекции прямого конуса со срезами плоскостями частного положения
На рис. 4.77 показан пример построения проекций прямого круговою конуса со срезами фронтально-проецирующей плоскостью  и профильной плоскостью
и профильной плоскостью  .
.

Для построения проекций конуса со срезами следует выполнить графический алгоритм, определяющий порядок действий при решении всех подобных задач.
1-е действие. Построить на чертеже тонкими линиями по заданному радиусу основания  и высоте
и высоте  фронтальную, горизонтальную и профильную проекции конуса без срезов, а затем выполнить на его фронтальной проекции заданные срезы фронтально-проецирующей плоскостью
фронтальную, горизонтальную и профильную проекции конуса без срезов, а затем выполнить на его фронтальной проекции заданные срезы фронтально-проецирующей плоскостью  и профильной плоскостью
и профильной плоскостью  ;
;
2-е действие. Обозначить на фронтальной проекции характерные точки пересечения плоскостей срезов с образующими и основанием конуса и выпол-иить графический анализ сечений:
1. Фронтально-проецирующая плоскость  параллельна одной образующей конуса
параллельна одной образующей конуса 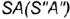 и пересекает его поверхность по участку параболы
и пересекает его поверхность по участку параболы 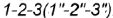 , которая проецируется в отрезок и ограничена вырожденной в точку фронтально-проецирующей линией пересечения
, которая проецируется в отрезок и ограничена вырожденной в точку фронтально-проецирующей линией пересечения 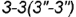 плоскостей срезов
плоскостей срезов  и
и  .
.
- Профильная плоскость
 параллельна двум образующим конуса
параллельна двум образующим конуса 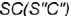 и
и 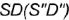 и пересекает его поверхность по участку гиперболы
и пересекает его поверхность по участку гиперболы 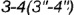 , которая проецируется в отрезок и ограничена вырожденными в точки фронтально-проецирующими линиями пересечения плоскостей срезов
, которая проецируется в отрезок и ограничена вырожденными в точки фронтально-проецирующими линиями пересечения плоскостей срезов  и
и 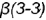 и плоскости
и плоскости  с основанием конуса (4-4).
с основанием конуса (4-4).
3-е действие. Достроить горизонтальную проекцию конуса со срезами, построив проекции плоскостей срезов по горизонтальным проекциям обозначенных точек и определить видимость плоскостей срезов:
1. Плоскость среза 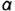 определяет видимая горизонтальная проекция участка параболы
определяет видимая горизонтальная проекция участка параболы 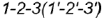 построенной по горизонтальным проекциям обозначенных точек:
построенной по горизонтальным проекциям обозначенных точек:
- Плоскость среза
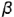 определяет вертикальный видимый отрезок
определяет вертикальный видимый отрезок 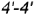 вырожденной в линию проекции профильной плоскости, точки
вырожденной в линию проекции профильной плоскости, точки 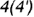 которой лежат на очерковой окружности основания конуса.
которой лежат на очерковой окружности основания конуса.
!!! Поскольку горизонтальная проекция имеет вертикальную симметрию, точки обозначены на одной ее половине (нижней).
4-е действие. Выполнить графический анализ построенной горизонтальной проекции конуса для определения ее очерка и внутреннего контура:
- Горизонтальный очерк определяют участок окружности и отрезок
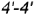 .
. - Внутренний контур определяет видимый участок параболы
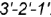 .
.
5-е действие. Достроить профильную проекцию конуса со срезами, пост-роив проекции плоскостей срезов по профильным проекциям обозначенных точек, и определить видимость плоскостей срезов:
1. Плоскость среза а определяет видимый участок параболы 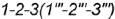 , построенный по профильным проекциям обозначенных точек:
, построенный по профильным проекциям обозначенных точек:
- Плоскость среза
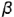 определяют видимые участки гиперболы
определяют видимые участки гиперболы 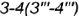 , ограниченные видимым отрезком
, ограниченные видимым отрезком 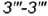 (построен) и видимым отрезком
(построен) и видимым отрезком  . точки которого построены но координате
. точки которого построены но координате  .
.
6-е действие. Выполнить графический анализ построенной профильной проекции конуса для определения ее очерка и внутреннего контура.
- Профильный очерк определяют:
- Внутренний контур определяют:
7-е действие. Оформить чертеж конуса, выполнив толстыми сплошными линиями очерки и видимый внутренний контур каждой его проекции (оставить сплошными тонкими линиями полные очерки проекций и линии построения).
Эта теория взята со страницы задач по начертательной геометрии:
- Решение задач по начертательной геометрии
Возможно эти страницы вам будут полезны:

Пересечение прямой с конусом
Пересечение прямой с конусом – это задача по определению точек встречи прямой с поверхностью конуса.
Поверхность конуса состоит:
– боковой поверхности представляющей собой поверхность вращения;
– поверхности основания представляющей собой окружность .
Пересечение прямой с конусом: d ∩ α.
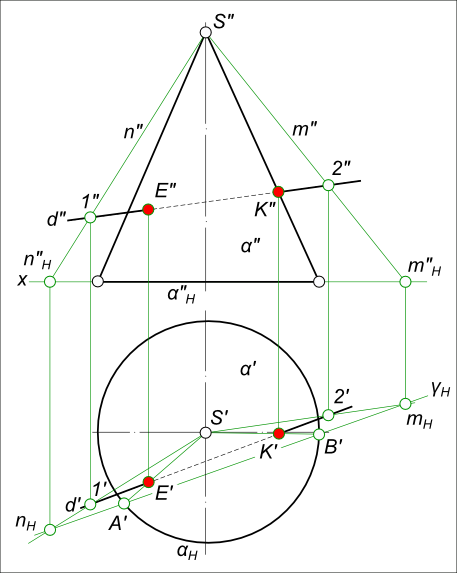
Пересечение прямой с конусом
Здесь прямая d занимают общее положение и поверхность прямого кругового конуса α формируется прямыми из вершины S. Решать задачу на пересечение прямой с конусом следует, применяя алгоритм пересечения прямой с поверхностью:
– Заключаем прямую d в вспомогательную плоскость γ, которая также проходит через вершину конуса S;
– Находим точки пересечения этой плоскости с основанием конуса, для чего строим горизонтальный след плоскости – γH по следам прямых nH и mH:
γH ∩ αH = A`, B`.
Соединив полученные точки с вершиной конуса S` прямыми линиями, находим линии пересечения этой плоскости с боковой поверхностью конуса S`A`, S`B`, которые пересекаются с прямой d:
– S`A` ∩ d` = E` ⇒ E”;
– S`B` ∩ d` = K` ⇒ K”.
Пересечение прямой с конусом – это задача по определению видимости:
– для горизонтальной плоскости проекций производим с помощью конкурирующих точек:
– перемещаясь вверх по линиям связи точек пересечения αH и прямой d` находим, что соответствующие точки прямой d” находится выше основания конуса α”H, а это означает что соответствующие им точки прямой d` на горизонтальной плоскости проекций видимы.
– для фронтальной плоскости проекций производим исходя из того, что образующие находящиеся:
– за очерковыми образующими не видимы;
– перед очерковыми образующими видимы.
Образующие S`A` и S`B` находятся перед очерковыми образующими и следовательно они видимы.
+
Конус с отверстием треугольника
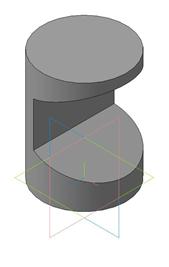
Построить три проекции тела с вырезом
Пример 1. Вырез на конусе (рис.142).
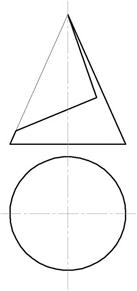
 Рис.142
Рис.142
Вырез произведен двумя плоскостями. Одна проходит через вершину конуса и рассечет его поверхность по образующим. Вторая плоскость – фронтально-проецирующая, линия пересечения – часть эллипса, ограниченная прямой принадлежащей линии пересечения плоскостей.
1. Отметим фронтальные проекции характерных точек для построения выреза – А”, В”, С”, M»,N» (рис. 143).
2. Точки D и Е выбраны произвольно для построения эллипса, т.к. линия среза от А до СN представляет собой часть эллипса.
3. Найдем горизонтальные проекции точек А, В, С, D, Е, N. Точки лежат на поверхности конуса, а значит, они лежат на линиях, принадлежащих поверхности конуса. Горизонтальные проекции точек М и В, D и E найдены на окружностях, принадлежащих поверхности конуса. Точки С и N – на образующих S1 и S2.
4. Соединяем полученные горизонтальные проекции. S’С’ и S’N‘ – прямые, C’, B’, D’, A’, E’, M’, N’ – кривая линия – часть эллипса (рис. 142).
Рис.143 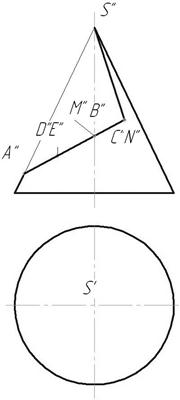
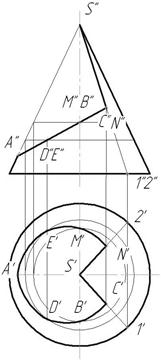 Рис.144
Рис.144
Строим профильную проекцию конуса и профильные проекции точек. Соединяем их (рис.145).
Пример 2. Вырез на цилиндре (рис.146).
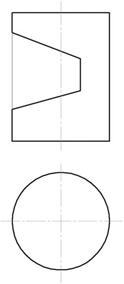
Вырез произведен тремя плоскостями. Наклонные фронтально-проецирующие плоскости рассекут цилиндр по части эллипса, ограниченного прямой. Плоскость, параллельная оси вращения, пересекает поверхность цилиндра по образующим.
1. Отметим на фронтальной проекции выреза фронтальные проекции A»,F»,G»,K»,L»,P». Характерные точки D»,E» ,M»,N» – на оси симметрии цилиндра, B»,C»,T»,V » – отмечены произвольно на линии, принадлежащей поверхности цилиндра. Все точки принадлежат боковой поверхности цилиндра, которая проецируется в окружность на горизонтальной плоскости проекций. Поэтому все горизонтальные проекции точек принадлежат этой окружности (рис.147).
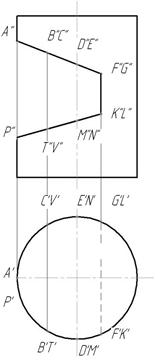 Рис.147
Рис.147
Найдем профильные проекции всех точек. Затем полученные точки соединяем. Линия GECABDF – часть эллипса, FK и GL отрезки прямых, GF и KL-отрезки прямых, LNVPTMK – часть эллипса (рис. 148).
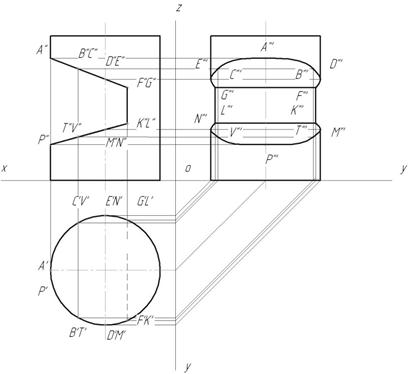 Рис.148
Рис.148
Пример 3. Вырез на призме (рис.149).
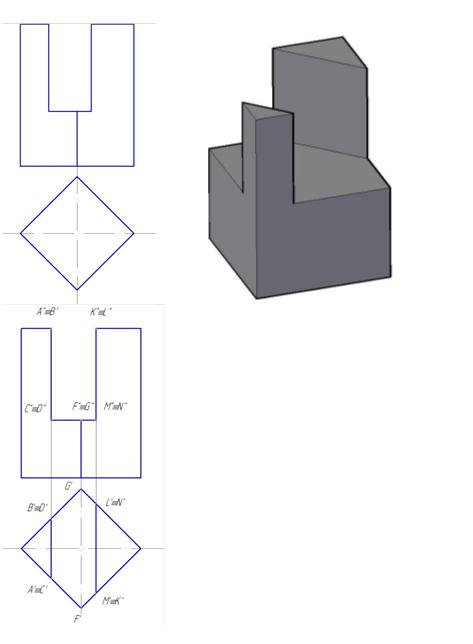 Рис.149
Рис.149 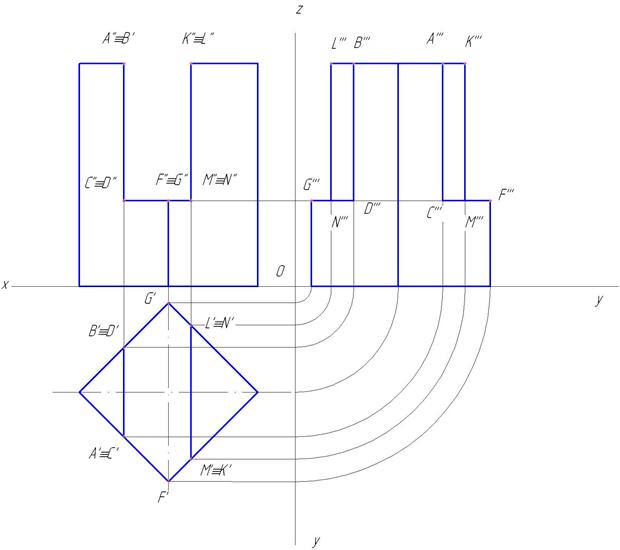 Hbc
Hbc
Пример 4. Вырез на пирамиде (рис.150).
Пример 5. Вырез на сфере (рис. 151
 p>
p>
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: На стипендию можно купить что-нибудь, но не больше. 9122 –  | 7289 –
| 7289 –  или читать все.
или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Пошаговое руководство решения задачи №6 — построение линии пересечения сферической поверхности от сквозного призматического выреза.
Необходимо построить линию пересечения сферической поверхности (шара) от сквозного призматического выреза, состоящего из четырех граней (проецирующих плоскостей). Фронтальная проекция линии пересечения заданных поверхностей (шара и многогранника) задана исходным чертежом, требуется построить ее в горизонтальную и профильную проекции.
Для решения такой задачи по начертательной геометрии необходимо знать:
— построение трех проекций сферической поверхности (шара) по заданным координатам, на комплексном чертеже;
— построение линии пересечения шаровой поверхности с гранным телом;
— частные случаи построения линии пересечения шаровой поверхности с проецирующей плоскостью.
Порядок решения Задачи
Рис.6.1
1. В правой части листа формата A3 наносятся оси координат и согласно варианту задания строится фронтальная, горизонтальная и профильная проекции сферы (шара) заданного радиуса.
По координатам точек, взятым из таблицы по своему варианту, наносятся вершины сквозного четырехгранного выреза во фронтальной проекции (рис.6.1).
2. Решение задачи заключается в построении горизонтальной и профильной проекции линии пересечения данного выреза.
Прежде чем приступить к построению этих проекций, необходимо вспомнить некоторые частные случаи сечений шаровой поверхности от проецирующей плоскости (сквозное отверстие можно рассматривать как гранное тело, образованное четырьмя плоскостями), а именно:
(а) если плоскость во фронтальной проекции рассекает шаровую поверхность параллельно экватору, то в горизонтальной проекции это сечение проецируется в виде окружности с радиусом, взятым в этом сечении от оси вращения шара до очерка, а в профильной проекции это сечение проецируется в виде прямой линии;
(b) если плоскость во фронтальной проекции рассекает шаровую поверхность перпендикулярно экватору, то в горизонтальной проекции это сечение проецируется в виде прямой линии, а в профильной — в виде окружности с радиусом, взятым тем же способом что и в первом случае;
(c) если плоскость во фронтальной проекции рассекает шаровую поверхность под некоторым (отличным от 0 и 90 градусов) углом к экватору, то в горизонтальной и фронтальной проекциях это сечение будет проецироваться в виде эллипса. Построение эллипса осуществляется по опорным (характерным) и некоторым промежуточным, взятым произвольно, точкам;
(d) все точки фронтальной проекции сферы, расположенные на очерке, в горизонтальной проекции будут проецироваться на экваторе, а в профильной — на главном меридиане;
(e) все точки фронтальной проекции сферы, расположенные на экваторе, в горизонтальной проекции будут проецироваться на очерке, а в профильной — на экваторе;
(f) все точки фронтальной проекции сферы, расположенные на главном меридиане, в горизонтальной проекции будут проецироваться также на главном меридиане, а в профильной — на очерке сферы.
Рис.6.2
3. С учетом приведенных частных случаев сечений построение выреза в горизонтальной и профильной проекциях не вызывает особых затруднений и начинается с определения характерных (опорных) точек сквозного выреза во фронтальной проекции. Этими точками являются А, В, С, D. Тогда берем проекцию стороны призмы B’C’ и рассматриваем ее как проецирующую плоскость ’, рассекающую шар параллельно экватору, — строим в горизонтальной проекции окружность с радиусом r1 взятым в этой плоскости, от оси шара до очерка. Проецируем на эту окружность точки B’ и C’, получаем B и C — их горизонтальные проекции. Вполне очевидно, что этих точек будет по две (точки входа и выхода), т.к. отверстие сквозное.
Аналогичным способом строится проекция сечения плоскости А’D’. Берется радиус от оси сферы до очерка (разумеется не до точки A’) и в горизонтальной проекции проводится окружность этим радиусом. Проецированием находятся проекции точек D (их будет две — точка входа и точка выхода) — D и D1 и промежуточной точки, расположенной на экваторе.
Рис.6.3
Сторона четырехугольника СD горизонтальной проекции проецируется в прямую линию, причем эта линия должна начинаться от очерка, т.к. во фронтальной проекции
она пересекает экватор шара и продолжается до точек С и D.
Рис.6.4
Горизонтальной проекцией сторон четырехугольника АВ будет эллипс, строим его по характерным (опорным) точкам. Проецируем точки, расположенные на меридиане, экваторе и очерке фронтальной проекции соответственно на меридиан, очерк и экватор горизонтальной проекции. Соединяя их по лекалу с уже имеющимися
проекциями точек B и B1, и получаем искомую проекцию эллипса.
4. Аналогичным способом строится третья профильная проекция данного выреза (вид слева), поэтому нет надобности в подробном изложении четырехугольника ВС и АD будут проецироваться в прямые линии, СD – в окружность, AB – в эллипс.
Рис.6.5
5. Заключительным этапом в решении задачи является определение видимости сторон сквозного выреза, которая определяется из расположения их на сопряженной плоскости проекций. Тогда видимыми точками и линиями в горизонтальной плоскости будут точки и линии, которые во фронтальной — расположены выше экватора и на профильной проекции видимыми будут точки и линии которые на фронтальной плоскости расположены левее меридианы.
Экватор и меридиан являются границами видимости. Точки и линии, расположенные ниже экватора и правее меридиана во фронтальной проекции, в горизонтальной и профильной проекциях будут невидимыми.
Пример 1. Построить три проекции цилиндра с вырезом (рис. 147).
Отмечаем характерные точки выреза А, В, С, Д, Е, F, а также произвольную точку к для построения профильной проекции части эллипса. Горизонтальные проекции точек отмечаем на горизонтальном очерке цилиндра, так как горизонтальная проекция боковой поверхности цилиндра совпадает с горизонтальным очерком (рис .148)
Построение профильной проекции выреза показано на рис. 149. Для этого целесообразно ось x 12 провести через ось симметрии горизонтальной проекции,а ось x 23 через профильную ось симметрии.
Пример 2. Построить три проекции конуса с вырезом (рис. 150).
Отмечаем характерные точки вареза А, В, С, Е, K, а также произвольную точку D для построения части эллипса. Горизонтальные проекции точек отмечаем на образующих конуса и вспомогательных окружностях (рис. 151).
На рис. 152 показано построение профильной проекции конуса с вырезом.Для этого целесообразно ось x 12 провести через ось симметрии горизонтальной проекции, а ось x 23 через профильную ось симметрии.
Пример 3. Построить три проекции вырезе на призме (рис. 153).
Решение показано на рис. 154
Пример 4. Построить три проекции выреза на пирамиде (рис. 155).
Отмечаем фронтальные проекции характерных точек выреза – это точки 12, 22, 32, 42, 52, 62. Для нахождения горизонтальных проекций точек 4 и 5 проводим по поверхности пирамиды две вспомогательные линии, параллельные основанию пирамиды ABC. Горизонтальные проекции этих линий являются треугольниками, параллельными горизонтальной проекции основания А1В1С1. На этих треугольниках отмечаем горизонтальные проекции точек 4 и 5 (рис. 156).
Затем строим профильную проекцию пирамиды и точек выреза. Для этого оси целесообразно провести как показано на рис. 157.
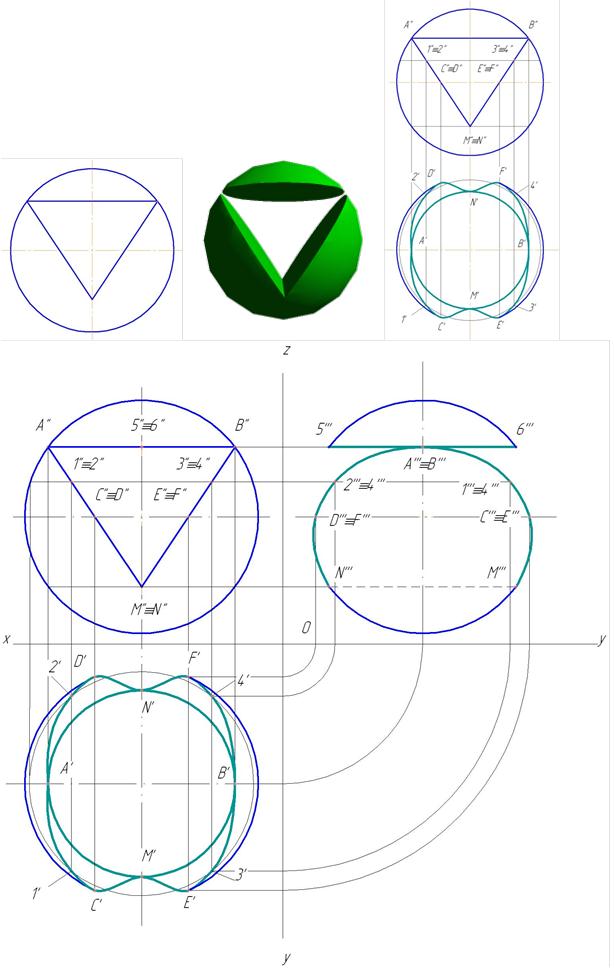
Пример 5. Построить три проекции выреза на сфере (рис. 158).
Вырез образован двумя фронтально-проецирующими плоскостями α и τ, горизонтальной плоскостью φ, двумя профильными плоскостями β и γ. Горизонтальная плоскость пересекает поверхность сферы по части окружности, ограниченной прямой. Фронтально-проецирующая плоскость пересекают поверхность сферы по окрухностям, которые на горизонтальной и профильной плоскости проецируются как части эллипсов. Профильная плоскость пересечет поверхность сферы по части окружности, которая на профильной плоскости спроецируется как часть окружности (рис. 159).
Построение профильной проекции показано на рис. 160
Метрические задачи
Дата добавления: 2018-10-15 ; просмотров: 1914 | Нарушение авторских прав
Черчение. Проецирование геометрического тела с отверстием на чертеже
В этот раз хочется повести речь, о чуть более сложных моделях, и их изображении на чертежах. В качестве примера рассмотрим сквозное отверстие в призматической фигуре, и подробно распишем последовательность построение этого отверстия в трех основных проекциях.
Первое, с чего стоит начинать чертеж модели – это конечно построение осевой линии. Это вертикальная или горизонтальная штрихпунктирная линия, идущая вдоль оси тела, которая в нашем случае является осью симметрии. Затем приступаем к построению контура фигуры и первым делом рисуем главный вид (рисунок 1) с которого в дальнейшем нарисуем два других вида модели. Для того, чтобы правильно вычертить отверстие на трех проекциях, используют проекционные связи. Т.е. если у вас есть отверстие на одном из видов, например, на главном, зная несколько простых правил, вы сможете вычертить это отверстие и на других двух видах.
Проекции геометрических тел с примерами и образцами выполнения
Содержание:
Формы деталей, встречающихся в технике, представляют собой сочетание различных геометрических тел или их частей.
Формы геометрических тел
Деталь любой формы можно представить как совокупность отдельных геометрических тел.
Для примера возьмем деталь (рис. 159. а) и проанализируем се форму. Мысленно разделив ее на отдельные элементы, получим следующие геометрические тела (рис. 159, б): 1 — усеченный прямой круговой конус с цилиндрическим отверстием, 2 — прямой круговой цилиндр, 3 — прямоугольный параллелепипед, 4 — два прямоугольных параллелепипеда с цилиндрическими отверстиями, 5 — два полых полуцилиндра. Для выполнения комплексных чертежей необходимо усвоить методы проецирования отдельных геометрических тел, а также точек и линий, расположенных на поверхности этих тел.
Геометрические тела, ограниченные плоскими многоугольниками, называются многогранниками (рис. 160, а). Эти многоугольники называются гранями, их пересечения — ребрами. Угол, образованный гранями, сходящимися в одной точке — вершине, называется многогранным углом.
Тела вращения ограничены поверхностями, которые получаются в результате вращения какой-либо линии вокруг неподвижной оси (рис. 160, б и в). Линия АВ, которая при своем движении образует поверхность, называется образующей. Наиболее часто встречаются такие тела вращения, как цилиндр, конус, шар, тор.
Проекции призм
Построение проекций правильной прямой шестиугольной призмы (рис. 161) начинается с выполнения ее горизонтальной проекции — правильного шестиугольника. Из вершин этого шестиугольника провопят вертикальные линии связи и строят фронтальную проекцию нижнего основания призмы. Эта проекция изображается отрезком горизонтальной прямой. От этой прямой вверх откладывают высоту призмы и строят фронтальную проекцию верхнего основания. Затем вычерчивают фронтальные проекции ребер — отрезки вертикальных прямых, равные высоте призмы. Фронтальные проекции передних и задних ребер совпадают. Горизонтальные проекции боковых граней изображаются в виде отрезков прямых. Передняя боковая грань 1243 изображается на плоскости V без искажения, а на плоскости W— в виде прямой линии. Фронтальные и профильные проекции остальных боковых граней изображаются с искажением.
На чертеже оси х, у и z не показывают, что делает чертеж более простым.
Несколько сложнее построение проекций наклонной призмы.
Рассмотрим порядок построения проекций наклонной шестиугольной призмы.
1. Призма, основание которой лежит на плоскости Н, наклонена к этой плоскости под утлом α (рис. 162, а). Ребра призмы параллельны плоскости V, т.е. являются фронталями.
Вначале выполняется построение горизонтальной проекции основания призмы, которое проецируется на плоскость Н без искажения (правильный шестиугольник). Фронтальная проекция основания представляет собой отрезок прямой, параллельной оси х.
Из точек 1‘, 2′, 3’ фронтальной проекции основания проводят прямые проекции ребер под углом α к оси х и на них откладывают действительную длину бокового ребра призмы.
Строят фронтальную проекцию верхнего основания призмы в виде отрезка прямой, равного и параллельного фронтальной проекции нижнего основания.
Из точек 1, 2, 3, 4. 5. 6 горизонтальной проекции нижнего основания проводят прямые — проекции ребер — параллельно оси х и на них с помощью вертикальных линий связи находят шесть точек — горизонтальные проекции вершин верхнего основания призмы.
2. Прямая правильная шестиугольная призма наклонена под углом α к плоскости Н. Основание призмы наклонено к плоскости Н под углом β (рис. 162, б).
В этом случае необходимо вначале построить фронтальную проекцию основания. Эта проекция представляет собой отрезок, равный расстоянию между параллельными сторонами шестиугольника. Если этот отрезок разделить пополам и из его середины провести линию связи, то на ней будут расположены точки 2 и 5 — горизонтальные проекции вершин основания призмы. Расстояние между точками 2, 5 равно действительному расстоянию между вершинами основания призмы. Так как горизонтальные проекции сторон 16 и 34 представляют собой их действительные длины, то, воспользовавшись этим обстоятельством, можно построить полностью горизонтальную проекцию основания.
Дальнейший процесс построения, показанный на рис. 162, б, аналогичен приведенному на рис. 162, а.
На комплексных чертежах предметов часто приходится строить проекции линий и точек, расположенных на поверхности этих тел, имея только одну проекцию линии или точки. Рассмотрим решение такой задачи.
Дан комплексный чертеж четырехугольной прямой призмы и фронтальная проекция а’ точки А.
Прежде всего надо отыскать на комплексном чертеже две проекции грани, на которой расположена точка А. На комплексном чертеже видно (рис. 163, а), что точка А лежит на грани призмы 1265. Фронтальная проекция а’ точки А лежит на фронтальной проекции 1‘2’6’5‘ грани призмы. Горизонтальная проекция 1562 этой грани — отрезок 56. На этом отрезке и находится горизонтальная проекция а точки А. Профильную проекцию призмы и точки А строят, применяя линии связи.
По имеющемуся комплексному чертежу призмы можно выполнить ее изометрическую проекцию по координатам вершин. Для этого вначале строят нижнее основание призмы (рис. 163, б), а затем вертикальные ребра и верхнее основание (рис. 163, в).
По координатам т и п точки А, взятым с комплексного чертежа, можно построить аксонометрическую проекцию этой точки.
Проекции пирамид
Построение проекций треугольной пирамиды начинается с построения основания, горизонтальная проекция которого представляет собой треугольник без искажения (рис. 164, а). фронтальная проекция основания — отрезок горизонтальной прямой.
Из горизонтальной проекции точки s (вершины. пирамиды) проводят вертикальную линию связи, на которой от оси х откладывают высоту пирамиды и получают фронтальную проекцию s’ вершины. Соединяя точку s’ с точками 1‘, 2′ и 3′, получают фронтальные проекции ребер пирамиды.
Горизонтальные проекции ребер получают, соединяя горизонтальную проекцию точки s с горизонтальными проекциями точек 1, 2 и 3.
Пусть, например, дана фронтальная проекция а’ точки А, расположенной на грани пирамиды 1s2, и требуется найти другую проекцию этой точки. Для решения этой задачи проведем через а’ произвольную вспомогательную прямую и продолжим ее до пересечения с фронтальными проекциями 1’s’ и 2’s’ ребер в точках п’ и т‘. Затем проведем из точек п’ и т‘ линии связи до пересечения с горизонтальными проекциями 1s и 2s этих ребер в точках п и т. Соединив п с т, получим горизонтальную проекцию вспомогательной прямой, на которой с помощью линии связи найдем искомую горизонтальную проекцию а точки А Профильную проекцию этой точки находят по линиям связи.
Другой способ решения задачи на построение проекции точки по заданной ее проекции показан на рис. 164, б. Дана четырехугольная правильная пирамида. Через заданную фронтальную проекцию а’ точки А проводят вспомогательную прямую, проходящую через вершину пирамиды и расположенную на ее грани. Горизонтальную проекцию ns вспомогательной прямой находят с помощью линии связи. Искомая горизонтальная проекция а точки А находится на пересечении линии связи, проведенной из точки а’, с горизонтальной проекцией ns вспомогательной прямой.
Фронтальная диметрическая проекция рассматриваемой пирамиды выполняется следующим образом (рис. 164, в).
Вначале строят основание, для чего по оси х откладывают длину диагонали 13, а по оси у — половину длины диагонали 24. Из точки О пересечения диагоналей проводят ось z и на ней откладывают высоту пирамиды. Вершину S соединяют с вершинами основания прямыми линиями — ребрами.
Фронтальную диметрическую проекцию точки А, расположенной на грани пирамиды, строят по координатам, которые берут с комплексного чертежа. От качала координат О по оси х откладывают координату xА, из се конца параллельно оси у — половину координаты yА и из конца этой координаты параллельно оси z — третью координату zА. Построение точки В, расположенной на ребре пирамиды, более простое. От точки О по оси х откладывают координату xB и из конца ее проводят прямую, параллельную оси z, до пересечения с ребром пирамиды в точке В.
Проекции цилиндров
Боковая поверхность прямого кругового цилиндра получается вращением отрезка АВ образующей вокруг оси, параллельной этому отрезку. На рис. 165, а представлена изометрическая проекция цилиндра.
Построение горизонтальной и фронтальной проекций цилиндра показано на рис. 165, б и в.
Построение начинают с изображения основания цилиндра, т.е. двух проекций окружности (рис. 165, б). Так как окружность расположена на плоскости Н, то она проецируется на эту плоскость без искажения. Фронтальная проекция окружности представляет собой отрезок горизонтальной прямой линии, равный диаметру окружности основания.
После построения основания на фронтальной проекции проводят две очерковые (крайние) образующие и на них откладывают высоту цилиндра. Проводят отрезок горизонтальной прямой, который является фронтальной проекцией верхнего основания цилиндра (рис. 165, в).
Определение недостающих проекции точек А и В, расположенных на поверхности цилиндра, по заданным фронтальным проекциям в данном случае затруднений нс вызывает, так как вся горизонтальная проекция боковой поверхности цилиндра представляет собой окружность (рис. 166. а). Следовательно, горизонтальные проекции точек А и В можно найти, проводя из данных точек а’ и b‘ вертикальные линии связи до их пересечения с окружностью в искомых точках а и Ь.
Профильные проекции точек А и В строят также с помощью вертикальных и горизонтальных линий связи.
Изометрическую проекцию цилиндра вычерчивают, как показано на рис. 166, б.
В изометрии точки A и В строят по координатам. Например, для построения точки В от начала координат О по оси х откладывают координату xB = n, а затем через ее конец проводят прямую, параллельную оси у, до пересечения с контуром основания в точке 1. Из этой точки параллельно оси x проводят прямую, на которой откладывают координату xB = h1 точки В.
Проекции конусов
Нагляднее изображение прямого кругового конуса показано на рис. 167, а. Боковая поверхность конуса получена вращением отрезка BS вокруг оси, пересекающей отрезок в точке S. Последовательность построения двух проекций конуса показана на рис. 167, б и в. Сначала строят две проекции основания. Горизонтальная проекция основания — окружность. Фронтальной проекцией будет отрезок горизонтальной прямой, равный диаметру этой окружности (рис. 167, б). На фронтальной проекции из середины основания восставляют перпендикуляр и на нем откладывают высоту конуса (рис. 167, в). Полученную фронтальную проекцию вершины конуса соединяют прямыми с концами фронтальной проекции основания и получают фронтальную проекцию конуса.
Если на поверхности конуса задана одна проекция точки А (например, фронтальная проекция на рис. 168, а). то две другие проекции этой точки определяют с помощью вспомогательных линий — образующей, расположенной на поверхности конуса и проведенной через точку А, или окружности, расположенной в плоскости, параллельной основанию конуса.
В первом случае (рис 168. а) проводят фронтальную проекцию s’a‘f ’ вспомогательной образующей. Пользуясь вертикальной линией связи, проведенной из точки f, расположенной на фронтальной проекции окружности основания, находят горизонтальную проекцию sf этой образующей, на которой с помощью линии связи, проходящей через а’, находят искомую точку а.
Во втором случае (рис. 168. б) вспомогательной линией, проходящей через точку А, будет окружность. расположенная на конической поверхности и параллельная плоскости Н. Фронтальная проекция этой окружности изображается в виде отрезка Ь’с’ горизонтальной прямой, величина которого равна диаметру вспомогательной окружности. Искомая горизонтальная проекция а точки А находится на пересечении линии связи, опущенной из точки а’, с горизонтальной проекцией вспомогательной окружности.
Если заданная фронтальная проекция Ь’ точки В расположена на контурной (очерковой) образующей SK, то горизонтальная проекция точки находится без вспомогательных линий (рис. 168. б).
В изометрической проекции точку А, находящуюся на поверхности конуса, строят по трем координатам (рис. 168, в): xА = n, yА = m, zА = h. Эти координаты последовательно откладывают по направлениям, параллельным изометрическим осям. В рассматриваемом примере от точки О по оси х отложена координата xА = n; из конца ее параллельно оси у проведена прямая, на которой отложена координата yА = m; из конца отрезка, равного т, параллельно оси z проведена прямая, на которой отложена координата zА = h. В результате построений получим искомую точку А.
Проекции шара
На рис. 169, а изображена половина шара, сферическая поверхность этого шара образована вращением четверти окружности АВ вокруг радиуса АО.
Проекции этой фигуры приведены на рис. 169, б. Горизонтальная проекция — окружность радиуса, равного радиусу сферы, а фронтальная — полуокружность того же радиуса.
Если точка А расположена на сферической поверхности (рис. 169, в), то вспомогательная линия Ь’с’, проведенная через эту точку параллельно горизонтальной плоскости проекций, проецируется на горизонтальную плоскость проекций окружностью. На горизонтальной проекции вспомогательной окружности находят с помощью линии связи искомую горизонтальную проекцию а точки А.
Величина диаметра вспомогательной окружности равна фронтальной проекции Ь’с’.
Проекции кольца и тора
Поверхность кругового кольца (рис. 170, а) образована вращением образующей окружности ABCD вокруг оси ОО1.
Тор — поверхность, образованная вращением части дуги окружности, являющейся образующей, вокруг оси ОО1, расположенной в плоскости этой окружности и не проходящей через ее центр.
На рис. 171, а и б приведены два вида тора. В первом случае образующая дуга окружности радиуса R отстоит от оси вращения на расстоянии меньше радиуса R, а во втором случае — больше.
В обоих случаях фронтальные проекции тора представляют собой действительный вид двух образующих дуг окружности радиуса R, расположенных симметрично относительно фронтальной проекции оси вращения. Профильными проекциями тора будут окружности.
Круговое кольцо (или открытый тор) имеет горизонтальную проекцию в виде двух концентрических окружностей, разность радиусов которых равна толщине кольца или диаметру образующей окружности (рис. 170, б). Фронтальная проекция ограничивается справа и слева дугами полуокружностей диаметра образующей окружности.
В случае, когда точка А лежит на поверхности кругового кольца и дана одна се проекция, для нахождения второй проекции этой точки применяется вспомогательная окружность, проходящая через данную точку А и расположенная на поверхности кольца в плоскости, перпендикулярной оси кольца (рис. 172).
Если задана фронтальная проекция а’ точки А, лежащей на поверхности кольца, то для нахождения ее второй проекции (в данном случае — профильной) через а’ проводят фронтальную проекцию вспомогательной окружности — отрезок вертикальной прямой линии b‘c‘. Затем строят профильную проекцию b«с» этой окружности и на ней, применяя линию связи, находят точку а“.
Если задана профильная проекция а» точки D, расположенной на поверхности этого кольца, то для нахождения фронтальной проекции точки D через d« проводят профильную проекцию вспомогательной окружности радиуса O«d“. Затем через верхнюю и нижнюю точки е» f« этой окружности проводят горизонтальные линии связи до пересечения с фронтальными проекциями образующей окружности радиуса r и получают точки e‘ и f‘. Эти точки соединяют вертикальной прямой, которая представляет собой фронтальную проекцию вспомогательной окружности (она будет невидима). Проводя горизонтальную линию связи из точки d« до пересечения с прямой e‘f ‘, получаем искомую точку d‘.
Такие же приемы построения применимы и для точек, находящихся на поверхности тора.
Комплексные чертежи группы геометрических тел и моделей
Для развития пространственного воображения полезно выполнять комплексные чертежи группы геометрических тел и несложных моделей с натуры.
Наглядное изображение группы геометрических тел показано на рис. 173, а. Построение комплексного чертежа этой группы геометрических тел следует начинать с горизонтальной проекции, так как основания цилиндра, конуса и шестигранной пирамиды проецируются на горизонтальную плоскость проекции без искажений. С помощью вертикальных линий связи строят фронтальную проекцию. Профильную проекцию строят с помощью вертикальных и горизонтальных линий связи (рис. 173, б).
Чтобы перейти к более сложным моделям, необходимо усвоить построение простых комплексных чертежей. Проекции моделей следует располагать таким образом, чтобы фронтальная проекция давала наиболее полное представление о форме и размерах модели (рис. 174).
Примеры и образцы решения задач:
Услуги по выполнению чертежей:
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Отверстие в конусе треугольник
В машиностроении, наряду с цилиндрическими, широко применяются детали с коническими поверхностями в виде наружных конусов или в виде конических отверстий. Например, центр токарного станка имеет два наружных конуса, из которых один служит для установки и закрепления его в коническом отверстии шпинделя; наружный конус для установки и закрепления имеют также сверло, зенкер, развертка и т. д. Переходная втулка для закрепления сверл с коническим хвостовиком имеет наружный конус и коническое отверстие
1. Понятие о конусе и его элементах
Элементы конуса . Если вращать прямоугольный треугольник АБВ вокруг катета АБ (рис. 202, а), то образуется тело АВГ, называемое полным конусом. Линия АБ называется осью или высотой конуса, линия АВ — образующей конуса. Точка А является вершиной конуса.
При вращении катета БВ вокруг оси АБ образуется поверхность круга, называемая основанием конуса.
Угол ВАГ между боковыми сторонами АВ и АГ называется углом конуса и обозначается 2α. Половина этого угла, образуемая боковой стороной АГ и осью АБ, называется углом уклона конуса и обозначается α. Углы выражаются в градусах, минутах и секундах.
Если от полного конуса отрезать его верхнюю часть плоскостью, параллельной егооснованию (рис. 202, б), то получим тело, называемое усеченным конусом. Оно имеет два основания верхнее и нижнее. Расстояние OO1 по оси между основаниями называется высотой усеченного конуса. Так как в машиностроении большей частью приходится иметь дело с частями конусов, т. е. усеченными конусами, то обычно их просто называют конусами; дальше будем называть все конические поверхности конусами.
Связь между элементами конуса. На чертеже указывают обычно три основных размера конуса: больший диаметр D, меньший — d и высоту конуса l (рис. 203).
Иногда на чертеже указывается только один из диаметров конуса, например, больший D, высота конуса l и так называемая конусность. Конусностью называется отношение разности диаметров конуса к его длине. Обозначим конусность буквой K, тогда
Если конус имеет размеры: D =80 мм, d = 70 мм и l = 100 мм, то согласно формуле (10):
Это значит, что на длине 10 мм диаметр конуса уменьшается на 1 мм или на каждый миллиметр длины конуса разница между его диаметрами изменяется на
Иногда на чертеже вместо угла конуса указывается уклон конуса. Уклон конуса показывает, в какой мере отклоняется образующая конуса от его оси.
Уклон конуса определяется по формуле
где tg α — уклон конуса;
D — диаметр большого основания конуса в мм;
d — диаметр малого основания конуса в мм;
l — высота конуса в мм.
Пользуясь формулой (11), можно при помощи тригонометрических таблиц определить угол а уклона конуса.
Уклон конуса и конусность обычно выражают простой дробью, например: 1 : 10; 1 : 50, или десятичной дробью, например, 0,1; 0,05; 0,02 и т. д.
2. Способы получения конических поверхностей на токарном станке
На токарном станке обработка конических поверхностей производится одним из следующих способов:
а) поворотом верхней части суппорта;
б) поперечным смещением корпуса задней бабки;
в) с помощью конусной линейки;
г) с помощью широкого резца.
3. Обработка конических поверхностей поворотом верхней части суппорта
При изготовлении на токарном станке коротких наружных и внутренних конических поверхностей с большим углом уклона нужно повернуть верхнюю часть суппорта относительно оси станка под углом α уклона конуса (см. рис. 204). При таком способе работы подачу можно производить только от руки, вращая рукоятку ходового винта верхней части суппорта, и лишь в наиболее современных токарных станках имеется механическая подача верхней части суппорта.
Для установки верхней части суппорта 1 на требуемый угол можно использовать деления, нанесенные на фланце 2 поворотной части суппорта (рис. 204). Если угол α уклона конуса задан по чертежу, то верхнюю часть суппорта повертывают вместе с его поворотной частью на требуемое число делений, обозначающих градусы. Число делений отсчитывают относительно риски, нанесенной на нижней части суппорта.
Если на чертеже угол α не дан, а указаны больший и меньший диаметры конуса и длина его конической части, то величину угла поворота суппорта определяют по формуле (11)
Способ обтачивания конических поверхностей поворотом верхней части суппорта имеет следующие недостатки: он допускает обычно применение только ручной подачи, что отражается на производительности труда и чистоте обработанной поверхности; позволяет обтачивать сравнительно короткие конические поверхности, ограниченные длиной хода верхней части суппорта.
4. Обработка конических поверхностей способом поперечного смещения корпуса задней бабки
Для получения конической поверхности на токарном станке необходимо при вращении заготовки вершину резца перемещать не параллельно, а под некоторым углом к оси центров. Этот угол должен равняться углу α уклона конуса. Наиболее простой способ получения угла между осью центров и направлением подачи — сместить линию центров, сдвинув задний центр в поперечном направлении. Путем смещения заднего центра в сторону резца (на себя) в результате обтачивания получают конус, у которого большее основание направлено в сторону передней бабки; при смещении заднего центра в противоположную сторону, т. е. от резца (от себя), большее основание конуса окажется со стороны задней бабки (рис. 205).
Смещение корпуса задней бабки определяют по формуле
где S — смещение корпуса задней бабки от оси шпинделя передней бабки в мм;
D — диаметр большого основания конуса в мм;
d — диаметр малого основания конуса в мм;
L — длина всей детали или расстояние между центрами в мм;
l — длина конической части детали в мм.
Смещение корпуса задней бабки производят, используя деления 1 (рис 206), нанесенные на торце опорной плиты, и риску 2 на торце корпуса задней бабки.
Если на торце плиты делений нет, то смещают корпус задней бабки, пользуясь измерительной линейкой, как показано на рис. 207.
Преимущество обработки конических поверхностей путем смещения корпуса задней бабки заключается в том, что этим способом можно обтачивать конусы большой длины и вести обтачивание с механической подачей.
Недостатки этого способа: невозможность растачивать конические отверстия; потеря времени на перестановку задней бабки; возможность обрабатывать лишь пологие конусы; перекос центров в центровых отверстиях, что приводит к быстрому и неравномерному износу центров и центровых отверстий и служит причиной брака при вторичной установке детали в этих же центровых отверстиях.
Неравномерного износа центровых отверстий можно избежать, если вместо обычного применять специальный шаровой центр (рис. 208). Такие центры используют преимущественно при обработке точных конусов.
5. Обработка конических поверхностей с применением конусной линейки
Для обработки конических поверхностей с углом уклона а до 10—12° современные токарные станки обычно имеют особое приспособление, называемое конусной линейкой. Схема обработки конуса с применением конусной линейки приводится на рис. 209.
К станине станка прикреплена плита 11, на которой установлена конусная линейка 9. Линейку можно поворачивать вокруг пальца 8 под требуемым углом а к оси обрабатываемой детали. Для закрепления линейки в требуемом положении служат два болта 4 и 10. По линейке свободно скользит ползун 7, соединяющийся с нижней поперечной частью 12 суппорта при помощи тяги 5 и зажима 6. Чтобы эта часть суппорта могла свободно скользить по направляющим, ее отсоединяют от каретки 3, вывинчивая поперечный винт или отсоединяя от суппорта его гайку.
Если сообщить каретке продольную подачу, то ползун 7, захватываемый тягой 5, начнет перемещаться вдоль линейки 9. Так как ползун скреплен с поперечными салазками суппорта, то они вместе с резцом будут перемещаться параллельно линейке 9. Благодаря этому резец будет обрабатывать коническую поверхность с углом уклона, равным углу α поворота конусной линейки.
После каждого прохода резец устанавливают на глубину резания с помощью рукоятки 1 верхней части 2 суппорта. Эта часть суппорта должна быть повернута на 90° относительно нормального положения, т. е. так, как это показано на рис. 209.
Если даны диаметры оснований конуса D и d и его длина l, то угол поворота линейки можно найти по формуле (11).
Подсчитав величину tg α, легко определить значение угла α по таблице тангенсов.
Применение конусной линейки имеет ряд преимуществ:
1) наладка линейки удобна и производится быстро;
2) при переходе к обработке конусов не требуется нарушать нормальную наладку станка, т. е. не нужно смещать корпус задней бабки; центры станка остаются в нормальном положении, т. е. на одной оси, благодаря чему центровые отверстия в детали и центры станка не срабатываются;
3) при помощи конусной линейки можно не только обтачивать наружные конические поверхности, но и растачивать конические отверстия;
4) возможна работа е продольным самоходом, что увеличивает производительность труда и улучшает качество обработки.
Недостатком конусной линейки является необходимость отсоединять салазки суппорта от винта поперечной подачи. Этот недостаток устранен в конструкции некоторых токарных станков, у которых винт не связан жестко со своим маховичком и зубчатыми колесами поперечного самохода.
6. Обработка конических поверхностей широким резцом
Обработку конических поверхностей (наружных и внутренних) с небольшой длиной конуса можно производить широким резцом с углом в плане, соответствующим углу α уклона конуса (рис. 210). Подача резца может быть продольная и поперечная.
Однако использование широкого резца на обычных станках возможно только при длине конуса, не превышающей примерно 20 мм. Применять более широкие резцы можно лишь на особо жестких станках и деталях, если это не вызывает вибрации резца и обрабатываемой детали.
7. Растачивание и развертывание конических отверстий
Обработка конических отверстий является одной из наиболее трудных токарных работ; она значительно труднее, чем обработка наружных конусов.
Обработку конических отверстий на токарных станках в большинстве случаев производят растачиванием резцом с поворотом верхней части суппорта и реже с помощью конусной линейки. Все подсчеты, связанные с поворотом верхней части суппорта или конусной линейки, выполняются так же, как при обтачивании наружных конических поверхностей.
Если отверстие должно быть в сплошном материале, то сначала сверлят цилиндрическое отверстие, которое затем растачивают резцом на конус или обрабатывают коническими зенкерами и развертками.
Чтобы ускорить растачивание или развертывание, следует предварительно просверлить отверстие сверлом, диаметр d, которого на 1—2 мм меньше диаметра малого основания конуса (рис. 211, а). После этого рассверливают отверстие одним (рис. 211, б) или двумя (рис. 211, в) сверлами для получения ступеней.
После чистового растачивания конуса его развертывают конической разверткой соответствующей конусности. Для конусов с небольшой конусностью выгоднее производить обработку конических отверстий непосредственно после сверления набором специальных разверток, как показано на рис. 212.
8. Режимы резания при обработке отверстий коническими развертками
Конические развертки работают в более тяжелых условиях, чем цилиндрические: в то время как цилиндрические развертки снимают незначительный припуск небольшими режущими кромками, конические развертки режут всей длиной их режущих кромок, расположенных на образующей конуса. Поэтому при работе коническими развертками применяют подачи и скорости резания меньше, чем при работе цилиндрическими развертками.
При обработке отверстий коническими развертками подачу производят вручную, вращая маховичок задней бабки. Необходимо следить за тем, чтобы пиноль задней бабки перемещалась равномерно.
Подачи при развертывании стали 0,1—0,2 мм/об, при развертывании чугуна 0,2—0,4 мм/об.
Скорость резания при развертывании конических отверстий развертками из быстрорежущей стали 6—10 м/мин.
Для облегчения работы конических разверток и получения чистой и гладкой поверхности следует применять охлаждение. При обработке стали и чугуна применяют эмульсию или сульфофрезол.
9. Измерение конических поверхностей
Поверхности конусов проверяют шаблонами и калибрами; измерение и одновременно проверку углов конуса производят угломерами. На рис. 213 показан способ проверки конуса с помощью шаблона.
Наружные и внутренние углы различных деталей можно измерять универсальным угломером (рис. 214). Он состоит из основания 1, На котором на дуге 130 нанесена основная шкала. С основанием 1 жестко скреплена линейка 5. По дуге основания перемещается сектор 4, несущий нониус 3. К сектору 4 посредством державки 7 может быть прикреплен угольник 2, в котором, в свою очередь, закрепляется съемная линейка 5. Угольник 2 и съемная линейка 5 имеют возможность перемещаться по грани сектора 4.
Путем различных комбинаций в установке измерительных деталей угломера можно производить измерение углов от 0 до 320°. Величина отсчета по нониусу 2′. Отсчет, полученный при измерении углов, производится по шкале и нониусу (рис. 215) следующим образом: нулевой штрих нониуса показывает число градусов, а штрих нониуса, совпадающий со штрихом шкалы основания, — число минут. На рис. 215 со штрихом шкалы основания совпадает 11-й штрих нониуса, что означает 2’Х 11 = 22′. Следовательно, угол в данном случае равен 76°22′.
На рис. 216 показаны комбинации измерительных деталей универсального угломера, позволяющие производить измерение различных углов от 0 до 320°.
Для более точной проверки конусов в серийном производстве применяют специальные калибры. На рис. 217, а показан кониче-ский калибр-втулка для проверки наружных конусов, а на рис. 217, б—конический калибр-пробка для проверки конических отверстий.
На калибрах делаются уступы 1 и 2 на торцах или наносятся риски 3, служащие для определения точности проверяемых поверхностей.
На. рис. 218 приводится пример проверки конического отверстия калибром-пробкой.
Для проверки отверстия калибр (см. рис. 218), имеющий уступ 1 на определенном расстоянии от торца 2 и две риски 3, вводят с легким нажимом в отверстие и проверяют, нет ли качания калибра в отверстии. Отсутствие качания показывает, что угол конуса правилен. Убедившись, что угол конуса правилен, приступают к проверке его размера. Для этого наблюдают, до какого места калибр войдет в проверяемую деталь. Если конец конуса детали совпадает с левым торцом уступа 1 или с одной из рисок 3 или находится между рисками, то размеры конуса правильны. Но может случиться, что калибр войдет в деталь настолько глубоко, что обе риски 3 войдут в отверстие или оба торца уступа 1 выйдут из него наружу. Это показывает, что диаметр отверстия больше заданного. Если, наоборот, обе риски окажутся вне отверстия или ни один из торцов уступа не выйдет из него, то диаметр отверстия меньше требуемого.
Для точной проверки конусности применяют следующий способ. На измеряемой поверхности детали или калибра проводят мелом или карандашом две-три линии вдоль образующей конуса, затем вставляют или надевают калибр на деталь и повертывают его на часть оборота. Если линии сотрутся неравномерно, это значит, что конус детали обработан неточно и необходимо его исправить. Стирание линий по концам калибра говорит о неправильной конусности; стирание линий в средней части калибра показывает, что конус имеет небольшую вогнутость, причиной чего обычно является неточное расположение вершины резца по высоте центров. Вместо меловых линий можно нанести на всю коническую поверхность детали или калибра тонкий слой специальной краски (синьки). Такой способ дает большую точность измерения.
10. Брак при обработке конических поверхностей и меры его предупреждения
При обработке конических поверхностей, помимо упомянутых видов брака для цилиндрических поверхностей, дополнительно возможны следующие виды брака:
1) неправильная конусность;
2) отклонения в размерах конуса;
3) отклонения в размерах диаметров оснований при правильной конусности;
4) непрямолинейность образующей конической поверхности.
1. Неправильная конусность получается главным образом вследствие неточного смещения корпуса задней бабки, неточного поворота верхней части суппорта, неправильной установки конусной линейки, неправильной заточки или установки широкого резца. Следовательно, точной установкой корпуса задней бабки, верхней части суппорта или конусной линейки перед началом обработки можно брак предупредить. Этот вид брака исправим только в том случае, если ошибка во всей длине конуса направлена в тело детали, т. е. все диаметры у втулки меньше, а у конического стержня больше требуемых.
2. Неправильный размер конуса при правильном угле его, т. е. неправильная величина диаметров по всей длине конуса, получается, если снято недостаточно или слишком много материала. Предупредить брак можно только внимательной установкой глубины резания по лимбу на чистовых проходах. Брак исправим, если снято недостаточно материала.
3. Может получиться, что при правильной конусности и точных размерах одного конца конуса диаметр второго конца неправилен. Единственной причиной является несоблюдение требуемой длины всего конического участка детали. Брак исправим, если деталь излишне длинна. Чтобы избежать этого вида брака, необходимо перед обработкой конуса тщательно проверить его длину.
4. Непрямолинейность образующей обрабатываемого конуса получается при установке резца выше (рис. 219, б) или ниже (рис. 219, в) центра (на этих рисунках для большей наглядности искажения образующей конуса показаны в сильно преувеличенном виде). Таким образом, и этот вид брака является результатом невнимательной работы токаря.
Черчение. Проецирование геометрического тела с отверстием на чертеже
В этот раз хочется повести речь, о чуть более сложных моделях, и их изображении на чертежах. В качестве примера рассмотрим сквозное отверстие в призматической фигуре, и подробно распишем последовательность построение этого отверстия в трех основных проекциях.
Первое, с чего стоит начинать чертеж модели – это конечно построение осевой линии. Это вертикальная или горизонтальная штрихпунктирная линия, идущая вдоль оси тела, которая в нашем случае является осью симметрии. Затем приступаем к построению контура фигуры и первым делом рисуем главный вид (рисунок 1) с которого в дальнейшем нарисуем два других вида модели. Для того, чтобы правильно вычертить отверстие на трех проекциях, используют проекционные связи. Т.е. если у вас есть отверстие на одном из видов, например, на главном, зная несколько простых правил, вы сможете вычертить это отверстие и на других двух видах.
[spoiler title=”источники:”]
http://www.tehinfor.ru/s_3/konus.html
[/spoiler]
