Найти площадь прямоугольного треугольника
- Главная
- /
- Математика
- /
- Геометрия
- /
- Найти площадь прямоугольного треугольника
Чтобы посчитать площадь прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор

Чтобы вычислить площадь прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- длины катетов a и b
- длину гипотенузы с и длину любого из катетов (a или b)
- длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
- длину гипотенузы с и один из острых углов (α или β)
Найти площадь прямоугольного треугольника по двум катетам
Катет a =
Катет b =
S =
0
Просто введите длины двух катетов, и получите ответ.
Теория
Чему равна площадь (S) прямоугольного треугольника если известны оба катета (a и b)?
Формула
S = ½ ⋅ a ⋅ b
Пример
К примеру найдём площадь прямоугольного треугольника у которого сторона a = 2 см, а сторона b = 4 см:
S = 2 ⋅ 4 / 2 = 8 / 2 = 4 см²
Найти площадь прямоугольного треугольника по катету и гипотенузе
Гипотенуза c =
Катет (a или b) =
S =
0
Введите длины гипотенузы и одного из катетов, и получите ответ.
Теория
Чему равна площадь (S) прямоугольного треугольника если известны его гипотенуза (c) и один из катетов (a или b)?
Формула
S = ½ ⋅ a ⋅ √c² – a² = ½ ⋅ b ⋅ √c² – b²
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 2 см, а гипотенуза c = 5 см:
S = 2 ⋅ √5² – 2² / 2 = √25 – 4 ≈ 4.58 см²
Найти площадь прямоугольного треугольника по катету и прилежащему к нему острому углу
Катет (a или b) =
Прилежащий угол (β или α) = °
S =
0
Введите длину одного из катетов и прилежащий к нему острый угол в градусах.
То есть к катету a прилежащий ∠β, а к катету b – ∠α
Теория
Чему равна площадь (S) прямоугольного треугольника если известны один из катетов (a или b) и прилежащий к нему угол?
Формула
S = ½ ⋅ a² ⋅ tg(β) = ½ ⋅ b² ⋅ tg(α)
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 4 см, а прилежащий к нему ∠β = 45°:
S = ½ ⋅ 4² ⋅ tg(45) = ½ ⋅ 16 ⋅ 1 = 16 / 2 = 8 см²
Найти площадь прямоугольного треугольника по катету и противолежащему к нему острому углу
Катет (a или b) =
Противолежащий угол (α или β) = °
S =
0
Введите длину одного из катетов и противолежащий к нему острый угол в градусах.
То есть к катету a противолежащий ∠α, а к катету b – ∠β
Теория
Чему равна площадь (S) прямоугольного треугольника если известны один из катетов (a или b) и противолежащий к нему угол?
Формула
S = ½ ⋅ a² ⋅ tg(90 – α) = ½ ⋅ b² ⋅ tg(90 – β)
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 4 см, а противолежащий к нему ∠α = 45°:
S = 4² / 2⋅ tg(45) = 16 / 2 ⋅ 1 = 8 см²
Найти площадь прямоугольного треугольника зная длину гипотенузы и один из острых углов
Гипотенуза c =
Угол (α или β) = °
S =
0
Введите длину гипотенузы и один из острых угол в градусах.
Теория
Чему равна площадь (S) прямоугольного треугольника если известны длина гипотенузы (c) и один из острых углов?
Формула
S = ½ ⋅ c² ⋅ sin(α) ⋅ cos(α) = ½ ⋅ c² ⋅ sin(β) ⋅ cos(β)
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого гипотенуза c = 8 см, а ∠α = 45°:
S = ½ ⋅ 8² ⋅ sin(45) ⋅ cos(45) ≈ ½ ⋅ 64 ⋅ 0.7071067812 ⋅ 0.7071067812 ≈ 16 см²

Формула:
S
=
1
2
ab
Где: a, b – стороны.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
1
4
С2
·sin(2α)
Где: C – гипотенуза, α – острый угол.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
1
2
a2
·tg(α)
Где: a – катет, α – острый угол.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
R·(R+C)
Где: С – гипотенуза, R – радиус вписанной окружности.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
D
2
·(
D
2
+ C
)
Где: С – гипотенуза, D – диаметр вписанной окружности.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
S
π
·(
S
π
+ C
)
Где: С – гипотенуза, S – площадь вписанной окружности.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
P
2π
·(
P
2π
+ C
)
Где: С – гипотенуза, P – длина вписанной окружности.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
C1
·
C2
Где: C1 , C2 – части гипотенузы.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
1
2
ch
Где: c – гипотенуза, h – высота.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано
Площадь треугольника равна одной четверной квадрата гипотенузы умноженной на синус двойного угла.
Калькуляторы площади прямоугольного треугольника
Площадь прямоугольного треугольника онлайн
С помощю этого онлайн калькулятора можно найти площадь прямоугольного треугольника. Для нахождения площади прямоугольного треугольника введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть и численные примеры смотрите ниже.
Содержание
- Площадь прямоугольного треугольника по двум катетам
- Площадь прямоугольного треугольника по катету и гипотенузе
- Площадь прямоугольного треугольника по гипотенузе и углу
- Площадь прямоугольного треугольника по катету и прилежащему углу
- Площадь прямоугольного треугольника по катету и противолежащему углу
- Площадь прямоугольного треугольника по гипотенузе и вписанной окружности
- Площадь прямоугольного треугольника по отрезкам, на которые делит гипотенузу вписанная окружность
Площадь прямоугольного треугольника по двум катетам
Как известно, площадь треугольника равна половине произведения его основания на высоту (см. страницу Площадь треугольника онлайн).В прямоугольном треугольнике катеты перпендикулярны друг другу. Поэтому можно один из них считать как основание, а другой − как высоту.
На рисунке 1 можем считать a как основание, а b − как высоту. Тогда площадь прямоугольного треугольника равна:
Пример 1. Известны катеты прямоугольного треугольника: 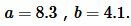 Найти площадь треугольника.
Найти площадь треугольника.
Решение. Для вычисления площади треугольника воспользуемся формулой (1). Подставляя значения 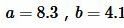 в (1), получим:
в (1), получим:
Ответ: 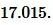
Площадь прямоугольного треугольника по катету и гипотенузе
Пусть в прямоугольном треугольнике известны катет a и гипотенуза c (Рис.2):
Найдем площадь треугольника. Из формулы Пифагора имеем:
Подставляя (2) в (1), получим формулу вычисления площади прямоугольного треугольника по катету и гипотенузе:
Пример 2. Известны катет и гипотенуза прямоугольного треугольника: 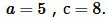 Найти площадь треугольника.
Найти площадь треугольника.
Решение. Для вычисления площади треугольника воспользуемся формулой (3). Подставляя значения 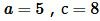 в (3), получим:
в (3), получим:
Ответ: 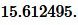
Площадь прямоугольного треугольника по гипотенузе и углу
Пусть в прямоугольном треугольнике известны гипотенуза с и угол α (Рис.3):
Найдем площадь прямоугольного треугольника. Из теоремы синусов имеем:
или
Подставим (4) в (1):
Из формулы произведения тригонометрических функций имеем:
Подставим в (6) ( small beta=alpha ):
Применяя (7) относительно формулы (5), получим:
Пример 3. Известны гипотенуза и прилегающий угол прямоугольного треугольника: 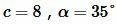 . Найти площадь треугольника.
. Найти площадь треугольника.
Решение. Для вычисления площади треугольника воспользуемся формулой (8). Подставляя значения 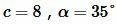 в (8), получим:
в (8), получим:
Ответ: 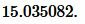
Площадь прямоугольного треугольника по катету и прилежащему углу
Пусть в прямоугольном треугольнике известны катет a и прилежащий угол α (Рис.4):
Найдем площадь прямоугольного треугольника. Тангенс угла α прямоугольного треугольника равна:
Откуда
Подставляя (9) в (1), получим формулу площади прямоугольного треугольника по катету и прилежащему углу:
Пример 4. Известны катет и прилегающий угол прямоугольного треугольника: 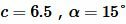 . Найти площадь треугольника.
. Найти площадь треугольника.
Решение. Для вычисления площади треугольника воспользуемся формулой (10). Подставляя значения 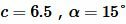 в (10), получим:
в (10), получим:
Ответ: 
Площадь прямоугольного треугольника по катету и противолежащему углу
Пусть в прямоугольном треугольнике известны катет a и противолежащий угол α (Рис.5):
Найдем площадь прямоугольного треугольника. Коангенс угла α прямоугольного треугольника равна:
Откуда
Подставляя (12) в (1), получим формулу площади прямоугольного треугольника по катету и противожащему углу:
Пример 5. Известны катет и противолежащий угол прямоугольного треугольника: 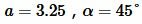 . Найти площадь треугольника.
. Найти площадь треугольника.
Решение. Для вычисления площади треугольника воспользуемся формулой (13). Подставляя значения 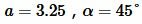 в (13), получим:
в (13), получим:
Ответ: 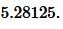
Площадь прямоугольного треугольника по гипотенузе и вписанной окружности
Пусть в прямоугольном треугольнике известны гипотенуза с и радиус вписанной окружности r (Рис.6):
Найдем площадь прямоугольного треугольника. Соединим центр окружности O c вершинами A, B и с точками D, E, F.
Треугольники AOD, AOF, BOD, BOE прямоугольные, поскольку 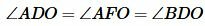
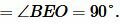 Прямоугольные треугольники AOD и AOF равны по гипотенузе и катету (сторона AO общая, OD=OF):
Прямоугольные треугольники AOD и AOF равны по гипотенузе и катету (сторона AO общая, OD=OF):
Прямоугольные треугольники BOD и BOE равны по гипотенузе и катету (сторона BO общая, OD=OE):
Запишем формулы площадей прямоугольных треугольников AOD и BOD и квадрата OECF:
Тогда, учитывая (14) и (15), площадь прямоугольного треугольника ABC равна:
Подставляя (16), (17) в (18), получим:
или
Пример 6. Известны гипотенуза и радиус вписанной окружности прямоугольного треугольника: 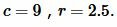 Найти площадь треугольника.
Найти площадь треугольника.
Решение. Для вычисления площади треугольника воспользуемся формулой (19). Подставляя значения 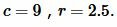 в (19), получим:
в (19), получим:
Ответ: 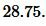
Площадь прямоугольного треугольника по отрезкам, на которые делит гипотенузу вписанная окружность
Пусть в прямоугольном треугольнике известны отрезки AD и DB (Рис.6). Найдем площадь прямоугольного треугольника выраженные через эти отрезки. Площадь прямоугольного треугольника через катеты имеет вид:
Учитывая, что 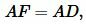
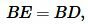
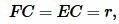
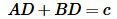 , (20) примет вид:
, (20) примет вид:
То есть
Сравнивая формулы (19) и (21) можем записать:
Таким образом формула площади прямоугольного треугольника по отрезкам, на которые делит гипотенузу вписанная окружность имеет следующий вид:
Пример 7. Известны отрезки гипотенузы разделенные вписанной окружностью прямоугольного треугольника (Рис.6) 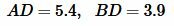 Найти площадь треугольника.
Найти площадь треугольника.
Решение. Для вычисления площади треугольника воспользуемся формулой (22). Подставляя значения 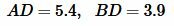 в (22), получим:
в (22), получим:
Ответ: 
Смотрите также:
- Площадь треугольника онлайн
- Площадь равностороннего треугольника онлайн
- Площадь равнобедренного треугольника онлайн
Рассматривается треугольник АВС, в котором угол С — прямой.
Стороны этого треугольника, прилегающие к прямому углу (т.е. стороны АС и ВС) называются катетами, а сторона, противолежащая прямому углу (т.е. сторона АВ) — гипотенузой.
Площадь прямоугольного треугольника, если известны катеты
Площадь прямоугольного треугольника равна половине произведения его катетов.
Примеры.
В треугольнике АВС (угол С = 90º) катет АС равен 5 см, а катет ВС равен 3 см. Площадь треугольника АВС равна:
SАВС = 0,5 · 5 · 3 = 7,5 см2.
В треугольнике MNP (угол N = 90º) катет PN равен 102 мм, а катет MN равен 76 мм. Площадь треугольника MNP равна:
SАВС = 0,5 · 102 · 76 = 3876 мм2.
Площадь прямоугольного треугольника, если известны две стороны
Нужно разобраться, длины каких именно сторон прямоугольного треугольника известны: двух катетов или же гипотенузы и одного из катетов, т.к. подход к решению будет совершенно разный. Случай, когда известны длины двух катетов, рассмотрен выше. Ниже рассмотрен случай, когда известна длина гипотенузы и одного из катетов.
Площадь прямоугольного треугольника по катету и гипотенузе
Последовательность решения следующая:
- используя теорему Пифагора, нужно определить длину второго катета;
- нужно найти площадь прямоугольного треугольника по двум катетам.
Пример.
В треугольнике АВС (угол С = 90º) катет АС равен 6 см, а гипотенуза АВ равна 9,22 см. Длина второго катета равна
ВС = КОРЕНЬ из (9,222 − 62) = 7 см.
Теперь по двум известным катетам (АС = 6 см, ВС = 7 см) можно определить площадь треугольника:
SАВС = 0,5 · 6 · 7 = 21 см2.
Площадь прямоугольного треугольника, если известна гипотенуза
Невозможно найти площадь треугольника, зная одну лишь длину его гипотенузы, потому что гипотенуза не определяет однозначно прямоугольный треугольник. Ведь несколько треугольников могут иметь одинаковую длину гипотенузы, но совершенно разные длины катетов и, соответственно, разную площадь.
Например:
- гипотенуза АС = 10 см, катеты АС = 6 см, ВС = 8 см, площадь S = 0,5 · 6 · 8 = 24 см2;
- гипотенуза АС = 10 см, катеты АС = 5 см, ВС = 8,66 см, площадь S = 0,5 · 5 · 8,66 = 21,65 см2;
- гипотенуза АС = 10 см, катеты АС = 4 см, ВС = 9,165 см, площадь S = 0,5 · 4 · 9,165 = 18,33 см2.
Помимо длины гипотенузы, для однозначного определения треугольника необходимо знать либо длину одного из катетов, либо величину одного из острых углов.
Определение площади прямоугольного треугольника по гипотенузе и одному из катетов рассмотрено выше.
Площадь прямоугольного треугольника по гипотенузе и углу
Зная длину гипотенузы и величину одного из его острых углов, можно найти длины обоих катетов — прилежащего к этому острому углу и противолежащего от этого угла. Далее, зная длины обоих катетов, без труда можно определить площадь треугольника.
Источники:
- П.Ф. Фильчакова. Справочник по элементарной математике. — К.: Наукова думка, 1967. — 442 с.
- М.Я. Выгодский. Справочник по элементарной математике. — М.: Государственное издательство технико-теоретической литературы. — 412 с.
- Е. Хлебалиной. Универсальная школьная энциклопедия. В 2-х томах. Том 2 (М — Я). — М.: Аванта+, 2003. — 592 с.
Дополнительно на Геноне:
- Что такое гипотенуза?
- Что такое катет?
- Как найти площадь прямоугольного треугольника?
Содержание:
- Формула
- Примеры вычисления площади прямоугольного треугольника
Формула
Чтобы найти площадь прямоугольного треугольника $ABC$ (рис. 1),
надо найти произведение катетов
$a$ и
$b$ и поделить его на два. То есть
$$mathrm{S}_{Delta A B C}=frac{a b}{2}$$
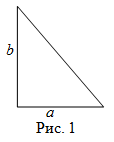
Напомним, что катетами прямоугольного треугольника называются стороны, которые пересекаются под прямым углом.
Примеры вычисления площади прямоугольного треугольника
Пример
Задание. Найти площадь прямоугольного треугольника
$ABC$, если известно, что длины его катетов равны 3 см и 4 см.
Решение. Искомая площадь равна половине произведения катетов, то есть
$mathrm{S}_{Delta A B C}=frac{3 cdot 4}{2}=frac{12}{2}=6$ (см2)
Ответ. $mathrm{S}_{Delta A B C}=6$ (см2)

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Вычислить площадь прямоугольного треугольника, один из катетов которого равен 6 см, а гипотенуза 10 см.
Решение. Искомая площадь равна половине произведения катетов. Используя теорему Пифагора,
найдем второй катет заданного треугольника:
$b=sqrt{10^{2}-6^{2}}=sqrt{100-36}=sqrt{64}=8$ (см)
Тогда площадь
$S=frac{6 cdot 8}{2}=frac{48}{2}=24$ (см2)
Ответ. $S=24$ (см2)
Читать дальше: как найти площадь равнобедренного треугольника.
