Статьи / Python

Встроенный модуль itertools в Python — простой инструментарий, позволяющий генерировать полный список возможных комбинаций из заданного набора символов. Как с этим работать и справляться – далее в статье.
Что ж, в преддверии Нового года KOTOFF.net вновь расправляет крылья.
И сразу к делу. Рассмотрим всего 3 функции и их различия.
1. Нахождение всевозможных комбинаций из набора символов
Допустим, у нас есть некий алфавит из трёх букв (А, Б, В), и из него необходимо составить максимальное количество трёхзначных слов (комбинаций). Причём в данном случае буквы могут повторяться. Алфавит короткий, однако у нас получится составить целых 27 слов. На каждую позицию приходится по 3 варианта букв, соответственно, общее количество комбинаций можно посчитать так: nk (n – количество доступных символов в степени k – длина конечной комбинации). Для нашего случая: 33 = 27
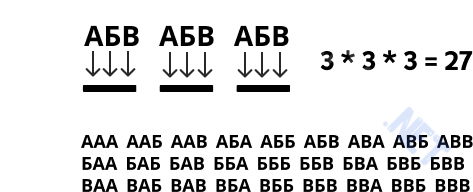
Теперь импортирую itertools и сгенерирую всё то, что выше считали руками, но теперь уже с помощью функции product():
from itertools import product
for i in product('АБВ', repeat=3):
print(''.join(i), end=' ')Функция принимает два параметра (набор символов и длина конечного объекта). С помощью join() получили строковое представление полученной комбинации.
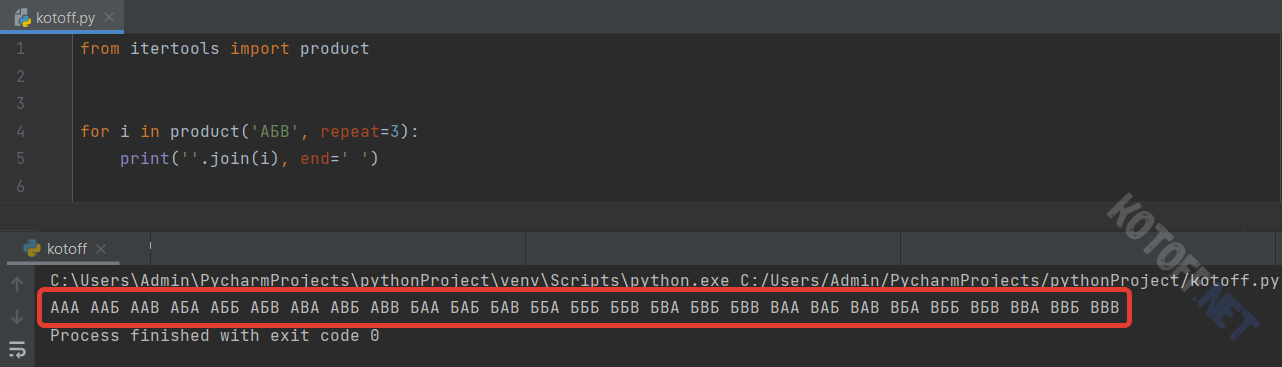 И, как можно заметить, в результате мы получили те самые 27 так называемых слов.
И, как можно заметить, в результате мы получили те самые 27 так называемых слов.
Можно добавить в цикл некий фильтр (условие). Например, сделаю так, чтобы комбинируемые слова начинались только с “X” и заканчивались на “YZY”:
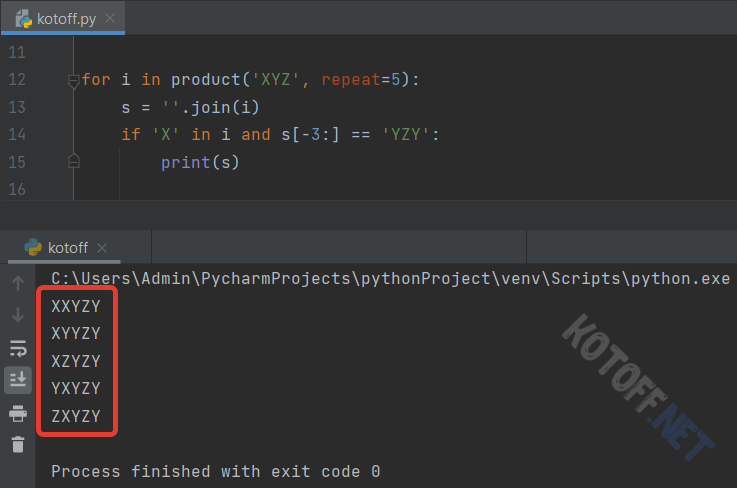
Попробуем сгенерировать всевозможные автомобильные номера для одного региона. Способ, конечно, не особо рациональный, но для примера сгодится:
from itertools import product
import re
chars = '0123456789АВЕКМНОРСТУХ'
reg = '[АВЕКМНОРСТУХ]{1}d{3}[АВЕКМНОРСТУХ]{2}'
for i in product(chars, repeat=6):
if re.fullmatch(reg, ''.join(i)):
print(''.join(i))Кстати, если добавить в цикл счётчик, то в итоге получим цифру 1.728.000 (12*10*10*10*12*12). Именно столько номеров формата x000xx можно наклепать для одного региона 🙂
2. Перестановка символов в наборе
В отличие от предыдущего примера, теперь мы не можем использовать по несколько раз один и тот же символ. Можем только переставлять их местами. Принцип подсчёта количества комбинаций остаётся тот же: необходимо перемножить количество вариантов символов на каждую позицию слова между собой. Но поскольку по мере составления слова на каждую последующую позицию символов будет оставаться всё меньше и меньше, то и формула также меняется на: n! / (n-k)! (n – количество доступных символов, k – длина слова). Если n = k, то можно использовать упрощённую формулу: n! (факториал числа n).
В питоне для таких целей используется функция permutations(). Принимает тоже два параметра: набор символов и длину генерируемой комбинации:
from itertools import permutations
for i in permutations('АБВ'):
print(''.join(i))Из трёх букв будет сгенерировано 6 различных слов с неповторяющимися символами (1! = 1 * 2 * 3 = 6)
Попробуем составить трёхзначные слова в 5-символьном алфавите (5! / (5-3)! = 120 / 2 = 60):
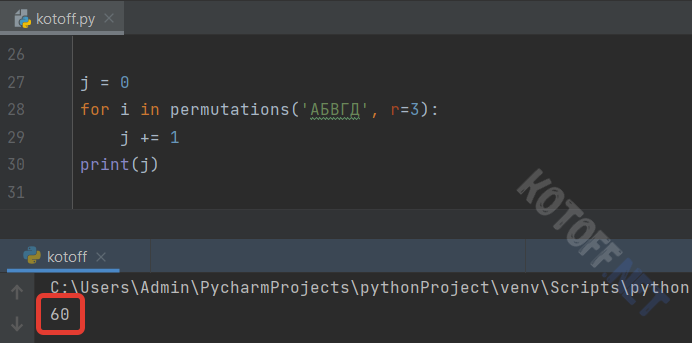
Кстати, если в заданном “алфавите” есть повторяющиеся символы, то они будут повторяться и в комбинациях:
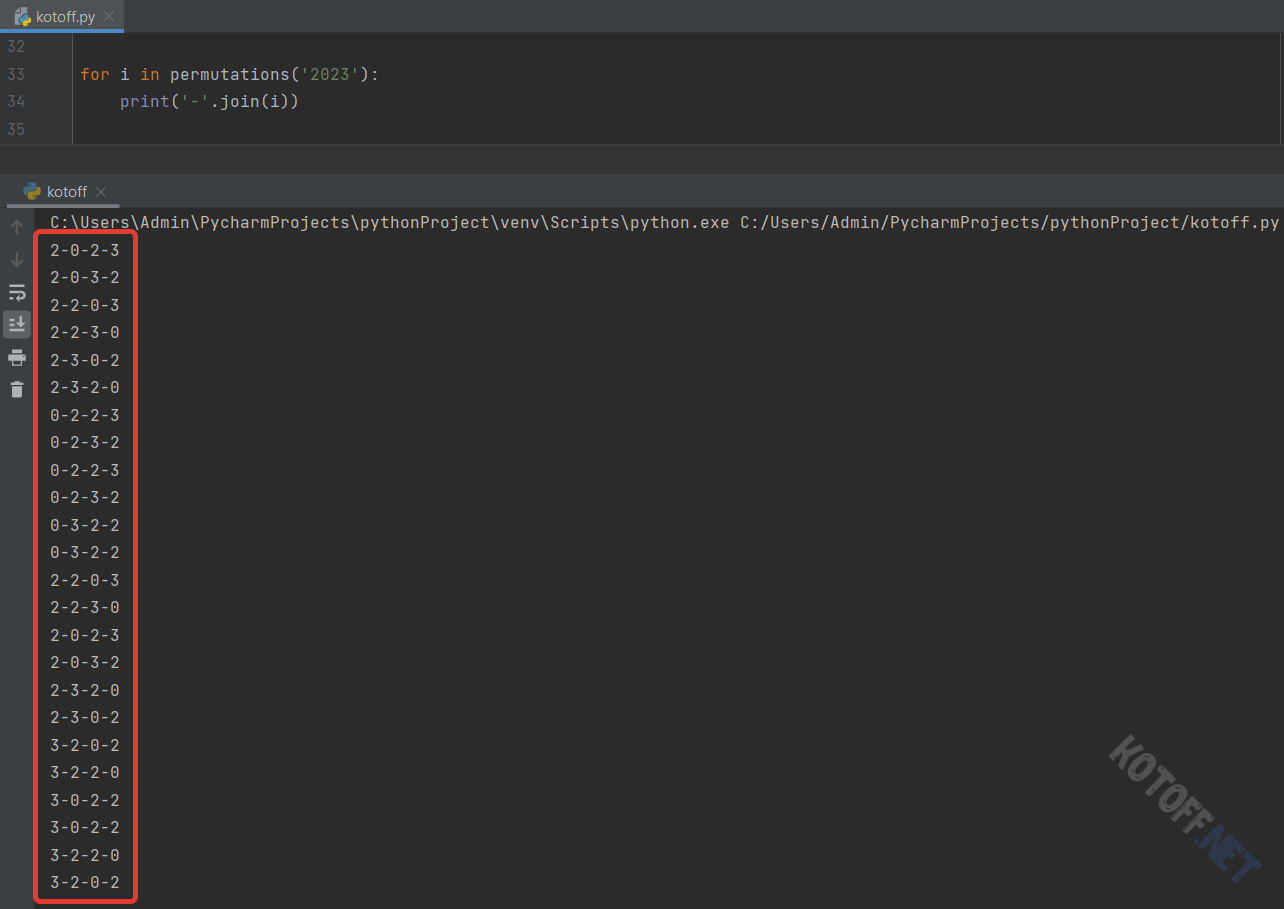
3. Сочетания без повторений
А если нужно составить не комбинации, а отдельные неповторяющиеся сочетания? Например, есть 6 человек. Вопрос: какими способами их можно разбить по парам? Опять же, пользуемся формулой: n! / (n-k)! / k! (n – количество доступных объектов/символов, k – количество сочетаний). Соответственно, существует 6! / (6-2)! / 2! = 720 / 24 / 2 = 15 вариантов разбиения этих 6 персон по парам.
Теперь реализуем эту задачу на питоне с помощью функции combinations(). Принимает она два параметра – список и кол-во сочетаний:
from itertools import combinations
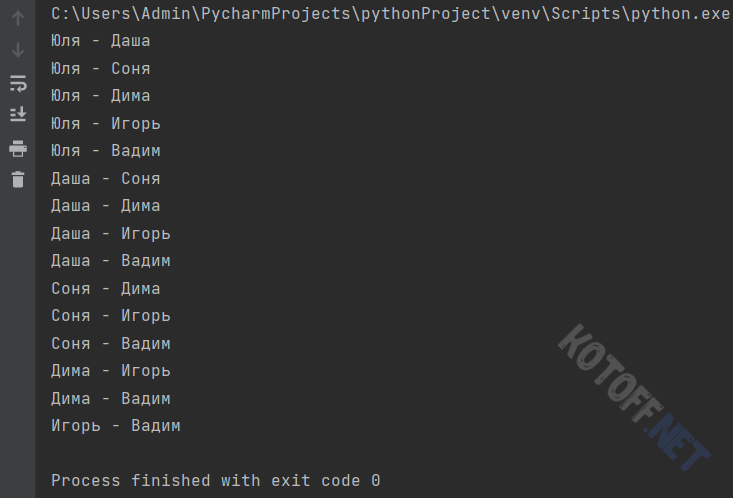
for i in combinations(['Юля', 'Даша', 'Соня', 'Дима', 'Игорь', 'Вадим'], 2):
print(' - '.join(i))Результат работы программы будет таков:
На этом, пожалуй, на сегодня всё. С наступающим! 

You’re going to have to be more specific on exactly WHAT you want your function to get. There are many different definitions of “combinations” and you haven’t specified whether you want ordered or unordered combinations.
Mathematically, if you have n elements and want a LIST of k of them (ordered with repeats), that gives you
n ^ k
combinations. (6 ^ 4 = 1296 combinations in your original example, which is a lot!). However, if you have n elements and want a MULTISET of k of them (unordered with repeats), that gives you
(n + k - 1)! / (k! * (n - 1)!)
combinations and is a much harder enumeration.
If k is small, you can generate the first one with a limited number of for loops but this becomes cumbersome very quickly as k grows. This strongly hints at the need for a RECURSIVE method:
public static String[] getAllLists(String[] elements, int lengthOfList)
{
//initialize our returned list with the number of elements calculated above
String[] allLists = new String[(int)Math.pow(elements.length, lengthOfList)];
//lists of length 1 are just the original elements
if(lengthOfList == 1) return elements;
else
{
//the recursion--get all lists of length 3, length 2, all the way up to 1
String[] allSublists = getAllLists(elements, lengthOfList - 1);
//append the sublists to each element
int arrayIndex = 0;
for(int i = 0; i < elements.length; i++)
{
for(int j = 0; j < allSublists.length; j++)
{
//add the newly appended combination to the list
allLists[arrayIndex] = elements[i] + allSublists[j];
arrayIndex++;
}
}
return allLists;
}
}
Not only will this method generate all the lists, but it will enumerate them in order. That is, the output will be
aaaa
aaab
aaac
aaa1
aaa2
aaa3
aaba
aabb
aabc
aab1
...
3323
333a
333b
333c
3331
3332
3333
using your original input. It can also generate any length of words (be very careful with this! Just with words of length 8 I wound up with 1,679,616 combinations!).
If the method confuses you (it’s a recursive method, so it’s a bit hard to follow) or if you want a solution to the second combination problem, feel free to ask. Also, this method is somewhat inefficient because it recalculates the combinations for all the sublists, so it’s not viable for really long lists. If you really wanted efficiency you would store the already-calculated tuples in a global list.
Необходимо получить все возможные комбинации расстановки + и – для заданной длины, например для 2 это будет ++, –, +-, -+.
задан 26 мая 2018 в 11:49
![]()
Если +- и -+ различаются в вашем случае, то вам не комбинации (сочетания) нужны (которые порядок не учитывают), а itertools.product() (размещение с повторениями):
>>> import itertools
>>> print(*map(''.join, itertools.combinations('+-', r=2)))
+-
>>> print(*map(''.join, itertools.combinations_with_replacement('+-', r=2)))
++ +- --
>>> print(*map(''.join, itertools.product('+-', repeat=2)))
++ +- -+ --
ответ дан 26 мая 2018 в 13:40
jfsjfs
51.8k11 золотых знаков107 серебряных знаков306 бронзовых знаков
Заметьте, что каждая такая расстановка соответствует бинарной записи некоторого числа, только вместо 0 пишется -, а вместо единицы – плюс.
Отсюда простой способ генерации – перечислить в цикле все числа от 0 до 2^N-1, выводя их бинарное представление с использованием алфавита "-+"
N = 4
for k in range(1<<N):
print(''.join('+' if (1 & (k >> i)) else '-' for i in range(N)))
Если строки перевернуть [::-1], порядок будет лексикографический
ответ дан 26 мая 2018 в 16:36
MBoMBo
47.8k1 золотой знак17 серебряных знаков40 бронзовых знаков
5
С такой задачей отлично справляется itertools.cobinations()
Чтобы не терялись зеркальные комбинации '+-', '-+' передаем двойную строку '+-+-', а для того чтобы комбинации не повторялись используем set().
from itertools import combinations
print(set(combinations('+-'*2, 2)))
ответ дан 26 мая 2018 в 12:11
pinguinpinguin
1,8232 золотых знака10 серебряных знаков22 бронзовых знака
2
С подстановочными знаками можно поэкспериментировать. Все они перечислены на странице поддержки MS Office в разделе о работе с Word.
Если ввести в форму поиска пять вопросительных знаков “?????”, то система выдаст очень плачевную картину, потому что во-первых, без указания границ слова результат выделит слова с этими пятью знаками в середине слова и во-вторых, среди вопросительных знаков могут быть пробелы. Даже если по краям установить угловые скобки “<?????>”, то избежать попадания пробела в середину слова не удастся. Так что поиск с вопросительными знаками отметаем.
Тогда нужно брать подстановочные знаки.
Границы слова отметить нужно обязательно – “<” и “>”. Далее можно попробовать ввести любой символ в диапазоне от “а” до “я” пять раз. Получим вот такую формулу: “<[а-я][а-я][а-я][а-я][а-я]>”.
Есть и более экономичный вариант, если указать количество символов (кроме пробелов) после заданного знака с помощью фигурных скобок. А этот заданный знак в диапазоне от “а” до “я”. (Если указать просто знак, то количество этих повторяющихся знаков будет 5 и нет гарантий, что в тексте есть слово с одинаковыми пятью буквами). И не забудем про границы слова
Итак, формула – “<[а-я]{5}>”. Количество букв в слове будет равно 5, а буква может быть любой в диапазоне от “а” до “я”.
|
SiNn3R 0 / 0 / 0 Регистрация: 19.09.2008 Сообщений: 10 |
||||
|
1 |
||||
Перебор возможных комбинаций символов23.09.2008, 21:19. Показов 46212. Ответов 51 Метки нет (Все метки)
Чет мой чайник совсем не варит! Помогите сделать следущее:
Логика мне ясна, а вот с реализацией туго! Число возможных вариантов: 3*3*3 = 27 Код ->->->->-> aaa aab aac aba abb abc aca acb acc baa bab bac bba bbb bbc bca bcb bcc caa cab cac cba cbb cbc cca ccb ccc Я думаю начать с конца слова, с постепенным смещением влево. Но вот запутался в циклах… Допустим меняю последний символ: Затем смещаюсь влево: Опять последний: И у меня ступор… Исходник пустил под скальпель, пытаясь что-то сделать, так что не просите показать А где есть исходники подобных алгоритмов?
0 |
|
Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782 |
23.09.2008, 21:19 |
|
51 |
|
qwone 10 / 10 / 2 Регистрация: 18.08.2008 Сообщений: 127 |
||||
|
23.09.2008, 22:20 |
2 |
|||
Смотри
0 |
|
SiNn3R 0 / 0 / 0 Регистрация: 19.09.2008 Сообщений: 10 |
||||
|
24.09.2008, 09:51 [ТС] |
3 |
|||
|
Смотри Хм, а если символов в слове 20? 20 циклов делать под каждый? Не есть хорошо. Ура, написал…
0 |
|
0 / 0 / 0 Регистрация: 29.09.2008 Сообщений: 9 |
|
|
24.07.2009, 18:47 |
4 |
|
Ура, написал… напиши реализацию плиз
0 |
|
Временно недоступен 957 / 228 / 14 Регистрация: 12.04.2009 Сообщений: 926 |
|
|
24.07.2009, 20:01 |
5 |
|
А это за сколько посчитает?
0 |
|
47 / 47 / 3 Регистрация: 07.01.2009 Сообщений: 297 |
|
|
24.07.2009, 21:02 |
6 |
|
Это комбинаторика. В данном случае, когда слово из 3 букв, то можно тупо все вариации подобрать циклами вложенных(и так можно до 6 вложенных циклов),т.е. получается перебор. Посмотри здесь(алгоритм похожий):
0 |
|
Search.. Заказ софта 343 / 188 / 21 Регистрация: 26.05.2009 Сообщений: 863 |
||||
|
24.07.2009, 21:08 |
7 |
|||
0 |
|
Ёрик 47 / 47 / 3 Регистрация: 07.01.2009 Сообщений: 297 |
||||
|
24.07.2009, 21:21 |
8 |
|||
|
Уже написали,что тройной цикл не пойдет ))
0 |
|
odip
7175 / 3234 / 81 Регистрация: 17.06.2009 Сообщений: 14,164 |
||||
|
24.07.2009, 22:04 |
9 |
|||
|
Нужно завести массив, где хранить номера в таблице символов.
Элементы word_num[] – это числа от 0 до char_count-1.
0 |
|
mirso 561 / 372 / 55 Регистрация: 05.04.2009 Сообщений: 767 |
||||
|
30.07.2009, 23:39 |
10 |
|||
|
Вывести все возможные комбинации слов
А это за сколько посчитает? “За сколько?” – это уже второй вопрос!
0 |
|
zim22 depict1 281 / 146 / 4 Регистрация: 11.07.2009 Сообщений: 606 |
||||
|
31.07.2009, 09:12 |
11 |
|||
|
А где есть исходники подобных алгоритмов?
1 |
|
schdub
3069 / 1407 / 425 Регистрация: 19.01.2009 Сообщений: 3,850 |
||||
|
31.07.2009, 11:05 |
12 |
|||
|
Вот небольшой исходничек, написаный, после прочтения “Техники Сетевых Атак”, Криса Касперски:
0 |
|
Gravity 577 / 571 / 65 Регистрация: 29.01.2009 Сообщений: 1,274 |
||||
|
31.07.2009, 14:04 |
13 |
|||
|
polivets, если делать цикл с таким условием
то будет затираться завершающий нуль-символ. Правильнее тогда задать буфер как buff[BUFFMAX+1].
0 |
|
mirso 561 / 372 / 55 Регистрация: 05.04.2009 Сообщений: 767 |
||||
|
31.07.2009, 18:09 |
14 |
|||
|
zim22,
Сообщение от SiNn3R zim22 они делают немножко ни то о чем просил автор вопроса
aaa aab aac
Вывод такой -> abc acb
0 |
|
depict1 281 / 146 / 4 Регистрация: 11.07.2009 Сообщений: 606 |
|
|
31.07.2009, 19:01 |
15 |
|
они делают немножко ни то о чем просил автор вопроса я понял это уже после того, как запостил
0 |
|
0 / 0 / 0 Регистрация: 28.10.2009 Сообщений: 4 |
|
|
28.10.2009, 17:40 |
16 |
|
Люди хелп ми по другому никак ..мне нужно найти комбинацию из abc по 5 разов ВОТ пример (составить смог только 47 комбинаций а их должнобыть 120): ababc, bbbab, cbbcc ну и т.д. не могу больше мозг кипит а программы так до сих пор и не нашёл=(((((
0 |
|
эволюционирую потихоньку 468 / 466 / 91 Регистрация: 30.06.2009 Сообщений: 1,401 |
|
|
28.10.2009, 17:48 |
17 |
|
по-другому ? в смысле решение отличное от решения в 14м посте?
0 |
|
0 / 0 / 0 Регистрация: 28.10.2009 Сообщений: 4 |
|
|
28.10.2009, 18:07 |
18 |
|
по-другому ? в смысле решение отличное от решения в 14м посте? нет я подставил символы тобишь буквы абс , но эти буквы обозначают для меня кое что иное , код который мне нужно подобрать состоит из 5 раз по 3 буквы , ещё раз приведу пример , : aaaaa, bbbbb, ccccc, ababc, bbbcb, aabcc…. что то в этом роде код зашифрован в 5 – и значениях а в одно значение можно подставить только a,b, или с . Теперь думаю понятней похожий пример я видел на этом сайте уже только там было из 3 по 3 , ; aaa, bbb, ccc, aab,aac,abb , abc, acc ….и т.д.
0 |
|
эволюционирую потихоньку 468 / 466 / 91 Регистрация: 30.06.2009 Сообщений: 1,401 |
|
|
28.10.2009, 18:27 |
19 |
|
короче, в твоём слове 5 символов каждый из которых может принимать одно из 3х значений Добавлено через 3 минуты
0 |
|
0 / 0 / 0 Регистрация: 28.10.2009 Сообщений: 4 |
|
|
28.10.2009, 18:38 |
20 |
|
Да вот именно это я и хотел сказать , просто времени мало спешу=) Добавлено через 8 минут Добавлено через 39 секунд Сочетаниями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются хотя бы одним элементом. Число сочетаний
0 |




 rev_permutation
rev_permutation
