Для вычисления арксинуса в Паскале нет стандартной функции, зато его можно выразить через арктангенс. Чтобы найти ArcSin(X), нужно сначала по формуле Пифагора найти косинус того же угла, синус которого равен X.
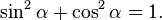
Затем, поделив синус на косинус, находим тангенс искомого угла, а затем, используя стандартную функцию арктангенса, и сам угол, который и будет искомым значением ArcSin(X).
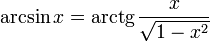
Борьба с погрешностью
С точки зрения математики, все действия проделаны корректно, кроме случаев X = ±1, приводящих к делению на 0, но и до того, как случится деление на 0, учитывая особенности машинного представления, имеет смысл находить арксинус другим путём, чтобы избегать стремящихся к бесконечности аргументов арктангенса. Разбиваем область определения арксинуса на центр, в котором производятся вычисления по выше приведённым формулам, и края. Разбить можно разными способами, но одно из способов разбиения примечательно тем, что аргументы, с которыми будет вызван ArcTan(X), будут не больше 1.0, что соответствует углу 45°, синус которого Sqrt(2)/2. Для правого края (Sqrt(2)/2 <= X <= 1) найдём арксинус другим способом: наоборот, поделим косинус (полученный по теореме Пифагора) на синус и получим котангенс, затем найдём угол, используя арккотангенс. Стандартной функции арккотангенса в Паскале нет, но арккотангенс очень просто выражается через арктангенс: ArcCot(X) := Pi/2 – ArcTan(X). Для левого края всё аналогично.
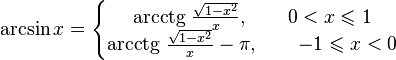
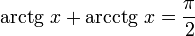
Реализация
program MyArcSin;
function ArcSin(X: Real): Real;
begin
if X <= –1.0 then
ArcSin := –Pi / 2
else if X < –Sqrt(2) / 2 then
ArcSin := –Pi / 2 – ArcTan(Sqrt(1 – Sqr(X)) / X) { левый край }
else if X <= Sqrt(2) / 2 then
ArcSin := ArcTan(X / Sqrt(1 – Sqr(X))) { центр }
else if X < 1.0 then
ArcSin := Pi / 2 – ArcTan(Sqrt(1 – Sqr(X)) / X) { правый край }
else
ArcSin := Pi / 2
end;
begin
WriteLn(ArcSin(–1.0):0:3, ‘ ‘, ArcSin(–0.9):0:3, ‘ ‘,
ArcSin(0.3):0:3, ‘ ‘, ArcSin(0.9):0:3, ‘ ‘,
ArcSin(1.0):0:3);
{ -1.571 -1.120 0.305 1.120 1.1571 }
end.
См. также
- Sin
- Pi
- ArcCos
- ArcTan
- ArcTan2
- Арксинус в Wikipedia
Как известно, ядро Паскаля предельно компактно, и многие математические функции в модуле System просто отсутствуют. Поэтому у людей, изучающих основы программирования именно на этом языке, типовые математические расчёты зачастую вызывают проблемы. Далее приводятся пути решения наиболее типичных из этих проблем.
Возведение в произвольную степень на Паскале
Требуется вычислить значение с = ab. В зависимости от значений
основания a и показателя степени b,
вычисление степени может быть реализовано по-разному.
Если a > 0, а b может принимать произвольные вещественные значения, используем известную формулу
ab = exp (b * ln a):
c:=exp(b*ln(a));
Если b – целое число (вообще говоря, “не слишком большое” по модулю),
а a – любое (не равное нулю при b < 0),
возведение в степень может быть реализовано с помощью цикла:
var i:integer;
{...}
c:=1;
for i:=1 to abs(b) do c:=c*a; {перемножение одинаковых сомножителей b раз}
if b<0 then c:=1/c; {учёт знака показателя}
Для целого b и не равного нулю a выгоднее считать с помощью экспоненты и логарифма, не забывая о том, что не существует логарифмов от отрицательных чисел:
c:=exp(b*ln(abs(a))); {степень положительного основания}
if (odd(b)=true) and (a<0) then c:=-c; {если основание отрицательно, а показатель нечетный, то меняем знак}
Вычисление корня произвольной степени на Паскале
Стандартная функция sqrt умеет извлекать только квадратный корень.
Извлечь корень степени n (где n – натуральное)
из числа a можно всегда, кроме случая, когда a < 0
и при этом n четно. Извлечь корень степени n
из числа a означает возвести число a в степень 1/n.
При этом знак корня совпадает со знаком a.
Ниже приводится код функции, вычисляющей корень произвольной степени
n от своего аргумента a:
function root(a:real;n:word):real;
{Тип word здесь указывает, что n положительно}
var r: real;
begin
r:=exp(ln(abs(a))/n); {корень из модуля}
if a<0 then root:=-r else root:=r {учет знака}
end;
Вычисление логарифмов на Паскале
Стандартная функция ln вычисляет только натуральный логарифм.
Для вычисления логарифмов по другим основаниям можно применить формулу
log a b = ln b / ln a:
c:=ln(b)/ln(a);
В частности, для вычисления десятичного логарифма lg b можно записать:
c:=ln(b)/ln(10);
Вычисление обратных тригонометрических функций (арксинусов и арккосинусов) на Паскале
В Паскале имеется стандартная функция arctan для вычисления арктангенса.
Другие обратные тригонометрические функции могут быть выражены через неё с помощью формул тригонометрии.
Для вычисления y = arcsin x, где, конечно, |x| <= 1,
можно применить один из следующих способов:
if x=1 then y:=pi/2 else if x=-1 then y:=-pi/2 else y:=arctan(x/sqrt(1-sqr(x)));
или
y:=2*arctan(x/(1+sqrt(1-sqr(x))));
на практике следует помнить о возможных погрешностях при сравнении вещественных чисел (глава учебника, п.7.2).
Для вычисления z = arccos x, где |x| <= 1,
можно использовать тот факт, что
сумма арксинуса и арккосинуса некоторого значения
равна прямому углу:
if x=1 then z:=0 else if x=-1 then z:=pi else z:=pi/2-arctan(x/sqrt(1-sqr(x)));
или
z:=pi/2-2*arctan(x/(1+sqrt(1-sqr(x))));
Вычисление полярных углов на Паскале
Полярным углом точки с координатами (x,y),
отличной от начала координат,
называют угол между положительным направлением оси Ox и
направлением из начала координат на данную точку. При этом угол
отсчитывается против часовой стрелки.
Строго говоря, полярный угол не всегда
равен arctg (y/x), это верно лишь при x > 0.
Кроме того, при делении большого значения y на малое x
возможно переполнение. Показанная ниже функция вычисляет полярный угол fi,
лежащий в промежутке от -pi до +pi,
для любой точки с координатами (x,y), не совпадающей с началом координат:
function fi(x:real; y:real):real; var f:real; begin if abs(x)>abs(y) then begin f:=arctan(y/x); if x>0 then fi:=f else if y>=0 then fi:=f+pi else fi:=f-pi end else begin f:=arctan(x/y); if y>0 then fi:=pi/2-f else fi:=-pi/2-f end end;
Проблема с приведением типов на Паскале
Начинающие “паскалисты” нередко не понимают строгой типизированности этого языка, из-за чего находят в нём несуществующие “баги”. Вот простейший пример.
var a,b:integer;
r:longint;
begin
a:=1000;
b:=200;
r:=a*b;
writeln (r);
end.
Эта программа выдаст отнюдь не 200000, как может показаться. Ответ будет равен 3392 (результат переполнения). Никакого бага нет. Тип выражения в Паскале определяется только типом входящих в него переменных, но не типом переменной, куда записывается результат. То есть, мы вычислили с переполнением произведение двух переменных типа Integer, а потом “испорченный” результат переписали в переменную типа Longint. ничего не изменит и
r:=Longint(a*b);
Здесь тоже сначала вычислен результат с переполнением, затем преобразован к типу Longint. А вот
r:=Longint(a)*b;
рулит, получите свои 200000 🙂 Указанная ошибка часто встречается в программах начинающих. Чтобы её не повторять, помните – выражение в Паскале должно быть приведено к нужному типу в процессе его вычисления, а не после его окончания или при присваивании.
![]()
| Description | |||||||||||||||
| The ArcSin function is a mathematical function giving the value in radians of the Arc Sine of Number. | |||||||||||||||
| Notes | |||||||||||||||
|
The System unit supports only the following angular functions:ArcTan Sin Cos |
|||||||||||||||
| Related commands | |||||||||||||||
|
| Example code : The ArcSin of 0.5 gives 30 degrees |
// Full Unit code. // ———————————————————– // You must store this code in a unit called Unit1 with a form // called Form1 that has an OnCreate event called FormCreate. unit Unit1; interface uses Math, // Unit containing the ArcSin command type var Form1: TForm1; implementation procedure TForm1.FormCreate(Sender: TObject); var float : single; begin // The ArcSin of 0.5 should give 30 degrees float := ArcSin(0.5); float := RadToDeg(float); // Convert result to degrees ShowMessage(‘ArcSin of 0.5 = ‘+FloatToStr(float)+’ degrees’); end; end. |
| Hide full unit code |
ArcSin of 0.5 = 30 degrees |
