Содержание
- Задание №21. Профиль рельефа местности.
- Страница 4 — 5. План местности — Контурные карты по географии. 6 класс. Дрофа
- Коварные невидимые горизонтали
- Постановка задачи
- Комментарий к решению
- Вопрос №2 — формальное решение
- Вопрос №2 — решение для внимательных
- Вопрос №5
Задание №21. Профиль рельефа местности.
Теория
Перед тем, как приступить к разбору задания №21, повторим тему «Изображение рельефа на карте»
Рельеф – это все неровности земной поверхности.
Так как рельеф, это что-то объемное (3D формат), то его сложно изобразить на плоской карте или плане (2D формат). И, тем не менее, выход был найден.
Рельеф может быть изображен при помощи:
а) послойной окраски (для карт мелкого масштаба);
б) горизонталей (для карт крупного масштаба).
Для планов местности и крупномасштабных карт для изображения рельефа используют горизонтали.
Горизонтали (изогипсы) — линии, соединяющие точки с одинаковой высотой (= лежащие на одинаковой высоте). Горизонтали всегда проводятся через одинаковое расстояние и зная количество горизонталей, а также расстояние между ними, возможно узнать высоту форм рельефа.

Например, высота у подножия холма 130 метров над уровнем моря, а на плане холм изображен 8 горизонталями с расстоянием 5 метров. Это значит, что относительная высота (высота от подножия) у холма порядком 40 метров, а абсолютная высота (высота над уровнем моря), 170 метров.
Обратите внимание на несколько моментов!
Для определения высот используют значения, подписанные на горизонтали, но не все горизонтали подписаны (= не у всех горизонталей указана высота).Это сделано для того, чтобы не перегружать цифрами изображение. Чтобы определить высоту не подписанной горизонтали нужно найти ближайшую подписанную горизонталь и по числу интервалов между ними с учётом направления ската определить высоту искомой горизонтали.
При этом необходимо правильно установить направление ската, т. е. в какую сторону от данной горизонтали высоты увеличиваются, а в какую – уменьшаются. Местность всегда понижается к водотокам (реки, ручьи).
Чем чаще и ближе к друг другу расположены горизонтали, тем круче склон. И наоборот, если горизонтали отдалены друг от друга, то склон пологий. Если на участке не изображены горизонтали, то на участке нет уклона.
Практика
Найдем высоты точек А и В. Под планом написано, что горизонтали проведены через 2,5 метра.

Точка А лежит на подписанной горизонтали с высотой 150 метров. И значит, точка А имеет высоту 150 метров.
Точка В лежит на не подписанной горизонтали, но тем не менее, ее высоту узнать не трудно. Рядом с точкой В, через одну горизонталь находится точка с высотой 153 м. Это самая высокая точка данного участка местности. Рядом с этой точкой горизонталь с высотой 152,5 м. Точка В расположена на еще одну горизонталь ниже (152,5-2,5=150 м). Точка В также имеет высоту 150 метров.
Теория Профиль местности – это рельеф местности как бы разрезанный вертикально.
На профиле рельефа, построенном между двумя точками, изображаются все формы рельефа «в разрезе», которые встречаются на карте (местности) между этими двумя точками.
Профиль выглядит как график, по двум осям которого отображена шкала высот и отмечены высоты начальной и конечной точки. Между ними отмечены высоты промежуточных форм рельефа, которые встречаются по линии от первой точки до второй.

Для того, чтобы понять, правильно ли построен профиль местности необходимо:
1.Найти высоту начальной и конечной точки при помощи горизонталей.
- Оценить, какие высоты расположены между двумя точками. Есть ли между данными точками повышение или понижение в рельефе, на каких склонах располагаются точки: на крутом склоне или на более пологом, протекает ли между ними река.
Обратите внимание! В большинстве случаев для того, чтобы понять, какой профиль рельефа рельеф правильный, необходимо только верно определить высоту начальной и конечной точки.
Практика
По условию задания, на рисунках представлены варианты профиля рельефа местности, построенные на основе карты по линии А – В разными учащимися. Нужно найти тот профиль, который построен корректно для данной линии.
Обратите внимание! Так как строить и анализировать профиль нужно именно по линии А-В, то первая отметка высоты на профиле будет принадлежать точке А, а последняя — точке В.
В ОГЭ необходимо определить какой из профилей рельефа местности построен верно для линии А — В. В ЕГЭ же необходимо данный профиль построить, что сложнее
Задача №1

Решение задачи №1
В данной задаче точка А расположена на берегу реки Черная. Ближайшая подписанная горизонталь к ней имеет высоту 140 метров. Точка А лежит на 3 горизонтали ниже высоты 140 метров. По условию горизонтали проведены через 2,5 метра. Соответственно, высота точки Апримерно 140- (2,5*3)=132,5метра и даже ниже. Так как точка А лежит все ниже горизонтали 132,5.
Ближайшая подписанная горизонталь к точке В имеет высоту 150 метров. Так как точка В располагается выше это подписанной горизонтали, то и высоту он будет иметь большую. От подписанной горизонтали до точки В две горизонтали. Соответственно, высота точки В примерно 150+ (2,5*2)=155 метров и даже выше. Так как точка В лежит выше горизонтали 155 метров.
Рассмотрим предложенные варианты: 1,2 и 3 профили рельефа нам не подходят. Так как на этих профилях отображены некорректные высоты точек А и В. А вот в четвертом профиле все верно.
Ответ: 4.

Решение задачи №2
Ближайшая подписанная горизонталь к точке А имеет высоту 90 метров. Точка А лежит на следующей горизонтали выше. По условию горизонтали проведены через 2,5 метра. Соответственно, высота точки А — 92,5 метра.
Ближайшая подписанная горизонталь к точке В имеет высоту 100 метров. Точка В лежит на следующей горизонтали выше. По условию горизонтали проведены через 2,5 метра. Соответственно, высота точки В — 102,5 метра.
Между точками протекает река, и, это значит, что к реке идет понижение в рельефе. При этом точки А и В располагаются на разных склонах. Склон, где расположена точка А — более пологий, а где точка В — более крутой.
Рассмотрим предложенные варианты: 1,2 и 4 профили рельефа нам не подходят. Так как на этих профилях отображены некорректные высоты точек А и В. А вот на третьем профиле все верно.
Ответ: 3.
Задача №3

Решение задачи №3
Ближайшая подписанная горизонталь к точке А имеет высоту 140 метров. Точка А лежит на 3 горизонтали ниже высоты 140 метров. По условию горизонтали проведены через 2,5 метра. Соответственно, высота точки А примерно 140- (2,5*3)=132,5 метра и даже ниже. Так как точка А лежит ниже горизонтали 132,5.
Ближайшая подписанная горизонталь к точке В имеет высоту 150 метров. Так как точка В располагается выше это подписанной горизонтали, то и высоту он будет иметь большую. От подписанной горизонтали до точки В две горизонтали. Соответственно, высота точки В примерно 150+ (2,5*2)=155 метров и даже выше. Так как точка В лежит выше горизонтали 155 метров. Но ниже 157 метров, так как 157 — наивысшая точка данного участка местности, обозначена отдельно.
Рассмотрим предложенные варианты: 1,2 и 3 профили рельефа нам не подходят. Так как на этих профилях отображены некорректные высоты точек А и В. А вот в четвертом профиле все верно.
Ответ: 4.
Дата добавления: 2019-03-09 ; просмотров: 4943 ; Мы поможем в написании вашей работы!
Источник
Страница 4 — 5. План местности — Контурные карты по географии. 6 класс. Дрофа
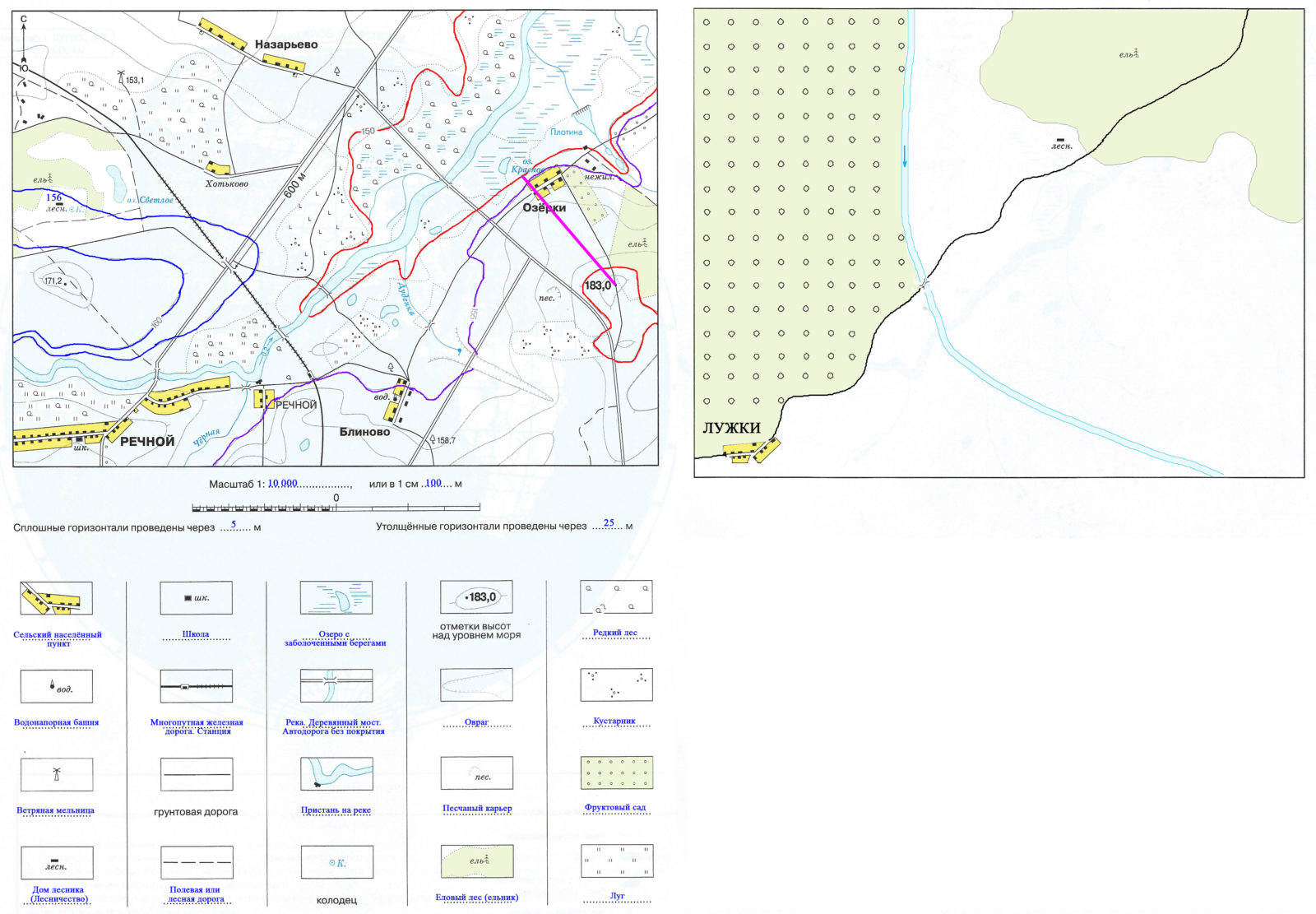
Комментарий: Перед выполнением работы, обязательно изучите Правила оформления контурных карт. В них вы найдёте информацию о том, как должны быть сделаны надписи к различным географическим объектам. Например, что все водные объекты подписываются синим цветом, а остальные — чёрным.
При этом, если вы внимательно рассмотрите наши ГДЗ, то увидите, что на наших картах объекты подписаны самыми разными цветами. Это сделано специально, ведь наша главная цель — помочь вам сориентироваться в огромном количестве информации, которой насыщена любая карта. Разноцветные надписи помогут вам быстро найти нужное: города и реки, моря и равнины. Вы сможете быстро увидеть что добавилось на карте в результате выполнения следующего задания и лучше понять что и где находится.
Так что пользуйтесь нашими картами «с умом», чтобы ваши оценки не были снижены из-за тонкостей оформления. Работу лучше выполнять по шагам, последовательно выполняя задания к контурным картам. Для того, чтобы увеличить карту, просто нажмите на неё. Также можно увеличивать и уменьшать размер страницы при помощи одновременного клавиш Ctrl и «+» или Ctrl и «-«.
Для выполнения заданий будем рассматривать карту атласа на страницах 8 и 9.
1. Подпишите значения условных знаков.
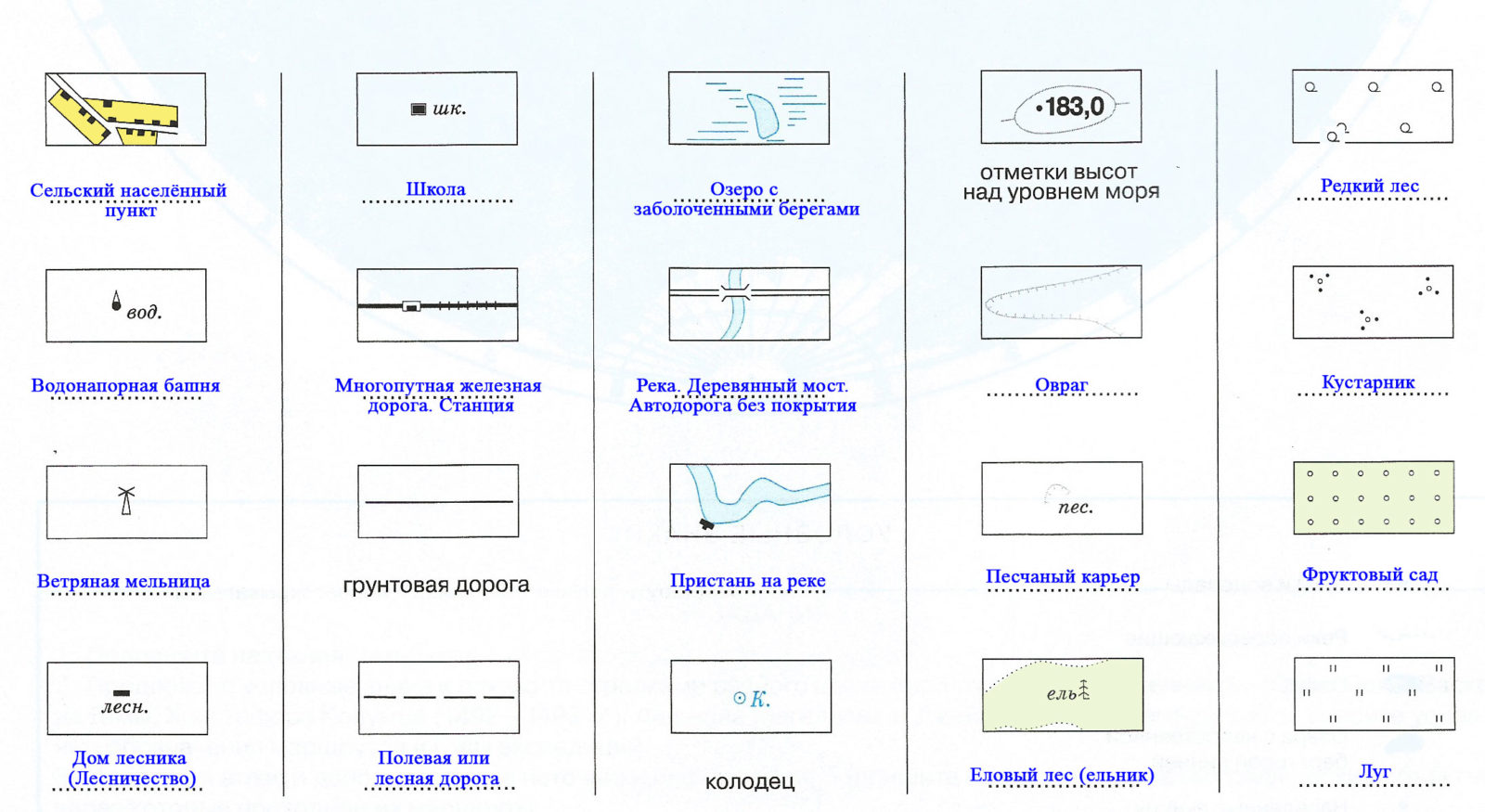 2. Обозначьте принятыми условными знаками подписанные на плане объекты: редкий лес на болоте, еловый лес, редкий лес на лугу, луг с кустарником, плотину, кустарник.
2. Обозначьте принятыми условными знаками подписанные на плане объекты: редкий лес на болоте, еловый лес, редкий лес на лугу, луг с кустарником, плотину, кустарник.
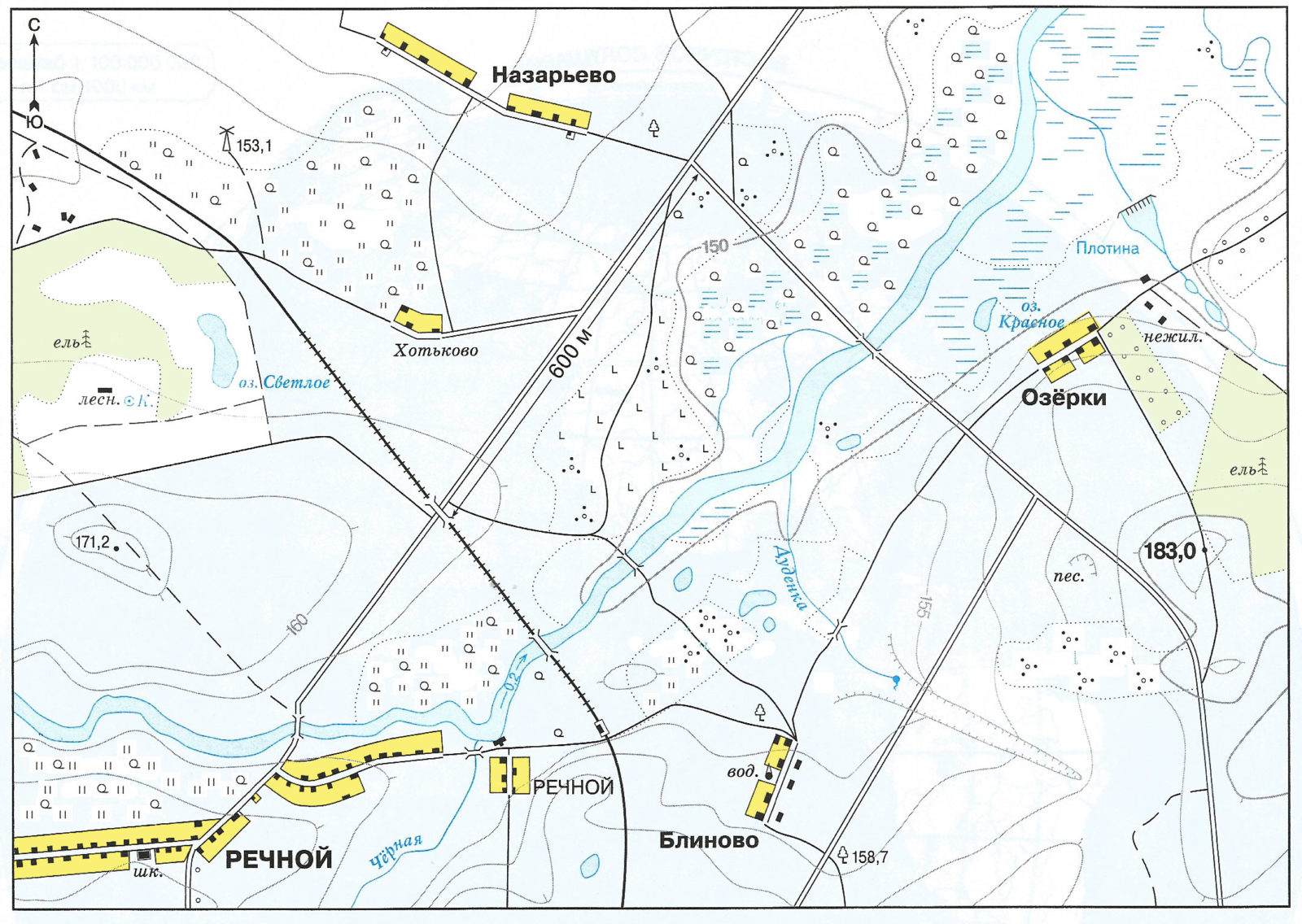
3. Известно, что расстояние на местности от железнодорожного моста до перекрёстка автомобильных дорог составляет 600 м. Определите масштаб плана и впишите его в легенду плана.
Измерим это расстояние на карте линейкой. Получается, что 600 метров на местности = 6 см на карте. Значит 1 см на карте равен 100 метрам на местности. Переведем метры в сантиметры: 100 м = 10 000 см, то есть масштаб карты 1:10 000.
4. Определите, через сколько метров проведены сплошные и утолщённые горизонтали, и укажите их в легенде плана.
Рассмотрим карту. Для удобства обведём утолщенные горизонтали красной линией, а ближайшую сплошную горизонталь с обозначением высоты — фиолетовой линией.
Мы видим, что красная горизонталь с отметкой расположена на уровне 150 м, а ближайшая к ней фиолетовая — на уровне 155 м. Значит расстояние между сплошными горизонталями на этой карте составляет 5 метров.
По правилам, утолщенные диагонали проводятся по каждой пятой сплошной горизонтали. То есть расстояние между утолщенными горизонталями составляет 5 • 5 = 25 м. Можно вычислить, что вторая обведенная нами красным цветом утолщенная горизонталь находится на высоте 150 + 25 = 175 м.
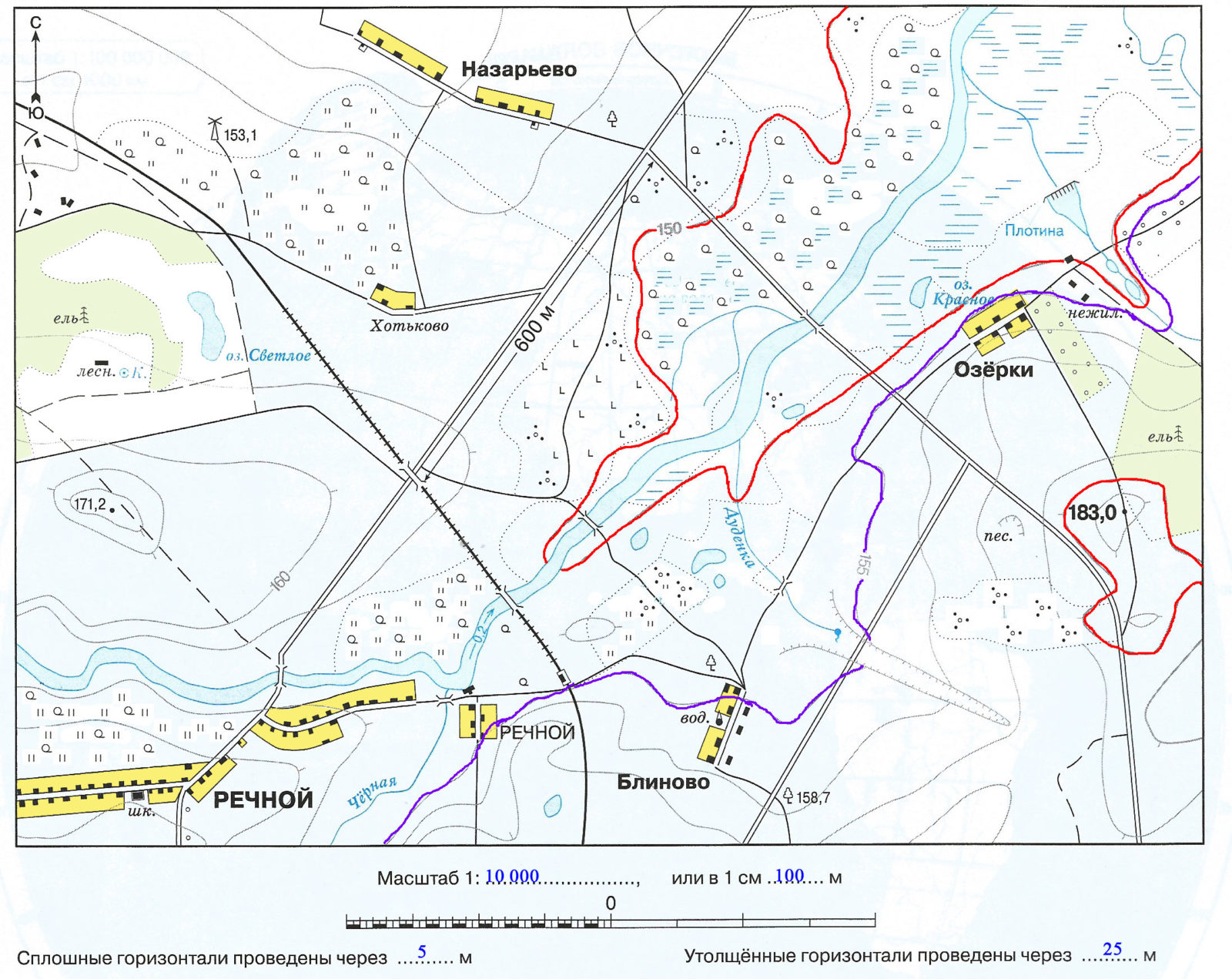
5. Определите максимальную и минимальную абсолютные высоты, подписанные на плане. Проведите между ними линию и подпишите расстояние между отметками высот. Определите относительную высоту.
- Максимальная абсолютная высота, отмеченная на карте — это холм высотой 183 метра.
- Минимальная абсолютная высота, отмеченная на карте — это утолщенная горизонталь с отметкой 150 м (отмечена красной линией).
- Между максимальной и минимальной высотами проведена толстая розовая линия (перпендикуляр к горизонтали). Относительная высота равна 183 — 150 = 33 метра.
- Расстояние между этими точками на карте составляет 4 см. То есть на местности между самой высокой и самой низкой точкой расстояние составляет 400 метров.
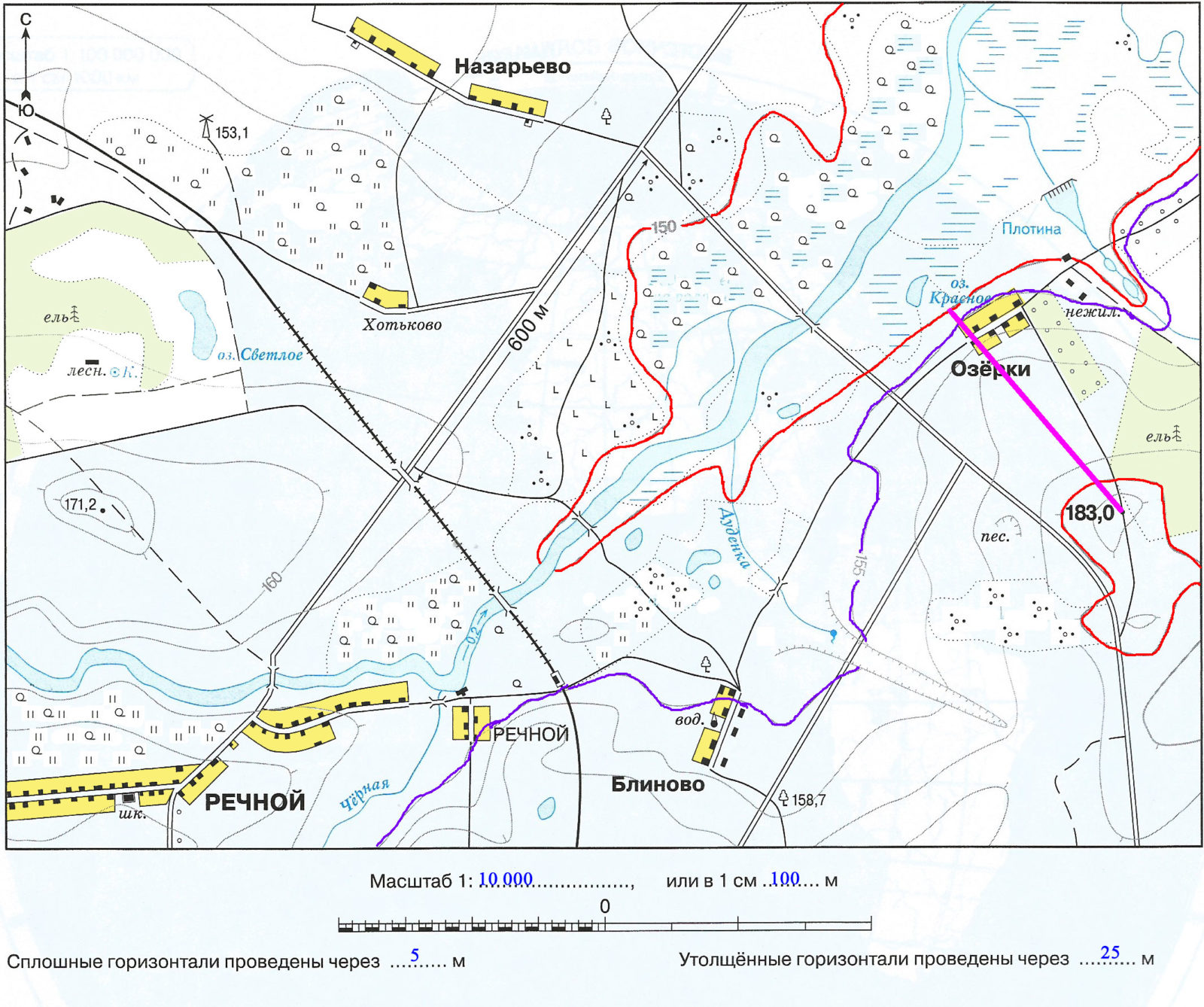
6. Определите и подпишите абсолютную высоту домика лесника, расположенного в западной части плана.
Для удобства обведём ближайшие к домику лесника горизонтали синими линиями. Мы видим, что горизонталь, расположенная выше домика лесника имеет отметку 160 метров. Так как расстояние между сплошными горизонталями составляет 5 метров, то горизонталь, расположенная ниже домика лесника находится на отметке 155 м.
Можно предположить, что домик лесника находится на высоте 156 метров над уровнем моря.

7. Составьте план местности по описанию:
«От посёлка Лужки, расположенного на юго-западе, к хвойному лесу, расположенному на северо-востоке, ведёт грунтовая дорога. Примерно на середине пути к лесу протекает небольшая речка, перебраться через которую можно по деревянному мосту. Речка течёт с севера и вскоре после моста поворачивает на юго-восток. От посёлка и до речки, слева от дороги, тянутся фруктовые сады. На самом краю леса, к северу от дороги, стоит избушка лесника».
Источник
Коварные невидимые горизонтали
Постановка задачи
Принесли мне недавно посмотреть актуальные задания по географии для 5-ого класса. Так как на оригинальной карте уже был выполнен ряд построений, то здесь привожу свою «кавер-версию» оной:
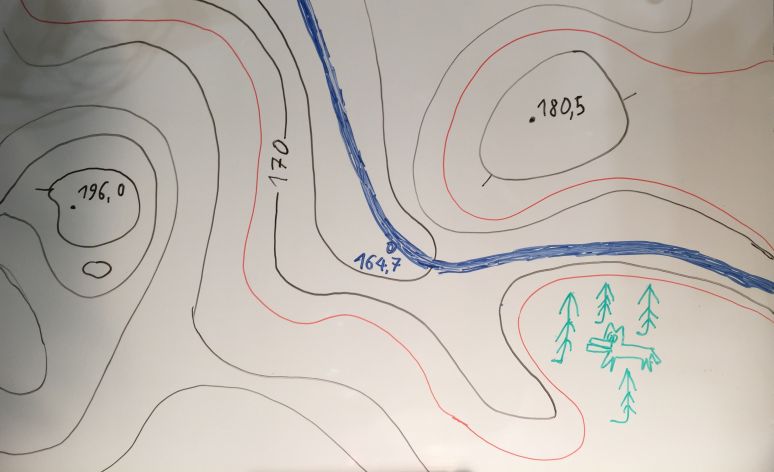
Итак, парочка заданий:
Комментарий к решению
Никогда особо не увлекался географией, поэтому подошёл к решению с формальной стороны. Я предлагаю алгоритм решения, который любителям географии может показаться странным и отрешённым от сути проблемы.
Вопрос №2 — формальное решение
Ну, тут всё просто: находим известную горизонталь (тут подписана только одна — 170 м.) — обозначим её высоту как H, находим ещё одну отметку, желательно, с максимально удалённой по модулю величиной. Из известных высот остаются 196 м., 164,7 м. и 180,5 м. Точка с наибольшим перепадом высот, относительно 170 м. — 196 м., обозначим её высоту как P.
Теперь надо посчитать количество горизонталей (N) между двумя выбранными точками. Необходимо учесть, что в процессе движения от первой точки ко второй, одна и та же высота может повторяться. Для правильного подсчёта, необходимо выбрать ближайшую к точке P точку на горизонтали H. (Или не считать повторяющиеся горизонтали: здесь аналогия с открывающимися/закрывающимися скобками и уровнем вложенности.)
Например, если двигаться к точке 180,5 из точки A (см. рисунок), то N=5, а если из точки B (и это правильно), то — 2.
Двигаясь из точки A к отметке 196 м., мы пересечём N=5 горизонталей.
Искомая величина Δ, удовлетворяет системе неравенств:
Эту систему я собрал из двух простых условий: расстояние между горизонталями должно быть таким, чтобы одноврменно
- его хватало на N горизонталей;
В нашем случае: H=170, P=196, N=5 — таким образом:
Логично предположив, что ответ должен быть целым, найдём решение системы:
Ответ: Δ=5 м.
Мы могли выбрать и любую другую высоту в качестве точки P, например, 164,7 м. В этом случае:
Этой системе, помимо найденного Δ=5, удовлетворяет и Δ=3 и Δ=4.
Вопрос №2 — решение для внимательных
Если прежде чем отвечать на второй вопрос, прочитать все предложенные задания, то из пятого можно узнать, что утолщённая горизонталь соединяет точки с высотой 175 м. Так как соседняя горизонталь подписана (170 м.), то:
Вопрос №5
Не знаю как Вас, а меня этот вопрос поразил формулировкой: на плане, мол, есть ещё особые горизонтали, но я Вам их не покажу — сами угадайте. Какого цвета невидимая линия? И, кстати, если это вопрос — почему в конце предложения нет вопросительного знака? Ах, да — мы же не на «русском».
Я, конечно, не блещу соображалкой, поэтому потребовалось перечитать вопрос несколько раз, пока, наконец, он не развернулся в понимании в следующую формулировку:
Рассуждая таким образом, можно заключить, что максимальный перепад высот относительно утолщённой горизонтали (175 м.) меньше искомого шага ΔB.

Проанализировав план, приходим к выводу:
Второе условие избыточно, таким образом:
Анализируя план ранее, мы пришли к выводу, что расстояние между горизонталями (некоторые из которых утолщённые) — Δ=5 м. Значит, ΔB делится на 5 без остатка (иначе не попадёт в сетку).
Известная нам утолщённая горизонталь должна удовлетворять искомой ΔB, то есть 175 должно делиться на ΔB без остатка.
Алгоритм следующий: найдём минимальное ΔB из условий (1) и (2), полученную оценку подставим в условие (3), получив максимальный делитель для последующего перебора (если x минимален, то y=const/x — максимален).
— округление в большую сторону):
Так как 175/ΔB min =7, то осталось проверить числа 6, 5, 4, … Приступим к перебору.
| I | ΔB=175/I |
| 7 | 25 |
| 6 | дробное |
| 5 | 35 |
| 4 | дробное |
| 3 | дробное |
| 2 | дробное |
| 1 | 175 |
Таким образом, получаем три возможных ΔB:
но нас и предупреждали: «Предложите свои варианты ответа».
Если уж выбирать единственный ответ, то число должно быть удобным в использовании в качестве шага по высоте. Думается адекватным, сформулировать в качестве критерия «эргономичности числа» следующее выражение:
— десятичный логарифм, k, n — целые, положительные числа. ΔB, для которого будет выполняться указанное тождество при минимальном k — подходит. Данное тождество позволит нам найти число, которое быстрее всего (иначе говоря — при умножении на минимальный множитель) даст число вида 10 n , то есть 10, 100, 1000 и так далее, если такое вообще возможно.
Источник
Постановка задачи
Принесли мне недавно посмотреть актуальные задания по географии для 5-ого класса. Так как на оригинальной карте уже был выполнен ряд построений, то здесь привожу свою “кавер-версию” оной:

Итак, парочка заданий:
2. Определите, через сколько метров проведены горизонтали на плане местности.
…
5. Выделите коричневым (у меня только красный маркер – не обессудьте) цветом утолщённую горизонталь, соединяющую точки с абсолютной высотой 175 м. Через сколько метров проведены утолщённые горизонтали, если на плане показана только одна из них – 175 м. Предложите свои варианты ответа.
Комментарий к решению
Никогда особо не увлекался географией, поэтому подошёл к решению с формальной стороны. Я предлагаю алгоритм решения, который любителям географии может показаться странным и отрешённым от сути проблемы.
Вопрос №2 – формальное решение
Ну, тут всё просто: находим известную горизонталь (тут подписана только одна – 170 м.) – обозначим её высоту как H, находим ещё одну отметку, желательно, с максимально удалённой по модулю величиной. Из известных высот остаются 196 м., 164,7 м. и 180,5 м. Точка с наибольшим перепадом высот, относительно 170 м. – 196 м., обозначим её высоту как P.

Теперь надо посчитать количество горизонталей (N) между двумя выбранными точками. Необходимо учесть, что в процессе движения от первой точки ко второй, одна и та же высота может повторяться. Для правильного подсчёта, необходимо выбрать ближайшую к точке P точку на горизонтали H. (Или не считать повторяющиеся горизонтали: здесь аналогия с открывающимися/закрывающимися скобками и уровнем вложенности.)
Например, если двигаться к точке 180,5 из точки A (см. рисунок), то N=5, а если из точки B (и это правильно), то – 2.
Двигаясь из точки A к отметке 196 м., мы пересечём N=5 горизонталей.
Искомая величина Δ, удовлетворяет системе неравенств:
Δ<|H-P|/N,
Δ>|H-P|/(N+1).
Эту систему я собрал из двух простых условий: расстояние между горизонталями должно быть таким, чтобы одноврменно
- его хватало на N горизонталей;
- его не хватало на (N+1) горизонталь.
В нашем случае: H=170, P=196, N=5 – таким образом:
Δ<|170-196|/5,
Δ>|170-196|/(5+1).
Вычислим:
|170-196|/5=|-26|/5=26/5=5,2;
|170-196|/(5+1)=26/6=4,(3).
Логично предположив, что ответ должен быть целым, найдём решение системы:
Δ<5,2,
Δ>4,(3).
Ответ: Δ=5 м.
Мы могли выбрать и любую другую высоту в качестве точки P, например, 164,7 м. В этом случае:
Δ<5,3,
Δ>2,65.
Этой системе, помимо найденного Δ=5, удовлетворяет и Δ=3 и Δ=4.
Вопрос №2 – решение для внимательных
Если прежде чем отвечать на второй вопрос, прочитать все предложенные задания, то из пятого можно узнать, что утолщённая горизонталь соединяет точки с высотой 175 м. Так как соседняя горизонталь подписана (170 м.), то:
Δ=175-170=5 м.
Вопрос №5
Через сколько метров проведены утолщённые горизонтали, если на плане показана только одна из них
Не знаю как Вас, а меня этот вопрос поразил формулировкой: на плане, мол, есть ещё особые горизонтали, но я Вам их не покажу – сами угадайте. Какого цвета невидимая линия? И, кстати, если это вопрос – почему в конце предложения нет вопросительного знака? Ах, да – мы же не на “русском”.
Я, конечно, не блещу соображалкой, поэтому потребовалось перечитать вопрос несколько раз, пока, наконец, он не развернулся в понимании в следующую формулировку:
Характер рельефа (диапазон высот) фрагмента местности, отображённого на плане, таков, что содержит только одну особую горизонталь. Исходя из этого, определите: с каким шагом по высоте проведены особые горизонтали (которые, возможно, присутствуют на большем фрагменте плана)?
Рассуждая таким образом, можно заключить, что максимальный перепад высот относительно утолщённой горизонтали (175 м.) меньше искомого шага ΔB.

Проанализировав план, приходим к выводу:
ΔB>196-175,
ΔB>175-164,7.
Вычислим:
ΔB>21,
ΔB>10,3.
Второе условие избыточно, таким образом:
ΔB>21.
Анализируя план ранее, мы пришли к выводу, что расстояние между горизонталями (некоторые из которых утолщённые) – Δ=5 м. Значит, ΔB делится на 5 без остатка (иначе не попадёт в сетку).
Известная нам утолщённая горизонталь должна удовлетворять искомой ΔB, то есть 175 должно делиться на ΔB без остатка.
Резюмируя:
- ΔB>21;
- ΔB/5 – целое;
- 175/ΔB – целое.
Алгоритм следующий: найдём минимальное ΔB из условий (1) и (2), полученную оценку подставим в условие (3), получив максимальный делитель для последующего перебора (если x минимален, то y=const/x – максимален).
- ΔB>21;
- ΔB/5 – целое;
Находим минимальное ΔBmin, как (
– округление в большую сторону):
ΔBmin=ceil(21/5)*5=ceil(4,2)*5=5*5=25.
Так как 175/ΔBmin=7, то осталось проверить числа 6, 5, 4, … Приступим к перебору.
| I | ΔB=175/I |
| 7 | 25 |
| 6 | дробное |
| 5 | 35 |
| 4 | дробное |
| 3 | дробное |
| 2 | дробное |
| 1 | 175 |
Таким образом, получаем три возможных ΔB:
ΔB1=25, ΔB2=35, ΔB3=175 –
но нас и предупреждали: “Предложите свои варианты ответа”.
Если уж выбирать единственный ответ, то число должно быть удобным в использовании в качестве шага по высоте. Думается адекватным, сформулировать в качестве критерия “эргономичности числа” следующее выражение:
n=lg(ΔB*k),
где
– десятичный логарифм, k, n – целые, положительные числа. ΔB, для которого будет выполняться указанное тождество при минимальном k – подходит. Данное тождество позволит нам найти число, которое быстрее всего (иначе говоря – при умножении на минимальный множитель) даст число вида 10n, то есть 10, 100, 1000 и так далее, если такое вообще возможно.
| k | n для ΔB1 | n для ΔB2 | n для ΔB3 |
| 1 | дробное | дробное | дробное |
| 2 | дробное | дробное | дробное |
| 3 | дробное | дробное | дробное |
| 4 | 2 | дробное | дробное |
Таким образом,
Ответ: ΔB=ΔB1=25 м.
Чтобы на планах местности и географических картах наглядно изобразить рельеф, картографы пользуются специальными линиями — горизонталями. Впервые горизонтали использовал в (1774) году английский математик Чарльз Хаттон, когда решил графически показать результаты обмера одной из гор в Шотландии.
Горизонтали — это линии, соединяющие точки с одинаковой абсолютной высотой.

Изображения холма (а) и впадины (б) горизонталями
Горизонтали обычно наносят коричневым цветом и указывают значения абсолютной высоты в метрах. В легенде карты указывают, через сколько метров высоты проведены горизонтали. Горизонтали помогают определять и крутизну склонов. Если промежутки между соседними горизонталями большие, то склон пологий. Если горизонтали близки друг к другу, то склон крутой.

У термина «горизонталь» есть слово-синоним — изогипса (от двух греческих слов isos — «равный» и hypsos — «высота»). Способ изображения неровностей поверхности Земли изогипсами (горизонталями) был изобретён ещё в (1774) году английским математиком Ч. Хаттоном.
Чтобы отличить холм от впадины, изображают короткие чёрточки — бергштрихи, которые всегда направлены от горизонталей вниз по склону.


Изобаты — линии, соединяющие точки с одинаковыми значениями глубины.
Это линии обозначаются, как правило, синим цветом.
В пределах материков область между горизонталями в зависимости от высоты окрашивают оттенками зелёного, жёлтого и коричневого цветов. Области между изобатами закрашивают оттенками синего и голубого цветов. В легенде карты для удобства изображают шкалу высот и глубин. Таким образом, рельеф изображают с помощью послойной окраски.

Для большей наглядности при составлении современных карт используют светотеневую пластику. Склоны гор при таком способе затемняют или, наоборот, осветляют. Изображение при этом становится более объёмным.

Источники:
Изображение: светотеневая пластика. https://pixabay.com/ru/illustrations/африка-карта-земля-континент-11115/. В изображение внесены изменения.
1 .Определите и подпишите в легенде плана, что означает каждый условный знак.
2.Определите, через сколько метров проведены горизонтали на плане местности.
3.Определите, используя цифровые данные, указанные вдоль железной дороги в центральной части плана, именованный и численный масштабы плана местности. Подпишите линейный, именованный и численный масштабы плана.
4.Используя атлас, выделите зелёным цветом растительные объекты. Обозначьте условными знаками подписанные на плане объекты: луг с редким лесом, плотина, еловый лес, луг с кустарником, редкий лес.
5.Выделите коричневым цветом утолщённую горизонталь, соединяющую точки с абсолютной высотой 175 м. Через сколько метров проведены утолщённые горизонтали, если на плане показана только одна из них — 175 м. Предложите свои варианты ответа.
6. Используя атлас, выделите коричневым цветом формы рельефа: карьер, овраг.
7. Подпишите название главной реки (Белая). Определите направление и скорость её течения.
8.Перечислите объекты, которые можно встретить, двигаясь по шоссе от посёлка Лесков на северо-запад.
9.Определите азимут школы в посёлке Лесков, если вы находитесь рядом с мельницей в юго-восточной части плана.
10. Укажите место на плане, где необходимо нанести мост на одной из автодорог. Какие доводы вы можете привести для обоснования своего выбора?
Определите Через сколько метров проведены горизонтали на плане.
На этой странице сайта, в категории География размещен ответ на вопрос
Определите Через сколько метров проведены горизонтали на плане?. По уровню сложности вопрос рассчитан на учащихся
10 – 11 классов. Чтобы получить дополнительную информацию по
интересующей теме, воспользуйтесь автоматическим поиском в этой же категории,
чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы
расположена кнопка, с помощью которой можно сформулировать новый вопрос,
который наиболее полно отвечает критериям поиска. Удобный интерфейс
позволяет обсудить интересующую тему с посетителями в комментариях.

