Download Article
Download Article
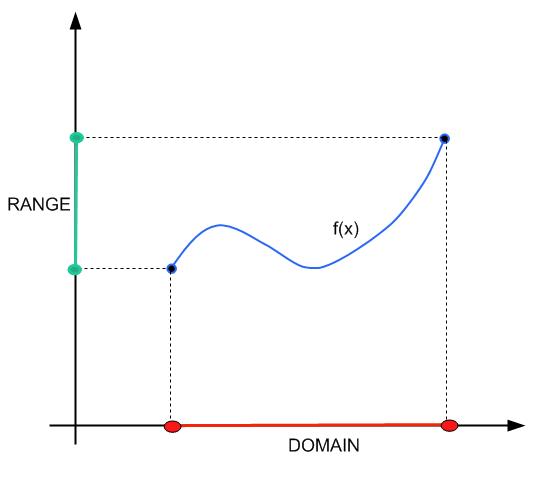
The domain of a function is the set of numbers that can go into a given function. In other words, it is the set of x-values that you can put into any given equation. The set of possible y-values is called the range. If you want to know how to find the domain of a function in a variety of situations, just follow these steps.
Things You Should Know
- The domain of a function is the set of input values (x) for which the function produces an output value (y).
- Solve for the domain depending on things like whether there is a variable in the denominator or inside a radical sign.
- Notate the domain as 2 endpoints separated by a comma. Use brackets if the point(s) is included in the domain, or parentheses if not.
-

1
Learn the definition of the domain. The domain is defined as the set of input values for which the function produces an output value. In other words, the domain is the full set of x-values that can be plugged into a function to produce a y-value.
-

2
Learn how to find the domain of a variety of functions. The type of function will determine the best method for finding a domain. Here are the basics that you need to know about each type of function, which will be explained in the next section:
- A polynomial function without radicals or variables in the denominator. For this type of function, the domain is all real numbers.
- A function with a fraction with a variable in the denominator. To find the domain of this type of function, set the bottom equal to zero and exclude the x value you find when you solve the equation.
- A function with a variable inside a radical sign. To find the domain of this type of function, just set the terms inside the radical sign to >0 and solve to find the values that would work for x.
- A function using the natural log (ln). Just set the terms in the parentheses to >0 and solve.
- A graph. Check out the graph to see which values work for x.
- A relation. This will be a list of x and y coordinates. Your domain will simply be a list of x coordinates.
Advertisement
-

3
Correctly state the domain. The proper notation for the domain is easy to learn, but it is important that you write it correctly to express the correct answer and get full points on assignments and tests. Here are a few things you need to know about writing the domain of a function:
- The format for expressing the domain is an open bracket/parenthesis, followed by the 2 endpoints of the domain separated by a comma, followed by a closed bracket/parenthesis.[1]
- For example, [-1,5). This means that the domain goes from -1 to 5.
-
Use brackets such as [ and ] to indicate that a number is included in the domain.
- So in the example, [-1,5), the domain includes -1.
-
Use parentheses such as ( and ) to indicate that a number is not included in the domain.
- So in the example, [-1,5), 5 is not included in the domain. The domain stops arbitrarily short of 5, i.e. 4.999…
-
Use “U” (meaning “union”) to connect parts of the domain that are separated by a gap.’
- For example, [-1,5) U (5,10]. This means that the domain goes from -1 to 10, inclusive, but that there is a gap in the domain at 5. This could be the result of, for example, a function with “x – 5” in the denominator.
- You can use as many “U” symbols as necessary if the domain has multiple gaps in it.
-
Use infinity and negative infinity signs to express that the domain goes on infinitely in either direction.
- Always use ( ), not [ ], with infinity symbols.
-
Keep in mind that this notation may be different depending on where you live.
- The rules outlined above apply to the UK and USA.
- Some regions use arrows instead of infinity signs to express that the domain goes on infinitely in either direction.
- Usage of brackets varies wildly across regions. For example, Belgium uses reverse square brackets instead of round ones.
- The format for expressing the domain is an open bracket/parenthesis, followed by the 2 endpoints of the domain separated by a comma, followed by a closed bracket/parenthesis.[1]
Advertisement
-

1
Write the problem. Let’s say you’re working with the following problem:
- f(x) = 2x/(x2 – 4)
-

2
Set the denominator equal to zero for fractions with a variable in the denominator. When finding the domain of a fractional function, you must exclude all the x-values that make the denominator equal to zero, because you can never divide by zero. So, write the denominator as an equation and set it equal to 0.[2]
Here’s how you do it:- f(x) = 2x/(x2 – 4)
- x2 – 4 = 0
- (x – 2 )(x + 2) = 0
- x ≠ (2, – 2)
-

3
State the domain. Here’s how you do it:
- x = all real numbers except 2 and -2
Advertisement
-

1
Write the problem. Let’s say you’re working with the following problem: Y =√(x-7)
-

2
Set the terms inside the radicand to be greater than or equal to 0. You cannot take the square root of a negative number, though you can take the square root of 0. So, set the terms inside the radicand to be greater than or equal to 0.[3]
Note that this applies not just to square roots, but to all even-numbered roots. It does not, however, apply to odd-numbered roots, because it is perfectly fine to have negatives under odd roots. Here’s how:- x-7 ≧ 0
-

3
Isolate the variable. Now, to isolate x on the left side of the equation, just add 7 to both sides, so you’re left with the following:[4]
- x ≧ 7
-

4
State the domain correctly. Here is how you would write it:
- D = [7,∞)
-

5
Find the domain of a function with a square root when there are multiple solutions. Let’s say you’re working with the following function: Y = 1/√( ̅x2 -4). When you factor the denominator and set it equal to zero, you’ll get x ≠ (2, – 2). Here’s where you go from there:
- Now, check the area below -2 (by plugging in -3, for example), to see if the numbers below -2 can be plugged into the denominator to yield a number higher than 0. They do.
- (-3)2 – 4 = 5
- Now, check the area between -2 and 2. Pick 0, for example.
- 02 – 4 = -4, so you know the numbers between -2 and 2 don’t work.
- Now try a number above 2, such as +3.
- 32 – 4 = 5, so the numbers over 2 do work.
- Write the domain when you’re done. Here is how you would write the domain:
- D = (-∞, -2) U (2, ∞)
- Now, check the area below -2 (by plugging in -3, for example), to see if the numbers below -2 can be plugged into the denominator to yield a number higher than 0. They do.
Advertisement
-

1
Write the problem. Let’s say you’re working with this one:
- f(x) = ln(x-8)
-

2
Set the terms inside the parentheses to greater than zero. The natural log has to be a positive number,[5]
so set the terms inside the parentheses to greater than zero to make it so. Here’s what you do:- x – 8 > 0
-

3
Solve. Just isolate the variable x by adding 8 to both sides.[6]
Here’s how:- x – 8 + 8 > 0 + 8
- x > 8
-

4
State the domain. Show that the domain for this equation is equal to all numbers greater than 8 until infinity.[7]
Here’s how:- D = (8,∞)
Advertisement
-

1
Look at the graph.
-

2
Check out the x-values that are included in the graph.[8]
This may be easier said than done, but here are some tips:- A line. If you see a non-vertical line on the graph that extends to infinity in both directions, then all versions of x will be covered eventually, so the domain is equal to all real numbers.
- A normal parabola. If you see a parabola that is facing upwards or downwards, then yes, the domain will be all real numbers, because all numbers on the x-axis will eventually be covered.
- A sideways parabola. Now, if you have a parabola with a vertex at (4,0) which extends infinitely to the right, then your domain is D = [4,∞)
-

3
State the domain. Just state the domain based on the type of graph you’re working with. If you’re uncertain and know the equation of the line, plug the x-coordinates back into the function to check.[9]
Advertisement
-

1
Write down the relation. A relation is simply a set of ordered pairs. Let’s say you’re working with the following coordinates: {(1, 3), (2, 4), (5, 7)}
-

2
Write down the x coordinates. They are: 1, 2, 5.[10]
-

3
State the domain. D = {1, 2, 5}
-

4
Make sure the relation is a function. For a relation to be a function, every time you put in one numerical x coordinate, you should get the same y coordinate. So, if you put in 3 for x, you should always get 6 for y, and so on. The following relation is not a function because the x coordinate, 1, has two different corresponding values of y, 4 and 5. {(1,4), (3,5), (1,5)}. [11]
Advertisement
Calculator, Practice Problems, and Answers
Add New Question
-
Question
How do you find the domain of a function algebraically?

Mario Banuelos is an Assistant Professor of Mathematics at California State University, Fresno. With over eight years of teaching experience, Mario specializes in mathematical biology, optimization, statistical models for genome evolution, and data science. Mario holds a BA in Mathematics from California State University, Fresno, and a Ph.D. in Applied Mathematics from the University of California, Merced. Mario has taught at both the high school and collegiate levels.

Assistant Professor of Mathematics
Expert Answer
If your function is a fraction, set the denominator equal to 0 and solve. The domain would then be all real numbers except for whatever input makes your denominator equal to 0. For a square root, set whatever is inside the radical to greater than or equal to 0 and solve, since you can’t use any inputs that produce an imaginary number (i.e., the square root of a negative).
-
Question
Can I find the domain of a function with a calculator?

Mario Banuelos is an Assistant Professor of Mathematics at California State University, Fresno. With over eight years of teaching experience, Mario specializes in mathematical biology, optimization, statistical models for genome evolution, and data science. Mario holds a BA in Mathematics from California State University, Fresno, and a Ph.D. in Applied Mathematics from the University of California, Merced. Mario has taught at both the high school and collegiate levels.

Assistant Professor of Mathematics
Expert Answer
Yes. You can use a graphing calculator to calculate domain by plotting the function. There are also a variety of domain and range calculators online. Simply input your function to find the domain, which is a set of x-values that will successfully generate y-values.
-
Question
How do I find the domain of 1/2 tan(90x/2)?

The function tan(90x/2) is undefined at 90x/2 = pi/2 + pi*n, where n is an integer. Simply solve for x to obtain pi/90 + pi*n/45, where n is an integer.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Thanks for submitting a tip for review!
References
About This Article
Article SummaryX
In mathematics, the domain of a function refers to the set of all possible numbers that you can use as inputs, or x-values, in the function. For example, if your function is f(x) = 2x+3, then the domain is any number that you can use in place of x. In this example, and with many other functions, the domain includes all real numbers. However, there are special cases where the domain will be more limited. For instance, if the function includes a fraction with a variable in the denominator, you’ll need to exclude any numbers from your domain that would result in the denominator of the fraction being equal to 0. To figure this out, set the denominator as an equation equal to 0 and solve for x. Let’s say you have a function f(x) = 2x/x^2-4. Start by writing out x^2-4 = 0. Factor the expression to get (x – 2) (x + 2) = 0. When you solve for 0, you’ll get two possible inputs: 2 and -2. This means you must exclude 2 and -2 from the domain. Define the domain as “x = all real numbers except for 2 and -2.” You could also write it as D = (-∞, -2) U (2, ∞). Functions that include natural logs and square roots also require special care when defining the domain. For instance, if the variable is under a square root, you must exclude any values that would result in a negative number under the root sign. The same goes for functions with a natural log. For example, if your function is either f(x) = ln(x – 8) or f(x) = √(x – 8), you’d define the domain as any real number greater than or equal to 8. Another way to write this out is D = [8, ∞). In many cases you can also define the domain of a function by looking at a graph. Look at which values are represented or excluded on the x-axis to help you find the domain. For example, if you’re looking at a graph of a line or a parabola, the domain would be all real numbers, since the graph continues infinitely in both directions. On the other hand, a function with a vertical asymptote at x = 3 would have a domain of all real numbers except for 3. If you want to learn how to find the domain of a function on a coordinate plane, keep reading the article!
Did this summary help you?
Thanks to all authors for creating a page that has been read 2,226,648 times.
Did this article help you?
Когда вы впервые начинаете изучать функции, вам, возможно, придется рассматривать их как машину: вы вводите значение x в функцию, и как только оно обрабатывается через машину, другое значение – назовем его y – выскакивает на дальнем конце., Диапазон возможных входов x, которые могут пройти через машину для возврата действительного вывода, называется областью функции. Поэтому, если вас попросят найти домен функции, вам действительно нужно выяснить, какие возможные входные данные вернут действительный вывод.
Стратегия поиска домена
Если вы просто изучаете функции и домены, обычно предполагается, что доменом функции являются «все действительные числа». Поэтому, когда вы приступаете к определению домена, часто проще всего использовать свои знания по математике – особенно по алгебре – чтобы определить, какие числа не являются действительными членами домена. Поэтому, когда вы видите инструкции «найти домен», часто проще всего прочитать их в своей голове как «найти и исключить любые числа, которые не могут быть в домене».
В большинстве случаев это сводится к проверке (и устранению) потенциальных входных данных, которые могут привести к тому, что дроби станут неопределенными или имеющими 0 в знаменателе, а также к поиску потенциальных входных данных, которые дадут вам отрицательные числа под знаком квадратного корня.
Пример поиска домена
Рассмотрим функцию f ( x ) = 3 / ( x – 2), которая действительно означает, что любое введенное вами число будет сброшено вместо x в правой части уравнения. Например, если вы вычислили f (4), вы бы получили f (4) = 3 / (4 – 2), что составляет 3/2.
Но что, если вы вычислили f (2) или, другими словами, введите 2 вместо x ? Тогда бы вы имели f (2) = 3 / (2 – 2), что упрощается до 3/0, что является неопределенной дробью.
Это иллюстрирует один из двух распространенных случаев, которые могут исключать число из домена функции. Если задействована дробь, и ввод приведет к тому, что знаменатель этой дроби будет равен нулю, то вход должен быть исключен из области функции.
Небольшое исследование покажет вам, что абсолютно любое число, кроме 2, вернёт действительный (если иногда грязный) результат для рассматриваемой функции, поэтому доменом этой функции являются все числа, кроме 2.
Еще один пример поиска домена
Есть еще один распространенный случай, который исключает возможных членов домена функции: наличие отрицательного количества под знаком квадратного корня или любого радикала с четным индексом. Рассмотрим пример функции f ( x ) = √ (5 – x ).
Если x ≤ 5, то величина под знаком радикала будет либо 0, либо положительной, и вернет действительный результат. Например, если x = 4.5, вы бы имели f (4.5) = √ (5 – 4.5) = √ (.5), который, хотя и грязный, по-прежнему возвращает действительный результат. И если x = -10, вы получите f (4.5) = √ (5 – (-10)) = √ (5 + 10) = √ (15, что опять-таки возвращает действительный, если получится беспорядочный результат.
Но представьте, что х = 5, 1. В тот момент, когда вы на цыпочках пересечете разделительную линию между 5 и любыми числами, большими, чем она, вы получите отрицательное число под радикалом:
f (5.1) = √ (5 – 5.1) = √ (-. 1)
Много позже в вашей математической карьере вы научитесь понимать отрицательные квадратные корни, используя концепцию, называемую мнимыми числами или комплексными числами. Но пока наличие отрицательного числа под знаком радикала исключает этот вход как действительный член домена функции.
Таким образом, в этом случае, поскольку любое число x ≤ 5 возвращает действительный результат для этой функции, а любое число x > 5 возвращает недопустимый результат, доменом функции являются все числа x ≤ 5.
Умение находить область определения функции – важный навык в алгебре, потому что он дает вам возможность оценить, где функция определена правильно. Или, другими словами, регион, в котором допустимо использовать функцию
Задача найти, где допустимо использовать функцию, является полезной. Например, рассмотрим функцию (f(x) = sqrt x). Мы знаем, что функция оперирует такими значениями, что (x ge 0). Мы не можем работать с отрицательными числами, потому что мы получили бы что-то вроде (f(-1) = sqrt{-1}), что не совсем точно (по крайней мере, как действительное число)
Вы можете проверить наш предыдущий урок, в котором мы подробно говорили о
домен и диапазон
. Это руководство будет ориентировано на оперативную часть поиска домена.
Зачем нам нужно искать домен?
Причина, по которой нам нужно найти область определения функции, заключается в том, что каждая функция имеет определенный набор значений, в которых она определена. Не все функции определены везде в реальной строке.
Домен, область на реальной линии, где он находится
действительный
для работы с функцией (f(x)) в терминах значений, которые может принимать (x).
Что нам нужно сделать, чтобы найти домен?
На самом деле не существует одной хитрости, подходящей для всех размеров. Каждая функция отличается, и для поиска области необходимо использовать разные стратегии в зависимости от функции.
Вы ВСЕГДА должны учитывать два метода:
![]()
Техника 1.
: Убедитесь, что есть деления на ноль.
Причем те точки, которые приводят к делению на ноль, нужно исключить из области.
![]()
Техника 2.
: Убедитесь, что есть квадратные корни делений с отрицательными аргументами (например, (sqrt{-1})).
Более того, те точки, которые приводят к извлечению квадратного корня из отрицательного числа, необходимо исключить из домена.
В конечном итоге, используя эти два метода, вы сможете отсеять точки, которых нет в домене. Остальные точки на реальной линии просто ЯВЛЯЮТСЯ частью домена.
Итак, эти два метода решают проблему знания того, как найти область определения функции алгебраически. Другой способ сделать это – посмотреть на график, если он доступен.
ПРИМЕР 1
Найдите домен функции (f(x) = sqrt{x+4}+3)
ОТВЕЧАТЬ:
Первое, что нам нужно сделать, и именно в этом заключается наш успех в поиске домена, – это определить, где потенциально мы могли бы найти недопустимые операции, такие как деление на ноль или отрицательные квадратные корни.
Для функции (f(x) = sqrt{x+4}+3) нет потенциальных делений на ноль, но есть квадратный корень. Чтобы иметь действительный аргумент, аргумент внутри квадратного корня должен быть неотрицательным.
Следовательно, чтобы (x) находилось в домене функции, нам нужно иметь (xge 0). Это означает, что домен (f) – это ({x: xge 0}) или ([0, +infty)), если мы используем обозначение интервала.
Всегда ли это просто ?? Не совсем, это может быть так сложно, как вы, в зависимости от сложности функции (f(x)).
Однако обычно примеры, которые вы видите в своих тестах и домашних заданиях, довольно просты. Давайте поднимемся на ступеньку выше с точки зрения сложности.
ПРИМЕР 2
Теперь найдите домен функции (displaystyle f(x) = sqrt{frac{x+4}{x-3}})
ОТВЕЧАТЬ:
Эта функция немного сложнее и требует более внимательного отношения. В этом случае нам нужно беспокоиться как о возможных делениях на ноль, так и на отрицательные квадратные корни.
Во-первых, может быть потенциальное деление на ноль, когда (x = 3), что указывает на то, что (x = 3) следует исключить из домена.
Теперь нам нужно позаботиться о потенциальном отрицательном квадратном корне. Нам нужно оценить признак (displaystyle frac{x+4}{x-3}). Более того, нам нужно, чтобы он был неотрицательным, поэтому нам нужно решить:
[displaystyle frac{x+4}{x-3} ge 0]
Чтобы деление было неотрицательным, нам нужно, чтобы числитель и знаменатель были положительными, либо числитель и знаменатель были отрицательными.
Другими словами, нам нужны оба (x+4 ge 0) и (x-3 > 0), или оба (x+4 le 0) и (x-3 < 0).
Это то же самое, что и (x ge -4), и (x > 3), или оба (x le -4) и (x < 3).
И это может быть записано как (x > 3) или как (x le -4), что соответствует интервалу ( (-infty, -4] cup (3, +infty)).
Напрашивается вывод, что область определения функции (displaystyle f(x) = sqrt{frac{x+4}{x-3}}):
[ dom(f) = (-infty, -4] cup (3, +infty)]
Как видите, уровень сложности немного увеличился, и вы можете увеличивать его сколько угодно.
Как найти область рациональной функции
Прежде всего, напомним, что рациональная функция – это частное двух многочленов вида:
[f(x) = frac{p(x)}{q(x)} = frac{a_0 + a_1 x + …+ a_m x^m}{b_0 + b_1 x + …+ b_n x^n}]
Как найти область для указанной выше рациональной функции? Нам нужно следовать нашему правилу: ищите возможные деления на ноль и отрицательные квадратные корни.
В этом случае нет потенциальных отрицательных квадратных корней, но может быть деление на ноль, если многочлен в знаменателе равен нулю.
Вывод очень простой: область определения рациональной функции – это вся вещественная прямая, ЗА ИСКЛЮЧЕНИЕМ тех точек, в которых многочлен в знаменателе равен нулю.
ПРИМЕР 3
Найдите домен
[f(x) = frac{x^2 + x + 1}{x^3 – 6x^2 + 11x – 6}]
ОТВЕЧАТЬ:
Прежде всего, нам нужно понять, что это рациональная функция, потому что у вас есть два полинома (p(x) = x^2 + x + 1) и (q(x) = x^3 – 6x^2 + 11x – 6) в числителе и знаменателе соответственно.
Итак, первый шаг – найти нули многочлена в знаменателе, поэтому нам нужно решить: [ x^3 – 6x^2 + 11x – 6 = 0]
Это уравнение довольно сложно решить, поэтому я дам вам это действительно (x^3 – 6x^2 + 11x – 6 = (x-1)(x-2)(x-3)), поэтому нам нужно решить:
[ x^3 – 6x^2 + 11x – 6 = (x-1)(x-2)(x-3) = 0]
что означает, что корни многочлена в знаменателе равны (x_1 = 1, x_2 = 2, x_3 = 3). Вывод состоит в том, что область определения функции – это вся вещественная линия, за исключением точек 1, 2 и 3. При использовании интервальной записи область определения ((-infty, +infty) backslash {1,2,3}).
Другие стратегии поиска области определения функции
Альтернативой поиска области определения функции путем рассмотрения возможных делений на нулевые или отрицательные квадратные корни, что является аналитическим способом, является просмотр графика.
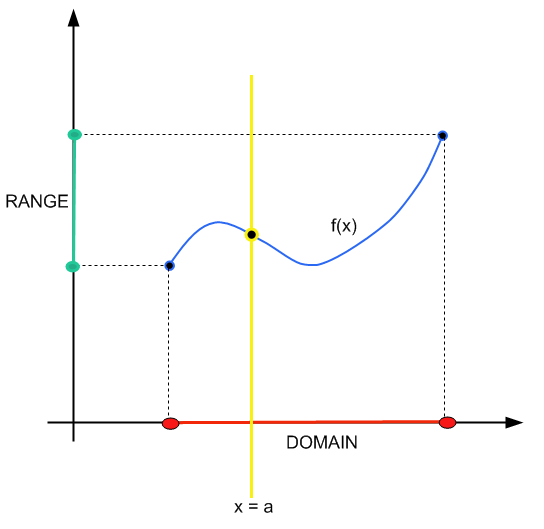
Метод прост: вы строите вертикальную линию (x = a). Если эта вертикальная линия пересекает график функции в одной и только одной точке, то (x = a) принадлежит домену.
Коротко и мило.
Наконец, как найти область определения функции с квадратным корнем
Это суть одной из техник, о которых мы говорили, а именно нахождения потенциальных отрицательных квадратных корней. Итак, когда у вас есть функция с одним или несколькими квадратными корнями, вы знаете, что очень вероятно, что у вас будет потенциальный отрицательный корень, и вам нужно его обнаружить.
Однако это не всегда так. Подумайте о функции (f(x) = sqrt{x^2}). Эта функция имеет квадратный корень, но аргумент внутри – (x^2), который не может быть отрицательным, поэтому мы имеем дело с функцией с квадратным корнем, которая не имеет отрицательных квадратных корней.
Автор:
Lewis Jackson
Дата создания:
11 Май 2021
Дата обновления:
11 Май 2023

Содержание
- меры
- Об этом Villagemonkland
Эта статья была написана в сотрудничестве с нашей командой редакторов и опытных исследователей, которые одобрили ее точно и исчерпывающе.
Команда управления контентом Villagemonkland тщательно следит за работой редакции, чтобы убедиться, что каждый элемент соответствует нашим стандартам качества.
Домен функции – это набор чисел, которые могут быть введены в самой функции. Другими словами, это набор X, которые вы можете поместить в определенное уравнение. Множество возможных значений Y называется кодоменом или рангом функции. Если вы хотите узнать, как найти домен функции в различных ситуациях, просто выполните следующие действия.
меры
Об этом Villagemonkland
Написано в сотрудничестве с: редакцией Villagemonkland. Эта статья была написана в сотрудничестве с нашей командой редакторов и опытных исследователей, которые подтвердили их точность и полноту. Категории: Математика Краткое содержание статьи
Чтобы найти область функции, которая содержит дробь, установите знаменатель так, чтобы он был 0. Затем исключите все значения переменных, которые делают знаменатель равным 0, потому что невозможно разделить на 0. Как только эти значения найдены, запишите домен как набор всех действительных чисел, кроме исключаемых. Если функция содержит квадратный корень, установите термины внутри radicand больше или равно 0. Наконец, выделите переменную и найдите домен.
На других языках. Определение области образования: Нидерланды: Het Domein Van Een Functie Vinden, Бахаса, Индонезия: Домен Менкари, Себау Фанги: 関 数 定義 域 求 る ü ü る る る る る る る る る る る る る る る る る る Bir Bir Bir 한국어 한국어 한국어 한국어 한국어 한국어 한국어 한국어 한국어 한국어 한국어 한국어 한국어 한국어 한국어 한국어 한국어 한국어 한국어 한국어 한국어 한국어 한국어 구하기
Когда вы впервые начинаете изучать функции, вам, возможно, придется рассматривать их как машину: вы вводите значение,Икс, в функцию, и как только оно будет обработано машиной, другое значение – назовем егоу– выскакивает дальний конец. Диапазон возможныхИксвходные данные, которые могут проходить через машину для возврата действительного вывода, называются областью действия функции. Поэтому, если вас просят найти домен функции, вам действительно нужно выяснить, какие возможные входные данные вернут действительный результат.
Стратегия поиска домена
Если вы только изучаете функции и домены, обычно предполагается, что домен функции – «все действительные числа». Итак, когда вы приступив к определению предметной области, часто проще всего использовать свои знания математики, особенно алгебры, чтобы определить, какие числанедействительные члены домена. Поэтому, когда вы видите инструкции «найдите домен», их проще всего прочитать в уме как «найти и удалить любые числа, которыене могубыть в домене “.
В большинстве случаев это сводится к проверке (и исключению) потенциальных входов, которые могут привести к тому, что дроби станут неопределенными, или иметь 0 в знаменателе и искать потенциальные входные данные, которые дадут вам отрицательные числа под квадратным корнем знак.
Пример поиска домена
Рассмотрим функцию
f (x) = frac {3} {x – 2}
что на самом деле означает, что любое введенное вами число будет сброшено на место вместоИксв правой части уравнения. Например, если вы рассчиталиж(4) у вас будет
f (4) = frac {3} {4–2}
который работает до 3/2.
Но что, если вы подсчиталиж(2) или, другими словами, введите 2 вместоИкс? Тогда у тебя было бы
f (2) = frac {3} {2–2}
что упрощается до 3/0, что является неопределенной дробью.
Это иллюстрирует один из двух распространенных примеров, которые могут исключать число из домена функции. Если задействована дробь, и ввод приведет к тому, что знаменатель этой дроби будет равен нулю, то ввод должен быть исключен из области определения функции.
Небольшой осмотр покажет вам, что абсолютно любое числоКроме2 вернет действительный (если иногда и беспорядочный) результат для рассматриваемой функции, поэтому домен этой функции – все числа, кроме 2.
Еще один пример поиска домена
Есть еще один распространенный случай, который исключает возможные члены домена функции: отрицательное число под знаком квадратного корня или любой радикал с четным индексом. Рассмотрим пример функции
f (x) = sqrt {5 – x}
ЕслиИкс≤ 5, то величина под знаком корня будет либо 0, либо положительной, и вернет действительный результат. Например, еслиИкс= 4.5 у вас будет
f (4.5) = sqrt {5 – 4.5} = sqrt {0.5}
который, хотя и беспорядочный, все же возвращает действительный результат. И еслиИкс= −10 у вас будет
f (-10) = sqrt {5 – (-10)} = sqrt {5 + 10} = sqrt {15}
который, опять же, возвращает действительный, если нечеткий результат.
Но представьте, чтоИкс= 5,1. В тот момент, когда вы на цыпочках преодолеете разделительную линию между 5 и любыми числами, превышающими ее, вы получите отрицательное число под корнем:
f (5.1) = sqrt {5 – 5.1} = sqrt {-0.1}
Намного позже в своей математической карьере вы научитесь понимать отрицательные квадратные корни, используя концепцию, называемую мнимыми числами или комплексными числами. Но на данный момент наличие отрицательного числа под знаком радикала исключает этот ввод как действительный член домена функции.
Итак, в данном случае, потому что любое числоИкс≤ 5 возвращает действительный результат для этой функции и любое числоИкс> 5 возвращает неверный результат, домен функции – все числаИкс ≤ 5.
