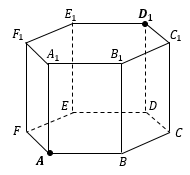
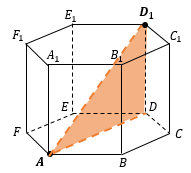
при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки,
Окружность и круг – определение и вычисление с примерами решения
Содержание:
Пусть в природе не существовало бы ни одного круга или треугольника, и все-таки истины, доказанные Евклидом, навсегда сохранили бы свою достоверность и очевидность.
Раньше вы знакомились с основными геометрическими фигурами, устанавливали особенности этих фигур и их взаимное расположение. Но на практике довольно часто приходится решать «обратную» задачу — по определенным особенностям находить фигуру, имеющую их. Именно таково содержание задач на построение, которые будут рассматриваться в этом разделе.
Еще в работах древнегреческих математиков описаны задачи на построение и методы их решения.
Многие из этих задач составляют классику евклидовой геометрии. Кроме практической ценности, такие задачи представляют значительный исследовательский интерес, поскольку в ходе их решения определяются новые особенности построенных фигур.
Окружность и круг:
Определение. Окружностью называется геометрическая фигура, состоящая из всех точек плоскости, равноудаленных от данной точки, которая называется центром окружности.
Радиусом окружности называется отрезок, соединяющий центр окружности с любой точкой на окружности (или длина этого отрезка).
Хордой окружности называется отрезок, соединяющий две точки окружности.
Диаметром окружности называется хорда, проходящая через центр окружности.
Дугой окружности называется часть окружности, ограниченная двумя точками.
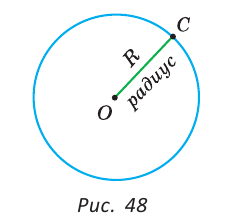
На рисунке 48 точка О — центр, отрезок ОС — радиус окружности. Радиус обозначают буквой R (или 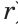
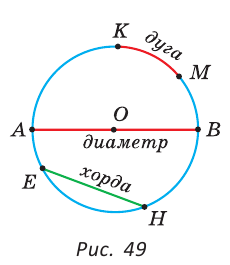
На рисунке 49 изображены: хорда ЕН, дуга КМ (обозначается: 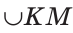 ), диаметр АВ. Диаметр состоит из двух радиусов. Поэтому диаметры окружности равны между собой. Диаметр АВ состоит из радиусов OA и ОВ, откуда
), диаметр АВ. Диаметр состоит из двух радиусов. Поэтому диаметры окружности равны между собой. Диаметр АВ состоит из радиусов OA и ОВ, откуда 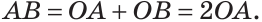 Диаметр обозначают буквой D (или d). Тогда
Диаметр обозначают буквой D (или d). Тогда 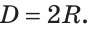
Любые две точки окружности разбивают ее на две дуги, которые дополняют друг друга до окружности. Эти дуги так и называются — дополнительными. Чтобы различать такие дуги, их иногда обозначают тремя буквами. На рисунке 49 дуги АКМ и АНМ — дополнительные.
Определение. Кругом называется часть плоскости, ограниченная окружностью.
Точки окружности также принадлежат кругу (рис. 50). Поэтому центр, радиус, хорда и диаметр у круга те же, что и у его окружности.
Часть круга, заключенная между двумя радиусами, называется сектором. Часть круга, заключенная между дугой окружности и хордой, соединяющей концы дуги, называется сегментом (рис. 51). Два радиуса разбивают круг на два сектора, хорда разбивает круг на два сегмента.
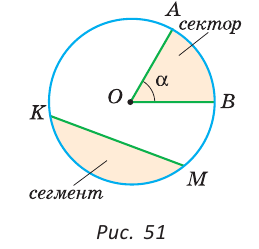
Полуокружностью называется дуга окружности, концы которой являются концами диаметра. Полукругом называется часть круга, ограниченная полуокружностью и диаметром, соединяющим концы полуокружности. На рисунке 49 дуга АКВ — полуокружность, сегмент АКВ — полукруг.
Угол, вершина которого находится в центре окружности, называется центральным углом. На рисунке 51 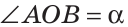 — центральный угол.
— центральный угол.
Окружности (круги) равны, если равны их радиусы.
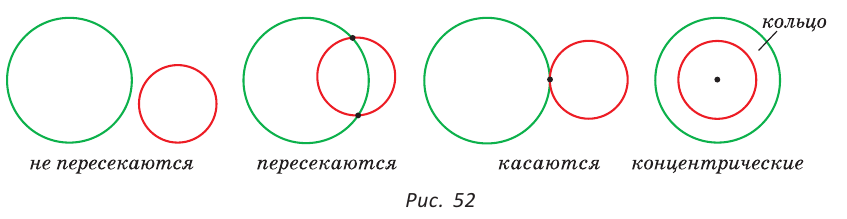
Две окружности могут не иметь общих точек, могут пересекаться в двух точках или касаться друг друга в одной точке. Окружности разного радиуса с общим центром называются концентрическими. Часть плоскости между двумя концентрическими окружностями называется кольцом (рис. 52).
Определение окружности и круга
Окружность — это замкнутая линия на плоскости, все точки которой находятся на одинаковом расстоянии от одной точки — центра окружности.
Круг — это внутренняя часть плоскости, ограниченная окружностью.
Размеры окружности и круга определяются их радиусом — отрезком, который соединяет центр с точкой на окружности (рис. 3).
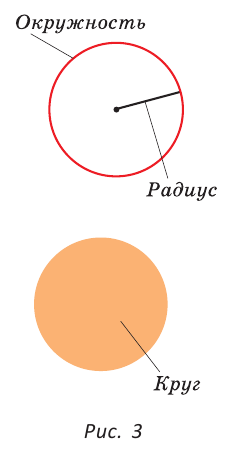
В математике «окружность» и «круг» — два различных, хотя и связанных между собой, понятия. Окружность, например, является моделью обруча, а круг — моделью крышки люка. 
Определение окружности и ее элементов
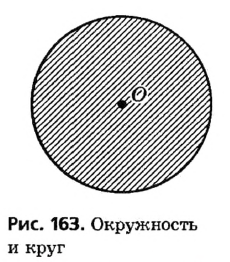
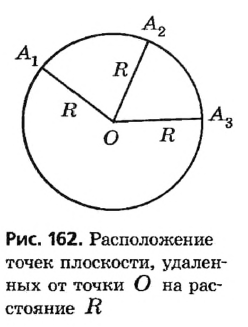
Пусть на плоскости отмечена точка О. Очевидно, что от точки О можно отложить бесконечное множество отрезков длиной R (рис. 162). Концы всех таких отрезков на плоскости образуют окружность — фигуру, уже известную из курса математики. Определение Окружностью называется геометрическая фигура, состоящая из всех точек плоскости, удаленных от данной точки (центра окружности) на одинаковое расстояние. Иначе говорят, что все точки окружности равноудалены от ее центра. Определение Кругом называется часть плоскости, ограниченная окружностью и содержащая ее центр. Иначе говоря, круг состоит из всех точек плоскости, удаленных от данной точки (центра круга) на расстояние, не превышающее заданного. На рисунке 163 заштрихованная часть плоскости — круг, ограниченный окружностью с тем же центром. Центр окружности и круга является точкой круга, но не является точкой окружности.
Определение Радиусом окружности (круга) называется расстояние от центра окружности до любой ее точки. Радиусом также называется любой отрезок, соединяющий точку окружности с ее центром. На рисунке 162 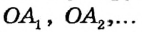 — радиусы окружности с центром О. Как правило, радиус обозначается буквой R (или r ).
— радиусы окружности с центром О. Как правило, радиус обозначается буквой R (или r ).
Радиус – от латинского «радиус» – луч, спица
Хорда – от греческого «хорда» — струна, тетива
Диаметр — от греческого «диа» — насквозь и «метрео» – измеряющий насквозь; другое значение этого слова — поперечник
Радиусом также называется любой отрезок, соединяющий точку окружности с ее центром. На рисунке 162 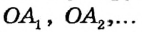 — радиусы окружности с центром О. Как правило, радиус обозначается буквой R (или r ).
— радиусы окружности с центром О. Как правило, радиус обозначается буквой R (или r ).
Определение:
Хордой называется отрезок, соединяющий две точки окружности.
Диаметром называется хорда, проходящая через центр окружности.
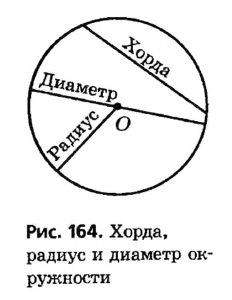
На рисунке 164 изображены две хорды окружности, одна из которых является ее диаметром. Обычно диаметр обозначают буквой d. Очевидно, что диаметр вдвое больше радиуса, то есть d = 2R.
Построение окружности выполняют с помощью циркуля.
Что такое окружность и круг
Окружность — это фигура, состоящая из всех точек плоскости, равноудален ных от данной точки. Эту точку называют центром окружности.
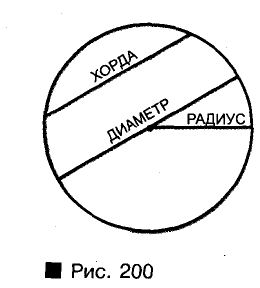
Отрезок, соединяющий любую точку окружности с ее центром, называют ради усом. Отрезок, соединяющий две против вольные точки окружности, — хорда окружности. Хорда, проходящая через центр окружности, — диаметр (рис. 200). Каждый диаметр окружности состоит’ из двух радиусов, поэтому его длина вдвое больше длины радиуса. Длина хорды, не проходящей через центр окружности, меньше длины диаметра, (Почему?)
Окружность на бумаге описывают МА и MB — перпендикуляры на ОА и ОВ (см. рис. 216), то 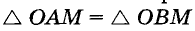 (по гипотенузе и острому углу). Поэтом МА = MB, следовательно, точка М равноудалена от сторон данного угла.
(по гипотенузе и острому углу). Поэтом МА = MB, следовательно, точка М равноудалена от сторон данного угла.
Геометрическим местом точек угла, равноудаленных от его сторон, является биссектриса этого угла.
Здесь имеются в виду углы меньше развернутого.
Верно ли, что геометрическим местом точек, равноудален-ных от сторон угла, является биссектриса этого угла? Нет. Когда в планиметрии говорят о геометрическом месте точек, не уточняя, о каких именно точках идет речь, то имеют в виду точки плоскости, которой принадлежит данная фигура. При таком условии геометрическим местом точек, равноудаленных от ф сторон угла, является объединение биссектрисы I данного угле g и всех точек некоего другого угла, показанного на рисунке 217,
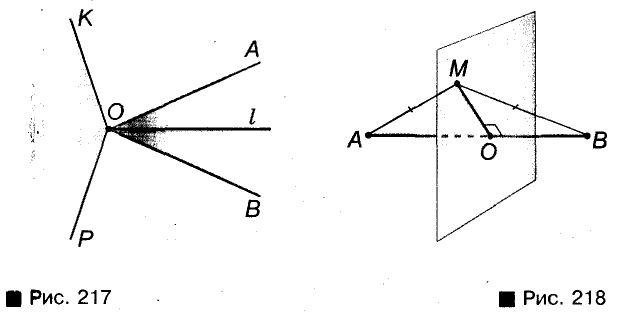
Ведь каждая точка угла КОР также равноудалена от сторон донного угла АО В (речь идет об углах меньше развернутого).
Когда мы говорим, что геометрическим местом точек, равноудаленных от концов отрезка, является серединный перпендикуляр этого отрезка, то мы имеем в виду, что речь идет о геометрическом месте точек плоскости, на которой лежит отрезок.
А геометрическим местом точек пространства, равноудаленных от концов отрезка, является некая плоскость (мал. 218).
Подумайте, как расположена эта плоскость относительно денного отрезка.
Геометрические места точек пространства изучают в старших классах.
Пример №3
Докажите, что серединные перпендикуляры двух сторон треугольника пересекаются.
Решение:
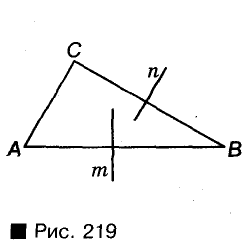
Пусть n и m— серединные перпендикуляры сторон ВС и АВ треугольника (рис. 219). Докажем, что они не могут быть параллельны. Доказывать будем от противного. Допустим, что n || m. Тогда прямая, перпендикулярная к п, должна быть перпендикулярной и к m, то есть 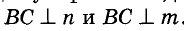 . Но по условию
. Но по условию 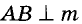 А две прямые, перпендикулярные к третьей прямой, параллельны. Таким образом, из допущения, что п || т, следует параллельность сторон АВ и ВС треугольника. А этого не может быть. Поэтому прямые ли т не могут быть параллельными. Они пересекаются.
А две прямые, перпендикулярные к третьей прямой, параллельны. Таким образом, из допущения, что п || т, следует параллельность сторон АВ и ВС треугольника. А этого не может быть. Поэтому прямые ли т не могут быть параллельными. Они пересекаются.
Окружность и треугольник
Окружность и треугольник могут не иметь общих точек или иметь 1, 2, 3, 4, 5, 6 общих точек (соответствующие рисунки выполните самостоятельно). Заслуживаем внимания случаи, когда окружность проходит через все три вершины треугольника или когда она касается всех и сторон треугольника. Рассмотрим такие случаи подробнее.
Описанная окружность
Окружность называется описанной около треугольника, если она проходит через все вершины треугольника (рис. 223).
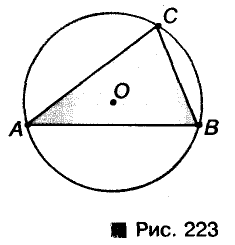
Теорема: Около каждого треугольника можно описать только одну окружность. Ее центром является точка пересечения серединных перпендикуляров двух сторон треугольника.
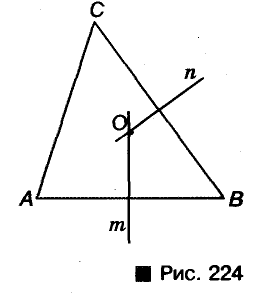
Пусть ABC — произвольный треугольник (рис. 224). Найдем точку, равноудаленную от вершин А, В и С.’ Метрическое место точек, равноудаленных от А и В, — серединный перпендикуляр m отрезка АВ; геометрическое место точек, равноудаленна от В и С, — серединный перпендикуляр n отрезка ВС. Эти два серединных перпендикуляра не могут быть параллельными, они пересекаются в точке О. А она равноудалена от Н и С. Следовательно, ОА = ОВ = ОС, поэтому О — центр окружности, описанной около ABC.
Для каждого отрезка АВ существует серединный перпендикуляр, и только один, а для ВС — серединный перпендикуляр и только один. И точка их пересечения существует всегда, только одна. Таким образом, около каждого треугольника можно описать одну окружность, и только одну. 
- Серединные перпендикуляры всех трех сторон произвольного треугольника проходят через одну и ту же точку.
- Через любые три точки, не лежащие на одной прямой, можно провести окружность, и только одну.
Из доказанной теоремы следует cnocof построения окружности, описанной около треугольника. Чтобы описать около треугольника ABC окружность, достаточно:
- построить серединные перпендикуляры двух сторон данного треугольника;
- определить точку О, в которой эти серединные перпендикуляры пересекаются;
- ) из центра О провести окружность радиуса ОА.
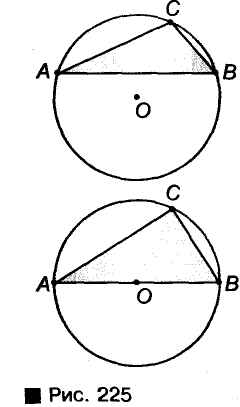
Центр окружности, описанной около треугольника, может лежать во внутренней или внешней области данного треугольника либо на его сторон (рис. 225).
Вписанная окружность
Окружность называется вписанной в треугольник если она касается всех сторон треугольника (рис. 226). Центр окружности, вписанной в треугольник, лежим’ и внутренней области этого треугольник.
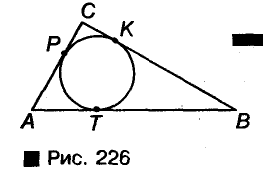
Теорема: В каждый треугольник можно вписан только одну окружность. Ее центром является точка пересечения двух биссектрис треугольника.
Доказательство:
Пусть ABC — произвольный треугольник. Определим точи О, равноудаленную от всех его сторон (рис. 227). Геометрическое место точек, лежащих внутри угла А и равноудаленных второй АВ и АС, — биссектриса l угла А. Гtjметрическое место точек, равноудаленных от сторон АВ и ВС и лежащих внутри угла В, — биссектриса t угла B. Эти две биссектрисы обязательно Пересекаются (докажите это!). Точка U, в которой пересекаются биссектрисы l и t, равноудалена от всех трех сторон данного треугольника. Следовательно, точка О — центр окружности, Вписанной в треугольник АВС. 
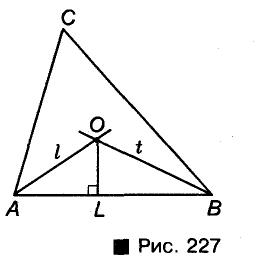
В каждом треугольнике все три биссектрисы пересекаются в одной точке.
Из доказанной теоремы следует способ построения окружности, вписанной в треугольник. Чтобы вписать в данный треугольник окружность, достаточно:
- провести две его биссектрисы;
- из точки их пересечения О опустить перпендикуляр OL на произвольную сторону треугольника;
- из центра О радиуса OL описать окружность. Она касается каждой стороны треугольника, следовательно, является вписанной в данный треугольник.
Теорема: Центром окружности, описанной около прямоугольного треугольника, является середина его гипотенузы.
Пусть ABC — произвольный треугольник с прямым углом С, t— серединный перпендикуляр катета АС, пересекающий гипотенузу АВ в точке О (рис. 228).
Поскольку точка О лежит на серединном перпендикуляре отрезка АС, то 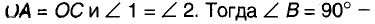
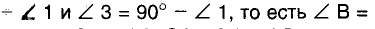 .
. 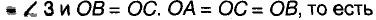
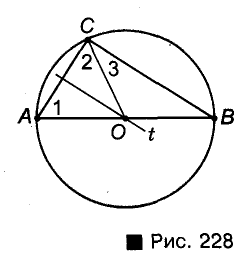
точка О—середина гипотенузы АВ, равноудаленная от всех вершин треугольника. Таким образом, окружность с центром О и радиусом ОА проходит через все вершины данного треугольника.
Диаметр окружности, описанной около прямоугольного треугольника, равен его гипотенузе.
Теорема: Из любой точки окружности ее Диаметр, не выходящий из этой точки, виден под прямым углом.
Доказательство:
Пусть АВ — произвольный диаметр окружности с центром О, а С— произвольная точка окружности, отличная от А и В (рис. 229). Покажем, что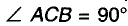 Поскольку
Поскольку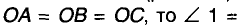
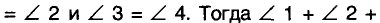
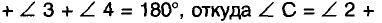
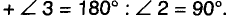
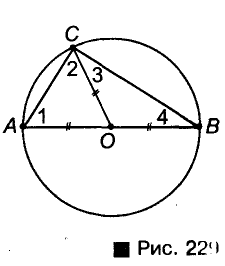
Геометрическим местом точек плоскости, из которых отрезок АВ виден под прямым углом, является окружность диаметра АВ. На самом деле этому ГМТ точки А и В не принадлежат. Подробнее об этом вы узнаете в старших классах.
Пример №4
Найдите радиус окружности, описанной около прямоугольного треугольника с гипотенузой 6 см.
Решение:
Диаметр окружности, описанной около прямоугольного треугольника, является его гипотенузой. Радиус вдвое меньше: 3 см.
Пример №5
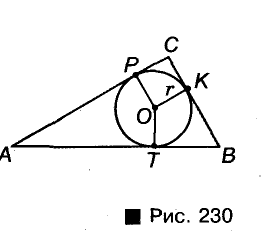
Докажите, что диаметр окружности, вписанной в прямоугольный треугольник с катетами а и Ь и гипотенузой с, равен a + b — c.
Решение:
Пусть в 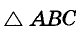 угол С прямой, а К, Р, Т — точки касания вписанной в треугольник окружности (рис. 230). Поскольку АР =АТ и ВК = ВТ, то АС + ВС – АВ = PC + СК = 2r, или 2r = a + b- с.
угол С прямой, а К, Р, Т — точки касания вписанной в треугольник окружности (рис. 230). Поскольку АР =АТ и ВК = ВТ, то АС + ВС – АВ = PC + СК = 2r, или 2r = a + b- с.
Геометрические построения
Пользуясь линейкой’ и циркулем, моле но выполнить много геометрических построений, то есть начертить геометрические фигуры. Рассмотрим сначала, как выполняются самые простые геометрические построения.
Пример №6
Постройте треугольник по данным сторонам.
Решение:
Пусть даны три отрезки а, b и с (рис. 232). Нужно построить, треугольник, стороны которого были бы равны этим отрезкам. С помощью линейки проводим произвольную прямую, обозначаем на ней произвольную точку В и циркулем откладываем на этой прямой отрезок ВС = а. Раствором циркуля, равным с описываем дугу окружности с центром В. С той же стороны от прямой СВ описываем дугу окружности радиуса b с центром С. Точку пересечения А этих дуг соединяем отрезками с С и В. Треугольник ABC — именно тот, который требовалось построить, так как его стороны ВС, АС и АВ равны данным отрезкам.
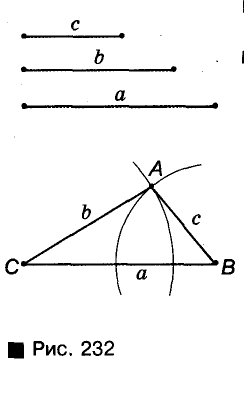
Если построенные дуги не пересекаются, требуемый треугольник построить невозможно. Это бывшие в том случае, когда один из данных отрезков больше суммы двух других или равен их сумме.
Пример №7
Постройте угол, равный данному углу.
Решение:
Пусть дан угол АОВ и требуется построить угол КРТ, равный 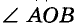 (рис. 233). Проводим луч РТ и дуг* равных радиусов с центрами О и Р. Пусть одна из этих д пересекает стороны угла АОВ в точках А и В, а другая луч РТ в точке Т. Дальше раствором циркуля, равным А/ описываем третью дугу с центром Т. Если она пересекает другую дугу в точке К, проводим луч РК. Угол КРТ — то 1 Будем считать, что линейка без делений.
(рис. 233). Проводим луч РТ и дуг* равных радиусов с центрами О и Р. Пусть одна из этих д пересекает стороны угла АОВ в точках А и В, а другая луч РТ в точке Т. Дальше раствором циркуля, равным А/ описываем третью дугу с центром Т. Если она пересекает другую дугу в точке К, проводим луч РК. Угол КРТ — то 1 Будем считать, что линейка без делений.
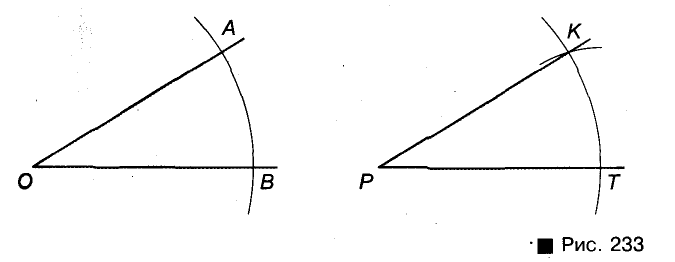
который требовалось построить. Ведь треугольники КРТ и АОВ равны (по трем сторонам), поэтому 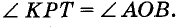
Пример №8
Постройте биссектрису данного угла.
Решение:
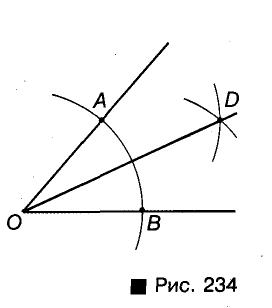
Пусть АОВ — данный угол (рис. 234). Произвольным раствором циркуля опишем дугу с центром О. Пусть А и В — точки пересечения этой дуги с лучами О А и ОВ. Из центров А и В опишем дуги такими же радиусами. Если D — точка пересечения этих дуг, то луч OD — биссектриса угла АОВ.
Действительно, 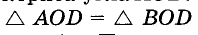 (по трем сторонам). Поэтому
(по трем сторонам). Поэтому 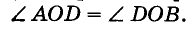
Пример №9
Разделите данный отрезок пополам.
Решение:
Пусть АВ — данный отрезок (рис. 235). Из точек А и В радиусом АВ описываем дуги. Они пересекутся в неких точках С и D.
Прямая CD точкой М разделит данный отрезок пополам.
Действительно, по трем сторонам 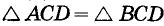 , поэтому
, поэтому 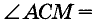
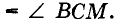 По первому признаку равенства треугольников
По первому признаку равенства треугольников 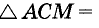
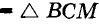 . Итак, AM = ВМ.
. Итак, AM = ВМ.
Пример №10
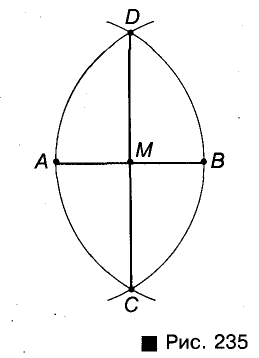
Через данную точку Р проведите прямую, перпендикулярную и данной прямой а.
Решение:
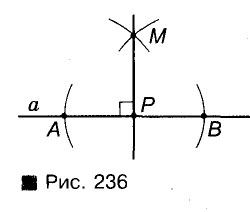
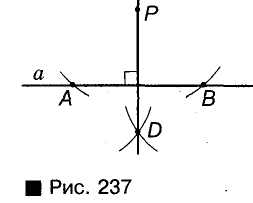
В зависимости от того, лежит или не лежит точка Р на прямой а, задачу можно решить, как показа но на рисунках 236 и 237. Опишите и аргументируйте эти построения самостоятельно.
Пример №11
Через точку Р, не лежащую на прямой АВ, проведите прямую, параллельную прямой АВ.
Решение:
Через точку Р и про из вольную точку А прямой АВ проводим прямую АТ (рис. 238). Строим угол ТРМ, равный углу РАВ, так, что бы эти углы стали соответственны ми при прямых РК, АВ и секущей АР. Построенная таким образом пря мая РК удовлетворяет задачу: она проходит через данную точку Р и параллельна прямой АВ, поскольку 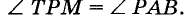
Геометрическими построениями часто приходилось заниматься многим людям. Еще в доисторические времена мастера, изготавливающие колеса к колесницам, умели делить окружность на несколько равных частей. В наше время выполнять такие построения приходится специалистам, проектирующим или изготавливающим шестеренки, дисковые пилы (рис. 239), турбины и различные роторные механизмы. Как бы вы разделили окружность, например, на 5, 6 или 7 равных частей? 
Основные чертежные инструменты — линейка и циркуль — были известны еще несколько тысячелетий назад.
Слово линейка происходит от слова линия, которое на латинском языке сначала означало «льняная нитка», «черта, проведенная ниткой, бечевкой» (производное от лат. Плит — лен). Слово циркуль тоже латинского происхождения, первоначально слово циркулюс означало «окружность, круг», а потом стало означать инструмент, с помощью которого проводят окружности.
В Древней Греции линейку и циркуль признавали единственными приборами геометрических построений. Задачу на построение считали решенной, если все построения в ней выполнялись только с помощью линейки и циркуля. Сейчас специалисты при выполнении построений пользуются угольником, транспортиром, рейсмусом, рейсшиной и другими чертежными приспособлениями.
Пример №12
Разделите данную дугу окружности на две равные части.
Решение:
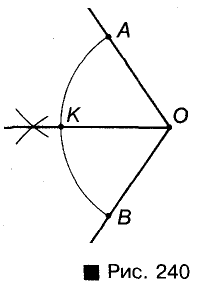
Пусть дана дуга АВ окружности с центром О (рис. 240). Представим угол АОВ и проведем его биссектрису ОК. Треугольники АОК и КОВ равны, поэтому и дуги АК и КВ равны.
Пример №13
Постройте угол вдвое больше данною.
Решение:
Пусть АОВ — данный угол (рис. 241) Опишем дугу окружности с центром О Если она пересечет стороны данного угла в точках А и В, из В как из центра сделаем засечку ВС = ВА и проведем луч ОС. Угол АОС вдвое больше 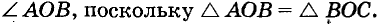
Задачи на построение
С геометрическими построениями имеют дело различные специалисты. Геометрические построении выполняют чертежники, архитекторы, конструкторы, топографы, геодезисты, штурманы. Разные геометрические фигуры строят также: слесарь — на жести, столяр — на доске, портной— на ткани, садовник — на земле.
В задаче на построение требуется построить геометрическую фигуру, которая должна удовлетворять определенные условия. В геометрии построения выполняют чаще всего с помощь к линейки и циркуля. Условимся: если в задаче не сказано, какими инструментами следует выполнить построение, то имеются в виду только линейка (без делений) и циркуль.
Более сложные задачи на построение часто решают методом геометрических мест. Пусть, например, в задаче требуете!’ найти точку X, удовлетворяющую два условия. Если первое условие удовлетворяют точки фигуры К, а второе — точки фигуры Р, то X должна принадлежать каждой из этих фигур. Тс есть X — точка пересечения фигур К и Р.
Пример №14
Постройте прямоугольный треугольник по да» ному катету а и гипотенузе с (рис. 243).
Решение:
Строим прямой угол АСВ, на его стороне откладываем отрезок СВ = а. Точки С и В — две вершины треугольника, который требуется построить. Третья верши» должна лежать, во-первых, на луче СА, во-вторых, на pfti стоянии с от В, то есть на окружности радиуса с с центр В. Если эту окружность пересекает луч СА в точке А, 1 треугольник ABC — именно тот, который требовалось не строить. Ведь его угол С прямой, ВС = а, ВА = с.
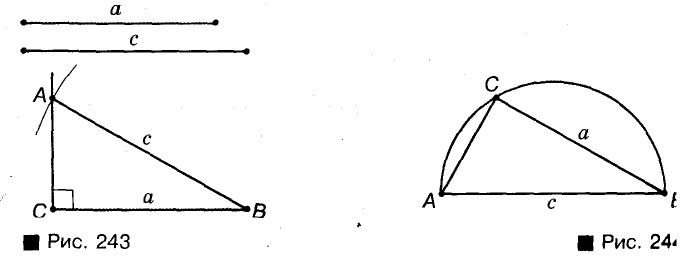
Второй способ (рис. 244). Откладываем отрезок АВ = с и проводим окружность диаметра АВ — ГМТ, из которых АВ виден под прямым углом. Дальше строим полуокружность радиуса а с центром В — ГМТ, удаленных от В на расстояние а и лежащих по одну сторону от прямой АВ. Если два ГМТ пересекаются в точке С, то треугольник ABC — именно тот, который требовалось построить.
Составные части решения задачи на построение — анализ, построение, доказательство и исследование. В анализе ищут способ решения задачи, в построении выполняется само построение, в доказательстве обосновывается правильность выполненного построения, в исследовании выясняется, сколько решений имеет задача.
Пример №15
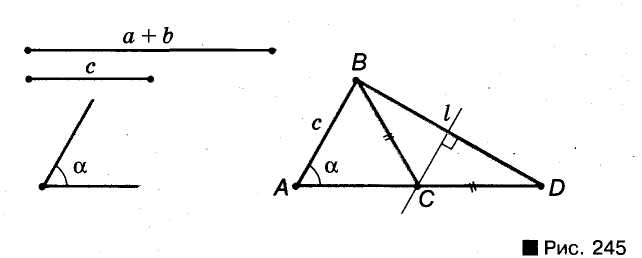
Постройте треугольник по данной стороне, прилежащему к ней углу и сумме двух других сторон (рис. 245).
Решение:
Анализ. Допустим, что требуемый треугольник ABC построен. Его сторона с и угол А = а — даны. Дан также отрезок, равный сумме сторон а и b. По данным отрезкам с и а + b и углу А между ними можно построить A ABD. Вершиной С искомого треугольника будет такая точка отрезка AD, для которой CD = СВ. Следовательно, точка С должна лежать и на серединном перпендикуляре отрезка BD.
Построение. По двум данным отрезкам и углу между ними строим 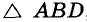 , после чего проводим серединный перпендикуляр I отрезка BD. Пусть прямая I пересекает отрезок АВ в точке С. Проводим отрезок СВ. Треугольник ABC — такой, который требовалось построить.
, после чего проводим серединный перпендикуляр I отрезка BD. Пусть прямая I пересекает отрезок АВ в точке С. Проводим отрезок СВ. Треугольник ABC — такой, который требовалось построить.
Доказательство:
В треугольнике 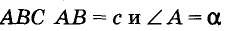 по построению. АС + СВ – АС + CD — а + b. Следовательно,
по построению. АС + СВ – АС + CD — а + b. Следовательно, 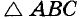 удовлетворяет все условия задачи.
удовлетворяет все условия задачи.
Исследование. Задача имеет решение только при условии, что а + b > с.
Если задача несложная и способ ее решения известен, анализ можно не описывать. А в решении не обязательно выделять анализ, построение, доказательство и исследование.
В математике чаще всего имеют дело с задачами: на вычисление, на доказательство, на построение, на преобразование и на исследование. Геометрическими задачами на построение активно интересовались античные геометры. Допуская лишь классические построения (выполняемые только линейкой и циркулем), они исследовали, какие из построений можно вы-полнить, а какие невозможно. В частности, выясняли:
- можно ли любой угол разделить на три равные части;
- можно ли построить квадрат, площадь которого была бы равна площади данного круга;
- можно ли построить ребро такого куба, объем которого был бы в 2 раза больше объема данного куба.
Много столетий выдающиеся геометры пытались решить эти задачи и не смогли. Эти три классические задачи древности получили специальные названия:
- трисекция угла,
- 2квадратура круга,
- удвоение куба.
Последнюю задачу называют еще делосской задачей, связывая ее с древнегреческой легендой. согласно которой оракул бога Аполлона согласился спасти жителей острова Делос от чумы, если кубический жертовник в делосском храме заменят на жертовник такой же формы, но вдвое большего объема. Только почти через 2000 лет ученые убедились, что ни одну из этих трех задач с помощью лишь линейки и циркуля решить невозможно.
В настоящее время специалисты, которым приходится выполнять геометрические построения, пользуются не только линейкой и циркулем. С точки зрения классических методов такие построения приближенные. Но для практических нужд точности, которую обеспечивают приближенные методы, вполне достаточно
Пример №16
Найдите центр данной окружности.
Решение:
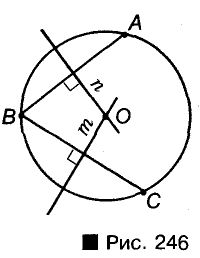
Обозначим на данной окружности три производные точки А, В и С (рис. 246).
Представим хорды АВ, ВС и проведем их серединные перпендикуляры n и m. Точка О, в которой пересекаются прямые n и m., — центр данной окружности. Ведь ОА = ОВ = ОС.
Пример №17
Через данную точку проведите касательную к данной окружности.
Решение:
Если данная точка А лежит на окружности центра О (рис. 247, а), проводим луч ОА, потом — прямую АК, перпендикулярную к ОА. Прямая АК — касательная, которую и требовалось построить.
Если точка А лежит вне данной окружности центра О (рис. 247, б), то на диаметре ОА описываем окружность. Она пересечется с данной окружностью в двух точках К и Р. Прямые АК и АР — искомые касательные, поскольку 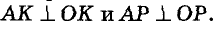 (Из точек К и Р вспомогательной окружности ее диаметр ОМ виден под прямыми углами АКО и АРО.) В этом случае задача имеет два решения.
(Из точек К и Р вспомогательной окружности ее диаметр ОМ виден под прямыми углами АКО и АРО.) В этом случае задача имеет два решения.
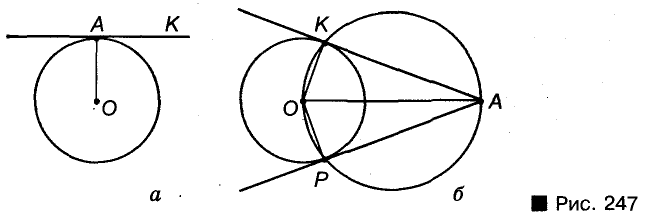
Свойство диаметра, перпендикулярного хорде
Диаметр, перпендикулярный хорде, проходит через ее середину. Докажите.
Решение
Пусть СО — диаметр окружности с центром О, АВ — хорда этой окружности, 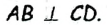 Докажем, что М — точка пересечения отрезков АВ и СD— середина отрезка АВ.
Докажем, что М — точка пересечения отрезков АВ и СD— середина отрезка АВ.
В случае, когда хорда АВ сама является диаметром, точка М совпадает с центром О и утверждение задачи очевидно. Пусть хорда АВ не является диаметром (рис. 165). Проведем радиусы OA и ОВ. Тогда в равнобедренном треугольнике АОВ высота ОМ является медианой. Итак, AM = ВМ, что и требовалось доказать.
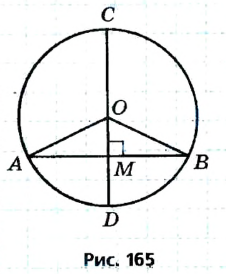
Докажите самостоятельно еще одно утверждение (опорное): диаметр окружности, проведенной через середину хорды, не являющейся диаметром, перпендикулярен этой хорде.
Касательная к окружности
Определение и свойство касательной
Любая прямая, проходящая через точки окружности, называется секущей; ее отрезок, лежащий внутри окружности, является хордой. На рисунке 167 хорда CD — отрезок секущей b . Рассмотрим теперь прямую, имеющую с окружностью только одну общую точку.
Определение:
Касательной к окружности называется прямая, имеющая с окружностью единственную общую точку. Общая точка касательной и окружности называется точкой касания.
На рисунке 167 прямая а является касательной к окружности с центром О. Иначе говоря, прямая а касается окружности с центром О в точке А . 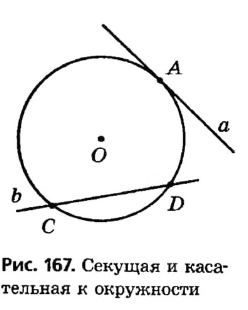
Определим взаимное расположение касательной и радиуса окружности, проведенного в точку касания.
Теорема (свойство касательной)
Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.
Доказательство:
Пусть прямая а касается окружности с центром О в точке А (рис. 168). Докажем, что 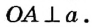 Применим метод доказательства от противного.
Применим метод доказательства от противного. 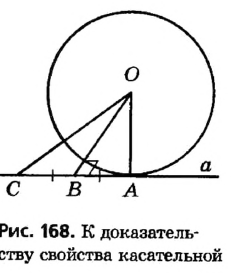
Пусть отрезок OA не является перпендикуляром к прямой а. Тогда, по теореме о существовании и единственности перпендикуляра к прямой, из точки О можно провести перпендикуляр ОB к прямой а . На луче АВ от точки В отложим отрезок ВС, равный АВ , и соединим точки О и С . Поскольку по построению отрезок ОВ — медиана и высота треугольника АОС, то этот треугольник равнобедренный с основанием АС, то есть OA = ОС . Таким образом, расстояние между точками О и С равно радиусу окружности, и, по определению радиуса, точка С должна лежать на данной окружности. Но это противоречит определению касательной, поскольку А — единственная общая точка окружности с прямой а. Из этого противоречия следует, что наше предположение неверно, то есть OA 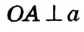 . Теорема доказана.
. Теорема доказана.
Признак касательной
Докажем теорему, обратную предыдущей.
Теорема: (признак касательной)
Если прямая проходит через точку окружности перпендикулярно радиусу, проведенному в эту точку, то она является касательной к окружности.
Доказательство:
Пусть прямая а проходит через точку А, лежащую на окружности с центром О, причем 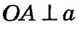 . Докажем, что а — касательная к окружности. Согласно определению касательной, нам необходимо доказать, что окружность имеет с прямой а единственную общую точку. Применим метод доказательства от противного.
. Докажем, что а — касательная к окружности. Согласно определению касательной, нам необходимо доказать, что окружность имеет с прямой а единственную общую точку. Применим метод доказательства от противного.
Пусть прямая а имеет с окружностью общую точку В , отличную от А (рис. 169). Тогда из определения окружности ОА = ОВ как радиусы, то есть треугольник АОВ равнобедренный с основанием АВ. По свойству углов равнобедренного треугольника 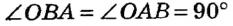 , что противоречит теореме о сумме углов треугольника.
, что противоречит теореме о сумме углов треугольника.
Следовательно, точка А — единственная общая точка окружности и прямой а, значит, прямая а — касательная к окружности.
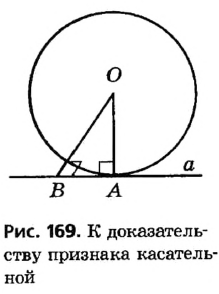
Свойство отрезков касательных
Пусть даны окружность с центром О и точка А, не принадлежащая кругу, ограниченному данной окружностью (рис. 170).
Через точку А можно провести две касательные к данной окружности. Отрезки, соединяющие данную точку А с точками касания, называют отрезками касательных, проведенных из точки А к данной окружности. На рисунке 170 АВ и АС — отрезки касательных, проведенных к окружности из точки А .
Опорная задача
Отрезки касательных, проведенных из данной точки к окружности, равны. Докажите.
Решение
Пусть АВ и АС — отрезки касательных, проведенных к окружности с центром О из точки А (рис. 170). Рассмотрим треугольники АОВ и АОС. По свойству касательной 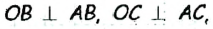 то есть эти треугольники являются прямоугольными с общей гипотенузой АО и равными катетами ОВ = ОС как радиусы окружности). Следовательно,
то есть эти треугольники являются прямоугольными с общей гипотенузой АО и равными катетами ОВ = ОС как радиусы окружности). Следовательно, 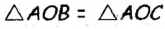 по гипотенузе и катету, откуда АВ = АС.
по гипотенузе и катету, откуда АВ = АС. 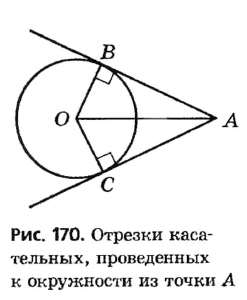
Касание двух окружностей
Определение:
Две окружности, имеющие общую точку, касаются в этой точке, если они имеют в ней общую касательную.
Общая точка двух окружностей в таком случае называется точкой касания окружностей.
Различают два вида касания окружностей: внутреннее и внешнее.
Касание окружностей называется внутренним, если центры окружностей лежат по одну сторону от общей касательной, проведенной через точку касания (рис. 171, а);
Касание окружностей называется внешним, если центры окружностей лежат по разные стороны от общей касательной, проведенной через точку касания (рис. 171, б).
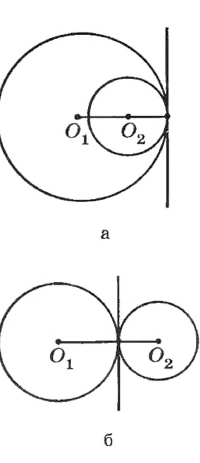
Рис. 171 Касание двух окружностей. 1. внутреннее; 2. внешнее.
По свойству касательной радиусы данных окружностей, проведенные в точку касания, перпендикулярны общей касательной. Из теоремы о существовании и единственности прямой, перпендикулярной данной, следует, что центры касающихся окружностей и точка касания окружнос тей лежат на одной прямой.
Касающиеся окружности имеют единствен ную общую точку — точку касания.
Если данные окружности имеют радиусы R и r (R > r), то расстояние между центрами окружностей равно R-r в случае внутреннего касания и R+r в случае внешнего касания.
Задачи на построение
Что такое задачи на построение?
Задачи на построение представляют собой отдельный класс геометрических задач, решение которых подчиняется определенным правилам. Цель решения этих задач — построение геометрических фигур с заданными свойствами с помощью чертежных инструментов. Если в условии задачи нет специальных примечаний, то имеются в виду построения с помощью циркуля и линейки. С помощью линейки можно провести:
- произвольную прямую;
- прямую, проходящую через данную точку;
- прямую, проходящую через две данные точки.
Заметим, что никаких других построений линейкой выполнять нельзя. В частности, с помощью линейки нельзя откладывать отрезки заданной длины.
Циркуль – от латинского “циркулус” – окружность, круг.
С помощью циркуля можно:
- провести окружность (часть окружности) произвольного или заданного радиуса с произвольным или заданным центром;
- отложить от начала данного луча отрезок заданной длины.
Кроме того, можно отмечать на плоскости точки и находить точки пересечения прямых и окружностей.
Все перечисленные операции называют элементарными построениями, а решить задачу на построение — это значит найти последовательность элементарных построений, после выполнения которых искомая фигура считается построенной, и доказать, что именно эта фигура удовлетворяет условию задачи.
Итак, решение задач на построение заключается не столько в самом построении фигуры, сколько в нахождении способа построения и доказательстве того, что полученная фигура искомая.
Основные задачи на построение
Если каждый шаг построений описывать полностью, решение некоторых задач может оказаться довольно громоздким. С целью упрощения работы выделяют несколько важнейших задач, которые считаются основными и не детализируются каждый раз при решении более сложных задач.
Пусть даны отрезки длиной а , b и с . Построим треугольник со сторонами, b и с.
Проведем произвольный луч и отметим на нем точку А . Раствором циркуля, равным а , построим окружность с центром А . Пусть В — точка пересечения этой окружности с лучом.
Раствором циркуля, равным b , опишем окружность с центром А , а раствором циркуля, равным с ,— окружность с центром В . Пусть С — точка пересечения этих окружностей.
Проведем отрезки АС и ВС. По построению треугольник ABC имеет стороны длиной а , b и с, то есть треугольник ABC искомый 1 .
1 По данным задачи можно построить четыре разных треугольника с общей стороной АВ. По третьему признаку эти треугольники равны, то есть совмещаются наложением. В таких случаях решением задачи считают любой из этих равных треугольников.
Отметим, что эта задача имеет решение при условии, что длины отрезков а , b и с удовлетворяют неравенству треугольника.
С помощью описанных операций несложно решить задачу о построении угла, равного данному неразвернутому углу А. Для этого достаточно отложить на сторонах данного угла А отрезки АВ и АС и построить треугольник, равный треугольнику ABC.
Построим окружность произвольного радиуса с центром О. Пусть А и B — точки пересечения этой окружности с прямой а .
| Построение перпендикулярной прямой | |
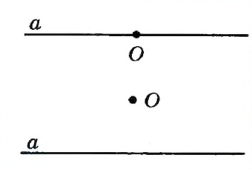 |
Пусть даны прямая а и точка О . Построим прямую, проходящую через точку О и перпендикулярную прямой а . Рассмотрим два случая |
| Точка O лежит на прямой а | |
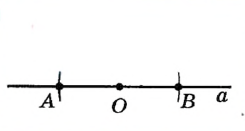 |
|
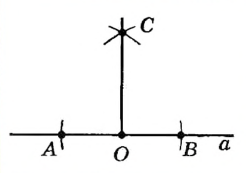 |
Построим окружности радиуса АВ с центрами А и В. Пусть С — одна из точек их пересечения. Проведем прямую через точки С и О. |
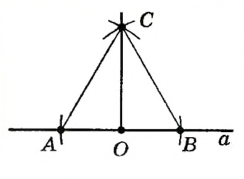 |
По построению отрезок СО — медиана равностороннего треугольника ABC , которая является также его высотой. Итак, 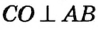 , то есть прямая СО — искомая. , то есть прямая СО — искомая. |
| Точка O не лежит на прямой а | |
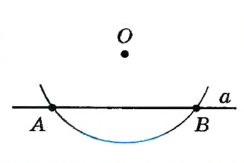 |
Построим окружность с центром О , которая пересекает прямую O, в точках А и В . |
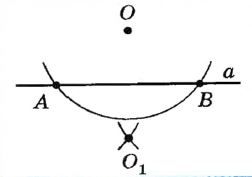 |
Построими окружности того же радиуса с центрами A и В . Пусть Ol — точка пересечения этих окружностей, причем точки О и Ol лежат по разные стороны от прямой а . |
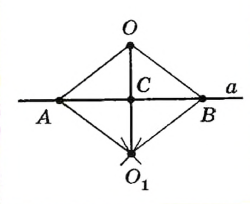 |
Проведем прямую 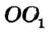 . Пусть С — точка пересечения прямых . Пусть С — точка пересечения прямых 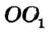 и а . По построению и а . По построению 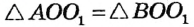 (по третьему признаку). Отсюда (по третьему признаку). Отсюда 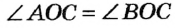 . Тогда ОС — биссектриса равнобедренного треугольника АОВ , проведенная к основанию. Она также является медианой и высотой треугольника. Следовательно, . Тогда ОС — биссектриса равнобедренного треугольника АОВ , проведенная к основанию. Она также является медианой и высотой треугольника. Следовательно, 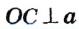 а , то есть прямая а , то есть прямая 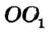 — искомая. — искомая. |
Отметим, что построенная прямая 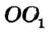 перпендикулярна отрезку АВ и проходит через его середину. Такую прямую называют серединным перпендикуляром к отрезку.
перпендикулярна отрезку АВ и проходит через его середину. Такую прямую называют серединным перпендикуляром к отрезку.
Пользуясь описанными построениями, несложно решить задачи на построение середины данного отрезка и на построение прямой, параллельной данной.
Для построения середины отрезка АВ достаточно провести две окружности радиуса АВ с центрами в точках А к В (рис. 172). Обозначив точки пересечения этих окружностей через 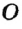 и
и 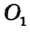 можно определить середину отрезка AB как точку пересечения прямых АВ и
можно определить середину отрезка AB как точку пересечения прямых АВ и 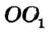 , после чего провести доказательство, аналогичное доказательству предыдущей задачи.
, после чего провести доказательство, аналогичное доказательству предыдущей задачи.
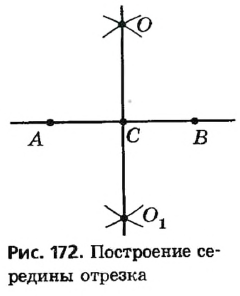
Для построения прямой, проходящей через данную точку О параллельно данной прямой а, достаточно провести через точку О прямую b , перпендикулярную а, и прямую с, перпендикулярную b (рис. 173). Тогда а || с по теореме о двух прямых, перпендикулярных третьей.
Таким образом, основными задачами на построение будем считать следующие:
- построение треугольника с данными сторонами;
- построение угла, равного данному неразвернутому углу;
- построение биссектрисы данного неразвернутого угла;
- построение прямой, проходящей через данную точку перпендикулярно данной прямой;
- построение серединного перпендикуляра к данному отрезку;
- построение середины данного отрезка;
- построение прямой, проходящей через данную точку параллельно данной прямой.
Если эти задачи применяются как вспомогательные при решение более сложных задач, соответствующие построения можно подробно не описывать.
Решение задач на построение
Решение задач на построение состоит из четырех основных этапов: анализ, построение, доказательство, исследование.
Выполнение рисунка-эскиза искомой фигуры и установление связи между ее элементами и данными задачи. Определение плана построения искомой фигуры.
Осуществление плана, разработанного в ходе анализа.
Обоснование того, что построенная фигура имеет заданную форму, а размеры и расположение ее элементов удовлетворяют условию задачи.
Определение количества решений и условий существования искомой фигуры или обоснование невозможности ее построения.
Если задача достаточно проста, то отдельные этапы ее решения можно проводить устно.
1] В некоторых задачах для исследования необходимы геометрические утверждения и соотношения, изучаемые в 8—9 классах. В этих случаях исследования мы будем проводить в сокращенном виде или вообще опускать.
Рассмотрим на конкретных примерах некоторые методы решения задач на построение.
Пример №18
Постройте треугольник по двум сторонам и медиане, проведенной к одной из них.
Решение:
Анализ
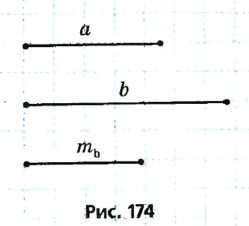
Пусть a, b, 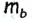 — две стороны и медиана треугольника ABC, который необходимо построить (рис. 174).
— две стороны и медиана треугольника ABC, который необходимо построить (рис. 174).
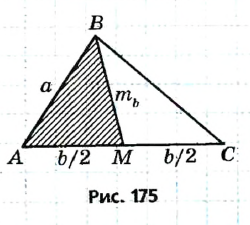
Допустим, что треугольник ABC построен (рис. 175). Если ВМ — данная медиана треугольника ABC, то в треугольнике АВМ известны длины трех сторон 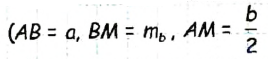 по условию задачи). Таким образом, мы можем построить треугольник АВМ и найти вершины А и В искомого треугольника. Чтобы найти вершину С, достаточно отложить на луче AM отрез ок МС длиной
по условию задачи). Таким образом, мы можем построить треугольник АВМ и найти вершины А и В искомого треугольника. Чтобы найти вершину С, достаточно отложить на луче AM отрез ок МС длиной 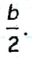
Построение
- Разделим отрезок bпополам.
- Построим треугольник АВМ со сторонами АВ = а,
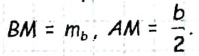
- Отложим на луче AM отрезок
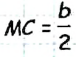 .
. - Соединим точки В и С.
Доказательство
В треугольнике 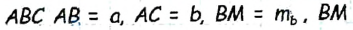 — медиана (по построению). Следовательно, треугольник ABC искомый.
— медиана (по построению). Следовательно, треугольник ABC искомый.
Исследование
Задача имеет решение при условии существования треугольника АВМ, то есть, если числа 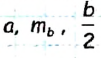 – удовлетворяют неравенству треугольника.
– удовлетворяют неравенству треугольника.
Сравним только что решенную задачу с задачей о доказательстве равенства треугольников но двум сторонам и медиане, проведенной к одной из них (п. 13.1). Решая обе эти задачи, мы использовали треугольник АВМ в котором все стороны известны по условию. Его рассмотрение помогло в задаче на доказательство получить необходимые соотношения для углов данных треугольников, а в задаче на построение — найти две вершины искомого треугольника. Треугольник АВМ называют вспомогательным а соответствующий метод решения — методом вспомогательного треугольника.
Решение задач на построение с помощью метода вспомогательной треугольника подробно рассмотрено в Приложении 2.
Геометрическое место точек
Понятие о геометрическом месте точек
До сих пор мы описывали геометрические фигуры с помощью определений и устанавливали их особенности путем доказательства свойств и признаков, относящихся к фигуре в целом. Для случаев, когда определенное свойство и соответствующий ему признак имеет каждая точка фигуры, существует еще один способ описания.
Определение:
Геометрическим местом точек (сокращенно ГМТ) на плоскости называется фигура, которая состоит из всех точек плоскости, удовлетворяющих определенному условию.
Например, по определению окружность является геометрическим местом точек, удаленных от данной точки плоскости на одинаковое расстояние.
В определении ГМТ обратим внимание на слово «всех». Оно указывает на то, что для выяснения геометрического места точек недостаточно доказать, что точки указанной фигуры удовлетворяют определенному условию (то есть установить свойство точек). Необходимо также показать, что других точек, удовлетворяющих данному условию, на плоскости нет, то есть доказать соответствующий признак: если точка удовлетворяет указанному условию, то она принадлежит данной фигуре.
Иначе говоря, доказательство того, что некоторая фигура F является геометрическим местом точек, удовлетворяющих условию Р, состоит из доказательства двух утверждений — прямого и обратного:
- если определенная точка P принадлежит фигуре F, то она удовлетворяет условию Р ;
- если определенная точка удовлетворяет условию Р, то она принадлежит фигуре F .
Основные теоремы о ГМТ
Часто геометрическим местом точек является прямая или часть прямой. Докажем две важные теоремы о ГМТ.
Теорема: (о серединном перпендикуляре)
Серединный перпендикуляр к отрезку является геометрическим местом точек, равноудаленных от концов этого отрезка.
Доказательство:
Нам необходимо доказать два утверждения:
- если точка принадлежит серединному перпендикуляру к отрезку, то она равноудалена от концов этого отрезка;
- если точка равноудалена от концов отрезка, то она принадлежит серединному перпендикуляру к этому отрезку.
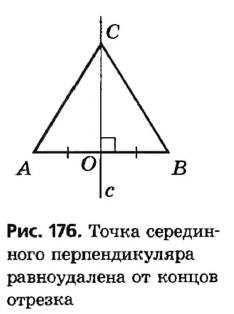
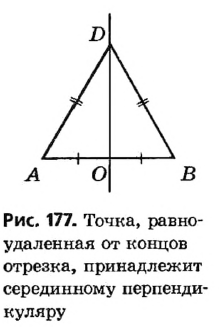
Докажем первое из этих утверждений. Пусть точка С лежит на прямой с, перпендикулярной отрезку АВ и проходящей через его середину — точку О (рис. 176). В треугольнике АСВ отрезок СО — медиана и высота, значит, этот треугольник равнобедренный с основанием АВ. Отсюда АС=ВС , то есть расстояния от точки С до концов отрезка АВ равны. Докажем второе утверждение. Пусть точка D равноудалена от точек А и В , то есть AD = BD (рис. 177). Тогда в равнобедренном треугольнике ADB отрезок DO — медиана, проведенная к основанию, которая является также и высотой. Таким образом, прямая DO — серединный перпендикуляр к отрезку АВ. Теорема доказана.
Теорема: (о биссектрисе угла)
Биссектриса неразвернутого угла является геометрическим местом точек, равноудаленных от сторон этого угла.
Доказательство
По аналогии с предыдущей теоремой докажем сначала, что любая точка биссектрисы равноудалена от сторон угла.
Пусть даны неразвернутый угол с вершиной А и точка D на его биссектрисе (рис. 178). Опустим из точки D перпендикуляры DB и DC на стороны данного угла. По определению, DB и DC — расстояния от точки D до сторон угла А.
Прямоугольные треугольники DBA и DCA имеют общую гипотенузу 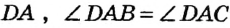 по условию. Тогда
по условию. Тогда 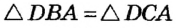 по гипотенузе и острому углу. Отсюда DB = DC , то есть точка D равноудалена от сторон данного угла.
по гипотенузе и острому углу. Отсюда DB = DC , то есть точка D равноудалена от сторон данного угла.
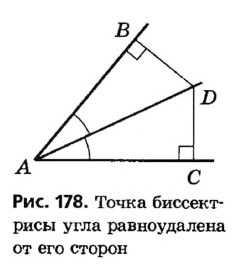
Теперь докажем, что любая точка, равноудаленная от сторон угла, принадлежит его биссектрисе. Пусть F — некоторая точка, равноудаленная от сторон угла А, то есть перпендикуляры FB и FC, опущенные из точки F на стороны данного угла, равны (рис. 179). Соединим точки F и А . Тогда прямоугольные треугольники FBA и FCA равны по гипотенузе и катету.
Отсюда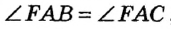 , то есть луч AF — биссектриса угла А.
, то есть луч AF — биссектриса угла А.
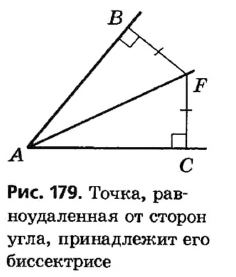
*Здесь и далее, говоря о точках, равноудаленных от сторон угла, мы имеем в виду точки, лежащие внутри угла и равноудаленные от прямых, содержащих его стороны.
Метод геометрических мест
Понятие ГМТ часто используется при решении задач на построение. Например, пусть необходимо построить точку, удовлетворяющую условиям 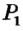 и
и 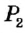 . Если геометрическим местом точек, удовлетворяющих условию
. Если геометрическим местом точек, удовлетворяющих условию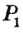 , является фигура
, является фигура 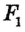 , а геометрическим местом точек, удовлетворяющих условию
, а геометрическим местом точек, удовлетворяющих условию 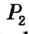 — фигура
— фигура 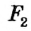 то искомая точка будет общей для фигур
то искомая точка будет общей для фигур 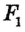 и
и 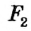 то есть точкой их пересечения.
то есть точкой их пересечения.
Рассуждения по такой схеме лежат в основе метода геометрических мест.
Пример №19
Постройте прямоугольный треугольник по гипотенузе и катету.
Решение:
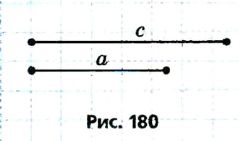
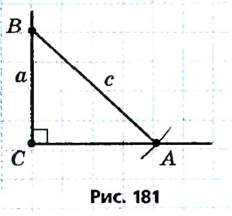
Пусть в искомом прямоугольном треугольнике ABC гипотенуза АВ равна с , катет ВС равен а (рис. 180). Для построения треугольника воспользуемся методом геометрических мест. Для этого на стороне прямого угла С отложим катет ВС, ВС = а (рис. 181). Точка А должна принадлежать второй стороне прямого угла и быть удаленной от точки В на расстояние с, то есть А — точка пересечения окружности с центром В радиуса с со второй стороной прямого угла. Построенные точки А, В и С являются вершинами искомого прямоугольного треугольника ABC. В соответствии со следствием теоремы о сравнении сторон и углов треугольника задача имеет решение при условии а 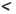 с.
с.
Описанная и вписанная окружности треугольника
Окружность, описанная около треугольника
Определение:
Окружность называется описанной около треугольника, если все вершины треугольника лежат на данной окружности.
В этом случае говорят, что треугольник является вписанным в данную окружность.
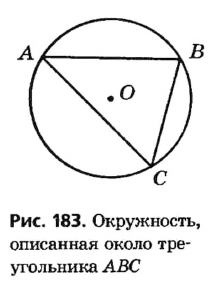
На рисунке 183 окружность с центром О описана около треугольника ABC.
Поскольку все вершины треугольника лежат на описанной окружности, то все они равноудалены от центра окружности. Этот факт лежит в основе доказательства теоремы об описанной окружности.
Теорема: (об окружности, описанной около треугольника)
Около любого треугольника можно описать единственную окружность. Центр этой окружности является точкой пересечения серединных перпендикуляров к сторонам треугольника.
Доказательство:
Пусть прямые а и b — серединные перпендикуляры к сторонам АВ и ВС данного треугольника ABC (рис. 184).
Сначала докажем методом от противного, что прямые а и b пересекаются. Предположим, что эти прямые не пересекаются, то есть а || b . Тогда поскольку 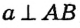 , то
, то 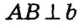 по следствию из теоремы о свойствах углов при параллельных прямых. Но
по следствию из теоремы о свойствах углов при параллельных прямых. Но 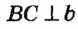 по построению, отсюда
по построению, отсюда 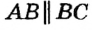 что невозможно по условию. Следовательно, прямые а и b пересекаются в некоторой точке О.
что невозможно по условию. Следовательно, прямые а и b пересекаются в некоторой точке О.
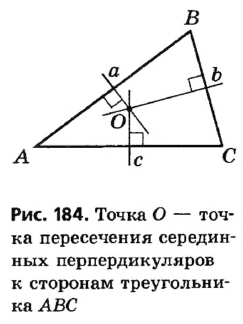
По теореме о серединном перпендикуляре точка О равноудалена от точек А и В (то есть OA = OB ) и равноудалена от точек В и С (то есть ОВ = ОС ). Отсюда OA = OB = ОС. Следовательно, существует окружность с центром О, проходящая через все вершины треугольника ABC.
Докажем методом от противного, что такая окружность единственна.
Допустим, что около треугольника можно описать еще одну окружность, отличную от построенной. Тогда центр этой окружности равноудален от вершин треугольника и потому совпадает с О, точкой пересечения серединных перпендикуляров к сторонам треугольника. Радиус этой окружности равен расстоянию от точки О до вершин треугольника. Значит, эта окружность совпадает с построенной.
И наконец, серединный перпендикуляр с к стороне АС содержит вое точки, равноудаленные от точек А и С . Поскольку точка О также равноудалена от точек А и С , то этот серединный перпендикуляр проходит через точку О. Теорема доказана.
Три серединных перпендикуляра к сторонам треугольника пересекаются в одной точке.
Отметим, что центр описанной окружности не всегда лежит внутри треугольника; он также может лежать на одной из его сторон или вне треугольника (рис. 185).
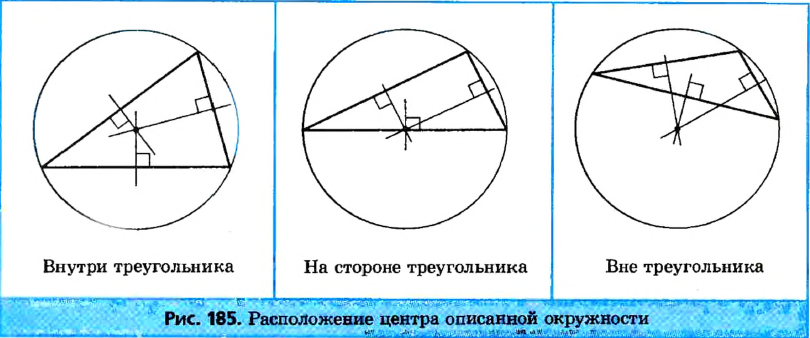
Окружность, вписанная в треугольник
Определение:
Окружность называется вписанной в треугольник, если она касается всех его сторон.
В этом случае треугольник является описанным около данной окружности.
На рисунке 186 окружность с центром О вписана в треугольник ABC. Прямые, содержащие стороны треугольника, являются касательными к вписанной окружности, а точки касания лежат на сторонах треугольника. Радиусы вписанной окружности, проведенные в точки касания, перпендикулярны сторонам данного треугольника.
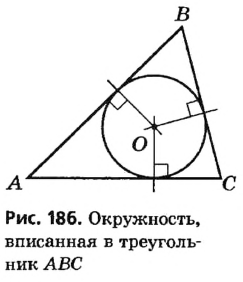
Далее в таком случае мы будем говорить, что центр вписанной окружности равноудален от сторон треугольника.
Теорема: (об окружности, вписанной в треугольник)
В любой треугольник можно вписать единственную окружность. Центр этой окружности является точкой пересечения биссектрис треугольника.
Доказательство:
Пусть AD и BE — биссектрисы данного треугольника ABC (рис. 187).
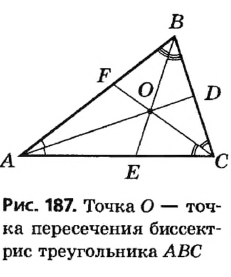
Докажем методом от противного, что эти биссектрисы пересекаются. Пусть AD и BE не пересекаются. Тогда AD || BE, а углы BAD и ABE — внутренние односторонние при параллельных прямых AD и BE и секущей АВ. Сумма этих углов должна быть равна 180°, что противоречит теореме о сумме углов треугольника.
Итак, биссектрисы AD и BE пересекаются в некоторой точке О. Тогда по теореме о биссектрисе угла точка О равноудалена от сторон АВ и АС, а также равноудалена от сторон АВ и ВС . Таким образом, три перпендикуляра, опущенные из точки О на стороны данного треугольника, равны. Следовательно, существует окружность с центром О, которая касается всех сторон треугольника ABC.
Докажем методом от противного, что эта окружность единственна.
Допустим, что в треугольник можно вписать еще одну окружность, отличную от построенной. Тогда ее центр одинаково удален от сторон треугольника и совпадает с О, точкой пересечения биссектрис треугольника. Радиус этой окружности равен расстоянию от точки О до сторон треугольника. Таким образом, эта окружность совпадает с построенной.
И наконец, биссектриса CF содержит все точки, равноудаленные от сторон СА и СВ. Поскольку точка О также равноудалена от СА и СВ, то эта биссектриса проходит через точку О. Теорема доказана.
Три биссектрисы треугольника пересекаются в одной точке.
Поскольку все биссектрисы треугольника лежат внутри него, то и центр вписанной окружности всегда лежит внутри треугольника.
Пример №20
В равностороннем треугольнике центры описанной и вписанной окружностей совпадают. Докажите.
Решение:
В равностороннем треугольнике ABC биссектрисы 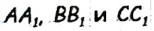 являются также медианами и высотами (рис. 188). Это означает, что. прямые
являются также медианами и высотами (рис. 188). Это означает, что. прямые 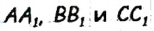 — серединные перпендикуляры к сторонам треугольника ABC. Поскольку все они пересекаются в одной точке, то эта точка — центр описанной и вписанной окружностей треугольника ABC.
— серединные перпендикуляры к сторонам треугольника ABC. Поскольку все они пересекаются в одной точке, то эта точка — центр описанной и вписанной окружностей треугольника ABC.
Верно также и обратное утверждение: если в треугольнике центры описанной и вписанной окружностей совпадают, то этот треугольник равносторонний. Попробуйте доказать это самостоятельно.
Историческая справка:
Простейшие геометрические задачи на построение:
Возникновение задан на построение было обусловлено необходимостью измерений земельных участков и строительством. Значительных успехов в решении таких задач достигли древнегреческие ученые, прежде всего Евклид и Платон, в VII – III в. до н. з. Именно со времен Платона в решении задач на построение стали выделять четыре этапа: анализ, собственно построение, доказательство и исследование.
Задачи, которые невозможно решить с помощью циркуля и линейки
Особый интерес математиков древности вызывали три классические задачи, которые не удавалось решить с помощью циркуля и линейки – о квадратуре круга, трисекции угла и удвоении куба. Задача о квадратуре круга состояла в построении квадрата, площадь которого равна площади данного круга. В задаче о трисекции угла пытались разделить данный угол на три равные части. Такую задачу несложно решить для некоторых конкретных углов, например развернутого, прямого, но не для любого угла. Задача об удвоении куба состояла в построении куба, объем которого вдвое больше объема данного куба. Невозможность решить эти задачи с помощью циркуля и линейки была доказана в XIX в.
Циркуль или линейка
Интересна историй ограничений в выборе инструментов для решения задач на построение. В X веке арабский математик Абу-ль-Вафа предложил ограничиться в геометрических построениях односторонней линейкой и циркулем постоянного раствора. В 1797 г. итальянец Лоренцо Маскерони доказал: любая задача на построение, решенная с помощью циркуля и линейки, может быть решена и с помощью одного циркуля (при этом предполагалось, что через любые две точки может быть проведена прямая). А еще раньше, в 1672 г. к такому же выводу пришел датчанин Г. Мор. Так, теорема о возможности построений только циркулем получила название «теоремы Мора – Маскерони». В 1833 г. швейцарский геометр Якоб Штейнер показал, что, при наличии на плоскости окружности с отмеченным центром, любую задачу на построение можно решить с помощью одной линейки. Задачи на построение играют особую роль в обучении геометрии, ведь они прекрасно развивают логику и абстрактное мышление. Специалисты считают задачи на построение одними из самых полезных и красивых задач геометрии.
Об аксиомах геометрии
Вы ознакомились с начальными понятиями геометрии: точкой и прямой, а также лучом, отрезком и углом. Их основные свойства — аксиомы — не доказываются, но являются фундаментом для доказательства других утверждений. Первую попытку провести логическое обоснование геометрии с помощью систематизированного перечня исходных положений (аксиом или постулатов) осуществил древнегреческий математик Евклид в своей знаменитой книге «Начала». На протяжении многих веков ученые-геометры опирались именно на евклидовы аксиомы. Но в XIX—XX вв., после создания Лобачевским неевклидовой геометрии, исследования системы геометрических аксиом вышли на качественно новый уровень. Одним из тех, кто внес заметный вклад в усовершенствование аксиоматики, был выдающийся украинский математик Алексей Васильевич Погорелов. В своей фундаментальной работе «Основания геометрии» (1983) он разработал собственную усовершенствованную систему аксиом евклидовой геометрии, которая решила проблему преодоления ряда существенных трудностей, возникших при введении понятия меры для отрезков и углов. Более того, А. В. Погорелов предложил упрощенный вариант геометрической аксиоматики, предназначенный именно для преподавания геометрии в школе. Этот вариант был положен в основу учебника «Геометрия», по которому свыше четверти века изучали и, без сомнения, будут изучать геометрию в школе. Вот как выглядит система аксиом школьного курса, предложенная А. В. Погореловым.
- Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей. Через любые две точки можно провести прямую, и только одну.
- Из трех точек на прямой одна и только одна лежит между двумя другими.
- Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
- Прямая разбивает плоскость на две полуплоскости.
Каждый угол имеет градусную меру, большую нуля. Развернутый угол равен 180°. Градусная мера угла равна сумме градусных мер углов, на
- которые он разбивается любым лучом, проходящим между его сторонами.
- На любой полупрямой от ее начальной точки можно отложить отрезок заданной длины, и только один.
- От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180°, и только один.
- Каков бы ни был треугольник, существует равный ему треугольник, в заданном расположении относительно данной полупрямой.
- Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной.
Этой системы аксиом мы придерживаемся и в нашем учебнике с учетом принятой нами терминологии. Некоторые аксиомы были сформулированы в главе I, другие аксиомы не формулировались, но фактически использовались в рассуждениях. Отметим, что авторы не ставили цель представлять в этом учебнике абсолютно совершенную и логически завершенную систему аксиом, а сосредоточили основное внимание на практическом применении основных свойств простейших геометрических фигур при доказательстве теорем и решении задач. В дальнейшем, при изучении свойств фигур в пространстве, формулировки некоторых аксиом будут уточнены, а сама система аксиом — расширена.
Вообще же, система аксиом должна удовлетворять условиям независимости (не содержать аксиомы, которые можно вывести с помощью других аксиом), непротиворечивости (не иметь явных или скрытых противоречий) и полноты (содержать достаточное количество аксиом, чтобы доказать основные утверждения). Исследование проблем построения таких систем аксиом является содержанием одного из разделов современной геометрии.
Метод вспомогательного треугольника
Метод вспомогательного треугольника применяется при решении многих задач на построение. Используя этот метод, необходимо придерживаться следующей последовательности действий:
- предположив, что искомый треугольник построен, выполнить рисунок- эскиз и найти на нем вспомогательный треугольник, способ построения которого известен (или получить такой треугольник путем дополнительных построений);
- установить, какие вершины искомого треугольника мы получим, построив вспомогательный треугольник;
- определить на основании данных задачи последовательность построения других вершин, предположив, что вспомогательный треугольник построен;
- осуществить все намеченные построения;
- провести необходимые доказательства и исследования.
Довольно часто метод вспомогательного треугольника используют в сочетании с другими методами. Рассмотрим такие случаи на примерах.
Пример №21
Постройте прямоугольный треугольник по катету и сумме второго катета и гипотенузы.
Решение:
Пусть а и b + с — катет и сумма второго катета и гипотенузы треугольника ABC, который необходимо построить (рис. 194). 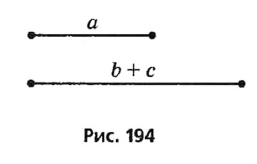
Анализ
Допустим, что треугольник ABC построен (рис. 195). Отложим на луче ВС отрезок CD длиной с и соединим точки А и D. Треугольник АВD прямоугольный с катетами а и b+с, то есть может быть построен по данным задачи и является вспомогательным. Построив его, получим вершины А и В искомого треугольника. Для построения вершины С воспользуемся одним из признаков равнобедренного треугольника. Точка С является точкой пересечения серединного перпендикуляра к стороне АD с лучом BD.
Построение
- 1. Построим прямой угол с вершиной В.
- 2. Отложим на сторонах этого угла отрезки АВ = а и ВD = b+с и соединим точки А и О. Треугольник АВD вспомогательный.
- 3. Построим перпендикуляр к отрезку АО. который проходит через его середину В. Пусть С— точка его пересечения с лучом ВD.
- 4. Соединим точки А и С.
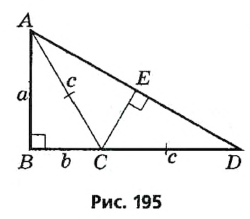
Доказательство:
В треугольнике 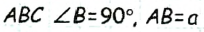 по построению. В треугольнике
по построению. В треугольнике 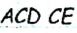 — высота и медиана (по построению). Значит, треугольник АСD равнобедренный с основанием AD), откуда СА=СD=с. По построению
— высота и медиана (по построению). Значит, треугольник АСD равнобедренный с основанием AD), откуда СА=СD=с. По построению 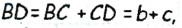 , следовательно,
, следовательно, 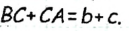 Таким образом, треугольник ABC искомый.
Таким образом, треугольник ABC искомый.
В соответствии с неравенством треугольника, задача имеет решение при условии a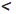 c+b
c+b
При решении этой задачи мы использовали метод спрямления. Суть его такова: если в условии задачи на построение заданы сумма (или разность) отрезков, то на рисунке-эскизе их необходимо отложить на одной прямой от общего конца так, чтобы другие концы этих отрезков образовали заданный отрезок-сумму (разность). Благодаря такому дополнительному построению, удается получить вспомогательный треугольник.
Пример №22
Постройте треугольник по медиане и двум углам, на которые она делит угол треугольника.
Решение:
Пусть m — медиана треугольника ABC, который необходимо построить, 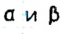 — углы, на которые медиана делит угол треугольника (рис. 196).
— углы, на которые медиана делит угол треугольника (рис. 196).
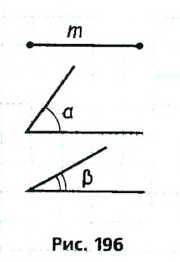
Анализ
Допустим, что треугольник ABC построен (рис. 197). Применим метод удвоения медианы. Для этого на луче ВМ отложим отрезок МD, равный m, и соединим точки O и А. По первому признаку равенства треугольников 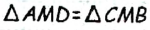 (АМ=СМ по определению медианы, ВМ =DМ по построению,
(АМ=СМ по определению медианы, ВМ =DМ по построению, 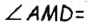
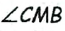 как вертикальные). Тогда
как вертикальные). Тогда 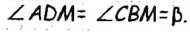
Следовательно, треугольник АВD вспомогательный, поскольку его можно построить по стороне и прилежащим к ней углам 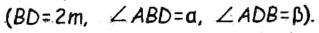 Построив этот треугольник, получим вершины А и В скомого треугольника. Для построения вершины С достаточно удвоить в треугольнике АВD медиану AM.
Построив этот треугольник, получим вершины А и В скомого треугольника. Для построения вершины С достаточно удвоить в треугольнике АВD медиану AM.
Построение (сокращенный план)
- 1. Построим треугольник АВD, в котором BD=2m
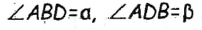 . Треугольник АВй вспомогательный.
. Треугольник АВй вспомогательный. - 2. Построим в треугольнике АВD медиану AM и на ее продолжении отложим отрезок МС, равный Am. >
- 3. Соединим точки Bи С.
Доказательство
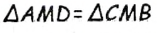 по первому признаку равенства треугольников
по первому признаку равенства треугольников 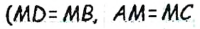 по построению,
по построению, 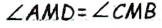 как вертикальные). Тогда
как вертикальные). Тогда 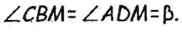 Также по построению
Также по построению 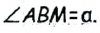 В треугольнике
В треугольнике 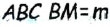 — медиана, поскольку по построению
— медиана, поскольку по построению 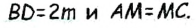 Таким образом, треугольник ABC — искомый.
Таким образом, треугольник ABC — искомый.
Пример №23
Постройте треугольник по стороне, медиане, проведенной к этой стороне, и высоте, опущенной на другую сторону.
Решение:
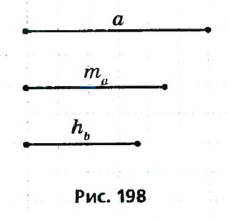
Пусть а — сторона искомого треугольника ABC, 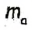 — проведенная к ней медиана,
— проведенная к ней медиана, 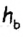 — высота треугольника, проведенная к другой стороне (рис. 198). Построим этот треугольник.
— высота треугольника, проведенная к другой стороне (рис. 198). Построим этот треугольник.
Анализ
Пусть треугольник ABC построен (рис. 199). Тогда прямоугольный треугольник ВСН можно построить по гипотенузе BC и катету ВН : на стороне прямого угла Н отложим катет BH=hb , тогда С — точка пересечения окружности с центром В радиуса а со второй стороной прямого угла.
Таким образом, мы построим вершины В и С искомого треугольника. Для построения вершины А снова используем метод геометрических мест. Поскольку основание высоты ВН принадлежит стороне АС, то точка А лежит на прямой НС. Поскольку 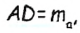 то точка А должна лежать на расстоянии
то точка А должна лежать на расстоянии 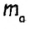 от точки D. Это означает, что A — точка пересечения прямой СH и окружности радиуса
от точки D. Это означает, что A — точка пересечения прямой СH и окружности радиуса 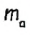 с центром D.
с центром D.
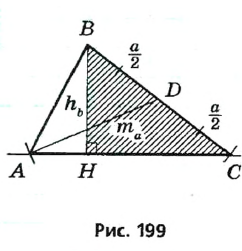
Построение
- 1. Построим прямой угол с вершиной Н.
- 2. Отложим на стороне этого угла отрезокВН, ВН= hb.
- 3. Построим окружность с центром В радиуса а. Пусть С — точка пересечения этой окружности с другой стороной прямого угла.
- 4. Соединим точки В и Си разделим отрезок ВС пополам. Пусть точка D — его середина.
- 5. Проведем прямую СН.
- 6. Построим окружность с центром D радиуса mа. ПустьА — точка пересечения этой окружности с прямой СН.
- 7. Соединим точкиА и В.
Доказательство
В треугольнике 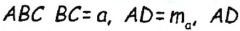 — медиана,
— медиана, 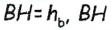 — высота (по построению). Следовательно, треугольник ABC — искомый.
— высота (по построению). Следовательно, треугольник ABC — искомый.
Исследование
В соответствии со следствием теоремы о сравнении сторон и углов треугольника вспомогательный треугольник существует, если hb 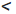 a. В зависимости от длины медианы
a. В зависимости от длины медианы 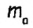 задача имеет одно или два решения, или не имеет ни одного.
задача имеет одно или два решения, или не имеет ни одного.
Реальная геометрия
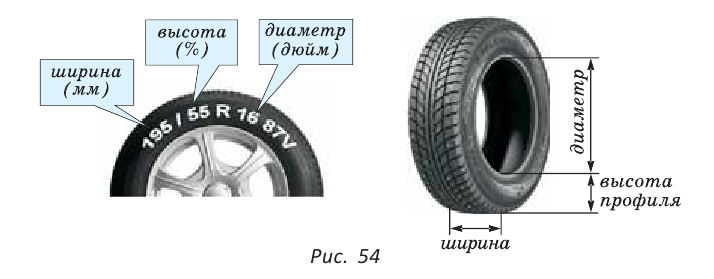
На любой шине от автомобиля есть маркировка, указывающая на ее размеры, например, 195/55 R16 (рис. 54). Число 195 означает ширину шины в мм. В данном случае ширина шины равна 195 мм или 19,5 см.
Второе число 55 означает высоту шины или высоту ее профиля, выраженную в процентах от ее ширины. В нашем случае это 55 % от 195 мм, то есть примерно 107 мм или 10,7 см.
И наконец надпись R16 обозначает внутренний диаметр шины, выраженный в дюймах. Так как 1 дюйм 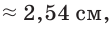 то для нашей шины получим
то для нашей шины получим 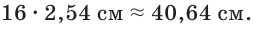
Интересно знать:
Если круг вращать около своего диаметра, получим геометрическое тело, которое вы хорошо знаете, — шар (рис. 55). Он также имеет центр, радиус, диаметр. Поверхность шара называется сферой. Сфера — это оболочка шара. Расстояние от центра шара до любой точки сферы равно радиусу шара. Диаметр шара равен двум радиусам.
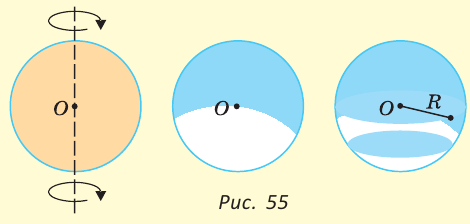
Если провести плоскость, пересекающую шар, то в сечении получим круг. Когда секущая плоскость будет проходить через центр шара, радиус R полученного круга будет равен радиусу шара.
Справочный материал по окружности и кругу
18. Геометрическое место точек
- ✓ Геометрическим местом точек (ГМТ) называют множество всех точек, обладающих определенным свойством.
- ✓ Серединный перпендикуляр отрезка является геометрическим местом точек, равноудаленных от концов этого отрезка.
- ✓ Биссектриса угла является геометрическим местом точек, принадлежащих углу и равноудаленных от его сторон.
19. Окружность и круг, их элементы
- ✓ Окружностью называют геометрическое место точек, расстояния от которых до заданной точки равны данному положительному числу. Данную точку называют центром окружности.
- ✓ Любой отрезок, соединяющий точку окружности с ее центром, называют радиусом окружности.
- ✓ Отрезок, соединяющий две точки окружности, называют хордой окружности. Хорду, проходящую через центр окружности, называют диаметром.
- ✓ Диаметр окружности в два раза больше ее радиуса.
- ✓ Кругом называют геометрическое место точек, расстояния от которых до заданной точки не больше данного положительного числа. Заданную точку называют центром круга. Радиус окружности, ограничивающей круг, называют радиусом круга. Если X — произвольная точка круга с центром О и радиусом
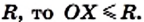
- ✓ Окружность, ограничивающая круг, ему принадлежит.
- ✓ Хорда и диаметр круга — это хорда и диаметр окружности, ограничивающей круг.
20. Свойства окружности
- ✓ Диаметр окружности, перпендикулярный хорде, делит эту хорду пополам.
- ✓ Диаметр окружности, который делит хорду, отличную от диаметра, пополам, перпендикулярен этой хорде.
21. Взаимное расположение прямой и окружности. Касательная к окружности
- ✓ Прямая и окружность могут не иметь общих точек, иметь две общие точки или иметь одну общую точку.
- ✓ Прямую, имеющую с окружностью только одну общую точку, называют касательной к окружности.
- ✓ Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.
- ✓ Если прямая, проходящая через точку окружности, перпендикулярна радиусу, проведенному в эту точку, то эта прямая является касательной к данной окружности.
- ✓ Если расстояние от центра окружности до некоторой прямой равно радиусу окружности, то эта прямая является касательной к данной окружности.
- ✓ Если через данную точку к окружности проведены две касательные, то отрезки касательных, соединяющие данную точку с точками касания, равны.
Описанная и вписанная окружности треугольника
Окружность называют описанной около треугольника, если она проходит через все его вершины.
На рисунке 247 изображена окружность, описанная около треугольника. В этом случае также говорят, что треугольник вписан в окружность.
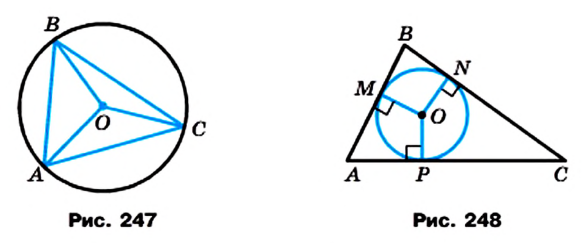
- ✓ Центр описанной окружности треугольника равноудален от всех его вершин.
- ✓ Около любого треугольника можно описать окружность. Центр окружности, описанной около треугольника, — это точка пересечения серединных перпендикуляров сторон треугольника.
- ✓ Серединные перпендикуляры сторон треугольника пересекаются в одной точке.
- ✓ Окружность называют вписанной в треугольник, если она касается всех его сторон.
- ✓ На рисунке 248 изображена окружность, вписанная в треугольник. В этом случае также говорят, что треугольник описан около окружности.
- ✓ Центр вписанной окружности треугольника равноудален от всех его сторон.
- ✓ В любой треугольник можно вписать окружность. Центр окружности, вписанной в треугольник, — это точка пересечения биссектрис треугольника.
- ✓ Биссектрисы треугольника пересекаются в одной точке.
- ✓ Радиус окружности, вписанной в прямоугольный треугольник, вычисляют по формуле
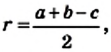 где r — радиус вписанной окружности, а и b — катеты, с — гипотенуза.
где r — радиус вписанной окружности, а и b — катеты, с — гипотенуза.
Что называют окружностью
Окружностью называют геометрическую фигуру, состоящую из всех точек плоскости, равноудаленных от данной точки (рис. 282).
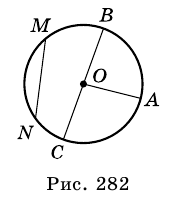
Эту точку называют центром окружности; отрезок, соединяющий точку окружности с ее центром, называют радиусом окружности.
На рисунке 282 точка 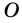 – центр окружности,
– центр окружности, 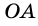 – радиус окружности.
– радиус окружности.
Отрезок, соединяющий две точки окружности, называют хордой. Хорду, проходящую через центр окружности, называют диаметром. На рисунке 282 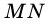 – хорда,
– хорда, 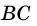 – диаметр. Часть плоскости, ограниченную окружностью, вместе с самой окружностью называют кругом (рис. 283).
– диаметр. Часть плоскости, ограниченную окружностью, вместе с самой окружностью называют кругом (рис. 283).

Центром, радиусом, диаметром, хордой круга называют соответственно центр, радиус, диаметр, хорду окружности, ограничивающей круг.
Свойства элементов окружности.
- Диаметр окружности вдвое больше его радиуса.
- Диаметр является наибольшей из хорд.
- Диаметр из любой точки окружности виден под прямым углом.
- Диаметр окружности, перпендикулярный хорде, делит ее пополам.
- Диаметр окружности, проходящий через середину хорды, которая не является диаметром, перпендикулярен этой хорде.
Касательной к окружности называют прямую, которая имеет с окружностью одну общую точку. Эту точку называют точкой касания.
На рисунке 284 прямая 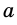 — касательная к окружности, точка
— касательная к окружности, точка 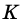 – точка касания.
– точка касания.
Свойство касательной. Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.
Свойство отрезков касательных, проведенных из одной точки. Отрезки касательных, проведенных к окружности из одной точки, равны. На рисунке 285
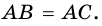
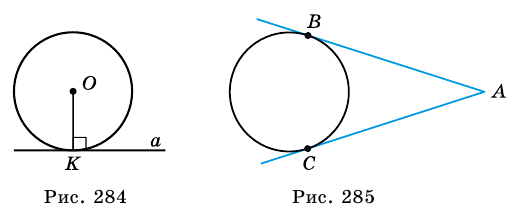
Окружность, вписанная в треугольник
Окружность называют вписанной в треугольник, если она касается всех его сторон. При этом треугольник называют описанным около окружности (рис. 286).
В любой треугольник можно вписать окружность. Центром окружности, вписанной в треугольник, является точка пересечения биссектрис треугольника.
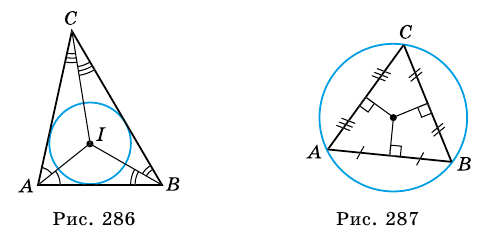
Окружность, описанная около треугольника
Окружность называют описанной около треугольника, если она проходит через все вершины треугольника. При этом треугольник называют вписанным в окружность (рис. 287).
Около любого треугольника можно описать окружность. Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к его сторонам.
Геометрическое место точек в окружности и круге
Любое множество точек — это геометрическая фигура. Изобразить произвольную фигуру легко: все, что нарисуете, — это геометрическая фигура (рис. 272). Однако изучать фигуры, состоящие из хаотически расположенных точек, вряд ли целесообразно. Поэтому разумно выделить тот класс фигур, все точки которых обладают каким-то характерным свойством. Каждую из таких фигур называют геометрическим местом точек.

Определение. Геометрическим местом точек (ГМТ) называют множество всех точек, обладающих определенным свойством.
Образно ГМТ можно представить так: задают некоторое свойство, а потом на белой плоскости все точки, обладающие этим свойством, красят в красный цвет. Та «красная фигура», которая при этом получится, и будет ГМТ.
Например, зафиксируем две точки 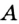 и
и 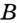 . Для всех точек зададим свойство: одновременно принадлежать лучам
. Для всех точек зададим свойство: одновременно принадлежать лучам 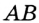 и
и 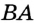 . Ясно, что указанным свойством обладают все точки отрезка
. Ясно, что указанным свойством обладают все точки отрезка 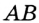 и только они (рис. 273). Поэтому искомым ГМТ является отрезок
и только они (рис. 273). Поэтому искомым ГМТ является отрезок 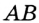 .
.

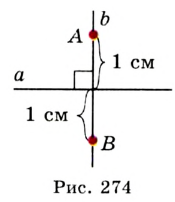
Рассмотрим перпендикулярные прямые 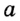 и
и 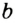 . Для всех точек зададим свойство: принадлежать прямой
. Для всех точек зададим свойство: принадлежать прямой 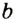 и находиться на расстоянии 1 см от прямой
и находиться на расстоянии 1 см от прямой 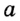 . Очевидно, что точки
. Очевидно, что точки 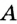 и
и 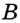 (рис. 274) удовлетворяют этим условиям. Также понятно, что никакая другая точка, отличная от
(рис. 274) удовлетворяют этим условиям. Также понятно, что никакая другая точка, отличная от 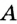 и
и 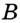 , этим свойством не обладает. Следовательно, искомое ГМТ — это фигура, состоящая из двух точек
, этим свойством не обладает. Следовательно, искомое ГМТ — это фигура, состоящая из двух точек 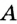 и
и 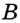 (рис. 274).
(рис. 274).
Вообще, чтобы иметь право какое-то множество точек называть ГМТ, надо доказать две взаимно обратные теоремы:
- каждая точка данного множества обладает заданным свойством;
- если точка обладает заданным свойством, то она принадлежит данному множеству.
Теорема 19.1. Серединный перпендикуляр отрезка является геометрическим местом точек, равноудаленных от концов этого отрезка.
Доказательство: По теореме 8.2 каждая точка серединного перпендикуляра обладает заданным свойством. По теореме 11.2, если точка обладает заданным свойством, то она принадлежит серединному перпендикуляру.
Теорема 19.2. Биссектриса угла является геометрическим местом точек, принадлежащих углу и равноудаленных от его сторон.
Прямая теорема. Каждая точка биссектрисы угла равноудалена от его сторон.
Доказательство: Очевидно, что вершина угла обладает доказываемым свойством.
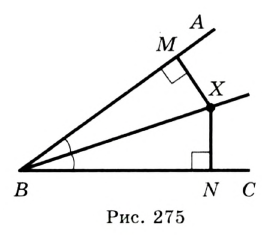
Пусть какая-то точка 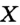 не совпадает с вершиной угла
не совпадает с вершиной угла 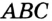 и принадлежит его биссектрисе (рис. 275). Опустим перпендикуляры
и принадлежит его биссектрисе (рис. 275). Опустим перпендикуляры 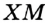 и
и 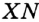 соответственно на стороны
соответственно на стороны 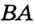 и
и 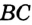 . Надо доказать, что
. Надо доказать, что 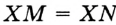 .
.
В прямоугольных треугольниках 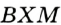 и
и 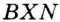 гипотенуза
гипотенуза 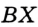 — общая,
— общая, 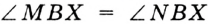 , так как
, так как 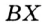 — биссектриса угла
— биссектриса угла 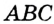 . Следовательно,
. Следовательно, 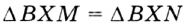 по гипотенузе и острому углу. Отсюда
по гипотенузе и острому углу. Отсюда  . Обратная теорема. Если точка, принадлежащая углу, равноудалена от его сторон, то она лежит на биссектрисе этого угла.
. Обратная теорема. Если точка, принадлежащая углу, равноудалена от его сторон, то она лежит на биссектрисе этого угла.
Доказательство: Очевидно, что вершина угла обладает доказываемым свойством.
Пусть какая-то точка 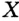 , принадлежащая углу
, принадлежащая углу 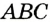 , не совпадает с его вершиной и равноудалена от его сторон. Опустим перпендикуляры
, не совпадает с его вершиной и равноудалена от его сторон. Опустим перпендикуляры 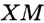 и
и 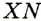 соответственно на стороны
соответственно на стороны 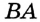 и
и 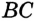 . Надо доказать, что
. Надо доказать, что 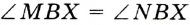 (рис. 275).
(рис. 275).
В прямоугольных треугольниках 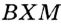 и
и 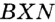 гипотенуза
гипотенуза 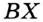 — общая,
— общая, 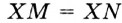 по условию. Следовательно,
по условию. Следовательно, 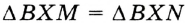 по гипотенузе и катету. Отсюда
по гипотенузе и катету. Отсюда 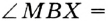
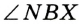 .
.
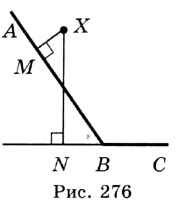
Заметим, что доказательство теоремы будет полным, если показать, что равноудаленность точки угла от его сторон исключает возможность, когда одна из точек к 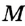 или
или  принадлежит продолжению стороны угла (рис. 276). Исследовать эту ситуацию вы можете на занятии математического кружка. Также отметим, что теорема остается справедливой и для развернутого угла.
принадлежит продолжению стороны угла (рис. 276). Исследовать эту ситуацию вы можете на занятии математического кружка. Также отметим, что теорема остается справедливой и для развернутого угла.
Определение. Окружностью называют геометрическое место точек, равноудаленных от заданной точки.
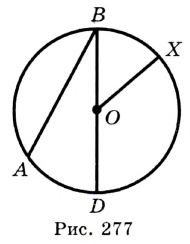
Заданную точку называют центром окружности. На рисунке 277 точка  — центр окружности.
— центр окружности.
Любой отрезок, соединяющий точку окружности с ее центром, называют радиусом окружности. На рисунке 277 отрезок 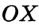 — радиус. Из определения следует, что все радиусы одной окружности равны.
— радиус. Из определения следует, что все радиусы одной окружности равны.
Отрезок, соединяющий две точки окружности, называют хордой окружности. На рисунке 277 отрезок 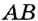 — хорда. Хорду, проходящую через центр окружности, называют диаметром. На рисунке 277 отрезок
— хорда. Хорду, проходящую через центр окружности, называют диаметром. На рисунке 277 отрезок 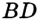 — диаметр окружности. Очевидно, что
— диаметр окружности. Очевидно, что 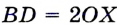 , т. е. диаметр окружности в два раза больше ее радиуса.
, т. е. диаметр окружности в два раза больше ее радиуса.
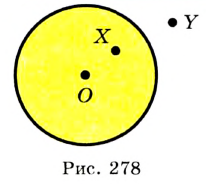
Из курса математики шестого класса вы знаете, что фигуру, ограниченную окружностью, называют кругом (рис. 278). Теперь с помощью понятия ГМТ можно дать другое
Определение. Кругом называют геометрическое место точек, расстояние от которых до заданной точки не больше данного положительного числа.
Заданную точку называют центром круга, данное число — радиусом круга. Если 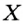 — произвольная точка круга с центром
— произвольная точка круга с центром 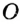 радиуса
радиуса 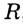 , то
, то 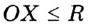 (рис. 278). Если
(рис. 278). Если 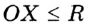 , то говорят, что точка
, то говорят, что точка 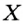 лежит внутри окружности, ограничивающей данный круг. Точка
лежит внутри окружности, ограничивающей данный круг. Точка 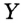 кругу не принадлежит (рис. 278). Также говорят, что точка
кругу не принадлежит (рис. 278). Также говорят, что точка 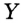 лежит вне окружности, ограничивающей круг. Из определения круга следует, что окружность, ограничивающая круг, ему принадлежит.
лежит вне окружности, ограничивающей круг. Из определения круга следует, что окружность, ограничивающая круг, ему принадлежит.
Хорда и диаметр круга — это хорда и диаметр окружности, ограничивающей круг.
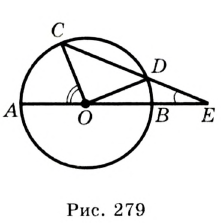
На продолжении хорды 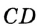 окружности с центром
окружности с центром 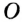 за точку
за точку 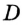 отметили точку
отметили точку 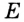 такую, что отрезок
такую, что отрезок 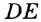 равен радиусу окружности (рис. 279). Прямая
равен радиусу окружности (рис. 279). Прямая 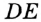 пересекает данную окружность в точках
пересекает данную окружность в точках 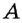 и
и  . Докажите, что
. Докажите, что 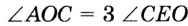 .
.
Решение:
Пусть 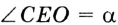 . Так как
. Так как 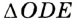 — равнобедренный, то
— равнобедренный, то 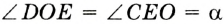 .
. 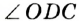 — внешний угол треугольника
— внешний угол треугольника 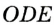 ,
, 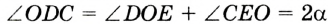 . Так как
. Так как 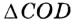 — равнобедренный, то имеем:
— равнобедренный, то имеем: 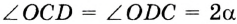 .
. 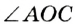 — внешний угол треугольника
— внешний угол треугольника 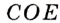 . Тогда
. Тогда 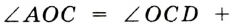
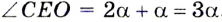 , то есть
, то есть 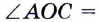
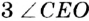 .
.
Некоторые свойства окружности. Касательная к окружности
Теорема 20.1. Диаметр окружности, перпендикулярный хорде, делит эту хорду пополам.
Доказательство: Если хорда является диаметром, то теорема очевидна.
На рисунке 286 изображена окружность с центром 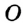 ,
,  — точка пересечения диаметра
— точка пересечения диаметра  и хорды
и хорды 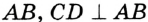 . Надо доказать, что
. Надо доказать, что 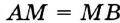 . Проведем радиусы
. Проведем радиусы 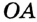 и
и 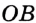 . В равнобедренном треугольнике
. В равнобедренном треугольнике  отрезок
отрезок 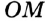 — высота, а значит, и медиана, т. е.
— высота, а значит, и медиана, т. е. 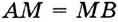 .
.
Теорема 20.2. Диаметр окружности, делящий хорду, отличную от диаметра, пополам, перпендикулярен этой хорде.
Докажите эту теорему самостоятельно. Подумайте, будет ли верным это утверждение, если хорда является диаметром.
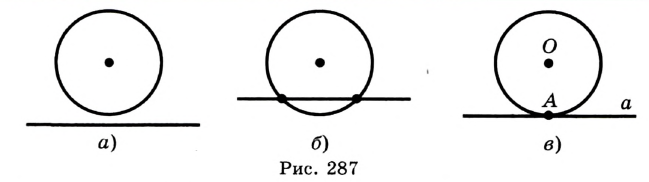
На рисунке 287 изображены прямая и окружность, которые на рисунке 287, а не имеют общих точек, на рисунке 287, б имеют две общие точки, на рисунке 287, в — одну.
Определение. Прямую, имеющую с окружностью только одну общую точку, называют касательной к окружности.
Очевидно, что касательная к окружности имеет только одну общую точку с кругом, ограниченным этой окружностью. На рисунке 287, в прямая 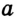 — касательная,
— касательная, 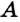 — точка касания.
— точка касания.
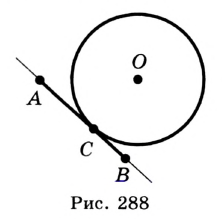
Если отрезок (луч) принадлежит касательной к окружности и имеет с этой окружностью общую точку, то говорят, что отрезок (луч) касается окружности. Например, на рисунке 288 изображен отрезок 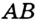 , который касается окружности в точке
, который касается окружности в точке 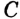 .
.
Теорема 20.3 (свойство касательной). Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.
Доказательство: На рисунке 289 изображена окружность с центром  ,
,  — точка касания прямой
— точка касания прямой 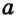 и окружности. Надо доказать, что
и окружности. Надо доказать, что 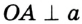 .
.
Предположим, что это не так, то есть 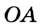 — наклонная к прямой
— наклонная к прямой 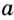 . Тогда из точки
. Тогда из точки 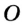 опустим перпендикуляр
опустим перпендикуляр 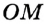 на прямую
на прямую 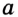 (рис. 289). Поскольку точка
(рис. 289). Поскольку точка 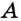 — единственная общая точка прямой а и круга с центром
— единственная общая точка прямой а и круга с центром 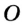 , то точка
, то точка 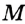 не принадлежит этому кругу. Отсюда
не принадлежит этому кругу. Отсюда 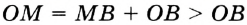
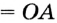 . Получили противоречие: перпендикуляр
. Получили противоречие: перпендикуляр 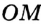 больше наклонной
больше наклонной 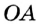 . Следовательно,
. Следовательно, 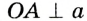 .
.
Теорема 20.4 (признак касательной к окружности). Если прямая, проходящая через точку окружности, перпендикулярна радиусу, проведенному в эту точку, то эта прямая является касательной к данной окружности.
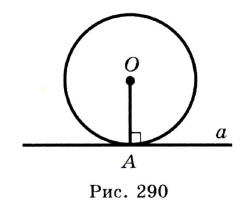
Доказательство: На рисунке 290 изображена окружность с центром в точке 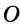 , отрезок
, отрезок 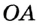 — ее радиус, точка
— ее радиус, точка 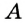 принадлежит прямой
принадлежит прямой 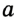 ,
, 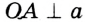 . Докажем, что прямая
. Докажем, что прямая 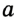 — касательная к окружности.
— касательная к окружности.
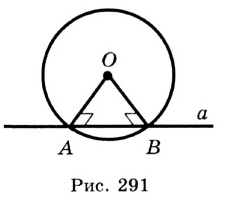
Пусть прямая 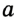 не является касательной, а имеет еще одну общую точку
не является касательной, а имеет еще одну общую точку 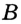 с окружностью (рис. 291). Тогда
с окружностью (рис. 291). Тогда 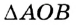 — равнобедренный (
— равнобедренный ( 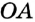 и
и 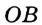 равны как радиусы). Отсюда получаем противоречие: в треугольнике
равны как радиусы). Отсюда получаем противоречие: в треугольнике 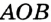 есть два прямых угла. Следовательно, прямая
есть два прямых угла. Следовательно, прямая 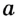 является касательной к окружности. Следствие. Если расстояние от центра окружности до некоторой прямой равно радиусу окружности, то эта прямая является касательной к данной окружности.
является касательной к окружности. Следствие. Если расстояние от центра окружности до некоторой прямой равно радиусу окружности, то эта прямая является касательной к данной окружности.
Часто при решении целого класса задач используют результат следующей задачи.
Если из данной точки к окружности проведены две касательные, то отрезки касательных, соединяющих данную точку с точками касания, равны.
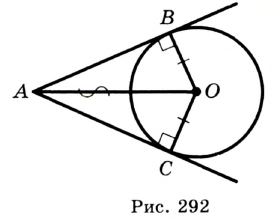
Решение:
На рисунке 292 изображена окружность с центром 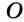 . Прямые
. Прямые 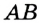 и
и 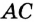 — касательные,
— касательные, 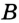 и
и 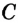 — точки касания. Надо доказать, что
— точки касания. Надо доказать, что 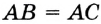 . Проведем радиусы
. Проведем радиусы 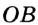 и
и 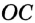 в точки касания. По свойству касательной
в точки касания. По свойству касательной 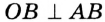 и
и 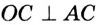 . В прямоугольных треугольниках
. В прямоугольных треугольниках 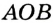 и
и 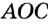 катеты
катеты 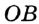 и
и 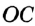 равны как радиусы одной окружности,
равны как радиусы одной окружности, 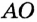 — общая гипотенуза. Следовательно,
— общая гипотенуза. Следовательно, 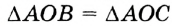 по гипотенузе и катету. Отсюда
по гипотенузе и катету. Отсюда 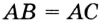 .
.
| Общая схема решения задач на построение |
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Описанные и вписанные окружности
- Плоские и пространственные фигуры
- Взаимное расположение точек и прямых
- Сравнение и измерение отрезков и углов
- Решение треугольников
- Треугольники и окружность
- Площадь треугольника
- Соотношения между сторонами и углами произвольного треугольника
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
[spoiler title=”источники:”]
http://math-ege.sdamgia.ru/problem?id=519683
http://www.evkova.org/okruzhnost-i-krug
[/spoiler]
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
В кубе ABCDA1B1C1D1 все ребра равны 1.
а) Докажите, что
б) Найдите расстояние от точки C до прямой BD1.
2
Дана правильная треугольная пирамида DABC с вершиной D. Боковое ребро пирамиды равно высота равна
а) Докажите, что сечение пирамиды, проходящее через середины ребер BD, AC и AD, является прямоугольником.
б) Найдите расстояние от середины бокового ребра BD до прямой MT, где точки M и T — середины ребер AC и AD соответственно.
3
В правильной шестиугольной призме ABCDEF A1B1C1D1E1F1, все рёбра которой равны 1, найдите расстояние от точки C до прямой F1E1.
4
В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB = 12 и Длины боковых рёбер пирамиды SA = 5, SB = 13, SD = 10.
а) Докажите, что SA — высота пирамиды.
б) Найдите расстояние от вершины A до плоскости SBC.
Источник: Материалы для экспертов ЕГЭ 2016
5
В кубе ABCDA1B1C1D1 все ребра равны 1.
а) Докажите, что расстояние от точки C до плоскости меньше, чем расстояние от точки C до прямой
б) Найдите расстояние от точки C до прямой AD1
Пройти тестирование по этим заданиям
Расстояния
Задача на нахождения расстояния в стереометрической фигуре является главной и самой важной из всех. Прежде всего определимся с тем, что имеется ввиду под словом «расстояние», ведь их может быть бесконечно много.
Расстояние между объектами в геометрии – это кратчайшее из расстояний между ними.
Обозначение:

В стереометрии найти расстояние можно между следующими комбинациями фигур:
РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ
Расстояние между точками– это длина отрезка, соединяющего эти точки.
В задачах на стереометрию мы не можем просто воспользоваться линейкой, и длину этого отрезка должны найти аналитически. Поэтому длину отрезка AB между точками A и B находят как сторону треугольника, если отрезок AB удается включить в некоторый треугольник в качестве одной из его сторон.
То есть если в задаче предлагается найти расстояние между точками, нужно задать себе вопрос: «В каком треугольнике этот отрезок является стороной?», затем построить этот треугольник и найти в нем нужную сторону.
Например:

|
|
|
РАССТОЯНИЕ МЕЖДУ ТОЧКОЙ И ПРЯМОЙ
Расстояние от точки до прямой – длина перпендикуляра, опущенного из точки на прямую.

Этот отрезок перпендикуляра можно вычислить, включив его в треугольник (или трапецию) в качестве одной из высот. То есть нужно задать себе вопрос: «В каком треугольнике этот отрезок является высотой?», затем построить этот треугольник и найти в нем высоту.
Например:
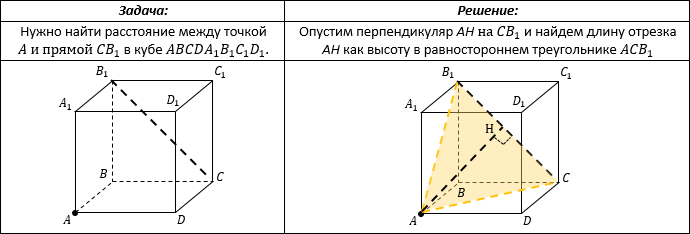
РАССТОЯНИЕ МЕЖДУ ТОЧКОЙ И ПЛОСКОСТЬЮ
Существует несколько способов нахождения расстояния от точки до плоскости:
- Построение перпендикуляра из точки на плоскость.
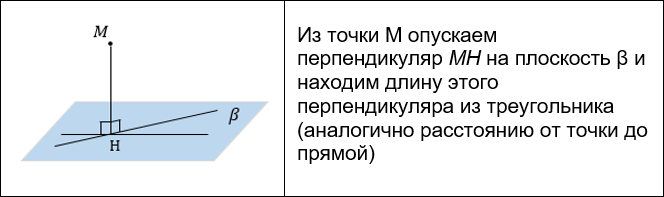
- К этому способу обращаются, если расстояние из точки M на плоскость опускать неудобно, а удобно опустить равный ему перпендикуляр из другой точки, лежащей на одной линии с M.
- Построение перпендикуляра из точки прямой к плоскости.
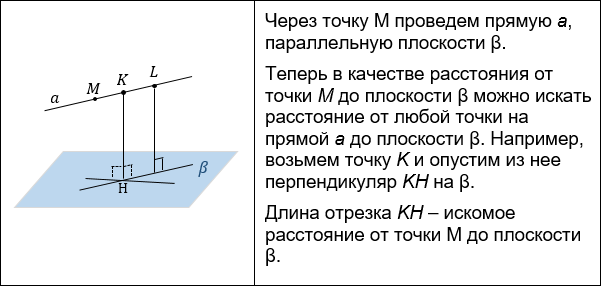
- Построение перпендикуляра из точки плоскости на плоскость.
К этому способу, аналогично, обращаются, если расстояние из точки M на плоскость опускать неудобно, а удобно опустить равный ему перпендикуляр из другой точки, лежащей на одной плоскости с M.

- Через двойное выражение объема.
Расстояние от точки M до плоскости β – это перпендикуляр, опущенный из точки на плоскость, то есть по сути это высота в некоторой пирамиде с вершиной M и плоскостью основания, лежащей на β. Если легко вычислить объем этой пирамиды, используя другое основание и другую высоту, то через этот объем можно найти нужное расстояние.
Например:

РАССТОЯНИЕ МЕЖДУ СКРЕЩИВАЮЩИМИСЯ ПРЯМЫМИ
Существует несколько способов нахождения расстояния между скрещивающимися прямыми:
1. Построение взаимного перпендикуляра.

2. Построение параллельной прямой.
К этому способу обращаются, если строить взаимный перпендикуляр неудобно и одна из скрещивающихся прямых уже заключена в удобную плоскость.
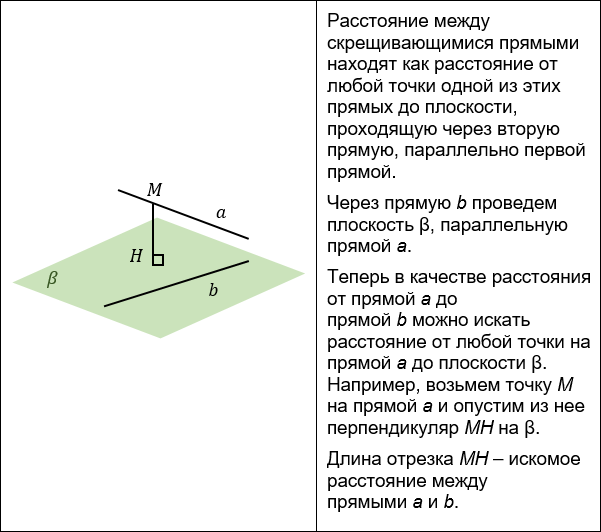 К этому способу обращаются, если строить взаимный перпендикуляр неудобно и скрещивающиеся прямые уже заключены в удобные плоскости.
К этому способу обращаются, если строить взаимный перпендикуляр неудобно и скрещивающиеся прямые уже заключены в удобные плоскости.
3. Построение параллельной плоскости.
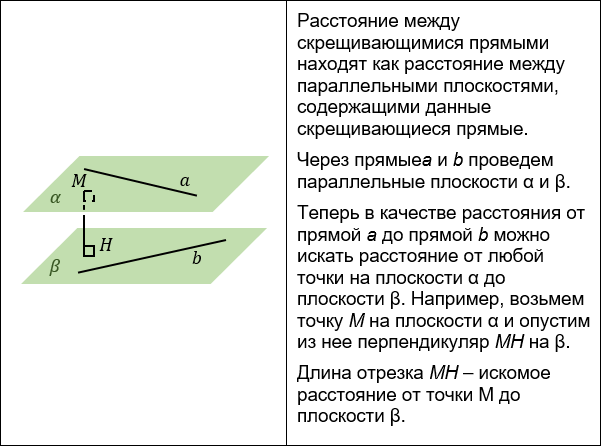
Данная статья рассказывает об определении расстояния от точки до плоскости. произведем разбор методом координат, который позволит находить расстояние от заданной точки трехмерного пространства. Для закрепления рассмотрим примеры нескольких задач.
Расстояние от точки до плоскости – определение
Расстояние от точки до плоскости находится посредством известного расстояния от точки до точки, где одна из них заданная, а другая – проекция на заданную плоскость.
Когда в пространстве задается точка М1 с плоскостью χ, то через точку можно провести перпендикулярную плоскости прямую. Н1 является общей точкой их пересечения. Отсюда получаем, что отрезок М1Н1 – это перпендикуляр, который провели из точки М1 к плоскости χ, где точка Н1 – основание перпендикуляра.
Расстоянием от точки до плоскости называют расстояние от заданной точки к основанию перпендикуляра, который провели из заданной точки к заданной плоскости.
Определение может быть записано разными формулировками.
Расстоянием от точки до плоскости называют длину перпендикуляра, который провели из заданной точки к заданной плоскости.
Расстояние от точки М1 к плоскости χ определяется так: расстояние от точки М1 до плоскости χ будет являться наименьшим от заданной точки до любой точки плоскости. Если точка Н2 располагается в плоскости χ и не равна точке Н2, тогда получаем прямоугольный треугольник вида М2H1H2 , который является прямоугольным, где имеется катет М2H1, М2H2 – гипотенуза. Значит, отсюда следует, что M1H1<M1H2. Тогда отрезок М2H1 считается наклонной, которая проводится из точки М1 до плоскости χ. Мы имеем, что перпендикуляр, проведенный из заданной точки к плоскости, меньше наклонной, которую проводят из точки к заданной плоскости. Рассмотрим этот случай на рисунке, приведенном ниже.
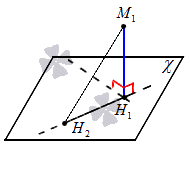
Расстояние от точки до плоскости – теория, примеры, решения
Существует ряд геометрических задач, решения которых должны содержать расстояние от точки до плоскости. Способы выявления этого могут быть разными. Для разрешения применяют теорему Пифагора или подобия треугольников. Когда по условию необходимо рассчитать расстояние от точки до плоскости, заданные в прямоугольной системе координат трехмерного пространства, решают методом координат. Данный пункт рассматривает этот метод.
По условию задачи имеем, что задана точка трехмерного пространства с координатами M1(x1, y1, z1) с плоскостью χ, необходимо определить расстояние от М1 к плоскости χ. Для решения применяется несколько способов решения.
Первый способ
Данный способ основывается на нахождении расстояния от точки до плоскости при помощи координат точки Н1, которые являются основанием перпендикуляра из точки М1 к плоскости χ. Далее необходимо вычислить расстояние между М1 и Н1.
Для решения задачи вторым способом применяют нормальное уравнение заданной плоскости.
Второй способ
По условию имеем, что Н1 является основанием перпендикуляра, который опустили из точки М1 на плоскость χ. Тогда определяем координаты (x2, y2, z2) точки Н1. Искомое расстояние от М1 к плоскости χ находится по формуле M1H1=(x2-x1)2+(y2-y1)2+(z2-z1)2, где M1(x1, y1, z1) и H1(x2, y2, z2). Для решения необходимо узнать координаты точки Н1.
Имеем, что Н1 является точкой пересечения плоскости χ с прямой a, которая проходит через точку М1, расположенную перпендикулярно плоскости χ. Отсюда следует, что необходимо составление уравнения прямой, проходящей через заданную точку перпендикулярно к заданной плоскости. Именно тогда сможем определить координаты точки Н1. Необходимо произвести вычисление координат точки пересечения прямой и плоскости.
Алгоритм нахождения расстояния от точки с координатами M1(x1, y1, z1) к плоскости χ:
- составить уравнение прямой а, проходящей через точку М1 и одновременно
- перпендикулярной к плоскости χ;
- найти и вычислить координаты (x2, y2, z2) точки Н1, являющимися точками
- пересечения прямой a с плоскостью χ;
- вычислить расстояние от М1 до χ, используя формулу M1H1=(x2-x1)2+(y2-y1)2+z2-z12.
Третий способ
В заданной прямоугольной системе координат Охуz имеется плоскость χ, тогда получаем нормальное уравнение плоскости вида cos α· x+cos β·y+cos γ·z-p=0. Отсюда получаем, что расстояние M1H1 с точкой M1(x1, y1, z1) , проведенной на плоскость χ, вычисляемое по формуле M1H1=cos α· x+cos β·y+cos γ·z-p. Эта формула справедлива, так как это установлено благодаря теореме.
Если задана точка M1(x1, y1, z1) в трехмерном пространстве, имеющая нормальное уравнение плоскости χ вида cos α· x+cos β·y+cos γ·z-p=0, тогда вычисление расстояния от точки до плоскости M1H1 производится из формулы M1H1=cos α· x+cos β·y+cos γ·z-p, так как x=x1, y=y1, z=z1.
Доказательство теоремы сводится к нахождению расстояния от точки до прямой. Отсюда получаем, что расстояние от M1 до плоскости χ – это и есть модуль разности числовой проекции радиус-вектора M1 с расстоянием от начала координат к плоскости χ. Тогда получаем выражение M1H1=npn→OM→-p. Нормальный вектор плоскости χ имеет вид n→=cos α, cos β, cos γ, а его длина равняется единице, npn→OM→ – числовая проекция вектора OM→=(x1, y1, z1) по направлению, определяемым вектором n→.
Применим формулу вычисления скалярных векторов. Тогда получаем выражение для нахождения вектора вида n→, OM→=n→·npn→OM→=1·npn→OM→=npn→OM→, так как n→=cos α, cos β, cos γ·z и OM→=(x1, y1, z1). Координатная форма записи примет вид n→, OM→=cos α· x1+cos β·y1+cos γ·z1, тогда M1H1=npn→OM→-p=cos α· x1+cos β·y1+cos γ·z1-p. Теорема доказана.
Отсюда получаем, что расстояние от точки M1(x1, y1, z1) к плоскости χ вычисляется при помощи подстановки в левую часть нормального уравнения плоскости cos α· x+cos β·y+cos γ·z-p=0 вместо х, у, z координаты x1, y1 и z1 ,относящиеся к точке М1, взяв абсолютную величину полученного значения.
Рассмотрим примеры нахождения расстояния от точки с координатами до заданной плоскости.
Вычислить расстояние от точки с координатами M1(5, -3, 10) к плоскости 2x-y+5z-3=0.
Решение
Решим задачу двумя способами.
Первый способ начнется с вычисления направляющего вектора прямой a. По условию имеем, что заданное уравнение 2x-y+5z-3=0 является уравнением плоскости общего вида, а n→=(2, -1, 5) является нормальным вектором заданной плоскости. Его применяют в качестве направляющего вектора прямой a, которая перпендикулярна относительно заданной плоскости. Следует записать каноническое уравнение прямой в пространстве, проходящее через M1(5, -3, 10) с направляющим вектором с координатами 2, -1, 5.
Уравнение получит вид x-52=y-(-3)-1=z-105⇔x-52=y+3-1=z-105.
Следует определить точки пересечения. Для этого нежно объединить уравнения в систему для перехода от канонического к уравнениям двух пересекающихся прямых. Данную точку примем за Н1. Получим, что
x-52=y+3-1=z-105⇔-1·(x-5)=2·(y+3)5·(x-5)=2·(z-10)5·(y+3)=-1·(z-10)⇔⇔x+2y+1=05x-2z-5=05y+z+5=0⇔x+2y+1=05x-2z-5=0
После чего необходимо разрешить систему
x+2y+1=05x-2z-5=02x-y+5z-3=0⇔x+2y=15x-2z=52x-y+5z=3
Обратимся к правилу решения системы по Гауссу:
120-150-252-153~120-10-10-2100-555~120-10-10-2100060⇒⇒z=06=0, y=-110·10+2·z=-1, x=-1-2·y=1
Получаем, что H1(1, -1, 0).
Производим вычисления расстояния от заданной точки до плоскости. Берем точки M1(5, -3, 10) и H1(1, -1, 0) и получаем
M1H1=(1-5)2+(-1-(-3))2+(0-10)2=230
Второй способ решения заключается в том, чтобы для начала привести заданное уравнение 2x-y+5z-3=0 к нормальному виду. Определяем нормирующий множитель и получаем 122+(-1)2+52=130. Отсюда выводим уравнение плоскости 230·x-130·y+530·z-330=0. Вычисление левой части уравнения производится посредствам подстановки x=5, y=-3, z=10, причем нужно взять расстояние от M1(5, -3, 10) до 2x-y+5z-3=0 по модулю. Получаем выражение:
M1H1=230·5-130·-3+530·10-330=6030=230
Ответ: 230.
Когда плоскость χ задается одним из способов раздела способы задания плоскости, тогда нужно для начала получить уравнение плоскости χ и вычислять искомое расстояние при помощи любого метода.
В трехмерном пространстве задаются точки с координатами M1(5, -3, 10), A(0, 2, 1), B(2, 6, 1), C(4, 0, -1). Вычислить расстяние от М1 к плоскости АВС.
Решение
Для начала необходимо записать уравнение плоскости, проходящее через заданные три точки с координатами M1(5, -3, 10), A(0, 2, 1), B(2, 6, 1), C(4, 0, -1).
Получим:
x-0y-2z-12-06-21-14-00-2-1-1=0⇔xy-2z-12404-2-2=0⇔⇔-8x+4y-20z+12=0⇔2x-y+5z-3=0
Отсюда следует, что задача имеет аналогичное предыдущему решение. Значит, расстояние от точки М1 к плоскости АВС имеет значение 230.
Ответ: 230.
Нахождение расстояния от заданной точки на плоскости или к плоскости, которым они параллельны, удобнее, применив формулу M1H1=cos α·x1+cos β·y1+cos γ·z1-p. Отсюда получим, что нормальные уравнения плоскостей получают в несколько действий.
Найти расстояние от заданной точки с координатами M1(-3, 2, -7) к координатной плоскости Охуz и плоскости, заданной уравнением 2y-5=0.
Решение
Координатная плоскость Оуz соответствует уравнению вида х=0. Для плоскости Оуz оно является нормальным. Поэтому необходимо подставить в левую часть выражения значения х=-3 и взять модуль значения расстояния от точки с координатами M1(-3, 2, -7) к плоскости. Получаем значение, равное -3=3.
После преобразования нормальное уравнение плоскости 2y-5=0 получит вид y-52=0. Тогда можно найти искомое расстояние от точки с координатами M1(-3, 2, -7) к плоскости2y-5=0. Подставив и вычислив, получаем 2-52=52-2.
Ответ: Искомое расстояние от M1(-3, 2, -7) до Оуz имеет значение 3, а до 2y-5=0 имеет значение 52-2.
Всем привет. Рада то, что вы меня читаете и комментируете
Сегодня разберем 13 задание, это стереометрия.
Вот условие задачи
Сначала строим сечение. Я делала методом следов.
Теперь сделаем несколько выносных чертежей
И через подобие найдем нужное нам соотношение.
Теперь найдем расстояние от точки С до плоскости ALR
В треугольнике CRM проведем CS – высоту к гипотенузе RM
Найдем дины RM, CS и QS
Теперь используя метод объёмов найдем требуемое расстояние
Найдем объём пирамиды QCRM, если вершина Q(первая строчка) и С (вторая строчка).
Также рекомендую по построению сечений (метод следов) почитать, например:
Открытый урок 1 сентября и инфоурок
Спасибо за внимание
Буду рада вашим лайкам, комментариям, а также вашей подписке
Также приглашаю в свои группы в Телеграм и Вконтакте
До новых встреч на канале Простаяматематика.рф
#математикаэтопросто
#блогрепетитора
#егэпоматематике
#геометрия