Алгебра
Лучшие условия по продуктам Тинькофф по этой ссылке
Дарим 500 ₽ на баланс сим-карты и 1000 ₽ при сохранении номера
. 500 руб. на счет при заказе сим-карты по этой ссылке
Лучшие условия по продуктам
ТИНЬКОФФ по данной ссылке
План урока:
Числовая и единичная окружность
В средней школе мы уже познакомились с координатной, или числовой прямой. Так называют абстрактную прямую, на которой выбрана точка отсчета, определен единичный отрезок, а также задано направление, в котором следует откладывать положительные числа. С помощью координатной прямой удается наглядно представлять сложение и вычитание как положительных, так и отрицательных чисел, решать задачи, связанные с перемещением по прямой, и делать многое другое.
Однако порою приходится рассматривать задачи, связанные с движением по окружности, а также складывать и вычитать углы. Здесь математикам помогает другая абстракция – числовая окружность. Пусть два гонщика (Вася и Петя) едут по круговой трассе, чья протяженность составляет 1 км. За минуту Вася проехал 1250 м, а Петя преодолел только 500 м. Попытаемся показать их положение графически.
Построим на координатной плоскости окружность с центром в начале координат длиной 1 км. Будем считать, старт находится в крайней правой точке трассы, на пересечении оси Ох и окружности. Также условимся, что гонщики едут против часовой стрелки. Тогда получим такую картинку:
Петя проедет ровно половину окружности и окажется в крайней левой точке трассы. Вася же за минуту успел сделать полный круг (1 км) и проехать ещё 250 м, а потому оказался в верхней точке.
Теперь предположим, что Петя стоит на месте, а Вася проехал ещё 250 м (четверть круга). В результате оба пилота оказались в одной точке, но проехали они разное расстояние! Получается, что по положению гонщика невозможно однозначно определить, сколько именно метров он проехал.
Заметим, что очень удобно характеризовать положение точки на числовой окружности с помощью угла. Достаточно соединить точку отрезком с началом координат. Полученный отрезок образует с прямой Ох некоторый угол α:
В тригонометрии предпочитают использовать особую числовую прямую, радиус которой равен единице. По ряду причин, которые станут ясны чуть позже, с ней очень удобно работать. Такую фигуру называют единичной окружностью.
Выглядит единичная окружность так:
Откладывание углов на единичной окружности
Положение каждой точки на единичной окружности можно указать с помощью угла. Пусть надо найти точку, соответствующую углу 60°. Для этого просто строим угол следующим образом:
Углы, которые откладывают на единичной окружности, называют углами поворота. В данном случае можно утверждать, что точке А соответствует угол поворота, равный 60°.
Отложить можно и угол, больший 90° и даже 180°. Выглядеть они будут примерно так:
Углы можно складывать друг с другом и вычитать. Предположим, нам надо построить угол, равный сумме углов 120° и 110°. Для этого сначала совершить поворот на 120°, а потом от полученного отрезка отложить ещё один угол в 110°:
Ясно, что возможно построить любой угол в диапазоне от 0° до 360°. А можно ли отложить угол, который будет больше 360°? В обычной планиметрии мы не работаем с такими углами, однако в тригонометрии они существуют. Действительно, мы же можем, например, сложить углы 250° и 140°. В итоге получится 250 + 140 = 390°:
В результате мы совершили полный оборот (360°) и вдобавок повернули отрезок ещё на 30°. Получается, что углам в 390° и 30° соответствует одна и та же точка.
Углы можно и вычитать друг из друга. Для этого вычитаемый угол надо отложить в противоположном направлении – не против часовой, а по часовой стрелке. Например, вычитая из 150° угол в 70°, придем в точку, соответствующую 150 – 70 = 80°:
Из арифметики мы помним, что вычитание можно заменить прибавлением противоположного (то есть отрицательного) числа:
Получается, что отложив угол 70° по часовой стрелке, мы прибавили к 150° отрицательный угол (– 70°). То есть на единичной окружности можно откладывать отрицательные углы! Для их получения поворот надо осуществлять по часовой стрелке. Например, угол – 60° будет выглядеть так:
Итак, мы можем откладывать и положительные, и отрицательные углы, а также углы, большие 360°. Вообще в тригонометрии угол может быть равен любому действительному числу. На единичной окружности можно отложить углы величиной 1000°, 1000000° и (– 999999999°) и любые другие, самые большие и самые малые углы. В этом смысле единичная окружность схожа с координатной прямой. Разница лишь в том, что на прямой разным числам всегда соответствуют разные точки, а на окружности разным углам могут соответствовать одни и те же точки.
Ещё раз отметим, что один полный оборот равен 360°. Если отложить на окружности произвольную точку А, которой соответствует угол α, а потом добавить к α ещё 360°, то мы попадем в ту же самую точку:
С точки зрения тригонометрии те углы поворота, которые соответствуют одной точке на единичной окружности, равны друг другу. Поэтому можно записать формулу:
Естественно, при вычитании 360° из угла мы тоже совершим полный поворот, только по часовой стрелке, поэтому верна и другая запись:
Угол, не изменится и в том случае, если мы совершим не один, а два полных оборота, то есть добавим к нему 2•360° = 720°. Можно добавлять к углу два, три, четыре полных поворота, но он не изменится от этого. Обозначим буквой n количество оборотов, которые мы добавляем к углу. Естественно, что n – целое число. Справедливой будет формула:
Например, верны следующие равенства:
15° + 3•360° = 15° + 1080° = 1095°
100° + 10•360° = 100° + 3600° = 3700°
1000° = 1000° – 2•360° = 1000° – 720° = 280°
Очевидно, что любой точке на окружности соответствует какой-то угол α из промежутка 0 ≤ α 1 5
Координаты точек тригонометрической окружности
Использование радианной меры при измерении углов позволяет для каждой точки Ра тригонометрической окружности указать длину дуги Р0Ра. Это дает возможность определить отображение множества действительных чисел М на единичную окружность, т.е. поставить в соответствие каждой точке Ра действительное число. Это можно осуществить следующим образом.
Сначала множество R отображают на координатную прямую, приняв радиус окружности за единицу длины на прямой. Вообразим эту прямую в виде нерастяжимой нити и закрепим ее на окружности так, чтобы начало координат на прямой совпало с точкой Р0. Далее будем «наматывать» эту прямую (нить) на тригонометрическую окружность так, что луч, на котором отложены положительные числа, наматывается в положительном направлении, а луч, на котором отложены отрицательные числа, наматывается в отрицательном направлении. При этом точки координатной прямой переходят соответственно в точки окружности. Таким образом, каждой точке прямой ставится в соответствие некоторая точка окружности.
Поскольку после полного оборота числам вида а и a + Ink, k е Z, соответствует одна и та же точка тригонометрической окружности, то считается, что все они изображаются на окружности одной точкой.
В итоге вся числовая прямая разбивается на промежутки [2кп; 2п(п + 1)], п е Z. Если а е [2кп 2п(п + 1)], то числу а ставят в соответствие точку Ра такую, что дуга Р$Ра, пробегаемая в положительном направлении, имеет длину а – 2кп, если а > 0 (например,
рис. 2.4 при а = у), и дуга Р0Ра, пробегаемая в отрицательном направлении, имеет длину 2к(п + 1) – а, если а Р 30 Р Р Р 30
- 2) 390° = — ? 390 рад = рад. Так как = 2л + ^, то точка
- 180 6 66 РПп совпадает на тригонометрической окружности с точкой Рп и ее
рад. Значит, искомая координата
Единичная окружность

О чем эта статья:
10 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Единичная окружность в тригонометрии
Все процессы тригонометрии изучают на единичной окружности. Сейчас узнаем, какую окружность называют единичной и дадим определение.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат и радиусом, равным единице.
Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат.
Радиус — отрезок, который соединяет центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка. Радиус составляет половину диаметра.
Единичную окружность с установленным соответствием между действительными числами и точками окружности называют числовой окружностью.
Поясним, как единичная окружность связана с тригонометрией.
В тригонометрии мы постоянно сталкиваемся с углами поворота. А углы поворота связаны с вращением по окружности.
Угол поворота — это угол, который образован положительным направлением оси OX и лучом OA.
Величины углов поворота не зависят от радиуса окружности, по которой происходит вращение, поэтому удобно работать именно с окружностью единичного радиуса. Это позволяет избавиться от коэффициентов при математическом описании. Вот и все объяснение полезности единичной тригонометрической окружности.
Все углы, которые принадлежат одному семейству, дают одинаковые абсолютные значения тригонометрических функций, но эти значения могут различаться по знаку. Вот как:
- Если угол находится в первом квадранте, все тригонометрические функции имеют положительные значения.
- Для угла во втором квадранте все функции, за исключением sin и cos, отрицательны.
- В третьем квадранте значения всех функций, кроме tg и ctg, меньше нуля.
- В четвертом квадранте все функции, за исключением cos и sec, имеют отрицательные значения.
Градусная мера окружности равна 360°. Чтобы решать задачи быстро, важно запомнить, где находятся углы 0°; 90°; 180°; 270°; 360°. Единичная окружность с градусами выглядит так:
Радиан — одна из мер для определения величины угла.
Один радиан — это величина угла между двумя радиусами, проведенными так, что длина дуги между ними равна величине радиуса.
Число радиан для полной окружности — 360 градусов.
Длина окружности равна 2πr, что превышает длину радиуса в 2π раза.
Поскольку по определению 1 радиан — это угол между концами дуги, длина которой равна радиусу, в полной окружности заключен угол, равный 2π радиан.
Потренируемся переводить радианы в градусы. В полной окружности содержится 2π радиан, или 360 градусов. Таким образом:
- 2π радиан = 360°
- 1 радиан = (360/2π) градусов
- 1 радиан = (180/π) градусов
- 360° = 2π радиан
- 1° = (2π/360) радиан
- 1° = (π/180) радиан
Кстати, определение синуса, косинуса, тангенса и котангенса в тригонометрии дается через координаты точек на единичной окружности. Эти определения дают возможность раскрыть свойства синуса, косинуса, тангенса и котангенса.
Уравнение единичной окружности
При помощи этого уравнения, вместе с определениями синуса и косинуса, можно записать основное тригонометрическое тождество:
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
[spoiler title=”источники:”]
http://studref.com/535683/informatika/koordinaty_tochek_trigonometricheskoy_okruzhnosti
http://skysmart.ru/articles/mathematic/edinichnaya-okruzhnost
[/spoiler]
Для нахождения координат точки эллипса по углу существует простое и элегантное решение. Понимаю, что для маститого математика это решение является очевидным. Однако, для меня в то далекое время, когда инет был диким, связь модемной, а я сильно молодым, это таковым не являлось.
ВНИМАНИЕ! Если Вы искали как найти координаты точки по углу от произвольной прямой и совсем не подразумевали эллипс, то Вам сюда.
Калькулятор точки на эллипсе
Давайте посмотрим, как это выглядит на практике. Потом теория. Оранжевый маркер отвечает за угол, на основании которого считаем координаты. Красный — параметрический угол, о котором ниже.
Маркеры кликабельны и таскабельны.
Если есть вопросы, предложения по калькулятору или заметили ошибку, буду очень рад обратной связиx
Эллипс:
a:
b:
Углы (град.):
Get a better browser, bro…
Параметрическое уравнение эллипса
Обратимся, как обычно, к Википедии. Находим там следующее:
Каноническое уравнение эллипса может быть параметризовано:

Очевидно, что t — это угол, и это не «наш» угол. Это какой-то другой угол, который функционально связан с «нашим». «Нашим» называю угол, от которого требуется посчитать координаты.
Таким образом, задача нахождения координат точки эллипса по углу сводится к задаче нахождения угла t, зависящим от требуемого. Нахождением этой зависимости и займемся.
Подготовка

У нас есть эллипс, описанный двумя полуосями a и b. Представим две окружности, имеющих общий центр. Меньшая окружность (зеленая) имеет радиус b. Большая окружность (синяя) имеет радиус a.
Проведем прямую из общего центра [X0;Y0] в произвольную точку плоскости [X;Y]. В результате пересечения с этими окружностями получаются две точки [X1;Y1] и [X2;Y2].
α – угол между прямой и осью X.
| Малая окружность | X1 = b × cos α | Y1 = b × sin α |
| Большая окружность | X2 = a × cos α | Y2 = a × sin α |
Нахождение зависимости

Используя уравнение (1) посчитаем координаты точки на эллипсе [X’;Y’] для угла α. Проведем прямую из центра [X0;Y0] в точку [X’;Y’]. Угол β – угол между этой прямой и осью X.
Задача сводится к тому, чтобы найти такой α, при котором β был бы равен интересующему нас углу. Таким образом, угол α будет являться параметром в уравнении (1) для требуемого угла β.
Найдем зависимость между получившимся углом β и углом α. На рисунке видно, что прилегающий к углу катет (синий) равен ранее рассчитанному X2, а противолежащий (зеленый) равен Y1:
X’ = X2 = a × cos α
Y’ = Y1 = b × sin α
Опыт показывает, что тут зачастую возникает легкий ступор. Возможно, рисунок вводит в некое заблуждение. Видим треугольник, и если с синим катетом вопросов нет, то с зеленым — масса. Почему синус от α? Угол «вона где», тут синус вообще не от того угла и т.д.
Смотрим на пересечение прямой и малой (зеленой) окружности. Зеленый катет прилетает именно оттуда. Именно так координату Y’ и рассчитывали, согласно уравнению(1). Рисунок — это иллюстрация, не метод решения.
Тангенс угла β в этом случае равен:
(3) Тангенс угла β
Используя формулу тангенса произведем дальнейшие преобразования:
(4) Зависимость тангенса α от тангенса β
Таким образом, видим прямую зависимость угла α, который нужен нам в качестве параметра в уравнении(1), от угла β, координаты точки от которого хотим получить.
Нахождение координат
Угол α находим через арктангенс. В Delphi (и не только) для этих целей используется функция ArcTan2 из модуля math. Она корректно возвращает знак ± угла в зависимости от квадранта, а также предусмотрительно нечувствительна к возможным коллизиям, типа деления на 0.
Находим синус и косинус от требуемого угла β и подставляем в параметры функции ArcTan2, согласно последней формуле (4):
|
//– находим параметр (некий угол) для уравнения — SinCos(Angle,sn,cs); t := ArcTan2(a*sn, b*cs); |
Получившийся в результате вызова ArcTan2 угол есть ничто иное, как параметр t в параметрическом уравнении (1). Подставив его в уравнение, находим координаты точки на эллипсе, отстоящей на заданный угол от оси X.
О параметре
Практический смысл параметра t состоит в том, что это угол окружности до «сплющивания». Этот тот угол окружности, который будет соответствовать точке эллипса при заданном угле. Попытаюсь на практике показать.
В JavaScript’е нет понятия эллипс. Тем более нет понятия дуги эллипса. Но можно нарисовать окружность (через дугу) и «сплющить». Может быть такой номер пройдет и с дугой?
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
// рисует дугу эллипса function drawArcEllipse(ctx, center, a, b, start, finish, colorLine=‘none’, widthLine=0.0, angle=0.0) { if (a==0.0) return; var t1 = start; var t2 = finish; ctx.beginPath(); // сохраняем контекст ctx.save(); // перемещение координат в центр эллипса ctx.translate(center.x, center.y); // поворот плоскости на угол, если требуется if (angle!=0.0) ctx.rotate(angle); // сжимаем по вертикали ctx.scale(1, b/a); // рисуем дугу ctx.arc(0, 0, a, t1, t2); // восстанавливает контекст ctx.restore(); if (colorLine!=‘none’) ctx.strokeStyle = colorLine; if (widthLine>0.0) ctx.lineWidth = widthLine; ctx.stroke(); ctx.closePath(); } |
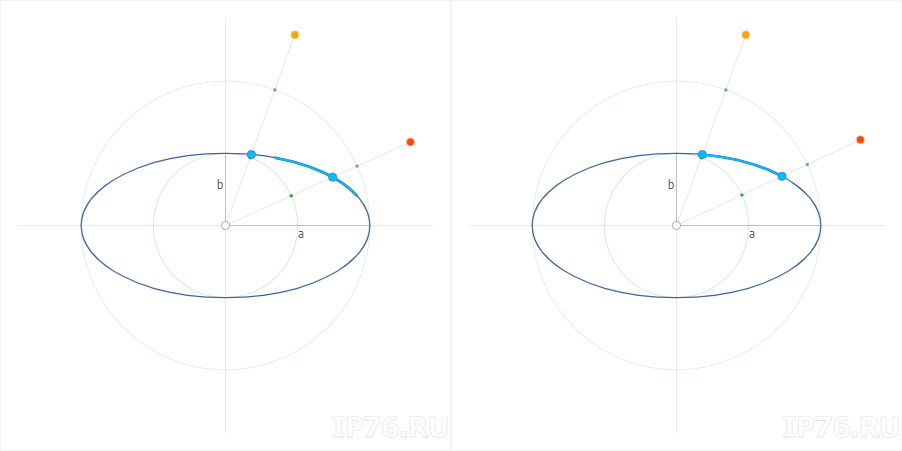
На рисунке слева видим, что дуга расположена совершенно неправильно. Очевидно, что надо использовать какие-то другие углы. Вот тут на помощь приходит параметр эллипса. Это как раз тот самый угол, который обеспечивает «попадание» в нужный нам угол при «сплющивании» окружности.
Перепишем функцию с учетом нахождения параметра:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
// рисует дугу эллипса function drawArcEllipse(ctx, center, a, b, start, finish, colorLine=‘none’, widthLine=0.0, angle=0.0) { if (a==0.0) return; var sn = Math.sin(start); var cs = Math.cos(start); var t1 = Math.atan2(a*sn, b*cs); sn = Math.sin(finish); cs = Math.cos(finish); var t2 = Math.atan2(a*sn, b*cs); ctx.beginPath(); // сохраняем контекст ctx.save(); // перемещение координат в центр эллипса ctx.translate(center.x, center.y); // поворот плоскости на угол, если требуется if (angle!=0.0) ctx.rotate(angle); // сжимаем по вертикали ctx.scale(1, b/a); // рисуем дугу ctx.arc(0, 0, a, t1, t2); // восстанавливает контекст ctx.restore(); if (colorLine!=‘none’) ctx.strokeStyle = colorLine; if (widthLine>0.0) ctx.lineWidth = widthLine; ctx.stroke(); ctx.closePath(); } |
На рисунке справа видим, что все встало на свои места. Идеальная дуга )
Координаты точки наклонного эллипса

Перенесено в отдельную статью.
Практика
Две функции. Первая находит параметр t по углу. Вторая производит расчет координат. Из второй не вызываю первую, т.к. получится двойное вычисление полуосей. Код не настолько велик, чтобы его нельзя было продублировать.
|
//****************************************************************** // Найти угол, который будет использован в расчете точки на элипсе // Т.е. тот самый параметр t в параметрическом уравнении эллипса: // x = a * cos t // y = b * sin t //****************************************************************** function GetEllipseAngleParam(ARect : TRectF; Angle : Extended) : Extended; var sn,cs : Extended; // синус/косинус a,b : Extended; // полуоси по X/Y begin a := ARect.Width/2; b := ARect.Height/2; SinCos(Angle,sn,cs); result := ArcTan2(a * sn, b * cs); end; |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
//******************************************************************** // Найти координату точки на эллипсе по углу отклонения //******************************************************************** function CalcEllipsePointCoord(ARect : TRectF; Angle : extended) : TPointF; var sn,cs : Extended; // синус/косинус a,b : Extended; // полуоси по X/Y cnt : TPointF; // центр t : Extended; // параметр для уравнения эллипса begin // инициализация полуосей a := ARect.Width/2; b := ARect.Height/2; // центр эллипса cnt := ARect.CenterPoint; // находим параметр (некий угол) для уравнения SinCos(Angle,sn,cs); t := ArcTan2(a * sn, b * cs); // считаем результат по параметрическому уравнению SinCos (t, sn, cs); result.X := cnt.x + a * cs; result.Y := cnt.Y + b * sn; end; |
Скачать исходник + исполнямый файл
Друзья, спасибо за внимание!
Надеюсь, материал после правок стал понятней.
Подписывайтесь на телегу.
Если есть вопросы, с удовольствием отвечу )
Сегодня поговорим об единичной окружности 🧑🏫

Можно ли найти точку (её координаты) на окружности, зная координаты центра окружности, её радиус и угол поворота?🤔
Ну, конечно, можно! Записывай и запоминай общую формулу для нахождения координат точки:
x=x0+r⋅cos δ
y=y0+r⋅sin δ
x0,y0 — координаты центра окружности;
r — радиус окружности;
δ —угол поворота радиуса вектора.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!
Как найти координаты точки на окружности, зная радиус и угол прямой к точке из окружности?
Михаил
Оракул
(50492),
закрыт
12 лет назад
Угол задаётся в градусах, координаты нужно получить в полярной системе.
Нужно чтобы для всех 360 градусов работало.
У меня почему-то получается точки в 300 и 60 градусах на одном и том же месте располагаются.
Дополнен 12 лет назад
*угол прямой к точке из центра окружности
Содержание:
Окружность:
Определение: Кривой второго порядка называется линия, описываемая уравнением 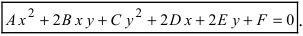
Замечание: Если коэффициенты 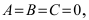
При определенных значениях параметров, входящих в это уравнение, оно дает канонические у равнения окружности, эллипса (не путать с овалом), гиперболы и параболы. Рассмотрим эти кривые второго порядка в указанной последовательности.
Определение: Окружностью называется геометрическое место точек равноудаленных от выделенной точки 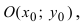 называемой центром окружности, на расстояние R, которое называется радиусом окружности.
называемой центром окружности, на расстояние R, которое называется радиусом окружности.
Получим уравнение окружности (Рис. 27). Пусть точка М(х;у) лежит на окружности:
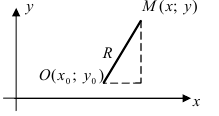
Рис. 27. Вывод уравнения окружности.
Из рисунка видно, что по теореме Пифагора 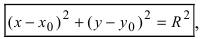 которое определяет уравнение окружности (Рис. 28):
которое определяет уравнение окружности (Рис. 28): 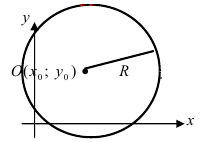
Рис. 28. Окружность. 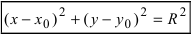
Если 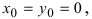 то уравнение принимает вид
то уравнение принимает вид 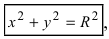 который называется каноническим уравнением окружности.
который называется каноническим уравнением окружности.
Пример:
Составить уравнение окружности, центр которой совпадает с точкой М (2; 1), прямая линия 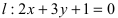 является касательной к окружности.
является касательной к окружности.
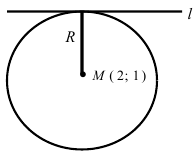
Решение:
Радиус окружности равен расстоянию от центра окружности точки М (2; 1) до прямой l, т.е.
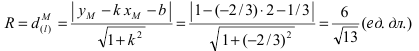
В уравнении окружности 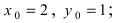 таким образом оно имеет вид:
таким образом оно имеет вид: 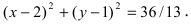
Пример:
Составить уравнение окружности, касающейся двух параллельных прямых 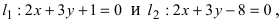 причем одной из них в т. А (1; 2).
причем одной из них в т. А (1; 2).
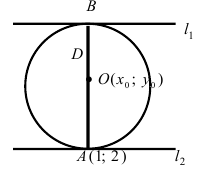
Решение:
Прежде всего определим, на какой из прямых 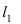 или
или 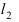 лежит точка A(1; 2). Для этого подставим ее координаты в уравнения прямых
лежит точка A(1; 2). Для этого подставим ее координаты в уравнения прямых 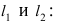
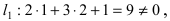 следовательно, точка A(1; 2) принадлежит линии
следовательно, точка A(1; 2) принадлежит линии 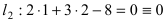 (в сокращенной форме это предложение пишут так:
(в сокращенной форме это предложение пишут так: 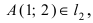 где значок
где значок 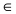 означает “принадлежит”. Таким образом, диаметр окружности D равен расстоянию от точки A(1; 2) до прямой
означает “принадлежит”. Таким образом, диаметр окружности D равен расстоянию от точки A(1; 2) до прямой 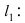
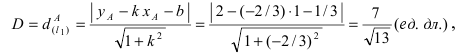
а радиус окружности 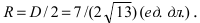 Найдём координаты центра окружности точки
Найдём координаты центра окружности точки 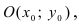 которая делит отрезок АВ пополам. Вначале составим уравнение прямой (АВ) и вычислим координаты точки
которая делит отрезок АВ пополам. Вначале составим уравнение прямой (АВ) и вычислим координаты точки 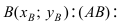 перейдем от общего уравнения прямой
перейдем от общего уравнения прямой 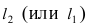 к уравнению прямой с угловым коэффициентом
к уравнению прямой с угловым коэффициентом 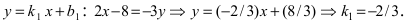 Так как прямая
Так как прямая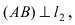 то её угловой коэффициент
то её угловой коэффициент 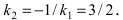 Прямая (АВ) проходит через известную точку A(1;2), следовательно,
Прямая (АВ) проходит через известную точку A(1;2), следовательно, 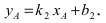 Отсюда находим
Отсюда находим 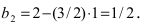 Таким образом,уравнение прямой (АВ):
Таким образом,уравнение прямой (АВ):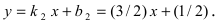
Найдем координаты точки B, которая является пересечением прямых 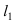 и (АВ), т.е. решим систему линейных алгебраических уравнений, составленную из уравнений прямых
и (АВ), т.е. решим систему линейных алгебраических уравнений, составленную из уравнений прямых 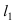 и (АВ): (В):
и (АВ): (В): 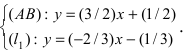 Подставим выражение для переменной у из второго у равнения в первое, получим
Подставим выражение для переменной у из второго у равнения в первое, получим 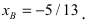 Подставив это значение во второе уравнение системы, найдем
Подставив это значение во второе уравнение системы, найдем 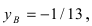 т.е.
т.е. 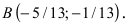
Для вычисления координат точки О применим формулы деления отрезка пополам (О): 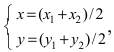 в этой формуле
в этой формуле 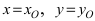 (координаты точки О),
(координаты точки О), 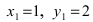 (координаты точки А),
(координаты точки А), 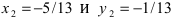 (координаты точки В), следовательно,
(координаты точки В), следовательно, 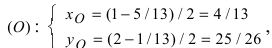 т.е. координаты точки О
т.е. координаты точки О 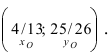
Таким образом, уравнение искомой окружности имеет вид: 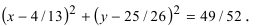
Окружность в высшей математике
Рассмотрим уравнение

которое получается из уравнения (I), если положить 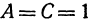 ,
, 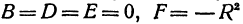 .
.
Если в формулу, выражающую расстояние между двумя точками, подставить 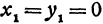 ,
, 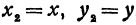 , то получим
, то получим 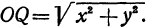 Из уравнения (1) находим, что
Из уравнения (1) находим, что 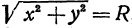 , т. е.
, т. е. 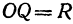 . Это значит, что все точки
. Это значит, что все точки 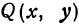 , координаты которых удовлетворяют уравнению (1), находятся на расстоянии
, координаты которых удовлетворяют уравнению (1), находятся на расстоянии 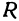 от начала координат. Следовательно, геометрическое место точек, координаты которых удовлетворяют уравнению (1), есть окружность радиуса
от начала координат. Следовательно, геометрическое место точек, координаты которых удовлетворяют уравнению (1), есть окружность радиуса  с центром в начале координат. Аналогично получаем, что уравнение
с центром в начале координат. Аналогично получаем, что уравнение 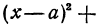
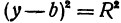 определяет окружность радиуса
определяет окружность радиуса  с центром в точке
с центром в точке 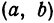 .
.
Пример:
Найдем уравнение окружности с центром в точке  и радиусом, равным 10.
и радиусом, равным 10.
Решение:
Полагая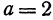 ,
, 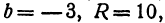 получим
получим 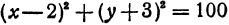 .
.
Разрешим это уравнение относительно 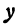 , будем иметь
, будем иметь
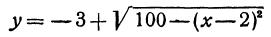
и
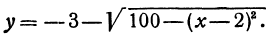
Первое из этих уравнений есть уравнение верхней половины окружности, второе—нижней.
Центральный угол. Градусная мера дуги
Дуга окружности. Если отметить на окружности точки  и
и  , то окружность разделится на две дуги: большую дугу (мажорная дуга) и меньшую дугу (минорная дуга). Если точка
, то окружность разделится на две дуги: большую дугу (мажорная дуга) и меньшую дугу (минорная дуга). Если точка 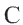 является какой-либо точкой дуги
является какой-либо точкой дуги 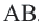 , то
, то 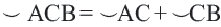 . Если точки
. Если точки  и
и  являются концами диаметра, го каждая дуга является полуокружностью.
являются концами диаметра, го каждая дуга является полуокружностью.
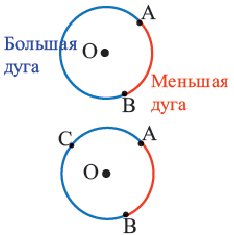
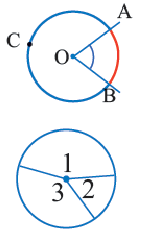
Центральный угол. Угол, вершина которого находится в центре окружности, называется центральным углом. Дугу окружности можно измерять в градусах. Градусная мера дуги равна градусной мере соответствующего центрального угла: 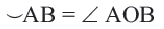
Сумма всех центральных углов окружности, не имеющих общую внутреннюю точку, равна 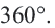
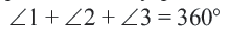
Дуги окружности и их величины

Пример: 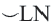 минорная дуга:
минорная дуга: 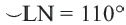
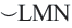 мажорная дуга:
мажорная дуга: 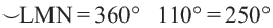
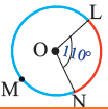
Конгруэнтные дуги
В окружности конгруэнтным центральным углам соответствуют конгруэнтные дуги и наоборот.
Если 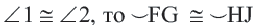
Если 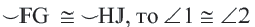
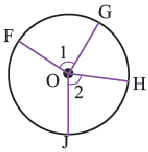
Длина дуги
Какую часть составляет центральный угол от всей окружности, такую же часть длина дуги составляет от длины всей окружности.
Длина дуги в 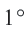 равна
равна 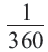 части длины окружности.
части длины окружности.
Длина дуги, соответствующей центральному углу с градусной мерой 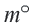 , составляет
, составляет 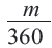 части длины окружности:
части длины окружности: 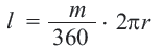
Длина дуги выражается единицами измерения длины (мм, см, м, и т.д.)
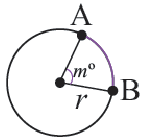
Пример №1
Длина окружности равна 72 см. Найдите длину дуги, соответствующей центральному углу 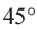 .
.
Решение:
Так как центральный угол 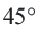 составляет
составляет 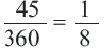 часть полного угла, то длина искомой дуги:
часть полного угла, то длина искомой дуги: 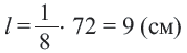
Пример №2
Найдите длину дуги, соответствующей центральному углу 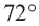 в окружности радиусом 15 см.
в окружности радиусом 15 см.
Решение: подставляя значения 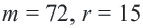 в формулу длины дуги находим:
в формулу длины дуги находим: 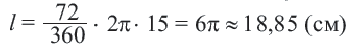
Окружность и хорда
Теорема о конгруэнтных хордах
Теорема 1. Хорды, стягивающие конгруэнтные дуги окружности, конгруэнтны.
Обратная теорема 1. Дуги, стягиваемые конгруэнтными хордами окружности, конгруэнтны.
1)Если 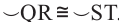 , то
, то 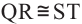
2)Если 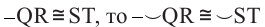
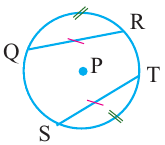
Доказательство теоремы 1:
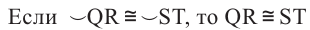

Теорема о серединном перпендикуляре хорд
Теорема 2.
Диаметр, перпендикулярный хорде, делит хорду и соответствующую дугу пополам.
Если 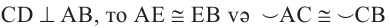
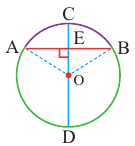
Доказательство теоремы 2.
Дано:  – центральный угол,
– центральный угол, 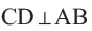
Докажите: 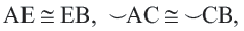
Начертите радиусы 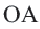 и
и 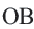 окружности.
окружности.
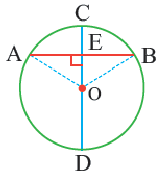
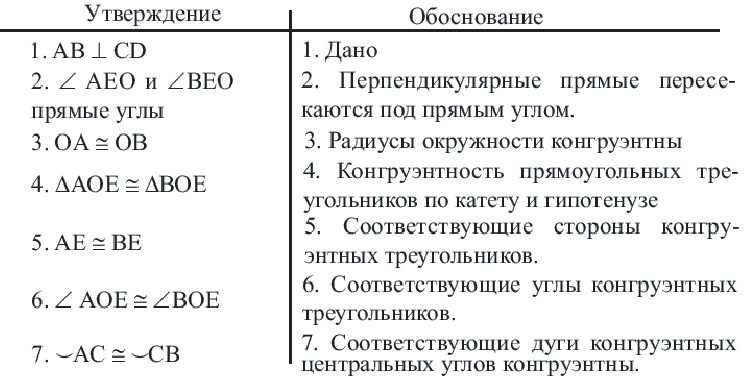
Следствие 1. Прямая, проходящая через центр окружности и перпендикулярная хорде, делит хорду и ее дугу пополам.
Следствие 2. Центр окружности расположен на серединном перпендикуляре хорды. Серединный перпендикуляр хорды проходит через центр окружности.
Пример: Найдите расстояние от центра до хорды длиной 30 единиц в окружности радиусом 17 единиц. Если 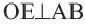 , то
, то 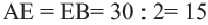 . Из
. Из 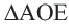 по теореме Пифагора имеем:
по теореме Пифагора имеем: 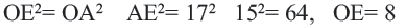
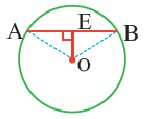
Теорема о хордах, находящихся на одинаковом расстоянии от центра окружности
Теорема 3.
Конгруэнтные хорды окружности находятся на одинаковом расстоянии от центра окружности.
Если 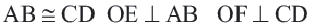 , то
, то 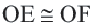
Обратная теорема 3. Хорды, находящиеся на одинаковом расстоянии от центра окружности, конгруэнтны.
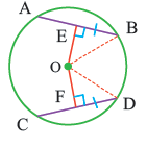
Доказательство теоремы 3
Дано: Окружность с центром 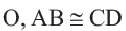
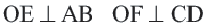
Докажите: 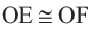
Доказательство (текстовое): Прямая, проходящая через центр окружности и перпендикулярная хорде, делит хорду и стягивающую ее дугу пополам.  и
и  – серединные перпендикуляры конгруэнтных хорд
– серединные перпендикуляры конгруэнтных хорд 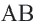 и
и 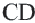 .
.  , так как они являются половиной конгруэнтных хорд. Начертим радиусы окружности
, так как они являются половиной конгруэнтных хорд. Начертим радиусы окружности 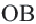 и
и 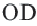 :
: 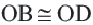 . Прямоугольные треугольники,
. Прямоугольные треугольники, 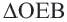 и
и 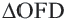 конгруэнтны (по катету и гипотенузе). Так как
конгруэнтны (по катету и гипотенузе). Так как  и
и  являются соответствующими сторонами данных треугольников, то они конгруэнтны:
являются соответствующими сторонами данных треугольников, то они конгруэнтны: 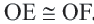 . Теорема доказана.
. Теорема доказана.
Задача. Хорды  и
и  находятся на одинаковом расстоянии от центра окружности.
находятся на одинаковом расстоянии от центра окружности. 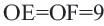 . Если радиус окружности равен 41 единице, то найдите
. Если радиус окружности равен 41 единице, то найдите 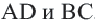 .
.
Решение: Так как хорды  и
и  находятся на одинаковом расстоянии от центра, то они конгруэнтны:
находятся на одинаковом расстоянии от центра, то они конгруэнтны: 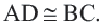
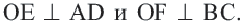 Соединим точки
Соединим точки 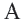 и
и 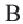 с точкой
с точкой 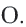 В прямоугольном треугольнике
В прямоугольном треугольнике 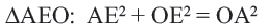
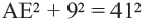 ;
; 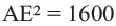 ;
; 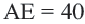 ;
; 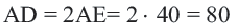
Так как 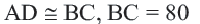
Угол, вписанный в окружность
Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется углом вписанным в окружность. Дуга, соответствующая углу, вписанному в окружность, называется дугой, на которую опирается этот угол.
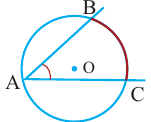
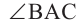 является углом вписанным в окружность с центром
является углом вписанным в окружность с центром  , а
, а 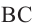 дуга, на которую опирается этот угол. Ниже показаны три разных угла, вписанных в окружность.
дуга, на которую опирается этот угол. Ниже показаны три разных угла, вписанных в окружность.
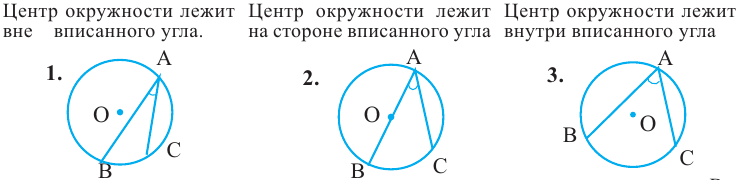
Угол, вписанный в окружность:
Теорема 1. Градусная мера угла, вписанного в окружность, равна половине градусной меры дуги, на которую он опирается. 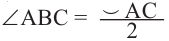
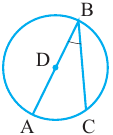
Доказательство (текстовое): 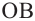 и
и 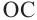 радиусы окружности и
радиусы окружности и 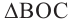 равнобедренный треугольник. Значит,
равнобедренный треугольник. Значит, 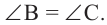 Так как
Так как 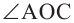 является внешним углом
является внешним углом 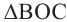 ,
, 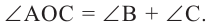 Если примем, что
Если примем, что 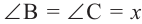 , то
, то 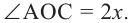 Так как градусные меры центрального угла и опирающейся на него дуги равны, то
Так как градусные меры центрального угла и опирающейся на него дуги равны, то 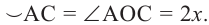 Следовательно,
Следовательно, 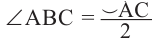 .
.
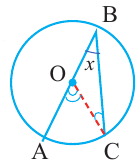
Следствие 1. Угол, вписанный в окружность, равен половине соответствующего центрального угла.
Следствие 2. Угол, вписанный в окружность и опирающийся на диаметр (полуокружность), является прямым углом.
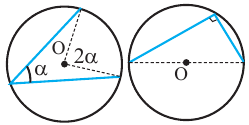
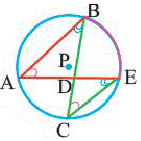
Конгруэнтные углы, вписанные в окружность
Следствие 3. Вписанные углы, опирающиеся на одну и ту же дугу, конгруэнтны. 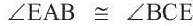 ,
, 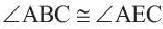 .
.
Следствие 4. Вписанные углы, опирающиеся на конгруэнтные дуги, конгруэнтны. Если 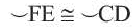 , то
, то 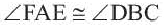 .
.

Касательная к окружности
Касательная. Признак касательной
Прямая, имеющая одну общую точку с окружностью, называется касательной. Теорема 1. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
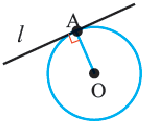
Прямая 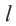 является касательной к окружности. Значит,
является касательной к окружности. Значит, 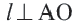 Обратная теорема (признак касательной): Прямая, проходящая через точку окружности и перпендикулярная радиусу, проведенному в эту точку, является касательной окружности.
Обратная теорема (признак касательной): Прямая, проходящая через точку окружности и перпендикулярная радиусу, проведенному в эту точку, является касательной окружности.
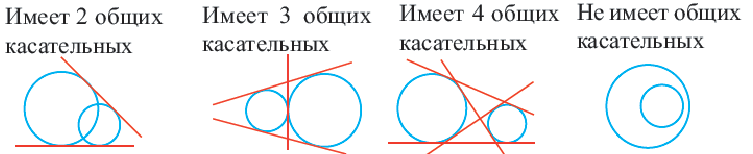
Прямая, касающаяся обеих окружностей, называется общей касательной этих окружностей. Окружности, касаясь друг друга изнутри или извне, могут иметь общую касательную в одной точке. Также окружности могут касаться одной касательной в разных точках.

Две окружности могут иметь несколько общих касательных или вообще не иметь общих касательных.
Доказательство теоремы 1. Если прямая  – касательная к окружности, значит, она имеет единственную общую точку с окружностью. Допустим, что прямая
– касательная к окружности, значит, она имеет единственную общую точку с окружностью. Допустим, что прямая  не перпендикулярна радиусу
не перпендикулярна радиусу 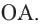 Проведем
Проведем 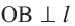 и на прямой
и на прямой  выделим отрезок
выделим отрезок 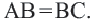 Тогда
Тогда 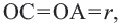 так как
так как 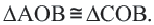 Значит, точка
Значит, точка 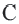 также находится на окружности. То есть прямая
также находится на окружности. То есть прямая  имеет с окружностью две общие точки, что противоречит условию. Значит,
имеет с окружностью две общие точки, что противоречит условию. Значит, 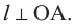
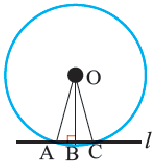
Свойства касательных, проведенных к окружности из одной точки
Теорема 2. Отрезки касательных к окружности, проведенных из одной точки, конгруэнтны, и центр окружности находится на биссектрисе угла, образованного касательными.
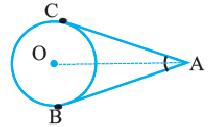
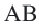 и
и 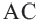 касательные, проведенные из точки
касательные, проведенные из точки 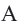 к окружности с центром
к окружности с центром 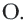
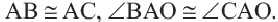
Углы, образованные секущими и касательными
Прямая, имеющая две общие точки с окружностью, называется секущей окружности.
Углы между двумя секущими
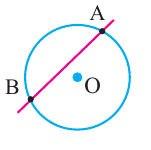
Вершина угла находится внутри окружности
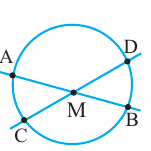
Теорема. Если вершина угла, образованного двумя секущими, находится внутри окружности, то градусная мера угла равна полусумме величин дуг на которые опирается этот угол и угол вертикальный данному. 
Углы между касательной и секущей
Вершина угла находится на окружности
Теорема. Если вершина угла, образованного касательной и секущей, находится на окружности, то градусная мера угла равна половине градусной меры дуги, на которую он опирается.
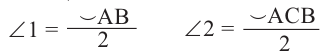
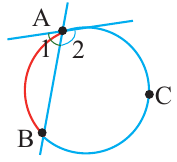
Углы, образованные касательной и секущей
Вершина угла находится вне окружности
Теорема 1.
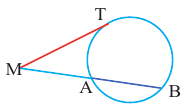
Градусная мера угла, образованного секущей и касательной, двумя касательными, двумя секущими окружности (если вершина угла находится вне окружности), равна половине разности градусных мер дуг, находящихся между сторонами угла.
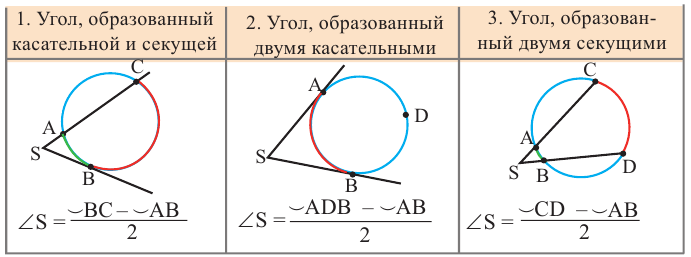
Отрезки секущих и касательных
Длина отрезков, секущих окружность
Теорема 1. При пересечении двух хорд, произведение отрезков одной хорды, полученных точкой пересечения, равно произведению отрезков второй хорды.
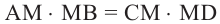
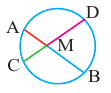
Теорема 2. Если из точки  провести две прямые, пересекающие окружность соответственно в точках
провести две прямые, пересекающие окружность соответственно в точках  и
и 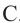 ,
, 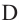 и
и 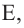 то верно равенство
то верно равенство 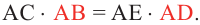
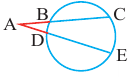
Теорема 3. Если из точки 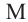 проведены прямая, которая пересекает окружность в точках
проведены прямая, которая пересекает окружность в точках  и
и  и касательная к окружности в точке
и касательная к окружности в точке 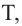 то верно равенство:
то верно равенство: 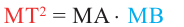
Уравнение окружности
Используя формулу расстояния между двумя точками, можно написать уравнение окружности с радиусом  и с центром в начале координат. Расстояние между центром окружности
и с центром в начале координат. Расстояние между центром окружности 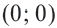 и ее любой точкой
и ее любой точкой 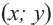 равно радиусу
равно радиусу  окружности.
окружности.
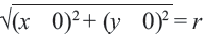 Расстояние между двумя точками
Расстояние между двумя точками
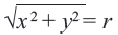 Упрощение
Упрощение
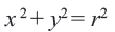 Возведение обеих частей в квадрат
Возведение обеих частей в квадрат
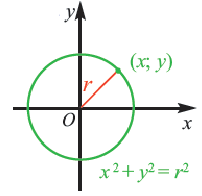
Уравнение окружности с центром в начале координат и радиусом 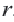 :
: 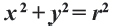
Например, уравнение окружности с центром в начале координат 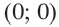 и радиусом 2 имеет вид:
и радиусом 2 имеет вид: 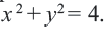
По формуле расстояния между центром окружности 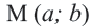 и точки
и точки 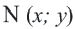 на окружности радиуса
на окружности радиуса 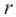 имеем
имеем 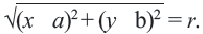 Возведя в квадрат обе части, получаем уравнение окружности с центром в точке
Возведя в квадрат обе части, получаем уравнение окружности с центром в точке 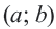 и радиусом
и радиусом 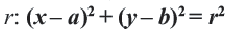
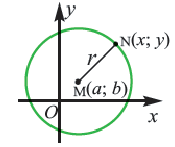
Например, уравнение окружности с центром в точке 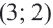 и радиусом 4 имеет вид:
и радиусом 4 имеет вид: 
Пример №3
Постройте на координатной плоскости окружность, заданную уравнением 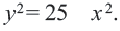
Решение: Напишем уравнение в виде 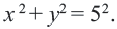 Как видно,
Как видно, 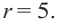
Отметим 4 точки, находящиеся на расстоянии 5 единиц от начала координат. Например, 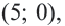
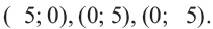 Проведем окружность через эти точки.
Проведем окружность через эти точки.
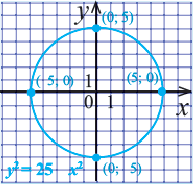
Пример №4
Точка 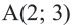 находится на окружности, центром которой является начало координат. Напишите уравнение этой окружности.
находится на окружности, центром которой является начало координат. Напишите уравнение этой окружности.
Решение: Записав координаты точки 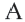 в уравнении
в уравнении 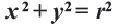 , получим:
, получим: 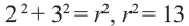 Уравнение этой окружности:
Уравнение этой окружности: 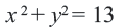
Пример №5
Найдем центр и радиус окружности, заданной уравнением 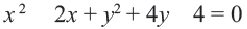
Решение: 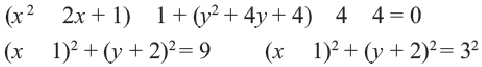
Центр окружности точка 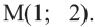 Радиус
Радиус 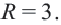
Пример №6
Мобильные телефоны работают с помощью передачи сигналов посредством спутников из одной передающей станции в другую. Компания мобильного оператора старается расположить передающую станцию так, чтобы обслуживать больше пользователей. Представим, что три больших города находятся в точках 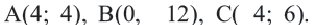 На координатной плоскости 1 единица равна расстоянию в 100 км. Передающая станция должна быть расположена в точке, находящейся на одинаковом расстоянии от этих городов. Напишите координаты этой точки и уравнение соответствующей окружности.
На координатной плоскости 1 единица равна расстоянию в 100 км. Передающая станция должна быть расположена в точке, находящейся на одинаковом расстоянии от этих городов. Напишите координаты этой точки и уравнение соответствующей окружности.
Решение: Сначала соединим эти точки и найдем точку пересечения серединных перпендикуляров сторон полученного треугольника. Эта точка 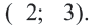 Эта точка, являясь центром окружности, показывает месторасположение станции. Расстояние между центром и любой из заданных точек является радиусом окружности,
Эта точка, являясь центром окружности, показывает месторасположение станции. Расстояние между центром и любой из заданных точек является радиусом окружности, 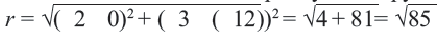
Уравнение окружности: 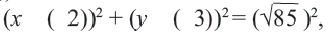
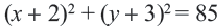
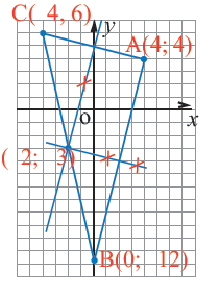
Заметка. Определив линейные уравнения, соответствующие серединным перпендикулярам, можно найти координаты центра окружности решением системы уравнений.
Координаты точек, находящихся на окружности, и тригонометрические отношения
Если точка 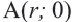 при повороте радиуса
при повороте радиуса 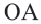 вокруг точки
вокруг точки 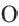 против движения часовой стрелки на угол
против движения часовой стрелки на угол 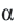 преобразуется в точку
преобразуется в точку 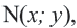 то
то 
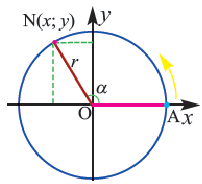
Для координат точки 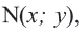 соответствующей углу поворота
соответствующей углу поворота  на окружности, верны формулы
на окружности, верны формулы 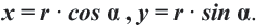 В этих формулах
В этих формулах  – угол, отсчитываемый от положительной оси
– угол, отсчитываемый от положительной оси 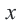 против движения часовой стрелки. Если точка
против движения часовой стрелки. Если точка 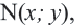 не находится на оси ординат, то
не находится на оси ординат, то 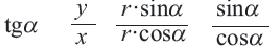 .
.
Синусы смежных углов равны, а косинусы взаимно противоположны.

Из этих формул при 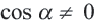 почленным делением получаем:
почленным делением получаем:
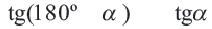
С помощью формул, приведенных выше, вычисление синуса, косинуса, тангенса для тупого угла можно свести к вычислению синуса, косинуса, тангенса острого угла, соответственно.
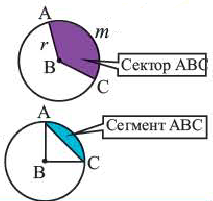
Сектор и сегмент
Сектор часть круга, ограниченная центральным углом, образованным двумя радиусами и соответствующей этому углу дугой. Площадь сектора, соответствующего центральному углу, составляет ту часть площади круга, которую составляет центральный угол от полного угла.
Например, часть круга, соответствующая центральному углу 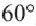 , составляет
, составляет 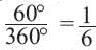 часть всего круга. Так как площадь круга
часть всего круга. Так как площадь круга 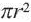 , то площадь этого сектора будет
, то площадь этого сектора будет  Сегмент часть круга, ограниченная хордой и соответствующей дугой.
Сегмент часть круга, ограниченная хордой и соответствующей дугой.
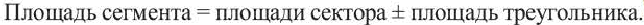
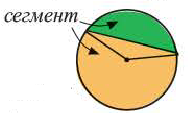
Площадь сектора
Площадь сектора: 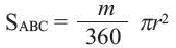
Площадь сегмента: 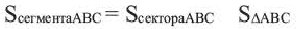
Указание: При нахождении площади сегмента, соответствующего большей дуге, к площади соответствующего сектора прибавляется площадь 
- Эллипс
- Гипербола
- Парабола
- Многогранник
- Сфера в геометрии
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники
