В общем случае уравнение, имеющее степень выше 4, нельзя разрешить в радикалах. Но иногда мы все же можем найти корни многочлена, стоящего слева в уравнении высшей степени, если представим его в виде произведения многочленов в степени не более 4-х. Решение таких уравнений базируется на разложении многочлена на множители, поэтому советуем вам повторить эту тему перед изучением данной статьи.
Чаще всего приходится иметь дело с уравнениями высших степеней с целыми коэффициентами. В этих случаях мы можем попробовать найти рациональные корни, а потом разложить многочлен на множители, чтобы потом преобразовать его в уравнение более низкой степени, которое будет просто решить. В рамках этого материала мы рассмотрим как раз такие примеры.
Уравнения высшей степени с целыми коэффициентами
Все уравнения, имеющие вид anxn+an-1xn-1+…+a1x+a0=0, мы можем привести к уравнению той же степени с помощью умножения обеих частей на ann-1 и осуществив замену переменной вида y=anx:
anxn+an-1xn-1+…+a1x+a0=0ann·xn+an-1·ann-1·xn-1+…+a1·(an)n-1·x+a0·(an)n-1=0y=anx⇒yn+bn-1yn-1+…+b1y+b0=0
Те коэффициенты, что получились в итоге, также будут целыми. Таким образом, нам нужно будет решить приведенное уравнение n-ной степени с целыми коэффициентами, имеющее вид xn+anxn-1+…+a1x+a0=0.
Схема решения уравнения
Вычисляем целые корни уравнения. Если уравнение имеет целые корни, нужно искать их среди делителей свободного члена a0. Выпишем их и будем подставлять в исходное равенство по очереди, проверяя результат. Как только мы получили тождество и нашли один из корней уравнения, то можем записать его в виде x-x1·Pn-1(x)=0. Здесь x1 является корнем уравнения, а Pn-1(x) представляет собой частное от деления xn+anxn-1+…+a1x+a0 на x-x1.
Подставляем остальные выписанные делители в Pn-1(x)=0, начав с x1, поскольку корни могут повторяться. После получения тождества корень x2 считается найденным, а уравнение может быть записано в виде (x-x1)(x-x2)·Pn-2(x)=0.Здесь Pn-2(x) будет частным от деления Pn-1(x) на x-x2.
Продолжаем и дальше перебирать делители. Найдем все целые корни и обозначим их количество как m. После этого исходное уравнение можно представить как x-x1x-x2·…·x-xm·Pn-m(x)=0. Здесь Pn-m(x) является многочленом n-m-ной степени. Для подсчета удобно использовать схему Горнера.
Если у нас исходное уравнение имеет целые коэффициенты, мы не можем получить в итоге дробные корни.
У нас в итоге получилось уравнение Pn-m(x)=0, корни которого могут быть найдены любым удобным способом. Они могут быть иррациональными или комплексными.
Покажем на конкретном примере, как применяется такая схема решения.
Условие: найдите решение уравнения x4+x3+2×2-x-3=0.
Решение
Начнем с нахождений целых корней.
У нас есть свободный член, равный минус трем. У него есть делители, равные 1, -1, 3 и -3. Подставим их в исходное уравнение и посмотрим, какие из них дадут в итоге тождества.
При x, равном единице, мы получим 14+13+2·12-1-3=0, значит, единица будет корнем данного уравнения.
Теперь выполним деления многочлена x4+x3+2×2-x-3 на (х-1) в столбик:
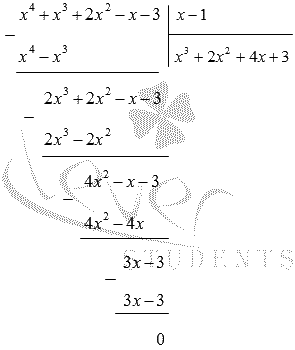
Значит, x4+x3+2×2-x-3=x-1×3+2×2+4x+3.
Перебираем возможные делители дальше, но подставляем их в равенство x3+2×2+4x+3=0:
13+2·12+4·1+3=10≠0(-1)3+2·(-1)2+4·-1+3=0
У нас получилось тождество, значит, мы нашли еще один корень уравнения, равный -1.
Делим многочлен x3+2×2+4x+3 на (х+1) в столбик:
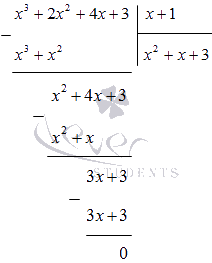
Получаем, что
x4+x3+2×2-x-3=(x-1)(x3+2×2+4x+3)==(x-1)(x+1)(x2+x+3)
Подставляем очередной делитель в равенство x2+x+3=0, начиная с -1:
-12+(-1)+3=3≠032+3+3=15≠0(-3)2+(-3)+3=9≠0
Равенства, полученные в итоге, будут неверными, значит, у уравнения больше нет целых корней.
Оставшиеся корни будут корнями выражения x2+x+3.
D=12-4·1·3=-11<0
Из этого следует, что у данного квадратного трехчлена нет действительных корней, но есть комплексно сопряженные: x=-12±i112.
Уточним, что вместо деления в столбик можно применять схему Горнера. Это делается так: после того, как мы определили первый корень уравнения, заполняем таблицу.
| xi | коэффициенты многочлена | ||||
| 1 | 1 | 2 | -1 | -3 | |
| 1 | 1 | 1+1·1=2 | 2+2·1=4 | -1+4·1=3 | -3+3·1=0 |
В таблице коэффициентов мы сразу можем увидеть коэффициенты частного от деления многочленов, значит, x4+x3+2×2-x-3=x-1×3+2×2+4x+3.
После нахождения следующего корня, равного -1, мы получаем следующее:
| xi | коэффициенты многочлена | |||
| 1 | 2 | 4 | 3 | |
| 1 | 1 | 2+1·(-1)=1 | 4+1·(-1)=3 | 3+3·(-1)=0 |
Далее мы приходим к разложению x-1x+1×2+x+3=0. Потом, проверив оставшиеся делители равенства x2+x+3=0, вычисляем оставшиеся корни.
Ответ: х=-1, х=1, x=-12±i112.
Условие: решите уравнение x4-x3-5×2+12=0.
Решение
У свободного члена есть делители 1, -1, 2, -2, 3, -3, 4, -4, 6, -6, 12, -12.
Проверяем их по порядку:
14-13-5·12+12=7≠0(-1)4-(-1)3-5·(-1)2+12=9≠024·23-5·22+12=0
Значит, x=2 будет корнем уравнения. Разделим x4-x3-5×2+12 на х-2, воспользовавшись схемой Горнера:
| xi | коэффициенты многочлена | ||||
| 1 | -1 | -5 | 0 | 12 | |
| 2 | 1 | -1+1·2=1 | -5+1·2=-3 | 0-3·2=3 | 12-6·2=0 |
В итоге мы получим x-2(x3+x2-3x-6)=0.
Проверяем делители дальше, но уже для равенства x3+x2-3x-6=0, начиная с двойки.
23+22-3·2-6=0
Значит, 2 опять будет корнем. Разделим x3+x2-3x-6=0 на x-2:
| xi | коэффициенты многочлена | |||
| 1 | 1 | -3 | -6 | |
| 2 | 1 | 1+1·2=3 | -3+3·2=3 | -6+3·2=0 |
В итоге получим (x-2)2·(x2+3x+3)=0.
Проверка оставшихся делителей смысла не имеет, поскольку равенство x2+3x+3=0 быстрее и удобнее решить с помощью дискриминанта.
Решим квадратное уравнение:
x2+3x+3=0D=32-4·1·3=-3<0
Получаем комплексно сопряженную пару корней: x=-32±i32.
Ответ: x=-32±i32.
Условие: найдите для уравнения x4+12×3-52x-3=0 действительные корни.
Решение
x4+12×3-52x-3=02×4+x3-5x-6=0
Выполняем домножение 23обеих частей уравнения:
2×4+x3-5x-6=024·x4+23×3-20·2·x-48=0
Заменяем переменные y=2x:
24·x4+23×3-20·2·x-48=0y4+y3-20y-48=0
В итоге у нас получилось стандартное уравнение 4-й степени, которое можно решить по стандартной схеме. Проверим делители, разделим и получим в итоге, что оно имеет 2 действительных корня y=-2, y=3 и два комплексных. Решение целиком здесь мы не будем приводить. В силу замены действительными корнями данного уравнения будут x=y2=-22=-1 и x=y2=32.
Ответ: x1=-1, x2=32
Советуем также ознакомиться с материалами, посвященными решению кубических уравнений и уравнений четвертой степени.
![]()
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Определение:
Целым
уравнением с одной переменной называется уравнение, левая и
правая части которого – целые выражения.
Отличие
целого уравнения от дробно-рационального заключается в том, что областью определения
целого уравнения является множество всех действительных чисел. То есть
аргумент может принимать любые значения.
Среди
уравнений найдем те, которые являются целыми уравнениями с одной переменной.
Целыми
будут следующие уравнения.
Каждое
из этих уравнений можно преобразовать.
Первое
уравнение:
Во
втором уравнении:
В
третьем уравнении:
Определение:
Степень
многочлена P(x)
называют степенью уравнения P(x)=0.
Степень
первого уравнения P(x)=3,
степень второго уравнения P(x)=4,
степень третьего уравнения P(x)=4.
Рассмотрим
пример: определить степень уравнений.
1.
2.
3.
4.
Любое
уравнение 1 – й степени можно привести к виду –
это линейное уравнение, и оно имеет не более одного корня.
Уравнение
2 – й степени можно привести к виду –
это квадратное уравнение и оно имеет не более двух корней.
Уравнение
3 – й степени можно записать в виде ,
оно имеет не более трёх корней.
Уравнения
4 – й степени можно представить в виде ,
оно имеет не более четырёх корней.
Любое
целое уравнение n
–
й степени можно представить в таком виде ,
оно имеет не более n
корней.
Причём,
во всех этих случаях, a≠0.
Пример.
Решить
уравнение:
Данное
уравнение имеет три корня.
Рассмотрим
пример: решить уравнение.
Так
как для него трудно найти способ решения, будем работать с исходной записью.
Введём замену.
Получим
новое уравнение, решим его:
При
решении этого уравнения мы применили способ введения новой переменной. С
помощью этого способа легко решать уравнения вида .
Такие уравнения имеют специальное название – «биквадратные уравнения».
Алгоритм
решения биквадратного уравнения:
1.
Ввести
новую переменную .
2.
Решить
уравнение ,
полученное после подстановки новой переменной.
3.
Выполняю
обратную подстановку .
4.
Найти
корни исходного биквадратного уравнения.
Пример.
Решить
уравнение:
Приведем
его к биквадратному уравнению:
Введём
новую переменную и выполним подстановку:
Рассмотрим уравнение.
31x3 – 10x = (x – 5)2 + 6x2
И левая и правая части уравнения являются целыми выражениями.
Напомним, что подобные уравнения называются целыми уравнениями.
Вернёмся к нашему изначальному уравнению и раскроем скобки, используя формулу квадрата разности.
Перенесем все члены уравнения в левую часть и приведем подобные члены.
Выражения «минус десять икс» и «плюс десять икс» взаимно уничтожаются.
После приведения подобных членов получаем уравнение, в левой части которого стоит многочлен стандартного вида (в общем виде будем называть его «Пэ от икс»), а в правой части — нуль.
Чтобы определить степень целого уравнения, необходимо привести его к виду пэ от икс равно нулю, то есть к уравнению, в левой части которого стоит многочлен стандартного вида, а в правой — нуль.
После этого необходимо определить степень многочлена пэ от икс. Это и будет степенью уравнения.
Рассмотрим пример. Попробуем определить степень данного уравнения.
Раскроем скобки, используя формулу квадрата суммы.
Далее перенесём все члены уравнения в левую часть и приведём подобные члены.
Итак, мы получили уравнение, в левой части которого многочлен стандартного вида второй степени, а в правой нуль. Это значит, что степень данного уравнения – вторая.
От степени уравнения зависит сколько корней оно имеет.
Можно доказать, что уравнение первой степени имеет один корень, уравнение второй степени имеет не более двух корней, уравнение третьей степени – не более трёх корней и так далее.
Степень уравнения также подсказывает нам, каким образом можно это уравнение решить.
Например, уравнение первой степени мы приводим к виду а икс плюс бэ равно цэ, где а не равно нулю.
Уравнение второй степени мы приводим к равносильному уравнению, в левой части которого квадратный трёхчлен, а в правой — нуль. Такое уравнение решается с помощью формулы корней квадратного уравнения или теоремы Виета.
Для решения уравнений более высоких степеней универсального способа нет, но есть основные методы, которые мы рассмотрим на примерах.
Решим уравнение третьей степени икс в третьей степени минус восемь икс во второй степени минус икс плюс восемь равно нулю.
Чтобы решить данное уравнение разложим его левую часть на множители способом группировки и воспользовавшись формулой разности квадратов.
Далее необходимо вспомнить, что произведение равно нули, когда один из множителей равен нулю. На основании этого делаем вывод, что либо икс минус 8 равно нулю, либо икс минус 1 равно нулю, либо икс плюс один равно нулю. Следовательно, корнями уравнения будут числа минус один, один и восемь.
Иногда для решения уравнений степени выше второй удобно использовать введение новой переменной.
Рассмотрим подобный пример.
Если раскрыть скобки, перенести все члены уравнения в левую часть, привести подобные члены и представить левую часть уравнения в виде многочлена стандартного вида, то ни один из известных нам способов не поможет решить это уравнение. В таком случае стоит обратить внимание на то, что в обеих скобках есть одинаковые выражения.
Именно это выражение мы и обозначим новой переменной игрик.
Тогда наше уравнение сведётся к уравнению с переменной игрек..
Далее просто раскроем скобки и перенесём все члены уравнения в левую часть.
Приведём подобные члены и получим уже знакомое нам квадратное уравнение.
Нетрудно найти корни этого уравнения. Игрик один равен шести, игрик два равен минус шестнадцати.
Теперь вернёмся к изначальному уравнению, выполнив обратную замену.
Изначально за игрик мы принимали выражение два икс в квадрате минус икс. А так как у нас два значения переменной игрек, мы получаем два уравнения. В каждом уравнении переносим все члены в левую часть, решаем получившиеся два квадратных уравнения. Корнями первого уравнения являются числа минус одна целая пять десятых и два, а второе уравнение корней не имеет, так как его дискриминант меньше нуля.
Итак, решением данного уравнения четвёртой степени являются числа минус одна целая пять десятых и два.
Особое место в классификации целых уравнений имеет уравнение вида а икс в четвёртой степени плюс бэ икс во второй степени плюс цэ равно нулю. Уравнения такого вида называют биквадратными уравнениями.
Решать подобные уравнения можно с помощью замены переменной.
Рассмотрим на примере.
В данном уравнении обозначим икс квадрат через игрик. При этом стоит обратить внимание, что переменная игрик не может принимать отрицательные значения.
Получим квадратное уравнение, корнями которого являются числа одна двадцать пятая и один.
Выполним обратную замену.
Корни первого уравнения: одна пятая и минус одна пятая, а корни второго: один и минус один.
Таким образом, мы нашли четыре корня исходного биквадратного уравнения.
Алгебраические уравнения выше второй степени мы называем уравнениями высших степеней. Изучение их в общем виде выходит за рамки программы средней школы. В нашем курсе рассматриваются лишь некоторые частные Еопросы, относящиеся к уравнениям высших степеней. Здесь мы покажем, как можно находить целые корни уравнения с целочисленными коэффициентами (если такие корни имеются).
Пусть старший коэффициент уравнения равен единице (приведенное уравнение), а остальные коэффициенты — целые числа. Пусть такое уравнение

имеет корнем целое число  подставляя
подставляя  в уравнение, получим
в уравнение, получим

откуда

где оба сомножителя в правой части равенства — целые; таким образом, свободный член  уравнения должен делиться на k. Все целые корни приведенного алгебраического уравнения с целыми коэффициентами являются делителями его свободного члена. Отсюда следует, что в качестве целых корней надлежит испытывать не какие-либо произвольные целые числа, а лишь делители свободного члена уравнения, которых имеется лишь конечное множество.
уравнения должен делиться на k. Все целые корни приведенного алгебраического уравнения с целыми коэффициентами являются делителями его свободного члена. Отсюда следует, что в качестве целых корней надлежит испытывать не какие-либо произвольные целые числа, а лишь делители свободного члена уравнения, которых имеется лишь конечное множество.
Можно доказать, что приведенное уравнение с целыми коэффициентами не имеет других рациональных корней, кроме целых; поэтому наш метод дает все рациональные решения уравнения (62.1).
Пример 1. Решить уравнение  Решение. Выписываем (положительные и отрицательные) делители свободного члена
Решение. Выписываем (положительные и отрицательные) делители свободного члена 
Подставляя эти числа в уравнение, находим, что корнем данного уравнения служит число  поскольку
поскольку  Многочлен, расположенный в левой части уравнения, по теореме Безу (п. 51) должен без остатка делиться на двучлен,
Многочлен, расположенный в левой части уравнения, по теореме Безу (п. 51) должен без остатка делиться на двучлен,  Проделав деление, найдем в частном квадратный трехчлен
Проделав деление, найдем в частном квадратный трехчлен  Его два корня присоединим к ранее найденному корню и, таким образом, найдем все три корня данного уравнения:
Его два корня присоединим к ранее найденному корню и, таким образом, найдем все три корня данного уравнения: 
Пример 2. Имеет ли уравнение  целые корни?
целые корни?
Решение. Целыми корнями могут быть лишь делители свободного члена 2, т. е. числа ±1, ±2. Непосредственной подстановкой этих чисел в уравнение убеждаемся, что ни одно из них ему не удовлетворяет. Данное уравнение целых и вообще рациональных корней не имеет.
Если старший коэффициент  уравнения с целыми коэффициентами
уравнения с целыми коэффициентами

отличен от единицы, то можно ввести новую неизвестную у с помощью формулы  тогда для у получится уравнение
тогда для у получится уравнение

или

которое уже имеет) старший коэффициент, равный единице, и к которому применим способ отыскания целых корней, указанный выше. Целые корни для у Кадут рациональные, вообще говоря, дробные корни для 
Пример 3. Решить уравнение

Решение. Делаем подстановку  . После очевидных преобразований имеем
. После очевидных преобразований имеем

Подбираем целый корень для у, находим

Делим левую часть уравнения на  и получаем уравнение
и получаем уравнение

с корнями  . Окончательно выписываем решения исходного уравнения:
. Окончательно выписываем решения исходного уравнения:

10.5. НАХОЖДЕНИЕ РАЦИОНАЛЬНЫХ КОРНЕЙ МНОГОЧЛЕНА С ЦЕЛЫМИ КОЭФФИЦИЕНТАМИ
Теорема 4. Если многочлен с целыми коэффициентами f (x) = anxn + an-1xn-1 + … + a1x+a0 имеет рациональный корень x=p/q (q ≠ 0, дробь p/q несократимая), то р является делителем свободного члена (a0), а q — делителем коэффициента при старшем члене аn.
Если p/q является корнем многочлена f (х), то f(p/q) = 0. Подставляем p/q вместо х в f(x) и из последнего равенства имеем
|
an * pn/qn + an-1 * pn-1/qn-1 + … + a1 * p/q + a0 = 0. |
(1) |
Умножим обе части равенства (1) на (q ≠ 0). Получаем
|
аnрn + an-1pn-1q + … + a1pqn-1 + a0qn = 0. |
(2) |
В равенстве (2) все слагаемые, кроме последнего, делятся на р. Поэтому
a0qn = -(аnрn + an-1pn-1q + … + a1pqn-1) делится на р.
Но когда мы записываем рациональное число в виде p/q, то эта дробь считается несократимой, то есть р и q не имеют общих делителей. Произведение a0qn может делиться на р (если р и q — взаимно простые числа) только тогда, когда a0 делится на р. Таким образом, р — делитель свободного члена a0.
Аналогично все слагаемые равенства (2), кроме первого, делятся на q. Тогда
anpn = -(an-1pn-1q + … + a1pq-1 + a0qn) делится на q. Поскольку р и q — взаимно простые числа, то an делится на q, следовательно, q — делитель коэффициента при старшем члене.
Отметим два следствия из этой теоремы. Если взять q = 1, то корнем многочлена будет целое число р — делитель a0. Таким образом, имеет место:
Следствие 1. Любой целый корень многочлена с целыми коэффициентами является делителем его свободного члена.
Если в заданном многочлене f (х) коэффициент аn = 1, то делителями аn могут быть только числа ±1, то есть q =±1, и имеет место:
Следствие 2. Если коэффициент при старшем члене уравнения с целыми коэффициентами равен 1, то все рациональные корни этого уравнения (если они существуют) — целые числа.
Задача 1 Найдите рациональные корни многочлена 2х3 – х2 + 12х – 6.
Пусть несократимая дробь p/q является корнем многочлена. Тогда р необходимо искать среди делителей свободного члена, то есть среди чисел ±1, ±2, ±3, ±6, а q — среди делителей старшего коэффициента: ±1, ±2.
Таким образом, рациональные корни многочлена необходимо искать среди чисел ±1/2, ±1, +±3/2, ±2, ±3, ±6. Проверять, является ли данное число корнем многочлена, целесообразно с помощью схемы Горнера. При x = 1/2 имеем следующую таблицу.

Кроме того, по схеме Горнера можно записать, что
2х3 – х2 + 12х – 6 = (x – 1/2) (2x2 + 12).
Многочлен 2х2 + 12 не имеет действительных корней (а тем более рациональных), поэтому заданный многочлен имеет единственный рациональный корень x =1/2.
Задача 2 Разложите многочлен Р (х) = 2х4 + 3х3 – 2х2 – х – 2 на множители.
Ищем целые корни многочлена среди делителей свободного члена: ±1, ±2. Подходит 1. Делим Р (х) на х – 1 с помощью схемы Горнера.

Тогда Р (х) = (х – 1)(2х3 + 5х2 + 3х + 2). Ищем целые корни кубического многочлена 2х3 + 5х2 + 3х + 2 среди делителей его свободного члена: ±1, ±2. Подходит (–2). Делим на х + 2

Имеем Р (х) = (х – 1)(х + 2)(2х2 + х +1).
Квадратный трехчлен 2х2 + х +1 не имеет действительных корней и на линейные множители не раскладывается.
Ответ: Р (х) = (х – 1)(х + 2)(2х2 + х +1).
Отметим, что во множестве действительных чисел не всегда можно найти все корни многочлена (например, квадратный трехчлен х2 + х + 1 не имеет действительных корней). Таким образом, многочлен n-й степени не всегда можно разложить на линейные множители. В курсах высшей алгебры доказывается, что многочлен нечетной степени всегда можно разложить на линейные и квадратные множители, а многочлен четной степени представить в виде произведения квадратных трехчленов.
Например, многочлен четвертой степени раскладывается в произведение двух квадратных трехчленов. Для нахождения коэффициентов этого разложения иногда можно применить метод неопределенных коэффициентов.
Задача 3 Разложите на множители многочлен х4 + х3 + 3х2 + х + 6.
Попытка найти рациональные корни ничего не дает: многочлен не имеет рациональных (целых) корней.
Попытаемся разложить этот многочлен в произведение двух квадратных трехчленов. Поскольку старший коэффициент многочлена равен 1, то и у квадратных трехчленов возьмем старшие коэффициенты равными 1. То есть будем искать разложение нашего многочлена в виде:
|
х4 + х3 + 3х2 + х + 6 = (х2 + ах + b)(х2 + сх + d), |
(3) |
где а, b, с и d — неопределенные (пока что) коэффициенты. Многочлены, стоящие в левой и правой частях этого равенства, тождественно равны, поэтому и коэффициенты при одинаковых степенях х у них равны. Раскроем скобки в правой части равенства и приравняем соответствующие коэффициенты. Это удобно записать так:
х4 + х3 + 3х2 + х + 6 = x4 + cx3 + dx2 +
+ ax3 + acx2 + adx +
+ bx2 + bcx + bd.
Получаем систему
 |
(4) |
Попытка решить эту систему методом подстановки приводит к уравнению 4-й степени, поэтому попробуем решить систему (4) в целых числах. Из последнего равенства системы (4) получаем, что b и d могут быть только делителями числа 6. Все возможные варианты запишем в таблицу.

Коэффициенты b и d в равенстве (3) равноправны, поэтому мы не рассматриваем случаи b = 6 и d = 1 или b = –6 и d = –1 и т. д.
Для каждой пары значений b и d из третьего равенства системы (4) найдем ас = 3 – (b + d), а из второго равенства имеем а + с = 1.
Зная а + с и ас, по теореме, обратной теореме Виета, находим а и с как корни квадратного уравнения. Найденные таким образом значения а, b, с, d подставим в четвертое равенство системы (4) bс + ad = 1, чтобы выбрать те числа, которые являются решениями системы (4). Удобно эти рассуждения оформить в виде таблицы:

Как видим, системе (4) удовлетворяет набор целых чисел а = –1, b = 2, с = 2, d = 3. Тогда равенство (3) имеет вид
|
x4 + х3 + 3х2 + х + 6 = (х2 – х + 2)(х2 + 2х + 3). |
(5) |
Поскольку квадратные трехчлены х2 – х + 2 и х2 + 2х + 3 не имеют не только рациональных, но и действительных корней, то равенство (5) дает окончательный ответ.
Упражнения
- Найдите целые корни многочлена:
1) х3 – 5х + 4;
2) 2x3 + x2 – 13x + 6;
3) 5х3 + 18х2 – 10х – 8;
4) 4х4 – 11х2 + 9х – 2.
- Найдите рациональные корни уравнения:
1) х3 – 3х2 + 2 = 0;
2) 2х3 – 5х2 – х + 1 = 0;
3) 3х4 + 5х3 – х2 – 5х – 2 = 0;
4) 3х4 – 8х3 – 2х2 + 7х – 2 = 0.
- Разложите многочлен на множители:
1) 2х3 – х2 – 5х – 2;
2) х3 + 9х2 + 23х +15;
3) х4 – 2х3 + 2х – 1;
4) х4 – 2х3 – 24х2 + 50х – 25.
- Найдите действительные корни уравнения:
1) х3 + х2 – 4х + 2 = 0;
2) х3 – 7х – 6 = 0;
3) 2х4 – 5х3 + 5х2 – 2 = 0;
4) 2х3 – 5х2 + 1 = 0.
5*. Разложите многочлен на множители методом неопределенных коэффициентов:
1) х4 + х3 – 5х2 + 13х – 6;
2) х4 – 4х3 – 20х2 + 13х – 2.
6*. Разложите многочлен на множители, заранее записав его с помощью метода неопределенных коэффициентов в виде (х2 + bх + с)2 – (mх + n)2: :
1) х4+ 4х – 1;
2) х4 – 4х3 – 1;
3) х4 + 4а3х – а4.
