У меня есть отрезок с известными координатами концов. На этом отрезке есть точка. Я знаю расстояние от начала отрезка до этой точки. Мне надо найти координаты этой точки. Как найти эти координаты?
Пример: Есть 2 точки А(3,3) и В(6,4). Длина отрезка примерно 3,16. И есть точка С(?,?) на отрезке. Как найти координаты, если от А до С =1,8 ???
![]()
Dmytro
6,7011 золотой знак20 серебряных знаков55 бронзовых знаков
задан 3 мар 2016 в 20:40
4
Имеется отрезок AB с координатами A(Xa, Ya) и B(Xb, Yb).
Требуется найти координаты точки C(Xc, Yc), лежащей на отрезке AB на расстоянии Rac от точки A.
Rab = sqrt((Xb - Xa) ^ 2 + (Yb - Ya) ^ 2)
k = Rac / Rab
Xc = Xa + (Xb - Xa) * k
Yc = Ya + (Yb - Ya) * k
Обозначения:
f ^ n – возведение f в степень n, в нашем случае (первом) f будет Xb - Xa и n будет 2.
sqrt(f) – квадратный корень из f, в нашем случае f будет (Xb - Xa) ^ 2 + (Yb - Ya) ^ 2.
f / n – деление f на n, в нашем случае f будет Rac и n будет Rab.
f * n – умножение f на n, в нашем случае (первом) f будет Xb - Xa и n будет k.
ответ дан 4 мар 2016 в 6:54
![]()
Konstantin LesKonstantin Les
1,5388 серебряных знаков12 бронзовых знаков
2
Алгоритм без кода (довольно элементарный):
Имеем:
Две точки A, B; len – расстояние от точки А до требуемой точки C
full_len = |B - A| // длина вектора, соединяющего две точки == длина отрезка
C = A + (B - A) * (len / full_len)
Сложение векторов и умножение на число – очевидные операции.
ответ дан 3 мар 2016 в 20:56
int3int3
2,4579 серебряных знаков19 бронзовых знаков
8
nodet – точка конец вектора, в твоем случае точка b
nodef – точка начало вектора, в твоем случае точка a
dx = nodet.x - nodef.x
dy = nodet.y - nodef.y
dz = nodet.z - nodef.z
r = math.sqrt(dx ** 2 + dy ** 2 + dz ** 2)
xx = dx * (step/r)
yy = dy * (step /r)
zz = dz * (step /r)
newnode = node(nodef.x + xx,nodef.y + yy,nodef.z + zz)
newnode – новая точка на заданом расстоянии
ответ дан 12 ноя 2019 в 16:31
qvuer7qvuer7
113 бронзовых знака
Найти координаты точки на отрезке
Dmitry
Ученик
(135),
закрыт
9 лет назад
Leonid
Высший разум
(388685)
11 лет назад
Если некоторя точка делит отрезок в отношении А: В, то и отдельно коордиаты отрезка (х, у) делятся в этом же отношении. А координата отрезка – это разность координат его концов.
То есть, к примеру, конкретно для этого случая: х1 = 100, х2 = 0. То есть тупо отсчитывает от точки х1 расстояние, равное (100-0)*(23*141) = чему-то там. И вычитаем из х1. Аналогично для у.
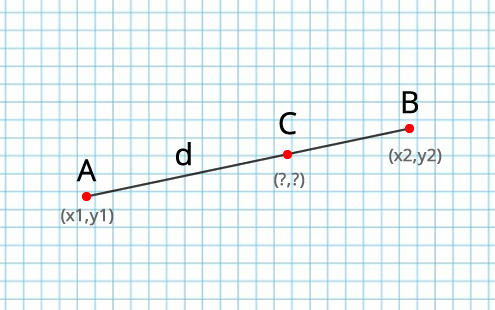
Имеем отрезок AB с координатам x1,y1 и x2, y2:
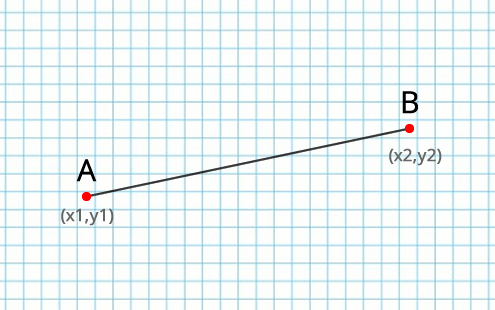
Необходимо найти координаты новой точки С, которая находится на отрезке, на определенном расстоянии от точки A.
1
PHP-функция
$x1, $y1 – координаты точки A,
$x2, $y2 – координаты точки B,
$d – расстояние от точки A до точки C.
function pointToLine($x1, $y1, $x2, $y2, $d)
{
$Rab = sqrt(pow($x2 - $x1, 2) + pow($y2 - $y1, 2));
$k = $d / $Rab;
$Xc = $x1 + ($x2 - $x1) * $k;
$Yc = $y1 + ($y2 - $y1) * $k;
return array('x' => $Xc, 'y' => $Yc);
}PHP
2
JS-функция
function pointToLine(x1, y1, x2, y2, d)
{
var Rab = Math.sqrt(Math.pow(x2 - x1, 2) + Math.pow(y2 - y1, 2));
var k = d / Rab;
var Xc = x1 + (x2 - x1) * k;
var Yc = y1 + (y2 - y1) * k;
return {x: Xc, y: Yc};
}JS
3
Координата точки на отрезке онлайн
|
0 / 0 / 0 Регистрация: 22.12.2014 Сообщений: 21 |
|
|
1 |
|
Определить координаты точки на отрезке15.01.2015, 23:06. Показов 2224. Ответов 4
Определить координаты точки C на отрезке AB, если A (0; 1; 2), B(4; 5; – 6) и |AC|:|BC|=1: 3
0 |
|
Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782 |
15.01.2015, 23:06 |
|
Ответы с готовыми решениями: Наути координаты точки на отрезке
Имеется 2… Найти координаты точки на отрезке Даны две…
4 |
|
Диссидент
27462 / 17151 / 3780 Регистрация: 24.12.2010 Сообщений: 38,627 |
|
|
16.01.2015, 00:08 |
2 |
|
С = (1*A + 3*B)/4 Все буквы – векторы
1 |
|
0 / 0 / 0 Регистрация: 22.12.2014 Сообщений: 21 |
|
|
16.01.2015, 00:23 [ТС] |
3 |
|
С = (1*A + 3*B)/4 Все буквы – векторы Формулу вижу, даже записал ее, а что именно подставлять в формуле под векторами А и В? Если Вам не сложно, напишите решение до конца, пожалуйста
0 |
|
6352 / 4061 / 1509 Регистрация: 09.10.2009 Сообщений: 7,550 Записей в блоге: 4 |
|
|
16.01.2015, 03:00 |
4 |
|
Решение
С = (1*A + 3*B)/4 Все буквы – векторы Как говорится, при всём уважении…, но при координатах точки нужно ставить противоположный коэффициент, а не прилежащий.
2 |
|
0 / 0 / 0 Регистрация: 22.12.2014 Сообщений: 21 |
|
|
16.01.2015, 03:41 [ТС] |
5 |
|
bizabrazen, можно это же записать полностью векторами: Премного благодарен!!!
0 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
16.01.2015, 03:41 |
|
Помогаю со студенческими работами здесь
Известны координаты точек А и В, а… Определить координаты точки, симметричной точке M относительно прямой Определить координаты третьей точки, лежащей на этой прямой Вычислить координаты точки, лежащей на отрезке
Искать еще темы с ответами Или воспользуйтесь поиском по форуму: 5 |
Даны точки
![]() Требуется найти координаты точкиK(x,y),
Требуется найти координаты точкиK(x,y),
 делящей
делящей
отрезокMN
в отношении
![]() Рассмотрим векторы
Рассмотрим векторы![]() Эти векторы коллинеарны
Эти векторы коллинеарны![]() Из векторной алгебры известно, что если
Из векторной алгебры известно, что если
векторы коллинеарны, то соответствующие
координаты пропорциональны. Имеем:
![]()
![]() (по условию).
(по условию).
Из этих уравнений
легко найти x
и y
![]()
![]() (2.1.1)
(2.1.1)
Если
![]() то точкаK
то точкаK
является серединой отрезка MN.
Формулы (2.1) примут вид:
![]() (2.1.2)
(2.1.2)
Это формулы
координат середины отрезка.
Пример 1.
Найти
координаты
точки K,
делящей отрезок MN,
где M(-1,4)
и N(2,1),
в отношении 2 : 1.
Решение.
По условию
![]() Подставим координаты точкиM
Подставим координаты точкиM
и N
в формулы (2.1.1). Имеем:
![]()
Точка K
имеет координаты: x=1,
y=2.
Ответ: K(1,2).
Пример 2.
Отрезок АВ разделен на три равные части.
Определить координаты точек деления,
если А(3,-2), В(6,4).
Решение.
Обозначим точки деления С и D.
Точка D
делит отрезок АВ в отно-
шении АD:DB
= 2. Координаты точки D
найдем по формулам (2.1.1).
![]()
Итак, D(5,2).
Координаты точки
С можно найти аналогично, взяв
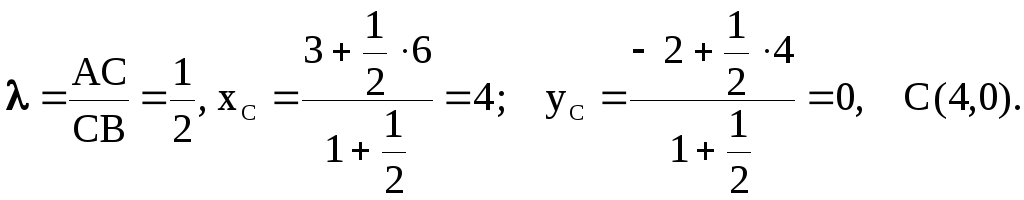
Существует другой
способ нахождения координат точки С.
Точка С является серединой отрезка АD.
По формулам (2.1.2) имеем
![]()
Ответ:
D(5,2)
; C(4,0).
Пример 3.
Найти точку пересечения медиан
треугольника АВС, где А(-1,3) ;
B(3,-2);
C(5,3).
Р ешение:
ешение:
Пусть точка О – точка пересечения медиан
AM
и BN
треугольника ABC.
Точка М является серединой отрезка ВС.
По формулам (2.1.2) получим координаты
точки М:
![]()
![]() Из школьного курса
Из школьного курса
планиметрии известно, что точка О делит
медиану АМ в отношении АО:ОМ = 2:1.
![]() По формулам (2.1.1) получим
По формулам (2.1.1) получим
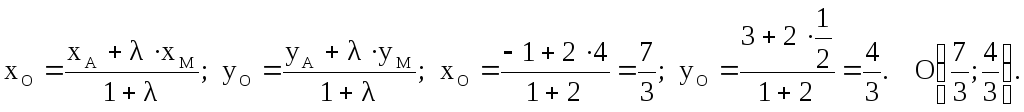
Ответ:
Точка пересечения медиан ![]()
Замечание: Точка
пересечения медиан треугольника является
его центром тяжести.
3. Прямая на плоскости.
3.1. Простейшей из
линий является прямая. Всякую прямую,
не параллельную оси ординат, можно
представить уравнением вида
![]() ,
,
(3.1.1)
где к есть тангенс
угла
![]() образованного прямой с положительным
образованного прямой с положительным
направлением оси абсцисс (ox).

![]()
Величину к называют
угловым
коэффициентом.
Величину b
– начальной
ординатой.
Если прямая
параллельна оси ox,
то
![]() Уравнение прямой примет вид:y
Уравнение прямой примет вид:y
= b
(3.1.2)

Если прямая
параллельна оси oy,
то
![]() не существует. В этом случае уравнение
не существует. В этом случае уравнение
прямой будет иметь вид:x
= a
(3.1.3),
где а – абсцисса точки, через которую
проходит данная прямая ( точки пересечения
прямой с осью ox).

Пример 1.
Какую прямую представляет уравнение
![]()
Р ешение. Данное
ешение. Данное
уравнение задает прямую, у которой
![]() Так как
Так как![]() Поэтому данное уравнение представляет
Поэтому данное уравнение представляет
прямую, проходящую через начало координат
(b
= 0) и образующую с осью ox
угол
![]()
Пример 2.
Написать
уравнение прямой, параллельной оси ox
и имеющей на-
 чальную
чальную
ординату b
=
![]() .
.
Решение: По
формуле (3.1.2) имеем y
=![]() где
где![]()
Итак, искомая
прямая задается уравнением
![]()
Ответ:
![]()
Пример 3.
Написать уравнение прямой, параллельной
оси oy
и проходящей
через точку
M(3,1).
 Решение:
Решение:
По формуле (3.1.3) уравнение прямой имеет
вид x
= a
, где а – абсцисса точки М. а = 3. Уравнение
прямой x
= 3.
Ответ:
x
= 3.
3.2. Уравнение
прямой по точке и угловому коэффициенту.
Пусть прямая
проходит через точку
![]() и имеет угловой коэффициент к. Уравнение
и имеет угловой коэффициент к. Уравнение
такой прямой можно записать в виде
(3.1.1)![]() гдеb
гдеb
– неизв естная
естная
величина. Так как прямая проходит через
точку![]() ,
,
то координаты точки удовлетворяют
уравнению (3.1.1). Имеем![]() Отсюда
Отсюда![]()
Подставим значение
“b”
в уравнение (3.1.1), получим
![]() –
–![]() или
или
![]() (3.2.1)
(3.2.1)
Полученное уравнение
называется уравнением прямой по точке
и угловому коэффициенту.
Пример 1.
Составить уравнение прямой, проходящей
через точку
![]()
и образующей с
положительным направлением оси ox
угол
![]()
Решение:
Так как
![]() то
то![]() Применив формулу (3.2.1), получимy-(-2)=-1(x-1)
Применив формулу (3.2.1), получимy-(-2)=-1(x-1)
![]() y+2
y+2
= -x+1
![]() y=-x-1.
y=-x-1.
Ответ:
y=-x-1.![]()
Пример 2.
Составить
уравнение прямой, проходящей через
точку А(-3,4) и имеющей угловой коэффициент
к = 2.
Решение:
Применяем
формулу (3.2.1) y
– 4 = 2 (x+3)
![]() y
y
– 4 = 2x
+ 6
![]()
y
= 2x
+
10.
Ответ:
y
= 2x
+ 10.
Пример 3.
Составить
уравнение прямой, проходящей через
точку М(-1, 2) параллельно оси ox.
Решение:
Если прямая параллельна оси ox,
то угол между прямой и положительным
направлением оси ox
равен нулю. Следовательно,
![]() По формуле (3.2.1) получимy
По формуле (3.2.1) получимy
– 2 = 0 (x
+ 1)
![]()
y
– 2 = 0
![]()
Ответ:
y
= 2.
3 .3.Уравнение
.3.Уравнение
прямой по точке и нормальному вектору.
Пусть прямая
проходит через точку
![]() Поднормальным
Поднормальным
вектором
понимают вектор, который перпендикулярен
данной прямой. Обозначим его
![]() Возьмем на прямой произвольную точкуM(x,y)
Возьмем на прямой произвольную точкуM(x,y)
и рассмотрим вектор
![]() Используя векторную алгебру, найдем
Используя векторную алгебру, найдем
координаты вектора![]() Вектор
Вектор![]() перпендикулярен вектору
перпендикулярен вектору![]() .Из векторной
.Из векторной
алгебры известно, что скалярное
произведение этих векторов равно нулю.
Следовательно,
![]() (3.3.1)
(3.3.1)
Полученное уравнение
называется уравнением
прямой по точке и нормальному вектору.
Преобразуем полученное уравнение:
Ax + By –
A![]() – B
– B![]() =
=
0.Пусть
C = -A![]() -B
-B![]() ,тогда
,тогда
получим:
Ax
+ By + C = 0 (3.3.2)
Уравнение (3.3.2)
называется общим
уравнением прямой.
Напомним, что коэффициенты А и В в
уравнении определяют координаты
нормального вектора
![]()
Рассмотрим общее
уравнение прямой подробнее.
1). Если А = 0, то
![]() уравнение примет вид
уравнение примет вид
By
+ C
= 0 ; y
= –![]() Прямая параллельна осиox.
Прямая параллельна осиox.
(3.1.2)
2). Если В = 0, то
![]() уравнение примет вид:
уравнение примет вид:
Ax
+ C
= 0, x
= –![]()
Прямая параллельна оси oy.
(3.1.3.)
3). Если С = 0, то
уравнение примет вид: Ax
+ By
= 0. y
= –
![]()
Прямая проходит через начало координат
и имеет угловой коэффициент k
= –
![]() См. пример 1 пункт 3.1.
См. пример 1 пункт 3.1.
Из общего
уравнения прямой, если
![]() можно найти угловой коэффициент к. Для
можно найти угловой коэффициент к. Для
этого выразимy
из этого уравнения : Ax
+ By
+ C
= 0.
By = – Ax –
C ; y = –![]() –
–![]() Отсюда,
Отсюда,
k
= –
![]() (3.3.3)
(3.3.3)
Пример 1.
Прямая задана уравнением 3x
– 4y
+5 = 0. Найти координаты нормального
вектора.
Решение:
Координатами
нормального вектора
![]() являются коэффициенты приx
являются коэффициенты приx
и y
данного уравнения прямой. Имеем А = 3;
В = – 4.
Ответ:
![]()
Пример 2.
Составить уравнение прямой, проходящей
через точку М(2,-1) и имеющей нормальный
вектор
![]()
Решение:
Применяем
формулу (3.3.1). Имеем 0(x
– 2) + 2(y
+ 1) = 0
![]()
2y
+ 2 = 0
![]()
y
+ 1 = 0.
Ответ:
y
+ 1 = 0.
Пример 3.
Составить уравнение прямой, проходящей
через точку М(0; 1) перпендикулярно вектору
![]() где А(-1; 2), В(1; -1).
где А(-1; 2), В(1; -1).
Решение:
Найдем координаты вектора
![]()
![]() –
–
(-1); -1-2);
![]() (2;
(2;
-3).
Вектор ![]() является нормальным
является нормальным
векторомискомой
прямой. По формуле (3.3.1) имеем 2(x
– 0) -3(y
-1) = 0
![]()
2x
– 3y
+ 3 = 0.
Ответ:
2x
– 3y
+ 3 = 0.
3.4. Уравнение
прямой по точке и направляющему вектору.
Пусть прямая
проходит через точку
![]() Направляющим вектором
Направляющим вектором![]() данной прямой называется вектор,
данной прямой называется вектор,
параллельный этой прямой. Пусть дан
вектор![]() Возьмем на прямой произвольную точкуM(x,y)
Возьмем на прямой произвольную точкуM(x,y)
и рассмотрим вектор
![]()
![]() Векторы
Векторы
![]() и
и![]() коллинеарны,следовательно, их
коллинеарны,следовательно, их
соответствующие координаты пропорциональны.
![]() (3.4.1)
(3.4.1)
Полученное уравнение
является уравнением прямой по
точке и направляющему вектору.
Пример 1.
Прямая задана
уравнением:
![]() Написать координаты
Написать координаты
направляющего вектора; найти координаты
точки, лежащей на прямой; составить
общее уравнение прямой.
Решение:
Направляющий
вектор
![]() = (−1; 2). Точку
= (−1; 2). Точку![]() мы получим, приравняв нулю числители
мы получим, приравняв нулю числители
данного уравнения:x
+ 2 = 0
![]()
x
=−2; y
– 3 = 0
![]()
![]()
y
= 3.
Итак,
![]() (−2; 3).
(−2; 3).
Общее уравнение
прямой получим по свойству пропорций:
(x+2)∙2
= (y−3)∙(−
1)
![]()
2x
+ 4 = −y
+ 3
![]()
2x
+ y
+ 1 = 0.
Ответ:
![]() (−1;
(−1;
2),
![]() (−2;
(−2;
3), 2x
+ y
+ 1 = 0.
Пример 2.
Составить
уравнение прямой по точке М(2,-5) и
направляющему вектору
![]() (-2,4).
(-2,4).
Решение:
Применяем
формулу
(3.4.1). Имеем:
![]()
4(x-2)
= -2(y+5)
4x
– 8 = – 2y
– 10
![]()
4x
+ 2y
+ 2 = 0
![]()
2x
+ y
+ 1 =0.
Ответ: 2x
+ y
+ 1 = 0.
Пример 3.
Через точку
С(- 2, 1) провести прямую, параллельную
вектору
![]() где А(2,-1), В(3,4).
где А(2,-1), В(3,4).
Решение:
Вектор ![]() можно взять за
можно взять за
направляющий вектор данной прямой. ![]() (3-2; 4-(-1)) = (1;
(3-2; 4-(-1)) = (1;
5). Применяем
формулу (3.4.1). Имеем:
![]()
5(x
+ 2) = y
– 1
![]()
5x
+ 10 = y
– 1
![]()
5x
– y
+ 11 = 0.
Ответ:
5x
– y
+11 = 0.
3.5. Уравнение
прямой, проходящей через две заданные
точки.
Известно, что
через две данные точки можно провести
единственную прямую. П усть
усть
прямая проходит через точки![]() За направляющий вектор
За направляющий вектор![]() данной прямой можно взять вектор
данной прямой можно взять вектор![]() .
.
![]()
Составим уравнение
прямой по точке ![]() и направляющему
и направляющему
вектору
![]()
По формуле (3.4.1)
имеем:
![]() (3.5.1)
(3.5.1)
Если
![]() то прямая параллельна осиoy.
то прямая параллельна осиoy.
Ее уравнение имеет вид:
![]() (3.5.2)
(3.5.2)
Если
![]() то прямая параллельна осиox.
то прямая параллельна осиox.
Ее уравнение :
y
=
![]()
(3.5.3)
Пример 1.
Составить уравнение прямой АВ, если
А(2,-1); В(1,3).
Решение:
Применяем
формулу (3.5.1):
![]() 4(x
4(x
– 2) = -(y
+ 1)
![]() 4x
4x
+ y
– 7 = 0.
Ответ:
4x
+ y
– 7 = 0.
Пример 2.
Составить уравнение прямой, проходящей
через точки М(4,-2) и N(4,5).
Решение:
Так как
![]()
то по формуле (3.5.2) уравнение прямой
имеет вид:
x = 4.
Прямая
параллельна оси oy.
Пример 3. Дан
треугольник АВС, у которого А(1,2), В(4,3),
С(1,3). Составить уравнения его сторон.
Решение: 1)
Найдем уравнение стороны АВ. ПО формуле
(3.5.1) имеем:
![]() x
x
– 1 = 3(y
– 2)
![]() x
x
– 3y
+ 5 = 0.
2) Сторона ВС
находится по формуле (3.5.3), так как
![]() y
y
= 3.
3) Уравнение стороны
АС выпишем по формуле (3.5.2), так как
![]() x
x
= 1.
Ответ:
AB:
x
– 3y
+ 5 = 0; BC:
y
= 3; AC:
x
= 1.
Пример 4.
Даны вершины треугольника АВС А(- 1, 3),
В(3,-2), С(5,3). Составить уравнение медианы,
проведенной из вершины В.
 Решение: Пусть
Решение: Пусть
ВМ – медиана, тогда точка М является
серединой отрезка АС. По формулам (2.1.2)
имеем:
![]()
![]() M(2,3).
M(2,3).
Уравнение медианы
ВМ получим по формуле (3.5.1):
![]()
![]() 5(x-
5(x-
3) = -(y
+2)
![]()
5x
+ y
– 13 = 0.
Ответ:
BM:
5x
+ y
– 13 = 0.
3.6. Уравнение
прямой в отрезках.
Если прямая отсекает
на осях отрезки а и b,
не равные нулю, то ее уравнение можно
записать в виде:
![]() .
.
(3.6.1)
Такое уравнение
называется уравнением
в отрезках.
Рассмотрим это уравнение. Пусть x
= 0, тогда
![]()
Пусть y
= 0, тогда
![]()
Прямая проходит
через точки А(а,0) и B(0,b).
 Пример.
Пример.
Записать
уравнение прямой в отрезках. Построить
эту прямую.
3x
– 2y + 12 = 0.
Решение:
3x
– 2y
= – 12. Разделим обе части этого уравнения
на – 12. П олучим:
олучим:
![]() a = – 4, b = 6.
a = – 4, b = 6.
Построим полученную
прямую. Для этого отложим на оси ox
a
= – 4, на оси oy
b
= 6 и соединим полученные точки.
3.7. Расстояние
от точки до прямой.
Пусть прямая
задана уравнением Ax
+ By
+ C
= 0. Найдем расстояние от точки
![]() до этой прямой. Подрасстоянием
до этой прямой. Подрасстоянием
от точки до прямой понимают длину о трезка
трезка![]() где М – основание перпендикуляра,
где М – основание перпендикуляра,
опущенного из точки![]() на данную прямую. Расстояние
на данную прямую. Расстояние![]()
![]() находим по формуле:
находим по формуле:
![]() (3.7.1)
(3.7.1)
Пример. Найти
расстояние от точки
![]() до прямой 3x
до прямой 3x
+ 4y
– 22 =0.
Решение: По
формуле (3.7.1) получим:
![]()
Ответ:
d
= 4.
Соседние файлы в предмете Математика
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
03.03.20154.96 Кб8Содержание OneNote.onetoc2
- #

 Найти координаты точки на отрезке
Найти координаты точки на отрезке
