Задание 5. Определить
диаметр свободной осесимметричной
изотермической струи, скорость движения
воздуха, расход воздуха в струе, построить
профиль скорости на расстояние Х1
и Х2
, м,
от начального сечения цилиндрического
насадка
с поджатием
(без поджатия – последняя цифра шифра
– нечетная). Выходное отверстие
цилиндрического насадка имеет диаметр
d0,
мм; скорость выхода воздуха из насадка
– v0,
м/с. Исходные данные принять по приложению
3.
Свободные
струи образуются при истечении в
пространство, заполненное той же средой,
находящейся в относительно спокойном
состоянии.
Свободная
изотермическая струя.
Струя по выходе из отверстия расширяется,
ширина её растёт пропорционально
увеличению расстояния от места истечения.
Измерениями давлений установлено, что
статическое давление в струе остаётся
постоянным и равным статическому
давлению в окружающейсреде.
Потери энергии вследствие торможения,
оказываемого окружающим воздухом,
компенсируются за счёт кинетической
энергии, поэтому скорость в струе
затухает.
Структура
и свойства
струи.
Осевая
скорость на протяжении длины начального
участка l0
одинакова
и равна скорости выходного сечения v0
(рис.3).
Благодаря
турбулентному перемешиванию с окружающим
воздухом масса приточной струи по мере
удаления от приточного отверстия
возрастает, а скорость в ней уменьшается.
Боковые границы струи соответствуют
приблизительно лучам, исходящим из
точки, называемой полюсом струи (точка
О).
На структуру струи
оказывает влияние начальная турбулентность:
чем она выше, тем интенсивнее протекает
перемешивание его с воздухом атмосферы,
тем больше угол расширения струи, тем
короче длина начального участка и тем
быстрее уменьшение осевой скорости в
основном участке.
Экспериментально
показано, что эпюры скоростей в различных
поперечных сечениях струи подобны и
при построении их в безразмерных
координатах y/(![]() x)
x)
и
![]() совпадают
совпадают
друг с другом. Это совпадение наблюдается
и у различных струй, если в безразмерные
координаты вводить коэффициент
![]() ,
,
характеризующий начальную турбулентность.
Значения
коэффициента
![]() ,
,
получены опытным путём и приведены в
таблице 7.
Таблица 7 –
Коэффициент
![]() ,
,
характеризующий начальную турбулентность
|
Конструкция насадков |
|
|
Цилиндрический |
0,07 |
|
То же, без поджатия |
0,08 |
|
Щелевидный насадок |
0,09 |
|
То же, без поджатия |
0,12 |
|
Квадратный насадок |
0,09-0,1 |
|
Прямоугольный насадок |
0,17-0,2 |
Формулы Г.Н.
Абрамовича, полученные на основании
экспериментальных данных и определяющие
основные параметры свободных струй,
приведены в таблице 8.
Таблица 8 -Формулы для
свободной осесимметричной струи
|
№ |
Наименование |
Обзначение |
Начальный участок струи |
Основной участок струи |
|
1 |
Расстояние |
h0/d0 |
0,145/а |
– |
|
2 |
Длина |
|
0,335d0/а |
– |
|
3 |
Осевая скорость |
|
1 |
0,48/(ax/d0+0,145) |
|
4 |
Расход |
Lx/L0 |
1+1,52ax/d0+5,28(ax/d0)2 |
4,36/(ax/d0+0,145) |
|
5 |
Средние скорости по площади |
|
|
0,0945/(ax/d0+0,14) |
|
6 |
Средние скорости по расходу |
|
|
0,226/(ax/d0+0,145) |
|
7 |
Диаметр струи |
dx/d0 |
6,8ax/d+1 |
6,8(ax/d0+0,145) |
|
8 |
Перепад температур на оси струи |
|
– |
0,35/(ax/d0+0,145) |
|
9 |
Средняя температура (или концентрация) |
|
|
0,226/(ax/d0+0,145) |
|
10 |
Эпюра скоростей |
|
h0
– полюсное
расстояние, м;
x
– расстояние от выходного сечения
насадка до расчётного сечения струи, м
dx
–
диаметр струи в сечении Х,
м.

Рис.3.
Структурная схема истечения свободной
осесимметричной
изотермической
струи
Пример 5. Выходное
отверстие имеет диаметр 300 мм, скорость
выхода воздуха υнач
= 10 м/с.
Определить скорость движения воздуха,
диаметр струи, расход воздуха в струе,
построить профили скоростей для
сечений на расстоянии Х1
= 2 м и Х2
= 10 м от начального сечения цилиндрического
насадка с поджатием.
Решение:
1. При решении
задачи применяем формулы для свободной
осесимметрической струи. Выясняем на
каком участке находится заданное
сечение струи на начальном или на
основном.
Определяем длину
начального участка струи
![]()
![]() м.
м.
Так как 2 > 1,44, то
заданное сечение находится на основном
участке, формулами для которого и
воспользуемся.
Осевая скорость
на расстоянии Х = 2 м
![]()
 м/с.
м/с.
Средняя по расходу
скорость на расстоянии Х = 2 м
![]() м/с.
м/с.
Средняя скорость
по площади заданного сечения струи при
Х = 2 м
 м/с.
м/с.
Теоретический
диаметр струи на расстоянии Х = 2 м
dx=d0∙6,8 (![]() + 0,145) = 0,3∙6,8(
+ 0,145) = 0,3∙6,8(![]() + 0,145) = 1,24 м.
+ 0,145) = 1,24 м.
Начальный расход
воздуха на выходе из цилиндрического
насадка
L0=
![]() м3/ч.
м3/ч.
Расход
воздуха в струе на расстоянии Х = 2 м
Lх=L0
∙4,36 (![]() + 0,145) = 2 543,4∙4,36 (
+ 0,145) = 2 543,4∙4,36 (![]() + 0,145) = 5383м3/ч.
+ 0,145) = 5383м3/ч.
Для
построения эпюры скоростей в сечении
на расстоянии Х = 2 м используем формулу
Г. Шлихтинга
![]() ,(12)
,(12)
где
![]()
– скорость в точке струи с координатами
Х = 2 м и y;
![]() – ордината
– ордината
границы струи м.
Ордината
границы струи
при dх
= 1,24 м составляет
угр=
![]() .
.
Определяем
значения скорости в сечении струи для
различных задаваемых ординат в пределах
от y
= 0 до угр
= 0,62 м.
при у
= 0
![]() м/с,
м/с,
при у
= 0,1 м
![]() м/с.
м/с.
Результаты
дальнейших расчетов сведены в таблицу
9.
Таблица
9 – Расчет скоростей движения воздуха
в струе
|
Расстояние Х, |
Ордината |
|||||||
|
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,62 |
|
|
2 |
7,87 |
7,01 |
5,2 |
3,4 |
1,8 |
0,62 |
0,18 |
0 |
Аналогично следует
определить параметры для сечения на
расстоянии 10 м. По результатам расчёта
построить структурную схему струи
и эпюры скоростей ( рис. 3) для сечений
Х = 2 м и Х = 10 м, сделать выводы.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
|
Как определить диаметр отверстия на дне сосуда, зная начальный объем воды и время за которое этот объем воды полностью вытекает из сосуда. Сосуд цилиндрический, поверхность воды свободная.
Если считать скорость истечения неизменной, то диаметр отверстия на дне сосуда можно определить следующим образом. Пусть вся вода объемом V вытекает за время t, тогда скорость истечения V/t в литрах на секунду. С другой стороны за секунду через отверстие протекает такой же объем или V/t = S*l,l = g/2, путь который проходит струя воды за секунду. Оттуда площадь отверстия S = 2*V/ (l*g*t), или диаметр d = под кв корнем 4*S/pi Знаете ответ? |
Главная страница
Содержание
Введение
Основы гидростатики
Основы гидродинамики
Гидравлические сопротивления
Истечние жидкости из отверстий, насадков и из-под затворов
Гидравлический расчет простых трубопроводов
Гидравлические машины
Лекция 5. ИСТЕЧЕНИЕ ЖИДКОСТИ ИЗ ОТВЕРСТИЙ, НАСАДКОВ И ИЗ-ПОД ЗАТВОРОВ
Рассмотрим различные случаи истечения жидкости из резервуаров, баков, котлов через отверстия и насадки
(коротки трубки различной формы) в атмосферу или пространство, заполненное газом или той же жидкость. В
процессе такого истечения запас потенциальной энергии, которым обладает жидкость, находящаяся в резервуаре,
превращается в кинетическую энергию свободной струи.
Основным вопросом, который интересует в данном случае, является определение скорости истечения и
расхода жидкости для различных форм отверстий и насадков.
Рассмотрим большой резервуар с жидкостью под давлением Р0, имеющий малое круглое
отверстие в стенке на достаточно большой глубине Н0 от свободной поверхности (рис.5.1).
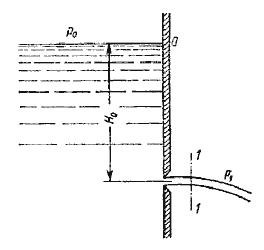
Рис. 5.1. Истечение из резервуара через малое отверстие
Жидкость вытекает в воздушное пространство с давлением Р1. Пусть отверстие имеет форму,
показанную на рис.5.2, а, т.е. выполнено в виде сверления в тонкой стенке без обработки входной кромки или
имеет форму, показанную на рис.5.2, б, т.е. выполнено в толстой стенке, но с заострением входной кромки с
внешней стороны. Струя, отрываясь от кромки отверстия, несколько сжимается (рис.5.2, а). Такое сжатие
обусловлено движением жидкости от различных направлений, в том числе и от радиального движения по стенке,
к осевому движению в струе.
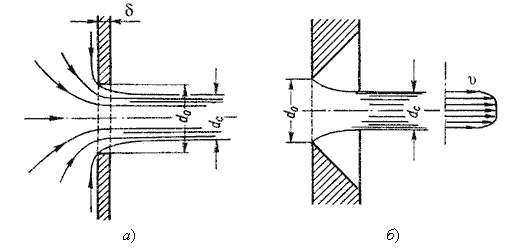
Рис. 5.2. Истечение через круглое отверстие
Степень сжатия оценивается коэффициентом сжатия.
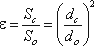
где Sс и Sо – площади поперечного сечения струи и отверстия
соответственно; dс и dо – диаметры струи и отверстия соответственно.
Скорость истечения жидкости через отверстие такое отверстие
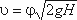
где Н – напор жидкости, определяется как
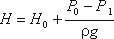
φ- коэффициент скорости
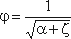
где α – коэффициент Кориолиса;
ζ- коэффициент сопротивления отверстия.
Расход жидкости определяется как произведение действительной скорости истечения на фактическую площадь
сечения:
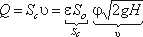
Произведение ε и φ принято обозначать буквой и называть коэффициентом
расхода, т.е. μ = εφ.
В итоге получаем расход
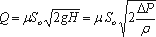
где ΔР – расчетная разность давлений, под действием которой происходит истечение.
При помощи этого выражения решается основная задача – определяется расход.
Значение коэффициента сжатия ε, сопротивления ζ, скорости φ и расхода μ для круглого
отверстия можно определить по эмпирически построенным зависимостям. На рис.5.3 показаны зависимости
коэффициентов ε, ζ и μ от числа Рейнольдса, подсчитанного для идеальной скорости
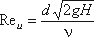
где ν – кинематическая вязкость.
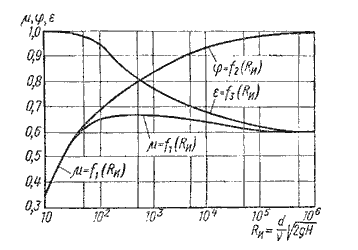
| Рис. 5.3. Зависимость ε, φ и от числа Reu | Рис. 5.4. Инверсия струй |
При истечении струи в атмосферу из малого отверстия в тонкой стенке происходит изменение формы струи по ее
длине, называемое инверсией струи (рис.5.4). Обуславливается это явление в основном действием сил
поверхностного натяжения на вытекающие криволинейные струйки и различными условиями сжатия по периметру
отверстия. Инверсия больше всего проявляется при истечении из некруглых отверстий.
Несовершенное сжатие наблюдается в том случае, когда на истечение жидкости через отверстие и на
формирование струи оказывает влияние близость боковых стенок резервуара (рис.5.5).
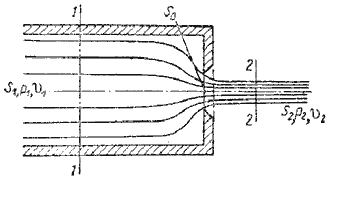
Рис. 5.5. Схема несовершенного сжатия струи
Так как боковые стенки частично направляют движение жидкости при подходе к отверстию, то струя по выходе
из отверстия сжимается в меньшей степени, чем из резервуара неограниченных размеров, как это было описано в
п.5.1.
При истечении жидкостей из цилиндрического резервуара круглого сечения через круглое отверстие,
расположенное в центре торцевой стенки, при больших числах Re коэффициент сжатия для идеальной жидкости можно
найти по формуле, представленной Н.Е. Жуковским:
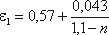
где n – отношение площади отверстия Sо к площади поперечного сечения
резервуара S1
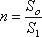
Расход жидкости при несовершенном сжатии
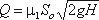
где напор Н нужно находить с учетом скоростного напора в резервуаре
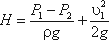
Часто приходится иметь дело с истечением жидкости не в атмосферу, а в пространство, заполненное этой же
жидкостью (рис.5.6). такой случай называется истечением под уровень, или истечением через затопленное
отверстие.
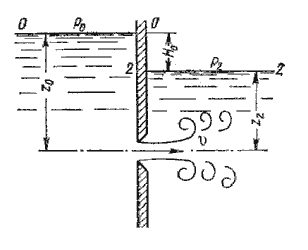
Рис. 5.6. Истечение по уровень
В этом случае вся кинетическая энергия струи теряется на вихреобразование, как при внезапном расширении.
Скорость истечения в сжатом сечении струи
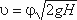
где φ – коэффициент скорости;
Н – расчетный напор,
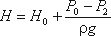
Расход жидкости равен
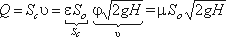
Таким образом, имеем те же расчетные формулы, что и при истечении в воздух (газ), только расчетный напор
Н в данном случае представляет собой разность гидростатических напоров по обе стенки, т.е. скорость
и расход жидкости в данном случае не зависят от высот расположения отверстия.
Коэффициенты сжатия и расхода при истечении под уровень можно принимать те же, что и при истечении в
воздушную среду.
Внешним цилиндрическим насадком называется короткая трубка длиной, равной нескольким диаметрам без
закругления входной кромки (рис. 5.7). На практике такой насадок часто получается в тех случаях, когда
выполняют сверление в толстой стенке и не обрабатывают входную кромку. Истечение через такой насадок в
газовую среду может происходить в двух режимах.
Первый режим – безотрывный режим. При истечении струя, после входа в насадок сжимается примерно
так же, как и при истечении через отверстие в тонкой стенке. Затем струя постепенно расширяется до размеров
отверстия из насадка выходит полным сечением (рис.5.7).
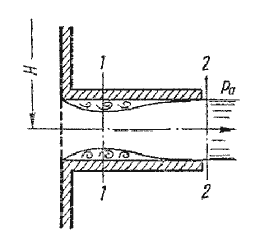
Рис. 5.7. Истечение через насадок
Коэффициент расхода μ, зависящий от относительной длины насадка l / d и числа
Рейнольдса, определяется по эмпирической формуле:
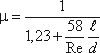
Так как на выходе из насадка диаметр струи равен диаметру отверстия, то коэффициент сжатия
ε = 1 и, следовательно, μ = φ , а коэффициент сопротивления ζ = 0,5.
Если составить уравнение Бернулли для сжатого сечения 1-1 и сечения за насадком 2-2 и
преобразовать его, то можно получить падение давления внутри насадка
P2 – P1  0,75Hgρ
0,75Hgρ
При некотором критическом напоре Нкр абсолютное давление внутри насадка (сечение
1-1) становится равным нулю (P1 = 0), и поэтому
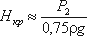
Следовательно, при Н > Нкр давление P1 должно было бы стать
отрицательным, но так как в жидкостях отрицательных давлений не бывает, то первый режим движения становится
невозможным. Поэтому при Н  Нкр происходит изменение режима истечения, переход от первого
Нкр происходит изменение режима истечения, переход от первого
режима ко второму (рис.5.8).
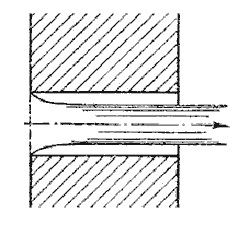
Рис. 5.8. Второй режим истечения через насадок
Второй режим характеризуется тем, что струя после сжатия уже не расширяется, а сохраняет цилиндрическую
форму и перемещается внутри насадка, не соприкасаясь с его стенками. Истечение становится точно таким же,
как и из отверстия в тонкой стенке, с теми же значениями коэффициентов. Следовательно, при переходе от
первого режима ко второму скорость возрастает, а расход уменьшается благодаря сжатию струи.
При истечении через цилиндрический насадок под уровень первый режим истечения не будет отличаться от
описанного выше. Но при Н > Нкр перехода ко второму режиму не происходит, а начинается
кавитационный режим.
Таким образом, внешний цилиндрический насадок имеет существенные недостатки: на первом режиме – большое
сопротивление и недостаточно высокий коэффициент расхода, а на втором – очень низкий коэффициент расхода.
Недостатком также является возможность кавитации при истечении под уровень.
Внешний цилиндрический насадок может быть значительно улучшен путем закругления входной кромки или
устройства конического входа. На рис.5.9 даны различные типы насадков и указаны значения соответствующих
коэффициентов.

Рис. 5.9. Истечение жидкости через насадки а – расширяющиеся конические; б – сужающиеся
конические; в – коноидальные; г – внутренние цилиндрические
Конически сходящиеся и коноидальные насадки применяют там, где необходимо получить хорошую компактную
струю сравнительно большой длины при малых потерях энергии (в напорных брандспойтах, гидромониторах и т.д.).
Конически сходящиеся насадки используют для увеличения расхода истечения при малых выходных скоростях.
Рассмотрим случай опорожнения открытого в атмосферу сосуда при постоянно уменьшающемся напоре, при котором
течение является неустановившемся (рис.5.10).
Однако если напор, а следовательно, и скорость истечения изменяются медленно, то движение в каждый момент
времени можно рассматривать как установившееся, и для решения задачи применить уравнение Бернулли.
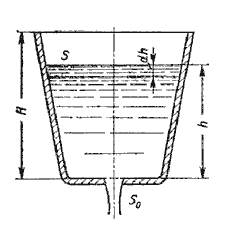
Рис. 5.10. Схема опорожнения резервуара
Обозначим переменную высоту уровня жидкости в сосуде за h, площадь сечения резервуара на этом
уровне S, площадь отверстия Sо, и взяв бесконечно малый отрезок времени dt,
можно записать следующее уравнение объемов:
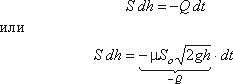
где dh – изменение уровня жидкости за время dt.
Отсюда время полного опорожнения сосуда высотой Н
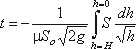
Если будет известен закон изменения площади S по высоте h, то интеграл можно
подсчитать. Для призматического сосуда S = const (рис.5.11), следовательно, время его полного
опорожнения
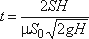
Из этого выражения следует, что время полного опорожнения призматического сосуда в два раза
больше времени истечения того же объема жидкости при постоянном напоре, равном первоначальному.
Для определения времени истечения жидкости из горизонтального цилиндрического сосуда (цистерны) (рис. 5.12)
выразим зависимость переменной площади S от h:
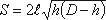
где l – длина цистерны; D – диаметр цистерны.
Тогда время полного опорожнения такой цистерны, т.е. время изменения напора от h1 = D
до h2 = 0, получится равным
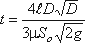
Во многих водозаборных и водопропускных гидротехнических сооружениях расходы воды проходят через отверстия,
перекрываемые затворами. Затворы поднимают на определенную высоту над дном и пропускают через отверстия
необходимые расходы. Чаще всего на гидромелиоративных сооружениях устраивают отверстия прямоугольного сечения,
истечение из которых и рассмотрим.
Отверстия могут быть незатопленными (истечение свободное) и затопленными, когда уровень воды за затвором
влияет на истечение.
Если отверстие незатопленное, то вытекающая из-под затвора струя находится под атмосферным давлением
(рис. 5.13). При истечении через затопленное отверстие струя за затвором находится под некоторым слоем воды
(рис. 5.14).
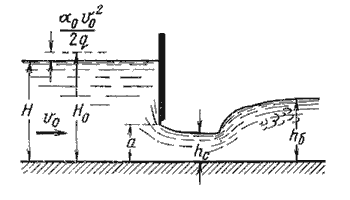
Рис. 5.13. Истечение из-под затвора через незатопленное отверстие
Когда затвор приподнят над дном, вытекающая из-под него струя испытывает сжатие в вертикальной плоскости.
На расстоянии, примерно равном высоте отверстия а (высоте поднятия затвора), наблюдается наиболее
сжатое сечение. Глубина в сжатом сечении hc связана с высотой отверстия а следующей
зависимостью:
hc = ε’a
где ε’ – коэффициент вертикального сжатия струи.
Коэффициент вертикального сжатия ε’ зависит от отношения высоты отверстия а
к напору (глубине воды перед затвором) Н. Для ориентировочных расчетов можно принимать
ε’ = 0,64.
Если составить уравнение Бернулли для сечений, проведенных перед затвором и в сжатом сечении, после
преобразований получим:
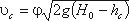
где φ – коэффициент скорости,
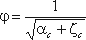
где Н0 – напор с учетом скорости подхода,
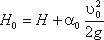
Тогда расход при истечении из-под затвора при незатопленном отверстии определится по формуле:
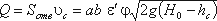
где S – площадь отверстия, S = ab.
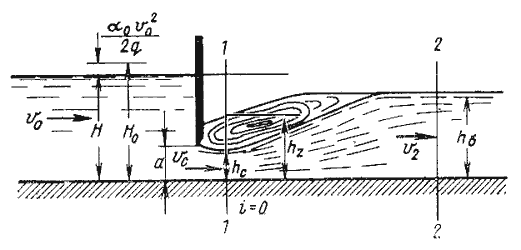
Рис. 5.14. Истечение из-под затвора при затопленном отверстии
При истечении через затопленное отверстие (рис. 5.14) расход определится по формуле:
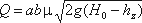
где hz – глубина в том сечении, где наблюдается максимальное сжатие истекающей из-под
затвора струи.
Глубина hz определяется из зависимости
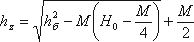
в которой
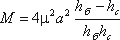
а hб – глубина в отводящем канале (бытовая глубина).
Если вытекающая из отверстия или насадка струя попадает на неподвижную стенку, то она с определенным
давлением воздействует на нее. Основное уравнение, по которому вычисляется давление струи на площадку,
имеет вид
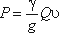
На рис. 5.15 приведены наиболее часто встречающиеся в практике ограждающие поверхности (преграды) и
уравнения, по которым вычисляется давление струи на соответствующую поверхность.
Величина давления струи, естественно, зависит от расстояния насадка до преграды. С увеличением расстояния
струя рассеивается и давление уменьшается. Соответствующие исследования показывают, что в данном случае
струя может быть разбита на три характерные части: компактную, раздробленную и распыленную (рис.5.16).
В пределах компактной части сохраняется цилиндрическая форма струи без нарушения сплошности движения.
В пределах раздробленной части сплошность потока нарушается, причем струя постепенно расширяется. Наконец,
в пределах распыленной части струи происходит окончательный распад потока на отдельные капли.
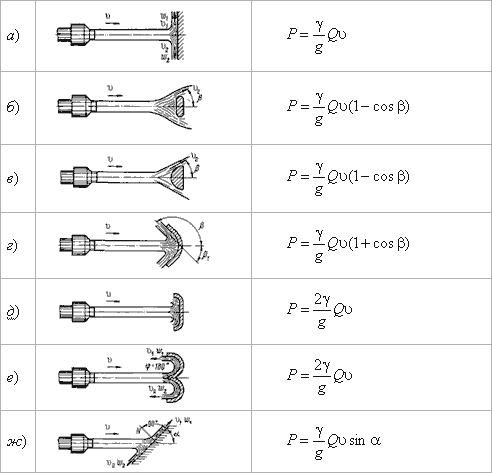
Рис. 5.15. Взаимодействие струи жидкости с неподвижной поверхностью
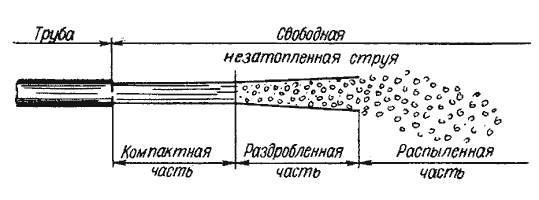
Рис. 5.16. Составные части свободной струи
Проверить себя ( Тест )
Наверх страницы
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,651 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,896 -
разное
16,900
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
12-я лекция, 2010
8. ИСТЕЧЕНИЕ ЖИДКОСТИ
ЧЕРЕЗ ОТВЕРСТИЯ И НАСАДКИ
8.1 Истечение через отверстия в тонкой стенке и насадки (короткие трубки)
при постоянном напоре.
8.2. Истечение при совершенном сжатии.
8.3 Скорость истечения при совершенном сжатии. Коэффициенты:ε, ξ, φ, μ
8.4 Истечение при несовершенном сжатии
8.5. Истечение под уровень
8.6. Истечение через насадки при постоянном напоре.
8.7 Первый режим течения.
8.8 Второй режим истечения
8.1. Истечение через
отверстия и насадки (короткие трубки)
при постоянном напоре.
Рассматривается
процесс истечение жидкости из резервуаров через отверстия и насадки в атмосферу
и в пространство, заполненное жидкостью.
При истечении запас
потенциальной энергии жидкости в
резервуаре, переходит в кинетическую энергию свободной струи, при переходе есть
потери энергии на трение и завихрение
частиц жидкости.
Задачей изучения
процесса истечения является определение скорости истечения и расхода жидкости.
Истечение
производится из резервуара с жидкостью под давлением Р0 на
свободной поверхности через круглое отверстие в тонкой стенке на глубине (во
много раз большей диаметра отверстия) Н0 >> dот (рис. 12.1).
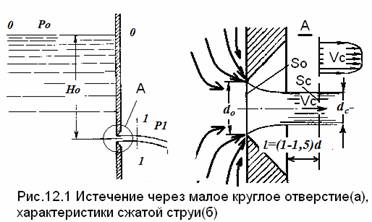
Через отверстие
жидкость вытекает в воздушное пространство с давлением Р1.
Отверстие в стенке
имеет острую кромку. Частицы жидкости приближаются к отверстию из всего
прилежащего объема, двигаясь ускоренно по различным плавным траекториям (см.
рис.12.1б). Струя отрывается от стенки у кромки отверстия и затем сжимается. Формирование
сжатого сечения струи происходит на расстоянии
примерно одного диаметра отверстия.
Сжатие струи происходит
при плавном переходе от различных направлений движения жидкости в резервуаре.
12.2. Истечение при
совершенном сжатии.
Совершенным сжатием называется наибольшее
сжатие струи, когда диаметр отверстия во
много раз меньше напора Н0.
Н0 >> dот
В этом случае боковые
стенки и свободная поверхность жидкости не влияют на поток жидкости к отверстию.
Сжатие струи оценивается
коэффициентом сжатия ε, равным отношению площади
поперечного сечения струи к площади отверстия
ε = Sc/S0 = (dc/d0)2. (12.1)
Для определения
скорости истечения и расхода из отверстия запишем уравнение Бернулли для движения
жидкости от свободной поверхности «0 – 0» в резервуаре и сечением
струи «1 – 1» (на рис.12.1а).
В рассматриваемом
случае уравнение Бернулли записывается для установившейся скорости, истечение происходит под постоянным напором,
над свободной поверхностью «0 – 0» давление
равно Р0, скорость
также равна нулю.
В сечении «1 – 1», струя примет цилиндрическую форму, давление Р1, скорость V1 предстоит определить из уравнения Бернулли для
потока реальной жидкости.
![]()
где ξ—
коэффициент, характеризующий сопротивление отверстия,  -коэффициент Кориолиса из уравнения Бернулли
-коэффициент Кориолиса из уравнения Бернулли
для потока вязкой жидкости, характеризующий неравномерность распределения
скоростей в потоке.
Если умножить
числитель и знаменатель выражения для α на ρ/2, можно убедиться, что α
является отношением действительной кинетической энергии потока в данном сечении
к кинетической энергии этого потока в этом сечения при равномерном распределении скоростей.
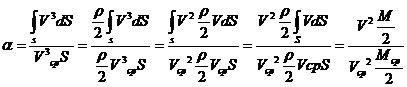
Выделив сумму
геометрического и пьезометрического напора Н = Н0 + (Р0 – Р1)/(ρg), получаем выражение,
связывающее скорость истечения и скоростной напор.
![]()
12.3 Скорость истечения
реальной жидкости при совершенном сжатии.
Коэффициенты:ε, ξ, φ, μ
Из выражения для
гидростатического напора, получим формулу для определения скорости истечения из
отверстия с острой кромкой для реальной жидкости
![]() , (12.2)
, (12.2)
где φ —
коэффициент скорости
![]() . (12.3)
. (12.3)
Для идеальной
жидкости, так как у нее отсутствует вязкость, трения и потерь на трение
нет ξ = 0, α = 1, следовательно,
φ
= 1.
Скорость
истечения идеальной жидкости из отверстия с острой кромкой
![]() (12.4)
(12.4)
Из формулы (12.2) можно заключить, что коэффициент
скорости φ есть отношение скорости истечения реальной жидкости к скорости истечения
идеальной жидкости.
![]() , (12.5)
, (12.5)
Скорость
истечения реальной жидкости меньше идеальной
из-за вязкости и трения, поэтому коэффициент скорости φ всегда меньше единицы.
Измерения
показывают, что в средней части сечения струи эпюра скоростей является
равномерной, поэтому скорость в средней части струи близка к идеальной ![]() , наружный слой жидкости притормаживается при трении о края
, наружный слой жидкости притормаживается при трении о края
стенки отверстия. Коэффициент φ
рассматривается, как коэффициент по средней скорости.
Умножив скорость истечения на площадь сечения струи, получим
выражение для расхода жидкости через отверстие с острой кромкой при совершенном
сжатии
![]() . (12.6)
. (12.6)
Коэффициентом
расхода μ называют произведение
значений коэффициентов сжатия ε и скорости
φ
μ = ε * φ.
Формула для
расхода через отверстие с острой кромкой с учетом выражения для μ
![]() (12.7) или
(12.7) или
![]() (12.8)
(12.8)
где ΔР
— расчетная разность давлений, под действием которой происходит истечение.
По этим формулам
определяется расход для всех случаев связанных с истечением из отверстия с острой кромкой и через насадки различных
форм.
Из уравнения (12.7)
следует, что
![]() (12.9)
(12.9)
Коэффициент
расхода есть отношение действительного
расхода Q к расходу идеальной
жидкости Qи,
определенному по ее скорости ![]() . Действительный
. Действительный
расход всегда меньше расхода идеальной жидкости, следовательно, коэффициент
расхода всегда меньше единицы из-за сжатия струи и трения.
Коэффициенты
сжатия струи ε, сопротивления ξ, скорости φ, расхода μ = ε * φ зависят от
типа отверстия и насадка и от числа Рейнольдса.
На рис. 12.2
показаны составленные Альтшулем зависимости
для коэффициентов ε, φ и μ
для круглого отверстия в функции
числа Rеи, подсчитанного по
скорости истечения идеальной жидкости
Rеи=Vиd/ν = ![]() .
.
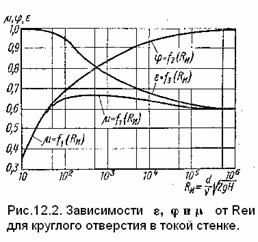
Увеличение числа Re означает
уменьшение сил вязкости, поэтому коэффициент φ возрастает в связи
с уменьшением коэффициента сопротивления ξ
(влияние трения становится меньше), коэффициент ε уменьшается из-за уменьшения торможения жидкости
у кромки отверстия и увеличения радиусов кривизны струи на входе в цилиндрическую
часть. При Rеи
→∞ значения коэффициентов приближаются к φ→1
и ε→0,6
и соответствуют истечению идеальной жидкости.
Коэффициент
расхода μ, определяемый
произведением ε на φ с увеличением Re сначала растет, что связано с сростом
φ,
а затем уменьшается в связи со
значительным падением ε
и при больших Rеи
равен μ = 0,60÷061.
В области малых Re (Rеи < 25) роль
вязкости велика, торможение жидкости у кромки значительно так, что сжатие струи отсутствует ε
= 1, φ = μ. В этом
случае можно пользоваться формулой:
![]() (12.10)
(12.10)
12.3. Истечение при
несовершенном сжатии
Несовершенным
сжатием струи тогда, когда на формирование струи оказывает влияние близость боковых
стенок резервуара.
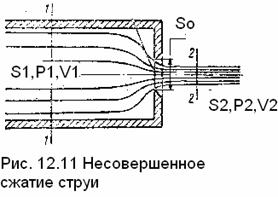
Боковые стенки успевают
направлять жидкость при подходе к отверстию, и струя сжимается в меньшей степени, чем при истечении
из резервуара неограниченных размеров при совершенном сжатии. Увеличивается коэффициент сжатия и коэффициент расхода.
При истечении из
цилиндрического резервуара через круглое отверстие, расположенное в центре торцевой
стенки при больших числах Re, коэффициент сжатия ε1 можно
находить по формуле Жуковского для идеальной жидкости
ε1 = 0,57 +0,043/(1,1 – n)
(12.11)
где n = S0/S1 отношение площади
отверстия S0 к
площади S1 поперечного
сечения резервуара.
Коэффициент
скорости φ при несовершенном сжатии мало зависит от отношения n и его
находят по графику на рис.12.2, коэффициент сопротивления отверстия ξ можно найти из формулы, связывающей ![]()
Коэффициент
расхода μ1 = ε1 φ
, уравнение Бернулли записывается для сечения «1-1» в резервуаре и сечения в
наиболее сжатой части струи, где давление равно Р0 –атмосферному.
Выразим V1 через V2 V1S1=V2 ε1S0;
V1=V2 ε1S0/S1;
V1=V2 ε1n
![]() .
.
(12.12)
Откуда получаем:
скорость для несовершенного
сжатия струи
 ; (12.13)
; (12.13)
расход для несовершенного
сжатия струи
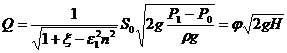 (12.14)
(12.14)
12.5. Истечение под
уровень
Истечением под
уровень называется истечение жидкости в пространство, заполненное этой же жидкостью
(рис. 12.12).

Вся кинетическая
энергия струи теряется на вихреобразование, как при внезапном расширении.
Составляя уравнение
Бернулли относительно свободных поверхностей «0 – 0» и «2 –
2» скорости считаем равными нулю, а приравнивая к
первой и второй части члены уранения для сжатого сечения получим с учетом
коффициента α :
![]() или
или
1-я сумма, 2-я сумма, 3- сжатое сечение
![]()
где Н – обозначен
расчетный напор, ξ – коэффициент сопротивления отверстия, имеющий примерно
то же значение, что и при истечении в атмосферу, V – скорость истечения в сжатом сечении
струи.
Скорость в этом
случае
![]() (12.15)
(12.15)
Расход
![]() , (12.16)
, (12.16)
где Sc – площадь
сжатого сечения струи, S0
– площадь отверстия.
Получились такие же расчетные формулы, что и при истечении в
воздух, только расчетный напор Н в данном
случае представляет собой разность
гидростатических напоров по обе стороны стенки, т.е. скорость и расход
не зависят от высоты расположения
отверстия.
Коэффициенты
сжатия и расхода при истечении под уровень можно принимать те же, что и при истечении в воздушную среду.
12.6.
Истечение через насадки при постоянном напоре.
Внешним
цилиндрическим насадком называется короткая трубка длиной, равной l = (2÷6)d без
закругления входной кромки (рис.12.4а). Истечение через такой насадок в атмосферу может
происходить в двух режимах.
12.5.1.Первый режим течения- безотрывный:
струя после входа в насадок сжимается
примерно как при истечении через
отверстие в тонкой стенке.
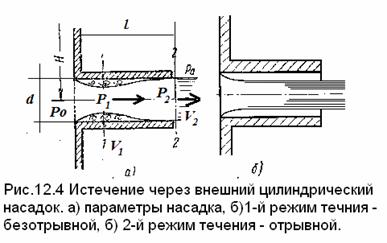
Затем сжатая часть
струи расширяется до размеров отверстия, и из насадка выходит полным сечением. Такой
режим истечения называют безотрывным. На выходе диаметр струи равен диаметру отверстия.
Для маловязких
жидкостей средние значения коэффициентов
для этого режима при больших числах Re равны: μ=φ = 0,8, ξ = 0,5-0,63.
Коэффициент μ
расхода такого насадка при этом режиме истечения жидкости зависит от относительной
длины насадка l/d и числа Re. Однако и при достаточном значении
l/d не всегда возможен
этот режим.
Пусть
истечение жидкости происходит под действием давления Р0 в среду
газа с давлением Р2. Расчетный напор в этом случае
H = (P0 – Р2)/(ρg)
В
струе на выходе из насадка давление равно Р2, в суженном месте
струи внутри насадка, где скорость увеличена, давление Р1 меньше, чем
Р2.
Чем больше напор, под которым происходит истечение и расход через насадок, тем
меньше абсолютное давление Р1.
Разность давлений Р2 – Р1
растет пропорционально напору Н.
Покажем
это, составив уравнение Бернулли для сечений 1 – 1 и 2 – 2,α = 1 (см. рис.12.4а):
![]()
Последний
член уравнения представляет собой потерю напора на расширение потока, которое в
данном случае происходит примерно так же, как и при внезапном расширении трубы (формула
Борда). Сжатие струи внутри насадка можно оценить коэффициентом сжатия ε,
как и в случае отверстия, поэтому на основании уравнения расхода
ε=S1/S2; V1S1=V2S2;
V1/V2=S2/S1=1/ ε;
V1=V2/ε. (12.17)
Заменив
с помощью этого соотношения скорость V1 в уравнении
Бернулли на скорость V2, а ее скорость V2 выражением через ![]() , найдем падение давления внутри насадка:
, найдем падение давления внутри насадка:
![]() (12.18)
(12.18)
Подставляя сюда φ = 0,8 и
ε=0.63, получаем
(Р2 – Р1 ) ≈ 0,75ρgH (12.19)
Если
истечение происходит в среду, где Р2 равно постоянному ,
например, атмосферному давлению, увеличение
напора до критической величины Нкр приводит
к уменьшению Р1 – абсолютное давление в сжатом сечение «1 – 1» внутри насадка может уменьшиться до давления насыщенных паров. Поэтому существует
величина напора, называемая критическим
напором
Hкр ≈ Р2 /(0,75ρg). (12.20)
Следовательно,
при Н
> Hкр
давление Р1 должно
стать отрицательным, но отрицательных давлений в жидкости не бывает, поэтому
первый режим истечения при
Н
> Hкр
делается невозможным. При Н ≈ Hкр происходит внезапное
изменение режима истечения, переход от первого режима ко второму (см. рис.12.4в).
12.5.2. Второй режим истечения
характеризуется тем, что струя после сжатия уже не расширяется, сохраня
цилиндрическую форму, и перемещается внутри насадка, не соприкасаясь с его
стенками. Течение становится таким же, как из отверстия в тонкой стенке, с теми
же значениями коэффициентов. Следовательно, при переходе от первого режима ко
второму скорость возрастает, расход
уменьшается, благодаря сжатию струи.
Если
через насадок происходит истечение воды в атмосферу, то
Hкр ≈ Ра /(0,75ρg) = 10,33/0,75 ≈ 14 м.
Когда
давление Рн.п.
насыщенных паров истекающей жидкости соизмеримо с давлением Р2
среды, в которую происходит истечение,
пренебречь величиной Рн.п. нельзя, в формуле (12.19) следует принять Р1
= Рн.п.
Hкр = (Ра – Рн.п.)
/(0,75ρg) (12.21)
Если
после перехода от первого режима истечения ко второму уменьшить напор Н,
то второй режим будет сохраняться вплоть до самых малых Н. Это значит, что второй
режим истечения возможен при любых напорах, следовательно, при Н < Нкр возможны оба
режима.
При
истечении через цилиндрический насадок под уровень первый режим истечения не
будет отличаться от описанного выше. Но когда абсолютное давление внутри
насадка благодаря увеличению Н падает до давления насыщенных
паров перехода ко второму режиму не происходит, а начинается кавитационный
режим, при котором расход перестает зависеть от противодавления Р2,
получается эффект стабилизации расхода. При этом чем меньше относительное противодавление
Р2/Р0
= Рвых/Рвх =![]() , которое является критерием кавитации, тем шире
, которое является критерием кавитации, тем шире
область кавитации внутри насадка и тем меньше коэффициент расхода μ.
Таким
образом, при истечении жидкости через внешний цилиндрический насадок под
уровень коэффициент является функцией трех безразмерных критериев, а именно
μ = f (l/d, Re, ![]() ).
).
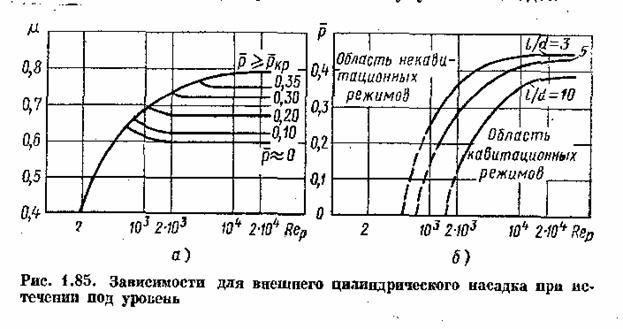
Результаты
новых экспериментальных исследований этого случаи истечения представлены в
безразмерных координатах на рис. 1.85. На рис.1.85а даны зависимости от Re при l/d = 3
для ряда значений ![]() , начиная от
, начиная от ![]() = 0 и до
= 0 и до ![]() >
> ![]() , где
, где ![]() – критическое
– критическое
значение ![]() , соответствующее началу кавитации и, следовательно,
, соответствующее началу кавитации и, следовательно,
критерию ηкр(см. п. 1.23). На рис. 1.85б показаны области кавитационных и
безкавитационных режимов истечения через насадки с l/d = 3; 5 и 10. Увеличение![]() при возрастании Re объясняется уменьшением коэффициента ε сжатия струи
при возрастании Re объясняется уменьшением коэффициента ε сжатия струи
внутри насадка, т. е. увеличением степени сжатия, а уменьшение ![]() при увеличении l/d происходит из-за возрастания давления в сжатом сечении вследствие
при увеличении l/d происходит из-за возрастания давления в сжатом сечении вследствие
увеличения потерь на трение по длине насадка.
Таким
образом, внешний цилиндрический насадок имеет существенные недостатки: на
первом режиме – большое сопротивление и недостаточно высокий коэффициент расхода,
а на втором – очень низкий коэффициент расхода. Недостатком является также двойст-венность
режима истечения в газовую среду при Н < Нкр, а следовательно двузначность
расхода при данном Н и возможность кавитации при истечении под уровень.
При
использовании цилиндрического насадка (сверления в толстой стенке), например в
качество жиклеров, дросселей или форсунок эти недостатки следует учитывать или
улучшать насадок.
Внешний
цилиндрический насадок может быть значительно улучшен путем закругления входной
кромки (см. штриховые линии на рис. 1.83) или устройства конического входа с
углом конусности около 60° (см. жиклер на рис. 1.75).
Чем
больше радиус закругления, тем выше коэффициент расхода и ниже коэффициент
сопротивления. В пределе при радиусе кривизны, равном толщине стенки, цилиндрический
насадок приближается к коноидальному насадку, или соплу.
Коноидальный
насадок (рис. 1.86) очерчивается приблизительно по форме естественно сжимающейся
струи и, благодаря этому, обеспечивает безотрывность течения внутри насадка в
параллельноструйность в выходном сечении. Это весьма распространеный насадок, так
как он имеет коэффициент расхода, близкий к единице, и очень малые потери
(коэффициент сжатия ε = 1), а также устойчивый режим течения без кавитации.
Значения
коэффициента сопротивления те же, что и при плавном сужении (см. п. 1.32), т.
е. ξ= 0,03 ÷ 0,1 (большим Re соответствуют малые ξ ‚ и наоборот). В соответствии с этим
μ =φ= 0,99÷0,96.
Диффузорный
насадок представляет собой комбинацию сопла и диффузора (рис. 1.87).

Приставка
диффузора к соплу влечет за собой снижение давления в узком месте насадка, а
следовательно, увеличение скорости и расхода жидкости через него. При том жедиаметре
узкого сечения, что и у сопла, и том же напоре диффузорный насадок может дать
значительно больший расход (увеличение до 2,5 раза), чем сопло.
Такие насадки
применяют в том случае, когда заданы диаметр узкого сечения и напор и требуется
получить возможно больший расход. Однако, использовать диффузорных насадков
можно лишь при небольших напорах Н = 1 ÷4
м, так как иначе в узком месте насадка возникает кавитация. Следствием кавитации являются увеличение
сопротивления и уменьшение пропускной способности насадка.
На рис.1.88
показано падение коэффициента расхода диффузорного насадка с увеличением напора
вследствие кавитации, возникающей в узком месте насадка при истечении воды в атмосферу.
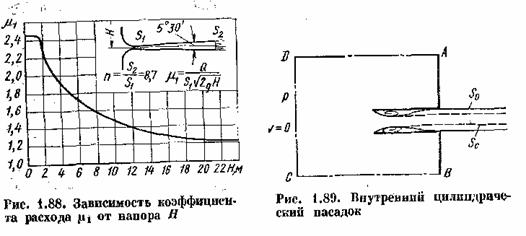
Коэффициент
расхода отнесен к площади узкого сечения, т. е. ![]() . Приведенная кривая получена в результате испытания диффузорного
. Приведенная кривая получена в результате испытания диффузорного
насадка, обладающего наивыгоднейшим углом и степенью расширения, которые
обеспечивают наибольший коэффициент расхода.
Внутренний
цилиндрический насадок или насадок Борда, изображен на рис.1.89. Там же
схематически показаны два режима истечения , аналогичные режимам истечения
через внешний цилиндрический насадок. Очертания струи при первом режиме
показаны сплошными линиями, а при втором – штриховыми. Так как частицы жидкости
приближаются к входному отверстию
насадка из всего прилежащего объема, а некоторые из них, попадающие на
периферию струи, изменяют направление своего движения на 180°, то степень
сжатия струи в данном насадке больше, а коэффициент ε меньше, чем во внешнем
цилиндрическом насадке. Значение ε в этом случае при истечении идеальной
жидкости может быть получено на основании
теоремы Эйлера об изменения количества движения (см. п. 1.15). Применим эту
теорему к фиксированному объему в виде кругового цилиндра ABCD соосного с насадком, и с основанием
CD, достаточно удаленным от насадка, где V=0. Пренебрегая толщиной стенки
насадка на основании указанной теоремы при втором режиме истечения получим
PS0 = ρSс*V2,
где
P— давление в центре
основания CD, S0 и Sс —
площади отверстия насадка и сечения струи (силы давления жидкости на кольцевые
площади оснований цилиндра ABCD уравновешиваются, а избыточное
давление по площади S0 в
плоскости АВ равно нулю.
С
другой стороны, для скорости истечения имеем
![]() 1 .
1 .
IIосле
подстановки второго уравнения в первое и сокращения на Р и ρ получим
ε = Sс / S0 = ½.
Этому
значению ε соответствуют значения коэффициентов расхода μ = 0,71 и потерь
ξ =1, что подтверждается опытами при первом режиме истечения и больших
числах Рейнольдса.

