Шестиугольник описанный около окружности формулы
На чтение 2 мин Просмотров 1.2к. Опубликовано 13.11.2021
Калькулятор для вычисления стороны правильного шестиугольника по известным данным.
При известном радиусе R описанной вокруг правильного шестиугольника окружности сторона a имеет такое же значение как и радиус R описанной вокруг шестиугольника окружности.
При известном радиусе r окружности вписанной в правильный шестиугольник сторона a вычисляется как отношение двух радиусов вписанной в правильный шестиугольник окружности и корня из числа 3.
Формула для вычисления стороны правильного шестиугольника при известном радиусе вписанной в правильный шестиугольник окружности:
r – радиус окружности вписанной в правильный шестиугольник,
a – сторона правильного шестиугольника.
При вводе данных дробную часть от целой, отделяйте точкой, а не запятой.
На данной странице калькулятор поможет рассчитать площадь правильного шестиугольника онлайн. Для расчета задайте длину стороны или радиус окружности.
Шестиугольник – многоугольник у которого все стороны равны, а все внутренние углы равны 120°.
Через сторону
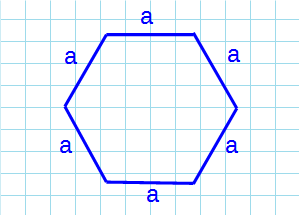
Формула для нахождения площади правильного шестиугольника через сторону:
Через радиус описанной окружности
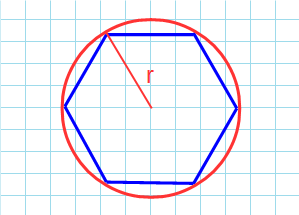
Формула для нахождения площади правильного шестиугольника через радиус описанной окружности:
Определение длины стороны правильного многоугольника по радиусу вписанной окружности
От нашего нового пользователя поступил вот такой запрос:
«Калькулятор должен вычислять длину стороны правильного многоугольника (шестиугольник, пятигольник) по указанному диаметру (или радиусу) описанной окружности».
Удовлетворяем запрос оперативно. Заметим, что для решения задачи нужно найти длину третьей стороны треугольника, исходящего из центра описанной окружности и опирающегося на две соседние вершины правильного многоугольника. Про этот треугольник известно многое: длины двух сторон — это радиусы описанной окружности, и угол, как нетрудно заметить, — это 360, деленное на число вершин правильного многоугольника. Далее используется соотношение из теоремы синусов — две стороны относятся друг к другу также как и синусы противолежащих им углов. Поскольку треугольник равнобедренный и сумма углов в треугольнике равна 180 градусам, угол, противолежащий радиусу вычисляется тривиально. Результат — ниже.
Сторона правильный шестиугольник описанный около окружности
Задание 6. Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен √3.

Рассмотрим равносторонний треугольник AOB (известно, что правильный шестиугольник разбивается на шесть правильных треугольников) с высотой, равной радиусу вписанной окружности r=√3 (см. рисунок ниже).

Так как все углы правильного треугольника равны 60°, то сторона AO равна:
 ,
,
Сторона правильный шестиугольник описанный около окружности
Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен
Рассмотрим равносторонний треугольник AOB (см. рис.). В этом треугольнике
Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен
Рассмотрим равносторонний треугольник AOB (см. рис.). В этом треугольнике
Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен
Рассмотрим равносторонний треугольник AOB (см. рис.). В этом треугольнике
Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен
Это задание ещё не решено, приводим решение прототипа.
Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен
Пусть точка О — центр окружности. Треугольник АОВ является равнобедренным с углом при вершине 60° (см. рис.), поэтому этот треугольник равносторонний. Радиус ОН вписанной в шестиугольник окружности является высотой, биссектрисой и медианой треугольника АОВ, поэтому:
Шестиугольник описанный около окружности построение
 Тему многоугольников проходят в школьной программе, но не уделяют ей достаточного внимания. А между тем она интересна, и особенно это касается правильного шестиугольника или гексагона — ведь эту форму имеют многие природные объекты. К ним относятся пчелиные соты и многое другое. Эта форма очень хорошо применяется на практике.
Тему многоугольников проходят в школьной программе, но не уделяют ей достаточного внимания. А между тем она интересна, и особенно это касается правильного шестиугольника или гексагона — ведь эту форму имеют многие природные объекты. К ним относятся пчелиные соты и многое другое. Эта форма очень хорошо применяется на практике.
Определение и построение
Правильным шестиугольником называется плоскостная фигура, имеющая шесть равных по длине сторон и столько же равных углов.
Если вспомнить формулу суммы углов многоугольника
то получается, что в этой фигуре она равна 720°. Ну а поскольку все углы фигуры равны, нетрудно посчитать, что каждый из них равен 120°.
Начертить шестиугольник очень просто, для этого достаточно циркуля и линейки.
Пошаговая инструкция будет выглядеть так:
 чертится прямая линия и на ней ставится точка;
чертится прямая линия и на ней ставится точка;- из этой точки строится окружность (она является ее центром);
- из мест пересечения окружности с линией строятся еще две таких же, они должны сойтись в центре.
- после этого отрезками последовательно соединяются все точки на первой окружности.
При желании можно обойтись и без линии, начертив пять равных по радиусу окружностей.
Полученная таким образом фигура будет правильным шестиугольником, и это можно доказать ниже.
Свойства простые и интересные
Чтобы понять свойства правильного шестиугольника, его имеет смысл разбить на шесть треугольников:
Это поможет в дальнейшем нагляднее отобразить его свойства, главные из которых:
- диаметр описанной окружности;
- диаметр вписанной окружности;
- площадь;
- периметр.
Описанная окружность и возможность построения
 Вокруг гексагона можно описать окружность, и притом только одну. Поскольку фигура эта правильная, то можно поступить довольно просто: от двух соседних углов провести внутрь биссектрисы. Они пересекутся в точке О, и образуют вместе со стороной между ними треугольник.
Вокруг гексагона можно описать окружность, и притом только одну. Поскольку фигура эта правильная, то можно поступить довольно просто: от двух соседних углов провести внутрь биссектрисы. Они пересекутся в точке О, и образуют вместе со стороной между ними треугольник.
Углы между стороной гексагона и биссектрисами будут по 60°, поэтому можно определенно сказать, что треугольник, к примеру, АОВ — равнобедренный. А поскольку третий угол тоже будет равен 60°, то он еще и равносторонний. Отсюда следует, что отрезки ОА и ОВ равны, значит, могут служить радиусом окружности.
После этого можно перейти к следующей стороне, и из угла при точке С тоже вывести биссектрису. Получится очередной равносторонний треугольник, причем сторона АВ будет общей сразу для двух, а ОС — очередным радиусом, через который идет та же окружность. Всего таких треугольников получится шесть, и у них будет общая вершина в точке О. Получается, что описать окружность будет можно, и она всего одна, а ее радиус равен стороне гексагона:
R=а.
Именно поэтому и возможно построение этой фигуры с помощью циркуля и линейки.
Ну а площадь этой окружности будет стандартная:
S=πR²
Вписанная окружность
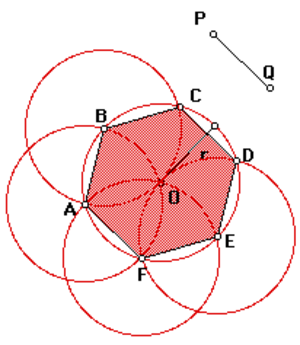 Центр описанной окружности совпадет с центром вписанной. Чтобы в этом убедиться, можно провести из точки О перпендикуляры к сторонам шестиугольника. Они будут являться высотами тех треугольников, из которых составлен гексагон. А в равнобедренном треугольнике высота является медианой по отношению к стороне, на которую она опирается. Таким образом, эта высота не что иное, как серединный перпендикуляр, являющийся радиусом вписанной окружности.
Центр описанной окружности совпадет с центром вписанной. Чтобы в этом убедиться, можно провести из точки О перпендикуляры к сторонам шестиугольника. Они будут являться высотами тех треугольников, из которых составлен гексагон. А в равнобедренном треугольнике высота является медианой по отношению к стороне, на которую она опирается. Таким образом, эта высота не что иное, как серединный перпендикуляр, являющийся радиусом вписанной окружности.
Высота равностороннего треугольника вычисляется просто:
h²=а²-(а/2)²= а²3/4, h=а(√3)/2
А поскольку R=a и r=h, то получается, что
r=R(√3)/2.
Таким образом, вписанная окружность проходит через центры сторон правильного шестиугольника.
Ее площадь будет составлять:
S=3πa²/4,
то есть три четверти от описанной.
Периметр и площадь
С периметром все ясно, это сумма длин сторон:
P=6а, или P=6R
А вот площадь будет равна сумме всех шести треугольников, на которые можно разбить гексагон. Поскольку площадь треугольника вычисляется как половина произведения основания на высоту, то:
S=6(а/2)(а(√3)/2)= 6а²(√3)/4=3а²(√3)/2 или
S=3R²(√3)/2
Желающим вычислять эту площадь через радиус вписанной окружности можно сделать и так:
Занимательные построения
В гексагон можно вписать треугольник, стороны которого будут соединять вершины через одну:
Всего их получится два, и их наложение друг на друга даст звезду Давида. Каждый из этих треугольников — равносторонний. В этом нетрудно убедиться. Если посмотреть на сторону АС, то она принадлежит сразу двум треугольникам — ВАС и АЕС. Если в первом из них АВ=ВС, а угол между ними 120°, то каждый из оставшихся будет 30°. Отсюда можно сделать закономерные выводы:
- Высота АВС из вершины В будет равна половине стороны шестиугольника, поскольку sin30°=1/2. Желающим убедиться в этом можно посоветовать пересчитать по теореме Пифагора, она здесь подходит как нельзя лучше.
- Сторона АС будет равна двум радиусам вписанной окружности, что опять-таки вычисляется по той же теореме. То есть АС=2(a(√3)/2)=а(√3).
- Треугольники АВС, СДЕ и АЕF равны по двум сторонам и углу между ними, и отсюда вытекает равенство сторон АС, СЕ и ЕА.
Пересекаясь друг с другом, треугольники образуют новый гексагон, и он тоже правильный. Доказывается это просто:
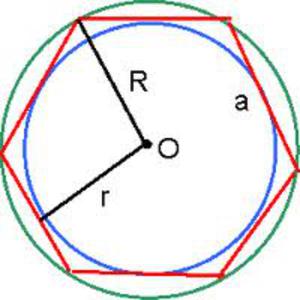 Угол АВF равен углу ВАС. Таким образом, получившийся треугольник с основанием АВ и безымянной вершиной напротив него — равнобедренный.
Угол АВF равен углу ВАС. Таким образом, получившийся треугольник с основанием АВ и безымянной вершиной напротив него — равнобедренный.- Все такие же треугольники, основанием которых служит сторона гексагона, равны по стороне и прилегающей к ней углам.
- Треугольники при вершинах гексагона являются равносторонними и равными, что вытекает из предыдущего пункта.
- Углы новообразованного шестиугольника равняются 360-120-60-60=120°.
Таким образом, фигура отвечает признакам правильного шестиугольника — у нее шесть равных сторон и углов. Из равенства треугольников при вершинах легко вывести длину стороны нового гексагона:
d=а(√3)/3
Она же будет радиусом описанной вокруг него окружности. Радиус вписанной будет вдвое меньше стороны большого шестиугольника, что было доказано при рассмотрении треугольника АВС. Его высота составляет как раз половину стороны, следовательно, вторая половина — это радиус вписанной в маленький гексагон окружности:
r₂=а/2
Площадь нового шестиугольника можно посчитать так:
Получается, что площадь гексагона внутри звезды Давида в три раза меньше, чем у большого, в который вписана звезда.
От теории к практике
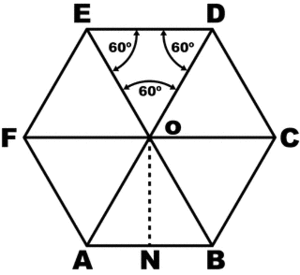 Свойства шестиугольника очень активно используются как в природе, так и в различных областях деятельности человека. В первую очередь это касается болтов и гаек — шляпки первых и вторые представляют собой ничто иное, как правильный шестигранник, если не брать в расчет фаски. Размер гаечных ключей соответствует диаметру вписанной окружности — то есть расстоянию между противоположными гранями.
Свойства шестиугольника очень активно используются как в природе, так и в различных областях деятельности человека. В первую очередь это касается болтов и гаек — шляпки первых и вторые представляют собой ничто иное, как правильный шестигранник, если не брать в расчет фаски. Размер гаечных ключей соответствует диаметру вписанной окружности — то есть расстоянию между противоположными гранями.
Нашла свое применение и гексагональная плитка. Она распространена куда меньше четырехугольной, но класть ее удобнее: в одной точке смыкаются три плитки, а не четыре. Композиции могут получаться очень интересные:
Выпускается и бетонная плитка для мощения.
Распространенность гексагона в природе объясняется просто. Таким образом, проще всего плотно уместить круги и шары на плоскости, если у них одинаковый диаметр. Из-за этого у пчелиных сот такая форма.
Презентация была опубликована 5 лет назад пользователемГригорий Оськин
Похожие презентации
Презентация на тему: ” а) Для построения правильного шестиугольника можно воспользоваться тем, что а 6 = R. Построение. 1. Строим ω(О; R). О 2. Строим произвольную точку, принадлежащую.” — Транскрипт:
2 а) Для построения правильного шестиугольника можно воспользоваться тем, что а 6 = R. Построение. 1. Строим ω(О; R). О 2. Строим произвольную точку, принадлежащую окружности. 3. Из данной точки раствором циркуля равным R на окружности откладываем последовательно один за другим отрезки. (таким образом окружность разделиться на 6 равных частей). 4. Соединив последовательно данные точки, получим правильный шестиугольник. б) Для построения правильного шестиугольника можно воспользоваться другим способом (см. учебник стр.206, п. 117).
3 Построение. 1. Строим ω(О; R). О 2. Строим произвольную точку, принадлежащую окружности. 3. Из данной точки раствором циркуля равным R на окружности откладываем последовательно один за другим отрезки. (таким образом окружность разделиться на 6 равных частей). 4. Соединив последовательно через одну данные точки, получим правильный треугольник. Для построения правильного треугольника воспользуемся тем же алгоритмом, что и для построения правильного шестиугольника, только получив 6 точек на окружности, соединим их через одну.
4 Построение. 1. Строим ω(О; R). О 4. Соединив последовательно точки пересечения прямых с окружностью, получим правильный треугольник. Для построения правильного четырехугольника следует провести две перпендикулярные прямые, проходящие через центр окружности. Соединив последовательно точки пересечения прямых с окружностью, получим правильный четырехугольник (квадрат). 2. Проведем произвольную прямую, проходящую через центр окружности. 3. Проведем прямую, перпендикулярную данной и проходящую через центр окружности.
5 Построение. О 3. Соединив последовательно точки на окружности получим правильный восьмиугольник. Для построения правильного восьмиугольника сначала строим правильный четырехугольник ( по описанному алгоритму), а затем проводим две прямые через середины противолежащих сторон. При этом окружность окажется разделенной на 8 раваных частей. Соединив последовательно точки на окружности, получим правильный восьмиугольник. 1. Строим правильный четырехугольник, вписанный в окружность. 2. Проводим две прямые через середины сторон квадрата (вершины квадрата и точки пересечения прямых с окружностью делят окружность на 8 равных частей).
6 Рассмотренные способы построения правильных многоугольников дают возможность построить многоугольники, вписанные в окружность. Чтобы построить многоугольник, описанный около окружности, пользуются теми же способами, только на последнем этапе не соединяют полученные точки на окружности, а проводят через них касательные. Построим правильный шестиугольник, описанный около окружности. Построение. 1. Строим ω(О; R). О 2. Строим произвольную точку, принадлежащую окружности. 3. Из данной точки раствором циркуля равным R на окружности откладываем последовательно один за другим отрезки. 4. Через каждую полученную точку на окружности проводим касательные. Получим правильный шестиугольник.
Правильный описанный треугольник строят следующим образом (рисунок 38). Из центра заданной окружности радиуса R1 проводят окружность радиусом R2 = 2R1 и делят ее на три равные части. Точки деления А, В, С являются вершинами правильного треугольника, описанного около окружности радиуса R1.
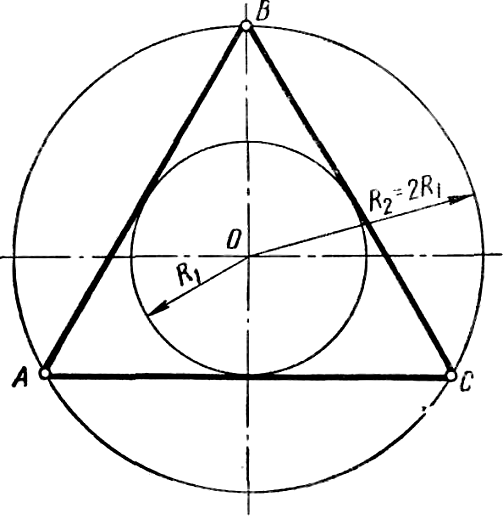
Правильный описанный четырехугольник (квадрат) можно построить с помощью циркуля и линейки (рисунок 39). В заданной окружности проводят два взаимно перпендикулярных диаметра. Приняв точки пересечения диаметров с окружностью за центры, радиусом окружности R описывают дуги до взаимного их пересечения в точках А, В, С,D. Точки A, B, C, D и являются вершинами квадрата, описанного около данной окружности.
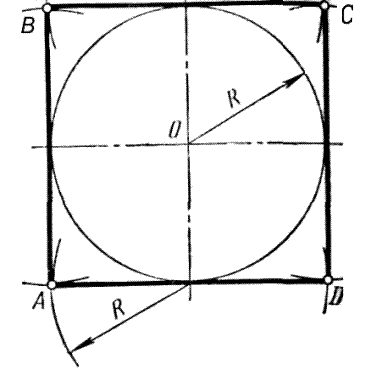
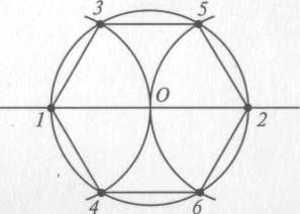
Для построения правильного описанного шестиугольника необходимо вначале построить вершины описанного квадрата указанным выше способом (рисунок 40, а). Одновременно с определением вершин квадрата заданную окружность радиуса R делят на шесть равных частей в точках 1, 2, 3, 4, 5, 6 и проводят вертикальные стороны квадрата. Проведя через точки деления окружности 2–5 и 3–6 прямые до пересечения их с вертикальными сторонами квадрата (рисунок 40, б), получают вершины А, В, D, Е описанного правильного шестиугольника.

Остальные вершины C и F определяют с помощью дуги окружности радиуса OA, которая проводится до пересечения ее с продолжением вертикального диаметра заданной окружности.
3 СОПРЯЖЕНИЯ
Дата добавления: 2014-11-06 ; Просмотров: 4403 ; Нарушение авторских прав? ;
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
[spoiler title=”источники:”]
http://ege.sdamgia.ru/test?likes=27916
http://morflot.su/shestiugolnik-opisannyj-okolo-okruzhnosti/
[/spoiler]
Задания
Версия для печати и копирования в MS Word
Тип 1 № 27916 

i
Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен
Спрятать решение
Решение.
Пусть точка О — центр окружности. Треугольник АОВ является равнобедренным с углом при вершине 60° (см. рис.), поэтому этот треугольник равносторонний. Радиус ОН вписанной в шестиугольник окружности является высотой, биссектрисой и медианой треугольника АОВ, поэтому:
Ответ: 2.
Аналоги к заданию № 27916: 53571 53613 53619 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.1.7 Вписанная окружность и описанная окружность правильного многоугольника
Спрятать решение
·
Видеокурс
·
Помощь
Как найти сторону правильного шестиугольника
Шестиугольную – «гексагональную» – форму имеют, например, сечения гаек и карандашей, пчелиных сот и снежинок. Правильные геометрические фигуры такой формы имеют некую особенность, отличающую их от прочих плоских многоугольников. Заключается она в том, что радиус описанной около гексагона окружности равен длине его стороны – во многих случаях это значительно упрощает вычисление параметров многоугольника.

Инструкция
Если в условиях задачи дан радиус (R) описанной около правильного шестиугольника окружности, вычислять ничего не придется – эта величина тождественна длине стороны (t) гексагона: t = R. При известном диметре (D) просто поделите его пополам: t = D/2.
Периметр (Р) правильного шестиугольника позволяет вычислить длину стороны (t) простой операцией деления. В качестве делителя используйте число сторон, т.е. шестерку: t = Р/6.
Радиус (r) вписанной в такой многоугольник окружности связан с длиной его стороны (t) немного более сложным коэффициентом – удвойте радиус, а полученный результат разделите на квадратный корень из тройки: t = 2*r/√3. Эта же формула с использованием диаметра (d) вписанной окружности станет на одно математическое действие короче: t = d/√3. Например, при радиусе в 50 см длина стороны шестиугольника должна быть приблизительно равна 2*50/√3 ≈ 57,735 см.
Известная площадь (S) многоугольника с шестью вершинами тоже позволяет вычислить длину его стороны (t), но численный коэффициент, связывающий их, точно выражается через дробь из трех натуральных чисел. Две трети площади делите на квадратный корень из тройки, а из полученного значения извлекайте квадратный корень: t = √(2*S/(3*√3)). Например, если площадь фигуры составляет 400 см², длина ее стороны должна составлять примерно √(2*400/(3*√3)) ≈ √(800/5,196) ≈ √153,965 ≈ 12,408 см.
Длина окружности (L), описанной около правильного шестиугольника, связана с радиусом, а значит и с длиной стороны (t) через число Пи. Если он дана в условиях задачи, поделите ее величину на два числа Пи: t = L/(2*π). Скажем, если эта величина равна 400 см, длина стороны должна составлять приблизительно 400/(2*3,142) = 400/6,284 ≈ 63,654 см.
Этот же параметр (l) для вписанной окружности позволяет рассчитать длину стороны шестиугольника (t) вычислением соотношения между ней и произведением числа Пи на квадратный корень из тройки: t = l/(π*√3). Например, если длина вписанной окружности составляет 300 см, сторона шестиугольника должна иметь величину, примерно равную 300/(3,142*√3) ≈ 300/(3,142*1,732) ≈ 300/5,442 ≈ 55,127 см.
Видео по теме
Источники:
- сторона шестиугольника
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
