Характеристический полином
матрицы
A, вычисляется следующим образом:
| A − λ E |
где
E
– единичная матрица, размеры которой совпадают с размерами исходной матрицы
A.
Разберем подробнее приведенную выше формулу. Если матрица
A
задана в виде:
тогда выражение
A − λ E
имеет вид:
Наконец, нам нужно найти определитель:
Раскрыв этот определитель, мы получим полином
n-ой степени
(n
– порядок исходной матрицы), зависящий от
λ:
P ( λ )
=
cn λ n
+
cn−1 λ n−1
+ … +
ci λ i
+ … +
c1 λ
+
c0
Поскольку для вычисления характеристического полинома, требуется нахождение определителя матрицы, то характеристический полином может быть найден только для квадратной матрицы.
Наш онлайн калькулятор находит
характеристический полином матрицы, причем в качестве элементов матрицы, можно вводить не только числа и дроби, но и параметры.

| bold{mathrm{Basic}} | bold{alphabetagamma} | bold{mathrm{ABGamma}} | bold{sincos} | bold{gedivrightarrow} | bold{overline{x}spacemathbb{C}forall} | bold{sumspaceintspaceproduct} | bold{begin{pmatrix}square&square\square&squareend{pmatrix}} | bold{H_{2}O} | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|

Подпишитесь, чтобы подтвердить свой ответ
Подписаться
Войдите, чтобы сохранять заметки
Войти
Номер Строки

Примеры
-
характеристический:многочлен:begin{pmatrix}1&-4\4&-7end{pmatrix}
-
характеристический:многочлен:begin{pmatrix}1&2&1\6&-1&0\-1&-2&-1end{pmatrix}
-
характеристический:многочлен:begin{pmatrix}a&1\0&2aend{pmatrix}
-
характеристический:многочлен:begin{pmatrix}1&2\3&4end{pmatrix}
- Показать больше
Описание
Пошаговый поиск характеристического полинома матрицы
matrix-characteristic-polynomial-calculator
характеристический многочлен begin{pmatrix}1&2&1\6&-1&0\-1&-2&-1end{pmatrix}
ru
Блог-сообщения, имеющие отношение к Symbolab
The Matrix… Symbolab Version
Matrix, the one with numbers, arranged with rows and columns, is extremely useful in most scientific fields. There…
Read More
Введите Задачу
Сохранить в блокнот!
Войти
|
01:26 Многочлен от матрицы |
||
|
Тема: Линейная алгебра.Калькулятор для вычисления многочлена от матрицы. Пример. Найти многочлен f(x)= x^2-5x+3 от матрицы
Пусть дан многочлен Определение. Многочленом Пример 12. а) Найти значение многочлена Решение. Многочлен
б) Найти значение многочлена
Тема: Линейная алгебра.Калькулятор для вычисления многочлена от матрицы. $CUT$ Пример. Найти многочлен f(x)= x^2-5x+3 от матрицы |
||
Категория: Линейная алгебра | Просмотров: 58621 | | Теги: Многочлен от матрицы, Возведение матрицы в степень | Рейтинг: 3.3/14 |
| Всего комментариев: 1 | |
|
Порядок вывода комментариев: |
|
Многочлен и матрица как аргумент
| Исходный полином f(x) (его коэффициенты) |
| Аргумент является квадратной матрицей с элементами |
| Многочлен |
| Переменная x= |
| Результат вычислений |
Расссмотрим в данном материале одну из трудоёмких задач в высшей математике, которая звучит так: Найти чему задан многочлен
если аргумент есть квадратная матрица, то есть
И если сам принцип вычисления понятен, особенно если вы в совершенстве поняли как умножать матрицы, то непосредственное вычисление, для меня лично считается рутиной, которую по возможности нужно избежать.
Сразу хотелось бы сказать, где этот калькулятор пригодится. Для учителей, преподавателей, для создателей учебников, для тех, кому необходимо создавать оригинальные задачи по данной теме.
Также пригодится для студентов или аспирантов которые пишут рефераты, курсовые, дипломы.
Для всех остальных, это легкий способ проверить ошибку в заданном примере, решить, без долгих промежуточных вычислений, поставленную задачу.
Когда калькулятор был написан, оказалось что сайты, которые были посвещенны этой теме, содержали ошибки в промежуточных вычислениях и как как результат были неверные.
Данный калькулятор, я надеюсь избавлен от ошибок и Вы сможете безопасно решать любые примеры.
Как и подавляющее большинство калькуляторов на этом сайте, значениями как коэффициентов полинома, так и элементов матрицы, могут быть комплексные значения.
Такого на конец 2017 года, больше нигде не найдете, не считая конечно специальных созданных математических программ.
Приступим к примерам?
Найти значение полинома =2x^2-3x+4)
Еще один пример
Чему равен полином =ix^5+(2-i)x^2-11x)
Найти значение многочлена =x^4-x-1)
Удачный расчетов !
Определение 14. Пусть дан многочлен
![]()
и пусть
![]()
– квадратная матрица, тогда значением
многочлена
![]()
от матрицы
называется матрица
![]()
,
где
![]()
– единичная матрица,
![]()
– матрица, получающаяся при умножении
матрицы
на себя
раз.
№ 827 (П).
Найти значение многочлена
![]()
от матрицы

.
Р е ш е н и е.
Найдем
![]()
.


;
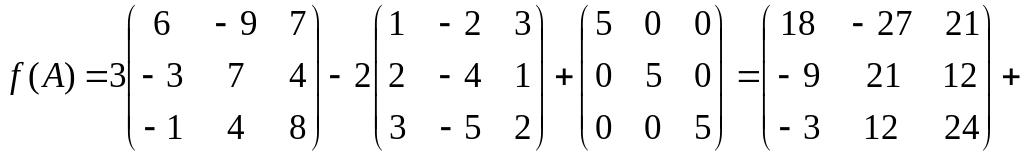

.
Ответ:

.
-
Обратная матрица
Определение 15. Матрица
![]()
называется обратной к квадратной
матрице
,
если
![]()
.
Определение 16. Квадратная матрица
называется невырожденной, если
она имеет единственную обратную матрицу
![]()
.
В противном случае
– вырожденная матрица.
Утверждение. Квадратная матрица
порядка
является невырож-денной в том и только
том случае, если определитель этой
матрицы отличен от нуля.
Для отыскания обратной матрицы
существуют два способа.
-
Припишем
к матрицесправа единичную матрицу и, применяя
метод Гаусса (см. §5), преобразуем
расширенную матрицу так, чтобы слева
стояла единичная матрица, тогда справа
будет находиться обратная матрица

:

.

.
Обоснование этого способа состоит в
следующем.
Пусть нам дана невырожденная квадратная
матрица. Задачу нахождения обратной
матрицы можно рассматривать как задачу
решения матричного уравнения
![]()
,
которое эквивалентно системе
![]()
уравнений с
неизвестными.
Эта система является объединением
систем уравнений, каждая из которых
содержит
неизвестных. Умножая поочередно строки
матрицы
на 1-й столбец матрицы
![]()
и приравнивая к 1-му столбцу матрицы
,
получим систему уравнений, матричная
форма записи которой имеет вид

(1.2.1)
С помощью элементарных операций над
строками матрицы систему уравнений
можно привести к виду
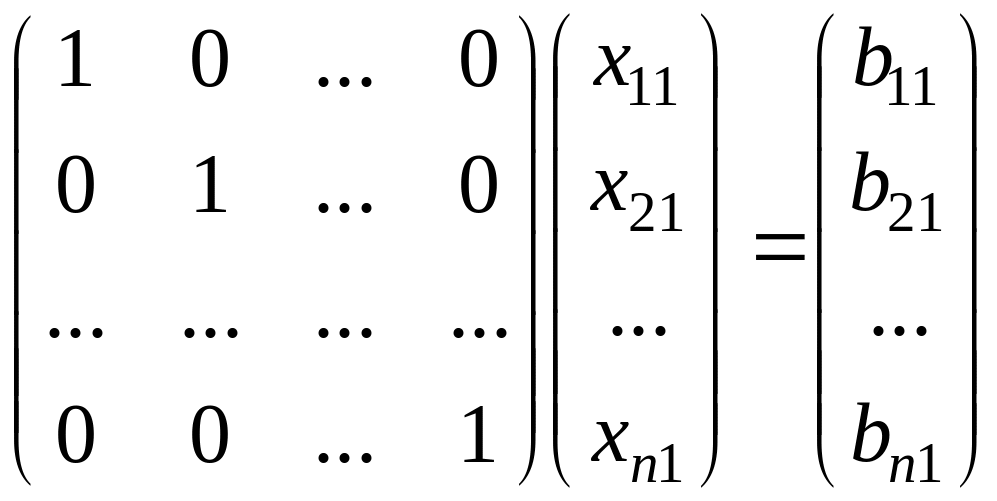
Умножая
поочередно строки матрицы
на второй столбец матрицы
и приравняв ко второму столбцу матрицы
,
получим систему уравнений

.
(1.2.2)
С помощью тех же элементарных операций,
что применялись для решения системы
(1.2.1), мы приведем систему (1.2.2) к виду

и т.д.
Поэтому
для нахождения обратной матрицы и был
предложен описанный выше способ.
-
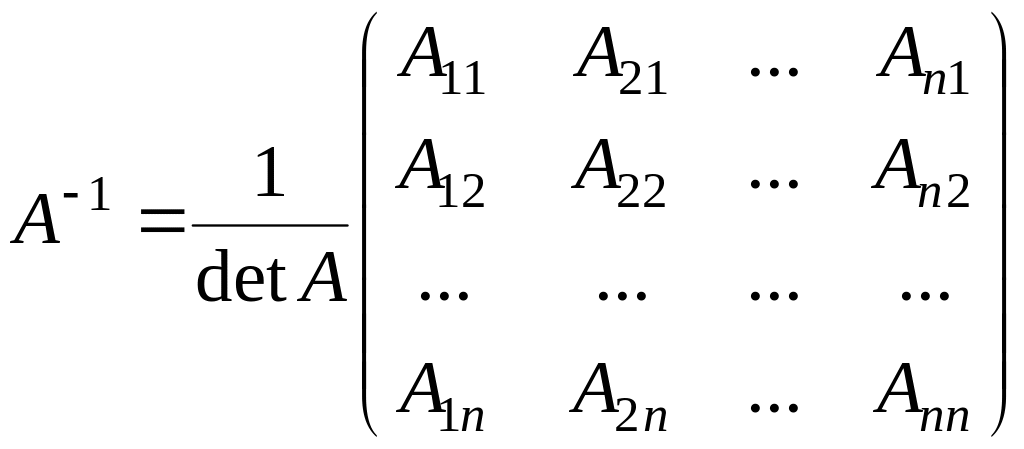
,
где


– алгебраические дополнения к элементу
,

– определитель матрицы
(см. §2).
№ 840 (П).
Найти обратную матрицу для матрицы
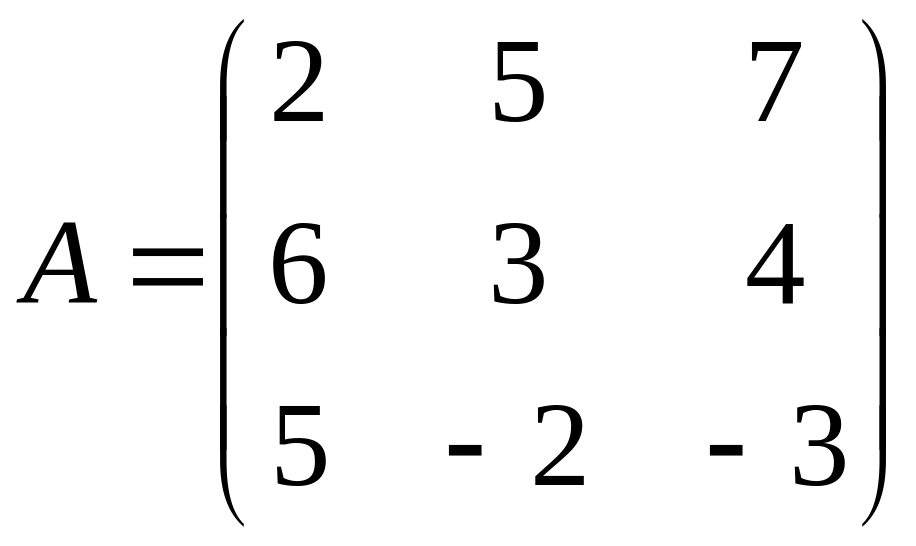
.
Р е ш е н и е.
I
способ.




.
Ответ:

.
II
способ.

![]()
;
![]()
;
![]()
;
![]()
;
![]()
;
![]()
;
![]()
;
![]()
;
![]()
;
![]()
.
Таким образом,

.
Ответ:
.
№ 861 (П).
Решить матричное уравнение
![]()
.
Р е ш е н и е.
1 вариант.
Пусть
![]()
,
тогда
![]()
![]()
![]()

.
![]()
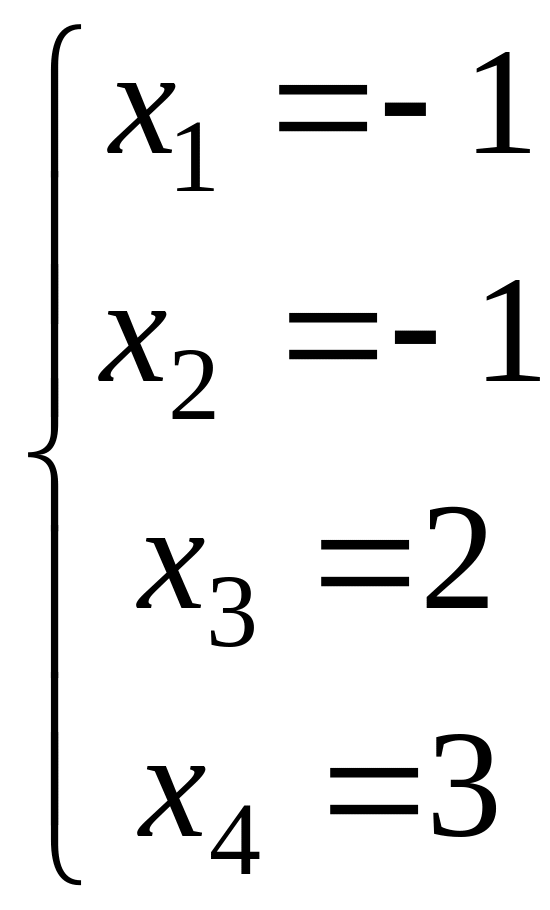
.
Ответ:
![]()
.
2 вариант.
Очевидно, что
![]()
.
Найдем матрицу, обратную к матрице
![]()
.
I
способ:
![]()

.
II
способ:

.
Таким образом,

.
Ответ:
![]()
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #





=a_0x^{n}+a_1x^{n-1}+a_2x^{n-2}+.....+a_{n-1}x+a_n)




