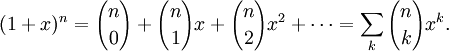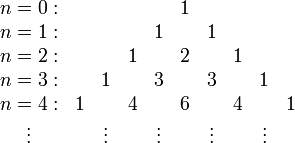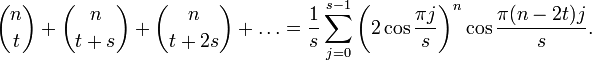Что такое биномиальные коэффициенты как их найти

Что такое биномиальные коэффициенты как их найти

Биномиальный коэффициент — коэффициент перед членом разложения бинома Ньютона (1+x)^{n} по степеням x. Коэффициент при x^{k} обозначается textstyle {binom {n}{k}} или textstyle C_n^k и читается «биномиальный коэффициент из n по k» (или «число сочетаний из n по k»):

{displaystyle (1+x)^{n}={binom {n}{0}}+{binom {n}{1}}x+{binom {n}{2}}x^{2}+ldots +{binom {n}{n}}x^{n}=sum _{k=0}^{n}{binom {n}{k}}x^{k}}

для натуральных степеней n.

Биномиальные коэффициенты могут быть также определены для произвольных действительных показателей n. В случае произвольного действительного числа n биномиальные коэффициенты определяются как коэффициенты разложения выражения (1+x)^{n} в бесконечный степенной ряд:

{displaystyle (1+x)^{n}=sum _{k=0}^{infty }{binom {n}{k}}x^{k}},

где в случае неотрицательных целых n все коэффициенты textstyle {binom {n}{k}} при k>n обращаются в нуль и поэтому данное разложение является конечной суммой.

В комбинаторике биномиальный коэффициент textstyle {binom {n}{k}} для неотрицательных целых чисел n и k интерпретируется как количество сочетаний из n по k, то есть как количество всех (нестрогих) подмножеств (выборок) размера k в n-элементном множестве.

Биномиальные коэффициенты часто возникают в задачах комбинаторики и теории вероятностей. Обобщением биномиальных коэффициентов являются мультиномиальные коэффициенты.

Явные формулы[править | править код]

Вычисляя коэффициенты в разложении (1+x)^{n} в степенной ряд, можно получить явные формулы для биномиальных коэффициентов textstyle {binom {n}{k}}.

Для всех действительных чисел n и целых чисел k:

{displaystyle {binom {n}{k}}={begin{cases}{frac {n(n-1)(n-2)cdot ldots cdot (n-k+1)}{k!}},&kgeqslant 0\0,&k<0end{cases}}},

где k! обозначает факториал числа k.

Для неотрицательных целых n и k также справедливы формулы:

{displaystyle {binom {n}{k}}={begin{cases}{frac {n!}{k!(n-k)!}},&0leqslant kleqslant n\0,&k>nend{cases}}}.

Для целых отрицательных показателей коэффициенты разложения бинома {displaystyle (1+x)^{-n}} равны:

{displaystyle {binom {-n}{k}}={begin{cases}(-1)^{k}cdot {frac {(n+k-1)!}{k!(n-1)!}},&kgeqslant 0\0,&k<0end{cases}}}.

Треугольник Паскаля[править | править код]

Треугольник Паскаля.svg

Visualisation of binomial expansion up to the 4th power

Визуализация биномиального коэффициента до 4 степени

Тождество:

{n choose k}={n-1 choose k-1}+{n-1 choose k}

позволяет расположить биномиальные коэффициенты для неотрицательных целых чисел n, k в виде треугольника Паскаля, в котором каждое число равно сумме двух вышестоящих:

{begin{matrix}n=0:&&&&&1&&&&\n=1:&&&&1&&1&&&\n=2:&&&1&&2&&1&&\n=3:&&1&&3&&3&&1&\n=4:&1&&4&&6&&4&&1\vdots &&vdots &&vdots &&vdots &&vdots &end{matrix}}.

Треугольная таблица, предложенная Паскалем в «Трактате об арифметическом треугольнике» (1654), отличается от той, что выписана здесь, поворотом на 45°. Таблицы для изображения биномиальных коэффициентов были известны и ранее (Тарталье, Омару Хайяму).

Если в каждой строке треугольника Паскаля все числа разделить на 2^{n} (это сумма всех чисел в строке), то все строки при стремлении n к бесконечности примут вид функции нормального распределения.

Свойства[править | править код]

Производящие функции[править | править код]

Для фиксированного значения n производящей функцией последовательности биномиальных коэффициентов {displaystyle {tbinom {n}{0}},;{tbinom {n}{1}},;{tbinom {n}{2}},dots } является:

{displaystyle sum _{k=0}^{infty }{binom {n}{k}}x^{k}=(1+x)^{n}}.

Для фиксированного значения k производящая функция последовательности коэффициентов {displaystyle {tbinom {0}{k}},;{tbinom {1}{k}},;{tbinom {2}{k}},dots } равна:

{displaystyle sum _{n}{binom {n}{k}}y^{n}={frac {y^{k}}{(1-y)^{k+1}}}}.

Двумерной производящей функцией биномиальных коэффициентов tbinom{n}{k} для целых n,k является:

{displaystyle sum _{n,k}{binom {n}{k}}x^{k}y^{n}={frac {1}{1-y-xy}}}, или {displaystyle sum _{n=0}^{infty }sum _{k=0}^{n}{binom {n}{k}}x^{k}y^{n}={frac {1}{1-y-xy}}}.

Делимость[править | править код]

Из теоремы Люка следует, что:

Основные тождества[править | править код]

  • {n choose k}={n-1 choose k-1}+{n-1 choose k}.
  • {displaystyle {binom {n}{k}}=(-1)^{k}{binom {-n+k-1}{k}}}.
  • {n choose k}={n choose n-k} (правило симметрии).
  • {displaystyle {n choose k}={frac {n}{k}}{n-1 choose k-1}} (вынесение за скобки).
  • {displaystyle {n choose {color {Green}m}}{{color {Green}m} choose n-{color {Green}k}}={n choose {color {Green}k}}{{color {Green}k} choose n-{color {Green}m}}} (замена индексов).
  • {displaystyle (n-k){n choose k}=n{n-1 choose k}}.

Бином Ньютона и следствия[править | править код]

а более общем виде

{displaystyle sum _{k=-a}^{a}(-1)^{k}{a+b choose a+k}{b+c choose b+k}{c+a choose c+k}={frac {(a+b+c)!}{a!,b!,c!}}}.

Свёртка Вандермонда и следствия[править | править код]

Свёртка Вандермонда:

{displaystyle sum _{k}{r choose m+k}{s choose n-k}={r+s choose m+n}},

где {displaystyle m,nin mathbb {Z} ,} а {displaystyle r,sin mathbb {R} }. Это тождество получается вычислением коэффициента при {displaystyle x^{m+n}} в разложении {displaystyle (1+x)^{r}(1+x)^{s}} с учётом тождества {displaystyle (1+x)^{r+s}=(1+x)^{r}(1+x)^{s}}. Сумма берётся по всем целым k, для которых {displaystyle textstyle {r choose m+k}{s choose n-k}neq 0}. Для произвольных действительных r, s число ненулевых слагаемых в сумме будет конечно.

Следствие свёртки Вандермонда:

{n choose 0}{a choose a}-{n choose 1}{a+1 choose a}+ldots +(-1)^{n}{n choose n}{a+n choose a}=(-1)^{n}{a choose n}.

Более общее тождество:

sum _{{i=0}}^{{p}}(-1)^{i}{p choose i}prod _{{m=1}}^{{n}}{i+s_{m} choose s_{m}}=0, если sum _{{m=1}}^{n}{s_{m}}<p.

Ещё одним следствием свёртки является следующее тождество:
{displaystyle {n choose 0}^{2}+{n choose 1}^{2}+ldots +{n choose n}^{2}={2n choose n}}.

Другие тождества[править | править код]

{displaystyle {binom {n}{t}}+{binom {n}{t+s}}+{binom {n}{t+2s}}+ldots ={frac {1}{s}}sum _{j=0}^{s-1}left(2cos {frac {pi j}{s}}right)^{n}cos {frac {pi (n-2t)j}{s}}}.

Также имеют место равенства:

{displaystyle {begin{alignedat}{2}{binom {n}{3}}&={frac {n(n-1)(n-2)}{color {Green}2}}-sum _{i=2}^{n-1}{(n-i)(n-i+1)}=\&=n(n-1)(n-2)-sum _{i=2}^{n-1}{(n-i)({color {Green}2}n-i+1)}=\&=3{binom {n}{3}}-2{binom {n}{3}};\end{alignedat}}}
{displaystyle {begin{alignedat}{2}{binom {n}{4}}&={frac {n(n-1)(n-2)(n-3)}{color {Green}2}}-sum _{i=3}^{n-1}{(n-i)left(n(n-1)-sum _{i_{0}=1}^{i-2}i_{0}right)}=\&=n(n-1)(n-2)(n-3)-sum _{i=3}^{n-1}{(n-i)left({color {Green}2}n(n-1)-sum _{i_{0}=1}^{i-2}i_{0}right)}=\&=24{binom {n}{4}}-23{binom {n}{4}};\end{alignedat}}}
{displaystyle {begin{alignedat}{2}{binom {n}{5}}&={frac {n(n-1)(n-2)(n-3)(n-4)}{color {Green}2}}-\&-sum _{i=4}^{n-1}{(n-i)left(n(n-1)(n-2)-sum _{i_{0}=1}^{i-3}sum _{i_{1}=1}^{i_{0}}i_{1}right)}=\&=n(n-1)(n-2)(n-3)(n-4)-\&-sum _{i=4}^{n-1}{(n-i)left({color {Green}2}n(n-1)(n-2)-sum _{i_{0}=1}^{i-3}sum _{i_{1}=1}^{i_{0}}i_{1}right)}=\&=120{binom {n}{5}}-119{binom {n}{5}}.end{alignedat}}}

Откуда следует:

{displaystyle {binom {n}{3}}={frac {sum limits _{i=2}^{n-1}{(n-i)(2n-i+1)}}{2}}={frac {sum limits _{i=2}^{n-1}{(n-i)left(2A_{n}^{1}-{binom {i-1}{1}}right)}}{2}};}
{displaystyle {binom {n}{4}}={frac {sum limits _{i=3}^{n-1}{(n-i)left(2n(n-1)-sum limits _{i_{0}=1}^{i-2}i_{0}right)}}{23}}={frac {sum limits _{i=3}^{n-1}{(n-i)left(2A_{n}^{2}-{binom {i-1}{2}}right)}}{23}};}
{displaystyle {begin{alignedat}{2}&{binom {n}{5}}={frac {sum limits _{i=4}^{n-1}{(n-i)left(2n(n-1)(n-2)-sum limits _{i_{0}=1}^{i-3}sum limits _{i_{1}=1}^{i_{0}}i_{1}right)}}{119}}=\&={frac {sum limits _{i=4}^{n-1}{(n-i)left(2A_{n}^{3}-{binom {i-1}{3}}right)}}{119}};\end{alignedat}}}
{displaystyle {binom {n}{k}}={frac {sum limits _{i=k-1}^{n-1}{(n-i)left(2A_{n}^{k-2}-{binom {i-1}{k-2}}right)}}{k!-1}}},

где A_{n}^{k} — количество размещений из n по k.

Матричные соотношения[править | править код]

Если взять квадратную матрицу, отсчитав N элементов по катетам треугольника Паскаля и повернув матрицу на любой из четырёх углов, то детерминант этих четырёх матриц равен ±1 при любом N, причём детерминант матрицы с вершиной треугольника в верхнем левом углу равен 1.

В матрице {begin{bmatrix}{tbinom {i+j}{i}}end{bmatrix}} числа на диагонали {displaystyle i+j=mathrm {Const} } повторяют числа строк треугольника Паскаля ({displaystyle i,j=0,1,dots }). Её можно разложить в произведение двух строго диагональных матриц: нижнетреугольной и получаемой из неё транспонированием:

{displaystyle {begin{bmatrix}{binom {i+j}{i}}end{bmatrix}}=UU^{T}},

где U={begin{bmatrix}{tbinom {i}{j}}end{bmatrix}}. Обратная матрица к U имеет вид:

{displaystyle U^{-1}={begin{bmatrix}(-1)^{i+j}{binom {i}{j}}end{bmatrix}}}.

Таким образом, можно разложить обратную матрицу к {begin{bmatrix}{tbinom {i+j}{i}}end{bmatrix}} в произведение двух строго диагональных матриц: первая матрица — верхнетреугольная, а вторая получается из первой путём транспонирования, что позволяет дать явное выражение для обратных элементов:

{begin{bmatrix}{binom {i+j}{i}}end{bmatrix}}_{{m,n}}^{{-1}}=sum _{{k=0}}^{{p}}(-1)^{{m+n}}{binom {k}{m}}{binom {k}{n}}, где i, j, m, {displaystyle n=0dots p}.

Элементы обратной матрицы меняются при изменении её размера и, в отличие от матрицы {begin{bmatrix}{tbinom {i+j}{i}}end{bmatrix}}, недостаточно приписать новую строку и столбец. Столбец j матрицы {begin{bmatrix}{tbinom {i+j}{i}}end{bmatrix}} есть многочлен степени j по аргументу i, следовательно, первые p столбцов образуют полный базис в пространстве векторов длины p+1, чьи координаты могут быть интерполированы многочленом равной или меньшей степени p-1. Нижняя строка матрицы {begin{bmatrix}{binom {i+j}{i}}end{bmatrix}}_{{m,n}}^{{-1}} ортогональна любому такому вектору.

{begin{bmatrix}{binom {i+j}{i}}end{bmatrix}}_{{p,n}}^{{-1}}=sum _{{k=0}}^{{p}}(-1)^{{p+n}}{binom {k}{p}}{binom {k}{n}}=(-1)^{{p+n}}{binom {p}{n}}
sum _{{n=0}}^{{p}}(-1)^{{p+n}}{binom {p}{n}}{P}_{{a}}(n)=0 при a<p, где {P}_{{a}}(n) многочлен степени a.

Если произвольный вектор длины p+1 можно интерполировать многочленом степени i<p, то скалярное произведение со строками i+1,i+2,dots ,p (нумерация с 0) матрицы {begin{bmatrix}{binom {i+j}{i}}end{bmatrix}}_{{m,n}}^{{-1}} равно нулю.
Используя тождество выше и равенство единицы скалярного произведения нижней строки матрицы {begin{bmatrix}{binom {i+j}{i}}end{bmatrix}}_{{m,n}}^{{-1}} на последний столбец матрицы {begin{bmatrix}{tbinom {i+j}{i}}end{bmatrix}}, получаем:

{displaystyle sum _{n=0}^{p}(-1)^{p+n}{binom {p}{n}}{n}^{p}=p!}.

Для показателя большего p можно задать рекуррентную формулу:

{displaystyle sum _{n=0}^{p}(-1)^{p+n}{binom {p}{n}}{n}^{p+a}=p!{P}_{2a}(p)={f}_{a}(p)},

где многочлен

{displaystyle {P}_{2a+2}(p)=sum _{x=1}^{p}x{P}_{2a}(x);quad ageqslant 0;quad {P}_{0}(p)=1}.

Для доказательства сперва устанавливается тождество:

{displaystyle {f}_{a}(p+1)=sum _{x=0}^{a}{(p+1)}^{x+1}{f}_{a-x}(p)}.

Если требуется найти формулу не для всех показателей степени, то:

{displaystyle {P}_{2a}(p)={frac {p}{{2}^{a}}}{binom {p+a}{a}}{Q}_{a-1}(p);quad a>0}.

Старший коэффициент {Q}_{{a-1}}(p) равен 1, потребуется a-1 значений, чтобы найти другие коэффициенты:

{Q}_{{a-1}}(p)=p(p+1){T}_{{a-3}}(p) для {displaystyle aequiv 1{pmod {2}};ageqslant 3}.

Асимптотика и оценки[править | править код]

Непосредственно из формулы Стирлинга следует, что для alpha in (0;1) верно C_{n}^{{alpha n}}sim {sqrt {{frac {1}{2pi alpha (1-alpha )n}}}}left({{frac {1}{alpha }}}right)^{{alpha n}}left({{frac {1}{1-alpha }}}right)^{{(1-alpha )n}}=left({{frac {1}{alpha ^{alpha }{(1-alpha )}^{{(1-alpha )}}}}+o(1)}right)^{{n}}.

Целозначные полиномы[править | править код]

Биномиальные коэффициенты {displaystyle {tbinom {x}{0}}=1,{tbinom {x}{1}}=x,{tbinom {x}{2}}={tfrac {x^{2}}{2}}-{tfrac {x}{2}}}, … являются целозначными полиномами от x, то есть принимают целые значения при целых значениях x, — это нетрудно понять, например, по треугольнику Паскаля. Более того, они образуют базис целозначных полиномов, в котором все целозначные полиномы выражаются как линейные комбинации с целыми коэффициентами.[1]

В то же время стандартный базис {displaystyle 1,x,x^{2}}, … не позволяет выразить все целочисленные полиномы, если использовать только целые коэффициенты, так как уже {displaystyle {tbinom {x}{2}}={tfrac {x^{2}}{2}}-{tfrac {x}{2}}} имеет дробные коэффициенты при степенях x.

Этот результат обобщается на полиномы многих переменных. А именно, если полином R(x_1, dots, x_m) степени k имеет вещественные коэффициенты и принимает целые значения при целых значениях переменных, то

{displaystyle R(x_{1},dots ,x_{m})=Pleft({binom {x_{1}}{1}},dots ,{binom {x_{1}}{k}},dots ,{binom {x_{m}}{1}},dots ,{binom {x_{m}}{k}}right)},

где P — полином с целыми коэффициентами.[2]

Алгоритмы вычисления[править | править код]

Биномиальные коэффициенты можно вычислить с помощью рекуррентной формулы {tbinom {n}{k}}={tbinom {n-1}{k}}+{tbinom {n-1}{k-1}}, если на каждом шаге n хранить значения tbinom{n}{k} при {displaystyle k={overline {0,1,;ldots ,n}}}. Этот алгоритм особенно эффективен, если нужно получить все значения tbinom{n}{k} при фиксированном n. Алгоритм требует O(n) памяти (O(n^{2}) при вычислении всей таблицы биномиальных коэффициентов) и O(n^{2}) времени (в предположении, что каждое число занимает единицу памяти и операции с числами выполняются за единицу времени), где O — «o» большое.

При фиксированном значении k биномиальные коэффициенты могут быть вычислены по рекуррентной формуле {displaystyle {tbinom {n}{k}}={tfrac {n}{n-k}}cdot {tbinom {n-1}{k}}} с начальным значением {tbinom {k}{k}}=1. Для вычисления значения tbinom{n}{k} этот метод требует O(1) памяти и O(n) времени.

Если требуется вычислить коэффициенты tbinom{n}{k} при фиксированном значении n, можно воспользоваться формулой {displaystyle {tbinom {n}{k}}={tfrac {n-k+1}{k}}cdot {tbinom {n}{k-1}}} при начальном условии {displaystyle {tbinom {n}{0}}=1}. При каждом шаге итерации числитель уменьшается на 1 (начальное значение равно n), а знаменатель соответственно увеличивается на 1 (начальное значение — 1). Для вычисления значения tbinom{n}{k} этот метод требует O(1) памяти и O(k) времени.

Примечания[править | править код]

  1. ↑ Прасолов В. В. Глава 12. Целозначные многочлены // Многочлены. — М.: МЦНМО, 1999, 2001, 2003. Архивная копия от 21 января 2022 на Wayback Machine
  2. ↑ Ю. Матиясевич. Десятая проблема Гильберта. — Наука, 1993.

Литература[править | править код]

  • Биномиальные коэффициенты // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
  • Фукс Д., Фукс М. Арифметика биномиальных коэффициентов // Квант. — 1970. — № 6. — С. 17—25.
  • Кузьмин О. В. Треугольник и пирамида Паскаля: свойства и обобщения // Соросовский Образовательный Журнал. — 2000. — Т. 6, № 5. — С. 101—109.
  • Ландо С. К. Теневое исчисление // VIII летняя школа «Современная математика». — Дубна, 2008.
  • Винберг Э. Б. Удивительные арифметические свойства биномиальных коэффициентов // Математическое просвещение. — 2008. — Вып. 12. — С. 33–42.
  • Дональд Кнут, Роналд Грэхем, Орен Паташник. Конкретная математика. Математические основы информатики = Concrete Mathematics. A Foundation for Computer Science. — 2-е. — М.: Мир; Бином. Лаборатория знаний; «Вильямс», 1998—2009. — 703, 784 с. — ISBN 95-94774-560-7, 78-5-8459-1588-7.
Источник

Бином Ньютона – формула

Определение 1

С натуральным n формула Бинома Ньютона принимает вид a+bn=Cn0·an+Cn1·an-1·b+Cn2·an-2·b2+…+Cnn-1·a·bn-1+Cnn·bn, где имеем, что Cnk=(n)!(k)!·(n-k)!=n(n-1)·(n-2)·…·(n-(k-1))(k)!- биномиальные коэффициенты, где есть n по k, k=0,1,2,…,n, а “!” является знаком факториала.

В формуле сокращенного умножения a+b2=C20·a2+C21·a1·b+C22·b2=a2+2ab+b2
просматривается формула бинома Ньютона, так как при n=2 является его частным случаем.

Первая часть бинома называют разложением (a+b)n, а Сnk·an-k·bk – (k+1)-ым членом разложения, где k=0,1,2, …,n.

Коэффициенты бинома Ньютона, свойства биномиальных коэффициентов, треугольник Паскаля

Представление биномиальных коэффициентов для различных n осуществляется при помощи таблицы, которая имеет название арифметического треугольника Паскаля. Общий вид таблицы:

Показатель степени Биноминальные коэффициенты
0           C00          
1         C10   C11        
2       C20   C21   C22      
3     C30   C31   C32   C33    
⋮   … … … … … … … … …  
n Cn0   Cn1 … … … … … Cnn-1   Cnn

При натуральных n такой треугольник Паскаля состоит из значений коэффициентов бинома:

Показатель степени Биноминальные коэффициенты
0               1              
1             1   1            
2           1   2   1          
3         1   3   3   1        
4       1   4   6   4   1      
5     1   5   10   10   5   1    
⋮   … … … … … … … … … … … … …  
n Cn0   Cn1 … … … … … … … … … Cnn-1   Cnn

Боковые стороны треугольника имеют значение единиц. Внутри располагаются числа, которые получаются при сложении двух чисел соседних сторон. Значения, которые выделены красным, получают как сумму четверки, а синим – шестерки. Правило применимо для всех внутренних чисел, которые входят в состав треугольника. Свойства коэффициентов объясняются при помощи бинома Ньютона.

Доказательство формулы бинома Ньютона

Имеются равенства, которые справедливы для коэффициентов бинома Ньютона:

  • коэффициента располагаются равноудалено от начала и конца, причем равны, что видно по формуле Cnp=Cnn-p, где р=0, 1, 2, …, n;
  • Cnp=Cnp+1=Cn+1p+1;
  • биномиальные коэффициенты в сумме дают 2 в степени показателя степени бинома, то есть Cn0+Cn1+Cn2+…+Cnn=2n;
  • при четном расположении биноминальных коэффициентов их сумма равняется сумме биномиальных коэффициентов, расположенных в нечетных местах.

Равенство вида a+bn=Cn0·an+Cn1·an-1·b+Cn2·an-2·b2+…+Cnn-1·a·bn-1+Cnn·bn считается справедливым. Докажем его существование.

Для этого необходимо применить метод математической индукции.

Для доказательства необходимо выполнить несколько пунктов:

  1. Проверка справедливости разложения при n=3. Имеем, что
    a+b3=a+ba+ba+b=a2+ab+ba+b2a+b==a2+2ab+b2a+b=a3+2a2b+ab2+a2b+2ab+b3==a3+3a2b+3ab2+b3=C30a3+C31a2b+C32ab2+C33b3
  2. Если неравенство верно при n-1, тогда выражение вида a+bn-1=Cn-10·an-1·Cn-11·an-2·b·Cn-12·an-3·b2+…+Cn-1n-2·a·bn-2+Cn-1n-1·bn-1

считается справедливым.

  1. Доказательство равенства a+bn-1=Cn-10·an-1·Cn-11·an-2·b·Cn-12·an-3·b2+…+Cn-1n-2·a·bn-2+Cn-1n-1·bn-1, основываясь на 2 пункте.
Доказательство 1

Выражению

a+bn=a+ba+bn-1==(a+b)Cn-10·an-1·Cn-11·an-2·b·Cn-12·an-3·b2+…+Cn-1n-2·a·bn-2+Cn-1n-1·bn-1

Необходимо раскрыть скобки, тогда получимa+bn=Cn-10·an+Cn-11·an-1·b+Cn-12·an-2·b2+…+Cn-1n-2·a2·bn-2++Cn-1n-1·a·bn-1+Cn-10·an-1·b+Cn-11·an-2·b2+Cn-12·an-3·b3+…+Cn-1n-2·a·bn-1+Cn-1n-1·bn

Производим группировку слагаемых

a+bn==Cn-10·an+Cn-11+Cn-10·an-1·b+Cn-12+Cn-11·an-2·b2+…++Cn-1n-1+Cn-1n-2·a·bn-1+Cn-1n-1·bn

Имеем, что Cn-10=1 и Cn0=1, тогда Cn-10=Cn0. Если Cn-1n-1=1 и Cnn=1, тогда Cn-1n-1=Cnn. При применении свойства сочетаний Cnp+Cnp+1=Cn+1p+1, получаем выражение вида

Cn-11+Cn-10=Cn1Cn-12+Cn-11=Cn2⋮Cn-1n-1+Cn-1n-2=Cnn-1

Произведем подстановку в полученное равенство. Получим, что

a+bn==Cn-10·an+Cn-11+Cn-10·an-1·b+Cn-12+Cn-11·an-2·b2+…++Cn-1n-1+Cn-1n-2·a·bn-1=Cn-1n-1·bn

После чего можно переходить к биному Ньютона, тогда a+bn=Cn0·an+Cn1·an-1·b+Cn2·an-2·b2+…+Cnn-1·a·bn-1+Cnn·bn.

Формула бинома доказана.

Бином Ньютона – применение при решении примеров и задач

Для полного понятия использования формулы рассмотрим примеры.

Пример 1

Разложить выражение (a+b)5 , используя формулу бинома Ньютона.

Решение

По треугольнику Паскаля с пятой степенью видно, что биноминальные коэффициенты – это 1, 5, 10, 10, 5, 1. То есть, получаем, что a+b5=a5+5a4b+10a3b2+10a2b3+5ab4+b5 является искомым разложением.

Ответ: a+b5=a5+5a4b+10a3b2+10a2b3+5ab4+b5

Пример 2

Найти коэффициенты бинома Ньютона для шестого члена разложения выражения вида a+b10.

Решение

По условию имеем, что n=10, k=6-1=5. Тогда можно перейти к вычислению биномиального коэффициента:

Cnk=C105=(10)!(5)!·10-5!=(10)!(5)!·(5)!==10·9·8·7·6(5)!=10·9·8·7·61·2·3·4·5=252

Ответ: Cnk=C105=252

Ниже приведен пример, где используется бином для доказательства делимости выражения с заданным числом.

Пример 3

Доказать, что значение выражения 5n+28·n-1, при n, являющимся натуральным числом, делится на 16 без остатка.

Решение

Необходимо представить выражение в виде 5n=4+1n и воспользоваться биномом Ньютона. Тогда получим, что

5n+28·n-1=4+1n+28·n-1==Cn0·4n+Cn1·4n-1·1+…+Cnn-2·42·1n-2+Cnn-1·4·1n-1+Cnn·1n+28·n-1==4n+Cn1·4n-1+…+Cnn-2·42+n·4+1+28·n-1==4n+Cn1·4n-1+…+Cnn-2·42+32·n==16·(4n-2+Cn1·4n-3+…+Cnn-2+2·n)

Ответ: Исходя из полученного выражения, видно, что исходное выражение делится на 16.

Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Источник

Продолжаем рассказывать о разных формулах и подходах из математики, которые часто применяются в ИТ и в привычных алгоритмах. Сегодня будет про бином Ньютона — про него много кто слышал, но не все представляют, что это и зачем это нужно. Сейчас разложим по полочкам. 

Чтобы понять бином Ньютона, нам понадобится треугольник Паскаля.

Что такое треугольник Паскаля

Треугольник Паскаля — это одно из названий треугольной таблицы чисел. Его назвали в честь математика Блеза Паскаля, но про такой треугольник математики знали тысячу лет назад. 

Работает треугольник так: берём единицу (это будет вершина треугольника), а все остальные числа в каждом ряду получаем сложением левых и правых чисел, которые стоят выше. Если нарисовать, то получится так:

Что такое бином Ньютона и почему им всех пугают

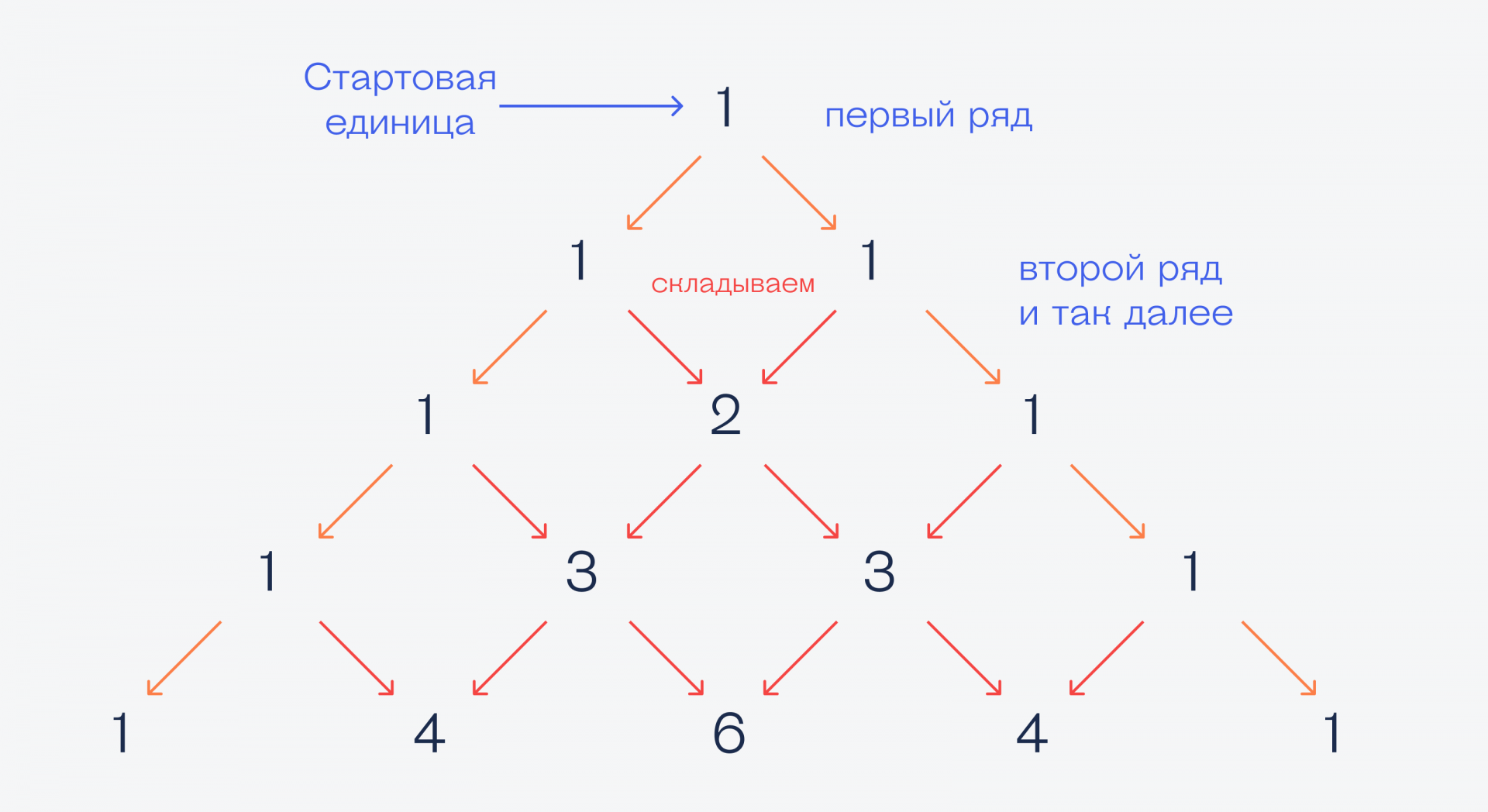
Такой треугольник можно продолжать бесконечно. В математике этот треугольник обладает разными полезными свойствами, но нам он нужен для биномиальных коэффициентов в биноме Ньютона. Вот теперь поговорим про бином.

Что такое бином Ньютона (просто)

Бином Ньютона — это формула, которая помогает посчитать сумму двух чисел, возведенную в какую-то степень.

Разбираем по полочкам: 

  • У нас есть некие числа a и b. Мы не знаем какие, потому что алгебра.
  • Не зная, что это за числа, мы их складываем.
  • Эту сумму почему-то очень хочется возвести в какую-то степень — в квадрат, в куб, в четвертую, хоть в девятьсот девяносто девятую — алгебре плевать на ваши чувства.
  • Нам нужна формула, как это сделать. Вот эта формула и есть бином Ньютона. 

Из школьной программы мы помним такую формулу: (a + b)2 = a2 + 2ab + b2 — это частный случай бинома Ньютона для квадрата суммы. 

Может быть, вы помните сумму в кубе: (a + b)3 = a3 + 3a2b + 3ab2 + b3 — это тоже бином Ньютона. 

А что если нам нужно возвести сумму не в квадрат, не в куб, а в сто сорок шестую степень? Какая тогда будет формула? Вот для этого нам нужна более обобщенная формула, которая опишет вообще все варианты биномов для любой степени.

Вот как эта формула выглядит в общем виде:

Что такое бином Ньютона и почему им всех пугают

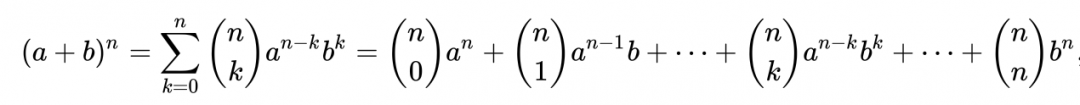
Про знак Σ мы уже говорили — это обозначение суммы, а цифры в больших скобках — это биномиальные коэффициенты. В общем виде они считаются так:

Что такое бином Ньютона и почему им всех пугают

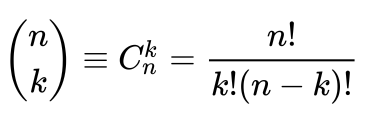
Исходя из этой адской формулы для расчета бинома на компьютере нам нужно будет много раз посчитать факториал — это произведение всех целых чисел от единицы до заданного числа. Например, 5! = 1 × 2 × 3 × 4 × 5 = 120. А факториалы в силу своей цикличности жрут довольно много оперативной памяти. Может так получиться, что мы не сможем посчитать коэффициенты бинома, потому что закончилась оперативка.

Но, оказывается, необязательно считать факториалы — есть способ проще.

Биномиальные коэффициенты и треугольник Паскаля (простая теория в картинках)

Тут нам приходит на помощь треугольник Паскаля. Оказывается, числа в каждом ряду — это биномиальные коэффициенты для каждой степени n:

Что такое бином Ньютона и почему им всех пугают

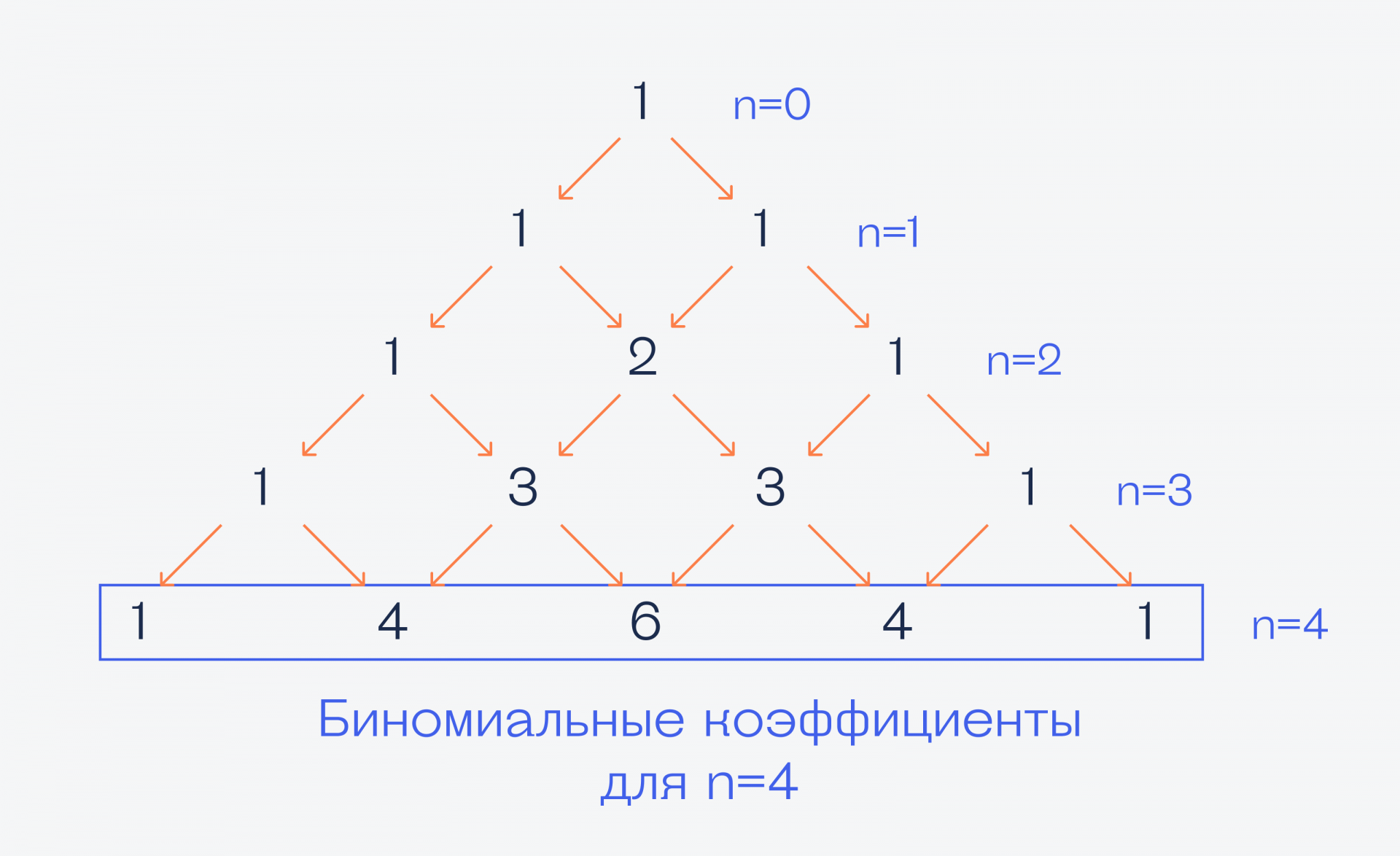
На практике это работает так: допустим, что по ходу работы алгоритма нам нужно раскрыть скобки и вычислить (x + y)⁴. Применим сюда бином Ньютона и треугольник Паскаля:

Что такое бином Ньютона и почему им всех пугают

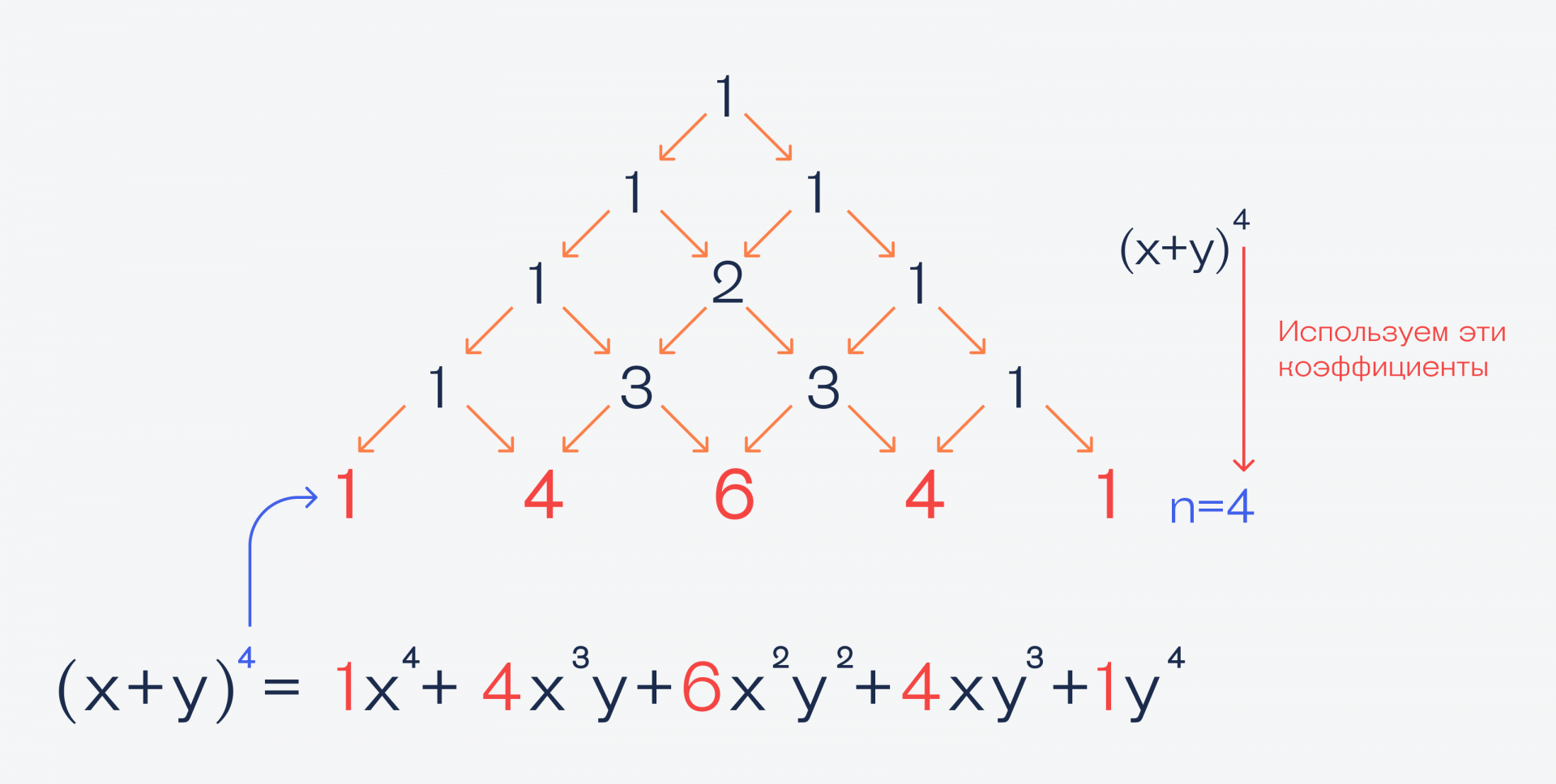
Получается, что с помощью этого треугольника можно не считать все эти формулы с факториалами, а быстро находить нужные коэффициенты, подставлять их в формулу бинома и сразу получать ответ. Так можно разложить любой бином и получить ответ гораздо быстрее, чем вычисляя все факториалы подряд.

Где используется бином Ньютона

Кроме математики, где бином нужен для комбинаторики и разных полезных формул, он часто применяется в программировании. Например, с его помощью можно обойти ограничение на размер оперативной памяти при возведении большого числа в степень: его можно разложить на сумму двух чисел поменьше и посчитать слагаемые через бином. 

Также биномиальные коэффициенты часто применяются в матрицах и операциях с векторами — а именно на матрицах построены почти все нейросети. Поэтому если мы сможем быстро находить нужный коэффициент и применять его к матрице, то сможем быстрее создавать дипфейки и генерировать реалистичные пейзажи. Строго говоря, для этого сейчас нужно просто знать команду import, потому что готовых библиотек на эту тему — вагон, без всяких биномов. 

А ещё на биномиальных коэффициентах работает отдельная непозиционная система счисления — её применяют в проектах, где надо быстро перебирать много различных вариантов и их возможных сочетаний.

Что дальше

Дальше мы попробуем применить эти знания и алгоритмы на практике: напишем код, который использует бином Ньютона для решения разных хитрых бытовых задач. 

Вёрстка:

Кирилл Климентьев

Источник

Бином Ньютона и треугольник Паскаля

18 декабря 2021

Сегодня мы детально разберём Бином Ньютона. Это формула, по которой можно раскрыть скобки ${{left( a+b right)}^{n}}$ и получить готовый многочлен. Сама формула выглядит так:

[{{left( a+b right)}^{n}}=sumlimits_{k=0}^{n}{C_{n}^{k}cdot {{a}^{n-k}}{{b}^{k}}}]

где $C_{n}^{k}$ — биноминальные коэффициенты (они же — «число сочетаний из $n$ по $k$»), которые считаются по формуле

[C_{n}^{k}=frac{n!}{k!left( n-k right)!}]

Вот и всё. На этом можно было бы закончить, но есть одно но: большинство начинающих учеников не понимают эту формулу, не умеют пользоваться её, а уж чтобы доказать её — об этом даже речи не идёт.

Сегодня мы всё это исправим. Вы узнаете буквально всё, что нужно знать про Бином Ньютона:

  1. Постановка задачи — в чём вообще проблема?
  2. Формула бинома Ньютона — что значат все эти значки?
  3. Знак суммы — чрезвычайно полезный материал для всех, кто хочет понять математику.
  4. Биноминальные коэффициенты — минутка комбинаторики.
  5. Треугольник Паскаля — лайфхак для быстрых вычислений.
  6. Доказательство Бинома Ньютона — для тех, кто хочет познать Истину.:)

Материала много, но всё будет максимально понятно и — главное — чрезвычайно полезно. Погнали!

1. Постановка задачи

Итак, мы хотим быстро раскрывать скобки в конструкциях вида ${{left( a+b right)}^{n}}$. Начнём с того, что мы и так знаем. Например:

[{{left( a+b right)}^{1}}=a+b]

Спасибо, кэп. Теперь вспомним формулы сокращённого умножения. Квадрат суммы:

[{{left( a+b right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}]

И куб суммы:

[{{left( a+b right)}^{3}}={{a}^{3}}+3{{a}^{2}}b+3a{{b}^{2}}+{{b}^{3}}]

Видим, что с ростом степени растёт и количество слагаемых-одночленов: их всегда на одно больше, чем степень. Но это не проблема. Проблема в другом: у этих одночленов появляются некие коэффициенты, принцип вычисления которых не ясен. Пока не ясен…

Именно для нахождения этих коэффициентов придумали бином Ньютона.

2. Бином Ньютона

Пусть $nin mathbb{N}$. Тогда верно равенство

[{{left( a+b right)}^{n}}=sumlimits_{k=0}^{n}{C_{n}^{k}cdot {{a}^{n-k}}{{b}^{k}}}]

где $sum{left( … right)}$ — краткая запись суммы, $C_{n}^{k}$ — биноминальный коэффициент, который считается по формуле

[C_{n}^{k}=frac{n!}{k!left( n-k right)!}]

В этой формуле прекрасно всё. Одних пугает знак суммы. Другие не понимают, что за $C_{n}^{k}$ такое (ещё раз: это объект из мира комбинаторики, читается «число сочетаний из $n$ по $k$»). Третьи более-менее понимают, о чём речь, но применить эту формулу на практике не могут.

Сегодня мы решим все эти проблемы. Начнём со знака суммы.

3. Знак суммы

Знак суммы — это краткая запись суммы нескольких однотипных слагаемых:

[sumlimits_{k=a}^{k=b}{fleft( k right)}]

Формула $fleft( k right)$ задаёт общий вид однотипных слагаемых, а нижний и верхний индексы $k=a$ и $k=b$ (сверху вместо $k=b$ обычно пишут просто $b$) определяют диапазон значений, которые «пробегает» $k$ и которые нужно подставить в $fleft( k right)$. Например:

[sumlimits_{k=3}^{5}{2k}=2cdot 3+2cdot 4+2cdot 5]

Более привычный формат:

[sumlimits_{k=1}^{n}{fleft( k right)=fleft( 1 right)+fleft( 2 right)+…+fleft( n right)}]

То же самое с индексами:

[sumlimits_{k=1}^{n}{{{a}_{k}}={{a}_{1}}+{{a}_{2}}+…+{{a}_{n}}}]

Обратите внимание: если $k$ пробегает значения от $k=a$ до $k=b$, то всего таких слагаемых будет ровно $b-a+1$:

[sumlimits_{k=a}^{b}{fleft( k right)=underbrace{fleft( a right)+fleft( a+1 right)+ldots +fleft( b right)}_{b-a+1text{ слагаемых!}}}]

Кроме того, полезно потренироваться и с обратным переходом — от полной записи к краткой:

[frac{1}{1}+frac{1}{3}+frac{1}{5}+frac{1}{7}+frac{1}{9}=sumlimits_{n=1}^{5}{frac{1}{2n-1}}]

[frac{2}{3}+frac{4}{9}+frac{6}{27}+frac{8}{81}=sumlimits_{n=1}^{4}{frac{2n}{{{3}^{n}}}}]

В приложении к уроку — куча задач для самостоятельной тренировки.

Но вернёмся к биному Ньютона. Распишем его без знака суммы:

[begin{align} {{left( a+b right)}^{n}} & =C_{n}^{0}cdot {{a}^{n}}{{b}^{0}}+C_{n}^{1}cdot {{a}^{n-1}}{{b}^{1}}+ \ & +ldots +C_{n}^{k}cdot {{a}^{n-k}}{{b}^{k}}+ldots + \ & +C_{n}^{n-1}cdot {{a}^{1}}{{b}^{n-1}}+C_{n}^{n}cdot {{a}^{0}}{{b}^{n}} end{align}]

В целом, всё понятно: степени буквы $a$ уменьшаются с ${{a}^{n}}$ до ${{a}^{0}}$; одновременно степени буквы $b$ растут с ${{b}^{0}}$ до ${{b}^{n}}$. Сумма степеней этих букв в каждом одночлене равна $n$. Но что такое $C_{n}^{k}$?

4. Биноминальные коэффициенты

Немного комбинаторики.

Определение. Число сочетаний из $n$ по $k$ — это число способов, которыми можно выбрать $k$ элементов среди $n$ элементов, если порядок выбора не имеет значения. Обозначается $C_{n}^{k}$ и считается по формуле

[C_{n}^{k}=frac{n!}{k!left( n-k right)!}]

Обратите внимание: в числителе и знаменателе стоят факториалы. Стандартное определение: $n!$ — это произведение всех чисел от единицы до $n$:

[n!=1cdot 2cdot 3cdot …cdot n]

У факториалов много интересных свойств. Чуть позже мы рассмотрим их и даже введём более корректное определение самого факториала. А пока просто потренируемся считать биноминальные коэффициенты.

Пример. На пруду плавают 5 уток. Сколькими способами можно выбрать 2 из них, чтобы покормить?

Очевидно, порядок кормления уток неважен. Покормить сначала утку №1, а затем №2 — это то же самое, что покормить сначала утку №2, затем №1. Результат один и тот же: накормлены лишь эти две утки, а остальные три — нет. Поэтому считаем $C_{5}^{2}$:

[begin{align} C_{5}^{2} & =frac{5!}{2!cdot 3!} \ & =frac{5cdot 4cdot 3cdot 2cdot 1}{2cdot 1cdot 3cdot 2cdot 1}= \ & =10 end{align}]

Вот и всё. Однако при больших $n$ и $k$ посчитать число сочетаний напрямую становится затруднительно. Тут на помощь приходит сокращение дробей.

Пример. На пруду 150 уток. Сколькими способами можно выбрать 2 из них, чтобы покормить?

Порядок вновь неважен, просто уток стало больше. Поэтому считаем $C_{150}^{2}$:

[begin{align} C_{150}^{2} & =frac{150!}{2!cdot 148!}= \ & =frac{150cdot 149cdot 148cdot …cdot 1}{2cdot 1cdot 148cdot …cdot 1}= \ & =frac{150cdot 149}{2cdot 1}= \ & =11175 end{align}]

Видим, что факториалы образуют «длинные хвосты» в числителе и знаменателе, которые легко сокращаются. Однако для корректной работы с биномом Ньютона нам потребуется расширить определение факториала.

4.1. Новое определение факториала

Стандартное определение мы уже привели выше:

[n!=1cdot 2cdot 3cdot …cdot n,quad nin mathbb{N}]

Но как посчитать, например, факториал нуля? И как сокращать «длинные хвосты», не расписывая факториалы? Здесь нам поможет более грамотное определение.

Определение. Пусть $nin mathbb{N}bigcup left{ 0 right}$ — целое неотрицательное число. Тогда факториал считается по формуле:

[n!=left{ begin{align} & 1,quad n=0 \ & ncdot left( n-1 right)!,quad n gt 0 \ end{align} right.]

В частности, $0!=1$ по определению.

Простейшие коэффициенты:

[begin{align} C_{n}^{0} & =frac{n!}{0!left( n-0 right)!}=frac{n!}{1cdot n!}=1; \ C_{n}^{1} & =frac{n!}{1!left( n-1 right)!}=frac{ncdot left( n-1 right)!}{1cdot left( n-1 right)!}=n; \ end{align}]

А вот ещё парочка весёлых примеров:

[begin{align} C_{7}^{3} & =frac{7cdot 6cdot 5cdot 4cdot ldots cdot 1}{3cdot 2cdot 1cdot 4cdot ldots cdot 1}=35 \ C_{8}^{2} & =frac{8cdot 7cdot 6cdot ldots cdot 1}{2cdot 1cdot 6cdot ldots cdot 1}=28 \ C_{64}^{3} & =frac{64cdot 63cdot 62cdot 61cdot ldots cdot 1}{3cdot 2cdot 1cdot 61cdot ldots cdot 1}= \ & =41664 end{align}]

5. Треугольник Паскаля

Посчитаем бином Ньютона для $n=0$, $n=1$, $n=2$, $n=3$:

[begin{align} & {{left( a+b right)}^{0}}=1 \ & {{left( a+b right)}^{1}}=1cdot a+1cdot b \ & {{left( a+b right)}^{2}}=1cdot {{a}^{2}}+2cdot ab+1cdot {{b}^{2}} \ & {{left( a+b right)}^{3}}=1cdot {{a}^{3}}+3cdot {{a}^{2}}b+3cdot a{{b}^{2}}+1cdot {{b}^{3}} \ end{align}]

Составим таблицу:

[begin{matrix} 1 \ 1quad 1 \ 1quad 2quad 1 \ 1quad 3quad 3quad 1 \ 1quad 4quad 6quad 4quad 1 \ end{matrix}]

Получили треугольник, который в народе называют «Треугольник Паскаля»: по бокам единицы, а внутри каждое число равно сумме двух ближайших, стоящих этажом выше:

[begin{align} & 3=1+2 \ & 4=1+3 \ & 6=3+3 \ end{align}]

И это не случайность. Перед нами важнейшее свойство биноминальных коэффициентов, которое мы оформим в виде теоремы и докажем.

Теорема. Биноминальные коэффициенты вычисляются по формуле

[C_{n}^{k}+C_{n}^{k+1}=C_{n+1}^{k+1}]

Доказывается напролом.

Распишем доказательство детально:

[C_{n}^{k}+C_{n}^{k+1}=frac{n!}{k!left( n-k right)!}+frac{n!}{left( k+1 right)!left( n-k-1 right)!}]

[begin{align} & C_{n}^{k}+C_{n}^{k+1}= \ = & frac{n!}{k!left( n-k right)!}+frac{n!}{left( k+1 right)!left( n-k-1 right)!} \ end{align}]

Заметим, что по определению факториала

[begin{align} & left( k+1 right)!=left( k+1 right)cdot k! \ & left( n-k right)!=left( n-k right)cdot left( n-k-1 right)! end{align}]

Поэтому знаменатели биноминальных коэффициентов можно переписать:

[C_{n}^{k}+C_{n}^{k+1}=frac{n!}{k!left( n-k right)left( n-k-1 right)!}+frac{n!}{left( k+1 right)k!left( n-k-1 right)!}]

[begin{align} C_{n}^{k}+C_{n}^{k+1} & =frac{n!}{k!left( n-k right)left( n-k-1 right)!}+ \ & +frac{n!}{left( k+1 right)k!left( n-k-1 right)!} end{align}]

Приведём к общему знаменателю:

[begin{align} C_{n}^{k}+C_{n}^{k+1} & =frac{left( k+1 right)cdot n!}{left( k+1 right)!left( n-k right)!}+frac{left( n-k right)cdot n!}{left( k+1 right)!left( n-k right)!}= \ & =frac{left( k+1+n-k right)cdot n!}{left( k+1 right)!left( n-k right)!}= \ & =frac{left( n+1 right)cdot n!}{left( k+1 right)!left( n-k right)!} end{align}]

[begin{align} & C_{n}^{k}+C_{n}^{k+1}= \ = & frac{left( k+1 right)cdot n!}{left( k+1 right)!left( n-k right)!}+frac{left( n-k right)cdot n!}{left( k+1 right)!left( n-k right)!}= \ = & frac{left( k+1+n-k right)cdot n!}{left( k+1 right)!left( n-k right)!}=frac{left( n+1 right)cdot n!}{left( k+1 right)!left( n-k right)!} \ end{align}]

Окончательно получим:

[begin{align} C_{n}^{k}+C_{n}^{k+1} & =frac{left( n+1 right)!}{left( k+1 right)!left( n-k right)!}= \ & =frac{left( n+1 right)!}{left( k+1 right)!left( n+1-left( k+1 right) right)!}= \ & = C_{n+1}^{k+1} end{align}]

Теорема доказана. Теперь мы знаем, как формируется треугольник Паскаля. Осталось доказать сам Бином Ньютона.

6. Доказательство Бинома Ньютона

Итак, нужно доказать, что

[{{left( a+b right)}^{n}}=sumlimits_{k=0}^{n}{C_{n}^{k}cdot {{a}^{n-k}}{{b}^{k}}}]

где $C_{n}^{k}$ — биноминальные коэффициенты с теми чудесными свойствами, которые мы рассмотрели и доказали выше.

Будем доказывать по индукции.

6.1. База индукции

Рассмотрим $n=1$. Формула Бинома Ньютона для него:

[begin{align} {{left( a+b right)}^{1}} & =sumlimits_{k=0}^{1}{C_{1}^{k}{{a}^{1-k}}{{b}^{k}}}= \ & =C_{1}^{0}{{a}^{1}}{{b}^{0}}+C_{1}^{1}{{a}^{0}}{{b}^{1}}= \ & =a+bend{align}]

Очевидно, для $n=1$ формула верна. Переходим к индуктивному предположению.

6.2. Индуктивное предположение

Пусть Бином Ньютона верен для некоторого $n=t$:

[{{left( a+b right)}^{t}}=sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k}}}]

Используя этот факт, докажем верность и для $n=t+1$, т.е. выполним индуктивный переход.

6.3. Индуктивный переход

Докажем, что бином Ньютона верен для $n=t+1$:

[{{left( a+b right)}^{t+1}}=sumlimits_{k=0}^{t+1}{C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}]

Для этого сначала заметим, что

[{{left( a+b right)}^{t+1}}={{left( a+b right)}^{t}}cdot left( a+b right)]

Однако согласно индуктивному предположению, ${{left( a+b right)}^{t}}$ допускает разложение по Биному Ньютона, поэтому

[begin{align} left( a+b right)cdot {{left( a+b right)}^{t}} & =left( a+b right)cdot sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k}}}= \ & =acdot sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k}}}+bcdot sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k}}}= \ & =sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}} end{align}]

[begin{align} & left( a+b right)cdot {{left( a+b right)}^{t}}= \ = & left( a+b right)cdot sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k}}}= \ = & acdot sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k}}}+bcdot sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k}}}= \ = & sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}} \ end{align}]

Запишем отдельно первое слагаемое первой суммы и учтём, что $C_{t}^{0}=C_{t+1}^{0}=1$:

[begin{align} sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}} & = C_{t}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}} \ & = C_{t+1}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}} end{align}]

[begin{align} & sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}= \ = & C_{t}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}} \ = & C_{t+1}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}} \ end{align}]

И последнее слагаемое последней второй суммы и учтём, что $C_{t}^{t}=C_{t+1}^{t+1}=1$:

[begin{align} sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}} & =sumlimits_{k=0}^{t-1}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}+C_{t}^{t}cdot {{b}^{t+1}} \ & =sumlimits_{k=0}^{t-1}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}} end{align}]

[begin{align} & sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}= \ = & sumlimits_{k=0}^{t-1}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}+C_{t}^{t}cdot {{b}^{t+1}} \ = & sumlimits_{k=0}^{t-1}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}} \ end{align}]

Сейчас будет самая нетривиальная операция. Меняем индекс суммирования в последней сумме: выполняем подстановку $k=m-1$. При этом меняются и пределы суммирования:

[left[ begin{align} k & =m-1 \ k & =0Rightarrow m=1 \ k & =t-1Rightarrow m=t \ k+1 & =m \ t-k & =t+1-m \ end{align} right]]

В итоге последняя сумма перепишется так:

[sumlimits_{k=0}^{t-1}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}}=sumlimits_{m=1}^{t}{C_{t}^{m-1}cdot {{a}^{t+1-m}}{{b}^{m}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}}]

[begin{align} & sumlimits_{k=0}^{t-1}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}}= \ = & sumlimits_{m=1}^{t}{C_{t}^{m-1}cdot {{a}^{t+1-m}}{{b}^{m}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}} \ end{align}]

Объединяем суммы вместе:

[begin{align} & sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}= \ = & C_{t+1}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+sumlimits_{m=1}^{t}{C_{t}^{m-1}cdot {{a}^{t+1-m}}{{b}^{m}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}} \ end{align}]

[begin{align} & sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}= \ = & C_{t+1}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+ \ + & sumlimits_{m=1}^{t}{C_{t}^{m-1}cdot {{a}^{t+1-m}}{{b}^{m}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}} \ end{align}]

Заметим, что два знака суммы различаются лишь названием индекса и биноминальными коэффициентами. Всё остальное — диапазоны суммирования, степени буквы $a$ и буквы $b$ — всё идеально совпадает и никак не меняется, если написать вместо $k$ индекс $m$ или наоборот.

Такие суммы можно записать под единым знаком:

[C_{t+1}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{left( C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}+C_{t}^{k-1}cdot {{a}^{t+1-k}}{{b}^{k}} right)}+C_{t+1}^{t+1}cdot {{b}^{t+1}}]

[begin{align} & C_{t+1}^{0}cdot {{a}^{t+1}}+ \ + & sumlimits_{k=1}^{t}{left( C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}+C_{t}^{k-1}cdot {{a}^{t+1-k}}{{b}^{k}} right)}+ \ + & C_{t+1}^{t+1}cdot {{b}^{t+1}} \ end{align}]

Выражение под знаком суммы легко раскладывается на множители:

[begin{align} C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}+C_{t}^{k-1}cdot {{a}^{t+1-k}}{{b}^{k}} & =left( C_{t}^{k}+C_{t}^{k-1} right)cdot {{a}^{t+1-k}}{{b}^{k}}= \ & =C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}} end{align}]

[begin{align} & C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}+C_{t}^{k-1}cdot {{a}^{t+1-k}}{{b}^{k}}= \ = & left( C_{t}^{k}+C_{t}^{k-1} right)cdot {{a}^{t+1-k}}{{b}^{k}}= \ = & C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}} \ end{align}]

Здесь в последнем шаге мы использовали свойство биноминальных коэффициентов, доказанное выше:

[C_{n}^{k}+C_{n}^{k+1}=C_{n+1}^{k+1}]

Или, что то же самое

[C_{n}^{k-1}+C_{n}^{k}=C_{n+1}^{k}]

Таким образом, всю сумму можно переписать более компактно, а затем внести под знак суммы первое и последнее слагаемое:

[ C_{t+1}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}}=sumlimits_{k=0}^{t+1}{C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}]

[begin{align} C_{t+1}^{0}cdot {{a}^{t+1}} & +sumlimits_{k=1}^{t}{C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}}= \ & =sumlimits_{k=0}^{t+1}{C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}} \ end{align}]

Сопоставляя исходное выражение и конечное, получим

[{{left( a+b right)}^{t+1}}=sumlimits_{k=0}^{t+1}{C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}]

Именно это и требовалось доказать. Следовательно, исходная формула Бинома Ньютона верна.

Смотрите также:

  1. Схема Горнера
  2. Теорема Безу и корни многочленов
  3. Знаки тригонометрических функций
  4. Уравнение касательной к графику функции
  5. Как представить обычную дробь в виде десятичной
  6. Сложные задачи B2 на проценты: вычисление полной стоимости
Источник

Биномиальные коэффициенты

Биномиальные коэффициенты

Биномиальные коэффициенты — коэффициенты в разложении (1 + x)n по степеням x (т. н. бином Ньютона):

(1+x)^n = {nchoose 0} + {nchoose 1}x + {nchoose 2}x^2 + cdots = sum_k {nchoose k} x^k.

Иначе говоря, (1 + x)n является производящей функцией для биномиальных коэффициентов.

Значение биномиального коэффициента {nchoose k} определено для всех целых чисел n и k. Явные формулы для вычисления биномиальных коэффициентов:

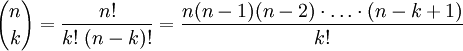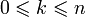{nchoose k} = frac{n!}{k!;(n-k)!}= frac{n(n-1)(n-2)cdotdotscdot(n-k+1)}{k!} для 0leqslant k leqslant n;
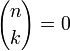{nchoose k} = 0 для k < 0 или 0leqslant n &amp;lt; k;
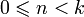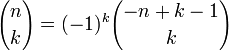{nchoose k} = (-1)^k {-n+k-1choose k} для n&amp;lt;0leqslant k,

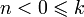где n! и k! — факториалы чисел n и k.

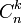Биномиальный коэффициент {nchoose k} является обобщением числа сочетаний C^k_n, которое определено только для неотрицательных целых чисел n, k.

Биномиальные коэффициенты часто возникают в комбинаторных задачах и теории вероятностей.

Обобщением биномиальных коэффициентов являются мультиномиальные коэффициенты.

Содержание

  • 1 Треугольник Паскаля
  • 2 Свойства
  • 3 Тождества
  • 4 Асимптотика и оценки
  • 5 Алгоритмы вычисления биномиальных коэффициентов
  • 6 См. также
  • 7 Ссылки

Треугольник Паскаля

Тождество

{nchoose k}={n-1choose k-1} + {n-1choose k}

позволяет расположить биномиальные коэффициенты для неотрицательных n, k в виде треугольника Паскаля, в котором каждое число равно сумме двух вышестоящих:

begin{matrix} n=0: &amp;amp; &amp;amp; &amp;amp; &amp;amp; &amp;amp; 1 &amp;amp; &amp;amp; &amp;amp; &amp;amp;\ n=1: &amp;amp; &amp;amp; &amp;amp; &amp;amp; 1 &amp;amp; &amp;amp; 1 &amp;amp; &amp;amp; &amp;amp;\ n=2: &amp;amp; &amp;amp; &amp;amp; 1 &amp;amp; &amp;amp; 2 &amp;amp; &amp;amp; 1 &amp;amp; &amp;amp;\ n=3: &amp;amp; &amp;amp; 1 &amp;amp; &amp;amp; 3 &amp;amp; &amp;amp; 3 &amp;amp; &amp;amp; 1 &amp;amp;\ n=4: &amp;amp; 1 &amp;amp; &amp;amp; 4 &amp;amp; &amp;amp; 6 &amp;amp; &amp;amp; 4 &amp;amp; &amp;amp; 1\ vdots &amp;amp; &amp;amp; vdots &amp;amp; &amp;amp; vdots &amp;amp; &amp;amp; vdots &amp;amp; &amp;amp; vdots &amp;amp; end{matrix}

Треугольная таблица, предложенная Паскалем в «Трактате об арифметическом треугольнике» (1654), отличается от выписанной здесь поворотом на 45°. Таблицы для изображения биномиальных коэффициентов были известны и ранее (Тарталье, О. Хайяму и др.).

Свойства

Интересно, что если рассмотреть ряды в треугольнике Паскаля, состоящие из биномиальных коэффициентов, то в пределе получим функцию нормального распределения — распределение Гаусса.

Из теоремы Люка следует, что:

Тождества

binom{n}{t} + binom{n}{t+s} + binom{n}{t+2s} + ldots = frac{1}{s} sum_{j=0}^{s-1} left(2cosfrac{pi j}{s}right)^n cosfrac{pi(n-2t)j}{s}.

Асимптотика и оценки

Алгоритмы вычисления биномиальных коэффициентов

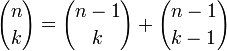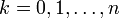Биномиальные коэффициенты могут быть вычислены с помощью формулы {nchoose k}={n-1choose k}+{n-1choose k-1}, если на каждом шаге хранить значения {nchoose k} при k=0,1,dots,n. Этот алгоритм особенно эффективен, если нужно получить все значения {nchoose k} при фиксированном n. Алгоритм требует O(n) памяти (O(n2) при вычислении всей таблицы биномиальных коэффициентов) и O(n2) времени (в предположении, что каждое число занимает единицу памяти и операции с числами выполняются за единицу времени).

Второй способ основан на тождестве 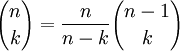{nchoose k}=frac{n}{n-k}{n-1choose k}. Он позволяет вычислить значения {nchoose k} при фиксированном k. Алгоритм требует O(1) памяти (O(l) если нужно посчитать l последовательных коэффициентов с фиксированным k) и O(k) времени.

См. также

  • Биномиальное распределение
  • Треугольное число
  • Треугольник Паскаля
  • Пирамида Паскаля
  • Композиция (теория чисел)
  • Разбиение числа

Ссылки

  • О. В. Кузьмин Треугольник и пирамида Паскаля: свойства и обобщения // Соросовский Образовательный Журнал. — 2000. — Т. 6. — № 5. — С. 101—109.
  • С. К. Абачиев Радужная фрактальность треугольника Паскаля

Wikimedia Foundation.
2010.

Полезное

Смотреть что такое “Биномиальные коэффициенты” в других словарях:

  • Биномиальные коэффициенты —         коэффициенты в формуле разложения Ньютона бинома …   Большая советская энциклопедия

  • БИНОМИАЛЬНЫЕ КОЭФФИЦИЕНТЫ — коэффициенты при степенях z в разложений Ньютона бинома . Б. к. обозначается или и равен Обозначение восходит к Л. Эйлеру (L. Euler); второе обозначение появилось в 19 в. и связано, по видимому, с интерпретацией Б. к. как числа различимых… …   Математическая энциклопедия

  • Биномиальные коэффициенты — так называются количества: l, n/1, n(n 1)/(1.2), n(n 1)(n 2)/(1.2.3)…, n(n 1)(n 2)…(n m + 1)/(1.2.3…m), составляющие коэффициенты последовательных членов бинома Ньютона (см. Бином). Их обозначают в настоящее время часто знаком . Общий вид Б …   Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

  • Паскаля треугольник — Биномиальные коэффициенты коэффициенты в разложении (1 + x)n по степеням x (т. н. бином Ньютона): Иначе говоря, (1 + x)n является производящей функцией для биномиальных коэффициентов. Значение биномиального коэффициента определено для всех целых… …   Википедия

  • Биномиальный коэффициент — В математике биномиальные коэффициенты  это коэффициенты в разложении бинома Ньютона по степеням x. Коэффициент при обозначается или и читается «биномиальный коэффициент из n по k» (или «це из n по k»): В …   Википедия

  • Ньютона бином —         название формулы, выражающей любую целую положительную степень суммы двух слагаемых (бинома, двучлена) через степени этих слагаемых, а именно:                  (1)          (1) где n целое положительное число, а и b какие угодно числа.… …   Большая советская энциклопедия

  • Бином Ньютона — Бином Ньютона  формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных, имеющая вид , где   биномиальные коэффициенты,   неотрицательное целое число. В таком виде эта формула была известна… …   Википедия

  • биномиальное распределение — (распределение Бернулли), распределение вероятностей числа появлений некоторого события при повторных независимых испытаниях, если вероятность появления этого события в каждом испытании равна р (0≤р≤1). Именно, число μ появлений этого события… …   Энциклопедический словарь

  • Последовательность Падована — Последовательность Падована  это целочисленная последовательность P(n) с начальными значениями и линейным рекуррентным соотношением Первые значения P(n) таковы 1, 1, 1, 2, 2, 3, 4, 5, 7, 9, 12, 16, 21, 28, 37, 49, 65, 86, 114, 151, 200, 265 …   Википедия

  • Бином ньютона — Бином Ньютона  это формула , где   биномиальные коэффициенты, n  неотрицательное целое число. Содержание 1 Доказательство …   Википедия

Источник

Добавить комментарий