Функция вида y=ax2+bx+c, где а, b, с – некоторые числа, причем, а≠0 число, х – переменная, называется квадратичной функцией.
Графиком квадратичной функции является парабола, она имеет вершину и две ветви, которые могут быть направлены либо вверх, либо вниз (рис.1). Красной точкой обозначена вершина параболы, из которой выходят ветви. Её координаты по графику – (3; –4). Направление ветвей зависит от значения коэффициента «а», то есть, если «а» – положительное число, то ветви направлены вверх; если число «а» – отрицательное, то ветви направлены вверх. На данном рисунке ветви направлены вверх, значит коэффициент «а» у формулы, которая задает эту функцию – положительное число. Коэффициент «с» показывает ординату (у) точки пересечения ветви параболы с осью у. Так, на рисунке №1 парабола пересекает ось у в точке (5;0), значит коэффициент с=5.

Рисунок №1.
Вершина параболы. Формула.
Чтобы найти координаты вершины параболы (х0; у0), надо воспользоваться формулой:
х0=−b2a
для нахождения у0 можно просто подставить значение х0 в формулу данной функции y0=ax2+bx+c вместо х.
Рассмотрим это на примере конкретно заданной функции.
Пример №1
Найти вершину параболы, заданной формулой у=2х2 – 8х + 5.
Найдем, чему равны коэффициенты: а=2; b= – 8
Подставим их в формулу и вычислим значение х0:
х0=−b2a=82∙2=84=2
Теперь в заданную по условию формулу вместо х подставим найденное значение у0=2∙22 – 8∙2 + 5=8 – 16 + 5= –3
Итак, мы нашли координаты вершины параболы: (2; –3).
Ответ: (2; –3).
Нули параболы
Значения х, при которых функция принимает значения, равные нулю, называются нулями функции. Другими словами, Значения абсцисс (х) точек пересечения ветвей параболы с осью х, называются нулями функции. На рисунке №1 точки координаты точек пересечения ветвей параболы с осью х следующие: (1;0) и (5;0). Значит, нули функции – это значения х, равные 1 и 5.
Рассмотрим, как найти нули функции не по рисунку, а по заданной формуле.
Пример №2
Найти нули функции у=х2 +4х – 5
Так как нули функции это абсциссы точек пересечения ветвей параболы с осью х, то их координаты будут (х;0), то есть у=0. Значит, вместо у подставляем нуль в нашу формулу 0=х2 +4х – 5 и получаем квадратное уравнение, решив которое, мы и найдем значения нулей функции:
х2 +4х – 5=0
а=1, b=4, с= –5
D=b2 – 4ac=42 – 4∙1∙(−5)=36
x=−b±√D2a
x=−4±√362; х1=–5; х2=1
Значит, нули функции равны –5 и 1
Ответ: –5 и 1
Примечание к заданию по нахождению нулей функции без графика
Если дискриминант уравнения отрицательный, значит, нулей функции нет, то есть парабола не пересекает ось х (вершина находится выше неё, если ветви направлены вверх и ниже, если ветви направлены вниз).
Рассмотрим нахождение соответствия рисунков парабол, расположенных в системе координат значениям а и с.
Пример №3

Для выполнения данного задания на соответствие необходимо сначала поработать с графиками, подписав на них, какими – отрицательными или положительными являются коэффициенты а и с.

Теперь можно выполнить соответствие:
Ответ: 231
Пример №4
Рассмотрим еще пример на соответствие

В данном задании рассмотрим коэффициенты в формулах и подчеркнем их: так, в формуле под буквой А коэффициент а=-2, т.е. отрицательный, значит, ветви направлены вниз, а это график под номером 2. В формулах под буквами Б и В первые и третьи коэффициенты одинаковые, значит, сравнить по рисунку их невозможно, следовательно, будем сравнивать по расположению вершины (справа или слева от оси у), а именно х0. 
Итак, найдем х0 для формулы «Б»:
х0=−b2a=−42∙2=−44=−1
Видим, что х0 отрицательное, значит, вершина расположена слева от оси у, а это рисунок 3. Ну и осталось привести в соответствие В и 1.
Запишем в таблицу
Ответ: 231
Задание 11OM21R
На рисунках изображены графики функций вида . Установите соответствие между знаками коэффициентов а и с и графиками функций.
КОЭФФИЦИЕНТЫ
А) a>0, с >0 Б) а<0; с>0 В) а>0, с<0
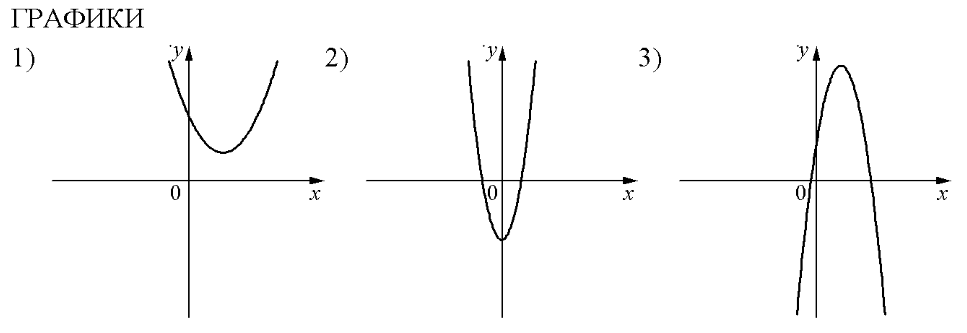
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
Решение
На рисунках в задании изображены параболы. Вспомним, что обозначают коэффициенты а и с: а – направление ветвей (a<0 – ветви вниз; а>0 – ветви вверх); коэффициент с показывает ординату точку пересечения параболы с осью х (с >0 – пересечение в положительном направлении; с<0 – пересечение в отрицательном направлении).
Теперь поработаем с графиками и подпишем на каждом из них соответствующие коэффициенты.
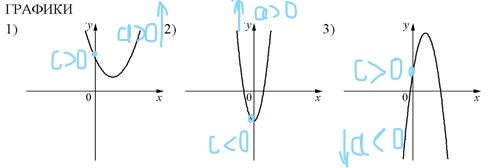
Теперь расставим в соответствии с указанными коэффициентами:
А) a>0, с >0 – это график №1
Б) а<0; с>0 – это график №3
В) а>0, с<0 – это график №2
Ответ: 132
pазбирался: Даниил Романович | обсудить разбор
Задание OM1105o
Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) у=–х2–4х–3 Б) у=–х2+4х–3 В) у=х2+4х+3

Сразу обратим внимание на вариант В. Эта функция единственная, имеющая положительный коэффициент при х2 (здесь а=1, т.е. а>0). При а>0 график параболы направлен ветками вверх. Такой график имеется только один – под №3. Кроме того, можно обратить внимание на коэфициент с. Она равен 3, т.е. с>0. Это указывает на то, что парабола должна пересечь ось Оу выше начала координат. Что и отображено на графике В. Получаем соответствие: В–3.
Оба других графика – 1-й и 2-й – пересекают ось Оу ниже начала координат, что соответствует значению с=–3<0 в обоих случаях.
Далее надежнее всего вычислить вершины оставшихся двух парабол из уравнений А и Б по формуле -b/2a. Видим, что случае А (- (-4)) / (2 • -1) = -2, следовательно, вершина левее оси Y, так как x0 отрицателен, значит, А-1, а Б-2.
Ответ: 123
pазбирался: Даниил Романович | обсудить разбор
Задание OM1101o
На рисунках изображены графики функций вида
y = ax² + bx + c
Установите соответствие между знаками коэффициентов a и c и графиками функций.
Коэффициенты:
А) a > 0, c > 0
Б) a < 0, c > 0
В) a > 0, c < 0
Графики:
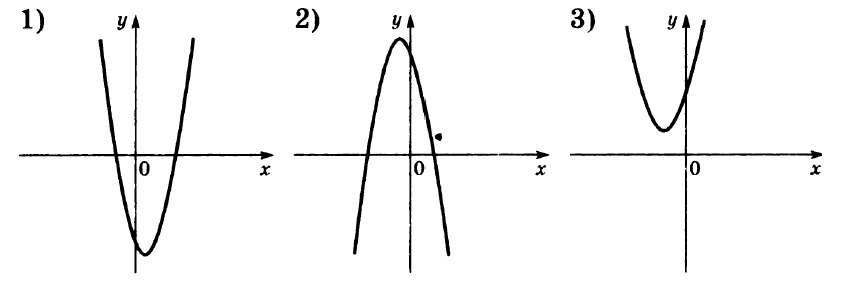
Мы вспоминаем, за что отвечают коэффициенты a и b при построении графиков функции вида
y = ax² + bx + c
Коэффициент a определяет направление ветвей параболы: если a > 0, то ветви направлены вверх, а если a < 0, то ветви направлены вниз.
Таким образом, мы видим, что только у второй параболы ветви направлены вниз, а значит a < 0.
У первой и третьей ветви направлены вверх, то есть a > 0.
Далее мы смотрим, на что влияет коэффициент c.
Коэффициент c отвечает за положение параболы относительно оси x, или же отвечает за сдвиг по оси y, а именно:
если c > 0, то вершина параболы расположена выше оси х
если c < 0, то вершина параболы расположена ниже оси x
Так, у первой параболы c < 0, у второй и третьей c > 0.
Из всего вышеперечисленного можно найти ответ:
А) 3
Б) 2
В) 1
Ответ: 321
pазбирался: Даниил Романович | обсудить разбор
Даниил Романович | Просмотров: 10.4k
Вершина параболы
Содержание:
- Что такое вершина параболы
- Вывод формулы координат вершины параболы
- Как найти координаты, основные способы
- Примеры решения задач
Что такое вершина параболы
Определение
Вершина параболы — это точка, в которой наблюдается пересечение параболой оси координат и ее невозможность держать направление выше или ниже в координатной плоскости.
Чтобы найти ВП, необходимо применить формулу:
(lbrackfrac{-b}{2a};-frac{b^2-4ac}{4a}rbrack)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Исходя из координат, можно узнать расположение вершины параболы и построить ее.
Вывод формулы координат вершины параболы
Рассматриваемую формулу используют для решения квадратных уравнений, которые имеют вид:
(y;=;ax^2;+;bx;+;c)
Ее график представляет собой параболу, формулу которой мы определили выше. Но не всегда требуется пользоваться данной формулой, так как сначала можно найти значение х, а затем подставить его в уравнение и найти y.
Для того, чтобы вывести формулу ВП, нужно преобразовать квадратную функцию к виду:
(y;=;f(x;+;l);+;m)
Делают это с помощью метода выделения полного квадрата, то есть (left(a+bright)^2) преобразуют в (a^2+2ab+b^2.)
Функции вида (y;=;f(x;+;l);+;m) отличаются от (y;=;f(x)) сдвигом из графиков по оси абсцисс на –l и по оси ординат на m. l в переписанной квадратичной функции равняется:
(frac{-b}{2a}, а frac{left(4ac-b^2right)}{4a})
Получается, что l и m — это координаты x0 и y0.
Приведем доказательство:
- Соединяем первые два члена многочлена: (y;=;(ax^2;+;bx);+;c.)
- Выносим коэффициент a за скобку, b при этом делим на a: (y=aleft(x^2+frac baxright)+c.)
- Представляем, что у нас есть квадрат суммы, в котором x является слагаемым, а из выражения в скобках необходимо рассчитать его полный квадрат суммы. Одночлен (frac bax) умножаем на два и делим на два одновременно. Далее прибавляем и вычитаем квадрат второго слагаемого квадрата суммы. Получаем: (y=aleft(x^2+2frac b{2a}x+frac{b^2}{4a^2}-frac{b^2}{4a^2}right)+c.)
- Выделяем квадрат суммы: (y=aleft(left(x+frac b{2a}right)^2-frac{b^2}{4a}right)+c.)
- Умножаем на a: (y=aleft(x+frac b{2a}right)^2-frac{b^2}{4a}+c.)
- Приводим свободные члены к общему знаменателю: (y=aleft(x+frac b{2a}right)^2-frac{b^2+4ac}{4a}.)
- Меняем знак: (y=aleft(x+frac b{2a}right)^2+frac{b^2-4ac}{4a}.)
Мы привели функцию (y;=;ax^2;+;bx;+;c) к виду (y;=;a{(x;+;l)}^2;+;m,) что соответствует (y;=;f(x;+;l);+;m,) где (f(x);=;ax^2. )
Как найти координаты, основные способы
Существует несколько способов нахождения координат ВП:
- (x_0=frac{-b}{2a}) — подходит в том случае, если дискриминант квадратного уравнения равен нулю.
- (y_0=-frac{b^2-4ac}{4a}) — это формула дискриминанта, поделенная на 4а.
- (x_0=frac{x_1+x_2}2) — среднее арифметическое между нулями функции. Можно использовать, если в выражении есть нули.
- Если функция имеет вид (y=aleft(x-x_0right)^2+y_0), то в ее вершиной совпадают координаты (left(x_0;y_0right).)
Примеры решения задач
Задача №1
Найти вершину параболы для уравнения: (y=x^2-5x+7.)
Решение: В выражение (x=-frac b{2a}) подставляем известные числа и получаем (x=frac52=2,5). Теперь подставляем x в исходное уравнение: (2,5^2-5times2,5+7=0,75.)
Ответ: (2,5; 0,75).
Задача №2
Найти ВП для уравнения: y=5(x-1)(x+7).
Решение: Ищем нули функции: 5(x-1)(x+7)=0. Тогда x-1=0 либо x+7=0. Из этого x=1; x=-7.
Подставляем и получаем: (x_0=frac{x_1+x_2}2=frac{1+left(-7right)}2=-3.)
Второе: (y_0=5timesleft(-3-1right)left(-3+7right)=-80.)
Ответ: (-3; -80).
Задача №3
Найти вершину параболы для уравнения: (y=x^2-7x+3 ).
Решение: (х_0=-frac b{2a}=-frac{left(-7right)}{2times1}=3,5.)
Второе: (y_0=3,5^2-7times3,5+3=-9,25.)
Ответ: (3,5; -9,25).
Насколько полезной была для вас статья?
Рейтинг: 2.50 (Голосов: 8)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Формула нахождения вершины параболы
Ирина Алексеевна Антоненко
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Определение 1
Парабола – это геометрическое множество точек, равноудалённых от точки F, не лежащей на параболе, и прямой $d$, не проходящей через точку $F$.
Что значит вершина параболы
Определение 2
Вершина параболы – это точка, ближайшая к директрисе параболы. Она является центром отрезка, ограниченного точкой фокуса параболы $F$ и директрисой $d$.
Производная в вершине квадратичной параболы равна нулю.
Каноническое уравнение параболы $y^2 = 2px$ справедливо для параболы, вершина которой находится в центре осей.
Для того, чтобы определить, принадлежит ли точка графику заданной параболы, необходимо подставить её координаты в формулу $y = ax^2 + bx + c$.
Если равенство выполняется — точка принадлежит графику.
Как найти вершины параболы, задающейся квадратичной функцией
Рисунок 1. Пример уравнения и графика квадратичной параболы
Довольно часто парабола задаётся квадратичной функцией вида $y = ax^2 + bx + c$, вершина такой параболы находится в произвольной точке.
Какой-то единой формулы для нахождения сразу обеих координат вершины параболы нет, но при этом определить координаты вершины параболы по уравнению довольно просто.
Алгоритм для нахождения вершины параболы такой:
- Запишите коэффициенты $a, b, c$ из уравнения. Если коэффициент $a$ при $y$ положительный, то ветви параболы будут смотреть вверх, а если отрицательный, то вниз.
- Найдите абсциссу вершины параболы ($x$ вершины) по формуле $x = – frac{b}{2a}$, для этого воспользуйтесь коэффициентами $a, b, c$ из уравнения.
- Подставьте найденный $x$ в уравнение параболы и вычислите ординату вершины параболы $y$.
- Запишите полученные координаты x и y вершины параболы в форме точки $(x; y)$.
Пример 1
Рассмотрим уравнение параболы $y = x^2 – 5x + 7$
- Коэффициенты этой параболы $a = 1$, $b = -5$, $c = 7$.
- Для вычисления x вершины параболы подставьте $a = 1$ и $b = -5$ в формулу $x = – frac{b}{2a}= frac{5}{2}=2.5$
- Подставьте найденный $x$ в исходное уравнение:
- $y = 2,5^2 – 5 cdot 2.5 + 7$
- $y = 0,75$
- Координаты вершины этой параболы $(2.5;0.75)$.
Вершина кубической параболы
Чтобы найти вершины (точки локальных минимумов и максимумов) кубической параболы, необходимо найти её производную, приравнять её к нулю и затем вычислить $x$ и $y$.
Если же необходимо найти точку перегиба кубической параболы, необходимо найти вторую производную и также приравнять её к нулю.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 04.12.2022
Загрузить PDF
Загрузить PDF
Вершина параболы квадратного уравнения — это самая высокая или самая низкая ее точка. Чтобы найти вершину параболы, вы можете воспользоваться специальной формулой или методом дополнения до полного квадрата. Ниже описано, как это сделать.
-

1
Найдите величины a, b, и c. В квадратном уравнении коэффициент при x2 = a, при x = b, постоянная (коэффициент без переменной) = c. Например, возьмем уравнение: y = x2 + 9x + 18. Здесь a = 1, b = 9, and c = 18.[1]
-

2
Воспользуйтесь формулой для вычисления значения координаты x вершины. Вершина также является точкой симметрии параболы. Формула для нахождения координаты x параболы: x = -b/2a. Подставьте в нее соответствующие значения для вычисления x.
- x=-b/2a
- x=-(9)/(2)(1)
- x=-9/2
-

3
Подставьте найденное значение x в исходное уравнение для вычисления значения y. Теперь, когда вам известно значение x, просто подставьте его в исходное уравнение для нахождения y. Таким образом, формулу для нахождения вершины параболы можно записать в виде функции: (x, y) = [(-b/2a), f(-b/2a)]. Это значит, что для нахождения y необходимо сначала найти x по формуле, а затем подставить значение x в исходное уравнение. Вот, как это делается:
- y = x2 + 9x + 18
- y = (-9/2)2 + 9(-9/2) +18
- y = 81/4 -81/2 + 18
- y = 81/4 -162/4 + 72/4
- y = (81 – 162 + 72)/4
- y = -9/4
-

4
Запишите значения x и y в виде пары координат. Теперь, когда вам известно, что x = -9/2, а y = -9/4, запишите их как координаты в виде: (-9/2, -9/4). Вершина параболы находится по координатам (-9/2, -9/4). Если вам нужно нарисовать эту параболу, то ее вершина лежит в нижней точке, так как коэффициент при x2 положительный.
Реклама
-

1
Запишите уравнение. Дополнение до полного квадрата — еще один способ найти вершину параболы. Применив этот метод, вы найдете координаты x и y сразу, без необходимости подставлять x в исходное уравнение. Например, дано уравнение: x2 + 4x + 1 = 0.[2]
-

2
Разделите каждый коэффициент на коэффициент при x2. В нашем случае коэффициент при x2 равен 1, поэтому мы можем пропустить этот шаг. Деление на 1 ничего не изменит.
-

3
Перенесите постоянную в правую часть уравнения. Постоянная — коэффициент без переменной. Здесь это 1. Перенесите 1 вправо путем вычитания 1 из обеих частей уравнения. Вот, как это сделать:[3]
- x2 + 4x + 1 = 0
- x2 + 4x + 1 -1 = 0 – 1
- x2 + 4x = – 1
-

4
Дополните до полного квадрата левую часть уравнения. Для этого просто найдите (b/2)2 и прибавьте результат к обеим частям уравнения. Подставьте 4 вместо b, так как 4x — это коэффициент b нашего уравнения.
- (4/2)2 = 22 = 4. Теперь прибавьте 4 к обеим частям уравнения и получите:
- x2 + 4x + 4 = -1 + 4
- x2 + 4x + 4 = 3
- (4/2)2 = 22 = 4. Теперь прибавьте 4 к обеим частям уравнения и получите:
-

5
Упрощаем левую часть уравнения. Мы видим, что x2 + 4x + 4 — полный квадрат. Он может быть записан в виде: (x + 2)2 = 3
-

6
Используйте его для нахождения координат x и y. Вы можете найти x, просто приравняв (x + 2)2 к 0. Теперь, когда (x + 2)2 = 0, вычисляем x: x =-2. Координата y — это постоянная в правой части полного квадрата. Итак, y = 3. Вершина параболы уравнения x2 + 4x + 1 = (-2, 3)
Реклама
Советы
- Правильно определяйте a, b, и c.
- Записывайте предварительные вычисления. Это не только поможет в процессе работы, но и позволит увидеть, где сделаны ошибки.
- Не нарушайте порядок вычислений.
Реклама
Предупреждения
- Проверьте ваш ответ!
- Удостоверьтесь, что вы знаете, как определить коэффициента a, b, и c. Если вы не знаете, ответ будет неправильным.
- Не паникуйте — решение таких задач требует практики.
Реклама
Что вам понадобится
- Бумага или компьютер
- Калькулятор
Об этой статье
Эту страницу просматривали 507 321 раз.
Была ли эта статья полезной?

Общие сведения
Парабола — кривая, состоящая из равноудаленных точек от заданной точки (вершина) и прямой. Последняя называется директрисой. График функции имеет ось симметрии, которая проходит по определенной траектории и зависит от функции кривой (рис. 1). Ее вершина находится в центре координат.
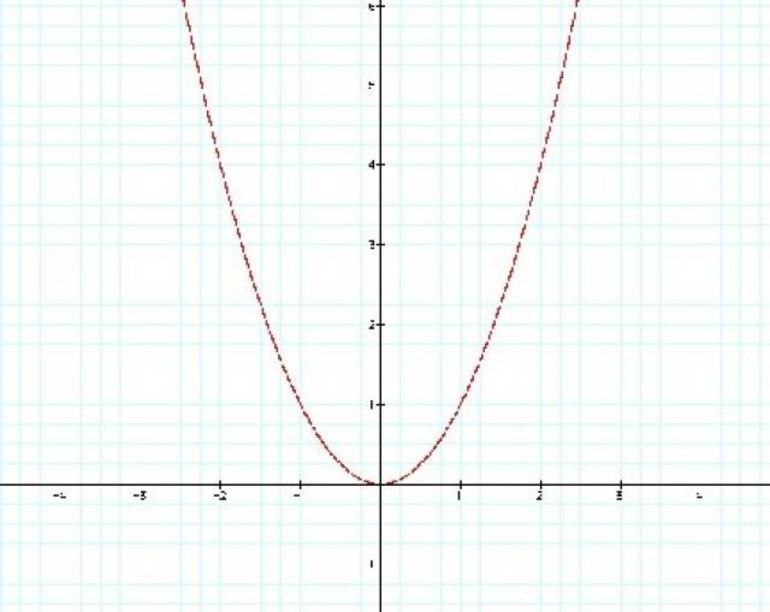
Рисунок 1. График квадратичной функции с вершиной в начале координат.
Однако существуют и другие случаи прохождения кривой. Она может пересекать оси абсцисс или ординат. В некоторых случаях ее ветви направлены вниз. При вращении вокруг оси симметрии получается поверхность, которая используется в различных устройствах. По этому принципу изготовлены фары автомобиля, зеркала в телескопах и т. д. Кроме того, парабола — это квадратичная зависимость переменных друг от друга. Парабола имеет некоторые свойства:

- Парабола — кривая второго порядка.
- Ось симметрии перпендикулярна директрисе и проходит через фокус и вершины.
- Оптическое свойство отражения.
- Отрезок, который соединяет середину любой хорды параболы и точку пересечения касательных прямых, является перпендикуляром относительно директрисы.
- Подобность всех парабол.
- Траектория фокуса, которая катится по произвольной прямой — цепная молния.
Следует отметить, что оптическое свойство — это способность отражать свет от источника. Если пучок лучей, которые являются параллельными ее оси, отражаются в параболе, то они собираются в фокусе кривой. При нахождении источника света в фокусе происходит отражение параллельного пучка лучей относительно ее оси.
Уравнения квадратичной функции
Параболу можно описать несколькими способами. Каждый из них нужно применять в конкретных случаях для удобства вычислений. Существует три формы описания кривой:
- Каноническая.
- Квадратичная.
- Общая.
В первой форме она имеет следующий вид: y 2 = 2px. Если поменять местами оси декартовой системы, то получится следующий вид: x 2 = 2yp. Коэффициент p — фокальный параметр. Он соответствует расстоянию между фокусом и директрисой. Кроме того, его значение всегда больше нуля. Вершина лежит всегда между фокусом и директрисой кривой на расстоянии, равном p/2 (рис. 2).
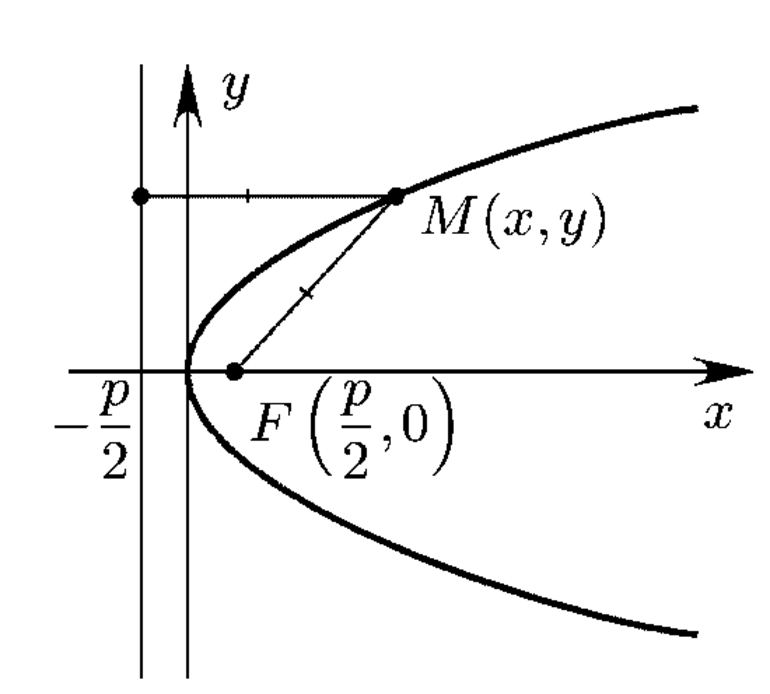
Рисунок 2. Директриса и фокус.
Пусть уравнение директрисы (прямая, которая параллельна оси ОУ) имеет следующий вид: х + p/2 = 0. Координаты фокуса F — (р/2;0). Начало координат делит луч, проходящий из точки F и точки пересечения с директрисой на 2 равных отрезка. Величина FM рассчитывается таким образом: FM = [(x — p/2)^2 + y 2 ]^0.5. Отрезок (луч) из точки М до директрисы равен p/2 + x. Если приравнять оба выражения, то равенство имеет такой вид: p/2 + x = [(x — p/2)^2 + y 2 ]^0.5. При возведении в квадрат и приведении подобных слагаемых, получается искомое уравнение параболы (y 2 = 2px).
Парабола может задаваться квадратичной функцией. Она имеет такой вид: y = ax 2 + bx + c. Следует учитывать, что коэффициент «a» не должен быть равен 0. Если a=1, b = 0 и с = 0, функция принимает такой вид: y = ax 2 . В этом случае формула нахождения вершины параболы выглядит таким образом:

- Абсцисса вершины параболы: xa = -b / 2a.
- Координата «игрек» по оси ординат: yb = – D / 2a.
В последней формуле переменная D является дискриминантом квадратного уравнения искомой функции. Он вычисляется с помощью такого соотношения: D = b 2 — 4ac. При а>0 фокус лежит на оси, и находится над вершиной. Ось симметрии параллельна оси ординат. Кроме того, она проходит через вершину кривой. Расстояние до нее равно ¼ величины «а». Если а<0, то ось ее симметрии параллельна оси абсцисс. Расстояние до фокуса также равно ¼а. Уравнение y = a (x — xa)^2 + ya — функция, определяющая кривую II порядка, как параболу.
Поскольку искомую функцию можно назвать кривой второго порядка, то ее уравнение может быть записано в виде квадратного многочлена в декартовой системе координат. Вид его имеет такой вид: Ax 2 + Bxy + Cy 2 + Dx + Ey + F = 0. Дискриминант равен нулю (при старших членах).
В полярной системе координат с осями p и v уравнение квадратичной функции имеет такой вид: p (1 + cos (v)) = p. Расстояние от фокуса до директрисы обозначается фокальным коэффициентом p. Кроме того, p соответствует удвоенной длине отрезка, проведенного от фокуса до вершины.
Методы нахождения вершины
В математике есть три способа нахождения координат точки вершины кривой: по формуле, выделением полного квадрата и нахождением производной. Следует отметить, что первый способ не подойдет в том случае, когда функция отличается от вида y = ax 2 + bx + c. Первый способ — расчет по формуле вершины параболы квадратичной функции. Координата x0 вычисляется таким образом: x0 = -b / 2a. Для нахождения координаты y0 следует подставить в функцию найденное значение x0.
Когда функция представлена неполным квадратом, нужно прибавить или отнять одинаковое число к двум частям уравнения. Если воспользоваться этим методом, то можно вычислить сразу значения х и у. Алгоритм нахождения вершины для функции у = x 2 + 4x + 2 имеет такой вид:

- Приравнять многочлен к нулю, и перенести свободный член в правую сторону с противоположным знаком: x 2 + 4x = -2.
- Дополнить до полного квадрата. Необходимо вычислить свободный член по такому соотношению: с = (b/2)^2 = (4/2)^2 = 4.
- Записать полный квадрат, отняв и прибавив свободный член: x 2 + 4x + 4 — 4 = -2.
- Выделить квадрат: (x 2 + 2x + 4) — 4 = -2.
- Перенести свободное число в правую сторону с противоположным знаком: (x 2 + 2x + 4) = 4 — 2.
- Уравнение принимает следующий вид: (x + 2)^2 = 2.
- Для того чтобы вычислить x0, нужно решить уравнение (x + 2)^2 = 0. Следовательно, x = -2.
- Ординату точки определить очень просто, поскольку ее значение соответствует числу (нужно брать с противоположным знаком), которое находится в правой части уравнения, т. е. у = -2.
При изображении графика вершину нужно сместить в точку (-2;2). Третий способ позволяет узнать координаты вершины с помощью определения производной. Находить ее следует от заданной функции. Для вычисления координат вершины нужно действовать по следующему алгоритму:
- Найти производную и приравнять ее к нулю: f'(x) = (ax 2 + bx + c)’ = 2ax + b.
- Выразить х: х = -b / (2a).
- Подставить в функцию для вычисления y.
- Записать координаты точки.
Однако эти все три метода относятся к ручному вычислению. Автоматизация действий осуществляется с помощью специализированного программного обеспечения. Для этой цели подойдет онлайн-калькулятор, поддерживающий функцию нахождения точек вершины квадратичной кривой. Программы рекомендуется применять только для проверки решения, поскольку очень важно знать методы нахождения этой точки.
Алгоритм построения
В различных задачах нужно выполнить построение графика функции. В некоторых случаях даются координаты вершины, а в других — их следует искать, используя какой-либо метод. Чтобы построить квадратичную функцию, нужно воспользоваться таким алгоритмом:
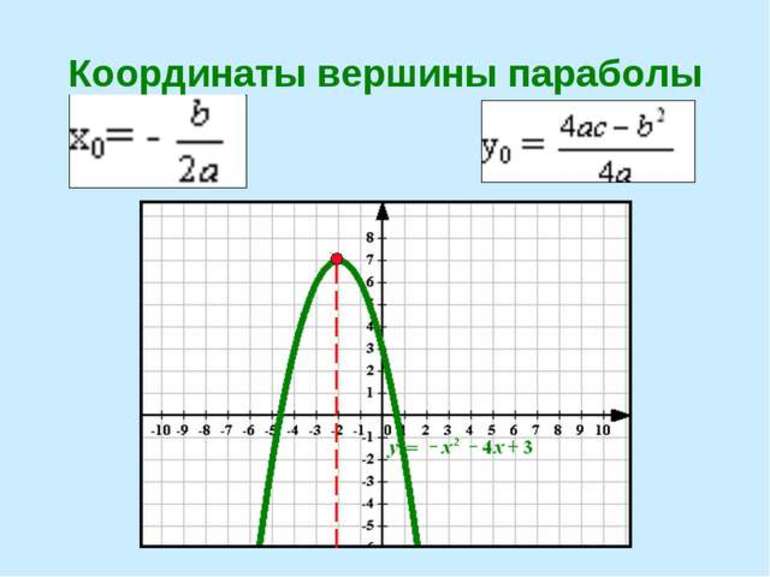
- Если вершина не задана, то нужно найти ее любым из методов.
- Определить точки пересечения с осями декартовой системы координат.
- Построить таблицу зависимости ординаты от абсциссы. Для этой цели нужно выделить минимум 3 значения «х». Вершина должна находиться по центру таблицы.
- Выполнить построение, соединив точки.
Если необходим более точный график, то необходимо брать больше точек. Значения рассчитываются при подстановке значений «х» в функцию. Когда парабола задана функцией y = x 2 + c, нет смысла брать разные значения. Нужно использовать для построения искомой таблицы числа с противоположными знаками. Например, x1 = 2 и x2 = -2.
Специалисты-математики настоятельно рекомендуют не усложнять вычисления. Возможно, в школьных программах и рассматриваются различные случаи. Однако в высших учебных заведениях основной аспект изучения дисциплин с физико-математическим уклоном сводится к оптимизации процесса решения задачи.
Примеры решений
В математике существует определенная классификация заданий на простые и сложные типы. Все они считаются однотипными, но отличаются только объемами вычислений и необходимостью построения графиков. Для решения нужно воспользоваться рекомендуемыми алгоритмами, которые существенно оптимизируют вычисления.
«Корень» трудностей при расчете — отсутствие систематизации вычислений. Не все ими пользуются. В результате простая задача становится очень сложной, поскольку в ней присутствует много ненужных вычислений. Кроме того, как отмечалось выше, рекомендуется «набить руку» на ручных вычислениях, ведь не всегда можно будет воспользоваться программами.
Упрощенная задача
Простым примером задания является следующий: необходимо вычислить координаты вершины точки параболы y = x 2 + 3x — 18. Следует продемонстрировать решение тремя способами. Решение первым методом:
- Координата по оси абсцисс: х0 = -3 / (2 * 1) = -1,5.
- По ординате: (-1,5)^2 + 3 * (-1,5) — 18 — y= 0. Отсюда, y = -20,25.
Следовательно, вершина находится в точке (-1,5;20,25). Второй способ решения данной задачи имеет такой вид:
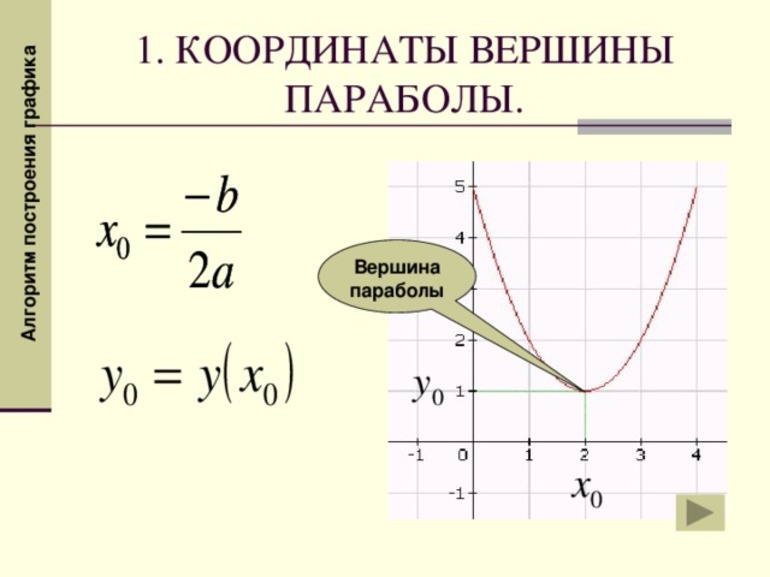
- Составить уравнение и перенести свободный член: x 2 + 3x = 18.
- Вычислить свободный член: с = (b/2)^2 = 2,25.
- Записать выражение: x 2 + 3x + 2,25 — 2,25 = 18.
- Выделить квадрат: (x 2 + 3x + 2,25) = 20,25.
- Определить координаты: (x + 1,5)^2 = 20,25.
- Искомая точка: (-1,5;20,25).
Для решения третьим методом следует найти производную: y’ = (x 2 + 3x — 18)’ = 2x + 3. Затем нужно приравнять ее к нулю: 2х + 3 = 0. Уравнение является простым, а его переменная легко находится: x = -3 / 2 = -1,5. После этого необходимо подставить абсциссу в функцию, приравняв ее к 0: y = 20,25.
Повышенная сложность
Задания повышенной сложности сводятся к вычислению нескольких значений. Кроме того, в некоторых случаях следует построить график параболы y = x 2 — 7x +10. Необходимо выполнить такие действия:
- Пересечение с осями.
- Вычислить экстремум (вершину) всеми методами.
- Выполнить графический эскиз (график).
Точек пересечения по ОУ нет. Они есть по оси абсцисс. Следует приравнять функцию к 0. Нахождение корней выполняется по теореме Виета: x1 = 2 и x2 = 5.
Для нахождения вершины необходимо воспользоваться тремя методами. При решении первым способом находится координата x0 = 7 / (2 * 1) = 3,5. Ордината определяется таким образом: y0 = (3,5)^2 — (7 * 3,5) + 10 = -2,25. Точка экстремума имеет координаты (3,5;-2,25). Находить вершину параболы необходимо по такому алгоритму:
- Записать уравнение, и выполнить перенос свободного члена: x 2 — 7x = -10.
- Найти свободный член: с = (7/2)^2 = 12,25.
- Составить уравнение: x 2 — 7x + 12,25 — 12,25 = -10.
- Выделить квадрат: (x — 3,5)^2 = 2,25.
- Экстремум: (3,5;-2,25).
Для следующего метода нужно найти производную: y’ = (x 2 — 7x +10)’ = 2x — 7. Далее нужно приравнять y’ к нулю: 2x — 7 = 0. Значение по оси абсцисс равно х0 = 3,5, а y0 = -2,25. Далее нужно заполнить таблицу зависимостей ординаты от переменной.
| y | 4 | 0 | -2 | -2,25 | -2 | 0 | 4 |
| x | 1 | 2 | 3 | 3,5 | 4 | 5 | 6 |
Таблица 1. Зависимость y от x.
После заполнения таблицы следует построить график искомой функции (рис. 3). Таблица состоит из следующих элементов: вершины, точек пересечения с осью абсцисс и 4 произвольных значений.

Рисунок 3. График функции.
Математики рекомендуют использовать для построения графика полученные значения при расчетах, поскольку подстановка и вычисление произвольных х существенно снижает скорость вычислений.
Таким образом, нахождение координат вершины параболы является довольно простой задачей, поскольку существует несколько методов. Из них можно выбрать оптимальный, который подходит в конкретной ситуации.

