Найти площадь прямоугольного треугольника
- Главная
- /
- Математика
- /
- Геометрия
- /
- Найти площадь прямоугольного треугольника
Чтобы посчитать площадь прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор

Чтобы вычислить площадь прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- длины катетов a и b
- длину гипотенузы с и длину любого из катетов (a или b)
- длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
- длину гипотенузы с и один из острых углов (α или β)
Найти площадь прямоугольного треугольника по двум катетам
Катет a =
Катет b =
S =
0
Просто введите длины двух катетов, и получите ответ.
Теория
Чему равна площадь (S) прямоугольного треугольника если известны оба катета (a и b)?
Формула
S = ½ ⋅ a ⋅ b
Пример
К примеру найдём площадь прямоугольного треугольника у которого сторона a = 2 см, а сторона b = 4 см:
S = 2 ⋅ 4 / 2 = 8 / 2 = 4 см²
Найти площадь прямоугольного треугольника по катету и гипотенузе
Гипотенуза c =
Катет (a или b) =
S =
0
Введите длины гипотенузы и одного из катетов, и получите ответ.
Теория
Чему равна площадь (S) прямоугольного треугольника если известны его гипотенуза (c) и один из катетов (a или b)?
Формула
S = ½ ⋅ a ⋅ √c² – a² = ½ ⋅ b ⋅ √c² – b²
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 2 см, а гипотенуза c = 5 см:
S = 2 ⋅ √5² – 2² / 2 = √25 – 4 ≈ 4.58 см²
Найти площадь прямоугольного треугольника по катету и прилежащему к нему острому углу
Катет (a или b) =
Прилежащий угол (β или α) = °
S =
0
Введите длину одного из катетов и прилежащий к нему острый угол в градусах.
То есть к катету a прилежащий ∠β, а к катету b – ∠α
Теория
Чему равна площадь (S) прямоугольного треугольника если известны один из катетов (a или b) и прилежащий к нему угол?
Формула
S = ½ ⋅ a² ⋅ tg(β) = ½ ⋅ b² ⋅ tg(α)
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 4 см, а прилежащий к нему ∠β = 45°:
S = ½ ⋅ 4² ⋅ tg(45) = ½ ⋅ 16 ⋅ 1 = 16 / 2 = 8 см²
Найти площадь прямоугольного треугольника по катету и противолежащему к нему острому углу
Катет (a или b) =
Противолежащий угол (α или β) = °
S =
0
Введите длину одного из катетов и противолежащий к нему острый угол в градусах.
То есть к катету a противолежащий ∠α, а к катету b – ∠β
Теория
Чему равна площадь (S) прямоугольного треугольника если известны один из катетов (a или b) и противолежащий к нему угол?
Формула
S = ½ ⋅ a² ⋅ tg(90 – α) = ½ ⋅ b² ⋅ tg(90 – β)
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 4 см, а противолежащий к нему ∠α = 45°:
S = 4² / 2⋅ tg(45) = 16 / 2 ⋅ 1 = 8 см²
Найти площадь прямоугольного треугольника зная длину гипотенузы и один из острых углов
Гипотенуза c =
Угол (α или β) = °
S =
0
Введите длину гипотенузы и один из острых угол в градусах.
Теория
Чему равна площадь (S) прямоугольного треугольника если известны длина гипотенузы (c) и один из острых углов?
Формула
S = ½ ⋅ c² ⋅ sin(α) ⋅ cos(α) = ½ ⋅ c² ⋅ sin(β) ⋅ cos(β)
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого гипотенуза c = 8 см, а ∠α = 45°:
S = ½ ⋅ 8² ⋅ sin(45) ⋅ cos(45) ≈ ½ ⋅ 64 ⋅ 0.7071067812 ⋅ 0.7071067812 ≈ 16 см²
Площадь прямоугольного треугольника
Ирина Алексеевна Антоненко
Эксперт по предмету «Калькуляторы»
Задать вопрос автору статьи
На этой странице вы узнаете, как вычислить площадь прямоугольного треугольника, также здесь вы найдёте онлайн-калькуляторы для вычисления площади прямоугольного треугольника по различным заданным величинам.
Определение 1
Прямоугольный треугольник — это треугольник, один из углов которого является прямым, при этом два другие угла — острые.
Для того чтобы воспользоваться приведёнными онлайн-калькуляторами для расчётов, введите известные величины.
Одной из самых простых формул для вычисления площади прямоугольного треугольника является формула через катеты.
Площадь прямоугольного треугольника по двум катетам

Формула площади прямоугольного треугольника по двум катетам выглядит как:
$S = frac12 cdot a cdot b$, где
$S$ – площадь треугольника,
$a$ – первый катет данного треугольника,
$b$ – второй катет данного треугольника.
Пример 1
Задача
Дан прямоугольный треугольник, две меньшие стороны которого равны $3$ и $4$. Чему равна его площадь?
Решение:
Самой длинной стороной в треугольнике является гипотенуза, поэтому воспользуемся формулой вычисления площади через катеты:
$S = frac12 cdot a cdot b = frac12 cdot 3 cdot 4 = 6$.
Ответ: $6$.
Также площадь прямоугольного треугольника можно вычислить если известна гипотенуза и угол между гипотенузой и одним из катетов.
Площадь прямоугольного треугольника по гипотенузе и углу

Площадь прямоугольного треугольника через гипотенузу можно найти по формуле для площади треугольника через 2 стороны и синус угла между ними:
$S = frac12 cdot a cdot c cdot sin (α)$ (1).
Для начала необходимо найти одну из его сторон.
Для этого вспомним определение косинуса:
$cos (α) = frac{a}{c}$.
Из него выразим сторону $a$:
$a = c cdot cos (α)$.
Подставим $a$ в формулу (1):
$S = frac12 c^2 cdot cos (α) cdot sin (α)$, здесь
$c$ — гипотенуза;
$α$ — угол между сторонами $a$ и $c$.
Пример 2
Задача
Гипотенуза прямоугольного треугольника равна $7$, а угол $α$ между гипотенузой и катетом $a$ равен $30°$. Найдите, чему равна площадь треугольника.
Решение:
Найдём сторону $a$:
$a = c cdot cos (30°) ≈ 7 cdot 0.866 ≈ 6.06$
Подставим полученное значение для вычисления площади треугольника через синус угла:
$S = frac12 cdot a cdot c cdot sin (α) = frac12 cdot 6.06 cdot 7 cdot 0.5 = 10.605$.
Ответ: $10.605$.
Другим способом вычисления площади прямого треугольника является вычисление через формулу Герона.
Площадь прямоугольного треугольника по формуле Герона

Рассчитать площадь прямоугольного треугольника по формуле Герона можно следующим образом:
$S = (p – a) cdot (p – b)$, где
$S$ – площадь треугольника,
$a$ – первый катет,
$b$ – второй катет,
$p$ – полупериметр данного треугольника, вычисляемый по формуле:
$p = frac{a + b + c}{2}$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата написания статьи: 10.06.2019
Площадь прямоугольного треугольника онлайн
С помощю этого онлайн калькулятора можно найти площадь прямоугольного треугольника. Для нахождения площади прямоугольного треугольника введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть и численные примеры смотрите ниже.
Содержание
- Площадь прямоугольного треугольника по двум катетам
- Площадь прямоугольного треугольника по катету и гипотенузе
- Площадь прямоугольного треугольника по гипотенузе и углу
- Площадь прямоугольного треугольника по катету и прилежащему углу
- Площадь прямоугольного треугольника по катету и противолежащему углу
- Площадь прямоугольного треугольника по гипотенузе и вписанной окружности
- Площадь прямоугольного треугольника по отрезкам, на которые делит гипотенузу вписанная окружность
Площадь прямоугольного треугольника по двум катетам
Как известно, площадь треугольника равна половине произведения его основания на высоту (см. страницу Площадь треугольника онлайн).В прямоугольном треугольнике катеты перпендикулярны друг другу. Поэтому можно один из них считать как основание, а другой − как высоту.
На рисунке 1 можем считать a как основание, а b − как высоту. Тогда площадь прямоугольного треугольника равна:
Пример 1. Известны катеты прямоугольного треугольника: 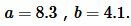 Найти площадь треугольника.
Найти площадь треугольника.
Решение. Для вычисления площади треугольника воспользуемся формулой (1). Подставляя значения 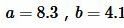 в (1), получим:
в (1), получим:
Ответ: 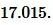
Площадь прямоугольного треугольника по катету и гипотенузе
Пусть в прямоугольном треугольнике известны катет a и гипотенуза c (Рис.2):
Найдем площадь треугольника. Из формулы Пифагора имеем:
Подставляя (2) в (1), получим формулу вычисления площади прямоугольного треугольника по катету и гипотенузе:
Пример 2. Известны катет и гипотенуза прямоугольного треугольника: 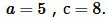 Найти площадь треугольника.
Найти площадь треугольника.
Решение. Для вычисления площади треугольника воспользуемся формулой (3). Подставляя значения 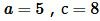 в (3), получим:
в (3), получим:
Ответ: 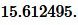
Площадь прямоугольного треугольника по гипотенузе и углу
Пусть в прямоугольном треугольнике известны гипотенуза с и угол α (Рис.3):
Найдем площадь прямоугольного треугольника. Из теоремы синусов имеем:
или
Подставим (4) в (1):
Из формулы произведения тригонометрических функций имеем:
Подставим в (6) ( small beta=alpha ):
Применяя (7) относительно формулы (5), получим:
Пример 3. Известны гипотенуза и прилегающий угол прямоугольного треугольника: 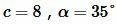 . Найти площадь треугольника.
. Найти площадь треугольника.
Решение. Для вычисления площади треугольника воспользуемся формулой (8). Подставляя значения 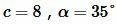 в (8), получим:
в (8), получим:
Ответ: 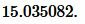
Площадь прямоугольного треугольника по катету и прилежащему углу
Пусть в прямоугольном треугольнике известны катет a и прилежащий угол α (Рис.4):
Найдем площадь прямоугольного треугольника. Тангенс угла α прямоугольного треугольника равна:
Откуда
Подставляя (9) в (1), получим формулу площади прямоугольного треугольника по катету и прилежащему углу:
Пример 4. Известны катет и прилегающий угол прямоугольного треугольника: 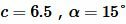 . Найти площадь треугольника.
. Найти площадь треугольника.
Решение. Для вычисления площади треугольника воспользуемся формулой (10). Подставляя значения 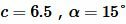 в (10), получим:
в (10), получим:
Ответ: 
Площадь прямоугольного треугольника по катету и противолежащему углу
Пусть в прямоугольном треугольнике известны катет a и противолежащий угол α (Рис.5):
Найдем площадь прямоугольного треугольника. Коангенс угла α прямоугольного треугольника равна:
Откуда
Подставляя (12) в (1), получим формулу площади прямоугольного треугольника по катету и противожащему углу:
Пример 5. Известны катет и противолежащий угол прямоугольного треугольника: 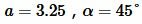 . Найти площадь треугольника.
. Найти площадь треугольника.
Решение. Для вычисления площади треугольника воспользуемся формулой (13). Подставляя значения 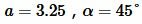 в (13), получим:
в (13), получим:
Ответ: 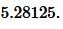
Площадь прямоугольного треугольника по гипотенузе и вписанной окружности
Пусть в прямоугольном треугольнике известны гипотенуза с и радиус вписанной окружности r (Рис.6):
Найдем площадь прямоугольного треугольника. Соединим центр окружности O c вершинами A, B и с точками D, E, F.
Треугольники AOD, AOF, BOD, BOE прямоугольные, поскольку 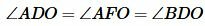
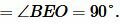 Прямоугольные треугольники AOD и AOF равны по гипотенузе и катету (сторона AO общая, OD=OF):
Прямоугольные треугольники AOD и AOF равны по гипотенузе и катету (сторона AO общая, OD=OF):
Прямоугольные треугольники BOD и BOE равны по гипотенузе и катету (сторона BO общая, OD=OE):
Запишем формулы площадей прямоугольных треугольников AOD и BOD и квадрата OECF:
Тогда, учитывая (14) и (15), площадь прямоугольного треугольника ABC равна:
Подставляя (16), (17) в (18), получим:
или
Пример 6. Известны гипотенуза и радиус вписанной окружности прямоугольного треугольника: 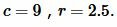 Найти площадь треугольника.
Найти площадь треугольника.
Решение. Для вычисления площади треугольника воспользуемся формулой (19). Подставляя значения 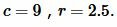 в (19), получим:
в (19), получим:
Ответ: 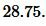
Площадь прямоугольного треугольника по отрезкам, на которые делит гипотенузу вписанная окружность
Пусть в прямоугольном треугольнике известны отрезки AD и DB (Рис.6). Найдем площадь прямоугольного треугольника выраженные через эти отрезки. Площадь прямоугольного треугольника через катеты имеет вид:
Учитывая, что 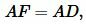
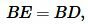
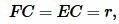
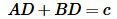 , (20) примет вид:
, (20) примет вид:
То есть
Сравнивая формулы (19) и (21) можем записать:
Таким образом формула площади прямоугольного треугольника по отрезкам, на которые делит гипотенузу вписанная окружность имеет следующий вид:
Пример 7. Известны отрезки гипотенузы разделенные вписанной окружностью прямоугольного треугольника (Рис.6) 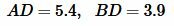 Найти площадь треугольника.
Найти площадь треугольника.
Решение. Для вычисления площади треугольника воспользуемся формулой (22). Подставляя значения 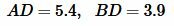 в (22), получим:
в (22), получим:
Ответ: 
Смотрите также:
- Площадь треугольника онлайн
- Площадь равностороннего треугольника онлайн
- Площадь равнобедренного треугольника онлайн
Как найти площадь треугольника
На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.
Треугольник – это многоугольник с тремя сторонами.
По формуле Герона

Формула Герона для нахождения площади треугольника:
– полупериметр треугольника; a,b,c – стороны треугольника.
Через основание и высоту

Формула нахождения площади треугольника с помощью половины его основания и высоту:
a – основание треугольника; h – высота треугольника.
Через две стороны и угол

Формула нахождения площади треугольника через две стороны и угол между ними:
a,b – стороны треугольника; α – угол между сторонами.
Через сторону и два прилежащих угла

Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:
<
a– сторона треугольника; α и β – прилежащие углы.
Площадь прямоугольного треугольника

Прямоугольный треугольник – треугольник у которого один из углов прямой, т.е. равен 90°.
Формула нахождения площади прямоугольного треугольника через катеты:
a, b – катеты треугольника.
Площадь равнобедренного треугольника через стороны

Равнобедренный треугольник – треугольник, в котором две стороны равны. А значит, равны и два угла.
Формула нахождения площади равнобедренного треугольника через две стороны:
a, b – стороны треугольника.
Площадь равнобедренного треугольника через основание и угол

Формула нахождения площади равнобедренного треугольника через основание и угол:
a – основание равнобедренного треугольника; α – угол между сторонами.
Площадь равностороннего треугольника через стороны

Равносторонний треугольник – треугольник, в котором все стороны равны, а каждый угол равен 60°.
Формула нахождения площади равностороннего треугольника через сторону:
a – сторона равностороннего треугольника.
Площадь равностороннего треугольника через высоту

Формула нахождения площади равностороннего треугольника через высоту:
h – высота равностороннего треугольника.
Площадь равностороннего треугольника через радиус вписанной окружности

Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:
r – радиус вписанной окружности равностороннего треугольника.
Площадь равностороннего треугольника через радиус описанной окружности

Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:
r – радиус описанной окружности равностороннего треугольника.
Площадь треугольника через радиус описанной окружности и три стороны

Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:
a, b, c – стороны треугольника; r – радиус описанной окружности треугольника.
Площадь треугольника через радиус вписанной окружности и три стороны

Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:
p – полупериметр треугольника;a, b, c – стороны треугольника; r – радиус вписанной окружности треугольника.
Как найти площадь любого треугольника
Вспоминаем геометрию: формулы для произвольных, прямоугольных, равнобедренных и равносторонних фигур.

Как найти площадь любого треугольника
Посчитать площадь треугольника можно разными способами. Выбирайте формулу в зависимости от известных вам величин.
Зная сторону и высоту
- Умножьте сторону треугольника на высоту, проведённую к этой стороне.
- Поделите результат на два.
- S — искомая площадь треугольника.
- a — сторона треугольника.
- h — высота треугольника. Это перпендикуляр, опущенный на сторону или её продолжение из противоположной вершины.
Зная две стороны и угол между ними
- Посчитайте произведение двух известных сторон треугольника.
- Найдите синус угла между выбранными сторонами.
- Перемножьте полученные числа.
- Поделите результат на два.
- S — искомая площадь треугольника.
- a и b — стороны треугольника.
- α — угол между сторонами a и b.
Зная три стороны (формула Герона)
- Посчитайте разности полупериметра треугольника и каждой из его сторон.
- Найдите произведение полученных чисел.
- Умножьте результат на полупериметр.
- Найдите корень из полученного числа.
- S — искомая площадь треугольника.
- a, b, c — стороны треугольника.
- p — полупериметр (равен половине от суммы всех сторон треугольника).
Зная три стороны и радиус описанной окружности
- Найдите произведение всех сторон треугольника.
- Поделите результат на четыре радиуса окружности, описанной вокруг прямоугольника.
- S — искомая площадь треугольника.
- R — радиус описанной окружности.
- a, b, c — стороны треугольника.
Зная радиус вписанной окружности и полупериметр
Умножьте радиус окружности, вписанной в треугольник, на полупериметр.
- S — искомая площадь треугольника.
- r — радиус вписанной окружности.
- p — полупериметр треугольника (равен половине от суммы всех сторон).
Как найти площадь прямоугольного треугольника
- Посчитайте произведение катетов треугольника.
- Поделите результат на два.
- S — искомая площадь треугольника.
- a, b — катеты треугольника, то есть стороны, которые пересекаются под прямым углом.
Как найти площадь равнобедренного треугольника
- Умножьте основание на высоту треугольника.
- Поделите результат на два.
- S — искомая площадь треугольника.
- a — основание треугольника. Это та сторона, которая не равняется двум другим. Напомним, в равнобедренном треугольнике две из трёх сторон имеют одинаковую длину.
- h — высота треугольника. Это перпендикуляр, опущенный на основание из противоположной вершины.
Как найти площадь равностороннего треугольника
- Умножьте квадрат стороны треугольника на корень из трёх.
- Поделите результат на четыре.
- S — искомая площадь треугольника.
- a — сторона треугольника. Напомним, в равностороннем треугольнике все стороны имеют одинаковую длину.
Читайте также 🧠👨🏻🎓✍🏻
- 7 причин полюбить математику
- ТЕСТ: Помните ли вы геометрию?
- 10 хитрых головоломок со спичками для тренировки воображения
- Интересные математические факты для тех, кто хочет больше узнать о мире вокруг
- ТЕСТ: Сможете ли вы решить простые математические примеры?
