Нами были рассмотрены действия сложения, вычитания и умножения матриц на число. Еще одним действием над ними является умножение. Выполняется оно сложнее, а само правило может показаться немного странным. При его выполнении важно уметь определять размер матриц. Это понятие было рассмотрено в теме «Что такое матрица».
Онлайн-калькулятор
Как умножать матрицы
Приступим к рассмотрению умножения матриц.
Нам известно, что складывать и вычитать можно матрицы, которые имеют одинаковый размер. С умножением дела обстоят немного сложнее.
Какие матрицы можно умножать
Матрицу P можно умножить на матрицу K только в том случае, если число столбцов матрицы P равняется числу строк матрицы K. Матрицы, для которых данное условие не выполняется, умножать нельзя.
Пример 1
Определим, можно ли умножить матрицу
K=(15271810)K=begin{pmatrix}15&27\18&10end{pmatrix} на матрицу L=(3516)L=begin{pmatrix}35\16end{pmatrix}.
Матрица KK состоит из 2 строк и 2 столбцов, а матрица LL — из 2 строк и 1 столбца. Число столбцов матрицы KK равно числу строк матрицы LL, значит, матрицу KK можно умножить на матрицу LL.
Пример 2
Переставим матрицы местами и определим, можно ли умножить матрицу
F=(3516)F=begin{pmatrix}35\16end{pmatrix} на матрицу C=(15271810)C=begin{pmatrix}15&27\18&10end{pmatrix}.
Матрица FF состоит из 2 строк и 1 столбца, а матрица CC — из 2 строк и 2 столбцов. Число столбцов матрицы FF не равно числу строк матрицы CC, значит, матрицу FF нельзя умножить на матрицу CC.
Произведение матрицы AA размера m×nmtimes n и матрицы BB размера n×kntimes k — это матрица CC размера m×kmtimes k, в которой элемент cijc_{ij} равен сумме произведений элементов ii строки матрицы AA на соответствующие элементы jj столбца матрицы B:cij=ai1b1j+ai2b2j+…+ainbnjB: c_{ij}=a_{i1}b_{1j}+a_{i2}b_{2j}+…+a_{in}b_{nj}.
Умножение матриц осуществляется путем умножения строки на столбец. Находятся произведения первого элемента строки и первого элемента столбца, второго элемента строки и второго элемента столбца и т.д. Затем полученные произведения суммируются.
Алгоритм нахождения произведения матриц
- определить размеры матриц;
- если число столбцов первой матрицы совпадает с числом строк второй матрицы, то выполнять умножение.
Рассмотрим пример умножения матрицы
A=(a11a12a21a22a31a32a41a42)A=begin{pmatrix}a_{11}&a_{12}\a_{21}&a_{22}\a_{31}&a_{32}\a_{41}&a_{42}end{pmatrix}
на матрицу
B=(b11b12b13b21b22b23)B=begin{pmatrix}b_{11}&b_{12}&b_{13}\b_{21}&b_{22}&b_{23}end{pmatrix}.
Матрица AA состоит из 4 строк и 2 столбцов, а матрица BB — из 2 строк и 3 столбцов. Число столбцов матрицы AA равно числу строк матрицы BB, значит, можно найти произведение C=A⋅BC=Acdot B. Причем матрица CC будет иметь размер 4×34times 3. Найдем элементы c12c_{12} (выделен красными стрелками) и c33c_{33} (выделен синими стрелками):
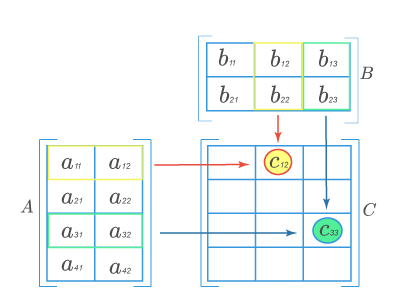
Для того чтобы найти элемент c12c_{12} нужно перемножать соответствующие элементы 1 строки матрицы AA и 2 столбца матрицы B:c12=a11⋅b12+a12⋅b22B: c_{12}=a_{11}cdot b_{12}+a_{12}cdot b_{22}. Для того чтобы найти элемент c33c_{33} нужно перемножать соответствующие элементы 3 строки матрицы AA и 3 столбца матрицы BB: c33=a31⋅b13+a32⋅b23c_{33}=a_{31}cdot b_{13}+a_{32}cdot b_{23}. Так находят все элементы.
Таким образом, матрица CC может быть найдена следующим образом:
A⋅B=(a11a12a21a22a31a32a41a42)⋅(b11b12b13b21b22b23)=Acdot B=begin{pmatrix}a_{11}&a_{12}\a_{21}&a_{22}\a_{31}&a_{32}\a_{41}&a_{42}end{pmatrix}cdot begin{pmatrix}b_{11}&b_{12}&b_{13}\b_{21}&b_{22}&b_{23}end{pmatrix}=
=(a11⋅b11+a12⋅b21a11⋅b12+a12⋅b22a11⋅b13+a12⋅b23a21⋅b11+a22⋅b21a21⋅b12+a22⋅b22a21⋅b13+a22⋅b23a31⋅b11+a32⋅b21a31⋅b12+a32⋅b22a31⋅b13+a32⋅b23a41⋅b11+a42⋅b21a41⋅b12+a42⋅b22a41⋅b13+a42⋅b23)=begin{pmatrix}a_{11}cdot b_{11}+a_{12}cdot b_{21}&a_{11}cdot b_{12}+a_{12}cdot b_{22}&a_{11}cdot b_{13}+a_{12}cdot b_{23}\a_{21}cdot b_{11}+a_{22}cdot b_{21}&a_{21}cdot b_{12}+a_{22}cdot b_{22}&a_{21}cdot b_{13}+a_{22}cdot b_{23}\a_{31}cdot b_{11}+a_{32}cdot b_{21}&a_{31}cdot b_{12}+a_{32}cdot b_{22}&a_{31}cdot b_{13}+a_{32}cdot b_{23}\a_{41}cdot b_{11}+a_{42}cdot b_{21}&a_{41}cdot b_{12}+a_{42}cdot b_{22}&a_{41}cdot b_{13}+a_{42}cdot b_{23}end{pmatrix}
Произведение B⋅ABcdot A нельзя найти, поскольку число столбцов матрицы BB неравно числу строк матрицы AA.
Найти произведение матрицы C=(15271810)C=begin{pmatrix}15&27\18&10end{pmatrix} на матрицу F=(3516)F=begin{pmatrix}35\16end{pmatrix}.
Матрица CC имеет размер 2×22times 2, матрица FF имеет размер 2×12times 1, значит, размер матрицы произведения будет 2×12times 1.
C⋅F=(15271810)⋅(3516)=(15⋅35+27⋅1618⋅35+10⋅16)=(957790)Ccdot F=begin{pmatrix}15&27\18&10end{pmatrix}cdot begin{pmatrix}35\16end{pmatrix}=begin{pmatrix}15cdot 35+27cdot 16\18cdot 35+10cdot 16end{pmatrix}=begin{pmatrix}957\790end{pmatrix}.
Как отмечалось выше, произведение матриц F⋅CFcdot C невозможно.
Найти произведение матриц K⋅LKcdot L и L⋅KLcdot K, если K=(12171314)K=begin{pmatrix}12&17\13&14end{pmatrix} на матрицу L=(18111210)L=begin{pmatrix}18&11\12&10end{pmatrix}.
Матрица KK имеет размер 2×22times 2, матрица LL имеет размер 2×22times 2, значит, размер матрицы произведения будет 2×22times 2.
K⋅L=(12171314)⋅(18111210)=(12⋅18+17⋅1212⋅11+17⋅1013⋅18+14⋅1213⋅11+14⋅10)=(420302402283)Kcdot L=begin{pmatrix}12&17\13&14end{pmatrix}cdot begin{pmatrix}18&11\12&10end{pmatrix}=begin{pmatrix}12cdot 18+17cdot 12&12cdot 11+17cdot 10\13cdot 18+14cdot 12&13cdot 11+14cdot 10end{pmatrix}=begin{pmatrix}420&302\402&283end{pmatrix}
Произведение L⋅KLcdot K существует и его размер — 2×22times 2.
L⋅K=(18111210)⋅(12171314)=(18⋅12+11⋅1318⋅17+11⋅1412⋅12+10⋅1312⋅17+10⋅14)=(359460274344)Lcdot K=begin{pmatrix}18&11\12&10end{pmatrix}cdot begin{pmatrix}12&17\13&14end{pmatrix}=begin{pmatrix}18cdot 12+11cdot 13&18cdot 17+11cdot 14\12cdot 12+10cdot 13&12cdot 17+10cdot 14end{pmatrix}=begin{pmatrix}359&460\274&344end{pmatrix}
Произведение двух матриц в общем случае зависит от порядка сомножителей, т.е. оно некоммутативно: A⋅B≠B⋅AAcdot Bneq Bcdot A.
Так, для матриц K=(12171314)K=begin{pmatrix}12&17\13&14end{pmatrix} и L=(18111210)L=begin{pmatrix}18&11\12&10end{pmatrix} из рассмотренного примера K⋅L≠L⋅KKcdot L neq Lcdot K.
Перестановочные матрицы
Перестановочные, или коммутирующие, матрицы – матрицы, для которых выполняется равенство A⋅B=B⋅AAcdot B=Bcdot A. Они обязательно квадратные.
Проверить, являются ли перестановочными матрицы CC и DD, если C=(2342)C=begin{pmatrix}2&3\4&2end{pmatrix}, D=(3343)D=begin{pmatrix}3&3\4&3end{pmatrix}.
Найдем произведения этих матриц C⋅DCcdot D и D⋅CDcdot C.
C⋅D=(2342)⋅(3343)=(2⋅3+3⋅42⋅3+3⋅34⋅3+2⋅44⋅3+2⋅3)=(18152018)Ccdot D=begin{pmatrix}2&3\4&2end{pmatrix}cdot begin{pmatrix}3&3\4&3end{pmatrix}=begin{pmatrix}2cdot 3+3cdot 4&2cdot 3+3cdot 3\4cdot 3+2cdot 4&4cdot 3+2cdot 3end{pmatrix}=begin{pmatrix}18&15\20&18end{pmatrix},
D⋅C=(3343)⋅(2342)=(3⋅2+3⋅43⋅3+3⋅24⋅2+3⋅44⋅3+3⋅2)=(18152018)Dcdot C=begin{pmatrix}3&3\4&3end{pmatrix}cdot begin{pmatrix}2&3\4&2end{pmatrix}=begin{pmatrix}3cdot 2+3cdot 4&3cdot 3+3cdot 2\4cdot 2+3cdot 4&4cdot 3+3cdot 2end{pmatrix}=begin{pmatrix}18&15\20&18end{pmatrix}.
Таким образом, для заданных матриц выполняется равенство C⋅DCcdot D и D⋅CDcdot C, поэтому они являются перестановочными.
Проверить, являются ли перестановочными матрицы FF и HH, если F=(3421)F=begin{pmatrix}3&4\2&1end{pmatrix}, H=(0593)H=begin{pmatrix}0&5\9&3end{pmatrix}.
Найдем произведения этих матриц F⋅HFcdot H и H⋅FHcdot F.
F⋅H=(3421)⋅(0593)=(3⋅0+4⋅93⋅5+4⋅32⋅0+1⋅92⋅5+1⋅3)=(3627913)Fcdot H=begin{pmatrix}3&4\2&1end{pmatrix}cdot begin{pmatrix}0&5\9&3end{pmatrix}=begin{pmatrix}3cdot 0+4cdot 9&3cdot 5+4cdot 3\2cdot 0+1cdot 9&2cdot 5+1cdot 3end{pmatrix}=begin{pmatrix}36&27\9&13end{pmatrix},
H⋅F=(0593)⋅(3421)=(0⋅3+5⋅20⋅4+5⋅19⋅3+3⋅29⋅4+3⋅1)=(1053339)Hcdot F=begin{pmatrix}0&5\9&3end{pmatrix}cdot begin{pmatrix}3&4\2&1end{pmatrix}=begin{pmatrix}0cdot 3+5cdot 2&0cdot 4+5cdot 1\9cdot 3+3cdot 2&9cdot 4+3cdot 1end{pmatrix}=begin{pmatrix}10&5\33&39end{pmatrix}.
Таким образом, для заданных матриц не выполняется равенство F⋅HFcdot H и H⋅FHcdot F, поэтому они не являются перестановочными.
Контрольные работы на заказ онлайн от практикующих исполнителей!
Умножение матриц: примеры, алгоритм действий, свойства произведения
Произведение двух матриц
Произведение матриц (С= АВ) — операция только для согласованных матриц А и В, у которых число столбцов матрицы А равно числу строк матрицы В:
C⏟m×n=A⏟m×p×B⏟p×n
Даны матрицы:
- A=a(ij) размеров m×n;
- B=b(ij) размеров p×n
Матрицу C, элементы cij которой вычисляются по следующей формуле:
cij=ai1×b1j+ai2×b2j+…+aip×bpj, i=1,…m, j=1,…m
Вычислим произведения АВ=ВА:
А=121012, В=100111
Решение, используя правило умножения матриц:
А⏟2×3×В⏟3×2=121012×100111=1×1+2×0+1×11×0+2×1+1×10×1+1×0+2×10×0+1×1+2×1==2323⏟2×2
В⏟3×2×А⏟2×3=100111×121012=1×1+0×01×2+0×11×1+0×20×1+1×00×2+1×10×1+1×21×1+1×01×2+1×11×1+1×2=121012133⏟3×3
Произведение АВ и ВА найдены, но являются матрицами разных размеров: АВ не равна ВА.
Свойства умножения матриц
Свойства умножения матриц:
- (АВ)С = А(ВС) — ассоциативность умножения матриц;
- А(В+С) = АВ + АС — дистрибутивность умножения;
- (А+В)С = АС + ВС — дистрибутивность умножения;
- λ(АВ)=(λА)В
Проверяем свойство №1: (АВ)С = А(ВС):
(А×В)×А=1234×5678×1002=19224350×1002=194443100,
А(В×С)=1234×56781002=1234×512716=194443100.
Проверяем свойство №2: А(В+С) = АВ + АС:
А×(В+С)=1234×5678+1002=1234×66710=20264658,
АВ+АС=1234×5678+1234×1002=19224350+1438=20264658.
Произведение трех матриц
Произведение трех матриц АВС вычисляют 2-мя способами:
- найти АВ и умножить на С: (АВ)С;
- либо найти сначала ВС, а затем умножить А(ВС).
Перемножить матрицы 2-мя способами:
4375×-289338-126×7321
Алгоритм действий:
- найти произведение 2-х матриц;
- затем снова найти произведение 2-х матриц.
1). АВ=4375×-289338-126=4(-28)+3×384×93+3(-126)7(-28)+5×387×93+5(-126)=2-6-621
2). АВС=(АВ)С=2-6-6217321=2×7-6×22×3-6×1-6×7+21×2-6×3+21×1=2003.
Используем формулу АВС=(АВ)С:
1). ВС=-289338-1267321=-28×7+93×2-28×3+93×138×7-126×238×3-126×1=-10914-12
2). АВС=(АВ)С=7321-10914-12=4(-10)+3×144×9+3(-12)7(-10)+5×147×9+5(-12)=2003
Ответ: 4375-289338-1267321=2003
Умножение матрицы на число
Произведение матрицы А на число k — это матрица В=Аk того же размера, которая получена из исходной умножением на заданное число всех ее элементов:
bi,j=k×ai,j
Свойства умножения матрицы на число:
- 1×А=А
- 0×А=нулевая матрица
- k(A+B)=kA+kB
- (k+n)A=kA+nA
- (k×n)×A=k(n×A)
Найдем произведение матрицы А=4290 на 5.
Решение:
5А=542905×45×25×95×0=2010450
Умножение матрицы на вектор
Чтобы найти произведение матрицы и вектора, необходимо умножать по правилу «строка на столбец»:
- если умножить матрицу на вектор-столбец число столбцов в матрице должно совпадать с числом строк в векторе-столбце;
- результатом умножения вектора-столбца является только вектор-столбец:
АВ=а11а12⋯а1nа21а22⋯а2n⋯⋯⋯⋯аm1аm2⋯аmnb1b2⋯b1n=a11×b1+a12×b2+⋯+a1n×bna21×b1+a22×b2+⋯+a2n×bn⋯⋯⋯⋯am1×b1+am2×b2+⋯+amn×bn=c1c2⋯c1m
- если умножить матрицу на вектор-строку, то умножаемая матрица должна быть исключительно вектором-столбцом, причем количество столбцов должно совпадать с количеством столбцов в векторе-строке:
АВ=аа⋯аbb⋯b=a1×b1a1×b2⋯a1×bna2×b1a2×b2⋯a2×bn⋯⋯⋯⋯an×b1an×b2⋯an×bn=c11c12⋯c1nc21c22⋯c2n⋯⋯⋯⋯cn1cn2⋯cnn
Найдем произведение матрицы А и вектора-столбца В:
АВ=240-213-10112-1=2×1+4×2+0×(-1)-2×1+1×2+3×(-1)-1×1+0×2+1×(-1)=2+8+0-2+2-3-1+0-1=10-3-2
Найдем произведение матрицы А и вектора-строку В:
А=320-1, В=-1102
Решение:
АВ=3201×-1102=3×(-1)3×13×03×22×(-1)2×12×02×20×(-1)0×10×00×21×(-1)1×11×01×2=-3306-22040000-1102
Ответ: АВ=-3306-22040000-1102
![]()
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Уважаемые студенты!
Заказать задачи по физике, информатике, экономике, праву и другим 200 предметам можно здесь всего за 10 минут.
Произведение матриц
Для того, чтобы найти произведение матриц нужно строки левой матрицы умножить на столбцы правой матрицы. $$begin{pmatrix} a_{11}&a_{12}&a_{13} \ *&*&* \ *&*&* end{pmatrix} times begin{pmatrix} b_{11}&*&* \ b_{21}&*&* \ b_{31}&*&* end{pmatrix} = begin{pmatrix} c_{11}&*&* \ *&*&* \ *&*&* end{pmatrix}$$
Умножение строки на столбец производим по правилу скалярного произведения. То есть находим сумму произведений соответствующих элементов. Например, при умножении первой строки на первый столбец получаем $$c_{11}=a_{11}b_{11}+a_{12}b_{21}+a_{13}b_{31}.$$
Обязательно перед умножением матриц необходимо убедиться, чтобы число столбцов левой матрицы совпадало с числом строк правой матрицы. Только в этом случае матрицы можно перемножать. В результате получается матрица, у которой число строк равняется количеству строк левой матрицы, а количество столбцов равно числу столбцов правой матрицы. $$ underbrace{A}_{n times p} times underbrace{B}_{p times m} = underbrace{C}_{ntimes m}$$
Важное замечание!
Умножение матриц не коммутативно, т.е. $AB neq BA$.
| Пример 1 |
| Найти произведение матриц $Atimes B$ $$A=begin{pmatrix} 2&1 \ -3&4 end{pmatrix}, B = begin{pmatrix} 1&-3 \ 2&0 end{pmatrix}.$$ |
| Решение |
|
Проверяем, что число столбцов матрицы $A$ равно числу строк матрицы $B$. Далее берем первую строчку левой матрицы и умножаем её на первый столбец второй матрицы. $$A times B = begin{pmatrix} 2&1 \*&* end{pmatrix} times begin{pmatrix} 1&* \ 2&* end{pmatrix}= begin{pmatrix} 2cdot1+1cdot2 &* \*&* end{pmatrix} = begin{pmatrix} 4&* \*&* end{pmatrix}$$ Теперь умножаем первую строку левой матрицы на второй столбец правой матрицы. $$A times B = begin{pmatrix} 2&1 \*&* end{pmatrix} times begin{pmatrix} *&-3 \ *&0 end{pmatrix}= begin{pmatrix} *&2cdot(-3)+1cdot0 \*&* end{pmatrix}=begin{pmatrix} *&-6 \*&* end{pmatrix}$$ Далее вторую строчку левой матрицы и умножаем на первый столбец второй матрицы. $$A times B = begin{pmatrix} *&* \-3&4 end{pmatrix} times begin{pmatrix} 1&* \ 2&* end{pmatrix}= begin{pmatrix} *&* \(-3)cdot1+4cdot2&* end{pmatrix}=begin{pmatrix} *&* \5&* end{pmatrix}$$ И осталось умножить первую строку левой матрицы на второй столбец правой матрицы. $$A times B = begin{pmatrix} *&* \-3&4 end{pmatrix} times begin{pmatrix} *&-3 \ *&0 end{pmatrix}= begin{pmatrix} *&* \ *&(-3)cdot(-3)+4cdot0 end{pmatrix}=begin{pmatrix} *&* \*&9 end{pmatrix}$$ Вот теперь можно составить полный ответ. $$Atimes B=begin{pmatrix} 2&1 \ -3&4 end{pmatrix} times begin{pmatrix} 1&-3 \ 2&0 end{pmatrix} = begin{pmatrix} 4&-6 \ 5&9 end{pmatrix}$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$A times B = begin{pmatrix} 4&-6 \ 5&9 end{pmatrix}$$ |
| Пример 2 |
| Умножить матрицы $Atimes B$ $$A = begin{pmatrix} 2&3&0 \ 1&-1&2 end{pmatrix}, B = begin{pmatrix} 1&0 \ 2&-1 \ 1&-2 end{pmatrix}.$$ |
| Решение |
|
Убеждаемся, что число столбцов матрицы $A$ равно количеству строк матрицы $B$ для того, чтобы можно было выполнить умножение. Так как количество строк в $A$ равно двум, а количество столбцов в $B$ равно 2, то в результате должна получиться матрица с размерностью два на два. $$A times B = begin{pmatrix} 2&3&0 \ 1&-1&2 end{pmatrix} times begin{pmatrix} 1&0 \ 2&-1 \ 1&-2 end{pmatrix} = begin{pmatrix} *&* \ *&* end{pmatrix}$$ Умножаем первую строку левой матрицы на второй столбец правой матрицы. $$begin{pmatrix} 2&3&0 \ 1&-1&2 end{pmatrix} times begin{pmatrix} 1&0 \ 2&-1 \ 1&-2 end{pmatrix} = begin{pmatrix} 2cdot1+3cdot2+0cdot1&* \ *&* end{pmatrix} = begin{pmatrix} 8&* \*&* end{pmatrix}$$ Умножим первую строку левой матрицы на второй столбец правой матрицы. $$begin{pmatrix} 2&3&0 \ 1&-1&2 end{pmatrix} times begin{pmatrix} 1&0 \ 2&-1 \ 1&-2 end{pmatrix} = begin{pmatrix} 8&2cdot0+3cdot(-1)+0cdot(-2) \ *&* end{pmatrix} = begin{pmatrix} 8&-3 \*&* end{pmatrix}$$ Аналогично поступаем теперь со второй строкой левой матрицы. Умножаем её на первый столбец правой матрицы. $$begin{pmatrix} 2&3&0 \ 1&-1&2 end{pmatrix} times begin{pmatrix} 1&0 \ 2&-1 \ 1&-2 end{pmatrix} = begin{pmatrix} 8&-3 \ 1cdot1+(-1)cdot2+2cdot1&* end{pmatrix} = begin{pmatrix} 8&-3 \1&* end{pmatrix}$$ Умножим вторую строку левой матрицы на второй столбец правой матрицы.$$begin{pmatrix} 2&3&0 \ 1&-1&2 end{pmatrix} times begin{pmatrix} 1&0 \ 2&-1 \ 1&-2 end{pmatrix} = begin{pmatrix} 8&-3 \ 1&1cdot0+(-1)cdot(-1)+2cdot(-2) end{pmatrix} = begin{pmatrix} 8&-3 \1&-3 end{pmatrix}$$ Вот таким образом можно перемножить матрицы разной размерности. |
| Ответ |
| $$Atimes B = begin{pmatrix} 8&-3 \1&-3 end{pmatrix}$$ |
| Пример 3 |
| Найти произведение матриц $Atimes B$ $$A = begin{pmatrix} 2&3&0 \ -1&2&3 \ 1&-1&2 end{pmatrix}, B = begin{pmatrix} 1&0&2 \ 2&-1&-2 \ 1&-2&4 end{pmatrix}.$$ |
| Решение |
|
Умножаем первую строку левой матрицы на первый столбец правой матрицы. $$begin{pmatrix} 2&3&0 \ -1&2&3 \ 1&-1&2 end{pmatrix} times begin{pmatrix} 1&0&2 \ 2&-1&-2 \ 1&-2&4 end{pmatrix} = begin{pmatrix} 2cdot1+3cdot2+0cdot1 &*&* \*&*&* \ *&*&* end{pmatrix} = begin{pmatrix} 8&*&* \ *&*&* \ *&*&* end{pmatrix}$$ Перемножим первую строку матрицы $A$ со вторым столбцом матрицы $B$. $$begin{pmatrix} 2&3&0 \ -1&2&3 \ 1&-1&2 end{pmatrix} times begin{pmatrix} 1&0&2 \ 2&-1&-2 \ 1&-2&4 end{pmatrix} = begin{pmatrix} 8&2cdot0+3cdot(-1)+0cdot(-2)&* \*&*&* \ *&*&* end{pmatrix} = begin{pmatrix} 8&-3&* \ *&*&* \ *&*&* end{pmatrix}$$ Найдем произведение первой строки матрицы $A$ на третий столбец матрицы $B$. $$begin{pmatrix} 2&3&0 \ -1&2&3 \ 1&-1&2 end{pmatrix} times begin{pmatrix} 1&0&2 \ 2&-1&-2 \ 1&-2&4 end{pmatrix} = begin{pmatrix} 8&-3&2cdot2+3cdot(-2)+0cdot4 \*&*&* \ *&*&* end{pmatrix} = begin{pmatrix} 8&-3&-2 \ *&*&* \ *&*&* end{pmatrix}$$ Возьмем вторую строку левой матрицы и умножим на первый столбец правой матрицы. $$begin{pmatrix} 2&3&0 \ -1&2&3 \ 1&-1&2 end{pmatrix} times begin{pmatrix} 1&0&2 \ 2&-1&-2 \ 1&-2&4 end{pmatrix} = begin{pmatrix} 8&-3&-2 \(-1)cdot1+2cdot2+3cdot1&*&* \ *&*&* end{pmatrix} = begin{pmatrix} 8&-3&-2 \ 6&*&* \ *&*&* end{pmatrix}$$ Аналогично умножим вторую строчку на второй столбец. $$begin{pmatrix} 2&3&0 \ -1&2&3 \ 1&-1&2 end{pmatrix} times begin{pmatrix} 1&0&2 \ 2&-1&-2 \ 1&-2&4 end{pmatrix} = begin{pmatrix} 8&-3&-2 \ 6&(-1)cdot0+2cdot(-1)+3cdot(-2)&* \ *&*&* end{pmatrix} = begin{pmatrix} 8&-3&-2 \ 6&-8&* \ *&*&* end{pmatrix}$$ Таким же образом перемножим вторую строчку с третьим столбцом. $$begin{pmatrix} 2&3&0 \ -1&2&3 \ 1&-1&2 end{pmatrix} times begin{pmatrix} 1&0&2 \ 2&-1&-2 \ 1&-2&4 end{pmatrix} = begin{pmatrix} 8&-3&-2 \ 6&-8&(-1)cdot2+2cdot(-2)+3cdot4 \ *&*&* end{pmatrix} = begin{pmatrix} 8&-3&-2 \ 6&-8&6 \ *&*&* end{pmatrix}$$ Аналогично поступаем с третьей строкой левой матрицы, умножая её на три столбца правой матрицы. $$begin{pmatrix} 2&3&0 \ -1&2&3 \ 1&-1&2 end{pmatrix} times begin{pmatrix} 1&0&2 \ 2&-1&-2 \ 1&-2&4 end{pmatrix} = begin{pmatrix} 8&-3&-2 \ 6&-8&6 \ 1cdot1+(-1)cdot2+2cdot1&*&* end{pmatrix} = begin{pmatrix} 8&-3&-2 \ 6&-8&6 \ 1&*&* end{pmatrix}$$ $$begin{pmatrix} 2&3&0 \ -1&2&3 \ 1&-1&2 end{pmatrix} times begin{pmatrix} 1&0&2 \ 2&-1&-2 \ 1&-2&4 end{pmatrix} = begin{pmatrix} 8&-3&-2 \ 6&-8&6 \ 1&1cdot0+(-1)cdot(-1)+2cdot(-2)&* end{pmatrix} = begin{pmatrix} 8&-3&-2 \ 6&-8&6 \ 1&-3&* end{pmatrix}$$ $$begin{pmatrix} 2&3&0 \ -1&2&3 \ 1&-1&2 end{pmatrix} times begin{pmatrix} 1&0&2 \ 2&-1&-2 \ 1&-2&4 end{pmatrix} = begin{pmatrix} 8&-3&-2 \ 6&-8&6 \ 1&-3&1cdot2+(-1)cdot(-2)+2cdot4 end{pmatrix} = begin{pmatrix} 8&-3&-2 \ 6&-8&6 \ 1&-3&12 end{pmatrix}$$ |
| Ответ |
| $$Atimes B = begin{pmatrix} 8&-3&-2 \ 6&-8&6 \ 1&-3&12 end{pmatrix}$$ |
| Пример 4 |
| Найти произведение матриц $Atimes B$ $$A = begin{pmatrix} 2&3&0 \ -1&2&3 \ 1&-1&2 end{pmatrix}, B = begin{pmatrix} 1&0&2 \ 1&-2&4 end{pmatrix}.$$ |
| Решение |
| Количество столбцов в матрице $A$ равно трём и не совпадает с числом строк в матрице $B$, поэтому нельзя выполнить произведение $A times B$, но вот наоборот произведение $B times A$ можно сделать, так как количество столбцов в матрице $B$ равно количеству строк в $A$. Но так как в условии требуется вариант $Atimes B$, то ответ прост: нельзя выполнить умножение. |
| Ответ |
| Матрицы нельзя перемножить |
Линейная алгебра и, в частности, матрицы — это основа математики нейросетей. Когда говорят «машинное обучение», на самом деле говорят «перемножение матриц», «решение матричных уравнений» и «поиск коэффициентов в матричных уравнениях».
Понятно, что между простой матрицей в линейной алгебре и нейросетью, которая генерирует котов, много слоёв усложнений, дополнительной логики, обучения и т. д. Но здесь мы говорим именно о фундаменте. Цель — чтобы стало понятно, из чего оно сделано.
Краткое содержание прошлых частей:
- Линейная алгебра изучает векторы, матрицы и другие понятия, которые относятся к упорядоченным наборам данных. Линейной алгебре интересно, как можно трансформировать эти упорядоченные данные, складывать и умножать, всячески обсчитывать и находить в них закономерности.
- Вектор — это набор упорядоченных данных в одном измерении. Можно упрощённо сказать, что это последовательность чисел.
- Матрица — это тоже набор упорядоченных данных, только уже не в одном измерении, а в двух (или даже больше).
- Матрицу можно представить как упорядоченную сумку с данными. И с этой сумкой как с единым целым можно совершать какие-то действия. Например, делить, умножать, менять знаки.
- Матрицы можно складывать и умножать на другие матрицы. Это как взять две сумки с данными и получить третью сумку, тоже с данными, только теперь какими-то новыми.
- Матрицы перемножаются по довольно замороченному алгоритму. Арифметика простая, а порядок перемножения довольно запутанный.
И вот наконец мы здесь: если мы можем перемножать матрицы, то мы можем и решить матричное уравнение.
❌ Никакого практического применения следующего материала в народном хозяйстве вы не увидите. Это чистая алгебра в несколько упрощённом виде. Отсюда до практики далёкий путь, поэтому, если нужно что-то практическое, — посмотрите, как мы генерим Чехова на цепях Маркова.
Что такое матричное уравнение
Матричное уравнение — это когда мы умножаем известную матрицу на матрицу Х и получаем новую матрицу. Наша задача — найти неизвестную матрицу Х.
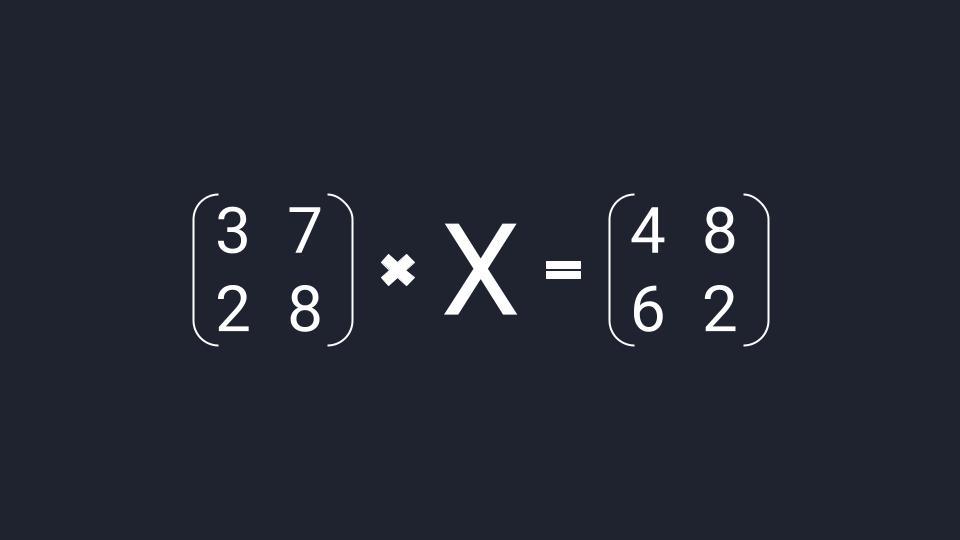
Шаг 1. Упрощаем уравнение
Вместо известных числовых матриц вводим в уравнение буквы: первую матрицу обозначаем буквой A, вторую — буквой B. Неизвестную матрицу X оставляем. Это упрощение поможет составить формулу и выразить X через известную матрицу.
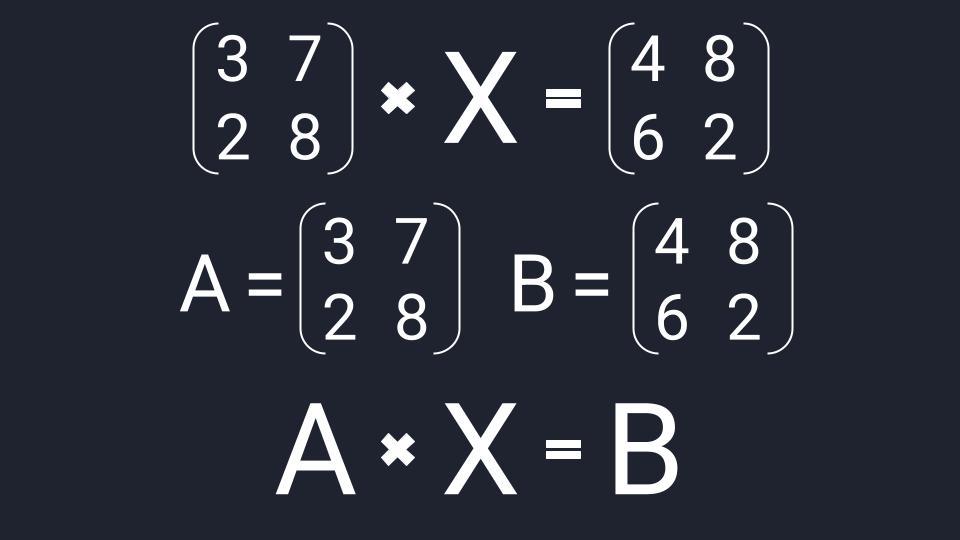
Шаг 2. Вводим единичную матрицу
В линейной алгебре есть два вспомогательных понятия: обратная матрица и единичная матрица. Единичная матрица состоит из нулей, а по диагонали у неё единицы. Обратная матрица — это такая, которая при умножении на исходную даёт единичную матрицу.
Можно представить, что есть число 100 — это «сто в первой степени», 1001
И есть число 0,01 — это «сто в минус первой степени», 100-1
При перемножении этих двух чисел получится единица:
1001 × 100-1 = 100 × 0,01 = 1.
Вот такое, только в мире матриц.
Зная свойства единичных и обратных матриц, делаем алгебраическое колдунство. Умножаем обе известные матрицы на обратную матрицу А-1. Неизвестную матрицу Х оставляем без изменений и переписываем уравнение:
А-1 × А × Х = А-1 × В
Добавляем единичную матрицу и упрощаем запись:
А-1 × А = E — единичная матрица
E × Х = А-1 × В — единичная матрица, умноженная на исходную матрицу, даёт исходную матрицу. Единичную матрицу убираем
Х = А-1 × В — новая запись уравнения
После введения единичной матрицы мы нашли способ выражения неизвестной матрицы X через известные матрицы A и B.
💡 Смотрите, что произошло: раньше нам нужно было найти неизвестную матрицу. А теперь мы точно знаем, как её найти: нужно рассчитать обратную матрицу A-1 и умножить её на известную матрицу B. И то и другое — замороченные процедуры, но с точки зрения арифметики — просто.
Шаг 3. Находим обратную матрицу
Вспоминаем формулу и порядок расчёта обратной матрицы:
- Делим единицу на определитель матрицы A.
- Считаем транспонированную матрицу алгебраических дополнений.
- Перемножаем значения и получаем нужную матрицу.
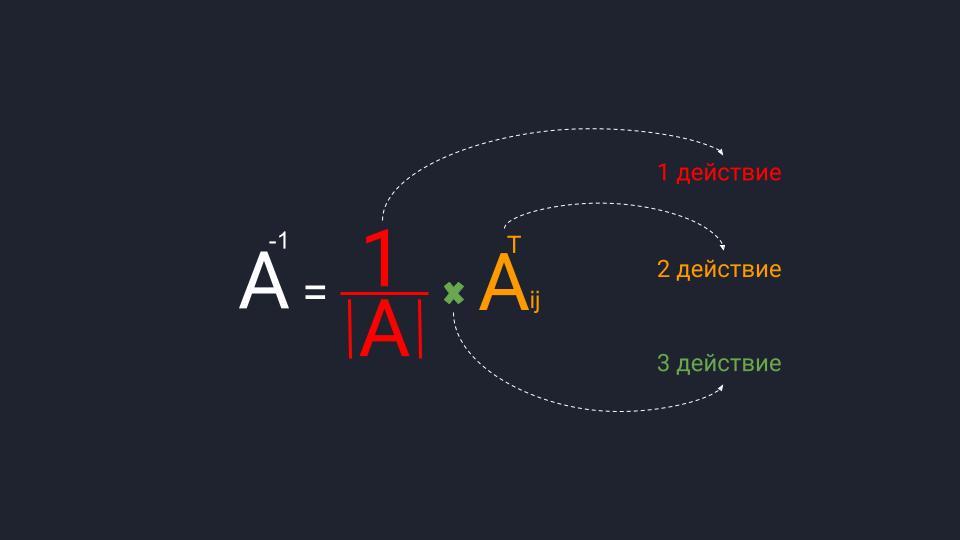

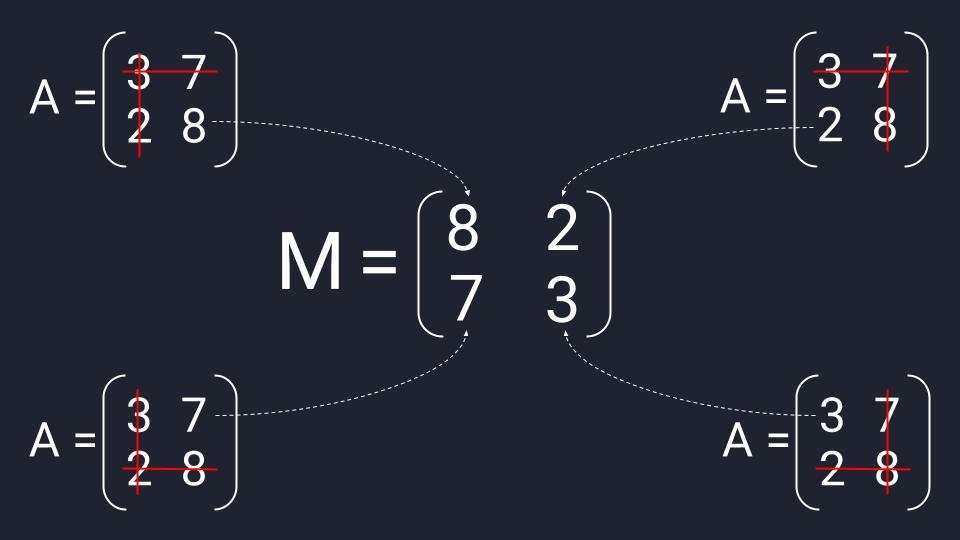

Собираем формулу и получаем обратную матрицу. Для удобства умышленно оставляем перед матрицей дробное число, чтобы было проще считать.

Шаг 4. Вычисляем неизвестную матрицу
Нам остаётся посчитать матрицу X: умножаем обратную матрицу А-1 на матрицу B. Дробь держим за скобками и вносим в матрицу только при условии, что элементы новой матрицы будут кратны десяти — их можно умножить на дробь и получить целое число. Если кратных элементов не будет — дробь оставим за скобками.

Шаг 5. Проверяем уравнение
Мы решили матричное уравнение и получили красивый ответ с целыми числами. Выглядит правильно, но в случае с матрицами этого недостаточно. Чтобы проверить ответ, нам нужно вернуться к условию и умножить исходную матрицу A на матрицу X. В результате должна появиться матрица B. Если расчёты совпадут — мы всё сделали правильно. Если будут отличия — придётся решать заново.
👉 Часто начинающие математики пренебрегают финальной проверкой и считают её лишней тратой времени. Сегодня мы разобрали простое уравнение с двумя квадратными матрицами с четырьмя элементами в каждой. Когда элементов будет больше, в них легко запутаться и допустить ошибку.

Ну и что
Алгоритм решения матричных уравнений несложный, если знать отдельные его компоненты. Дальше на основе этих компонентов математики переходят в более сложные пространства: работают с многомерными матрицами, решают более сложные уравнения, постепенно выходят на всё более и более абстрактные уровни. И дальше, в конце пути, появляется датасет из миллионов котиков. Этот датасет раскладывается на пиксели, каждый пиксель оцифровывается, цифры подставляются в матрицы, и уже огромный алгоритм в автоматическом режиме генерирует изображение нейрокотика:

Этого котика не существует, а матрицы — существуют.
Умножение матриц.
Определение.
Результатом умножения матриц Am×n и Bn×k будет матрица Cm×k такая, что элемент матрицы C, стоящий в i-той строке и j-том столбце (cij), равен сумме произведений элементов i-той строки матрицы A на соответствующие элементы j-того столбца матрицы B:
cij = ai1 · b1j + ai2 · b2j + … + ain · bnj
Замечание.
Две матрицы можно перемножить между собой тогда и только тогда, когда количество столбцов первой матрицы равно количеству строк второй матрицы.
Свойства умножения матриц
- (A · B) · C= A · (B · C) – произведение матриц ассоциативно;
- (z · A) · B= z · (A · B), где z – число;
- A · (B + C) = A · B + A · C – произведение матриц дистрибутивно;
- En · Anm = Anm · Em= Anm – умножение на единичную матрицу;
- A · B ≠ B · A – в общем случае произведение матриц не коммутативно.
- Произведением двух матриц есть матрица, у которой столько строк, сколько их у левого сомножителя, и столько столбцов, сколько их у правого сомножителя.
Примеры задач на умножение матриц
Пример 1.
Найти матрицу C равную произведению матриц A =
42
90
и
B =
31
-34
Решение:
С = A · B =
42
90
·
31
-34
=
612
279
Элементы матрицы C вычисляются следующим образом:
c11 = a11·b11 + a12·b21 = 4·3 + 2·(-3) = 12 – 6 = 6
c12 = a11·b12 + a12·b22 = 4·1 + 2·4 = 4 + 8 = 12
c21 = a21·b11 + a22·b21 = 9·3 + 0·(-3) = 27 + 0 = 27
c22 = a21·b12 + a22·b22 = 9·1 + 0·4 = 9 + 0 = 9
Пример 2
Найти матрицу C равную произведению матриц A =
21
-30
4-1
и
B =
5-16
-307
.
Решение:
C = A · B =
21
-30
4-1
·
5-16
-307
=
7-219
-153-18
23-417
Элементы матрицы C вычисляются следующим образом:
c11 = a11·b11 + a12·b21 = 2·5 + 1·(-3) = 10 – 3 = 7
c12 = a11·b12 + a12·b22 = 2·(-1) + 1·0 = -2 + 0 = -2
c13 = a11·b13 + a12·b23 = 2·6 + 1·7 = 12 + 7 = 19
c21 = a21·b11 + a22·b21 = (-3)·5 + 0·(-3) = -15 + 0 = -15
c22 = a21·b12 + a22·b22 = (-3)·(-1) + 0·0 = 3 + 0 = 3
c23 = a21·b13 + a22·b23 = (-3)·6 + 0·7 = -18 + 0 = -18
c31 = a31·b11 + a32·b21 = 4·5 + (-1)·(-3) = 20 + 3 = 23
c32 = a31·b12 + a32·b22 = (4)·(-1) + (-1)·0 = -4 + 0 = -4
c33 = a31·b13 + a32·b23 = 4·6 + (-1)·7 = 24 – 7 = 17
