Загрузить PDF
Загрузить PDF
Существует множество причин, в связи с которыми вам, возможно, необходимо вычислить процентные выплаты. Из этой статьи вы узнаете, как рассчитать простые и сложные проценты.
-

1
Определите основной (начальный) капитал (P). Прежде всего, необходимо определить сумму денег, с которой вы начинаете. Это ваш основной капитал или переменная (Р).
- Например, если вы одалживаете $2000, то ваш основной капитал будет $2000.
-

2
Определите процентную ставку (r). Прежде чем подсчитать, насколько прирастет ваш основной капитал, вам нужно знать темп этого прироста. Это и есть процентная ставка или переменная (r).
- Например, если вы одолжили деньги под 1,5% на 6 месяцев, то через 6 месяцев вам вернут $2000 плюс 1,5%. Но, прежде чем перейти к вычислениям, необходимо преобразовать 1,5% в десятичное число. Для преобразования процентов в десятичное число разделите проценты на 100: 1,5% ÷ 100 = 0,015. Теперь переменная r = 0,015.
-

3
Вычислите простой процент. Для этого просто перемножьте основной капитал и процентную ставку: простой процент = Р х r.
-
4
Например, если вы подставите значения переменных, определенных выше (Р = 2000 и r = 0,015), то получите: 2000 х 0,015 = 30. Теперь вы знаете, что через полгода вам вернут $2000 (основной капитал) + $30 (процентные выплаты).
Реклама
-

1
Определите основной (начальный) капитал (P). Прежде всего, необходимо определить сумму денег, с которой вы начинаете. Это ваш основной капитал или переменная (Р). При расчете сложных процентов учитывается тот факт, что начальный капитал прирастает со временем и проценты вычисляются с такой растущей суммы.
- Например, вы кладете на сберегательный счет $2000 (это ваш основной капитал).
-

2
Определите процентную ставку (r). Прежде чем подсчитать, насколько прирастет ваш основной капитал, вам нужно знать темп этого прироста. Это и есть процентная ставка или переменная (r). Обратите внимание, что для расчетов (r) должна быть представлена в виде десятичного числа, а не в процентах.
- Например, вы кладете деньги на сберегательный счет под 1,5% годовых. Но, прежде чем перейти к вычислениям, необходимо преобразовать 1,5% в десятичное число. Для преобразования процентов в десятичное число разделите проценты на 100: 1,5% ÷ 100 = 0,015. Теперь переменная r = 0,015.
-

3
Определите график платежей (n). Вы должны знать, как часто будут начисляться и выплачиваться процентные выплаты, потому что они будут прибавляться к вашему основному капиталу и влиять на последующие процентные выплаты. График платежей будет переменной n.
- Например, если проценты по вашему сберегательному счету начисляются ежеквартально, то это означает, что четыре раза в год (каждые три месяца) проценты начисляются и добавляются к основному капиталу. Таким образом, если проценты начисляются ежеквартально, то n = 4.
- В качестве альтернативы проценты могут начисляться ежедневно и в этом случае n = 365; или ежемесячно и в этом случае n = 12.
-

4
Определите количество лет. Определите, за какое количество лет вы хотите вычислить процентные выплаты. Это будет переменная t.
- Например, если вы хотите узнать, какие процентные выплаты вы получите через 10 лет, то t = 10.
-

5
Подставьте значения переменных в формулу. Формула для расчета сложных процентов: P(1+r/n)nt[1]
. По этой формуле вы найдете общую сумму денег на вашем счету (то есть процентные выплаты плюс начальный капитал).- Например, подставим значения переменных, описанных выше (Р = 2000; r = 0,015; n = 4; t = 10), в формулу: 2000(1+0,015/4)4×10
-

6
Найдите общую сумму денег на вашем счету. При решении помните о порядке выполнения операций. Во-первых, решите выражение в скобках, потом возведите в степень, а потом умножайте.
- Например, 2000(1+0,015/4)4×10 = $2323,01. Теперь вы знаете, что если вы положите на счет $2000 под 1,5% годовых, начисляемых ежеквартально, то через 10 лет на вашем счету будет лежать сумма $2323,01.
-

7
Вычисление процентных выплат. Если вы хотите узнать, насколько приросла ваша начальная сумма, вычтете ее из общей суммы на счету (через 10 лет).
- Например, $2323,01 – $2000 = $323,01. Таким образом, положив на счет $2000, через 10 лет вы заработаете $323,01 в виде процентных выплат.
Реклама
Об этой статье
Эту страницу просматривали 10 018 раз.
Была ли эта статья полезной?
Формулы расчета процентов
Онлайн калькулятор
- Процент
- это одна сотая доля, обозначается знаком %. Само слово процент происходит от латинского pro centum, что означает сотая доля. Используется для обозначения части чего-либо по отношению к целому, выражается в сотых долях. Например, 5 процентов это пять сотых долей.
Проценты незаменимы в страховании, финансовой сфере, в экономических расчетах. В процентах выражаются ставки налогов, доходность капиталовложений, плата за заемные денежные средства (например, кредиты банка), темпы роста экономики и многое другое.
Содержание
Формула расчета доли в процентном отношении
Формула расчета процента от числа
Формула увеличения числа на заданный процент. Сумма с НДС
Формула уменьшения числа на заданный процент
Формула расчета исходной суммы. Сумма без НДС
Формула расчета простых процентов. Расчет процентов на банковский вклад
Формула расчета сложных процентов
Формула сложных процентов если процентная ставка дана не в годовом исчислении
1. Формула расчета доли в процентном отношении
Пусть задано два числа: A1 и A2. Надо рассчитать, какую долю в процентном отношении составляет число A1 от A2.
P = A1 / A2 * 100
В финансовых расчетах часто пишут
P = A1 / A2 * 100%
Пример 1.1 Рассчитаем какую долю в процентном отношении составляет 10 от 200
P = 10 / 200 * 100 = 5 (%).
Онлайн калькулятор
Доля в процентах
P =
2. Формула расчета процента от числа
Пусть задано число A2. Надо вычислить число A1, составляющее заданный процент P от A2.
A1= A2 * P / 100
Пример 2.1 Банковский кредит 10 000 рублей под 5% за весь срок кредита. Сумма процентов составит:
A1 = 10000 * 5 / 100 = 500
Онлайн калькулятор
Процент от числа
A1 =
3. Формула увеличения числа на заданный процент. Сумма с НДС
Пусть задано число A1. Надо вычислить число A2, которое больше A1 на заданный процент P. Используя формулу расчета процента от числа, получаем:
A2= A1 + A1 * P / 100
или
A2= A1 * (1 + P / 100)
Пример 3.1 Банковский кредит 10 000 рублей под 5% за весь срок кредита. Общая сумма долга составит:
A2= 10000 * (1 + 5 / 100) = 10000 * 1.05 = 10500
Пример 3.2 Сумма без НДС равна 1000 рублей, НДС 18%.
Рассчитаем сумму с НДС:
A2= 1000 * (1 + 18 / 100) = 1000 * 1.18 = 1180
Онлайн калькулятор
Увеличение числа на заданный процент
Сумма с НДС
A2 =
4. Формула уменьшения числа на заданный процент
Пусть задано число A1. Надо вычислить число A2, которое меньше A1 на заданный процент P. Используя формулу расчета процента от числа, получаем:
A2= A1 – A1 * P / 100
или
A2= A1 * (1 – P / 100)
Пример 4.1 Оклад за минусом подоходного налога (13%).
Пусть оклад составляет 10 000 рублей. Тогда сумма к выдаче составляет:
A2= 10000 * (1 – 13 / 100) = 10000 * 0.87 = 8700
Онлайн калькулятор
Уменьшение числа на заданный процент
A2 =
5. Формула расчета исходной суммы. Сумма без НДС
Пусть задано число A1, равное некоторому исходному числу A2 с прибавленным процентом P. Надо вычислить A2. Например, знаем денежную сумму с НДС, надо рассчитать сумму без НДС.
Обозначим p = P / 100, тогда:
A1= A2 + p * A2
или
A1= A2 * (1 + p)
тогда
A2= A1 / (1 + p)
окончательная формула расчета:
A2= A1 / (1 + P/100)
Пример 5.1 Сумма с НДС равна 1180 рублей, НДС 18%.
Стоимость без НДС составляет:
A2= 1180 / (1 + 0.18) = 1000
Онлайн калькулятор
Вычисление исходной суммы
Сумма без НДС
A2 =
6. Формула расчета простых процентов. Расчет процентов на банковский вклад
Если проценты на депозит начисляются один раз в конце срока вклада, то расчет процентов выполняется по формуле простых процентов:
Sp = K * P/100 * d/D
Формула расчета вклада с процентами:
S = K + K * P/100 * d/D
Иногда удобнее использовать формулу расчета в таком виде:
S = K * (1 + P/100 * d/D)
Где:
S — сумма банковского вклада с процентами,
Sp — сумма процентов (доход),
K — первоначальный вклад (капитал),
P — годовая процентная ставка,
d — количество дней начисления процентов по привлеченному вкладу,
D — количество дней в календарном году (365 или 366).
Пример 6.1 Банком принят вклад 100 тыс. рублей сроком на 1 год по ставке 20%.
S = 100000 + 100000 * 20/100 * 365/365 = 120000
Sp = 100000 * 20/100 * 365/365 = 20000
Пример 6.2 Банком принят вклад 100 тыс. рублей сроком на 30 дней по ставке 20% годовых.
S = 100000 + 100000 * 20/100 * 30/365 = 101643.84
Sp = 100000 * 20/100 * 30/365 = 1643.84
Онлайн калькулятор
Расчет вклада с процентами
S =
Расчет процентов
Sp =
7. Формула расчета сложных процентов. Расчет процентов на банковский вклад при начислении процента на процент
Если проценты на депозит начисляются несколько раз через равные промежутки времени и зачисляются во вклад, то расчет вклада с процентами выполняется по формуле сложных процентов.
S = K * ( 1 + P/100 * d/D )N
Где:
S — сумма вклада с процентами,
К — первоначальный вклад (капитал),
P — годовая процентная ставка,
d — продолжительность периода в конце которого начисляются проценты,
N — количество периодов начисления процентов.
При расчете сложных процентов проще вычислить общую сумму с процентами, а потом вычислить сумму процентов (доход), вычтя сумму начального вклада (капитал).
Формула расчета процентов:
Sp = S – K
или
Sp = K * ( 1 + P/100 * d/D )N – K
Иногда удобнее использовать формулу расчета в таком виде:
Sp = K * (( 1 + P/100 * d/D )N – 1)
Пример 7.1 Принят вклад 100 тыс. рублей сроком на 90 дней по ставке 20% годовых с начислением процентов каждые 30 дней.
S = 100000 * (1 + 20/100 * 30/365)3 = 105 013.02
Sp = 100000 * ((1 + 20/100 * 30/365)3 – 1) = 5 013.02
Онлайн калькулятор
Расчет вклада с процентами
S =
Расчет процентов
Sp =
Пример 7.2 Проверим формулу расчета сложных процентов для случая из предыдущего примера.
Разобьем срок вклада на 3 периода и сделаем расчет процентов для каждого периода, использую формулу простых процентов.
S1 = 100000 + 100000*20/100 * 30/365 = 101643.84
Sp1 = 100000 * 20/100 * 30/365 = 1643.84
S2 = 101643.84 + 101643.84*20/100 * 30/365 = 103314.70
Sp2 = 101643.84 * 20/100 * 30/365 = 1670.86
S3 = 103314.70 + 103314.70*20/100 * 30/365 = 105013.02
Sp3 = 103314.70 * 20/100 * 30/365 = 1698.32
Общая сумма процентов с учетом начисления процентов на проценты (сложные проценты)
Sp = Sp1 + Sp2 + Sp3 = 5013.02
Таким образом, формула расчета сложных процентов верна.
8. Формула сложных процентов если процентная ставка дана не в годовом исчислении
Если процентная ставка дана не в годовом исчислении, а непосредственно для периода начисления, то формула расчета сложных процентов выглядит так:
S = K * ( 1 + P/100 )N
Где:
S — сумма вклада с процентами,
К — первоначальный вклад (капитал),
P — процентная ставка,
N — количество периодов начисления процентов.
Формула расчета процентов на вклад:
Sp = S – K
или
Sp = K * ( 1 + P/100 )N – K
Иногда удобнее использовать формулу расчета в таком виде:
Sp = K * (( 1 + P/100 )N – 1)
Пример 8.1 Принят депозит 100 тыс. рублей сроком на 3 месяца с ежемесячным начислением процентов по ставке 1.5% в месяц.
S = 100000 * (1 + 1.5/100)3 = 104 567.84
Sp = 100000 * ((1 + 1.5/100)3 – 1) = 4 567.84
Онлайн калькулятор
Расчет вклада с процентами
S =
Расчет процентов
Sp =
Общие сведения о ПС
Процентная ставка, установленная банком, определяет, сколько процентов вы заплатите за пользование кредитными средствами, а значит, выгодно ли брать займ. Мы все знаем, насколько ПС важна для заимствования или экономии денег. Так что же на практике означает их изменение? Влияние увеличения или уменьшения ПС отражено в таблице 1 ниже.
Таблица 1. Свойства процентной ставки
| Высокие процентные ставки | Низкие процентные ставки |
| Местная валюта становится более устойчивой | Местная валюта теряет свою устойчивость |
| Меньшая доходность для покупателей валюты за рубежом | Для зарубежных покупателей местная валюта становится более доступной |
| Увеличивается экономия | Увеличиваются расходы |
| Меньше доходов | Больше доходов |
| Выплаты по кредитам увеличиваются | Выплаты по кредитам уменьшаются |
| Больше процентов по депозитам | Меньше процентов по депозитам |
Как рассчитывается процент – примеры формул
Проценты могут быть простыми и сложными. От этого зависит и метод их определения:
- Простые ПС рассчитываются только в процентах от вашей начальной суммы.
- Сложные проценты начисляются (обычно каждый месяц) на весь баланс ваших сбережений или займов, включая предыдущие выплаты и начисления процентов.
Формула для простой ПС:
Сумма переплаты по простой процентной ставке = сумма кредита х годовая ПС х количество лет
Важно! Если вы оформили срочный кредит или займ, скорее всего, получите простую ПС.
Формула для сложной процентной ставки:
Вся сумма = сумма кредита x (1 + процентная ставка / 100)лет
Важно! Сложные ПС используются для выплат по сберегательным и банковским вкладам, кредитным картам, автокредитам и ипотекам. Процент по кредитным картам может рассчитываться бесконечно долго, поэтому погашать задолженность по ним стоит как можно быстрее.
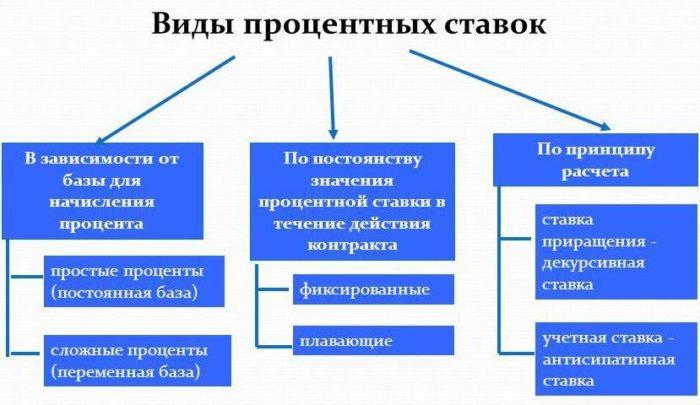
Виды процентных ставок
Различают фиксированные и переменные ПС.
Фиксированные проценты
Фиксированная ставка, как следует из названия, на какое-то время остается неизменной и не зависит от колебаний рынка. Обычно этот период составляет от 1 до 7 лет и служит отличным способом защитить себя от повышения рыночных процентных ставок. Наличие фиксированной ПС означает, что ваши выплаты будут оставаться неизменными. Это, в свою очередь, упрощает формирование бюджета.
Фиксированные ПС также могут быть огромным преимуществом, особенно когда вы можете “закрепить” за собой выплату невысоких процентов. Это будет означать, что ваши платежи по кредиту будут оставаться небольшими до полной выплаты. Однако здесь также есть подводные камни – досрочное погашение такого кредита обычно может стоить гораздо дороже. Поэтому при подписании кредитного договора с фиксированной ПС будьте особо внимательны.
Важно! Банк всеми способами будет стараться удерживать вас в качестве должника. В большинстве случаев фиксированные ставки обычно выше, чем переменные, поскольку банки должны защитить себя. Если рыночные ставки внезапно увеличатся, ваши выплаты останутся неизменными, что для банка является убытком.
Где можно встретить кредит с фиксированной процентной ставкой? Чаще всего они привязаны к обычным потребительским кредитным продуктам – личным кредитам и ипотекам. Учитывая, что для выплаты долга требуется от трех до семи лет, ставка на весь срок погашения обычно будет оставаться неизменной.
Переменные процентные ставки
Переменные ставки, в отличие от фиксированных, будут меняться со ставками на рынке. На них влияет текущий экономический климат, а также доступ банков к наличным средствам. В конце концов деньги, которые они предоставляют, могут быть чужими сбережениями. Если рыночные ставки увеличиваются, ваши выплаты будут расти, и наоборот. Как правило, кредиты с переменной ПС будут иметь больше возможностей, например, меньшие комиссионные. Но при этом сформировать бюджет, когда ваши выплаты постоянно меняются, будет гораздо сложнее. Кредиты с переменной ставкой для большинства часто считаются лучшим выбором, поскольку первоначальная ставка обычно ниже, чем аналогичный продукт с фиксированной ПС. Однако будьте осторожны, поскольку они, как известно, на протяжении всей жизни кредита могут расти.
Важно! Переменные ставки не всегда доступны для личных займов, но их использование с ипотекой является гораздо более распространенным явлением.
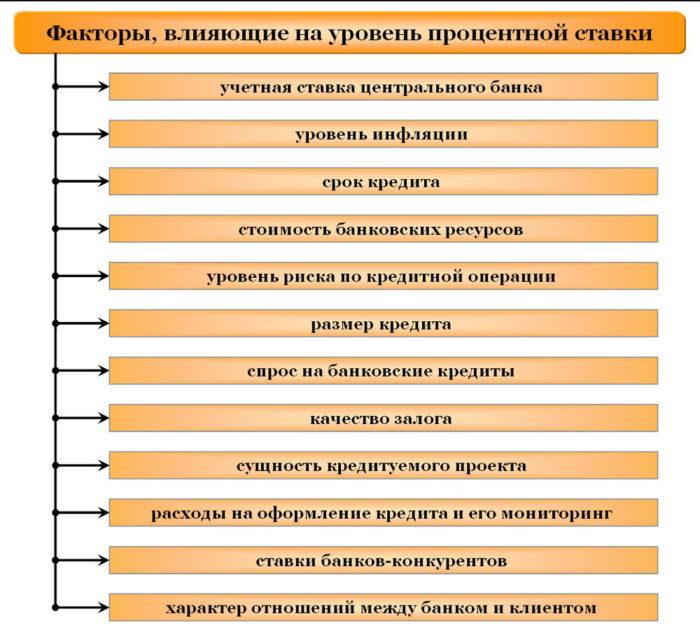
Факторы влияния
ПС изменяются в зависимости от:
- правительственных указов центральному банку для достижения своих целей;
- основной валюты кредита или депозита;
- срока до полного погашения;
- ожидаемой вероятности заемщика получить средства;
- спроса и предложения на рынке.
Существуют и другие причины. Рассмотрим их подробнее.
Политическая краткосрочная прибыль
Снижение ПС может дать экономике краткосрочный толчок. В нормальных условиях большинство экономистов считают, что снижение процентных ставок приведет лишь к краткосрочной выгоде, которая вскоре будет компенсирована инфляцией. Быстрый толчок может повлиять на выборы. Большинство экономистов выступают за независимые центральные банки, чтобы ограничить влияние политики на процентные ставки.
Отложенное потребление
В соответствии с теорией экономии времени, люди предпочитают “товары сейчас”, чем “товары позже”, на свободном рынке будет существовать положительная процентная ставка.
Прогнозы инфляции
Инфляция обычно наблюдается в большинстве стран, а это означает, что за данную сумму в будущем можно будет купить меньше товаров, чем сейчас. Заемщик должен это компенсировать кредитору.
Альтернативные инвестиции
Рынок потребительских и бизнес-кредитов довольно широк, поэтому каждый здесь сможет подобрать для себя подходящие условия.
Риски инвестиций
Всегда существует риск того, что заемщик может обанкротиться, скрыться, умереть или иным образом избежать выплат по кредиту. Именно поэтому кредитор обычно взимает аванс. Так он гарантирует, что при потере инвестиций получит компенсацию.
Подходящая форма сбережения средств
Люди предпочитают хранить свои сбережения в форме, которая удобна им и может быть обменена на настоящую валюту без особых усилий, а не в форме, требующей для обмена определенного, даже самого минимального, времени.
Налоги
Поскольку некоторые процентные ставки могут облагаться налогами, чтобы компенсировать эту потерю, кредитор может настаивать на более высокой ставке.
Банки
Банки могут менять процентную ставку, чтобы либо замедлить, либо ускорить рост экономики. Повышение процентных ставок приводит к замедлению роста экономики, а их снижение способствует экономическому росту.
Экономика
Процентные ставки могут колебаться в зависимости от состояния экономики. Как правило, при стабильной экономике процентные ставки будут высокими. И наоборот, если экономика будет слабой, процентные ставки будут низкими. Проценты – это стоимость использования денег. Вы платите за возможность использовать деньги, которые еще не накопили. Поэтому процентная ставка представляет собой стимул для банка одолжить вам деньги, и служат в то же время доходом за риск от кредитования. Процентная ставка – это один из основных способов получения прибыли кредиторами. Для лучшего понимания темы предлагаем вам для ознакомления также видео про процентные ставки.

Привет всем читателям Блога Вебинвестора! Думаю, каждый из вас сталкивался с начислением процентов на денежную сумму — по депозиту, по кредиту, расчётом доходности инвестиций и так далее. Так вот, если повторить эту процедуру много раз, вложения начинают расти всё быстрее и быстрее благодаря эффекту сложного процента! Воистину, это один из главных секретов, как с помощью инвестирования увеличить количество нулей в сумме на вашем банковском счёте.
Эта статья входит в бесплатное обучение инвестициям с нуля на Блоге Вебинвестора. В комментариях к статье вы можете оставлять любые вопросы по теме и я постараюсь подробно на них ответить.
Приглашаю подписываться на мой Telegram-канал Блог Вебинвестора! Там вы найдёте еженедельные отчёты по инвестициям, аналитические материалы, комментарии по важным новостям и многое другое. Также прошу делиться ссылкой на блог в социальных сетях и мессенджерах:
Что такое простой и сложный процент
и чем они отличаются
Понятие простых и сложных процентов — один из самых важных уроков по финансовой грамотности, которые вы должны знать. Они встречаются в нашей жизни повсюду: от ежедневных покупок (кэшбек, бонусы) до инвестирования (проценты на депозит, дивиденды, комиссии и т.д.) и оказывают незаметное, но существенное влияние на ваш кошелек на длинной дистанции. Чтобы наглядно увидеть различия между простыми и сложными процентами, давайте рассмотрим примеры.
Простой процент — прибыль в % начисляется только на первоначальную сумму вклада и сразу выводится.
Допустим, вы открыли депозит 10000$ под 10% годовых, проценты начисляются раз в год. По схеме простого процента каждые 12 месяцев вы будете получать 1000$ прибыли, но она не остаётся на депозите и сразу же выводится. В итоге прирост прибыли будет выглядеть так:

Всё «просто» — каждый год плюс тысяча в карман. Простой процент используется в случаях, когда база начисления процентов не изменяется. Это могут быть специальные банковские депозиты, проценты по кредиту. Также простой процент используется, когда инвестор регулярно выводит прибыль — в каждый период времени работает первоначальная сумма.
Сложный процент — проценты начисляются на первоначальную сумму вклада плюс всю полученную до этого прибыль. Понятия «реинвестирование» и «капитализация» по сути означают использование сложного процента.
Для сравнения пусть будет тот же депозит 10000$ под 10%, но банк в этот раз разрешает оставить прибыль на счёте. Вот что произойдёт с вкладом за 10 лет:

В первый год разницы нет — всё та же тысяча, но поскольку сумма на депозите теперь растёт, уже на втором году прибыль увеличивается: 2100$ вместо 2000$, за третий год 3310$ вместо 3000$ и так далее. За 10 лет доходность нашего депозита составила 159% вместо 100% когда мы выводили прибыль. Неплохая прибавка, не так ли? А вот что случится еще через несколько десятилетий:

Впечатляет! Чем дольше открыт депозит, тем сильнее работает эффект сложного процента — за 50 лет можно увеличить депозит не в 6, а более чем в 100 раз. Вот как это выглядит на графике:

без капитализации депозит растёт линейно,
а с капитализацией — по экспоненте
Теперь киношные истории про забытые банковские счета, на которых накопились миллионы долларов выглядят вполне реальными 🙂 Конечно, 50 лет это много, но правило сложного процента неплохо работает и на более коротких промежутках времени — всё зависит от доходности вклада. Если хочется заработать больше, стоит использовать более прибыльные способы инвестирования: акции, драгоценные металлы, криптовалюты, валютный рынок и так далее.
Думаю, суть понятна, теперь давайте пройдемся по математической стороне вопроса, а потом рассмотрим несколько типичных примеров задач.
⬆️ К СОДЕРЖАНИЮ ⬆️
Формулы простых и сложных процентов
Поскольку простые и сложные проценты чаще всего используются при расчете прибыли от банковских вкладов, продолжим на их примере. Для решения задач нам понадобится такая информация:
- К0 — начальная сумма вклада;
- К — конечная сумма вклада;
- R — ставка доходности, переводится из процентов в число (10% = 0.1);
- N — количество периодов (лет).
Формула простого процента

По этой формуле мы можем рассчитать конечную сумму вклада без капитализации полученной прибыли. Для этого нужно знать начальную сумму вклада, процентную ставку за 1 период инвестирования и временной интервал. Если конечная сумма задана сразу и нужно найти другую неизвестную переменную, используйте производные формулы простого процента:

Формула сложного процента

По этой формуле мы можем посчитать конечную сумму вклада с учётом капитализации полученной прибыли, зная начальный депозит, процентную ставку и нужный временной интервал. Для решения задач также можно использовать производные формулы сложного процента:

На практике часто дело не заканчивается первоначальным депозитом — многие пользуются регулярными пополнениями, например делают регулярные инвестиции из зарплаты. Для этих случаев формула сложного процента становится длиннее:

где D — сумма регулярных пополнений банковского депозита. Обратите внимание, степень N-1 означает, что доливки начинаются со второго инвестиционного периода (если сумма дополнительных инвестиций вносится сразу, то N-1 меняется на N).
Ну что, удачи на экзаменах всем читающим меня студентам 🙂 Для закрепления далее мы разберем несколько примеров задач на сложные проценты.
⬆️ К СОДЕРЖАНИЮ ⬆️
Примеры решения задач
по сложным процентам
В этом разделе мы пройдемся по некоторым типичным задачам на сложные проценты. Также вы найдете шаблоны расчётов в Excel, в которых можно поменять вводные данные и получить нужное вам решение.
Задача №1. Рассчитать прибыль по вкладу на 5 лет под 10% годовых, начальная сумма вложений 100000 рублей (с капитализацией).
Находим конечную сумму вклада по формуле сложных процентов:
Вычисляем прибыль:
Результат: инвестор через 5 лет получит 61051 рублей прибыли.
Задача №2. Рассчитать прибыль по вкладу на 10 лет под 10% годовых с капитализацией. Начальная сумма вложений 50000 рублей, дополнительно каждый год начиная с первого счёт пополняется на 10000 рублей.
Сначала находим конечную сумму по формуле сложного процента с регулярными пополнениями:

Учитывая, сколько инвестировано за 10 лет (50000 сразу и еще 9 раз по 10000), вычисляем прибыль:
Результат: инвестор через 10 лет получит 139061 рубль прибыли, инвестировав 140000 рублей.
Задача №3. Рассчитать, сколько времени понадобится инвестору, чтобы увеличить капитал с 500000 до 1000000 рублей. Средняя доходность портфеля — 12% годовых, прибыль реинвестируется.
У нас есть все необходимые данные, используем одну из производных формул сложных процентов:

Решение: инвестору понадобится чуть больше 6 лет.
Задача №4. Посчитать среднюю процентную ставку, которая позволит превратить 100000 рублей в 500000 рублей за 10 лет путём инвестирования. Прибыль реинвестируется.
Используем одну из производных формул сложных процентов:

Решение: инвестору нужно вложить деньги под 17.5% годовых (довольно сложно на практике, кстати).
Думаю, этого достаточно. Если ваша задача не похожа ни на одну из предыдущих, возможно вам поможет информация из следующего раздела статьи.
⬆️ К СОДЕРЖАНИЮ ⬆️
Калькулятор сложных процентов в Excel
Конечно же, задачи на сложные проценты целесообразнее решать в MS Excel по уже известным вам из предыдущих разделов формулам. По ходу статьи вы уже могли скачать некоторые примеры типичных задач, но если этого мало — предлагаю полную подборку калькуляторов по сложным процентам, реализованную в одном Excel-файле. Получить его можно бесплатно, просто заполните форму ниже:
Если письмо не пришло, проверяйте папку «Спам», иногда попадает туда. Если не видите форму подписки, оставьте комментарий к статье и я добавлю ваш электронный адрес вручную.
Вот какие задачи по простым и сложным процентам может решать «Коллекция калькуляторов для инвестора»:
- расчёт конечной суммы вклада;
- расчёт начальной суммы вклада;
- расчёт необходимой процентной ставки;
- расчёт срока инвестирования;
- расчёт конечной суммы вклада с учётом регулярных пополнений и капитализацией;
- ожидаемый пассивный доход в каждом из случаев.
В будущем я планирую добавить много калькуляторов по самым разным темам, оставляйте свои пожелания в комментариях!
Пример одного из калькуляторов для расчёта сложных процентов в Excel:

Дополнительно к каждому калькулятору автоматически строится график доходности вклада с капитализацией и без:

А также уже знакомые вам таблицы:

Думаю, файл будет полезен и для практического использования, и в обучающих целях — в готовом виде есть все формулы, по которым можно считать сложные проценты в Excel.
⬆️ К СОДЕРЖАНИЮ ⬆️
Как использовать сложные проценты
в инвестировании
Как вы уже знаете, получаемая от инвестиций прибыль — это важный инструмент, который на большой дистанции может во много раз увеличить доходность ваших вложений. Метод повторного вложения прибыли называется реинвестированием.
Статья в тему: Как деньги делают еще больше денег или Что такое реинвестирование
Безусловно, использовать эффект сложного процента должен каждый инвестор, однако на практике это не так просто как кажется. Существует несколько проблем, которые мешают теоретически супервыгодное реинвестирование реализовать в реальных условиях. Например, вряд ли вы слышали о людях, ставших миллиардерами через банковские депозиты. Дело в том, что деньги постоянно обесцениваются из-за инфляции — постоянного повышения цен на товары и услуги. На самом деле ставка банковских депозитов обычно примерно равна инфляции или даже ниже, поэтому реальная доходность вкладов не впечатляет:

Источники: statbureau.org
Даже если оставить удачный бескризисный отрезок 2010-2020 годов, доходность банковского вклада с учётом инфляции была в районе 1-2% годовых в рублях. Не говоря уже о доходности в долларах, которая после 2014 года, очевидно, находится в еще большем минусе.
Кроме инфляции сильно повлиять на итоговую доходность инвестиций могут разнообразные комиссии. Если их размер зависит от суммы инвестиций, убытки накапливаются по правилу сложных процентов, но уже с негативным эффектом. Это значит, что за несколько десятков лет инвестор может потерять сотни или даже тысячи процентов прибыли.
Такое часто встречается при инвестициях в ETF, где комиссия за управление достигает несколько процентов от депозита в год. Один из самых старых ETF под тикером SPY (инвестиционная стратегия — следование за индексом S&P 500) работает с 1993 года и берет с клиентов 0.09% в год — немного, по сравнению с другими биржевыми фондами. Эта ставка со временем может меняться, но давайте для эксперимента представим что она всегда была такой — и сравним, как будет отличаться доходность инвестиций при комиссиях от 0 до 2% в год:

Источник: ru.investing.com
Как видите, даже из-за несчастных 0.09% инвестор на дистанции 27 лет потерял 25% прибыли. А вроде бы небольшая комиссия в 2% годовых срезает доходность почти в 3 раза — с 723% до 270%, и это еще не учтена инфляция. По причине скрытых комиссий высокая доходность активов на самом деле может оказаться в разы ниже, поэтому перед принятием решения об инвестировании важно учитывать даже мизерные расходы.
Куда же стоит инвестировать, чтобы использовать эффект сложного процента на максимум и минимизировать влияние инфляции и комиссий? Я бы выделил такие инструменты:
- Акции, в особенности американские. Сейчас это один из немногих активов, которые растут большую часть времени. Кроме того, многие компании платят дивиденды, которые можно реинвестировать и еще сильнее разгонять сложный процент. Плюс, рост цен на сами акции способен перекрыть влияние инфляции, а комиссии зависят от объема торгов, а не от вашего вклада. Взгляните на самых богатых людей планеты — почти все сделали состояние, владея большим количеством акций в своих компаниях.
- Инвестиционные фонды (в т.ч. ETF). Чаще всего это тоже инвестиции в акции, но вам не нужно самостоятельно подбирать портфель — аналитики фонда все сделают за вас. Если в портфеле фонда есть дивидендные акции, вы опять же сможете реинвестировать выплаты. При комиссии за участие ниже 1% в год катастрофического влияния на доходность ваших инвестиций не будет.
- Облигации. Обычно они дают чуть большую доходность, чем банковский депозит и способны практически без рисков приносить небольшую прибыль с учётом инфляции. В любом случае в вашем инвестиционном портфеле должны быть надёжные долгосрочные вложения, и облигации для этих целей подходят неплохо. Расходы при вложении в облигации идут на услуги фондового брокера и не зависят от общей суммы инвестиций.
Оптимальный портфель инвестора предполагает использование всех этих инструментов, поскольку генерируемый ими денежный поток позволяет гибко управлять вложениями: делать ребалансировку, выводить прибыль или реинвестировать. Использовать правило сложных процентов можно в любых инвестициях, но не везде это рекомендуется делать. Чем выше риски вложений, тем выгоднее просто выводить прибыль, поскольку при неудачных раскладах депозит может быть потерян.
⬆️ К СОДЕРЖАНИЮ ⬆️
Использование сложных процентов — теоретически очень выгодное занятие, но как всегда дьявол кроется в деталях. Тем не менее, реинвестирование/капитализация остаётся одним из главных инструментов для накопления большого капитала, грех его игнорировать. И даже вне инвестирования начисление процентов по простому или сложному принципу встречается часто, поэтому полезно знать как это все работает. Надеюсь, подробный разбор формул и решения задач будут вам полезны.
Удачных инвестиций и не болейте!
Представим, что вы изучаете рынок финансовых инструментов и сравниваете их, чтобы выбрать оптимальный, берете кредит или открываете депозит, во всех этих случаях вы столкнетесь с понятием процентной ставки.
Эта основное свойство всех финансовых продуктов и финансовая концепция, которую можно назвать фундаментальной для всей финансовой индустрии.
Именно на значение в процентах вы будете обращать внимание, если хотите найти кредит на выгодных условиях или депозит. В первом случае – чем выше ставка, тем хуже условия, во втором – чем выше ставка, тем условия привлекательнее. Но это только для вас, а для банка все выглядит ровно наоборот.
Процентная ставка.
Давайте разберемся с определением чтобы не путаться в понятиях. Если вы будете читать описания инвестиционных продуктов на английском, то встретите слово “interest rate” – процентная ставка. Дословно в английском любую доходность называют “интерес”. То есть доходность – это “интерес” инвестора. Процентная ставка – “интерес” банка. Проценты в этом случае, это только форма выражения такого интереса. Процентная ставка в случае с кредитом – это тот процент, который вы заплатите банку за кредит. То есть, если максимально упростить – это стоимость денег, которые вам дает банк. Кредитор требует от заемщика заплатить за то, чтобы пользоваться капиталом. Оплата будет выражена в проценте от суммы долга.
Итак, суммируем.
Процентная ставка – это стоимость заимствования денег
Это сумма, которую кредитор взимает с заемщика за использование своих активов.
Какие виды активов готов предоставить вам банк? В большинстве случаев это будет некоторая сумма наличных, которые вы берете в заем на какие-то нужды – для того, например, чтобы улучшить жилищные условия или открыть бизнес, а возможно, чтобы сделать крупную покупку. Когда вы берете личный займ, ипотеку или автокредит, банк ссужает вам наличные для совершения покупки и назначает проценты с суммы, которую вы получили. Когда вы кладете наличные на сберегательный счет, ситуация меняется зеркально – теперь уже банк выплачивает вам проценты за то, что вы одалживаете ему свои деньги.
В некоторых случаях для кредита понадобится обеспечение – кредитор может предоставить какое-то материальное доказательство, что сможет расплатиться по кредиту. Например – товары и запасы на складе или крупные активы, ценное имущество, недвижимость, транспортные средства. Нередко на основе стоимости этих активов банк может принять решение об условиях кредитования.
Как работает процентная ставка
Когда вы занимаете деньги, вы платите проценты. Проценты компенсируют кредитору тот риск, который он несет, сотрудничая с вами, ведь он рискует своими деньгами, позволяя вам их использовать. Но вы, как потребитель финансовых услуг, тоже рискуете – заплатить по кредиту больше, чем могли бы по рынку, ведь если вы заняли деньги у одного банка, то, возможно, прошли мимо более выгодного предложения от кого-то другого, поэтому среди кредиторов тоже есть конкуренция и они конкурируют с помощью процентной ставки по кредиту, различных условий, предложений от партнеров и тд. Не думайте, что только вам нужны деньги банка, банку тоже нужны деньги, которые он заработает на вашей сделке. Так что и риски и интересы должны быть в равновесии.
О выплате процентов по кредиту можно думать, как об аренде.
Представим, что вы арендуете автомобиль, вы платите кому-то за привилегию им пользоваться. Ваш интерес в том, чтобы пользоваться автомобилем, а интерес владельца автомобиля в том, чтобы заработать на этом. По окончанию аренды вы возвращаете хозяину его имущество и платите за услугу. Та же история с процентной ставкой по кредиту. Вы делаете то же самое – берете у банка деньги, чтобы или пользоваться. После того, как использовали – должны вернуть и деньги и процент за их использование.
Допустим, вы занимаете 2000 долларов в банке. Банк ссужает вам деньги на один год и взимает 7% процентов. По истечении года вы заплатите банку 2140 долларов. Дополнительные 140 долларов – это компенсация банка за то, что он одолжил вам свои деньги. Про то, как рассчитывают процентную ставку, поговорим дальше.
Теперь представьте, что вы поменялись с банком местами. Когда вы даете деньги взаймы – вы зарабатываете проценты. Скорее всего, пополняя свой счет, вы не считаете себя кредитором, но на самом деле, именно так и есть. Когда вы вносите деньги на банковский счет, вы одалживаете эти деньги банку. И банк готов вознаградить вас за это. Банк ссужает эти деньги своим заемщикам и взимает с них проценты, отдает часть этих процентов вам, а разницу оставляет себе.
Когда вы зарабатываете проценты, это ваши деньги. Вы можете снять их и потратить, как вам заблагорассудится. Или вы можете не трогать деньги на счете, чтобы продолжать зарабатывать больше процентов. Или даже – процентов от процентов. Чем выше процентная ставка по депозиту и чем больше банк смог получить от вас чтобы кредитовать других своих клиентов, тем выгоднее и ему и им и вам.
Годовая Процентная ставка (APR)
Если вы когда-либо изучали финансовые продукты в зарубежных банк, то, вероятно, слышали термин APR (annual percentage rate). APR это – годовая процентная ставка банка по продукту. Есть еще одна величина, о которой нужно знать, APY (annual percentage yield). В переводе на русский “годовая процентная доходность”. Эта цифра показывает какую прибыль в процентах вы получите за год, вложившись в тот или иной финансовый продукт.
Зачем вам знать разницу? Отличать понятия “процентная ставка” и “доходность” важно потому, что они могут не совпадать. Если у вас возникнут дополнительные расходы при использовании продукта, например, какие-то комиссии, то ваша доходность по продукту будет ниже, чем ставка по нему.
Это важно и в случае с кредитом. Поскольку кредиторы часто взимают различные виды сборов сверх процентов, трудно сравнивать кредиты друг с другом. Но важно понимать, что APR создает эталон, на который можно ориентироваться, выбирая продукт, но APY (ваша годовая процентная доходность или банковская годовая процентная доходность) может с ним не совпадать. Этот вопрос стоит задать консультанту в банке или вашему брокеру, особенно, если речь идет о работе с иностранными банками.
История вопроса
Люди одалживали друг другу деньги и брали друг с друга проценты еще за 3000 лет до нашей эры. Уже тогда кредиторы требовали компенсацию за то, что берут на себя риск (в конце концов, заемщик может не заплатить), а также за то, что теряли возможность инвестировать эти деньги другим способом.
В неблагополучные для экономики времена и в те времена, когда экономика не была развитой индустрией, не было ничего необычного в том, что процентные ставки достигали 20% или 25%. Еще не так давно для всего мира такие проценты по кредитам были фантастикой. Но в свете последних событий в мире, похоже, мы не далеки от кого, чтобы снова увидеть такие цифры по кредитам.
Что делает процентные ставки высокими? Неблагоприятная экономическая ситуация. Почему процентные ставки падают? За это, в основном, можно благодарить конкуренцию в банковской индустрии. Сегодня инвестиционный сектор бизнеса стал разнообразнее, чем когда-либо. У любого инвестора в любой стране мира, даже в ситуации кризиса есть возможность приумножить свои деньги. Это означает, что кредиторы должны поднимать процентные ставки, чтобы привлекать вкладчиков. Это также означает, что они должны снизить свои ставки по кредитам, чтобы привлекать заемщиков.
Причины высоких и низких процентных ставок
Рынок финансовых продуктов – это конкурентный рынок. Как и на любом рынке, величина процентных ставок растет и падает вслед за спросом и предложением. Если у кредиторов много наличных денег для кредитования (высокое предложение), процентные ставки падают, поскольку они конкурируют друг с другом. Если предложение кредитов падает, процентные ставки растут. Аналогичным образом, ставки растут, когда все больше людей хотят брать кредиты (высокий спрос), и падают, когда никто не хочет брать кредиты (низкий спрос).
Инфляция – это способ повышения процентных ставок
Когда на рынке появляется большой объем денег, они теряют покупательную способность. Это означает, что деньги в вашем кармане прямо сейчас стоят меньше, чем вчера и могут купить все меньше с течением времени.
Кредиторы требуют более высоких процентных ставок, чтобы компенсировать снижение покупательной способности денег. Представьте логику банка, который дал вам 1000 рублей: завтра вы вернете ему ту же 1000, но в реальности она уже подешевеет до 500 рублей, теперь, чтобы восстановить покупательную способность капитала, нужно повысить ставку в два раза.
Правительство может влиять на процентные ставки с помощью денежно-кредитной политики. Центральные банки (такие как Федеральная резервная система США, Банк Канады, Банк Англии, Центробанк РФ) предоставляют деньги кредитоспособным клиентам, чаще всего это другие банки. Это создает волновой эффект в экономике.
Банки-заемщики используют процентную ставку центрального банка чтобы установить процентные ставки по своим продуктам – по кредитным картам, ипотечным кредитам и автокредитам. Низкие процентные ставки означают, что занимать деньги дешево, поэтому у бизнеса есть стимул инвестировать в экономический рост. Более высокие процентные ставки ослабляют этот эффект и снижают вероятность того, что предприятия будут брать кредиты.
Не означает ли это, что центральные банки всегда должны поддерживать свои процентные ставки на низком уровне, чтобы экономический рост был постоянным? Не совсем так. Если процентные ставки останутся низкими, центральные банки не смогут снизить их во время экономического спада, чтобы стимулировать экономику.
