Как найти сферические координаты точки

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 25 декабря 2020 года; проверки требуют 4 правки.

Сферическая система координат — трёхмерная система координат, в которой каждая точка пространства определяется тремя числами $(r,;theta ,;varphi )$ , где $r$ — расстояние до начала координат (радиальное расстояние), а $theta$ и $varphi$ — зенитный и азимутальный углы соответственно.

Понятия зенит и азимут широко используются в астрономии. Зенит — направление вертикального подъёма над произвольно выбранной точкой (точкой наблюдения), принадлежащей фундаментальной плоскости. В качестве фундаментальной плоскости в астрономии может быть выбрана плоскость, в которой лежит экватор, или плоскость, в которой лежит горизонт, или плоскость эклиптики и т. д., что порождает разные системы небесных координат. Азимут — угол между произвольно выбранным лучом фундаментальной плоскости с началом в точке наблюдения и другим лучом этой плоскости, имеющим общее начало с первым.

Рис. 1.Точка имеет три декартовых и три сферических координаты

Если рассматривать сферическую систему координат относительно декартовой системы $Oxyz$ , фундаментальной плоскостью будет плоскость $xy$ , зенитным углом точки, заданной радиус-вектором $P$ , будет угол между $P$ и осью $z$ , а азимутом — угол между проекцией $P$ на плоскость $xy$ и осью $x$ . Это объясняет названия углов и то, что сферическая система координат может служить обобщением множества видов систем небесных координат.

Определения[править | править код]

Положение точки $P$ в сферической системе координат определяется тройкой $(r,;theta ,;varphi )$ , где

Угол $theta$ называется зенитным, или полярным, также он может называться наклонением, или коширотой, а угол $varphi$ — азимутальным. Углы $theta$ и $varphi$ не определены при $r=0$ , также не определён угол $varphi$ при $sin(theta )=0$ (то есть при $theta =0$ или $theta =180^{circ }$ ).

Такое соглашение установлено в стандарте (ISO 31-11). Кроме того может использоваться соглашение, когда вместо зенитного угла $theta$ , используется угол между радиус-вектором точки $P$ и плоскостью $xy$ , равный ${displaystyle 90^{circ }-theta }$ . Он называется широтой и может быть обозначен той же буквой $theta$ . Широта может изменяться в пределах $-90^{circ }leqslant theta leqslant 90^{circ }$ . При этом соглашении углы $theta$ и $varphi$ не имеют значения при $r=0$ , так же как и в первом случае, а $varphi$ не имеет значения при $cos(theta )=0$ (то есть при $theta =-90^{circ }$ или $theta =90^{circ }$ ).

Переход к другим системам координат[править | править код]

Декартова система координат[править | править код]

Если заданы сферические координаты точки $(r,;theta ,;varphi )$ , то переход к декартовым осуществляется по формулам:

${begin{cases}x=rsin theta cos varphi ,\y=rsin theta sin varphi ,\z=rcos theta .end{cases}}$

Обратно, от декартовых к сферическим:

${displaystyle {begin{cases}r={sqrt {x^{2}+y^{2}+z^{2}}},\theta =arccos {dfrac {z}{sqrt {x^{2}+y^{2}+z^{2}}}}=mathrm {arctg} {dfrac {sqrt {x^{2}+y^{2}}}{z}},\varphi =mathrm {arctg} {dfrac {y}{x}}.end{cases}}}$

Якобиан преобразования к сферическим координатам равен

${displaystyle {begin{alignedat}{2}J&={frac {partial (x,y,z)}{partial (r,theta ,varphi )}}={begin{vmatrix}sin theta cos varphi &rcos theta cos varphi &-rsin theta sin varphi \sin theta sin varphi &rcos theta sin varphi &rsin theta cos varphi \cos theta &-rsin theta &0end{vmatrix}}=\&=cos theta (r^{2}cos varphi ^{2}cos theta sin theta +r^{2}sin ^{2}varphi cos theta sin theta )+rsin theta (rsin ^{2}theta cos ^{2}varphi +rsin ^{2}theta sin ^{2}varphi )=\&=r^{2}cos ^{2}theta sin theta +r^{2}sin ^{2}theta sin theta =\&=r^{2}sin theta .end{alignedat}}}$

Таким образом, элемент объёма при переходе от декартовых к сферическим координатам будет выглядеть следующим образом:

${displaystyle mathrm {d} V=mathrm {d} x,mathrm {d} y,mathrm {d} z=J(r,theta ,varphi ),mathrm {d} r,mathrm {d} theta ,mathrm {d} varphi =r^{2}sin theta ,,mathrm {d} r,mathrm {d} theta ,mathrm {d} varphi }$

Цилиндрическая система координат[править | править код]

Если заданы сферические координаты точки, то переход к цилиндрическим осуществляется по формулам:

${begin{cases}rho =rsin theta ,\varphi =varphi ,\z=rcos theta .end{cases}}$

Обратно от цилиндрических к сферическим:

${displaystyle {begin{cases}r={sqrt {rho ^{2}+z^{2}}},\theta =mathrm {arctg} {dfrac {rho }{z}},\varphi =varphi .end{cases}}}$

Якобиан преобразования от сферических к цилиндрическим ${displaystyle J=r}$ .

Дифференциальные характеристики[править | править код]

Вектор $mathrm {d} mathbf {r}$ , проведённый из точки $(r,theta ,varphi )$ в точку $(r+mathrm {d} r,,theta +mathrm {d} theta ,,varphi +mathrm {d} varphi )$ , равен

$mathrm {d} mathbf {r} =mathrm {d} r,{boldsymbol {hat {r}}}+r,mathrm {d} theta ,{boldsymbol {hat {theta }}}+rsin {theta },mathrm {d} varphi ,mathbf {boldsymbol {hat {varphi }}} ,$

где

${displaystyle {boldsymbol {hat {r}}}=sin theta cos varphi {boldsymbol {hat {imath }}}+sin theta sin varphi {boldsymbol {hat {jmath }}}+cos theta {boldsymbol {hat {k}}}}$

${displaystyle {boldsymbol {hat {theta }}}=cos theta cos varphi {boldsymbol {hat {imath }}}+cos theta sin varphi {boldsymbol {hat {jmath }}}-sin theta {boldsymbol {hat {k}}}}$

${displaystyle {boldsymbol {hat {varphi }}}=-sin varphi {boldsymbol {hat {imath }}}+cos varphi {boldsymbol {hat {jmath }}}}$

ортогональные единичные векторы сферических координат в направлении увеличения $r,theta ,varphi$ , соответственно, а ${boldsymbol {hat {imath }}},{boldsymbol {hat {jmath }}},{boldsymbol {hat {k}}}$ — единичные векторы декартовых координат. Сферические координаты являются ортогональными, поэтому метрический тензор имеет в них диагональный вид:

$g_{ij}={begin{pmatrix}1&0&0\0&r^{2}&0\0&0&r^{2}sin ^{2}theta end{pmatrix}},quad g^{ij}={begin{pmatrix}1&0&0\0&{dfrac {1}{r^{2}}}&0\0&0&{dfrac {1}{r^{2}sin ^{2}theta }}end{pmatrix}}$

$det(g_{ij})=r^{4}sin ^{2}theta .$
Квадрат дифференциала длины дуги:

$ds^{2}=dr^{2}+r^{2},dtheta ^{2}+r^{2}sin ^{2}theta ,dvarphi ^{2}.$

Коэффициенты Ламе:

$H_{r}=1,quad H_{theta }=r,quad H_{varphi }=rsin theta .$

Символы Кристоффеля ${r,;theta ,;varphi }$ :

$Gamma _{22}^{1}=-r,quad Gamma _{33}^{1}=-rsin ^{2}theta ,$

$Gamma _{21}^{2}=Gamma _{12}^{2}=Gamma _{13}^{3}=Gamma _{31}^{3}={frac {1}{r}},$

$Gamma _{33}^{2}=-cos theta sin theta ,quad Gamma _{23}^{3}=Gamma _{32}^{3}=mathrm {ctg} ,theta .$

Остальные равны нулю.

Математическое моделирование Земли[править | править код]

Сферическая географическая система координат[править | править код]

Сферическая географическая система координат строится следующим образом^[1]:

Вектор магнитной индукции магнитного поля Земли $mathbf {B}$ имеет компоненты

${displaystyle B_{r}=-Bsin I,;B_{theta }=-Bcos Icos D,;B_{varphi }=Bcos Isin D,}$

где $I$ — магнитное наклонение; $D$ — магнитное склонение.

Компоненты вектора ускорения свободного падения ${mathbf {g}}$ равны

${displaystyle g_{r}=-g,;g_{theta }=g_{varphi }=0.}$

Наконец, компоненты вектора угловой скорости вращения Земли ${displaystyle mathbf {Omega } }$ такие:

${displaystyle Omega _{r}=Omega cos theta ,;Omega _{theta }=-Omega sin theta ,;Omega _{varphi }=0.}$

В сферических географических координатах оптимально решать уравнения, описывающие поведение нейтральных частиц околоземного пространства^[1].

Сферическая геомагнитная система координат[править | править код]

Сферическая геомагнитная система координат строится следующим образом^[1]:

Географические координаты северного магнитного полюса равны

${displaystyle theta _{0}=4,6^{circ },;varphi _{0}=43,0^{circ };(2012).}$

В сферической геомагнитной системе координат склонение $D=0$ и

${displaystyle B_{r}=-Bsin I,;B_{Theta }=-Bcos I,;B_{Lambda }=0,}$

${displaystyle g_{r}=-g,;g_{Theta }=g_{Lambda }=0.}$

${displaystyle Omega _{r}=Omega (cos theta _{0}cos Theta -sin theta _{0}sin Theta cos Lambda ),}$

${displaystyle Omega _{Theta }=-Omega (cos theta _{0}sin Theta +sin theta _{0}cos Theta cos Lambda ),}$

${displaystyle Omega _{Lambda }=Omega sin theta _{0}sin Lambda .}$

Формулы, связывающие географические и геомагнитные сферические координаты^[1]:

${displaystyle cos Theta =cos theta _{0}cos theta +sin theta _{0}sin theta cos(varphi -varphi _{0}),}$

${displaystyle cos Lambda ={frac {-sin theta _{0}cos theta +cos theta _{0}sin theta cos(varphi -varphi _{0})}{sin Theta }},}$

${displaystyle cos theta =cos theta _{0}cos Theta -sin theta _{0}sin Theta cos Lambda ,}$

${displaystyle cos(varphi -varphi _{0})={frac {sin theta _{0}cos Theta +cos theta _{0}sin Theta cos Lambda }{sin theta }}.}$

В сферических геомагнитных координатах проще, чем в сферических географических координатах, описывать влияние геомагнитного поля на заряженные частицы околоземного пространства^[1].

См. также[править | править код]

Углы Эйлера
Гиперсферические координаты

Примечания[править | править код]

↑ ¹ ² ³ ⁴ ⁵ Брюнелли Б. Е., Намгаладзе А. А. Физика ионосферы. М.: Наука, 1988. § 3.5, С. 172—173. ISBN 5-02-000716-1

Ссылки[править | править код]

Weisstein, Eric W. Сферические координаты (англ.) на сайте Wolfram MathWorld.

Источник

Конев В.В. Скалярные и векторные поля

Сферическая система координат

Положение точки М в сферической системе координат задается тройкой чисел r, φ и θ, где r – расстояние от начала координат до точки M (

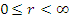); φ – угол, образованный проекцией радиус-вектора точки M на плоскость 0ху с положительным направлением оси 0х (

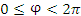); θ – угол между положительным направлением оси Oz и радиус-вектором точки М (

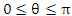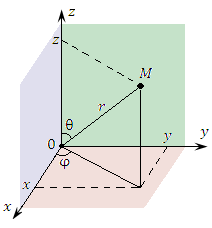
Рис. 1. Сферические координаты точки M.

Связь между декартовыми и сферическими координатами описывается формулами

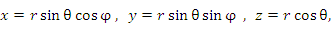
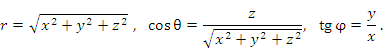
Связь между сферическими и цилиндрическими координатами описывается формулами

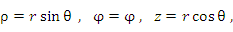
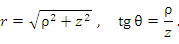
Поверхность, на которой одна из координат сохраняет постоянное значение, называется координатной поверхностью.

Линия, вдоль которой изменяется только одна координата, а остальные координаты остаются неизменными, называется координатной линией.

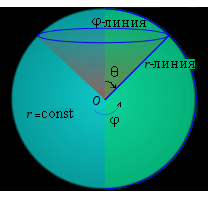
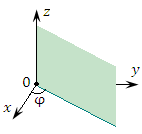
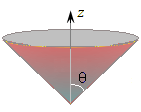
Рис. 2. Координатные поверхности сферической системы координат:

сфера (r = const);

полуплоскость (φ = const);

конус (θ = const).

В сферической системе координатные линии, проходящие через любую точку M пространства, пересекаются под прямым углом. Такие системы координат называются ортогональными.


Единичный касательный вектор к координатной линии в точке М, направленный в сторону возрастания координаты, называется ортом в точке М. Поскольку сферическая система координат является ортогональной, то в любой точке пространства векторы 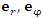и 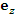попарно ортогональны.


Отметим, что каждая координатная линия перпендикулярна соответствующей координатной поверхности.

Некоторые полезные формулы:

Элемент длины дуги:
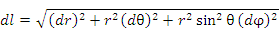
Якобиан перехода от декартовой системы координат к сферической:
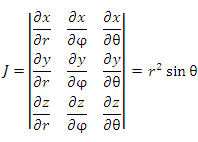
Элемент объема:

Источник

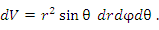
Сферические координаты (сферическая система координат)

Для введения сферической системы координат в пространстве выбирается плоскость (основная плоскость) и на ней задается полярная система координат с полюсом (начало сферической системы координат) и полярной осью . Через точку перпендикулярно основной плоскости проведем ось (ось аппликат) и выберем ее направление так, чтобы возрастание полярного угла со стороны положительного направления оси происходило против часовой стрелки (рис.2.36,а).

В сферической системе координат положение точки , не лежащей на оси аппликат, характеризуется расстоянием rho=|overrightarrow{OM}| до начала координат, полярным углом varphi точки M_0 – ортогональной проекции точки на основную плоскость, и углом theta между вектором и положительным направлением оси аппликат. Таким образом, сферические координаты точки – это упорядоченная тройка чисел rho,varphi,theta – радиус (rhogeqslant0) , долгота (-pi<varphileqslantpi) и широта (0leqslantthetaleqslantpi) . У точек, принадлежащих оси аппликат, не определена долгота, их положение задается радиусом rho и широтой theta=0 для положительной части оси и theta=pi для отрицательной ее части. Начало координат задается нулевым значением радиуса rho . Иногда вместо угла theta широтой называют угол $psi=frac{pi}{2}-theta$ , принимающий значения $-frac{pi}{2}leqslantpsileqslantfrac{pi}{2}$ .

Сферическая система координат и её связь с прямоугольными координатами

Со сферической системой координат Orhovarphitheta можно связать прямоугольную систему координат Ovec{i}vec{j}vec{k} (рис.2.36,б), у которой начало и базисные векторы vec{i},vec{k} совпадают с началом сферической системы координат и единичными векторами на полярной оси и оси аппликат соответственно, а базисный вектор vec{j} выбирается так, чтобы тройка vec{i},vec{j},vec{k} была правой (при этом базис оказывается стандартным).

Наоборот, если в пространстве задана правая прямоугольная система координат, то, приняв положительную полуось абсцисс за полярную ось, получим сферическую систему координат (связанную с данной прямоугольной).

Переход от сферических координат к декартовым (прямоугольным)

Получим формулы, связывающие между собой прямоугольные координаты x,y,z точки и её сферические координаты rho,varphi,theta . По рис.2.36,б получаем

$begin{cases}x=rhocdotcosvarphicdotsintheta,\y=rhocdotsinvarphicdotsintheta,\z=rhocdotcostheta.end{cases}$

(2.21)

Эти формулы перехода позволяют найти прямоугольные координаты по известным сферическим координатам. Обратный переход выполняется по формулам

$left{!begin{aligned} rho&=sqrt{x^2+y^2+z^2},\ cosvarphi&=frac{x}{sqrt{x^2+y^2}},\ sinvarphi&=frac{y}{sqrt{x^2+y^2}},\ theta&=arccosfrac{z}{rho}=arccosfrac{z}{sqrt{x^2+y^2+z^2}}. end{aligned}right.$

(2.22)

Формулы (2.22) определяют долготу varphi с точностью до слагаемых 2pi n , где ninmathbb{Z} . При xne0 из них следует, что $operatorname{tg}varphi=frac{y}{x}$ . Главное значение долготы varphi~(-pi<varphileqslantpi) находится по формулам (см. рис.2.29).

Пример 2.13. В сферической системе координат Orhovarphitheta :

а) построить координатные поверхности rho=R,~varphi=varphi_0,~z=z_0 ;

б) найти сферические координаты rho,varphi,theta точки , если известны её прямоугольные координаты A(4,-3,12) ;

в) найти прямоугольные координаты x,y,z точки , если известны её сферические координаты: $rho=4,~varphi=frac{2pi}{3},~theta=frac{3pi}{4}$ .

Построение поверхностей в сферической системе координат

Решение. а) Координатной поверхностью rho=R , т.е. геометрическим местом точек M(R,varphi,theta) при фиксированном значении радиуса rho=R , является сфера с центром в начале координат (рис.2.37). Этим объясняется название сферической системы координат. Координатной поверхностью varphi=varphi_0 , т.е. геометрическим местом точек M(rho,varphi_0,theta) при фиксированном значении долготы , является полуплоскость, ограниченная осью аппликат (на рис.2.37 изображена полуплоскость varphi=0 ). Координатной поверхностью theta=theta_0 , т.е. геометрическим местом точек M(rho,varphi,theta_0) при фиксированном значении широты $theta=thetanefrac{pi}{2}$ , является конус, ось которого совпадает с осью аппликат, а вершина – с началом координат. При $theta=frac{pi}{2}$ получаем основную плоскость. На рис.2.37 изображены конус $theta=thetanefrac{pi}{2}$ и основная плоскость $theta=frac{pi}{2}$ .

б) Найдем сферические координаты точки A(4,-3,12) . По формулам (2.22), учитывая рис.2.29 (см. пример 2.12), получаем

$rho=sqrt{4^2+(-3)^2+12^2}=13;quad varphi=-operatorname{arctg}frac{3}{4};quad theta=arccosfrac{12}{13}.$

в) По формулам (2.21) получаем

$begin{gathered} x=rhocdotcosvarphicdotsintheta=4cdot!left(-frac{1}{2}right)!cdot!left(frac{sqrt{2}}{2}right)=-sqrt{2};\[2pt] y=rhocdotsinvarphicdotsintheta=4cdot!left(frac{sqrt{3}}{2}right)!cdot!left(frac{sqrt{2}}{2}right)=sqrt{6};\[2pt] z=rhocdotcostheta=4cdot!left(-frac{sqrt{2}}{2}right)=-2sqrt{2}. end{gathered}$

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Рассмотрим
в пространстве координатную плоскость
Р, на которой задана полярная система
координат. ПустьOz –координатная
ось, перпендикулярная плоскостиРи пересекающая ее в полюсеО.
Координатная осьOz направлена так,
чтобы из конца положительного направления
осиOz направление отсчета положительных
значений полярного углаφот полярной
осиОхбыло видно против часовой
стрелки. Совокупность этих элементов
называетсяполярной системой
координат в пространстве(рис.3.2).

Координатная
плоскость Рназываетсяэкваториальной,
а координатная осьOz–зенитной.
Для удобства будем полагать, что
масштабные отрезки одинаковы (ОЕ₁=ОЕ₂) и точка отсчетаОкоординатной осиOzсовпадает с
полюсомО.

Цилиндрическими
координатами точкиМ, не лежащими
на зенитной оси, называется упорядоченная
тройка чиселρ, φ, z, гдеρиφ– полярные координаты ортогональной
проекцииМ_р точкиМна экваториальную плоскость, аz–
координата на зенитной осиOzпроекцииМ_zточкиМна зенитную
ось (рис. 3.3). Для точек зенитной оси
считаютρ = 0,φ– любое число, аzопределяется так, как указано выше.
Тот факт, чтоρ, φ иzесть
цилиндрические координаты точкиМ в
пространстве, записывают так:М(ρ,φ,z).

Заметим,
что при помощи цилиндрических координат
не устанавливается взаимно однозначного
соответствия между множеством всех
точек геометрического пространства и
множеством упорядоченных троек
действительных чисел.

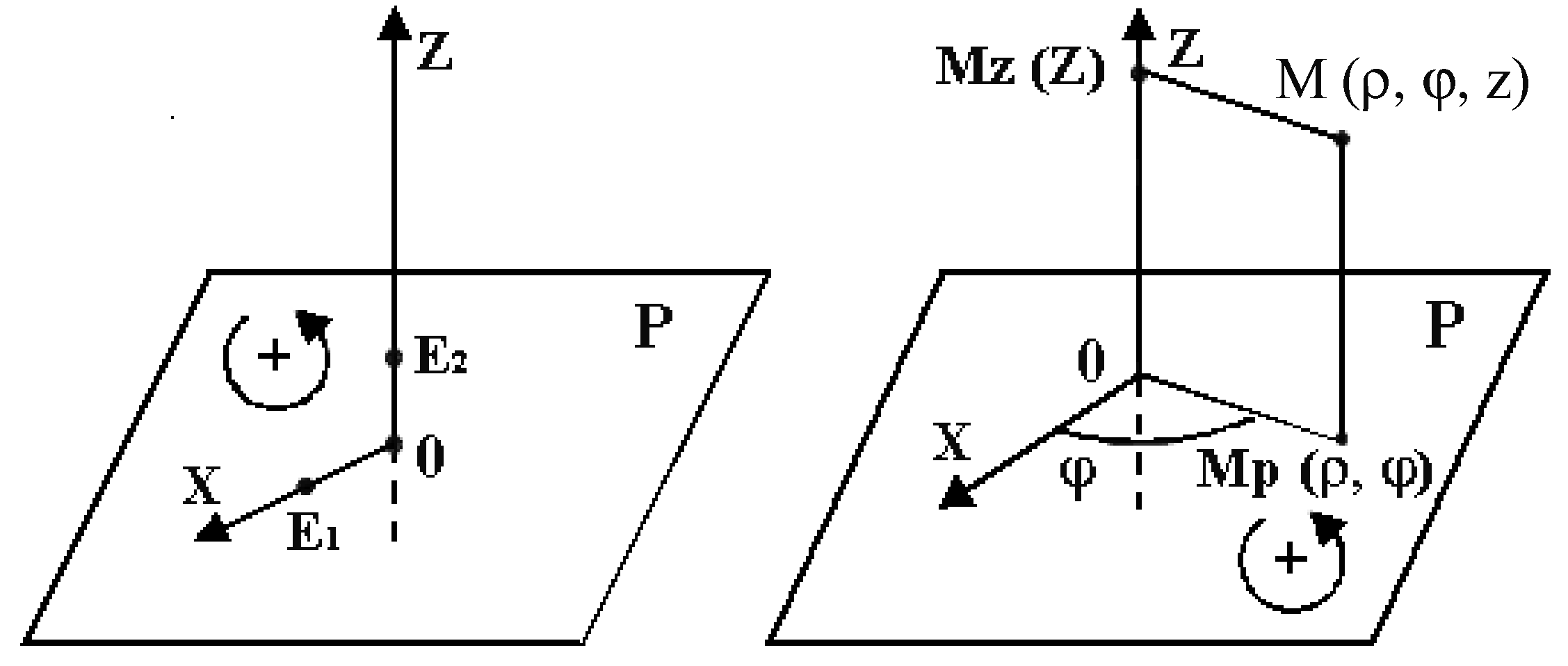
Рис. 3.2
Рис. 3.3

Сферическими
координатами точкиМ, не лежащей
на зенитной оси, называется упорядоченная
тройка чиселr, φ, Θ, гдеr– длина отрезкаОМ,φ– угол от
полярной осиОхдо лучаОМ_р(М_р– проекция точкиМна экваториальную плоскость), аΘ–
угол между лучамиОМ_риОМ, который принимает значения в
интервале,
причем считается, чтоΘ= 0, если точкаМлежит в экваториальной плоскости,Θ> 0, если лучОМобразует острый
угол с зенитной осью, иΘ< 0, если
лучОМобразует тупой угол с зенитной
осью (рис.3.4).

Рис. 3.4

Если
точка М лежит на зенитной оси и не
совпадает с полюсомО, то считают,
чтоφ– любое число, аилив зависимости от того, совпадает ли
направление лучаОМ с направлением
зенитной оси или противоположно ему.
Для полюса считаютr= 0,φиΘ– любые числа. При помощи сферических
координат не устанавливается взаимно
однозначного соответствия между
множеством всех точек пространства и
множеством упорядоченных троек
действительных чисел.

Найдем
зависимости между прямоугольными
декартовыми координатами точки М(х,
у, z) и ее цилиндрическими координатамиМ(ρ, φ, z) и сферическими
координатамиМ(r, φ, θ).
Введем декартову прямоугольную систему
координат, принимая за положительную
полуосьОхполярную ось, за осьОу– ось, полученную из осиОхповоротом
ее вокруг полюса в экваториальной
плоскости на уголи зенитную ось за осьОz
(рис.3.4.).

Из
рис.3.4, учитывая формулы (1.7) и рис.3.3.
находим

,,z= z(1.12)

Cдругой стороны,,
а,
значит,

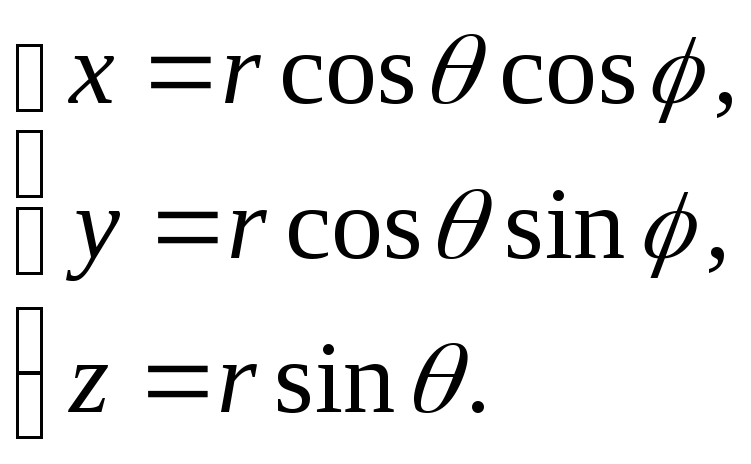(1.13)

Формулы
(1.12) и (1.13) верны и для того случая, когда
точка Млежит на зенитной оси и когда
она совпадает с полюсом (при дополнительных
соглашениях о величинахρ иφв
этом случае).

По
формулам (1.12) вычисляются декартовы
прямоугольные координаты точки Мв случае, если известны ее цилиндрические
координаты, а по формулам (1.13) – если
известны ее сферические координаты.

Из
формул (1.13) следует, что

откуда

значит,

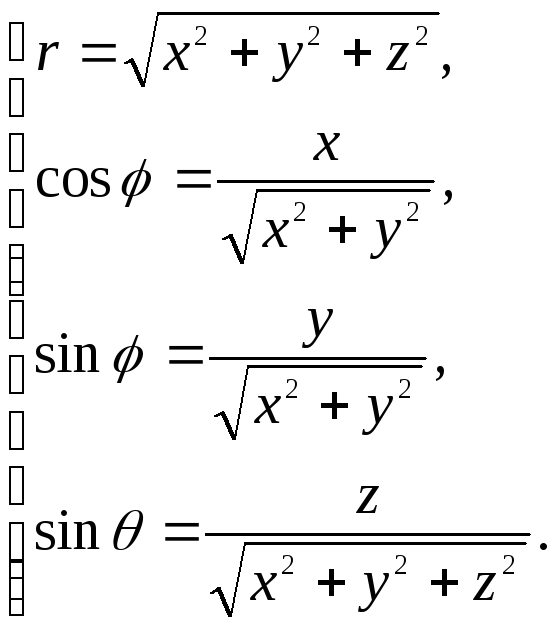(1.14)

По этим
формулам вычисляются сферические
координаты r,φ, ΘточкиМ,
не лежащей на зенитной оси по ее декартовым
прямоугольным координатамx,y,z
(при указанном взаимном расположении
этих двух систем координат).

Цилиндрические
координаты ρ, φ, zточкиМ
вычисляются по ее декартовым
прямоугольным координатамx, y,
zиз формул (1.12) с учетом формул (1.8) и
(1.9) или (1.10).

Аналогично
декартовым координатам определяется
уравнение поверхности в сферических
координатах:

и в цилиндрических
координатах
.

Замечание.Вторую сферическую координатуφчасто называютдолготой, третьюΘ – широтой. Иногда вместо
широтыΘрассматривают уголψ
между положительным направлением
зенитной оси и лучомОМ, идущим из
полюсаО в данную точкуМ; величинаψизменяется в пределах от 0 доπ.
Величинаψназываетсязенитным
расстоянием.

Так
как
,
то в формулах (1.13) и (1.14) (в случае, если
за третью сферическую координату
принимается зенитное расстояние)иследует заменить соответственно наи
.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Spherical coordinates (r, θ, φ) as commonly used in physics (ISO 80000-2:2019 convention): radial distance r (distance to origin), polar angle θ (theta) (angle with respect to polar axis), and azimuthal angle φ (phi) (angle of rotation from the initial meridian plane). This is the convention followed in this article.

Spherical coordinates (r, θ, φ) as often used in mathematics: radial distance r, azimuthal angle θ, and polar angle φ. The meanings of θ and φ have been swapped compared to the physics convention. As in physics, ρ (rho) is often used instead of r, to avoid confusion with the value r in cylindrical and 2D polar coordinates.

A globe showing the radial distance, polar angle and azimuthal angle of a point P with respect to a unit sphere, in the mathematics convention. In this image, r equals 4/6, θ equals 90°, and φ equals 30°.

In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the radial distance of that point from a fixed origin, its polar angle measured from a fixed zenith direction, and the azimuthal angle of its orthogonal projection on a reference plane that passes through the origin and is orthogonal to the zenith, measured from a fixed reference direction on that plane. It can be seen as the three-dimensional version of the polar coordinate system.

The radial distance is also called the radius or radial coordinate. The polar angle may be called colatitude, zenith angle, normal angle, or inclination angle.

When radius is fixed, the two angular coordinates make a coordinate system on the sphere sometimes called spherical polar coordinates.

The use of symbols and the order of the coordinates differs among sources and disciplines. This article will use the ISO convention^[1] frequently encountered in physics: $(r,theta ,varphi )$ gives the radial distance, polar angle, and azimuthal angle. By contrast, in many mathematics books, ${displaystyle (rho ,theta ,varphi )}$ or $(r,theta ,varphi )$ gives the radial distance, azimuthal angle, and polar angle, switching the meanings of θ and φ. Other conventions are also used, such as r for radius from the z-axis, so great care needs to be taken to check the meaning of the symbols.

According to the conventions of geographical coordinate systems, positions are measured by latitude, longitude, and height (altitude). There are a number of celestial coordinate systems based on different fundamental planes and with different terms for the various coordinates. The spherical coordinate systems used in mathematics normally use radians rather than degrees and measure the azimuthal angle counterclockwise from the x-axis to the y-axis rather than clockwise from north (0°) to east (+90°) like the horizontal coordinate system.^[2] The polar angle is often replaced by the elevation angle measured from the reference plane towards the positive Z axis, so that the elevation angle of zero is at the horizon; the depression angle is the negative of the elevation angle.

The spherical coordinate system generalizes the two-dimensional polar coordinate system. It can also be extended to higher-dimensional spaces and is then referred to as a hyperspherical coordinate system.

Definition[edit]

To define a spherical coordinate system, one must choose two orthogonal directions, the zenith and the azimuth reference, and an origin point in space. These choices determine a reference plane that contains the origin and is perpendicular to the zenith. The spherical coordinates of a point P are then defined as follows:

The radius or radial distance is the Euclidean distance from the origin O to P.
The azimuth (or azimuthal angle) is the signed angle measured from the azimuth reference direction to the orthogonal projection of the line segment OP on the reference plane.
The inclination (or polar angle) is the angle between the zenith direction and the line segment OP.

The sign of the azimuth is determined by choosing what is a positive sense of turning about the zenith. This choice is arbitrary, and is part of the coordinate system’s definition.

The elevation angle is the signed angle between the reference plane and the line segment OP, where positive angles are oriented towards the zenith. Equivalently, it is 90 degrees (π/2 radians) minus the inclination angle.

If the inclination is zero or 180 degrees (π radians), the azimuth is arbitrary. If the radius is zero, both azimuth and inclination are arbitrary.

In linear algebra, the vector from the origin O to the point P is often called the position vector of P.

Conventions[edit]

Several different conventions exist for representing the three coordinates, and for the order in which they should be written. The use of $(r,theta ,varphi )$ to denote radial distance, inclination (or elevation), and azimuth, respectively, is common practice in physics, and is specified by ISO standard 80000-2:2019, and earlier in ISO 31-11 (1992).

This article, as stated above, will use the ISO convention: ${displaystyle (r,theta ,varphi )}$ gives the radial distance, polar angle, and azimuthal angle.

However, some authors (including mathematicians) use ρ for radial distance, φ for inclination (or elevation) and θ for azimuth, and r for radius from the z-axis, which “provides a logical extension of the usual polar coordinates notation”.^[3] Some authors may also list the azimuth before the inclination (or elevation). Some combinations of these choices result in a left-handed coordinate system. The standard convention $(r,theta ,varphi )$ conflicts with the usual notation for two-dimensional polar coordinates and three-dimensional cylindrical coordinates, where θ is often used for the azimuth.^[3]

The angles are typically measured in degrees (°) or radians (rad), where 360° = 2π rad. Degrees are most common in geography, astronomy, and engineering, whereas radians are commonly used in mathematics and theoretical physics. The unit for radial distance is usually determined by the context.

When the system is used for physical three-space, it is customary to use positive sign for azimuth angles that are measured in the counter-clockwise sense from the reference direction on the reference plane, as seen from the zenith side of the plane. This convention is used, in particular, for geographical coordinates, where the “zenith” direction is north and positive azimuth (longitude) angles are measured eastwards from some prime meridian.

Major conventions

coordinates	corresponding local geographical directions (Z, X, Y)	right/left-handed
(r, θ_inc, φ_az,right)	(U, S, E)	right
(r, φ_az,right, θ_el)	(U, E, N)	right
(r, θ_el, φ_az,right)	(U, N, E)	left

Note: easting (E), northing (N), upwardness (U). Local azimuth angle would be measured, e.g., counterclockwise from S to E in the case of (U, S, E).

Unique coordinates[edit]

Any spherical coordinate triplet $(r,theta ,varphi )$ specifies a single point of three-dimensional space. On the other hand, every point has infinitely many equivalent spherical coordinates. One can add or subtract any number of full turns to either angular measure without changing the angles themselves, and therefore without changing the point. It is also convenient, in many contexts, to allow negative radial distances, with the convention that ${displaystyle (-r,-theta ,varphi )}$ is equivalent to $(r,theta ,varphi )$ for any r, θ, and φ. Moreover, ${displaystyle (r,-theta ,varphi )}$ is equivalent to ${displaystyle (r,theta ,varphi {+}180^{circ })}$ .

If it is necessary to define a unique set of spherical coordinates for each point, one must restrict their ranges. A common choice is

radial distance: r ≥ 0,

polar angle: 0° ≤ θ ≤ 180° (π rad),

azimuth : 0° ≤ φ < 360° (2π rad).

However, the azimuth φ is often restricted to the interval (−180°, +180°], or (−π, +π] in radians, instead of [0, 360°). This is the standard convention for geographic longitude.

For the polar angle θ, the range [0°, 180°] for inclination is equivalent to [−90°, +90°] for elevation. In geography, the latitude is the elevation.

Even with these restrictions, if polar angle is 0° or 180° (elevation is 90° or −90°) then the azimuth angle is arbitrary; and if r is zero, both azimuth and polar angle are arbitrary. To make the coordinates unique, one can use the convention that in these cases the arbitrary coordinates are set to zero.

Plotting[edit]

To plot a dot from its spherical coordinates (r, θ, φ), where θ is inclination, move r units from the origin in the zenith direction, rotate by θ about the origin towards the azimuth reference direction, and rotate by φ about the zenith in the proper direction.

Applications[edit]

Just as the two-dimensional Cartesian coordinate system is useful on the plane, a two-dimensional spherical coordinate system is useful on the surface of a sphere. In this system, the sphere is taken as a unit sphere, so the radius is unity and can generally be ignored. This simplification can also be very useful when dealing with objects such as rotational matrices.

Spherical coordinates are useful in analyzing systems that have some degree of symmetry about a point, such as volume integrals inside a sphere, the potential energy field surrounding a concentrated mass or charge, or global weather simulation in a planet’s atmosphere. A sphere that has the Cartesian equation x² + y² + z² = c² has the simple equation r = c in spherical coordinates.

Two important partial differential equations that arise in many physical problems, Laplace’s equation and the Helmholtz equation, allow a separation of variables in spherical coordinates. The angular portions of the solutions to such equations take the form of spherical harmonics.

Another application is ergonomic design, where r is the arm length of a stationary person and the angles describe the direction of the arm as it reaches out.

The output pattern of an industrial loudspeaker shown using spherical polar plots taken at six frequencies

Three dimensional modeling of loudspeaker output patterns can be used to predict their performance. A number of polar plots are required, taken at a wide selection of frequencies, as the pattern changes greatly with frequency. Polar plots help to show that many loudspeakers tend toward omnidirectionality at lower frequencies.

The spherical coordinate system is also commonly used in 3D game development to rotate the camera around the player’s position^[4]

In geography[edit]

To a first approximation, the geographic coordinate system uses elevation angle (latitude) in degrees north of the equator plane, in the range −90° ≤ φ ≤ 90°, instead of inclination. Latitude is either geocentric latitude, measured at the Earth’s center and designated variously by ψ, q, φ′, φ_c, φ_g or geodetic latitude, measured by the observer’s local vertical, and commonly designated φ.
The polar angle, which is 90° minus the latitude and ranges from 0 to 180°, is called colatitude in geography.

The azimuth angle (longitude), commonly denoted by λ, is measured in degrees east or west from some conventional reference meridian (most commonly the IERS Reference Meridian), so its domain is −180° ≤ λ ≤ 180°. For positions on the Earth or other solid celestial body, the reference plane is usually taken to be the plane perpendicular to the axis of rotation.

Instead of the radial distance, geographers commonly use altitude above or below some reference surface (vertical datum), which may be the mean sea level. The radial distance r can be computed from the altitude by adding the radius of Earth, which is approximately 6,360 ± 11 km (3,952 ± 7 miles).

However, modern geographical coordinate systems are quite complex, and the positions implied by these simple formulae may be wrong by several kilometers. The precise standard meanings of latitude, longitude and altitude are currently defined by the World Geodetic System (WGS), and take into account the flattening of the Earth at the poles (about 21 km or 13 miles) and many other details.

Planetary coordinate systems use formulations analogous to the geographic coordinate system.

In astronomy[edit]

A series of astronomical coordinate systems are used to measure the elevation angle from different fundamental planes. These reference planes are the observer’s horizon, the celestial equator (defined by Earth’s rotation), the plane of the ecliptic (defined by Earth’s orbit around the Sun), the plane of the earth terminator (normal to the instantaneous direction to the Sun), and the galactic equator (defined by the rotation of the Milky Way).

Coordinate system conversions[edit]

As the spherical coordinate system is only one of many three-dimensional coordinate systems, there exist equations for converting coordinates between the spherical coordinate system and others.

Cartesian coordinates[edit]

The spherical coordinates of a point in the ISO convention (i.e. for physics: radius r, inclination θ, azimuth φ) can be obtained from its Cartesian coordinates (x, y, z) by the formulae

${displaystyle {begin{aligned}r&={sqrt {x^{2}+y^{2}+z^{2}}}\theta &=arccos {frac {z}{sqrt {x^{2}+y^{2}+z^{2}}}}=arccos {frac {z}{r}}={begin{cases}arctan {frac {sqrt {x^{2}+y^{2}}}{z}}&{text{if }}z>0\pi +arctan {frac {sqrt {x^{2}+y^{2}}}{z}}&{text{if }}z<0\+{frac {pi }{2}}&{text{if }}z=0{text{ and }}xyneq 0\{text{undefined}}&{text{if }}x=y=z=0\end{cases}}\varphi &=operatorname {sgn}(y)arccos {frac {x}{sqrt {x^{2}+y^{2}}}}={begin{cases}arctan({frac {y}{x}})&{text{if }}x>0,\arctan({frac {y}{x}})+pi &{text{if }}x<0{text{ and }}ygeq 0,\arctan({frac {y}{x}})-pi &{text{if }}x<0{text{ and }}y<0,\+{frac {pi }{2}}&{text{if }}x=0{text{ and }}y>0,\-{frac {pi }{2}}&{text{if }}x=0{text{ and }}y<0,\{text{undefined}}&{text{if }}x=0{text{ and }}y=0.end{cases}}end{aligned}}}$

The inverse tangent denoted in φ = arctan y/x must be suitably defined, taking into account the correct quadrant of (x, y). See the article on atan2.

Alternatively, the conversion can be considered as two sequential rectangular to polar conversions: the first in the Cartesian xy plane from (x, y) to (R, φ), where R is the projection of r onto the xy-plane, and the second in the Cartesian zR-plane from (z, R) to (r, θ). The correct quadrants for φ and θ are implied by the correctness of the planar rectangular to polar conversions.

These formulae assume that the two systems have the same origin, that the spherical reference plane is the Cartesian xy plane, that θ is inclination from the z direction, and that the azimuth angles are measured from the Cartesian x axis (so that the y axis has φ = +90°). If θ measures elevation from the reference plane instead of inclination from the zenith the arccos above becomes an arcsin, and the cos θ and sin θ below become switched.

Conversely, the Cartesian coordinates may be retrieved from the spherical coordinates (radius r, inclination θ, azimuth φ), where r ∈ [0, ∞), θ ∈ [0, π], φ ∈ [0, 2π), by

${displaystyle {begin{aligned}x&=rsin theta ,cos varphi ,\y&=rsin theta ,sin varphi ,\z&=rcos theta .end{aligned}}}$

Cylindrical coordinates[edit]

Cylindrical coordinates (axial radius ρ, azimuth φ, elevation z) may be converted into spherical coordinates (central radius r, inclination θ, azimuth φ), by the formulas

${displaystyle {begin{aligned}r&={sqrt {rho ^{2}+z^{2}}},\theta &=arctan {frac {rho }{z}}=arccos {frac {z}{sqrt {rho ^{2}+z^{2}}}},\varphi &=varphi .end{aligned}}}$

Conversely, the spherical coordinates may be converted into cylindrical coordinates by the formulae

${displaystyle {begin{aligned}rho &=rsin theta ,\varphi &=varphi ,\z&=rcos theta .end{aligned}}}$

These formulae assume that the two systems have the same origin and same reference plane, measure the azimuth angle φ in the same senses from the same axis, and that the spherical angle θ is inclination from the cylindrical z axis.

Generalization[edit]

It is also possible to deal with ellipsoids in Cartesian coordinates by using a modified version of the spherical coordinates.

Let P be an ellipsoid specified by the level set

${displaystyle ax^{2}+by^{2}+cz^{2}=d.}$

The modified spherical coordinates of a point in P in the ISO convention (i.e. for physics: radius r, inclination θ, azimuth φ) can be obtained from its Cartesian coordinates (x, y, z) by the formulae

${displaystyle {begin{aligned}x&={frac {1}{sqrt {a}}}rsin theta ,cos varphi ,\y&={frac {1}{sqrt {b}}}rsin theta ,sin varphi ,\z&={frac {1}{sqrt {c}}}rcos theta ,\r^{2}&=ax^{2}+by^{2}+cz^{2}.end{aligned}}}$

An infinitesimal volume element is given by

${displaystyle mathrm {d} V=left|{frac {partial (x,y,z)}{partial (r,theta ,varphi )}}right|,dr,dtheta ,dvarphi ={frac {1}{sqrt {abc}}}r^{2}sin theta ,mathrm {d} r,mathrm {d} theta ,mathrm {d} varphi ={frac {1}{sqrt {abc}}}r^{2},mathrm {d} r,mathrm {d} Omega .}$

The square-root factor comes from the property of the determinant that allows a constant to be pulled out from a column:

${displaystyle {begin{vmatrix}ka&b&c\kd&e&f\kg&h&iend{vmatrix}}=k{begin{vmatrix}a&b&c\d&e&f\g&h&iend{vmatrix}}.}$

Integration and differentiation in spherical coordinates[edit]

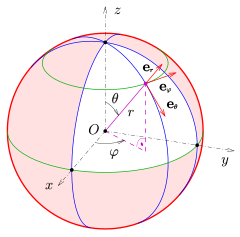
Unit vectors in spherical coordinates

The following equations (Iyanaga 1977) assume that the colatitude θ is the inclination from the z (polar) axis (ambiguous since x, y, and z are mutually normal), as in the physics convention discussed.

The line element for an infinitesimal displacement from (r, θ, φ) to (r + dr, θ + dθ, φ + dφ) is

${displaystyle mathrm {d} mathbf {r} =mathrm {d} r,{hat {mathbf {r} }}+r,mathrm {d} theta ,{hat {boldsymbol {theta }}}+rsin {theta },mathrm {d} varphi ,mathbf {hat {boldsymbol {varphi }}} ,}$

where

${displaystyle {begin{aligned}{hat {mathbf {r} }}&=sin theta cos varphi ,{hat {mathbf {x} }}+sin theta sin varphi ,{hat {mathbf {y} }}+cos theta ,{hat {mathbf {z} }},\{hat {boldsymbol {theta }}}&=cos theta cos varphi ,{hat {mathbf {x} }}+cos theta sin varphi ,{hat {mathbf {y} }}-sin theta ,{hat {mathbf {z} }},\{hat {boldsymbol {varphi }}}&=-sin varphi ,{hat {mathbf {x} }}+cos varphi ,{hat {mathbf {y} }}end{aligned}}}$

are the local orthogonal unit vectors in the directions of increasing r, θ, and φ, respectively,
and x̂, ŷ, and ẑ are the unit vectors in Cartesian coordinates. The linear transformation to this right-handed coordinate triplet is a rotation matrix,

${displaystyle R={begin{pmatrix}sin theta cos varphi &sin theta sin varphi &cos theta \cos theta cos varphi &cos theta sin varphi &-sin theta \-sin varphi &cos varphi &0end{pmatrix}}.}$

This gives the transformation from the spherical to the cartesian, the other way around is given by its inverse.
Note: the matrix is an orthogonal matrix, that is, its inverse is simply its transpose.

The Cartesian unit vectors are thus related to the spherical unit vectors by:

${displaystyle {begin{bmatrix}mathbf {hat {x}} \mathbf {hat {y}} \mathbf {hat {z}} end{bmatrix}}={begin{bmatrix}sin theta cos varphi &cos theta cos varphi &-sin varphi \sin theta sin varphi &cos theta sin varphi &cos varphi \cos theta &-sin theta &0end{bmatrix}}{begin{bmatrix}{boldsymbol {hat {r}}}\{boldsymbol {hat {theta }}}\{boldsymbol {hat {varphi }}}end{bmatrix}}}$

The general form of the formula to prove the differential line element, is^[5]

${displaystyle mathrm {d} mathbf {r} =sum _{i}{frac {partial mathbf {r} }{partial x_{i}}},mathrm {d} x_{i}=sum _{i}left|{frac {partial mathbf {r} }{partial x_{i}}}right|{frac {frac {partial mathbf {r} }{partial x_{i}}}{left|{frac {partial mathbf {r} }{partial x_{i}}}right|}},mathrm {d} x_{i}=sum _{i}left|{frac {partial mathbf {r} }{partial x_{i}}}right|,mathrm {d} x_{i},{hat {boldsymbol {x}}}_{i},}$

that is, the change in $mathbf {r}$ is decomposed into individual changes corresponding to changes in the individual coordinates.

To apply this to the present case, one needs to calculate how $mathbf {r}$ changes with each of the coordinates. In the conventions used,

${displaystyle mathbf {r} ={begin{bmatrix}rsin theta ,cos varphi \rsin theta ,sin varphi \rcos theta end{bmatrix}}.}$

Thus,

${displaystyle {frac {partial mathbf {r} }{partial r}}={begin{bmatrix}sin theta ,cos varphi \sin theta ,sin varphi \cos theta end{bmatrix}}=mathbf {hat {r}} ,quad {frac {partial mathbf {r} }{partial theta }}={begin{bmatrix}rcos theta ,cos varphi \rcos theta ,sin varphi \-rsin theta end{bmatrix}}=r,{hat {boldsymbol {theta }}},quad {frac {partial mathbf {r} }{partial varphi }}={begin{bmatrix}-rsin theta ,sin varphi \rsin theta ,cos varphi \0end{bmatrix}}=rsin theta ,mathbf {hat {boldsymbol {varphi }}} .}$

The desired coefficients are the magnitudes of these vectors:^[5]

${displaystyle left|{frac {partial mathbf {r} }{partial r}}right|=1,quad left|{frac {partial mathbf {r} }{partial theta }}right|=r,quad left|{frac {partial mathbf {r} }{partial varphi }}right|=rsin theta .}$

The surface element spanning from θ to θ + dθ and φ to φ + dφ on a spherical surface at (constant) radius r is then

${displaystyle mathrm {d} S_{r}=left|{frac {partial {mathbf {r} }}{partial theta }}times {frac {partial {mathbf {r} }}{partial varphi }}right|mathrm {d} theta ,mathrm {d} varphi =left|r{hat {boldsymbol {theta }}}times rsin theta {boldsymbol {hat {varphi }}}right|=r^{2}sin theta ,mathrm {d} theta ,mathrm {d} varphi ~.}$

Thus the differential solid angle is

${displaystyle mathrm {d} Omega ={frac {mathrm {d} S_{r}}{r^{2}}}=sin theta ,mathrm {d} theta ,mathrm {d} varphi .}$

The surface element in a surface of polar angle θ constant (a cone with vertex the origin) is

${displaystyle mathrm {d} S_{theta }=rsin theta ,mathrm {d} varphi ,mathrm {d} r.}$

The surface element in a surface of azimuth φ constant (a vertical half-plane) is

${displaystyle mathrm {d} S_{varphi }=r,mathrm {d} r,mathrm {d} theta .}$

The volume element spanning from r to r + dr, θ to θ + dθ, and φ to φ + dφ is specified by the determinant of the Jacobian matrix of partial derivatives,

${displaystyle J={frac {partial (x,y,z)}{partial (r,theta ,varphi )}}={begin{pmatrix}sin theta cos varphi &rcos theta cos varphi &-rsin theta sin varphi \sin theta sin varphi &rcos theta sin varphi &rsin theta cos varphi \cos theta &-rsin theta &0end{pmatrix}},}$

namely

${displaystyle mathrm {d} V=left|{frac {partial (x,y,z)}{partial (r,theta ,varphi )}}right|,mathrm {d} r,mathrm {d} theta ,mathrm {d} varphi =r^{2}sin theta ,mathrm {d} r,mathrm {d} theta ,mathrm {d} varphi =r^{2},mathrm {d} r,mathrm {d} Omega ~.}$

Thus, for example, a function f(r, θ, φ) can be integrated over every point in R³ by the triple integral

${displaystyle int limits _{0}^{2pi }int limits _{0}^{pi }int limits _{0}^{infty }f(r,theta ,varphi )r^{2}sin theta ,mathrm {d} r,mathrm {d} theta ,mathrm {d} varphi ~.}$

The del operator in this system leads to the following expressions for the gradient, divergence, curl and (scalar) Laplacian,

${displaystyle {begin{aligned}nabla f={}&{partial f over partial r}{hat {mathbf {r} }}+{1 over r}{partial f over partial theta }{hat {boldsymbol {theta }}}+{1 over rsin theta }{partial f over partial varphi }{hat {boldsymbol {varphi }}},\[8pt]nabla cdot mathbf {A} ={}&{frac {1}{r^{2}}}{partial over partial r}left(r^{2}A_{r}right)+{frac {1}{rsin theta }}{partial over partial theta }left(sin theta A_{theta }right)+{frac {1}{rsin theta }}{partial A_{varphi } over partial varphi },\[8pt]nabla times mathbf {A} ={}&{frac {1}{rsin theta }}left({partial over partial theta }left(A_{varphi }sin theta right)-{partial A_{theta } over partial varphi }right){hat {mathbf {r} }}\[8pt]&{}+{frac {1}{r}}left({1 over sin theta }{partial A_{r} over partial varphi }-{partial over partial r}left(rA_{varphi }right)right){hat {boldsymbol {theta }}}\[8pt]&{}+{frac {1}{r}}left({partial over partial r}left(rA_{theta }right)-{partial A_{r} over partial theta }right){hat {boldsymbol {varphi }}},\[8pt]nabla ^{2}f={}&{1 over r^{2}}{partial over partial r}left(r^{2}{partial f over partial r}right)+{1 over r^{2}sin theta }{partial over partial theta }left(sin theta {partial f over partial theta }right)+{1 over r^{2}sin ^{2}theta }{partial ^{2}f over partial varphi ^{2}}\[8pt]={}&left({frac {partial ^{2}}{partial r^{2}}}+{frac {2}{r}}{frac {partial }{partial r}}right)f+{1 over r^{2}sin theta }{partial over partial theta }left(sin theta {frac {partial }{partial theta }}right)f+{frac {1}{r^{2}sin ^{2}theta }}{frac {partial ^{2}}{partial varphi ^{2}}}f~.end{aligned}}}$

Further, the inverse Jacobian in Cartesian coordinates is

${displaystyle J^{-1}={begin{pmatrix}{dfrac {x}{r}}&{dfrac {y}{r}}&{dfrac {z}{r}}\\{dfrac {xz}{r^{2}{sqrt {x^{2}+y^{2}}}}}&{dfrac {yz}{r^{2}{sqrt {x^{2}+y^{2}}}}}&{dfrac {-(x^{2}+y^{2})}{r^{2}{sqrt {x^{2}+y^{2}}}}}\\{dfrac {-y}{x^{2}+y^{2}}}&{dfrac {x}{x^{2}+y^{2}}}&0end{pmatrix}}.}$

The metric tensor in the spherical coordinate system is ${displaystyle g=J^{T}J}$ .

Distance in spherical coordinates[edit]

In spherical coordinates, given two points with φ being the azimuthal coordinate

${displaystyle {begin{aligned}{mathbf {r} }&=(r,theta ,varphi ),\{mathbf {r} '}&=(r',theta ',varphi ')end{aligned}}}$

The distance between the two points can be expressed as

${displaystyle {begin{aligned}{mathbf {D} }&={sqrt {r^{2}+r'^{2}-2rr'(sin {theta }sin {theta '}cos {(varphi -varphi ')}+cos {theta }cos {theta '})}}end{aligned}}}$

Kinematics[edit]

In spherical coordinates, the position of a point or particle (although better written as a triple ${displaystyle (r,theta ,varphi )}$ ) can be written as^[6]

${mathbf {r}}=r{mathbf {{hat r}}}.$

Its velocity is then^[6]

${displaystyle mathbf {v} ={frac {mathrm {d} mathbf {r} }{mathrm {d} t}}={dot {r}}mathbf {hat {r}} +r,{dot {theta }},{hat {boldsymbol {theta }}}+r,{dot {varphi }}sin theta ,mathbf {hat {boldsymbol {varphi }}} }$

and its acceleration is^[6]

${displaystyle {begin{aligned}mathbf {a} ={frac {mathrm {d} mathbf {v} }{mathrm {d} t}}={}&left({ddot {r}}-r,{dot {theta }}^{2}-r,{dot {varphi }}^{2}sin ^{2}theta right)mathbf {hat {r}} \&{}+left(r,{ddot {theta }}+2{dot {r}},{dot {theta }}-r,{dot {varphi }}^{2}sin theta cos theta right){hat {boldsymbol {theta }}}\&{}+left(r{ddot {varphi }},sin theta +2{dot {r}},{dot {varphi }},sin theta +2r,{dot {theta }},{dot {varphi }},cos theta right){hat {boldsymbol {varphi }}}end{aligned}}}$

The angular momentum is

${displaystyle mathbf {L} =mathbf {r} times mathbf {p} =mathbf {r} times mmathbf {v} =mr^{2}(-{dot {varphi }}sin theta ,mathbf {hat {boldsymbol {theta }}} +{dot {theta }},{hat {boldsymbol {varphi }}})}$

Where $m$ is mass. In the case of a constant φ or else θ = π/2, this reduces to vector calculus in polar coordinates.

The corresponding angular momentum operator then follows from the phase-space reformulation of the above,

${displaystyle mathbf {L} =-ihbar ~mathbf {r} times nabla =ihbar left({frac {hat {boldsymbol {theta }}}{sin(theta )}}{frac {partial }{partial phi }}-{hat {boldsymbol {phi }}}{frac {partial }{partial theta }}right).}$

The torque is given as^[6]

${displaystyle mathbf {tau } ={frac {mathrm {d} mathbf {L} }{mathrm {d} t}}=mathbf {r} times mathbf {F} =-mleft(2r{dot {r}}{dot {varphi }}sin theta +r^{2}{ddot {varphi }}sin {theta }+2r^{2}{dot {theta }}{dot {varphi }}cos {theta }right){hat {boldsymbol {theta }}}+mleft(r^{2}{ddot {theta }}+2r{dot {r}}{dot {theta }}-r^{2}{dot {varphi }}^{2}sin theta cos theta right){hat {boldsymbol {varphi }}}}$

The kinetic energy is given as^[6]

${displaystyle E_{k}={frac {1}{2}}mleft[left({dot {r}}^{2}right)+left(r{dot {theta }}right)^{2}+left(r{dot {varphi }}sin theta right)^{2}right]}$

Notes[edit]

^ “ISO 80000-2:2019 Quantities and units — Part 2: Mathematics”. ISO. pp. 20–21. Item no. 2-17.3. Retrieved 2020-08-12.
^ Duffett-Smith, P and Zwart, J, p. 34.
^ ^a ^b Eric W. Weisstein (2005-10-26). “Spherical Coordinates”. MathWorld. Retrieved 2010-01-15.
^ “Video Game Math: Polar and Spherical Notation”. Academy of Interactive Entertainment (AIE). Retrieved 2022-02-16.
^ ^a ^b “Line element (dl) in spherical coordinates derivation/diagram”. Stack Exchange. October 21, 2011.
^ ^a ^b ^c ^d ^e Reed, Bruce Cameron (2019). Keplerian ellipses : the physics of the gravitational two-body problem. Morgan & Claypool Publishers, Institute of Physics. San Rafael [California] (40 Oak Drive, San Rafael, CA, 94903, US). ISBN 978-1-64327-470-6. OCLC 1104053368.{{cite book}}: CS1 maint: location (link)

Bibliography[edit]

Iyanaga, Shōkichi; Kawada, Yukiyosi (1977). Encyclopedic Dictionary of Mathematics. MIT Press. ISBN 978-0262090162.
Morse PM, Feshbach H (1953). Methods of Theoretical Physics, Part I. New York: McGraw-Hill. p. 658. ISBN 0-07-043316-X. LCCN 52011515.
Margenau H, Murphy GM (1956). The Mathematics of Physics and Chemistry. New York: D. van Nostrand. pp. 177–178. LCCN 55010911.
Korn GA, Korn TM (1961). Mathematical Handbook for Scientists and Engineers. New York: McGraw-Hill. pp. 174–175. LCCN 59014456. ASIN B0000CKZX7.
Sauer R, Szabó I (1967). Mathematische Hilfsmittel des Ingenieurs. New York: Springer Verlag. pp. 95–96. LCCN 67025285.
Moon P, Spencer DE (1988). “Spherical Coordinates (r, θ, ψ)”. Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions (corrected 2nd ed., 3rd print ed.). New York: Springer-Verlag. pp. 24–27 (Table 1.05). ISBN 978-0-387-18430-2.
Duffett-Smith P, Zwart J (2011). Practical Astronomy with your Calculator or Spreadsheet, 4th Edition. New York: Cambridge University Press. p. 34. ISBN 978-0521146548.

External links[edit]

“Spherical coordinates”, Encyclopedia of Mathematics, EMS Press, 2001 [1994]
MathWorld description of spherical coordinates
Coordinate Converter — converts between polar, Cartesian and spherical coordinates

Источник

Определения[править | править код]

Переход к другим системам координат[править | править код]

Декартова система координат[править | править код]

Цилиндрическая система координат[править | править код]

Дифференциальные характеристики[править | править код]

Математическое моделирование Земли[править | править код]

Сферическая географическая система координат[править | править код]

Сферическая геомагнитная система координат[править | править код]

См. также[править | править код]

Примечания[править | править код]

Ссылки[править | править код]

Конев В.В. Скалярные и векторные поля

Сферические координаты (сферическая система координат)

Переход от сферических координат к декартовым (прямоугольным)