Искать “а” ради “ускорения”-пустое занятие. Искать надо F-Силу,которая вызывает движение,и изменяет его. S/tt=F/m. S,t,m можно измерить. F=?
Ошибка Ньютон: S=att/2. S=att ! (без /2).
“а”-это ЭНЕРГИЯ движения. Она НЕ зависит от графика движения, и численно = S/tt (V/t).
У падающего “яблока..” несколько скоростей: нач. скорость, кон.скорость,средняя скорость, at, 2at. “средняя скорость”-(S/t)-это та-же скорость at,но выраженная через ЭНЕРГИЮ и ВРЕМЯ: F/m*t.
ВСЕ расчёты на движение надо делать ТОЛЬКО из СРЕДНЕЙ скорости! (Энергия одинакова, и НЕ зависит от графика движения). И нет “надобности” в “интегралах”. …Задачка: машина m=1165 кг, прошла 250 м. за 18 с.(набрала скорость от 0 до 27,7 м/с за 18 сек.) (“Жигули”). Вопрос: какая мощность мотора?
Всякий механизм имеет КПД. КПД ДВС (у бензиновых двс=16%).Решение: S/tt=F/m. 250/324=F/1165, (или 13,9/18=F/1165). F=900 кг.м/сс. Это 12 л.с. при 100% КПД ! При 16% мощность=75 л.с. (а,Да! “ускорение”? оно =0,77 м/сс….). Но и без “а”не обойтись…
Грубая ошибка, находить “а”: Vo=0. V кон.=27,7. t=18 сек. а=(27,7-0)/18. а=1,5 м/сс. Мощность мотора=150 л.с.
То-же с “яблоком…” Vo=0, Vкон.=9,8. t=1 c. Правильно: (0+9,8)/2t. a=4,9 м/cc S=4,9 м.
“Если тело упало на Землю с высоты h, то S/tt ВСЕГДА !!! РАВНО числу 4,9… Это число 4,9 м/сс и ЕСТЬ “УСКОРЕНИЕ СВОБОДНОГО ПАДЕНИЯ”! Скорость: м/с. Ускорение-м/сек.сек. 9,8-это скорость,(но НЕ ускорение).
Сколько ошибок (и слёз) при решении задач:
Vo=5. t=10. a=2. S=? a=? V кон.=?
Решение: S=Vot+att. S=5/10+2*10*10. S=250. a=S/tt. a=2,5. V кон.=Vo+2at. Vкон.=5+2*2*10. V кон.=45. Проверка:S=att. 2,5*10*10=250. S=(v+V)/2*t. (5+45)/2*10. S=250 м.
По принятым формулам: S=(vo+att/2)*t. S=5*10+2*10/10/2=150 м. a=2S/tt. 300/100=3 м/сс
V кон.=v0+at. 5+20=25. S=(5+5+25)*10. S=350 м. (“ОГОРОД!”)
Предположим, вам попался график функции (y=ax^2+bx+c) и нужно по этому графику определить коэффициенты (a), (b) и (c). В этой статье я расскажу 3 простых способа сделать это.
1 способ – ищем коэффициенты на графике
Данный способ хорош, когда координаты вершины и точка пересечения параболы с осью (y) – целые числа. Если это не так, советую использовать способ 2.
-
Коэффициент (a) можно найти с помощью следующих фактов:
– Если (a>0), то ветви параболы направленных вверх, если (a<0), то ветви параболы направлены вниз.

– Если (a>1), то график вытянут вверх в (a) раз по сравнению с «базовым» графиком (у которого (a=1)). Вершина при этом остается на месте. Это наглядно видно по выделенным точкам.

– Аналогично с (a<-1), только график вытянут вниз.

– Если (a∈(0;1)), то график сжат в (a) раз (по сравнению с «базовым» графиком с (a=1)). Вершина при этом остается на месте.

– Аналогично (a∈(-1;0)), только ветви направлены вниз.

-
Парабола пересекает ось y в точке (c).

-
(b) напрямую по графику не видно, но его можно посчитать с помощью (x_в) – абсциссы (икса) вершины параболы:
(x_в=-frac{b}{2a})
(b=-x_вcdot 2a)

Пример (ЕГЭ):

Решение:
Во-первых, надо разобраться, где тут (f(x)), а где (g(x)). По коэффициенту (c) видно, что (f(x)) это функция, которая лежит ниже – именно она пересекает ось игрек в точке (4).

Значит нужно найти коэффициенты у параболы, которая лежит повыше.
Коэффициент (c) у неё равен (1).
Ветви параболы направлены вниз – значит (a<0). При этом форма этой параболы стандартная, базовая, значит (a=-1).

Найдем (b). (x_в=-2), (a=-1).
(x_в=-frac{b}{2a})
(-2=-frac{b}{-2})
(b=-4)
Получается (g(x)=-x^2-4x+1). Теперь найдем в каких точках функции пересекаются:
(-x^2-4x+1=-2x^2-2x+4)
(-x^2-4x+1+2x^2+2x-4=0)
(x^2-2x-3=0)
(D=4+4cdot 3=16=4^2)
(x_1=frac{2-4}{2}=-1); (x_2=frac{2+4}{2}=3).
Ответ: (3).
2 способ – находим формулу по точкам
Это самый надежный способ, потому что его можно применить практически в любой ситуации, но и самый не интересный, потому что думать тут особо не надо, только уметь решать системы линейных уравнений. Алгоритм прост:
-
Ищем 3 точки с целыми координатами, принадлежащие параболе.
Пример:
-
Выписываем координаты этих точек и подставляем в формулу квадратичной функции: (y=ax^2+bx+c). Получится система с тремя уравнениями.
Пример: (A(-4;5)), (B(-5;5)), (C(-6;3)).
(begin{cases}5=a(-4)^2+b(-4)+c\5=a(-5)^2+b(-5)+c\3=a(-6)^2+b(-6)+c end{cases})
-
Решаем систему.
Пример:(begin{cases}5=16a-4b+c\5=25a-5b+c\3=36a-6b+c end{cases})
Вычтем из второго уравнения первое:
(0=9a-b)
(b=9a)Подставим (9a) вместо (b):
(begin{cases}5=16a-36a+c\5=25a-45a+c\3=36a-54a+c end{cases})
(begin{cases}5=-20a+c\5=-20a+c\3=-18a+c end{cases})Первое и второе уравнения совпали (это нормально для точек, симметричных относительно прямой проходящей через вершину – как точки (A) и (B) в нашем случае), но нас это не остановит – мы вычтем из второго уравнение третье:
(2=-2a)
(a=-1)Найдем (b):
(b=-9)
Подставим в первое уравнение (a):
(5=20+c)
(c=-15).Получается квадратичная функция: (y=-x^2-9x-15).
Пример (ЕГЭ):

Решение:
Сразу заметим, что по графику можно сразу определить, что (c=4). Это сильно облегчит нашу систему – нам хватит 2 точек. Выберем их на параболе: (C(-1;8)), (D(1;2)) (на самом деле, если присмотреться, то можно заметить, что эти точки выделены жирно на изначальной картинке – это вам подсказка от авторов задачи).

Таким образом имеем систему:
(begin{cases}8=a(-1)^2+b(-1)+4\2=a+b+4 end{cases})
(begin{cases}8=a-b+4\2=a+b+4 end{cases})
(begin{cases}4=a-b\-2=a+b end{cases})
Сложим 2 уравнения:
(2=2a)
(a=1)
Подставим во второе уравнение:
(-2=1+b)
(b=-3)
Получается:
(g(x)=x^2-3x+4)
Теперь найдем точки пересечения двух функций:
(-3x+13=x^2-3x+4)
(x^2-9=0)
(x=±3)
Теперь можно найти ординату второй точки пересечения:
(f(-3)=-3cdot (-3)+13)
(f(-3)=9+13)
(f(-3)=22)
Ответ: (22).
3 способ – используем преобразование графиков функций
Этот способ быстрее первого и более универсальный, в частности он может пригодится и в задачах на другие функции.
Главный недостаток этого способа – вершина должна иметь целые координаты.
Сам способ базируется на следующих идеях:
-
График (y=-x^2) симметричен относительно оси (x) графику (y=x^2).

-
– Если (a>1) график (y=ax^2) получается растяжением графика (y=x^2) вдоль оси (y) в (a) раз.
– Если (a∈(0;1)) график (y=ax^2) получается сжатием графика (y=x^2) вдоль оси (y) в (a) раз.
-
– График (y=a(x+d)^2) получается сдвигом графика (y=ax^2) влево на (d) единиц.
– График (y=a(x-d)^2) получается сдвигом графика (y=ax^2) вправо на (d) единиц.
-
График (y=a(x+d)^2+e) получается переносом графика (y=a(x+d)^2) на (e) единиц вверх.
График (y=a(x+d)^2-e) получается переносом графика (y=a(x+d)^2) на (e) единиц вниз.
У вас наверно остался вопрос – как этим пользоваться? Предположим, мы видим такую параболу:

Сначала смотрим на её форму и направленность её ветвей. Видим, что форма стандартная, базовая и ветви направлены вверх, поэтому (a=1). То есть она получена перемещениями графика базовой параболы (y=x^2).

А как надо было перемещать зеленый график чтоб получить оранжевый? Надо сдвинуться вправо на пять единиц и вниз на (4).

То есть наша функция выглядит так: (y=(x-5)^2-4).
После раскрытия скобок и приведения подобных получаем искомую формулу:
(y=x^2-10x+25-4)
(y=x^2-10x+21)
Готово.
Пример (ЕГЭ):

Чтобы найти (f(6)), надо сначала узнать формулу функции (f(x)). Найдем её:
-
Парабола растянута на (2) и ветви направлены вниз, поэтому (a=-2). Иными словами, первоначальной, перемещаемой функцией является функция (y=-2x^2).

-
Парабола смещена на 2 клеточки вправо, поэтому (y=-2(x-2)^2).
-
Парабола поднята на 4 клеточки вверх, поэтому (y=-2(x-2)^2+4).
-
Получается (y=-2(x^2-4x+4)+4=)(-2x^2+8x-8+4=-2x^2+8x-4).
-
(f(6)=-2cdot 6^2+8cdot 6-4=-72+48-4=-28)
Смотрите также:
Как найти k и b по графику линейной функции?
Описание презентации по отдельным слайдам:
-

1 слайд
Алгоритм
нахождения значения коэффициентов a, b, c
по графику квадратичной функции
y= ax2 +bx+c. -

2 слайд
Нахождение коэффициента a
1) по графику параболы определяем координаты вершины (m,n)
2) по графику параболы определяем координаты любой точки А (х1;у1)
3) подставляем эти значения в формулу квадратичной функции, заданной в другом виде:
4) решаем полученное уравнение. -

3 слайд
Нахождение коэффициента b
1) Сначала находим значение коэффициента a
(шаг I, смотри выше)2)В формулу для абсциссы параболы m= -b/2a подставляем значения
m и a3) Вычисляем значение коэффициента b.
-

4 слайд
Нахождение коэффициента с:
1)Находим координату у точки пересечения графика параболы с осью Оу, это значение равно коэффициенту с, т.е. точка (0;с)-точка пересечения графика параболы с осью Оу.
2)Если по графику невозможно найти точку пересечения с осью Оу, то выполняем шаги I, II (находим коэффициенты a,b)
3)Подставляем найденные значения a, b , А(х1 ;у1) в уравнение
у=ax2 +bx+c и находим с. -

5 слайд
По графику функции найдите значения коэффициентов a, b, c
-

-

-

Содержание:
- Определение и формула силы Ампера
- Закон Ампера
- Силы, действующие на проводники с током в магнитном поле
- Единицы измерения силы Ампера
- Примеры решения задач
Определение и формула силы Ампера
Определение
Сила, действующая на проводник с током в магнитном поле, называется силой Ампера. Ее обозначения:
$bar{F}, bar{F}_A$ . Сила Ампера векторная величина. Ее направление определяет
правило левой руки: следует расположить ладонь левой руки так, чтобы силовые линии магнитного поля входили в нее.
Вытянутые четыре пальца указывали направление силы тока. В таком случае отогнутый на
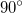 большой палец укажет направление силы Ампера (рис.1).
большой палец укажет направление силы Ампера (рис.1).
Закон Ампера
Элементарная сила Ампера
($dbar{F}_A$) определена законом (или формулой) Ампера:
$$d bar{F}_{A}=I d bar{l} times bar{B}(1)$$
где I – сила тока,
$d bar{l}$ – малый элемент длины проводника – это вектор, равный
по модулю длине проводника, направленный в таком же направлении как вектор плотности тока,
$bar{B}$ – индукция магнитного поля, в которое помещен проводник с током.
Иначе эту формулу для силы Ампера записывают как:
$$d bar{F}_{A}=bar{j} times bar{B} d V(2)$$
где $bar{j}$ – вектор плотности тока, dV – элемент объема проводника.
Модуль силы Ампера находят в соответствии с выражением:
$$d F=I cdot B cdot d l cdot sin alpha(3)$$
где $alpha$ – угол между векторами магнитной индукции и направление течения тока. Из выражения (3) очевидно, что
сила Ампера максимальна в случае перпендикулярности линий магнитной индукции поля по отношению к проводнику с током.
Силы, действующие на проводники с током в магнитном поле
Из закона Ампера следует, что на проводник с током, равным I, действует сила равная:
$$bar{F}_{A}=I int_{l} d bar{l} times bar{B}(4)$$
где $bar{B}$ магнитная индукция, рассматриваемая в пределах малого кусочка проводника dl.
Интегрирование в формуле (4) проводят по всей длине проводника (l). Из выражения (4) следует, что на замкнутый контур с током I,
в однородном магнитном поле действует сила Ампера равная $bar{F}_{A}=0(H)$
Сила Ампера, которая действует на элемент (dl) прямого проводника с током I1, помещённый в магнитное поле, которое
создает другой прямой проводник, параллельный первому с током I2, равна по модулю:
$$d F=frac{mu_{0}}{2 pi} frac{I_{1} I_{2}}{d} d l(5)$$
где d – расстояние между проводниками, $mu_{0}=4 pi cdot 10^{7}$ Гн/м(или Н/А2 ) – магнитная постоянная.
Проводники с токами одного направления притягиваются. Если направления токов в проводниках различны, то они отталкиваются.
Для рассмотренных выше параллельных проводников бесконечной длины сила Амперана единицу длины может быть вычислена по формуле:
$$frac{F}{l}=frac{mu_{0}}{2 pi} frac{I_{1} I_{2}}{d}$$
Формулу (6) в системе СИ применяют для получения количественного значения магнитной постоянной.
Единицы измерения силы Ампера
Основной единицей измерения силы Ампер (как и любой другой силы) в системе СИ является: [FA]=H
В СГС: [FA]=дин
Примеры решения задач
Пример
Задание. Прямой проводник длины l с током I находится в однородном магнитном поле B. На проводник
действует сила F. Каков угол между направлением течения тока и вектором магнитной индукции?
Решение. На проводник с током, находящийся в магнитном поле действует сила Ампера, модуль которой для
прямолинейного проводника с током расположенном в однородном поле можно представить как:
$$F=F_{A}=I B operatorname{lsin} alpha$$
где $alpha$ – искомый угол. Следовательно:
$$alpha=arcsin left(frac{F}{I B l}right)$$
Ответ. $alpha=arcsin left(frac{F}{I B l}right)$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Два тонких, длинных проводника с токами лежат в одной плоскости на расстоянии d друг от друга.
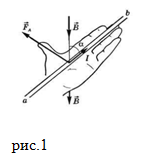
Ширина правого проводника равна a. По проводникам текут токи I1 и I2 (рис.1). Какова, сила Ампера, действующая
на проводники в расчете на единицу длины?
Решение. За основу решения задачи примем формулу элементарной силы Ампера:
$$d bar{F}_{A}=I d bar{l} times bar{B}(2.1)$$
Будем считать, что проводник с током I1 создает магнитное поле, а другой проводник в нем находится.Станем искать силу
Ампера, действующую на проводник с током I2. Выделим в проводнике (2) маленький элемент dx (рис.1), который находится
на расстоянии x от первого проводника. Магнитное поле, которое создает проводник 1 (магнитное поле бесконечного прямолинейного проводника с
током) в точке нахождения элементаdxпо теореме о циркуляции можно найти как:
$$B cdot 2 pi x=mu_{0} I_{1} rightarrow B=frac{mu_{0} I_{1}}{2 pi x}$$
Вектор магнитной индукции в точке нахождения элемента dx направлен перпендикулярно плоскости
рисунка, следовательно, модуль элементарной силы Ампера, действующий на него можно представить как:
$$B cdot 2 pi x=mu_{0} I_{1} rightarrow B=frac{mu_{0} I_{1}}{2 pi x}$$
где ток, который течет в элементе проводника dx, выразим как:
$$B cdot 2 pi x=mu_{0} I_{1} rightarrow B=frac{mu_{0} I_{1}}{2 pi x}$$
Тогда выражение для dFA, учитывая (2.2) и (2.4) запишем как:
$$B cdot 2 pi x=mu_{0} I_{1} rightarrow B=frac{mu_{0} I_{1}}{2 pi x}$$
где из рис.1 видно, что $a leq x leq a+b$, по условию задачи силу следует
найти на единицу длины, значит $0 leq l leq 1$ . Для нахождения суммарной силы Ампера, действующей на проводник (2) возьмем двойной интеграл от выражения (2.5):
$$F_{A}=int_{a}^{a+b} int_{0}^{1} frac{mu_{0} I_{1}}{2 pi x} cdot frac{I_{2}}{b} d x d l=int_{a}^{a+b} frac{mu_{0} I_{1}}{2 pi x} cdot frac{I_{2}}{b} d x=frac{mu_{0} I_{1}}{2 pi} cdot frac{I_{2}}{b} ln left|frac{a+b}{a}right|$$
Проводники действуют друг на друга с силами равными по модулю и так как токи направлены одинаково, то они притягиваются.
Ответ. $F_{A}=frac{mu_{0} I_{1}}{2 pi} cdot frac{I_{2}}{b} ln left|frac{a+b}{a}right|$
Читать дальше: Формула силы выталкивания.
Все формулы по физике за 9 класс: определения, пояснения
Содержание:
- Формулы по физике за 9 класс: основные разделы
-
Кинематика
- Равномерное прямолинейное движение
- Равноускоренное прямолинейное движение
- Равномерное движение по окружности
-
Динамика
- Законы Ньютона
- Силы в природе
- Сила всемирного тяготения
- Движение тела под действием силы тяжести
- Силы трения
- Движение тела под действием нескольких сил
- Закон сохранения в механике
- Движение жидкостей и газов по трубам
- Примеры задач
Содержание
- Формулы по физике за 9 класс: основные разделы
-
Кинематика
- Равномерное прямолинейное движение
- Равноускоренное прямолинейное движение
- Равномерное движение по окружности
-
Динамика
- Законы Ньютона
- Силы в природе
- Сила всемирного тяготения
-
Движение тела под действием силы тяжести
- Силы трения
- Движение тела под действием нескольких сил
- Закон сохранения в механике
- Движение жидкостей и газов по трубам
- Примеры задач
Формулы по физике за 9 класс: основные разделы
Программа обучения по предмету физика в 9 классе включает в себя несколько разделов: кинематика и динамика, которые в свою очередь состоят из подразделов.
Таким образом ученики старшей школы изучают механические колебания и волны, законы взаимодействия и движения тел, электромагнитные явления, строение атомов и их ядер, основные законы механики. В школьную программу девятого года обучения также входят основные свойства света: интерференция, преломление и дисперсия.
Кинематика
Кинематика — один из разделов механики. Кинематика изучает механическое движение тел и способы его описания, независимо от причин этого движения. В данном случае под механическим движением подразумевается любое изменение положения какого-либо тела полностью или частично относительно других тел, случившееся с течением времени.
В Кинематике изучают простые виды движения.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Равномерное прямолинейное движение
Понятие равномерного прямолинейного движения заключается в том, что тело движется по прямой с одинаковой скоростью, то есть за равные промежутки времени тело перемещается на одинаковое расстояние. В таком случае скорость тела остается постоянной, однако является векторной величиной.
В таком случае скорость тела остается постоянной, однако является векторной величиной.
Скорость может быть как положительной, так и отрицательной. Все зависит от того, в каком направлении оси X (положительном или отрицательно) направлен вектор скорости. Если тело находится в покое, то его скорость равняется нулю, а координата не меняется в течение времени.
При равномерном прямолинейном движении координата тела вычисляется по следующей формуле:
x = x0 + v · t
В этой формуле x0 – начальная координата, x – конечная координата, v – скорость, t – время.
Если начальная координата — это начало движения и x
0 = 0, то формулу можно сократить до x1 = v · t.
Если x0 = 0, то пройденный путь S будет равен координате x. Из этого утверждения можно получить формулу прямолинейного равномерного движения относительно пройденного телом расстояния:
S = v · t.
Из этого можно вывести формулы относительно скорости и времени:
v= S/t и t = S/v.
Скорость и время также можно выразить из полной формулы для тех случаев, когда x0 не равно 0:
v = (x1 — x0)/t и t = (x1 — x0)/v.
Равноускоренное прямолинейное движение
В случае равноускоренного прямолинейного движения тело изменяет скорость своего движения на одинаковую величину за любые равные промежутки времени. Под ускорением в контексте данного определения понимается изменение значения скорости за единицу времени.
Скорость тела вычисляется по формуле:
v = v0 + a · t
В данной формуле v – конечная скорость, v0 – начальная скорость, a – ускорение, t – время.
В равноускоренном прямолинейном движении постоянной величиной является ускорение, а не скорость. Ускорение может быть больше или меньше нуля. В случае увеличения скорость, значение ускорения будет больше нуля, а в случае уменьшения — меньше.
Рассмотрим случай, если начальная скорость тела равно 0. Тогда его скорость через какое-либо время t будет равна произведению ускорения и этого времени:
Тогда его скорость через какое-либо время t будет равна произведению ускорения и этого времени:
v = at
Допустим, что нам известны текущая скорость тела и время, за которое тело развило указанную скорость из состояния покоя. Тогда мы можем определить ускорение:
a = v/t
В том случае, если начальная скорость тела не равна нулю, мы можем рассчитать конечную скорость тела по следующей формуле:
v = v0 + at
Взглянем на случаи, когда вектор скорости направлен в противоположном направлении (например, подброшенный камень, его скорость направлена в противоположную сторону от ускорения свободного падения) или в случае торможения. Тогда формула будет выглядеть следующим образом:
v = v0 – at
В случае свободного ускорения остальные формулы будут записываться так:
at = v – v0, a = (v – v)/t
А говоря о торможении, мы используем эти формулы:
at = v0 – v, a = (v0 – v)/t
Если тело останавливается, то нам следует использовать эту формулу:
a = v0/t
А если необходимо узнать, через какой отрезок времени тело остановится, то мы запишем формулу так:
t = v0/a
Обратимся к формуле, которая поможет найти путь, которое тело проходит при прямолинейном ускорении.
Если при равномерном движении, оси времени и расстояния параллельны, то в случае равноускоренного движения ось движения либо возрастает, либо убывает. Тогда вместо прямоугольника, чью площадь мы вычисляли при равномерном движении, необходимо вычислить площадь трапеции.
Площадь трапеции равна полусумме оснований на высоту, таким образом мы получаем:
s = ½ · (v0 + v) · t
Пройденный путь определяется по формуле:
s = v0t + at2/2
Путь торможения рассчитывается с помощью этой формулы:
s = v02/(2a)
Равномерное движение по окружности
Говоря о равномерном движении по окружности, нужно понимать, что в этом случае вектор скорости тела изменяется (скорость направлена по касательным к окружности), а модуль скорости тела (числовое значение) остается постоянным.
Предположим, что необходимо вычислить модуль скорости за один оборот тела по окружности. Обозначим оборот как S, а время, за которое тело его совершило, как t.
Тогда формула будет записываться следующим образом: v = s/t.
Однако, если мы говорим об одном обороте, то это называется период. То есть время, за которое тело совершает один оборот вокруг окружности. Он обозначается как T. И тогда формула одного оборота будет выглядеть так: v = s/T
Если S в данном случае это длина окружности (l), то формула принимает вид v = 2πR/T, в соответствии с формулой окружности l = 2piR
Если необходимо найти период при известном модуле скорости, то формула примет вид T = 2piR/v
Аналогично радиус можно найти через формулу R = ½ vT/pi
Динамика
Динамика — раздел механики, изучающий предпосылки изменения в характере движения. Например, возникновение движения. Именно этот раздел изучает три закона Ньютона. В задачах динамики содержится решение таких вопросов как определение действующих на тело сил по характеру его движения и наоборот.
Законы Ньютона
Первый закон Ньютона гласит, что существуют такие системы отсчета, относительно которых тело движется прямолинейно и равномерно, или покоится, если на него не действуют другие тела или их действия скомпенсированы.
Введем основные величины:
Инерциальными называются системы отсчета, которые движутся равномерно прямолинейно относительно Земли. Все системы отсчета, которые движутся прямолинейно и равномерно относительно инерциальной, также являются таковыми. Если система отсчета движется с ускорением, то она — неинерциальная.
Сила — это физическая величина, которая характеризует действие одного тела на второе. В результате этого действия второе тело получает ускорение в инерциальной системе отсчета. Измеряется в ньютонах.
Масса — это физическая величина, которая количественно характеризует инертность тела. Измеряется в килограммах.
Взглянем на тело, на которое действует сила с модулем равным 1 Н. Так как изначально тело массой 1 кг находилось в покое в инерциальной системе, модуль его ускорения будет равен 1 м/с2.
В соответствии со вторым законом Ньютона сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение. Это основной закон динамики.
Для выведения второго закона Ньютона и формулы, где F = ma, необходимо обобщить два факта:
- если на два тела, масса которых различна, подействовать равной силой, то ускорения, которые приобретут тела, будут обратно пропорциональны массам;
- если на одно и то же тело действуют силы разной величины, то ускорения тела будут прямо пропорциональны приложенным силам.
Благодаря этому закону, возможно вычислить не только силу, действующую на тело, но и ускорение. Для этого нужно использовать формулу [w = frac{F}{m}]
В векторной форме второй закон Ньютона записывается как ma = mg + N + Fтр
Третий закон Ньютона гласит, что силы, с которыми две материальные точки воздействуют друг на друга, всегда равны по модулю и направлены в противоположные стороны вдоль прямой, соединяющей эти точки.
Выразить закон формулой можно следующим образом F1 = -F2
Примечание
В случае взаимодействия тел силы имеют одинаковую природу, однако, они приложены к разным телам. Таким образом эти силы не могут уравновешивать друг друга, а складывать можно только силы, приложенные к одному телу.
Таким образом эти силы не могут уравновешивать друг друга, а складывать можно только силы, приложенные к одному телу.
Силы в природе
В соответствии с законом Гука, при деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Природа этой силы состоит в электромагнитном взаимодействии между атомами и молекулами вещества. Эта сила называется упругость.
Говоря о малых деформациях (если |x| < l) сила упругости пропорциональна деформации тела и направлена в противоположную сторону от перемещения частиц тела при деформации. Исходя из этого формула выглядит следующим образом Fx = Fупр = -kx
В данном случае коэффициент k — жесткость тела, она измеряется в ньютонах на метр (Н/м).
Физике свойственен другой способ записи закона Гука. В его записи используются понятия относительной деформации и напряжения. Относительная деформация ε = x / l, а напряжение — это отношение силы к площади поперечного сечения деформированного тела δ = F / S = -Fупр / S.
Исходя из этого, закон Гука можно сформулировать так [ε = frac{E}{δ}]
Коэффициент Е — это модуль Юнга. Он зависит исключительно от свойств материала. Размеры и форма не имеют значения.
Если говорить о случаях сложных деформациях, например в случае деформации изгиба, в формуле появляется сила N — сила реакции опоры. Эта сила направлена перпендикулярно поверхности соприкосновения. N = -mg
Сила всемирного тяготения
Закон всемирного тяготения говорит, что все тела притягиваются друг к другу с силами, прямо пропорциональными их массам и обратно пропорциональна квадрату расстояния между ними.
Эту силу можно вычислить по формуле F = GfracMR32m = mg
g в данном случае — ускорение свободного падения, о котором говорилось выше. В данном случае g = GfracMR32. Среднее значение ускорения свободного падения равно 9,81 м/с2.
R3 — это радиус Земли. Он равен 6,38·106 м.
G в формуле обозначает гравитационную постоянную. Она равна 6,67·10–11 Н·м2/кг2.
Движение тела под действием силы тяжести
Ускорение свободного падение является частным случаем равноускоренного прямолинейного движения. В этом случае ускорение всегда будет равно 9,8 м/с2 и обозначается буквой g. Таким образом g — это ускорение свободного падения.
Ускорение свободного падения можно вычислить по следующей формуле: g = GM3/(R3+H)2
В данном случае H — это гравитационная постоянная, M — масса земли, R — радиус земли, а H — высота падения тела.
Скорость тела под действием силы тяжести можно вычислить по формуле: v = gt
Высоту, с которой падает тело, можно вычислить по формуле H=gt2/2
Силы трения
Силой трения называют силу, характеризующую взаимодействие, возникающее в месте соприкосновения тел и препятствующее их относительному движению. Сила трения имеет электромагнитную природу.
Сила трения имеет электромагнитную природу.
Трение можно разделить на три вида: трение покоя, трение скольжения и трение качения.
Трение покоя — это трение, которое возникает при отсутствии перемещения соприкасающихся тел относительно друг друга.
Можно сказать, что эта сила не позволяет одному телу двигаться относительно другого. Эта сила направлена противоположно силе, приложенной извне параллельно поверхности соприкосновения. Сила трения покоя возрастает вместе с силой, которая стремится сдвинуть тело с места.
Трение скольжения возникает при действии на тело силе, превышающей максимальную силу трения покоя.
Это тело сдвигается с места и начинает дальнейшее движение. Сила трения скольжения всегда направлена в противоположную сторону от относительной скорости соприкасающихся тел.
Трение качения возникает в случае, если тело не скользит по другому телу, а катится наподобие колеса или цилиндра. Трение качения — это трение, которое возникает на месте их соприкосновения.
В виде формулы сила трения выглядит следующим образом: Fтр = μmg
В данном случае μ – коэффициент трения, m – масса тела, а g — ускорение свободного падения (постоянная величина 9,81 м/с2).
Движение тела под действием нескольких сил
Если на тело действуют несколько сил одновременно, то необходимо найти равнодействующую всех сил по формуле F = F1 + F2 + F3
Равнодействующая сила может быть равна нулю. В таком случае тело находится в состоянии покоя.
Закон сохранения в механике
Закон сохранения импульса гласит, что геометрическая сумма импульсов тел, составляющих замкнутую систему, остается постоянной при любых движениях и взаимодействиях тел системы.
В виде формулы закон сохранения импульса выглядит следующим образом: p1 + p2 = p1’ + p2’ m1v + m2u = m1v’ + m2u’
В свою очередь импульсом тела называют величину, которая равна произведению массы тела на его скорость: p = mv.
Изменение импульса тела равно импульсу силы, который в свою очередь вычисляется по формуле P = Ft
Кинетическая энергия равна половине произведения массы тела и квадрата его скорости: Ek = mv2/2
Кинетическая энергия — это физическая величина, которая характеризует движущиеся тела. Выражается в Дж.
Закон сохранения энергии состоит в том, что полная механическая энергия замкнутой системы тел, взаимодействующих силами тяготения или силами упругости, остается неизменной при любых движениях тел системы.
Мощность — это величина, которая равна отношению совершенной работы к промежутку времени, за который она совершена. Выражается в Вт.
Вычисляется по формуле N = A/t
Коэффициент полезного действия (КПД) — это название величины, равной отношению полезной работы ко всей совершенной работе. Выражается в Дж.
КПД демонстрирует эффективность использования затраченной энергии. Коэффициент не может быть больше единицы, однако его можно выразить в процентах. 2}{2}])
2}{2}])
Примеры задач
Задача №1
На рисунке представлены графики зависимости координаты двух тел от времени. Графики каких зависимостей показаны? Какой вид имеют графики зависимости скорости и пути пройденного телом, от времени?
Решение
На рисунке показаны графики равномерного движения тел.
- В начальный момент времени t = 0 первое тело имеет начальную координату хо1 = 1 м, второе тело — координату хо2 = 0.
- Оба тела движутся в направлении оси Х, так как координата возрастает с течением времени.
- Уравнение движения для равномерного прямолинейного движения имеет вид: x=xо+vхt.
Тогда для первого, второго тела соответственно:
x1=xо1+v1хt и x2=xо2+v2хt
или x1=1+v1хt и x2=v2хt. 2}{2} = 2mgl + frac{mgl}{2}])
2}{2} = 2mgl + frac{mgl}{2}])
vo2 = g4l + gl = 5gl
vo = √(5gl)
Выполнив вычисления, получим: vo = √(5×10×0,5) = 5 (м/с).
Ответ: если шарик подвешен на нерастяжимой нити, его скорость должна составлять не менее 5 м/с.
Задача №3
Экваториальный радиус Земли равен 6370 км. Определить линейную и угловую скорости движения точек экватора при вращении Земли вокруг оси.
Решение:
Линейная скорость вращения ν точек земного экватора:
([v = frac{2piR}{T}])
При этом угловая скорость вращения w всех точек Земли равна:
([w = frac{2pi}{T}])
После вычислений у нас получится: ν = 463 м/с, w = 7,3×10−5 рад/с.
Насколько полезной была для вас статья?
Рейтинг: 2.60 (Голосов: 5)
Основные формулы раздела астрономии для ЕГЭ по физике
Астрономия — один из разделов физики. Она изучает космические тела и объекты: планеты, звезды, астероиды. В школе эту тему практически не рассматривают, хотя в ЕГЭ она встречается. Формулы по астрономии — это задание 24 из итоговой аттестации. Для его выполнения нужно анализировать таблицы с информацией о небесных телах, а также проводить некоторые расчеты. Если вам интересна эта тема, и вы хотите подготовиться к экзамену лучше, подумайте о посещении курсов. На них, помимо других разделов, разбираются небесные тела. А в статье мы дадим краткую теорию, перечислим формулы по астрономии для физики.
Она изучает космические тела и объекты: планеты, звезды, астероиды. В школе эту тему практически не рассматривают, хотя в ЕГЭ она встречается. Формулы по астрономии — это задание 24 из итоговой аттестации. Для его выполнения нужно анализировать таблицы с информацией о небесных телах, а также проводить некоторые расчеты. Если вам интересна эта тема, и вы хотите подготовиться к экзамену лучше, подумайте о посещении курсов. На них, помимо других разделов, разбираются небесные тела. А в статье мы дадим краткую теорию, перечислим формулы по астрономии для физики.
Теория
Теоретические вопросы и формулы по астрономии для ЕГЭ можно разделить на 4 группы:
- звезды;
- планеты Солнечной системы;
- спутники;
- остальные тела: кометы, астероиды.
Формул по теме «Звезды» нет. Для решения заданий нужно уметь пользоваться диаграммой Герцшпрунга-Расселла, показывающей классификацию небесных тел. Для этого разберитесь в светимости, температуре, спектральных классах.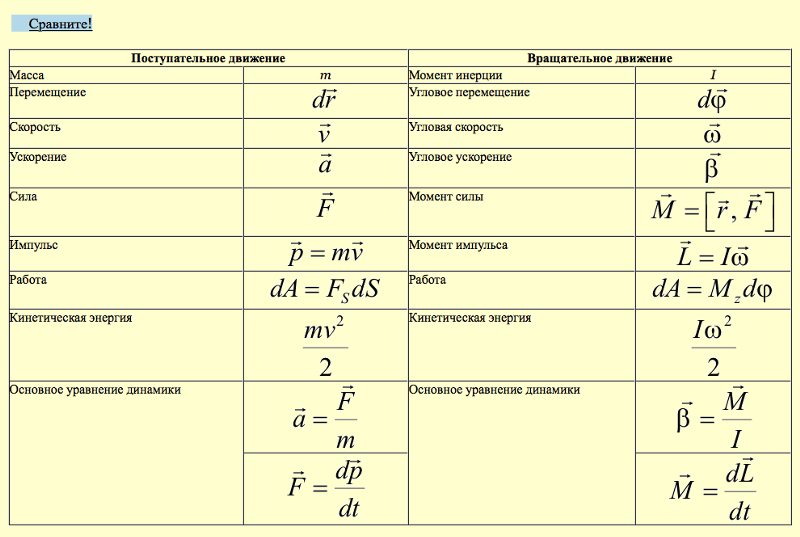
Планеты и спутники
Планеты и спутники Солнечной системы представляют собой шарообразные тела. К ним применимы многие формулы из геометрии. Одно из таких выражений — объем V = 4/3 • πR3 = πd3 / 6. Зная среднюю плотность небесного тела, можно вычислить ее массу m = 4/3 • ρπR3 = ρπd3 / 6. Еще одно важное определение — первая космическая скорость. При ее достижении небесное тело приобретает круговую орбиту и становится спутником. Если тело приобретет вторую космическую скорость, оно победит силу гравитационного притяжения, сможет покинуть свою орбиту и улететь в пространство на бесконечность. Важная характеристика — период вращения, показывающий отношение радиуса планеты к ее скорости. Период вращения определяет длительность суток или года.
Астероиды и другие тела
Астероиды движутся по эллиптическим орбитам. Из-за вытянутости траектории они то приближаются к Солнцу, то удаляются от него. В астрономии и математике «вытянутость» называется эксцентриситетом. Для расчета этой величины нужно знать размеры полуосей. Большая — расстояние от центра до самой дальней точки. Малая — до самой ближней. Эксцентриситет рассчитывается в астрономии формулой Кеплера: .
Для расчета этой величины нужно знать размеры полуосей. Большая — расстояние от центра до самой дальней точки. Малая — до самой ближней. Эксцентриситет рассчитывается в астрономии формулой Кеплера: .
Формулы
В этом разделе рассмотрим астрономические формулы с объяснениями:
- период вращения планеты: . R — радиус, v — скорость вращения;
- частота вращения: ;
- линейная скорость вращения: , — угловая скорость;
- угловая скорость: ;
- центростремительное ускорение: ;
- первая космическая скорость: . G — гравитационная постоянная, M — масса планеты, h — высота над поверхностью планеты;
- вторая космическая скорость: ;
- первый закон Кеплера (эксцентриситет): . a — большая полуось, b — малая полуось;
- третий закон Кеплера: . T — периоды вращения, a — большие полуоси;
- ускорение свободного падения: ;
- закон Хаббла (скорость удаления галактик и звезд): v=RH.
 R — расстояние до объекта, H — постоянная Хаббла.
R — расстояние до объекта, H — постоянная Хаббла.
Мы разобрали основные формулы для 24 задания ЕГЭ по физике, немного коснулись теоретического материала. Обязательно выучите уравнения из статьи — они пригодятся при решении задач. Чтобы выполнять номер без ошибок, не забывайте практиковаться. Примеры заданий можно найти на ФИПИ и Решу.ЕГЭ. Если решать задачи самостоятельно не получается, запишитесь на курсы подготовки к ЕГЭ. Там с вами разберут все сложные моменты. Мы уверены — вы справитесь и наберете высокие баллы на экзамене!
Физика: Не паникуйте! 10 шагов к решению (большинства) физических задач
Физика: не паникуйте! 10 шагов к решению (большинства) физических задач
Опубликовано:
6 октября 2010 г.
Автор
Мориэль Шоттлендер
Категории:
Аналитические статьи, физика, учебные пособия
В этом семестре я начала заниматься репетиторством в физико-математическом учебном центре. Я единственный «чистый» репетитор по физике — остальные репетиторы — математики или инженеры, которые очень хорошо разбираются в математике (правда, они все очень классные). Однако большинство из них уклоняются от задач по физике, позволяя мне — и горстке других репетиторов — заниматься этим страшным предметом.
Вообще кажется, что физика имеет ауру, которая пугает людей еще до того, как они начинают решать задачу. Это начинается с очень простой физики, но продолжается с материалом более высокого уровня. Разница, похоже, в том, что только те, кто любит физику и находит хороший способ с ней справиться, остаются, чтобы иметь дело с вещами более высокого уровня.
Физика и большинство естественных наук могут быть очень сложными. Описание нашего мира не всегда интуитивно понятно и иногда требует очень продвинутого математического и концептуального понимания. Это может объяснить, почему не все выбирают карьеру физика. Ну и зарплата.
В базовой физике — материале, изучаемом в старших классах и университетских курсах начального уровня — методология проста. Не нужно паниковать. Довольно часто именно паника мешает студентам внимательно относиться к предмету и получать максимальную отдачу от этих курсов.
Имея опыт репетиторства (и прохождения) занятий по физике начального уровня, я разработал несколько основных правил, которые помогут вам справиться с проблемами. Это поможет, если проблема в домашнем задании или на экзамене. Мы пройдемся по ним сейчас.
1. Не паникуйте.
Звучит очевидно, правда? И все же, это сложнее, чем кажется. Вы смотрите на вопрос, и предложения угрожающе вырисовываются перед вами, запутывая вас до бесконечности. Вы понятия не имеете, с чего начать, даже если знаете основные понятия. Чьи машины едут в каком направлении? Какая волна распространяется по струне? Помоги мне, думаешь ты с ужасом. Помоги мне…!
Вы понятия не имеете, с чего начать, даже если знаете основные понятия. Чьи машины едут в каком направлении? Какая волна распространяется по струне? Помоги мне, думаешь ты с ужасом. Помоги мне…!
Настало время сделать глубокий вдох, закрыть глаза и сосчитать до пяти.
В физике более низкого уровня большинство вопросов можно решить с помощью простых формул. Пока вы помните эти формулы, вы находитесь на большей части пути к ответу. С этого момента единственное, на чем вам нужно сосредоточиться, — это преобразование ужасного, запутанного куска текста в читаемые биты, которые вписываются в ваши формулы. Вы можете сделать это.
2. Попытайтесь понять ситуацию
Что происходит в этой задаче? Это мяч, свободно падающий с какой-то высоты? Это скорость Супермена, когда он летит, чтобы спасти Лоис Лейн на определенном расстоянии? Или, может быть, это вопрос о магнетизме? Электричество?
Сначала выясните контекст. Вам не нужно разбираться во всех мелких деталях, но как только вы узнаете, с чем имеете дело в целом, вы будете знать, как сформулировать свой ответ и какие уравнения использовать.
3. Внимательно прочитайте вопрос
Итак, теперь вы понимаете физическую ситуацию и знаете, к какому предмету относится этот вопрос (или к нескольким предметам). Теперь прочитайте вопрос еще раз и убедитесь, что вы четко понимаете, что он на самом деле требует от вас найти. В задаче того же типа — скажем, в прыгающем мяче — вас могут попросить найти начальную скорость, максимальную высоту или угол броска. Для каждого из них потребуется немного другая стратегия. Убедитесь, что вы знаете, что вам нужно делать.
Еще один хороший совет, который следует помнить на данном этапе, заключается в том, что формулировка многих физических задач содержит очень важную информацию. Например, автомобиль, трогающийся с места, означает, что ваша начальная скорость равна нулю. Два объекта, падающие из окна, могут вести себя по-разному, если они оба прикреплены друг к другу.
Внимательно прочитайте вопрос, сейчас не время бегло просматривать. Убедитесь, что вы не пропустите важную информацию.
4. Организуйте информацию
Задачи Word сбивают с толку только потому, что они скрывают в себе реальные переменные. Иногда вам будет предоставлена дополнительная информация, которая вам на самом деле не понадобится. В других случаях будут переменные, цель которых раскрывается в более поздней части вопроса.
Например, если в вопросе есть автомобиль, который начинает двигаться из состояния покоя и за 5 минут достигает скорости 20 км/ч, вы должны записать основные переменные следующим образом:
- v(начальная) = 0 км/ч
- t(окончание) = 5 минут
- v(конечная) = 20 км/ч
- а = ?
Сделайте это со всей информацией, которую вы получите из вопроса. Это поможет вам ясно увидеть переменные перед вами, найти правильное уравнение для использования и увидеть, что вы упускаете. Это также сделает исходный, запутанный текст ненужным. Если вы систематизируете информацию, ваш мозг сможет заниматься реальной физикой вместо понимания прочитанного.
5. Нарисуйте сцену
В физике рисование действительно может упростить задачу. Например, получение визуального представления о вашей системе отсчета или о разнице между верхом (положительным) и нижним (отрицательным) может означать разницу между правильным ответом и неправильным.
Вам не обязательно хорошо рисовать. Нарисуйте грубую схему в зависимости от ситуации. Стрелки — ваши друзья в вопросах физики — они показывают, в каком направлении движется объект или какова возможная сумма приложенных к нему сил. Они организуют информацию для вас. Используй их.
Некоторые вопросы уже приходят с чертежом — используйте его! Вопросы о силах, например, лучше всего решать с помощью схемы, и вы можете упустить важную информацию, которую сразу не увидите, если не зарисуете ее.
Давай, Пикассо, приложи все усилия и переходи к следующему шагу.
6. Проверка блоков
Иногда ваш профессор будет проверять ваши навыки преобразования единиц измерения. Это неспроста — в физике (и науке в целом) единицы измерения имеют решающее значение. Вы должны убедиться, что ваши единицы измерения одинаковы на протяжении всего упражнения, иначе формулы не будут работать. Если вы умножите скорость на время, вы получите расстояние (при постоянном ускорении), но если автомобиль двигался со скоростью 10 км в час в течение 5 минут, умножение 10 на 5 не даст вам правильного ответа. Скорее, вам нужно будет либо преобразовать километры в час в километры в минуту, либо (что, вероятно, проще) преобразовать 5 минут в единицы часов.
Это неспроста — в физике (и науке в целом) единицы измерения имеют решающее значение. Вы должны убедиться, что ваши единицы измерения одинаковы на протяжении всего упражнения, иначе формулы не будут работать. Если вы умножите скорость на время, вы получите расстояние (при постоянном ускорении), но если автомобиль двигался со скоростью 10 км в час в течение 5 минут, умножение 10 на 5 не даст вам правильного ответа. Скорее, вам нужно будет либо преобразовать километры в час в километры в минуту, либо (что, вероятно, проще) преобразовать 5 минут в единицы часов.
Лучше всего это делать с помощью дробей, но существует достаточно руководств по преобразованию единиц измерения, объясняющих эту концепцию. Не паникуйте, делайте это осторожно, и вы получите правильные значения.
Если мы продолжим наш пример из предыдущей части, мы должны преобразовать t(final) из минут в часы. Это не так сложно сделать:
(5 text{ минут} * frac{1 text{ час}}{60 text{ минут}} = frac{1}{12} text{ час})
(Посмотрите, как единицы «минуты» сокращаются с единицами «минут» в знаменателе, оставляя единицы «часы» с окончательным ответом? Это отличный способ проверить правильность вашего преобразования)
Теперь, когда все ваши переменные указаны в правильных единицах, вы можете продолжить решение вопроса.
7. Рассмотрите свои формулы
Это верно для большинства вопросов по физике и абсолютно верно для более низкого уровня физики. Как студент, изучающий основы физики, вы не должны заново изобретать колесо или даже понимать, как оно вообще было изобретено. Ожидается, что вы будете понимать концепции и использовать доступные вам инструменты.
Самым важным из этих инструментов являются формулы.
Некоторые профессора потребуют, чтобы вы запомнили соответствующие формулы, а другие дадут вам «шпаргалку». В любом случае, у вас есть то, что вам нужно. Запоминание может показаться ужасным, но большинству предметов физики не нужно запоминать так много уравнений. Я помню, как проходил продвинутый курс электромагнетизма, где мне нужно было запомнить около 20 различных формул. Сначала это казалось ужасным, и я продолжал запоминать их неправильно. Однако чем больше вы используете формулы и чем больше вы понимаете, что они означают, и — если вы достаточно внимательно относитесь к проверке — откуда они взялись, тем легче вам становится их запомнить.
Разложите свои формулы перед собой. Если у вас есть шпаргалка, выровняйте ее рядом с вашими переменными. Какую формулу можно заполнить, оставив наименьшее количество пропущенных переменных? Какая формула поможет вам решить вопрос?
Видишь? Используй это.
Но подождите, какую формулу мне использовать?!
Вы смотрите на свою таблицу формул, и у вас есть три разных формулы, отмеченных под темой задачи. Как узнать какой использовать?? Естественно, вы снова начинаете паниковать.
Не паникуйте.
Физические уравнения не просто приземлились на ученых с неба, все они красиво завернуты в математические формулировки. Они являются производными от физических свойств, и все они взаимосвязаны. В большинстве физических задач существует более одного способа найти решение, что часто означает, что может работать более одного уравнения. На самом деле, в подавляющем большинстве вопросов, независимо от того, какое уравнение вы используете — при условии, что оно имеет отношение к предмету, и что вы вводите правильные переменные — вы найдете решение.
Способ узнать, какое уравнение использовать, зависит от двух основных моментов: переменных, данных вам в уравнении, и вашего опыта. Чем больше проблем вы решите, тем больше вы будете знакомы со стратегиями выбора правильной формулы. Но пока этого не произошло, ищите формулу, в которой есть переменная, которую вы уже знаете (из вашего списка переменных), и которая связывает ее с одной переменной, которой вам не хватает. Если у вас есть две недостающие переменные, вам, скорее всего, понадобятся два уравнения.
Притормози, просмотри свой список переменных и найди нужные. Это как головоломка, и чем больше вы ее делаете, тем лучше у вас получается.
8. Решить
У вас есть свои переменные, у вас есть свой эскиз, вы знаете, что происходит — подключите, решите и получите ответ.
Просто помните: вам может понадобиться решить относительно длинное уравнение, а иногда и два (или больше). Не забывайте о своей цели. Продолжайте просматривать список переменных. 2 единиц, вы допустили ошибку. Если ваш вопрос требует минут, а ваш ответ в секундах, вы пропустили шаг.
2 единиц, вы допустили ошибку. Если ваш вопрос требует минут, а ваш ответ в секундах, вы пропустили шаг.
Внимательно прочитайте инструкции и проверьте свой метод. Это действительно важно.
10. Практика. Упражняться. Упражняться.
Да, да, да, ты сейчас думаешь про себя, держу пари. Все говорят это. Практика делает совершенным. Практикуйтесь, чтобы стать лучше. Как.. очевидно.
Но многим ученикам это не кажется очевидным.
Иногда я получаю изумленные взгляды студентов, которых я обучаю, когда я придумываю идеальный способ решения вопроса, на который они потратили полчаса, пытаясь решить. — Я бы никогда не подумал об этом! — восклицают они в благоговении перед моей гениальностью. Что ж, как бы моему эго ни хотелось принять этот комплимент, я не гений. Причина, по которой я быстро вижу решение, обычно заключается в том, что у меня есть опыт — я задавал так много вопросов, что уже предчувствую, какой метод, скорее всего, сработает лучше всего.
Я всегда прав? Конечно, нет. Иногда я начинаю с одного метода и обнаруживаю, что это неправильный путь. Но эти «ошибки» служат только для того, чтобы научить вас подходить к различным наборам вопросов. Чем больше вы их делаете, тем меньше времени требуется вам, чтобы распознать действительно эффективный способ их решения.
Все дело в опыте. Не паникуйте и не сдавайтесь. Физика менее сложна, чем вы думаете (в большинстве случаев).
Итак, мы попытались разработать метод решения проблем общей физики. Давайте посмотрим, как это работает на практике, выбрав пример вопроса, который я взял из этого онлайн-документа. 92 (трением можно пренебречь) под каким углом к горизонтали тянет человека?
Стратегия
- Не паникуйте.
- Попробуй разобраться в ситуации
В данном случае все довольно просто. Мужчина тянет коробку на полу, только тянет ее под углом. Ящик движется с ускорением вперед. Поскольку нам говорят только об ускорении вперед, нам нужно будет рассмотреть горизонтальные силы (или горизонтальную проекцию) — вертикальная проекция пока не имеет отношения к этой проблеме. 92
92
В этом случае в исходном документе уже есть рисунок, но я намеренно его не включил. Попробуйте нарисовать его самостоятельно. У нас есть ящик, сила тянет его под углом. Вот так:
Теперь мы можем видеть, что мы ожидаем найти, и что у нас уже есть.
Все наши блоки подходят для этого случая. Нет необходимости в преобразованиях.
Вот основные формулы, которые имеют дело с базовыми силами:
- Ф=ма
- (F_{text{x}}=F cos(theta))
- (F_{text{y}}=F sin(theta))
Формулы №2 и №3 представляют собой деконструкцию вектора силы (если вы не знаете, что это значит, вам следует просмотреть материал) – это формулы, связывающие силу (которую мы знаем) с углом (что мы хотим узнать)
Помните нашу часть «Понимание проблемы»? Мы сказали там, что, поскольку ускорение направлено по горизонтали, нам нужно будет рассмотреть горизонтальную силу или проекцию этой силы.
 И мы знаем, что F=ma, что означает, что ускорение является прямым результатом действия силы. Какова тогда сила, действующая на коробку? 9{-1}(frac{7}{8}))
И мы знаем, что F=ma, что означает, что ускорение является прямым результатом действия силы. Какова тогда сила, действующая на коробку? 9{-1}(frac{7}{8})) Что ж, давайте задумаемся об этом на мгновение. Человек тянет веревку под углом. Но проекция (35 Н) не слишком далека от фактической силы, которую он использует (40 Н) — тогда вполне логично, что угол будет относительно небольшим — даже меньше 45 градусов.
Пссс… Вы сделали это!
Не позволяйте предмету увлечь вас еще до того, как вы приступите к нему. Физика кажется ужасно сложной, но большинство ее вопросов базового уровня похожи — как только вы поймете концепцию, вы получите и решение.
Итак, подытожим:
- Не паникуйте.
- Постарайтесь разобраться в ситуации.
- Внимательно прочитайте вопрос.
- Организуйте информацию.
- Нарисуйте сцену.

- Проверка единиц.
- Подумайте о своих формулах.
- Решить.
- Проверьте свои результаты.
- Практика. Упражняться. Упражняться.
Есть. Это было не так уж плохо, не так ли?
Это опыт, уверенность и организованность. Хорошо изучите материал, чтобы понять концепции (даже если вы ненавидите математику) и понять уравнения, которые вам нужно использовать. Решайте задачи терпеливо и организованно, и вы увидите, как вдруг станете хороши в физике. Может быть, даже очень хорошо. Черт возьми, может быть, вы сделаете это своей специальностью в университете!
У вас есть еще какие-нибудь советы о том, как подходить к вопросам физики? Вы сталкиваетесь с проблемами регулярно с определенными типами проблем? Добавьте свой вклад в комментарии!
- UnintentonalChaos за невероятную помощь в редактировании.
- Дэниел Грррррррррррррррррренберг, за его (как всегда) зоркий взгляд и дельный совет.
- Тоби за указание на окончательные исправления, хотя она не очень любит физику (никто не идеален).

- Изображение предоставлено RLHyde из Flickr.
два больших сочных стейка
Как использовать формулу расстояния в физике
Jon Feingersh Photography Inc/Digital Vision Collection/Getty Images
Иногда решения не очевидны. Если вы хотите узнать, как далеко от вас находится объект, вы можете подумать: «Возьмите линейку, линейку, рулетку — все, что может измерять расстояние». Конечно, это сработает, но что, если у вас не было этих инструментов? В этой ситуации на помощь приходит уравнение расстояния в физике!
Физические задачи с формулой расстояния доказывают, что с помощью нескольких фрагментов информации можно решить неизвестную задачу. Теперь вы можете подумать: «Да, но когда мне когда-нибудь понадобится знать расстояние без измерительного инструмента?» Ну, почти любая работа, которая требует от вас постоянного использования физики, например:
- Астроном
- Геофизик
- Оптик
- Инженер
- Патентный поверенный
- Программатор
- Ученый
- Менеджер проекта
Человеческий мозг невероятно пластичен, а это означает, что он может понимать новые концепции, если вы дадите ему возможность. Через какое-то время вашему мозгу уже не понадобится измерительный инструмент, чтобы максимально приблизиться к правильному ответу. Если вы научитесь рассчитывать расстояние в физике, это пригодится ежедневно в любой из вышеперечисленных работ.
Через какое-то время вашему мозгу уже не понадобится измерительный инструмент, чтобы максимально приблизиться к правильному ответу. Если вы научитесь рассчитывать расстояние в физике, это пригодится ежедневно в любой из вышеперечисленных работ.
Можете ли вы привести примеры задач по физике с формулой расстояния?
Пекич / E+ / Getty Images
Абсолютно! Мы покажем вам, как рассчитать расстояние по скорости и времени. Эти три фундаментальных понятия взаимосвязаны и не могут существовать друг без друга. Вы, вероятно, уже понимаете эти концепции, но мы дадим им некоторые определения, прежде чем приступить к некоторым проблемам науки о формулах расстояния.
- Расстояние: насколько далеко два объекта друг от друга
- Скорость: скорость, с которой движется объект
- Время: секунды, минуты, часы и т. д., необходимые для расчета
Теперь, когда у нас есть некоторые рабочие определения, давайте рассмотрим, как рассчитать расстояние в физике.
Поскольку мы ищем расстояние, давайте начнем с него. Уравнение расстояния выглядит следующим образом:
Скорость×Время=Расстояние
Итак, если вы знаете скорость объекта и время, которое он двигался, вы можете использовать эти известные атрибуты, чтобы узнать пройденное расстояние.
Возможно, вы хотите знать, насколько далеко питчер от отбивающего на бейсбольном поле. Вы можете взять измерительный инструмент, например, длинную рулетку, и пройтись по полю, чтобы определить расстояние. Или вы могли бы провести некоторые измерения, которые вы могли бы рассчитать в своей гостиной, просто наблюдая за игрой.
Если вы застряли дома во время пандемии, почему бы не превратить время просмотра в время обучения?
Patrik Giardino / Stone / Getty Images
Во-первых, нам нужно знать, с какой скоростью движется мяч. Эту скорость не так уж сложно вычислить, потому что скорость подачи отображается на экране.
Предположим, что в нашей воображаемой игре с этой физической задачей по формуле расстояния мы только что наблюдали, как питчер бросает мяч с хорошей скоростью, ровно 100 миль в час или 100 миль в час. Большой! У нас есть своя скорость. Но как узнать время?
Большой! У нас есть своя скорость. Но как узнать время?
Допустим, у нас есть сверхточный секундомер. Мы бы определили, что шаг занял 375 миллисекунд или 375 мс. Оба числа должны использовать одну и ту же единицу измерения, поэтому в этом случае мы будем считать часы. Давайте конвертируем миллисекунды в часы, разделив 375 на 1000, чтобы перейти от миллисекунд к секундам:
375 ÷ 1000 = 0,375 секунды
, затем разделите 0,375 на 60 за минуты:
375 000 секунд ÷ 60 = 0,00625 минуты
Разделите на 60 снова на часы:
.
Это не так много времени! Для сравнения, время моргания человека составляет от 300 до 400 миллисекунд, что примерно в четыре раза быстрее, чем самая быстрая игра на гитаре. Не волнуйся; за цифрами будет намного легче следить. Подставьте цифры в нашу формулу:
100 миль в час × 0,00010416666 часов = 0,01041666666 миль
Давайте изменим это на футы, умножив на 5280:
0,01041666666 миль × 5,280 = 55 футов
5 м, которые мы знаем от дома.
Допустим, мы вычисляем, какое расстояние проехал автомобиль за свое путешествие. Мы не знаем расстояния, но знаем скорость и продолжительность пути. Допустим, скорость 50 километров в час или 50 км/ч. Ехал 2 часа. Теперь нам нужно подставить эти цифры в нашу задачу по физике с формулой расстояния:
50 км/ч×2 часа=100 километров
Теперь вы знаете, как найти расстояние в физике!
А как насчет других единиц скорости, времени и расстояния?
Хороший вопрос; это редко бывает резким и сухим. Если вы занимаетесь наукой, вам необходимо знать английские метрические единицы и . Допустим, мы ищем расстояние, пройденное двумя объектами, но нам даны разные измерения каждого из них.
В нашем первом примере мы использовали мили в час для бейсбольного мяча, а затем километры для автомобиля. Они оба использовали часы для времени, но давайте изменим это. Что, если бы нам нужно было сравнить расстояние, пройденное другим транспортным средством, но измерения для этого автомобиля были бы даны нам в милях для расстояния и в секундах для времени?
Снова наша первая машина в задаче физики уравнения расстояния проехала 100 километров. Наша вторая машина ехала со скоростью 100 миль в час (миль в час) в течение 900 секунд.
Наша вторая машина ехала со скоростью 100 миль в час (миль в час) в течение 900 секунд.
У нас есть еще одна проблема , потому что наше время и скорость выражены в разных единицах. Нам нужно преобразовать один из них, чтобы уравнение имело смысл.
Поскольку миля в час — это общепринятая мера скорости автомобиля, давайте изменим время на часы, как мы сделали это раньше с бейсбольным мячом. Сначала разделим 900 на 60, чтобы получить минуты: 9.0005
900÷60=15 минут
Затем разделите 15 на 60, чтобы получить часы:
15÷60=0,25 часа (¼ часа)
Девятьсот секунд равны четверти часа. Теперь мы можем найти расстояние!
100 миль в час × 0,25 часа = 25 миль.
Отлично, проблема с формулой расстояния решена, верно? Не совсем, потому что нам еще предстоит сравнить 100 километров с 25 милями. Мы знаем, что:
1 километр = 0,621371 мили
Давайте конвертируем наши мили в километры, а километры в мили. Мы сделаем это, умножив наше расстояние в 100 км на 0,621371 : 9. 0005
0005
100 километров × 0,621371=62,137 мили
И разделите наши 25 миль на 0,621371:
25 миль÷0,621371=40,233 километра
сравните расстояния, которые преодолели эти вымышленные автомобили, в наших задачах по физике уравнения расстояния.
Что еще мы можем вычислить в физике?
Помните, ранее мы говорили, что расстояние, скорость и время связаны друг с другом? Это правда! Зная любые два из этих измерений, можно найти и остальные.
И хотя хорошо иметь навыки работы с компьютером, иногда вам нужно уже иметь такие понятия в голове. Чтобы найти скорость и время, мы пойдем по уравнениям физики формулы расстояния с других направлений.
Определение скорости
Если вы знаете расстояние и время, но не скорость, вам поможет уравнение:
Расстояние÷Время=Скорость
Вернемся к нашим вымышленным автомобилям из предыдущих уравнений расстояния. Если мы знаем, что наша машина проехала 25 миль и проделала это за 15 минут или 0,25 часа, мы можем составить уравнение следующим образом:
25 миль÷. 25 часов=скорость
25 часов=скорость
25 миль÷.25 часов=100 миль.
Работает! Давайте попробуем это и для нашего метрического автомобиля:
100 километров ÷ 2 часа = 50 км/ч
Работает как шарм. Здесь применяются те же правила относительно эквивалентности измерений во всей формуле.
Нахождение времени
Допустим, мы знаем, с какой скоростью движется автомобиль и как далеко он едет, но мы не знаем, сколько времени это займет. Как и в предыдущих задачах физики с формулой расстояния, если мы знаем два измерения, мы можем найти третье. Возможно, вы не сможете сохраняет время , но вам не нужен ритм, чтобы найти время . Формула времени выглядит следующим образом:
Расстояние÷Скорость=Время Итак, мы знаем, что каждый час машина из нашей задачи по физике уравнения расстояния проезжает 100 миль. Давайте возьмем цифры из нашей задачи и подставим их:
25 миль÷100 миль в час=0,25 часа
И то же самое работает для нашего метрического автомобиля:
100 километров÷50 км/ч=2 часа
Как рассчитать расстояние в физике также можно наглядно продемонстрировать.
Пирамида
Расстояние
÷ ÷
Время × Скорость
. Расстояние находится сверху, потому что, если вы хотите найти одно из двух других измерений, вы всегда хотите разделить расстояние на них. Расстояние, деленное на время, есть скорость, расстояние, деленное на скорость, есть время.
Взгляните на пирамиду выше. Расстояние находится сверху, потому что, если вы хотите найти одно из двух других измерений, вы всегда хотите разделить расстояние на них. Расстояние, деленное на время, есть скорость, расстояние, деленное на скорость, есть время.
Время и скорость умножаются, чтобы найти расстояние. Вы можете скрыть одно из измерений и найти другое. Подставим информацию об автомобиле:
25 миль
÷ ÷
¼ часа × 100 миль в час
Вы можете увидеть их отношения в пирамиде. Умножьте ¼ часа на 100 миль в час, чтобы получить 25 миль. Разделите 25 миль на ¼ часа, чтобы получить 100 миль в час. Разделите 25 миль на 100 миль в час, чтобы получить ¼ часа.
Разделите 25 миль на ¼ часа, чтобы получить 100 миль в час. Разделите 25 миль на 100 миль в час, чтобы получить ¼ часа.
Физика: как понять мир SDI Productions / E+ / Getty Images
О физике и математике можно узнать гораздо больше, и найти учителя, который поможет понять большие понятия, поможет вам стать инженер, ученый или изобретатель.
Понимание физики дает вам представление о том, как силы, управляющие Вселенной, взаимодействуют друг с другом, и такая простая вещь, как научиться вычислять расстояние со скоростью и временем, является началом этого понимания.
Математика может быть сложной; этого никто не отрицает! Но чем больше вы применяете его к физическим проблемам, которые легче обдумать, тем более конкретными будут становиться эти возвышенные идеи.
Практикуйтесь, применяйте уроки к реальным вопросам и наблюдайте, как ваш мозг начинает усваивать эти принципы и трансформирует то, как вы воспринимаете окружающую среду.
