Алгоритмом (algorithm) называют чёткое описание последовательности действий, направленных на решение конкретной задачи. О важности и типах алгоритмических последовательностей сказано уже немало. В этой статье пойдёт речь о способах их представления при записи алгоритмов.

Словесный способ
Словесное описание алгоритма предполагает наличие некого словесного перечня действий. Пример — вам говорят что-то типа следующего: «Вычислите Z при условии, что Z = X + Y, когда X равен 0,89, а Y равен 1,286. Полученное значение Z следует возвести в куб и вычислить корень».
Можно представить ситуацию туристического посещения незнакомого города. Когда вы спрашиваете, как пройти в интересующее место, вам объясняют, что надо через 100 метров повернуть направо, потом пройти прямо, пока не увидите перед собой здание кинотеатра, далее потребуется перейти дорогу, повернуть налево и не сворачивая идти до нужного объекта.
Все эти примеры можно назвать словесным способом представления. У такого способа есть недостаток: отсутствие наглядности выполнения процесса и чёткой формализации объектов алгоритма.
Формульно-словесный способ
При использовании формульно-словесного способа инструкции задаются более чётко. Этот тот случай, когда словесные пояснения сопровождаются перечнем конкретных действий, плюс эти пояснения характеризуются наличием формальных символов и выражений (формул).
Для примера составим формульно-словесный алгоритм вычисления выражения: z=2∙x–(y+6):
• вводим значения х и y;
• находим сумму (y+6);
• находим произведение (2∙x);
• вычисляем z как разность уже полученных выше значений: z=2∙x–(y+6);
• выводим z как результат вычисления выражения.
Это более компактный и лаконичный метод, он нагляднее, но всё же строго формальным не является.
Табличный способ
В случае применения табличного метода алгоритм задаётся в виде входных данных: расчётных форм и таблиц. Способ широко применяется в экономических расчетах. Исходные данные, как и результаты, заносятся в заголовки столбцов используемой таблицы. Простейший пример такого способа представления — та же таблица умножения:
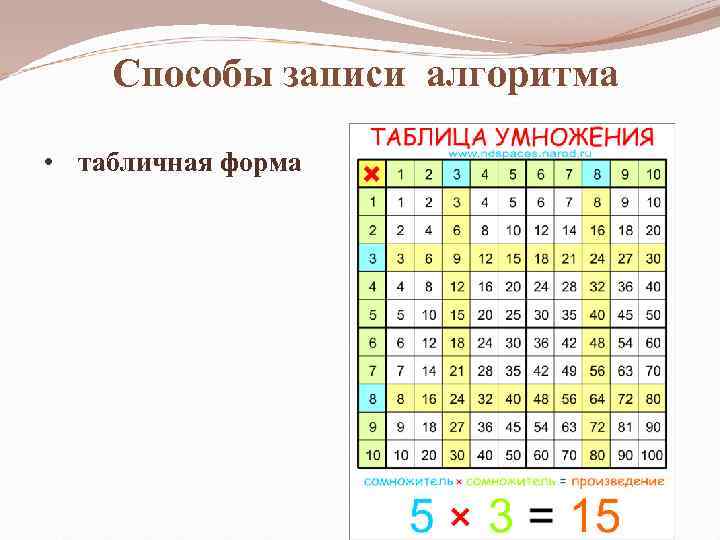
Графический способ
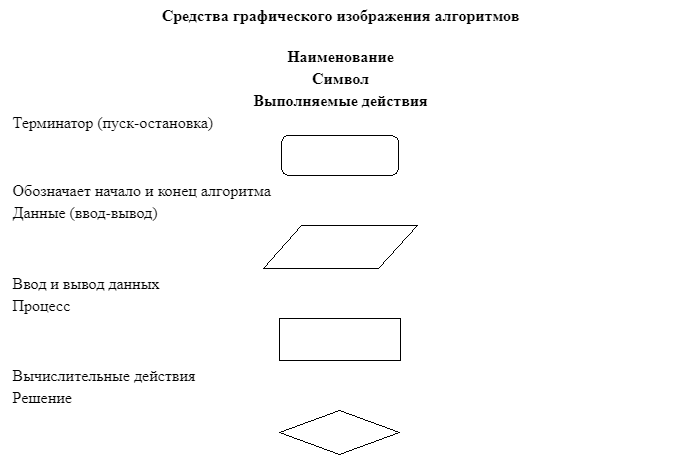
Этот метод ещё называют способом блок-схем. В данной ситуации каждый этап прохождения алгоритма представляется в виде геометрических фигур — так называемых «блоков», причём конкретная форма фигур зависит от выполняемой операции. Существует стандарт, регламентирующий размеры используемых графических блоков, а также их отображение, функции, формы и взаимное расположение. Направление работы алгоритма показывают линии соединения блоков.

Другое название способа — визуальное представление. При проектировании алгоритмов, представленных графически, придерживаются ряда правил:
• в начале алгоритма располагаются блоки ввода значений (входные данные);
• после ввода значений располагаются блоки обработки и блоки условия;
• алгоритм завершается блоками вывода значений, полученных в результате работы алгоритма (выходные данные);
• должен быть лишь один блок начала и один — окончания;
• межблочная связь указывается линиями (направленными либо ненаправленными);
• вычислительные формулы, данные и логические выражения размещаются внутри соответствующих блоков;
• возможно наличие комментариев в виде выносок.
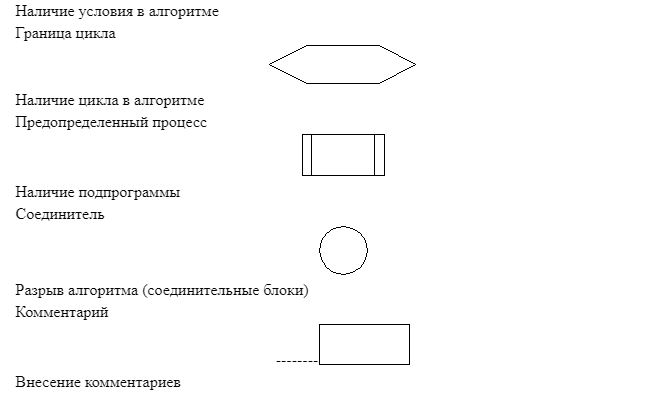
Графический способ представления имеет практическое значение и используется не только в случае программирования. Его применяют при составлении информационных и структурных схем, инфографики и в иных ситуациях, когда нужно обеспечить чёткую визуализацию данных и графически отобразить последовательность расположения объектов алгоритма.
Создание блок-схемы алгоритма — важный и нужный этап решения поставленной задачи. Но при некоторых обстоятельствах этот этап можно считать промежуточным, так как в таком виде описанный алгоритм невозможно выполнить средствами ЭВМ. Зато графический способ представления значительно облегчает процесс дальнейшего создания компьютерной программы. О ней ниже.
Программный способ (текстовая запись)
Программа представляет собой алгоритм, который записан как последовательность команд. Речь идёт о командах, понятных компьютеру, для чего используются различные языки программирования, представляющие собой системы кодирования предписаний с правилами их применения. Языки программирования характеризуются строго определённым синтаксисом, то есть свободное толкование конструкций не допускается.
В случае программного способа представления алгоритмическая последовательность записывается в виде компьютерной программы с высокой степенью формализации. В результате появляется возможность решать прикладные задачи.
Пример — простейший алгоритм сложения 2-ч чисел, который записан средствами языка программирования Qbasic:

О взаимодополнении способов представления
Способы, представленные выше, нередко являются взаимодополняемыми:
— на этапе обсуждения используются словесные и словесно-формульные способы;
— на этапе проектирования рекомендуется использовать графические алгоритмы (графическое представление);
— на этапе проверки возможно табличное описание;
— на этапе непосредственного применения и решения прикладных задач используют текстовую запись, представленную в виде компьютерной программы.

Источники:
• http://csaa.ru/sposoby-predstavlenija-algoritmov-2/;
• https://infourok.ru/konspekt-sposobi-opisaniya-algoritmov-966802.html.
Алгоритмы можно
записывать разными способами, называемыми
формой
представления алгоритма.
На практике наиболее распространены
следующие формы представления алгоритмов:
– словесная
(записи на естественном языке);
– графическая
(изображения из графических символов);
– псевдокоды
(полуформализованные описания алгоритмов
на условном алгоритмическом языке,
включающие в себя как элементы языка
программирования, так и фразы естественного
языка, общепринятые математические
обозначения и др.);
– программная
(тексты на языках программирования).
Словесная форма представления алгоритмов
Словесная
форма записи не так широко распространена
в литературе из-за ее многословности
и отсутствия наглядности.
Рассмотрим
запись алгоритма в словесной форме на
примере алгоритма нахождения максимального
из двух значений:
Определим
форматы переменных X, Y, M, где X и Y –
значения для сравнения, M – переменная
для хранения максимального значения.
-
Получим два
значения чисел X и Y для сравнения; -
сравним X и Y;
-
если X меньше Y,
значит большее число Y; -
поместим в
переменную M значение Y; -
если X не меньше
(больше) Y, значит большее число X; -
поместим в
переменную M значение X.
Как видно из данного
примера словесный способ описания
обладает следующими недостатками:
-
описание строго
не формализуемо; -
запись получилась
многословной; -
отдельные
предписания (действия) допускают
неоднозначность толкования.
Именно эти три
причины не позволили получить широкое
распространение словесной форме записи.
Графический
способ представления алгоритмов
Графический способ
оказался очень удобным средством
изображения алгоритмов и получил
широкое распространение в научной и
учебной литературе.
Структурная (блок-)
схема алгоритма – графическое изображение
алгоритма в виде схемы связанных между
собой с помощью стрелок (линий перехода)
блоков – графических символов, каждый
из которых соответствует одному шагу
алгоритма. Внутри каждого блока дается
описание соответствующего действия.
Графическое
изображение алгоритма широко используется
перед программированием задачи
вследствие его наглядности, т.к.
зрительное восприятие обычно облегчает
процесс написания программы, ее
корректировки при возможных ошибках,
осмысливание процесса обработки
информации.
Можно встретить
даже такое утверждение: «Внешне алгоритм
представляет собой схему – набор
прямоугольников и других символов,
внутри которых записывается, что
вычисляется, что вводится в машину и
что выдается на печать и другие средства
отображения информации». Здесь форма
представления алгоритма смешивается
с самим алгоритмом.
Принцип
программирования «сверху вниз» требует,
чтобы блок-схема поэтапно конкретизировалась
и каждый блок «расписывался» до
элементарных операций. Но такой подход
можно осуществить при решении несложных
задач. При решении сколько-нибудь
серьезной задачи блок-схема «расползется»
до такой степени, что ее невозможно
будет охватить одним взглядом.
Блок-схемы алгоритмов
удобно использовать для объяснения
работы уже готового алгоритма, при этом
в качестве блоков берутся действительно
блоки алгоритма, работа которых не
требует пояснений. Блок-схема алгоритма
должна служить для упрощения изображения
алгоритма, а не для усложнения.
В таблице приведены
наиболее часто употребляемые символы.
|
Название |
Обозначение |
Пояснение |
|
Процесс |
|
Вычислительное |
|
Решение |
|
Проверка |
|
Модификация |
|
Начало |
|
Предопределенный |
|
Вычисления |
|
Ввод-вывод |
|
Ввод-вывод |
|
Пуск-останов |
|
Начало, |
|
Документ |
|
Вывод |
Блок «процесс»
применяется для обозначения действия
или последовательности действий,
изменяющих значение, форму представления
или размещения данных. Для улучшения
наглядности схемы несколько отдельных
блоков обработки можно объединять в
один блок. Представление отдельных
операций достаточно свободно.
Блок «решение»
используется для обозначения переходов
управления по условию. В каждом блоке
«решение» должны быть указаны вопрос,
условие или сравнение, которые он
определяет.
Блок «модификация»
используется для организации циклических
конструкций. (Слово модификация означает
видоизменение, преобразование). Внутри
блока записывается параметр цикла, для
которого указываются его начальное
значение, граничное условие и шаг
изменения значения параметра для
каждого повторения.
Блок «предопределенный
процесс» используется для указания
обращений к вспомогательным алгоритмам,
существующим автономно в виде некоторых
самостоятельных модулей, и для обращений
к библиотечным подпрограммам.
Псевдокод
Псевдокод
представляет собой систему обозначений
и правил, предназначенную для единообразной
записи алгоритмов. Он занимает
промежуточное место между естественным
и формальным языками. С одной стороны,
псевдокод близок к обычному естественному
языку, поэтому алгоритмы могут на нем
записываться и читаться как обычный
текст. С другой стороны, в псевдокоде
используются некоторые формальные
конструкции и математическая символика,
что приближает запись алгоритма к
общепринятой математической записи.
В псевдокоде не приняты строгие
синтаксические правила для записи
команд, присущие формальным языкам,
что облегчает запись алгоритма на
стадии его проектирования и дает
возможность использовать более широкий
набор команд, рассчитанный на абстрактного
исполнителя. Однако в псевдокоде обычно
имеются некоторые конструкции, присущие
формальным языкам, что облегчает переход
от записи на псевдокоде к записи
алгоритма на формальном языке. В
частности, в псевдокоде, так же, как и
в формальных языках, есть служебные
слова, смысл которых определен раз и
навсегда. Они выделяются в печатном
тексте жирным шрифтом, а в рукописном
тексте подчеркиваются. Единого или
формального определения псевдокода
не существует, поэтому возможны различные
псевдокоды, отличающиеся набором
служебных слов и основных (базовых)
конструкций. К таким конструкциям
обычно относят ветвления (если
…то … иначе …)
и циклы (цикл
от … до …,
цикл пока,
цикл до…).
При записи алгоритма
в словесной форме, в виде блок-схемы
или на псевдокоде допускается определенный
произвол при изображении команд. Вместе
с тем такая запись точна настолько, что
позволяет человеку понять суть дела и
исполнить алгоритм.
Однако на практике
в качестве исполнителей алгоритмов
используются специальные автоматы —
компьютеры. Поэтому алгоритм,
предназначенный для исполнения на
компьютере, должен быть записан на
«понятном» ему языке. И здесь на первый
план выдвигается необходимость точной
записи команд, не оставляющей места
для произвольного толкования их
исполнителем. Следовательно, язык для
записи алгоритмов должен быть
формализован. Такой язык принято
называть языком программирования, а
запись алгоритма на этом языке —
программой для компьютера.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
11.02.20156.4 Mб11EVaDi.pdf
- #
Основные понятия алгоритмизации
Работа по решению любой задачи с использованием компьютера делится на следующие этапы:
- Постановка задачи.
- Формализация задачи.
- Построение алгоритма.
- Составление программы на языке программирования.
- Отладка и тестирование программы.
- Использование программы.
Часто эту последовательность называют технологической цепочкой решения задачи. Непосредственно к программированию в этом списке относятся пункты 3, 4, 5.
На этапе постановки задачи должно быть четко сформулировано, что дано и что требуется найти. Здесь очень важно определить полный набор исходных данных, необходимых для получения решения.
Второй этап — формализация задачи. Здесь чаще всего задача переводится на язык математических формул, уравнений, отношений. Если решение требует математического описания какого-то реального объекта, явления или процесса, то формализация равносильна получению соответствующей математической модели.
Третий этап — построение алгоритма. Опытные программисты часто сразу пишут программы на языках, не прибегая к каким-либо специальным способам описания алгоритмов (блок-схемам, псевдокодам). Однако в учебных целях полезно использовать эти средства, а затем переводить полученный алгоритм на язык программирования.
Первые три этапа предусматривают работу без компьютера. Дальше следует собственно программирование на определенном языке, в определенной системе программирования. Последний (шестой) этап — это использование уже разработанной программы в практических целях.
Таким образом, программист должен обладать следующими знаниями и навыками:
- уметь строить алгоритмы;
- знать языки программирования;
- уметь работать в соответствующей системе программирования.
Понятие алгоритма
Одним из фундаментальных понятий в информатике является понятие алгоритма. Происхождение самого термина «алгоритм» связано с математикой. Это слово происходит от Algorithmi — латинского написания имени Мухаммеда альХорезми (787 — 850), выдающегося математика средневекового Востока. В XII в. был выполнен латинский перевод его математического трактата, из которого европейцы узнали о десятичной позиционной системе счисления и правилах арифметики многозначных чисел. Именно эти правила в то время называли алгоритмами. Сложение, вычитание, умножение столбиком, деление уголком многозначных чисел — вот первые алгоритмы в математике.
В наше время понятие алгоритма трактуется шире. Алгоритм — это последовательность команд управления каким-либо исполнителем.
Алгоритм может быть предназначен для выполнения его человеком или автоматическим устройством — формальным исполнителем. Задача исполнителя — точная реализация уже имеющегося алгоритма. Формальный исполнитель не обязан вникать в сущность алгоритма, а возможно, и неспособен его понять.
Примером формального исполнителя может служить автоматическая стиральная машина, которая неукоснительно исполняет предписанные ей действия, даже если вы забыли положить в нее порошок. Человек тоже может выступать в роли формального исполнителя, но в первую очередь формальными исполнителями являются различные автоматические устройства, и компьютер в том числе.
В разделе информатики под названием Программирование изучаются методы программного управления работой ЭВМ. Следовательно, в качестве исполнителя выступает компьютер.
Компьютер работает с величинами — различными информационными объектами: числами, символами, кодами и т.п. Поэтому алгоритмы, предназначенные для управления компьютером, принято называть алгоритмами работы с величинами.
Данные и величины. Совокупность величин, с которыми работает компьютер, принято называть данными. По отношению к программе данные делятся на исходные, результаты (окончательные данные) и промежуточные, которые получаются в процессе вычислений.

Например, при решении квадратного уравнения ах2 + Ьх + с = 0
исходными данными являются коэффициенты а, Ь, с; результатами — корни уравнения х1, х2; промежуточным данным — дискриминант уравнения D = b2 – 4ас.
Для успешного освоения программирования необходимо усвоить следующее правило: всякая величина занимает свое определенное место в памяти ЭВМ (иногда говорят — ячейку памяти). Хотя термин «ячейка» с точки зрения архитектуры современных ЭВМ несколько устарел, однако в учебных целях его удобно использовать.
У всякой величины имеются три основных свойства: имя, значение и тип (на самом деле многие современные языки, такие как PHP или JS, обходятся без явного указания типа, интерпретируя тип переменной в зависимости от контекста операции). На уровне команд процессора величина идентифицируется при помощи адреса ячейки памяти, в которой она хранится. В алгоритмах и языках программирования величины делятся на константы и переменные. Константа — неизменная величина, и в алгоритме она представляется собственным значением, например: 15, 34.7, k, true и т.д. Переменные величины могут изменять свои значения в ходе выполнения программы и представляются символическими именами — идентификаторами, например: X, S2, cod15. Любая константа, как и переменная, занимает ячейку памяти, а значение этих величин определяется двоичным кодом в этой ячейке.
Теперь о типах величин — типах данных. С понятием типа данных вы уже, возможно, встречались, изучая в курсе информатики базы данных и электронные таблицы. Это понятие является фундаментальным для программирования.
В каждом языке программирования существует своя концепция типов данных, своя система типов. Тем не менее в любой язык входит минимально необходимый набор основных типов данных, к которому относятся: целый, вещественный, логический и символьный типы. С типом величины связаны три ее характеристики: множество допустимых значений, множество допустимых операций, форма внутреннего представления. Ниже представлены эти характеристики для основных типов данных.
| Тип | Значения | Операции | Внутреннее представление |
|---|---|---|---|
| Целый | Целые положительные и отрицательные числа в некотором диапазоне. Примеры: 23, —12, 387 |
Арифметические операции с целыми числами: +, —, *, целое деление и остаток от деления. Операции отношений (<, >, = и др.) |
Формат с фиксированной точкой |
| Вещественный | Любые (целые и дробные) числа в некотором диапазоне. Примеры: 2.5, -0.01, 45.0, 3.6-109 |
Арифметические операции: +, —, *, /. Операции отношений |
Формат с плавающей точкой |
| Логический | True (истина), False (ложь) |
Логические операции: И (&), ИЛИ (|), HE (~). Операции отношений | 1 бит: 1 – true; 0 – false |
| Символьный | Любые символы компьютерного алфавита. Примеры: ‘а’, ‘5’, ‘+’, ‘$’ |
Операции отношений | Коды таблицы символьной кодировки. 1 символ – 1 байт (Сейчас используются многобайтные кодировки: UTF-8, UTF-16…) |
Типы констант определяются по контексту (т.е. по форме записи в тексте), а типы переменных устанавливаются в описаниях переменных (не во всех языках; Python, например, не имеет явного определения типа, тип переменной определяетя при первом присваивании).
Есть еще один вариант классификации данных — классификация по структуре. Данные делятся на простые и структурированные. Для простых величин (их еще называют скалярными) справедливо утверждение: одна величина — одно значение, для структурированных: одна величина — множество значений. К структурированным величинам относятся массивы, строки, множества и т.д.
Свойства алгоритма
Массовость — алгоритм решения задачи разрабатывается в общем виде, то есть он должен быть применим для некоторого класса задач, различающихся только исходными данными. При этом исходные данные могут выбираться из некоторой области, которая называется областью применимости алгоритма.
Понятность – команды, используемые в алгоритме, должны быть понятны исполнителю.
Дискретность (прерывность, раздельность) — алгоритм должен представлять процесс решения задачи как последовательное выполнение простых шагов. Каждое действие, предусмотренное алгоритмом, исполняется только после того, как закончилось исполнение предыдущего.
Определенность (детерминнированность) — предполагает получение однозначного результата вычислительного процecca при заданных исходных данных. Благодаря этому свойству процесс выполнения алгоритма носит механический характер.
Результативность (конечность) — алгоритм должен приводить к решению задачи за конечное число шагов.
Формы записи алгоритмов
На практике наиболее распространены следующие формы представления алгоритмов:
- словесная (запись на естественном языке)
- графическая (изображения из графических символов)
- псевдокоды (полуформализованные описания алгоритмов на условном алгоритмическом языке, включающие в себя как элементы языка программирования, так и фразы естественного языка, общепринятые математические обозначения и др.
- программная (тексты на языках программирования)
Пример: написать алгоритм “Одеться по погоде”. Если на улице температура ниже 0, то необходимо надеть шубу, иначе – куртку.
Словесный способ записи алгоритма
Словесный способ записи алгоритмов представляет собой описание последовательных этапов обработки данных. Алгоритм задается в произвольном изложении на естественном языке.
Алгоритм ПОГОДА
Начало
определить температуру воздуха
если температура ниже 0, то надеть шубу, иначе надеть куртку
Конец.
Словесный способ не имеет широкого распространения, так как такие описания:
- строго не формализуемы;
- страдают многословностью записей;
- допускают неоднозначность толкования отдельных предписаний.
Графический способ записи алгоритмов
Наибольшее распространение благодаря своей наглядности получил графический способ записи алгоритмов. При графическом представлении алгоритм изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий.
Такое графическое представление называется схемой алгоритма или блок-схемой. В блок-схеме каждому типу действий (вводу исходных данных, вычислению значений выражений, проверке условий, управлению повторением действий, окончанию обработки и т.п.) соответствует геометрическая фигура, представленная в виде блочного символа. Блочные символы соединяются линиями переходов, определяющими очередность выполнения действий. В таблице приведены наиболее часто употребляемые символы.
| Название символа | Обозначение и пример заполнения | Пояснение |
|---|---|---|
| Процесс |  |
Вычислительное действие или последовательность действий |
| Решение |  |
Проверка условий |
| Модификация |  |
Начало цикла |
| Предопределенный процесс |  |
Вычисления по подпрограмме, стандартной подпрограмме |
| Ввод-вывод |  |
Ввод-вывод в общем виде |
| Пуск-останов |  |
Начало, конец алгоритма, вход и выход в подпрограмму |
| Документ |  |
Вывод результатов на печать |
Блок процесс применяется для обозначения действия или последовательности действий,изменяющих значение, форму представления или размещения данных. Для улучшения наглядности схемы несколько отдельных блоков обработки можно объединять в один блок. Представление отдельных операций достаточно свободно.
Блок решение используется для обозначения переходов управления по условию. В каждом блоке решение должны быть указаны вопрос, условие или сравнение, которые он определяет.
Блок модификация используется для организации циклических конструкций. (Слово модификация означает видоизменение, преобразование). Внутри блока записывается параметр цикла, для которого указываются его начальное значение, граничное условие и шаг изменения значения параметра для каждого повторения.
Блок предопределенный процесс используется для указания обращений к вспомогательным алгоритмам, существующим автономно в виде некоторых самостоятельных модулей, и для обращений к библиотечным подпрограммам.
Блок Ввод-вывод используется для преобразования данных в форму, пригодную для обработки (ввод) или отображения результатов обработки (вывод). Отдельным логическим устройствам компьютера или отдельным функциям обмена соответствуют определенные блочные символы. В каждом из них указываются тип устройства или файла данных, тип информации, участвующий в обмене, а также вид операции обмена.
Блок Пуск-останов используется для обозначения начала, конца, прерывания процесса обработки данных или выполнения программы.
Блок Документ предназначен для ввода-вывода данных, носителем которых служит бумага.

Псевдокод
Псевдокод представляет собой систему обозначений и правил, предназначенную для единообразной записи алгоритмов.
Псевдокод занимает промежуточное место между естественным и формальным языками. С одной стороны, он близок к обычному естественному языку, поэтому алгоритмы могут на нем записываться и читаться как обычный текст. С другой стороны, в псевдокоде используются некоторые формальные конструкции и математическая символика, что приближает запись алгоритма к общепринятой математической записи.
В псевдокоде не приняты строгие синтаксические правила для записи команд, присущие формальным языкам, что облегчает запись алгоритма на стадии его проектирования и дает возможность использовать более широкий набор команд, рассчитанный на абстрактного исполнителя.
Однако в псевдокоде обычно имеются некоторые конструкции, присущие формальным языкам, что облегчает переход от записи на псевдокоде к записи алгоритма на формальном языке. В частности, в псевдокоде, так же, как и в формальных языках, есть служебные слова, смысл которых определен раз и навсегда. Они выделяются в печатном тексте жирным шрифтом, а в рукописном тексте подчеркиваются.
Единого или формального определения псевдокода не существует, поэтому возможны различные псевдокоды, отличающиеся набором служебных слов и основных (базовых) конструкций.
Программный способ записи алгоритмов
При записи алгоритма в словесной форме, в виде блок-схемы или на псевдокоде допускается определенный произвол при изображении команд. Вместе с тем такая запись точна настолько, что позволяет человеку понять суть дела и исполнить алгоритм.
Однако на практике в качестве исполнителей алгоритмов используются специальные автоматы – компьютеры. Поэтому алгоритм, предназначенный для исполнения на компьютере, должен быть записан на понятном ему языке. И здесь на первый план выдвигается необходимость точной записи команд, не оставляющей места для произвольного толкования их исполнителем.
Следовательно, язык для записи алгоритмов должен быть формализован. Такой язык принято называть языком программирования, а запись алгоритма на этом языке – программой для компьютера.
Программа, создаваемая человеком – программистом, представляет собой текст, состоящий из знаков, как правило букв, цифр и специальных знаков. Знаки в тексте программы часто объединены в последовательности – ключевые слова, слова объединены в предложения языка программирования – операторы. Каждый оператор, как правило, записывается в отдельную строку текста программы.
Таким образом текстовое программирование представляет собой иерархическую последовательность знаков, слов, операторов, записываемых и читаемых последовательно, как обычный текст человеческой письменности.
//Пример программы на языке C# namespace oap { class Program { static void Main(string[] args) { Console.WriteLine("введите температуру воздуха t: "); var t = int.Parse( Console.ReadLine() ); if (t < 0) Console.WriteLine("одеть шубу"); else Console.WriteLine("одеть куртку"); } } }
Структурное программирование
Запись алгоритмов решения сложных задач в любой форме, в том числе в виде блок-схемы, может быть слишком объемной и сложной. Поэтому на практике используют некоторые методы, облегчающие построение и реализацию алгоритмов.
Одним из наиболее распространенных является метод структурного программирования, или конструирование алгоритмов методом последовательной детализации. При пошаговой детализации алгоритмы записываются в виде множества вспомогательных алгоритмов, решающих вспомогательные подзадачи, а каждая из них требует получения определенных промежуточных результатов.
Разработав основной алгоритм, можно приступить к разработке алгоритмов «второго уровня», которые, в свою очередь, могут требовать дальнейшей детализации. Процесс детализации продолжается до тех пор, пока не будут написаны все нужные вспомогательные алгоритмы. Таким образом, основной алгоритм представляет собой план действий, которые необходимо выполнить для достижения поставленной цели, а суть каждого действия расшифровывается в соответствующем вспомогательном алгоритме.
Каждый вспомогательный алгоритм описывает способ решения некоторой вспомогательной задачи или даже общий способ решения некоторого класса вспомогательных подзадач.
Для реализации вспомогательных алгоритмов служат подпрограммы, или процедуры. Подпрограмма — часть алгоритма (программы), оформленная в виде, допускающем многократное обращение к ней из разных точек программы. Обращение к подпрограмме — переход к выполнению подпрограммы с заданием информации, необходимой для ее выполнения и возврата.
Общие принципы построения алгоритмов
При разработке алгоритма используют следующие основные принципы.
Принцип поэтапной детализации алгоритма (другое название — “проектирование сверху-вниз”). Этот принцип предполагает первоначальную разработку алгоритма в виде укрупненных блоков (разбиение задачи на подзадачи) и их постепенную детализацию.
Принцип “от главного к второстепенному”, предполагающий составление алгоритма, начиная с главной конструкции. При этом, часто, приходится “достраивать” алгоритм в обратную сторону, например, от середины к началу.
Принцип структурирования, т.е. использования только типовых алгоритмических структур при построении алгоритма. Нетиповой структурой считается, например, циклическая конструкция, содержащая в теле цикла дополнительные выходы из цикла. В программировании нетиповые структуры появляются в результате злоупотребления командой безусловного перехода (GoTo). При этом программа хуже читается и труднее отлаживается.
Определение сложности работы алгоритмов
Существует несколько способов измерения сложности алгоритма. Программисты обычно сосредотачивают внимание на скорости алгоритма, но не менее важны и другие показатели – требования к объёму памяти, свободному месте на диске. Использование быстрого алгоритма не приведёт к ожидаемым результатам, если для его работы понадобится больше памяти, чем есть у компьютера.
Память или время
Многие алгоритмы предлагают выбор между объёмом памяти и скоростью. Задачу можно решить быстро, использую большой объём памяти, или медленнее, занимая меньший объём.
Типичным примером в данном случае служит алгоритм поиска кратчайшего пути. Представив карту города в виде сети, можно написать алгоритм для определения кратчайшего расстояния между двумя любыми точками этой сети. Чтобы не вычислять эти расстояния всякий раз, когда они нам нужны, мы можем вывести кратчайшие расстояния между всеми точками и сохранить результаты в таблице. Когда нам понадобится узнать кратчайшее расстояние между двумя заданными точками, мы можем просто взять готовое расстояние из таблицы.
Результат будет получен мгновенно, но это потребует огромного объёма памяти. Карта большого города может содержать десятки тысяч точек. Тогда, описанная выше таблица, должна содержать более 10 млрд. ячеек. Т.е. для того, чтобы повысить быстродействие алгоритма, необходимо использовать дополнительные 10 Гб памяти.
Из этой зависимости проистекает идея объёмно-временной сложности. При таком подходе алгоритм оценивается, как с точки зрении скорости выполнения, так и с точки зрения потреблённой памяти.
Мы будем уделять основное внимание временной сложности, но, тем не менее, обязательно будем оговаривать и объём потребляемой памяти.
Оценка порядка
При сравнении различных алгоритмов важно знать, как их сложность зависит от объёма входных данных. Допустим, при сортировке одним методом обработка тысячи чисел занимает 1 с., а обработка миллиона чисел – 10 с., при использовании другого алгоритма может потребоваться 2 с. и 5 с. соответственно. В таких условиях нельзя однозначно сказать, какой алгоритм лучше.
В общем случае сложность алгоритма можно оценить по порядку величины. Алгоритм имеет сложность O(f(n)), если при увеличении размерности входных данных N, время выполнения алгоритма возрастает с той же скоростью, что и функция f(N). Рассмотрим код, который для матрицы A[NxN] находит максимальный элемент в каждой строке.
for i:=1 to N do begin max:=A[i,1]; for j:=1 to N do begin if A[i,j]>max then max:=A[i,j] end; writeln(max); end;
В этом алгоритме переменная i меняется от 1 до N. При каждом изменении i, переменная j тоже меняется от 1 до N. Во время каждой из N итераций внешнего цикла, внутренний цикл тоже выполняется N раз. Общее количество итераций внутреннего цикла равно N*N. Это определяет сложность алгоритма O(N2).
Оценивая порядок сложности алгоритма, необходимо использовать только ту часть, которая возрастает быстрее всего. Предположим, что рабочий цикл описывается выражением N3+N. В таком случае его сложность будет равна O(N3). Рассмотрение быстро растущей части функции позволяет оценить поведение алгоритма при увеличении N. Например, при N=100, то разница между N3+N=1000100 и N=1000000 равна всего лишь 100, что составляет 0,01%.
При вычислении O можно не учитывать постоянные множители в выражениях. Алгоритм с рабочим шагом 3N3 рассматривается, как O(N3). Это делает зависимость отношения O(N) от изменения размера задачи более очевидной.
Определение сложности
Наиболее сложными частями программы обычно является выполнение циклов и вызов процедур. В предыдущем примере весь алгоритм выполнен с помощью двух циклов.
Если одна процедура вызывает другую, то необходимо более тщательно оценить сложность последней. Если в ней выполняется определённое число инструкций (например, вывод на печать),то на оценку сложности это практически не влияет. Если же в вызываемой процедуре выполняется O(N) шагов, то функция может значительно усложнить алгоритм. Если же процедура вызывается внутри цикла, то влияние может быть намного больше.
В качестве примера рассмотрим две процедуры: Slow со сложностью O(N3) и Fast со сложностью O(N2).
procedure Slow; var i,j,k: integer; begin for i:=1 to N do for j:=1 to N do for k:=1 to N do //какое-то действие end; procedure Fast; var i,j: integer; begin for i:=1 to N do for j:=1 to N do Slow; end; procedure Both; begin Fast; end;
Если во внутренних циклах процедуры Fast происходит вызов процедуры Slow, то сложности процедур перемножаются. В данном случае сложность алгоритма составляет O(N2)*O(N3)=O(N5).
Если же основная программа вызывает процедуры по очереди, то их сложности складываются:
O(N2)+O(N3)=O(N3).
Следующий фрагмент имеет именно такую сложность:
procedure Slow; var i,j,k: integer; begin for i:=1 to N do for j:=1 to N do for k:=1 to N do {какое-то действие} end; procedure Fast; var i,j: integer; begin for i:=1 to N do for j:=1 to N do {какое-то действие} end; procedure Both; begin Fast; Slow; end;
Сложность рекурсивных алгоритмов
Простая рекурсия
Рекурсивными процедурами называются процедуры, которые вызывают сами себя. Их сложность определить довольно тяжело. Сложность этих алгоритмов зависит не только от сложности внутренних циклов, но и от количества итераций рекурсии. Рекурсивная процедура может выглядеть достаточно простой, но она может серьёзно усложнить программу, многократно вызывая себя.
Рассмотрим рекурсивную реализацию вычисления факториала:
function Factorial(n: Word): integer; begin if n > 1 then Factorial:=n*Factorial(n-1) else Factorial:=1; end;
Эта процедура выполняется N раз, таким образом, вычислительная сложность этого алгоритма равна O(N).
Многократная рекурсия
Рекурсивный алгоритм, который вызывает себя несколько раз, называется многократной рекурсией. Такие процедуры гораздо сложнее анализировать, кроме того, они могут сделать алгоритм гораздо сложнее.
Рассмотрим такую процедуру:
procedure DoubleRecursive(N: integer); begin if N>0 then begin DoubleRecursive(N-1); DoubleRecursive(N-1); end; end;
Поскольку процедура вызывается дважды, можно было бы предположить, что её рабочий цикл будет равен O(2N)=O(N). Но на самом деле ситуация гораздо сложнее. Если внимательно исследовать этот алгоритм, то станет очевидно, что его сложность равна O(2(N+1)-1)=O(2N).
Всегда надо помнить, что анализ сложности рекурсивных алгоритмов весьма нетривиальная задача.
Объёмная сложность рекурсивных алгоритмов
Для всех рекурсивных алгоритмов очень важно понятие объёмной сложности. При каждом вызове процедура запрашивает небольшой объём памяти, но этот объём может значительно увеличиваться в процессе рекурсивных вызовов. По этой причине всегда необходимо проводить хотя бы поверхностный анализ объёмной сложности рекурсивных процедур.
Средний и наихудший случай
Оценка сложности алгоритма до порядка является верхней границей сложности алгоритмов. Если программа имеет большой порядок сложности, это вовсе не означает, что алгоритм будет выполняться действительно долго. На некоторых наборах данных выполнение алгоритма занимает намного меньше времени, чем можно предположить на основе их сложности. Например, рассмотрим код, который ищет заданный элемент в векторе A.
function Locate(data: integer): integer; var i: integer; fl: boolean; begin fl:=false; i:=1; while (not fl) and (i<=N) do begin if A[i]=data then fl:=true else i:=i+1; end; if not fl then i:=0; Locate:=i; end;
Если искомый элемент находится в конце списка, то программе придётся выполнить N шагов. В таком случае сложность алгоритма составит O(N). В этом наихудшем случае время работы алгоритма будем максимальным.
С другой стороны, искомый элемент может находится в списке на первой позиции. Алгоритму придётся сделать всего один шаг. Такой случай называется наилучшим и его сложность можно оценить, как O(1).
Оба эти случая маловероятны. Нас больше всего интересует ожидаемый вариант. Если элемента списка изначально беспорядочно смешаны, то искомый элемент может оказаться в любом месте списка. В среднем потребуется сделать N/2 сравнений, чтобы найти требуемый элемент. Значит сложность этого алгоритма в среднем составляет O(N/2)=O(N).
В данном случае средняя и ожидаемая сложность совпадают, но для многих алгоритмов наихудший случай сильно отличается от ожидаемого. Например, алгоритм быстрой сортировки в наихудшем случае имеет сложность порядка O(N2), в то время как ожидаемое поведение описывается оценкой O(N*log(N)), что много быстрее.
Общие функции оценки сложности
Сейчас мы перечислим некоторые функции, которые чаще всего используются для вычисления сложности. Функции перечислены в порядке возрастания сложности. Чем выше в этом списке находится функция, тем быстрее будет выполняться алгоритм с такой оценкой.
- C – константа (время выполнения алгоритма не зависит от входных параметров, линейные алгоритмы)
- log(log(N))
- log(N) – (поиск в сортированном массиве)
- NC, 0<C<1
- N – линейная сложность (поиск в не сортированном массиве)
- N*log(N)
- NC, C>1
- CN, C>1
- N!
Если мы хотим оценить сложность алгоритма, уравнение сложности которого содержит несколько этих функций, то уравнение можно сократить до функции, расположенной ниже в таблице. Например, O(log(N)+N!)=O(N!).
Если алгоритм вызывается редко и для небольших объёмов данных, то приемлемой можно считать сложность O(N2), если же алгоритм работает в реальном времени, то не всегда достаточно производительности O(N).
Обычно алгоритмы со сложностью N*log(N) работают с хорошей скоростью. Алгоритмы со сложностью NC можно использовать только при небольших значениях C. Вычислительная сложность алгоритмов, порядок которых определяется функциями CN и N! очень велика, поэтому такие алгоритмы могут использоваться только для обработки небольшого объёма данных.
В заключение приведём таблицу, которая показывает, как долго компьютер, осуществляющий миллион операций в секунду, будет выполнять некоторые медленные алгоритмы.
| Сложность | N=10 | N=20 | N=30 | N=40 | N=50 |
|---|---|---|---|---|---|
| N3 | 0.001 c | 0.008 c | 0.027 c | 0.064 c | 0.125 c |
| 2N | 0.001 c | 1.05 c | 17.9 мин | 1.29 дней | 35.7 лет |
| 3N | 0.059 c | 58.1 мин | 6.53 лет | 3.86*105 лет | 2.28*1010 лет |
| N! | 3.63 c | 7.71*104 лет | 8.41*1018 лет | 2.59*1034 лет | 9.64*1050 лет |
Википедия: Временная сложность алгоритма
КОНТРОЛЬНЫЕ ВОПРОСЫ
-
Этапы решения задачи на компьютере? Охарактеризуйте их. Проиллюстрируйте этапы постановки и формализации на примере задачи: вычислить время движения моторной лодки между двумя пунктами.
-
Понятие алгоритма.
-
Основные типы данных.
-
Свойства алгоритма.
-
Формы записи алгоритмов.
-
Что такое структурное программирование? Каковы основные прнципы структурной методики построения алгоритмов?
У этого термина существуют и другие значения, см. Блок.
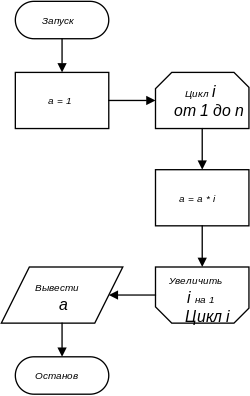
Блок-схема — распространённый тип схем (графических моделей), описывающих алгоритмы или процессы, в которых отдельные шаги изображаются в виде блоков различной формы, соединённых между собой линиями, указывающими направление последовательности.
Основные элементы схем алгоритма[править | править код]
При начертании элементов рекомендуется придерживаться строгих размеров, определяемых двумя значениями a и b. Значение a выбирается из ряда 15, 20, 25.. мм, b рассчитывается из соотношения 2⋅a = 3⋅b. Определение размеров несёт рекомендательный характер, однако, при соблюдении выполнения размеров блок-схемы имеют более аккуратный вид.
Действие[править | править код]
Символ отображает функцию обработки данных любого вида (выполнение определённой операции или группы операций, приводящее к изменению значения, формы или размещения информации или к определению, по которому из нескольких направлений потока следует двигаться).

Данные (ввод-вывод)[править | править код]
Символ отображает данные, носитель данных не определён.

Преобразование данных в форму, пригодную для обработки (ввода) или отображения результатов обработки (вывода). Данный символ не определяет носителя данных (для указания типа носителя данных используются специфические символы).
Предопределённый процесс (функция)[править | править код]
Символ отображает предопределённый процесс, состоящий из одной или нескольких операций или шагов программы, которые определены в другом месте (в подпрограмме, модуле). Например, в программировании − вызов процедуры или функции.
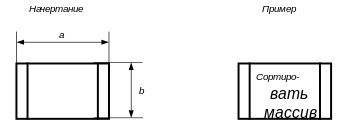
Вопрос (условие или решение)[править | править код]
Символ отображает решение или функцию переключательного типа, имеющую один вход и ряд альтернативных выходов, один и только один из которых может быть активизирован после вычисления условий, определённых внутри этого символа. Соответствующие результаты вычисления могут быть записаны по соседству с линиями, отображающими эти пути.

Отображает решение или функцию переключательного типа с одним входом и двумя или более альтернативными выходами, из которых только один может быть выбран после вычисления условий, определённых внутри этого элемента. Вход в элемент обозначается линией, входящей обычно в верхнюю вершину элемента. Если выходов два или три, то обычно каждый выход обозначается линией, выходящей из оставшихся вершин (боковых и нижней). Если выходов больше трёх, то их следует показывать одной линией, выходящей из вершины (чаще нижней) элемента, которая затем разветвляется. Соответствующие результаты вычислений могут записываться рядом с линиями, отображающими эти пути. Примеры решения: в общем случае — сравнение (три выхода: >, <, =); в программировании — условные операторы if (два выхода: true, false) и case (множество выходов).
Ограничитель[править | править код]
Символ отображает вход из внешней среды и выход во внешнюю среду (начало или конец схемы программы, внешнее использование и источник или пункт назначения данных).

На практике имеют смысл следующие описания ограничителей: начало/конец, запуск/останов, перезапуск (подразумевает перезапуск данной блок-схемы), ошибка (подразумевает завершение алгоритма с ошибкой), исключение (подразумевает исполнение программного исключения)
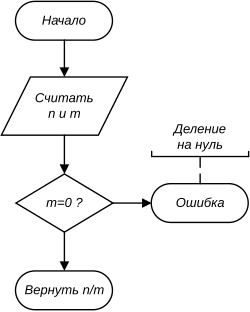
Цикл[править | править код]
Символ, состоящий из двух частей, отображает начало и конец цикла. Обе части символа имеют один и тот же идентификатор. Условия для инициализации, приращения, завершения и т. д. помещаются внутри символа в начале или в конце в зависимости от расположения операции, проверяющей условие.
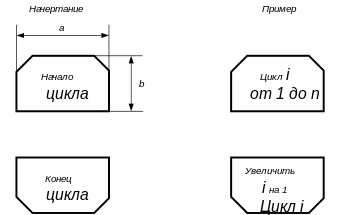
Пример блок-схемы расчёта факториала с использованием цикла[править | править код]

Пример вложенных циклов[править | править код]

Соединитель[править | править код]
Символ отображает выход в часть схемы и вход из другой части этой схемы и используется для обрыва линии и продолжения её в другом месте. Соответствующие символы-соединители должны содержать одно и то же уникальное обозначение.

Разделение алгоритма на две части с использованием соединителей[править | править код]

Комментарий[править | править код]
Символ используют для добавления описательных комментариев или пояснительных записей в целях объяснения или примечаний. Пунктирные линии в символе комментария связаны с соответствующим символом или могут обводить группу символов. Текст комментариев или примечаний должен быть помещён около ограничивающей фигуры.
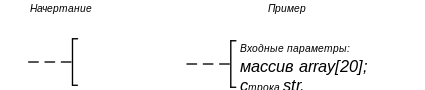
Также символ комментария следует использовать в тех случаях, когда объём текста, помещаемого внутри некоего символа (например, символ процесса, символ данных и др.), превышает размер самого этого символа.
Комментарии используют совместно с терминаторами для описания входных аргументов алгоритма при описании функций.
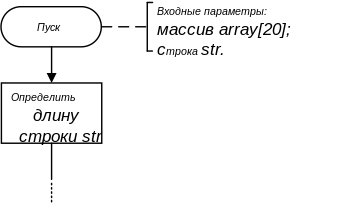
Параллельные действия[править | править код]
Символ представляется двумя параллельными линиями, отображает синхронизацию двух или более параллельных операций. В случае входа нескольких операций в параллельные линии, выполнение алгоритма будет продолжено только в случае окончания всех входящих процессов.

Параллельные действия могут быть использованы для асинхронных процессов или для процессов, последовательность которых не важна. В представленном примере стоит обратить внимание, что созданные в одних параллельных линиях процессы не обязаны также параллельно заканчиваться.
Описание других элементов схем можно найти в соответствующих ГОСТ[1]. Среди элементов существуют:
- Запоминаемые данные
- Документ
- Ручной ввод
- Карта
- Дисплей
- Передача управления
- Альтернативная связь между двумя или более символами
- и др.
Представление алгоритмов в виде графов[править | править код]
Порядок выполнения действий задаётся путём соединения вершин дугами, что позволяет рассматривать блок-схемы не только как наглядную интерпретацию алгоритма, удобную для восприятия человеком, но и как ориентированный граф (т. н. граф-схема алгоритма, ГСА). Подобное представление алгоритмов используется при построении систем логического управления, реализующих заданные управляющие алгоритмы, в задачах распараллеливания вычислений и так далее.
Критика[править | править код]
Распространённой и ошибочной практикой является попытка использования блок-схем для иллюстрации алгоритма на низком уровне (на уровне кода) — то есть попытка вписывать в блоки схемы фрагменты кода на каком-либо искусственном языке. Такой подход применим только к программам, организованным согласно структурному подходу, и не может отразить, к примеру, алгоритм, который реализуется во взаимодействии абстракций при объектно-ориентированном подходе. Для целей описания алгоритмов, взаимодействия частей системы и иллюстрации многих других сопутствующих вещей существует нотация UML [источник не указан 943 дня].
Примечания[править | править код]
- ↑ ГОСТ 19.701-90. Схемы алгоритмов, программ, данных и систем. Условные обозначения и правила выполнения. Дата обращения: 23 мая 2007. Архивировано 1 июня 2007 года.
Выделяют три наиболее распространенные на практике способа записи алгоритмов:
- словесный (запись на естественном языке);
- графический (запись с использованием графических символов);
- программный (тексты на языках программирования).
Словесный способ записи алгоритмов
Словесный способ – способ записи алгоритма на естественном языке. Данный способ очень удобен, если нужно приближенно описать суть алгоритма. Однако при словесном описании не всегда удается ясно и точно выразить логику действий.
В качестве примера словесного способа записи алгоритма рассмотрим алгоритм нахождения площади прямоугольника
S=a*b,
где S – площадь прямоугольника; а, b – длины его сторон.
Очевидно, что a, b должны быть заданы заранее, иначе задачу решить невозможно.
Словестный способ записи алгоритма выглядит так:
- Начало алгоритма.
- Задать численное значение стороны a.
- Задать численное значение стороны b.
- Вычислить площадь S прямоугольника по формуле S=a*b.
- Вывести результат вычислений.
- Конец алгоритма.
Графический способ описания алгоритмов
Для более наглядного представления алгоритма используется графический способ. Существует несколько способов графического описания алгоритмов. Наиболее широко используемым на практике графическим описанием алгоритмов является использование блок-схем. Несомненное достоинство блок схем – наглядность и простота записи алгоритма.
Каждому действию алгоритма соответствует геометрическая фигура (блочный символ). Перечень наиболее часто употребляемых символов приведен в таблице:
| Название символа | Обозначение и пример заполнения |
Пояснения |
| Пуск-останов | Начало, завершение алгоритма или подпрограммы | |
| Ввод-вывод данных | |
Ввод исходных данных или вывод результатов |
| Процесс | |
Внутри прямоугольника записывается действие, например, расчетная формула |
| Решение |  |
Проверка условия, в зависимости от которого меняется направление выполнения алгоритма |
| Модификация |  |
Организация цикла |
| Предопределенный процесс | |
Использование ранее созданных подпрограмм |
| Комментарий | |
Пояснения |
Пояснения:
- блок Процесс обозначает вычислительный процесс и применяется для обозначения действия или последовательности действий, изменяющих значения переменных или данных

- блок Решение обозначает проверку условия

Если условие выполняется, то есть a>b, то следующим выполняется действие по стрелке «Да». Если условие не выполняется, то осуществляется переход по стрелке «Нет».
- блок Модификация используется для организации циклических (повторяющихся) действий.

- блок Предопределенный процесс используется для указания обращений к ранее созданным алгоритмам и программам, в том числе и библиотечным подпрограммам.
- блок Ввод-Вывод. При решении задачи на компьютере ввод исходных данных может осуществляться различными способами, например, с клавиатуры, с жесткого диска, с флэш-карты т. д. Задание численных значений исходных данных называется вводом, а отображение результатов расчета на экране монитора или с помощью принтера на бумаге – выводом. Если ввод-вывод не привязан к конкретному устройству, то обозначается параллелограммом. Если необходимо указать конкретное устройство ввода или вывода, то используются специальные геометрические фигуры.
В качестве примера графического способа описания алгоритмов с помощью блок-схем запишем алгоритм нахождения площади прямоугольника:

Внутри каждого блока записывается соответствующее действие. Последовательность выполнения задается соединительной линией со стрелочкой.
Последовательность выполнения сверху вниз и слева направо принята за основную.
Если в алгоритме не нарушается основная последовательность, то стрелочки можно не указывать. В остальных случаях последовательность выполнения блоков обозначается стрелочкой обязательно. В нашем примере основная последовательность выполнения – сверху вниз.
Программный способ записи алгоритмов
Способ записи алгоритмов с помощью блок-схем нагляден и точен для понимания сути алгоритма, тем не менее, алгоритм предназначен для исполнения на компьютере, а язык блок-схем компьютер не воспринимает. Поэтому алгоритм должен быть записан на языке, понятном компьютеру с абсолютно точной и однозначной записью команд.
Таким образом, алгоритм должен быть записан на каком-то промежуточном языке, с точными и однозначными правилами и отличном от естественного языка и языка блок-схем, но понятном компьютеру. Такой язык принято называть языком программирования.
Программный способ записи алгоритма – это запись алгоритма на языке программирования, позволяющем на основе строго определенных правил формировать последовательность предписаний, однозначно отражающих смысл и содержание алгоритма, с целью его последующего исполнения на компьютере.
|
Запись алгоритма на языке программирования называется компьютерной программой. |

