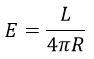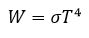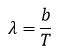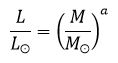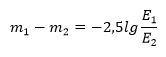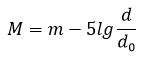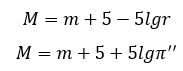Как найти звездную величину скопления

Звездная величина или блеск – это безразмерная величина, характеризующая видимость космического объекта на ночном небе. Обозначается буквой m, что пошло от латинского magnitude – величина, размер. Звездная величина зависит как от физических свойств объекта, так и от расстояния до него.

История

Считается, что понятие звездой величины ввел Гиппарх Никейский. Однако, письменных подтверждений этому нет. Гиппарх составил первый каталог звезд, где разделили их на шесть величин – по яркости на небе, где первая – самые яркие, шестая – самые тусклые – предел человеческого восприятия невооруженным глазом.

Птолемей описал данную систему в Альмогесте, тем самым дав ей широкую огласку.

Норман Погсон в 1856 году ввел ясность в определение звездных величин, обозначив звезды первой величины в 100 раз ярче чем звезды шестой величин. Тем самым введя логарифмическую шкалу. Такой ее вид используется и по ныне.

В качестве эталонной звезды изначально была принятая Полярная, ее видимая звездная величина была определена как 2,00m. Но с развитием телескопов, стало понятно, что Полярная – переменная звезда, ее видимая величина меняется со временем. Тогда, в качестве эталона взяли Вегу, приняв ее звездную величину равную 0,00m.

В современной шкале используется и отрицательные звездные величины, так как под их описание попадают и планеты, и Луна, и Солнце.

Классификация звездных величин

В зависимости от спектральной чувствительности приемника (глаза, фотопластины, фотодетектора и т.п.) можно выделить 5 звездных величин:

• болометрическая – распространяется на весь спектр излучения, на все длины волн. Удобна, когда основная часть излучения звезды находится не в видимом спектре;
• визуальная – распространяется только на видимую часть спектра, максимум восприятия приходится на 555 нм (зеленый цвет);
• синяя – распространяется только на синюю часть спектра, как следует из названия, максимум восприятия приходится на 445 нм;
• ультрафиолетовая – распространяется на ультрафиолетовый спектр излучения с максимумом на 350 нм;
• фотографическая – показывает видимую звездную величину, если бы чувствительность человеческого глаза совпадала с чувствительностью фотоприбора. Максиму приходится на 425 нм.

Видимая звездная величина

Тем самым, исторически, видимая звездная величина – это сугубо человеческая характеристика яркости космического объекта на звездном небе и опирается она на чувствительность человеческого глаза.

Но в настоящее время, для определения видимой звездой величины используется логарифмические зависимости, основываясь на освещенности (отношение светового потока к площади на которую он падает) от этих объектов.

Абсолютная звездная величина

Абсолютная звездная величина уравнивает все объекты на одно расстояние, то есть, абсолютная звездная величина звезды – это видимая величина светила, если бы оно находилось на расстоянии 10 персек (32, 616 световых лет), без учета атмосферного или межзвездного поглощения.

Абсолютная звездная величина планет Солнечной системы – видимая величина на расстоянии 1 астрономической единицы от наблюдателя.

Для метеоров – видимая звездная величина, если бы метеор находился на расстоянии 100 км в зените.

Если же космический объект по своим размерам больше 10 парсек (галактика, туманность, звездное скопление), то тогда этот объект считают, как точечный объект, со суммарной светимостью.

Применение звездных величин

В астрономии используются все виды звездных величин, в зависимости от характера объекта и тех данных, которые надо сравнить. Особых предпочтений ученые не делают. Зная видимую и абсолютные звездные величины можно рассчитать расстояние до объекта.

Видимые звёздные величины различных объектов

1. Видимая звёздная величина. При первоначальном знакомстве со звёздным небом (§ 2) мы рассмотрели понятие «звёздная величина» (m). Вы уже знаете, что звёзды 1-й звёздной величины создают в 2,512 раза большую освещённость (отношение светового потока к площади, им освещаемой), чем звёзды 2-й звёздной величины, которые, в свою очередь, дают световые потоки в 2,512 раза больше, чем звёзды 3-й звёздной величины, и т. д. Таким образом, за интервал в одну видимую звёздную величину (обозначается 1m) принято отношение освещённостей (Е) в 2,512 раза. В виде формулы эти соотношения выразил Н. Погсон:

формула (1)

Измеряя при помощи фотометра отношение блеска звёзд, можно определить разность звёздных величин по формуле Погсона. Нуль-пункт же выбирают условно, по соглашениям. При этом договорено, чтобы стандартная звезда 1-й звёздной величины (средняя из 20 самых ярких звёзд) давала бы в 100 раз больше света, чем звезда 6-й звёздной величины, находящаяся на пределе зрения.

Видимая звёздная величина Луны в полнолуние равна -12,7m, а в фазе первой четверти составляет -9,0m. По формуле (1) можем найти, что освещённость Луны в полнолуние (Еп) больше освещённости Луны в фазе первой четверти (Е1) в 30 раз:

Метод параллакса

Видимую звёздную величину Солнца определил Витольд Карлович Цераский. Она оказалась равной -26,8m. Шкала звёздных величин позволяет выражать в звёздных величинах блеск слабых светил, невидимых невооружённым глазом. В настоящее время крупнейшие телескопы с диаметром зеркал 8—10 м и современной приёмной аппаратурой позволяют регистрировать объекты до 28-й звёздной величины.

2. Определение расстояний до звёзд. Учёные давно предполагали, что звёзды имеют такую же физическую природу, как и Солнце. Из-за колоссальных расстояний диски звёзд не видны даже в сильные телескопы. Чтобы сравнивать звёзды между собой и с Солнцем, необходимо найти методы определения расстояний до них. Основным методом является метод параллактического смещения звёзд, рассмотренный нами ранее. Так как радиус Земли слишком мал по сравнению с расстоянием до звёзд, необходимо выбрать больший базис для измерения параллактического смещения звёзд. Ещё Н. Коперник понимал, что, согласно его гелиоцентрической системе, близкие звёзды на фоне далёких звёзд должны описывать эллипсы в результате годового движения Земли вокруг Солнца.

Рис. 122. Параллактическое смещение звезды на протяжении года: С — Солнце; М — звезда; а — полуось земной орбиты; π — годичный параллакс

Кажущееся перемещение более близкой звезды М на фоне очень далеких звезд происходит по эллипсу с периодом в 1 год и отражает движение наблюдателя вместе с Землей вокруг Солнца (рис. 122). Положение Земли на орбите и видимые с Земли положения звезды на небе прослеживаются на рисунке 122.
Маленький эллипс, описываемый звездой, называется параллактическим эллипсом. В угловой мере большая полуось этого эллипса равна величине угла, под которым со звезды видна большая полуось земной орбиты, перпендикулярная направлению на звезду. Этот угол называется годичным параллаксом (π). Параллактические смещения звезд служат неопровержимым доказательством обращения Земли вокруг Солнца.

Расстояния до звезд определяются по их годичному параллактическому смещению. Из рисунка 122 видно, что если СТ = а — средний радиус земной орбиты, СМ = r — расстояние до звезды М от Солнца С, а угол π — годичный параллакс звезды, то

 ​( r=frac{a}{sin(pi)} ).​

Так как годичные параллаксы звёзд оцениваются десятичными долями секунды, а 1 радиан равен 206265″, то расстояние до звезды можно определить из соотношения

формула (2).

Для измерения расстояний до звёзд астрономическая единица слишком мала. Поэтому для удобства определения расстояний до звёзд в астрономии применяется специальная единица длины — парсек (пк), название которой происходит от слов «параллакс» и «секунда». Парсек — это расстояние, с которого радиус земной орбиты был бы виден под углом в 1″.
Согласно формуле (2), 1 _пк = 206 265 а. е. = 3,086 • 10¹³ км. Таким образом, расстояние до звёзд в парсеках будет определяться выражением

формула (3).

В астрономических единицах обычно выражаются расстояния до тел Солнечной системы. Расстояния до небесных тел, находящихся за пределами Солнечной системы, обычно выражаются в парсеках, килопарсеках (1 _кпк = 10³ пк) и мегапарсеках (1 _Мпк = 10⁶ пк), а также в световых годах (1 св. г. = 9,46 • 10¹² км = 63 240 а. е. = 0,3067 пк или 1 _пк = 3,26 св. г.). Световой год — расстояние, которое электромагнитное излучение (в вакууме) проходит за один год.

Нижний предел измерений параллаксов не превышает 0,005″, что позволяет определять расстояния не свыше 200 пк. Расстояния до ещё более далёких объектов определяются менее точно и иными методами.

3. Абсолютная звёздная величина. Видимый блеск звёзд не характеризует их реального излучения. Он определяется двумя факторами: истинным излучением звезды и расстоянием до неё. Солнце, например, гораздо ближе к Земле, чем любая другая звезда, поэтому оно — самое яркое светило на небе. Следовательно, для сравнения истинного блеска звёзд необходимо вычислять их звёздную величину на определённом одинаковом расстоянии. За такое одинаковое (или стандартное) расстояние принято 10 пк. Видимая звёздная величина, которую имела бы звезда, если бы находилась от нас на расстоянии 10 пк, называется абсолютной звёздной величиной.

Рис. 123. Что такое парсек?

Пусть видимая звёздная величина звезды на расстоянии r равна m, а освещённость, создаваемая этой звездой, — E. По определению, видимая звёздная величина с расстояния r₀ = 10 пк будет равна абсолютной звёздной величине М, а Е₀ — освещённость (или излучение) звезды с расстояния 10 пк. Тогда, используя формулу (1), можем записать: ​( frac{E}{E_0}=2.512^{M-m} )​ формула (4).

Из физики известно, что освещённости, создаваемые одним и тем же источником излучения, обратно пропорциональны квадратам расстояний до него, т. е.  ( frac{E}{E_0}= frac{R_0^2}{r^2} ) формула (5).

Подставляя (5) в (4), получим, что ​( 2.512^{M-m}=frac{100}{r^2} )​. Прологарифмировав данное равенство и упростив его, получим:

формула (6).

Учитывая, что ​( r=frac{1}{pi} )​, формулу (6) можно записать в виде:

формула (7).

По формуле (6) вычислим абсолютную звёздную величину Солнца. Расстояние до Солнца ​( r=1_{a.e.}=frac{1}{206265}пк );​видимая звёздная величина Солнца равна -26,8^m. После подстановки этих значений в формулу получим, что М_{( bigodot )} = -26,8^m + 5^m + 26,6^m = 4,8^m. Это означает, что со стандартного расстояния в 10 пк Солнце выглядит слабой звёздочкой почти 5-й звёздной величины. Абсолютные звёздные величины звёзд колеблются от -9^m до 19^m, т. е. отличаются на 28^m, или по освещённости в 160 миллиардов раз, друг от друга.

4. Светимость звёзд. Зная абсолютную звёздную величину звезды, можно вычислить действительное общее излучение звезды или её светимость. Светимостью называется полная энергия, излучаемая звездой за 1 с. Светимость звезды можно выразить в ваттах, но чаще её выражают в светимостях Солнца. Напомним, что светимость Солнца равна 3,85 • 10²⁶ Вт (см. § 19).
Используя формулу (1), можно записать соотношение между светимостями и абсолютными звёздными величинами какой-либо звезды и Солнца:

формула (8),

где L и L_{( bigodot )} — светимости звезды и Солнца; М и М_{( bigodot )} — соответственно их абсолютные звёздные величины. Если принять L_{( bigodot )} = 1 и с учётом того, что М = 4,8^m, формула (8) примет вид:

или

или или через логарифм:

Если абсолютная звёздная величина определена другим способом, например по спектру звезды, то из формулы M = m + 5 – 5·lg(r) можно найти расстояние до звезды:

Звёзды-сверхгиганты, имеющие М = -9^m, обладают мощностью излучения больше Солнца в 330 тыс. раз, а самые неяркие звёзды с абсолютной звёздной величиной М = 19^m излучают свет в 480 тыс. раз слабее Солнца.

Главные выводы
1. Звёзды движутся в пространстве и находятся от нас на различных расстояниях.
2. Видимая звёздная величина — мера наблюдаемого блеска (освещённости, создаваемой светилом на приёмнике лучистой энергии) небесного объекта, видимого с Земли. Интервал в одну звёздную величину соответствует разности освещённостей в 2,512 раза.
3. Расстояние до недалёких звёзд определяется методом годичного параллакса, основанного на измерении угла, под которым виден радиус земной орбиты с исследуемой звезды.
4. Единицами измерения расстояний до звёзд являются парсек и световой год.
5. Абсолютная звёздная величина — видимая звёздная величина, которую имела бы звезда, находясь на стандартном расстоянии 10 пк.
6. Полная энергия, излучаемая звездой по всем направлениям за единицу времени, называется её светимостью. Обычно светимость звезды выражается в единицах светимости Солнца.

Контрольные вопросы и задания

1. Что понимают под годичным параллаксом звезды?
2. Что такое парсек и световой год?
3. Чем отличается абсолютная звездная величина от видимой звездной величины?
4. Что понимают под светимостью звезды? Какова светимость Солнца?
5. Какая зависимость существует между светимостью звезды и ее абсолютной звездной величиной?
6. Расстояние до звезды Бетельгейзе 652 св. г. Чему равен ее параллакс?
7. Вычислите расстояние до звезды Веги в парсеках и световых годах, если известно, что ее видимая и абсолютная звездные величины соответственно равны 0^m,0 и 0^m,5.
8. Абсолютная звездная величина Солнца равна М = 5^m. Определите расстояние, на котором оно будет наблюдаться как звезда 15-й звездной величины.
9. Звездное скопление содержит 100 звезд одинакового блеска m = 8^m. Найдите суммарную звездную величину скопления.

Проверь себя

Выбор тем

Абсолютная и видимая звездная величина светила

В этой статье собраны задачи на определение абсолютной и видимой звездной величины светил,  подобранные Шатовской Натальей Евгеньевной, учителем школы 179 г. Москвы.

Задача 1.

а) Сколько слабых звёзд () может заменить по блеску одну звезду ? одну звезду ? одну звезду ?

Отношение блеска  и  двух светил связано с их видимой звездной величиной и  формулой Погсона:

Для звёзд :

Для звёзд :

Для звёзд :

Ответ: одну звезду могут заменить 100 звезд ; одну звезду могут заменить 40 звезд ; одну звезду могут заменить 16 звезд .

б) Сколько звёзд может заменить по блеску Венеру ()?

Ответ: 10000.

в) Лучшим современным наземным телескопам доступны объекты до . Во сколько раз более слабые объекты могут они зафиксировать по сравнению с невооружённым глазом?

Ответ: в раз.

Задача 2.

Во сколько раз ярчайшая звезда Сириус () превосходит по блеску вторую по яркости звезду Вегу ()?

Ответ: в 4,9 раза.

Задача 3.

Звёздная величина Солнца , звёздная величина полной Луны . Во сколько раз освещённость, создаваемая Солнцем, больше освещённости, создаваемой полной Луной (при одинаковой высоте светил над горизонтом)?

Здесь тоже можно воспользоваться той же формулой Погсона:

Ответ: в 437 тыс. раз.

Задача 4.

При наблюдении с Земли Альдебаран и Альтаир имеют одинаковую видимую звёздную величину ().  Во сколько раз отличаются их светимости, если расстояние до Альдебарана 21 пк, а до Альтаира – 5 пк?

Где   – светимость Альдебарана,   – Альтаира, – расстояние до Альдебарана, – до Альтаира. Отношение блесков будет равно 1 вследствие равенства видимых звёздных величин.

Поэтому

Ответ: почти в 18 раз.

Задача 5.

Какова звёздная величина Солнца при наблюдении его с Плутона, находящегося на среднем расстоянии 40 а.е.?

Светимость звезд вычисляется по их абсолютной звездной величине , которая связана с видимой звездной величиной соотношениями

Тогда

Ответ: .

Задача 6.

Абсолютной называется звёздная величина светила при наблюдении его со стандартного расстояния 10 пк. Вычислите абсолютную величину Солнца, если видимая с Земли его звёздная величина составляет .

Ответ: .

Задача 7.

а) Вычислите абсолютную звёздную величину Сириуса, если его параллакс , а видимая звёздная величина .

Абсолютная звездная величина связана с видимой звездной величиной соотношением

Ответ: .

б) Вычислите абсолютную звёздную величину Антареса, если его параллакс , а видимая звёздная величина .

Ответ: .

Задача 8.

Какова абсолютная звёздная величина звезды Альтаир ( Орла), имеющей видимую звёздную величину и находящейся на расстоянии 16,8 св. лет?

Расстояние в 16,8 св. лет – это парсека.

Ответ: .

Задача 9.

Определите максимальное расстояние, с которого Солнце ещё можно видеть невооружённым глазом.

Глаз различает звезды . Надо определить, с какого расстояния видимая звездная величина Солнца такова.

Ответ: с расстояния в 17,62 парсека.

Задача 10.

Какая из двух звёзд ярче на земном небе: звезда видимой звёздной величины или звезда с абсолютной величиной , находящаяся на расстоянии 100 пк от Земли?

Определим видимую звездную величину второй звезды:

Звезда, видимая звездная величина которой меньше, видна лучше.

Ответ: вторая видна лучше.

Задача 11.

Телескопу доступны звёзды до . Можно ли с его помощью зарегистрировать шаровое скопление из миллиона звезд, подобных Солнцу, находящееся в соседней галактике на расстоянии 10 Мпк от нас?

Определяем видимую звездную величину звезды, подобной Солнцу, с расстояния 10 Мпк:

Блеск одной звезды

Блеск миллиона звезд будет

Видимая звездная величина скопления

Следовательно, в такой телескоп это скопление можно увидеть.

Ответ: да.

Задача 12.

В некотором созвездии расстояние между звёздами Альфа и Бета на небесной сфере составляет , а их звёздные величины равны и соответственно. Известно, что абсолютные звёздные величины этих звёзд одинаковы. Какую звёздную величину будет иметь звезда Альфа, если смотреть на неё из окрестностей звезды Бета?

Так как абсолютные звездные величины одинаковы, определим отношение расстояний до этих звезд.

Тогда

 Или

По теореме косинусов расстояние между и

По формуле Погсона

Ответ: .

Задача 13.

Видимая с Земли звёздная величина планеты в противостоянии на  меньше, чем в соединении. Какая это планета?

Во-первых,  планета внешняя – противостояние возможно для внешних планет. Пусть – расстояние от Земли до этой планеты в противостоянии, а – в соединении. Тогда а.е., и по формуле Погсона

Следовательно,

На такое расстояние – 0,5 а.е. – подходит к Земле Марс во время противостояний.

Ответ: Марс.

Задача 14.

Вследствие эллиптичности орбит Земли и Луны видимый с Земли угловой диаметр Солнца изменяется от 31’31” до 32’36”, а Луны – от 29’20” до 33’32”. На сколько изменяется наблюдаемая звёздная величина Солнца в ходе самого яркого кольцеобразного затмения? Потемнением солнечного диска к краю пренебречь.

Линейные размеры светил пропорциональны угловым. Видимые звездные величины пропорциональны блеску, а тот – зависит от светимости. То есть видимая звездная величина Солнца соответствует угловому размеру 32’36” – полноразмерному Солнцу, а во время затмения часть диска Солнца закроет Луна и площадь поверхности уменьшится, и пропорционально этой площади уменьшится видимая звездная величина. Самое яркое затмение – при наибольшем угловом диаметре Солнца и наименьшем – Луны. Тогда , и

Откуда

Следовательно, видимая звездная величина изменяется на

Ответ: на .

Звезда — массивный газовый шар, излучающий свет и удерживаемый силами собственной гравитации и внутренним давлением, в недрах которого происходят (или происходили ранее) реакции термоядерного синтеза.

Физические характеристики звезд

Звезды представляются нам светящимися точками. Одни из них видны лучше, другие едва различимы невооруженным глазом, третьи видны только в телескоп. Единственной характеристикой звезды, которую можно измерить, является освещенность, создаваемая звездой на земной поверхности.

где E– освещенность, L– светимость, R – расстояние до звезды.

Зная освещенность и расстояние до звезды, можно определить ее светимость, одну из основных ее характеристик. Светимости звезд лежат в очень широких пределах. У большинства звезд светимость меньше солнечной (у самых маломощных в миллион раз), а у белых или голубых сверхгигантов в десятки тысяч раз больше.

Согласно закону Стефана-Больцмана,

W – энергия, излучаемая поверхностью в 1 м² за 1 с,

σ = 5,67·10^-8 Вт/(м²·К⁴) – постоянная Стефана-Больцмана,

T – температура поверхности.

Вся поверхность звезды равна 4πR², поэтому светимость звезды определяется выражением

L = 4πR²·σT⁴

Зная светимость и температуру, можно определить радиус звезды. С помощью самых мощных телескопов и специальных наблюдений удалось получить изображения дисков звезд, которые совпали с вычисленными по формуле светимости.

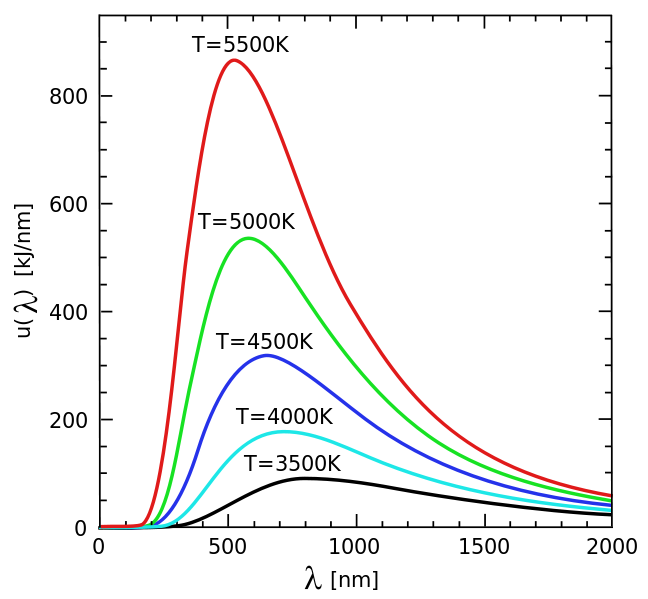
Внимательный наблюдатель заметит, что звезды имеют разный цвет. Цвет звезды определяется ее температурой, что следует из закона Вина

Положение максимума излучения определяет цвет звезды.

Спектральные классы — классификация звёзд по спектру излучения, в первую очередь, по температуре фотосферы. Различия в спектрах звезд обусловливаются различием физических свойств их атмосфер, в основном, температуры и давления (определяющих степень ионизации атомов).

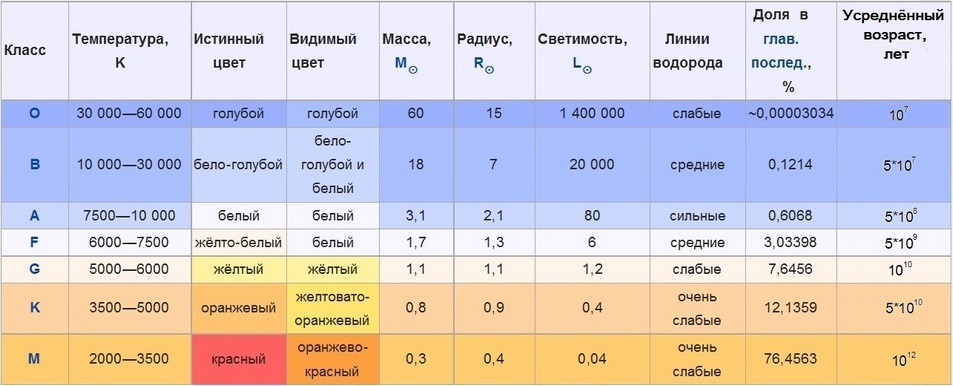
Солнце относится к спектральному классу G, имеет температуру поверхности фотосферы 5700 К.

Вскоре после открытия спектрального анализа ученые смогли определить и истинный химический состав звезд. Он оказался удивительно одинаковым. Во всех звездах преобладающими элементами по массе являются водород (около 65%) и гелий (около 35%). На долю всех остальных элементов приходится не более 1% массы звезды.

Химический состав зависит и от возраста. В самых старых звездах количество тяжелых (тяжелее гелия) элементов не превышает 0,1%, в самых молодых доходит до 4%. Это очень важно для теории эволюции звезд, галактик и Вселенной.

Массы звезд лежат в очень узких пределах. Если светимости могут быть 10^-4L_ʘ < L< 10⁴L_ʘ, радиусы от 0,01R_ʘ  до 3·10³R_ʘ, то массы всего от 0,02 M_ʘ  до 100 M_ʘ. Тело меньшей массы уже не является звездой, а большей не может существовать и уже при возникновении либо сбросит избыточную массу, либо распадется на несколько.

Сопоставление масс, радиусов и светимостей показывает, что между ними есть связь.

Соотношение масса – светимость – уравнение, показывающее зависимость этих величин для звезд главной последовательности.

a = 3,5 для звезд главной последовательности с массами 2М_ʘ < M< 20M_ʘ. Не применима к красным гигантам и белым карликам.

Чем больше масса звезды на главной последовательности, тем больше ее радиус и светимость и выше эффективная температура. По этой причине звезды ранних спектральных классов (О, B, A, F) лежат левее Солнца на диаграмме Герцшпрунга-Рессела (цвет-светимость), так как цвет (спектральный класс) звезды определяется ее эффективной температурой.

R~M^α

где 0 < α < 1, для звезд главной последовательности α = 0,75.

Наблюдаемые характеристики звезд

Видимая звёздная величина (m) — мера яркости небесного тела (точнее, освещённости, создаваемой этим телом) с точки зрения земного наблюдателя. Чем ярче объект, тем меньше его звёздная величина.

Уточнение «видимая» указывает только на то, что эта звёздная величина наблюдается с Земли; это уточнение нужно, чтобы отличить её от абсолютной. Оно не указывает на видимый диапазон: видимыми называют и величины, измеренные в инфракрасном или каком-либо другом диапазоне.

Оказалось, что изменение блеска на одну звездную величину соответствует изменению светового потока в 2,512 раза.

m₁ иm₂ –звездные величины объектов, E₁ и E₂– освещенности от этих объектов.

Принято, что Вега (α Лиры) имеет звездную величину, равную 0^m. Более яркие светила имеют отрицательную звездную величину.

Абсолютная звёздная величина (M) для звёзд определяется как видимая звёздная величина объекта, если бы он был расположен на расстоянии 10 парсек от наблюдателя. Абсолютная болометрическая (учитывающая полное излучение во всех диапазонах электромагнитных волн) звёздная величина Солнца +4,8.

Если известна видимая звёздная величина m и расстояние до объекта d, можно вычислить абсолютную звёздную величину по формуле:

где d₀= 10 пк ≈ 32,616 световых лет.

Зная расстояние до звезды r в парсеках или годичный параллакс π΄΄ в секундах можно рассчитать абсолютную звездную величину по формулам:

Видимая и абсолютная звездная величина некоторых звезд

Звезда	Видимая величина	Абсолютная величина
Вега	0,04	0,5
Ригель	0,11	-7
Полярная	2,3	-4,6
Сириус	-1,45	1,41
Процион	0,37	2,64
Тау Кита	3,5	5,2
Солнце	-26,74	4,83

 

Задачи

Крупнейшим наземным телескопам (в частности, двум самым большим в мире 10-метровым телескопам Кека) доступны звезды 28^m. Во сколько раз они слабее звезд, едва различимых невооруженным глазом?

Переменная o Cet (Мира Кита) в максимуме имеет визуальный блеск -2,5^m, в минимуме -9,2^m. Во сколько примерно раз меняется ее светимость в видимом диапазоне?

Разность звездных величин двух звезд одинаковой светимости равна 2,5^m. Во сколько раз одна из них дальше другой?

Где светлее – днем на Плутоне или в лунную ночь на Земле?

Из вещества Луны в полнолуние сделали миллион одинаковых сферических спутников, оставив их примерно в том же месте, но так, чтобы они не затеняли друг друга. Какова звездная величина получившегося роя? Звездная величина полной Луны вам известна.

Двойная звезда имеет компоненты 2^m и 3^m. Найти суммарную звездную величину двойной.

Затменно-двойная система имеет одинаковые компоненты. На сколько звездных величин меняется блеск системы в момент полного затмения одной компоненты другой?

В звездном скоплении N звезд звездной величины m каждая. Найти суммарную звездную величину скопления.

На небе около 6000 звезд ярче 6-й звездной величины. Считая, что у всех звезд одинаковая светимость и что они распределены в пространстве равномерно, оценить, сколько на небе звезд ярче m-й звездной величины.

* На каком примерно расстоянии надо поместить 100-ваттную лампочку, чтобы она выглядела как звезда 0-й звездной величины?

* Можно ли с Луны невооруженным глазом увидеть города на Земле?

* Один из четырех галилеевых спутников Юпитера – Европа – имеет радиус 1600 км и полностью покрыт льдом. Оцените звездную величину Европы в тот момент, когда Юпитер ближе всего к Земле.

Оцените максимальное расстояние (в пк), с которого Солнце еще видно невооруженным глазом.

В 1987 году в Большом Магеллановом облаке вспыхнула сверхновая звезда, которая в максимуме имела видимую звездную величину m = +3. Определить абсолютную звездную величину сверхновой, если расстояние до БМО R = 52 кпк.

Во сколько раз отличаются светимости двух звезд одинакового цвета, если радиус одной из них больше, чем другой, в 25 раз?

Во сколько раз красный гигант больше красного карлика, если их светимости отличаются в 100 раз?

Параллакс Солнца p₀ = 8″,8, а видимый угловой радиус Солнца примерно 30′. Во сколько раз радиус Солнца больше радиуса Земли?

Фотографические абсолютные звездные величины М цефеид с периодом свыше 40 дней достигают –7 звездной величины. Определить расстояние до ближайшей галактики, если такая цефеида наблюдается как звезда с видимой звездной величиной +18. 

Источники:

https://ru.wikipedia.org/wiki/

http://www.astronet.ru/db/msg/

Порфирьев В.В., Астрономия: Учебник для 11 кл. – М.: Просвещение, 2004 – 174 с.: ил.

http://www.astro.spbu.ru/staff/viva/Book/ch4L/node8.html

Звездными
скоплениями
называются гравитационно связанные
системы звезд, выделяющиеся как области
повышенной звездной плотности. По
внешнему виду звездные скопления делятся
на две группы: рассеянные
скопления,
содержащие несколько десятков и сотен
звезд, и шаровые
скопления,
состоящие из десятков и сотен тысяч
звезд.

Рисунок 6.2. Рассеянное скопление «Плеяды».

Рисунок 6.3. Шаровое скопление в созвездии Центавра.

Рассеянные звездные
скопления встречаются вблизи галактической
плоскости. Всего известно более 1500 таких
объектов в радиусе нескольких килопарсеков
от Солнца. Наиболее известны рассеянное
звездное скопление Плеяды (рис. 6.2),
удаленное от нас на расстояние 120 пс,
и Гиады, которое находится в сорока пяти
парсеках от нас.

 Чтобы отделить
звезды, принадлежащие скоплению, от
звезд поля, случайно проектирующихся
в ту же область неба, можно построить
диаграмму спектр-светимость. Для
скоплений обычно строят диаграмму
цвет-видимая звездная величина, откладывая
по осям показатель цвета (вместо
спектрального класса) и видимую
звездную
величину, которая одинаково для всех
звезд скопления отличается от абсолютной.

Рисунок 6.4. Диаграмма «цвет-звездная величина» для рассеянного скопления NGC 2254.

Рисунок 6.5. Диаграмма «цвет-видимая звездная величина» для шарового звездного скопления М3.

На диаграмме
спектр-светимость для рассеянных
скоплений,
как правило, хорошо заметна главная
последовательность. Ветвь гигантов в
большинстве случаев отсутствует или
почти отсутствует.
Поскольку все звезды скопления практически
находятся на одинаковом расстоянии,
его диаграмма цвет-видимая звездная
величина (рис. 6.4) отличается от обычной
сдвигом по вертикальной оси на величину
модуля расстояния, а из-за влияния
межзвездного поглощения света (см .§
6.4),
и по горизонтальной оси. Ясно, что звезды,
не попадающие на “свои” места на
диаграмме, могут не принадлежать
скоплению.

Проверить
принадлежность этих звезд скоплению
можно, изучив их собственные движения
и лучевые скорости. Если звезды относятся
к одному и тому же скоплению, то собственные
движения всех звезд должны пересекаться
в одной точке — радианте скопления.
Тогда, зная угол 
между направлением на звезду скопления
и на радиант, а также лучевую скорость
звезды v_r
и ее собственное движение ,
можно найти расстояние до звезды (в
парсеках), а, значит, и до скопления:

.

(6.7)

Рассмотренный
метод определения расстояний до скоплений
называется методом
группового параллакса.

Коль скоро расстояние
до звездного скопления установлено,
легко вычислить его линейные размеры,
которые для большинства рассеянных
скоплений в среднем составляют от 2 до
20 пс.

В отличие от
рассеянных, шаровые
звездные скопления
сильно выделяются на окружающем фоне
благодаря значительно большему числу
входящих в них звезд и четкой своей
сферической или эллиптической форме,
обусловленной сильной концентрацией
звезд к центру (рис. 6.3). В среднем диаметры
шаровых скоплений составляют около 40
пс.
Вследствие своей большой светимости
шаровые скопления видны на больших
расстояниях в нашей Галактике. Поэтому
наблюдаемое их число близко к общему
числу этих объектов в Галактике. Шаровые
скопления обнаружены также и в ближайших
к нам других галактиках (например, в
Магеллановых Облаках, туманности
Андромеды).

 Диаграмма
цвет-видимая звездная величина для
звезд шаровых звездных скоплений имеет
особый вид (рис. 6.5). На ней обычно четко
выделяется характерная для шаровых
скоплений горизонтальная ветвь, ветвь
гигантов, соединяющаяся с главной
последовательностью, и сама главная
последовательность, начинающаяся в
области меньших светимостей, чем на
обычной диаграмме Герцшпрунга-Рессела.
В шаровых скоплениях часто наблюдается
значительное количество переменных
звезд, особенно типа RR
Лиры, которые позволяют определить
расстояния до этих объектов.

В 1947 г. В.А.
Амбарцумяном и его сотрудниками были
обнаружены наиболее молодые звездные
группировки, названные звездными
ассоциациями.
В них входят звезды определенного типа,
а их звездная плотность заметно больше
средней звездной плотности звезд того
же типа в Галактике.

Известны два типа
ассоциаций. Первый — О-B
ассоциации —
содержит звезды ранних спектральных
классов О и В. Их. Их размеры составляют
десятки и сотни парсеков, т.е. во много
pаз
превышают
размеры рассеянных звездных скоплений.
Ассоциации второго типа состоят из
звезд типа Т Тельца и поэтому называются
Т-ассоциациями.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #