Разделы:
Математика
Класс:
9
В школьный курс математики включена новая
содержательная линия – элементы статистики,
комбинаторики и теории вероятностей. Включение в
курс алгебры элементарных сведений из
статистики имеет важное общеобразовательное
значение, так как без этих знаний невозможно
разобраться в разнообразной информации.
Простейшие методы обработки и анализа
статистических данных являются главной целью
урока по теме “Варианты и их кратности”.
Использование информационных технологий на
данном уроке позволило отразить поэтапность
проведения урока, сконцентрировать внимание на
основных моментах и объективно оценить знания
учащихся за более короткий срок.
Цель:
- Ввести понятие варианта, показать примеры
обработки статистических данных, используя
введенные понятия. - Закрепить навыки решения комбинаторных задач
простейшего типа; - Повторить понятия и определения комбинаторики.
Девиз урока:
Не нужно нам владеть клинком.
Не ищем славы громкой
Тот побеждает, кто знаком
С искусством мыслить, тонким.
1. Оргмомент.
Сегодня по всей стране проходит “День
здоровья”, поэтому на уроке нам предстоит
выяснить насколько мы выносливы.
2. Разминка.
- Исход эксперимента или наблюдения которого при
реализации данного комплекса условий может
произойти, а может и не произойти? (случайное
событие) - Событие, которое при реализации данного
комплекса условий непременно произойдет?
(достоверное событие) - Событие, которое заведомо не может произойти
при реализации данного комплекса условий.
(невозможное) - Размещения, отличающиеся друг от друга только
порядком расположения элементов. (перестановки) - Выборки, составляемые из элементов, не
отличающиеся по своему объему, но отличающиеся
по составу хотя бы одним элементом. (сочетания с
повторениями)
3. Проверка домашнего задания.
А) 1 ряд “Ловкачи”: выполняет тест по
вариантам, затем взаимопроверка по готовым
ответам.
Б) 3 ряда “Прыжки в длину”: 2 человека с
работают у доски с домашними задачами,
2 человека работают по карточкам. (задачи), 1
человек на интердоске выполняет задание
| Сколькими способами в игре “Спортлото” можно выбрать шесть номеров из 49? (С649= |
У Робина – Бобина Барабека 40 соседей. Он решил пригласить двоих из них на обед. Сколько у него способов это сделать (С240 |
В) 2 ряд соревнуются в эстафете 1 вариант и 2
вариант. (Выбрать капитанов)
1 этап эстафеты: “Бег с препятствиями”
| Какие из следующих событий достоверные: А – “два попадания при трёх В – “появление не более 18 очков при бросании С – “наугад выбранное трёхзначное число не Д – “наугад выбранное число, составленное из (В, С и Д) |
Какие из следующих событий невозможные: А – “опаздывание ленинградского В – “появление 17 очков при бросании 3 игральных С – “появление слова “мама” при случайном Д – “появление составленного из цифр 1, 2, 3, 7, 8 и (Д) |
2 этап эстафеты: “Состязание капитанов”
О каком событии идёт речь?
| 1) Измерены длины сторон треугольника. Оказалось, что длина каждой стороны меньше суммы длин двух других сторон. (Достоверное событие) 2) В полночь выпадет снег, а через 24 часа |
1) Произведено три выстрела по мишени. Произошло пять попаданий. (Невозможное событие) 2) Завтра будет контрольная по |
3 этап эстафеты: “Кто быстрее?” (Решить
задачи.)
| 1) В урне 15 белых и 25 чёрных шаров. Из урны наугад вынимается один шар. Какова вероятность того, что он будет белым? (15/40 = 3/8 = 0, 2) Из слова СОБЫТИЕ случайным образом (4/7 = 0, 571) 3) Одновременно бросают 3 монеты. Сколько (8) |
1) Из русского алфавита случайным образом выбирается одна буква. Какова вероятность того, что она окажется гласной? (10/ 33 2) Абонент забыл последнюю цифру телефонного (5/10 = 1/2 = 0, 5) 3) Одновременно бросают 3 монеты. С какой (2/8 = 1/4 = 0, 25) |
Если выполнили задание 1 ряд, то дополнительно
решить задачи
(Решить задачу.)
| Имеется шесть перчаток различных размеров. Сколькими способами можно выбрать из них одну перчатку на левую руку и одну на правую руку так, чтобы эти перчатки были различных размеров? (Решается по правилу |
Гера, Афина и Афродит попросили Париса не только назвать самую красивую из них, но и указать, кто на “втором и третьем месте”. Сколько есть вариантов ответа? (Решается по |
4. Подведение итогов, выставление оценок.
5. Изучение нового материала.
Как только человеку в его деятельности
потребовались количественные характеристики, то
есть числа, тут же появилась статистика.
“Статистика знает все”, утверждал Ильф и
Петров в романе “двенадцать стульев”.
Для изучения, обработки и анализа
количественных данных различных массовых
социально-экономических процессов и явлений
проводят статистические исследования.
“Независимо от того, в какой отрасли знания
получены числовые данные, они обладают
определенными свойствами, для выявления которых
может потребоваться особого рода научный метод
обработки. Последний известен как
статистический метод или, короче, статистика.”
Дж.Юз. М. Кендалл. “Теория статистики”.
Каждое статистическое исследование состоит из
сбора и обработки информации. На основе
полученных данных проводятся выработка
различных прогнозов, оценка их достоверности.
Важной задачей, без которой статистические
данные теряют всякий смысл, является обработка
полученных данных.
Предложить учащимся выполнить задание №1.
№1. Посчитайте длины слов (количество букв) в
приведенном ниже отрывке.
Если хочешь быть здоров, закаляйся 4, 6, 4, 6, 9.
Позабудь про докторов 8, 3, 8.
Водой холодной умывайся. 5, 8, 8.
После его выполнения учащимся задаются
вопросы:
– Что вы сейчас делали? (собирали информацию)
– Какие выводы можно сделать? (можно вычислить
самое длинное слово, самую длинную строку, самую
распространенную букву и т. д.)
Займемся статистическим методами обработки
информации. Для этого нужны новые термины,
принятые в статистике.
Учащимся предлагается раздаточный материал.
| 1) Все понятно | 2) Почти понятно | 3) Ничего не понятно |
|
Новый термин |
Простое описание |
Более научный |
Определение |
| Общий ряд данных | То, откуда выбирают | Генеральная совокупность |
Множество всех в принципе возможных данных измерения |
| Выборка | То, что выбрали | Статистическая выборка, статистический ряд |
Множество данных, реально полученных в данном измерении. |
| Варианта | Значение одного из результатов измерения |
Варианта | Одно из значений элементов выборки |
| Ряд данных | Значение всех результатов измерения, перечисленных по порядку |
Вариационный ряд | Упорядоченное множество всех вариант |
| Кратность варианты | Это сколько раз каждая варианта из ряда данных наблюдается в выборке. |
||
|
Объем выборки |
Если сложить все кратности | Количество всех произведенных при выборке измерений |
|
| Частота варианты | Отношение кратности варианты к объему выборки |
№2.
30 абитуриентов на четырех
вступительных экзаменах набрали в сумме такое
количество баллов (оценки на экзаменах
выставлялись по 5 бальной системе):
20; 19; 12; 13; 16; 17; 15; 14; 16; 20; 15; 19; 20; 20;15; 13; 19; 14;
18; 17; 12; 14; 12; 17; 18; 17; 20; 17; 16; 17.
Составить общий ряд данных выборки.
Выборку из результатов, стоящих на четных местах
и соответствующий ряд данных.
Решение:
После получения 2 дальнейшие экзамены не
сдаются, поэтому сумма баллов не может быть
меньше 12(12 – это 4”тройки”)
Общий ряд данных – все реальные данные
измерения, выписанные в определенном порядке без
повторений. Значит, общий ряд данных состоит из
чисел.
Общий ряд данных: 12; 13; 14; 15; 16; 17; 18; 19; 20.
Выборка из результатов, стоящих на
четных местах состоит из 15 результатов; 19; 13; 17; 14;
20; 19; 20; 13; 14; 17; 14; 17; 17; 17; 17.
Ряд данных – это конечная возрастающая
последовательность: 13; 14; 17; 19; 20.
Перейдём к дальнейшей обработке информации.
Составим таблицу из двух строк. В первой из
которых будет ряд данных.
Каждая варианта из этого ряда какое – то
количество раз наблюдалось в выборке. Это
количество называется кратностью варианты.
Кратность варианты – это сколько
раз каждая варианта из ряда данных наблюдается в
выборке.
Вот и поставим во вторую строку
кратности соответствующих вариант.
Получим таблицу распределения
выборки. Вот как она выглядит.
| Варианта | 13 | 14 | 17 | 19 | 20 | Всего 5 вариант |
| Кратность варианты | 2 | 3 | 6 | 2 | 2 | Сумма = 15 (объем выборки) |
Если сложить все кратности, то
получится количество всех произведенных при
выборке измерений – объем выборки.
В данном случае объем выборки равен 15.
Далее, при общей оценке данных выборки
не очень важно, что, например, варианта 14 имеет
кратность 3 из общего объема в 15 данных. Удобнее
сказать, что эта варианта составляет или 20% числа
всех измерений. Так и поступают, т.е. делят
кратности вариант на объем выборки и получаем частоты
вариант.
Частотность варианты = КРАТНОСТЬ И
ВАРИАНТЫ
Частоты всех вариант удобно приписывать
третьей строкой уже составленной таблице. Новую
трехстрочную таблицу называют таблицей
распределения частот выборки.
Таблица распределения частот выборки:
| Варианта | 13 | 14 | 17 | 19 | 20 | Всего: 5 вариант |
| Кратность варианты | 2 | 3 | 6 | 2 | 2 | Сумма = 15 (объем выборки) |
| Частота варианты | Сумма = 1 | |||||
| 13,33% | 20% | 40% | 13,33% | 13,33% |
Обратите внимание, что сумма частот равна 1, и
так бывает всегда.
Иногда частоты удобно измерять в
процентах от общего объема выборки. Тогда
таблицу распределения дополняют еще частотой
частот в процентах. Она получается из предыдущей
строки умножением на 100%.
6. Закрепление
Решить задачу.
№1
После группировки данных эксперимента
получилась такая таблица их распределения:
| Варианта | -3 | 0 | 4 | 5 | 9 | 11 | 12 | 15 | 20 |
| Кратность варианты | 12 | 9 | 1 | 64 | 34 | 56 | 7 | 8 | 9 |
а) Определите объем выборки.
б) Найдите наиболее часто встретившуюся
варианту.
в) Допишите к таблице третью и четвертую строки
из частот и процентных частот вариант.
г) Найдите сумму чисел в третьей и четвертой
строках.
Решение:
| Варианта |
-3 |
0 |
4 |
5 |
9 |
11 |
12 |
15 |
20 |
Всего 9 вариант |
| Кратность варианты |
12 |
9 |
1 |
64 |
34 |
56 |
7 |
8 |
9 |
200 |
| Частота варианты |
|
|
|
|
Сумма 1 |
|||||
| Частота варианты в % |
6 |
4,5 |
0,5 |
32 |
17 |
28 |
3,5 |
4 |
4,5 |
100 |
а) Объем выборки 200; б) 5.
Работа в парах.
Задача № 2
1 ряд. Для выборочной переписи
населения в 20 квартирах были получены следующие
сведения о годах рождения их жильцов (первые две
цифры 1 и 9 не пишутся):
|
30 |
56 |
98 |
77 |
93 |
31 |
61 |
80 |
87 |
52 |
|
56 |
32 |
87 |
73 |
93 |
81 |
57 |
52 |
61 |
89 |
|
90 |
92 |
85 |
87 |
70 |
61 |
93 |
87 |
52 |
53 |
|
40 |
56 |
48 |
51 |
61 |
87 |
88 |
90 |
52 |
60 |
|
22 |
34 |
48 |
52 |
88 |
87 |
91 |
62 |
63 |
87 |
|
39 |
40 |
52 |
87 |
99 |
91 |
87 |
65 |
61 |
55 |
а) Составьте ряд данных.
б) Найдите кратность и частоту вариант 61 и 87.
в) Составьте таблицу кратностей, разбив данные
на интервалы по годам:
№1-от 22 до 30; №2 –от 31 до40;
№3-от 41 до 50; № 4 –от 51 до 60;
№5-от 61 до 70; № 6 – от 71 до 80;
№7 – от 81 до 90; №8 -от 91 до 99.
Решение:
а) 30, 31, 32, 34, 40, 48, 51, 52, 53, 55, 56, 57, 60, 61, 62, 63, 65, 70, 73, 77, 80,
81, 85, 87, 88, 90, 91, 92, 93, 98, 99.
б)
| Варианта |
61 |
87 |
| Кратность варианты |
5 |
9 |
| Частота варианты |
в)
| Варианта | 22– 30 | 31-40 | 41 -50 | 51-60 | 61-70 | 71-80 | 81-90 | 91-99 | |
| Кратность варианты |
2 |
6 |
2 |
14 |
9 |
3 |
16 |
8 |
Сумма 60 |
| Частота варианты | 1 | ||||||||
| Частота варианты в % | 3,3% | 10% | 3,3% | 23,3% | 15% | 5% | 26.6 % | 13,3% | 100% |
Самостоятельно определить частоту варианты и
частоту варианты в %
3 ряд. Предлагает задачу Морева С.
Проводя исследование
“Использование статистических методов при
изучении отношения школьников к математике.”
С этой целью был составлен тест,
содержащий 9 заданий. Работу выполняли учащиеся 9
А класса (23 человек). При проверке каждой работы
учитель математики отмечала число верно
выполненных заданий. Я приняла участие в анализе
данных по ее просьбе.
В результате был составлен такой ряд
чисел:
6, 5, 5, 7, 9, 6, 8, 7, 9, 8, 6, 7, 5, 7, 6, 4, 5, 8, 6, 7, 9, 9, 6.
а) Составьте ряд данных.
б) Найдите кратность и частоту вариант 5 и 9.
в) Составьте таблицу кратностей;
г) найдите частоту варианты и частоту варианты
в процентах.
Для того чтобы удобно было
анализировать полученные данные, упорядочим
этот ряд:
|
4 |
5, 5, 5, 5 |
6, 6, 6, 6, 6, 6 |
7, 7, 7, 7, 7 |
8, 8, 8 |
9, 9, 9, 9. |
Представим полученные данные в виде
таблицы, в которой для каждого числа верно
выполненных заданий, записанного в верхней
строке, укажем в нижней строке количество
появлений этого ила в ряду, т.е. частоту:
|
Число верно |
4 |
5 |
6 |
7 |
8 |
9 |
|
Кратность варианты |
1 |
4 |
6 |
5 |
3 |
4 |
|
Частота варианты |
||||||
|
Частота варианты в % |
4,3 |
17,4 |
26,1 |
21,7 |
13,1 |
17,4 |
В рассмотренном примере сумма частот
равна общему числу проверяемых работ, т.е. 23.
2 ряду предлагает задачу Ланцова
Татьяна
“Подтверждение статистических характеристик
на примере 7А класса МСОШ №1”
Мне стало интересно, какой средний
рост моих одноклассников. Я провела среди них
опрос, и в результате моего исследования
выяснилось следующее:
143, 157, 165,148, 168,161,159, 157, 164, 167,153, 170,159,158,167,166, 168,168, 173,
169,169,170, 168,
а) Составьте ряд данных.
б) Найдите кратность и частоту вариант 171 и 167.
в) Составьте таблицу кратностей, разбив данные
на интервалы по росту:
№1-от 143 до 149; №2 –от 150 до 155; №3-от 156 до 160; № 4
–от 161 до 165;
№5-от 166 до 170, №6 – от 171 до 175.
|
Рост, см |
Частота, |
Середина |
|
143-149 |
2 |
144,5 |
|
150-155 |
1 |
153,5 |
|
156-160 |
5 |
157,5 |
|
161-165 |
3 |
163,5 |
|
166-170 |
11 |
167,5 |
|
171-175 |
1 |
173,5 |
7. Домашнее задание:
Решить задачи: № 1; 2.
Задача № 1
В вашем классе соберите данные о месяцах
рождения учеников. Месяца удобнее перечислять по
порядковому номеру.
а) Выпишите ряд данных полученной вами выборки;
б) составьте таблицу распределения из четырех
строк: варианты, кратности, частоты, частоты в
процентах;
в) укажите наиболее и наименее часто
встретившуюся варианту.
Задача № 2
Выборка состоит из всех букв, входящих в
двустишье
“… Это дерево – сосна,
И судьба сосны ясна…”
а) выпишите ряд данных выборки;
б) найдите объем выборки;
в) определите кратность и частоту варианты “о”;
г) какова “наибольшая процентная частота
вариант выборки”.
Конспект.
8. Стадия рефлексии. Подводя итог урока,
необходимо добиться понимания учащимися
следующих важных положений:
На этапе рефлексии учащимся предлагается
составить синквейн и в поэтической форме
выразить свое отношение к изученном материалу.
Справка: СИНКВЕЙН – приём технологии
развития критического мышления, на стадии
рефлексии.
Это короткое литературное произведение,
характеризующее предмет (тему), состоящее из пяти
строк, которое пишется по определённому плану.
Слово “синквейн” происходит от французского
слова “пять”.
ПРАВИЛА НАПИСАНИЯ СИНКВЕЙНА
1 строчка – одно слово – название
стихотворения, тема, обычно существительное.
2 строчка – два слова (прилагательные или
причастия). Описание темы, слова можно соединять
союзами и предлогами.
3 строчка – три слова (глаголы). Действия,
относящиеся к теме.
4 строчка – четыре слова – предложение.
Фраза, которая показывает отношение автора к
теме в 1-ой строчке.
5 строчка – одно слово – ассоциация,
синоним, который повторяет суть темы в 1-ой
строчке, обычно существительное.
Пример синквейна:
Статистика
Ускользающая, непознанная.
Осознать, изучить, понять
Статистика есть дизайн информации.
Реальность.
9. Завершение урока
Завершить урок хочется такой историей.
– Доктор, – спрашивает пациент – пойдут ли у
меня дела на поправку?
– Несомненно, – отвечает врач, – потому что
статистика говорит, что один из ста
выздоравливает при этой болезни.
– Но почему же при этом именно я должен
выздороветь?
– Потому что вы как раз и есть мой сотый
пациент.
Презентация
Приложение
18.02.2010
Дата публикации: 09 апреля 2017.
Урок и презентация на тему: “Математическая статистика, элементы статистики”
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Скачать:
Математическая статистика, элементы статистики (PPTX)
Статистика, введение
Темой сегодняшнего урока будет математическая статистика.
Этот предмет занимается статистикой, используя различные математические методы. Математическая статистика – это самостоятельно развивающийся раздел математики, в котором существуют и свои уникальные способы решения различных задач.
Так чем же занимается и для чего нужна математическая статистика?
Предположим, что у учеников девятых классов измерили рост. Как представить полученные данные? Можно записать их в строчку друг за другом, можно разделить данные по классам, можно попробовать создать таблицу. Все эти способы довольно громоздки и неудобны. Будет сложно извлечь информацию из такого набора чисел. А теперь представьте, что измерили рост учеников девятых классов всех школ в городе. Количество измерений может перевалить за тысячу.
Математическая статистика занимается обработкой данных и представлением их в виде удобном для восприятия. Это только одна из задач статистики. Построение прогнозов и оценок; применение различных методов исследования; достоверность проведенных испытаний и многое другое – вот чем занимается статистика.
Как же обрабатывает информацию статистика?
- Данные измерений упорядочивают и группируют.
- Составляют таблицы распределений данных.
- По таблицам строят графики распределений.
- В итоге создается паспорт измерений, в котором собраны числовые характеристики полученной информации.
Давайте рассмотрим эти пункты.
Упорядочивание и группировка данных
Первое, что необходимо сделать при анализе данных, определить рамки, в которых находится исследователь. Выбираются наименьшее и наибольшее допустимые значения, которые могут не совпадать с полученными данными. Например, при измерении роста учеников, шансов, что кто-то будет ниже 140 сантиметров и выше 200 сантиметров очень мало. Если найдется такой вариант, то данные статистики можно подкорректировать.
При измерении роста могут получиться числа: 140,150,160,170,180,190,200 – это общий ряд данных, которые принято располагать в порядке возрастания. Общий ряд данных может быть и другим, например: 140,145,150,155,160,…,190,195,200. Как представить общий ряд данных зависит от конкретной задачи.
Пример. Составить общий ряд данных, включающих:
а) месяцы рождения одноклассников,
б) годов рождения родственников и друзей,
в) буквы, с которых начинается слово.
Решение.
а) Всего месяцев 12, если их перечислить по цифрам, то получим общий ряд: 1,2,3,4,5,6,7,8,9,10,11,12.
б) Шанс, что кто-то из родственников старше 100 лет – мал, а что, кто-то родился в этом году – есть. Тогда общий ряд годов рождения можно составить так: 1910,1911,1912,…, 2009,2010,2011,2012,2013,2014.
в) Слово может начинаться с любой буквы алфавита, кроме ь, ы, ъ. Тогда возможны 30 вариантов, если их представить численным рядом, то получим: 1,2,3,4,…,28,29,30.
Понятие “общий ряд” не является строгим, в примере б) мы могли начать ряд с 1900 года, ряд так же назывался “общим”.
При проведении эксперимента данные из общего ряда могут не встретиться. Вернемся к нашему примеру б) и рассмотрим конкретный случай.
Вова назвал года рождения родственников: 1935,1937,1960,1965,1980,1981,1997,2005.
Общий ряд представлял собой последовательность: 1910,1911,1912,…,2009,2010,2011,2012,2013,2014.
У Вовы встретились конкретные измерения, которые называются “вариантой измерения”.
Варианта измерения – это возможный вариант проведенного измерения.
Если все варианты измерений перечислить по порядку, то получится ряд данных измерения.
Для нашего примера составим таблицу:

Пример. Выписать ряд, состоящий из букв, которые встречаются в словах: мама, папа, брат, сестра, бабушка, дедушка, тетя, дядя.
Решение. Ряд будет выглядеть так: а, б, д, е, к, м, п, р, с, т, у, ш, я. Встретились 13 букв из 33.
Некоторые буквы встречаются несколько раз, например, буква а – девять раз, другие – реже.
Определение. Если среди всех данных конкретного измерения одна из вариант встретилась ровно к раз, то число к называют кратностью измерения.
В этом примере буква а имеет кратность – 9.
Запишем кратности для каждой из букв:

Далее варианты нужно сгруппировать. Создадим сгруппированный ряд данных:
а,а,а,а,а,а,а,а,а,б,б,б,д,д,д,д,е,е,е,к,к,м,м,п,п,р,р,с,с,т,т,т,т,у,у,ш,шя,я,я.
Число повторений каждой варианты равно кратности варианты.
Составление таблицы распределения данных

Если сложить все кратности, получится количество всех данных измерения или объем измерения. Объем измерения равен количеству букв встречающихся в наших словах. Для проверки всегда складывают кратности, сумма должна равняться количеству элементов измерения.
Далее вычисляют частоту варианты.
Частота варианты=Кратность варианты/Объем измерения.
Составим таблицу частот измерений:

Сумма всех частот всегда равна единице, так как это сумма всех дробей с одинаковым знаменателем, а сумма всех числителей как раз и равна знаменателю. Для удобства, часто переводят частоты в проценты от объема измерения. Составим таблицу еще одну таблицу, каждую частоту в новой строке помножим на 100.

Графическое представление данных
Давайте построим графики функций распределения по таблицам. Договоримся, что вместо букв будем использовать цифры 1,2,3,…,13.
Тогда наша таблица примет вид:

По оси абсцисс отложим цифры, соответствующие буквам, а по оси ординат – значения частот появления варианта. Графическое изображение имеющейся информации – график распределения частот.
Таблица значений:

График распределения частот:

График распределения частот также называют полигоном распределения.
Давайте построим график распределения частот процентов. Его тоже называют полигоном распределения процентов.
Таблица значений.

Полигон распределения процентов:

Даже не большая по объему данных задача, представляет собой довольно таки утомительную процедуру подсчета и составления таблиц и графиков распределений.
Числовые характеристики данных измерения
Наши данные обладают уникальными числовыми характеристиками. Давайте определим некоторые из них.
Разность между максимальной и минимальной вариантой называют размахом измерения.
На наших графиках – это область определения (разность крайнего правого значения и крайнего левого значения на оси абсцисс). В нашем примере размах равен $13-1=12$.
Варианта, которая встречается чаще других, называется модой. В нашем примере это буква а или число 1, в зависимости от обозначения.
Если у нас есть таблица распределения частот, то в строчке частот ищем наибольшее число, и смотрим, какому варианту оно соответствует. На графике, это точка в которой достигается максимальное значение.
Наиболее важная характеристика – среднее значение (среднее арифметическое или просто среднее).
Чтобы найти среднее значение нужно:
а) Просуммировать все данные измерения.
б) Полученную сумму разделить на количество вариантов.
Для нашего примера найдем среднее значение:
$frac{1*9+2*3+3*4+4*3+5*2+6*2+7*2+8*2+9*2+10*4+11*2+12*2+13*3}{40}=5,775$.
Среднее значение можно найти другим способом:
а) Каждую варианту умножить на ее частоту.
б) Сложить получившиеся значения.
Подсчитаем этим способом:

1*0,225+2*0,075+3*0,1+4*0,075+5*0,05+6*0,05+7*0,05+8*0,05+9*0,05+10*0,1+11*0,05+12*0,05+13*0,075=5,775.
Давайте рассмотрим еще один пример.
На экзамене по математике 25 учеников 9 класса получили такие оценки:
5,4,3,3,5,4,3,3,4,4,5,5,2,2,5,5,5,3,3,4,5,5,4,3,2.
а) Составить общий ряд данных. Упорядочить и сгруппировать.
б) Составить таблицы распределения и распределения частот.
в) Построить графики распределения и распределения частот.
г) Найти среднее, моду, размах.
Решение.
Возможны такие оценки: 1,2,3,4,5 – общий ряд данных.
В нашем примере встречаются оценки: 2,3,4,5 – ряд данных, все числа в ряде – варианты измерений.
Составим сгруппированный ряд: 2,2,2,3,3,3,3,3,3,3,4,4,4,4,4,4,5,5,5,5,5,5,5,5,5.
б) Объем измерения равен 25, так как 25 оценок выставлено.
Составим таблицу:

в) Нарисуем графики:
Полигон распределения данных:

Полигон распределения частот:

Полигон распределения частот процентов:

Все графики похожи между собой, различия только в масштабе оси ординат.
г)Найдем среднее значение:
$2*0,12+3*0,28+4*0,24+5*0,36=0,24+0,84+0,96+1,8=3,81$.
Мода: чаще всего встречается оценка пять, она и будет модой.
Размах: $5-2=3$.
Задачи статистики для самостоятельного решения
1.На экзамене по математике 50 учеников 9 класса получили такие оценки:
5,3,4,4,5,4,3,2,4,3,5,1,2,3,5,4,5,3,3,4,5,5,4,3,1,3,4,5,4,3,2,2,1,4,4,5,5,4,4,5,3,3,3,2,1,5,4,3,2,5.
а) Составить общий ряд данных. Упорядочить и сгруппировать.
б) Составить таблицы распределения и распределения частот.
в) Построить графики распределения и распределения частот.
г) Найти среднее, моду, размах.

3. Графическое представление информации.Распределение данных измерения рационально задавать в табличном виде. Однако нам известно, что и для функций есть табличный способ их задания. Таблицы являются связующим звеном. С их помощью осуществляется переход от распределения данных к функциям и графикам.
График распределения выборки является графическим представлением информации. Согласно табличным сведениям из примеров выше отметим точки, у которых абсциссы — это номер варианта, а ординаты — кратность. Соединяем отрезками полученные точки:
Пример:

Получили многоугольник или полигон распределения данных. Собственно, polygon и переводится как «многоугольник».
Чтобы представить большой объём информации в графическом виде, можно использовать гистограммы или столбчатые диаграммы.
Пример:


4. Числовые характеристики данных измерения.
У любого из нас имеются не только данные о рождении, но и ряд иных свойств и качеств.
Такие измерения имеют свои числовые характеристики.
Размах измерения — это разность между максимальной и минимальной вариантами.
Мода измерения — вариант, который в измерении встречался чаще других.
Медиана — число, стоящее в середине сгруппированного ряда.
Среднее значение — среднее арифметическое, или просто среднее. Для нахождения среднего значения нужно:
1) вычислить сумму всех данных измерения;
2) полученную сумму разделить на количество данных.
Итак,
выборки удобно задавать с помощью
таблиц. Но мы знаем, что и для функций
есть табличный
способ их
задания. Таблицы образуют «мостик», по
которому от выборок данных можно перейти
к функциям и их графикам.
Отложим
по оси абсцисс значения из первой строки
таблицы распределения, а по оси ординат
– значения из ее второй строки. Построим
соответствующие точки в координатной
плоскости. Получим графическое изображение
имеющейся информации – график
распределения выборки.
Часто, построенные точки для наглядности
соединяют отрезками. То же самое можно
сделать, заменив вторую строку таблицы
распределения ее третьей строкой.
Получится график
распределения частот выборки.
Термин «график распределения частот
выборки» чаще заменяют более кратким
– многоугольник
частот или
полигон
частот. Собственно,
роlуgоп
и переводится
как «многоугольник».
Пример
3. Постройте
график распределения и многоугольник
частот для следующих результатов
письменного экзамена по математике:
|
6, |
7, |
7, |
8, |
9, |
2, |
10, |
6, |
5, |
6, |
|
7, |
3, |
7, |
9, |
9, |
2, |
3, |
2, |
6, |
6, |
|
6, |
7, |
8, |
8, |
2, |
6, |
7, |
9, |
7, |
5, |
|
9, |
8, |
2, |
6, |
6, |
3, |
7, |
7, |
6, |
6, |
Решение.
Дана выборка объема 40. Ее ряд данных –
2; 3; 5; 6; 7; 8; 9; 10. Оценка в 2 балла встретилась
пять раз. Значит, кратность варианты 2
равна 5. Сделав то же для других оценок,
найдем их кратности. Они равны 5; 3; 2; 11;
9; 4; 5; 1. Можно себя проконтролировать,
вычислив сумму кратностей всех
рассмотренных вариант: 5 + 3 + 2 + 11 + 9 + 4 + +
5 + 1 = 40. Частота появления двух баллов
равна
![]() 0,125
0,125
или 12,5%. Вычислив остальные частоты,
составляем таблицу и строим графики
(см. рис. 6.1).
|
Варианта |
2 |
3 |
5 |
6 |
7 |
8 |
9 |
10 |
Всего |
|
Кратность |
5 |
3 |
2 |
11 |
9 |
4 |
5 |
1 |
Сумма |
|
Частота |
0,125 |
0,075 |
0,05 |
0,275 |
0,225 |
0,1 |
0,125 |
0,025 |
Сумма |
|
Частота |
12,5 |
7,5 |
5 |
27,5 |
22,5 |
10 |
12,5 |
2,5 |
Сумма |
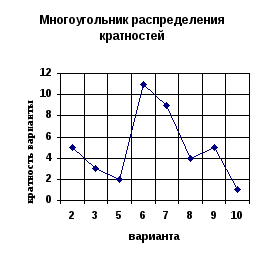
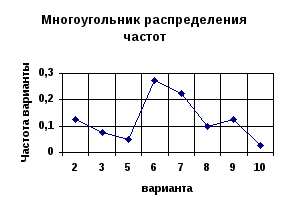
Рисунок 6.1
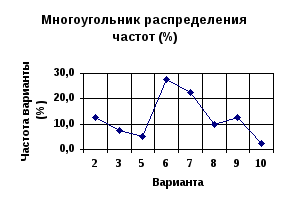
По существу,
различия этих трех графиков состоят
только в выборе единиц измерения и
масштаба по оси ординат. Для наглядного
оформления (дизайна) информации в каждом
конкретном случае приходится выбирать
между этими тремя возможностями. Чаще
всего в практических приложениях
используют многоугольники частот в
процентах. Для полноты картины можно
было бы приведенные ломаные дополнить
еще одной вершиной (4; 0), расположенной
на оси абсцисс. Эта вершина соответствует
тому, что в данной выборке отсутствует
оценка в 4 балла.
М ы
ы
видим, что даже для малого объема выборки
аккуратное «причесывание» информации
– довольно кропотливая вещь. Вот более
краткий, но менее точный способ.
Рисунок 6.2
Назовем
оценки 2, 3, 4 «плохими», оценки 5, 6, 7
«средними», а оценки 8, 9, 10 «хорошими».
Все «плохие» оценки принадлежат отрезку
[2; 4], «средние» – отрезку [5; 7], а «хорошие»
– отрезку [8; 10] (рис.). Тем самым мы разбили
промежуток между самой маленькой и
самой большой вариантой на участки и
получили интервальный
ряд данных: 2
– 4; 5 –7; 8 –
10.
|
Варианта |
«Плохая» |
«Средняя» |
«Хорошая» |
Для каждого участка
сложим кратности вариант, попавших в
него. Получим кратности каждого участка.
|
Варианта |
«Плохая» |
«Средняя» |
«Хорошая» |
|
Кратность |
8 |
22 |
10 |
Т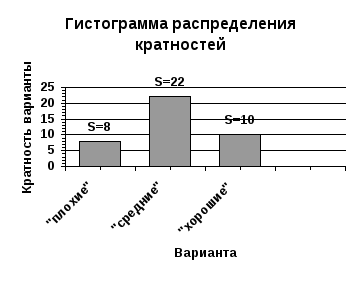 еперь
еперь
нарисуем три прямоугольника. Основание
первого – это отрезок [2; 4], его площадь
равна 8, т. е. равна кратности «плохой»
варианты. Аналогично поступим с двумя
другими вариантами. Получимстолбчатую
диаграмму, или
гистограмму распределения (рис. 6.3).
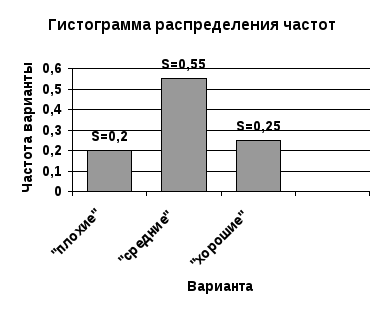 Рисунок 6.3
Рисунок 6.3
Поделив
высоты столбиков на объем всей выборки,
получим другую столбчатую диаграмму –
гистограмму распределения частот (рис.
6.4).
Рисунок 6.4
Как обычно, таблицу
можно дополнить и третьей строкой, в
которой частоты вариант выражены в
процентах:
|
Варианта |
«Плохая» |
«Средняя» |
«Хорошая» |
|
Кратность |
8 |
22 |
10 |
|
Частота |
0,2 |
0,55 |
0,25 |
|
Частота |
20 |
55 |
25 |
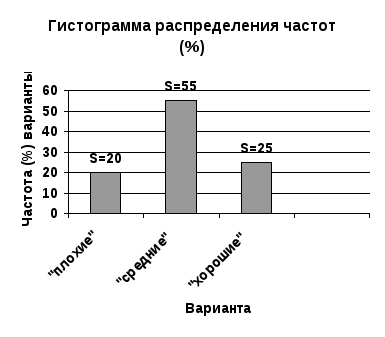
На
рисунке 6.5 приведена гистограмма
распределения частот в процентах.
С одной стороны,
в гистограмме потеряна первоначальная
точная информация: мы не знаем, например,
сколько именно человек получили 6 баллов.
С другой стороны, ответ получается более
быстро, и наглядно видна качественная
оценка распределения данных. Примерно
половина абитуриентов получила «средние»
баллы, а «плохиши» и
Рисунок
6.5 «хорошисты с отличниками» поделились
почти поровну. Для отчетов по результатам
экзаменов такой вид исходной информации
– в самый раз
Пример
4. Измерили
длины слов (количество букв) в приведенном
ниже отрывке из поэмы А. С. Пушкина
«Медный всадник». Нужно построить
гистограммы распределения кратностей
и частот, выбрав интервалы 1 – 3, 4 – 6, 7
– 9 для вариант выборки.
-
«…Ужасен
он в окрестной мгле!6,
2,
1,
9,
4
Какая
дума на челе!5,
4,
2,
4
Какая
сила в нем сокрыта,5,
4,
1,
3,
7
А
в сем коне какой огонь!1,
1,
3,
4,
5,
5
Куда
ты скачешь, гордый конь,4,
2,
7,
6,
4
И
где опустишь ты копыта?…»1,
3,
8,
2,
6
Решение.
Справа от текста вместо слов построчно
записаны их длины. После подсчета
составляем таблицу.
-
Длина
слова1
2
3
4
5
6
7
8
9
Всего
9 вариантКратность
5
4
3
7
4
3
2
1
1
Сумма
= 30
Для нужных гистограмм
составляем таблицу с меньшим числом
вариант.
-
Длины
слов1, 2 или 3
4, 5 или 6
7, 8 или 9
Всего
3 вариантыКратности
5+4+3=12
7+4+3=14
2+1+1=4
Сумма
= 30Частоты
(%)40
46,66
13,33
Сумма
≈ 100%
Осталось нарисовать
гистограммы:
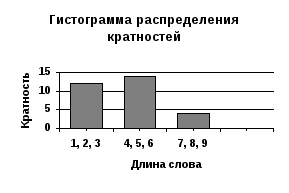
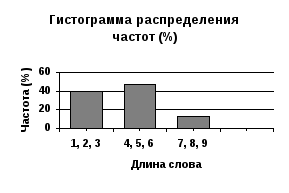
Рисунок 6.6
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Рядом данных называют результаты измерения, перечисленные в порядке их получения. Каждый из результатов называется вариантой измерения.
Например, результаты написания контрольной работы по математике для класса из 20 человек можно представить в виде следующего ряда данных: 3, 4, 4, 5, 3, 4, 3, 3, 3, 5, 5, 4, 5, 4, 5, 3, 3, 3, 4, 3. Эту же информацию можно представить в
виде таблицы:

Кратность варианты — количество её повторений в ряду данных. В нашем ряду оценка «3» появилась 9 раз, поэтому её кратность равна 9.
Понятно, что таблица распределения отображает данные более наглядно и компактно.
Числовые характеристики данных
Объём измерения — количество всех данных этого измерения. Одна из наиболее важных характеристик варианты — это её частота. Частота варианты показывает долю этой
варианты в ряду распределения. Она вычисляется по формуле:
частота =кратность варианты/объём измерения
В нашем примере частота варианты «4» равна .
Это означает, что оценка 4 составляет 0,3 всех полученных оценок.
Размах измерения — разность между максимальной и минимальной вариантами этого измерения. В нашем примере максимальная варианта равна 5, минимальная — 3, значит, размах равен .
Мода измерения — варианта, которая в измерении встретилась чаще других. В приведённом выше примере чаще всех встретилась оценка 3, значит, она и будет модой этого распределения.
Медиана распределения — это центральное число в упорядоченном ряду данных, если в ряду нечётное количество чисел, или полусумма двух центральных, если в ряду чётное количество чисел.
Например, для ряда распределения 1, 2, 3, 6, 9, объём измерения которого равен 5, медианой распределения будет третье число этого ряда, то есть 3.
Для ряда распределения 7, 3, 2, 1 с объёмом измерения, равным 4, медианой будет полусумма двух центральных чисел данного ряда, то есть число, равное .
Для нахождения медианы распределения необходимо
1. Упорядочить ряд распределения по возрастанию или по убыванию: .
2. Если объём измерения нечётный, то есть , то получим следующую ситуацию:
![]()
В этом случае медианой является число .
3. Если объём измерения чётный, то есть , то имеем
![]()
В этом случае медианой является число — .
Среднее ряда (среднее арифметическое) — сумма всех чисел ряда, делённая на их количество. Если имеется таблица распределения, то можно
1) умножить каждую варианту на её кратность;
2) просуммировать полученные значения;
3) разделить результат на объём измерения. Например, для ряда распределения 2, 4, б, 8, у которого объём измерения равен 4, среднее значение равно
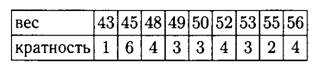
Задача 1. Даны результаты измерения веса школьников 9 класса: 55, 53, 56, 48, 45, 56, 49, 52, 53, 49, 50, 56, 45, 52, 56, 45, 45, 48, 55, 52, 43, 48, 52, 49, 50, 45, 48, 45, 50, 53.
а) Постройте таблицу распределения данных.
б) Найдите объём измерения.
в) Найдите размах ряда.
г) Найдите частоту появления каждого веса в указанном ряду.
д) Найдите медиану, моду и среднее указанного ряда.
Решение.
а) Наименьшее число в ряду — 43, оно встречается в ряду один раз, значит, его кратность равна 1. Следующее по величине — число 45, оно встречается шесть раз, значит, его кратность равна 6. Далее 48, оно встречалось 4 раза, значит, его кратность равна 4.
Продолжая аналогично, заполним таблицу:
б) Найти объём измерения можем несколькими способами.
1- й способ.
Посчитаем количество чисел в ряду, получим 30.
2- й способ.
Сложим кратности всех вариант:
Ответ: 30.
в) Наибольшее значение в ряду 56, наименьшее — 43, значит, размах равен
Ответ: 13.
г) Для каждой варианты делим её кратность на объём измерения (на 30), результаты пишем в таблицу.
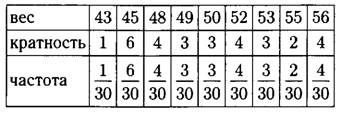
д) В данном ряду 30 чисел, значит, медиана равна полусумме 15-го и 16-го чисел в упорядоченном ряду.
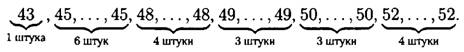
Как видно из такой записи чисел, от 43 до 49 — 14 чисел, значит, 15-ое и 16-ое числа равны 50, и значит, медиана равна
Мода — то значение, которое встречается чаще всех, то есть то, у которого больше кратность. Из таблицы распределения находим, что наибольшую кратность имеет число 45, значит, мода равна 45.
Для нахождения среднего необходимо найти сумму всех чисел ряда и разделить ее на количество этих чисел. Сумму можно найти просто складывая подряд все числа ряда. А можно поступить иначе: каждую варианту умножить на её кратность и сложить полученные результаты. Имеем:
.
Осталось разделить полученную сумму на количество всех чисел: .
Ответ: медиана: 50; мода: 45; среднее: 50,1.
Задача 2. Пятерых учеников попросили подсчитать, сколько времени (в минутах) они тратят на дорогу от дома до школы. Получили следующие результаты: 5,15,10,15,20.
1) На сколько среднее значение этого ряда меньше его размаха?
2) На сколько мода этого ряда больше медианы?
3) Найдите процентную частоту значения 10.
Решение.
1) Среднее ряда: , размах:
. Искомое значение равно
.
Ответ: 2.
2) Найдём медиану. Расположим числа в порядке возрастания: 5, 10, 15, 15, 20. Медианой этого набора будет третье число в упорядоченном ряду, то есть 15.
В данном ряду число 15 встретилось 2 раза, остальные — по одному разу. Мода ряда равна 15. Мода и медиана этого ряда равны, значит, ответ 0.
Ответ: 0.
3) Кратность значения 10 равна 1, объём измерения равен 5 (всего 5 чисел). Частота значения 10 равна , процентная частота равна
.
Ответ: 20.
Задача 3. Имеется 4 группы породистых котов. Для некоторого соревнования отбирают котов с длиной шерсти не менее 8 см.
Известно следующее:
1) в первой группе наибольшая длина шерсти равна 10 см;
2) во второй группе средняя длина шерсти равна 8 см;
3) в третьей группе мода длины шерсти равна 8 см;
4) в четвёртой группе медиана длины шерсти равна 9 см.
В какой из групп хотя бы половина котов гарантированно подходит по длине шерсти?
Решение.
1) Из того, что наибольшая длина шерсти равна 10 см, не следует никакой другой информации, то есть ничего не можем сказать про остальных котов этой группы.
2) Рассмотрим для примера группу котов с длиной шерсти 7 см, 7 см и 10 см. Среднее равно , но в этой группе нет половины котов, удовлетворяющих требованиям.
3) Рассмотрим для примера группу котов с шерстью длиной 8 см, 8 см, 7 см, б см, 5 см. Мода равна 8, но опять же нет половины котов, удовлетворяющих требованиям.
4) Если медиана равна 9 см, то есть половина котов с шерстью меньшей или равной длины и половина — с большей или равной длины. Значит, в этой группе найдётся половина котов с шерстью длиной не менее 8 см.
Ответ: 4.
Задача 4. По статистике автозавода из 1000 машин в среднем 20 бракованных. Сколько бракованных машин следует ожидать, если завод собирается выпустить 300 500 машин?
Решение.
Если из 1000 машин 20 бракованных, то частота появления бракованной машины равна . То есть доля бракованных машин будет равна 0,02, тогда из 300 500 машин будет
бракованных.
Ответ: 6010.
