Как вычислить площадь правильного пятиугольника по радиусу описанной вокруг него окружности?
 Популярные ответы
Популярные ответы
- Когда буквы е, ё, ю, я обозначают два звука?
- Каким членом предложения может быть местоимение?
- Как правильно произносятся слова термин, шинель, темп?
- Как найти точки экстремума функции по графику производной?
- Как правильно: по средам (ударение на «а» или на «е»)?
- Какой официальный сайт Московского энергетического института (МЭИ)?
- На какие вопросы отвечает наречие?
- Где найти примеры сравнительных оборотов и других конструкций со словом «как»?
- Как в физике обозначается скорость движения?
- Где скачать задания по английскому языку олимпиады для школьников «Покори Воробьевы горы!»?
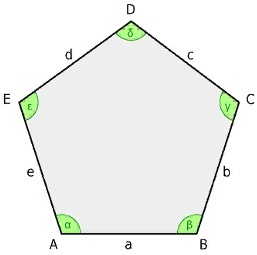
Правильный пятиугольник или пентагон (англ. regular pentagon) — это пятиугольник, все стороны и все углы которого равны между собой.
Формулы для правильного пятиугольника:
- Величина α внутренних углов правильного пятиугольника (n=5) составляет:
α = (n – 2)/n · 180° = (3/5) · 180° = 108°. - Площадь правильного пятиугольника со стороной a рассчитывается по формуле:
S = (5/4) a2 ctg(π/5) = (1/4) √5 √(5 + 2√5) a2 ≈ 1,720 a2. - Площадь правильного пятиугольника, вписанного в окружность радиуса R рассчитывается по формуле:
S = (5/2) R2 sin(2π/5) = (5√2/8) √(5 + √5) R2 ≈ 2,378 R2. - Площадь правильного пятиугольника, описанного вокруг окружности радиуса r рассчитывается по формуле:
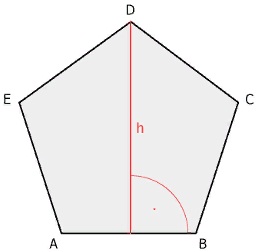
S = 5 r2 tg(π/5) = 5 √(5 – 2√5) r2 ≈ 3,633 r2. - Высота правильного пятиугольника со стороной a составляет:
h = (1/2) a tg 72° = (1/2) √(5 + 2√5) a2 = 1,539 a. - Отношение диагонали d правильного пятиугольника к его стороне a равно золотому сечению:
d/a = (1 + √5) / 2 ≈ 1,618. - Радиус r окружности, вписанной в правильный пятиугольник со стороной a составляет:
r = (1/10) √5 √(5 + 2√5) a ≈ 0,688 a. - Радиус R окружности, описанной вокруг правильного пятиугольника со стороной a составляет:
R = (1/10) √10 √(5 + √5) a ≈ 0,851 a. - Радиус R окружности, описанной вокруг правильного пятиугольника, можно найти по радиусу r вписанной в него окружности по формуле:
- R = (√5 – 1) r ≈ 1,236 r.
Факты о правильном пятиугольнике:
- Правильный пятиугольник может быть построен с помощью циркуля и линейки, или вписыванием его в заданную окружность, или построением на основе заданной стороны. Впервые это построение описал Евклид в своих «Началах» около 300 года до н.э.
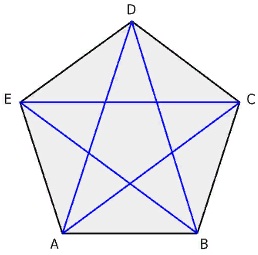
- Все диагонали правильного пятиугольника равны между собой. Вместе они образуют пятиконечную звезду, называемую также пентаграммой. Отношение длины диагонали к длине стороны правильного пятиугольника равно золотому сечению.
- Правильными пятиугольниками нельзя замостить плоскость без промежутков и наложений. Это наименьший по числу сторон правильный многоугольник, который обладает таким свойством.
- Додекаэдр — единственный правильный многогранник, грани которого представляют собой правильные пятиугольники. Правильный пятиугольник — наибольший по числу сторон правильный многоугольник, из которых можно собрать правильный многогранник.
- В природе не существует кристаллов с гранями в форме правильного пятиугольника. Однако, при формировании водяного льда на ровной поверхности меди при температурах 100—140 K на поверхности сначала возникают цепочки молекул шириной около 1 нм пентагональной структуры.
- Правильный пятиугольник можно получить, завязав узлом полоску бумаги, а затем сплющив узел.
- Пентагоном называют министерство обороны США, поскольку оно размещается в здании, имеющем в плане форму правильного пятиугольника (пентагона).
Источники:
- ru.wikipedia.org — Википедия: Правильный пятиугольник
- wolframalpha.com — Wolfram|Alpha: regular pentagon (англ. яз.)
Дополнительно на Геноне:
- Какой величины углы у правильного треугольника?
- Что такое пентаграмма?
- Сколько диагоналей у пятиугольника?
- Кто такой Евклид?
- Почему у здания Пентагона пять углов?
Последнее редактирование ответа: 20.10.2011
-

Оставить отзывОставить отзыв
Вы можете написать свои замечания к ответу, предложения об улучшении или просто поблагодарить автора. Комментарий, после проверки, увидят автор и редактор ответа. Будьте, пожалуйста, вежливыми. Спасибо!
Если Вы хотите получить уведомление об
исправлении ответа укажите свой e-mail:Неправильный формат адреса электронной почты
 Похожие вопросы
Похожие вопросы
«Как вычислить площадь правильного пятиугольника по радиусу описанной вокруг него окружности»
В других поисковых системах:
GoogleЯndexRamblerВикипедия
В соответствии с пользовательским соглашением администрация не несет ответственности за содержание материалов, которые размещают пользователи. Для урегулирования спорных вопросов и претензий Вы можете связаться с администрацией сайта genon.ru.
Размещенные на сайте материалы могут содержать информацию, предназначенную для пользователей старше 18 лет, согласно Федерального закона №436-ФЗ от 29.12.2010 года “О защите детей от информации, причиняющей вред их здоровью и развитию”. Обращение к пользователям 18+.
Правильный пятиугольник
По теореме о сумме углов выпуклого многоугольника, сумма углов правильного пятиугольника равна 180º(5-2)=540º.
Так как все углы правильного n-угольника равны между собой, каждый внутренний угол правильного пятиугольника равен 540º:5=108º (в частности, ∠A2A1A5=108º).
Сумма внешних углов многоугольника, взятых по одному при каждой вершине, равна 360º. Поскольку все внешние углы правильного пятиугольника равны между собой, градусная мера каждого, например, угла 1, равна
∠1=360º:5=72º (можно было внешний угол искать как смежный с внутренним).
Каждый центральный угол правильного пятиугольника, например, угол A1O A2, равен
Как и любой другой правильный многоугольник, правильный пятиугольник вписан в окружность и описан около окружности.
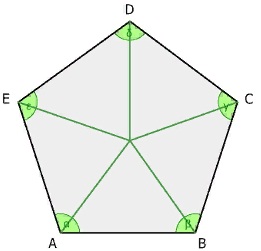
Соединив центр правильного многоугольника с его вершинами, получим пять равных равнобедренных треугольников.
Основанием каждого такого треугольника равно стороне 5-угольника, боковые стороны равны радиусу описанной окружности, угол при вершине — центральному углу 5-угольника.
Проведём из вершины высоту OF.
По свойству равнобедренного треугольника, OF является также медианой и биссектрисой треугольника A1OA5, то есть
Рассмотрим прямоугольный треугольник A1OF.
Таким образом, формула радиуса описанной около правильного пятиугольника окружности —
Подставив значение котангенса 36°, получаем:
Итак, формула радиуса вписанной в правильный пятиугольник окружности
можно найти площадь правильного пятиугольника. Здесь
Все диагонали правильного пятиугольника равны.
Площадь пятиугольника (пентагона).
Пятиугольник (пентагон) – представляет собой геометрическую фигуру с пятью углами. существует множество разных пятиугольников, однако если стороны равны, а каждый угол фигуры равен 108 градусам, то многоугольник называется правильным.
Формула расчёта площади пятиугольника (пентагона) зная длину сторон: S=n/4 × a 2 × ctg(pi/n).
Где (S) – площадь пятиугольника, (n) – количество сторон, в нашем случае 5, (a) – длина стороны, (ctg) – котангенс.
Формула расчёта площади пятиугольника (пентагона) зная радиус вписанной окружности: a = 1,4131 × r.
Где (r) – радиус вписанной окружности, дальше используем формулу расчёта площади пятиугольника (пентагона)
Формула расчёта площади пятиугольника (пентагона) зная радиус описанной окружности: a = 1,1756 × r.
Где (r) – радиус вписанной окружности, дальше используем формулу расчёта площади пятиугольника (пентагона)
Калькулятор для расчёта площади пятиугольника (пентагона), онлайн
Понравилась страница? Поделитесь ссылкой в социальных сетях. Поддержите проект!
Площадь правильного и неправильного пятиугольника: как рисовать, упражнения
Содержание:
Для расчета площадь пятиугольника для начала нам нужно определить, регулярно это или нет. Пятиугольник – это многоугольник, замкнутая плоская фигура с пятью сторонами. Когда многоугольник правильный, это означает, что длина его сторон одинакова, а его внутренние углы одинаковы.
В этом случае есть формула для вычисления точной площади правильного многоугольника, зная некоторые из его основных характеристик, которые мы выведем позже.
Если многоугольник не правильный, то есть имеет стороны разных размеров и неравные внутренние углы, единой формулы не существует.
Однако математики нашли методы вычислений, такие как разделение фигуры на другие с меньшим количеством сторон, такие как треугольники, квадраты и прямоугольники, размеры которых легко узнать или вычислить.
Еще одна процедура для вычисления площадей полигонов в целом, зная координаты их вершин, – это метод, называемый Гауссовские детерминанты, о котором мы расскажем позже.
Как найти площадь правильного пятиугольника?
Мы собираемся взять правильный пятиугольник со стороной a и разделить его на 5 равных треугольников, как показано на рисунке, проведя отрезки от центра (красный) до вершин (синий).
В свою очередь, треугольники, как и тот, который выделен желтым справа на рисунке выше, делятся на два равных прямоугольных треугольника благодаря зеленому сегменту, который называется апофема.
Апофема определяется как перпендикулярный сегмент, который соединяет центр многоугольника с центром одной из сторон. Его длина LК.
Площадь прямоугольного треугольника с основанием a / 2 и высотой LК это:
Пентагон состоит из 10 таких треугольников, поэтому его площадь равна:
А = 10 (а / 2) х LК
Но периметр п пятиугольника равно P =10а, поэтому площадь определяется как произведение периметра и длины апофемы:
Площадь правильного пятиугольника, знающая сторону a
Выражая длину апофемы LК как функция стороны a, зная, что указанный угол составляет половину центрального угла, то есть 36º, что эквивалентно:
Методом элементарной тригонометрии через тангенс острого угла 36º:
загар (π / 5) = (a / 2) ÷ LК
LК= (а / 2) ÷ загар (π / 5)
Подставив в область, выведенную в предыдущем разделе, и зная, что P = 5a:
Площадь правильного пятиугольника, зная его радиус
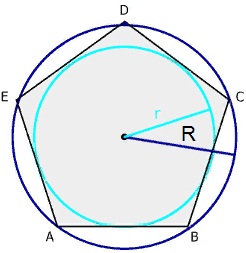
В радио правильного многоугольника – это отрезок, идущий от центра до одной из его вершин. Он соответствует радиусу описанной окружности, как показано на следующем рисунке:
Пусть R – мера указанного радиуса, которая совпадает с гипотенузой прямоугольного треугольника, выделенного синим цветом на предыдущем рисунке. По тригонометрии:
cos 36º = cos (π / 5) = LК ÷ R
sin 36º = sin (π / 5) = (a / 2) ÷ R
А = P x LК / 2 = 5р. sin (π / 5) x R. cos (π / 5) = 5R 2 [sin (π / 5) x cos (π / 5)]
Используя формулу двойного угла:
грех (2θ) = 2 греха θ. cos θ
[sin (π / 5) x cos (π / 5)] = (1/2) sin 72º
Итак, подставив это значение, мы получим следующую формулу для площади правильного пятиугольника:
А = (5/2) R 2 .sen 72º
Как рассчитать площадь неправильного пятиугольника?
Как мы уже говорили ранее, для неправильного многоугольника не существует уникальной формулы, но есть два метода, которые обычно работают очень хорошо: первый называется триангуляцией, а второй – методом детерминантов Гаусса.
Триангуляция
Он состоит из деления фигуры на треугольники, площадь которых легче вычислить, или ее также можно проверить с другими фигурами, площадь которых известна, такими как квадраты, прямоугольники и трапеции.
Гауссовские детерминанты
Другой способ найти площадь неправильного пятиугольника или другого неправильного многоугольника – это поместить фигуру в декартову систему координат, чтобы найти координаты вершин.
Зная эти координаты, применяется гауссовский метод определителей для вычисления площади, которая определяется следующей формулой:
Где A – площадь многоугольника, а (xп , Yп ) – координаты вершин. Многоугольник с n сторонами имеет 5 вершин, для пятиугольника это будет n = 5:
Полосы, сопровождающие формулу, представляют собой столбцы модуля или абсолютного значения.
Это означает, что даже если результат операции отрицательный, мы должны выразить его положительным знаком, а если он уже положительный, то его нужно оставить с этим знаком. Это потому, что площадь всегда является положительной величиной.
Процедура названа гауссовскими детерминантами в честь ее создателя, немецкого математика Карла Ф. Гаусса (1777-1855). Указанные операции эквивалентны определителю матрицы 2 × 2, например, первый определитель равен:
Чтобы найти площадь пятиугольника, мы должны решить 5 определителей, сложить результат алгебраически, разделить его на 2 и, наконец, выразить площадь всегда с положительным знаком.
Решенные упражнения
Упражнение 1
Найдите площадь правильного пятиугольника, апофема которого равна 4 см, а сторона – 5,9 см.
Решение
Поскольку это правильный пятиугольник, а у нас есть размеры стороны и апофемы, мы используем формулу, полученную выше:
Периметр P равен 5a = 5 x 5,9 см = 29,5 см.
A = 29,5 см x 4 см / 2 = 59 см 2
Упражнение 2.
Найдите площадь неправильного пятиугольника, как показано. Известны следующие размеры:
Решение
Площадь пятиугольника – это сумма площадей треугольников, которые являются прямоугольниками. В заявлении говорится, что DC ≈ DE, поэтому при применении теоремы Пифагора к треугольнику EDC мы имеем:
EC 2 = 2 ED 2 . Тогда EC = √2.ED.
Треугольники AEC и ABC имеют общую гипотенузу – отрезок AC, поэтому:
EA 2 + EC 2 = AB 2 + BC 2
Поскольку EA и AB измеряют одно и то же, отсюда следует, что:
Поскольку BC = 12, то ED = 12 / √2 = 8,485.
Используя эти значения, мы рассчитаем площадь каждого треугольника и добавим их в конце.
Площадь треугольника EDC
ED x DC / 2 = 8,485 2 / 2 = 36
Площадь треугольника AEC
EA x EC / 2 = EA x √2. ED / 2 = 5 x √2. 8 485/2 = 30
Площадь треугольника ABC
Тогда искомая область:
Это то же самое, что и треугольник AEC, поскольку они оба имеют одинаковые размеры.
Площадь неправильного пятиугольника
Наконец, запрашиваемая площадь представляет собой сумму площадей трех треугольников:
А = 36 + 30 + 30 единиц = 96 единиц.
Ссылки
- Александр, Д. 2013. Геометрия. 5-е. Издание. Cengage Learning.
- Открытый справочник по математике. Площадь многоугольника. Получено с: mathopenref.com.
- Формулы Вселенной. Площадь неправильного пятиугольника. Получено с: universaloformulas.com.
- Формулы Вселенной. Площадь правильного пятиугольника. Получено с: universaloformulas.com.
- Википедия. Пентагон. Получено с: es.wikipedia.com.
80 лучших слов о любви, которые затронут ваше сердце
Как удалить зубной камень с зубов? 5 советов
[spoiler title=”источники:”]
http://codemg.ru/geometry/ploshad_pyatiugolnika.php
http://ru1.warbletoncouncil.org/area-pentagono-12790
[/spoiler]
Загрузить PDF
Загрузить PDF
Пятиугольник — это многоугольник, у которого пять углов. В подавляющем большинстве задач вы столкнетесь с правильным пятиугольником, у которого все стороны равны. Есть два основных способа найти площадь пятиугольника (в зависимости от известных вам величин).
-

1
Даны сторона и апофема. Этот метод применим к правильным пятиугольникам, у которых все стороны равны. Апофема — это отрезок, соединяющий центр пятиугольника и середину любой из его сторон; апофема всегда перпендикулярна стороне пятиугольника.
- Не путайте апофему с радиусом описанной окружности. Такой радиус — это отрезок, соединяющий центр пятиугольника с его вершиной (а не серединой стороны). Если вам дана сторона и радиус описанной окружности, перейдите к следующей главе.
- Например, дан пятиугольник со стороной 3 см и апофемой 2 см.
-

2
Разделите пятиугольник на пять равных треугольников. Для этого соедините центр пятиугольника с каждой из его вершин.
-

3
Вычислите площадь треугольника. Основание каждого треугольника — это сторона пятиугольника, а высота каждого треугольника — это апофема пятиугольника. Для вычисления площади треугольника перемножьте половину основания и высоту, то есть площадь = ½ х основание х высоту.
- В нашем примере площадь треугольника = ½ х 3 х 2 = 3 квадратных сантиметра.
-

4
Умножьте найденную площадь треугольника на 5, чтобы вычислить площадь пятиугольника. Это верно, так как мы разделили пятиугольник на пять равных треугольников.
- В нашем примере площадь пятиугольника = 5 х площадь треугольника = 5 х 3 = 15 квадратных сантиметров.
Реклама
-

1
Если дана сторона. Этот метод применим к правильным пятиугольникам, у которых все стороны равны.
- Например, дан пятиугольник со стороной 7 см.
-

2
Разделите пятиугольник на пять равных треугольников. Для этого соедините центр пятиугольника с каждой из его вершин.
-

3
Разделите треугольник пополам. Для этого из вершины треугольника, которая лежит в центре пятиугольника, опустите перпендикуляр к противоположной стороне треугольника, которая равна стороне пятиугольника. Вы получите два равных прямоугольных треугольника.
-

4
Дайте обозначения одному из прямоугольных треугольников.
- Основание прямоугольного треугольника — это половина стороны пятиугольника. В нашем примере основание равно ½ х 7 = 3,5 см.
- Угол вокруг центра пятиугольника равен 360˚. Разделив пятиугольник на пять равных треугольников, а потом разделив каждый треугольник пополам, вы поделите угол вокруг центра пятиугольника на 10 равных частей, то есть угол прямоугольного треугольника, противолежащий основанию, равен 360°/10 = 36˚.
-

5
Вычислите высоту треугольника. Высота прямоугольного треугольника равна его катету, отличному от основания. Используйте тригонометрические функции, чтобы найти высоту треугольника.[1]
- В прямоугольном треугольнике тангенс угла равен отношению противолежащей стороны к прилежащей стороне.
- В нашем примере для угла в 36˚ противолежащей стороной является основание, а прилежащей — высота.
- tg 36˚ = противолежащая сторона/прилежащая сторона
- В нашем примере tg 36˚ = 3,5/высота
- Высота х tg 36˚ = 3,5
- Высота = 3,5/tg 36˚
- Высота = 4,8 см (примерно)
-

6
Найдите площадь треугольника. Площадь треугольника = ½ х основание х высота (А = ½bh). Зная основание и высоту, вы можете найти площадь прямоугольного треугольника.
- В нашем примере площадь прямоугольного треугольника = ½bh = ½(3,5)(4,8) = 8,4 квадратных сантиметров.
-

7
Умножьте найденную площадь прямоугольного треугольника на 10, чтобы вычислить площадь пятиугольника. Это верно, так как мы разделили пятиугольник на десять равных прямоугольных треугольников.
- В нашем примере площадь пятиугольника равна 8,4 х 10 = 84 квадратных сантиметра.
Реклама
-

1
Даны периметр и апофема. Апофема — это отрезок, соединяющий центр пятиугольника и середину любой из его сторон; апофема всегда перпендикулярна стороне пятиугольника.
- A = ра/2, где р — периметр, а — апофема. [2]
- Если дана сторона, вычислите периметр правильного пятиугольника по формуле: p = 5s, где s — сторона пятиугольника.
- A = ра/2, где р — периметр, а — апофема. [2]
-

2
Дана сторона. Если дана только сторона пятиугольника, используйте следующую формулу:[3]
- А = (5s2) / (4tg36˚), где s — сторона пятиугольника.
- tg36˚ = √(5-2√5).[4]
Если на калькуляторе нет функции тангенса, используйте следующую формулу: А = (5s2) / (4√(5-2√5)).
-

3
Дан радиус описанной окружности. В этом случае для вычисления площади пятиугольника используйте следующую формулу:[5]
- A = (5/2)r2sin72˚, где r — радиус описанной окружности.
Реклама
Советы
- Сложнее работать с неправильным пятиугольником (это пятиугольник, стороны которого имеют разную длину). В этом случае разделите пятиугольник на треугольники, найдите их площади и сложите значения площадей. Вы также можете обрисовать пятиугольник правильной фигурой, вычислить ее площадь, а затем вычесть площадь дополнительного пространства.
- Формулы, полученные геометрическим путем, аналогичны формулам, которые описаны в этой статье. Подумайте, сможете ли вы вывести эти формулы. Формулу, включающую радиус описанной окружности, вывести труднее (намек: рассматривайте удвоенный угол при центре пятиугольника).
- В приведенных в этой статье примерах используются округленные значения, чтобы упростить вычисления. Если вы работаете с реальным многоугольником, то вы получите другие результаты для других длин и площадей.
- Если возможно, вычислите площадь пятиугольника, используя оба описанных метода. Затем сравните результаты, чтобы подтвердить правильность ответа.
Реклама
Об этой статье
Эту страницу просматривали 234 675 раз.
Была ли эта статья полезной?
Правильном пятиугольнике это многоугольнике с 5 вершинами. Данная форма часто используется при строительстве и в архитектуре. Введите одно из известных значений, затем нажмите кнопку вычислить.
.
Поделиться расчетом:
Калькулятор пятиугольника
Длина стороны(a)
Диагноль(D)
Высота(h)
Периметр(p)
Площадь(S)
Радиус описанной окружности(R)
Радиус вписанной окружности(r)
Вычислить
Очистить
Формулы:
d = a / 2 * ( 1 + √5 )
h = a / 2 * √ 5 + 2 * √5
Р = 5 * а
S = a2 / 4 * √ 25 + 10 * √5
R = a / 10 * √ 50 + 10 * √5
r = a / 10 * √ 25 + 10 * √5
Угол: 72°, 5 сторон.
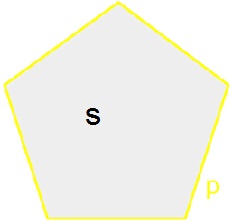
Ещё одна воскресная задача, у которой много общего с предыдущими двумя. На самом деле не очень сложная. Тут уж точно – только свойство площадей. Формул для нахождения площади пятиугольника у нас в школьной программе нет, ну кроме одной – через полупериметр и радиус вписанной окружности, но тут ни того, ни другого. Но формулу напомню:
S = p • r – площадь описанного около окружности многоугольника; p – полупериметр; r – радиус вписанной в многоугольник окружности.
Как всегда, нужно решение. Поехали?
Условие
Найдите площадь выпуклого пятиугольника ABCDE , в котором ∠ABC = ∠CDE = 90°, BC = CD = AE = 1 см, AB + DE = 1 см.
