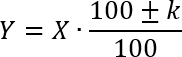Вычисление исходного числа по известному проценту от числа
Формула вычисления числа по его проценту.
Если дано число B которое составляет P процентов от числа A и необходимо найти значение числа A, то
Для вывода этого соотношения используем методику решения задач с процентами через пропорции
“все“”часть” =100%”часть в %“ =>
“все” = “часть” · “100%“часть в %
Примеры вычисления исходного числа по известному проценту от числа
Пример 1.
Найти исходное число, если 5% от этого числа равно 40.
Решение:
Ответ: 800.
Пример 2.
На заводе работает 270 женщины. Это 30% от всех работников. Сколько человек работает на заводе?
Решение:
Ответ: На заводе работает 900.
Пример 3.
Какую сумму нужно положить на депозит под 10% годовых, чтобы через год получить прибыль 1000 рублей.
Решение:
Ответ: на депозит необходимо положить 10000 рублей.
При изучении процентов вам также будут полезны:
Онлайн калькулятор для вы нахождения числа по его процентам, может решать примеры, сохранять историю вычисления и копировать ссылку на расчет.
Правило: Чтобы найти число по его проценту, нужно заданное число разделить на заданную величину процента, а результат умножить на 100.
Примеры вычисления исходного числа по известному проценту от числа:
Например: число 4 это 5% от неизвестного нам числа, чтобы найти это число нужно 4/5×100=80
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Формула простого процента: как найти исходное значение
13 ноября 2013
В этом коротком видеоуроке мы научимся решать задачи на проценты с помощью специальной формулы, которая так и называется: формула простого процента. Давайте оформим эту формулу в виде теоремы.
Теорема о простом проценте. Предположим, что есть некая исходная величина x, которая затем меняется на k%, и получается новая величина y. Тогда все три числа связаны формулой:
Плюс или минус перед коэффициентом k ставится в зависимости от условия задачи. Если по условию величина x возрастает, то перед k стоит плюс. Если же величина уменьшается, то перед коэффициентом k стоит минус.
Несмотря на кажущуюся мудреность этой формулы, многие задачи с ее помощью решаются очень быстро и красиво. Давайте попробуем.
Задача. Цена на товар была повышена на 10% и составила 2970 рублей. Сколько рублей стоил товар до повышения цены?
Чтобы решить эту задачу с помощью формулы простых процентов, нам необходимы три числа: исходное значение x, проценты k и итоговое значение y. Из всех трех чисел нам известны проценты k = 10 и итоговое значение y = 2970. Обратите внимание: 2970 — это именно итоговая цена, т.е. y. Потому что по условию задачи исходная цена на товар неизвестна (ее как раз требуется найти). Но затем она была повышена, и только тогда составила 2970 рублей.
Итак, нам нужно найти x, т.е. исходное значение. Что ж, подставляем наши числа в формулу и получаем:
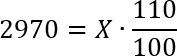
Складываем числа в числителе и получаем:
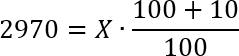
Сокращаем по одному нулю в числителе и знаменателе, а затем умножаем обе части уравнения на 10. Получим:
11x = 29 700
Чтобы найти x из этого простейшего линейного уравнения, нужно разделить обе стороны на 11:
x = 29 700 : 11 = 2700
Как видите, это довольно большие числа, поэтому в уме такие вычисления не провести. В случае, если такая задача встретится вам на ЕГЭ, придется делить уголком. При этом все разделилось без остатка, и мы получили значение x:
x = 2700
Именно столько стоил товар до повышения цены. И именно это число нам требовалось найти по условию задачи. Поэтому все: задача решена. Причем решена не «напролом», а с помощью формулы простого процента — быстро, красиво и наглядно.
Разумеется, эту задачу можно было решать по-другому. Например, через пропорции. Или экзотическим методом коэффициентов. Но будет гораздо лучше и надежнее, если у вас на вооружении будет несколько приемов для решения любой задачи на проценты. Так что обязательно попрактикуйтесь в использовании данной формулы.
А у меня на этом все. С вами был Павел Бердов. До новых встреч!:)
Смотрите также:
- Процент: неизвестно начальное значение (метод пропорции)

- Формула простого процента: неизвестно конечное значение

- Решение ЕГЭ-2011: вариант 1, часть B

- Метод коэффициентов, часть 1

- Деление многочленов уголком

- Сфера, вписанная в куб

Часто при работе с числами, нам нужно найти неизвестное число, зная только процент от него или процентное изменение. В этом посте мы рассмотрим, как найти неизвестное число, используя известное число и процент.
Найти число по его проценту
Если мы знаем процент исходного числа, который составляет неизвестное число, мы можем использовать следующую формулу:
Неизвестное число = (Известное число * Процент) / 100
Например, если мы знаем, что 20% от неизвестного числа равно 50, мы можем использовать формулу, чтобы найти неизвестное число:
Неизвестное число = (50 * 100) / 20 = 250
Таким образом, неизвестное число равно 250.
Нахождение числа, зная процентное изменение
Если мы знаем процентное изменение исходного числа, мы можем использовать следующую формулу:
Неизвестное число = Известное число / (1 + (Процентное изменение / 100))
Например, если мы знаем, что число увеличилось на 25%, и новое значение равно 125, мы можем использовать формулу, чтобы найти исходное число:
Неизвестное число = 125 / (1 + (25 / 100)) = 100
Таким образом, исходное число равно 100.
Нахождение числа, зная число и процент
Иногда нам может быть известно неизвестное число и процент, который оно составляет от известного числа. В этом случае мы можем использовать следующую формулу:
Известное число = Неизвестное число * 100 / Процент
Например, если мы знаем, что неизвестное число равно 75% от известного числа, и известное число равно 200, мы можем использовать формулу, чтобы найти неизвестное число:
Неизвестное число = 200 * 75 / 100 = 150
Таким образом, неизвестное число равно 150.
Заключение
Надеемся, что эти формулы помогут вам эффективно находить неизвестные числа, когда вам известны проценты или процентные изменения. Эти простые математические приемы могут быть полезными в повседневной жизни, а также при решении более сложных математических задач.
#Калькуляторы
Онлайн калькулятор вычисляет 100 процентов зная число и сколько процентов оно составляет от искомого числа. Для вычисления нужно число разделить на процент и умножить на 100.
Значащих цифр:
Вычислить число если
% от него равно
Вычислить число если 84% от него равно 26
Вычислить число если 95% от него равно 38
Вычислить число если 70% от него равно 37
Вычислить число если 54% от него равно 136
Вычислить число если 2% от него равно 120
Вычислить число если 60% от него равно 90