Видеоурок: закон Архимеда
Зако́н Архиме́да — закон гидростатики и аэростатики: на тело, погружённое в жидкость или газ, действует выталкивающая сила, численно равная весу объема жидкости или газа, вытесненного телом. Закон открыт Архимедом в III веке до н. э. Выталкивающая сила также называется архимедовой силой или гидростатической подъёмной силой[1][2] (её не следует путать с аэро- и гидродинамической подъёмной силой, возникающей при обтекании тела потоком газа или жидкости).
Так как сила Архимеда обусловлена силой тяжести, то в невесомости она не действует.
В соответствии с законом Архимеда для выталкивающей силы выполняется[3]:
где:
Описание[править | править код]
Выталкивающая или подъёмная сила по направлению противоположна силе тяжести, прикладывается к центру тяжести объёма, вытесняемого телом из жидкости или газа.
Если тело плавает (см. плавание тел) или равномерно движется вверх или вниз, то выталкивающая или подъёмная сила по модулю равна силе тяжести, действующей на вытесненный телом объём жидкости или газа.
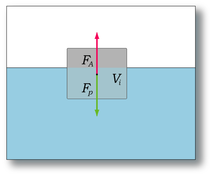
Плавание тела. Сила Архимеда (


ρж g Vж = ρт g Vт
Например, воздушный шарик объёмом 



Закон Архимеда можно объяснить при помощи разности гидростатических давлений на примере прямоугольного тела, погруженного в жидкость или газ. В силу симметрии прямоугольного тела, силы давления, действующие на боковые грани тела, уравновешиваются. Давление (

где:
Давление (

где:
Сила давления жидкости или газа на тело определяется разностью сил 

где:
Разница давлений:
В отсутствие гравитационного поля, то есть в состоянии невесомости, закон Архимеда не работает. Космонавты с этим явлением знакомы достаточно хорошо. В частности, в невесомости отсутствует явление (естественной) конвекции, поэтому, например, воздушное охлаждение и вентиляцию жилых отсеков космических аппаратов необходимо производить принудительно вентиляторами.
Обобщения[править | править код]
Некий аналог закона Архимеда справедлив также в любом поле сил, которое по-разному действуют на тело и на жидкость (газ), либо в неоднородном поле. Например, это относится к полю сил инерции (например, к полю центробежной силы) — на этом основано центрифугирование. Пример для поля немеханической природы: диамагнетик в вакууме вытесняется из области магнитного поля большей интенсивности в область с меньшей.
Вывод закона Архимеда для тела произвольной формы[править | править код]
Вывод через мысленный эксперимент[править | править код]
Если мысленно заменить погружённое в жидкость тело той же жидкостью, мысленно размещённая в том же объёме порция воды будет находиться в равновесии и действовать на окружающую воду с силой, равной силе тяжести, действующей на порцию воды. Так как перемешивания частиц воды не происходит, можно утверждать, что окружающая вода действует на выделенный объём с той же силой, но направленной в противоположном направлении, то есть с силой, равной 
Расчёт силы[править | править код]
Гидростатическое давление 










При переходе от интеграла по поверхности к интегралу по объёму пользуемся обобщённой теоремой Остроградского-Гаусса.
Получаем, что модуль силы Архимеда равен 
Вывод через закон сохранения энергии[править | править код]
Закон Архимеда можно также вывести из закона сохранения энергии. Работа силы, действующей со стороны погружённого тела на жидкость, приводит к изменению её потенциальной энергии:
где 

По третьему закону Ньютона эта сила, равна по модулю и противоположна по направлению силе Архимеда, действующей со стороны жидкости на тело. Объём вытесненной жидкости равен объёму погруженной части тела, поэтому массу вытесненной жидкости можно записать как:
где
— объем погружённой части тела.
Таким образом, для силы Архимеда имеем:
Условие плавания тел[править | править код]
Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести 

— тело тонет;
— тело плавает в жидкости или газе;
— тело всплывает до тех пор, пока не начнёт плавать.
Другая формулировка (где 

— тело тонет;
— тело плавает в жидкости или газе;
— тело всплывает до тех пор, пока не начнёт плавать.
Примечания[править | править код]
- ↑ Архимеда закон : [арх. 1 января 2023] // Анкилоз — Банка. — М. : Большая российская энциклопедия, 2005. — С. 331. — (Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов ; 2004—2017, т. 2). — ISBN 5-85270-330-3.
- ↑ Архимеда закон // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1988. — Т. 1: Ааронова — Бома эффект — Длинные линии. — С. 123. — 707 с. — 100 000 экз.
- ↑ Всё написанное ниже, если не оговорено иное, относится к однородному полю силы тяжести (например, к полю, действующему вблизи поверхности планеты).
- ↑ Перышкин А. , Оригинальное доказательство закона Архимеда. Дата обращения: 28 сентября 2020. Архивировано 20 июля 2020 года.
- ↑ Доказательство закона Архимеда для тела произвольной формы. Дата обращения: 28 сентября 2020. Архивировано 21 сентября 2020 года.
- ↑ Buoyancy (англ.). Архивировано 14 июля 2007 года.
Ссылки[править | править код]
- Архимедов закон // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- Закон Архимеда // Энциклопедия «Кругосвет».
Загрузить PDF
Загрузить PDF
Плавучесть – это выталкивающая сила, действующая на тело, погруженное в жидкость (или газ), и направленная противоположно силе тяжести. В общих случаях выталкивающая сила может быть вычислена по формуле: Fb = Vs × D × g, где Fb – выталкивающая сила; Vs – объем части тела, погруженной в жидкость; D – плотность жидкости, в которую погружают тело; g – сила тяжести.
-

1
Найдите объем части тела, погруженной в жидкость (погруженный объем). Выталкивающая сила прямо пропорциональна объему части тела, погруженной в жидкость. Другими словами, чем больше погружается тело, тем больше выталкивающая сила. Это означает, что даже на тонущие тела действует выталкивающая сила. Погруженный объем должен измеряться в м3.
- У тел, которые полностью погружены в жидкость, погруженный объем равен объему тела. У тел, плавающих в жидкости, погруженный объем равен объему части тела, скрытой под поверхностью жидкости.
- В качестве примера рассмотрим шар, плавающий в воде. Если диаметр шара равен 1 м, а поверхность воды доходит до середины шара (то есть он погружен в воду наполовину), то погруженный объем шара равен его объему, деленному на 2. Объем шара вычисляется по формуле V = (4/3)π(радиус)3 = (4/3)π(0,5)3 = 0,524 м3. Погруженный объем: 0,524/2 = 0,262 м3.
-

2
Найдите плотность жидкости (в кг/м3), в которую погружается тело. Плотность – это отношение массы тела к занимаемому этим телом объему. Если у двух тел одинаковый объем, то масса тела с большей плотностью будет больше. Как правило, чем больше плотность жидкости, в которую погружается тело, тем больше выталкивающая сила. Плотность жидкости можно найти в интернете или в различных справочниках.
- В нашем примере шар плавает в воде. Плотность воды приблизительно равна 1000 кг/м3.
- Плотности многих других жидкостей можно найти здесь.
-

3
Найдите силу тяжести (или любую другую силу, действующую на тело вертикально вниз). Не важно, плавает ли тело или тонет, на него всегда действует сила тяжести. В естественных условиях сила тяжести (а точнее сила тяжести, действующая на тело массой 1 кг) приблизительно равна 9,81 Н/кг. Тем не менее, если на тело действуют и другие силы, например, центробежная сила, такие силы необходимо учесть и вычислить результирующую силу, направленную вертикально вниз.
- В нашем примере мы имеем дело с обычной стационарной системой, поэтому на шар действует только сила тяжести, равная 9,81 Н/кг.
- Однако если шар плавает в емкости с водой, которая вращается вокруг некоторой точки, то на шар будет действовать центробежная сила, которая не позволяет шару и воде выплескиваться наружу и которую необходимо учесть в расчетах.
-

4
Если у вас есть значения погруженного объема тела (в м3), плотность жидкости (в кг/м3) и сила тяжести (или любая другая сила, направленная вертикально вниз), то вы можете вычислить выталкивающую силу. Для этого просто перемножьте указанные выше значения, и вы найдете выталкивающую силу (в Н).
- В нашем примере: Fb = Vs × D × g. Fb = 0,262 м3 × 1000 кг/м3 × 9,81 Н/кг = 2570 Н.
-

5
Выясните, будет ли тело плавать или тонуть. По приведенной выше формуле можно вычислить выталкивающую силу. Но, выполнив дополнительные расчеты, вы можете определить, будет ли тело плавать или тонуть. Для этого найдите выталкивающую силу для всего тела (то есть в вычислениях используйте весь объем тела, а не погруженный объем), а затем найдите силу тяжести по формуле G = (масса тела)*(9,81 м/с2). Если выталкивающая сила больше силы тяжести, то тело будет плавать; если же сила тяжести больше выталкивающей силы, то тело будет тонуть. Если силы равны, то тело обладает «нейтральной плавучестью».
- Например, рассмотрим 20 килограммовое бревно (цилиндрической формы) с диаметром 0,75 м и высотой 1,25 м, погруженное в воду.
- Найдите объем бревна (в нашем примере объем цилиндра) по формуле V = π(радиус)2 (высота) = π(0,375)2(1,25) = 0,55 м3.
- Далее вычислите выталкивающую силу: Fb = 0,55 м3 × 1000 кг/м3 × 9,81 Н/кг = 5395,5 Н.
- Теперь найдите силу тяжести: G = (20 кг)(9,81 м/с2) = 196,2 Н. Это значение намного меньше значения выталкивающей силы, поэтому бревно будет плавать.
- Например, рассмотрим 20 килограммовое бревно (цилиндрической формы) с диаметром 0,75 м и высотой 1,25 м, погруженное в воду.
-

6
Используйте описанные выше вычисления для тела, погруженного в газ. Помните, что тела могут плавать не только в жидкостях, но и в газах, которые вполне могут выталкивать некоторые тела, несмотря на очень небольшую плотность газов (вспомните про шар, наполненный гелием; плотность гелия меньше плотности воздуха, поэтому шар с гелием летает (плавает) в воздухе).
Реклама
-

1
Поместите небольшую чашку в ведро. В этом простом эксперименте мы покажем, что на тело, погруженное в жидкость, действует выталкивающая сила, так как тело выталкивает объем жидкости, равный погруженному объему тела. Мы также продемонстрируем, как найти выталкивающую силу при помощи эксперимента. Для начала поместите небольшую чашку в ведро (или кастрюлю).
-

2
Наполните чашку водой (до краев). Будьте осторожны! Если вода из чашки вылилась в ведро, вылейте воду и начните заново.
- Для эксперимента предположим, что плотность воды равна 1000 кг/м3 (только если вы не используете соленую воду или другую жидкость).
- Для наполнения чашки до краев используйте пипетку.
-

3
Возьмите небольшой предмет, который поместится в чашке и не будет поврежден водой. Найдите массу этого тела (в килограммах; для этого взвесьте тело на весах и конвертируйте значение в граммах в килограммы). Затем медленно опустите предмет в чашку с водой (то есть погрузите тело в воду, но при этом не погружайте пальцы). Вы увидите, что некоторое количество воды вылилось из чашки в ведро.
- В этом эксперименте мы опустим в чашку с водой игрушечный автомобиль массой 0,05 кг. Объем этого автомобиля нам не нужен, чтобы вычислить выталкивающую силу.
-

4
При погружении тела в воду оно выталкивает некоторый объем воды (иначе тело не погрузилось бы в воду). Когда тело выталкивает воду (то есть тело действует на воду), на тело начинает действовать выталкивающая сила (то есть вода действует на тело). Вылейте воду из ведра в мерный стакан. Объем воды в мерном стакане должен быть равен объему погруженного тела.
- Другими словами, если тело плавает, то объем вытесненной жидкости равен погруженному объему тела. Если тело утонуло, то объем вытесненной жидкости равен объему всего тела.
-

5
Вычислите массу вытесненной воды по известным значениям объема этой воды и плотности воды. Значение объема воды, показанного шкалой мерного стакана, конвертируйте в м3 (вы можете сделать это здесь), а затем умножьте объем вытесненной воды на плотность воды (1000 кг/м3).
- В нашем примере игрушечный автомобиль утонул, вытеснив около двух столовых ложек воды (0,00003 м3). Вычислим массу вытесненной воды: 1000 кг/м3 × 0,00003 м3 = 0,03 кг.
-

6
Сравните массу вытесненной воды с массой погруженного тела. Если масса погруженного тела больше массы вытесненной воды, то тело утонет. Если масса вытесненной воды больше массы тела, то оно плавает. Поэтому для того, чтобы тело плавало, оно должно вытеснять количество воды с массой, превышающей массу самого тела.
- Таким образом, тела, имеющие небольшую массу, но большой объем, обладают наилучшей плавучестью. Эти два параметра характерны для полых тел. Вспомните лодку – она обладает превосходной плавучестью, потому что она полая и вытесняет много воды при небольшой массе самой лодки. Если бы лодка не была полой, она бы вообще не плавала (а тонула).
- В нашем примере масса автомобиля (0,05 кг) больше массы вытесненной воды (0,03 кг). Поэтому автомобиль и утонул.
Реклама
Советы
- Используйте весы, показания которых можно сбросить до 0 перед каждым новым взвешиванием. В этом случае вы получите точные результаты.
Реклама
Что вам понадобится
- Маленькая чашка или миска
- Большая чашка или ведро
- Тело для погружения (например, резиновый мячик)
- Мерный стакан
Об этой статье
Эту страницу просматривали 61 047 раз.
Была ли эта статья полезной?
Содержание:
- Определение и формула силы выталкивания
- Примеры решения задач
На поверхность тела, которое находится в жидкости или газе действуют силы давления. Известно, что давление увеличивается с увеличением
глубины погружения. Значит, что силы давления, которые действуют на нижнюю часть тела и направлены вверх больше по модулю, чем силы,
которые действуют на верхнюю часть тела и направлены вниз.
Определение и формула силы выталкивания
Определение
Равнодействующую сил давления на тело, которое погружено в жидкость или газ называют выталкивающей силой. Выталкивающая сила
может быть больше, чем сила тяжести, которая действует на тело. Силы выталкивания появляются и в том случае,если тело находится
в жидкости или газе частично.
Если тело, находящееся в жидкости оставить в покое, то оно тонет, находится в равновесии или всплывает на поверхность.
Это зависит от соотношения силы тяжести и выталкивающей силы (FA),действующих на тело. В первом случае (тело тонет)
mg>FA . Если mg=FA, то тело находится в равновесии. При mgA
тело всплывает на поверхность.
На тело, погруженное в жидкость или газ, действует сила выталкивания (сила Архимеда FA), равная весу вытесненной им жидкости или газа.
В математическом виде данный закон выглядит как:
$$F_{A}=rho V g$$
где $rho$ – плотность жидкости (газа),
в которую погружено тело, g=9,8 м/с2 – ускорение свободного падения, V – объем тела (его части),
которое находится в жидкости (газе). Сила Архимеда приложена к центру тяжести объема части тела, которая находится в жидкости (газе).
Закон Архимеда можно применять для вычисления плотности однородного тела неправильной формы. При этом тело взвешивают два раза:
один раз в воздухе, второй раз, погрузив тело в жидкость, плотность которой известна.
Основной единицей измерения силы Архимеда, как и любой силы в системе СИ является: [FA]=Н
В СГС: FA]=дин
1Н= (кг•м)/с2
Примеры решения задач
Пример
Задание. Какова сила выталкивания, которая действует на куб, погруженный в систему жидкостей.
Сосуд наполнен водой, поверх воды налит керосин. Граница раздела жидкостей проходит посередине грани куба. Плотность воды считайте равной
$rho$1=103 кг/м3 ,
плотность керосина равна $rho$2=0,81•103
кг/м3 . Сторона куба равна a=0,1 м.
Решение. Сделаем рисунок.
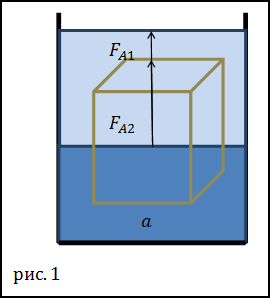
Сила выталкивания, которая действует со стороны воды, на половину куба равна:
$$F_{A 1}=rho_{1} frac{V}{2} g$$
где V=a3
Сила выталкивания, которая действует со стороны керосина, на половину куба равна:
$$F_{A 2}=rho_{2} frac{V}{2} g$$
Обе силы направлены вверх. Приложены они к разным точкам (центрам масс объемов тел, погруженных в соответствующие жидкости),
при суммировании векторы можно перенести в одну точку параллельно самим себе. Получим, результирующая сила выталкивания равна:
$$F_{A}=F_{A 1}+F_{A 2}(1.3)$$
Подставим компоненты силы (1.2), (1.3) в выражение (1.1), имеем:
$$F_{A}=rho_{1} frac{a^{3}}{2} g+rho_{2} frac{a^{3}}{2} g$$
Проведем вычисления:
$$F_{A}=10^{3} frac{(0,1)^{3}}{2} cdot 9,8+0,81 cdot 10^{3} frac{(0,1)^{3}}{2} cdot 9,8 approx 8,8(H)$$
Ответ. Ответ: FA=8,8 Н

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Какова плотность камня, если его вес в воздухе 3,2 Н, а вес в воде 1,8 Н.
Решение. Вес камня в воздухе:
$$P=rho g V rightarrow V=frac{P}{rho g}$$
где $rho$ – плотность камня, V – объем камня.
Взвешивая камень в воде, получаем вес камня в жидкости, равный:
$$P^{prime}=P-F_{A}(2.2)$$
где FA – сила выталкивания (сила Архимеда). В соответствии с законом Архимеда:
$$F_{A}=rho_{H_{2} O g V}$$
где $rho$H2O –
плотность воды. Подставим вместо V выражение (2.1), имеем:
$$F_{A}=rho_{H_{2} O g} frac{P}{rho g}=frac{rho_{H_{2} O}}{rho} P(2.4)$$
Подставим в уравнение (2.2) формулу (2.4), получаем:
$$rho=frac{P cdot rho_{H_{2} O}}{P-P^{prime}}(2.5)$$
Плотность воды будем считать равной
$rho$H2O=103 кг/м3 .
Можно провести вычисления:
$rho=frac{3,2 cdot 10^{3}}{3,2-1,8} approx 2,29 cdot 10^{3}$ кг/м3
Ответ. Плотность камня $ 2,29 cdot 10^{3}$ кг/м3
Читать дальше: Формула силы тока.
Выталкивающая сила, действующая на объекты в жидкой среде, прикладывается вверх к жидкости и обеспечивает плавание, погружение или подъем объекта в жидкости.
Выталкивающая сила, действующая на объект, следует принципам Архимеда: задействованы несколько сущностей, таких как вес, плотность и природа жидкой среды. Используя все эти объекты, давайте научимся рассчитывать выталкивающую силу и решать задачи, связанные с выталкивающей силой.
Чтобы рассчитать выталкивающую силу, необходимо выполнить шаги, указанные ниже:
- Найдите объем погруженного тела –Поскольку на объем объекта в жидкой среде в значительной степени влияет плавучесть; поэтому нам нужно их найти.
- Найти плотность тела и текучей среды –Плотность как объекта, так и жидкости необходима, потому что плотность играет жизненно важную роль в проявлении выталкивающей силы.
- Найдите силу тяжести или направленную вниз силу –выталкивающая сила направлена вверх, поэтому ее необходимо уравновешивать силой, направленной вниз; таким образом, необходимо выяснить либо гравитацию, либо любую направленную вниз силу, действующую на объект в среде.
Формула выталкивающей силы
Поскольку мы знаем, что плотность, объем и направленная вниз сила, такая как гравитация, напрямую влияют на выталкивающую силу, используя все эти объекты, общая формула для выталкивающей силы дается выражением
Fb=V×ρ×г
Где; V — объем жидкости, ρ — плотность жидкости, g — ускорение свободного падения.
Эта формула дает выталкивающую силу жидкой среды, действующую на объект в соответствии с принципом Архимеда.
Как найти выталкивающую силу с плотностью?
Плотность — это не что иное, как масса на единицу объема вещества, поэтому плотность жидкости необходимо знать для расчета выталкивающей силы.
- Плотность жидкости находится по формуле р=м/обf
- Где ρ — плотность жидкости, m — масса, а V — объем жидкости.
- Формула может рассчитать объем жидкости; Вf=л×ш×ч; где l — длина, w — ширина, h — высота.
Подставляя значения плотности и объема, выталкивающая сила рассчитывается по формуле Fb=ρgV.
Например, тело массой 4 кг погружено в жидкую среду объемом 8 м.3 как рассчитать выталкивающую силу жидкости? Примите ускорение свободного падения равным 9.8 м/с.2.
Дано – масса объекта, m=4кг
Объем V=8м3
Плотность жидкости ρ определяется выражением
р=м/обf
р=4/8
ρ = 0.5 кг/м3
Выталкивающая сила с плотностью определяется выражением
Fb= ρgV
Подставляя значения всех заданных значений, получаем
Fb=(0.5)(8)(9.8)
Fb= 39.2N
Как рассчитать выталкивающую силу плавучего объекта?
Приведенный выше расчет, связанный с выталкивающей силой, дает величину силы, действующей на объект, чтобы вытолкнуть его из подводного состояния. Рассчитать его довольно просто, но как рассчитать выталкивающую силу плавучего объекта?
- О предмете говорят, что он плавает, если выталкивающая сила больше силы тяжести. Необходимо выполнить некоторую дополнительную работу, чтобы найти выталкивающую силу, действующую на плавучий объект. Шаги, которые необходимо выполнить для определения плавучести, приведены ниже.
- Сначала рассчитайте всю выталкивающую силу, действующую на тело в жидкости, т. е. используйте весь объем.
- Затем найдите гравитационную силу, толкающую объект вниз, по уравнению W=mg; где m — масса объекта, а g — ускорение свободного падения, также известное как вес объекта.
- Если сила плавучести и сила тяжести меньше выталкивающей силы, то объект плавает в жидкости.
Изображение кредита: Wikimedia Commons
Решенный пример может быть ясен для понимания плавучий плавучий силовой расчет.
Объект массой 12 кг и плотностью 0.58 кг/м3 опускается в жидкость. Как рассчитать выталкивающую силу, действующую на тело, чтобы оно плавало в жидкости?
Дано – масса объекта m=12кг
Плотность объекта ρ=0.58 кг/м3
Объем объекта может быть задан как
V=м/р
Подставляя значения m и ρ,
V=12/0.63
V=20.68м3
Действующая выталкивающая сила определяется выражением
Fb=ρgV
Fb=(0.58)(9.8)(20.68)
Fb= 127.67N
Вес предмета определяется
Вт=мг
Вт=(12)(9.8)
Ш=117.6Н
Поскольку значение выталкивающей силы больше значения силы тяжести, объект плавает в жидкости.
Как рассчитать выталкивающую силу в воздухе?
Выталкивающая сила в воздухе связана со смещением воздуха вместе с объектом. Расчет выталкивающей силы в воздухе сильно отличается от обычного расчета выталкивающей силы, потому что плотность воздуха намного меньше.
- Расчетная плотность воздуха примерно равна 1.3×10-3кг / м3.
- Затем рассчитать плотность объекта, плавающего в воздушной среде.
Мы знаем, что когда сила плавучести действует в направлении вверх, сила тяжести пытается тянуть объект вниз. Объект может парить в воздухе только тогда, когда выталкивающая сила больше.
В воздушной среде выталкивающая сила должна быть равна весу объекта для эффективного плавания; таким образом, мы можем писать.
Fb=м*г
Где m — масса объекта, а g — ускорение свободного падения. Но в воздухе массу можно переписать как
м=рa/п; где рa – плотность воздуха, а ρ – плотность объекта.
Подставив значение массы в уравнение выталкивающей силы, получим
Fb=pa/п*г
Задача, приведенная ниже, поможет вам лучше понять.
Как рассчитать выталкивающую силу золотой монеты плотностью 19 г в воздушной среде?
Мы знаем, что плотность золотой монеты ρg=19 г/см3
Плотность воздуха ρa=0.0013 г/см3
Выталкивающая сила, действующая на золотую монету в воздухе, определяется выражением
Fb=pa/п*г
Fb= 0.0013 / 19 * 9.8
Fb=(6.83×10-5) 9.8
Fb= 6.705 × 10-4N
Как рассчитать выталкивающую силу в воде?
Объем вытесненной воды с плотностью воды используется для расчета выталкивающей силы в воде.
- Если объект полностью погружен в воду, то для расчета следует учитывать 100% объема.
- Если объект частично погружен в воду, следует учитывать 50% объема.
- Если объект погружен только на четверть, то следует учитывать только 25% объема.
Изображение кредита: Wikimedia Commons
Остальной расчет выталкивающей силы аналогичен общему расчету плавучести.
Масса тела 15 кг, плотность 0.55 кг/м.3 частично погружен в воду. Как рассчитать выталкивающую силу, действующую на тело?
Мы знаем, что плотность объекта ρ=0.55 кг/м3
Масса объекта m = 15 кг
Объем определяется по формуле; V=m/p
V=15/0.55
V=27.27м3
Поскольку объект частично погружен в воду, его объем в воде равен половине его общего объема; таким образом, объем V=13.635 м3.
Выталкивающую силу можно определить как
Fb=ρgV
Fb=(0.55)(9.8)(13.635)
Fb= 73.492Н.
Как рассчитать выталкивающую силу воздушного шара?
Чтобы найти выталкивающую силу воздушного шара, нам нужно знать заполненный воздухом объем внутри воздушного шара, что делает расчет несколько другим.
Сам воздух, обладая малой плотностью, все же поддерживает плавание в нем определенного предмета. Некоторые воздушные шары, например гелиевые, имеют меньшую плотность, чем воздух. Таким образом, воздушные шары легко парят на них.
Когда воздушные шары наполняются газом, он приобретает форму, напоминающую сферу; таким образом, нам нужно вычислить объем выражения сферы как,
V=4/3πr3
Затем зная плотность и масса, мы можем легко вычислить выталкивающую силу.
Воздушный шар, наполненный воздухом, образует сферу радиусом 5 см и может парить в воздухе. Как рассчитать выталкивающую силу, действующую на воздушный шар при подъеме в воздух?
Дано – радиус шарика r=5см.
Объем воздушного шара определяется выражением
V=4/3πr3
V=4/3(3.14)*23
V=33.49м3.
Выталкивающая сила определяется выражением
Fb=ρgV
Плотность воздуха ρ=1.3 кг/м3.
Подставляя значения, получаем
Fb=(1.3)(9.8)(33.49)
Fb= 426.66Н.
Как рассчитать выталкивающую силу лодки?
Лодка всегда плывет по поверхности воды; плавучесть лодки следует рассчитывать, учитывая весь объем лодки.
Согласно закону Архимеда, направленная вверх сила, действующая на погруженное тело, равна весу вытесненной жидкости. И это смещение также действует в направлении вверх к центру массы смещения жидкости.

Уравнение выталкивающей силы
Fb=v*f/v=v*мг/v
Но m/v=p
Fb=ρgV
Для лодки, плывущей по воде, выталкивающая сила равна
Fb=Вт/Втa
Где; W – вес объекта в воде, Втa вес предмета в воздухе.
Как рассчитать выталкивающую силу на подводном объекте?
Для затопленного объекта объем такой же, как перемещенный объем в жидкости, и, следовательно, мы можем легко найти выталкивающую силу затопленного объекта с помощью того же уравнения.
Fb=ρgV
Для затопленного объекта необходимо найти вес вытесненной жидкости. Вес вытесненной жидкости определяется выражением
Wf=ρ×V
Как рассчитать величину выталкивающей силы?
Величина выталкивающей силы всегда равна величине его веса. Это верно только тогда, когда объект плавает. Поясним эту концепцию, рассмотрев пример плиты толщиной t и плотностью ρs, плавающей на поверхности воды с массой m.
Поскольку величина выталкивающей силы равна величине веса воды, определяемой выражением
Ww=ρwАтг; где А – площадь плиты.
Величина веса плиты определяется выражением
Ws=ρsАтг+мг
Но по закону Архимеда
Ws=Ww
ρwAtg= ρsАтг+мг
мг= рwAtg- ρsАтг
м=рwAt-ρsAt
м = А (ρwт-рst)
А=м/Pwt-Pst
Как рассчитать выталкивающую силу куба?
Когда куб погружен в жидкость, его объем равен кубическому значению каждой стороны. Используя это в качестве эталона, мы можем рассчитать выталкивающую силу, действующую на куб.

Изображение кредита: Wikimedia Commons
Например, куб со стороной 2 см погружен в масло плотностью 800 кг/мXNUMX.3. Вычислите выталкивающую силу, действующую на куб.
Длина стороны куба l=2см=0.2м.
Объем куба можно рассчитать как
V=XNUMX3= (0.2)3= 0.008 м3
Выталкивающая сила Fb=ρgV
Возьмем g=9.8 м/с2.
Подставляя значения в приведенное выше уравнение,
Fb=(800)(9.8)(0.008)
Fb= 62.72Н.
Еще несколько решенных задач
Тело массой 0.56 кг погружено в жидкость с плотностью 910 кг/мXNUMX.3. Вычислите выталкивающую силу, действующую на тело в этой жидкости. И, следовательно, вычислить вес смещения жидкости.
Решение:
Дано – масса тела, m=0.56кг.
Плотность текучей среды ρ=910кг/м3
Ускорение свободного падения g=9.8 м/с2.
Объем тела в жидкости равен
V=м/р
V=0.56/910
V = 6.153 × 10-4m3
Выталкивающая сила, действующая на тело в жидкости
Fb=ρgV
Fb=(910)(9.8)(6.153×10-4)
Fb= 5.488Н.
Плитка длиной 20 см, шириной 9 см и высотой 0.88 см плавает в жидкости с плотностью 998 кг/м.3. Рассчитайте выталкивающую силу, действующую на объект, и, следовательно, рассчитайте вес объекта, который будет плавать в жидкости. (Примите ускорение свободного падения g=10 м/с.2)
Решение:
Дано – длина данной плиты, м=20см=0.2м
Ширина плиты w=9см=0.09м
Высота плиты h=0.88см=0.0088м
Плотность текучей среды ρ=998кг/м3
Сначала нужно найти объем плиты.
V=lwh=(0.2)(0.09)(0.0088)
V = 1.58 × 10-4m3
Выталкивающая сила, действующая на плиту в жидкой среде, равна
Fb=ρgV
Fb=(998)(10)(1.58×10-4)
Fb= 1.580Н.
Шар надувают газом плотностью 0.89 кг/мXNUMX.3 и позволили парить в воздухе с плотностью 1.22 кг/м3. Воздушный шар образовал сферическую структуру радиусом 0.32 м. Рассчитайте плавучесть, приложенную к воздушному шару, и объем воздушного шара.
Решение:
Дано – плотность баллона, наполненного газом ρb=0.89 кг/м3
Плотность воздуха ρa=1.22 кг/м3
Радиус баллона r=0.32м.
Выталкивающая сила рассчитывается как
Fb=Pa/Pb*g
Fb=1.22/0.89 г
Fb= 1.32Н.
Объем баллона, наполненного газом, равен
V=4/3πr3
V=4/3(3.14)(323)
V=0.137м3.
Проверить, тонет или всплывает данное тело в жидкости плотностью 1025 кг/мXNUMX.3. Учитывая, что масса объекта 46 кг.
Решение:
Дано – плотность жидкости ρ=1025кг/м3
Масса данного тела m=46кг.
Ускорение свободного падения g=9.8 м/с2.
Объем тела в жидкости v определяется выражением
V=46/1025
V=0.044м3
Выталкивающая сила, действующая на тело в жидкости
Fb=ρgV
Fb=(1025)(9.8)(0.044)
Fb= 450.8N
Сила тяжести, действующая на тело W=mg
Вт=(46)(9.8)
W = 450.8
Так как вес тела и выталкивающая сила, действующая на тело, равны; следовательно, тело находится в состоянии нейтральной плавучести. Тело не тонет в жидкости и не поднимается в ней.














