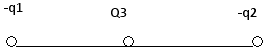Условие задачи:
Определить расстояние между двумя точечными зарядами 16 и -6 нКл, если напряженность поля в точке, находящейся на середине этого расстояния, равна 550 В/м.
Задача №6.2.21 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(q_1=16) нКл, (q_2=-6) нКл, (r=frac{l}{2}), (E=550) В/м, (l-?)
Решение задачи:
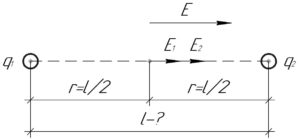Модули напряженностей электрических полей (E_1) и (E_2) от зарядов (q_1) и (q_2) соответственно на расстоянии (r) от каждого из них найдём по таким формулам:
[left{ begin{gathered}
{E_1} = frac{{k{q_1}}}{{{r^2}}} hfill \
{E_2} = frac{{kleft| {{q_2}} right|}}{{{r^2}}} hfill \
end{gathered} right.]
Здесь (k) – коэффициент пропорциональности (в законе Кулона), равный 9·109 Н·м2/Кл2.
Учитывая тот факт, что по условию (r=frac{l}{2}), и раскрывая модуль в нижней формуле (( left| {{q_2}} right| = – {q_2}) ), получим:
[left{ begin{gathered}
{E_1} = frac{{4k{q_1}}}{{{l^2}}} hfill \
{E_2} = frac{{ – 4k{q_2}}}{{{l^2}}} hfill \
end{gathered} right.]
На схеме к решению видно, что напряженности полей (E_1) и (E_2) сонаправлены, поэтому:
[E = {E_1} + {E_2}]
[E = frac{{4k{q_1}}}{{{l^2}}} + frac{{ – 4k{q_2}}}{{{l^2}}}]
[E = frac{{4k}}{{{l^2}}}left( {{q_1} – {q_2}} right)]
Откуда искомое расстояние между зарядами (l) равно:
[l = sqrt {frac{{4kleft( {{q_1} – {q_2}} right)}}{E}} ]
Посчитаем численный ответ:
[l = sqrt {frac{{4 cdot 9 cdot {{10}^9} cdot left( {16 cdot {{10}^{ – 9}} – left( { – 6 cdot {{10}^{ – 9}}} right)} right)}}{{550}}} = 1,2;м = 120;см]
Ответ: 120 см.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.2.20 Найти напряженность поля, создаваемого двумя точечными зарядами 2 и -4 нКл
6.2.22 В однородном электрическом поле напряженностью 40 кВ/м, направленным
6.2.23 Заряды по 0,1 мкКл расположены на расстоянии 6 см друг от друга. Найти
Как найти расстояние между зарядами
Многие физические явления, наблюдаемые в природе и окружающей нас жизни, не могут быть объяснены только на основе законов механики, молекулярно-кинетической теории и термодинамики. В этих явлениях проявляются силы, действующие между телами на расстоянии, причем эти силы не зависят от масс взаимодействующих тел и, следовательно, не являются гравитационными. Эти силы называют электромагнитными силами .
О существовании электромагнитных сил знали еще древние греки. Но систематическое, количественное изучение физических явлений, в которых проявляется электромагнитное взаимодействие тел, началось только в конце XVIII века. Трудами многих ученых в XIX веке завершилось создание стройной науки, изучающей электрические и магнитные явления. Эта наука, которая является одним из важнейших разделов физики, получила название электродинамики .
Основными объектами изучения в электродинамике являются электрические и магнитные поля, создаваемые электрическими зарядами и токами.
Электрическое поле
1.1. Электрический заряд. Закон Кулона
Подобно понятию гравитационной массы тела в механике Ньютона, понятие заряда в электродинамике является первичным, основным понятием.
Электрический заряд – это физическая величина, характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия.
Электрический заряд обычно обозначается буквами или .
Совокупность всех известных экспериментальных фактов позволяет сделать следующие выводы:
Существует два рода электрических зарядов, условно названных положительными и отрицательными.
Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд.
Одноименные заряды отталкиваются, разноименные – притягиваются. В этом также проявляется принципиальное отличие электромагнитных сил от гравитационных. Гравитационные силы всегда являются силами притяжения.
Одним из фундаментальных законов природы является экспериментально установленный закон сохранения электрического заряда .
Закон сохранения электрического заряда утверждает, что в замкнутой системе тел не могут наблюдаться процессы рождения или исчезновения зарядов только одного знака.
С современной точки зрения, носителями зарядов являются элементарные частицы. Все обычные тела состоят из атомов, в состав которых входят положительно заряженные протоны, отрицательно заряженные электроны и нейтральные частицы – нейтроны. Протоны и нейтроны входят в состав атомных ядер, электроны образуют электронную оболочку атомов. Электрические заряды протона и электрона по модулю в точности одинаковы и равны элементарному заряду .
В нейтральном атоме число протонов в ядре равно числу электронов в оболочке. Это число называется атомным номером . Атом данного вещества может потерять один или несколько электронов или приобрести лишний электрон. В этих случаях нейтральный атом превращается в положительно или отрицательно заряженный ион.
Заряд может передаваться от одного тела к другому только порциями, содержащими целое число элементарных зарядов. Таким образом, электрический заряд тела – дискретная величина:
Физические величины, которые могут принимать только дискретный ряд значений, называются квантованными . Элементарный заряд является квантом (наименьшей порцией) электрического заряда. Следует отметить, что в современной физике элементарных частиц предполагается существование так называемых кварков – частиц с дробным зарядом и Однако, в свободном состоянии кварки до сих пор наблюдать не удалось.
В обычных лабораторных опытах для обнаружения и измерения электрических зарядов используется электрометр – прибор, состоящий из металлического стержня и стрелки, которая может вращаться вокруг горизонтальной оси (рис. 1.1.1). Стержень со стрелкой изолирован от металлического корпуса. При соприкосновении заряженного тела со стержнем электрометра, электрические заряды одного знака распределяются по стержню и стрелке. Силы электрического отталкивания вызывают поворот стрелки на некоторый угол, по которому можно судить о заряде, переданном стержню электрометра.
Электрометр является достаточно грубым прибором; он не позволяет исследовать силы взаимодействия зарядов. Впервые закон взаимодействия неподвижных зарядов был открыт французским физиком Ш. Кулоном в 1785 г. В своих опытах Кулон измерял силы притяжения и отталкивания заряженных шариков с помощью сконструированного им прибора – крутильных весов (рис. 1.1.2), отличавшихся чрезвычайно высокой чувствительностью. Так, например, коромысло весов поворачивалось на 1° под действием силы порядка .
Идея измерений основывалась на блестящей догадке Кулона о том, что если заряженный шарик привести в контакт с точно таким же незаряженным, то заряд первого разделится между ними поровну. Таким образом, был указан способ изменять заряд шарика в два, три и т. д. раз. В опытах Кулона измерялось взаимодействие между шариками, размеры которых много меньше расстояния между ними. Такие заряженные тела принято называть точечными зарядами .
Точечным зарядом называют заряженное тело, размерами которого в условиях данной задачи можно пренебречь.
На основании многочисленных опытов Кулон установил следующий закон:
Силы взаимодействия неподвижных зарядов прямо пропорциональны произведению модулей зарядов и обратно пропорциональны квадрату расстояния между ними:
Силы взаимодействия подчиняются третьему закону Ньютона: Они являются силами отталкивания при одинаковых знаках зарядов и силами притяжения при разных знаках (рис. 1.1.3). Взаимодействие неподвижных электрических зарядов называют электростатическим или кулоновским взаимодействием. Раздел электродинамики, изучающий кулоновское взаимодействие, называют электростатикой .
Закон Кулона справедлив для точечных заряженных тел. Практически закон Кулона хорошо выполняется, если размеры заряженных тел много меньше расстояния между ними.
Коэффициент пропорциональности в законе Кулона зависит от выбора системы единиц. В Международной системе СИ за единицу заряда принят кулон (Кл).
Кулон – это заряд, проходящий за 1 с через поперечное сечение проводника при силе тока 1 А. Единица силы тока (ампер) в СИ является наряду с единицами длины, времени и массы основной единицей измерения .
Коэффициент в системе СИ обычно записывают в виде:
где – электрическая постоянная .
В системе СИ элементарный заряд равен:
Опыт показывает, что силы кулоновского взаимодействия подчиняются принципу суперпозиции.
Если заряженное тело взаимодействует одновременно с несколькими заряженными телами, то результирующая сила, действующая на данное тело, равна векторной сумме сил, действующих на это тело со стороны всех других заряженных тел.
Рис. 1.1.4 поясняет принцип суперпозиции на примере электростатического взаимодействия трех заряженных тел.
Принцип суперпозиции является фундаментальным законом природы. Однако, его применение требует определенной осторожности, в том случае, когда речь идет о взаимодействии заряженных тел конечных размеров (например, двух проводящих заряженных шаров 1 и 2). Если к системе из двух заряженных шаров поднсти третий заряженный шар, то взаимодействие между 1 и 2 изменится из-за перераспределения зарядов .
Принцип суперпозиции утверждает, что при заданном (фиксированном) распределении зарядов на всех телах силы электростатического взаимодействия между любыми двумя телами не зависят от наличия других заряженных тел.
Закон Кулона
Закон Кулона количественно описывает взаимодействие заряженных тел. Он является фундаментальным законом, то есть установлен при помощи эксперимента и не следует ни из какого другого закона природы. Он сформулирован для неподвижных точечных зарядов в вакууме. В реальности точечных зарядов не существует, но такими можно считать заряды, размеры которых значительно меньше расстояния между ними. Сила взаимодействия в воздухе почти не отличается от силы взаимодействия в вакууме (она слабее менее чем на одну тысячную).
Электрический заряд – это физическая величина, характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия.
Впервые закон взаимодействия неподвижных зарядов был открыт французским физиком Ш. Кулоном в 1785 г. В опытах Кулона измерялось взаимодействие между шариками, размеры которых много меньше расстояния между ними. Такие заряженные тела принято называть точечными зарядами.
На основании многочисленных опытов Кулон установил следующий закон:
Сила взаимодействия двух неподвижных точечных электрических зарядов в вакууме прямо пропорциональна произведению их модулей и обратно пропорциональна квадрату расстояния между ними. Она направлена вдоль прямой, соединяющей заряды, и является силой притяжения, если заряды разноименные, и силой отталкивания, если заряды одноименные.
Если обозначить модули зарядов через |q1| и |q2|, то закон Кулона можно записать в следующей форме:
Коэффициент пропорциональности k в законе Кулона зависит от выбора системы единиц.
Полная формула закона Кулона:
( F ) — Сила Кулона
( q_1 q_2 ) — Электрический заряд тела
( r ) — Расстояние между зарядами
( varepsilon_0 = 8,85*10^ ) — Электрическая постоянная
( varepsilon ) — Диэлектрическая проницаемость среды
( k = 9*10^9 ) — Коэффициент пропорциональности в законе Кулона
Силы взаимодействия подчиняются третьему закону Ньютона: ( vec_=vec_ ) . Они являются силами отталкивания при одинаковых знаках зарядов и силами притяжения при разных знаках.
Электрический заряд обычно обозначается буквами q или Q .
Совокупность всех известных экспериментальных фактов позволяет сделать следующие выводы:
Существует два рода электрических зарядов, условно названных положительными и отрицательными.
Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд.
Одноименные заряды отталкиваются, разноименные – притягиваются. В этом также проявляется принципиальное отличие электромагнитных сил от гравитационных. Гравитационные силы всегда являются силами притяжения.
Взаимодействие неподвижных электрических зарядов называют электростатическим или кулоновским взаимодействием. Раздел электродинамики, изучающий кулоновское взаимодействие, называют электростатикой.
Закон Кулона справедлив для точечных заряженных тел. Практически закон Кулона хорошо выполняется, если размеры заряженных тел много меньше расстояния между ними.
Отметим, чтоб выполнялся закон Кулона необходимо 3 условия:
- Точечность зарядов — то есть расстояние между заряженными телами много больше их размеров.
- Неподвижность зарядов. Иначе вступают в силу дополнительные эффекты: магнитное поле движущегося заряда и соответствующая ему дополнительная сила Лоренца, действующая на другой движущийся заряд .
- Взаимодействие зарядов в вакууме.
В Международной системе СИ за единицу заряда принят кулон (Кл) .
Кулон – это заряд, проходящий за 1 с через поперечное сечение проводника при силе тока 1 А . Единица силы тока (Ампер) в СИ является наряду с единицами длины, времени и массы основной единицей измерения.
Закон Кулона простым языком
Взаимодействия электрических зарядов исследовали ещё до Шарля Кулона. В частности, английский физик Кавендиш в своих исследованиях пришёл к выводу, что неподвижные заряды при взаимодействии подчиняются определённому закону. Однако он не обнародовал своих выводов. Повторно закон Кулона был открыт французским физиком, именем которого был назван этот фундаментальный закон.
Рисунок 1. Закон Кулона
История открытия
Эксперименты с заряженными частицами проводили много физиков:
- Г. В. Рихман;
- профессор физики Ф. Эпинус;
- Д. Бернулли;
- Пристли;
- Джон Робисон и многие другие.
Все эти учёные очень близко подошли к открытию закона, но никому из них не удалось математически обосновать свои догадки. Несомненно, они наблюдали взаимодействие заряженных шариков, но установить закономерность в этом процессе было непросто.
Кулон проводил тщательные измерения сил взаимодействия. Для этого он даже сконструировал уникальный прибор – крутильные весы (см. Рис. 2).
Рис. 2. Крутильные весы
У придуманных Кулоном весов была чрезвычайно высокая чувствительность. Прибор реагировал на силы порядка 10 -9 Н. Коромысло весов, под действием этой крошечной силы, поворачивалось на 1 º . Экспериментатор мог измерять угол поворота, а значит и приложенную силу, пользуясь точной шкалой.
Благодаря гениальной догадке учёного, идея которой состояла в том, что при соприкосновении заряженного и незаряженного шариков, электрический заряд делился между ними поровну. На это сразу реагировали крутильные весы, коромысло которых поворачивалось на определённый угол. Заземляя неподвижный шарик, Кулон мог нейтрализовать на нём полученный заряд.
Таким образом, учёный смог уменьшать первоначальный заряд подвижного шарика кратное число раз. Измеряя угол отклонения после каждого деления заряда, Кулон увидел закономерность в действии отталкивающей силы, что помогло ему сформулировать свой знаменитый закон.
Формулировка
Кулон исследовал взаимодействие между шариками, ничтожно малых размеров, по сравнению с расстояниями между ними. В физике такие заряженные тела называются точечными. Другими словами, под определение точечных зарядов подпадают такие заряженные тела, если их размерами, в условиях конкретного эксперимента, можно пренебречь.
Для точечных зарядов справедливо утверждение: Силы взаимодействия между ними направлены вдоль линии, проходящей через центры заряженных тел. Абсолютная величина каждой силы прямо пропорциональна произведению зарядов и обратно пропорциональна квадрату расстояния между ними (см. рис. 3). Данную зависимость можно выразить формулой: |F1|=|F2|=(ke*q1*q2) / r 2
Рис. 3. Взаимодействие точечных зарядов
Остаётся добавить, что векторы сил направлены друг к другу для разноименных зарядов, и противоположно, в случае с одноимёнными зарядами. То есть между разноимёнными зарядами действует электрическое притяжение, а между одноимёнными – отталкивание.
Таким образом, закон Кулона описывает взаимодействие между двумя электрическими зарядами, которое лежит в основе всех электромагнитных взаимодействий.
Для того чтобы действовал сформулированный выше закон, необходимо выполнение следующий условий:
- соблюдение точечности зарядов;
- неподвижность заряженных тел;
- закон выражает зависимости между зарядами в вакууме.
Границы применения
Описанная выше закономерность при определённых условиях применима для описания процессов квантовой механики. Правда, закон Кулона формулируется без понятия силы. Вместо силы используется понятие потенциальной энергии кулоновского взаимодействия. Закономерность получена путём обобщения экспериментальных данных.
Следует отметить, что на сверхмалых расстояниях (при взаимодействиях элементарных частиц) порядка 10 – 18 м проявляются электрослабые эффекты. В этих случаях закон Кулона, строго говоря, уже не соблюдается. Формулу можно применять с учётом поправок.
Нарушение закона Кулона наблюдается и в сильных электромагнитных полях (порядка 10 18 В/м), например поблизости магнитаров (тип электронных звёзд). В такой среде кулоновский потенциал уменьшается не обратно пропорционально, а экспоненциально.
Кулоновские силы подпадают под действие третьего закона Ньютона: F1 = – F2. Они используются для описания законов всемирного тяготения. В этом случае формула приобретает вид: F = ( m1* m2 ) / r 2 , где m1 и m2 – массы взаимодействующих тел, а r – расстояние между ними.
Закон Кулона стал первым открытым количественным фундаментальным законом, обоснованным математически. Его значение в исследованиях электромагнитных явлений трудно переоценить. С момента открытия и обнародования закона Кулона началась эра изучения электромагнетизма, имеющего огромное значение в современной жизни.
Коэффициент k
Формула содержит коэффициент пропорциональности k, который для согласования соразмерностей в международной системе СИ. В этой системе единицей измерения заряда принято называть кулоном (Кл) – заряд, проходящий за 1 секунду сквозь проводник, где силы тока составляет 1 А.
Коэффициент k в СИ выражается следующим образом: k = 1/4πε0, где ε0 – электрическая постоянная: ε0 = 8,85 ∙10 -12 Кл 2 /Н∙м 2 . Выполнив несложные вычисления, мы находим: k = 9×10 9 H*м 2 / Кл 2 . В метрической системе СГС k =1.
На основании экспериментов было установлено, что кулоновские силы, как и принцип суперпозиции электрических полей, в законах электростатики описывают уравнения Максвелла.
Если между собой взаимодействуют несколько заряженных тел, то в замкнутой системе результирующая сила этого взаимодействия равняется векторной сумме всех заряженных тел. В такой системе электрические заряды не исчезают – они передаются от тела к телу.
Закон Кулона в диэлектриках
Выше было упомянуто, что формула, определяющая зависимость силы от величины точечных зарядов и расстояния между ними, справедлива для вакуума. В среде сила взаимодействия уменьшается благодаря явлению поляризации. В однородной изотопной среде уменьшение силы пропорционально определённой величине, характерной для данной среды. Эту величину называют диэлектрической постоянной. Другое название – диэлектрическая проницаемость. Обозначают её символом ε. В этом случае k = 1/4πεε0.
Диэлектрическая постоянная воздуха очень близка к 1. Поэтому закон Кулона в воздушном пространстве проявляется так же как в вакууме.
Интересен тот факт, что диэлектрики могут накапливать электрические заряды, которые образуют электрическое поле. Проводники лишены такого свойства, так как заряды, попадающие на проводник, практически сразу нейтрализуются. Для поддержания электрического поля в проводнике необходимо непрерывно подавать на него заряженные частицы, образуя замкнутую цепь.
Применение на практике
Вся современная электротехника построена на принципах взаимодействия кулоновских сил. Благодаря открытию Клоном этого фундаментального закона развилась целая наука, изучающая электромагнитные взаимодействия. Понятие термина электрического поля также базируется на знаниях кулоновских сил. Доказано, что электрическое поле неразрывно связано с зарядами элементарных частиц.
Грозовые облака не что иное как скопление электрических зарядов. Они притягивают к себе индуцированные заряды земли, в результате чего появляется молния. Это открытие позволило создавать эффективные молниеотводы для защиты зданий и электротехнических сооружений.
На базе электростатики появилось много изобретений:
- конденсатор;
- различные диэлектрики;
- антистатические материалы для защиты чувствительных электронных деталей;
- защитная одежда для работников электронной промышленности и многое другое.
На законе Кулона базируется работа ускорителей заряженных частиц, в частности, функционирование Большого адронного коллайдера (см. Рис. 4).
Рис. 4. Большой адронный коллайдер
Ускорение заряженных частиц до околосветовых скоростей происходит под действием электромагнитного поля, создаваемого катушками, расположенными вдоль трассы. От столкновения распадаются элементарные частицы, следы которых фиксируются электронными приборами. На основании этих фотографий, применяя закон Кулона, учёные делают выводы о строении элементарных кирпичиков материи.
Калькулятор вычисления расстояния от заряда онлайн
Калькулятор вычисления расстояния от заряда онлайн позволяет найти расстояние от заряда через заряд и напряженность электрического поля в данной точке.
Единицы измерения, могут включать любые приставки Си. Калькулятор автоматически переведет одни единицы в другие и даст подробное решение.
Расстояние r от заряда через заряд q и напряженность электрического поля E в данной точке
Расстояние r от заряда равно квадратному корню из частного, где числителем выступает произведение коэффициента пропорциональности k и заряда q, а знаменателем – напряженность электрического поля E. Коэффициент пропорциональности k = 8.9875517873681764 × 109. Единицей измерения расстояния является – Метр (м)
Заряд q =
Напряженность E =
Единица измерения r
Так же для вычисления расстояния r между зарядами, можно воспользоваться калькулятором Закона Кулона.
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы (физика) |
|
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
| Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
|
Оптика |
| Калькулятор отражения и преломления света |
|
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
|
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
| Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор упрощения выражений |
| Калькулятор со скобками |
| Калькулятор уравнений |
| Калькулятор суммы |
| Калькулятор пределов функций |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Калькулятор делителей числа |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
| Длина отрезка. Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажер по математике |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
| Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Для школьников.
Приведём решение трёх задач на применение принципа суперпозиции (наложения) электростатических полей.
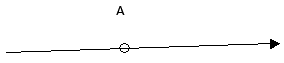
Задача 1. Два точечных одинаковых положительных заряда по 20 нКл каждый расположены в двух вершинах равностороннего треугольника со стороной 2 м в вакууме. Найти напряжённость поля в третьей вершине треугольника.
В точке А вектора напряженности электрических полей каждого заряда направлены вдоль их силовых линий (от зарядов).
Применим принцип суперпозиции для проекций указанных векторов на оси х и у:
Таким образом, вектор напряжённости результирующего электрического поля в точке А направлен вертикально вверх, а модуль напряжённости равен 77 В/м.
Задача 2. Электрическое поле образовано двумя одинаковыми разноимёнными точечными зарядами по 5 нКл. Расстояние между зарядами 10 см. Определить напряжённость поля: 1) в точке, лежащей посередине между зарядами; 2) в точке, лежащей на продолжении линии, соединяющей центры зарядов, на расстоянии 10 см от отрицательного заряда; 3) в точке, лежащей на расстоянии 10 см от положительного и отрицательного зарядов.
В точке А оба вектора напряжённости, создаваемых положительным и отрицательным зарядами, направлены вправо (на рисунке не показаны). Тогда результирующее поле находится через сумму полей, создаваемых первым и вторым зарядами:
В точке В результирующее поле направлено влево и равно:
В точке С вектор напряжённости результирующего электрического поля направлен вправо. Его модуль найдём из треугольника:
Ответ: 36000 В/м; 3400 В/м; 4500 В/м.
Задача 3. Электрическое поле создано двумя точечными зарядами 30 нКл и -10 нКл. Расстояние между зарядами 20 см. Определить напряжённость электрического поля в точке, находящейся на расстоянии 15 см от первого и на расстоянии второго (отрицательного) зарядов.
Покажем направления векторов напряжённости, создаваемых в искомой точке первым и вторым зарядами. Их модули найдём из формул:
Складывая вектора находим вектор результирующего поля. Модуль напряжённости результирующего поля находим по теореме косинусов:
Косинус угла найдём отдельно из треугольника образованного расстояниями:
Косинус угла оказался равным 0,25. Подставив все численные значения в формулу, получим результирующую напряжённость равную 16, 7 кВ/м.
Итак, приведено решение трёх задач на применение принципа суперпозиции (наложения) полей. Сначала в интересующей точке поля рисуем вектора напряжённости электрического поля, создаваемого каждым зарядом в отдельности. Затем, складывая их, находим напряжённость суммарного поля. В первой задаче проще просуммировать проекции векторов напряжённости на оси. Там, где угол между векторами напряжённости, создаваемыми отдельными зарядами, отличен от нуля, пользуются теоремой косинусов (задачи 2 и 3).
К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.
Предыдущая запись: Нахождение напряжённости электростатического поля.
Следующая запись:Как рассчитать напряжённость поля заряженной пластины. Поле конденсатора.
Ссылки на другие занятия (до электростатики) даны в Занятии 1.
Ссылки на занятия (начиная с электростатики) даны в Занятии 45.
Цель урока: дать понятие напряжённости электрического поля и ее
определения в любой точке поля.
Задачи урока:
- формирование понятия напряжённости электрического поля; дать понятие о
линиях напряжённости и графическое представление электрического поля; - научить учащихся применять формулу E=kq/r2 в решении
несложных задач на расчёт напряжённости.
Электрическое поле – это особая форма материи, о существовании которой можно
судить только по ее действию. Экспериментально доказано, что существуют два рода
зарядов, вокруг которых существуют электрические поля, характеризующиеся
силовыми линиями.
Графически изображая поле, следует помнить, что линии напряженности
электрического поля:
- нигде не пересекаются друг с другом;
- имеют начало на положительном заряде (или в бесконечности) и конец на
отрицательном (или в бесконечности), т. е. являются незамкнутыми линиями; - между зарядами нигде не прерываются.
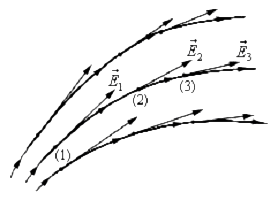
Рис.1
Силовые линии положительного заряда:
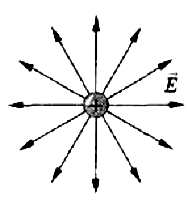
Рис.2
Силовые линии отрицательного заряда:
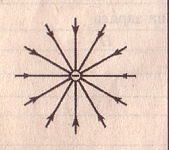
Рис.3
Силовые линии одноименных взаимодействующих зарядов:
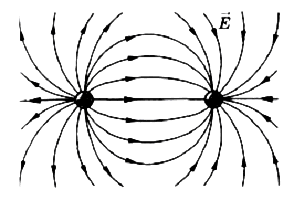
Рис.4
Силовые линии разноименных взаимодействующих зарядов:
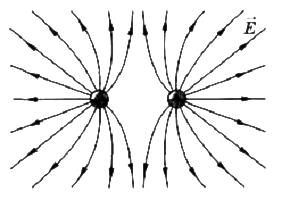
Рис.5
Силовой характеристикой электрического поля является напряженность, которая
обозначается буквой Е и имеет единицы измерения
или
.
Напряженность является векторной величиной, так как определяется отношением силы
Кулона к величине единичного положительного заряда
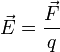
В результате преобразования формулы закона Кулона и формулы напряженности
имеем зависимость напряженности поля от расстояния, на котором она определяется
относительно данного заряда
где: k – коэффициент пропорциональности, значение которого зависит от
выбора единиц электрического заряда.
В системе СИ
Н·м2/Кл2,
где ε0 – электрическая
постоянная, равная 8,85·10-12 Кл2/Н·м2;
q – электрический заряд (Кл);
r – расстояние от заряда до точки в которой определяется напряженность.
Направление вектора напряженности совпадает с направлением силы Кулона.
Электрическое поле, напряженность которого одинакова во всех точках
пространства, называется однородным. В ограниченной области пространства
электрическое поле можно считать приблизительно однородным, если напряженность
поля внутри этой области меняется незначительно.
Общая напряженность поля нескольких взаимодействующих зарядов будет равна
геометрической сумме векторов напряженности, в чем и заключается принцип
суперпозиции полей:
Рассмотрим несколько случаев определения напряженности.
1. Пусть взаимодействуют два разноименных заряда. Поместим точечный
положительный заряд между ними, тогда в данной точке будут действовать два
вектора напряженности, направленные в одну сторону:
Е31 – напряженность точечного заряда 3 со стороны заряда 1;
Е32 – напряженность точечного заряда 3 со стороны заряда 2.
Согласно принципу суперпозиции полей общая напряженность поля в данной точке
равна геометрической сумме векторов напряженности Е31 и Е32.
Напряженность в данной точке определяется по формуле:
Е = kq1/x2 + kq2/(r – x)2
где: r – расстояние между первым и вторым зарядом;
х – расстояние между первым и точечным зарядом.
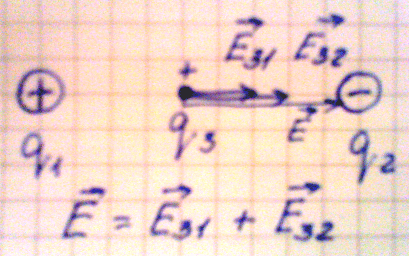
Рис.6
2. Рассмотрим случай, когда необходимо найти напряженность в точке удаленной
на расстояние а от второго заряда. Если учесть, что поле первого заряда больше,
чем поле второго заряда, то напряженность в данной точке поля равна
геометрической разности напряженности Е31 и Е32.
Формула напряженности в данной точке равна:
Е = kq1/(r + a)2 – kq2/a2
Где: r – расстояние между взаимодействующими зарядами;
а – расстояние между вторым и точечным зарядом.
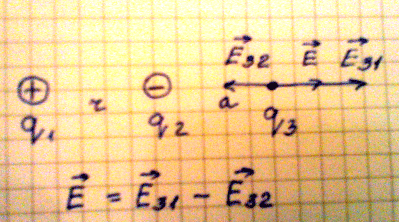
Рис.7
3. Рассмотрим пример, когда необходимо определить напряженность поля в
некоторой удаленности и от первого и от второго заряда, в данном случае на
расстоянии r от первого и на расстоянии bот второго заряда. Так как одноименные
заряды отталкиваются , а разноименные притягиваются, имеем два вектора
напряженности исходящие из одной точки, то для их сложения можно применить метод
противоположному углу параллелограмма будет являться суммарным вектором
напряженности. Алгебраическую сумму векторов находим из теоремы Пифагора:
Е = (Е312 +Е322)1/2
Следовательно:
Е = ((kq1/r2 )2 + (kq2/b2)2)1/2
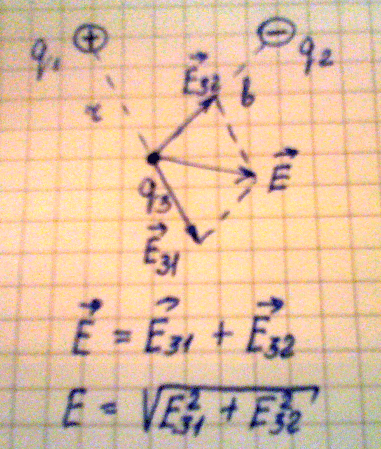
Рис.8
Исходя из данной работы, следует, что напряженность в любой точке поля можно
определить, зная величины взаимодействующих зарядов, расстояние от каждого
заряда до данной точки и электрическую постоянную.
4. Закрепление темы.
Проверочная работа.
Вариант № 1.
1. Продолжить фразу: “электростатика – это …
2. Продолжить фразу: электрическое поле – это ….
3. Как направлены силовые линии напряженности данного заряда?
4. Определить знаки зарядов:
5. Указать вектор напряженности.
6. Определить напряженность в точке В исходя из суперпозиции полей.
| Своя оценка работы | Оценка работы другим учеником |
Вариант № 2.
1. Продолжить фразу: “электростатика – это …
2. Продолжить фразу: напряженностью называется …
3. Как направлены силовые линии напряженности данного заряда?
4. Определить заряды.
5. Указать вектор напряженности.
6. Определить напряженность в точке В исходя из суперпозиции полей.
| Своя оценка работы | Оценка работы другим учеником |
Задачи на дом:
1. Два заряда q1 = +3·10-7 Кл и q2 = −2·10-7
Кл находятся в вакууме на расстоянии 0,2 м друг от друга. Определите
напряженность поля в точке С, расположенной на линии, соединяющей заряды, на
расстоянии 0,05 м вправо от заряда q2.
2. В некоторой точке поля на заряд 5·10-9 Кл действует сила 3·10-4
Н. Найти напряженность поля в этой точке и определите величину заряда,
создающего поле, если точка удалена от него на 0,1 м.
