Алгоритм решения задачи с помощью системы линейных уравнений
- Обозначить неизвестные величины переменными («от смысла к буквам»).
- По условию задачи записать уравнения, связывающие обозначенные переменные.
- Решить полученную систему уравнений.
- Истолковать результат в соответствии с условием задачи («от букв к смыслу»).
Например:
Задуманы два числа. Если от первого отнять второе, то получается 10. Если к первому прибавить удвоенное второе, то получается 91. Найдите задуманные числа.
Шаг 1
«От смысла к буквам»:
Пусть x и y – задуманные числа.
Шаг 2
Уравнения по условию задачи::
${left{ begin{array}{c} x-y = 10 \ x+2y = 91 end{array} right.}$
Шаг 3
Решение системы уравнений:
$(-) {left{ begin{array}{c} x-y = 10 \ x+2y = 91 end{array} right.} Rightarrow {left{ begin{array}{c} -3y = -81 \ x = y+10 end{array} right.} Rightarrow$
$ Rightarrow {left{ begin{array}{c} x = 37 \ y = 27 end{array} right.} $
Шаг 4
«От букв к смыслу»:
Задуманы числа 37 и 27.
Примеры
Пример 1. Периметр прямоугольника равен 48 см. Его длина больше ширины в 3 раза.
Найдите стороны прямоугольника.
Пусть a и b – длина и ширина прямоугольника.
По условию:
$$ {left{ begin{array}{c} P = 2(a+b) = 48 \ a = 3b end{array} right.} Rightarrow {left{ begin{array}{c} a+b = 24 \ a = 3b end{array} right.} Rightarrow {left{ begin{array}{c} 3b+b = 24 \ a = 3b end{array} right.} Rightarrow {left{ begin{array}{c} 4b = 24 \ a = 3b end{array} right.} Rightarrow {left{ begin{array}{c} a = 18 \ b = 6 end{array} right.} $$
Ответ: длина прямоугольника 18 см, ширина 6 см.
Пример 2. Два программиста из Бомбея, работающие в одном проекте, написали 100500 строк кода. Первый работал 70 дней, второй – 100 дней. Сколько строк писал каждый программист ежедневно, если за первые 30 дней первый написал на 5550 строк больше, чем второй?
Пусть x – ежедневное количество строк для 1-го программиста, y- для 2-го.
По условию:
$$ {left{ begin{array}{c} 70x+100y = 100500 |:10 \ 30x-30y = 5550 |:30 end{array} right.} (-) Rightarrow {left{ begin{array}{c} 7x+10y = 10050 \ x-y=185 | times 10 end{array} right.}$$
$$ Rightarrow (+) {left{ begin{array}{c} 7x+10y = 10050 \ 10x-10y = 1850 end{array} right.} Rightarrow {left{ begin{array}{c} 17x = 11900 \ y = x-185 end{array} right.} Rightarrow {left{ begin{array}{c} x = 700 \ y = 515 end{array} right.} $$
Ответ: 700 строк и 515 строк
Пример 3. За 2 кг конфет и 3 кг печенья заплатили 1540 руб. Сколько стоит 1 кг конфет и 1 кг печенья, если 2 кг печенья дороже 1 кг конфет на 210 руб.?
Пусть x – цена за 1 кг конфет, y – за 1 кг печенья.
По условию:
$$ {left{ begin{array}{c} 2x+3y = 1540 \ 2y-x = 210 | times 2 end{array} right.} Rightarrow (+) {left{ begin{array}{c} 2x+3y = 1540 \ -2x+4y = 420 end{array} right.} Rightarrow {left{ begin{array}{c} 7y = 1960 \ x = 2y-210 end{array} right.} Rightarrow {left{ begin{array}{c} x = 350 \ y = 280 end{array} right.} $$
Ответ: 1 кг конфет – 350 руб. и 1 кг печенья – 280 руб.
Пример 4. Катер за 3 ч движения против течения реки и 2 часа по течению проходит 73 км. Найдите собственную скорость катера и скорость течения, если за 4 ч движения по течению катер проходит на 29 км больше, чем за 3 ч движения против течения.
Пусть v – скорость катера (км/ч), u – скорость течения (км/ч).
По условию:
$$ {left{ begin{array}{c} 3(v-u)+2(v+u) = 73 \ 4(v+u)-3(v-u) = 29 end{array} right.} Rightarrow {left{ begin{array}{c} 3v-3u+2v+2u = 73 \ 4v+4u-3v+3u = 29 end{array} right.}$$
$$ Rightarrow {left{ begin{array}{c} 5v-u = 73 \ v+7u = 29 end{array} right.} Rightarrow {left{ begin{array}{c} 5(29-7u)-u = 73 \ v = 29-7u end{array} right.} Rightarrow {left{ begin{array}{c} 145-35u-u = 73 \ v = 29-7u end{array} right.} Rightarrow$$
$$ Rightarrow {left{ begin{array}{c} -36u = -72 \ v = 29-7u end{array} right.} Rightarrow {left{ begin{array}{c} v = 15 \ u = 2 end{array} right.} $$
Ответ: скорость катера 15 км/ч и скорость течения 2 км/ч
Пример 5. 5 карандашей и 3 тетрадки вместе стоили 170 руб. После того, как карандаши подешевели на 20%, а тетрадки подорожали на 30%, за 3 карандаша и 5 тетрадок заплатили 284 руб. Найдите первоначальную цену карандаша и тетрадки.
Пусть x – первоначальная цена карандаша, y – тетрадки.
По условию:
$$ {left{ begin{array}{c} 5x+3y = 170 \ 3cdot0,8x+5cdot1,3y = 284 end{array} right.} Rightarrow {left{ begin{array}{c} 5x+3y = 170 |times frac{2,4}{5} \ 2,4x+6,5y = 284 end{array} right.} Rightarrow (-) {left{ begin{array}{c} 2,4x+1,44y = 81,6 \ 2,4x+6,5y = 284 end{array} right.} $$
$$ Rightarrow {left{ begin{array}{c} (6,5-1,44)y = 284-81,6 \ x = frac{170-3y}{5} end{array} right.}Rightarrow {left{ begin{array}{c} y = 202,4:5,06 = 40 \ x = frac{170-120}{5} = 10 end{array} right.} $$
Ответ: карандаш сначала стоил 10 руб., тетрадка – 40 руб.
Пример 6*. Велосипедист планирует добраться из пункта А в пункт В. Если он будет ехать на 3 км/ч быстрее, чем обычно, он доберётся на 1 час раньше. А если он будет ехать на 2 км/ч медленней, чем обычно, то – на 1 час позже. Найдите обычную скорость велосипедиста и время поездки при этой скорости.
Пусть v – обычная скорость велосипедиста (км/ч), t – обычное время (ч).
Расстояние между А и В неизменно, и по условию равно:
$$ s_{AB} = vt = (v+3)(t-1) = (v-2)(t+1) $$
Получаем систему:
$$ {left{ begin{array}{c} vt = (v+3)(t-1) \ vt = (v-2)(t+1) end{array} right.} Rightarrow (-) {left{ begin{array}{c} vt = vt-v+3t-3 \ vt = vt+v-2t-2 end{array} right.} Rightarrow (+) {left{ begin{array}{c} v-3t = -3 \ -v+2t = -2 end{array} right.} Rightarrow $$
$$ Rightarrow {left{ begin{array}{c} -t = -5 \ v = 2t+2 end{array} right.} Rightarrow {left{ begin{array}{c} t = 5 \ v = 12 end{array} right.} $$
Ответ: обычная скорость 12 км/ч, время 5 ч
Пример 7*. В одной бочке налито 12 л, во второй – 32 л. Если первую бочку доверху наполнить водой из второй, то вторая бочка будет наполнена ровно наполовину своего объёма. Если вторую бочку доверху наполнить водой из первой, то первая бочка будет наполнена на 1/6 своего объёма. Найдите объём каждой бочки.
Пусть x – объём первой бочки (л), y – объём второй (л).
Пусть a л перелито из второй бочки, и первая наполнилась до краёв, а во второй воды осталось наполовину:
$$ (+) {left{ begin{array}{c} 12+a = x \ 32-a = frac{1}{2} y end{array} right.} Rightarrow x+ frac{1}{2} y = 44 $$
Теперь пусть b л перелито из первой бочки, и вторая наполнилась до краёв, а в первой воды осталось на 1/6:
$$ (+) {left{ begin{array}{c} 32+b = y \ 12-b = frac{1}{6} x end{array} right.} Rightarrow frac{1}{6}x+y = 44 $$
Получаем систему:
$$ {left{ begin{array}{c} x+ frac{1}{2} y = 44 | times 2 \ frac{1}{6} x+y = 44 end{array} right.} Rightarrow (-) {left{ begin{array}{c} 2x+y = 88 \ frac{1}{6} x+y = 44 end{array} right.} Rightarrow (+) {left{ begin{array}{c} 1frac{5}{6} x = 44 \ y = 88-2x end{array} right.} Rightarrow $$
$$ {left{ begin{array}{c} x = 44: frac{11}{6} = 44cdot frac{6}{11} = 24 \ y = 88-2cdot24 = 40 end{array} right.} $$
Ответ: первая бочка 24 л, вторая – 40 л
Пример 8*. Если школьник едет в школу на автобусе, а возвращается домой пешком, то он тратит на всю дорогу полтора часа. Если он едет туда и обратно на автобусе, то он тратит полчаса. Сколько времени потратит школьник, если он пойдёт туда и обратно пешком?
Пусть s – расстояние между домом и школой, v – скорость автобуса, u – скорость школьника, t – искомое время, потраченное на дорогу туда и обратно пешком.
По условию задачи:
$$ {left{ begin{array}{c} 1,5 = frac{s}{v} + frac{s}{u} \ 0,5 = frac{2s}{v} \ t = frac{2s}{u} end{array} right.} $$
Из второго уравнения $ frac{s}{v} = frac{0,5}{2} = 0,25 $. Подставляем в первое уравнение:
$$ frac{s}{u} = 1,5-frac{s}{v} = 1,5-0,25 = 1,25 $$
И тогда искомое время:
$$ t = frac{2s}{v} = 2cdot1,25 = 2,5 (ч) $$
Ответ: 2,5 ч
Прежде чем перейти к разбору как решать системы уравнений, давайте разберёмся, что называют системой уравнений
с двумя неизвестными.
Запомните!
![]()
Системой уравнений называют два уравнения с двумя неизвестными (чаще всего неизвестные в них называют
«x» и «y»),
которые объединены в общую систему фигурной скобкой.
Например, система уравнений может быть задана следующим образом.
Чтобы решить систему уравнений, нужно найти и «x», и «y».
Как решить систему уравнений
Существуют два основных способа решения систем уравнений. Рассмотрим оба способа решения.
Способ подстановки
или
«железобетонный» метод
Первый способ решения системы уравнений называют способом подстановки или «железобетонным».
Название «железобетонный» метод получил из-за того, что с помощью этого метода практически всегда можно
решить систему уравнений. Другими словами, если у вас не получается решить систему уравнений,
всегда пробуйте решить её методом подстановки.
Разберем способ подстановки на примере.
Выразим из первого уравнения «x + 5y = 7»
неизвестное «x».
Важно!

Чтобы выразить неизвестное, нужно выполнить два условия:
- перенести неизвестное, которое хотим выразить, в левую часть уравнения;
- разделить и левую и правую часть уравнения на нужное число так,
чтобы коэффициент при неизвестном стал равным единице.
Перенесём в первом уравнении «x + 5 y = 7» всё что
содержит «x» в левую часть,
а остальное в правую часть по
правилу переносу.
При «x» стоит коэффициент равный единице, поэтому дополнительно делить уравнение
на число не требуется.
Теперь, вместо «x» подставим во второе уравнение полученное выражение
«x = 7 − 5y» из первого уравнения.
| x = 7 − 5y | |
| 3(7 − 5y) − 2y = 4 |
Подставив вместо «x» выражение «(7 − 5y)»
во второе уравнение,
мы получили обычное линейное уравнение с одним неизвестным «y».
Решим его по правилам
решения линейных уравнений.
Чтобы каждый раз не писать всю систему уравнений заново, решим полученное уравнение
«3(7 − 5y) − 2y = 4» отдельно.
Вынесем его решение отдельно с помощью
обозначения звездочка (*).
| x = 7 − 5y | |
| 3(7 − 5y) − 2y = 4 (*) |
(*) 3(7 − 5y) − 2y = 4
21 − 15y − 2y = 4
− 17y = 4 − 21
− 17y = − 17 | :(−17)
y = 1
Мы нашли, что «y = 1».
Вернемся к первому уравнению «x = 7 − 5y» и вместо «y» подставим в него полученное числовое значение.
Таким образом можно найти «x».
Запишем в ответ оба полученных значения.
Ответ: x = 2; y = 1
Способ сложения
Рассмотрим другой способ решения системы уравнений. Метод называется способ сложения.
Вернемся к нашей системе уравнений еще раз.
По правилам математики уравнения системы можно складывать. Наша задача в том, чтобы сложив исходные
уравнения, получить такое уравнение, в котором останется только одно неизвестное.
Давайте сейчас сложим уравнения системы и посмотрим, что из этого выйдет.
Запомните!
![]()
При сложения уравнений системы
левая часть первого уравнения полностью складывается
с левой частью второго уравнения,
а правая часть полностью складывается с
правой частью.
| x + 5y = 7 | (x + 5y) + (3x − 2y) = 7 + 4 | ||
| + => |
x + 5y + 3x − 2y = 11 |
||
| 3x − 2y = 4 | 4x + 3y = 11 |
При сложении уравнений мы получили уравнение «4x + 3y = 11».
По сути, сложение уравнений в исходном виде нам ничего
не дало, так как в полученном уравнении мы по прежнему имеем оба неизвестных.
Вернемся снова к исходной системе уравнений.
Чтобы при сложении неизвестное «x» взаимноуничтожилось,
нужно сделать так, чтобы в первом уравнении при «x» стоял коэффициент
«−3».
Для этого умножим первое уравнение на «−3».
Важно!

При умножении уравнения на число, на это число умножается каждый член уравнения.
| x + 5y = 7 | ·(−3) | |
| 3x − 2y = 4 |
| x ·(−3) + 5y · (−3) = 7 · (−3) |
|
| 3x − 2y = 4 |
| −3x −15y = −21 | |
| 3x − 2y = 4 |
Теперь сложим уравнения.
| −3x −15y = −21 | (−3x −15y ) + (3x − 2y) = −21 + 4 | ||
| + => |
−3x −15y + 3x − 2y = −21 + 4 |
||
| 3x − 2y = 4 | −17y = −17 |:(−17) | ||
| y = 1 |
Мы нашли «y = 1».
Вернемся к первому уравнению и подставим вместо «y» полученное числовое
значение и найдем «x».
Ответ: x = 2; y = 1
Пример решения системы уравнения
способом подстановки
Выразим из первого уравнения «x».
Подставим вместо «x» во второе уравнение полученное выражение.
| x = 17 + 3y | |
| (17 + 3y) − 2y = −13 (*) |
(*) (17 + 3y) − 2y = −13
17 + 3y − 2y = −13
17 + y = −13
y = −13 − 17
y = −30
Подставим в первое уравнение полученное числовое значение «y = −30» и
найдем «x».
| x = 17 + 3 · (−30) | |
| y = −30 |
Ответ: x = −73; y = −30
Пример решения системы уравнения
способом сложения
Рассмотрим систему уравнений.
| 3(x − y) + 5x = 2(3x − 2) | |
| 4x − 2(x + y) = 4 − 3y |
Раскроем скобки и упростим выражения в обоих уравнениях.
| 3x − 3y + 5x = 6x − 4 | |
| 4x − 2x − 2y = 4 − 3y |
| 8x − 3y = 6x − 4 | |
| 2x −2y = 4 − 3y |
| 8x − 3y − 6x = −4 | |
| 2x −2y + 3y = 4 |
Мы видим, что в обоих уравнениях есть «2x».
Наша задача, чтобы при сложении уравнений «2x» взаимноуничтожились и в
полученном уравнении осталось только «y».
Для этого достаточно умножить первое уравнение на «−1».
| 2x − 3y = −4 |·(−1) | |
| 2x + y = 4 |
|
2x · (−1) − 3y · (−1) = −4 · (−1) |
|
| 2x + y = 4 |
Теперь при сложении уравнений у нас останется только «y» в уравнении.
| −2x + 3y = 4 | (−2x + 3y ) + (2x + y) = 4 + 4 | ||
| + => |
−2x + 3y + 2x + y = 4 + 4 |
||
| 2x + y = 4 | 4y = 8 | :4 | ||
| y = 2 |
Подставим в первое уравнение полученное числовое значение «y = 2» и
найдем «x».
Ответ: x = 1; y = 2
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
8 мая 2020 в 16:20
Алина Козлова

Профиль
Благодарили: 0
Сообщений: 1

Алина Козлова
Профиль
Благодарили: 0
Сообщений: 1
у-2х=-3
х+у=3
0
Спасибо
Ответить
9 мая 2020 в 21:50
Ответ для Алина Козлова
Evgeny Bayron

Профиль
Благодарили: 0
Сообщений: 1

Evgeny Bayron
Профиль
Благодарили: 0
Сообщений: 1
y=3-x
3-x-2x=-3
x=2
y-2*2=-3
y=1
0
Спасибо
Ответить
15 мая 2019 в 13:21
Марина Чернявская

Профиль
Благодарили: 0
Сообщений: 1

Марина Чернявская
Профиль
Благодарили: 0
Сообщений: 1
Решительно систему уравнений.
4x+3y =22.
-x+7y =10.
a)графическим способом.
б)способом подстановки
в)способом сложения
0
Спасибо
Ответить
15 мая 2019 в 22:31
Ответ для Марина Чернявская
Лёха Чешуйка

Профиль
Благодарили: 0
Сообщений: 2

Лёха Чешуйка
Профиль
Благодарили: 0
Сообщений: 2
в): Домножаем первое на 1, второе на 4:
4x+3y=22
-4x+28y=40
Складываем:
4x+(-4x)+3y+28y=22+40
31y=62
y=62/31
y=2
Подставляем y в первое:
4x+3 · 2=22
4x=22-6
4x=16
x=4
0
Спасибо
Ответить
15 мая 2019 в 22:41
Ответ для Марина Чернявская
Лёха Чешуйка

Профиль
Благодарили: 0
Сообщений: 2

Лёха Чешуйка
Профиль
Благодарили: 0
Сообщений: 2
б): Выражаем из второго x:
-x=10-7y
x=7y-10
Подставляем x в первое:
4(7y-10)+3y=22
28y-40+3y=22
31y=22+40
31y=62
y=2
Подставляем y в первое:
4x+3 · 2=22
4x=22-6
4x=16
x=4
0
Спасибо
Ответить
20 октября 2015 в 13:24
Елена Тутуликова

Профиль
Благодарили: 0
Сообщений: 1

Елена Тутуликова
Профиль
Благодарили: 0
Сообщений: 1
Помогите, пожалуйста, решить систему уравнений.{y + sinx = 5; {4y + 2 sinx = 19
Спасибо!
0
Спасибо
Ответить
23 октября 2015 в 21:25
Ответ для Елена Тутуликова
Елизавета Яременко

Профиль
Благодарили: 0
Сообщений: 5

Елизавета Яременко
Профиль
Благодарили: 0
Сообщений: 5
Я думаю{y + sinx =5; {4y + 2 sinx =19
0
Спасибо
Ответить
9 июня 2016 в 14:19
Ответ для Елена Тутуликова
Евгений Фёдоров

Профиль
Благодарили: 0
Сообщений: 60

Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
sinx = 1/2
y = 9/2
0
Спасибо
Ответить
Алгебра
7 класс
Урок № 49
Решение задач при помощи систем уравнений первой степени
Перечень рассматриваемых вопросов:
• Решение задач.
• Система уравнений.
• Решение системы уравнений.
Тезаурус:
Система уравнений – это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких (или одной) переменных.
Решить систему – это значит найти все её решения.
Алгебраический способ состоит в получении ответа на вопрос задачи с помощью составления уравнения или системы уравнений и последующего решения уравнения или системы.
Основная литература:
- Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.
Дополнительная литература:
- Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.
- Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.
- Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.
Теоретический материал для самостоятельного изучения.
Рассмотрим задачу. Сошлись два пастуха, Иван и Пётр. Иван и говорит Петру: «Отдай-ка ты мне одну овцу, тогда у меня будет овец ровно вдвое больше, чем у тебя!» А Пётр ему отвечает: «Нет, лучше ты мне отдай одну овцу, тогда у нас будет овец поровну!» Сколько же было у каждого овец?
Мы не знаем, сколько овец у Ивана, и сколько у Петра.
Обозначим за х число овец у Ивана, а за у – число овец у Петра.
Мысленно разделим условие задачи на две независимые части:
1. Иван и говорит Петру: «Отдай-ка ты мне одну овцу, тогда у меня будет овец ровно вдвое больше, чем у тебя!»
2. А Пётр ему отвечает: «Нет, лучше ты мне отдай одну овцу, тогда у нас будет овец поровну!»
Для каждой из частей составим уравнение с двумя неизвестными.
Начнем с первой части.
Если бы Пётр отдал Ивану одну овцу, то у Петра осталось бы (у – 1) овец.
А у Ивана стало бы (х + 1) овец.
Но тогда у Ивана было бы вдвое больше овец, чем у Петра.
Можем составить уравнение x + 1 = 2(y – 1).
Составим уравнение с двумя неизвестными для второй части. Если бы Иван отдал Петру 1 овцу, то у Ивана осталось бы (x – 1) овец. А у Петра стало бы (y + 1) овец, и тогда они имели бы овец поровну. Можем составить уравнение: x – 1 = y + 1
Мы составили два уравнения.
И в первом и во втором уравнении х обозначает число овец у Ивана, а у – число овец у Петра. Другими словами, каждое неизвестное число обозначает одно и то же в обоих уравнениях. Значит, эти уравнения можно рассматривать совместно, то есть объединить их в систему уравнений:

Решим эту систему способом подстановки.
Раскроем скобки в правой части первого уравнения.
Выразим х через у.
Подставим (2у – 3) вместо х во второе уравнение системы. Получим уравнение с одним неизвестным у.
Решим его. Упростим левую часть уравнения.
Перенесем неизвестные в левую часть. уравнения, а числа – в правую.
Подставим у = 5 в первое уравнение.
Получим х = 7.
Система имеет единственное решение: х = 7, у = 5.
Вернемся к исходным обозначениям.
Получаем, что у Ивана было 7 овец, а у Петра 5 овец.
Таким образом, мы решили задачу при помощи системы уравнений первой степени.
Задачи с помощью системы уравнений можно решать по следующей схеме.
Сначала вводим обозначения неизвестных.
Мысленно разделив условие задачи на две части, составляем 2 уравнения и объединяем их в систему.
Решаем полученную систему уравнений.
Возвращаемся к условию задачи и использованным обозначениям.
Отбираем решения и записываем ответ.
Разбор заданий из тренировочного модуля.
1. Решим задачу алгебраическим способом.
Задача.
Даны 3 числа, сумма которых равна 23. Если к удвоенному первому числу прибавить второе число и вычесть третье, то получится 32. А если из первого числа вычесть удвоенное второе и прибавить третье, то получится 8.
В задаче 3 неизвестные, поэтому введем следующие обозначения:
Пусть х – первое число, у – второе число, z – третье число.
Мысленно разделим условие задачи на 3 части, по каждой из которых составим уравнение с тремя неизвестными:


Вернёмся к условию задачи: первое число 15, второе число 5, третье число 3.
Ответ: 15, 5, 3.
Составим систему уравнений по условию задачи.
В трех сосудах 54л воды. Если из первого перелить во второй сосуд 4л, то в обоих сосудах будет воды поровну, а если из третьего сосуда перелить во второй 17л, то во втором сосуде окажется в 4 раза больше воды, чем в третьем. Сколько воды в каждом сосуде?
Пусть x л воды было в первом сосуде, y л воды – во втором, z воды – в третьем. Значит, всего в трёх сосудах было x + y + z л воды, что равно 54 л. Составим уравнение: x + y + z = 54.
Когда из первого сосуда перелили 4 л воды во второй сосуд, то во втором сосуде стало y + 4 л воды, а в первом сосуде x – 4 л воды. По условию задачи воды стало в сосудах поровну. Составляем уравнение:
y + 4 = x – 4.
Если из третьего сосуда перелить во второй 17 л, то в третьем останется z – 17 л, а во втором станет y + 17 л. По условию задачи во втором сосуде окажется в 4 раза больше воды, чем в третьем. Можем составить уравнение: y + 17 = 4(z – 17).
Записываем систему уравнений:
2. Система уравнений по условию задачи.
Составим систему уравнений по условию задачи: 5% одного числа и 4% другого вместе составляют 46, а 4% первого числа и 5% второго вместе составляют 44. Найдите эти числа.

Множество задач можно решить путем составления систем двух линейных уравнений. Такое решение состоит из трех этапов:
1. построение математической модели (обозначить через x и y неизвестные величины);
2. составление системы двух уравнений;
3. решение системы и нахождение ответа к задаче.
Пример 1. Расстояние между городами – 564 км. Навстречу друг другу из городов одновременно вышли поезда и встретились через 6 часов. Скорость одного поезда на 10 км больше скорости другого. Чему равна скорость каждого поезда?
Решение: Пусть х км/ч – скорость первого поезда, а у км/ч – скорость второго поезда. По условию задачи, поезда встретились через 6 часов. Тогда, 6х км пройдет до встречи первый поезд, 6у км пройдет до встречи второй поезд. Их встреча означает, что суммарно они прошли до встречи путь в 564 км, то есть 6х + 6у = 564 – первое уравнение.
Скорость первого поезда на 10 км/ч больше скорости второго, то есть, разность между скоростями равняется 10. Получим второе уравнение: х – у = 10.
В итоге получим систему уравнений:
(left{ begin{array}{l} 6x+6y=564 \ x-y=10 \ end{array} right. Rightarrow left{ begin{array}{l} x+y=94 \ x-y=10\ end{array} right. )(Rightarrow left{ begin{array}{l} x=52 \ y=52-10 \ end{array} right. Rightarrow left{ begin{array}{l} x=52 \ y=42 \ end{array} right.)
Ответ: 52 км/ч, 42 км/ч.
Пример 2. На двух полках лежат 84 книги. Если с одной полки снять 12 книг, то на обоих полках книг станет поровну. Сколько книг станет на каждой полке? А сколько было сначала?
Решение: Пусть х книг – на первой полке, а у книг – на второй полке. По условию задачи, количество книг на двух полках суммарно составляет 84 книги, то есть х + у = 84 – первое уравнение.
Если с первой полки снять 12 книг, то количество книг на обоих полках будет поровну. Получим второе уравнение: х – 12 = у.
В итоге получим систему уравнений:
(begin{cases} x+y=84 \ x-12=y \ end{cases} Rightarrow left{ begin{array}{l} x+y=84 \ x-y=12\ end{array} right. Rightarrow2x=96; x=48)
48 (книг) – было на первой полке.
84 – 48 = 36 (к.) – было на второй полке.
48 – 12 = 36 (к.) – станет на каждой полке.
Ответ: по 36 книг, 48 книг и 36 книг.
Содержание:
Системы уравнений, как и отдельные уравнения, используют для решения сложных и необходимых задач. Системы уравнений бывают с двумя, тремя и более переменными. В этой главе вы ознакомитесь с простейшими системами двух уравнений с двумя переменными. Основные темы лекции:
- уравнения с двумя переменными;
- график линейного уравнения;
- системы уравнений;
- способ подстановки;
- способ сложения;
- решение задач составлением системы уравнений.
Уравнения с двумя переменными
До сих пор мы рассматривали уравнение с одной переменной. Однако существуют задачи, решение которых приводит к уравнениям с двумя переменными.
Пример:
На 22 руб. купили несколько книжек по 5 руб. и географических карт — по 3 руб. Сколько купили книжек и карт?
Решение:
Пусть купили х книжки у карт. За книжки заплатили 5х руб., а за карты — 3у руб. Всего заплатили 22 руб., то есть, 5х + Зу = 22.
Это уравнение с двумя переменными. Приведём и другие примеры таких уравнений с двумя переменными:
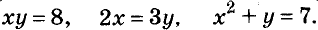
Уравнение вида ах + by = с, где а, b, с — данные числа, называется линейным уравнением с двумя переменными х и у. Если 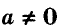
Примеры линейных уравнений:
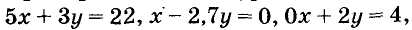 два первых из них — уравнение первой степени с двумя переменными.
два первых из них — уравнение первой степени с двумя переменными.
Паре чисел х = -1 и у = 9 удовлетворяет уравнение 5х + Зу -= 22, так как 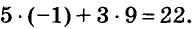 А пара чисел х = 1 и у = 2 этому уравнению не удовлетворяет, поскольку
А пара чисел х = 1 и у = 2 этому уравнению не удовлетворяет, поскольку 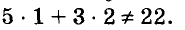
Каждая пара чисел, удовлетворяющая уравнение с двумя переменными, т. е. обращающая это уравнение в верное равенство, называется решением этого уравнения.
Обратите внимание: одно решение состоит из двух чисел, на первом месте записывают значение х, на втором — у. Корнями их не называют.
Чтобы найти решение уравнения с двумя переменными, следует подставить в уравнение произвольное значение первой неременной и, решив полученное уравнение, найти соответствующее значение второй переменной.
Для примера найдем несколько решений уравнения
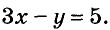
Если х = 1, то 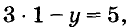 отсюда у = -2. Пара чисел х = 1 и у = -2 — решение данного уравнения. Его записывают ещё и так: (1; -2). Придавая переменной х значения 2, 3, 4, … , так же можно найти сколько угодно решений уравнения: (2; 1), (3; 4), (4; 7), (5; 10), …. Каждое уравнение первой степени с двумя переменными имеет бесконечно много решений.
отсюда у = -2. Пара чисел х = 1 и у = -2 — решение данного уравнения. Его записывают ещё и так: (1; -2). Придавая переменной х значения 2, 3, 4, … , так же можно найти сколько угодно решений уравнения: (2; 1), (3; 4), (4; 7), (5; 10), …. Каждое уравнение первой степени с двумя переменными имеет бесконечно много решений.
Уравнение 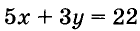 также имеет бесконечно много решений, но сформулированную выше задачу удовлетворяет только одно из них: (2; 4).
также имеет бесконечно много решений, но сформулированную выше задачу удовлетворяет только одно из них: (2; 4).
Два уравнения с двумя переменными называют равносильными, если каждое из них имеет те же решения, что и другое. Уравнения, не имеющие решений, также считаются равносильными.
Для уравнения с двумя переменными остаются справедливыми свойства, сформулированные для уравнений с одной переменной.
Обе части уравнения с двумя переменными можно умножить или разделить на одно и то же число, отличное от нуля. Любой член такого уравнения можно перенести из одной части уравнения в другую, изменив его знак на противоположный. В результате получается уравнение, равносильное данному.
Например, уравнение 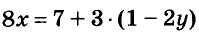 можно преобразовать так:
можно преобразовать так: 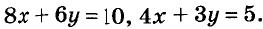 . Каждое из этих уравнений равносильно друг другу.
. Каждое из этих уравнений равносильно друг другу.
Иногда возникает потребность решить уравнение с двумя переменными во множестве целых чисел, то есть определить решения, являющиеся парами целых чисел. Способы решения таких уравнений определил древнегреческий математик Диофант (III в.), поэтому их называют диофантовыми уравнениями. Например, задача о книжках и картах сводится к уравнению 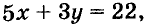 где х и у могут быть только целыми (иногда натуральными) числами.
где х и у могут быть только целыми (иногда натуральными) числами.
Переменную у из этого уравнения выразим через х:
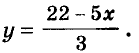
Будем подставлять в равенство вместо х первые натуральные числа до тех пор, пока не получим целое значение переменной у. Это можно делать устно. Если х = 2, то у = 4. Других натуральных решений уравнение не имеет. Поэтому задача имеет единственное решение: 2 книги и 4 карты.
Пример:
Решите уравнение:
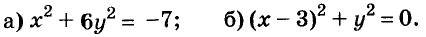
Решение:
а) При любых значениях х и у значения выражения 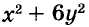 не может быть отрицательным числом. Поэтому уравнение не имеет решений.
не может быть отрицательным числом. Поэтому уравнение не имеет решений.
б) Значение выражения 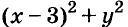 равно нулю только при условии, когда x -3 = 0 и y = 0. Значит, уравнение имеет только одно решение: х = 3, у = 0.
равно нулю только при условии, когда x -3 = 0 и y = 0. Значит, уравнение имеет только одно решение: х = 3, у = 0.
Пример:
Составьте уравнение с двумя переменными, решением которого будет пара чисел (1; -5).
Решение:
Пишем любой двучлен с переменными х и у, например 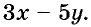 Если х = 1, а у = -5, то значение даного двучлена равно 28. Следовательно, уравнение
Если х = 1, а у = -5, то значение даного двучлена равно 28. Следовательно, уравнение 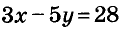 удовлетворяет условие задачи.
удовлетворяет условие задачи.
Есть много других линейных уравнений с двумя переменными, имеющих такое же решение (1; -5).
График линейного уравнения с двумя переменными
Рассмотрим уравнение 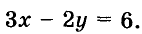 Давая переменной х значения -2, -1,0,1,2, 3,…, найдём соответствующие значения переменной у. Будем иметь решение данного уравнения: (-2; -б), (-1; -4,5), (0; -3), <1; -1,5), (2; 0), (3; 1,5),….
Давая переменной х значения -2, -1,0,1,2, 3,…, найдём соответствующие значения переменной у. Будем иметь решение данного уравнения: (-2; -б), (-1; -4,5), (0; -3), <1; -1,5), (2; 0), (3; 1,5),….
Если на координатной плоскости обозначить соответствующие этим парам точки, то окажется, что все они размещены на одной прямой (рис. 89). Эту прямую (рис. 90) называют графиком данного уравнения.
Выразим из уравнения 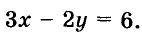 его переменную у через х:
его переменную у через х:
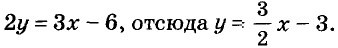
Это функция, график которой изображён на рисунке 90. Вообще, если 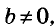 то из уравнения ах + by = с переменную у можно выразить через х. Получим равенство
то из уравнения ах + by = с переменную у можно выразить через х. Получим равенство 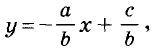 являющееся формулой линейной функции. А её график — прямая.
являющееся формулой линейной функции. А её график — прямая.
График каждого уравнения первой степени с двумя переменными — прямая. И каждая прямая координатной плоскости — график некоторого линейного уравнения с двумя переменными.
Каждая точка графика уравнения имеет координаты, удовлетворяющие данное уравнение. Например, точка М графика уравнения 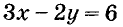 имеет абсциссу 5 и ординату 4,5 (см. рис. 90). Эти значения х и у удовлетворяют данное уравнение: 3 5-2-4,5 = 6.
имеет абсциссу 5 и ординату 4,5 (см. рис. 90). Эти значения х и у удовлетворяют данное уравнение: 3 5-2-4,5 = 6.
График линейной функции одновременно является графиком некоторого линейного уравнения с двумя переменными. Например, уравнения 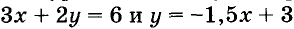 равносильны, а равносильные уравнения имеют одинаковые графики.
равносильны, а равносильные уравнения имеют одинаковые графики.
Чтобы построить график уравнения первой степени о ‘ 1 двумя переменными, достаточно найти два его решения, обозначить на координатной плоскости соответствующие им точки и провести через них прямую.
Такое уравнение удовлетворяет любая пара чисел. Его графиком является вся координатная плоскость.
•Если 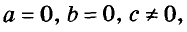 то будем иметь уравнение
то будем иметь уравнение
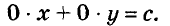
Такое уравнение не имеет ни одного решения.
Известно, что две прямые на плоскости могут пересекаться, быть параллельными или совпадать. Так же могут располагаться на координатной плоскости и графики двух уравнений первой степени с двумя переменными (рис. 91).
Взаимное расположение графиков уравнений
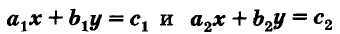
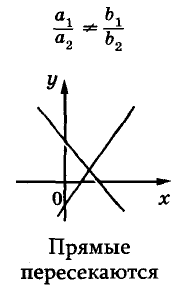
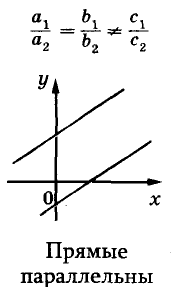
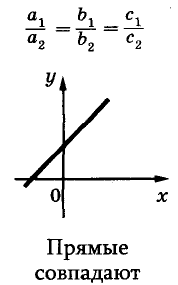
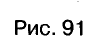
Пример:
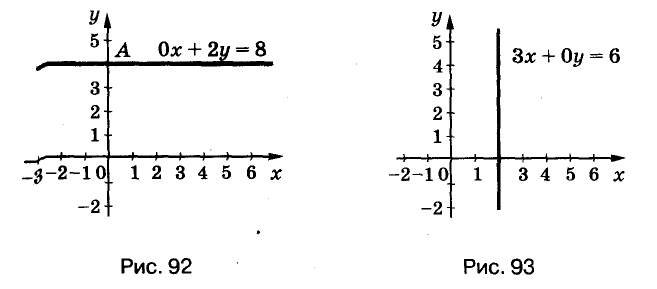
Постройте график уравнения:
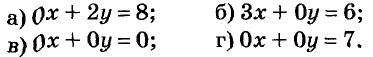
Решение:
Уравнению а) удовлетворяет каждая пара чисел (c ; 4), где с — произвольное число. График этого уравнений — прямая, параллельная оси х, проходящая через точку A(0 ; 4) (рис. 92).
Бесконечно много решений уравнения б) — множество пар (2 ; p), где p — произвольное число. График этого уравнения — прямая параллельная оси у (рис. 93).
Уравнение в) удовлетворяет каждая пара чисел, график этого уравнения — вся координатная плоскость.
Уравнение г) не имеет ни одного решения, его график — пустое множество.
Определение и вычисление систем уравнений
Пример:
4 кг конфет и 3 кг пряников стоят 26 руб., а 6 кг конфет и 2 кг пряников — 34 руб. Сколько стоит 1 кг конфет и 1 кг пряников?
Эту задачу можно решить, составив уравнение с одной переменной, а можно воспользоваться другим способом.
Пусть 1 кг конфет стоит х руб., а 1 кг пряников — у руб.
Тогда
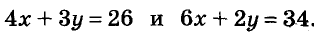
Имеем два уравнения с двумя переменными. Надо найти такие значения переменных х и у, которые удовлетворяют одновременно и первое, и второе уравнения, то есть обращающие каждое из уравнений в верное равенство. Другими словами: надо найти общее решение обоих уравнений, или решить систему данных уравнений.
Если требуется найти общие решение двух или нескольких уравнений, говорят, что эти уравнения образуют систему. Записывают систему уравнений, объединяя их фигурной скобкой:
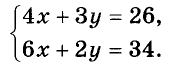
Решением системы уравнений называют общее решение всех её уравнений.
Например, пара чисел (3; 2) является решением системы
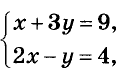
то есть: 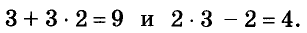
Решить систему уравнений —это означает найти множество всех её решений .
Решать системы уравнений можно графическим способом. Решим, например, систему (*). Для этого построим на одной координатной плоскости графики обоих её уравнений (рис. 95). Координаты каждой точки графика уравнения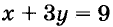 удовлетворяют это уравнение. Координаты каждой точки графика уравнения
удовлетворяют это уравнение. Координаты каждой точки графика уравнения 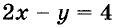 удовлетворяют это уравнение. Построенные графики пересекаются в точке А (3; 2). Поэтому пара чисел (3; 2) — единственное решение данной системы уравнений.
удовлетворяют это уравнение. Построенные графики пересекаются в точке А (3; 2). Поэтому пара чисел (3; 2) — единственное решение данной системы уравнений.
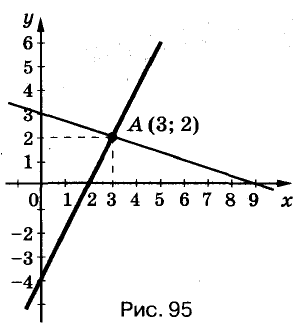
Графическим способом обычно находят приближённые решения. А подставив значения 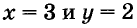 в данную систему уравнений, убедимся,что (3; 2) — точное решение.
в данную систему уравнений, убедимся,что (3; 2) — точное решение.
Каждая ли система двух уравнений имеет только одно решение? Нет. Например, система уравнений
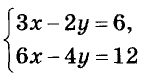
имеет бесконечно много решений. Ведь графики обоих этих уравнений — одна и та же прямая (убедитесь в этом самостоятельно). Следовательно, координаты каждой точки этой прямой, например(-2; -6), (-1; -4,5), (0; -3), (1; -1,5), (2; 0),… — решения данной системы уравнений.
Есть системы уравнений, которые не имеют ни одного решения. Графики таких уравнений — параллельные прямые (см. рис. 91).
Вы уже знаете, что уравнение и функции — удобные математические модели многих задач. Системы уравнений также используют как математические модели. Иногда, исходя из условия задачи, систему уравнений с двумя переменными легче составить, чем одно уравнение. И решать её бывает легче, чем уравнение с одной переменной, соответствующее условию той же задачи.
Пример:
Сколько решений имеет система уравнений
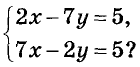
Решение:
Так как 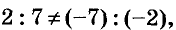 то эта система имеет одно решение (см. рис. 91). Проверьте графически.
то эта система имеет одно решение (см. рис. 91). Проверьте графически.
Пример:
Решите графически систему уравнений
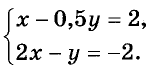
Решение:
Найдём координаты точек пересечения графиков уравнений системы с осями координат.
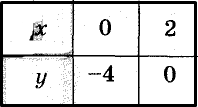

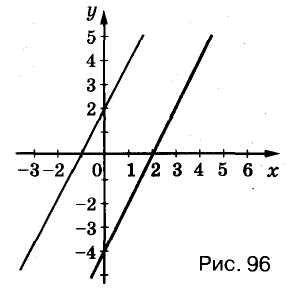
Построим графики данных уравнений (рис. 96). Эти графики — параллельные прямые, не имеющие общих точек. Ответ. Система уравнений решений не имеет.
Способ подстановки
Графический способ решения систем уравнений громоздок и даёт, как правило, приближённые решения. Поэтому чаще системы решают другими способами, в частности способом подстановки.
Пусть, например, надо решить систему
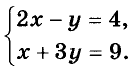
Выразим из второго её уравнения переменную х через у:
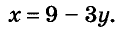
Так как первое уравнение системы должны удовлетворять те же значения переменных, что и второе, подставим найденное выражение 9-3у вместо х в первое уравнение. Получим уравнение с одной переменной:
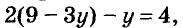 отсюда
отсюда 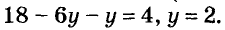
Подставим значение у = 2 в уравнение х = 9 – Зу и найдём соответствующее значение переменной х:
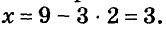
Следовательно, решением системы является пара чисел (3; 2).
Чтобы решить систему уравнений способом подстановки, надо:
- выразить из какого-нибудь её уравнения одну переменную через другую;
- подставить в другое уравнение системы вместо этой л временной полученное выражение;
- решить получившееся уравнение с одной переменной;
- найти соответствующее значение второй переменной.
Этим способом можно решать любую систему линейных уравнений с двумя переменными. Однако удобнее, если коэффициент при какой-либо переменной в уравнении равен 1.
Пример №1
Решите систему уравнений
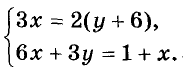
Решение:
Заменим данные уравнения линейными, получим систему:
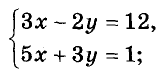
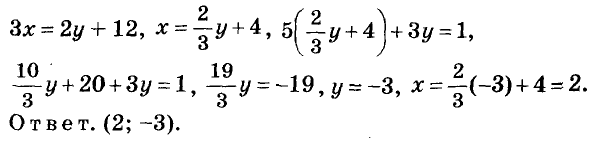
Иногда можно подставлять из одного уравнения системы во второе не значение отдельной переменной, а значение целого выражения.
Например, решая систему уравнений
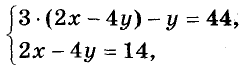
можно значение выражения 2х-4у из второго уравнения подставить в первое:
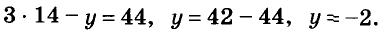
Тогда
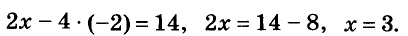
Ответ. х = 3, у = -2.
Проверка. 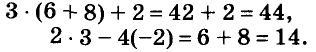
2 • 3 – 4(-2) = 6 + 8 = 14. Найденная пара чисел (3; -2) удовлетворяет данную систему уравнений.
Пример №2
Решите систему уравнений:
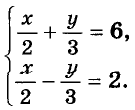
Решение:
Выразим из второго уравнения значение Дроби 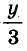 через х и подставим его в первое уравнение.
через х и подставим его в первое уравнение.
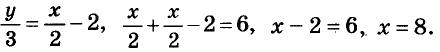
Тогда 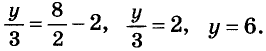
Ответ. (8; 6).
Способ сложения
Дана система уравнений:
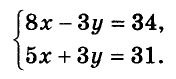
Сначала решим её способом подстановки. Выразим из первого уравнения переменную у через х и подставим полученное выражение вместо у во второе уравнение:
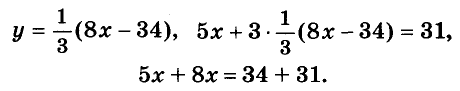
Дальше уже несложно закончить решение системы.
А можно ли уравнение 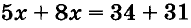 получить другим способом? Да, для этого достаточно сложить левые и правые части уравнений системы. Так как коэффициенты при у — противоположные числа, то члены с переменной у сокращаются. Поэтому, решая любую подобную систему, вместо подстановки можно выполнять почленно сложение уравнении. Оформлять решение будем, например, так:
получить другим способом? Да, для этого достаточно сложить левые и правые части уравнений системы. Так как коэффициенты при у — противоположные числа, то члены с переменной у сокращаются. Поэтому, решая любую подобную систему, вместо подстановки можно выполнять почленно сложение уравнении. Оформлять решение будем, например, так: 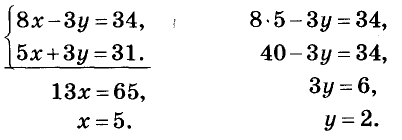 Ответ. (5; 2).
Ответ. (5; 2).
Таким образом решают системы, в которых коэффициенты при какой-либо переменной — противоположные числа. А к такому виду можно свести любую систему линейных уравнений с двумя переменными. Пусть, например, дана система
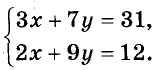
Умножим обе части её первого уравнения на 2, а второго — на -3; получим систему, в которой коэффициенты при переменной х — противоположные числа. Уравнения полученной системы равносильны уравнениям данной. Следовательно, она имеет такие же решения, что и данная.
Оформлять решение можно таким образом: 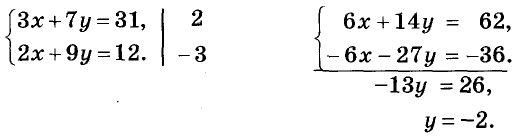
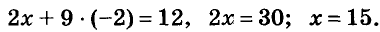
Решение. (15; -2).
Способом сложения можно решить не только системы линейных уравнений, а и многих нелинейных.
Пример №3
Решите систему уравнений
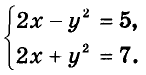
Решение:
Выполнив сложение левых и правых частей данных уравнений, получим:
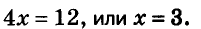
Значит, 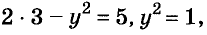 отсюда
отсюда 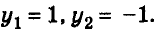
Проверка показывает, что найденные пары чисел (3; 1) и (3; -1) удовлетворяют данную систему уравнений.
Ответ. Система уравнений имеет два решения: (3; 1) и (3; -1).
Пример №4
Решите систему уравнений
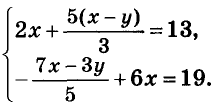
Решение:
Умножим все члены первого уравнения на 3, а второго — на 5. Упростим полученные уравнения:
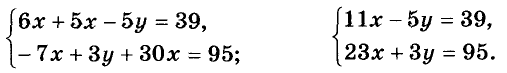
Чтобы воспользоваться способом сложения, ещё раз умножим все члены первого уравнения на 3, а второго — на 5 и почленно сложим их:

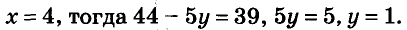
Ответ. (4; 1).
Решение задач составлением системы уравнений
Многие задачи, особенно такие, в которых надо найти значения двух величин, удобно решать с помощью систем уравнений.
Пример:
За 5 блокнотов и 6 тетрадей заплатили 6,9 руб. Сколько стоит один блокнот и одна тетрадь, если 4 блокнота дороже 3 тетрадей на 2,4 руб.?
Решение:
Допустим, что блокнот стоит х руб., а тетрадь — у руб. За 5 блокнотов заплатили 5х руб., а за б тетрадей — 6у руб. Вместе за них заплатили 6,9 руб., следовательно,
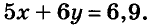
Так как 4 блокнота дороже 3 тетрадей на 2,4 руб., имеем ещё одно уравнение:
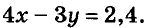
Переменные х и у в обоих уравнениях обозначают одни и те же цены. Значит, надо решить систему этих двух уравнений:
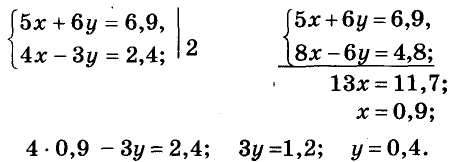
Ответ. Блокнот стоит 90 к., тетрадь — 40 к.
Эту задачу можно решить также составлением уравнения с одной переменной. Любую задачу, которая решается составлением системы линейных уравнений, можно решить и с помощью уравнения с одной переменной. Только систему уравнений чаще составить легче, чем уравнение с одной переменной.
Существует немало задач, которые удобно решать с помощью системы трёх уравнений с тремя переменными. Решим одну из них.
Пример:
Капитал в 10 000 руб. поделите на три части так, чтобы первая была на 2 000 руб. больше второй и на 3 000 руб. — третьей.
Решение:
Обозначим искомые части капитала буквами х,у и z. По условию задачи
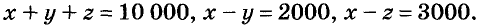
Искомые значения переменных должны удовлетворять системе трёх уравнений с тремя переменными:
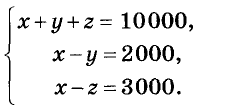
Сложив почленно левые и правые части этих уравнений, будем иметь Зх = 15 000, отсюда х = 5 000. Тогда из второго уравнения получим:
5000 -у = 2000, y = 3000, а из третьего вычислим:
5 000 -z = 3 000, z = 2 000. Ответ. 5000 руб., 3000 руб. и 2000 руб.
Обобщим задачу 1:
Пример:
За 5 блокнотов и 6 тетрадей заплатили m руб. Сколько стоит один блокнот и одна тетрадь, если 4 блокнота дороже 3 тетрадей на n руб.?
Здесь m и n – параметры, то есть буквы, считающиеся в условиях задачи данными, неизменными. Задачи с параметрами так же можно решать с помощью уравнений или системы уравнений, только ответами к ним будут не конкретные числа, а выражения, содержащие параметры.
Решим сформулированную задачу.
Решение:
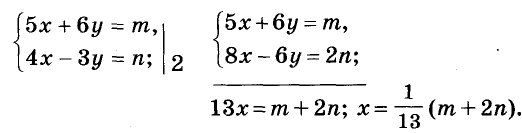
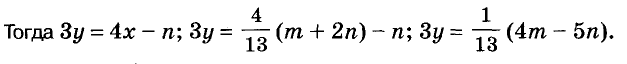
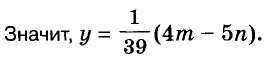
Ответ. Один блокнот и одна тетрадь стоят соответственно
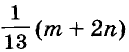 руб. и
руб. и 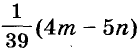 руб.
руб.
Пример:
Поделите капитал 8 100 руб. на две части так, чтобы меньшая часть составляла 80 % от большей.
Решение:
Пусть большая часть равна х руб., тогда меньшая — 80 % от х, то еть 0,8х. Имеем систему двух уравнений:
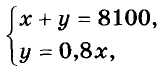
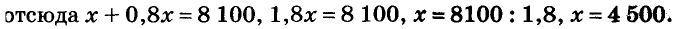
Ответ: 4500 руб. и 3600 руб.
Пример:
Найдите два числа, сумма которых равна 15, а разность их квадратов на 60 больше.
Решение:
Если искомые числа равны х и у, то
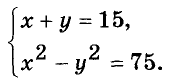
Так как 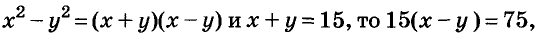 а х – у = 5. Имеем систему уравнений:
а х – у = 5. Имеем систему уравнений:
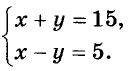
Её решение х = 10, у = 5 является решением и данной иидачи.
Ответ. 10 и 5.
История систем уравнений
Задачи, сводящиеся к системе уравнений с двумя переменными, учёные Вавилона умели решать ещё более 4 тысяч лет тому назад.
Китайские математики более 2 тысяч лeт тому назад разработали общий метод решения систем линейных уравнений с тремя и более неизвестными и описали его в трактате «Математика в девяти книгах».
Древнегреческий математик Диофант (III в.) находил натуральные решения и таких, например, задач: «Найдите два числа с данной разностью и таких, чтобы разность их квадратов была больше их разности на заданное число». Если искомые числа обозначить через х и у, а данные — через а и b, то задаче соответствует такая система уравнений:
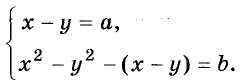
Графический способ решения уравнений одним из первых предложил выдающийся французский философ, математик, физик, физиолог Р. Декарт. Он ввёл понятие переменной величины и удобную математическую Рене Декарт символику. (1596-1650)
В 1637 г. Р. Декарт опубликовал работу «Размышления о методе», в которой описал метод координат, связывающий алгебру с геометрией. Пользуясь этим методом, геометрические задачи можно решать алгебраическими методами, а алгебраические — геометрическим.
Р. Декарт — основатель очень известного ранее философского учения картезианство. Это название произошло от латинизированного имени Декарта – Картезий.
Напомню:
Уравнение вида ах + by = с, где а,b,c — данные числа, называют линейным уравнением с двумя переменными хну. Если 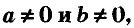 его называют уравнением первой степени с двумя переменными.
его называют уравнением первой степени с двумя переменными.
Пару чисел, удовлетворяющую уравнение с двумя переменными, называют решением этого уравнения. Например, пара чисел (3; -2) — решение уравнения 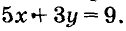 Уравнение первой степени с двумя переменными имеет бесконечно много решений. В декартовой системе координат каждому уравнению первой степени с двумя переменными соответствует прямая — график этого уравнения. И наоборот, каждая прямая координатной плоскости — график некоторого линейного уравнения с двумя переменными.
Уравнение первой степени с двумя переменными имеет бесконечно много решений. В декартовой системе координат каждому уравнению первой степени с двумя переменными соответствует прямая — график этого уравнения. И наоборот, каждая прямая координатной плоскости — график некоторого линейного уравнения с двумя переменными.
Два уравнения с двумя переменными называют равносильными, если они имеют те же решения. Равносильные уравнения с двумя переменными имеют одинаковые графики.
Если нужно найти общие решения двух или нескольких уравнений, говорят, что эти уравнения образуют систему уравнений.
Решением системы уравнений называют общее решение всех её уравнений. Пример системы двух линейных уравнений с переменными х и у:
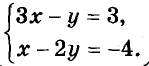 Каждое уравнение этой системы имеет бесконечно много решений и только одно из них — общее для обоих уравнений: пара (2; 3).
Каждое уравнение этой системы имеет бесконечно много решений и только одно из них — общее для обоих уравнений: пара (2; 3).
Системе двух уравнений первой степени с двумя переменными в декартовой системе координат соответствует пара прямых. Поскольку две прямые на плоскости могут пересекаться , совпадать или быть параллельными, то и соответствующая им система уравнений может иметь одно решение, бесконечно много или не иметь ни одного решения.
Решать системы уравнений с двумя переменными можно разными способами — подстановки, сложения или графическим способом.
Системы линейных уравнений
К системам линейных уравнений приводит множество прикладных, в том числе и экономических задач.
Основные понятия и определения
Система 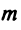 линейных уравнений с
линейных уравнений с 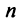 переменными имеет вид:
переменными имеет вид:
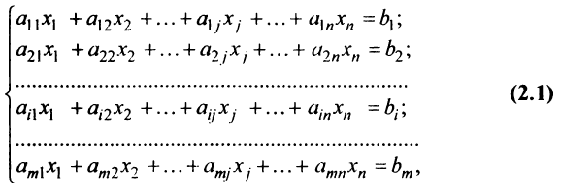
где 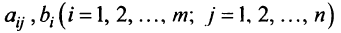 — произвольные числа, называемые соответственно коэффициентами при переменных и свободными членами уравнений.
— произвольные числа, называемые соответственно коэффициентами при переменных и свободными членами уравнений.
В более краткой записи с помощью знаков суммирования систему можно записать в виде: 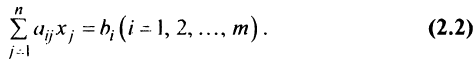
Решением системы (2.1) называется такая совокупность 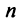 чисел
чисел 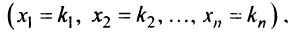 при подстановке которых каждое уравнение системы обращается в верное равенство.
при подстановке которых каждое уравнение системы обращается в верное равенство.
Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений.
Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. Например, система уравнений
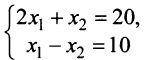 — совместная и определенная, так как имеет единственное решение
— совместная и определенная, так как имеет единственное решение 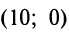 ; система
; система 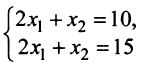 — несовместная; а система уравнении
— несовместная; а система уравнении 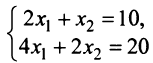 — совместная и неопределенная, так как имеет более одного, а точнее бесконечное множество решений
— совместная и неопределенная, так как имеет более одного, а точнее бесконечное множество решений  , где с — любое число.
, где с — любое число.
Две системы уравнений называются равносильными, или эквивалентными, если они имеют одно и то же множество решений. С помощью элементарных преобразований системы уравнений, рассмотренных в гл.1 применительно к матрицам (например, умножение обеих частей уравнений на числа, не равные нулю; сложение уравнений системы), получается система (2.1), равносильная данной.
Запишем систему (2.1) в матричной форме. Обозначим: 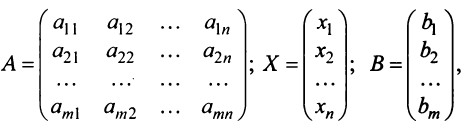
где  — матрица коэффициентов при переменных, или матрица системы,
— матрица коэффициентов при переменных, или матрица системы, 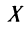 — матрица-столбец переменных;
— матрица-столбец переменных; 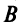 — матрица-столбец свободных членов.
— матрица-столбец свободных членов.
Так как число столбцов матрицы 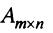 равно числу строк матрицы
равно числу строк матрицы 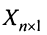 , то их произведение
, то их произведение
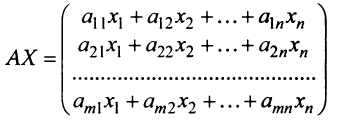
есть матрица-столбец. Элементами полученной матрицы являются левые части системы (2.1). На основании определения равенства матриц систему (2.1) можно записать в виде: 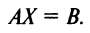
Система n линейных уравнений с n переменными.
Метод обратной матрицы и формулы Крамера
Пусть число уравнений системы (2.1) равно числу переменных, т.е. 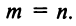 Тогда матрица системы является квадратной, а ее определитель
Тогда матрица системы является квадратной, а ее определитель 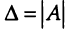 называется определителем системы.
называется определителем системы.
Рассмотрим решение системы двух уравнений с двумя переменными:

в которой хотя бы один из коэффициентов при переменных отличен от нуля.
Для решения этой системы исключим переменную 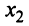 , умножив первое уравнение на
, умножив первое уравнение на 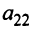 , второе — на
, второе — на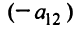 и сложив их. Затем исключим переменную
и сложив их. Затем исключим переменную 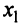 , умножив первое уравнение на
, умножив первое уравнение на 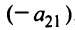 , второе — на
, второе — на 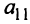 и также сложив их. В результате получим систему:
и также сложив их. В результате получим систему:
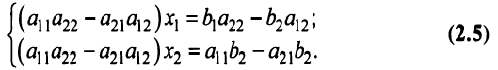
Выражение в скобках есть определитель системы
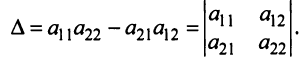
Обозначив 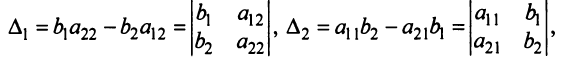 система (2.5) примет вид
система (2.5) примет вид

Из полученной системы следует, что если определитель системы 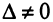 , то система (2.4) имеет единственное решение, определяемое по формулам:
, то система (2.4) имеет единственное решение, определяемое по формулам: 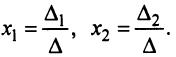
Если 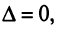
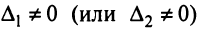 , то система (2.4) несовместная, так как в этом случае приводится к виду:
, то система (2.4) несовместная, так как в этом случае приводится к виду: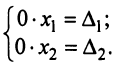
Если 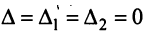 , то система (2.4) неопределенная и имеет бесконечное множество решений, так как в этом случае приводится к виду:
, то система (2.4) неопределенная и имеет бесконечное множество решений, так как в этом случае приводится к виду: 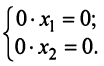
Для получения решения системы (2.1) при 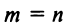 в общем виде предположим, что квадратная матрица системы
в общем виде предположим, что квадратная матрица системы 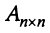 невырожденная, т.е. ее определитель
невырожденная, т.е. ее определитель 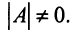 В этом случае существует обратная матрица
В этом случае существует обратная матрица 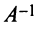 .
.
Умножая слева обе части матричного равенства (2.3) на матрицу 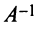 , получим
, получим 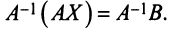 Так как
Так как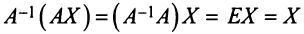 , то решением системы методом обратной матрицы будет матрица-столбец
, то решением системы методом обратной матрицы будет матрица-столбец

Теорема Крамера. Пусть  — определитель матрицы системы
— определитель матрицы системы 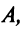 а
а 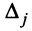 — определитель матрицы, получаемой из матрицы
— определитель матрицы, получаемой из матрицы 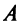 заменой
заменой 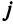 -го столбца столбцом свободных членов. Тогда, если
-го столбца столбцом свободных членов. Тогда, если 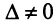 , то система имеет единственное решение, определяемое по формулам:
, то система имеет единственное решение, определяемое по формулам:
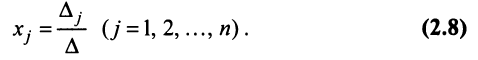
Формулы (2.8) получили название формул Крамера.
 В соответствии с (1.14) обратная матрица
В соответствии с (1.14) обратная матрица 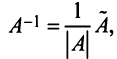 где
где 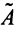 — матрица, присоединенная к матрице
— матрица, присоединенная к матрице 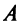 . Так как элементы матрицы
. Так как элементы матрицы 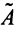 есть алгебраические дополнения элементов матрицы
есть алгебраические дополнения элементов матрицы 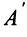 , транспонированной к
, транспонированной к 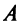 , то запишем равенство (2.7) в развернутой форме:
, то запишем равенство (2.7) в развернутой форме:
Учитывая, что 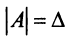 , получим после умножения матриц
, получим после умножения матриц
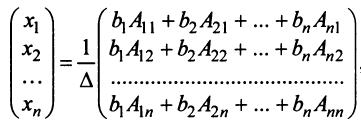 откуда следует, что для любого
откуда следует, что для любого 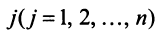
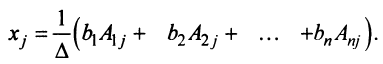
На основании свойства 9 определителей (см. § 1.4) 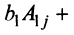
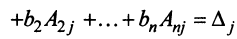 , где
, где 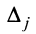 — определитель матрицы, полученной из матрицы
— определитель матрицы, полученной из матрицы 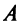 заменой
заменой 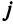 -го столбца
-го столбца 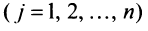 столбцом свободных членов. Следовательно,
столбцом свободных членов. Следовательно, 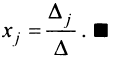
Заметим, что фактически формулы Крамера были получены нами в частном случае при решении системы (2.4) 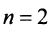 уравнений с двумя переменными.
уравнений с двумя переменными.
Пример №5
Решить систему уравнений
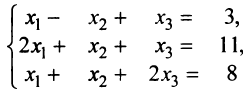 а) методом обратной матрицы; б) по формулам Крамера. Р е ш е н и е. а) Обозначим
а) методом обратной матрицы; б) по формулам Крамера. Р е ш е н и е. а) Обозначим 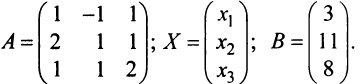
Решение:
Тогда в матричной форме данная система имеет вид: 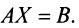 Найдем определитель
Найдем определитель 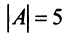 . Так как
. Так как 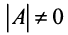 , то матрица
, то матрица 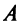 – невырожденная, и существует обратная матрица
– невырожденная, и существует обратная матрица 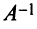 . Матрицу
. Матрицу 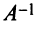 находим по алгоритму:
находим по алгоритму:
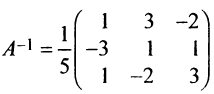 Теперь пo формуле (2.7)
Теперь пo формуле (2.7)
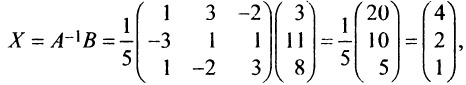
т.е. решение системы (4; 2; 1).
б) Найдем определитель системы 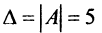 (см. п. а). Так как
(см. п. а). Так как 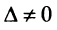 , то по теореме Крамера система имеет единственное решение.
, то по теореме Крамера система имеет единственное решение.
Вычислим определители матриц 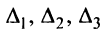 полученных из матрицы
полученных из матрицы 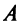 заменой соответственно первого, второго и третьего столбцов столбцом свободных членов:
заменой соответственно первого, второго и третьего столбцов столбцом свободных членов: 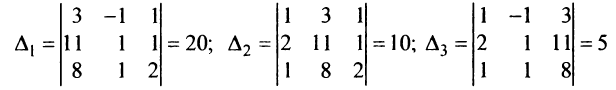 (рекомендуем читателю вычислить самостоятельно).
(рекомендуем читателю вычислить самостоятельно).
Теперь по формулам Крамера (2.8)
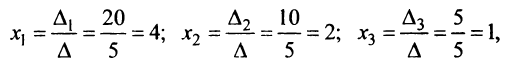
т.е. решение системы (4; 2; 1).
В конце решения системы (любым способом) рекомендуем сделать проверку, подставив найденные значения в уравнения системы, и убедиться в том, что они обращаются в верные равенства. ►
Существенным недостатком решения систем 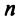 линейных уравнений с
линейных уравнений с 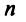 переменными по формулам Крамера и методом обратной матрицы является их большая трудоемкость, связанная с вычислением определителей и нахождением обратной матрицы. Поэтому эти методы представляют скорее теоретический интерес и на практике не могут быть использованы для решения реальных экономических задач, сводящихся часто к системам с большим числом уравнений и переменных.
переменными по формулам Крамера и методом обратной матрицы является их большая трудоемкость, связанная с вычислением определителей и нахождением обратной матрицы. Поэтому эти методы представляют скорее теоретический интерес и на практике не могут быть использованы для решения реальных экономических задач, сводящихся часто к системам с большим числом уравнений и переменных.
Метод Гаусса
Рассмотрим решение системы (2.1) т линейных уравнений с 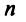 переменными в общем виде.
переменными в общем виде.
Метод Гаусса — метод последовательного исключения переменных — заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
Предположим, что в системе (2.1) коэффициент при переменной 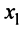 в первом уравнении
в первом уравнении 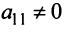 (если это не так, то перестановкой уравнений местами добьемся того, чтобы
(если это не так, то перестановкой уравнений местами добьемся того, чтобы 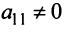 ).
).
Шаг 1. Умножая первое уравнение на подходящие числа (а именно на 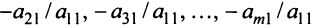 ) и прибавляя полученные уравнения соответственно ко второму, третьему, …,
) и прибавляя полученные уравнения соответственно ко второму, третьему, …, 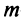 -му уравнению системы (2.1), исключим переменную х, из всех последующих уравнений, начиная со второго. Получим
-му уравнению системы (2.1), исключим переменную х, из всех последующих уравнений, начиная со второго. Получим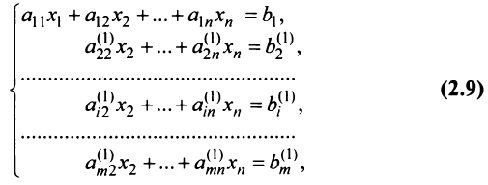
где буквами с верхним индексом (1) обозначены новые коэффициенты, полученные после первого шага.
Шаг 2. Предположим, что 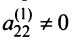 (если это не так, то соответствующей перестановкой уравнений или переменных с изменением их номеров добьемся того, чтобы
(если это не так, то соответствующей перестановкой уравнений или переменных с изменением их номеров добьемся того, чтобы 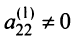 ).
).
Умножая второе уравнение на подходящие числа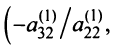
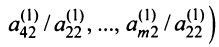 и прибавляя полученные уравнения соответственно к третьему, четвертому, …,
и прибавляя полученные уравнения соответственно к третьему, четвертому, …, 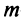 -му уравнению системы, исключим переменную
-му уравнению системы, исключим переменную 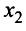 из всех последующих уравнений, начиная с третьего.
из всех последующих уравнений, начиная с третьего.
Продолжая процесс последовательного исключения переменных 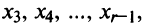 после
после 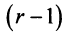 -гo шага получим систему
-гo шага получим систему
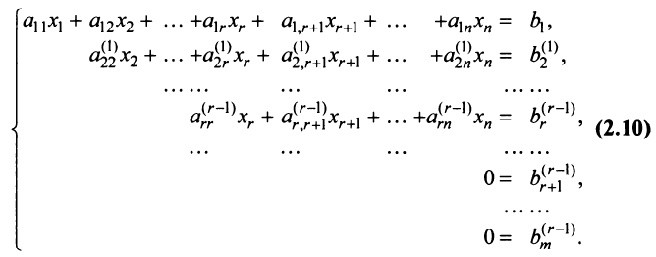
Число нуль в последних 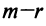 уравнениях означает, что их левые части имеют вид
уравнениях означает, что их левые части имеют вид 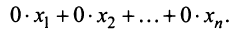 Если хотя бы одно из чисел
Если хотя бы одно из чисел 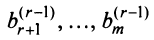 не равно нулю, то соответствующее равенство противоречиво, и система (2.1) несовместна.
не равно нулю, то соответствующее равенство противоречиво, и система (2.1) несовместна.
Таким образом, для любой совместной системы числа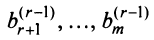 в системе (2.10) равны нулю. В этом случае последние
в системе (2.10) равны нулю. В этом случае последние 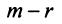 уравнений в системе (2.10) являются тождествами и их можно не принимать во внимание при решении системы (2.1). Очевидно, что после отбрасывания «лишних» уравнений возможны два случая: а) число уравнений системы (2.10) равно числу переменных, т.е.
уравнений в системе (2.10) являются тождествами и их можно не принимать во внимание при решении системы (2.1). Очевидно, что после отбрасывания «лишних» уравнений возможны два случая: а) число уравнений системы (2.10) равно числу переменных, т.е. 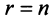 (в этом случае система (2.10) имеет треугольный вид); б)
(в этом случае система (2.10) имеет треугольный вид); б) 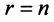 (в этом случае система (2.10) имеет ступенчатый вид).
(в этом случае система (2.10) имеет ступенчатый вид).
Переход системы (2.1) к равносильной ей системе (2.10) называется прямым ходом метода Гаусса, а нахождение переменных из системы (2.10) — обратным ходом.
Преобразования Гаусса удобно проводить, осуществляя преобразования не с самими уравнениями, а с матрицей их коэффициентов. Рассмотрим матрицу 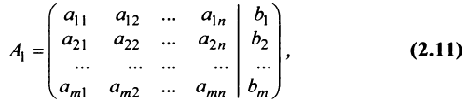
называемую расширенной матрицей системы (2.1), ибо в нее, кроме матрицы системы 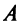 , дополнительно включен столбец свободных членов.
, дополнительно включен столбец свободных членов.
Пример №6
Решить систему уравнений: 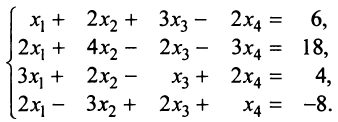
Решение:
Расширенная матрица системы имеет вид: 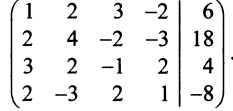 Шаг 1. Так как
Шаг 1. Так как 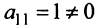 , то умножая первую строку матрицы на числа (-2), (—3), (-2) и прибавляя полученные строки соответственно ко второй, третьей, четвертой строкам, исключим переменную
, то умножая первую строку матрицы на числа (-2), (—3), (-2) и прибавляя полученные строки соответственно ко второй, третьей, четвертой строкам, исключим переменную 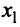 из всех строк, начиная со второй. Заметив, что в новой матрице
из всех строк, начиная со второй. Заметив, что в новой матрице 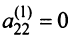 , поменяем местами вторую и третью строки:
, поменяем местами вторую и третью строки: 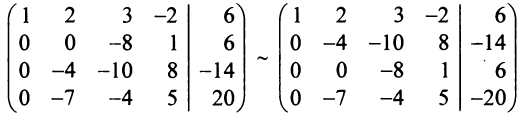
Шаг 2. Так как теперь 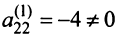 , то умножая вторую строку на (-7/4) и прибавляя полученную строку к четвертой, исключим переменную
, то умножая вторую строку на (-7/4) и прибавляя полученную строку к четвертой, исключим переменную 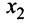 из всех строк, начиная с третьей:
из всех строк, начиная с третьей:
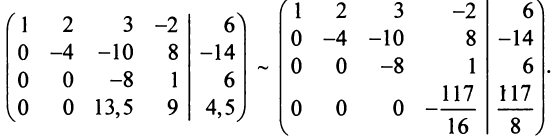
Шаг 3. Учитывая, что 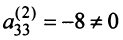 , умножаем третью строку на 13,5/8 = 27/16, и прибавляя полученную строку к четвертой, исключим из нее переменную
, умножаем третью строку на 13,5/8 = 27/16, и прибавляя полученную строку к четвертой, исключим из нее переменную 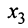 .
.
Получим (см. последнюю матрицу) систему уравнений
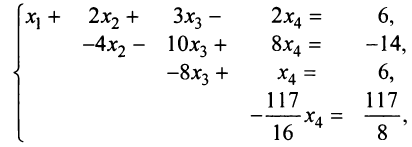
откуда, используя обратный ход метода Гаусса, найдем из четвертого уравнения 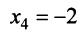 ; из третьего
; из третьего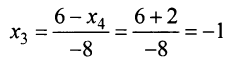 ; из второго
; из второго
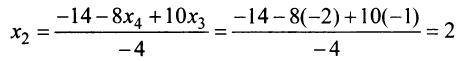 и из первого уравнения
и из первого уравнения
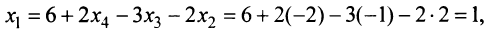 т.е. решение системы
т.е. решение системы
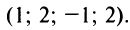 ►
►
Пример №7
Методом Гаусса решить систему уравнений:
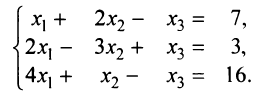
Решение:
Преобразуем расширенную матрицу системы
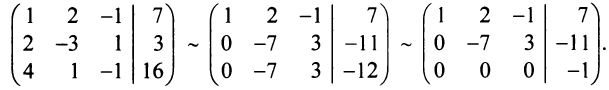
Итак, уравнение, соответствующее третьей строке последней матрицы, противоречиво — оно привелось к неверному равенству 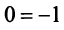 , следовательно, данная система несовместна. ►
, следовательно, данная система несовместна. ►
Система 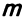 линейных уравнений с
линейных уравнений с 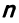 переменными
переменными
Ранее было установлено, что ранг матрицы равен максимальному числу ее линейно независимых строк (см. § 1.6). Поэтому, если строки расширенной матрицы 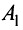 , т.е. уравнения системы (2.1), линейно независимы, то ранг матрицы
, т.е. уравнения системы (2.1), линейно независимы, то ранг матрицы 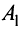 равен числу ее уравнений, т.е.
равен числу ее уравнений, т.е. 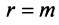 , если — линейно зависимы, то
, если — линейно зависимы, то 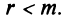
Вопрос о разрешимости системы (2.1) в общем виде рассматривается в следующей теореме.
Теорема Кронекера—Капелли. Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы.
 Не проводя строгого доказательства теоремы, поясним его. В процессе преобразования системы уравнений (2.1) к виду (2.10), т.е. элементарных преобразований матрицы системы
Не проводя строгого доказательства теоремы, поясним его. В процессе преобразования системы уравнений (2.1) к виду (2.10), т.е. элементарных преобразований матрицы системы 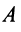 и расширенной матрицы
и расширенной матрицы 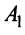 , ранги этих матриц не изменяются. Ранее (см. § 2.3) было установлено, что система (2.10) совместна тогда и только тогда, когда все свободные члены
, ранги этих матриц не изменяются. Ранее (см. § 2.3) было установлено, что система (2.10) совместна тогда и только тогда, когда все свободные члены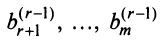
равны нулю. В этом случае, как нетрудно проверить, ранг матрицы и ранг расширенной матрицы системы (2.10), так же как и данной системы (2.1), совпадают (оба равны 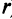 ).
). 
Для совместных систем линейных уравнений верны следующие теоремы.
- Если ранг матрицы совместной системы равен числу переменных, т.е.
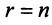 , то система (2.1) имеет единственное решение.
, то система (2.1) имеет единственное решение. - Если ранг матрицы совместной системы меньше числа переменных, т.е.
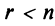 , то система (2.1) неопределенная и имеет бесконечное множество решений.
, то система (2.1) неопределенная и имеет бесконечное множество решений.
Результаты исследования системы (2.1) приведем в виде схемы (рис. 2.1):
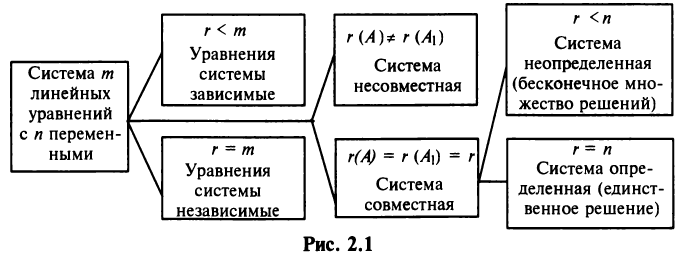 Пусть
Пусть 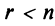 .
. 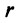 переменных
переменных  называются основными (или базисными), если определитель матрицы из коэффициентов при них (т.е. базисный минор) отличен от нуля. Остальные
называются основными (или базисными), если определитель матрицы из коэффициентов при них (т.е. базисный минор) отличен от нуля. Остальные 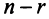 называются неосновными (или свободными).
называются неосновными (или свободными).
Решение системы (2.1), в котором все 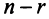 неосновных переменных равны нулю, называется базисным.
неосновных переменных равны нулю, называется базисным.
Так как каждому разбиению переменных на основные и неосновные соответствует одно базисное решение, а число способов разбиения не превосходит числа сочетаний 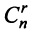 , то и базисных решений имеется не более
, то и базисных решений имеется не более 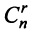 . Таким образом, совместная система
. Таким образом, совместная система 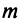 линейных уравнений с
линейных уравнений с 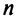 переменными
переменными 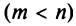 имеет бесконечное множество решений, среди которых базисных решений конечное число, не превосходящее
имеет бесконечное множество решений, среди которых базисных решений конечное число, не превосходящее 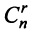 , где
, где 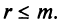
Приведенная на рис. 2.1 схема не означает, что для решения системы (2.1) в общем случае необходимо вычислять отдельно, а затем сравнивать ранги матрицы системы 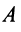 и расширенной матрицы
и расширенной матрицы 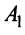 . Достаточно сразу применить метод Гаусса.
. Достаточно сразу применить метод Гаусса.
Достоинства метода Гаусса по сравнению с другими:
- значительно менее трудоемкий;
- позволяет однозначно установить, совместна система или нет, а в случае совместности найти ее решения (единственное или бесконечное множество);
- дает возможность найти максимальное число линейно независимых уравнений — ранг матрицы системы.
Пример №8
Методом Гаусса решить систему
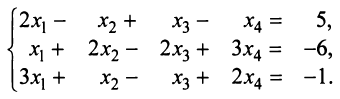
Решение:
Преобразуем расширенную матрицу системы (для удобства вычислений берем в качестве первой строки коэффициенты второго уравнения, у которого коэффициент при 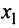 равен 1):
равен 1):
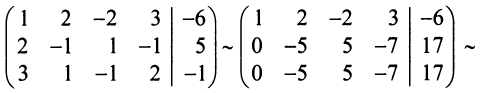
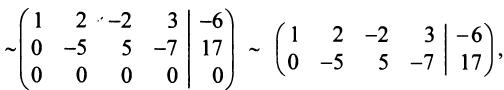 т.е. ранг матрицы системы
т.е. ранг матрицы системы 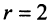
Оставляем в левой части переменные 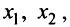 которые берем за основные (определитель из коэффициентов при них (базисный минор) отличен от нуля, т.е.
которые берем за основные (определитель из коэффициентов при них (базисный минор) отличен от нуля, т.е.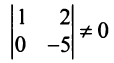 Остальные неосновные переменные
Остальные неосновные переменные 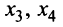 переносим в правые части уравнений. В результате получим систему
переносим в правые части уравнений. В результате получим систему
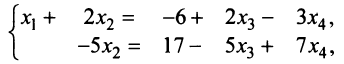 откуда
откуда
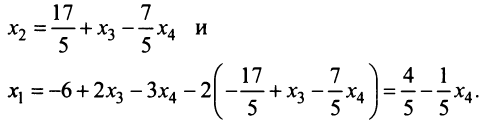
Задавая неосновным переменным произвольные значения 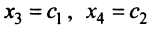 , найдем бесконечное множество решений системы
, найдем бесконечное множество решений системы
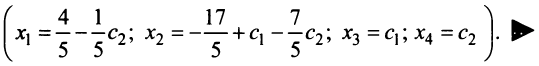
Пример №9
Найти все базисные решения системы, приведенной в примере 2.4.
Решение:
Ранг матрицы системы 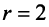 (это следует из примера 2.4), следовательно, одно из уравнений системы, например, третье, можно отбросить.
(это следует из примера 2.4), следовательно, одно из уравнений системы, например, третье, можно отбросить.
Общее число групп основных переменных не более чем 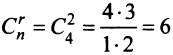 , поэтому возможны следующие группы основных переменных:
, поэтому возможны следующие группы основных переменных:
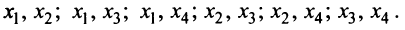
Выясним, могут ли переменные 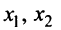 быть основными. Так как определитель матрицы из коэффициентов при этих переменных, т.е. базисный минор
быть основными. Так как определитель матрицы из коэффициентов при этих переменных, т.е. базисный минор
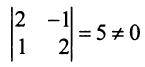 , то
, то 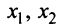 могут быть основными переменными. Рассуждая аналогично, найдем, что из всех возможных групп основных переменных только переменные
могут быть основными переменными. Рассуждая аналогично, найдем, что из всех возможных групп основных переменных только переменные 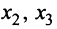 не могут быть основными, ибо
не могут быть основными, ибо 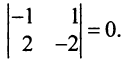 Найдем первое базисное решение, взяв в качестве основных переменных
Найдем первое базисное решение, взяв в качестве основных переменных 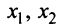 , а в качестве неосновных — переменные
, а в качестве неосновных — переменные 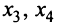 . Приравняв неосновные переменные нулю, т.е.
. Приравняв неосновные переменные нулю, т.е. 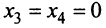 , получим систему уравнений в виде:
, получим систему уравнений в виде: 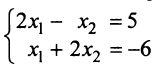 , откуда
, откуда 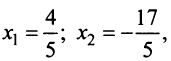 первое базисное решение (4/5; -17/5; 0; 0)
первое базисное решение (4/5; -17/5; 0; 0)
Если взять за основные переменные 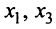 и приравнять нулю соответствующие неосновные переменные
и приравнять нулю соответствующие неосновные переменные 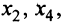 т.е.
т.е. 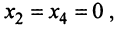 , то получим второе базисное решение (4/5; 0; 17/5; 0). Аналогично находятся и остальные базисные решения (9/7; 0; 0; -17/7), (0; -9; 0; 4) и (0; 0; 9; 4). ►
, то получим второе базисное решение (4/5; 0; 17/5; 0). Аналогично находятся и остальные базисные решения (9/7; 0; 0; -17/7), (0; -9; 0; 4) и (0; 0; 9; 4). ►
Системы линейных однородных уравнений
Фундаментальная система решений
Система 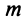 линейных уравнений с
линейных уравнений с 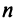 переменными называется системой линейных однородных уравнений, если все их свободные члены равны нулю. Такая система имеет вид:
переменными называется системой линейных однородных уравнений, если все их свободные члены равны нулю. Такая система имеет вид: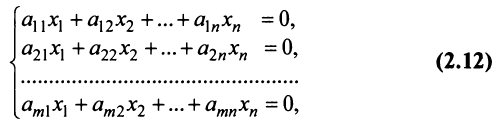
Система линейных однородных уравнений всегда совместна, так как она всегда имеет, по крайней мере, нулевое (или тривиальное) решение (0, 0, …, 0).
Если в системе (2.12)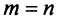 , а ее определитель отличен от нуля, то такая система имеет только нулевое решение, как это следует из теоремы и формул Крамера. Ненулевые решения, следовательно, возможны лишь для таких систем линейных однородных уравнений, в которых число уравнений меньше числа переменных или при их равенстве, когда определитель системы равен нулю.
, а ее определитель отличен от нуля, то такая система имеет только нулевое решение, как это следует из теоремы и формул Крамера. Ненулевые решения, следовательно, возможны лишь для таких систем линейных однородных уравнений, в которых число уравнений меньше числа переменных или при их равенстве, когда определитель системы равен нулю.
Иначе: система линейных однородных уравнений имеет ненулевые решения тогда и только тогда, когда ранг ее матрицы коэффициентов при переменных меньше числа переменных, т.е. при 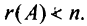
Обозначим решение системы (2.12) 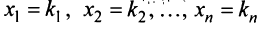 в виде строки
в виде строки 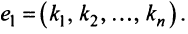
Решения системы линейных однородных уравнений обладают следующими свойствами:
- Если строка
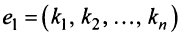 — решение системы (2.12), то и строка
— решение системы (2.12), то и строка 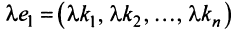 — также решение этой системы.
— также решение этой системы. - Если строки
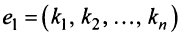 и
и 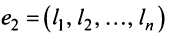 — решения системы (2.12), то при любых
— решения системы (2.12), то при любых 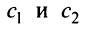 их линейная комбинация
их линейная комбинация 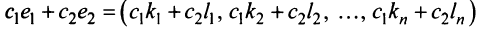 — также решение данной системы.
— также решение данной системы.
Убедиться в справедливости указанных свойств решений системы линейных однородных уравнений можно непосредственной подстановкой их в уравнения системы.
Из сформулированных свойств следует, что всякая линейная комбинация решений системы линейных однородных уравнений также является решением этой системы. Поэтому представляет интерес найти такие линейно независимые решения системы (2.12), через которые линейно выражались бы все остальные ее решения.
Определение. Система линейно независимых решений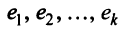 называется фундаментальной, если каждое решение системы (2.12) является линейной комбинацией решений
называется фундаментальной, если каждое решение системы (2.12) является линейной комбинацией решений 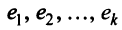 .
.
Теорема. Если ранг 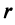 матрицы коэффициентов при переменных системы линейных однородных уравнений (2.12) меньше числа переменных
матрицы коэффициентов при переменных системы линейных однородных уравнений (2.12) меньше числа переменных 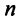 , то всякая фундаментальная система решений системы (2.12) состоит из
, то всякая фундаментальная система решений системы (2.12) состоит из 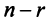 решений.
решений.
Поэтому общее решение системы (2.12) линейных однородных уравнений имеет вид:
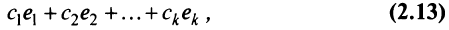
где 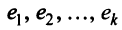 — любая фундаментальная система решений,
— любая фундаментальная система решений, 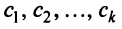 — произвольные числа и
— произвольные числа и 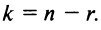
Можно показать, что общее решение системы т линейных уравнений с п переменными (2.1) равно сумме общего решения соответствующей ей системы однородных линейных уравнений (2.12) и произвольного частного решения этой системы (2.1).
Пример №10
Даны матрицы 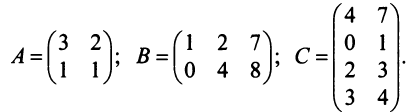 Решить уравнения:
Решить уравнения: 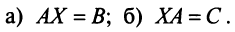
Решение:
а) Для невырожденной матрицы 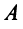 решение уравнения находится по той же формуле (2.7)
решение уравнения находится по той же формуле (2.7) 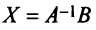 , но здесь необходимо учесть, что
, но здесь необходимо учесть, что 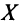 не является матрицей-столбцом (как это было в § 2.1), а имеет размер (2×3), ибо
не является матрицей-столбцом (как это было в § 2.1), а имеет размер (2×3), ибо
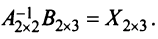
Найдем обратную матрицу 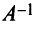 согласно алгоритму, приведенному в § 1.5:
согласно алгоритму, приведенному в § 1.5:
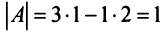 ; так как
; так как 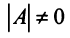 то
то 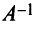 существует. Матрица
существует. Матрица 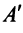 , транспонированная к
, транспонированная к 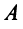 , имеет вид
, имеет вид 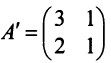 , а матрица
, а матрица 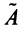 из алгебраических дополнений элементов матрицы
из алгебраических дополнений элементов матрицы 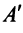 есть
есть 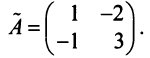 Теперь
Теперь 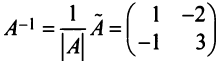 и матрица переменных
и матрица переменных
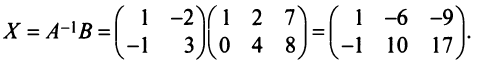
б) Полагая матрицу 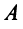 невырожденной, умножим обе части уравнения
невырожденной, умножим обе части уравнения 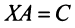 справа на обратную матрицу
справа на обратную матрицу 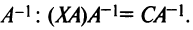 Так как
Так как
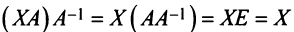 , то
, то 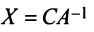 и размер
и размер
матрицы переменных (4 x 2), так как 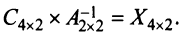 – Следовательно,
– Следовательно,
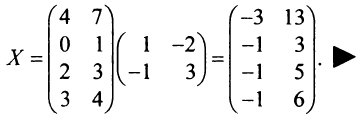
Пример №11
Решить уравнение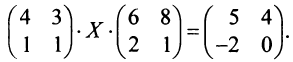
Решение:
Обозначив 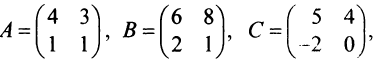 представим уравнение в виде
представим уравнение в виде 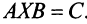 . Умножим обе части уравнения слева на обратную матрицу
. Умножим обе части уравнения слева на обратную матрицу 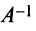 и справа на обратную матрицу
и справа на обратную матрицу 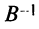 , учитывая, что
, учитывая, что 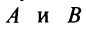 — невырожденные матрицы:
— невырожденные матрицы: 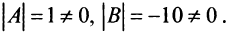
Получим 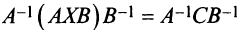 . Учитывая, что
. Учитывая, что
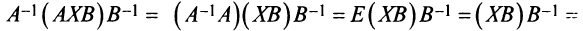
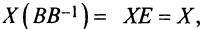 получим
получим 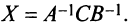
Теперь найдем 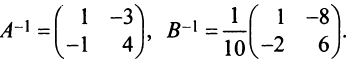
Поэтому 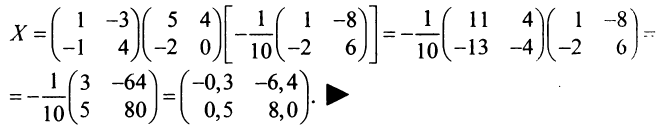
Пример №12
Обувная фабрика специализируется по выпуску изделий трех видов: сапог, кроссовок и ботинок; при этом используется сырье трех типов: 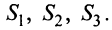 Нормы расхода каждого из них на одну пару обуви и объем расхода сырья на 1 день заданы таблицей:
Нормы расхода каждого из них на одну пару обуви и объем расхода сырья на 1 день заданы таблицей:
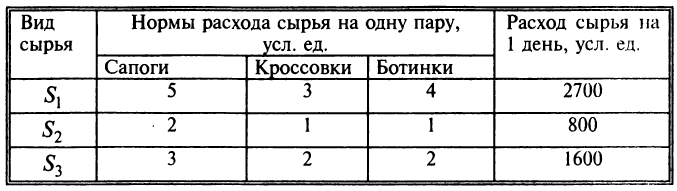
Найти ежедневный объем выпуска каждого вида обуви.
Решение:
Пусть ежедневно фабрика выпускает 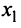 пар сапог,
пар сапог, 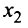 пар кроссовок и
пар кроссовок и 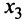 пар ботинок. Тогда в соответствии с расходом сырья каждого вида имеем систему:
пар ботинок. Тогда в соответствии с расходом сырья каждого вида имеем систему: 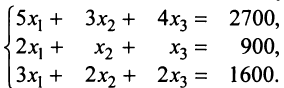 Решая систему любым способом, находим (200; 300; 200), т.е. фабрика выпускает 200 пар сапог, 300 — кроссовок и 200 пар ботинок. ►
Решая систему любым способом, находим (200; 300; 200), т.е. фабрика выпускает 200 пар сапог, 300 — кроссовок и 200 пар ботинок. ►
Пример №13
С двух заводов поставляются автомобили длядвух автохозяйств, потребности которых соответственно 200 и 300 машин. Первый завод выпустил 350 машин, а второй — 150 машин. Известны затраты на перевозку машин с завода в каждое автохозяйство (см. таблицу). 
Минимальные затраты на перевозку равны 7950 ден. ед. Найти оптимальный план перевозок машин.
Решение:
Пусть 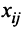 — количество машин, поставляемых с
— количество машин, поставляемых с 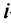 -го завода
-го завода 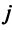 -му автохозяйству
-му автохозяйству 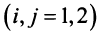 . Получаем систему
. Получаем систему 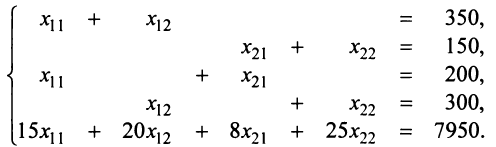 Решаем систему, например, методом Гаусса. (Рекомендуем сделать это читателю самостоятельно.) Найдем
Решаем систему, например, методом Гаусса. (Рекомендуем сделать это читателю самостоятельно.) Найдем 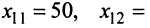
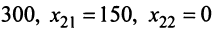 (обращаем внимание на то, что ранг матрицы системы
(обращаем внимание на то, что ранг матрицы системы 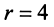 , т.е.
, т.е.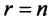 , и система имеет единственное решение). ►
, и система имеет единственное решение). ►
Модель Леонтьева многоотраслевой экономики (балансовый анализ)
Цель балансового анализа — ответить на вопрос, возникающий в макроэкономике и связанный с эффективностью ведения многоотраслевого хозяйства: каким должен быть объем производства каждой из я отраслей, чтобы удовлетворить все потребности в продукции этой отрасли? При этом каждая отрасль выступает, с одной стороны, как производитель некоторой продукции, а с другой — как потребитель продукции и своей, и произведенной другими отраслями.
Связь между отраслями, как правило, отражается в таблицах межотраслевого баланса, а математическая модель, позволяющая их анализировать, разработана в 1936 г. американским экономистом В. Леонтьевым.
Предположим, что рассматривается 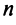 отраслей промышленности, каждая из которых производит свою продукцию. Часть продукции идет на внутрипроизводственное потребление данной отраслью и другими отраслями, а другая часть предназначена для целей конечного (вне сферы материального производства) личного и общественного потребления.
отраслей промышленности, каждая из которых производит свою продукцию. Часть продукции идет на внутрипроизводственное потребление данной отраслью и другими отраслями, а другая часть предназначена для целей конечного (вне сферы материального производства) личного и общественного потребления.
Рассмотрим процесс производства за некоторый период времени (например, год).
Введем следующие обозначения: 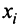 — общий (валовой) объем продукции
— общий (валовой) объем продукции 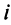 -й отрасли
-й отрасли 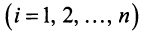 ;
;
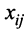 — объем продукции
— объем продукции 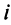 -й отрасли, потребляемой
-й отрасли, потребляемой 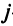 -й отраслью в процессе производства
-й отраслью в процессе производства 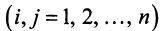 ;
;
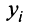 — объем конечного продукта
— объем конечного продукта 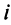 -й отрасли для непроизводственного потребления.
-й отрасли для непроизводственного потребления.
Так как валовой объем продукции любой 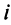 -й отрасли равен суммарному объему продукции, потребляемой
-й отрасли равен суммарному объему продукции, потребляемой 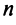 отраслями, и конечного продукта, то
отраслями, и конечного продукта, то
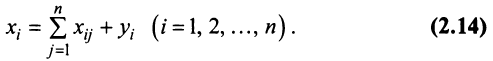
Уравнения (2.14) называются соотношениями баланса. Будем рассматривать стоимостный межотраслевой баланс, когда все величины, входящие в (2.14), имеют стоимостное выражение.
Введем коэффициенты прямых затрат
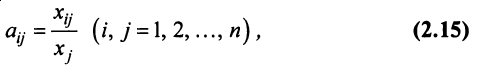
показывающие затраты продукции 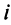 -й отрасли на производство единицы продукции
-й отрасли на производство единицы продукции 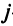 -й отрасли. Можно полагать, что в некотором промежутке времени коэффициенты
-й отрасли. Можно полагать, что в некотором промежутке времени коэффициенты 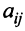 будут постоянными и зависящими от сложившейся технологии производства. Это означает линейную зависимость материальных затрат от валового выпуска, т.е.
будут постоянными и зависящими от сложившейся технологии производства. Это означает линейную зависимость материальных затрат от валового выпуска, т.е.
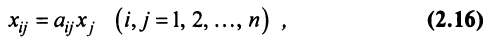
вследствие чего построенная на этом основании модель межотраслевого баланса получила название линейной. Теперь соотношения баланса (2.14) примут вид:
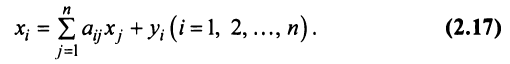
Обозначим 
где 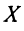 — вектор валового выпуска,
— вектор валового выпуска, 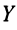 — вектор конечного продукта,
— вектор конечного продукта, 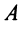 — матрица прямых затрат (технологическая или структурная матрица).
— матрица прямых затрат (технологическая или структурная матрица).
Тогда систему (2.14) можно записать в матричном виде:

Основная задача межотраслевого баланса состоит в отыскании такого вектора валового выпуска 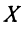 , который при известной матрице прямых затрат
, который при известной матрице прямых затрат 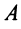 обеспечивает заданный вектор конечного продукта
обеспечивает заданный вектор конечного продукта 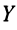 .
.
Перепишем уравнение (2.18) в виде:

Если матрица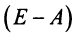 невырожденная, т.е.
невырожденная, т.е. 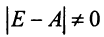 то по формуле (2.7)
то по формуле (2.7)
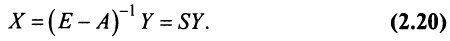
Матрица 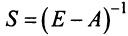 называется матрицей полных затрат.
называется матрицей полных затрат.
Чтобы выяснить экономический смысл элементов матрицы 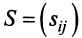 , будем задаваться единичными векторами конечного продукта
, будем задаваться единичными векторами конечного продукта
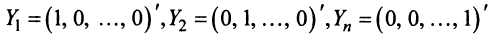 . Тогда по формуле (2.20) соответствующие векторы валового выпуска будут
. Тогда по формуле (2.20) соответствующие векторы валового выпуска будут
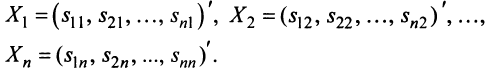
Следовательно, каждый элемент 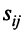 матрицы
матрицы 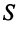 есть величина валового выпуска продукции
есть величина валового выпуска продукции 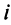 -й отрасли, необходимого для обеспечения выпуска единицы конечного продукта
-й отрасли, необходимого для обеспечения выпуска единицы конечного продукта 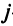 -й отрасли
-й отрасли 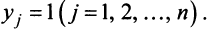
В соответствии с экономическим смыслом задачи значения 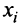 должны быть неотрицательны при неотрицательных значениях
должны быть неотрицательны при неотрицательных значениях
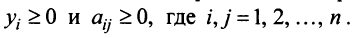
Матрица 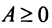 называется продуктивной, если для любого вектора
называется продуктивной, если для любого вектора 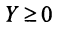 существует решение
существует решение 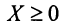 уравнения (2.19). В этом случае и модель Леонтьева называется продуктивной.
уравнения (2.19). В этом случае и модель Леонтьева называется продуктивной.
Существует несколько критериев продуктивности матрицы 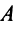 . Один из них говорит о том, что матрица
. Один из них говорит о том, что матрица 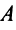 продуктивна, если максимум сумм элементов ее столбцов не превосходит единицы, причем хотя бы для одного из столбцов сумма элементов строго меньше единицы, т.е. матрица
продуктивна, если максимум сумм элементов ее столбцов не превосходит единицы, причем хотя бы для одного из столбцов сумма элементов строго меньше единицы, т.е. матрица 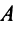 продуктивна, если
продуктивна, если 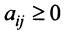 для любых
для любых 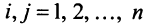 и
и 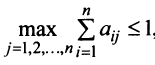 и существует номер
и существует номер 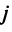 такой, что
такой, что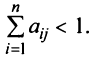
Пример №14
В таблице приведены данные об исполнении баланса за отчетный период, усл. ден. ед.: 
Вычислить необходимый объем валового выпуска каждой отрасли, если конечное потребление энергетической отрасли увеличится вдвое, а машиностроительной сохранится на прежнем уровне.
Решение:
Имеем
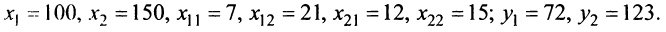
По формуле (2.15) находим коэффициенты прямых затрат:
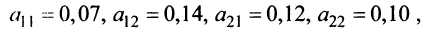 т.е матрица прямых затрат
т.е матрица прямых затрат
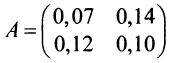 удовлетворяет критерию продуктивности:
удовлетворяет критерию продуктивности:
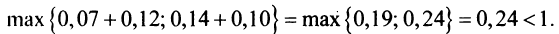
Поэтому для любого вектора конечного продукта 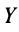 можно найти необходимый объем валового выпуска
можно найти необходимый объем валового выпуска 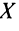 по формуле (2.20):
по формуле (2.20):
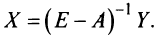
Найдем матрицу полных затрат 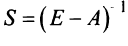 :
:
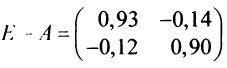 . Так как
. Так как 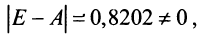 по формуле (1.14)
по формуле (1.14)
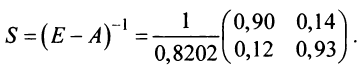 По условию вектор конечного продукта
По условию вектор конечного продукта 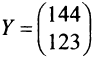 . Тогда по формуле (2.17) получаем вектор валового выпуска:
. Тогда по формуле (2.17) получаем вектор валового выпуска: 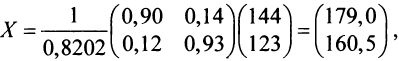
т.е. валовой выпуск в энергетической отрасли надо увеличить до 179,0 усл. ед., а в машиностроительной — до 160,5 усл. ед.
Системы линейных уравнений в линейной алгебре
Для исследования процессов функционирования экономики, при построении математических моделей конкретных задач, возникающих перед менеджером в процессе его деятельности, в ряде случаев используются системы линейных уравнений. Так, например, при межотраслевом анализе – изменение объема выпуска отрасли при фиксированном коэффициенте прямых затрат в случае изменения спроса необходимо искать путем решения системы линейных уравнений, которая является моделью изучаемого процесса.
Нахождение решений системы линейных уравнений может быть осуществлено различными методами. Выбор метода зависит от рассматриваемой задачи и соответствующей математической модели. В ряде случаев необходимо лишь знать – существует ли решение рассматриваемой системы.
Цель данного раздела – исследовать совместность системы линейных уравнений и дать некоторые методы их решения. Эти методы позволяют найти точное решение системы. Кроме этого, существуют методы, позволяющие находить приближенные решения, например, метод Якоби, метод Гаусса-Зейделя, метод пошагового агрегирования. В этом разделе они не рассматриваются.
Рассмотрим совокупность уравнений:
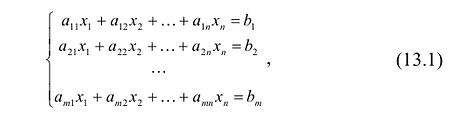
где 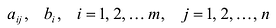 – действительные числа, а
– действительные числа, а 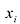 -неизвестные. Эту совокупность называют системой линейных уравнений с n неизвестными, числа
-неизвестные. Эту совокупность называют системой линейных уравнений с n неизвестными, числа 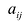 – коэффициенты системы (1),
– коэффициенты системы (1), 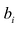 -свободные члены. Упорядоченный набор n действительных чисел
-свободные члены. Упорядоченный набор n действительных чисел 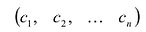 называется решением системы (13.1), если после подстановки в каждое из уравнений (13.1) вместо
называется решением системы (13.1), если после подстановки в каждое из уравнений (13.1) вместо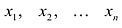 чисел
чисел 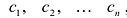 , это уравнение превращается в тождество.
, это уравнение превращается в тождество.
Система линейных уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если не имеет ни одного решения.
Система называется определенной, если она имеет единственное решение, и неопределенной, если у нее есть, по крайней мере, два различных решения.
Две системы с п неизвестными называются эквивалентными, если множества их решений совпадают. Матрица 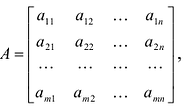 , составленная из коэффициентов системы (13.1), называется матрицей системы. Обозначив
, составленная из коэффициентов системы (13.1), называется матрицей системы. Обозначив 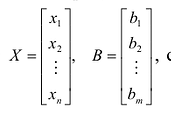 через систему (13.1) можно записать в виде матричного уравнения:
через систему (13.1) можно записать в виде матричного уравнения:
 Матрица
Матрица  полученная приписыванием к матрице А справа столбца свободных членов системы (13.1), называется расширенной матрицей системы (13.1).
полученная приписыванием к матрице А справа столбца свободных членов системы (13.1), называется расширенной матрицей системы (13.1).
При исследовании системы (13.1) ищут ответ на следующие три вопроса:
- когда система совместна;
- если система совместна, то определена ли она;
- как отыскать ее решения.
Критерий совместности системы линейных уравнений
Ответ на первый вопрос дает теорема Кронекера-Капелли – критерий совместности системы линейных уравнений.
Теорема. Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу ее расширенной матрицы.
Правило Крамера решения систем линейных уравнений
Рассмотрим невырожденные системы линейных уравнений, т.е. системы, у которых m= n и определитель матрицы системы отличен от нуля. Определитель матрицы называется определителем системы. Следующая теорема, называемая правилом Крамера, отвечает на второй вопрос.
Пусть дана система двух линейных уравнений с двумя неизвестными:

Коэффициенты этой системы составляют квадратную матрицу второго порядка:

Решим систему (13.3). Для этого умножим первое уравнение системы на 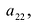 второе – на
второе – на 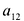 и вычтем из первого уравнения второе:
и вычтем из первого уравнения второе:
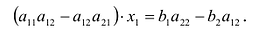
Аналогично, исключая 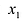 , получим –
, получим –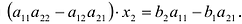
Если 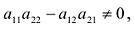 то найдем единственное решение системы:
то найдем единственное решение системы:
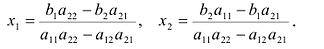
Общий знаменатель значений неизвестных 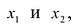 , обозначаемый через
, обозначаемый через 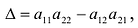 называется определителем матрицы А. Это определитель второго порядка. Числителями неизвестных
называется определителем матрицы А. Это определитель второго порядка. Числителями неизвестных 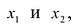 являются определители тоже второго порядка
являются определители тоже второго порядка 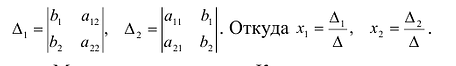 Мы получили правило Крамера решения системы двух линейных уравнений с двумя неизвестными.
Мы получили правило Крамера решения системы двух линейных уравнений с двумя неизвестными.
Правило Крамера. Если определитель  системы п линейных уравнений с n неизвестными отличен от нуля, то система имеет единственное решение:
системы п линейных уравнений с n неизвестными отличен от нуля, то система имеет единственное решение: 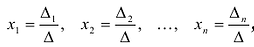 где
где 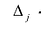 – определитель, получаемый из
– определитель, получаемый из  заменой j-го столбца столбцом свободных членов.
заменой j-го столбца столбцом свободных членов.
Невырожденную систему линейных уравнений АХ = В можно решить и иным способом.
Поскольку матрица А – невырожденная, то для нее существует единственная обратная матрица 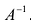 Умножив обе части уравнения АХ = В слева на матрицу
Умножив обе части уравнения АХ = В слева на матрицу 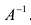 , получим
, получим 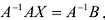 , откуда
, откуда 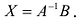 .
.
Мы ответили на три вопроса относительно систем линейных уравнений. Однако применение теоремы Крамера, которая позволила дать этот ответ, приводит к слишком громоздким вычислениям.
Практически для решения систем линейных уравнений чаще всего применяется метод Гаусса.
- Заказать решение задач по высшей математике
Метод Гаусса
Метод Гаусса основан на теореме: если к некоторому уравнению системы прибавить другое уравнение этой системы, умноженное на любое действительное число, или умножить любое уравнение системы на отличное от нуля действительное число, то полученная система будет эквивалентна исходной.
Метод Гаусса называют также методом последовательного исключения неизвестных, осуществляя его за несколько итераций. На каждой итерации выбирается разрешающее уравнение и базисное неизвестное. В качестве разрешающего уравнения можно взять любое уравнение системы, которое ранее не было выбрано разрешающим и не все коэффициенты которого равны нулю. За базисное неизвестное выбирают неизвестное, коэффициент при котором в разрешающем уравнении, называемый разрешающим коэффициентом, не равен нулю.
Алгоритм метода следующий:
- Выбирают разрешающее уравнение и базисное неизвестное.
- Делят обе части разрешающего уравнения на разрешающий коэффициент и исключают базисное неизвестное из всех уравнений системы, кроме разрешающего. Отбрасывают, если они появились, уравнения, все коэффициенты и свободный член в котором равны нулю. Если получилось уравнение, в котором коэффициенты нулевые, а свободный член не нуль, то система несовместна, конец. Если таких уравнений нет, то шаг 1. Если все уравнения были использованы в качестве разрешающих, то шаг 3.
- Если нет, то шаг 1.
- Базисные неизвестные оставляют слева, а небазисные (назовем их свободными, так как они могут принимать любые значения) переносят вправо. Тем самым получено общее решение системы. Конец.
Однородные системы уравнений
Линейное уравнение называется однородным, если его свободный член равен нулю, и неоднородным в противном случае. Система, состоящая из однородных уравнений, называется однородной и имеет общий вид:
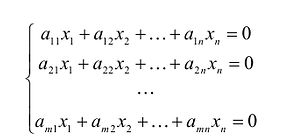
Очевидно, что всякая однородная система совместна и имеет нулевое (тривиальное) решение. Поэтому применительно к однородным системам линейных уравнений часто приходится искать ответ на вопрос о существовании ненулевых решений. Ответ на этот вопрос можно сформулировать в виде следующей теоремы.
Теорема. Однородная система линейных уравнений имеет ненулевое решение тогда и только тогда, когда ее ранг меньше числа неизвестных.
Доказательство: Допустим, система, ранг которой равен, имеет ненулевое решение. Очевидно, что г не превосходит п. В случае у = п система имеет единственное решение. Поскольку система однородных линейных уравнений всегда имеет нулевое решение, то именно нулевое решение и будет этим единственным решением. Таким образом, ненулевые решения возможны только при r < n.
Следствие. Однородная система уравнений в которой число уравнений меньше числа неизвестных, всегда имеет ненулевое решение.
Доказательство: Если у системы уравнений m
выполняется условие r < n и, значит, система имеет ненулевое решение.
Следствие: Однородная система n уравнений с n неизвестными имеет ненулевое решение тогда и только тогда, когда ее определитель равен нулю.
Доказательство: Допустим, система и линейных однородных уравнений, матрица которой 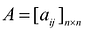 с определителем
с определителем 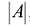 , имеет ненулевое решение. Тогда по доказанной теореме r < n, а это значит, что матрица А вырожденная, т.е.
, имеет ненулевое решение. Тогда по доказанной теореме r < n, а это значит, что матрица А вырожденная, т.е.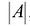 = 0.
= 0.
Разрешенные системы линейных уравнений
Переменная 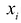 называется разрешенной, если какое-нибудь уравнение системы содержит
называется разрешенной, если какое-нибудь уравнение системы содержит 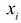 с коэффициентом, равным единице, а во все остальные уравнения системы переменная
с коэффициентом, равным единице, а во все остальные уравнения системы переменная 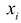 не входит, т.е. входит с коэффициентом, равным нулю.
не входит, т.е. входит с коэффициентом, равным нулю.
Например, система уравнений:
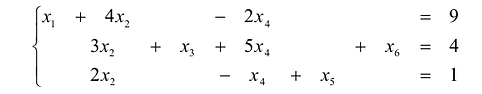
содержит разрешенные переменные 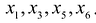 . Переменные
. Переменные 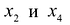 , разрешенными не являются.
, разрешенными не являются.
Если каждое уравнение содержит разрешенную переменную, то такую систему называют разрешенной. Очевидно, что приведенная в качестве примера система уравнений является разрешенной.
Выбрав из каждого уравнения разрешенной системы по одной разрешенной переменной, можно сформировать набор попарно различных переменных, который называется набором разрешенных переменных данной системы. В общем случае набор разрешенных переменных определен неоднозначно. Например, у рассмотренной выше системы можно выбрать два набора разрешенных переменных: 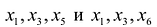
Переменные системы, которые не входят в данный набор разрешенных неизвестных, называются свободными. Если в системе фиксирован набор разрешенных переменных 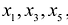 , то переменные
, то переменные 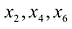 являются свободными; если в набор разрешенных переменных системы входят
являются свободными; если в набор разрешенных переменных системы входят 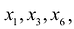 , то свободными переменными являются
, то свободными переменными являются 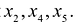 .
.
Допустим, что разрешенная система уравнений содержит переменные 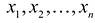 и что набор
и что набор 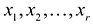 является набором разрешенных переменных данной системы. Возможны два случая: r= n и r < n.
является набором разрешенных переменных данной системы. Возможны два случая: r= n и r < n.
В первом случае, когда r = n, все переменные системы образуют набор разрешенных переменных системы 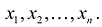 . Из определения набора разрешенных переменных вытекает, что данная система содержит n уравнений. Из определения разрешенных переменных следует, что переменная
. Из определения набора разрешенных переменных вытекает, что данная система содержит n уравнений. Из определения разрешенных переменных следует, что переменная 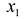 содержится только в первом уравнении, переменная
содержится только в первом уравнении, переменная 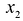 – только во втором и т.д., переменная
– только во втором и т.д., переменная 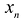 – только в n-м уравнении. Таким образом, разрешенная система имеет вид:
– только в n-м уравнении. Таким образом, разрешенная система имеет вид: 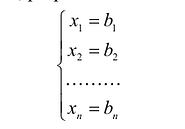
Очевидно, что такая система уравнений имеет только одно решение 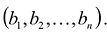 .
.
Во втором случае, когда r < n разрешенная система состоит из г уравнений вида:
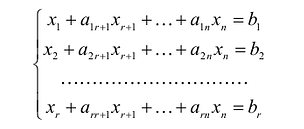
Переменные 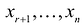 являются свободными переменными системы. Если выразить разрешенные переменные системы
являются свободными переменными системы. Если выразить разрешенные переменные системы 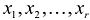 через ее свободные переменные
через ее свободные переменные 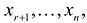 система примет вид:
система примет вид:
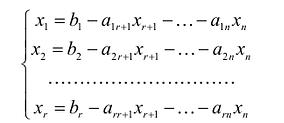
Теорема (свойство свободных переменных). Если свободным переменным системы придать 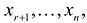 произвольные значения
произвольные значения 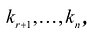 тогда:
тогда:
- можно построить решение К системы уравнений, у которого значения свободных переменных будут равны соответственно
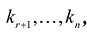
- если у решений К и L системы уравнений значения свободных переменных совпадают, то и сами решения совпадают.
Доказательство: Если значения свободных переменных 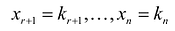 подставить в систему, то получится:
подставить в систему, то получится:
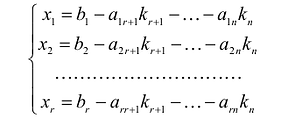
То есть 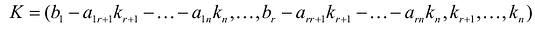 является решением системы уравнений, так как после подстановки координат АГ в эту систему получаются верные равенства. Поскольку у К значения свободных переменных равны, соответственно,
является решением системы уравнений, так как после подстановки координат АГ в эту систему получаются верные равенства. Поскольку у К значения свободных переменных равны, соответственно, 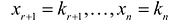 и есть искомое решение системы.
и есть искомое решение системы.
Следствие. Все решения системы получаются так же, как и решение К.
Значения для свободных переменных можно выбирать бесконечным числом различных способов, поэтому система уравнений является неопределенной.
Разрешенная система уравнений совместна всегда. Она будет определенной, если число уравнений равно числу неизвестных, и неопределенной, если число уравнений меньше числа неизвестных.
Системы линейных уравнений общего вида
Если система (5.1) оказалась совместной, т. е. матрицы 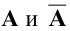 имеют один и тот же ранг, то могут представиться две возможности –
имеют один и тот же ранг, то могут представиться две возможности – 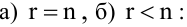
Перенесем лишние неизвестные 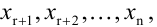 которые принято называть свободными, в правые части; наша система линейных уравнений примет вид:
которые принято называть свободными, в правые части; наша система линейных уравнений примет вид: 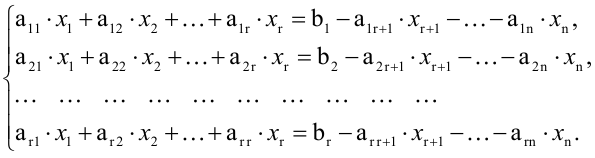
Ее можно решить относительно 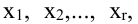 так как определитель этой системы (r-го порядка) отличен от нуля. Придавая свободным неизвестным произвольные числовые значения, получим по формулам Крамера соответствующие числовые значения для
так как определитель этой системы (r-го порядка) отличен от нуля. Придавая свободным неизвестным произвольные числовые значения, получим по формулам Крамера соответствующие числовые значения для 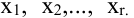 Таким образом, при r < n имеем бесчисленное множество решений.
Таким образом, при r < n имеем бесчисленное множество решений.
Система (5.1) называется однородной, если все 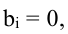 т. е. она имеет вид:
т. е. она имеет вид: 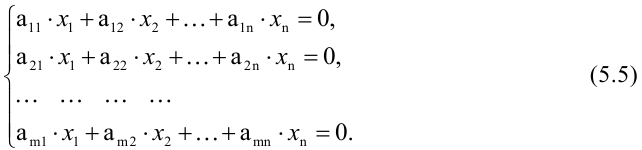
Из теоремы Кронекера-Капелли следует, что она всегда совместна, так как добавление столбца из нулей не может повысить ранга матрицы. Это, впрочем, видно и непосредственно -система (5.5) заведомо обладает нулевым, или тривиальным, решением 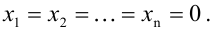 Пусть матрица А системы (5.5) имеет ранг r.
Пусть матрица А системы (5.5) имеет ранг r.
Если r = n, то нулевое решение будет единственным решением системы (5.5); при r < n система обладает решениями, отличными от нулевого, и для их разыскания применяют тот же прием, как и в случае произвольной системы уравнений.
Всякий ненулевой вектор – столбец 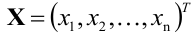 называется собственным вектором линейного преобразования (квадратной матрицы А), если найдется такое число
называется собственным вектором линейного преобразования (квадратной матрицы А), если найдется такое число 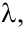 что будет выполняться равенство
что будет выполняться равенство 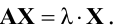
Число 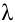 называется собственным значением линейного преобразования (матрицы А), соответствующим вектору X. Матрица А имеет порядок n.
называется собственным значением линейного преобразования (матрицы А), соответствующим вектору X. Матрица А имеет порядок n.
В математической экономике большую роль играют так называемые продуктивные матрицы. Доказано, что матрица А является продуктивной тогда и только тогда, когда все собственные значения матрицы А по модулю меньше единицы.
Для нахождения собственных значений матрицы А перепишем равенство 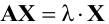 в виде
в виде 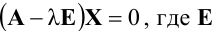 – единичная матрица n-го порядка или в координатной форме:
– единичная матрица n-го порядка или в координатной форме:
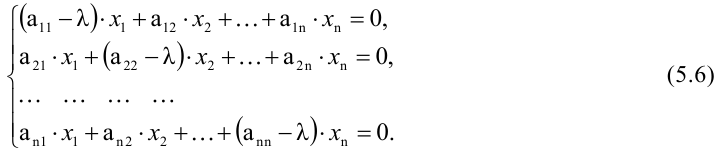
Получили систему линейных однородных уравнений, которая имеет ненулевые решения тогда и только тогда, когда определитель этой системы равен нулю, т.е. 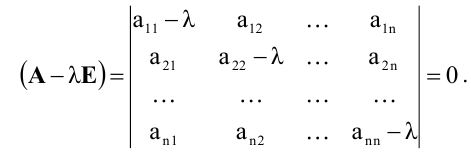
Получили уравнение n-ой степени относительно неизвестной 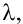 которое называется характеристическим уравнением матрицы А, многочлен
которое называется характеристическим уравнением матрицы А, многочлен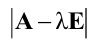 называется характеристическим многочленом матрицы А, а его корни – характеристическими числами, или собственными значениями, матрицы А.
называется характеристическим многочленом матрицы А, а его корни – характеристическими числами, или собственными значениями, матрицы А.
Для нахождения собственных векторов матрицы А в векторное уравнение 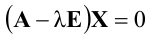 или в соответствующую систему однородных уравнений (5.6) нужно подставить найденные значения
или в соответствующую систему однородных уравнений (5.6) нужно подставить найденные значения 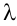 и решать обычным образом.
и решать обычным образом.
Пример №15
Исследовать систему уравнений и решить ее, если она совместна.
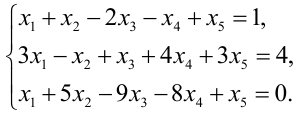
Решение:
Будем находить ранги матриц 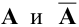 методом элементарных преобразований, приводя одновременно систему к ступенчатому виду:
методом элементарных преобразований, приводя одновременно систему к ступенчатому виду: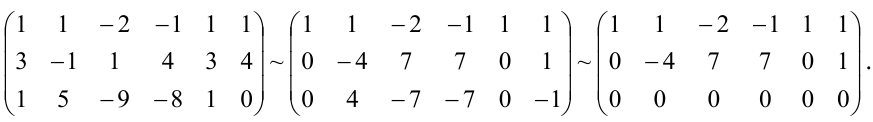
Очевидно, что 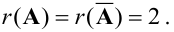 Исходная система равносильна следующей, приведенной к ступенчатому виду:
Исходная система равносильна следующей, приведенной к ступенчатому виду: 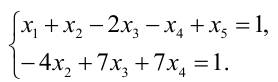
Поскольку определитель при неизвестных 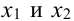 отличен от нуля, то их можно принять в качестве главных и переписать систему в виде:
отличен от нуля, то их можно принять в качестве главных и переписать систему в виде: 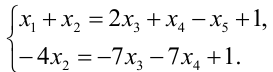
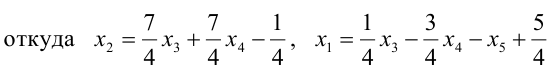 — общее решение системы, имеющей бесчисленное множество решений. Придавая свободным неизвестным
— общее решение системы, имеющей бесчисленное множество решений. Придавая свободным неизвестным 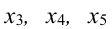 конкретные числовые значения, будем получать частные решения. Например, при
конкретные числовые значения, будем получать частные решения. Например, при 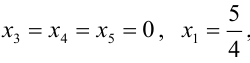
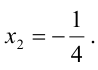
Вектор 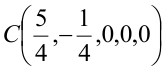 является частным решением данной системы.
является частным решением данной системы.
Пример №16
Исследовать систему уравнений и найти общее решение в зависимости от значения параметра а. 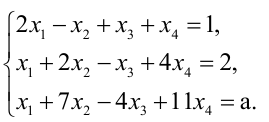
Решение:
Данной системе соответствует матрица 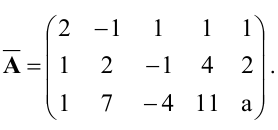 Имеем
Имеем 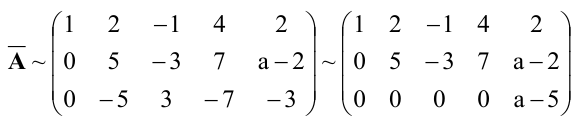
следовательно, исходная система равносильна такой: 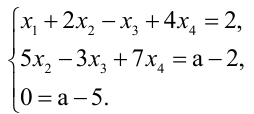
Отсюда видно, что система совместна только при а=5. Общее решение в этом случае имеет вид: 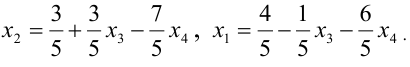
Пример №17
Выяснить, будет ли линейно зависимой система векторов:
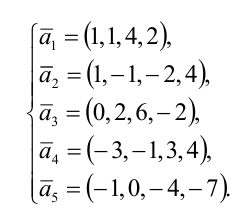
Решение:
Система векторов является линейно зависимой, если найдутся такие числа 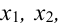
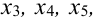 из которых хотя бы одно отлично от нуля (см. п. 1. разд. I), что выполняется векторное равенство:
из которых хотя бы одно отлично от нуля (см. п. 1. разд. I), что выполняется векторное равенство: 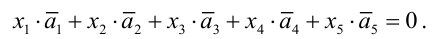
В координатной записи оно равносильно системе уравнений: 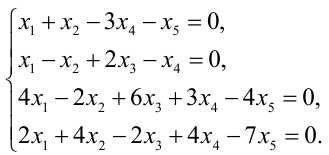
Итак, получили систему линейных однородных уравнений. Решаем ее методом исключения неизвестных:

Система приведена к ступенчатому виду, ранг матрицы равен 3, значит, однородная система уравнений имеет решения, отличные от нулевого г < n. Определитель при неизвестных 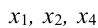 отличен от нуля, поэтому их можно выбрать в качестве главных и переписать систему в виде:
отличен от нуля, поэтому их можно выбрать в качестве главных и переписать систему в виде: 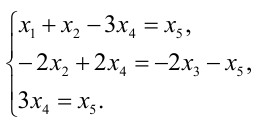 Имеем:
Имеем: 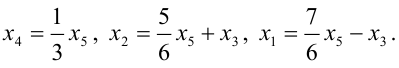
Система имеет бесчисленное множество решений; если свободные неизвестные 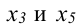 не равны нулю одновременно, то и главные неизвестные отличны от нуля. Следовательно, векторное уравнение
не равны нулю одновременно, то и главные неизвестные отличны от нуля. Следовательно, векторное уравнение 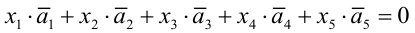 имеет коэффициенты, не равные нулю одновременно; пусть например,
имеет коэффициенты, не равные нулю одновременно; пусть например, 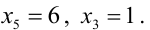 Тогда
Тогда 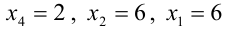 и мы получим соотношение
и мы получим соотношение 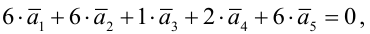 т.е. данная система векторов линейно независима.
т.е. данная система векторов линейно независима.
Пример №18
Найти собственные значения и собственные векторы матрицы
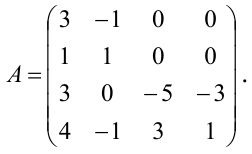
Решение:
Вычислим определитель матрицы А 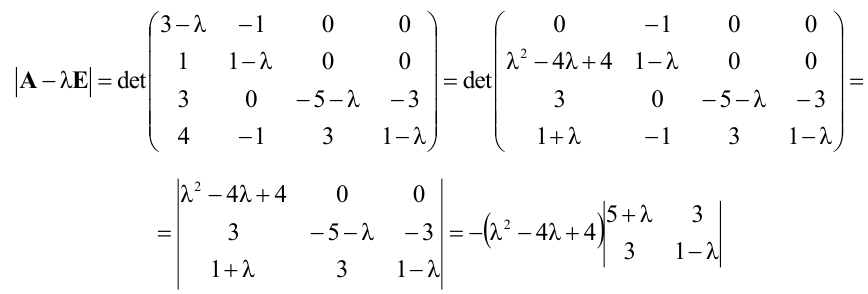
Итак, 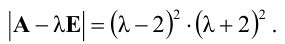 Корни характеристического уравнения
Корни характеристического уравнения 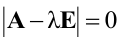 – это числа
– это числа 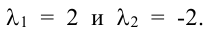 Другими словами, мы нашли собственные значения матрицы А. Для нахождения собственных векторов матрицы А подставим найденные значения
Другими словами, мы нашли собственные значения матрицы А. Для нахождения собственных векторов матрицы А подставим найденные значения 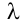 в систему (5.6): при
в систему (5.6): при 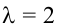 имеем систему линейных однородных уравнений
имеем систему линейных однородных уравнений 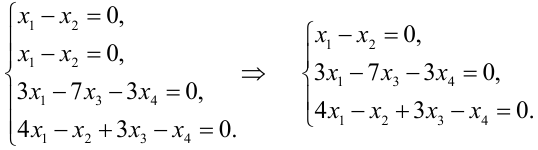
Следовательно, собственному значению 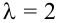 отвечают собственные векторы вида
отвечают собственные векторы вида 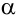 (8, 8, -3, 15), где
(8, 8, -3, 15), где 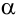 – любое отличное от нуля действительное число. При
– любое отличное от нуля действительное число. При 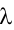 = -2 имеем:
= -2 имеем: 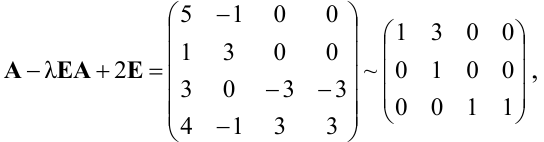 и поэтому координаты собственных векторов должны удовлетворять системе уравнений
и поэтому координаты собственных векторов должны удовлетворять системе уравнений
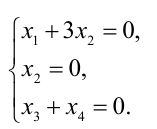
Поэтому собственному значению 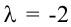 отвечают собственные векторы вида
отвечают собственные векторы вида 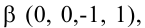 где
где 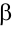 – любое отличное от нуля действительное число.
– любое отличное от нуля действительное число.
Системы линейных уравнений в высшей математике
Линейной системой m уравнений с n неизвестными 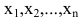 называется система вида
называется система вида
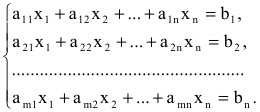
Числа 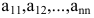 называются коэффициентами системы, a
называются коэффициентами системы, a 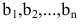 – ее свободными членами.
– ее свободными членами.
Линейную систему удобно записывать в матричной форме:
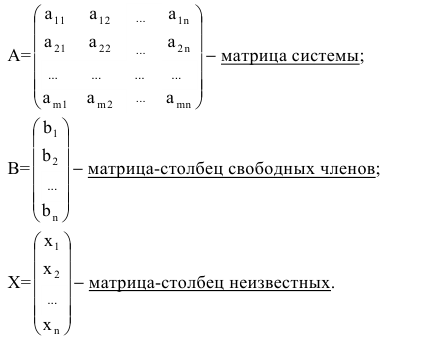 Матрица
Матрица 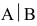 называется расширенной матрицей системы:
называется расширенной матрицей системы: 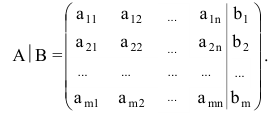
Система линейных уравнений называется однородной, если все свободные члены равны нулю. В противном случае она называется неоднородной.
Решением системы m уравнений с n неизвестными называется совокупность значений неизвестных
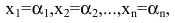
при подстановке которых все уравнения системы обращаются в тождества.
Система называется совместной, если она имеет хотя бы одно решение. В
противном случае она называется несовместной.
Замечание. Однородная система линейных уравнений всегда совместна,
т.к. имеет нулевое решение.
Решить систему – значит найти все ее решения.
Решение невырожденных систем линейных уравнений
Система n линейных уравнений с n неизвестными называется невырожденной, если матрица системы невырожденная.
Правило Крамера:
Невырожденная система имеет единственное решение, которое можно найти по формулам
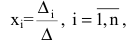 где
где 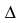 – определитель (матрицы) системы.
– определитель (матрицы) системы. 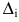 – определитель, полученный из
– определитель, полученный из 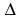 заменой i-гo столбца на столбец свободных членов.
заменой i-гo столбца на столбец свободных членов.
Пример №19
Решить систему уравнений по формулам Крамера.
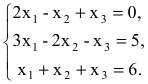
Решение:
Выпишем матрицу системы: 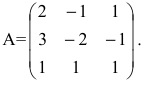 Найдем ее определитель:
Найдем ее определитель:
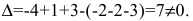
Следовательно, матрица А невырожденная и система имеет единственное решение, которое может быть найдено по формулам Крамера. Найдем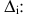
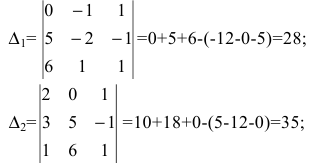
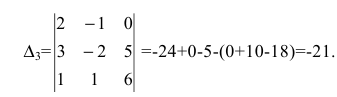
Тогда 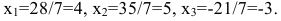
Решение произвольных систем линейных уравнений
Теорема Кронекера-Капелли:
Для того чтобы система линейных уравнений была совместной, необходимо и достаточно, чтобы ранг матрицы системы равнялся рангу расширенной матрицы системы.
Не ограничивая общности, можно считать, что базисный минор располагается в первых k строках и k столбцах матрицы системы. Отбросив m-k последних уравнений искомой системы, записывают укороченную систему:
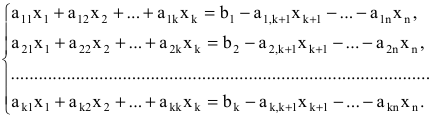
Неизвестные 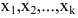 называются базисными, a
называются базисными, a 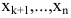 – свободными.
– свободными.
Придавая свободным неизвестным произвольные числовые значения, решают укороченную систему относительно базисных неизвестных. Решение укороченной (а следовательно, и исходной) системы будет являться функцией от n-k свободных неизвестных и называться общим решением системы.
Вывод. Если ранг расширенной системы не равен рангу основной матрицы, то система несовместна. Если ранг системы равен рангу расширенной системы и равен количеству неизвестных, то система имеет единственное решение. Если же ранг системы равен рангу расширенной системы и меньше числа неизвестных, то система имеет бесчисленное множество решений.
В общем случае для решения систем линейных уравнений применяют метод Жордана-Гаусса. Согласно ему расширенную матрицу системы с помощью элементарных преобразований над строками приводят к трапециевидной форме. Такой матрице соответствует система, которую легко решить, начиная с последнего уравнения.
Пример №20
Исследовать систему уравнений и в случае совместимости решить ее:
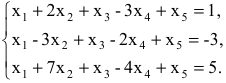
Решение:
Выпишем расширенную матрицу системы:
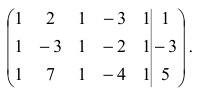
Найдем ранг матрицы методом Гаусса. Путем элементарных преобразований над строками приведем данную матрицу к трапециевидной форме: 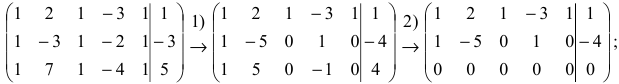
- первую строку умножили на -1 и прибавили ко второй, первую строку умножили на -1 и прибавили к третьей;
- вторую строку прибавили к третьей.
Отсюда rank A=rank 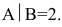 Система совместна.
Система совместна.
Очевидно, если мы проделаем над уравнениями системы любое из приведенных выше преобразований, то получим систему, равносильную исходной. Из коэффициентов преобразованной матрицы составим систему:
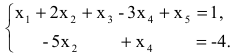
Выберем в качестве базисного минора стоящий в первых двух строках и столбцах: 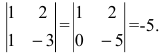
Тогда неизвестные  – базисные,
– базисные,  – свободные. Придадим свободным неизвестным произвольные числовые значения
– свободные. Придадим свободным неизвестным произвольные числовые значения 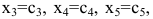 где
где 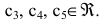 Решим укороченную систему относительно базисных неизвестных, начиная с последнего уравнения:
Решим укороченную систему относительно базисных неизвестных, начиная с последнего уравнения:
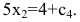
Следовательно,
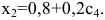
Тогда 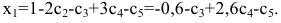 Общее решение системы имеет вид
Общее решение системы имеет вид
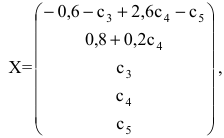 где
где 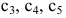 – произвольные постоянные.
– произвольные постоянные.
Для существования нетривиального решения однородной системы линейных уравнений необходимо и достаточно, чтобы ранг системы k был меньше числа неизвестных n. Тогда общее решение однородной системы может быть записано в виде
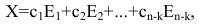
где 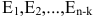 – векторы-столбцы, которые называются фундаментальной системой решений.
– векторы-столбцы, которые называются фундаментальной системой решений.
Пример №21
Найти фундаментальную систему решений:
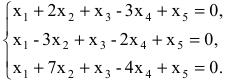
Решение:
На основании предыдущего примера выпишем общее решение системы: 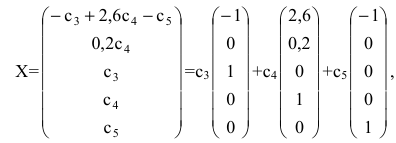
где 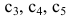 – произвольные постоянные. Тогда векторы
– произвольные постоянные. Тогда векторы 
образуют фундаментальную систему решений.
- Линейное программирование
- Дифференциальное исчисление функций одной переменной
- Исследование функции
- Пространство R”
- Матрица – виды, операции и действия с примерами
- Линейный оператор – свойства и определение
- Многочлен – виды, определение с примерами
- Квадратичные формы – определение и понятие
