я не знаю, как вас учат это решать. Решу, как понимаю.
Эластичность это отношение, насколько в процентах изменяется (в данном случае) выпуск продукции к изменению в процентах одного из (в данном случае) факторов производства.
В данный момент при таких значениях факторов производства компания производит следующий объем продукции
[math]75 cdot 43^{0,8} 846^{1,2} approx 4950858[/math]
при объеме “фондов” 846
Для определения эластичности нужно сначала определить скорость изменения объема продукции (в абсолютных единицах) относительно изменения интересующего фактора производства (в данном случае объема “фондов”) (тоже в абсолютных единицах) — эта скорость является частной производной объема производства по объему “фондов”.
По общему правилу производная функции типа
[math]f(x) = a cdot x^{n}[/math]
вычисляется следующим образом:
[math]f'(x) = a cdot n cdot x^{n-1}[/math]
соответственно производная функции
[math]Q(K) = 75 cdot 43^{0,8} cdot K^{1,2}[/math]
равна
[math]Q'(K) = 75 cdot 43^{0,8} cdot 1,2 cdot K^{1,2 – 1} approx 1824 cdot K^{0,2}[/math]
т.к. сейчас объеме “фондов” 846, в данной точке производная будет равна
[math]Q'(K) approx 1824 cdot 846^{0,2} approx 7022[/math]
Это число означается, что скорость нарастания объема производства в абсолютных единицах в данный момент времени соответствует 7022 единице на абсолютное увеличение “фондов” на 1 единицу. Но эластичность — это отношение процентов. Поэтому мы должны эту скорость пересчитать, учитывая, сколько сейчас в абсолютных единицах выпускается продукции (4950858) при каком объеме “фондов” (846).
Абсолютное изменение объема производства на 7022 единицы при текущих факторах производства соответствует изменению [math]frac{ 7022 }{ 4950858 } approx 0,142 %[/math]
Абсолютное изменение объема “фондов” на 1 единицу (т.к. производная функция идет в расчете на 1) при текущих факторах производства соответствует изменению [math]frac{ 1 }{ 846 } approx 0,118 %[/math]
Их отношение (а соответственно и эластичность) равны (примерно) [math]frac{ 7022 cdot 846 }{ 4950858 cdot 1 } approx frac{ 0,142 % }{ 0,118 % } approx 1,2[/math]
Значение > 1 говорит о наличии эластичности при текущих уровнях факторов производства.
Рассмотренные
в предыдущем подразделе экономические
понятия имеют размерность, что не вполне
удобно для анализа взаимосвязи
относительных изменений переменных.
Вводят понятия: эластичность
выпуска по труду EL
и эластичность выпуска по капиталу EK,
определяемые формулами
EL
=![]() ;
;
(2.6)
EK
=![]() .
.
(2.7)
Безразмерные
показатели EL
и EK
показывают, на сколько процентов
произойдет относительное увеличение
выпуска при относительном увеличении
соответствующего ресурса на 1%.
Сумма
значений эластичности выпуска по всем
ресурсам называется эластичностью
производства:
E
= EK
+ EL.
(2.8)
Для
эластичности
KL
предельной
нормы замещения труда капиталом
справедливо соотношение:
KL
= .
.
(2.9)
Эффективность
производственного процесса (эффект от
масштаба производства) можно оценить
математически, увеличив одновременно
все ресурсы в t
раз. Если
использовать более общую аппроксимирующую
формулу Кобба—Дугласа
Q
= AKL,
получаем: Q
(tK,
tL)
= AKtLt
= tt
Q
(K,
L)
= t+
Q
(K,
L).
Отсюда вытекает, что если
и
в сумме превышают единицу, то говорят,
что производственная функция имеет
возрастающий эффект от масштаба
производства (если ресурсы K
и L увеличиваются
в некоторой пропорции, то выпуск Q
растет в большей пропорции). Если их
сумма меньше, чем единица, то имеет место
убывающий эффект от масштаба производства.
В
своей первой статье Ч. Коббс и П. Дуглас
описывали производственную функцию в
виде (2.1), предполагающем постоянную
отдачу от масштаба:
и
в сумме точно составляют единицу.
Впоследствие они ослабили это допущение,
предпочитая оценивать степень отдачи
от масштаба производства. Как указывалось
нами ранее, при обработке исходных
данных, использованных Ч. Коббсом и П.
Дугласом, методом наименьших квадратов,
получаем значения
= 0,23 и
= 0,81. Сумма
и ,
равная 1,04, лишь несколько превышает
единицу, т.е. первоначальное предположение
Ч. Коббса и П. Дугласа о постоянной отдаче
от масштаба было вполне оправдано.
Пример
4. Рассчитать
эластичность выпуска по труду и капиталу
для производственной функции Q
= K1/4L3/4
в точке K
= 2, L
= 3. Оценить эффект от масштаба производства.
Решение.
Эластичность выпуска по труду определяется
формулой (2.6). Так как предельный продукт
труда
![]() =
=![]() =3/4
=3/4![]() ,
,
получаем:
EL
=![]() =
=![]() =
=![]() (3/4
(3/4![]() )
)
= (L /
K1/4L3/4)(3/4![]() )
)
= 3/4.
Эластичность
выпуска по капиталу определяется
формулой (2.7). Так как предельный продукт
капитала
![]() =
=![]() =1/4
=1/4![]() ,
,
получаем:
EK
=![]() =
=![]() =
=![]() (1/4
(1/4![]() )
)
= (K
/ K1/4L3/4)(1/4![]() )
)
= 1/4.
Таким
образом, эластичность выпуска по труду
и капиталу в случае производственной
функции Кобба—Дугласа
вида Q
= AKL
не зависит от точки производства и равна
показателям степени при соответствующих
переменных
= 0,75 и
= 0,25 соответственно.
Сумма
значений эластичности выпуска по всем
ресурсам (эластичность производства)
равна
+
= 1, т.е. в данном случае имеет место
постоянная отдача от масштаба производства.
Для
эластичности KL
предельной нормы замещения труда
капиталом в общем случае производственной
функции вида
Q = AKL
получаем:
KL
= =
= =
=
1,
т.е.
для функции Кобба—Дугласа
эластичность предельной нормы замещения
труда капиталом постоянна и равна
единице. Это важнейшее свойство функции
Кобба—Дугласа.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- Авторы
- Файлы
- Литература
Попова Е.С
1
Дырдасова А.С.
1
1 Самарский государственный экономический университет
1. Предельный анализ в экономике. Эластичность функции [Электронный ресурс]. – Режим доступа: http://www.mathelp.spb.ru/book1/lim_an_ec.htm. – (Дата обращения: 16.12.2015).
2. Яшина Ю.Е, Карнавская Н.В., Чехута В.А. и др. Эластичность функции и ее применение экономике [Электронный ресурс] / Ю.Е. Яшина, Н.В. Карнавская, В.А. Чехута и др./ Международный студенческий научный вестник: эл.науч.журн. – 2015. – №3. – Режим доступа: http://www.eduherald.ru/140–14166. – (Дата обращения:16.12.2015).
На современном этапе развития человечества одну из ведущих ролей в развитии общества играют экономические отношения, поскольку именно они являются той материальной основой, которая в свою очередь делает возможным формирование и развитие различных общественных институтов. Для наиболее полного изучения экономических явлений и процессов, происходящих в обществе, экономическая теория использует различные методы, прибегая к «помощи» других не менее важных наук. Одной из таких наук является математический анализ. Одними из базовых, ключевых понятий в экономической теории являются такие широко известные категории как спрос и предложение, которые, в свою очередь, обладают определенными признаками и свойствами, что и является главным предметом экономической теории. Спрос и предложение товаров обладают различной степенью чувствительности к изменению определяющих их факторов. Мерой такого изменения является эластичность спроса и эластичность предложения. В свою очередь, выделяется несколько основных видов эластичности: ценовая эластичность, эластичность по доходу и перекрестная эластичность.
Ценовая (прямая) эластичность спроса (предложения) показывает, какое процентное изменение спроса (предложения) последует за однопроцентным изменением цены товара.
Эластичность спроса по доходу показывает, какое процентное изменение спроса последует за однопроцентным изменением дохода потребителя.
Перекрестная эластичность спроса показывает, какое изменение спроса на товар A последует за однопроцентным изменением цены товара B, при условии, что товары A и B являются комплементарными (комплементами) или взаимозаменяемыми (субститутами). Количественным выражением эластичности спроса и предложения является коэффициент эластичности E, который рассчитывается в одной точке кривой спроса и предложения или на дуге этой кривой.
Эластичностью функции 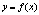 называется
называется
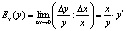 .
.
Таким образом, эластичность функции можно вычислить по формуле
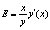 .
.
Эластичность функции также называется относительной производной. Эластичность функции по аргументу показывает, на сколько процентов изменится значение функции при изменении аргумента в точке x на 1 %. Пусть спрос задан функцией Q(d)=96–16P+P2, необходимо определить ценовую точечную эластичность спроса по цене при P=4.
Найдем первую производную функции
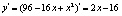 .
.
Подставим полученное выражение в формулу эластичности:
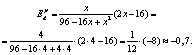
Таким образом, при изменении цены на 1 % величина спроса изменяется на 0,7 %. Спрос неэластичен.
Также в качестве примера можно рассмотреть производственную функцию Кобба-Дугласа. Данная функция устанавливает зависимость между величиной созданного общественного продукта и совокупными затратами живого труда, а также суммарным объемом применяемых производственных фондов.
Данная функция имеет следующий вид
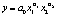 ,
,
где a0 – коэффициент, 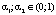 . Несмотря на то, что каждый из данных коэффициентов меньше 1, их сумма может быть меньше, равна или больше 1. Она показывает эффект одновременного пропорционального увеличения объема трудовых ресурсов и производственных фондов.
. Несмотря на то, что каждый из данных коэффициентов меньше 1, их сумма может быть меньше, равна или больше 1. Она показывает эффект одновременного пропорционального увеличения объема трудовых ресурсов и производственных фондов.
Каждый из используемых ресурсов характеризуется средней и предельной величинами. средняя производительность труда показывает, сколько единиц продукции приходится на единицу труда. Предельная производительность труда показывает, сколько дополнительных единиц продукции приносит дополнительная единица труда.
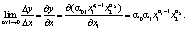
Рассчитаем вторую частную производную:
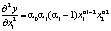 .
.
Вторая частная производная отрицательна, а значит, предельная производительность с увеличением  снижается.
снижается.
Для производственной функции Кобба-Дугласа предельная производительность всегда меньше средней.
Кроме того, можно определить показатель, характеризующий относительный прирост объема производства на единицу относительно увеличения труда
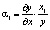 .
.
Полученный показатель называется эластичностью выпуска продукции по затратам труда. Он показывает, на сколько процентов увеличивается выпуск продукции при увеличении затрат труда на 1 %.
Подобные показатели можно рассчитать и для производственных фондов. Объем продукции в расчете на единицу производственных фондов называется фондоотдачей. Можно рассчитать среднюю и предельную фондоотдачу. Из функции Кобба_Дугласа имеем
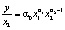 .
.
Предельная фондоотдача равна частной производной выпуска продукции по объему фондов:
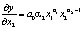 .
.
Предельная фондоотдача всегда ниже средней.
Относительная фондоотдача (эластичность выпуска продукции по объему производственных фондов) определяется как
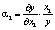 .
.
Если производственная функция задана формулой
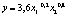 ,
,
где y – объем продукции в стоимостном выражении, x1 – фонд заработной платы, x2 – стоимость основных производственных фондов. 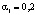 . Это означает, что при изменении затрат труда на 1 % выпуск продукции изменится на 0,2 % (увеличится или уменьшится).
. Это означает, что при изменении затрат труда на 1 % выпуск продукции изменится на 0,2 % (увеличится или уменьшится). 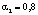 . Следовательно, при изменении объема основных производственных фондов на 1 %, выпуск продукции изменится на 0,8 % (увеличится или уменьшится).
. Следовательно, при изменении объема основных производственных фондов на 1 %, выпуск продукции изменится на 0,8 % (увеличится или уменьшится).
Библиографическая ссылка
Попова Е.С, Дырдасова А.С. ЭЛАСТИЧНОСТЬ В ПРОИЗВОДСТВЕННЫХ ФУНКЦИЯХ // Международный студенческий научный вестник. – 2016. – № 4-4.
;
URL: https://eduherald.ru/ru/article/view?id=16408 (дата обращения: 17.05.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
Анализ производственных функций
Курсовая работа :
“Анализ производственных функций”
Группа: ДИ 302
Студент: Шеломанов Р.Б.
Руководитель: Зуев Г.М
Москва 1999
Содержание
Теоретическая часть 3
Мультипликативная производственная функция 3
Линейная производственная функция 10
Производственная функция затраты-выпуск 10
Практическая часть 10
Задача 10
Решение 10
Заключение 11
Литература 12
Теоретическая часть
Мультипликативная производственная функция
Производственная функция (ПФ) выражает зависимость результата производства от затрат ресурсов. При описании экономики (точнее, ее производственной подсистемы) с помощью ПФ эта подсистема рассматривается как «черный ящик», на вход которого поступают ресурсы R1, …, Rn, а на выходе получается результат в виде годовых объемов производства различных видов продукции Х1, …, Хm .
В качестве ресурсов (факторов производства) на макроуровне наиболее часто рассматриваются накопленный труд в форме производственных фондов (капитал) К и настоящий (живой) труд L, а в качестве результата – валовой выпуск Х (либо валовой внутренний продукт Y, либо национальный доход N). Во всех случаях результат коротко будем называть выпуском и обозначать X, хотя это может быть и валовой выпуск, и ВВП, и национальный доход.
Остановимся несколько подробнее на обосновании состава фактора К. Накопленный прошлый труд проявляется в основных и оборотных, производственных и непроизводственных фондах. Выбор того или иного состава K определяется целью исследования, а также характером развития производственной и непроизводственной сфер в изучаемый период. Если в этот период в непроизводственную сферу вкладывается примерно постоянная доля вновь созданной стоимости и непроизводственная сфера оказывает на производство примерно одинаковое влияние, это служит основанием напрямую учитывать в ПФ только производственные фонды.
Но производственные фонды состоят из основных и оборотных производственных фондов. Если соотношение между этими составными частями производственных фондов примерно постоянное в течение всего изучаемого периода, то достаточно напрямую учитывать в ПФ только основные производственные фонды.
Если изучаемый период достаточно продолжителен и однороден по влиянию на производство указанных выше составных частей, следует испробовать все варианты включения их в модель (от всех вместе до какого-то одного из них). Чтобы не вдаваться в детали, далее будем К называть фондами.
Таким образом, экономика замещается своей моделью в форме нелинейной ПФ
Х= F(K, L),
т.е. выпуск (продукции) есть функция от затрат ресурсов (фондов и труда).
Теперь рассмотрим экономическую интерпретацию основных характеристик ПФ на примере мультипликативной функции (в частности, функции Кобба—Дугласа), некоторые другие ПФ, используемые в экономике, разберем в конце работы.
Производственная функция Х= F(K, L) называется неоклассической, если она является гладкой и удовлетворяет следующим условиям, поддающимся естественной экономической интерпретации:
1) F(0, L) = F(K, 0) = 0
– при отсутствии одного из ресурсов производство невозможно;
2)
– с ростом ресурсов выпуск растет;
3)
– с увеличением ресурсов скорость роста выпуска замедляется;
4) f(+¥, L) = F(K, +¥) = +¥
– при неограниченном увеличении одного из ресурсов выпуск неограниченно растет.
Мультипликативная ПФ задается выражением
a1>0 a2>0
где А — коэффициент нейтрального технического прогресса; а1, a2 -коэффициенты эластичности по труду и фондам .
Таким образом, ПФ обладает свойством 1, адекватным реальной экономике: при отсутствии одного из ресурсов производство невозможно. Частным случаем этой функции служит функция Кобба-Дугласа
Где a1=a, a2=1-a
Мультипликативная ПФ определяется по временному ряду выпусков и затрат ресурсов (Хt, Кt, Lt,), t= 1, …, Т, где T- длина временного ряда, при этом предполагается, что имеет место Т соотношений
где dt — корректировочный случайный коэффициент, который приводит в соответствие фактический и расчетный выпуск и отражает флюктуацию результата под воздействием других факторов, Мdt = 1. Поскольку в логарифмах эта функция линейна:
In Хt = In A + atIn Kt+ a2InLt + et, где et = In dt, Мet= 0,
получаем модель линейной множественной регрессии. Параметры функции А, a1, a2 могут быть определены по методу наименьших квадратов с помощью стандартных пакетов прикладных программ, содержащих метод множественной регрессии (например, STATGRAF или SAS для персональных ЭВМ).
В качестве примера приведем мультипликативную функцию валового выпуска Российской Федерации (млрд. руб.) в зависимости от стоимости основных производственных фондов (млрд. руб.) и числа занятых в народном хозяйстве (млн. чел.) по данным за 1960-1994 гг. (все стоимостные показатели даны в сопоставимых ценах для этого периода):
X=0,931K0,539L0,594
Мультипликативная функция обладает также свойством 2, адекватным реальной экономике: с ростом затрат ресурсов выпуск увеличивается, т.е.
Так как a1>0
Так как a2>0
Частные производные выпуска по факторам называются предельными продуктами или предельными (маржинальными) эффективностями факторов и представляют собой прирост выпуска на малую единицу прироста фактора:
– предельный продукт фондов, предельная фондоотдача (предельная эффективность фондов);
– предельный продукт труда, предельная производительность (предельная эффективность труда).
Для мультипликативной функции указанной выше вытекает, что предельная фондоотдача пропорциональна средней фондоотдаче — с коэффициентом a1 , а предельная производительность труда — средней производительности труда — с коэффициентом а2:
,
Из чего вытекает, что при а1 < 1, a2 < 1 предельные отдачи факторов меньше средних; при этих же условиях мультипликативная функции обладает свойством 3, которое очень часто наблюдается в реальной экономике: с ростом затрат ресурса его предельная отдача падает, т.е.
так как а1<1
так как а2<1
Из также видно, что мультипликативная функция обладает свойством 4 , т.е. при неограниченном увеличении одного из ресурсов выпуск неограниченно растет. Таким образом, мультипликативная функция при 0 < а1 < 1, 0<а2 < 1 является неоклассической.
Перейдем теперь к экономической интерпретации параметров А, а1, а2 мультипликативной ПФ. Параметр А обычно интерпретируется как параметр нейтрального технического прогресса: при тех же а1, а2 выпуск в точке (К, L) тем больше, чем больше А. Для интерпретации а1, а2 необходимо ввести понятие эластичностей как логарифмических производных факторов:
Поскольку в нашем случае In Х = In А + a1ln К + a1ln L, то
т.е. а1 — эластичность выпуска по основным фондам, а a2 – эластичность выпуска по труду.
Из
видно, что коэффициент эластичности фактора показывает, на сколько процентов увеличится выпуск, если фактор возрастет на 1%. Например, согласно ПФ X=0,931K0,539L0,594
при увеличении основных фондов (ОФ) на 1% валовой выпуск повысится на 0,539%, а при увеличении занятых на 1% — на 0,594%.
Если а1 >a2 имеет место трудосберегающий (интенсивный) рост, в противном случае – фондосберегающчй (экстенсивный) рост.
Рассмотрим темп роста выпуска
Если возвести обе части уравнения в степень , получим соотношение
в котором справа — взвешенное среднее геометрическое темпов роста затрат ресурсов, при этом в качестве весов выступают относительные эластичности факторов
При а1+ а2 > 1 выпуск растет быстрее, чем в среднем растут факторы , а при а1+ а2 < 1 – медленнее. В самом деле, если факторы растут (т.е. Kt+1>Kt, Lt+1>Lt) то согласно растет и выпуск (т.е. Xt+1>Xt), следовательно, при а1+ а2 > 1
т.е. действительно, темп роста выпуска больше среднего темпа роста факторов . Таким образом, при а1+ а2 > 1 ПФ описывает растущую экономику.
Линией уровня на плоскости К, L, или изоквантой, называется множество тех точек плоскости, для которых F(K, L) =Х0=const. Для мультипликативной ПФ изокванта имеет вид :
или
т.е. является степенной гиперболой, асимптотами которой служат оси координат.
Для разных К, L, лежащих на конкретной изокванте, выпуск равен одному и тому же значению X0, что эквивалентно утверждению о взаимозаменяемости ресурсов.
Поскольку на изокванте F(K, L) = Х0 = const, то
В этом соотношении , поэтому dK и dL имеют разные знаки: если dL<0 что означает сокращение объема труда, то dK>0, т.е выбывший в объеме труд замещается фондами в объеме dK.
Поэтому естественно следующее определение, вытекающее из .
Предельной нормой замены SK труда фондами называется отношение модулей дифференциалов ОФ и труда:
соответственно , предельная норма замены SL фондов трудом
при этом Sk SL=1
Для мультипликативной функции норма замещения труда фондами пропорциональна фондовооруженности:
,
что совершенно естественно: недостаток труда можно компенсировать его лучшей фондовооруженностью.
Изоклиналями называются линии наибольшего роста ПФ. Изоклинали ортогональны линиям нулевого роста, т.е. изоквантам. Поскольку направление наибольшего роста в каждой точке (К, L) задается градиентом
grad , то уравнение изоклинали записывается в форме
В частности, для мультипликативной ПФ получаем,
поэтому изоклиналь задается дифференциальным уравнением,
, которое имеет решение
,
где (L0; К0) – координаты точки, через которую проходит изоклиналь. Наиболее простая изоклиналь при а = 0 представляет собой прямую
На рис. 1 изображены изокванты и изоклинали мультипликативной ПФ.
При изучении факторов роста экономики выделяют экстенсивные факторы роста (за счет увеличения затрат ресурсов, т.е. увеличения масштаба производства) и
рис. 1
интенсивные факторы роста (за счет повышения эффективности использования ресурсов).
Возникает вопрос: как с помощью ПФ выразить масштаб и эффективность производства? Это сравнительно легко сделать, если выпуск и затраты выражены в соизмеримых единицах, например представлены в соизмеримой стоимостной форме. Однако проблема соизмерения настоящего и прошлого труда до сих пор не решена удовлетворительным образом. Поэтому воспользуемся переходом к относительным (безразмерным) показателям.В относительных показателях мультипликативная ПФ записывается следующим образом:
те X0, K0L0 — значения выпуска и затрат фондов и труда в базовый год.
Безразмерная форма , указанная выше , легко приводится к первоначальному виду
Таким образом, коэффициент
получает естественную интерпретацию – это коэффициент, который соизмеряет ресурсы с выпуском. Если обозначить выпуск и ресурсы в относительных (безразмерных) единицах измерения через x, k, l, то ПФ в форме
запишется так:
Найдем теперь эффективность экономики, представленной ПФ . Напомним, что эффективность — это отношение результата к затратам. В нашем случае два вида затрат: затраты прошлого труда в виде фондов k и настоящего труда l. Поэтому имеются два частных показателя эффективности: -фондоотдача , – производитель труда.
Поскольку частные показатели эффективности имеют одинаковую размерность (точнее, одинаково безразмерны), то можно находить любые средние из них. Так как ПФ выражена в мультипликативной форме, то и среднее естественно взять в такой же форме, т.е. среднегеометрическое значение.
Итак, обобщенный показатель экономической эффективности есть взвешенное среднее геометрическое частных показателей экономической эффективности:
в котором роль весов выполняют относительные эластичности
т.е. частные эффективности участвуют в образовании обобщенной эффективности с такими же приоритетами, с какими входят в ПФ соответствующие ресурсы.
Из вытекает, что с помощью коэффициента экономической эффективности ПФ преобразуется в форму, внешне совпадающую с функцией Кобба-Дугласа:
k=Eka l1-a
в соотношении с чем Е – не постоянный коэффициент, а функция от (К, L).
Поскольку масштаб производства М проявляется в объеме затраченных ресурсов, то по тем же соображениям, которые были приведены при расчете обобщенного показателя экономической эффективности, средний размер использованных ресурсов (т.е. масштаб производства)
M=kal1-a
В результате получаем , что выпуск Х есть произведение экономической эффективности и масштаба производства:
Х=ЕМ.
Линейная производственная функция
X=F(K,L)=EKK+ELL
Где EK и EL частные эффективности ресурсов.
EK = -фондоотдача , EL = – производитель труда.
Поскольку частные показатели эффективности имеют одинаковую размерность (точнее, одинаково безразмерны), то можно находить любые средние из них.
Эластичности замены труда фондами для линейной ПФ = ¥
эта величина показывает, на сколько процентов надо изменить фондовооруженность, чтобы добиться изменения нормы замены на 1%.
Производственная функция затраты-выпуск
X= F(K,L)=
Где:
Коэффициенты эластичности представленные в виде логарифмических производных факторов показывают, на сколько процентов увеличится выпуск, если фактор возрастет на 1%. Например, согласно ПФ X=0,931K0,539L0,594
при увеличении основных фондов (ОФ) на 1% валовой выпуск повысится на 0,539%, а при увеличении занятых на 1% — на 0,594%.
Практическая часть
Задача
Дана производственная функция валового внутреннего продукта США по данным 1960-1995 гг.
X=2,248K0,404L0,803
Валовой внутренний продукт США, измеренный в млрд. дол. в ценах 1987 г. возрос с 1960 по 1995 г. в 2,82 раза, основные производственные фонды за этот же период увеличились в 2,88 раза, число занятых – в 1,93 раза.
Необходимо рассчитать масштаб и эффективность производства.
Решение
Из условия x = 2,82 k=2,88 l=1,93;
(‘начала находим относительные эластичности по фондам и труду
Затем определяем частные эффективности ресурсов
после чего находим обобщенный показатель эффективности как среднее геометрическое частных:
Масштаб устанавливаем как среднее геометрическое темпов роста ресурсов
Таким образом , общий рост ВВП с 1960 по 1995 г. в 2,82 раза произошел за счет роста масштаба производства в 2,207 раза и за счет повышении эффективности производства в 1,278 раза (2,82 = 1,273 * 2,207).
Заключение
Выше достаточно подробно была изучена мультипликативная ПФ F(K,L). В частности, был выяснен экономический смысл ее параметров , показано, что при 0 <а1<1, i= 1, 2… эта функция –неоклассическая , построены изокванты и изоклинали этой функции, найдены нормы замены ресурсов.. Рассмотрены и другие производственные функции.
Литература
В.А. Колемаев «Математическая экономика»
Г.М. Зуев Ж.В. Самохвалова «Экономико-математические методы и модели. Межотраслевой анализ»
Теги:
Анализ производственных функций
Другое
Финансы, деньги, кредит
Просмотров: 21808
Найти в Wikkipedia статьи с фразой: Анализ производственных функций
