Условие задачи:
Определить число штрихов на 1 мм дифракционной решетки, если углу дифракции 30° соответствует максимум четвертого порядка для монохроматического света с длиной волны (lambda = 0,5) мкм.
Задача №10.7.4 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(l=1) мм, (varphi=30^circ), (k=4), (lambda=0,5) мкм, (N-?)
Решение задачи:
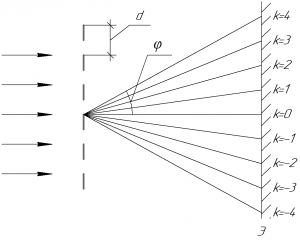 Запишем формулу дифракционной решетки:
Запишем формулу дифракционной решетки:
[dsin varphi = klambda;;;;(1)]
В этой формуле (d) – период решетки (также называют постоянной решетки), (varphi) – угол дифракции, (k) – порядок максимума (по условию задачи – четвертый максимум), (lambda) – длина волны, падающей нормально на решетку.
Период (постоянную) решетки (d) можно определить, разделив некоторую длину решетки (l) (в данном случае – 1 мм) на количество содержащихся на этой длине штрихов (N), то есть:
[d = frac{l}{N};;;;(2)]
Подставим (2) в (1), тогда будем иметь:
[frac{l}{N}sin varphi = klambda ]
Из полученной формулы выразим искомое количество штрихов:
[N = frac{{lsin varphi }}{{klambda }}]
Задача решена в общем виде, подставим данные из условия в полученную формулу и посчитаем численный ответ:
[N = frac{{{{10}^{ – 3}} cdot sin 30^circ }}{{4 cdot 0,5 cdot {{10}^{ – 6}}}} = 250]
Ответ: 250.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
10.7.3 Дифракционная решетка имеет 250 штрихов на миллиметр. Под каким углом виден максимум
10.7.5 Сколько штрихов на 1 мм должна иметь дифракционная решетка, чтобы зеленая линия
10.7.6 Сколько штрихов на 1 мм должна иметь дифракционная решетка для того, чтобы второй
Тема: Определить число штрихов дифракционной решётки (Прочитано 12462 раз)
0 Пользователей и 1 Гость просматривают эту тему.
Определить число штрихов на l =1,0 мм дифракционной решётки, если углу π/2 соответствует максимум пятого порядка для монохроматического света с длиной волны λ = 0,5 мкм.
« Последнее редактирование: 30 Сентября 2014, 21:16 от Сергей »

Записан
Решение: Максимум дифракционной решетки находится по формуле:
d∙sinφ = k∙λ;
φ = π/2, sinφ = 1,
d – период дифракционной решетки, d = l/N.
sinφ ∙ l/N = k∙λ, N = sinφ ∙ l/k∙λ,
Так как максимум пятый, k = 5, l = 10-3 м.
N = 400. Ответ: 400.
« Последнее редактирование: 06 Октября 2014, 13:51 от alsak »

Записан
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 17 декабря 2015 года; проверки требуют 66 правок.
У этого термина существуют и другие значения, см. Решётка.

Очень большая отражательная дифракционная решётка.
Дифракционная решётка — оптический прибор, действие которого основано на использовании явления дифракции света. Представляет собой совокупность большого числа регулярно расположенных штрихов (щелей, выступов), нанесённых на некоторую поверхность.
История[править | править код]
Первое описание явления сделал в 1673 году Джеймс Грегори, который наблюдал дифракцию на птичьих перьях:
Если вы сочтёте нужным, вы можете показать мистеру Ньютону небольшой эксперимент, который (если он еще не знает об этом) будет достоин его внимания. Впустите солнечный свет через маленькое отверстие в затемнённый дом, а в отверстие поместите перо (чем тоньше и белее, тем лучше для этой цели), и оно направит на белую стену или бумагу напротив нее ряд маленьких кругов и овалов (если я их не ошибаюсь), из которых один белый (а именно середина, которая противоположна Солнцу), а все остальные по-разному окрашены. Я с радостью выслушаю его мысли об этом.[1]
Дэвид Риттенхаус в 1786 году впервые изготовил дифракционную решётку и измерил углы отклонения для разных цветов[2].
В 1801 году Томас Юнг открыл и объяснил интерференцию света. В 1818 году Огюстен Жан Френель разработал теорию дифракции света.
Опираясь на представления Юнга и Френеля о световых волнах, Йозеф Фраунгофер в 1821 году впервые использовал дифракционную решётку (которую он и изготовил) для получения спектров и вычисления длин волн.
Виды решёток[править | править код]
- Отражательные — Штрихи нанесены на зеркальную (металлическую) поверхность, и наблюдение ведется в отражённом свете
- Прозрачные — Штрихи нанесены на прозрачную поверхность (или вырезаются в виде щелей на непрозрачном экране), наблюдение ведется в проходящем свете.
Описание явления[править | править код]

Так выглядит свет лампы накаливания фонарика, прошедший через прозрачную дифракционную решётку. Нулевой максимум (m=0) соответствует свету, прошедшему сквозь решётку без отклонений. В силу дисперсии решётки в первом (m=±1) максимуме можно наблюдать разложение света в спектр. Угол отклонения возрастает с ростом длины волны (от фиолетового цвета к красному)
Идеализированная решетка состоит из набора щелей с периодом d, который должен быть больше, чем длина волны, представляющая интерес, чтобы вызвать дифракцию. Пусть на решетку нормально(перпендикулярно решетке) падает плоская волна монохроматического света с длиной волны 
Формулы[править | править код]
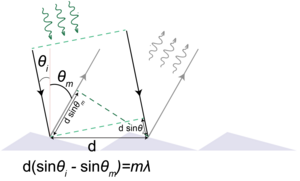
Иллюстрация к нахождению условия максимума при отражении от дифракционной решетки при наклонном падении.

Иллюстрация к нахождению порядков дифракции.
Расстояние, через которое повторяются штрихи на решётке, называют периодом дифракционной решётки. Обозначают буквой d.
Если известно число штрихов (

При нормальном падении плоской волны условия интерференционных максимумов дифракционной решётки, наблюдаемых под определёнными углами, имеют вид:
где
— период решётки,
— угол максимума данного цвета,
— порядок максимума, то есть порядковый номер максимума, отсчитанный от центра картинки,
— длина волны.
Это условие может быть выведено исходя из того, что разность фаз между лучами, отраженными от поверхностей на расстоянии, равном периоду решетки, должна быть кратна 
Если же свет падает на решётку под углом 
Эта формула может быть проиллюстрирована графически, для того, чтобы найти направление на какой-то порядок дифракции, необходимо нарисовать окружность с радиусом, равным периоду решетки, умноженному на показатель преломления вещества, в котором наблюдаются порядки. Затем через конец прошедшего или отражённого луча необходимо провести вертикальную прямую. После этого, необходимо провести еще несколько вертикальных прямых на расстоянии друг от друга, равным длине волны. Направления на порядки дифракции будут из центра окружности в точки, где она пересекается с вертикальными прямыми. Фактически, такая иллюстрация аналогична построению Эвальда в одномерном случае.
Характеристики[править | править код]
Одной из характеристик дифракционной решётки является угловая дисперсия. Предположим, что максимум какого-либо порядка наблюдается под углом 



Таким образом, угловая дисперсия увеличивается с уменьшением периода решётки d и возрастанием порядка спектра m.
Вторая характеристика дифракционной решетки — разрешающая способность. Она обусловлена угловой шириной главного максимума и определяет возможность раздельного наблюдения 2 близких спектральных линий. При увеличении порядка спектра m возрастает

Также существует еще одна характеристика дифракционной решетки — дисперсионная область. Она определяет для каждого порядка спектральный диапазон от перекрытия спектров. Данный параметр обратно-пропорционален порядку спектра m

Изготовление[править | править код]
Хорошие решётки требуют очень высокой точности изготовления. Если хоть одна щель из множества будет нанесена с ошибкой, то решётка будет бракована. Машина для изготовления решёток прочно и глубоко встраивается в специальный фундамент. Перед началом непосредственного изготовления решёток, машина работает 5—20 часов на холостом ходу для стабилизации всех своих узлов. Нарезание решётки длится до 7 суток, хотя время нанесения штриха составляет 2—3 секунды.
Применение[править | править код]
Дифракционную решётку применяют в спектральных приборах, также в качестве оптических датчиков линейных и угловых перемещений (измерительные дифракционные решётки).

Дифракция на примере одной щели
Примеры[править | править код]

Дифракция на компакт-диске
Один из простейших и распространённых в быту примеров отражательных дифракционных решёток — компакт-диск. На поверхности компакт-диска — дорожка в виде спирали с шагом 1,6 мкм между витками. Примерно треть ширины (0,5 мкм) этой дорожки занята углублением (это записанные данные), рассеивающим падающий на него свет, примерно две трети (1,1 мкм) — нетронутая подложка, отражающая свет. Таким образом, компакт-диск — отражательная дифракционная решётка с периодом 1,6 мкм. Кроме того, такой же отражательной дифракционной решёткой является и пустой CD-R диск, и пустой DVD диск, поскольку на них имеется спиральная дорожка для направления луча лазера при записи информации. Причём период решётки для DVD — 0,74 мкм.
См. также[править | править код]
Видеоурок: дифракционная решетка
- Дифракция на N щелях
- Дифракция Фраунгофера
- Дифракция Френеля
- Интерференция света
- Фурье-оптика
- Оптическая решётка
- Призма (оптика)
Примечания[править | править код]
- ↑ Letter from James Gregory to John Collins, dated 13 May 1673. Reprinted in: Correspondence of Scientific Men of the Seventeenth Century…., ed. Stephen Jordan Rigaud (Oxford, England: Oxford University Press, 1841), vol. 2, page 254. Books.Google.com Архивная копия от 16 сентября 2020 на Wayback Machine.
- ↑ И. Д. Багбая. К истории дифракционной решётки. Успехи физических наук, т. 108, вып. 2, октябрь 1972. стр. 335-337.. Дата обращения: 21 августа 2020. Архивировано 12 августа 2017 года.
Литература[править | править код]
- Эшелетты // Элоквенция — Яя. — М. : Советская энциклопедия, 1957. — С. 293. — (Большая советская энциклопедия : [в 51 т.] / гл. ред. Б. А. Введенский ; 1949—1958, т. 49).
- Ландсберг Г. С. Оптика, 1976
- Сивухин Д. В. Общий курс физики. — М.. — Т. IV. Оптика.
- Тарасов К. И. Спектральные приборы, 1968
Ссылки[править | править код]
- Экспериментальное определение периода решётки у компакт-диска — видео с пояснениями на английском языке
9
Санкт-Петербургский
Государственный
Университет
Информационных
Технологий
Механики и Оптики
Лабораторная
работа №13
ОПРЕДЕЛЕНИЕ ОСНОВНЫХ ХАРАКТЕРИСТИК
ДИФРАКЦИОННОЙ РЕШЕТКИ
Студент:
Лысак Андрей
Альбертович
Группа:
2840
Преподаватель:
Соловьев
Сергей
Михайлович
Цель работы – определение периода,
числа штрихов на 1 мм,
угловой дисперсии и разрешающей
способности дифракционной решетки.
Общие положения
Дифракционная решетка – оптический
прибор, представляющий собой совокупность
большого числа параллельных, равноотстоящих
друг от друга узких щелей (штрихов)
одинаковой формы, нанесенных на какую-либо
поверхность. Основное свойство
дифракционной решетки – способность
разлагать падающий на неё свет в спектр
по длинам волн, что используется в
современных приборах. Различают
отражательные и прозрачные дифракционные
решетки. У отражательных штрихи наносятся
на зеркальную (как правило, металлическую)
поверхность, и наблюдение спектра
ведется в отраженном свете. У прозрачных
решеток штрихи наносятся на поверхность
прозрачной (как правило, стеклянной)
пластины, либо вырезаются в виде узких
щелей в непрозрачном экране, и наблюдение
ведется в проходящем свете.
Р ассмотрим
ассмотрим
действие прозрачной дифракционной
решетки. Пусть на решетку нормально к
её поверхности падает параллельный
пучок лучей белого света (рис. 1).
На щелях (штрихах) решетки, соизмеримых
с длиной волны света, происходит явление
дифракции, связанное с отклонением волн
от прямолинейного распространения при
взаимодействии их с препятствием. В
результате за решеткой лучи пойдут под
разными углами во все стороны от каждой
точки щели. Эти лучи можно сгруппировать
в пучки параллельных между собой лучей.
Установим за решеткой положительную
линзу. Каждый пучок параллельных лучей
соберется в задней фокальной плоскости
линзы в одной точке (точка А для
лучей, дифрагировавших под углом φ
к нормали решетки). Параллельные лучи
других углов дифракции соберутся в
других точках фокальной плоскости
линзы. В этих точках произойдет
интерференция световых волн, исходящих
от разных щелей решетки. Если р
Рис. 1
азность хода между соответственными
лучами будет равна целому числу длин
волн какого-то монохроматического
света, то в точке встречи лучей возникнет
максимум света для данной длины волны,
т.е.
![]() ,
,
κ = 0, ±1, ±2, … Из рис. 1
видно, что разность хода Δ между двумя
параллельными лучами, выходящими из
соответствующих точек соседних щелей,
равна
![]() ,
,
где a – ширина щели;
b – ширина
непрозрачного промежутка между щелями.
Величина
![]()
называется периодом, или постоянной,
дифракционной решетки. Следовательно,
условие возникновения главных
интерференционных максимумов решетки
имеет вид:
![]() (1)
(1)
В фокальной плоскости линзы для лучей,
не испытавших дифракции, наблюдается
центральный белый максимум нулевого
порядка (φ = 0, κ = 0),
вправо и влево от которого располагаются
цветные максимумы (спектральные линии)
первого, второго и последующих порядков
(см. рис. 1). Интенсивность
максимумов сильно уменьшается с ростом
их порядка, т.е. с увеличением угла
дифракции.
Уравнение (1) позволяет рассчитать период
дифракционной решетки d, если
измерен угол дифракции φ,
соответствующий спектральной линии,
для которой известны её длина волны и
порядок спектра.
Зная период решетки, легко рассчитать
число штрихов, нанесенных на 1 мм
ширины решетки:
![]() (2)
(2)
Одной из основных характеристик
дифракционной решетки является её
угловая дисперсия. Угловой дисперсией
решетки называется величина, равная
производной от угла дифракции световых
волн по длине волны:
![]() (3)
(3)
Дисперсия определяет угловое расстояние
dφ между направлениями
для двух спектральных линий, отличающихся
по длине волны на 1 нм (![]() = 1 нм),
= 1 нм),
и характеризует степень растянутости
спектра вблизи данной длины волны.
Формула для расчета угловой дисперсии
решетки может быть получена при
дифференцировании уравнения, определяющего
положение главных максимумов
![]() ,
,
![]() .
.
Отсюда
![]() . (4)
. (4)
Из этой формулы следует, что угловая
дисперсия решетки тем больше, чем больше
порядок спектра. Этим объясняется
расширение спектра у решеток с ростом
порядка.
Для решеток с разными периодами ширина
спектра больше у решетки, характеризующейся
меньшим периодом. Обычно в пределах
одного порядка
![]()
меняется незначительно (особенно для
решеток с небольшим числом штрихов на
миллиметр), поэтому дисперсия в пределах
одного порядка почти не меняется. Спектр,
полученный при постоянной дисперсии,
растянут равномерно во всей области
длин волн, что выгодно отличает спектр
решетки от спектра, даваемого призмой.
В спектроскопии принято считать, что
оптический прибор разрешил две линии
спектра, если изображения этих линий в
спектре, полученном с помощью данного
прибора, видны раздельно. Если изображения
двух линий сливаются в одно, то говорят,
что прибор их не разрешил. Одни и те же
линии спектра могут быть разрешены
одним прибором и не разрешены другим.
Это связано с шириной максимумов
интенсивности этих линий.
П о
о
предложению Рэлея, подтверждённому и
проверенному опытом, принято считать
разрешение полным, когда максимум
интенсивности одной из линий совпадает
с минимумом другой (рис. 2). Если
максимумы располагаются ближе, чем
показанные на рис. 2, изображения
линий λ1 и λ2 сливаются в
одно – линии не разрешаются. Когда
максимумы разнесены дальше, линии
уверенно разрешены.
Разрешающей способностью (или разрешающей
силой) принято называть величину
![]()
Рис. 2
,
где
![]() –
–
средняя длина волны двух разрешаемых
линий;
![]() –
–
наименьшая разность двух длин волн,
которые ещё разрешаются данным прибором
(соответствует критерию Рэлея). Разрешающая
способность является величиной
безразмерной. Чем она больше, тем более
близкие по длине волны линии способен
разрешить прибор. Разрешающая способность
дифракционной решетки определяется
порядком спектра и полным числом штрихов
решетки N:
![]() (5)
(5)
Описание лабораторной установки
Лабораторная установка по определению
основных характеристик дифракционной
решетки включает в себя источник света
1 (рис. 3). Это ртутная лампа, дающая
линейчатый спектр, который состоит из
следующих спектральных линий: две желтые
λ1 = 579,1 нм; λ2 = 577,0 нм;
зеленая λ3 = 546,1 нм; голубая
λ4 = 491,6
нм (слабая); синяя λ5 = 435,8
нм; две фиолетовые λ6 = 407,8
нм (слабая); λ7 = 404,7 нм.
В
Рис. 3
се измерения углов дифракции
производятся на гониометре. Он состоит
из осветительного коллиматора 2,
который дает пучок параллельных лучей
(входная щель коллиматора расположена
в фокальной плоскости объектива трубы).
Ширина щели регулируется винтом,
расположенным сбоку. Параллельный пучок
лучей направляется на дифракционную
решетку 3, установленную на столике
гониометра, перпендикулярно оси
осветительного коллиматора. Спектр,
полученный с помощью дифракционной
решетки, наблюдается в зрительную трубу
4, которая может поворачиваться
вокруг вертикальной оси гониометра,
оставаясь при этом все время направленной
по радиусу кругового лимба гониометра
5. Лимб разделен на 360○
(цена деления лимба 30′ ). Вдоль
лимба вместе со зрительной трубой
движется скрепленный с ней нониус 6,
точность которого одна угловая минута.
В окуляре зрительной трубы имеется
вертикальная нить, которую совмещают
с исследуемой линией спектра.
Порядок выполнения работы
1. Установить решетку на столик гониометра,
перпендикулярно оси коллиматора 2.
При этом в поле зрении трубы будет
наблюдаться ряд ярких и четких спектральных
линий паров ртути первого, второго и
последующих порядков по обе стороны от
центрального белого максимума (κ = 0).
Для определения угла φ необходимо
совместить вертикальную нить в окуляре
зрительной трубы с зеленой линией в
спектре первого порядка сначала слева
от нулевого максимума. По лимбу гониометра
и нониусу снять отсчет N1
(градусы и полуградусы ‑ по
лимбу против нуля нониуса, минуты ‑ по
нониусу). Затем перемещать зрительную
трубу по направлению к нулевому максимуму
и дальше, пока вертикальная нить не
совпадет с зеленой линией в спектре
первого порядка справа от нулевого
максимума. Вновь произвести отсчет N2.
Искомый угол дифракции
![]() .
.
Угол φ измерить три раза. По среднему
значению измеренного угла, зная длину
волны зеленой линии, рассчитать период
решетки по формуле (1).
2. Зная период решетки, рассчитать число
штрихов на 1 мм ширины решетки по
формуле (2).
3. Произвести измерение угла дифракции
для синей линии спектра (λ = 435,8нм).
Зная углы дифракции на, зеленой и синей
линиях и их длины волн, рассчитать
угловую дисперсию по формуле (3). Кроме
того, зная период решетки, рассчитать
угловую дисперсию по формуле (4). Сравнить
результаты двух способов расчета угловой
дисперсии.
4. Рассчитать разрешающую способность
решетки в спектре рассматриваемого
первого порядка по формуле (5). Найти
полное число штрихов решетки, зная число
штрихов на 1 мм и измерив ширину
нарезанной части решетки (с точностью
до 1 мм).
5. Вывести формулу погрешности для
периода решетки и определить относительную
и абсолютную ошибки расчета периода
решетки.
Расчеты :
|
Порядок |
угол |
|
|
к |
φ(л) |
φ(пр) |
|
Зеленая |
175, |
166, |
|
176, |
166, |
|
|
176 |
166, |
|
|
среднее |
176, |
166, |
|
порядок |
Угол |
|
|
к |
φ(л) |
φ(пр) |
|
фиолетовая |
175, |
168, |
|
175, |
168, |
|
|
174, |
168, |
|
|
Среднее |
175, |
168, |
![]()
![]()
![]()
|
Порядок |
угол |
|
|
к |
φ(л) |
φ(пр) |
|
зеленая |
1810, |
1610, |
|
1800, |
1610, |
|
|
1810, |
1610, |
|
|
среднее |
1810, |
1660, |
|
Порядок |
угол |
|
|
к |
φ(л) |
φ(пр) |
|
фиолетового |
1780, |
1730, |
|
1780, |
1730, |
|
|
1780, |
1730, |
|
|
среднее |
1780, |
1730, |
![]()
![]()
Зеленая линия
![]()
Фиолетовая линия
![]()
Из условия
возникновения главных интерференционных
максимумов решетки находим период
дифракционной решетки
![]() :
:
Для зеленой линии
спектра, к=1
порядка:
![]() м
м
Для зеленой линии
спектра, к=2
порядка:
![]()
м
Зная период решетки,
рассчитываем число штрихов, нанесенных
на 1 мм ширины решетки:![]() :
:
Для зеленой линии
спектра, к=1
порядка:![]()
Для зеленой линии
спектра, к=2
порядка:![]()
Угловой дисперсией
решетки называется величина, равная
производной от угла дифракции световых
волн по длине волны:![]()
![]()
![]()
Для первого порядка
зеленой и фиолетовой линии:
![]()
![]()
![]() м-1
м-1
Для второго порядка
зеленой и фиолетовой волн:
![]()
![]()
![]()
Формула для расчета
угловой дисперсии решетки может быть
получена при дифференцировании уравнения,
определяющего положение главных
максимумов
![]() ,
,
![]() .
.
Отсюда![]()
Для зеленой линии
спектра, к=1
порядка:
![]()
Для зеленой линии
спектра, к=2
порядка:
![]()
L
— дифракционной
решетки 30 мм
Для зеленой линии
спектра, к=1
порядка:
![]() шт.
шт.
Для зеленой линии
спектра, к=2
порядка:
![]() шт.
шт.
Разрешающая
способность решетки в спектре
рассматриваемого первого порядка:
![]()
к–порядок
спектра и полное число штрихов решетки
N:
Для зеленой линии
спектра, к=1
порядка:
![]()
Для зеленой линии
спектра, к=2
порядка:
![]()
Соседние файлы в папке лабы 2 курс 3 семестр
- #
- #
- #
Период дифракционной решетки


4.2
Средняя оценка: 4.2
Всего получено оценок: 169.
4.2
Средняя оценка: 4.2
Всего получено оценок: 169.
Для измерения длины световой волны нередко используется специальный оптический прибор, который называется дифракционной решеткой. Важнейшей характеристикой любой дифракционной решетки является ее период. Рассмотрим эту характеристику подробнее.
Дифракция на тонкой щели
Основой работы дифракционной решетки является способность световых волн к дифракции на тонких узких щелях. Дифракционная картина на одной узкой щели представляет собой чередование максимумов и минимумов освещенности, причем главный максимум имеет наибольшую интенсивность, а на остальных максимумах интенсивность освещенности быстро падает.

Если взять две тонких щели, расположенные рядом, то волны от щелей начинают интерферировать между собой, давая на дифракционной картине дополнительные минимумы, основные же максимумы становятся выражены более четко. При трех щелях дополнительных минимумов становится больше, а основные максимумы выделяют еще лучше.
Если взять большое количество периодических тонких щелей, в результате получаем дифракционную решетку.
Дифракционная решетка
Измерительная дифракционная решетка имеет, как правило, несколько тысяч штрихов на миллиметр, общее количество штрихов доходит до сотен тысяч. Дифракционная решетка может быть прозрачной или отражающей. В прозрачной решетке чередуются прозрачные и непрозрачные участки. В отражающей чередуются отражающие и неотражающие участки.
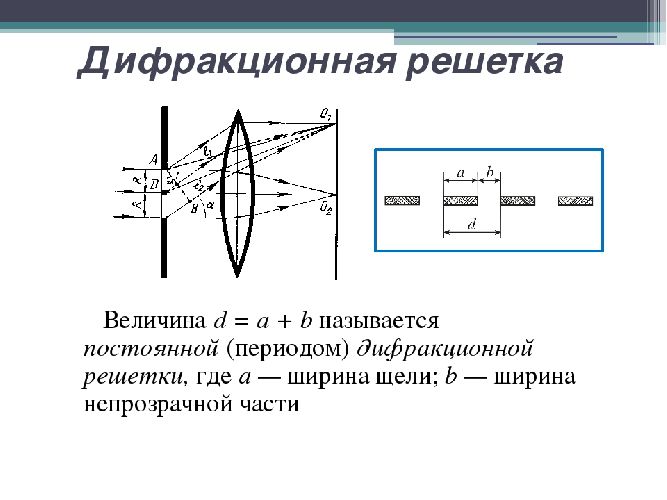
Расстояние между центрами соседних штрихов $d$ называется периодом дифракционной решетки и является важнейшей ее характеристикой. Формула периода дифракционной решетки:
$$d = S_{щели}+ S_{непрозр}$$
То есть период дифракционной решетки равен сумме ширины щели и ширине непрозрачной области между соседними щелями.
Если число щелей в решетке обозначить через $N$, то в создании интерференционной картины за решеткой участвует $N$ когерентных световых пучков. Положение главных максимумов определяется условием:
$$d sin varphi = k lambda$$
где:
- $varphi$ — угол отклонения для данного максимума;
- $lambda $ — длина волны света;
- $k$ — 0,1,2… — номер максимума.
Между главными максимумами на дифракционной картине имеется $N-1$ минимумов, максимумы же имеют интенсивность во столько же раз больше (по сравнению с дифракцией на одиночной щели).
Наиболее интенсивным остается центральный максимум ($k=0$). Кроме того, поскольку угол отклонения зависит от длины волны, дифракционная решетка разлагает белый свет в спектр.
Измерение длины волны с помощью дифракционной решетки
Дифракционная решетка позволяет очень точно определять длину волны падающего пучка. Для этого достаточно измерить угол $varphi$ отклонения, который соответствует некоторому максимуму.
При этом важным параметром является разрешающая способность дифракционной решетки $R$. Разрешающая способность прямо пропорциональна количеству штрихов и порядку максимума:
$$R=kN$$
Разрешающая способность показывает, во сколько раз длина волны больше абсолютной погрешности ее определения.


Что мы узнали?
Дифракционная решетка — это совокупность непрозрачных штрихов и прозрачных участков. Период дифракционной решетки — это сумма ширины прозрачного участка и ширины штриха. Дифракционная решетка применяется для измерения длины волны падающего света. Важнейшими параметрами дифракционной решетки является период и разрешающая способность.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.2
Средняя оценка: 4.2
Всего получено оценок: 169.
А какая ваша оценка?




