Как найти расстояние через скорость света

Как найти расстояние через скорость света

Unit Converter

Enter the total time of travel at light speed (s) into the Light Speed Distance Calculator. The calculator will evaluate and display the Light Speed Distance. This calculator can also evaluate the time if given the distance.

  • All Distance Calculators
  • Warp Speed Calculator
  • Speed of Sound Calculator
  • Milliradian Distance Calculator

Light Speed Distance Formula

The following formula is used to calculate the Light Speed Distance. 

  • Where LSD is the Light Speed Distance (m)
  • T is the total time of travel at light speed (s) 
  • LS is the speed of light (299,792,458 m/s)

To calculate light speed distance, multiply the total time of light speed travel by the speed of light.

How to Calculate Light Speed Distance?

The following example problems outline how to calculate Light Speed Distance.

Example Problem #1:

  1. First, determine the total time of travel at light speed (s). 
    • The total time of travel at light speed (s) is given as: 3s.
  2. Finally, calculate the Light Speed Distance using the equation above: 

LSD = LS * T

The values given above are inserted into the equation below and the solution is calculated:

LSD = 299,792,458 * 3 = 899377374 (m)

Example Problem #2: 

For this problem, the variables needed are provided below:

total time of travel at light speed (s) = 6

This example problem is a test of your knowledge on the subject. Use the calculator above to check your answer. 

LSD = LS * T = ?

light speed distance calculator

Источник


Загрузить PDF


Загрузить PDF

Многие полагают, что световой год — это единица измерения времени, потому что здесь присутствует слово «год». На самом деле световой год является единицей измерения расстояния. Например, если вы когда-либо говорили другу, что находитесь в пяти минутах ходьбы от него, вы использовали время как единицу измерения расстояния.[1]
 Во вселенной расстояние между небесными телами огромно, поэтому астрономы пользуются световым годом, потому что эта единица измерения расстояния во много раз больше километра или метра. Чтобы вычислить световой год (в километрах), нужно перемножить скорость света и количество секунд в году.

  1. Изображение с названием Calculate a Light Year Step 1

    1

    Запомните определение светового года. Светлый год — это единица измерения расстояния, равная дистанции, которую проходит луч света за один год. Расстояния во вселенной настолько велики, что астрономы пользуются световыми годами. Если расстояния во вселенной измерять в километрах, придется работать с огромными и неудобными числами.[2]

    • В астрономии используется еще одна единица измерения расстояния — парсек. Один парсек равен 3,26 световых лет. Эта единица измерения также служит для упрощения вычислений и представления расстояний в астрономии.[3]

  2. Изображение с названием Calculate a Light Year Step 2

    2

    Запишите формулу для вычисления расстояния. Из физики известно, что расстояние равно произведению скорости на время: d = v x t. (Расстояние «d» также обозначается как «S»). Таким образом, световой год = (скорость света) x (один год). Скорость света обозначается как «c», поэтому формулу можно записать так: d = c x t, где d — расстояние, c — скорость света, t — время.[4]

    • Чтобы вычислить значение светового года в километрах, скорость света должна измеряться в километрах в секунду (км/с).
    • Также нам понадобится количество секунд в одном году (365 дней).

  3. Изображение с названием Calculate a Light Year Step 3

    3

    Запишите скорость света (в вакууме). Она равна 299792 км/с ≈ 300000 км/с.[5]

    • Скорость света можно записать в экспоненциальном формате: 3 x 105 км/с.

  4. Изображение с названием Calculate a Light Year Step 4

    4

    Вычислите количество секунд в году. Для этого нужно перемножить количество дней в году, количество часов в одном дне, количество минут в одном часе и количество секунд в одной минуте.

    • 1 год x 365 дней/год x 24 часа/день x 60 минут/час x 60 секунд/минута = 31536000 секунд.[6]
    • Это число также можно записать в экспоненциальном формате: 3,154 x 107.

  5. Изображение с названием Calculate a Light Year Step 5

    5

    Подставьте значения в формулу. Теперь, когда вам известны значения скорости света и времени, подставьте их в формулу d = c x t и вычислите световой год. Вместо «с» подставьте 3 x 105 км/с, а вместо «t» подставьте 3,15 x 107 с.[7]

    • d = c x t
    • d = (3 x 105) x (3,154 x 107)
    • d = 9,5 x 1012 км, то есть 9,5 триллионов километров.

  6. Изображение с названием Calculate a Light Year Step 6

    6

    Вычислите расстояние в метрах. Чтобы вычислить световой год в метрах, вместо скорости света в километрах в секунду подставьте значение скорости света в метрах в секунду: с = 3 x 108 м/с. Количество секунд в году останется прежним.[8]

    • d = c x t
    • d = (3 x 108) x (3,154 x 10 7)
    • d = 9,5 x 1015 м.

    Реклама

  1. Изображение с названием Calculate a Light Year Step 7

    1

    Определите расстояние, которое нужно преобразовать. Лучше, если оно будет представлено в километрах. Нет смысла преобразовывать расстояние, измеренное в меньших единицах (например, в метрах или сантиметрах), но вы можете попробовать, если вам это интересно.

    • Чтобы преобразовать метры в километры, разделите значение в метрах на 1000.[9]
    • Чтобы преобразовать сантиметры в километры, разделите значение в сантиметрах на 100000.

  2. Изображение с названием Calculate a Light Year Step 8

    2

    Определите правильный коэффициент преобразования. Выясните, в каких единицах измерения представлено расстояние, которое нужно преобразовать в световые годы. Для расстояний, измеренных в километрах и метрах, коэффициент преобразования будет разным.

    • Чтобы километры преобразовать в световые годы, значение в километрах разделите на 9,5 x 1012.[10]
    • Чтобы метры преобразовать в световые годы, значение в метрах разделите на 9,5 x 1015.[11]

  3. Изображение с названием Calculate a Light Year Step 9

    3

    Исходное расстояние разделите на коэффициент преобразования. Теперь, когда вы знаете коэффициенты преобразования, исходное расстояние разделите на соответствующий коэффициент, чтобы представить расстояние в световых годах. Если вы работаете с большими числами, записывайте их в экспоненциальном формате.

    • Например: космический объект находится на расстоянии 14,2 x 1014 км от Земли. Представьте это расстояние в световых годах.
    • Здесь исходное значение нужно разделить на следующий коэффициент преобразования: 9,5 x 1012.
    • Разделите: 14,2 x 1014 / 9,5 x 1012 = 1,5 x 102 = 150 световых лет.
    • Космический объект находится на расстоянии 150 световых лет от Земли.

  4. Изображение с названием Calculate a Light Year Step 10

    4

    Если вы не справляетесь с задачей, попросите о помощи. Помощь можно получить со стороны одноклассников (однокурсников) или учителя (преподавателя). Также дополнительную информацию можно поискать в интернете и в учебнике. Не стесняйтесь обращаться за помощью, если она вам нужна.

    • Помните, что когда вы решаете задачу, помощь можно получить разными способами.

    Реклама

Об этой статье

Эту страницу просматривали 20 012 раз.

Была ли эта статья полезной?

Источник
Указано расстояние от Солнца до Земли, равное 150 миллионам километров.

солнечному свету требуется в среднем[Прим. 1] 8 минут 17 секунд, чтобы достигнуть Земли
точные значения
метров в секунду 299 792 458
Планковских единиц 1
приблизительные значения
километров в секунду 300 000
километров в час 1,08 млрд
астрономических единиц в сутки 173
приблизительное время путешествия светового сигнала
расстояние время
один метр 3,3 нс
один километр 3,3 мкс
от геостационарной орбиты до Земли 119 мс
длина экватора Земли 134 мс
от Луны до Земли 1,255 с
от Солнца до Земли (1 а. е.) 8,3 мин.
от Вояджера-1 до Земли 22 часа 05 минут (на март 2023)[1]
один световой год 1 год
один парсек 3,26 лет
от Проксимы Центавра до Земли 4,24 лет
от Альфы Центавра до Земли 4,37 лет
от ближайшей галактики (Карликовой галактики в Большом Псе) до Земли 25 000 лет
через Млечный Путь 100 000 лет
от галактики Андромеды до Земли 2,5 млн лет
от самой удалённой известной галактики до Земли 13,4 млрд лет[2]

Ско́рость све́та в вакууме[Прим. 2] — абсолютная величина скорости распространения электромагнитных волн, в точности равная 299 792 458 м/с (или приблизительно 3×108 м/с). В физике традиционно обозначается латинской буквой «c» (произносится как «цэ»), от лат. celeritas (скорость).

Скорость света в вакууме — фундаментальная постоянная, не зависящая от выбора инерциальной системы отсчёта (ИСО). Она относится к фундаментальным физическим постоянным, которые характеризуют не просто отдельные тела или поля, а свойства геометрии пространства-времени в целом[3]. Из постулата причинности (любое событие может оказывать влияние только на события, происходящие позже него, и не может оказывать влияние на события, произошедшие раньше него[4][5][6]) и постулата специальной теории относительности о независимости скорости света в вакууме от выбора инерциальной системы отсчёта (скорость света в вакууме одинакова во всех системах координат, движущихся прямолинейно и равномерно друг относительно друга[7]) следует, что скорость любого сигнала и элементарной частицы не может превышать скорость света[8][9][6]. Таким образом, скорость света в вакууме — предельная скорость движения частиц и распространения взаимодействий.

В вакууме[править | править код]

Время распространения светового луча в масштабной модели Земля-Луна. Для преодоления расстояния от поверхности Земли до поверхности Луны свету требуется 1,255 с

Наиболее точное измерение скорости света 299 792 458 ± 1,2 м/с на основе эталонного метра было проведено в 1975 году[Прим. 3].

На данный момент считают, что скорость света в вакууме — фундаментальная физическая постоянная, по определению, точно равная 299 792 458 м/с, или 1 079 252 848,8 км/ч. Точность значения связана с тем, что с 1983 года метр в Международной системе единиц (СИ) определён как расстояние, которое проходит свет в вакууме за промежуток времени, равный 1 / 299 792 458 секунды[11].

В планковской системе единиц скорость света в вакууме равна 1. Можно сказать, что свет проходит 1 планковскую длину за планковское время, но в планковской системе единиц скорость света c является основной единицей, а единицы времени и расстояния — производными (в отличие от СИ, где основными являются метр и секунда).

В природе со скоростью света распространяются (в вакууме):

Массивные частицы могут иметь скорость, приближающуюся почти вплотную к скорости света[Прим. 4], но всё же не достигающую её точно. Например, околосветовую скорость, лишь на 3 м/сек меньше скорости света, имеют массивные частицы (протоны), полученные на ускорителе (Большой адронный коллайдер) или входящие в состав космических лучей.[источник не указан 1988 дней]

В современной физике считается хорошо обоснованным утверждение, что причинное воздействие не может переноситься со скоростью, большей скорости света в вакууме (в том числе посредством переноса такого воздействия каким-либо физическим телом). Существует, однако, проблема «запутанных состояний» частиц, которые, судя по всему, «узнают» о состоянии друг друга мгновенно. Однако и в этом случае сверхсветовой передачи информации не происходит, поскольку для передачи информации таким способом необходимо привлечь дополнительный классический канал передачи со скоростью света[Прим. 5].

Хотя в принципе движение каких-то объектов со скоростью, большей скорости света в вакууме, вполне возможно, однако это могут быть, с современной точки зрения, только такие объекты, которые не могут быть использованы для переноса информации с их движением (например, солнечный зайчик в принципе может двигаться по стене со скоростью, большей скорости света, но никак не может быть использован для передачи информации с такой скоростью от одной точки стены к другой)[13]Перейти к разделу «#Сверхсветовое движение».

В прозрачной среде[править | править код]

Скорость света в прозрачной среде — скорость, с которой свет распространяется в среде, отличной от вакуума. В среде, обладающей дисперсией, различают фазовую и групповую скорость.

Фазовая скорость связывает частоту и длину волны монохроматического света в среде ({displaystyle lambda ={frac {c}{nu }}}). Эта скорость обычно (но не обязательно) меньше c. Отношение скорости света в вакууме к фазовой скорости света в среде называется показателем преломления среды. Если угловая частота omega волны в среде зависит от волнового числа k нелинейным образом, то групповая скорость равняется первой производной {displaystyle {frac {partial omega }{partial k}}}, в отличие от фазовой скорости {displaystyle {frac {omega }{k}}}.[14]

Групповая скорость света определяется как скорость распространения биений между двумя волнами с близкой частотой и в равновесной среде всегда меньше c. Однако в неравновесных средах, например, сильно поглощающих, она может превышать c. При этом, однако, передний фронт импульса всё равно движется со скоростью, не превышающей скорости света в вакууме. В результате сверхсветовая передача информации остаётся невозможной.

Арман Ипполит Луи Физо на опыте доказал, что движение среды относительно светового луча также способно влиять на скорость распространения света в этой среде.

Вывод скорости света из уравнений Максвелла[править | править код]

Уравнения Максвелла в дифференциальной форме:

{displaystyle operatorname {rot} mathbf {E} =-{frac {partial mathbf {B} }{partial t}}}

{displaystyle operatorname {rot} mathbf {H} =mathbf {j} +{frac {partial mathbf {D} }{partial t}}}

{displaystyle operatorname {div} mathbf {B} =0}

{displaystyle operatorname {div} mathbf {D} =rho }

{displaystyle mathbf {B} =mu mu _{0}mathbf {H} }

{displaystyle mathbf {D} =varepsilon varepsilon _{0}mathbf {E} }

mathbf {E} – вектор напряженности электрического поля

mathbf {H} – вектор напряженности магнитного поля

mathbf {B} – вектор магнитной индукции

mathbf {D} – вектор электрической индукции

mu – магнитная проницаемость

mu _{0} – магнитная постоянная

varepsilon – электрическая проницаемость

varepsilon _{0} – электрическая постоянная

mathbf {j} – плотность тока

rho – плотность заряда

operatorname{rot} – ротор, дифференциальный оператор, {displaystyle operatorname {rot} mathbf {E} =mathbf {nabla } times mathbf {E} ={begin{vmatrix}mathbf {i} &mathbf {j} &mathbf {k} \{frac {partial }{partial x}}&{frac {partial }{partial y}}&{frac {partial }{partial z}}\E_{x}&E_{y}&E_{z}end{vmatrix}}=left({frac {partial E_{z}}{partial y}}-{frac {partial E_{y}}{partial z}}right)mathbf {i} +left({frac {partial E_{x}}{partial z}}-{frac {partial E_{z}}{partial x}}right)mathbf {j} +left({frac {partial E_{y}}{partial x}}-{frac {partial E_{x}}{partial y}}right)mathbf {k} }

{displaystyle operatorname {div} } – дивергенция, дифференциальный оператор, {displaystyle operatorname {div} mathbf {E} =nabla cdot mathbf {E} ={frac {partial E_{x}}{partial x}}+{frac {partial E_{y}}{partial y}}+{frac {partial E_{z}}{partial z}}}

Delta – оператор Лапласа, {displaystyle Delta ={frac {partial ^{2}}{partial x^{2}}}+{frac {partial ^{2}}{partial y^{2}}}+{frac {partial ^{2}}{partial z^{2}}}}, {displaystyle Delta mathbf {E} =Delta E_{x}mathbf {i} +Delta E_{y}mathbf {j} +Delta E_{z}mathbf {k} }

Для электромагнитной волны mathbf {j} =0, {displaystyle rho =0} , поэтому:

{displaystyle operatorname {rot} mathbf {H} ={frac {partial mathbf {D} }{partial t}}}

{displaystyle operatorname {div} mathbf {D} =varepsilon varepsilon _{0}operatorname {div} mathbf {E} =0}

Согласно свойству ротора векторного поля {displaystyle operatorname {rot} operatorname {rot} mathbf {E} =mathbf {operatorname {grad} } (operatorname {div} mathbf {E} )-Delta E}. Подставив сюда {displaystyle operatorname {rot} mathbf {E} =-{frac {partial mathbf {B} }{partial t}}} и {displaystyle operatorname {div} mathbf {E} =0} , получим:

{displaystyle operatorname {rot} left(-{frac {partial mathbf {B} }{partial t}}right)=-Delta mathbf {E} }

{displaystyle Delta mathbf {E} =operatorname {rot} {frac {partial mathbf {B} }{partial t}}}

{displaystyle Delta mathbf {E} ={frac {partial }{partial t}}operatorname {rot} mathbf {B} }

{displaystyle Delta mathbf {E} =mu mu _{0}{frac {partial }{partial t}}operatorname {rot} mathbf {H} } подставляем сюда из уравнений Максвелла {displaystyle operatorname {rot} mathbf {H} ={frac {partial mathbf {D} }{partial t}}} , получаем:

{displaystyle Delta mathbf {E} =mu mu _{0}{frac {partial }{partial t}}left({frac {partial mathbf {D} }{partial t}}right)}

{displaystyle Delta mathbf {E} =mu mu _{0}{partial ^{2}mathbf {D} over partial t^{2}}}

{displaystyle Delta mathbf {E} =mu mu _{0}varepsilon varepsilon _{0}{partial ^{2}mathbf {E} over partial t^{2}}} [3] (1)

Уравнение волны:

{displaystyle square mathbf {E} =0}, где {displaystyle square } – оператор Д’Аламбера, {displaystyle square =Delta -{frac {1}{v^{2}}}{frac {partial ^{2}}{partial t^{2}}}}

{displaystyle Delta mathbf {E} -{frac {1}{c^{2}}}{frac {partial ^{2}mathbf {E} }{partial t^{2}}}=0}

{displaystyle Delta mathbf {E} ={frac {1}{c^{2}}}{frac {partial ^{2}mathbf {E} }{partial t^{2}}}} (2)

Подставляем (1) в (2), находим скорость:

{displaystyle c=1/{sqrt {mu mu _{0}epsilon epsilon _{0}}}}

{displaystyle epsilon _{0}=8{,}854;187;812times 10^{-12}} с{displaystyle ^{4}}A{displaystyle ^{2}}/м{displaystyle ^{3}}кг

{displaystyle mu _{0}=1{,}256;637;062times 10^{-6}} кг м/с{displaystyle ^{2}}А{displaystyle ^{2}}

В вакууме {displaystyle mu =1}, {displaystyle varepsilon =1}

{displaystyle c=299;792;458} м/с

Фундаментальная роль в физике[править | править код]

Лоренц-фактор gamma как функция скорости. Он растет от 1 (для нулевой скорости) до бесконечности (с приближением v к c)

Скорость, с которой световые волны распространяются в вакууме, не зависит ни от движения источника волн, ни от системы отсчёта наблюдателя[Прим. 6]. Эйнштейн постулировал такую инвариантность скорости света в 1905 году[15]. Он пришёл к этому выводу на основании теории электромагнетизма Максвелла и доказательства отсутствия светоносного эфира[16].

Инвариантность скорости света неизменно подтверждается множеством экспериментов[17]. Существует возможность проверить экспериментально лишь то, что скорость света в «двустороннем» эксперименте (например, от источника к зеркалу и обратно) не зависит от системы отсчёта, поскольку невозможно измерить скорость света в одну сторону (например, от источника к удалённому приёмнику) без дополнительных договоренностей относительно того, как синхронизировать часы источника и приёмника. Однако, если применить для этого синхронизацию Эйнштейна, односторонняя скорость света становится равной двусторонней по определению[18][19].

Специальная теория относительности исследует последствия инвариантности c в предположении, что законы физики одинаковы во всех инерциальных системах отсчёта[20][21]. Одним из последствий является то, что c — это та скорость, с которой должны двигаться в вакууме все безмассовые частицы и волны (в частности, и свет).

Специальная теория относительности имеет много экспериментально проверенных последствий, которые противоречат интуиции[22]. Такие последствия включают: эквивалентность массы и энергии (E_{0}=mc^{2}), сокращение длины (сокращение объектов во время движения)[Прим. 7] и замедление времени (движущиеся часы идут медленнее). Коэффициент gamma , показывающий, во сколько раз сокращается длина и замедляется время, известен как фактор Лоренца (Лоренц-фактор)

{displaystyle gamma ={frac {1}{sqrt {1-{frac {v^{2}}{c^{2}}}}}},}

где v — скорость объекта. Для скоростей гораздо меньших, чем c (например, для скоростей, с которыми мы имеем дело в быту) разница между gamma и 1 настолько мала, что ею можно пренебречь. В этом случае специальная теория относительности хорошо аппроксимируется относительностью Галилея. Но на релятивистских скоростях разница увеличивается и стремится к бесконечности при приближении v к c.

Объединение результатов специальной теории относительности требует выполнения двух условий: (1) пространство и время являются единой структурой, известной как пространство-время (где c связывает единицы измерения пространства и времени), и (2) физические законы удовлетворяют требованиям особой симметрии, которая называется инвариантность Лоренца (Лоренц-инвариантность), формула которой содержит параметр c[25]. Инвариантность Лоренца встречается повсеместно в современных физических теориях, таких как квантовая электродинамика, квантовая хромодинамика, стандартная модель физики элементарных частиц и общая теория относительности. Таким образом, параметр c встречается повсюду в современной физике и появляется во многих смыслах, которые не имеют отношения собственно к свету. Например, общая теория относительности предполагает, что гравитация и гравитационные волны распространяются со скоростью c[26][27]. В неинерциальных системах отсчёта (в гравитационно искривлённом пространстве или в системах отсчёта, движущихся с ускорением), локальная скорость света также является постоянной и равна c, однако скорость света вдоль траектории конечной длины может отличаться от c в зависимости от того, как определено пространство и время[28].

Считается, что фундаментальные константы, такие как c, имеют одинаковое значение во всём пространстве-времени, то есть они не зависят от места и не меняются со временем. Однако некоторые теории предполагают, что скорость света может изменяться со временем[29][30]. Пока нет убедительных доказательств таких изменений, но они остаются предметом исследований[31][32].

Кроме того, считается, что скорость света изотропна, то есть не зависит от направления его распространения. Наблюдения за излучением ядерных энергетических переходов как функции от ориентации ядер в магнитном поле (эксперимент Гугса — Древера), а также вращающихся оптических резонаторов (эксперимент Майкельсона — Морли и его новые вариации), наложили жёсткие ограничения на возможность двусторонней анизотропии[33][34].

В ряде естественных систем единиц скорость света является единицей измерения скорости[35]. В планковской системе единиц, также относящейся к естественным системам, она служит в качестве единицы скорости и является одной из основных единиц системы.

Верхний предел скорости[править | править код]

Согласно специальной теории относительности, энергия объекта с массой покоя m и скоростью v равна {displaystyle gamma mc^{2}}, где gamma  — определённый выше фактор Лоренца. Когда v равна нулю, gamma равен единице, что приводит к известной формуле эквивалентности массы и энергии E=mc^{2}. Поскольку фактор gamma приближается к бесконечности с приближением v к c, ускорение массивного объекта до скорости света потребует бесконечной энергии. Скорость света — это верхний предел скорости для объектов с ненулевой массой покоя. Это экспериментально установлено во многих тестах релятивистской энергии и импульса[36].

Относительность одновременности возникающая при преобразованиях Лоренца. Три цветные системы отсчета связаны с тремя разными наблюдателями, движущимися относительно оси x. По отношению к зеленому наблюдателю красный движется со скоростью +0,28c, а синий с −0,52c. Пусть в ситеме отсчета зеленого наблюдателя событие «B» произошло одновременно с событием «A», тогда для синего событие «B» произойдет раньше, чем «A», а для красного наоборот — «A» раньше, чем «B».

Вообще информация или энергия не могут передаваться в пространстве быстрее, чем со скоростью света. Один из аргументов в пользу этого следует из контринтуитивного заключения специальной теории относительности, известного как относительность одновременности. Если пространственное расстояние между двумя событиями А и В больше, чем промежуток времени между ними, умноженный на c, то существуют такие системы отсчёта, в которых А предшествует B, и другие, в которых B предшествует А, а также такие, в которых события А и B одновременны. В результате, если объект двигался бы быстрее скорости света относительно некоторой инерциальной системы отсчёта, то в другой системе отсчёта он бы путешествовал назад во времени, и принцип причинности был бы нарушен[Прим. 8][38]. В такой системе отсчёта «следствие» можно было бы наблюдать раньше его «первопричины». Такое нарушение причинности никогда не наблюдалось[19]. Оно также может приводить к парадоксам, таким как тахионный антителефон[39].

История измерений скорости света[править | править код]

Античные учёные, за редким исключением, считали скорость света бесконечной[40]. В Новое время этот вопрос стал предметом дискуссий. Галилей и Гук допускали, что она конечна, хотя и очень велика, в то время как Кеплер, Декарт и Ферма по-прежнему отстаивали бесконечность скорости света.

Наблюдения при измерении скорости света при затмениях Ио Юпитером

Первую оценку скорости света произвёл Олаф Рёмер (1676). Он заметил, что, когда Земля на своей орбите находится дальше от Юпитера, затмения Юпитером спутника Юпитера Ио запаздывают по сравнению с расчётами на 22 минуты. Отсюда он получил значение для скорости света около 220 000 км/с — неточное значение, но близкое к истинному. В 1676 году он сделал сообщение в Парижской Академии, но не опубликовал свои результаты в виде формальной научной работы. Поэтому научное сообщество приняло идею о конечной скорости света только полвека спустя[41], когда в 1728 году открытие аберрации позволило Дж. Брэдли подтвердить конечность скорости света и уточнить её оценку. Полученное Брэдли значение составило 308 000 км/с[42][43].

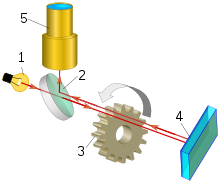
Схема опыта Физо по определению скорости света.
1 — Источник света.
2 — Светоделительное полупрозрачное зеркало.
3 — Зубчатое колесо-прерыватель светового пучка.
4 — Удалённое зеркало.
5 — Телескопическая труба.

Впервые измерения скорости света, основанные на определении времени прохождения светом точно измеренного расстояния в земных условиях, выполнил в 1849 году А. И. Л. Физо. В своих экспериментах Физо использовал разработанный им «метод прерываний», при этом расстояние, преодолеваемое светом в опытах Физо, составляло 8,63 км. Полученное в результате выполненных измерений значение оказалось равным 313 300 км/с.
В дальнейшем метод прерываний значительно усовершенствовали и его использовали для измерений М. А. Корню (1876 г.), А. Ж. Перротен (1902 г.) и Э. Бергштранд[sv]. Измерения, выполненные Э. Бергштрандом в 1950 году, дали для скорости света значение 299 793,1 км/с, при этом точность измерений была доведена до 0,25 км/с[42].

Другой лабораторный метод («метод вращающегося зеркала»), идея которого была высказана в 1838 году Ф. Араго, в 1862 году осуществил Леон Фуко. Измеряя малые промежутки времени с помощью вращающегося с большой скоростью (512 об/с) зеркала, он получил для скорости света значение 298 000 км/с с погрешностью 500 км/с. Длина базы в экспериментах Фуко была сравнительно небольшой — двадцать метров[43][42][44][45][46]. В последующем за счёт совершенствования техники эксперимента, увеличения используемой базы и более точного определения её длины точность измерений с помощью метода вращающегося зеркала была существенно повышена. Так, С. Ньюком в 1891 году получил значение 299 810 км/с с погрешностью 50 км/с, а А. А. Майкельсону в 1926 году удалось понизить погрешность до 4 км/с и получить для скорости величину 299 796 км/с. В своих экспериментах Майкельсон использовал базу, равную 35 373,21 м[42].

Дальнейший прогресс был связан с появлением мазеров и лазеров, которые отличаются очень высокой стабильностью частоты излучения, что позволило определять скорость света одновременным измерением длины волны и частоты их излучения. В начале 1970-х годов погрешность измерений скорости света приблизилась к 1 м/с[47]. После проверки и согласования результатов, полученных в различных лабораториях, XV Генеральная конференция по мерам и весам в 1975 году рекомендовала использовать в качестве значения скорости света в вакууме величину, равную 299 792 458 м/с, с относительной погрешностью (неопределённостью) 4⋅10-9[48], что соответствует абсолютной погрешности 1,2 м/с[49].

Существенно, что дальнейшее повышение точности измерений стало невозможным в силу обстоятельств принципиального характера: ограничивающим фактором стала величина неопределённости реализации определения метра, действовавшего в то время. Проще говоря, основной вклад в погрешность измерений скорости света вносила погрешность «изготовления» эталона метра, относительное значение которой составляло 4⋅10-9[49]. Исходя из этого, а также учитывая другие соображения, XVII Генеральная конференция по мерам и весам в 1983 году приняла новое определение метра, положив в его основу рекомендованное ранее значение скорости света и определив метр как расстояние, которое проходит свет в вакууме за промежуток времени, равный 1 / 299 792 458 секунды[50].

Сверхсветовое движение[править | править код]

Из специальной теории относительности следует, что превышение скорости света физическими частицами (массивными или безмассовыми) нарушило бы принцип причинности — в некоторых инерциальных системах отсчёта оказалась бы возможной передача сигналов из будущего в прошлое. Однако теория не исключает для гипотетических частиц, не взаимодействующих с обычными частицами[51], движение в пространстве-времени со сверхсветовой скоростью.

Гипотетические частицы, движущиеся со сверхсветовой скоростью, называются тахионами. Математически движение тахионов описывается преобразованиями Лоренца как движение частиц с мнимой массой. Чем выше скорость этих частиц, тем меньше энергии они несут, и наоборот, чем ближе их скорость к скорости света, тем больше их энергия — так же, как и энергия обычных частиц, энергия тахионов стремится к бесконечности при приближении к скорости света. Это самое очевидное следствие преобразования Лоренца, не позволяющее массивной частице (как с вещественной, так и с мнимой массой) достичь скорости света — сообщить частице бесконечное количество энергии просто невозможно.

Следует понимать, что, во-первых, тахионы — это класс частиц, а не один вид частиц, и во-вторых, тахионы не нарушают принцип причинности, если они никак не взаимодействуют с обычными частицами[51].

Обычные частицы, движущиеся медленнее света, называются тардионами. Тардионы не могут достичь скорости света, а только лишь сколь угодно близко подойти к ней, так как при этом их энергия становится неограниченно большой. Все тардионы обладают массой, в отличие от безмассовых частиц, называемых люксонами. Люксоны в вакууме всегда движутся со скоростью света, к ним относятся фотоны, глюоны и гипотетические гравитоны.

C 2006 года показано, что в так называемом эффекте квантовой телепортации кажущееся взаимовлияние частиц распространяется быстрее скорости света. Например, в 2008 г. исследовательская группа доктора Николаса Гизена (Nicolas Gisin) из университета Женевы, исследуя разнесённые на 18 км в пространстве запутанные фотонные состояния, показала, что это кажущееся «взаимодействие между частицами осуществляется со скоростью, примерно в сто тысяч раз большей скорости света». Ранее также обсуждался так называемый «парадокс Хартмана[en]» — кажущаяся сверхсветовая скорость при туннельном эффекте[52]. Анализ этих и подобных результатов показывает, что они не могут быть использованы для сверхсветовой передачи какого-либо несущего информацию сообщения или для перемещения вещества[53].

В результате обработки данных эксперимента OPERA[54], набранных с 2008 по 2011 год в лаборатории Гран-Сассо совместно с ЦЕРН, было зафиксировано статистически значимое указание на превышение скорости света мюонными нейтрино[55]. Сообщение об этом сопровождалось публикацией в архиве препринтов[56]. Полученные результаты специалисты подвергли сомнению, поскольку они не согласуются не только с теорией относительности, но и с другими экспериментами с нейтрино[57]. В марте 2012 года в том же тоннеле были проведены независимые измерения, и сверхсветовых скоростей нейтрино они не обнаружили[58]. В мае 2012 года OPERA провела ряд контрольных экспериментов и пришла к окончательному выводу, что причиной ошибочного предположения о сверхсветовой скорости стал технический дефект (плохо вставленный разъём оптического кабеля)[59].

См. также[править | править код]

  • Переменная скорость света
  • Односторонняя скорость света
  • Световой год
  • Скорость звука
  • Планковские единицы
  • Рациональная система единиц

Примечания[править | править код]

Комментарии
  1. ↑ От поверхности Солнца — от 8 мин 8,3 с в перигелии до 8 мин 25 с в афелии.
  2. ↑ Скорость распространения светового импульса в среде отличается от скорости его распространения в вакууме (меньше, чем в вакууме), и может быть различной для разных сред. Когда говорят просто о скорости света, обычно подразумевается именно скорость света в вакууме; если же говорят о скорости света в среде, это, как правило, оговаривается явно.
  3. ↑ В настоящее время наиболее точные методы измерения скорости света основаны на независимом определении значений длины волны lambda и частоты nu света или другого электромагнитного излучения и последующего расчёта в соответствии с равенством {displaystyle c=lambda nu }[10].
  4. ↑ См. например «Частица Oh-My-God».
  5. ↑ Аналогом может быть посылка наудачу двух заклеенных конвертов с белой и чёрной бумагой в разные места. Открытие одного конверта гарантирует, что во втором будет лежать второй лист — если первый чёрный, то второй белый, и наоборот. Эта «информация» может распространяться быстрее скорости света — ведь вскрыть второй конверт можно в любое время, и там всегда будет этот второй лист. При этом принципиальная разница с квантовым случаем состоит только в том, что в квантовом случае до «открытия конверта»-измерения состояние листа внутри принципиально неопределённо, как у кота Шрёдингера, и там может оказаться любой лист.
  6. ↑ Однако частота света зависит от движения источника света относительно наблюдателя, благодаря эффекту Доплера.
  7. ↑ Помимо того, что измеряемые движущиеся объекты оказываются короче вдоль линии относительного движения, они также выглядят повёрнутыми. Этот эффект, известный как вращение Террелла, связан с разницей во времени между пришедшими к наблюдателю сигналами от разных частей объекта[23][24].
  8. ↑ Считается, что эффект Шарнхорста позволяет сигналам распространяться немногим выше c, но особые условия, при которых эффект может возникать, мешают применить этот эффект для нарушения принципа причинности[37].
Источники
  1. ↑ Where Are the Voyagers – NASA Voyager. Voyager – The Interstellar Mission. Jet Propulsion Laboratory, California Istitute of Technology. Дата обращения: 12 июля 2011. Архивировано 3 февраля 2012 года.
  2. ↑ Amos, Jonathan. Hubble sets new cosmic distance record, BBC News (3 марта 2016). Архивировано 4 марта 2016 года. Дата обращения: 3 марта 2016.
  3. ↑ 1 2 Is The Speed of Light Everywhere the Same? Дата обращения: 10 сентября 2015. Архивировано 8 сентября 2015 года.
  4. ↑ Начала теоретической физики, 2007, с. 169.
  5. ↑ Неванлинна, 1966, с. 122.
  6. ↑ 1 2 Чудинов Э. М. Теория относительности и философия. — М.: Политиздат, 1974. — С. 222—227.
  7. ↑ Эволюция физики, 1948, с. 167.
  8. ↑ Начала теоретической физики, 2007, с. 170.
  9. ↑ Неванлинна, 1966, с. 184.
  10. ↑ Сажин М. В. Скорость света // Физика космоса : маленькая энциклопедия / Гл. ред. Р. А. Сюняев. — Изд. 2-е, перераб. и доп. — М.: Советская энциклопедия, 1986. — С. 622. — 783 с. — 70 000 экз.
  11. ↑ ГОСТ 8.417-2002. Государственная система обеспечения единства измерений. Единицы величин. Дата обращения: 14 августа 2012. Архивировано из оригинала 10 ноября 2012 года.
  12. ↑ Abbott B. P. et al. (LIGO Scientific Collaboration, Virgo Collaboration, Fermi Gamma-ray Burst Monitor, and INTEGRAL). Gravitational Waves and Gamma-Rays from a Binary Neutron Star Merger: GW170817 and GRB 170817A // The Astrophysical Journal. — 2017. — Vol. 848. — P. L13. — doi:10.3847/2041-8213/aa920c. [исправить]
  13. ↑ Болотовский Б. М., Гинзбург В. Л. Эффект Вавилова — Черенкова и эффект Допплера при движении источников со скоростью больше скорости света в вакууме // Успехи физических наук. — Российская академия наук, 1972. — Т. 106, № 4. — С. 577—592. Архивировано 25 сентября 2013 года.
  14. ↑ Миллер М. А., Суворов E. В. Групповая скорость // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1988. — Т. 1. — С. 544—545. — 704 с.
  15. ↑ Stachel, J. J. Einstein from “B” to “Z” – Volume 9 of Einstein studies (нем.). — Springer, 2002. — S. 226. — ISBN 0-8176-4143-2. Архивная копия от 16 ноября 2016 на Wayback Machine
  16. ↑ Einstein, A. Zur Elektrodynamik bewegter Körper (нем.) // Annalen der Physik. — 1905. — Bd. 17. — S. 890—921. — doi:10.1002/andp.19053221004. English translation: Perrett, W; Jeffery, GB (tr.); Walker, J (ed.) On the Electrodynamics of Moving Bodies. Fourmilab. Дата обращения: 27 ноября 2009. Архивировано 1 февраля 2013 года.
  17. ↑ Александров Е. Б. Теория относительности: прямой эксперимент с кривым пучком // Химия и жизнь. — 2012. — № 3. Архивировано 4 марта 2016 года.
  18. ↑
    Hsu, J-P; Zhang, Y. Z. Lorentz and Poincaré Invariance. — World Scientific, 2001. — Т. 8. — С. 543ff. — (Advanced Series on Theoretical Physical Science). — ISBN 981-02-4721-4.
  19. ↑ 1 2 Zhang, Y. Z. Special Relativity and Its Experimental Foundations (англ.). — World Scientific, 1997. — Vol. 4. — P. 172—173. — (Advanced Series on Theoretical Physical Science). — ISBN 981-02-2749-3. Архивная копия от 19 мая 2012 на Wayback Machine Архивированная копия. Дата обращения: 24 января 2013. Архивировано из оригинала 19 мая 2012 года.
  20. ↑
    d’Inverno, R. Introducing Einstein’s Relativity (англ.). — Oxford University Press, 1992. — P. 19—20. — ISBN 0-19-859686-3.
  21. ↑
    Sriranjan, B. Postulates of the special theory of relativity and their consequences // The Special Theory to Relativity. — PHI Learning, 2004. — С. 20 ff. — ISBN 81-203-1963-X.
  22. ↑ Roberts, T; Schleif, S; Dlugosz, JM (ed.) What is the experimental basis of Special Relativity? Usenet Physics FAQ. University of California, Riverside (2007). Дата обращения: 27 ноября 2009. Архивировано 1 февраля 2013 года.
  23. ↑
    Terrell, J. Invisibility of the Lorentz Contraction (англ.) // Physical Review : journal. — 1959. — Vol. 116, no. 4. — P. 1041—1045. — doi:10.1103/PhysRev.116.1041. — Bibcode: 1959PhRv..116.1041T.
  24. ↑
    Penrose, R. The Apparent Shape of a Relativistically Moving Sphere (англ.) // Proceedings of the Cambridge Philosophical Society  (англ.) (рус. : journal. — 1959. — Vol. 55, no. 01. — P. 137—139. — doi:10.1017/S0305004100033776. — Bibcode: 1959PCPS…55..137P.
  25. ↑
    Hartle, J. B. Gravity: An Introduction to Einstein’s General Relativity (англ.). — Addison-Wesley, 2003. — P. 52—9. — ISBN 981-02-2749-3.
  26. ↑
    Hartle, J. B. Gravity: An Introduction to Einstein’s General Relativity (англ.). — Addison-Wesley, 2003. — P. 332. — ISBN 981-02-2749-3.
  27. ↑ The interpretation of observations on binary systems used to determine the speed of gravity is considered doubtful by some authors, leaving the experimental situation uncertain; seeSchäfer, G; Brügmann, M. H. Propagation of light in the gravitational filed of binary systems to quadratic order in Newton’s gravitational constant: Part 3: ‘On the speed-of-gravity controversy’ // Lasers, clocks and drag-free control: Exploration of relativistic gravity in space (англ.) / Dittus, H; Lämmerzahl, C; Turyshev, S. G.. — Springer, 2008. — ISBN 3-540-34376-8.
  28. ↑ Gibbs, P Is The Speed of Light Constant? Usenet Physics FAQ. University of California, Riverside (1997). Дата обращения: 26 ноября 2009. Архивировано 17 ноября 2009 года.
  29. ↑
    Ellis, GFR; Uzan, J-P. ‘c’ is the speed of light, isn’t it? (англ.) // American Journal of Physics : journal. — 2005. — Vol. 73, no. 3. — P. 240—247. — doi:10.1119/1.1819929. — Bibcode: 2005AmJPh..73..240E. — arXiv:gr-qc/0305099.. — «The possibility that the fundamental constants may vary during the evolution of the universe offers an exceptional window onto higher dimensional theories and is probably linked with the nature of the dark energy that makes the universe accelerate today.».
  30. ↑ An overview can be found in the dissertation of Mota, DF (2006), Variations of the fine structure constant in space and time, arΧiv:astro-ph/0401631 [astro-ph].
  31. ↑
    Uzan, J-P. The fundamental constants and their variation: observational status and theoretical motivations (англ.) // Reviews of Modern Physics : journal. — 2003. — Vol. 75, no. 2. — P. 403. — doi:10.1103/RevModPhys.75.403. — Bibcode: 2003RvMP…75..403U. — arXiv:hep-ph/0205340.
  32. ↑
    Amelino-Camelia, G (2008), Quantum Gravity Phenomenology, arΧiv:0806.0339 [gr-qc].
  33. ↑ Herrmann, S; Senger, A; Möhle, K; Nagel, M; Kovalchuk, EV; Peters, A. Rotating optical cavity experiment testing Lorentz invariance at the 10−17 level (англ.) // Physical Review D : journal. — 2009. — Vol. 80, no. 100. — P. 105011. — doi:10.1103/PhysRevD.80.105011. — Bibcode: 2009PhRvD..80j5011H. — arXiv:1002.1284.
  34. ↑ Lang, K. R. Astrophysical formulae. — 3rd. — Birkhäuser  (англ.) (рус., 1999. — С. 152. — ISBN 3-540-29692-1.
  35. ↑ Tomilin K. A. Natural Systems of Units: To the Centenary Anniversary of the Planck System (англ.). Proc. of the XXII Internat. Workshop on high energy physics and field theory (июнь 1999). Дата обращения: 22 декабря 2016. Архивировано 12 мая 2016 года.
  36. ↑ Fowler, M Notes on Special Relativity 56. University of Virginia (март 2008). Дата обращения: 7 мая 2010. Архивировано 1 февраля 2013 года.
  37. ↑
    Liberati, S; Sonego, S; Visser, M. Faster-than-c signals, special relativity, and causality (англ.) // Annals of Physics  (англ.) (рус. : journal. — 2002. — Vol. 298, no. 1. — P. 167—185. — doi:10.1006/aphy.2002.6233. — Bibcode: 2002AnPhy.298..167L. — arXiv:gr-qc/0107091.
  38. ↑
    Taylor, EF; Wheeler, J. A. Spacetime Physics. — W. H. Freeman  (англ.) (рус., 1992. — С. 74—5. — ISBN 0-7167-2327-1.
  39. ↑
    Tolman, R. C. Velocities greater than that of light // The Theory of the Relativity of Motion. — Reprint. — BiblioLife  (англ.) (рус., 2009. — С. 54. — ISBN 978-1-103-17233-7.
  40. ↑ Гиндикин С. Г. Рассказы о физиках и математиках. — издание третье, расширенное. — М.: МЦНМО, 2001. — С. 105—108. — ISBN 5-900916-83-9. Архивная копия от 11 июля 2020 на Wayback Machine
  41. ↑ Стюарт, 2018, с. 178.
  42. ↑ 1 2 3 4 Ландсберг Г. С. Оптика. — М.: Физматлит, 2003. — С. 384—389. — 848 с. — ISBN 5-9221-0314-8.
  43. ↑ 1 2 Бонч-Бруевич А. М. Скорость света // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. — С. 548—549. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
  44. ↑ Léon Foucault. Détermination expérimentale de la vitesse de la lumière ; description des appareils (фр.) // Comptes rendus hebdomadaires des séances de l’Académie des Sciences. — Paris, 1862. — Vol. 55. — P. 792—796. Архивировано 24 сентября 2015 года.
  45. ↑ Léon Foucault. Détermination expérimentale de la vitesse de la lumière ; parallaxe du Soleil (фр.) // Comptes rendus hebdomadaires des séances de l’Académie des Sciences. — Paris, 1862. — Vol. 55. — P. 501—503. Архивировано 24 сентября 2015 года.
  46. ↑ Léon Foucault. Experimental Determination of the Velocity of Light: Description of the Apparatus (англ.) // Philosophical Magazine. Fourth Series. — London, 1863. — Vol. 25. — P. 76—79.
  47. ↑ Evenson K. M., Wells J. S., Petersen F. R., Danielson B. L., Day G. W. Speed of Light from Direct Frequency and Wavelength Measurements of the Methane-Stabilized Laser (англ.) // Phys. Rev. Lett.. — 1972. — Vol. 29, no. 19. — P. 1346—1349. — doi:10.1103/PhysRevLett.29.1346.
  48. ↑ Указанная погрешность представляет собой утроенное стандартное отклонение.
  49. ↑ 1 2 Рекомендованное значение скорости света Архивная копия от 7 октября 2008 на Wayback Machine (англ.) Резолюция 2 XV Генеральной конференции по мерам и весам (1975)
  50. ↑ Определение метра Архивная копия от 26 июня 2013 на Wayback Machine (англ.) Резолюция 1 XVII Генеральной конференции по мерам и весам (1983)
  51. ↑ 1 2 Введение в рассмотрение полевой квантовой природы этих сверхсветовых частиц, возможно, позволяет обойти это ограничение через принцип переинтерпретации наблюдений.
  52. ↑ Давидович М. В. О парадоксе Хартмана, туннелировании электромагнитных волн и сверхсветовых скоростях // Успехи физических наук. — М.: Российская академия наук, 2009 (апрель). — Вып. 179. — С. 443. Архивировано 24 октября 2020 года.
  53. ↑ И. Иванов. Проведены новые эксперименты по проверке механизма квантовой запутанности. Архивная копия от 31 августа 2008 на Wayback Machine Элементы.ру.
  54. ↑ Oscillation Project with Emulsion-tRacking Apparatus. Дата обращения: 23 сентября 2011. Архивировано 11 октября 2012 года.
  55. ↑ OPERA experiment reports anomaly in flight time of neutrinos from CERN to Gran Sasso. Дата обращения: 10 января 2016. Архивировано 5 апреля 2013 года.
  56. ↑ OPERA Collaboration (Adam T. et al.) (2011), Measurement of the neutrino velocity with the OPERA detector in the CNGS beam, arΧiv:1109.4897..
  57. ↑ И.Иванов. Эксперимент OPERA сообщает о наблюдении сверхсветовой скорости нейтрино. Архивная копия от 25 сентября 2012 на Wayback Machine Элементы.ру, 23 сентября 2011 года.
  58. ↑ ICARUS Collaboration et al. Measurement of the neutrino velocity with the ICARUS detector at the CNGS beam // Physics Letters B. — 2012. — Vol. 713 (18 июля). — P. 17–22. — arXiv:1203.3433. — doi:10.1016/j.physletb.2012.05.033.
  59. ↑ Эксперимент OPERA окончательно «закрыл» сверхсветовые нейтрино Архивная копия от 7 июля 2012 на Wayback Machine.

Литература[править | править код]

  • Александров Е. Б., Александров П. А., Запасский В. С., Корчуганов В. Н., Стирин А. И. Эксперименты по прямой демонстрации независимости скорости света от скорости движения источника // Успехи физических наук. — Российская академия наук, 2011. — Вып. 12.
  • Физические величины: Справочник./А. П. Бабичев, Н. А. Бабушкина, А. М. Братковский и др.; под ред. И. С. Григорьева, Е. З. Мейлихова М.: Энергоатомиздат, 1991, — 1232 с.— ISBN 5-283-04013-5.
  • Эйнштейн А., Инфельд Л. Эволюция физики. — М.: ОГИЗ, 1948. — 267 с.
  • Медведев Б. В. Начала теоретической физики. — М.: Физматлит, 2007. — 600 с.
  • Неванлинна Р. Пространство, время и относительность. — М.: Мир, 1966. — 229 с.
  • Иэн Стюарт. Математика космоса. Как современная наука расшифровывает Вселенную = Stewart Ian. Calculating the Cosmos: How Mathematics Unveils the Universe. — Альпина Паблишер, 2018. — 542 p. — ISBN 978-5-91671-814-0.
  • И.В.Савельев “Курс общей физики” том II

Ссылки[править | править код]

  • Скорость света — статья в Физической энциклопедии
  • Скорость света на astronet.ru
  • Rømer, O (1676). “Démonstration touchant le mouvement de la lumière trouvé par M. Römer de l’Academie Royale des Sciences” (PDF). Journal des sçavans [фр.]: 223—36.
  • Halley, E (1694). “Monsieur Cassini, his New and Exact Tables for the Eclipses of the First Satellite of Jupiter, reduced to the Julian Stile and Meridian of London”. Philosophical Transactions of the Royal Society. 18 (214): 237—56. Bibcode:1694RSPT…18..237C. DOI:10.1098/rstl.1694.0048.
  • Fizeau, HL (1849). “Sur une expérience relative à la vitesse de propagation de la lumière” (PDF). Comptes rendus de l’Académie des sciences [фр.]. 29: 90—92, 132.
  • Foucault, JL (1862). “Détermination expérimentale de la vitesse de la lumière: parallaxe du Soleil”. Comptes rendus de l’Académie des sciences [фр.]. 55: 501—03, 792—96.
Источник

В астрономии есть много интересных терминов. Многие из них человек использует в повседневной жизни и даже не задумывается о их значении.

в чем измеряется скорость света

Что такое скорость света и в чём измеряется данная величина?

Содержание

  1. Что под собой подразумевает скорость света
  2. Чему равняется скорость света
  3. Какое значение скорости света можно назвать самым точным
  4. Какое значение имеет скорость света в различных условиях и средах
  5. Формула определения скорости света
  6. Как изменялась скорость света
  7. Галилей и его открытия
  8. Рёмер и Бредли и их расчёты, касательно скорости света
  9. Физо и его расчёты
  10. Существует ли скорость быстрее световой

Что под собой подразумевает скорость света

Каждый из нас хоть раз слышал выражение “быстрее скорости света”, но далеко не все понимают, чему равна данная величина и в чём она измеряется. Если не использовать терминологию, и объяснять простыми словами, то скорость света – это некий временной промежуток.

скорость света в воздухе формула

Если быть точнее, то временной промежуток, за который преодолел солнечный луч определённое расстояние. Временные промежутки физика измеряет в секундах. Расстояние принято измерять в метрах.

Справка! Некоторые учёные используют в своих измерениях другие условные единицы.

Но если обратить внимание на измерение скорости света, то данная величина подразумевает измерение в метрах в секунду. Основная закономерность движения света заключается в том, что солнечный луч будет двигаться с постоянной быстротой и скоростью.

скорость света в вакууме формула

Это невозможно сделать человеку или автомобилю, потому что рано или поздно скорость увеличится или понизится, а некоторые условия заставят предмет остановиться. Солнечный луч движется без остановки.

Чему равняется скорость света

В физике также принято рассматривать положение света в безвоздушном пространстве, то есть вакууме. Если световой луч выходит за приделы этого вакуума, то на него начинают влиять различные условия.

Например, в вакууме нет кислорода и ветра, а в воздушном пространстве есть ветра. Свет проходит несколько медленнее через различный материал: стекло, воду, и так далее. Поскольку это является неким барьером, к таким предметам применяется понятие преломления.

относительно чего измеряется скорость света

Каждый из этих барьеров имеет свой уровень преломления, и при различных физических вычислениях эти преломления должны учитываться.

Справка! Также преломление света принято называть рефракцией. Активно используется при проектировании каких-либо изобретений. Зачастую это относится к изобретениям, где используется оптика и линзы: бинокли, телескопы, очки.

Меньше всего солнечный луч поддаётся преломлению, если проходит через воздушное пространство.

Какое значение скорости света можно назвать самым точным

Поскольку определение скорости света – термин не новый, учёные сделали достаточное количество открытий и провели множество исследований, касательно света и его преломления.

скорость света чему равна

На сегодняшний день самым точным значение скорости света является – 299 792 километра в секунду. Такое число было установлено еще в 1933 году, и это значение актуально по сей день.

Справка! Со временем произошли погрешности в измерении метра, поэтому число неоднократно искажалось.

Какое значение имеет скорость света в различных условиях и средах

Скорость света принято высчитывать, исходя из определённых условий. Стоит сразу уточнить, что процедура достаточно сложная и проблематичная. Важно учесть все возможные преломления.

На сегодняшний день рассматривают три основных показателя:

  • вода;
  • стекло;
  • воздух.

Как правило, величина преломления через воздух самая низкая. При высчитывании принято считать и сравнивать солнечные лучи в безвоздушном пространстве, а затем вводится коэффициент преломления. Только при правильно составленной формуле можно точно высчитать скорость света в различных условиях.

Формула определения скорости света

Как и любая физическая величина, скорость света имеет свою формулу. Выглядит она таким образом: C = λ/T.

Каждая буква имеет своё значение. Учёные берут эту формулу, как основу для расчёта скорости света в безвоздушном пространстве.

максимальная скорость света

Величина этой скорости в идеальном вакуумном пространстве составляет 299 792 458 метров в секунду. Создать такой вакуум можно только в космосе, поэтому физики рассматривают многие примеры только на примере космического пространства.

Тогда не нужно учитывать различную величину преломления и так далее. В условиях земли идеальный вакуум с постоянной скоростью света можно только в искусственных условиях.

Скорость света также принято называть скоростью фотона.

фотон

Справка! Фотоном называют малейшую частицу света, который больше всего во Вселенной.

В безвоздушном пространстве скорость света не будет никак изменяться. Она не сможет увеличиваться и уменьшаться в идеальных условиях, так как нет никаких дополнительных преломлений.

Если рассматривать пример скорости света на Земле, то минимальная скорость света будет изменяться в зависимости от дополнительных условий.

Как изменялась скорость света

Скорость света менялась со временем. Чем точнее становилась аппаратура и чем больше проводилось опытов, тем точнее можно было установить скорость света. Многие учёные пытались неоднократно измерить скорость света.

скорость света в воздухе в км час

Долгое время считалось, что она бесконечная и её невозможно изменить. Такой позиции придерживались вплоть до 17 века. После этого периода появились новый умы, который посчитали, что луч может иметь начало и конец и его можно измерить.

Справка! Первые измерения провел учёный Олаф Рёмер. Учёный из Дании заметил, что затмение Юпитера немного запаздывает.

скорость света в воздухе в км часЭто стало отправной точкой и учёный решил примерно пересчитать эту скорость. Значение было приближено в 220 тысячам километров в секунду. Чуть позже за примерные расчёты взялись и другие учёные. Он также был далёк от нынешнего значения, но получил более точное значение.

вычисления

Затем скоростью света начали интересоваться и другие служители науки. Вычисления пытались произвести учёные из разных стран и городов. Но до 70-х годов прошлого века не было введено более точных и новых измерений.

После 70-х годов начала появляться новая аппаратура, которая позволила произвести более точные измерения.

Галилей и его открытия

Измерения Галилея буквально поразили публику и своей простотой, и гениальностью. Он смог измерить примерную скорость света буквально подручными средствами.

Он со своим помощником посетили ближайшие холмы у дома, и заранее записали расстояние между ними. Запасаясь фонарями и заслонками, они приступили к осуществлению своего опыта.

что такое скорость света

Они начали поочерёдно закрывать и открывать фонари, тем самым пытались рассчитать скорость света. Они заранее договорились с каким временным промежутком будут открывать и закрывать фонарный свет.

Но, к сожалению, эксперимент не увенчался успехом. Для того, чтобы рассчитать скорость света, им бы пришлось находиться друг от друга на слишком большом расстоянии.

Рёмер и Бредли и их расчёты, касательно скорости света

определение скорости света

Один из опытов, который позволил узнать примерное значение скорости света. Этот тот самый опыт, который был связан с затмением Юпитера. Учёные сделали достаточно простой шаг и разделили расстояние на время и получили примерное значение в 214 тысяч километров.

измерение скорости

Это стало отправной точкой. Пускай, это было не точно и с большим количеством недочётов, но благодаря именно этим учёным величиной заинтересовались и начали изучать её более подробно.

Физо и его расчёты

Многие учёные отнеслись к расчётам предыдущих коллег достаточно скептически. Но не взирая на это, результаты были близки к настоящей длине, которая подтверждена сейчас официально и широко используется в расчётах, тогда этого не знали и пытались пересчитать.

физо

Подобно Галилею, Физо игнорировал наблюдение за космическими телами и проводит опыт в лабораторных условиях. Эксперимент был прост: луч направлялся на зеркало, и отразившись проходил через колёсные зубцы.

После этого свет отражался на дополнительную поверхность, расположенную на достаточном расстоянии. Вращение колеса увеличивалось до тех пор, пока луч не попадал на то самое зеркало. Тогда были получены цифры в 313 тысяч километров, после того, как пересмотрели эти расчёты, была определена более точная цифра.

Существует ли скорость быстрее световой

Такое возможно только при создании дополнительных условий. Быстрее солнечного света будет солнечный зайчик или энергия. Также электроны и другие частицы.

Такие условия возможны в искусственных условиях, либо при наличии каких-то дополнительных условий.

скорость света в метрах в секунду

Справка! Скорость времени также быстрее скорости света.

Физика и космос – это связанные между собой отрасли, которые постоянно подвергаются изучению. Благодаря этим измерениям можно проводить дальнейшие исследования и ставить более точные числа.

Источник

Этот материал написан посетителем сайта, и за него начислено вознаграждение.

В нашей Солнечной системе Сатурн – самая далекая от Земли планета, которую можно увидеть невооруженным глазом. И если он будет разрушен астероидом во время наблюдения за ним (с помощью телескопа или без него), эта окольцованная планета будет оставаться видимой для наблюдателя примерно в течение 80 минут, даже после того, как она разлетится на кусочки. Это объясняется тем, что среднее расстояние между Сатурном и Землей составляет 0,00015 световых лет, а это значит, что свету от Сатурна потребуется примерно 80 минут, чтобы достичь Земли.

Yuri_B/Pixabay

Таким образом, если какая-либо звезда, которую вы наблюдаете находится на расстоянии 100 световых лет от Земли, то вы следите в телескоп не за ее текущим состоянием, а за тем, какой звезда была 100 лет назад. Именно поэтому телескоп иногда называют астрономической машиной времени. Измерение астрономических расстояний в милях или километрах нецелесообразно из-за огромных размеров и масштабов используемых цифр. Измерение в световых годах также позволяет астрономам заглянуть в прошлое. Поскольку свету требуется стандартное количество времени, чтобы добраться до наших глаз, все, что мы можем увидеть в космосе, уже произошло. Поэтому, когда вы наблюдаете что-либо на расстоянии ровно двух световых лет, вы видите его таким, каким оно было ровно два года назад.

Что такое световой год?

рекомендации

-10000р на 3070 Ti Gigabyte Aorus

Дешевая 4070 MSI – надо брать

1Tb SSD Crucial в ДВА раза подешевел

RTX 3070 за 45 тр в Регарде

4080 Gigabyte Gaming дешево в Регарде

-15000р на Ryzen 3950X – пора брать

Ищем PHP-программиста для апгрейда конфы

Компьютеры от 10 тр в Ситилинке

<b>13900K</b> в Регарде по СТАРОМУ курсу 62

Много 4080 от 100тр – цены в рублях не растут

3060 дешевле 30тр цена – как при курсе 68

13700K дешевле 40 тр в Регарде

Скорость света – это константа. В вакууме свет распространяется со скоростью 670 616 629 миль в час (1 079 252 849 километров в час). За один земной год, длящийся 364,25 дня (8 766 часов), свет проходит расстояние в 5 878 625 370 000 миль (9,5 трлн км). Это расстояние называется световым годом.

Поскольку расстояния между космическими телами в основном исчисляются миллионами и миллиардами километров, потребовалась более удобная единица измерения, чтобы было проще выражать такие большие расстояния, и это привело к тому, что в качестве единицы измерения астрономических расстояний стал использоваться световой год.

Как следует из самого названия, световой год (в множественном числе световых лет) – это единица измерения расстояния. Одно из распространенных заблуждений относительно светового года заключается в том, что некоторые считают его единицей времени, что в корне неверно. Световой год обычно используется для выражения расстояния между Землей и небесными телами за пределами нашей Солнечной системы.

Скорость света и открытие светового года

Для того чтобы ученые правильно вычислили световой год, им было важно знать значение скорости света. Древнегреческие философы расходились во мнениях относительно природы скорости света. Философ Эмпедокл считал, что свет движется и поэтому должен иметь скорость движения. Аристотель, напротив, утверждал, что свет мгновенен.

В середине 1600-х годов Галилео Галилей провел эксперименты по определению скорости света с помощью людей, расположившихся на холмах на расстоянии около мили друг от друга и державших в руках фонари. Но расстояние было недостаточно большим, чтобы зафиксировать его скорость, в результате чего был сделан вывод, что свет распространяется быстрее звука.

Расстояние от Солнца до различных ближайших звезд в световых годах. Источник: atlasoftheuniverse.com/Wikimedia Commons

В 1676 году датский астроном Оле Рёмер, пытаясь создать надежные астрономические часы для моряков в море, случайно придумал новую оценку скорости света. Он использовал наблюдения за затмениями луны Юпитера, Ио, чтобы оценить скорость света в 124 000 миль в секунду (200 000 километров в секунду).

Однако она отличалась от известной нам сегодня скорости света (299 792 км/с), но эта аномалия возникла не потому, что метод Рёмера был несовершенен, а из-за того, что в то время не был известен реальный диаметр Земли (12 742 км). Позже голландский математик Христиан Гюйгенс рассчитал скорость света как 220 миллионов миль в секунду (гораздо ближе к реальной), применив истинное значение диаметра Земли в расчетах Рёмера.

В 1729 году английский астроном Джеймс Брэдли выдвинул свою теорию относительно аберрации света (изменение направления распространения света ) перед Королевским обществом. В своем исследовании он оценил скорость света в 185 000 миль в секунду (301 000 км/с), что находится в пределах примерно 1% от известной нам сегодня величины.

Две различные попытки, предпринятые в середине 1800-х годов французскими физиками Ипполитом Физо и Леоном Фуко, приблизились к скорости света примерно на 1 000 миль в секунду (1 609 километров в секунду).

В 1879 году физик Альберт А. Майкельсон с помощью зеркал и линз измерил скорость света, которая составила 186 355 миль в секунду (299 910 км/с). Сорок лет спустя он использовал трубы длиной в милю, находящиеся под давлением, пытаясь создать условия, близкие к вакууму, и получить более точное измерение, которое было лишь немного меньше, чем существующее сегодня.   

В 1838 году немецкий физик Фридрих Вильгельм Бессель использовал значение скорости света для измерения расстояния между Землей и бинарной звездной системой 61 Лебедя AB. Хотя он не упоминал слово “световой год”, он объяснил, что свету потребуется 10,3 года, чтобы добраться от 61 Лебедя AB до Земли. Это был первый случай, когда физик использовал световой год в качестве меры расстояния, поэтому Бесселя также считают человеком, открывшим световой год.

Впервые термин “световой год” был упомянут в 1851 году в немецком издании под названием Lichtjare. К тому времени, когда Эйнштейн разработал теорию специальной относительности (E=mc2), утверждающую, что свет всегда движется с конечной скоростью, световой год уже стал популярной единицей измерения астрономических расстояний среди ученых.

Световой год. Астрономическая единица. Лунное расстояние. Парсек

Помимо светового года, существуют и другие единицы, такие как астрономическая единица (AU), лунное расстояние (LD) и парсек (pc), которые используются для измерения расстояния между различными объектами в космосе. В астрономии лунное расстояние, или расстояние между Землей и Луной, – это средняя полуось геоцентрической лунной орбиты. Оно составляет приблизительно 400 000 км, то есть четверть миллиона миль, или 1,28 световых секунд. Лунное расстояние обычно используется для выражения расстояния до сближающихся с Землей объектов.

Астрономическая единица (AU) равна среднему расстоянию от центра Земли до центра Солнца.

Лунное расстояние и астрономические единицы используются для выражения расстояния между объектами внутри нашей Солнечной системы, в то время как световой год и парсек используются для измерения расстояний за пределами нашей Солнечной системы (например, расстояния между галактиками).

Парсек – это расстояние, на котором радиус земной орбиты составляет угол в одну секунду дуги (угол образуется дугой, когда два ее луча проходят через конечные точки этой дуги). Таким образом, параллакс звезды, находящейся на расстоянии одного парсека, (угловая разница в направлении небесного тела, измеренная из двух точек на орбите Земли) составляет одну секунду. Один световой год равен 63 241 AU, а один парсек равен 3,26 ly или 206 265 AU.  

Источник: CharlVera/Pixabay

Некоторые интересные факты о световых годах

Световой год можно разделить на световые часы, световые минуты, световые секунды и даже световые наносекунды. Например, свету от Солнца требуется восемь минут, чтобы достичь Земли, что также означает, что Солнце находится на расстоянии восьми световых минут от Земли. Вот несколько интересных фактов, связанных со световыми годами:

Космический зонд “Вояджер-1”, запущенный NASA в 1977 году, передал сигнал в ноябре 2021 года с расстояния 21,31 светового часа (14,45 миллиарда миль). Это самое дальнее расстояние, которое преодолел в космосе любой искусственный объект.

Ближайшая к Млечному пути (нашей галактике) карликовая галактика Большой Пёс  находится на расстоянии 25 000 световых лет от Солнца. Карликовая эллиптическая галактика Стрелец находится на расстоянии 70 000 световых лет от Солнца.  Самая удаленная от Земли известная галактика называется GN-z11, она была обнаружена телескопом Хаббл в 2016 году в созвездии Большой Медведицы и на тот момент считалось, что она находится на расстоянии 13,4 миллиарда световых лет от Земли, или 134 нониллиона километров (это 134 и 30 нулей).

Радарная система, использующая радиоволны для обнаружения летящего самолета, измеряет время в наносекундах, чтобы определить, насколько далеко находится цель, поскольку радиоволны распространяются со скоростью света. Наносекунда равна одной миллиардной части секунды. Свет проходит 1 фут (30 см) за наносекунду.  

Недавно NASA заявило, что его зонд Parker Solar “коснулся Солнца”. Он также считается самым быстрым из искусственных объектов в космосе и, как ожидается, достигнет скорости 430 000 миль в час (690 000 километров в час). Этого достаточно, чтобы добраться из Филадельфии в Вашингтон, округ Колумбия, менее чем за секунду.

Великий американский астроном Эдвин Хаббл однажды сказал: “Поиск будет продолжаться, это стремление старше истории, оно не утолено и не будет подавлено”. Освоение космоса тоже можно рассматривать как поиск того, что находится за пределами Земли и звезд. Будучи единицей измерения расстояния, световой год также напоминает нам о том, насколько огромна Вселенная и как много человечеству и науке еще предстоит узнать.

Этот материал написан посетителем сайта, и за него начислено вознаграждение.

Источник

Добавить комментарий