Главная » Справочник » Катушка индуктивности. Описание, характеристики, формула расчета
Катушка индуктивности является пассивным компонентом электронных схем, основное предназначение которой является сохранение энергии в виде магнитного поля. Свойство катушки индуктивности чем-то схоже с конденсатором, который хранит энергию в виде электрического поля.
Индуктивность (измеряется в Генри) — это эффект возникновения магнитного поля вокруг проводника с током. Ток, протекающий через катушку индуктивности, создает магнитное поле, которое имеет связь с электродвижущей силой (ЭДС) оказывающее противодействие приложенному напряжению.

Возникающая противодействующая сила (ЭДС) противостоит изменению переменного напряжения и силе тока в катушке индуктивности. Это свойство индуктивной катушки называется индуктивным сопротивлением. Следует отметить, что индуктивное сопротивление находится в противофазе к емкостному реактивному сопротивлению конденсатора в цепи переменного тока. Путем увеличения числа витков можно повысить индуктивность самой катушки.
Накопленная энергия в индуктивности
Как известно магнитное поле обладает энергией. Аналогично тому, как в полностью заряженном конденсаторе существует запас электрической энергии, в индуктивной катушке, по обмотке которой течет ток, тоже существует запас — только уже магнитной энергии.
Энергия, запасенная в катушке индуктивности равна затраченной энергии необходимой для обеспечения протекания тока I в противодействии ЭДС. Величина запасенной энергии в индуктивности можно рассчитать по следующей формуле:
![]()
где L — индуктивность, I — ток, протекающий через катушку индуктивности.
Гидравлическая модель
Работу катушки индуктивности можно сравнить с работой гидротурбины в потоке воды. Поток воды, направленный сквозь еще не раскрученную турбину, будет ощущать сопротивление до того момента, пока турбина полностью не раскрутится.
Далее турбина, имеющая определенную степень инерции, вращаясь в равномерном потоке, практически не оказывая влияния на скорость течения воды. В случае же если данный поток резко остановить, то турбина по инерции все еще будет вращаться, создавая движение воды. И чем выше инерция данной турбины, тем больше она будет оказывать сопротивление изменению потока.
Также и индуктивная катушка сопротивляется изменению электрического тока протекающего через неё.
Индуктивность в электрических цепях
В то время как конденсатор оказывает сопротивление изменению переменного напряжения, индуктивность же сопротивляется переменному тока. Идеальная индуктивность не будет оказывать сопротивление постоянному току, однако, в реальности все индуктивные катушки сами по себе обладают определенным сопротивлением.

Блок питания 0…30В/3A
Набор для сборки регулируемого блока питания…
В целом, отношение между изменяющимися во времени напряжением V(t) проходящим через катушку с индуктивностью L и изменяющимся во времени током I(t), проходящим через нее можно представить в виде дифференциального уравнения следующего вида:
![]()
Когда переменный синусоидальной ток (АС) протекает через катушку индуктивности, возникает синусоидальное переменное напряжение (ЭДС). Амплитуда ЭДС зависит от амплитуды тока и частоте синусоиды, которую можно выразить следующим уравнением:
![]()
где ω является угловой частотой резонансной частоты F:
![]()
Причем, фаза тока отстает от напряжения на 90 градусов. В конденсаторе же все наоборот, там ток опережает напряжение на 90 градусов. Когда индуктивная катушка соединена с конденсатором (последовательно либо параллельно), то образуется LC цепь, работающая на определенной резонансной частоте.
Индуктивное сопротивление ХL определяется по формуле:
![]()
где ХL — индуктивное сопротивление, ω — угловая частота, F — частота в герцах, и L индуктивность в генри.
Индуктивное сопротивление — это положительная составляющая импеданса. Оно измеряется в омах. Импеданс катушки индуктивности (индуктивное сопротивление) вычисляется по формуле:
![]()
Схемы соединения катушек индуктивностей
Параллельное соединение индуктивностей

Напряжение на каждой из катушек индуктивностей, соединенных параллельно, одинаково. Эквивалентную (общую) индуктивность параллельно соединенных катушек можно определить по формуле:
![]()
Последовательное соединение индуктивностей
![]()
Ток, протекающий через катушки индуктивности соединенных последовательно, одинаков, но напряжение на каждой катушке индуктивности отличается. Сумма разностей потенциалов (напряжений) равна общему напряжению. Общая индуктивность последовательно соединенных катушек можно высчитать по формуле:
![]()
Эти уравнения справедливы при условии, что магнитное поле каждой из катушек не оказывает влияние на соседние катушки.
Добротность катушки индуктивности
На практике катушка индуктивности имеет последовательное сопротивление, созданное медной обмоткой самой катушки. Это последовательное сопротивление преобразует протекающий через катушку электрический ток в тепло, что приводит к потере качества индукции, то есть добротности. Добротность является отношением индуктивности к сопротивлению.
Добротность катушки индуктивности может быть найдена через следующую формулу:
![]()
где R является собственным сопротивлением обмотки.
Катушка индуктивности. Формула индуктивности
Базовая формула индуктивности катушки:
![]()
- L = индуктивность в генри
- μ 0 = проницаемость свободного пространства = 4π × 10 -7 Гн / м
- μ г = относительная проницаемость материала сердечника
- N = число витков
- A = Площадь поперечного сечения катушки в квадратных метрах (м 2 )
- l = длина катушки в метрах (м)
Индуктивность прямого проводника:

- L = индуктивность в нГн
- l = длина проводника
- d = диаметр проводника в тех же единицах, что и l
Индуктивность катушки с воздушным сердечником:

- L = индуктивность в мкГн
- r = внешний радиус катушки
- l = длина катушки
- N = число витков
Индуктивность многослойной катушки с воздушным сердечником:
![]()
- L = индуктивность в мкГн
- r = средний радиус катушки
- l = длина катушки
- N = число витков
- d = глубина катушки
Индуктивность плоской катушки:
![]()
- L = индуктивность в мкГн
- r = средний радиус катушки
- N = число витков
- d = глубина катушки
Конструкция катушки индуктивности
Катушка индуктивности представляет собой обмотку из проводящего материала, как правило, медной проволоки, намотанной вокруг либо железосодержащего сердечника, либо вообще без сердечника.
Применение в качестве сердечника материалов с высокой магнитной проницаемостью, более высокой чем воздух, способствует удержанию магнитного поля вблизи катушки, тем самым увеличивая ее индуктивность. Индуктивные катушки бывают разных форм и размеров.
Большинство изготавливаются путем намотки эмалированного медного провода поверх ферритового сердечника.

Некоторые индуктивные катушки имеют регулируемый сердечник, при помощи которого обеспечивается изменение индуктивности.
Миниатюрные катушки могут быть вытравлены непосредственно на печатной плате в виде спирали. Индуктивности с малым значением могут быть расположены в микросхемах с использованием тех же технологических процессов, которые используются при создании транзисторов.
Применение катушек индуктивности
Индуктивности широко используются в аналоговых схемах и схемах обработки сигналов. Они в сочетании с конденсаторами и другими радиокомпонентами образуют специальные схемы, которые могут усилить или отфильтровать сигналы определенной частоты.
Катушки индуктивности получили широкое применение начиная от больших катушек индуктивности, таких как дроссели в источниках питания, которые в сочетании с конденсаторами фильтра устраняют остаточные помехи и другие колебания на выходе источника питания, и до столь малых индуктивностей, которые располагаются внутри интегральных микросхем.
Две (или более) катушки индуктивности, которые соединены единым магнитным потоком, образуют трансформатор, являющимся основным компонентом схем работающих с электрической сетью электроснабжения. Эффективность трансформатора возрастает с увеличением частоты напряжения.

По этой причине, в самолетах используется переменное напряжение с частотой 400 герц вместо обычных 50 или 60 герц, что в свою очередь позволяет значительно сэкономить на массе используемых трансформаторов в электроснабжении самолета.
Так же индуктивности используются в качестве устройства для хранения энергии в импульсных стабилизаторах напряжения, в высоковольтных электрических системах передачи электроэнергии для преднамеренного снижения системного напряжения или ограничения ток короткого замыкания.

Инвертор 12 В/ 220 В
Инвертор с чистой синусоидой, может обеспечивать питание переменно…
Продолжаем обсуждение катушек индуктивности, в первой части (ссылка) мы обсудили все основные аспекты, а именно устройство катушек, принцип работы и их поведение при использовании в цепях постоянного и переменного тока. Но некоторые моменты остались незатронутыми, собственно, их мы и обсудим в этой статье. И начнем с очень важной характеристики, а именно добротности катушки индуктивности.
Активное сопротивление и добротность катушки индуктивности.
Итак, начнем мы с того, что обсудим некоторые характеристики катушек индуктивности, с которыми мы не успели познакомиться в предыдущей статье. И для начала рассмотрим активное сопротивление катушки.
Разбирая примеры включения катушек в различные цепи, мы считали их активное сопротивление равным 0 (такие катушки называют идеальными). Но на практике любая катушка обладает ненулевым активным сопротивлением. Таким образом реальную катушку индуктивности можно представить как идеальную катушку и последовательно включенный резистор:
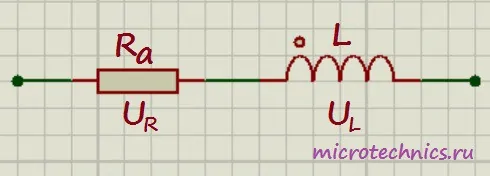
Идеальная катушка, как вы помните, не оказывает никакого сопротивления постоянному току, и напряжение на ней равно 0. В случае с реальной катушкой ситуация несколько меняется. При протекании по цепи постоянного тока напряжение на катушке будет равно:
Ну а поскольку частота тока равна 0 (постоянный ток), то реактивное сопротивление:
А что же будет происходить при включении реальной катушки индуктивности в цепь переменного тока? Давайте разбираться. Представим, что по данной цепи течет переменный ток i, тогда общее напряжение на цепи будет складываться из следующих компонент:
Напряжение на идеальной катушке, как вы помните, выражается через ЭДС самоиндукции:
u_L = -varepsilon_L = Lfrac{di}{dt}
И мы получаем для напряжения на реальной катушке индуктивности:
Отношение реактивного (индуктивного) сопротивления к активному называется добротностью и обозначается буквой Q:
Раз активное сопротивление R идеальной катушки равно 0, то значит ее добротность Q будет бесконечно большой. Соответственно, чем выше добротность катушки индуктивности, тем она ближе к идеальной. Таким образом активное сопротивление катушки мы рассмотрели, перейдем к следующему вопросу.
Энергия катушки индуктивности.
Электрический ток, протекающий через катушку способствует накоплению энергии в магнитном поле катушки. При пропадании/отключении тока эта энергия будет возвращена в электрическую цепь. С этим мы и столкнулись при рассмотрении катушек индуктивности в цепях постоянного тока. Больше тут добавить особо нечего, просто приведу формулу, по которой можно определить величину этой накопленной энергии:
Планомерно переходим к вариантам соединения катушек между собой. Все расчеты будем производить для идеальных катушек индуктивности, то есть их активные сопротивления равны 0. К слову, в большинстве теоретических задач и примеров, рассматриваются именно идеальные катушки. Но не стоит забывать о том, что в реальных цепях активное сопротивление не равно 0, и его необходимо учитывать при проведении любых расчетов.
Последовательное соединение катушек индуктивности.
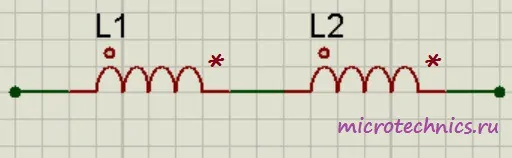
При последовательном соединении катушек индуктивности их можно заменить одной катушкой с величиной индуктивности, равной:
Вроде все просто, но тут есть один немаловажный нюанс. Данная формула справедлива только в том случае, если катушки расположены на таком расстоянии друг от друга, что магнитное поле одной катушки не пересекает витков другой:
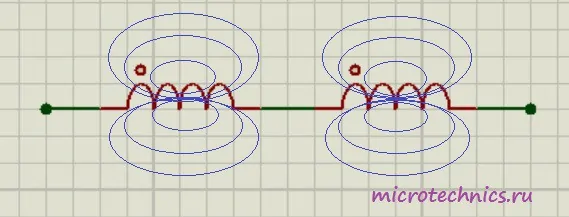
Если же катушки расположены близко друг к другу и часть магнитного поля одной катушки пронизывает вторую, то тут ситуация несколько другая. Возможны два варианта:
- магнитные потоки катушек имеют одинаковое направление
- магнитные потоки направлены навстречу друг другу
Первый случай называется согласным включением катушек – начало второй катушки подключается к концу первой. А второй вариант называют встречным включением – конец второй катушки подключается к началу первой. На схемах начало катушки обозначают символом “*“. Таким образом, на схеме, которая представлена на рисунке мы имеем согласное включение катушек индуктивности. Для этого случая общая индуктивность определяется так:
Где M – взаимная индуктивность катушек. При встречном включении последовательно соединенных катушек индуктивности:
L = L_1 + L_2medspace-medspace 2M
Можно заметить, что если потоки имеют одинаковое направление (согласное включение), то общая индуктивность увеличивается на двойную величину взаимной индуктивности. А если потоки направлены навстречу друг другу – уменьшается на ту же самую величину.
Параллельное соединение катушек индуктивности.
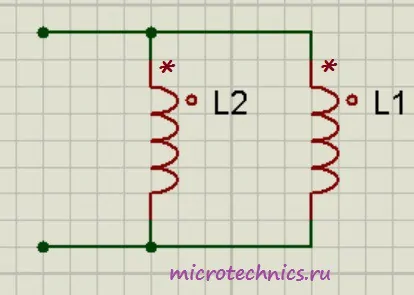
При параллельном соединении катушек индуктивности также возможны три варианта:
- Магнитное поле одной катушки не пересекает витков второй катушки, тогда: frac{1}{L_0} = frac{1}{L_1} +frac{1}{L_2} или L_0 = frac{L_1L_2}{L_1 + L_2}
- Часть магнитного потока одной катушки пронизывает витки второй и катушки включены согласно (как изображено на рисунке – то есть начала обеих катушек подключены к одному узлу). В этом случае: L_0 = frac{L_1L_2medspace-medspace M^2}{L_1 + L_2medspace-medspace 2M}
- Часть магнитного потока одной катушки пронизывает витки второй и катушки включены встречно. В этом случае: L_0 = frac{L_1L_2medspace-medspace M^2}{L_1 + L_2 + 2M}
Также как и в случае с последовательным соединением, при согласном включении общая индуктивность будет больше, чем при встречном включении, поскольку знаменатель дроби будет меньше.
Собственно, на этом заканчиваем разбор катушек индуктивности. Ранее мы изучили конденсаторы и резисторы, а в будущих статьях нам предстоит работать с цепями, включающими все эти элементы. Так что подписывайтесь на обновления и не пропускайте новые статьи 🤝
Если
в контуре с индуктивностью L
течёт ток I,
то в момент размыкания цепи возникает
индукционный ток и им совершается
работа. Эта работа совершается за счёт
энергии исчезнувшего при размыкании
цепи магнитного поля. На основании
закона сохранения и превращения энергию
магнитного поля превращается главным
образом в энергию электрического поля,
за счёт которой происходит нагревание
проводников. Работа может быть определена
из соотношения
dA=εсмIdt
Так
как
![]() ,
,
то
dA=-LIdI
Уменьшение
энергии магнитного поля равно работе
тока, поэтому
![]() (16.18)
(16.18)
Формула
справедлива для любого контура и
показывает, что энергия магнитного поля
зависит от индуктивности контура и силы
тока, протекающего по нему.
Рассчитаем
энергию однородного магнитного поля
длинного соленоида, индуктивность
которого определяется по формуле L
= μμ0n2V.
B
этом случае формула энергии примет вид
![]()
Учитывая,
что напряжённость поля внутри бесконечно
длинного соленоида Н=In,
получаем
![]() (16.19)
(16.19)
Выразим
энергию через индукцию магнитного поля
B=
μμ0H:
![]() (16.20)
(16.20)
Или
![]() (16.21)
(16.21)
Вследствие
того, что магнитное поле соленоида
однородно и локализовано внутри
соленоида, энергия распределена по
объёму соленоида с постоянной плотностью
![]() (16.22)
(16.22)
Учитывая
последние три формулы, получаем
![]()
![]()
![]()
Учитывая
правило Ленца, можно заметить, что
явление самоиндукции аналогично
проявлению инертности тел в механике.
Так, вследствие инертности тело не
мгновенно приобретает определённую
скорость, а постепенно. Так же постепенно
происходит и его торможение. То же самое,
как мы видели, происходит и с силой тока
при самоиндукции. Эту аналогию можно
провести и дальше.
![]()
и
![]()
эти
уравнения эквивалентны.
т.е.
m
~L
, υ~I
Эквивалентны
и формулы
![]()
![]()
Примеры решения задач
Пример.
В магнитном поле, изменяющемся по закону
B=B0cosωt
(B0=5мТл,
ω=5с-1),
помещён круговой проволочный виток
радиусом r=30см,
причём нормаль к витку образует с
направлением поля угол α=30º. Определите
ЭДС индукции, возникающую в витке в
момент времени t=10с.
Дано:
B=B0cosωt;
B0=5мТл=5∙10-3
Тл;
ω=5с-1;
r=30см=0,3
м;
α=30º; t=10 с.
Найти:
εi.
Решение:
Согласно
закону Фарадея,
![]() ,
,
(1)
Где
магнитный поток, сцепленный с витком
при произвольном его расположении
относительно магнитного поля.
Ф=BScosα.
По
условию задачи B=B0cosωt,
а площадь кольца S=πr2,
поэтому
Ф=πr2
B0cosωt∙cosα.
(2)
Подставив
выражение (2) в формулу (1) и продифференцировав,
получаем искомую ЭДС индукции в заданный
момент времени:
![]()
Ответ:
εi=4,69
мВ.
Пример
В
соленоиде длиной ℓ=50см и диаметром
d=6см
сила тока равномерно увеличивается на
0,3А за одну секунду. Определите число
витков соленоида, если сила индукционного
тока в кольце радиусом 3,1 см из медной
проволоки (ρ=17нОм∙м), надетом на катушку,
Iк=0,3
А.
Дано:
ℓ=50см=0,5
м; d=6см=0,06м;
![]() ;rк=3,1см=3.1∙10-2м;
;rк=3,1см=3.1∙10-2м;
ρ=17нОм∙м=17∙10-9
Ом∙м; Iк=0,3
А.
Найти:
N.
Решение.
При изменении силы тока в соленоиде
возникает ЭДС самоиндукции
![]() (1)
(1)
где
![]() –
–
индуктивность соленоида. Подставив это
выражение в (1)
с
учётом
![]()
![]() .
.
ЭДС
индукции, возникающая в одном кольце,
в N
раз меньше, чем найденное значение ЭДС
самоиндукции в соленоиде, состоящем из
N
витков, т.е.
![]() .
.
(2)
Согласно
закону Ома, сила индукционного тока в
кольце
![]() ,
,
(3)
где
![]() –
–
сопротивление кольца. Поскольку ℓк=πd,
а Sк=πrк2,
выражение (3) примет вид
![]()
Подставив
в эту формулу выражение (2), найдём искомое
число витков соленоид
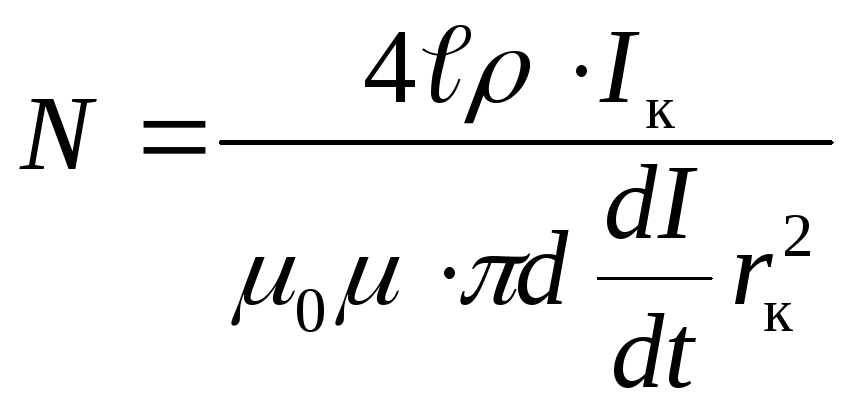 .
.
Ответ:
N=150
Пример
В
однородном магнитном поле подвижная
сторона (её длина ℓ=20см) прямоугольной
рамки (см. рисунок) перемещается
перпендикулярно линиям магнитной
индукции со скоростью υ=5 м/с. Определите
индукцию В магнитного поля, если
возникающая в рамке ЭДС индукции εi=0,2
В.
Дано:
ℓ=20см=0,2
м; υ=5 м/с; εi=0,2
В.
Найти:
B.
Р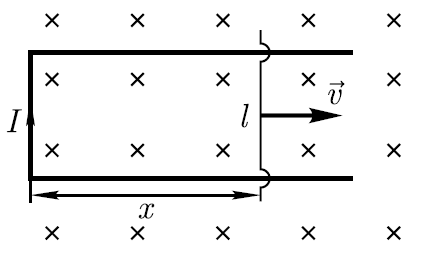 ешение.
ешение.
При движении в магнитном поле подвижной
стороны рамки поток Ф вектора магнитной
индукции сквозь рамку возрастает, что,
согласно закону Фарадея,
![]() ,
,
(1)
приводит
к возникновению ЭДС индукции.
Поток
вектора магнитной индукции, сцепленный
с рамкой,
Ф=Bℓx.
(2)
Подставив
выражение (2) в формулу (1) и учитывая, что
B
и ℓ – величины постоянные, получаем
![]()
откуда
искомая индукция магнитного поля
![]()
Ответ:
В=0,2 Тл.
Пример
В
однородном магнитном поле с индукцией
В=0,2 Тл равномерно вращается катушка,
содержащая N=600
витков, с частотой n=6
с-1.
Площадь
S
поперечного сечения катушка 100см2.
Ось вращения перпендикулярна оси катушки
и направлению магнитного поля. Определите
максимальную ЭДС индукции вращающейся
катушки.
Дано:
В=0,2
Тл; N=600;
n=6
с-1;
S=100см2=10-2
м2.
Найти:
(εi)max.
Решение.
Согласно закону Фарадея,
![]()
где
Ф – полный магнитный поток, сцеплённый
со всеми витками катушки. При произвольном
расположении катушки относительно
магнитного поля
Ф=NBScosωt,
(1)
где
круговая частота ω=2πn.
Подставив ω в (1), получим
Ф=NBScos2πnt.
Тогда
εi=-NBS2πn(-sin2πnt)=2πnNBSsin2πnt,
εi=(
εi)max
при
sin2πnt=1, поэтому
(εi)max=2πnNBS
Ответ:
(εi)max=45,2
В.
Пример
Однослойная
длинная катушка содержит N=300
витков, плотно прилегающих друг к другу.
Определите индуктивность катушки, если
диаметр проволоки d=0,7
мм (изоляция ничтожной толщины) и она
намотана на картонный цилиндр радиусом
r=1
см. .
Дано:
N=300;
d=0,7
мм=7∙10-4
м; r=1
см=10-2
м.
Найти:
L.
Решение.
Индуктивность катушки
![]() (1)
(1)
где
Ф – полный магнитный поток, сцепленный
со всеми витками катушки; I
– сила тока в катушке.
Учитывая,
что полный магнитный поток
Ф=NBS
(N-число
витков катушки; В – магнитная индукция;
S
– площадь поперечного сечения катушки);
магнитная индукция в катушке без
сердечника
![]()
(μ0
– магнитная постоянная; ℓ- длина
катушки), длина катушки
ℓ=Nd
(d-диаметр
проволоки; витки вплотную прилегают
друг к другу), площадь поперечного
сечения катушки
S=πr2,
Получим
осле подстановки записанных выражений
в формулу (1) искомую индуктивность
катушки:
![]()
Ответ:
L=1,69
мГн.
Пример
Первичная
обмотка понижающего трансформатора с
коэффициентом трансформации k=0,1
включена в сеть с источником переменного
напряжения с ЭДС ε1=220
В. Пренебрегая потерями энергии в
первичной обмотке, определите напряжение
U2
на зажимах вторичной обмотки, если её
сопротивление R2=5
Ом и сила тока в ней I2=2А.
Дано:
k=0,1;
ε1=220
В; R2=5
Ом; I2=2А.
Найти:
U2.
Решение.
В первичной обмотке под действием
переменной ЭДС ε1
возникает переменный ток I1,
создающий в сердечнике трансформатора
переменногый магнитный поток Ф, который
пронизывает вторичную обмотку. Согласно
закону Ома, для первичной обмотки
![]()
где
R1
– сопротивление первичной обмотки.
Падение напряжения I1R1
при быстропеременных полях мало по
сравнению с ε1
и ε2.
Тогда можем записать:
![]() (1)
(1)
ЭДС
взаимной индукции, возникающая во
вторичной обмотке,
![]() (2)
(2)
Из
выражений (1) и (2) получаем
![]() ,
,
где
![]() –
–
коэффициент трансформации, а знак «-»
показывает, что ЭДС в первичной и
вторичной обмотках противоположны по
фазе. Следовательно, ЭДС во вторичной
обмотке
ε2=k
ε2.
Напряжение
на зажимах вторичной обмотки
U2=
ε2-I2R2=
kε1-I2R2.
Ответ:
U2=12
В.
Пример
Соленоид
без сердечника с однослойной обмоткой
из проволоки диаметром d=0,4
мм имеет длину ℓ=0.5 м и поперечное сечение
S=60см2.
За какое время при напряжении U=10
В и силе тока I=1,5
А в обмотке выделится количество теплоты,
равное энергии поля внутри соленоида?
Поле считать однородным.
Дано:
d=0,4
мм=0,4∙10-4
м; ℓ=0,5 м; S=60см2=6∙10-3
м2;
I=1,5А;
U=10В;
Q=W.
Найти:
t.
Решение.
При прохождении тока I
при напряжении U
в обмотке за время t
выделяется теплота
Q=IUt.
(1)
Энергия
поля внутри соленоида
![]() (2)
(2)
где
![]() (N
(N
– общее число витков соленоида). Если
витки вплотную прилегают друг к другу,
то ℓ=Nd,
откуда
![]() .
.
Подставив выражение для В иN
в
(2), получаем
![]() .
.
(3)
Согласно
условию задачи, Q=W.
Приравняв выражение (1) и (3),найдём искомое
время:
![]()
Ответ:
t
=1,77 мс.
Пример
Катушка
без сердечника длиной ℓ=50 см содержит
N=200
витков. По катушке течёт ток I=1А.
Определите объёмную плотность энергии
магнитного поля внутри катушки..
Дано:
ℓ=50
см=0,5
м;
N=200; I=1 А.
Найти:
ω.
Решение.
Объёмная плотность энергии магнитного
поля (энергия единицы объёма)
![]() ,
,
(1)
где
![]() –
–
энергия магнитного поля (L
– индуктивность катушки); V=Sℓ-
объём катушки (S
– площадь катушки; ℓ- длина катушки).
Магнитная
индукция поля внутри соленоида с
сердечником с магнитной проницаемостью
μ равна
![]() .
.
Полный
магнитный поток, сцепленный со всеми
витками соленоида,
![]() .
.
Учитывая,
что Ф=LI,
получаем формулу для индуктивности
соленоида:
![]() (2)
(2)
Подставив
выражение (2) в формулу (1) с учётом того,
что
![]() ,
,
найдём искомую объёмную плотность
энергии магнитного поля внутри катушки:
![]()
Ответ:
ω=0,1
Дж/м3.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Катушка индуктивности

Катушка индуктивности – электронный компонент, представляющий собой винтовую либо спиральную конструкцию, выполненную с применением изолированного проводника. Основным свойством катушки индуктивности, как понятно из названия – индуктивность. Индуктивность – это свойство преобразовать энергию электрического тока в энергию магнитного поля. Величина индуктивности для цилиндрической или кольцевой катушки равна

Где ψ – потокосцепление, µ0 = 4π*10-7 – магнитная постоянная, N – количество витков, S – площадь поперечного сечения катушки, l – длина средней линии потока.
Также катушке индуктивности присущи такие свойства как небольшая ёмкость и малое активное сопротивление, а идеальная катушка и вовсе их лишена. Применение данного электронного компонента отмечается практически повсеместно в электротехнических устройствах. Цели применения различны:
– подавление помех в электрической цепи;
– сглаживание уровня пульсаций;
– накопление энергетического потенциала;
– ограничение токов переменной частоты;
– построение резонансных колебательных контуров;
– фильтрация частот в цепях прохождения электрического сигнала;
– формирование области магнитного поля;
– построение линий задержек, датчиков и т.д.
Энергия магнитного поля катушки индуктивности
Электрический ток способствует накоплению энергии в магнитном поле катушки. Если отключить подачу электричества, накопленная энергия будет возвращена в электрическую цепь. Значение напряжения при этом в цепи катушки возрастает многократно. Величина запасаемой энергии в магнитном поле равна примерно тому значению работы, которое необходимо получить, чтобы обеспечить появление необходимой силы тока в цепи. Значение энергии, запасаемой катушкой индуктивности можно рассчитать с помощью формулы.

Реактивное сопротивление
При протекании переменного тока, катушка обладает кроме активного, еще и реактивным сопротивлением, которое находится по формуле

По формуле видно, что в отличие от конденсатора, у катушки с увеличением частоты, реактивное сопротивление растет, это свойство применяется в фильтрах частот.
При построении векторных диаграмм важно помнить, что в катушке, напряжения опережает ток на 90 градусов.
Добротность катушки
Еще одним важным свойством катушки является добротность. Добротность показывает отношение реактивного сопротивления катушки к активному.

Чем выше добротность катушки, тем она ближе к идеальной, то есть она обладает только главным своим свойством – индуктивностью.
Конструкции катушек индуктивности

Конструктивно катушки индуктивности могут быть представлены в разном исполнении. Например, в исполнении однослойной или многослойной намотки проводника. При этом намотка провода может выполняться на диэлектрических каркасах разных форм: круглых, квадратных, прямоугольных. Нередко практикуется изготовление бескаркасных катушек. Широко применяется методика изготовления катушек тороидального типа.
Витки проводника, как правило, наматываются плотно один к одному. Однако в некоторых случаях намотка производится с шагом. Подобная методика отмечается, к примеру, когда изготавливаются высокочастотные дроссели. Намотка провода с шагом способствует снижению образования паразитной ёмкости, так же как и намотка, выполненная отдельными секциями.
Индуктивность катушки можно изменять, добавляя в конструкцию катушки ферромагнитный сердечник. Внедрение сердечников отражается на подавлении помех. Поэтому практически все дроссели, предназначенные для подавления высокочастотных помех, как правило, имеют ферродиэлектрические сердечники, изготовленные на основе феррита, флюкстрола, ферроксона, карбонильного железа. Низкочастотные помехи хорошо сглаживаются катушками на пермалоевых сердечниках или на сердечниках из электротехнической стали.
