Геометрическая вероятность
- Геометрическая вероятность на прямой
- Геометрическая вероятность на плоскости
- Геометрическая вероятность в пространстве
- Примеры
Понятие геометрической вероятности было сформулировано в §37 данного справочника. В этом параграфе мы рассмотрим различные задачи, при решении которых используется геометрическая вероятность.
п.1. Геометрическая вероятность на прямой
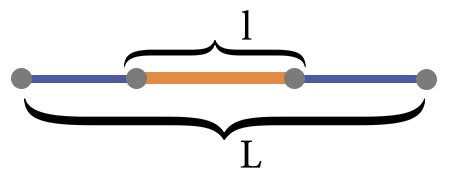
В одномерном случае пространству всех событий соответствует длина отрезка Ω ↔ L. Событие A ↔ lA – попадание в отрезок lA ≤ L.
Тогда вероятность события A $$ mathrm{ P(A)=frac{l_A}{L} } $$ Говорят, что мерой множеств событий в одномерном случае является длина.
Например:
Оптический кабель длиной 1 м случайно разрезают ножницами. Какова вероятность того, что длина обрезка составляет не меньше 80 см? 
Чтобы получить обрезок не менее 80 см, нужно попасть ножницами в отрезок 20 см справа или слева куска кабеля. Вероятности попадания (mathrm{P_{text{справа}}=frac{l_A}{L}, P_{text{слева}}=frac{l_A}{L}}). По правилу суммы, искомая вероятность при L=100 см, lA=20 см $$ mathrm{ P_{text{справа}}+P_{text{слева}}=frac{2l_A}{L}, P=frac{2cdot 20}{100}=0,4 } $$ Ответ: 0,4.
п.2. Геометрическая вероятность на плоскости
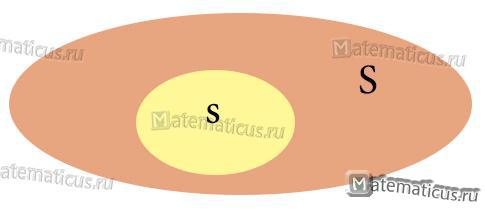
В двумерном случае пространству всех событий соответствует площадь некоторой замкнутой области Ω ↔ SΩ.
Событие A ↔ sA – попадание в замкнутую подобласть с площадью sA ≤ SΩ.
Тогда вероятность события A $$ mathrm{ P(A)=frac{s_A}{S_{Omega}} } $$ Говорят, что мерой множеств событий в двумерном случае является площадь.
Например:
Два друга договорились встретиться между 14 и 15 часами. Каждый может прийти в любой момент в течение назначенного часа. Тот, кто пришёл первым, ждёт другого в течение 15 минут, а затем уходит. Чему равна вероятность встречи? 
Пусть 0≤x≤60 (мин) и 0≤y≤60 (мин) – моменты прихода первого и второго друга соответственно. Тогда пространство событий – квадрат 60х60.
Область ожидания: |x–y|≤15. Раскроем модуль: –15≤x–y≤15. Получаем систему: (left{ begin{array}{ l} mathrm{yleq x+15} &\ mathrm{ygeq x-15} & end{array}right. ). На графике – это зелёная полоса. Событие A – встреча состоялась – соответствует площади зеленой полосы. Получаем: begin{gather*} mathrm{ S_{Omega}=60cdot 60=3600, s_A=3600-2S_{Delta}=3600-2cdot frac{1}{2}cdot 45^2=1575 }\ mathrm{ P(A)=frac{s_A}{S_{Omega}}=frac{1575}{3600}=frac{7}{16}=0,4375 } end{gather*} Ответ: 0,4375.
п.3. Геометрическая вероятность в пространстве
В трёхмерном случае пространству всех событий соответствует объём некоторой замкнутой области Ω ↔ VΩ.
Событие A ↔ vA – попадание в замкнутую подобласть с объёмом vA ≤ VΩ.
Тогда вероятность события A $$ mathrm{ P(A)=frac{v_A}{V_{Omega}} } $$ Говорят, что мерой множеств событий в трёхмерном случае является объём.
Например:
Телескоп находится на космической станции. В каждый момент времени он случайно направлен в одну из сторон и наблюдает часть неба. Пусть телескоп способен регистрировать все объекты в радиусе 10000 км. Какова вероятность, что он заметит астероид радиусом 100 км, залетевший в область регистрации? 
Пространству всех событий соответствует сфера объемом: $$ mathrm{ V_{Omega}=frac{4}{3}pi R^3, R=10000 text{км} } $$ Событие A – астероид замечен – соответствует объему астероида: $$ mathrm{ v_{A}=frac{4}{3}pi R^3, R=100 text{км} } $$ Вероятность того, что астероид будет замечен: $$ mathrm{ P(A)=frac{v_{A}}{V_{Omega}}=frac{frac{4}{3}pi R^3}{frac{4}{3}pi R^3}=left(frac{r}{R}right)^3, P(A)=left(frac{100}{10000}right)^3=10^{-6}=0,000001 } $$ Ответ: 0,000001.
п.4. Примеры
Пример 1. Для игры в «Дартс» используется круглая мишень радиусом 40 см. Центральный круг – «десятка» – имеет радиус 4 см. Если игрок всегда попадает в мишень в любую точку с одинаковой вероятностью, какова вероятность попасть в «десятку»?
Мерой для этой задачи является площадь.
Пространство всех событий – круг радиусом R = 40 см. Его площадь (mathrm{ S_{Omega;}=pi R^2}).
Событие A – попадание в «десятку» – круг радиусом r = 4 см. Его площадь (mathrm{ s_{A}=pi r^2}).
Вероятность попадания: $$ mathrm{ P(A)=frac{s_{A}}{S_{Omega}}=frac{pi r^2}{pi R^2}=left(frac{r}{R}right)^2, P(A)=left(frac{4}{40}right)^2=0,01 } $$ Ответ: 0,01.
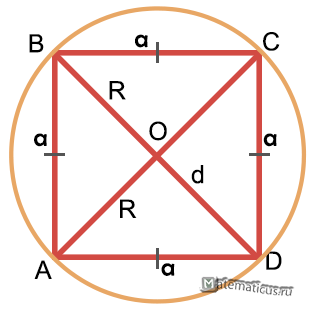
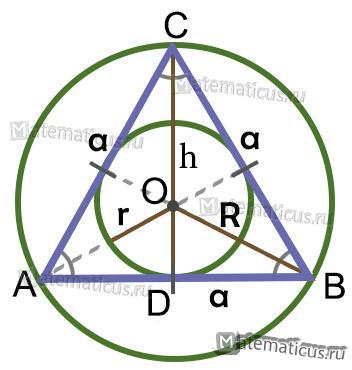
Пример 2. В правильный треугольник вписан полукруг. В треугольник случайно ставятся точки. Какова вероятность, что точка попадет в полукруг?
Мерой в данной задаче является площадь.
Пусть сторона треугольника a. Тогда пространство всех событий – треугольник площадью (mathrm{ S_{Omega}=frac{sqrt{3}}{4}a^2}).
Найдем радиус вписанного полукруга.
ΔCOB ~ ΔOEB – по двум углам. $$ mathrm{ frac{CO}{OE}=frac{CB}{OB}Rightarrowfrac{acdot sin60^{circ}}{r}=frac{a}{a/2}Rightarrow r=frac{a}{2}cdot sin60^{circ}=frac{sqrt{3}}{4}a } $$ Площадь вписанного полукруга: (mathrm{ s_{A}=frac{pi r^2}{2}=frac{pi}{2}left(frac{sqrt{3}}{4}aright)^2=frac{3pi}{32}a^2}).
Вероятность попасть в полукруг: $$ mathrm{ P(A)=frac{s_{A}}{S_{Omega}}=frac{frac{3pi}{32}a^2}{frac{sqrt{3}}{4}a^2}=frac{sqrt{3}}{8}pi approx 0,68 } $$ Ответ: (mathrm{ frac{sqrt{3}}{8}pi approx 0,68. })
Пример 3. На отрезке [0; 1] случайным образом выбирается точка. Найдите вероятность того, что её координата x удовлетворяет условиям:
1) x2 > 0,64
2) (left{ begin{array}{ l} mathrm{0,3x^2leq 0,027} &\ mathrm{2x^2geq 0,08} & end{array}right. )
1) (mathrm{x^2geq 0,64Rightarrow (x^2-0,64)geq 0Rightarrow (x-0,8)(x+0,8)geq 0Rightarrow} left{ begin{array}{ l} mathrm{xleq -0,8} &\ mathrm{xgeq 0,8} & end{array}right. )
Учитывая x ∈ [0; 1], получаем: $$ left{ begin{array}{ l} mathrm{0leq xleq 1} &\ left[ begin{array}{ l} mathrm{xleq -0,8Rightarrow 0,8leq xleq 1} &\ mathrm{xgeq 0,8} & end{array}right.& end{array}right. $$ Мерой в данной задаче является длина: LΩ = 1, lA = 1 – 0,8 = 0,2
Вероятность выбора точки при данных условиях: ( mathrm{P(A)=frac{0,2}{1}=0,2} )
begin{gather*} 2) left{ begin{array}{ l} mathrm{0,3x^2leq 0,027} &\ mathrm{2x^2geq 0,08} & end{array}right. Rightarrow left{ begin{array}{ l} mathrm{x^2leq 0,009} &\ mathrm{x^2geq 0,004} & end{array}right. Rightarrow left{ begin{array}{ l} mathrm{x^2-0,009leq 0} &\ mathrm{x^2-0,004geq 0} & end{array}right. Rightarrow left{ begin{array}{ l} mathrm{(x-0,3)(x+0,3)leq 0} &\ mathrm{(x-0,2)(x+0,2)geq 0} & end{array}right. Rightarrow \ Rightarrow left{ begin{array}{ l} mathrm{-0,3leq xleq 0,3} &\ left[ begin{array}{ l} mathrm{xleq -0,2} &\ mathrm{xgeq 0,2} & end{array}right.& end{array}right. Rightarrow left[ begin{array}{ l} mathrm{-0,3leq xleq -0,2} &\ mathrm{0,2leq xleq 0,3} & end{array}right. end{gather*} Учитывая x ∈ [0; 1], получаем: $$ left{ begin{array}{ l} mathrm{0leq xleq 1} &\ left[ begin{array}{ l} mathrm{-0,3leq xleq -0,2} &\ mathrm{0,2leq xleq 0,3} & end{array}right.& end{array}right. Rightarrow 0,2 leq x leq 0,3 $$ Мерой в данной задаче является длина: LΩ = 1, lA = 0,3 – 0,2 = 0,1
Вероятность выбора точки при данных условиях: (mathrm{P(A)=frac{0,1}{1}=0,1})
Ответ: 1) 0,2; 2) 0,1.
Пример 4. В сито, наполненное до краёв зерном, уронили жемчужину. Сито представляет собой цилиндр радиусом 20 см и высотой 12 см.
1) Какова вероятность случайно зачерпнуть горсть зерна вместе с жемчужиной, если объём горсти 0,1 л?
2) Если после неудачной попытки, высыпать зерно из горсти обратно в сито, перемешать, и снова зачерпнуть горсть, изменится ли вероятность?
3) Если после неудачной попытки, высыпать зерно из горсти в сторону и зачерпнуть следующую горсть, изменится ли вероятность?
4) Сколько «неудачных» горстей нужно отсыпать в сторону, чтобы вероятность удачи для следующей попытки превысила 1/3?
1) Мерой для этой задачи является объём.
Пространство всех событий – все возможные точки, где может оказаться жемчужина – это цилиндрическое сито, объемом
VΩ = πR2h, R = 20 см = 2 дм, h = 12 см = 1,2 дм
VΩ = π · 22 · 1,2 = 4,8 π дм3 = 4,8 π л
Событие A – зачерпнуть жемчужину в горсти объемом vA = 0,1 л
Вероятность: $$ mathrm{ P(A)=frac{v_{A}}{V_{Omega}}, P(A)=frac{0,1}{4,8pi} approx 0,0066 } $$ 2) Если высыпать зерно обратно из горсти и перемешать, то пространство всех событий останется тем же, VΩ = 4,8π л. Вероятность не изменится.
3) Если высыпать зерно в сторону, пространство всех событий уменьшится:
V‘Ω = VΩ – vA = (4,8π – 0,1) л
Вероятность увеличится: $$ mathrm{ P(A)=frac{v_{A}}{V_{Omega}^{‘}}, P(A)=frac{0,1}{4,8pi -0,1} approx 0,0071 } $$
4) После того, как мы отсыпаем N горстей, пространство всех событий $$ mathrm{ V_{Omega}^{”} = V_{Omega}-Nv_{A}=(4,8pi-0,1N) text{л} } $$ По условию: $$ mathrm{ P(A)frac{0,1}{4,8pi -0,1N}geq frac13 } $$ Получаем: (mathrm{4,8pi -0,1Nlt 0,3Rightarrow Ngt frac{4,8pi-0,3}{0,1}=147,8})
N = 148.
Ответ: 1) 0,0066; 2) нет; 3) увеличится, 0,0071; 4) 148.
Пример 5. Загадываются два действительных числа от 0 до 4.
1) Какова вероятность, что их сумма больше 3?
2) Какова вероятность, что их разность меньше 1?
По условию 0 ≤ x ≤ 4, 0 ≤ y ≤ 4
Мерой для этой задачи является площадь.
Пространство всех событий: квадрат 4х4, SΩ = 42 = 16.
Ответ: (mathrm{ 1) frac{23}{32}; 2) frac{7}{16}. })
Классическое определение вероятности оказывается эффективным для решения целого спектра задач, но с другой стороны, обладает и рядом ограничений. Одним из таких ограничений является тот факт, что оно неприменимо к испытаниям с бесконечным количеством исходов. Простейший пример:
На отрезок ![]() наудачу бросается точка. Какова вероятность того, что она попадёт в промежуток
наудачу бросается точка. Какова вероятность того, что она попадёт в промежуток ![]() ?
?

Поскольку на отрезке бесконечно много точек, то здесь нельзя применить формулу ![]() (ввиду бесконечно большого значения «эн») и поэтому на помощь приходит другой подход, называемый геометрическим определением вероятности:
(ввиду бесконечно большого значения «эн») и поэтому на помощь приходит другой подход, называемый геометрическим определением вероятности:
Вероятность наступления некоторого события ![]() в испытании равна отношению
в испытании равна отношению ![]() , где
, где ![]() – геометрическая мера, выражающая общее число всех возможных и равновозможных исходов данного испытания, а
– геометрическая мера, выражающая общее число всех возможных и равновозможных исходов данного испытания, а ![]() – мера, выражающая количество благоприятствующих событию
– мера, выражающая количество благоприятствующих событию ![]() исходов.
исходов.
На практике в качестве такой геометрической меры чаще всего выступает длина или площадь, реже – объём.
Рассмотрим событие: ![]() – брошенная на отрезок
– брошенная на отрезок ![]() точка, попала в промежуток
точка, попала в промежуток ![]() . Очевидно, что общее число исходов выражается длиной бОльшего отрезка:
. Очевидно, что общее число исходов выражается длиной бОльшего отрезка: ![]() , а благоприятствующие событию
, а благоприятствующие событию ![]() исходы – длиной вложенного отрезка:
исходы – длиной вложенного отрезка: ![]() По геометрическому определению вероятности:
По геометрическому определению вероятности:
![]()
Примечание:![]() – метрические единицы: метры, сантиметры или какие-то др.
– метрические единицы: метры, сантиметры или какие-то др.
Слишком просто? Как и в случае с классическим определением, это обманчивое впечатление. Обстоятельно и добросовестно разбираемся в практических примерах:
Задача 28
Метровую ленту случайным образом разрезают ножницами. Найти вероятность того, что длина обрезка составит не менее 80 см.
Решение: «чего тут сложного? Вероятность равна ![]() ». Это автоматическая ошибка, которую допускают по небрежности. Да, совершенно верно – длина обрезка составит не менее 80 см, если от ленты отрезать меньше 20 сантиметров. Но здесь часто забывают, что искомый разрез можно сделать как с одного конца ленты, так и с другого:
». Это автоматическая ошибка, которую допускают по небрежности. Да, совершенно верно – длина обрезка составит не менее 80 см, если от ленты отрезать меньше 20 сантиметров. Но здесь часто забывают, что искомый разрез можно сделать как с одного конца ленты, так и с другого:
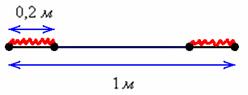
Рассмотрим событие: ![]() – длина обрезка составит не менее 0,8 м.
– длина обрезка составит не менее 0,8 м.
Поскольку ленту можно разрезать где угодно, то общему числу исходов соответствует её длина: ![]() Благоприятствующим исходам соответствуют участки, отмеченные красным цветом, и их суммарная длина равна:
Благоприятствующим исходам соответствуют участки, отмеченные красным цветом, и их суммарная длина равна: ![]()
По геометрическому определению:
![]()
Ответ: 0,4
Какой можно сделать вывод?
Даже если задача кажется вам очень простой, НЕ СПЕШИТЕ
При оформлении задач следует обязательно указывать размерность (единицы, метры, квадратные единицы, квадратные метры и т.д.). Кстати, обратите внимание, что на финальном этапе вычислений геометрическая мера сокращается. Так в рассмотренном примере, сократились метры:
![]() , в результате чего получилась привычная безразмерная вероятность.
, в результате чего получилась привычная безразмерная вероятность.
Следующая задача для самостоятельного решения:
Задача 29
После бури на участке между 40-м и 70-м километрами телефонной линии произошёл обрыв провода. Какова вероятность того, что он произошёл между 50-м и 55-м километрами линии?
Значительно чаще встречаются примеры, в которых фигурируют площади:
Задача 30
В треугольник со сторонами ![]() вписан круг. Точка
вписан круг. Точка ![]() произвольно ставится в треугольник. Найти вероятность того, что точка попадёт в круг.
произвольно ставится в треугольник. Найти вероятность того, что точка попадёт в круг.
Вспоминаем геометрию: вписанный круг лежит внутри треугольника и касается его сторон в трёх точках. …Представили? Отлично!
Решение: поскольку точка ставится в треугольник, а круг лежит внутри, то общему числу исходов соответствует площадь треугольника, а множеству благоприятствующих исходов – площадь вписанного круга.
Осталось вспомнить или отыскать (проще всего в Сети) школьные геометрические формулы. Если даны длины сторон треугольника, то его площадь удобно найти по формуле Герона:
![]() , где
, где ![]() – длины сторон треугольника, а
– длины сторон треугольника, а ![]() – полупериметр.
– полупериметр.
Сначала вычислим полупериметр треугольника: ![]() , а затем его площадь:
, а затем его площадь:
![]()
Площадь круга найдём по известной формуле ![]() . Если круг вписан в треугольник, то его радиус можно рассчитать по формуле
. Если круг вписан в треугольник, то его радиус можно рассчитать по формуле ![]() , этого я не вообще не знал – только что нашёл в Интернете.
, этого я не вообще не знал – только что нашёл в Интернете.
Итак, площадь вписанного круга:
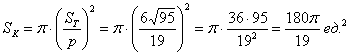
По геометрическому определению:
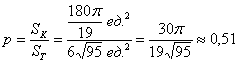 – вероятность того, что точка
– вероятность того, что точка ![]() попадёт во вписанный круг.
попадёт во вписанный круг.
Ответ: ![]()
Более простой пример для самостоятельного решения:
Задача 31
В круге радиуса 10 см находится прямоугольный треугольник с катетами 12 и 7 см. В круг наудачу ставится точка. Найти вероятность того, что она не попадёт в данный треугольник.
Следует отметить, что в этой задаче треугольник вовсе не обязан как-то касаться окружности, он просто расположен внутри круга и всё. Будьте внимательны!
А теперь рассмотрим широко известную задачу о встрече:
Задача 32
Две грузовые машины могут подойти на погрузку в промежуток времени от 19.00 до 20.30. Погрузка первой машины длится 10 минут, второй – 15 минут. Какова вероятность того, что одной машине придется ждать окончания погрузки другой?
Решение: сначала выясним длительность временнОго промежутка, на котором могут пересечься автомобили: это 90 минут (коль скоро, от 19.00 до 20.30). Изобразим прямоугольную систему координат, где в подходящем масштабе построим квадрат размером 90 на 90 единиц:
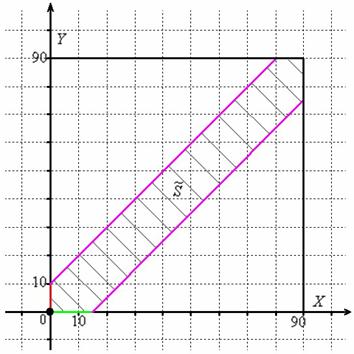
Общему множеству исходов соответствует площадь данного квадрата:
![]()
Далее по оси ![]() от начала координат откладываем время погрузки одного автомобиля (зелёная линия), а по оси
от начала координат откладываем время погрузки одного автомобиля (зелёная линия), а по оси ![]() – время погрузки другого автомобиля (красная линия) (можно наоборот, это не повлияет на решение).
– время погрузки другого автомобиля (красная линия) (можно наоборот, это не повлияет на решение).
Теперь из правого конца зелёного отрезка и из верхнего конца красного отрезка под углом 45 градусов проводим две линии внутри квадрата (малиновые отрезки).
Множеству благоприятствующих исходов (когда автомобили «пересекутся» во времени) соответствует площадь ![]() заштрихованной фигуры. В принципе, её можно вычислить «на пальцах», но технически проще использовать окольный путь, а именно, вычислить площади двух прямоугольных треугольников. Используем формулу:
заштрихованной фигуры. В принципе, её можно вычислить «на пальцах», но технически проще использовать окольный путь, а именно, вычислить площади двух прямоугольных треугольников. Используем формулу:
![]() , где
, где ![]() – длины катетов.
– длины катетов.
В нашей задаче: верхний треугольник имеет катеты длиной по 80 единиц, нижний треугольник – по 75 единиц. Обратите внимание, что в общем случае эти треугольники не равны.
Таким образом, суммарная площадь треугольников составляет:
![]()
И бесхитростный заключительный манёвр: из площади квадрата вычитаем площади треугольников, получая тем самым благоприятствующую площадь:
![]()
По геометрическому определению:
![]() – вероятность того, что одной машине придется ждать окончания погрузки другой.
– вероятность того, что одной машине придется ждать окончания погрузки другой.
Ответ: ![]()
Подробное объяснение этого способа решения можно найти, например, в учебном пособии В.Е. Гмурмана, я же остановился лишь на техническом алгоритме, дабы не тратить ваше драгоценное время.
И если в разобранной задаче встреча явно нежелательна, то в следующей, скорее, наоборот. Романтичный эпизод для самостоятельного изучения:
Задача 33
Студенты случайным образом приходят в столовую с 14.00 до 15.00, при этом обед каждого из них занимает примерно 20 минут. Найти вероятность того, что: а) Коля встретится с Олей во время обеда, б) данная встреча не состоится.
Не нужно печалиться по поводу пункта «бэ» – любовь приходит и уходит, а кушать хочется всегда! =)
Решение, чертёж и ответ в конце книги.
Оставшиеся примеры параграфа посвящены не менее распространённому типу задач, где фигурируют неравенства.
Для начала разогревающий пример:
Задача 34
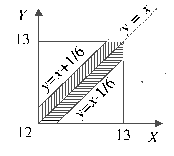
В квадрат с вершинами ![]() наудачу брошена точка
наудачу брошена точка ![]() . Найдите вероятность того, что координаты этой точки удовлетворяют неравенству
. Найдите вероятность того, что координаты этой точки удовлетворяют неравенству![]() .
.
Решение: изобразим на чертеже искомый квадрат и прямую ![]() :
:
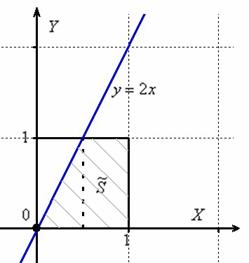
Общему множеству исходов соответствует площадь квадрата ![]()
Прямая ![]() делит квадрат на треугольник и трапецию. Как определить фигуру, которая удовлетворяет условию
делит квадрат на треугольник и трапецию. Как определить фигуру, которая удовлетворяет условию ![]() ? Вспоминаем линейные неравенства: нужно взять любую точку, не принадлежащую прямой
? Вспоминаем линейные неравенства: нужно взять любую точку, не принадлежащую прямой ![]() , например, точку
, например, точку ![]() и подставить её координаты в неравенство:
и подставить её координаты в неравенство:
![]()
Получено верное неравенство, значит, множеству благоприятствующих исходов соответствует площадь ![]() трапеции. Рассчитаем данную площадь как сумму площадей прямоугольного треугольника и прямоугольника (разделены на чертеже пунктиром):
трапеции. Рассчитаем данную площадь как сумму площадей прямоугольного треугольника и прямоугольника (разделены на чертеже пунктиром):
![]()
По геометрическому определению:
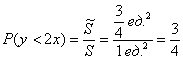 – вероятность того, что координаты брошенной в данный квадрат точки удовлетворяют неравенству
– вероятность того, что координаты брошенной в данный квадрат точки удовлетворяют неравенству![]() .
.
Ответ: ![]()
…аналитическую геометрию немного вспомнили, теперь на очереди математический анализ, ибо неравенства бывают не только линейными:
Задача 35
Загадываются два числа ![]() и
и ![]() в промежутке от 0 до 5. Какова вероятность, что
в промежутке от 0 до 5. Какова вероятность, что ![]() ?
?
Схема решения уже знакома: коль скоро загадываются 2 произвольных числа от нуля до пяти (они могут быть и иррациональными), то общему количеству исходов соответствует площадь квадрата ![]()
Изобразим ветвь гиперболы ![]() , которая делит квадрат на две части:
, которая делит квадрат на две части:
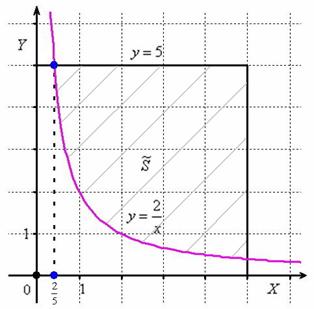
Теперь выясним, какой из этих двух «кусков» удовлетворяет неравенству ![]() . Для этого выберем любую точку, не принадлежащую гиперболе, проще всего взять
. Для этого выберем любую точку, не принадлежащую гиперболе, проще всего взять ![]() , и подставим её координаты в наше неравенство:
, и подставим её координаты в наше неравенство:
![]()
Получено неверное неравенство, а значит, условию ![]() соответствует «верхний кусок», площадь
соответствует «верхний кусок», площадь ![]() которого, деваться тут некуда, придётся вычислить с помощью определённого интеграла. Уточним нижний предел интегрирования аналитически (найдём точку пересечения гиперболы
которого, деваться тут некуда, придётся вычислить с помощью определённого интеграла. Уточним нижний предел интегрирования аналитически (найдём точку пересечения гиперболы ![]() и прямой
и прямой ![]() ):
):
![]()
На отрезке ![]() прямая
прямая ![]() расположена не ниже гиперболы
расположена не ниже гиперболы ![]() , по соответствующей формуле:
, по соответствующей формуле:
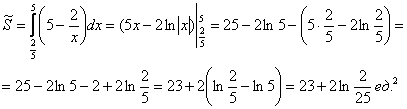
По геометрическому определению:
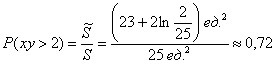 – вероятность того, что произведение двух загаданных в промежутке от 0 до 5 чисел окажется больше двух.
– вероятность того, что произведение двух загаданных в промежутке от 0 до 5 чисел окажется больше двух.
Ответ: ![]()
Аналогичный пример для самостоятельного решения:
Задача 36
Загадываются два числа ![]() и
и ![]() в промежутке от 0 до 10. Какова вероятность, что
в промежутке от 0 до 10. Какова вероятность, что ![]() ?
?
Данная задача (как, собственно, и предыдущая) допускает несколько способов расчёта площади, подумайте, какой путь более рационален.
В заключение следует отметить, что геометрическое определение вероятности тоже обладает своими недостатками. Один из них заключается в своеобразном парадоксе, давайте вспомним самый первый пример с отрезком ![]() , на который случайным образом падает точка. Возможно ли, что точка попадёт, например, на самый край отрезка? Да, такое событие возможно, но по геометрическому определению, его вероятность равна нулю! И то же самое можно сказать о любой точке отрезка! Дело в том, что с позиций геометрии размеры отдельно взятой точки равны нулю, и поэтому геометрическое определение вероятности здесь не срабатывает.
, на который случайным образом падает точка. Возможно ли, что точка попадёт, например, на самый край отрезка? Да, такое событие возможно, но по геометрическому определению, его вероятность равна нулю! И то же самое можно сказать о любой точке отрезка! Дело в том, что с позиций геометрии размеры отдельно взятой точки равны нулю, и поэтому геометрическое определение вероятности здесь не срабатывает.
 1.6.1. Теорема сложения вероятностей несовместных событий
1.6.1. Теорема сложения вероятностей несовместных событий
 1.4. Классическое определение вероятности
1.4. Классическое определение вероятности
| Оглавление |
Полную и свежую версию этой книги в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
Геометрическое определение вероятности применимо для несовместных событий, в которых число равновозможных исходов бесконечно, например, попадания точки на участок отрезка, плоскости, пространства, объёма.
Общая формула для определения геометрической вероятности:
$Pleft( A right) = frac{{mesleft( g right)}}{{mesleft( G right)}}$
Отношение меры области g, благоприятствующей событию А, к мере всей области G.
Формула геометрической вероятности попадания точки на участок отрезка L для одномерного пространства равна:
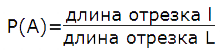
Формула геометрической вероятности попадания точки в область пространства S для фигур в двухмерном пространстве равна:
![]()
Формула геометрической вероятности попадания точки в заданный объём для фигур в трёхмерном пространстве V равна:
![]()

На отрезок OA длины L числовой оси Ох наудачу поставлена точка В(х). Найти вероятность того, что меньший из отрезков OB и BA имеет длину, большую, чем L/3. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения на числовой оси.
Решение
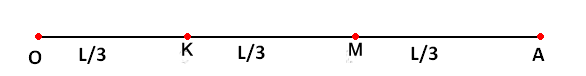

На отрезке L длины 20 см помещен меньший отрезок l длины 10 см. Найти вероятность того, что точка, наудачу поставленная на больший отрезок, попадет также и на меньший отрезок. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения.
Решение
Аналогично первому примеру, вероятность равна:
P(A)=l/L=10/20=1/2
В круг радиуса R помещен меньший круг радиуса r. Найти вероятность того, что точка, наудачу брошенная в большой круг, попадет также и в малый круг. Предполагается, что вероятность попадания точки в круг пропорциональна площади круга и не зависит от его расположения.
Решение
Вероятность того, что точка, наудачу брошенная в большой круг, попадет в малый круг равна:
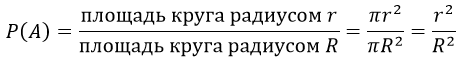
Данный ниже рисунок показывает графически отношение (нажмите на рисунок)
Пример 4
Быстро вращающийся диск разделен на четное число равных секторов, попеременно окрашенных в белый и черный цвет. По диску произведен выстрел. Найти вероятность того, что пуля попадет в один из белых секторов. Предполагается, что вероятность попадания пули в плоскую фигуру пропорциональна площади этой фигуры
Решение
P(A)=0.5·πr2/πr2=0.5
Пример 5
Два студента условились встретиться в определенном месте между 12 и 13 часами дня. Пришедший первым ждет второго в течение 1/4 часа, после чего уходит. Найти вероятность того, что встреча состоится, если каждый студент наудачу выбирает момент своего прихода (в промежутке от 12 до 13 часов).
Решение
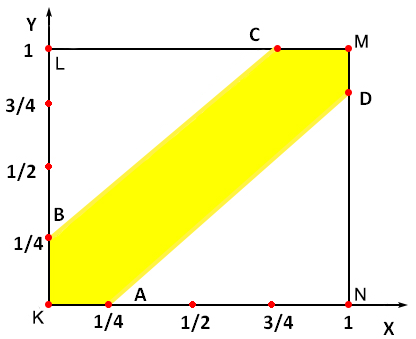
Многоугольник KBCMDA — есть многоугольник моментов встречи студентов, каждый из которых ждет другого не более 1/4 часа, то есть 15 минут, тогда
$Pleft( A right) = frac{{{S_{KBCMDA}}}}{{{S_{KLMN}}}}$
SKBCMDA=SKLMN–2 · SBLC
SKLMN=1
SBLC = 0,5·BL·LC = 1/2·3/4·3/4 = 9/32
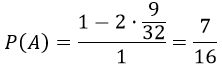
Пример 6
Внутрь круга радиуса R наудачу брошена точка. Найти вероятность того, что точка окажется внутри вписанного в круг:
а) квадрата;
б) правильного треугольника.
Предполагается, что вероятность попадания точки в часть круга пропорциональна площади этой части и не зависит от ее расположения относительно круга.
Решение
a)
Вероятность того, что точка окажется внутри вписанного в круг квадрата равна:
![]()
$AB = frac{{AC}}{{sqrt 2 }} = frac{{2R}}{{sqrt 2 }} = sqrt 2 R$
${S_{ABCD}} = A{B^2} = {left( {sqrt 2 R} right)^2} = 2{R^2}$
${S_{ABCD}} = 2 {R^2}$
Sкруга=πR2
$$Pleft( A right) = frac{{2 cdot {R^2}}}{{pi cdot {R^2}}} = frac{2}{pi }$$
б)

Геометрическая вероятность
В
одном специальном случае дадим правило
расчёта вероятности события для
случайного эксперимента с несчетным
множеством исходов.
Если
между множеством
элементарных исходов случайного
эксперимента и множеством точек некоторой
плоской фигуры
(сигма большая) можно установить
взаимно-однозначное соответствие, а
также можно установить взаимно-однозначное
соответствие между множеством элементарных
исходов, благоприятствующих событию
А, и
множеством точек плоской фигуры
(сигма малая), являющейся частью фигуры
,
то
![]()
,
где
s –
площадь фигуры ,
S —
площадь фигуры .
Здесь, естественно, подразумевается,
что фигуры
и
имеют площади. В частности, например,
фигура
может представлять собой отрезок прямой
линии, с площадью, равной нулю.
Заметим,
что в этом определении вместо плоской
фигуры
можно рассматривать промежуток ,
а вместо её части
– промежуток ,
целиком принадлежащий промежутку ,
и вероятность представлять как отношение
длин соответствующих промежутков.
Пример.
Два человека обедают в столовой, которая
открыта с 12 до 13 часов. Каждый из них
приходит в произвольный момент времени
и обедает в течение 10 минут. Какова
вероятность их встречи?
Пусть
x — время прихода первого
в столовую, а y
— время прихода второго
![]()
.

Рис.6
Можно
установить взаимно-однозначное
соответствие между всеми парами чисел
(x;y)
(или множеством исходов) и множеством
точек квадрата со стороной, равной 1, на
координатной плоскости, где начало
координат соответствует числу 12 по оси
X и по
оси Y,
как изображено на рисунке 6. Здесь,
например, точка А
соответствует исходу, заключающемуся
в том, что первый пришел в 12.30, а второй
– в 13.00. В этом случае, очевидно, встреча
не состоялась.
Если
первый пришел не позже второго (y
x), то встреча произойдет
при условии 0
y – x
1/6 (10 минут – это 1/6 часа).
Если
второй пришел не позже первого (x y),
то встреча произойдет при условии 0
x – y
1/6..
Между
множеством исходов, благоприятствующих
встрече, и множеством точек области ,
изображенной на рисунке 7 в заштрихованном
виде, можно установить взаимно-однозначное
соответствие.
Рис.
7
Искомая
вероятность p
равна отношению площади области
к площади всего квадрата. Площадь
квадрата равна единице, а площадь области
можно определить как разность единицы
и суммарной площади двух треугольников,
изображенных на рисунке 7. Отсюда
следует:
![]()
Задачи с решениями.
Задача
I.
На
шахматную доску с шириной клетки 5 см
брошена монета радиуса 1,5 см. Найти
вероятность того, что монета не попадёт
ни на одну границу клетки.
Задача
II.
Через
реку шириной 100 м перекинут мост. В
некоторый момент, когда на мосту находятся
два человека, мост рушится, и оба они
падают в реку. Первый умеет плавать и
спасётся. Второй плавать не умеет, и
спасётся, только если упадёт не далее
10-ти метров от берега или не далее, чем
в 10-ти метрах от первого. Какова
вероятность, что второй человек спасётся?
Задача
III.
Противотанковые
мины поставлены на прямой через 15 м.
Танк шириной в 2 м. едет перпендикулярно
этой прямой. Какова вероятность, что он
не подорвется на мине?
Задача
VI.
На
промежутке (0; 2) случайным образом
выбираются два числа. Найти вероятность
того, что квадрат большего числа меньше,
чем меньшее число
Задача
V.
На
отрезок бросаются наудачу две точки.
Они разбивают отрезок на три части.
Какова вероятность того, что из полученных
отрезков можно составить треугольник?
Задача
VI.
На
отрезок бросают наудачу три точки, одну
за другой. Какова вероятность того, что
третья по счёту точка упадёт между двумя
первыми?
Решения.
З
адача
I. Положение монеты
на шахматной доске полностью определяется
положением её геометрического центра.
Всё множество исходов можно изобразить
в виде квадрата
со стороной 5. Всё множество благоприятных
исходов тогда изображается в виде
квадрата ,
лежащего внутри квадрата ,
как это изображено на рисунке 1.
Искомая
вероятность тогда равна отношению
площади малого квадрата к площади
большого квадрата, то есть, 4/25
З
адача
II. Обозначим через
х
расстояние от левого берега реки до
точки падения первого человека, а через
у –
расстояние от левого берега до точки
падения второго человека. Очевидно, что
и х, и
у
принадлежат промежутку (0; 100). Таким
образом, можно заключить, что всё
множество исходов можно отобразить на
квадрат, левый нижний угол которого
лежит в начале координат, а правый
верхний – в точке с координатами
(100; 100). Две полосы: 0 < y < 10
и 90 < y < 100
являются изображениями тех исходов,
при которых второй упал в воду не далее
10-ти метров от берега. Если .у > x,
то есть второй упал ближе к правому
берегу, чем первый, то для того, чтобы
он был спасён, должно выполняться условие
у < х + 10.
Если у < x,
то есть второй упал ближе к левому
берегу, чем первый, то для его спасения
нужно, чтобы выполнялось условие
у > х – 10.
Из сказанного следует, что все благополучные
для второго человека исходы отображаются
в заштрихованную область на рисунке 2.
Площадь этой области легче всего
подсчитать, вычитая из площади всего
квадрата площади двух незаштрихованных
треугольников, что даёт в результате
10000–6400=3600. Искомая вероятность равна
0,36.
Задача
III.
П
о
условию задачи положение танка на
промежутке между двумя соседними минами
полностью определяется положением
прямой линии, равноотстоящей от бортов
танка. Эта линия перпендикулярна линии,
по которой установлены мины, и танк
подрывается на мине, если эта линия
расположена ближе, чем в 1-м метре от
края промежутка. Таким образом, всё
множество исходов отображается в
промежуток длиной 15, а множество
благоприятных исходов отображается в
промежуток длиной 13, как показано на
рисунке 3, Искомая вероятность равна
13/15.
Задача
IV.
О
бозначим
одно из чисел х,
а другое – у.
Всё множество возможных исходов
отображается в квадрат ОBCD
, две стороны которого совпадают с осями
координат и имеют длину, равную 2, как
показано на рисунке 4. Допустим, что
у – меньшее
число. Тогда множество исходов отображается
в треугольник ОCD
с площадью, равной 2. Выбранные числа
должны удовлетворять двум неравенствам:
у < х,
у > х2
Множество
чисел, удовлетворяющих этим неравенствам
отображается в заштрихованную область
на рисунке 4. Площадь этой области
определяется как разность площади
треугольника OEG,
равной 1/2, и площади криволинейного
треугольника OFEG.
Площадь
этого криволинейного
треугольника определяется формулой
![]()
и
равна 1/3. Отсюда получаем, что площадь
заштрихованной фигуры OEF
равна 1/6. Таким образом, искомая вероятность
равна 1/12.
Задача
V.
Пусть
длина отрезка равна l.
Если принять за х
и у
расстояния от левого конца отрезка до
точек, о которых говорится в условии
задачи, то множество всех исходов можно
отобразить на квадрат со стороной l,
одна из сторон которого лежит на
координатной оси х,
а другая – на координатной оси у.
Если принять условие у > х,
то множество исходов отобразится на
треугольник OВС,
изображенный на рисунке 5. Площадь этого
треугольника равна l2/2.
Полученные отрезки будут иметь длины:
х,
у – х
и l у.
Теперь вспомним геометрию. Из трёх
отрезков можно составить треугольник
тогда и только тогда, когда длина каждого
отрезка меньше суммы длин двух других
отрезков. Это условие в нашем случае
приводит к системе трёх неравенств


Первое
неравенство преобразуется к виду
х < l/2,
второе – к виду у > l/2,
а третье неравенство – к виду у < х + l/2.
Множество пар чисел х,
у,
являющееся решением системы неравенств
отображается в заштрихованный треугольник
на рисунке 5. Площадь этого треугольника
в 4 раза меньше площади треугольника
OВС. Отсюда
следует, что ответ задачи составляет
1/4.
З

адача
VI.
Примем
длину отрезка за l.
Пусть расстояние от левого конца отрезка
до первой точки равно х,
до второй точки – у,
а до третьей точки – z.
Тогда всё множество исходов отображается
в куб, три ребра которого лежат на осях
х, у
и z
прямоугольной системы координат, и с
ребром длиной l.
Допустим, что у > х.
Тогда множество исходов отобразится в
прямую призму АВСА1В1С1,
изображенную на рисунке 6. Условие z > x
означает, что все исходы будут отображаться
в область, лежащую выше плоскости AD1C1B,
показанной на рисунке 7. Эта плоскость
Теперь все допустимые исходы будут
отображаться в пирамиду с квадратом
АА1В1В
в основании и с высотой В1С1.
Все исходы, удовлетворяющие условию
z < y,
отображаются в область, лежащую ниже
плоскости DС1В1A,
которая отсекает от этой четырёхугольной
пирамиды треугольную пирамиду с
прямоугольным равнобедренным треугольником
АВ1В
в основании и с высотой В1С1.
Искомая вероятность равна отношению
объёма этой пирамиды, равного l3/6,
к объёму призмы АВСА1В1С1,
равному l3/2.
Таким образом, ответ задачи 1/3.
Задачи
для самостоятельного решения.
1.
Два парохода должны подойти к одному и
тому же причалу. Время прихода обоих
пароходов независимо и равновозможно
в течение данных суток. Определить
вероятность того, что одному из пароходов
придется ожидать освобождения причала,
если время стоянки первого парохода –
один час, а второго – два часа. Ответ:
139/1152.
2.
На перекрестке установлен автоматический
светофор, в котором одну минуту горит
зеленый свет и полминуты красный, затем
снова одну минуту – зеленый и полминуты
красный и т.д. В случайный момент времени
к перекрестку подъезжает автомобиль.
Какова вероятность того, что он проедет
перекресток без остановки? Ответ: 2/3
3.
На бесконечную шахматную доску с шириной
клетки 5 см брошена монета радиуса
1,5 см. Найти вероятность того, что
монета расположится не более чем в двух
клетках шахматной доски. Ответ: 16/25.
4.
В окружность наудачу вписывается
треугольник. Какова вероятность, что
он остроугольный? Ответ: 1/4.
5.
В окружность наудачу вписывается
треугольник. Какова вероятность, что
он прямоугольный? Ответ: 0.
6.
Стержень длины а
наудачу разломан на три части. Найдите
вероятность того, что длина каждой части
окажется больше а/4.
Ответ: 1/16.
7.
Найдите вероятность того, что сумма
двух наудачу взятых чисел из промежутка
[–1; 1] больше нуля, а их произведение
отрицательно. Ответ: 1/4.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Если опыт сводится к бесконечному числу равновозможных случаев, то применяется геометрическое определение вероятности
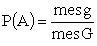 ,
,
где 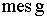 равно длине отрезка, если точки множества g расположены на прямой;
равно длине отрезка, если точки множества g расположены на прямой; 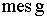 равно площади фигуры, если точки множества g расположены на плоскости;
равно площади фигуры, если точки множества g расположены на плоскости; 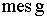 равно объему тела, если точки множества g расположены в пространстве.
равно объему тела, если точки множества g расположены в пространстве.
Примеры решения задач
ПРИМЕР 13.2.19. Территория нефтебазы имеет форму прямоугольника со сторонами 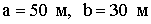 . На территории имеется емкость диаметром 10 м. (рис. 13.2.1). Какова вероятность поражения емкости бомбой, попавшей на территорию нефтебазы, если попадание бомбы в любую точку равновероятное?
. На территории имеется емкость диаметром 10 м. (рис. 13.2.1). Какова вероятность поражения емкости бомбой, попавшей на территорию нефтебазы, если попадание бомбы в любую точку равновероятное?
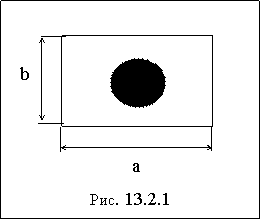
Решение: Событие А — поражение емкости бомбой, попавшей на территорию нефтебазы 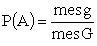 , где
, где 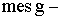 площадь заштрихованного круга;
площадь заштрихованного круга; 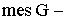 площадь прямоугольника
площадь прямоугольника
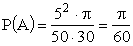 .
.
ПРИМЕР 13.2.20. Дети бросают мяч диаметром 0,2м в щит с круглым отверстием диаметром 1м. Какова вероятность попадания в это отверстие?
Решение: Ход решения ясен из рисунка 13.2.2, на котором “благоприятная” зона заштрихована и имеет диаметр 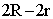 , где R=0,5м, r=0,1м.
, где R=0,5м, r=0,1м.
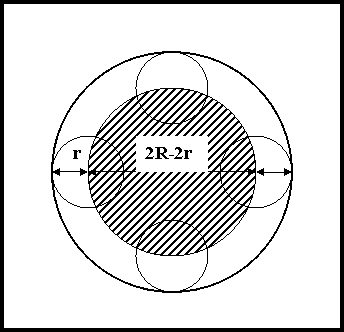 .
.
Рис.13.2.2
Тогда искомая вероятность есть 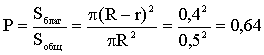 .
.
ПРИМЕР 13.2.21. Внутри круга с центром в точке (0,0) и радиусом R наудачу выбирается точка N(x,y). Найти вероятность события “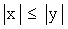 ”.
”.
Решение: В плоскости XOY построим круг и прямые 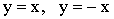 , которые разделят его на четыре области. На рисунке 13.2.3 “благоприятная” область показана штриховкой.
, которые разделят его на четыре области. На рисунке 13.2.3 “благоприятная” область показана штриховкой.
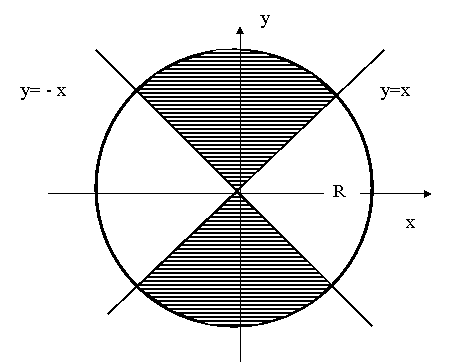
Рис.13.2.3
Непосредственно из рисунка ясно, что 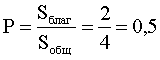 .
.
ПРИМЕР 13.2.22. Внутри квадрата с вершинами (0,0),(0,1),(1,0),(1,1) наудачу выбирается точка А(x,y). Найти вероятность события “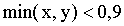 ”.
”.
Решение: В плоскости XOY построим заданный квадрат и прямые 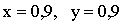 , которые разделят его на четыре области. На рисунке 13.2.4 “благоприятные” области показаны штриховкой.
, которые разделят его на четыре области. На рисунке 13.2.4 “благоприятные” области показаны штриховкой.
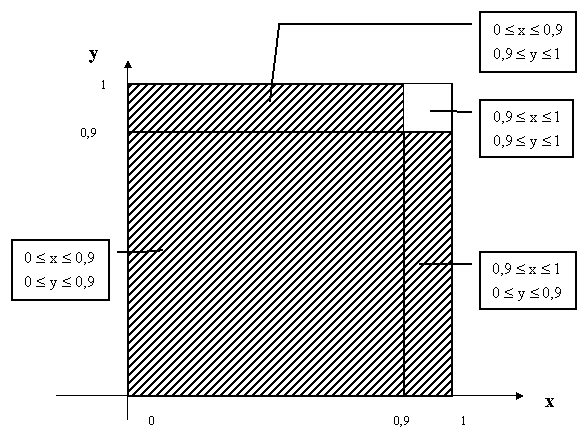
Рис.13.2.4
Непосредственно из рисунка ясно, что 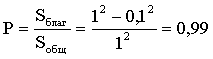 .
.
ПРИМЕР 13.2.23. Найти вероятность того, что сумма двух наудачу взятых положительных правильных дробей не больше 0,5.
Решение: Обозначим через x и y данные дроби. По условию задачи 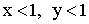 . Рассмотрим событие A сумма дробей не больше 0,5, то есть
. Рассмотрим событие A сумма дробей не больше 0,5, то есть 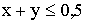 .
.
Будем рассматривать x,y как декартовы координаты точки на плоскости. Пусть g — площадь заштрихованного треугольника, G — площадь квадрата.
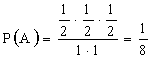
ПРИМЕР 13.2.24. Стержень единичной длины произвольным образом разламывается на три части x,y и z. Найти вероятность того, что из этих частей можно составить треугольник.
Решение: Элементарное событие характеризуется двумя параметрами x и y, ибо 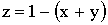 . На них наложены ограничения
. На них наложены ограничения 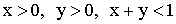 .
.
Пусть 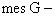 площадь полученного треугольника. Тогда
площадь полученного треугольника. Тогда 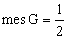 .
.
Чтобы можно было составить треугольник, необходимо, чтобы сумма двух любых сторон была больше третьей 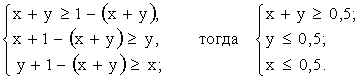 ;
;
Этим условиям соответствует заштрихованная область
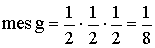 ;
; 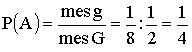 .
.
ПРИМЕР 13.2.25. Два студента условились встретиться в определенном месте между 12 и 13 часами дня. Пришедший первым ждет второго в течение 15 минут, после чего уходит. Найти вероятность того, что встреча состоится, если каждый студент наудачу выбирает момент своего прихода (в промежутке от 12 до 13 часов).
Решение: Пусть x и y моменты прихода соответственно первого и второго студентов. Будем изображать это событие точкой с координатами 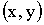 на плоскости
на плоскости 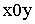 . Выберем за начало отсчета 12 часов, а за единицу измерения – 1 час. Построим на плоскости
. Выберем за начало отсчета 12 часов, а за единицу измерения – 1 час. Построим на плоскости 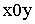 пространство элементарных событий G. Это есть квадрат со стороной 1.
пространство элементарных событий G. Это есть квадрат со стороной 1.
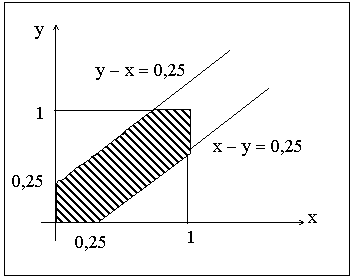
Рассмотрим событие A — студенты встретятся. Это событие произойдет, если разность между x и y по абсолютной величине не превзойдет 0,25 часа (15 минут), то есть 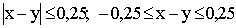 . Область, «благоприятная» этому событию, заштрихована. Ее площадь равна площади всего квадрата без суммы площадей двух угловых треугольников.
. Область, «благоприятная» этому событию, заштрихована. Ее площадь равна площади всего квадрата без суммы площадей двух угловых треугольников.
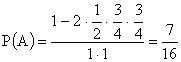 .
.
Если элементарные исходы испытания неравновозможны, то нельзя применять классическое определение вероятности. Вводится статистическое определение вероятности (относительная частота события).
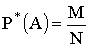 ,
,
где N — общее число произведенных испытаний,
M — число испытаний, в которых событие A наступило.
Примеры и задачи для самостоятельного решения
Решить задачи, используя формулы расчета геометрической и статистической вероятности
1. На отрезок OA длины L числовой оси Ox наудачу поставлена точка B(x). Найти вероятность того, что меньший из отрезков OB и BA имеет длину меньшую чем L/3. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения на числовой оси.
Отв.: 2/3
2. После бури на участке между 40-м и 55-м километрами телефонной линии произошел обрыв провода. Какова вероятность того, что разрыв произошел между 50-м и 55-м километрами линии?
Отв.: 1/3
3. В круг вписан квадрат. Найти вероятность того, что:
а) точка, брошенная наудачу внутрь круга, окажется и внутри квадрата;
б) из пяти точек, брошенных наудачу внутрь круга, одна окажется внутри квадрата и по одной точке попадет на каждый сегмент.
Предполагается, что вероятность попадания точки на какую-либо часть круга зависит только от площади этой части и пропорциональна ей.
Отв.:a) 0,63
4. Считается равновероятным попадание реактивного снаряда в любую точку площади в 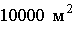 . Определить вероятность попадания снаряда в мост, находящийся на этой площади, если его длина 200 м и ширина 10 м.
. Определить вероятность попадания снаряда в мост, находящийся на этой площади, если его длина 200 м и ширина 10 м.
Отв.: 0,2
5. В круге радиуса R проводятся хорды параллельно заданному направлению. Какова вероятность того, что длина наугад взятой хорды не более R, если равновозможны любые положения точек пересечения хорды с диаметром, перпендикулярным выбранному направлению?
Отв.:0,134
6. К автобусной остановке через каждые четыре минуты подходит автобус линии A и через каждые шесть минут – автобус линии B . Интервал времени между моментами прихода автобуса линии A и ближайшего следующего автобуса линии B равновозможен в пределах от нуля до четырех минут. Определить вероятность того, что а) первый подошедший автобус окажется автобусом линии A; б) автобус какой-либо линии подойдет в течение двух минут.
Отв.:a) 2/3 б) 2/3
7. Какова вероятность того, что из трех взятых наудачу отрезков длиной не более  можно построить треугольник?
можно построить треугольник?
Отв.: 1/2
8. Наудачу взяты два положительных числа x и y, каждое из которых не превышает двух. Найти вероятность того, что произведение xy будет не больше единицы, а частное y/x не больше двух.
Отв.: 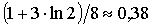
9. Внутри квадрата с вершинами (-1,-1),(-1,0),(0,0),(0,-1) наудачу выбирается точка А(x,y). Найти вероятность события “ 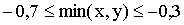 ”.
”.
Отв.: 0,16
10. Внутри прямоугольника с вершинами (-1,-1),(-1,1),(1,1), (1,-1) наудачу выбирается точка M(x,y). Найти вероятность события “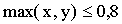 ”.
”.
Отв.: 0,81
11. Внутри квадрата с вершинами (0,0),(0,1),(1,0),(1,1) наудачу выбирается точка R(x,y). Найти вероятность события “ 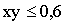 ”.
”.
Отв.: 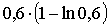
12. Внутри круга с центром в точке (0;0) и радиусом 1 наудачу выбирается точка P(x,y). Найти вероятность события “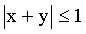 ”.
”.
Отв.: 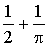
13. Внутри квадрата с вершинами (0,0),(0,1),(1,0),(1,1) наудачу выбирается точка N(x,y). Найти вероятность события “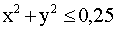 ”.
”.
Отв.: 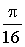
14. Наудачу взяты два положительных числа x и y, каждое из которых не превышает единицы. Найти вероятность того, что сумма x+y не превышает единицы, а произведение xy не меньше 0,09.
Отв.: 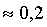
15. Плоскость разграфлена параллельными прямыми, находящимися друг от друга на расстоянии 2a. На плоскость наудачу брошена монета радиуса r < a. Найти вероятность того, что монета не пересечет ни одной из прямых.
Отв.: 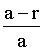
16. На плоскость с нанесенной сеткой квадратов со стороной a наудачу брошена монета радиуса 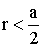 . Найти вероятность того, что монета не пересечет ни одной из сторон квадрата. Предполагается, что вероятность попадания точки в плоскую фигуру пропорциональна площади фигуры и не зависит от ее расположения.
. Найти вероятность того, что монета не пересечет ни одной из сторон квадрата. Предполагается, что вероятность попадания точки в плоскую фигуру пропорциональна площади фигуры и не зависит от ее расположения.
Отв.: 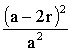
17. На плоскости начерчены две концентрические окружности, радиусы которых 5 и 10 см соответственно. Найти вероятность того, что точка, брошенная наудачу в большой круг, попадет также и в кольцо, образованное построенными окружностями. Предполагается, что вероятность попадания точки в плоскую фигуру пропорциональна площади этой фигуры и не зависит от ее расположения.
Отв.: 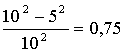
18. (Задача Бюффона) Плоскость разграфлена параллельными прямыми, отстоящими друг от друга на расстоянии 2a. На плоскость наудачу бросают иглу длины  . Найти вероятность того, что игла пересечет какую-нибудь прямую.
. Найти вероятность того, что игла пересечет какую-нибудь прямую.
Отв.: 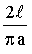
19. В партии из 100 деталей отдел технического контроля обнаружил 5 нестандартных деталей. Чему равна относительная частота появления нестандартных деталей?
Отв.: 0,05
20. При стрельбе из винтовки относительная частота попадания в цель оказалась равной 0,85. Найти число попаданий, если всего было произведено 120 выстрелов.
Отв.: 102
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >
