Формула скорости волны в физике
Формула скорости волны
Определение
Фронт волны (волновая поверхность) – это геометрическое место точек среды, для которых в некоторый момент времени фаза волны
имеет одно и то же значение.
Скоростью волны называют скорость, с которой движется фронт волны.
Формула фазовой скорости волны
Рассмотрим одномерный случай для гармонической волны. Уравнение волновой поверхности при это запишем как:
[Ф_s=omega t-kx+varphi left(1right),]
где${ Ф}_s$ – фаза волны; $k=frac{2pi }{lambda }$ – волновое число; $lambda $ – длина волны; $omega $ – циклическая частота; $varphi $ – начальная фаза. Уравнению (1) в каждый момент времени соответствует только одна точка оси X координата которой, равна:
[x=frac{omega t+varphi -Ф_s}{k}left(2right).]
Разным значениям фазы волны $Ф_s$ соответствуют разные волновые поверхности, каждая из которых в одномерной волне превращается в точку. Из формулы (2) видно, что волновые поверхности перемещаются в среде со скоростью:
[frac{dx}{dt}=frac{omega }{k}=frac{lambda }{T}=v left(3right),]
где $T$ – период колебаний точек в волне.
Если волны гармонические, то скорость движения волновой поверхности равна скорости распространения волны. Скорость, которую определяет выражение (3) является фазовой скоростью.
Фазовая скорость гармонической волны совпадает со скорость распространения энергии волны.
Скорость волны зависит от вещества, в котором распространяется волна и типа волны. Скорость волны – это не то же самое, что скорость колебания частиц среды в волне.
Формула для вычисления фазовой скорости распространения продольных волн
Скорость распространения продольных упругих волн в однородных в газах или жидкостях может быть вычислена как:
[v=sqrt{frac{K}{rho }}left(4right),]
где $K$ – модуль объемной упругости вещества; $rho =const$ – плотность среды. В газах формула (4) выполняется, если избыточное давление много меньше, равновесного давление газа в невозмущенном состоянии.
Для нахождения скорости распространения продольных волн в газе применяют выражение:
[v=sqrt{frac{gamma p}{rho }}left(5right),]
где $gamma $ – показатель адиабаты; $p$ – давление газа.
Продольные механические волны могут распространяться в твердых телах, их фазовая скорость равна:
[v=sqrt{frac{E}{rho }}left(6right),]
где $E$ – модуль Юнга вещества стержня.
Формула для фазовой скорости распространения поперечных волн
Поперечные механические волны способны распространяться только в твердых телах. Скорость ($v$) распространения поперечных волн в бесконечной изотропной среде при этом можно найти как:
[v=sqrt{frac{G}{rho }left(7right),}]
где $G$ – модуль сдвига среды; $rho $ – плотность вещества.
Упругие свойства и плотность твердого тела зависит от химического состава вещества, и она несущественно изменяется при изменении давления и температуры. Поэтому в большинстве случаев скорость распространения волны можно считать постоянной.
Формула для групповой скорости волн
Кроме фазовой скорости для описания распространения диспергирующих волн применяют понятие групповой скорости. При этом фазовая скорость может зависеть от частоты, при этом в веществе распространяются волны сложного негармонического характера, тогда с групповую скорость проще использовать, как характеристику скорости распространения волн.
Групповой скоростью называют скорость перемещения группы (цуга) волн, которые создают в каждый момент времени, локализованный в пространстве, волновой пакет. Любая реальная волна представляет собой суперпозицию гармонических волн. Скорость, с которой такая волна распространяется в веществе, имеющем дисперсию, равна фазовой скорости накрадывающихся волн. Распространение волны определяют перемещением энергии колебаний, которую переносит группа вол от источника.
Групповая скорость ($u$) связана с фазовой скоростью ($v$) формулой:
[u=v-frac{dv}{dlambda }left(8right).]
Если дисперсия отсутствует, то $frac{dv}{dlambda }=0$, тогда фазовая и групповая скорости равны и не зависят от длины волны.
Примеры задач с решением
Пример 1
Задание. За время равное $t=20$ c волне совершается $N=$100 колебаний, при этом расстояние между соседними максимумами волны составляет 1 м. Какова скорость распространения волны?
Решение. Сделаем рисунок.
В качестве основы для решения задачи используем формулу для вычисления фазовой скорости волны вида:
[v=frac{lambda }{T} left(1.1right).]
Найдем период колебаний как время одного полного колебания:
[T=frac{t}{N} left(1.2right).]
Используя формулу (1.2) скорость будем вычислять, применяя формулу:
[v=frac{lambda N}{t}.]
Вычислим искомую скорость:
[v=frac{1cdot 100}{20}=5left(frac{м}{с}right).]
Ответ. $v=5frac{м}{с}$
Пример 2
Задание. Уравнение плоской волны, которая распространяется вдоль положительного направления оси X, имеет вид: $xi left(x,tright)=2{cos left[omega left(t-frac{x}{v}right)right] }left(мright).$ Частота колебаний $nu =450$Гц, длина волны $lambda =0,8 $м. Какова скорость распространения волны, какой будет максимальная скорость колебания частиц среды?
Решение. Фазовую скорость движения волны найдем как:
[v=frac{lambda }{T}=lambda nu left(2.1right),]
где период – величина обратная частоте колебаний:
[T=frac{1}{nu }left(2.2right).]
Вычислим фазовую скорость:
[v=450cdot 0,8=360 left(frac{м}{с}right).]
Скорость колебания частиц равна:
[frac{dxi }{dt}=frac{d}{dt}left(2{cos left[omega left(t-frac{x}{v}right)right] }right)=-2omega {sin left[omega left(t-frac{x}{v}right)right]left(2.3right). }]
Максимальное значение скорости колебаний частиц в волне из (2.3) равно:
[{left(frac{dxi }{dt}right)}_{max}=left|2omega right|left(2.4right).]
Циклическую частоту найдем как:
[omega =2pi nu ,]
тогда:
[{left(frac{dxi }{dt}right)}_{max}=left|2cdot 2pi nu right|=4pi nu .]
Вычислим максимальную скорость колебаний частиц:
[{left(frac{dxi }{dt}right)}_{max}=4pi cdot 450=5,65cdot {10}^3left(frac{м}{с}right).]
Ответ. $v=360 frac{м}{с}$, ${left(frac{dxi }{dt}right)}_{max}=5,65cdot {10}^3frac{м}{с}$
Читать дальше: формула скорости свободного падения.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Скорость распространения волны


4.6
Средняя оценка: 4.6
Всего получено оценок: 149.
4.6
Средняя оценка: 4.6
Всего получено оценок: 149.
Волны любой природы распространяются в пространстве не мгновенно, следовательно, это распространение имеет конечную скорость. Поговорим об этой скорости более подробно.
Распространение колебаний
Далеко не любые колебательные процессы приводят к распространению волн. Колебательная система представляет собой лишь источник колебаний. Для того, чтобы эти колебания могли распространяться, необходимо также существование упругой среды без разрывов, связанной с этим источником. Природа упругих сил может быть различна в различных средах, однако, их наличие обязательно, без этого второго условия, распространение волн в среде невозможно.

Каждая точка среды, через которую проходит волна, в простейшем случае начинает колебаться по гармоническому закону (в более сложных случаях колебания точек можно представить в виде суммы таких функций с различными параметрами):
$$x=Asin(omega t+varphi)$$
Однако, уравнение колебания соседних точек будет немного различаться. Во-первых, чем дальше точка расположена от источника колебаний, тем больше потерь происходит по пути, и тем меньше амплитуда колебаний (параметр $A$ в представленной формуле). Однако, когда потери невелики, заметное изменение амплитуды происходит лишь на больших расстояниях.
Гораздо важнее другое отличие – отличие фазы колебаний (параметр $varphi$ ) для различных точек. По мере удаления от источника колебаний, фаза плавно изменяется, постоянно увеличиваясь. Поскольку синус – круговая функция, то рано или поздно разность фаз между двумя точками становится равной ${2pi}$, а значит, эти две точки колеблются одинаково – синфазно. Для более далеких точек фаза увеличивается дальше, и для точек, разность фаз которых составит ${4pi}$ колебания опять будут синфазны.
Таким образом, по мере удаления от источника колебаний в среде будет ряд точек, колеблющихся в одной фазе. Минимальное расстояние между двумя такими точками называется длиной волны. Она обозначается греческой буквой $lambda$ (лямбда).
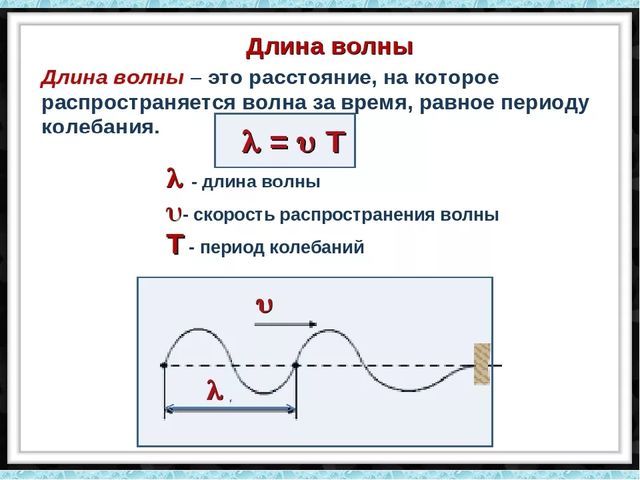
Скорость распространение волн
Плавное изменение фазы колебаний по мере удаления от источника колебаний можно представить в виде распространения этих колебаний, и определить скорость этого распространения. Разность фаз между ближайшими точками, колеблющимися синфазно, составляет $2pi$, это один период колебаний. А значит, волна проходит расстояние между этими точками за время одного периода $T$. Зная длину волны – можно вычислить скорость ее распространения:
$$v = {lambda over T}$$
Иногда известен не период, а частота колебаний $nu$. В этом случае формула скорости распространения волны примет вид:
$$v = {lambda nu}$$
Если среда первоначально была спокойна, то начало возмущений (иногда его называют «фронт волны») будет удаляться от источника колебаний как раз с указанной скоростью.


Что мы узнали?
Колебания среды распространяются не мгновенно, а с конечной скоростью. Каждая точка среды колеблется с некоторой фазой, которая изменяется, по мере удаления от источника колебаний. Минимальная длина между точками, колеблющимися синфазно, называется длиной волны, а отношение длины волны к периоду колебаний – скорости распространения волн.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.6
Средняя оценка: 4.6
Всего получено оценок: 149.
А какая ваша оценка?
Если бросить камень в воду водоема, то возникшие волны
дойдут до берега не сразу. Для продвижения волн на некоторое расстояние
необходимо время, следовательно, можно говорить о скорости распространения
волн. Например,
удар по торцу стального стержня вызывает в нем местное сжатие, которое затем
распространяется вдоль стержня со скоростью около 5 км/с.
Скорость волны зависит от свойств среды, в которой она
распространяется. При переходе из одной среды в другую, скорость волн меняется.
Кроме скорости, важной характеристикой
волны является длина волны. Длиной волны называется расстояние, на
которое распространяется волна за время, равное периоду колебаний в ней. ИЛИ Расстояние
между ближайшими друг к другу точками, колеблющимися в одинаковых фазах,
называется длиной волны.

Она равна расстоянию между соседними
гребнями или впадинами в поперечной волне и между соседними сгущениями или
разрежениями в продольной волне.
Поскольку скорость волны – величина
постоянная (для данной среды), то пройденное волной расстояние равно
произведению скорости на время ее распространения. Таким образом, чтобы
найти длину волны, надо скорость волны умножить на период колебаний в ней: λ=υT.
Так как период Т и частота v связаны соотношением T = 1 / v,
то скорость волны:
υ = λ / Т = λ v
Полученная
формула показывает, что скорость волны равна произведению длины волны на
частоту колебаний в ней.
Частота
колебаний в волне совпадает с частотой колебаний источника (так как колебания
частиц среды являются вынужденными) и не зависит от свойств среды, в которой
распространяется волна. При переходе волны из одной среды в другую ее
частота не изменяется, меняются лишь скорость и длина волны.
Скорость
упругой волны тем больше, чем плотнее среда и чем выше температура.
Величины, характеризующие волну:
длина волны, скорость волны, период колебаний, частота колебаний.
Единицы измерения в системе СИ:
длина волны [λ] = 1 м
скорость распространения волны [ v ] = 1м/с
период колебаний [ T ] = 1c
частота колебаний [ v ] = 1 Гц
Рассмотрим
неустановившееся движение в открытом
прямоугольном русле (с горизонтальным
дном), считая, что потерями на трение
можно пренебречь. В этом случае
![]() и уравнения (19.14) записываются в виде
и уравнения (19.14) записываются в виде
![]() ,
,
(19.20)
где
![]() –
–
скорость перемещения отдельных точек
фронта волны.
Интегрируя (19.15) с
учетом того, что
![]() ,
,![]() получим
получим
![]() const.
const.
(19.21)
Найдя постоянную
интегрирования из начальных условий,
когда
![]() =const
=const
и
![]() =const,
=const,
получим
![]()
и
![]() ,
,
(19.22)
где
![]() –
–
первоначальная глубина наполнения;![]() ,
,![]() –
–
высота волны (рис. 19.7).
Средняя скорость
движения при неустановившемся движении
в прямоугольном горизонтальном русле
при отсутствии гидравлических
сопротивлений определяется по (19.22). С
использованием (19 22) из (19.20) получим
![]() .
.
(19.23)
Далее
![]() ;
;
(19.24)
![]() ;
;
(19.25)
![]() ,
,
(19.26)
где
![]() –
–
произвольная функция.
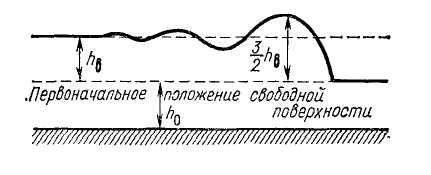
Рис. 19.7
В полученных
формулах знак плюс соответствует прямой
волне, знак минус – обратной. При этом
для положительной волны
![]() ,
,
для отрицательной![]() .
.
В соответствии с
(19.25) в волне, характеризующейся повышением
уровня (![]() ),
),
сечение с большей глубиной нагоняет
сечение с меньшей глубиной. Поэтому
мгновенные профили волны становятся
все более крутыми, при определенных
условиях волна может опрокинуться, т.е.
разрушиться. Для волн![]() сечение с меньшей глубиной отстает от
сечение с меньшей глубиной отстает от
сечения с большей глубиной и мгновенные
профили волны становятся все более
распластанными. Если изменение расхода,
вызвавшее появление положительной
волны, произошло достаточно быстро, то
фронт такой волны считают вертикальным,
хотя на самом деле положительная волна
в таких условиях начинается с переднего
вала высотой примерно![]() (рис. 19.7).
(рис. 19.7).
При медленном
изменении расхода (или отметки уровня,
или глубины), приведшем к появлению
положительной волны, ее фронт растянут.
От скорости
перемещения отдельных точек фронта
волны можно перейти к скорости
распространения фронта волны. Эту
скорость называют скоростью распространения
волны
![]() .
.
Ее находят из выражения
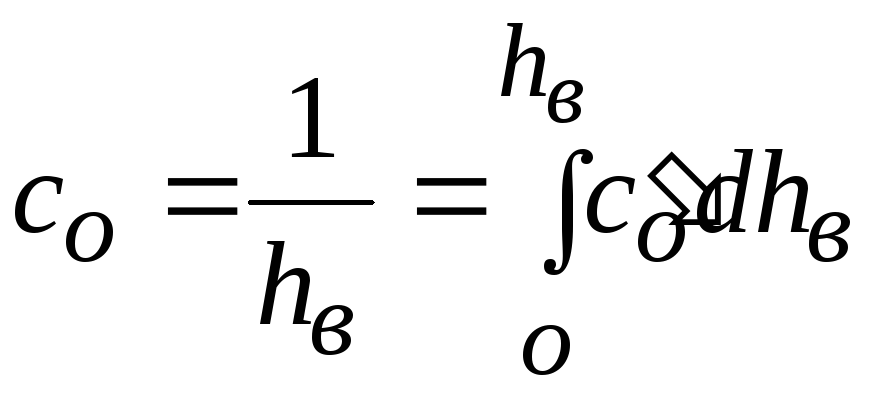 .
.
Подставив сюда
![]() по (19.25) и выполнив преобразования,
по (19.25) и выполнив преобразования,
получим
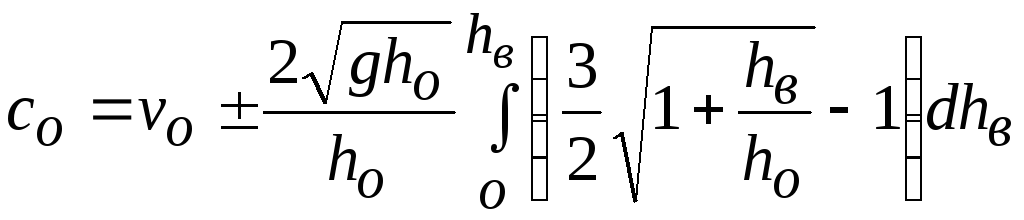 .
.
С учетом
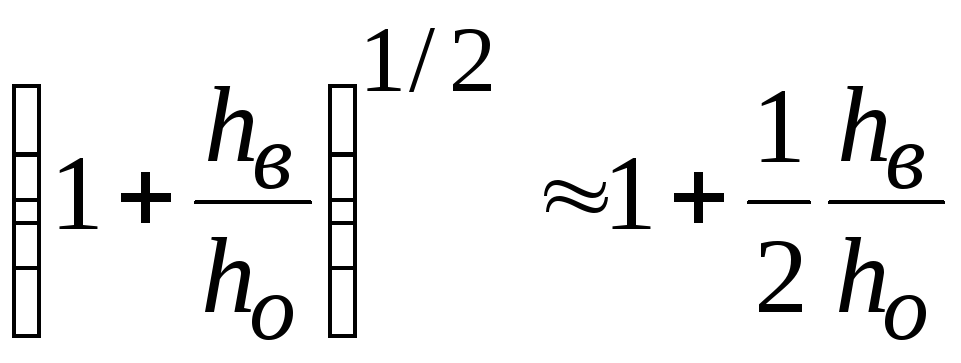
после интегрирования
получим
![]() .
.
(19.27)
Вновь для прямой
волны – знак плюс, для обратной волны –
знак минус.
При
![]() получим
получим
![]() .
.
(19.28)
Если волна
распространяется в неподвижной жидкости
(![]() ),
),
то получим формулу Лагранжа для этого
случая
![]() .
.
(19.29)
Все формулы даны
для случая, когда волна положительная,
т. е.
![]() .
.
При отрицательной
волне
![]() в формулах должна быть принята
в формулах должна быть принята
отрицательной.
Формулы, полученные
для прямоугольного русла, могут быть
применены для призматических русл с
другой формой поперечного сечения.
Следует при этом в формулах для
![]() и
и![]() заменить
заменить![]() на
на![]() ,
,
где![]() –
–
первоначальная площадь живого сечения;![]() –
–
ширина по верху живого сечения при![]() .
.
Формулы скорости
распространения волны (19.27) – (19.29) могут
быть применены и для реальных случаев,
когда силы сопротивления не равны нулю,
так как их влияние не сказывается
ощутимым образом на
![]() .
.
Соседние файлы в папке Штеренлихт
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Волны:
Стоя на берегу озера или пруда, вы могли наблюдать, как кольцами разбегаются волны от места, куда был брошен камень, как волны раскачивают лодку или катер. Ветер нарушает равновесие морской поверхности, кажется, что море надвигается на берег, но это не так. Не перемещаются по полю колосья, когда «волнуется» нива, они только наклоняются и опять выпрямляются. Вслед за кораблем или лодкой всегда возникает типичная картина волн.
Волновые процессы широко распространены в природе. Физические основы волновых движений различны, но все они объясняются одинаковыми законами.
Что же такое волна и каковы причины возникновения волн
Вам известно, что твердые, жидкие и газообразные тела состоят из частей, взаимодействующих между собой. Если частица тела начинает совершать колебания, то в результате взаимодействия ее с другими частицами тела это движение распространяется с определенной скоростью во всех направлениях.
Волна — процесс распространения колебаний в любой среде. Волна — это изменение состояния среды, распространяющееся в пространстве и переносящее энергию.
Наблюдения. Рассмотрим особенности распространения волн. Если рассматривать волны на поверхности воды (рис. 204), то они кажутся валами, движущимися в определенном направлении, причем расстояния между валами, или гребнями, одинаковы.

Если бросить в воду поплавок, его не будет относить волной, а он начнет совершать колебания вверх-вниз, оставаясь почти на одном месте.
При распространении волны изменяется состояние колеблющейся среды, но не перенос вещества. От брошенного камня начинает колебаться определенный участок воды, эти колебания передаются соседним участкам и постепенно распространяются во все стороны. Течение воды не возникает, перемещается только форма ее поверхности.
Опыт 1. Закрепим один конец длинного резинового шнура и легонько заставим шнур колебаться. По шнуру побежит волна (рис. 205). Чем сильнее колеблется шнур, тем больше скорость распространения волны. Волна добежит до точки крепежа, отразится и побежит в обратном направлении.

При распространении волны изменяется только форма шнура, а каждый его участок колеблется относительно своего положения равновесия, причем колебания происходят в направлении, перпендикулярном направлению распространения волны (рис. 206). Такие волны называют поперечными волнами.
Поперечные волны
Поперечные волны — это волны, в которых частицы совершают колебания в направлении, перпендикулярном направлению распространения волны.
Опыт 2. Если ударить по одному из концов длинной мягкой пружины большого диаметра, то по пружине «побежит» сжатие. Повторяя удары, можно возбудить в пружине волну, представляющую собой последовательные сжатия и растяжения пружины, «бегущие» друг за другом (рис. 207). Любой виток пружины совершает колебания вдоль направления распространения волны. Такую волну называют продольной волной.
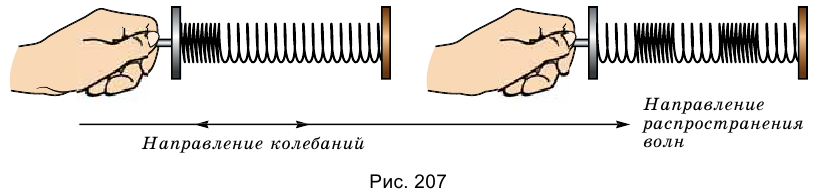
Продольные волны
Продольные волны — это волны, в которых частицы совершают колебания вдоль направления распространения волны.
При распространении волны движение передается от одного участка тела к другому. С передачей движения связана передача энергии. Передача энергии без передачи вещества – основное свойство всех волн.
Любые волны характеризуются длиной и скоростью их распространения.
Длина волны — это расстояние между ближайшими друг к другу точками волны, колеблющимися в одинаковых фазах (рис. 208).
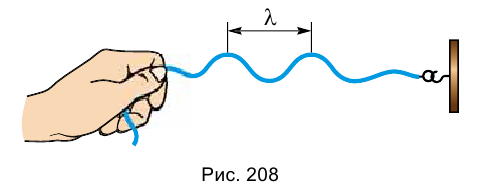
Длину волны обозначают греческой буквой А. (лямбда). Ее единицей является один метр (1 м).
Волны любого происхождения распространяются в пространстве не мгновенно, а с определенной скоростью. Например, можно увидеть, как чайка летит над морем будто все время над одним гребнем волны. В этом случае скорость полета чайки равна скорости распространения волны.
А как можно определить скорость распространения волны?
Вы уже знаете, что любое колебание характеризуется периодом колебаний, то есть временем, после которого колебания повторяются. Тогда можно сказать, что за один период волна распространяется на расстояние 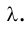 . Поэтому скорость ее распространения можно найти по формуле:
. Поэтому скорость ее распространения можно найти по формуле:
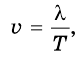
где v – скорость распространения волны (м/с); 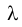 – длина волны (м); Т – период колебаний (с).
– длина волны (м); Т – период колебаний (с).
Так как период и частота связаны соотношением 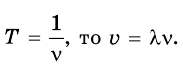
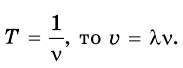
Пример №1
Определите скорость распространения волны на воде, если ее длина равна 180 м, а период колебаний – 15 с.
Дано:
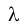 = 180 м
= 180 м
Т = 15 с
v – ?
Решение
По формуле 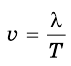 определяем скорость распространения волны на воде.
определяем скорость распространения волны на воде.
v = 180 м : 15 с = 12 м/с.
Ответ: 12 м/с.
Пример №2
Каково основное свойство механической волны?
Ответ: переносить энергию.
Интерференция волн
Для волн не очень больших амплитуд справедлив принцип суперпозиции: если в точку пространства приходят волны от нескольких источников, то эти волны накладываются друг на друга. В результате такого наложения в некоторых точках пространства может наблюдаться постоянное усиление колебаний, а в некоторых — ослабление. Выясним, почему и когда это происходит. Пусть в некоторую точку M поступают две когерентные волны — волны от двух источников 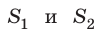 , колеблющихся синхронно, то есть в одинаковых фазах и с одинаковой частотой (рис. 22.6, а).
, колеблющихся синхронно, то есть в одинаковых фазах и с одинаковой частотой (рис. 22.6, а).
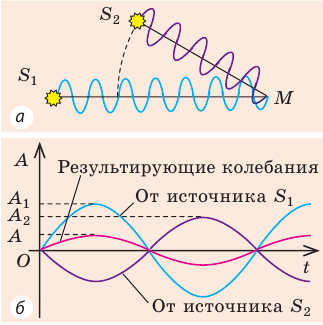
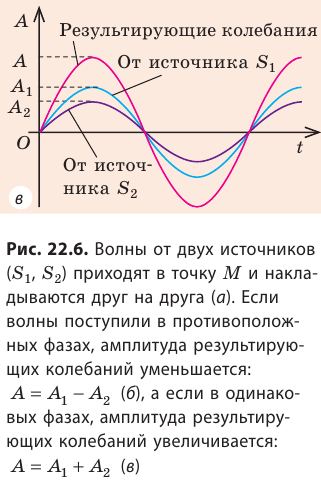
Если волны приходят в точку М в противоположных фазах (в один и тот же момент времени одна волна «толкает» точку М вверх, а вторая «толкает» ее вниз), то волны будут постоянно гасить друг друга (рис. 22.6, б). Если же волны приходят в точку М в одинаковых фазах, то в точке M будут все время наблюдаться колебания с увеличенной амплитудой (рис. 22.6, в). явление наложения волн, вследствие которого в некоторых точках пространства наблюдается устойчивое во времени усиление или ослабление результирующих колебаний, называют интерференцией.
Дифракция волн
Судно, плывущее по морю, образует на поверхности воды волну. Если на своем пути волна встретит скалу или торчащую из воды ветку, то за скалой образуется тень (то есть непосредственно за скалу волна не проникает), а за веткой тень не образуется (волна ветку огибает).
Явление огибания волнами препятствий называют дифракцией (от лат. difractus — разломанный) (рис. 22.8).
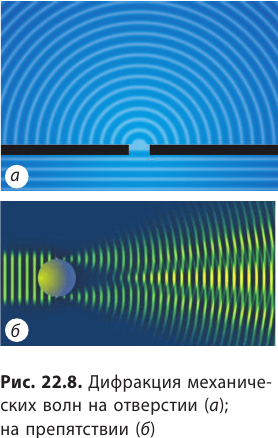
В приведенном примере дифракция волны происходит на ветке, но не происходит на скале. Но это не всегда так. Если скала достаточно удалена от берега, то на некотором расстоянии от скалы тень исчезнет — волна обогнет и скалу. Дело в том, что дифракция наблюдается в двух случаях: 1) когда линейные размеры препятствий, на которые находит волна (или размеры отверстий, сквозь которые проходит волна), сопоставимы с длиной волны; 2) когда расстояние от препятствия до места наблюдения намного больше размера препятствия.
Выводы:
- Распространение в пространстве колебаний вещества или поля называют волной. Механической волной называют распространение колебаний в упругой среде.
- Волна распространяется в пространстве не мгновенно, а с конечной скоростью. При распространении волны происходит перенос энергии без переноса вещества. В некоторых точках пространства вследствие наложения волн друг на друга может наблюдаться устойчивое во времени усиление или ослабление результирующих колебаний — это явление называют интерференцией. Волны могут огибать препятствия — это явление называют дифракцией.
- Волну, в которой частицы среды колеблются перпендикулярно направлению распространения волны, называют поперечной. Волну, в которой частицы среды колеблются вдоль направления распространения волны, называют продольной.
- Волна периодична во времени и пространстве. Периодичность волны во времени характеризуется периодом колебаний каждой отдельной точки волны. Периодичность волны в пространстве характеризуется длиной волны. Длина волны — это расстояние, на которое распространяется волна за время, равное периоду колебаний. Длина λ, частота ν и скорость v распространения волны связаны формулой волны: v = λν .
Звуковые волны
Звучание флейты, шум мегаполиса, шорох травы, грохот водопада, человеческая речь, музыкальный звук, шум, акустический резонанс… Все это связано с распространением в пространстве определенных механических волн, которые называют звуковыми волнами. Их изучает акустика — наука о звуке. С элементами акустики вы начали знакомиться в курсе физики 9 класса. Итак, вспоминаем и узнаем новое.
Звуковые (акустические) волны — это механические волны с частотами от 20 Гц до 20 кГц. Звуковые волны обычно доходят до уха через воздух — в виде последовательных сгущений и разрежений (то есть в воздухе звуковые волны являются продольными). В зонах сгущений (разрежений) давление воздуха незначительно больше (меньше) атмосферного (рис. 23.1).
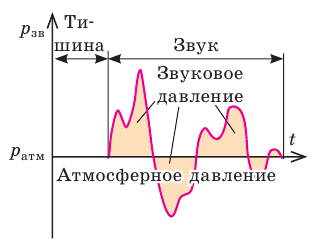
Рис. 23.1. Человеческое ухо воспринимает звуковые волны с избыточным (звуковым) давлением примерно от 20 мкПа (0 децибелов — порог слышимости) до 20 Па (120 децибелов — болевой порог). Для сравнения 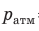 =100 000 Па
=100 000 Па
Звук — механическая волна, потому все свойства волнового движения касаются и звука.
- Звук распространяется в среде с конечной скоростью, зависящей от температуры, плотности, состава и других характеристик среды. Так, в жидкостях звук распространяется быстрее, чем в газах, и медленнее, чем в твердых телах. Скорость распространения звука обычно увеличивается с увеличением температуры среды (в воздухе при температуре 0 °С скорость распространения звука составляет около 330 м/с, а при 20 °С — 340 м/с). Кроме того, чем меньше масса молекул среды, тем быстрее распространяется звук.
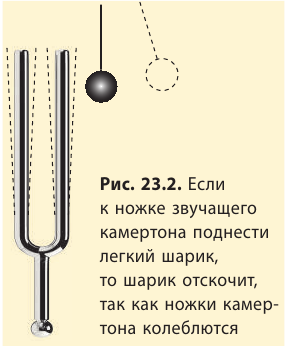
- Источником звука является колеблющееся тело (рис. 23.2). Такие колебания могут быть вынужденными (диффузор громкоговорителя), свободными (струна гитары), автоколебаниями (струны смычковых инструментов).
- Звук не распространяется в вакууме.
- При распространении звука не происходит переноса вещества, но происходит перенос энергии.
- Звуковые волны могут накладываться друг на друга (явление интерференции); могут огибать препятствия (явление дифракции).
Как связаны субъективные и объективные характеристики звука
Все физические величины, характеризующие механические волны (амплитуда, частота, длина, энергия), являются и характеристиками звука. Эти величины не зависят от особенностей восприятия звука человеком, поэтому их называют объективными, или физическими, характеристиками звука. Субъективные характеристики звука (громкость, высота, тембр) обусловлены особенностями слуха человека, поэтому их называют физиологическими. Понятно, что физические и физиологические характеристики звука связаны (см. таблицу).
- Заказать решение задач по физике
| Субъективные (физиологические) характеристики звука | |
|---|---|
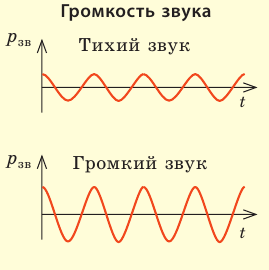 |
Громкость звука определяется прежде всего амплитудой звуковой волны (звуковым давлением), однако зависит и от частоты звуковой волны. Человеческое ухо плохо воспринимает звуки низких (около 20 Гц) и высоких (около 20 кГц) частот, лучше всего — средних частот (1–3 кГц). Громкость звука измеряют в децибелах (дБ). Так, при частоте звука 1 кГц и звуковом давлении 20 Па громкость звука составляет 120 дБ — это болевой порог звука — наиболее громкий звук, который может воспринимать человек, не чувствуя боли (звук такой громкости издает двигатель реактивного самолета). |
| Обратите внимание! Громкий звук может привести к ухудшению слуха и даже к глухоте, особенно это касается прослушивания громкой музыки в наушниках. Слушать музыку в наушниках следует при минимальной громкости! | |
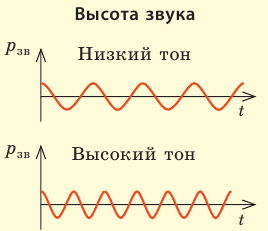 |
Высота звука определяется в основном частотой звуковой волны: чем больше ее частота, тем выше тон звука. Например, ноте «ля» первой октавы соответствует частота 440 Гц; ноте «ля» второй октавы — частота 880 Гц. Свойство человеческого уха различать звуки по их частоте также зависит от интенсивности звуков. При увеличении интенсивности звука его высота кажется более низкой. |
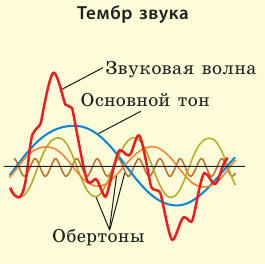 |
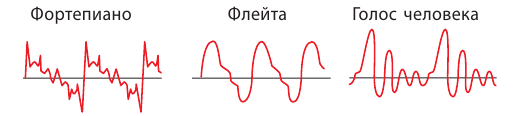
Тембр звука определяется составом звуковой волны: кроме основной частоты (по которой мы и оцениваем высоту звука) любой звук содержит несколько более слабых и более высоких дополнительных частот — обертонов. Именно благодаря тембру мы узнаем человека по голосу, отличаем звуки фортепиано от звуков флейты и т. д. Каждый музыкальный инструмент, каждый человек или животное имеют свой тембр.
|
Что такое акустический резонанс
На любое тело, расположенное в пределах распространения звуковой волны, действует периодическая сила, частота которой равна частоте волны. Под действием этой силы тело начинает совершать вынужденные колебания. Если частота собственных колебаний тела сов падает с частотой звуковой волны, то амплитуда колебаний тела увеличивается и оно начинает издавать звук — наблюдается акустический резонанс.
Акустический резонанс — это явление резкого возрастания амплитуды звукового сигнала при приближении частоты сигнала-возбудителя к частоте собственных колебаний системы.
Наблюдать акустический резонанс можно с помощью опыта с двумя камертонами, имеющими одинаковую частоту (рис. 23.3).
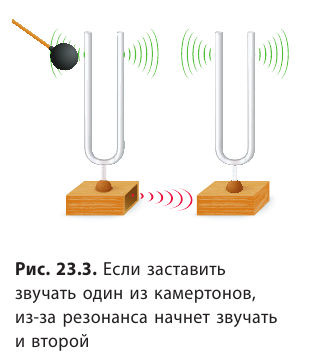
Акустический резонанс используют для увеличения интенсивности звука, созданного некоторым источником (струной, ножками камертона, голосовыми связками и т. д.). Например, для увеличения громкости камертона его присоединяют к деревянному ящику (резонатору), собственная частота колебаний воздуха в котором равна частоте колебаний камертона. Камертон, присоединенный к резонатору, звучит гораздо громче, чем тот, который держат в руке.
Акустический резонанс используют во многих музыкальных инструментах. Воздух в трубах органа, корпусах арф, бандур, гитар и т. д. резонирует с тонами и обертонами звуков, издаваемых колеблющимися телами, и усиливает их. Полость рта — резонатор для звуковых волн, которые создаются благодаря колебаниям голосовых связок. Рис. 23.3. Если заставить звучать один из камертонов, из-за резонанса начнет звучать и второй
Звуковая волна, достигнув уха, испытывает ряд преобразований. Сначала она действует на барабанную перепонку, заставляя ее вибрировать. Чем громче звук, тем сильнее вибрирует перепонка, передавая звуковые колебания в среднее ухо, где они усиливаются.
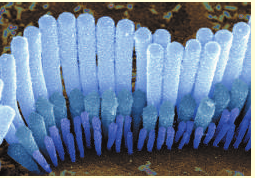
Усиленный звук попадает во внутреннее ухо с заполненной жидкостью улиткой. Поверхность улитки покрыта волосковыми клетками, количество которых достигает 15 000. Каждая клетка резонирует с определенным диапазоном частот. Обнаружив «собственную» частоту, клетка начинает колебаться, возбуждая нервные окончания, и в мозг идет нервный импульс — человек слышит звук.
С возрастом количество волосковых клеток уменьшается (от 15 000 у ребенка до 4 тысяч у пожилого человека). Первыми погибают клетки, «отвечающие» за высокую частоту, поэтому взрослый человек не слышит высоких звуков (подросток слышит звуки до 22 кГц, пожилой человек — до 12 кГц).
Вспоминаем инфра- и ультразвук
Инфразвук (от лат. infra — ниже, под) — это механические волны, частота которых меньше 20 Гц. Инфразвуковые волны возникают во время штормов, землетрясений, цунами, извержений вулканов, вследствие ударов о берег морских волн. Некоторые существа способны воспринимать инфразвуковые волны (рис. 23.4). Источником инфразвука могут быть и объекты, созданные человеком: турбины, двигатели внутреннего сгорания и т. д. В городах наибольший уровень инфразвука около автомагистралей.

Инфразвук очень опасен для животных и человека: он может вызывать симптомы морской болезни, головокружение, потерю зрения, стать причиной повышенной агрессивности. При длительном воздействии интенсивное инфразвуковое излучение может привести к остановке сердца. При этом человек даже не понимает, что происходит, ведь он не слышит инфразвука. Механические волны, частота которых превышает 20 кГц, называют ультразвуковыми волнами (от лат. ultra — сверх, за пределами).
Ультразвук есть в шуме ветра и водопада, в звуках, которые издают некоторые живые существа. Установлено, что ультразвук до 100 кГц воспринимают многие насекомые и грызуны; улавливают его и собаки.
Слабый ультразвук — основа ультразвуковой локации — определения расположения и характера движения объекта с помощью ультразвука. Так, летучие мыши и дельфины, излучая ультразвук и воспринимая его эхо, могут даже в полной темноте найти дорогу или поймать добычу. Ультразвуковое исследование позволяет «увидеть» еще не родившегося младенца, исследовать состояние внутренних органов, выявить инородные тела в тканях. Ультразвуковую локацию применяют также на морских судах — для выявления объектов в воде (сонары) и исследования рельефа морского дна (эхолоты); в металлургии — для выявления и установления размеров дефектов в изделиях (дефектоскопы).
Мощный ультразвук применяют в технике (обработка прочных материалов, сварка, очистка поверхностей от загрязнений); медицине (измельчение камней в организме, что позволяет избежать хирургических операций); пищевой промышленности (изготовление сыров, соусов); косметологии (изготовление кремов, зубной пасты).
Выводы:
- Механические волны с частотами 20 Гц — 20 кГц называют звуковыми волнами (звуком). Субъективные характеристики звука: высота звука (определяется частотой звуковой волны); громкость звука (определяется амплитудой и частотой звуковой волны); тембр звука (определяется спектром звуковой волны).
- Явление резкого возрастания амплитуды звукового сигнала в случае приближения частоты сигнала-возбудителя к частоте собственных колебаний системы называют акустическим резонансом. Акустические резонаторы имеют почти все музыкальные инструменты.
- Механические волны, частота которых меньше 20 Гц, называют инфразвуковыми волнами (инфразвук). Механические волны, частота которых превышает 20 кГц, называют ультразвуковыми волнами (ультразвук).
- Волновое движение в физике
- Продольные и поперечные волны в физике
- Звуковые волны в физике
- Электрическое поле в физике
- Электромагнитные явления в физике
- Электромагнитные волны и их свойства
- Магнитные явления в физике
- Магнитный поток