Урок по теории вероятностей и статистике в 7 классе
Тема “Отклонения. Дисперсия”. 7-й класс
Цель: сформировать у учащихся представление о понятиях “отклонение” и “дисперсия” и навыки их применения в реальных статистических исследованиях
Задачи урока:
- образовательные – показать, что окружающий нас изменчивый мир можно описать математическими понятиями, числовыми показателями;
- развивающие– формировать современное мировоззрение и умение ориентироваться в изменчивом информационном мире;
- воспитательные – учить мыслить категориями, имеющими вероятностный характер, применять вводимые понятия в практической жизни.
Планируемые результаты:
- знать, что такое отклонение от среднего арифметического и дисперсия;
- уметь вычислять отклонения, квадраты отклонений и дисперсию на коротких наборах;
- уметь применять понятия квадратов отклонений и дисперсии при анализе реальных ситуаций;
Оборудование:
- мультимедийный проектор, экран.
Дидактические материалы:
- карточки с таблицами.
Ход урока
I. Организационный момент
Сообщить тему и цели урока. (Слайд 1).
II. Актуализация знаний учащихся
На предыдущих уроках мы рассмотрели так называемые средние характеристики числового ряда, позволяющие оценить его поведение “в среднем”. Повторим их определения и способы нахождения.
Слайд 2 – задание на повторение (комментарии учителя, проверка ответов учеников с помощью слайда).
Задание. Дан числовой набор.
|
Х |
1 |
2 |
3 |
5 |
8 |
100 |
Найти среднее арифметическое и медиану, определить, какая из характеристик лучше характеризует числовой набор и почему?
III. Изучение нового материала, формирование знаний, умений и навыков
Слайд 3 – характеристики числового ряда (комментарии учителя).
Средние характеристики числового ряда (среднее арифметическое, медиана), позволяют оценить поведение ряда “в среднем”. Но это не всегда наиболее полно характеризуют выборку. Чтобы получить полное представление о поведении числового ряда, помимо средних характеристик надо знать характеристики разброса, показывающие, насколько сильно значения ряда отличаются друг от друга, как сильно они разбросаны вокруг средних.
Рассмотрим следующий пример ( раздать карточки с таблицами, которых нужно заполнять по ходу урока)
Слайд 4-5 – задание 1 (комментарий учителя).
Международные спортивные игры “Дети Азии” получили свое начало в 1996 г. по инициативе первого Президента Республики Саха (Якутия) М.Е.Николаева и были посвящены 100-летию олимпийского движения. С тех пор они проводятся совместно с Олимпийским комитетом России, Росспортом, Министерством иностранных дел Министерством образования и науки Российской Федерации. Летом 2012 года будет V международная спортивная игра «Дети Азии».
Для участия в V международных спортивных играх «Дети Азии» нужно выбрать лучших футболистов республики. На одно место футболиста претендуют двое. Для каждого из них установили испытательный срок, в течение которого они должны были участвовать в отборных играх. Результаты спортсменов представлены в таблице
Вопрос: кого из футболистов предпочтительнее взять на спортивные игры?
|
Номер сезона |
||
|
1-й футболист (Х) |
2-й футболист (Y) |
|
|
(кол-во голов) |
(кол-во голов) |
|
|
1 |
18 |
19 |
|
2 |
23 |
16 |
|
3 |
19 |
22 |
|
4 |
17 |
23 |
|
5 |
23 |
20 |
Рассчитаем, сколько голов забил каждый из футболистов за 5 сезонов.
|
Номер сезона |
||
|
1-й футболист (Х) |
2-й футболист (Y) |
|
|
(кол-во голов) |
(кол-во голов) |
|
|
1 |
18 |
19 |
|
2 |
23 |
16 |
|
3 |
19 |
22 |
|
4 |
17 |
23 |
|
5 |
23 |
20 |
|
Итого: |
100 |
100 |
Вывод: количество голов одинаково.
Рассчитаем, сколько голов в сезон забивал в среднем каждый футболист. Для этого найдём среднее арифметическое числовых наборов Х и Y.
|
Номер сезона |
||
|
1-й футболист (Х) |
2-й футболист (Y) |
|
|
(кол-во голов) |
(кол-во голов) |
|
|
1 |
18 |
19 |
|
2 |
23 |
16 |
|
3 |
19 |
22 |
|
4 |
17 |
23 |
|
5 |
23 |
20 |
|
Итого: |
100 |
100 |
|
Среднее арифметическое |
20 |
20 |
Среднее арифметическое у обоих футболистов тоже одинаковое.
На данном примере мы увидели, что с помощью средних характеристик сравнение выполнить не всегда возможно.
Как поступить?
В данном случае критерием сравнения может выступать стабильность игры– у какого футболиста количество забитых им голов в сезон менее отличается друг от друга, тот играет стабильнее.
Если количество забитых в сезон голов сильно разнится, то в какой-то сезон футболист играет не в полную силу, забивает меньше голов, а в какой-то сезон навёрстывает упущенное, а это всегда сказывается на качестве игры.
Стабильность можно оценивать с помощью отклонений элементов числового набора от среднего значения (отклонение – это разность между числом из данного набора и средним арифметическим этого набора)
Слайд 6 – пример вычисления отклонений (комментарии учителя).
Отклонение – разность между средним значением и числом набора
Набор отклонений:
|
X – X |
-2 |
-4 |
0 |
2 |
4 |
Логично предположить, что чем меньше будет разброс (отклонения от среднего значения) – тем стабильнее играет футболист.
Но когда набор чисел велик, рассматривать отклонения практически неудобно, нужно описать разнообразие чисел в наборе одним числом.
Попробуем найти сумму отклонений.
Слайд 6 – пример вычисления суммы отклонений (комментарии учителя, вывод).
-2-4+0+2+4=0
В сумме получилось 0 (т.к. при вычислении “среднего разброса” часть отклонений входит в сумму со знаком “+”, часть со знаком “-” и в сумме всегда получается 0). Следовательно сумма отклонений не может нести информацию о разбросе.
Какой же выход?
Можно суммировать квадраты отклонений (они всегда неотрицательны).
Слайд 7 – пример вычисления квадратов отклонений (комментарии учителя)
Набор квадратов отклонений:
|
(X – X)² |
4 |
16 |
0 |
4 |
16 |
Сумма квадратов отклонений:
4+16+0+4+16 = 40
Чем меньше сумма квадратов отклонений, тем меньше разброс чисел относительно среднего значения, тем более стабилен набор.
Итак, рассчитаем сумму квадратов отклонений для нашего примера.
|
Номер сезона |
||
|
1-й футболист (Х) |
2-й футболист (Y) |
|
|
(кол-во голов) |
(кол-во голов) |
|
|
1 |
18 |
19 |
|
2 |
23 |
16 |
|
3 |
19 |
22 |
|
4 |
17 |
23 |
|
5 |
23 |
20 |
|
Итого: |
100 |
100 |
|
Среднее арифметическое |
20 |
20 |
|
Сумма квадратов отклонений |
32 |
30 |
Вывод: второй футболист играет более стабильно, у него меньше сумма квадратов отклонений. Вероятно, тренер предпочтёт взять на соревнование его.
В данном примере футболисты играли одинаковое количество сезонов. А если они количество сезонов неодинаково?
Тогда стабильность игры каждого можно было бы оценить по величине среднего арифметического квадратов отклонений от среднего значения – дисперсии.
Слайд 8 – пример вычисления дисперсии (комментарии учителя).
Дисперсия – среднее арифметическое квадратов отклонений:
Dx= (4+16+0+4+16)/5 = 40/5 = 8
Дисперсия – характеристика разброса, мера стабильности.
Чем больше дисперсия, тем ниже стабильность
Рассмотрим следующий пример.
Слайд 9 – задание 2 (комментарии учителя).
(Ученикам открыть лист “Задание 2” файла с заданиями).
|
Номер сезона |
||
|
1-й футболист (Х) |
2-й футболист (Y) |
|
|
(кол-во голов) |
(кол-во голов) |
|
|
1 |
17 |
– |
|
2 |
21 |
17 |
|
3 |
20 |
20 |
|
4 |
16 |
18 |
|
5 |
15 |
21 |
|
6 |
19 |
14 |
Аналогично заданию 1 рассчитаем, сколько голов забил каждый футболист и сумму квадратов отклонений.
|
Номер сезона |
||
|
1-й футболист (Х) |
2-й футболист (Y) |
|
|
(кол-во голов) |
(кол-во голов) |
|
|
1 |
17 |
– |
|
2 |
21 |
17 |
|
3 |
20 |
20 |
|
4 |
16 |
18 |
|
5 |
15 |
21 |
|
6 |
19 |
14 |
|
Итого: |
108 |
90 |
|
Среднее арифметическое |
18 |
18 |
|
Сумма квадратов отклонений |
28 |
30 |
Т.к. футболисты играли разное количество сезонов, рассчитаем и сравним дисперсии числовых наборов X и Y.
|
Номер сезона |
||
|
1-й футболист (Х) |
2-й футболист (Y) |
|
|
(кол-во голов) |
(кол-во голов) |
|
|
1 |
17 |
– |
|
2 |
21 |
17 |
|
3 |
20 |
20 |
|
4 |
16 |
18 |
|
6 |
19 |
14 |
|
Итого: |
108 |
90 |
|
Среднее арифметическое |
18 |
18 |
|
Сумма квадратов отклонений |
28 |
30 |
|
Дисперсия |
4,6 |
6 |
Вывод: первый футболист играет стабильнее второго.
3. Самостоятельная практическая работа.
Слайд 10 – задание 3.
С 28 марта по 2 апреля в Южной Якутии пройдёт II Спартакиада зимних видов спорта Республики Саха (Якутия). Примут её опять Алдан и Нерюнгри.
Для участия в II Спартакиаде зимних видов спорта Республики Саха (Якутия)нужно выбрать лучших лыжников района. На одно место претендуют двое. Для каждого из них установили испытательный срок, в течение которого они должны были участвовать в отборных соревнованиях. Результаты спортсменов на 10 км.представлены в таблице
Вопрос: кого из спортсменов предпочтительнее взять на спартакиаду?
|
Номер сезона |
||
|
1-й спортсмен (Х) |
2-й спортсмен(Y) |
|
|
(время в мин.) |
(время в мин.) |
|
|
1 |
26,5 |
26,4 |
|
2 |
26,6 |
26,6 |
|
3 |
27 |
26,5 |
|
4 |
26 |
26,3 |
|
5 |
26,1 |
26,4 |
Подвести итог самостоятельной работы.
4. Итог урока.
Слайд 11 – выводы (комментарии учителя).
Слайд 12 – вопросы (ответы учеников).
Как найти дисперсию?
Спасибо за ваши закладки и рекомендации
Дисперсия – это мера разброса значений случайной величины $X$ относительно ее математического ожидания $M(X)$ (см. как найти математическое ожидание случайной величины). Дисперсия показывает, насколько в среднем значения сосредоточены, сгруппированы около $M(X)$: если дисперсия маленькая – значения сравнительно близки друг к другу, если большая – далеки друг от друга (см. примеры нахождения дисперсии ниже).
Если случайная величина описывает физические объекты с некоторой размерностью (метры, секунды, килограммы и т.п.), то дисперсия будет выражаться в квадратных единицах (метры в квадрате, секунды в квадрате и т.п.). Ясно, что это не совсем удобно для анализа, поэтому часто вычисляют также корень из дисперсии – среднеквадратическое отклонение $sigma(X)=sqrt{D(X)}$, которое имеет ту же размерность, что и исходная величина и также описывает разброс.
Еще одно формальное определение дисперсии звучит так: “Дисперсия – это второй центральный момент случайной величины” (напомним, что первый начальный момент – это как раз математическое ожидание).
Нужна помощь? Решаем теорию вероятностей на отлично
Формула дисперсии случайной величины
Дисперсия случайной величины Х вычисляется по следующей формуле:
$$
D(X)=M(X-M(X))^2,
$$
которую также часто записывают в более удобном для расчетов виде:
$$
D(X)=M(X^2)-(M(X))^2.
$$
Эта универсальная формула для дисперсии может быть расписана более подробно для двух случаев.
Если мы имеем дело с дискретной случайной величиной (которая задана перечнем значений $x_i$ и соответствующих вероятностей $p_i$), то формула принимает вид:
$$
D(X)=sum_{i=1}^{n}{x_i^2 cdot p_i}-left(sum_{i=1}^{n}{x_i cdot p_i} right)^2.
$$
Если же речь идет о непрерывной случайной величине (заданной плотностью вероятностей $f(x)$ в общем случае), формула дисперсии Х выглядит следующим образом:
$$
D(X)=int_{-infty}^{+infty} f(x) cdot x^2 dx – left( int_{-infty}^{+infty} f(x) cdot x dx right)^2.
$$
Пример нахождения дисперсии
Рассмотрим простые примеры, показывающие как найти дисперсию по формулам, введеным выше.
Пример 1. Вычислить и сравнить дисперсию двух законов распределения:
$$
x_i quad 1 quad 2 \
p_i quad 0.5 quad 0.5
$$
и
$$
y_i quad -10 quad 10 \
p_i quad 0.5 quad 0.5
$$
Для убедительности и наглядности расчетов мы взяли простые распределения с двумя значениями и одинаковыми вероятностями. Но в первом случае значения случайной величины расположены рядом (1 и 2), а во втором – дальше друг от друга (-10 и 10). А теперь посмотрим, насколько различаются дисперсии:
$$
D(X)=sum_{i=1}^{n}{x_i^2 cdot p_i}-left(sum_{i=1}^{n}{x_i cdot p_i} right)^2 =\
= 1^2cdot 0.5 + 2^2 cdot 0.5 – (1cdot 0.5 + 2cdot 0.5)^2=2.5-1.5^2=0.25.
$$
$$
D(Y)=sum_{i=1}^{n}{y_i^2 cdot p_i}-left(sum_{i=1}^{n}{y_i cdot p_i} right)^2 =\
= (-10)^2cdot 0.5 + 10^2 cdot 0.5 – (-10cdot 0.5 + 10cdot 0.5)^2=100-0^2=100.
$$
Итак, значения случайных величин различались на 1 и 20 единиц, тогда как дисперсия показывает меру разброса в 0.25 и 100. Если перейти к среднеквадратическому отклонению, получим $sigma(X)=0.5$, $sigma(Y)=10$, то есть вполне ожидаемые величины: в первом случае значения отстоят в обе стороны на 0.5 от среднего 1.5, а во втором – на 10 единиц от среднего 0.
Ясно, что для более сложных распределений, где число значений больше и вероятности не одинаковы, картина будет более сложной, прямой зависимости от значений уже не будет (но будет как раз оценка разброса).
Пример 2. Найти дисперсию случайной величины Х, заданной дискретным рядом распределения:
$$
x_i quad -1 quad 2 quad 5 quad 10 quad 20 \
p_i quad 0.1 quad 0.2 quad 0.3 quad 0.3 quad 0.1
$$
Снова используем формулу для дисперсии дискретной случайной величины:
$$
D(X)=M(X^2)-(M(X))^2.
$$
В случае, когда значений много, удобно разбить вычисления по шагам. Сначала найдем математическое ожидание:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i} =-1cdot 0.1 + 2 cdot 0.2 +5cdot 0.3 +10cdot 0.3+20cdot 0.1=6.8.
$$
Потом математическое ожидание квадрата случайной величины:
$$
M(X^2)=sum_{i=1}^{n}{x_i^2 cdot p_i}
= (-1)^2cdot 0.1 + 2^2 cdot 0.2 +5^2cdot 0.3 +10^2cdot 0.3+20^2cdot 0.1=78.4.
$$
А потом подставим все в формулу для дисперсии:
$$
D(X)=M(X^2)-(M(X))^2=78.4-6.8^2=32.16.
$$
Дисперсия равна 32.16 квадратных единиц.
Пример 3. Найти дисперсию по заданному непрерывному закону распределения случайной величины Х, заданному плотностью $f(x)=x/18$ при $x in(0,6)$ и $f(x)=0$ в остальных точках.
Используем для расчета формулу дисперсии непрерывной случайной величины:
$$
D(X)=int_{-infty}^{+infty} f(x) cdot x^2 dx – left( int_{-infty}^{+infty} f(x) cdot x dx right)^2.
$$
Вычислим сначала математическое ожидание:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx = int_{0}^{6} frac{x}{18} cdot x dx = int_{0}^{6} frac{x^2}{18} dx =
left.frac{x^3}{54} right|_0^6=frac{6^3}{54} = 4.
$$
Теперь вычислим
$$
M(X^2)=int_{-infty}^{+infty} f(x) cdot x^2 dx = int_{0}^{6} frac{x}{18} cdot x^2 dx = int_{0}^{6} frac{x^3}{18} dx = left.frac{x^4}{72} right|_0^6=frac{6^4}{72} = 18.
$$
Подставляем:
$$
D(X)=M(X^2)-(M(X))^2=18-4^2=2.
$$
Дисперсия равна 2.
Другие задачи с решениями по ТВ
Подробно решим ваши задачи на вычисление дисперсии
Вычисление дисперсии онлайн
Как найти дисперсию онлайн для дискретной случайной величины? Используйте калькулятор ниже.
- Введите число значений случайной величины К.
- Появится форма ввода для значений $x_i$ и соответствующих вероятностей $p_i$ (десятичные дроби вводятся с разделителем точкой, например: -10.3 или 0.5). Введите нужные значения (проверьте, что сумма вероятностей равна 1, то есть закон распределения корректный).
- Нажмите на кнопку “Вычислить”.
- Калькулятор покажет вычисленное математическое ожидание $M(X)$ и затем искомое значение дисперсии $D(X)$.
Видео. Полезные ссылки
Видеоролики: что такое дисперсия и как найти дисперсию
Если вам нужно более подробное объяснение того, что такое дисперсия, как она вычисляется и какими свойствами обладает, рекомендую два видео (для дискретной и непрерывной случайной величины соответственно).
Спасибо за ваши закладки и рекомендации
Полезные ссылки
Не забывайте сначала прочитать том, как найти математическое ожидание. А тут можно вычислить также СКО: Калькулятор математического ожидания, дисперсии и среднего квадратического отклонения.
Что еще может пригодиться? Например, для изучения основ теории вероятностей – онлайн учебник по ТВ. Для закрепления материала – еще примеры решений задач по теории вероятностей.
А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике или заказать в МатБюро:
Что такое дисперсия в статистике
Статистика, в частности, оперирует рядами данных, характеризующих какой-либо признак, явление. Интересует их изменение.
Вариация представляет собой отличие величин одинакового показателя у разных предметов. Ее изучение позволит понять причины отклонений от нормы, анализировать их и в какой-то мере прогнозировать. Также станет возможным выявить факторы, влияющие на значения, отсеяв случайные.
Характеристики равномерного распределения представлены на картинке:

При значительном объеме статистики, средняя величина очевидно близка к нормальной. Об этом говорят и законы распределения. Отклонения от нее будут являться объективной характеристикой.
Только вот отрицательные значения этих разбросов будут сбивать с толку при расчетах, погашая положительные. А оставлять лишь модули – для математика не корректно. Напрашивается возвести в четную степень, а именно – во вторую.
Решение оказалось не только удобным. Оно открыло бо́льшие возможности в изучении отклонений. А важны именно они, поскольку сама по себе средняя мало что дает.

В качестве одного из важных показателей вариации, вводится понятие «дисперсия» – усредненный квадрат отклонений численных значений каких-либо событий от средней величины.
Кратко записывается D[X] в русскоязычных источниках и Var[X] (от «variance») в английских. В статистических выкладках используется σ2.

Никакого наглядного смысла величина не несет. Другое дело, среднее квадратическое отклонение – корень квадратный из дисперсии.
Виды дисперсии дискретной случайной величины
Для анализа данных цифр в таком виде недостаточно. Гораздо больше можно выжать из последовательности, если разбить ее на группы по определенному признаку.
Общая дисперсия
Как можно заметить, вычисленная по приведенному выше определению величина характеризует отклонения в целом. Без учета определяющих вариацию факторов. Вернее, с учетом всех, включая совершенно случайные. Поэтому и называется «общей» и рассчитывается по формулам, указанным ниже.
Простая дисперсия, без разделения на группы:
![]()
Или в несколько преобразованном виде:
![]()
Взвешенная дисперсия, для вариационного ряда:
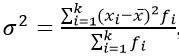
где xi – значение из ряда;
fi – частота, количество повторений;
k – групп;
n – число вариантов.
Черта сверху указывает на среднюю величину.
Межгрупповая дисперсия
Характеризует систематическое отклонение, возникающее из-за фактора, по которому производилось выделение признаков в группы. Поэтому также называется «факторной».
Как найти данную дисперсию? По формуле:
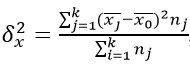
где k – количество групп;
nj – элементов в группе с индексом j.
Внутригрупповая дисперсия
Возникает по хаотичной причине, не связанной с причиной сделанной выборки. Неучтенный фактор. Еще обозначается как «остаточная».
Например, рассматривается количество выпущенных деталей за месяц каждым фрезеровщиком цеха.
В качестве критерия отбора в группу выбираем возраст оборудования. Он-то и не будет влиять на производительность внутри подборки: там станки у всех практически одинаковые.
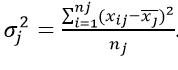
Если вычислить среднюю величину от всех групповых,
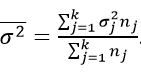
то получим характеристику случайного разброса. Иными словами, составляющую вариации, зависящую от чего угодно, кроме фактора отбора.
Взаимосвязь
В соответствии с правилом сложения, общая D[X] включает средние выражения остаточной и факторной. И это логично, поскольку учитывает и случайное изменение в группе, и систематическое в факторной.
Свойства дисперсии

Опишем основные:
-
Если последовательность состоит из одинаковых чисел, то D[X] будет нулевой.
-
Уменьшение всех значений на постоянную величину на дисперсию не влияет. Иначе говоря, рассчитать σ2 можно по отклонениям от фиксированного числа.
-
Уменьшение всех цифр в k раз приведет к падению D[X] в k2 раз. Можно, например, иметь в виду значения в метрах, а результат вычислить в футах. Достаточно учесть один раз то, на что следует умножить.
-
Средний квадрат отклонений от постоянной величины X отличается в большую сторону от того же с использованием среднего значения. Разница составит (Xcр – X)2.
Показатели вариаций
Кроме размаха (разницы максимального и минимального значений), среднего линейного и дисперсии, изменения описываются коэффициентом вариации:
![]()
Оценить масштаб разброса проще по относительной величине. Тем более, что измеряются в одних единицах.
Пример расчета дисперсии
Компания объявила конкурсный отбор для приема сотрудников. В качестве критерия принят стаж работы по специальности. Приведем исходные данные и расчеты.
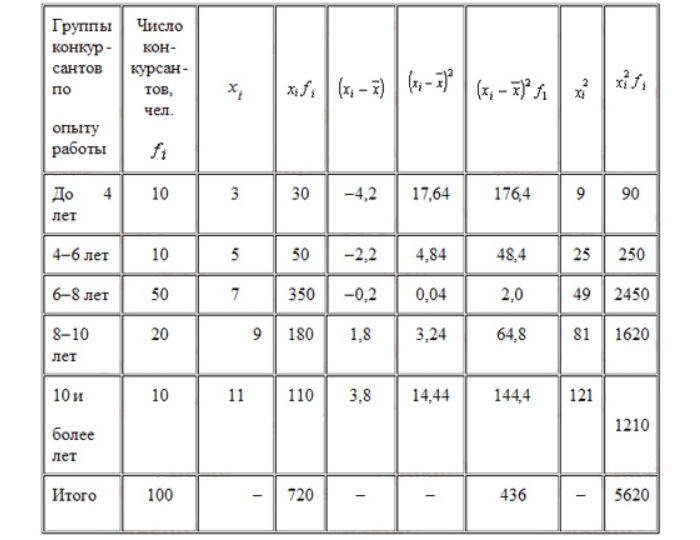
Усредненный стаж:
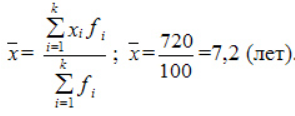
Дисперсия:
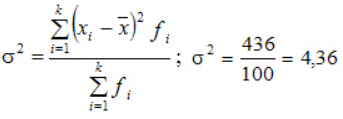
По альтернативной формуле:
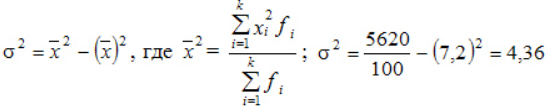
Среднеквадратическое:
![]()
Коэффициент вариации:
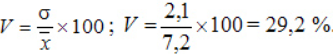
Заключение
Статистика оперирует значительными объемами данных. Вариация, как одно из основных понятий – не исключение. И дисперсия в качестве основной характеристики.
Для упрощения расчетов существует масса онлайн калькуляторов. Имеется упомянутый инструмент в MS Excel.
Слайды презентации
Слайд 1
Презентация № 5
по теме: «Описательная
статистика»
– 7 класс

Слайд 2
Описатель
ная
статистика
Наибольшее и наименьшее
значение.
Размах , мода
Отклонения
Дисперсия
Обозначения и формулы
Свойства среднего
арифметического и дисперсии

Слайд 3
Наибольшее и
наименьшее значение.
Пример
1
Петя и Вася поспорили, кто лучше
прыгает в длину с места. Чтобы
избежать случайности, они
решили,
что будут прыгать по очереди 5 раз.
Результаты своих
прыжков в
сантиметрах они записали в
таблицу.

Слайд 4
Результаты прыжков в
длину с места, см
Пример 1 (стр.54)
Номер прыжка
Петя
Вася
1 190 185
2 205 200
3 195 215
4 210 190
5
200 190

6. Производство пшеницы в России в 1995-2001 гг.
Год
1995
1996 1997 1998 1999 2000 2001
Млн.тонн
30,1 34,9 44,3 27,0 31,0
34,5 47,0
Размах показывает,
насколько велико
рассеивание значений в
числовом наборе.

Слайд 6
При изучении учебной нагрузки
учащихся выделили группу из 12
семиклассников.
Их попросили
отметить в определенный день
время (в минутах),
затраченное на
выполнение домашнего задания по
алгебре. Получили такие данные:
23,
18, 25, 20, 25, 25, 32, 37, 34, 26,
34, 25. 27
12324
12 253426343732252520252823
27 – среднее значение
Наибольшее значение – 37; наименьшее значение – 18;
Размах ряда равен 37 – 18 = 19

Слайд 7
При анализе сведений о времени,
затраченном семиклассниками на
выполнение домашнего
задания по алгебре,
нас могут интересовать не только среднее
арифметическое и размах полученного ряда
данных, но и другие показатели.
Интересно,
например, знать, какой расход времени
является типичным для выделенной группы
учащихся, то есть какое число встречается
в ряду данных чаще всего. Нетрудно
заметить, что таким числом является число
25. Говорят, что число 25 – мода
рассматриваемого
ряда .
Модой ряда чисел называется
число, чаще других
встречающееся в данном ряду.
Ряд чисел может иметь более одной
моды или не иметь моды совсем.

Слайд 8
Рассмотрим еще пример. Пусть,
проведя учет деталей, изготовленных
за смену
рабочими одной бригады,
получили такой ряд данных:
36, 35,
35, 36, 37, 37, 36, 37, 38, 36,
36, 36,
39, 39, 37, 39, 38, 38, 36, 39,
36.Найдем для него среднее арифметическое,
размах и моду. Для этого удобно
предварительно составить из полученных
данных упорядоченный ряд чисел , т. е. такой
ряд, в котором каждое последующее число не
меньше (или не больше) предыдущего.
Получим:
35, 35, 36, 36, 36, 36, 36, 36, 36, 36, 37, 37, 37,
37, 38, 38, 38, 39, 39, 39, 39.
Вычислим среднее арифметическое:
37
21
776
21
4 39 3 38 4 37 8 36 2 35
Размах ряда равен . Мода
данного ряда равна 36, так как число 36
чаще всего встречается в этом ряду.
4 35 39

Слайд 9
Например, в ряду чисел
47 , 46, 50, 52 ,
47 , 52 ,
49, 45, 43, 53
две моды –
это числа 47 и 52,
а в ряду чисел 69, 68, 66, 80, 67, 65,
71, 74, 63, 73, 72
моды нет.Моду ряда данных обычно находят тогда,
когда хотят выявить некоторый типичный
показатель. Например, если изучаются
данные о размерах мужских сорочек,
проданных в определенный день в
универмаге, то удобно воспользоваться
таким показателем, как мода, который
характеризует размер, пользующийся
наибольшим спросом. Находить в этом
случае среднее арифметическое не имеет
смысла. Мода является наиболее
приемлемым показателем при выявлении,
например, расфасовки некоторого товара,
которой отдают предпочтение покупатели;
цены на товар данного вида, наиболее
распространенной на рынке, и т. п.

Слайд 10
Итак, средняя выработка рабочих за
смену составляет примерно 37
деталей;
различие в выработке
рабочих не превосходит 4 деталей;
типичной
является выработка, равная
36 деталям.

Слайд 11
Упражне
ния
№ 1. Найдите наибольшее и
наименьшее значение, размах,
среднее значение,
медиану и моду
набора чисел:
а) 12, 7, 25, 3,
19, 15;
б) 17, 19, 5, 41, 47, 13, 19.

Слайд 12
Упражне
ния
№ 2. В таблице 7 приведены данные
о производстве зерновых
в России в
2000-2006 гг.показатель
2000 2001 2002 2003 2004
2005 2006
Производство
зерновых, млн.т 65,5 85,2 86,6 67,2 78,1 78,2
78,6
Урожайность, ц/га
15,6 19,4 19,6 17,8 18,8 18,5 18,9
Производство
пшеницы, млн. т 34,5 47,0 50,6 34,1 45,4 47,7 45,0
По таблице найдите наименьшее, наибольшее значение и размах:
а) производства зерновых в 2000-2006 гг.;
б) производства пшеницы в 2000-2006 гг.;
в) урожайности зерновых в 2000-2006 гг.

Слайд 13
Отклонен
ия
Попробуем узнать, как числа некоторого
набора расположены по отношению к
своему
среднему значению.
Зная только размах, разность между
наибольшим и
наименьшим значением, мы не
можем судить о том, как расположены
числа в
имеющемся наборе.
Для примера возьмем набор 1, 6, 7, 9, 12.
Вычислим среднее арифметическое:
(1+6+7+9+12):5=7.
Найдем отклонение каждого числа от
среднего: 1-7=-6, 6-7=-1, 7-7=0, 9-7=2, 12-7=5.

Слайд 14
Отклонения
(продолжение)
Получился новый набор -6, -1, 0, 2, 5 ,
который
состоит из отклонений.
Если число меньше среднего, то его
отклонение отрицательно, если число больше
среднего, то его отклонение положительно.
В одном
случае – для числа 7, которое совпало со средним
арифметическим, – отклонение равно нулю.
По набору отклонений можно судить о том,
насколько разнообразны числа в наборе.
Если отклонения малы, то числа в наборе
расположены близко к среднему арифметическому.
А если среди отклонений есть большие по
модулю, то числа в наборе сильно разбросаны.

Слайд 15
Отклонения
(продолжение)
Для любого набора, если только
не все числа в
нем равны, часть
отклонений будет положительна, а
часть –
отрицательна. При этом сумма
всех отклонений равна 0.
Убедимся в этом
на нашем
примере:
-6+(-1)+0+2+5=0.
В этом состоит основное
свойство отклонений:
сумма отклонений чисел от
среднего
арифметического этих
чисел равна нулю.

Слайд 16
Дисперсия
Наиболее полной
характеристикой разброса набора
чисел является набор их отклонений
от среднего арифметического. Но
когда набор чисел велик,
рассматривать
набор отклонений
практически неудобно. Нужно описать
разнообразие чисел в наборе
одной
характеристикой, одним числом.
Размах – слишком грубая мера
разброса чисел в наборе, поскольку
учитывает только два из них –
наименьшее и наибольшее. Можно
попробовать взять «среднее
отклонение». Но сумма отклонений
всегда равна нулю, поэтому среднее
арифметическое отклонений тоже
равно нулю и его нельзя использовать
как меру разброса.

Слайд 17
Дисперсия
Чтобы судить о разбросе, принято
складывать не сами отклонения, а
их
квадраты. Квадраты отклонений
неотрицательны, поэтому сумма
квадратов отклонений
зависит только
от абсолютных величин отклонений, а
не от их
знаков. Чем больше
отклонения чисел от среднего
арифметического, тем больше будет
сумма квадратов отклонений. Для
того чтобы мера разброса чисел не
зависела от их количества в наборе, в
качестве такой меры берут среднее
арифметическое квадратов
отклонений. Эту величину называют
дисперсией .

Слайд 18
Дисперсия
Определ
ение.
Среднее арифметическое
квадратов отклонений от
среднего значения называется
в статистике
дисперсией
набора чисел.

Слайд 19
Диспер
сия
Пример
1.
Обратим
ся к
таблице
произво
дства
пшениц
ы
(млн.тон
н) в
России.
Вычисли
ть
дисперс
ию. Год производство Отклонение
от среднего Квадрат
отклонения
1995 30,1
1996
34,9
1997 44,3
1998 27,0
1999 31,0
2000 34,5
2001 47,01.
Найдем
средне
е
арифме
ти-
ческое
произв
од-ства
пшени
цы Средн
ее
арифм
е-
тическ
ое
равно
35,5
млн.то
нн в
годНайдем
отклон
ения от
средне
го

Слайд 20
Диспер
сия
Пример
1. Год производство Отклонение
от среднего Квадрат
отклонения
1995 30,1
-5,4
1996 34,9 -0,6
1997 44,3 8,8
1998 27,0 -8,5
1999 31,0 -4,5
2000
34,5 -1,0
2001 47,0 11,5Найдем
отклон
ения от
средне
го Найдем
квадрат
ы
отклоне
ний

Слайд 21
Диспер
сия
Пример
1. Год производство Отклонение
от среднего Квадрат
отклонения
1995 30,1
-5,4 29,16
1996 34,9 -0,6 0,36
1997 44,3 8,8 77,44
1998 27,0
-8,5 72,25
1999 31,0 -4,5 20,25
2000 34,5 -1,0 1,00
2001 47,0 11,5
132,25Найдем
квадрат
ы
отклоне
нийВычисл
им
среднее
значени
е
квадрат
ов
отклоне
ний

Слайд 22
Диспер
сия Пример
1.
(29,16+0,36+77,44+72,25+20,25+1
,00+132,25) :7=47,53.
47,53 – дисперсия

Слайд 23
Диспер
сия Пример
2.
Покажем на простом примере, как
дисперсия характеризует разброс
отклонений. Возьмем два набора
чисел 1, 2, 3
и 0, 2, 4. Среднее
арифметическое значение обоих
наборов
равно 2. Для обоих
наборов вычислим отклонения и
квадраты отклонений и все
данные занесем в таблицу 9.

Слайд 24
Диспер
сия Пример
2.
1-й
набор Отклонение
от среднего Квадрат
отклонения
1
2
3 1-й
набор Отклонение
от среднего Квадрат
отклонения
0
2
4

Слайд 25
Диспер
сия Пример
2.
1-й
набор Отклонение
от среднего Квадрат
отклонения
1 -1
2
0
3 1 1-й
набор Отклонение
от среднего Квадрат
отклонения
0
-2
2 0
4 2

Слайд 26
Диспер
сия Пример
2.
1-й
набор Отклонение
от среднего Квадрат
отклонения
1 -1
1
2 0 0
3 1 1 1-й
набор Отклонение
от
среднего Квадрат
отклонения
0 -2 4
2 0 0
4 2 4

Слайд 27
Диспер
сия Пример
2.
1-й
набор Отклонение
от среднего Квадрат
отклонения
1 -1
1
2 0 0
3 1 1 1-й
набор Отклонение
от
среднего Квадрат
отклонения
0 -2 4
2 0 0
4 2 4
Дисперсия второго
набора:
(4 + 0 + 4): 3 = Дисперсия первого набора:
(1 + 0 + 1): 3 = 3
2
3
2
2
3
8

Слайд 28
Диспер
сия Пример
2.
1-й
набор Отклонение
от среднего Квадрат
отклонения
1 -1
1
2 0 0
3 1 1 1-й
набор Отклонение
от
среднего Квадрат
отклонения
0 -2 4
2 0 0
4 2 4
Дисперсия второго
набора:
(4 + 0 + 4): 3 = Дисперсия первого набора:
(1 + 0 + 1): 3 = 3
2
3
2
2
3
8
Числа в первом наборе расположены
более кучно – ближе друг к другу и к
своему среднему, – чем числа во
втором наборе. Поэтому дисперсия
первого набора меньше, чем второго.

Слайд 29
Диспер
сия Пример
3.
Континентальный климат отличается от
умеренного более резкими изменениями
температуры в течение года. В районах с
континентальным климатом
жаркое лето и
очень холодная зима. С помощью
дисперсии различия
между двумя видами
климата можно выразить количественно.
Сравним для примера изменение
температур в течение года в Москве и
Киеве, где климат умеренный, с
изменением температур в Новосибирске и
Хабаровске, где климат континентальный.
В таблице 10 приведены средние месячные
температуры за 80 лет в Москве, Киеве,
Новосибирске и Хабаровске.

Слайд 30
Диспер
сия Пример
3.
Месяцы Москва Киев Новосибирск Хабаровск
1 -9,3 -5,9 -19,0
-22,3
2 -8,6 -5,2 -17,2 -17,2
3 -3.4 -0,4 -10,7 -8,5
4
5,1 7,5 -0,1 3,1
5 12,4 14,7 10,0 11,1
6 16,7 17,8
16,3 17,4
7 18,4 19,8 18,7 21,1
8 16,6 18,7 16,0 20,0
9 10,9 13,9 9,9 13,9
10 4,4 7,5 1,5 4,7
11 -2,0 1,2 -9,7 -8,1
12 -6,8 -3,5 -16,9 -18,5
Среднее за год 4,5 6,0 -0,1 -1,4
Дисперсия 98,9 86,5 185,2 228,8

Слайд 31
Упражнени
я
№ 1 Для данных чисел вычислите
среднее значение. Составьте таблицу
отклонений от среднего и квадратов
отклонений от среднего и
вычислите
дисперсию:
а) -1, 0, 4; в) -3, 1, 2, 4;
д) -2, -1, 1, 2, 5;
б) 2, 3, 7; г) 2, 6, 7, 5; е) -1, -3, -2, 3, 3.

Слайд 32
Упражнени
я
№ 2. Даны два набора чисел. Отметьте
их на числовой
прямой. Вычислите
дисперсию каждого из этих наборов.
Дисперсия какого
набора больше?
а) 2, 3, 7 и 1, 2, 3; б)
2, 3, 4, 7 и 1, 5, 6, 8.

Слайд 33
Упражнени
я
№ 3. Даны два набора чисел.
Отметьте их на числовой
прямой.
Вычислите дисперсию каждого из
этих наборов. Сравните
дисперсии:
а)
2, 3, 4 и 6, 7, 8; б) 3, 5,
7, 9 и 12, 14, 16, 18.

Слайд 34
Обозначения и
формулы
Числа в наборах часто приходиться
обозначать буквами, подобно
тому, как
это делается при решении задач на
движение.
Но поскольку чисел может
быть много, использовать для каждого
числа
отдельную букву неудобно.
Поэтому поступают иначе: используют
одну и ту же букву с номером. Таким
образом, можно рассматривать набор
х
1 , х
2 , х
3 , х
4 , х
5 или у
1 , у
2 , у
3 , у
4 , у
5 , у
6 и т.п.
Номера чисел называются индексами.

Слайд 35
Обозначения и
формулы
Среднее арифметическое чисел х
1 , х
2 ,
х
3 ,
х
4 , х
5 принято
обозначать через
Например, среднее арифметическое
пяти чисел запишется так:x
5 54321
x x x x x
x

Слайд 36
Обозначения и
формулы
Отклонения от среднего значения
теперь запишутся так:
, 1 x x
,
2 xx ,
3 x x ,
4 xx . 5 x x
Разберем на примере набора
х
1 , х
2 , х
3 , х
4 ,
как
записывается в символьном виде
дисперсия. Дисперсия равна среднему
арифметическому квадратов
отклонений этих чисел от среднего
значения. Обозначают дисперсию
обысно через S 2
. Получается:
.
4 2
42
32
22
12
x x x x x x x x
s

Слайд 37
Обозначения и
формулы
№ 1. Запишите с помощью букв набор
чисел
17, 3, 6, 21, 15. Чему равно
значение х
2
в этом наборе? Чему равно
значение х
5 в этом
наборе?Упражнен
ия
№ 2. Пусть а – некоторое число.
Вычислите среднее
арифметическое и дисперсию
набора чисел:
а) х
1 = а +1, х
2 = а +2, х
3 = а + 3;
а) х
1 = а +2, х
2 = а +3, х
3 = а + 7.x2
S

Слайд 38
Свойства среднего
арифметического и дисперсии
Буквенные обозначения чисел в наборе и
введенные
обозначения для среднего
арифметического и
для дисперсии набора чисел позволяют
легко записать некоторые их свойства.
Для простоты записи сформулируем их
для набора из пяти чисел. Эти правила
верны для любого количества чисел в
наборе.x 2
S

Слайд 39
Свойства среднего
арифметического и дисперсии
Рассмотрим набор чисел х
1 ,
х
2 , х
3 , х
4 , х
5 .
Пусть
– его
среднее арифметическое, а
–
дисперсия.
Прибавим к каждому числу этого набора
постоянное число а. Получим набор
х
1 + а, х
2 + а , х
3 + а , х
4 + а , х
5 + а .x
2
S

Слайд 40
Свойств
о 1.
Среднее арифметическое набора
х
1 + а, х
2 +
а , х
3 + а , х
4 + а
, х
5 + а равно . a x

Слайд 41
Свойств
о 2.
Дисперсия набора
х
1 + а, х
2 + а
, х
3 + а , х
4 + а ,
х
5 + а равна
дисперсии набора х
1
, х
2 , х
3 , х
4 , х
5 .

Слайд 42
Свойств
о 3.
Среднее арифметическое набора а х
1 ,
ах
2 ,
ах
3 , ах
4 , ах
5
равно .xa
Свойств
о 4.
Среднее арифметическое
набора а х
1 ,
а х
2 , а х
3
, а х
4 , а х
5
равна 22
Sa

Чтобы скачать презентацию – поделитесь ей с друзьями с помощью
социальных кнопок.
Цель: познакомить учащихся с понятиями
“отклонение” и “дисперсия” и их применением в
реальных статистических исследованиях с
использованием средств табличного процессора
Excel.
Планируемые результаты:
- знать, что такое отклонение от среднего
арифметического и дисперсия; - уметь вычислять отклонения, квадраты
отклонений и дисперсию на коротких наборах; - уметь применять понятия квадратов отклонений и
дисперсии при анализе реальных ситуаций; - уметь использовать для вычисления
характеристик числовых наборов статистические
функции табличного процессора Excel.
Оборудование:
- компьютеры, мультимедийный проектор, экран;
- презентация <приложение 1>;
- файл Excel с заданиями к уроку и технологией их
выполнения <приложение 2> - файл Word с домашним заданием <приложение
3>
Программное обеспечение: табличный
процессор Excel.
Подготовительный этап:
- скопировать на компьютеры учеников файл с
заданиями; - подготовить распечатки домашнего задания.
Ход урока
Слайд 1 – тема и цели урока.
1. Актуализация знаний.
На предыдущих уроках мы рассмотрели так
называемые средние характеристики числового
ряда, позволяющие оценить его поведение “в
среднем”. Повторим их определения и способы
нахождения.
Слайд 2 – задание на повторение (комментарии
учителя, проверка ответов учеников с помощью
слайда).
2. Объяснение нового материала, практикум.
Слайд 3 – характеристики числового ряда
(комментарии учителя).
Средние характеристики числового ряда (среднее
арифметическое, медиана), позволяют оценить
поведение ряда “в среднем”. Но это не всегда
наиболее полно характеризуют выборку. Чтобы
получить полное представление о поведении
числового ряда, помимо средних характеристик
надо знать характеристики разброса,
показывающие, насколько сильно значения ряда
отличаются друг от друга, как сильно они
разбросаны вокруг средних.
Рассмотрим следующий пример.
Слайд 4 – задание 1 (комментарий учителя).
(Ученикам открыть файл с заданиями (приложение
2) и выбрать лист “Задание 1”).
| День недели | Дневная выработка | |
| 1-й рабочий (Х) | 2-й рабочий (Y) | |
| (кол-во деталей) | (кол-во деталей) | |
| Понедельник |
52 |
61 |
| Вторник |
54 |
40 |
| Среда |
50 |
55 |
| Четверг |
48 |
50 |
| Пятница |
46 |
44 |
Рассчитаем, сколько деталей изготовил каждый
из рабочих за 5 дней.
(Ученики выполняют задание, руководствуясь п. 1
“Подсчёт итога”).
| День недели | Дневная выработка | |
|
1-й рабочий (Х) |
2-й рабочий (Y) |
|
|
(кол-во деталей) |
(кол-во деталей) |
|
| Понедельник |
52 |
61 |
| Вторник |
54 |
40 |
| Среда |
50 |
55 |
| Четверг |
48 |
50 |
| Пятница |
46 |
44 |
| Итого: |
250 |
250 |
Вывод: количество деталей одинаково.
Рассчитаем, сколько деталей в день производил в
среднем каждый рабочий (среднюю
производительность труда). Для этого найдём среднее
арифметическое числовых наборов Х и Y.
(Ученики выполняют задание, руководствуясь п. 2
“Расчёт среднего арифметического”).
| День недели | Дневная выработка | |
| 1-й рабочий (Х) | 2-й рабочий (Y) | |
| (кол-во деталей) | (кол-во деталей) | |
| Понедельник |
52 |
61 |
| Вторник |
54 |
40 |
| Среда |
50 |
55 |
| Четверг |
48 |
50 |
| Пятница |
46 |
44 |
| Итого: |
250 |
250 |
| Среднее арифметическое |
50 |
50 |
Производительность труда за день у обоих
рабочих тоже одинаковая.
Найдём медианы числовых наборов X и Y.
(Ученики выполняют задание, руководствуясь п. 3
“Расчёт медианы”).
|
День недели |
Дневная |
|
|
1-й рабочий (Х) |
2-й рабочий (Y) |
|
|
(кол-во деталей) |
(кол-во деталей) |
|
| Понедельник |
52 |
61 |
| Вторник |
54 |
40 |
| Среда |
50 |
55 |
| Четверг |
48 |
50 |
| Пятница |
46 |
44 |
| Итого: |
250 |
250 |
| Среднее арифметическое |
50 |
50 |
| Медиана |
50 |
50 |
Медианы тоже получились одинаковые.
На данном примере мы увидели, что с помощью
средних характеристик сравнение выполнить не
всегда возможно.
Как поступить?
В данном случае критерием сравнения может
выступать стабильность работы токарей –
у какого токаря количество произведённых им
деталей в день менее отличается друг от друга,
тот работает стабильнее.
Если количество производимых в день деталей
сильно разнится, то в какие-то дни токарь
работает не в полную силу, производит меньше
деталей, а в какие-то дни навёрстывает упущенное,
а это всегда сказывается на качестве продукции.
Стабильность можно оценивать с помощью отклонений
элементов числового набора от среднего значения
(отклонение – это разность между числом из
данного набора и средним арифметическим этого
набора)
Слайд 5 – пример вычисления отклонений
(комментарии учителя).
Логично предположить, что чем меньше будет
разброс (отклонения от среднего значения) – тем стабильнее
работает токарь.
Но когда набор чисел велик, рассматривать
отклонения практически неудобно, нужно
описать разнообразие чисел в наборе одним
числом.
Попробуем найти сумму отклонений.
Слайд 5 – пример вычисления суммы отклонений
(комментарии учителя, вывод).
В сумме получилось 0 (т.к. при вычислении
“среднего разброса” часть отклонений входит в
сумму со знаком “+”, часть со знаком “-” и в
сумме всегда получается 0). Следовательно сумма
отклонений не может нести информацию о разбросе.
Какой же выход?
Можно суммировать квадраты отклонений (они
всегда неотрицательны).
Слайд 6 – пример вычисления квадратов
отклонений (комментарии учителя)
Чем меньше сумма квадратов отклонений, тем
меньше разброс чисел относительно среднего
значения, тем более стабилен набор.
Итак, рассчитаем сумму квадратов отклонений
для нашего примера.
(Ученики выполняют задание, руководствуясь п. 4
“Расчёт суммы квадратов отклонений”).
| День недели | Дневная выработка | |
| 1-й рабочий (Х) | 2-й рабочий (Y) | |
| (кол-во деталей) | (кол-во деталей) | |
| Понедельник |
52 |
61 |
| Вторник |
54 |
40 |
| Среда |
50 |
55 |
| Четверг |
48 |
50 |
| Пятница |
46 |
44 |
| Итого: |
250 |
250 |
| Среднее арифметическое |
50 |
50 |
| Медиана |
50 |
50 |
| Сумма квадратов отклонений |
40 |
282 |
Вывод: первый токарь работает более стабильно,
у него меньше сумма квадратов отклонений.
Вероятно, работодатель предпочтёт взять на
работу его.
В данном примере рабочие работали одинаковое
количество дней. А если они количество дней неодинаково?
Тогда стабильность работы каждого можно было
бы оценить по величине среднего
арифметического квадратов отклонений от
среднего значения – дисперсии.
Слайд 7 – пример вычисления дисперсии
(комментарии учителя).
Рассмотрим следующий пример.
Слайд 8 – задание 2 (комментарии учителя).
(Ученикам открыть лист “Задание 2” файла с
заданиями).
| День недели | Дневная выработка | |
| 1-й рабочий (Х) | 2-й рабочий (Y) | |
| (кол-во деталей) | (кол-во деталей) | |
| Понедельник |
53 |
52 |
| Вторник |
54 |
46 |
| Среда |
49 |
53 |
| Четверг |
48 |
49 |
| Пятница |
46 |
Аналогично заданию 1 рассчитаем, сколько
деталей произвёл каждый рабочий и сумму
квадратов отклонений.
(Ученики выполняют задание, руководствуясь п.
1-2).
| День недели | Дневная выработка | |
| 1-й рабочий (Х) | 2-й рабочий (Y) | |
| (кол-во деталей) | (кол-во деталей) | |
| Понедельник |
53 |
52 |
| Вторник |
54 |
46 |
| Среда |
49 |
53 |
| Четверг |
48 |
49 |
| Пятница |
46 |
|
| Итого: |
250 |
200 |
| Сумма квадратов отклонений |
46 |
30 |
Т.к. токари работали разное количество дней,
рассчитаем и сравним дисперсии числовых наборов
X и Y.
(Ученики выполняют задание, руководствуясь п. 3).
| День недели | Дневная выработка | |
| 1-й рабочий (Х) | 2-й рабочий (Y) | |
| (кол-во деталей) | (кол-во деталей) | |
| Понедельник |
53 |
52 |
| Вторник |
54 |
46 |
| Среда |
49 |
53 |
| Четверг |
48 |
49 |
| Пятница |
46 |
|
| Итого: |
250 |
200 |
| Сумма квадратов отклонений |
46 |
30 |
| Дисперсия |
9,2 |
7,5 |
Вывод: второй токарь работает стабильнее
первого.
3. Самостоятельная практическая работа (при
наличии времени).
Слайд 9 – задание 3.
(Ученикам открыть лист “Задание 3” файла
заданий и выполнить самостоятельную работу).
Подвести итог самостоятельной работы.
4. Итог урока.
Слайд 10 – выводы (комментарии учителя).
Слайд 11 – вопросы (ответы учеников).
5. Домашнее задание (§§ 13, 14 учебник Ю.Н. Тюрина,
А.А. Макарова, И.Р. Высоцкого, И.В. Ященко “Теория
вероятностей и статистика”, приложение 3).
Список использованной литературы
- М.В. Ткачёва, Н.Е. Фёдорова “Элементы статистики
и вероятность. 7-9”, Москва, “Просвещение”, 2005 г. - Ю.Н. Тюрин, А.А. Макаров, И.Р. Высоцкий, И.В. Ященко
“Теория вероятностей и статистика”, Москва,
“Просвещение”, 2008 г. - Е.А. Бунимович, В.А. Булычёв “Основы статистики и
вероятность 5-9”, Москва, “Дрофа”, 2004 г. - А.Г. Мордкович, П.В. Семёнов “События.
Вероятности. Статистическая обработка данных.
7-9”, Москва, “Мнемозина”, 2008 г.
