В данной публикации мы рассмотрим определение и разновидности тетраэдра, а также формулы для расчета площади его поверхности (одной грани и полной) и объема. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.
- Определение тетраэдра
- Виды тетраэдра
- Формулы площади и объема правильного тетраэдра
Определение тетраэдра
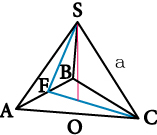
Тетраэдр – это разновидность пирамиды; четырехгранник, гранями которого являются треугольники.

Тетраэдр имеет 4 грани, 4 вершины и 6 ребер. Каждая грань фигуры может быть ее основанием.
Развертка тетраэдра на примере правильной фигуры представлена ниже:

Основные элементы и свойства тетраэдра (к нему применимы свойства правильной пирамиды) мы рассмотрели в отдельной публикации.
Виды тетраэдра
- Равногранный тетраэдр – боковые грани фигуры равны, а основанием является правильный (равносторонний) треугольник.

- Прямоугольный тетраэдр – угол между всеми тремя ребрами при одной вершине является прямым, т.е. равным 90°.

- Правильный тетраэдр – все ребра равны, а грани, соответственно, являются равносторонними треугольниками.

- Ортоцентричный тетраэдр – все высоты, проведенные из всех вершин фигуры к противолежащим граням, пересекаются в одной точке.
Формулы площади и объема правильного тетраэдра
Площадь поверхности

![]()
Объем
![]()
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 4 декабря 2019 года; проверки требуют 8 правок.
| Правильный тетраэдр | |||
|---|---|---|---|
 |
|||
 |
|||
| Тип | правильный многогранник | ||
| Комбинаторика | |||
| Элементы |
|
||
| Грани | правильные треугольники | ||
| Конфигурация вершины | 3.3.3 | ||
| Двойственный многогранник | тоже правильный тетраэдр | ||
| Классификация | |||
| Символ Шлефли | {3,3} | ||
| Группа симметрии |
 |
||
| Количественные данные | |||
| Длина ребра |
 |
||
| Площадь поверхности |
 |
||
| Объём |
 |
||
| Телесный угол при вершине |
 ср ср |
Тетраэдр называется правильным, если все его грани — равносторонние треугольники.
У правильного тетраэдра все двугранные углы при рёбрах и все трёхгранные углы при вершинах равны.
Свойства правильного тетраэдра[править | править код]
- Каждая его вершина является вершиной трех равносторонних треугольников. А значит, сумма плоских углов при каждой вершине будет равна
.
- В правильный тетраэдр можно вписать октаэдр, притом четыре из восьми граней октаэдра будут совмещены с серединными треугольниками четырёх граней тетраэдра, а все шесть вершин октаэдра будут совмещены с центрами шести рёбер тетраэдра.
- Правильный тетраэдр можно вписать в куб, притом четыре вершины тетраэдра будут совмещены с четырьмя вершинами куба, а все шесть рёбер тетраэдра будут совмещены с диагоналями граней куба.
Интересные факты[править | править код]
Середины граней правильного тетраэдра также образуют правильный тетраэдр.
Соотношения:
- рёбер и высот правильных тетрадров, радиусов переписанных, описанных и писанных сфер соответственно равны
;
- площадей поверхности равно
;
- объёмов равно
.

Autodualité du tétraèdre régulier.
Примечания[править | править код]
- ↑ 1 2 3 4 5 Coxeter, 1948.
Литература[править | править код]
- Harold Scott MacDonald Coxeter. Table I(i) // Regular Polytopes. — Methuen and Co., 1948.
Площадь поверхности тетраэдра
Площадь поверхности тел
Тетраэдром является геометрическая фигура, представляющая собой простейший многогранник с четырьмя гранями. Любая грань тетраэдра является треугольником. Кроме 4-х граней у тетраэдра имеется шесть ребер и четыре вершины. В правильном тетраэдре все ребра равны. Расчет S тетраэдра необходим при решении разных проектировочных задач, т.к. он является важным конструктивным элементом в сложных строительных и других конструкциях. Площадь поверхности тетраэдра несложно вычислить с помощью онлайн калькулятора, подставив исходные данные в приведенную ниже формулу:
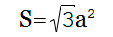
a — величина ребра тетраэдра.
Площадь тетраэдра рассчитывается как корень квадратный из произведения квадрата длины ребра на 3.
Расчет площади поверхности тетраэдра
- Категория: Математика
- Опубликовано: 21 декабря 2021
В таблице даны самые необходимые формулы для фигуры тетраэдр — это нахождения площади, объема, высоты, сечения, ребра, поверхности.
Эту таблицу с формулами можно не только сохранить на компьютере, в закладках или вашей социальной сети. Но можно скачать и распечатать для использования на уроках.

Сохраните материал в вашей социальной сети, чтобы легко найти его:
Ответы на домашние задания:
- Что такое рабочий план
- Английские слова по теме “Готовка”
- Пять забавных способов помочь вашим детям научиться считать и полюбить это!
- Значение символа мира
- Что такое химическая связь? Ковалентная полярная химическая связь.
- Таблица с формулами вычисления интегралов
- Открытие азота: эксперимент Резерфорда с Jar
- Разделы астрономии: какой и что изучает.
- Загадка теории относительности
- Литий-ионные аккумуляторы на основе твердого электролита безопаснее
- Электрохимические эквиваленты – таблица
- Значение гражданских ценностей
- Принцип Ле Шателье, химическое равновесие, примеры
- Английские слова на тему “Внешность”.
- Свойства твердых тел, жидкостей и газов
Зная площадь полной поверхности тетраэдра, можно сначала вычислить площадь одной грани, а затем ребро тетраэдра, через которое впоследствии легко найти все остальные значения параметров пирамиды. Площадь одной грани тетраэдра будет в четыре раза меньше площади полной поверхности.
S_1=S_(п.п.)/4
a=√(S_(п.п.)/√3)
P=6a=6√(S_(п.п.)/√3)=2√(3√3 S_(п.п.) )
Вычислив ребро через площадь тетраэдра, можно найти радиусы вписанной и описанной окружностей около грани тетраэдра, а затем через них рассчитать высоту и апофему тетраэдра. (рис. 60.1)
r=a/(2√3)=1/2 √(S_(п.п.)/(3√3))
R=a/√3=√(S_(п.п.)/(3√3))
h=√(2/3) a=√((2S_(п.п.))/(3√3))
l=(√3 a)/2=√(√3 S_(п.п.) )/2
Объем тетраэдра вычисляется как ребро в третьей степени, деленное на шесть корней из двух, а формула объема тетраэдра через площадь выглядит как
V=a^3/(6√2)=1/6 √(〖S_(п.п.)〗^3/(6√3))
Чтобы вычислить радиусы сфер вписанной и описанной около тетраэдра через площадь тетраэдра необходимо аналогично произвести алгебраические преобразования формул, чтобы получить следующий их вид. (рис.60.2, 60.3)
r_1=a/(2√6)=1/6 √(S_(п.п.)/√2)
R_1=(√3 a)/(2√2)=1/2 √(S_(п.п.)/√2)
