В этом разделе мы продолжим разбирать тему вычисления площадей плоских фигур. Рекомендуем тем, кто изучает темы не по порядку, сначала обратиться к статье «Геометрический смысл определенного интеграла» и разобрать способы вычисления площади криволинейной трапеции. Нам понадобится вычислять площади фигур, которые ограничены ограничены линиями y=f(x), x=g(y) в прямоугольной системе координат. А также раздел «Свойства площади фигур», где была разобрана квадрируемость плоских фигур.
Краткий обзор статьи
- Начнем с определения понятия криволинейного сектора, получим формулу для вычисления его площади. Для этого мы используем понятие определенного интеграла Дарбу.
- Подробно разберем решения задач с использованием таких кривых как кардиоида, архимедова спираль и лемниската Бернулли.
- В отдельную подтему мы выделили нахождение площади фигуры, которая представлена как разность двух криволинейных секторов.
Полярная система координат и криволинейный сектор
Точка, расположенная в полярной системе координат, имеет полярный угол φ0 и полярный радиус r0≥0. Полярный угол φ0 отсчитывается от полярной оси по часовой стрелке, а r0 – это расстояние от заданной точки до начала координат.
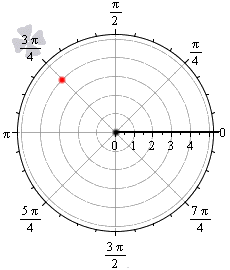
На рисунке мы отметили начало координат (полюс) жирной черной точкой, полярная ось имеет вид луча черного цвета, а красная точка определяется углом φ0=3π4 и расстоянием до полюса r0=4.
Мы можем рассматривать полярную систему координат одновременно с прямоугольной декартовой. Для этого необходимо совместить начала координат обеих систем, а ось абсцисс и полярной осью.
Задать связь полярных и декартовых координат можно соотношениями r=x2+y2φ=arctgyx, x≠0 и обратно x=r·cosφy=r·sinφ.
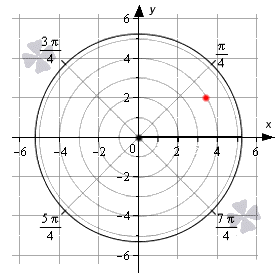
Координаты красной точки на чертеже 23; 2. Положение этой точки задается углом φ0=arctg223=π6 и расстоянием r0=232+22=4.
В полярной системе координат равенство φ=α задает луч, который выходит из точки начала координат и составляет угол α с полярной осью. При этом, угол α может быть задан как в радианах, так и в градусах. Полярную ось мы можем задать уравнением вида φ=0. Равенство r=C>0 задает окружность с центром в начале координат, где – это радиус.
Функция r=p(φ), φ∈α; β определяет некоторую линию в полярных координатах.
Следует учитывать тот факт, что с позиции геометрии функция r=p(φ), φ∈α; β во всех случаях будет неотрицательной. Связано это с тем, что она задает расстояние от начала координат до точки для заданного значения угла φ=φ0∈α; β. Однако мы будем встречать и отрицательные значенияr=p(φ) функции, что зависит от отношения к данному вопросу конкретных исследователей и преподавателей.
На рисунке мы изобразили несколько примеров линий в полярной системе координат.
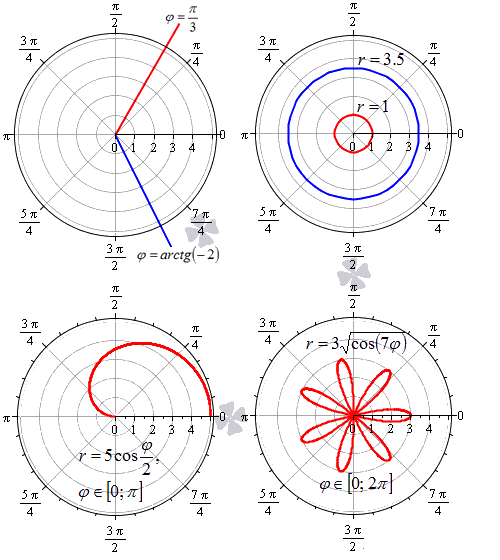
Дадим определение криволинейному сектору.
Криволинейный сектор представляет собой фигуру, которая ограничена лучами φ=α, φ=β и некоторой линией r=p(φ)≥0, непрерывной на участке α; β.
На рисунке мы привели несколько примеров криволинейных секторов.
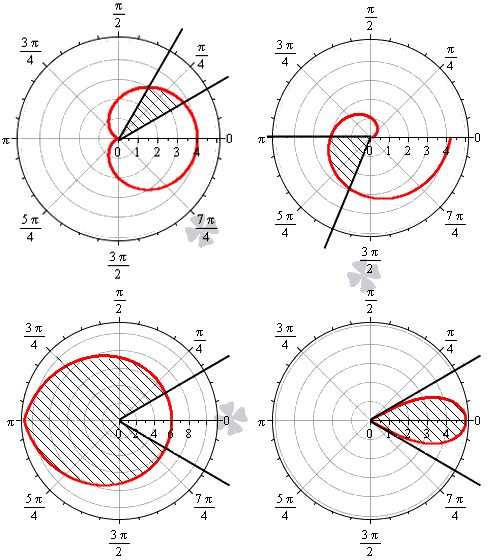
На последнем рисунке мы рассмотрели случай, когда фигура располагается между лучами φ=-π6, φ=π6, которые не являются ее границами.
Площадь криволинейного сектора – вывод формулы
Для вычисления площади криволинейного сектора мы можем вывести формулу. Для этого мы можем использовать формулу площади кругового сектора радиуса R с внутренним углом γ из школьного курса геометрии: Sкругового сектора=γ·R22. Задаем внутренний угол γ в радианах.
Разобьем криволинейный сектор на n частей такими лучами
φ=φ1, φ=φ2,…, φ=φn-1, что α=φ0<φ1<φ2<…<φn-1<β и λ=maxi=1, 2,…, nφi-φi-1→0 при n→+∞.
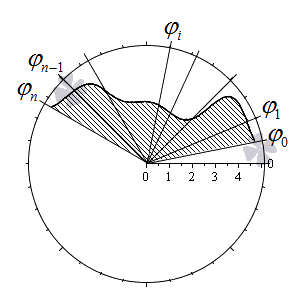
Учитывая свойства площади фигуры, мы можем представить площадь исходного криволинейного сектора S(G) как сумму площадей секторов S(Gi) на каждом из участков разбиения:
S(G)=∑i=1nS(Gi)
Обозначим наибольшее и наименьшее значения функции r=p(φ) на i-ом отрезке φi-1; φi, i=1, 2,…, n как Rmini и Rmaxi . На каждом из отрезков построим по два круговых сектора Pi и Qi с максимальным и минимальным радиусами Rmini и Rmaxi соответственно.
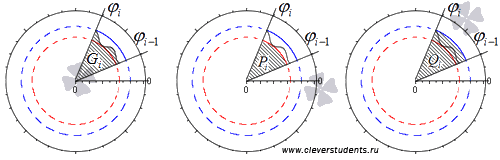
Фигуры, которые являются объединением круговых секторов Qi, i=1, 2,…, n; Pi, i=1, 2,…, n , обозначим как P и Q соответственно.
Их площади будут равны S(P)=∑i=1nS(Pi)=∑i=1n12(Rmini)2·φi-φi-1 и S(Q)=∑i=1nS(Qi)=∑i=1n12(Rmaxi)2·φi-φi-1, причем S(P)≤S(G)≤S(Q).
Так как функция r=pφ непрерывна на отрезке α; β, то функция 12p2φ будет непрерывна на этом отрезке. Если рассматривать S(P) и S(Q) для этой функции как нижнюю и верхнюю суммы Дарбу, то мы можем прийти к равенству:
limλ→0S(P)=limλ→0S(Q)=S(G)⇒S(G)=limλ→0∑ i=1n12(Rmini)2·φi-φi-1==limλ→0∑ i=1n12(Rmaxi)·φi-φi-1=12∫βαp2φdφ
Формула для определения площади криволинейного сектора имеет вид:
S(G)=12∫βαp2φdφ
Примеры вычисления площади криволинейного сектора
Рассмотрим алгоритмы вычисления площади криволинейного сектора с полярной системе координат на конкретных примерах.
Необходимо вычислить площадь плоской фигуры в полярных координатах, которая ограничена линией r=2sin2φи лучами φ=π6, φ=π3.
Решение
Для начала, изобразим описанную в условии задачи фигуру в полярной системе координат. Функция r=2sin(2φ)положительна и непрерывна на отрезке φ∈π6, π3.
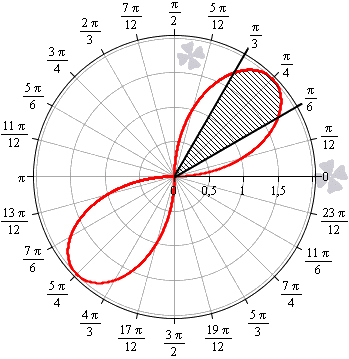
Полученная фигура является криволинейным сектором, что позволяет нам применить формулу для нахождения площади этого сектора.
S(G)=12∫π6π3(2sin(2φ)2dφ=∫π6π32(sin(2φ)2dφ=∫π6π32·1-cos4φ2dφ=∫π6π3(1-cos(4φ))dφ=φ-14sin(4φ)π6π3==π3-14sin4π3-π6-14sin4π6=π6+34
Ответ: S(G)=π6+34
Задача упрощается в тех случаях, когда лучи φ=φ1, φ=φ2, ограничивающие фигуру, заданы. Тогда нам не нужно задумываться о пределах интегрирования при проведении вычисления площади.
Чаще встречаются задачи, где фигуру ограничивает лишь кривая r=p(φ). В этих случаях применить формулу S(G)=12∫αβp2(φ)dφ сразу не получится. Для начала придется решить неравенство p(φ)≥0 для нахождения пределов интегрирования. Так мы можем поступить в тех случаях, когда функция r=pφ неотрицательная. В противном случае нам придется ориентироваться только на область определения и период функции.
Необходимо вычислить площадь фигуры, которая ограничена кривой в полярных координатах r=-3·cos3φ.
Решение
Функция определена для всех действительных значений аргумента. Решим неравенство -3·cos3φ≥0:
-3·cos3φ≥0⇔cos3φ≤0⇔cos φ≤0⇔⇔π2+2πk≤φ≤3π2+2πk, k∈Z
Построим функцию в полярных координатах на отрезке φ∈π2; 3π2 (при k=0). Для других значений k в силу периодичности косинуса мы будем получать ту же самую кривую.
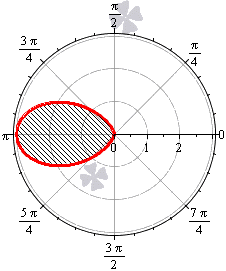
Применим формулу для вычисления площади фигуры в полярных координатах. В качестве нижнего и верхнего предела можно брать π2+2πk и 3π2+2πk соответственно для любого целого значения k.
S(G)=12∫π23π2(-3·cos3φ)dφ=92∫π23π2cos6φdφ
Для того, чтобы получить ответ, нам необходимо вычислить полученный определенный интеграл. Для этого мы можем использовать формулу Ньютона-Лейбница. Первообразную для формулы Ньютона-Лейбница мы можем с помощью рекуррентной формулы вида Kn(x)=sin x·cosn-1(x)n+n-1nKn-2(x), где Kn(x)=∫cosn(x)dx.
∫cos6φdφ=sin φ·cos5φ6+56∫cos4φdφ==sin φ·cos5φ6+56sin φ·cos3φ4+34cos2φdφ==sin φ·cos5φ6+5sin φ·cos3φ24+1524sin φ·cos φ2+12∫cos0φdφ==∫π23π2cos6φdφ=sin φ·cos5φ6+5sin φ·cos3φ24+15sin φ·cos φ48+15φ48π23π2==1548·3π2-1548·π2=5π16
Таким образом, искомая площадь фигуры, ограниченной линией в полярной системе координат, равна S(G)=92∫π23π2cos6φdφ=92·5π16=45π32.
Ответ: S(G)=45π32
В тех случаях, когда в полярной системе координат задается множество кривых, которые по форме напоминают листья клевера или цветка, площадь фигур, ограниченных этими кривыми, часто одинаковы. В этих случаях можно вычислить площадь одного «лепестка» и умножить ее на количество криволинейных фигур.
Необходимо вычислить площадь плоской фигуры в полярной системе координат, которая ограничена линией r=3·cos(3φ).
Решение
Найдем область определения, исходя из того, что эта функция неотрицательна для любого φ из области определения.
cos(3φ)≥0⇔-π2+2πk≤3φ≤π2+2πk, k∈Z-π6+2π3k≤φ≤π6+2π3k, k∈Z
Таким образом, период функции r=3·cos3φ равен 2π3. Это значит, что фигура состоит из трех областей одинаковой площади.
Построим фигуру на графике.
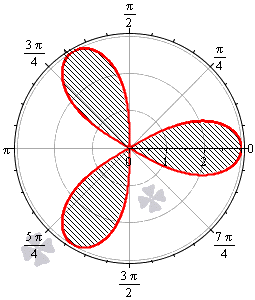
Вычислим площадь одного участка, расположенного на интервале φ∈π2; 5π6(при k=1):
12∫π25π69cos(3φ)dφ=12·3sin(3φ)π25π6=32sin3·5π6-sin3·π2=32(1-(-1)=3
Ответ: Площадь всей фигуры будет равна площади найденного участка, умноженной на 3.
Аналогичным образом можно найти площади фигур, имеющих сходное строение. Примером может служить лемниската Бернулли.
Площадь фигуры, которую ограничивает лемниската Бернулли
Лемниската Бернулли задается уравнением r=α·cos2φ где a – положительное число, влияющее на размер линии (но не на конфигурацию, схожую с символом бесконечности). Лемниската Бернулли строится при -π4+π·k≤φ≤π4+π·k, k∈Z.
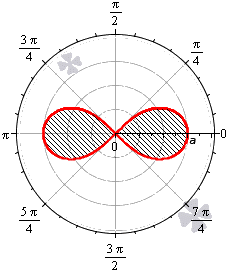
Лемниската служит границей фигуры, которую можно представить как два равных по площади участка.
Для вычисления площади используем нужную формулу:
S(G)=2·12∫-π4π4a2cos(2φ)2φ=a22(sin(2φ))-π4π4==a22sin2·π4-sin2·-π4=a2
Получается, что площадь фигуры, которую ограничивает лемниската Бернулли, равна квадрату коэффициента a.
Площадь фигуры, границей которой является кардиоида
В полярной системе координат кардиоида задается уравнением вида r=2a(1+cosφ). В этом уравнении a – некоторое положительное число. Задающая кардиоиду функция является периодической с периодом 2π. Она определена для всех действительных значений угла. Это значит, что для вычисления площади нижним пределом интегрирования мы будем считать любое число, а верхним, то, которое на 2π больше нижнего.
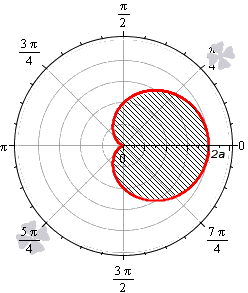
Вычислим площадь фигуры, ограниченной кардиоидой r=2a(1+cosφ), для φ∈0; 2π:
S(G)=12∫02π(2a(1+cosφ))2dφ=2a2∫02π(1+2cosφ+cos2φ)dφ==2a2∫02π1+2cosφ+1+cos2φ2dφ==2a2∫02π32+2cosφ+cos(2φ)2dφ==2a232φ+2sin φ+14sin2φ02π=6π·a2
Площадь фигуры, которую ограничивает улитка Паскаля
В полярной системе координат улитка Паскаля может быть задана уравнением r=b+2a·cosφ. В этом уравнении a – это некоторое положительное число, b – любое действительное число. Кардиоиду можно рассматривать как частный случай улитки Паскаля. Получить кардиоиду можно при b=2a.
Улитка Паскаля в зависимости от значений параметров a и b может принимать различный вид. В данном разделе мы рассмотрим случаи, когда функцию r неотрицательная.
При b<-2a функция r=b+2a·cosφ будет отрицательной для любого значения угла φ.
При b=-2a улитка Паскаля имеет вид точки, которая совпадает с полюсом.
При -2a< b< 0 функция r=b+2a·cosφ неотрицательна для φ∈-arccos-b2a+2πk; arccos-b2a+2πk, k∈Z.
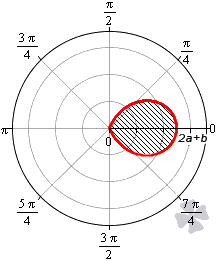
При 0<b<2a функция r=b+2a·cosφ неотрицательна для φ∈-arccos-b2a+2πk; arccos-b2a+2πk, k∈Z. Она ограничивает фигуру, которая по конфигурации напоминает кардиоиду.
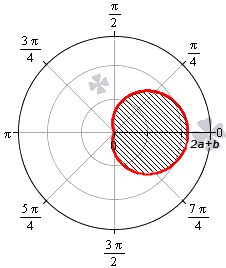
При b>2a функция r=b+2a·cosφ является неотрицательной для любого значения угла. Графическая иллюстрация этого случая приведена ниже
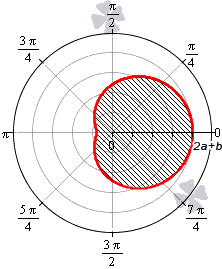
Для того, чтобы правильно определить пределы интегрирования, необходимо учитывать соотношение параметров a и b.
Необходимы вычислить площадь фигуры, которая ограничена линиями, заданными уравнениями r=-3+6cosφ и r=5+4cosφ в полярной системе координат.
Решение
Формула r=-3+6cosφ соответствует фигуре, известной как улитка Паскаля..
Функция r=-3+6cosφ определена для всех значений угла φ. Нам необходимо выяснить, при каких φ функция будет неотрицательной:
-3+6cosφ≥0⇔cosφ≥12⇔-π3+2πk≤φ≤π3+2πk, k∈Z
Проведем вычисление площади фигуры, которая ограничена данной улиткой Паскаля:
S(G)=12∫-π3π3(-3+6cosφ)2dφ=92∫-π3π3(1-4cosφ+4cos2φ)dφ==92∫-π3π31-4cosφ+4·1+cos2φ2dφ==92∫-π3π3(3-4cosφ+2cos(2φ))dφ=92·3φ-4sinφ+sin(2φ-π3π3==92·3·π3-4sinπ3+sin2π3-3·-π3-4sin-π3+sin-2π3==92·2π-33
Улитка Паскаля, определяемая формулой r=5+4cosφ, соответствует пятому пункту. Функция r=5+4cosφ определена и положительна для всех действительных значений φ. Поэтому, площадь фигуры в этом случае равна:
S(G)=12∫02π(5+4cosφ)2dφ=12∫02π(25+40cosφ+16cos2φ)dφ==12∫02π25+40cosφ+16·1+cos(2φ)2dφ==12∫02π(33+40cosφ+8cos(2φ))dφ=12·33φ+40sinφ+4sin(2φ02π==12·33·2π+40sin(2π+4sin(4π)-33·0+40sin 0+4sin 0=33π
Ответ: S(G)=33π
Площадь фигур, границей которых является спираль Архимеда или логарифмическая спираль
Сразу обратимся к примеру.
Необходимо вычислить площадь фигур в полярной системе координат, первая из которых ограничена первым витком спирали Архимеда r=αφ, α>0, а вторая первым витком логарифмической спирали r=αφ, α>1.
Решение
Если в задаче сказано, что фигура ограничена первым витком спирали Архимеда, то угол φ изменяется от нуля до двух пи.
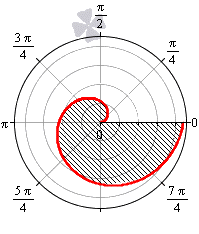
Исходя из этого, найдем площадь фигуры по формуле:
S(G)=12∫02π(αφ)2dϕ=α22∫02πφ2dφ=α22·φ3302π=4α3π33
Аналогично вычисляется площадь фигуры, ограниченной первым витком логарифмической спирали:
S(G)=12∫02π(αϕ)2dϕ=12∫02πa2φdφ=14ln a·a2φ02π==14ln a·a4π-1
Нахождение площади фигуры, которую можно представить как разность двух криволинейных секторов
Пусть фигура в полярной системе координат ограничена лучами φ=α, φ=β и непрерывными и неотрицательными на интервале φ∈α; β функциями r=p1(φ) и r=p2(φ), причем p1(φ)≤p2(φ) для любого угла φ=φ0∈α; β.
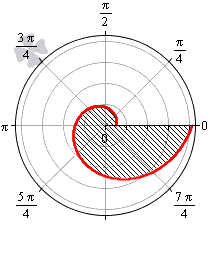
Находим площадь фигуры по формуле S(G)=12∫αβp22(φ)-p12(φ)dφ.
Действительно, в силу свойства аддитивности площади, фигуру G можно представить как разность двух криволинейных секторов G2 и G1.
Тогда площадь фигуры G равна разности площадей этих криволинейных секторов:
S(G)=S(G2)-S(G1)=12∫αβp22(φ)dφ-12∫αβp12(φ)dφ==12∫αβp22(φ)-p12(φ)dφ
Последний переход возможен в силу третьего свойства определенного интеграла.
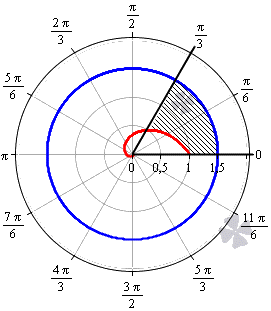
Необходимо вычислить площадь фигуры, которая ограничена линиями φ=0, φ=π3, r=32, r=12φв полярной системе координат.
Решение
Построим заданную фигуру на графике.
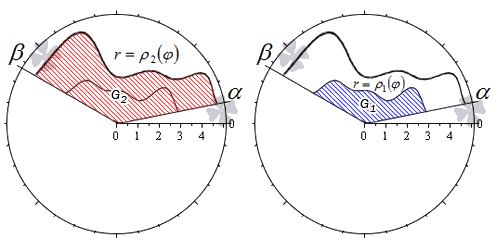
Очевидно, что r=32 больше r=12φ для любого φ∈0; π3. Применяем полученную формулу для вычисления площади фигуры:
S(G)=12∫0π3322-12φ2dφ=12∫0π394-2-2φdφ==12·94φ+12·2-2φln 20π3=12·94φ+1ln 2·122φ+10π3==12·94·π3+1ln 2·122·π3+1-94·0+1ln 2·122·0+1==12·3π4+2-2π3-12·ln 2
Ответ: S(G)=12·3π4+2-2π3-12·ln 2
А теперь рассмотрим пример, когда фигура ограничена линиями, заданными в прямоугольной системе координат. Площадь такой фигуры намного проще вычислять, используя полярные координаты.
Необходимо вычислить площадь фигуры, которая ограничена прямыми линиями y=13x, x=3x, окружностями (x-2)2+(y-3)2=13, (x-4)2+(y-3)2=25.
Решение
В прямоугольной системе координат вычислить площадь полученной фигуры можно, но дело это долгое и хлопотное. Намного проще перейти к полярной системе координат, воспользовавшись формулами перехода.
x=r·cosφy=r·sinφ⇒y=13x⇔r·sinφ=r·cosφ3⇔tgφ=13⇔φ=π6+πky=3x⇔r·sinφ=3·r·cosφ⇔tgφ=3⇔φ=π3+πk(x-2)2+(y-3)2=13⇔x2+y2=4x+6y⇔r=4cosφ+6sinφ(x-4)2+(y-3)2=25⇔x2+y2=8x+6y⇔r=8cosφ+6sinφ
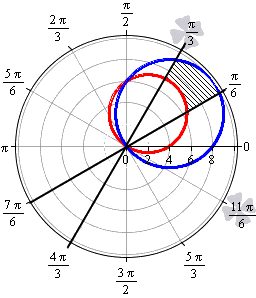
Функция r=8cosφ+6sinφ больше r=4cosφ+6sinφ для любого φ∈π6; π3. Вычисляем площадь фигуры в полярных координатах:
S(G)=12∫π6π38cosφ+6sinφ2-4cosφ+6sinφ2dφ==12∫π6π3(48cos2φ+48cosφ·sinφ)dφ==24∫π6π3cos2φdφ+24∫π6π3cosφ·sinφdφ==12∫π6π3(1+cos2φ)dφ+24∫π6π3sinφd(sinφ)==12·φ+12sin(2φ)π6π3+12·sin2φπ6π3==12·π3+12sin2π3-π6+12sin2π6+12·sin2π3-sin2π6==12·π6+12·322-122=2π+6
Ответ: S(G)=2π+6
| Автор | Сообщение | ||
|---|---|---|---|
|
Заголовок сообщения: Площадь улитки Паскаля
|
|||
|
Помогите найти площадь улитки Паскаля:
|
||
| Вернуться к началу |
|
||
 |
Добавлено: 11 апр 2013, 13:42 
|
Human |
Заголовок сообщения: Re: Площадь улитки Паскаля
|
|
Olga Aleshina писал(а): Какие пределы интегрирования будут в этом случае? Решите уравнение [math]sqrt2left(2-3sinleft(varphi+frac{pi}5right)right)=0[/math]. И ещё: Вы в своей формуле [math]frac12[/math] не забыли?
|
|
| Вернуться к началу |
|
|
|
| За это сообщение пользователю Human “Спасибо” сказали: Olga Aleshina |
|
|
|
Olga Aleshina |
Заголовок сообщения: Re: Площадь улитки Паскаля
|
|
Human писал(а): Olga Aleshina писал(а): Какие пределы интегрирования будут в этом случае? Решите уравнение [math]sqrt2left(2-3sinleft(varphi+frac{pi}5right)right)=0[/math]. И ещё: Вы в своей формуле [math]frac12[/math] не забыли? Спасибо за ответ. Уравнение решала. У меня получалось
|
|
| Вернуться к началу |
|
|
|
Avgust |
Заголовок сообщения: Re: Площадь улитки Паскаля
|
|
Надо очень внимательно отнестись к вычислению площади петли. Обязательно сверять результаты с графикой. Тогда ошибки исключатся.
Так же внимательно вычислим площадь большой фигуры:
PS. [math]-frac {pi}{5}+2pi[/math] 2) К сожалению, ответ не получился “красивым”. Зато получился “верным”.
|
|
| Вернуться к началу |
|
|
|
| За это сообщение пользователю Avgust “Спасибо” сказали: Olga Aleshina |
|
|
|
Olga Aleshina |
Заголовок сообщения: Re: Площадь улитки Паскаля
|
|
Большое спасибо за такой подробный ответ! [math]sin({varphi + frac{pi}{5}})= frac{2}{3}[/math] (т.е. [math]varphi = arcsin({frac{2}{3}})- frac{pi}{5}+2 pi k, k in Z[/math] ) А откуда берется предел интегрирования [math]frac{4}{5}pi – arcsin({frac{2}{3}})[/math] ?
|
|
| Вернуться к началу |
|
|
|
| За это сообщение пользователю Olga Aleshina “Спасибо” сказали: Avgust |
|
|
|
Avgust |
Заголовок сообщения: Re: Площадь улитки Паскаля
|
|
Посмотрите параболический график. Там два пересечения с осью ОХ. Это и есть корни, которые являются решением уравнения [math]2-3 sin left (t+frac{pi}{5} right )=0[/math] Общие решения: [math]t_1=2pi, n -frac{pi}{5}+arcsin left (frac{2}{3} right )[/math] [math]t_2=2pi, n +frac{4pi}{5}-arcsin left (frac{2}{3} right )[/math] Проверьте сами! Эти же корни дал Вольфрам: http://www.wolframalpha.com/input/?i=2- … *Pi%29%3D0
|
|
| Вернуться к началу |
|
|
|
| За это сообщение пользователю Avgust “Спасибо” сказали: Olga Aleshina |
|
|
|
Olga Aleshina |
Заголовок сообщения: Re: Площадь улитки Паскаля
|
|
Теперь поняла.
|
|
| Вернуться к началу |
|
|
Пусть кривая задана
параметрическими уравнениями
то площадь криволинейной трапеции,
ограниченной этой кривой, прямыми
и
и отрезком [a,b]
оси ОХ, выражается формулой
,
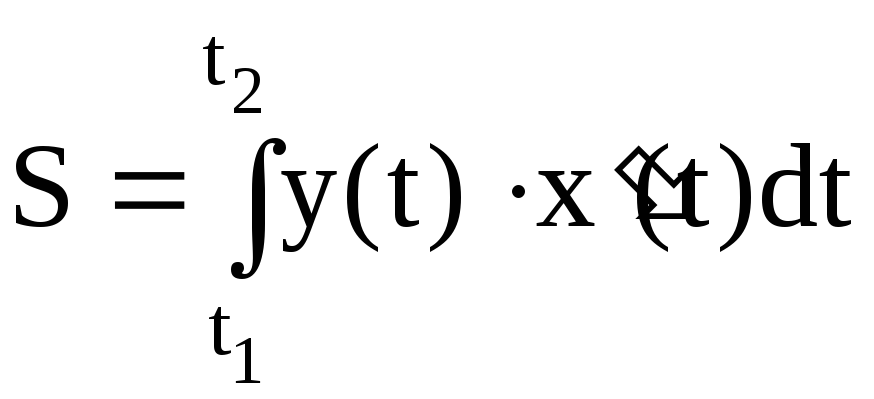(4.5)
где
,
,
и
определяются из условий
.
Пример 45.
Найти площадь фигуры, ограниченной осью
ОХ и одной аркой циклоиды
.
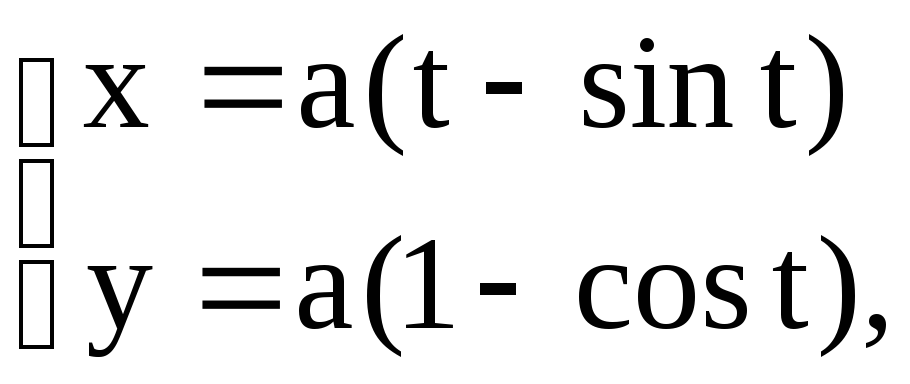
Решение.
Воспользуемся формулой (4.5). Предварительно
найдем
:
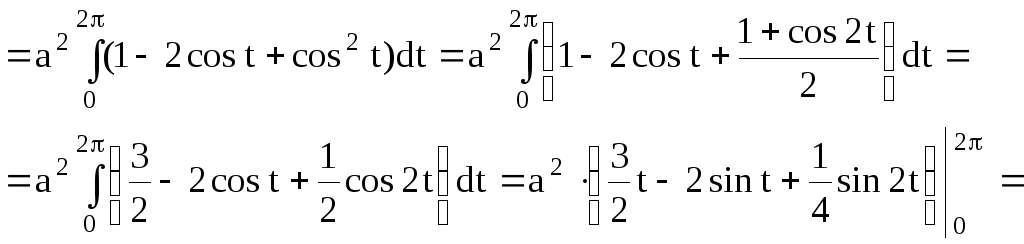
(кв.ед.)
4.3. Вычисление площади плоской фигуры в полярных координатах
В полярных
координатах положение точки на плоскости
определяется двумя координатами:
полярным радиусом
и полярным углом.
Связь между декартовыми координатами
(x,y)
и полярными (,
r)
осуществляется по формулам
.
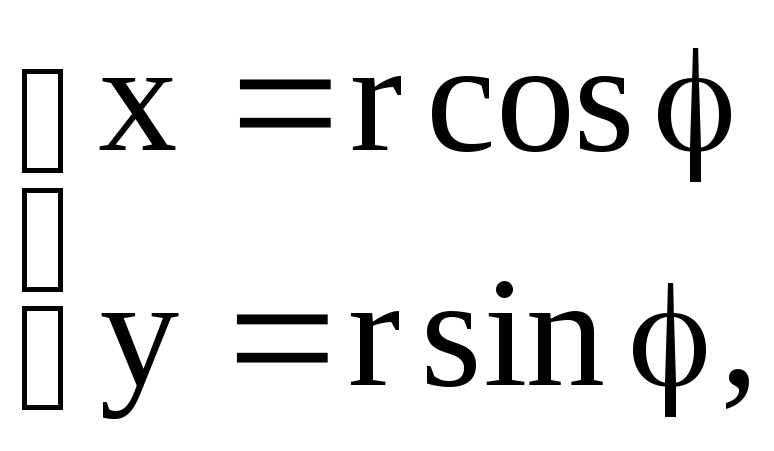
Площадь криволинейного
сектора,
ограниченного
кривой
и двумя
полярными радиусами
и
(рис.4.7), выражается
интегралом
.
(4.6)
Пример 46.
Найти площадь фигуры, ограниченной
улиткой Паскаля
.
Решение.
Воспользуемся формулой (4.6). Чтобы найти
пределы интегрирования
и ,
необходимо построить чертеж кривой
в полярных координатах. Результаты
вычислений занесем в таблицу 1.
Таблица 1
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
0 |
|
|
|
1 |
|
|
3 |
|
|
2,5 |
2 |
1,5 |
|
|
1 |
Так как функция
четная, то график функции
строим симметрично относительно
горизонтальной оси для значений углов
из промежутка
.
Для построения графика функции при
проводим полярную осьr;
на лучах, составляющих с осью r
углы, значение которых указано в таблице
1, откладываем соответствующее расстояние,
затем точки последовательно соединяем.
Получаем замкнутую кривую, называемую
улиткой Паскаля (рис.4.8).
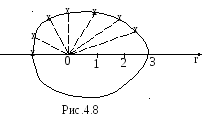
Площадь искомой
фигуры равна
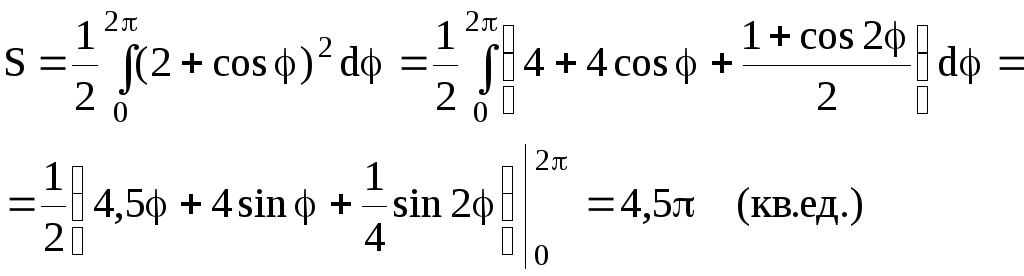
4.4. Вычисление длины дуги плоской кривой
Пусть функция f(x)
непрерывно дифференцируема на [a,b],
тогда длина дуги кривой
на указанном промежутке вычисляется
по формуле:
.
(4.7)
Если кривая гладкая
и задана параметрически, то длина дуги
этой кривой при
вычисляется по формуле:
.
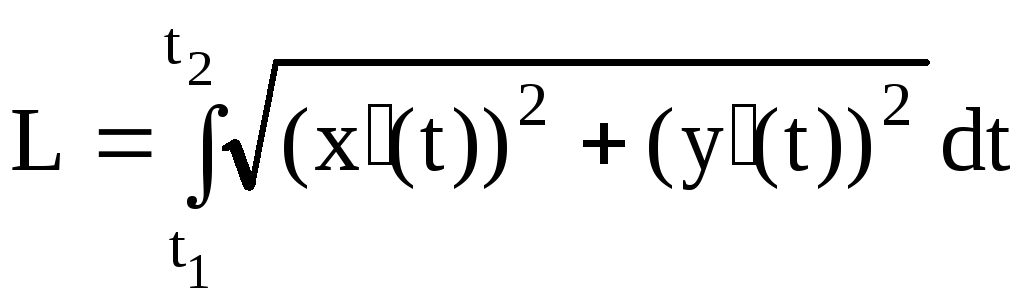(4.8)
Если гладкая кривая
задана в полярных координатах
и
,
то длина ее дуги равна
.
(4.9)
Пример 47.
Вычислить длину дуги развертки окружности
.
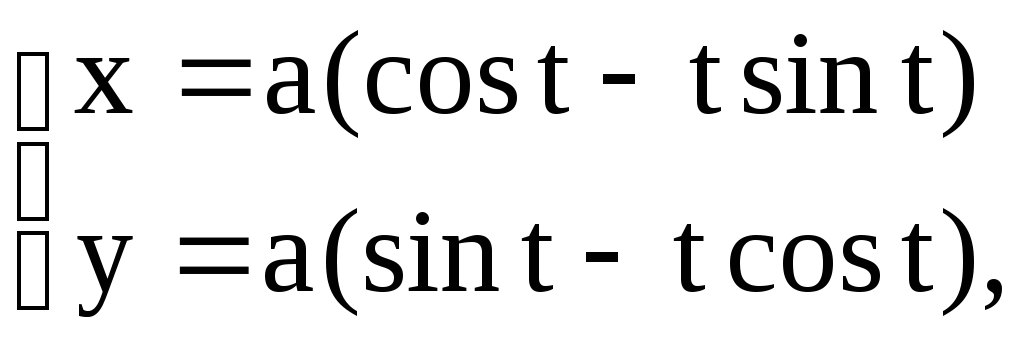
Решение.
В нашем случае кривая задана параметрически.
Воспользуемся формулой (4.8), предварительно
находим производные
и
.
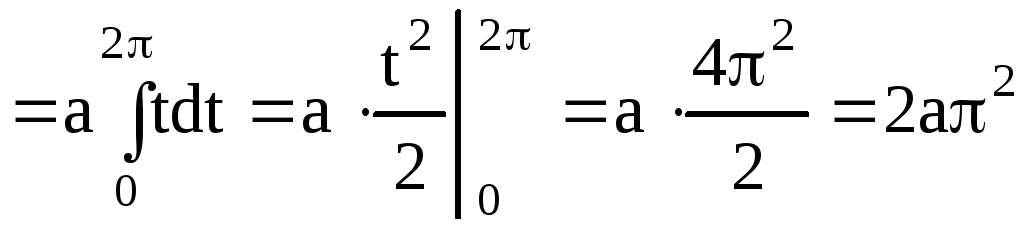(ед.длины).
Пример 48.
Найти длину дуги кривой
,
.
Решение.
Кривая
задана в полярных координатах.
Воспользуемся формулой (4.9). Находим
.
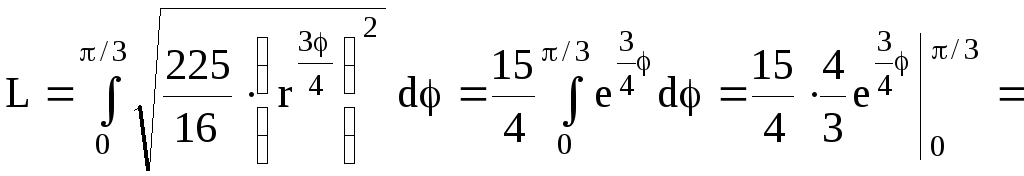
(ед.длины).
4.5. Вычисление объема тел вращения
Предположим, что
площадь сечения тела плоскостью,
перпендикулярной оси ОХ, может быть
выражена функцией от х:
при
,
тогда объем тела, заключенный между
перпендикулярными оси ОХ плоскостями
и
,
находится по формуле
.
(4.10)
Если криволинейную
трапецию (рис.4.10) вращать вокруг оси ОХ,
то объем тела вращения будет равен
.
(4.11)
Если плоская
область, ограниченная кривыми
и прямыми
и
,
вращается вокруг оси ОХ, то
(4.12)
Аналогично можно
записать формулы для вычисления объемов
тел вращения вокруг оси ОY:
(4.13)
(4.14)
Если кривые,
ограничивающие плоскую область заданы
в параметрическом виде, то к формулам
(4.10 – 4.14) следует применить соответствующие
замены переменной.
Если криволинейный
сектор вращать вокруг полярной оси
(см.рис.5.7), то
.
(4.15)
Пример 49.
Вычислить объем тела, полученного при
вращении дуги кривой
,
вокруг оси ОХ.
Р
ешение.
Данная кривая
называется цепной линией. График ее
изображен на рис.4.9. Объем тела вращения
(рис.4.10) вычислим по формуле (4.11)
.
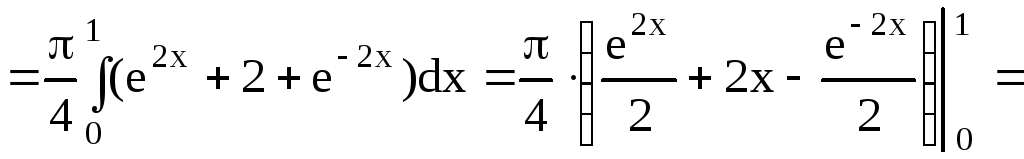
Пример 50.
Найти объем параболоида вращения, радиус
основания которого равен R,
а высота
Н.
Решение.
Искомый параболоид вращения с указанными
параметрами получится, если будем
вращать вокруг оси ОY
параболу
,
(рис.4.11; 4.12), где параметрk
легко вычислить исходя из данного
условия.
Если
,
то
,
поэтому
.
Далее воспользуемся
формулой (4.13)
.
Если
то
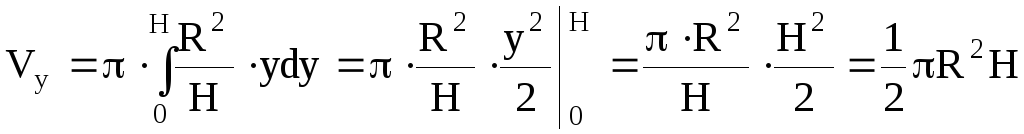(ед3).
Пример 51.
Найти объем тела вращения кривой
,
вокруг
оси ОХ.
Решение.
Данная кривая задана в параметрическом
виде
э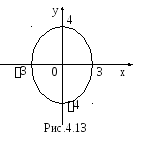
то
эллипс (рис.4.13). Искомой фигурой вращения
является эллипсоид.
Найдем
по формуле (4.11)
Если
,
то
,
.
Если
,
то
,
.
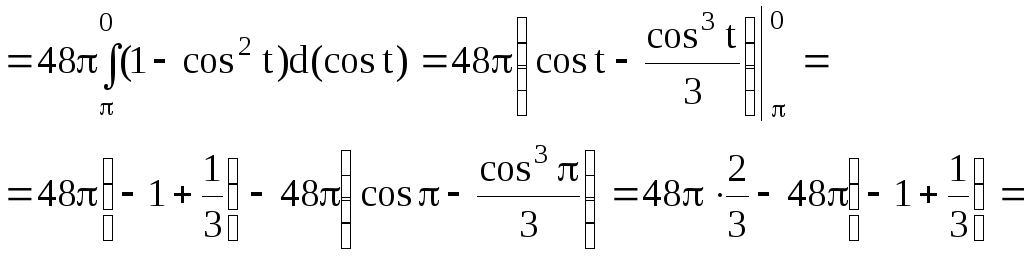
(куб.ед.).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
17.12.2018552.96 Кб33KA.doc
- #
Площадь окружности через интеграл в полярных координатах
Учасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів!
Контакты
Администратор, решение задач
Роман
Tel. +380685083397
[email protected]
skype, facebook:
roman.yukhym
Решение задач
Андрей
facebook:
dniprovets25
Вычисление площади фигуры в полярных координатах
В этом разделе мы продолжим разбирать тему вычисления площадей плоских фигур. Рекомендуем тем, кто изучает темы не по порядку, сначала обратиться к статье «Геометрический смысл определенного интеграла» и разобрать способы вычисления площади криволинейной трапеции. Нам понадобится вычислять площади фигур, которые ограничены ограничены линиями y = f ( x ) , x = g ( y ) в прямоугольной системе координат. А также раздел «Свойства площади фигур», где была разобрана квадрируемость плоских фигур.
Краткий обзор статьи
- Начнем с определения понятия криволинейного сектора, получим формулу для вычисления его площади. Для этого мы используем понятие определенного интеграла Дарбу.
- Подробно разберем решения задач с использованием таких кривых как кардиоида, архимедова спираль и лемниската Бернулли.
- В отдельную подтему мы выделили нахождение площади фигуры, которая представлена как разность двух криволинейных секторов.
Полярная система координат и криволинейный сектор
Точка, расположенная в полярной системе координат, имеет полярный угол φ 0 и полярный радиус r 0 ≥ 0 . Полярный угол φ 0 отсчитывается от полярной оси по часовой стрелке, а r 0 – это расстояние от заданной точки до начала координат.
На рисунке мы отметили начало координат (полюс) жирной черной точкой, полярная ось имеет вид луча черного цвета, а красная точка определяется углом φ 0 = 3 π 4 и расстоянием до полюса r 0 = 4 .
Мы можем рассматривать полярную систему координат одновременно с прямоугольной декартовой. Для этого необходимо совместить начала координат обеих систем, а ось абсцисс и полярной осью.
Задать связь полярных и декартовых координат можно соотношениями r = x 2 + y 2 φ = a r c t g y x , x ≠ 0 и обратно x = r · cos φ y = r · sin φ .
Координаты красной точки на чертеже 2 3 ; 2 . Положение этой точки задается углом φ 0 = a r c t g 2 2 3 = π 6 и расстоянием r 0 = 2 3 2 + 2 2 = 4 .
В полярной системе координат равенство φ = α задает луч, который выходит из точки начала координат и составляет угол α с полярной осью. При этом, угол α может быть задан как в радианах, так и в градусах. Полярную ось мы можем задать уравнением вида φ = 0 . Равенство r = C > 0 задает окружность с центром в начале координат, где – это радиус.
Функция r = p ( φ ) , φ ∈ α ; β определяет некоторую линию в полярных координатах.
Следует учитывать тот факт, что с позиции геометрии функция r = p ( φ ) , φ ∈ α ; β во всех случаях будет неотрицательной. Связано это с тем, что она задает расстояние от начала координат до точки для заданного значения угла φ = φ 0 ∈ α ; β . Однако мы будем встречать и отрицательные значения r = p ( φ ) функции, что зависит от отношения к данному вопросу конкретных исследователей и преподавателей.
На рисунке мы изобразили несколько примеров линий в полярной системе координат.
Дадим определение криволинейному сектору.
Криволинейный сектор представляет собой фигуру, которая ограничена лучами φ = α , φ = β и некоторой линией r = p ( φ ) ≥ 0 , непрерывной на участке α ; β .
На рисунке мы привели несколько примеров криволинейных секторов.
На последнем рисунке мы рассмотрели случай, когда фигура располагается между лучами φ = – π 6 , φ = π 6 , которые не являются ее границами.
Площадь криволинейного сектора – вывод формулы
Для вычисления площади криволинейного сектора мы можем вывести формулу. Для этого мы можем использовать формулу площади кругового сектора радиуса R с внутренним углом γ из школьного курса геометрии: S к р у г о в о г о с е к т о р а = γ · R 2 2 . Задаем внутренний угол γ в радианах.
Разобьем криволинейный сектор на n частей такими лучами
φ = φ 1 , φ = φ 2 , . . . , φ = φ n – 1 , что α = φ 0 φ 1 φ 2 . . . φ n – 1 β и λ = m a x i = 1 , 2 , . . . , n φ i – φ i – 1 → 0 при n → + ∞ .
Учитывая свойства площади фигуры, мы можем представить площадь исходного криволинейного сектора S ( G ) как сумму площадей секторов S ( G i ) на каждом из участков разбиения:
S ( G ) = ∑ i = 1 n S ( G i )
Обозначим наибольшее и наименьшее значения функции r = p ( φ ) на i -ом отрезке φ i – 1 ; φ i , i = 1 , 2 , . . . , n как R m i n i и R m a x i . На каждом из отрезков построим по два круговых сектора P i и Q i с максимальным и минимальным радиусами R m i n i и R m a x i соответственно.
Фигуры, которые являются объединением круговых секторов Q i , i = 1 , 2 , . . . , n ; P i , i = 1 , 2 , . . . , n , обозначим как P и Q соответственно.
Их площади будут равны S ( P ) = ∑ i = 1 n S ( P i ) = ∑ i = 1 n 1 2 ( R m i n i ) 2 · φ i – φ i – 1 и S ( Q ) = ∑ i = 1 n S ( Q i ) = ∑ i = 1 n 1 2 ( R m a x i ) 2 · φ i – φ i – 1 , причем S ( P ) ≤ S ( G ) ≤ S ( Q ) .
Так как функция r = p φ непрерывна на отрезке α ; β , то функция 1 2 p 2 φ будет непрерывна на этом отрезке. Если рассматривать S ( P ) и S ( Q ) для этой функции как нижнюю и верхнюю суммы Дарбу, то мы можем прийти к равенству:
lim λ → 0 S ( P ) = lim λ → 0 S ( Q ) = S ( G ) ⇒ S ( G ) = lim λ → 0 ∑ i = 1 n 1 2 ( R m i n i ) 2 · φ i – φ i – 1 = = lim λ → 0 ∑ i = 1 n 1 2 ( R m a x i ) · φ i – φ i – 1 = 1 2 ∫ β α p 2 φ d φ
Формула для определения площади криволинейного сектора имеет вид:
S ( G ) = 1 2 ∫ β α p 2 φ d φ
Примеры вычисления площади криволинейного сектора
Рассмотрим алгоритмы вычисления площади криволинейного сектора с полярной системе координат на конкретных примерах.
Необходимо вычислить площадь плоской фигуры в полярных координатах, которая ограничена линией r = 2 sin 2 φ и лучами φ = π 6 , φ = π 3 .
Решение
Для начала, изобразим описанную в условии задачи фигуру в полярной системе координат. Функция r = 2 sin ( 2 φ ) положительна и непрерывна на отрезке φ ∈ π 6 , π 3 .
Полученная фигура является криволинейным сектором, что позволяет нам применить формулу для нахождения площади этого сектора.
S ( G ) = 1 2 ∫ π 6 π 3 ( 2 sin ( 2 φ ) 2 d φ = ∫ π 6 π 3 2 ( sin ( 2 φ ) 2 d φ = ∫ π 6 π 3 2 · 1 – cos 4 φ 2 d φ = ∫ π 6 π 3 ( 1 – cos ( 4 φ ) ) d φ = φ – 1 4 sin ( 4 φ ) π 6 π 3 = = π 3 – 1 4 sin 4 π 3 – π 6 – 1 4 sin 4 π 6 = π 6 + 3 4
Ответ: S ( G ) = π 6 + 3 4
Задача упрощается в тех случаях, когда лучи φ = φ 1 , φ = φ 2 , ограничивающие фигуру, заданы. Тогда нам не нужно задумываться о пределах интегрирования при проведении вычисления площади.
Чаще встречаются задачи, где фигуру ограничивает лишь кривая r = p ( φ ) . В этих случаях применить формулу S ( G ) = 1 2 ∫ α β p 2 ( φ ) d φ сразу не получится. Для начала придется решить неравенство p ( φ ) ≥ 0 для нахождения пределов интегрирования. Так мы можем поступить в тех случаях, когда функция r = p φ неотрицательная. В противном случае нам придется ориентироваться только на область определения и период функции.
Необходимо вычислить площадь фигуры, которая ограничена кривой в полярных координатах r = – 3 · cos 3 φ .
Решение
Функция определена для всех действительных значений аргумента. Решим неравенство – 3 · cos 3 φ ≥ 0 :
– 3 · cos 3 φ ≥ 0 ⇔ cos 3 φ ≤ 0 ⇔ cos φ ≤ 0 ⇔ ⇔ π 2 + 2 πk ≤ φ ≤ 3 π 2 + 2 πk , k ∈ Z
Построим функцию в полярных координатах на отрезке φ ∈ π 2 ; 3 π 2 (при k = 0 ). Для других значений k в силу периодичности косинуса мы будем получать ту же самую кривую.
Применим формулу для вычисления площади фигуры в полярных координатах. В качестве нижнего и верхнего предела можно брать π 2 + 2 πk и 3 π 2 + 2 πk соответственно для любого целого значения k .
S ( G ) = 1 2 ∫ π 2 3 π 2 ( – 3 · cos 3 φ ) d φ = 9 2 ∫ π 2 3 π 2 cos 6 φ d φ
Для того, чтобы получить ответ, нам необходимо вычислить полученный определенный интеграл. Для этого мы можем использовать формулу Ньютона-Лейбница. Первообразную для формулы Ньютона-Лейбница мы можем с помощью рекуррентной формулы вида K n ( x ) = sin x · cos n – 1 ( x ) n + n – 1 n K n – 2 ( x ) , где K n ( x ) = ∫ cos n ( x ) d x .
∫ cos 6 φ d φ = sin φ · cos 5 φ 6 + 5 6 ∫ cos 4 φ d φ = = sin φ · cos 5 φ 6 + 5 6 sin φ · cos 3 φ 4 + 3 4 cos 2 φ d φ = = sin φ · cos 5 φ 6 + 5 sin φ · cos 3 φ 24 + 15 24 sin φ · cos φ 2 + 1 2 ∫ cos 0 φ d φ = = ∫ π 2 3 π 2 cos 6 φ d φ = sin φ · cos 5 φ 6 + 5 sin φ · cos 3 φ 24 + 15 sin φ · cos φ 48 + 15 φ 48 π 2 3 π 2 = = 15 48 · 3 π 2 – 15 48 · π 2 = 5 π 16
Таким образом, искомая площадь фигуры, ограниченной линией в полярной системе координат, равна S ( G ) = 9 2 ∫ π 2 3 π 2 cos 6 φ d φ = 9 2 · 5 π 16 = 45 π 32 .
Ответ: S ( G ) = 45 π 32
В тех случаях, когда в полярной системе координат задается множество кривых, которые по форме напоминают листья клевера или цветка, площадь фигур, ограниченных этими кривыми, часто одинаковы. В этих случаях можно вычислить площадь одного «лепестка» и умножить ее на количество криволинейных фигур.
Необходимо вычислить площадь плоской фигуры в полярной системе координат, которая ограничена линией r = 3 · cos ( 3 φ ) .
Решение
Найдем область определения, исходя из того, что эта функция неотрицательна для любого φ из области определения.
cos ( 3 φ ) ≥ 0 ⇔ – π 2 + 2 πk ≤ 3 φ ≤ π 2 + 2 πk , k ∈ Z – π 6 + 2 π 3 k ≤ φ ≤ π 6 + 2 π 3 k , k ∈ Z
Таким образом, период функции r = 3 · cos 3 φ равен 2 π 3 . Это значит, что фигура состоит из трех областей одинаковой площади.
Построим фигуру на графике.
Вычислим площадь одного участка, расположенного на интервале φ ∈ π 2 ; 5 π 6 (при k = 1 ):
1 2 ∫ π 2 5 π 6 9 cos ( 3 φ ) d φ = 1 2 · 3 sin ( 3 φ ) π 2 5 π 6 = 3 2 sin 3 · 5 π 6 – sin 3 · π 2 = 3 2 ( 1 – ( – 1 ) = 3
Ответ: Площадь всей фигуры будет равна площади найденного участка, умноженной на 3.
Аналогичным образом можно найти площади фигур, имеющих сходное строение. Примером может служить лемниската Бернулли.
Площадь фигуры, которую ограничивает лемниската Бернулли
Лемниската Бернулли задается уравнением r = α · cos 2 φ где a – положительное число, влияющее на размер линии (но не на конфигурацию, схожую с символом бесконечности). Лемниската Бернулли строится при – π 4 + π · k ≤ φ ≤ π 4 + π · k , k ∈ Z .
Лемниската служит границей фигуры, которую можно представить как два равных по площади участка.
Для вычисления площади используем нужную формулу:
S ( G ) = 2 · 1 2 ∫ – π 4 π 4 a 2 cos ( 2 φ ) 2 φ = a 2 2 ( sin ( 2 φ ) ) – π 4 π 4 = = a 2 2 sin 2 · π 4 – sin 2 · – π 4 = a 2
Получается, что площадь фигуры, которую ограничивает лемниската Бернулли, равна квадрату коэффициента a .
Площадь фигуры, границей которой является кардиоида
В полярной системе координат кардиоида задается уравнением вида r = 2 a ( 1 + cos φ ) . В этом уравнении a – некоторое положительное число. Задающая кардиоиду функция является периодической с периодом 2 π . Она определена для всех действительных значений угла. Это значит, что для вычисления площади нижним пределом интегрирования мы будем считать любое число, а верхним, то, которое на 2 π больше нижнего.
Вычислим площадь фигуры, ограниченной кардиоидой r = 2 a ( 1 + cos φ ) , для φ ∈ 0 ; 2 π :
S ( G ) = 1 2 ∫ 0 2 π ( 2 a ( 1 + cos φ ) ) 2 d φ = 2 a 2 ∫ 0 2 π ( 1 + 2 cos φ + cos 2 φ ) d φ = = 2 a 2 ∫ 0 2 π 1 + 2 cos φ + 1 + cos 2 φ 2 d φ = = 2 a 2 ∫ 0 2 π 3 2 + 2 cos φ + cos ( 2 φ ) 2 d φ = = 2 a 2 3 2 φ + 2 sin φ + 1 4 sin 2 φ 0 2 π = 6 π · a 2
Площадь фигуры, которую ограничивает улитка Паскаля
В полярной системе координат улитка Паскаля может быть задана уравнением r = b + 2 a · cos φ . В этом уравнении a – это некоторое положительное число, b – любое действительное число. Кардиоиду можно рассматривать как частный случай улитки Паскаля. Получить кардиоиду можно при b = 2 a .
Улитка Паскаля в зависимости от значений параметров a и b может принимать различный вид. В данном разделе мы рассмотрим случаи, когда функцию r неотрицательная.
При b – 2 a функция r = b + 2 a · cos φ будет отрицательной для любого значения угла φ .
При b = – 2 a улитка Паскаля имеет вид точки, которая совпадает с полюсом.
При – 2 a b 0 функция r = b + 2 a · cos φ неотрицательна для φ ∈ – a r c cos – b 2 a + 2 πk ; arccos – b 2 a + 2 πk , k ∈ Z .
При 0 b 2 a функция r = b + 2 a · cos φ неотрицательна для φ ∈ – a r c cos – b 2 a + 2 πk ; arccos – b 2 a + 2 πk , k ∈ Z . Она ограничивает фигуру, которая по конфигурации напоминает кардиоиду.
При b > 2 a функция r = b + 2 a · cos φ является неотрицательной для любого значения угла. Графическая иллюстрация этого случая приведена ниже
Для того, чтобы правильно определить пределы интегрирования, необходимо учитывать соотношение параметров a и b .
Необходимы вычислить площадь фигуры, которая ограничена линиями, заданными уравнениями r = – 3 + 6 cos φ и r = 5 + 4 cos φ в полярной системе координат.
Решение
Формула r = – 3 + 6 cos φ соответствует фигуре, известной как улитка Паскаля..
Функция r = – 3 + 6 cos φ определена для всех значений угла φ . Нам необходимо выяснить, при каких φ функция будет неотрицательной:
– 3 + 6 cos φ ≥ 0 ⇔ cos φ ≥ 1 2 ⇔ – π 3 + 2 π k ≤ φ ≤ π 3 + 2 πk , k ∈ Z
Проведем вычисление площади фигуры, которая ограничена данной улиткой Паскаля:
S ( G ) = 1 2 ∫ – π 3 π 3 ( – 3 + 6 cos φ ) 2 d φ = 9 2 ∫ – π 3 π 3 ( 1 – 4 cos φ + 4 cos 2 φ ) d φ = = 9 2 ∫ – π 3 π 3 1 – 4 cos φ + 4 · 1 + cos 2 φ 2 d φ = = 9 2 ∫ – π 3 π 3 ( 3 – 4 cos φ + 2 cos ( 2 φ ) ) d φ = 9 2 · 3 φ – 4 sin φ + sin ( 2 φ – π 3 π 3 = = 9 2 · 3 · π 3 – 4 sin π 3 + sin 2 π 3 – 3 · – π 3 – 4 sin – π 3 + sin – 2 π 3 = = 9 2 · 2 π – 3 3
Улитка Паскаля, определяемая формулой r = 5 + 4 cos φ , соответствует пятому пункту. Функция r = 5 + 4 cos φ определена и положительна для всех действительных значений φ . Поэтому, площадь фигуры в этом случае равна:
S ( G ) = 1 2 ∫ 0 2 π ( 5 + 4 cos φ ) 2 d φ = 1 2 ∫ 0 2 π ( 25 + 40 cos φ + 16 cos 2 φ ) d φ = = 1 2 ∫ 0 2 π 25 + 40 cos φ + 16 · 1 + cos ( 2 φ ) 2 d φ = = 1 2 ∫ 0 2 π ( 33 + 40 cos φ + 8 cos ( 2 φ ) ) d φ = 1 2 · 33 φ + 40 sin φ + 4 sin ( 2 φ 0 2 π = = 1 2 · 33 · 2 π + 40 sin ( 2 π + 4 sin ( 4 π ) – 33 · 0 + 40 sin 0 + 4 sin 0 = 33 π
Ответ: S ( G ) = 33 π
Площадь фигур, границей которых является спираль Архимеда или логарифмическая спираль
Сразу обратимся к примеру.
Необходимо вычислить площадь фигур в полярной системе координат, первая из которых ограничена первым витком спирали Архимеда r = α φ , α > 0 , а вторая первым витком логарифмической спирали r = α φ , α > 1 .
Решение
Если в задаче сказано, что фигура ограничена первым витком спирали Архимеда, то угол φ изменяется от нуля до двух пи.
Исходя из этого, найдем площадь фигуры по формуле:
S ( G ) = 1 2 ∫ 0 2 π ( α φ ) 2 d ϕ = α 2 2 ∫ 0 2 π φ 2 d φ = α 2 2 · φ 3 3 0 2 π = 4 α 3 π 3 3
Аналогично вычисляется площадь фигуры, ограниченной первым витком логарифмической спирали:
S ( G ) = 1 2 ∫ 0 2 π ( α ϕ ) 2 d ϕ = 1 2 ∫ 0 2 π a 2 φ d φ = 1 4 ln a · a 2 φ 0 2 π = = 1 4 ln a · a 4 π – 1
Нахождение площади фигуры, которую можно представить как разность двух криволинейных секторов
Пусть фигура в полярной системе координат ограничена лучами φ = α , φ = β и непрерывными и неотрицательными на интервале φ ∈ α ; β функциями r = p 1 ( φ ) и r = p 2 ( φ ) , причем p 1 ( φ ) ≤ p 2 ( φ ) для любого угла φ = φ 0 ∈ α ; β .
Находим площадь фигуры по формуле S ( G ) = 1 2 ∫ α β p 2 2 ( φ ) – p 1 2 ( φ ) d φ .
Действительно, в силу свойства аддитивности площади, фигуру G можно представить как разность двух криволинейных секторов G 2 и G 1 .
Тогда площадь фигуры G равна разности площадей этих криволинейных секторов:
S ( G ) = S ( G 2 ) – S ( G 1 ) = 1 2 ∫ α β p 2 2 ( φ ) d φ – 1 2 ∫ α β p 1 2 ( φ ) d φ = = 1 2 ∫ α β p 2 2 ( φ ) – p 1 2 ( φ ) d φ
Последний переход возможен в силу третьего свойства определенного интеграла.
Необходимо вычислить площадь фигуры, которая ограничена линиями φ = 0 , φ = π 3 , r = 3 2 , r = 1 2 φ в полярной системе координат.
Решение
Построим заданную фигуру на графике.
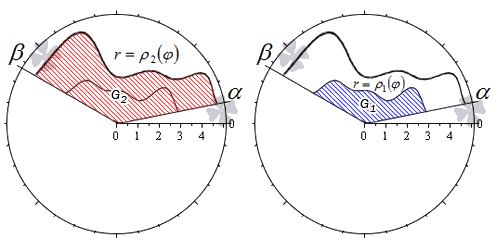
Очевидно, что r = 3 2 больше r = 1 2 φ для любого φ ∈ 0 ; π 3 . Применяем полученную формулу для вычисления площади фигуры:
S ( G ) = 1 2 ∫ 0 π 3 3 2 2 – 1 2 φ 2 d φ = 1 2 ∫ 0 π 3 9 4 – 2 – 2 φ d φ = = 1 2 · 9 4 φ + 1 2 · 2 – 2 φ ln 2 0 π 3 = 1 2 · 9 4 φ + 1 ln 2 · 1 2 2 φ + 1 0 π 3 = = 1 2 · 9 4 · π 3 + 1 ln 2 · 1 2 2 · π 3 + 1 – 9 4 · 0 + 1 ln 2 · 1 2 2 · 0 + 1 = = 1 2 · 3 π 4 + 2 – 2 π 3 – 1 2 · ln 2
Ответ: S ( G ) = 1 2 · 3 π 4 + 2 – 2 π 3 – 1 2 · ln 2
А теперь рассмотрим пример, когда фигура ограничена линиями, заданными в прямоугольной системе координат. Площадь такой фигуры намного проще вычислять, используя полярные координаты.
Необходимо вычислить площадь фигуры, которая ограничена прямыми линиями y = 1 3 x , x = 3 x , окружностями ( x – 2 ) 2 + ( y – 3 ) 2 = 13 , ( x – 4 ) 2 + ( y – 3 ) 2 = 25 .
Решение
В прямоугольной системе координат вычислить площадь полученной фигуры можно, но дело это долгое и хлопотное. Намного проще перейти к полярной системе координат, воспользовавшись формулами перехода.
x = r · cos φ y = r · sin φ ⇒ y = 1 3 x ⇔ r · sin φ = r · cos φ 3 ⇔ t g φ = 1 3 ⇔ φ = π 6 + πk y = 3 x ⇔ r · sinφ = 3 · r · cosφ ⇔ tgφ = 3 ⇔ φ = π 3 + πk ( x – 2 ) 2 + ( y – 3 ) 2 = 13 ⇔ x 2 + y 2 = 4 x + 6 y ⇔ r = 4 cosφ + 6 sinφ ( x – 4 ) 2 + ( y – 3 ) 2 = 25 ⇔ x 2 + y 2 = 8 x + 6 y ⇔ r = 8 cosφ + 6 sinφ
Функция r = 8 cos φ + 6 sin φ больше r = 4 cos φ + 6 sin φ для любого φ ∈ π 6 ; π 3 . Вычисляем площадь фигуры в полярных координатах:
S ( G ) = 1 2 ∫ π 6 π 3 8 cos φ + 6 sin φ 2 – 4 cos φ + 6 sin φ 2 d φ = = 1 2 ∫ π 6 π 3 ( 48 cos 2 φ + 48 cos φ · sin φ ) d φ = = 24 ∫ π 6 π 3 cos 2 φ d φ + 24 ∫ π 6 π 3 cos φ · sin φ d φ = = 12 ∫ π 6 π 3 ( 1 + cos 2 φ ) d φ + 24 ∫ π 6 π 3 sin φ d ( sin φ ) = = 12 · φ + 1 2 sin ( 2 φ ) π 6 π 3 + 12 · sin 2 φ π 6 π 3 = = 12 · π 3 + 1 2 sin 2 π 3 – π 6 + 1 2 sin 2 π 6 + 12 · sin 2 π 3 – sin 2 π 6 = = 12 · π 6 + 12 · 3 2 2 – 1 2 2 = 2 π + 6
Вычисление площади фигуры в полярных координатах с помощью интеграла Текст научной статьи по специальности « Математика»
Аннотация научной статьи по математике, автор научной работы — Махсуд Тулқин Ўғли Усмонов
Это, пожалуй, одно из самых популярных приложений определённого интеграла после вычисления площади в прямоугольных координатах и объёма тела вращения . Ручное построение чертежа в полярных координатах процесс длительный и трудоёмкий.
Похожие темы научных работ по математике , автор научной работы — Махсуд Тулқин Ўғли Усмонов
Текст научной работы на тему «Вычисление площади фигуры в полярных координатах с помощью интеграла»
Вычисление площади фигуры в полярных координатах с
Махсуд Тулкин угли Усмонов maqsudu32@gmail .com Ташкентский университет информационных технологий
Аннотация: Это, пожалуй, одно из самых популярных приложений определённого интеграла после вычисления площади в прямоугольных координатах и объёма тела вращения. Ручное построение чертежа в полярных координатах – процесс длительный и трудоёмкий.
Ключевые слова: определённый интеграл, вычисление площади в прямоугольных координатах, объём тела вращения.
Calculating the area of a figure in polar coordinates using an
Mahsud Tulgin oglu Usmonov maqsudu32@gmail.com Tashkent University of Information Technologies
Abstract: This is perhaps one of the most popular applications of the definite integral after calculating the area in rectangular coordinates and the volume of a body of revolution. Manual construction of a drawing in polar coordinates is a long and laborious process.
Keywords: definite integral, calculation of area in rectangular coordinates, volume of a body of revolution.
Всё очень и очень напоминает привычную задачу нахождения площади. Полярным аналогом криволинейной трапеции является криволинейный сектор.
Рассмотрим некоторую функцию r ^ заданную в полярной системе
координат, которая принимает неотрицательные значения на отрезке ^ е ^ ^ и непрерывна на нём. Криволинейным сектором называется фигура,
ограниченная отрезками лучей Ф
Площадь криволинейного сектора рассчитывается по формуле
2 я . Как видите, перед интегралом ставится дробь 2 , сама функция
возводится в квадрат, а интегрирование осуществляется по переменной «фи».
В качестве демонстрационного примера, вычислим площадь круга, ограниченного окружностью г – 2 с центром в полюсе, радиуса 2. Очевидно, что а = 0> и по формуле:
Вычислить площадь фигуры, ограниченной линией = Ф Ручное построение чертежа в полярных координатах – процесс длительный и трудоёмкий. В нашем случае задача облегчается ещё и тем, что
т = для любого «фи»,
а значит, угол, как и в примере с площадью круга, принимает все значения
от а = 0 д0 2л- до рабочей формуле:
Стандартно понижаем степень с помощью известной тригонометрической формулы:
Забавно, что можно вообще не иметь ни малейшего представления о том,
какую фигуру ограничивает линия г( = J cos2 2 qdq> = 2jcos2 2qdtp–
(*) На данном шаге использовали чётность подынтегральной функции на симметричном относительно нуля отрезке интегрирования. С геометрической точки зрения это означает, что лепесток розы симметричен относительно своей центральной оси. В предыдущих двух примерах фигуры тоже были симметричными, но, как ни странно, в рассматриваемом типе задач излишнее обмусоливание данного факта зачастую только удлиняет решение.
Если считать, что уравнение ‘”‘Ж1 – i::0Sзадано в обобщенных полярных координатах, то данная роза будет иметь 4 лепестка, и, соответственно, результат следует умножить ещё на два. Но, как я уже советовал в курсе аналитической геометрии, осмотрительнее рассматривать классику, где полярный радиус неотрицателен.
Кривая 4-го примера называется лемнискатой Бернулли, в 5-м примере дана трёхлепесковая роза. Напоминаю, что если есть возможность быстро построить чертеж, то его лучше построить. А здесь они, к слову, быстро строятся и вручную.
После интенсивной разминки на опушке надеваем хоккейную маску и с воодушевлением углубляемся в лес за новыми жертвами: Пример 6
Вычислить площадь фигуры, ограниченной линиями r
^ г – 2 sin ^ Решение: в условии даны две линии, и здесь хоть о чертеже и молчок, но
без него уже трудно. Какую кривую задаёт уравнение в статье о
полярных координатах мы подробно разбирали и строили график полярной
розы ^ с лепестками на промежутках
«минус» всё перевернёт с ног на голову (а если академичнее – отобразит симметрично относительно полярной оси и её продолжения) и лепестки розы
расположатся в секторах
2 зт ^ значительно проще, оно определяет типовую окружность:
Y>4 Г = 2 sin Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
3) Площадь искомой фигуры:
Ответ: 3 , что весьма правдоподобно
В рассмотренном примере фигурировали разные отрезки интегрирования,
s = Т. – Г33( , г = sin д>
, не определена однозначно и
поэтому в условии наложено дополнительное ограничение на угол из которого следует, что необходимо вычислить заштрихованную площадь
If ■ a , – sin q>dq>=—
2) На промежутке
фигура ограничена тем же отрезком луча
Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
3. Margulis A. Ya., Andrey Petrovich Kiselev, “Mathematics at school”, 1948,
4. Depman I. Ya., History of arithmetic, M., 1959.
5. Morgulis A. Ya., Trostnikov V. Legislator of school mathematics // Science and life. 1968. No. 1
6. Pylnev-Rogachev, Luneva MI Servant of the “queen of sciences” // Koltsovsky square. 2002. No. 3
[spoiler title=”источники:”]
http://zaochnik.com/spravochnik/matematika/integraly-integrirovanie/vychislenie-ploschadi-figury-v-poljarnyh-koordinat/
http://cyberleninka.ru/article/n/vychislenie-ploschadi-figury-v-polyarnyh-koordinatah-s-pomoschyu-integrala
[/spoiler]
интегралы – Площадь в полярных координатах
|
Приветсвую. Нужно найти площадь фигуры (улитка Паскаля) в полярных координатах (через интеграл): $$ Если бы была кардиоида, то проблем бы не возникло, а тут не знаю с какой стороны подойти. |
Здравствуйте
Математика – это совместно редактируемый форум вопросов и ответов для начинающих и опытных математиков, с особенным акцентом на компьютерные науки.
Присоединяйтесь!
отмечен:
интегралы
×1,505
площадь
×276
задан
24 Окт ’14 3:36
показан
1437 раз
обновлен
29 Окт ’14 1:35
Связанные вопросы
Отслеживать вопрос
по почте:
Зарегистрировавшись, вы сможете подписаться на любые обновления
по RSS:
Ответы
Ответы и Комментарии
