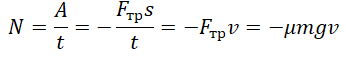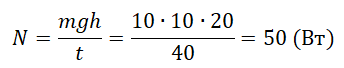У этого термина существуют и другие значения, см. Работа.
| Работа | |
|---|---|
 |
|
| Размерность | L2MT−2 |
| Единицы измерения | |
| СИ | Дж |
| СГС | эрг |
| Примечания | |
| скалярная величина |
| Механическая работа |
|---|
| Ключевые статьи |
|
Работа в физике Механическая работа Закон сохранения энергии Термодинамическая работа Первое начало термодинамики |
|
Размерность Джоуль Эрг |
| См. также: Портал:Физика |
Механи́ческая рабо́та — физическая величина — скалярная количественная мера действия силы (равнодействующей сил) на тело или сил на систему тел. Зависит от численной величины и направления силы (сил) и от перемещения тела (системы тел)[1].
При постоянной силе и прямолинейном движении материальной точки, работа рассчитывается как произведение величины силы на перемещение и на косинус угла между векторами перемещения и силы: 
В механике совершение работы над телом является единственной причиной изменения его энергии; в других областях физики энергия изменяется и за счёт иных факторов (например, в термодинамике — теплообмена).
Определение работы[править | править код]
По определению, «элементарная» (совершаемая за бесконечно малое время) работа — скалярное произведение действующей на материальную точку силы 

.
Использование символа δ (а не 
Работа за конечный промежуток времени — интеграл элементарной работы:
.
Если имеется система материальных точек, выполняется суммирование по всем точкам. При наличии нескольких сил их работа определяется как работа равнодействующей (векторной суммы) этих сил.
Обозначения, размерность[править | править код]
Работа обычно обозначается заглавной буквой 

Единицей измерения (размерностью) работы в Международной системе единиц (СИ) является джоуль, в СГС — эрг. При этом
- 1 Дж = 1 кг·м²/с² = 1 Н·м;
- 1 эрг = 1 г·см²/с² = 1 дин·см;
- 1 эрг = 10−7 Дж.
Вычисление работы[править | править код]
Случай одной материальной точки[править | править код]
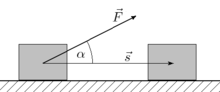
При прямолинейном движении материальной точки и постоянном значении приложенной к ней силы, работа (этой силы) равна произведению проекции вектора силы на направление движения и длины вектора перемещения, совершённого точкой:
Здесь «

Если направление приложенной силы ортогонально перемещению тела или перемещение равно нулю, то работа этой силы равна нулю.
В общем случае, когда сила не постоянна, а движение не прямолинейно, работа вычисляется как криволинейный интеграл второго рода по траектории точки[2]:
(подразумевается суммирование по кривой, которая является пределом ломаной, составленной из перемещений 
Если существует зависимость силы от координат[3], интеграл определяется[4] следующим образом:
,
где 









Если сила 
Случай системы точек или тела[править | править код]
Работа сил по перемещению системы из 
.
Если тело не является системой дискретных точек, его можно разбить (мысленно) на множество бесконечно малых элементов (кусочков), каждый из которых можно считать материальной точкой, и вычислить работу в соответствии с определением выше. В этом случае дискретная сумма заменяется на интеграл:
,
где 



Эти формулы могут быть использованы как для вычисления работы конкретной силы или класса сил, так и для вычисления полной работы, совершаемой всеми силами, действующими на систему.
Работа и кинетическая энергия[править | править код]
Кинетическая энергия вводится в механике в прямой связи с понятием работы.
С использованием второго закона Ньютона, позволяющего выразить силу через ускорение как 



.
При интегрировании от начального до финального момента получится
,
где 

Работа и потенциальная энергия[править | править код]
Сила называется потенциальной, если существует скалярная функция координат, известная как потенциальная энергия и обозначаемая 
.
Здесь 

.
Данный результат известен как закон сохранения механической энергии и утверждает, что полная механическая энергия
в замкнутой системе, в которой действуют консервативные силы, является постоянной во времени. Этот закон широко используется при решении задач классической механики.
Работа силы в теоретической механике[править | править код]
Пусть материальная точка 




Величина 






В соответствии с определением интеграла Римана, можем дать определение работе:
Предел, к которому стремится сумма 




Таким образом, если обозначить эту работу буквой 
.
Если положение точки на траектории её движения описывается с помощью какого-либо другого параметра 


.
Работа в термодинамике[править | править код]
В термодинамике работа, совершённая газом при расширении[6], рассчитывается как интеграл давления по объёму:
.
Работа, совершённая над газом, совпадает с этим выражением по абсолютной величине, но противоположна по знаку.
- Естественное обобщение этой формулы применимо не только к процессам, где давление есть однозначная функция объёма, но и к любому процессу (изображаемому любой кривой в плоскости
), в частности, к циклическим процессам.
- В принципе, формула применима не только к газу, но и к чему угодно, способному оказывать давление (надо только чтобы давление в сосуде было всюду одинаковым, что неявно подразумевается в формуле).
Эта формула непосредственно связана с механической работой, хотя, казалось бы, относится к другому разделу физики. Сила давления газа направлена ортогонально к каждой элементарной площадке и равна произведению давления 

При расширении сосуда, работа, совершаемая газом для смещения 
.
Это и есть произведение давления на приращение объёма вблизи элементарной площадки. После суммирования по всем 
См. также[править | править код]
- Закон сохранения энергии
- Теорема о кинетической энергии системы
- Механические приложения криволинейных интегралов
Примечания[править | править код]
- ↑ Тарг С. М. Работа силы // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. — С. 193-194. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
- ↑ Это делается исходя из того, что можно разбить суммарное конечное перемещение на маленькие последовательные перемещения
, на каждом из которых сила будет почти постоянной, а значит можно будет воспользоваться определением для постоянной силы, введённым выше. Затем работы на всех этих перемещениях
суммируется, что и даёт в результате интеграл.
- ↑ Как это очень часто бывает. Например, в случае кулоновского поля, растягивающейся пружины, силы тяготения планеты итд.
- ↑ По сути через предыдущий, поскольку здесь
; вектор же малого перемещения
совпадает с
.
- ↑ Тарг С. М. Кинетическая энергия // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2. — С. 360. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
- ↑ Работа, совершаемая газом при его сжатии, очевидно отрицательна, но вычисляется по той же формуле. Работа, совершаемая газом (или над газом) без его расширения или сжатия (например, в процессе перемешивания мешалкой), в принципе может быть выражена подобной формулой, но всё же не прямо этой, так как она требует обобщения: дело в том, что в формуле
давление подразумевается одинаковым по всему объёму (что часто выполняется в термодинамике, поскольку речь там часто идёт о процессах, близких к равновесным), что и приводит к наиболее простой формуле (в случае же вращающейся мешалки, например, давление будет разным на передней и задней стороне лопасти, что приведёт к необходимому усложнению формулы, если мы захотим применить её к такому случаю; эти соображения относятся и ко всем другим неравновесным случаям, когда давление неодинаково в разных частях системы).
Литература[править | править код]
- История механики с древнейших времён до конца XVIII в. В 2 т. М.: Наука, 1972.
- Кирпичёв В. Л. Беседы о механике. М.-Л.: Гостехиздат, 1950.
- Льоцци М. История физики. М.: Мир, 1970.
- Мах Э. Принцип сохранения работы: История и корень его. СПб., 1909.
- Мах Э. Механика. Историко-критический очерк её развития. Ижевск: РХД, 2000.
- Тюлина И. А. История и методология механики. М.: Изд-во МГУ, 1979.
п.1. От ускорения к скорости и координате
Рассматривая применение производной в физике и технике (см. §51 данного справочника), мы во второй производной от уравнения прямолинейного равномерного движения (x(t)) пришли к постоянному ускорению (a=const).
С помощью интегрирования можно пройти обратный путь.
Начнем с постоянного ускорения (a=const).
Интеграл от ускорения по времени – это скорость: $$ v(t)=int adt=aint dt=at+C $$ Физический смысл постоянной интегрирования (C) в этом случае – начальная скорость (v_0). Получаем: $$ v(t)=at+v_0 $$ Интеграл от скорости по времени – это координата: $$ x(t)=int v(t)dt=int (at+v_0)dt=frac{at^2}{2}+v_0 t+C $$ Физический смысл постоянной интегрирования (C) в этом случае – начальная координата (x_0). Получаем: $$ x(t)=frac{at^2}{2}+v_0 t+x_0 $$ Таким образом, если нам известны ускорение (a), начальная скорость (v_0) и начальная координата (x_0), мы всегда сможем получить уравнение движения (x(t)).
п.2. Физические величины как интегралы других величин
Если (v(t)) – скорость некоторого физического процесса, уравнение этого процесса можно найти интегрированием: $$ f(t)=int v(t)dt $$ Такие величины часто встречаются в различных разделах физики и техники.
Исходная величина (скорость)
Уравнение процесса (интеграл по времени)
Ускорение (a(t))
Скорость (v(t)=int a(t)dt)
Скорость (v(t))
Координата (x(t)=int v(t)dt)
Угловое ускорение (beta(t))
Угловая скорость (omega(t)=int beta(t) dt)
Угловая скорость (omega(t))
Угол поворота (varphi(t)=intomega(t)dt)
Скорость расходования горючего (u(t))
Масса горючего ракеты (m(t)=int u(t)dt)
Сила тока (I(t))
Заряд (q(t)=int I(t)dt)
Мощность (N(t))
Работа (A(t)=int N(t)dt)
ЭДС индукции (varepsilon(t))
Магнитный поток (Ф(t)=-intvarepsilon(t)dt)
Скорость радиоактивного распада (I(t))
Число атомов радиоактивного вещества (N(t)=int I(t)dt)
Берутся интегралы и по другим переменным. Например, чтобы найти работу переменной силы (F(x)), нужно взять интеграл по координате: $$ A=int_{x_1}^{x_2}F(x)dx $$ В трехмерном пространстве интегралы могут браться по всем трем координатам.
При решении уравнений в частных производных интегралы берутся и по времени и по координатам.
В современной физике интеграл по времени берётся также и от самого уравнение движения. Полученная скалярная величина называется действием и носит фундаментальный характер. В простейшем случае: $$ S_0=int overrightarrow{p}cdot overrightarrow{v}dt $$ где (overrightarrow{p}cdot overrightarrow{v}) – скалярное произведение векторов импульса и скорости.
п.3. Примеры
Пример 1. Тело движется со скоростью (v(t)) (м/с). Найдите путь, пройденный за промежуток времени от (t_1) до (t_2) (с):
a) (v(t)=3t+2t^2, t_1=0, t_2=6)
Путь: begin{gather*} s(t)=int_{t_1}^{t_2}v(t)dt\ s=int_{0}^{6}(3t+2t^2)dt=left(frac{3t^2}{2}+frac{2t^3}{3}right)|_{0}^{6}=frac{3cdot 36}{2}+frac{2cdot 36cdot 6}{3}-0=\ =3cdot 18+4cdot 36=54+144=198 text{(м)} end{gather*}
б) (v(t)=2(t+2)^{5/2}, t_1=0, t_2=7) begin{gather*} s=int_{0}^{7}2(t+2)^{5/2}dt =2cdotfrac{(t+2)^{frac52+1}}{frac72}|_{0}^{7}=frac47cdot 9^{frac72}-0=frac47cdot 3^7approx 1250 text{(м)} end{gather*}
Пример 2. . Сила тока в проводнике изменяется по закону (I(t)=e^{-t}+2t) (время в секундах, ток в амперах). Какой заряд пройдет через поперечное сечение проводника за время от второй до шестой секунды?
Заряд: begin{gather*} Q(t)=int_{t_1}^{t_2}I(t)dt end{gather*} По условию: begin{gather*} Q=int_{2}^{6}(e^{-t}+2t)dt=(-e^{-t}+t^2)|_{2}^{6}=-e^{-6}+6^2+e^{-2}-2^2=frac{1}{e^2}-frac{1}{e^6}+32=\ =frac{e^4-1}{e^6}+32approx 32,1 text{(Кл)} end{gather*}
Пример 3*. Найдите путь, который пройдет тело от начала движения до возвращения в исходную точку, если его скорость (v(t)=18t-9t^2) (время в секундах, скорость в м/с). Движение тела прямолинейное.
Если тело вернулось в исходную точку, оно меняло направление движения.
В момент разворота скорость равна нулю. Решаем уравнение: $$ 18t-9t^2=0Rightarrow 9t(2-t)=0Rightarrow left[ begin{array}{l} t=0\ t=2 end{array} right. $$ (t=0) – начало движения, (t=2) – разворот.
 |
Уравнение движения: $$ x(t)=int(18t-9t^2)dt=9t^2-3t^3+C $$ В начальный момент времени (x_0=0Rightarrow C=0) $$ x(t)=9t^2-3t^3 $$ В точке C(2;12) кривая (x(t)) имеет максимум. Тело двигалось в течение 2 с в одну сторону и прошло 12 м, а затем за 1 с вернулось обратно. Общий путь: 12+12 = 24 м. |
Ответ: 24 м
Пример 4*. Найдите работу, которую необходимо совершить, чтобы выкачать воду из полусферического котла радиуса R м.

Найдем работу (dA), которую нужно совершить, чтобы выкачать слой воды толщиной (dH) с глубины (H).
Радиус слоя на глубине (H: r^2=R^2-H^2) – по теореме Пифагора.
Объем слоя воды: (dV=pi r^2 dH=pi(R^2-H^2)dH)
Масса слоя воды: (dm=rho dV=pirho(R^2-H^2)dH)
Работа по подъему слоя на высоту (H): $$ dA=dmcdot gH=pirho gH(R^2-H^2)dH $$ Получаем интеграл: begin{gather*} A=int_{0}^{R}dA=int_{0}^{R}pirho gH(R^2-H^2)dH=pirho gint_{0}^{R}(HR^2-H^3)dH=\ =pirho gleft(frac{H^2}{2}R^2-frac{H^4}{4}right)|_{0}^{R}=pirho gleft(frac{R^4}{2}-frac{R^4}{4}-0right)=fracpi 4=rho gR^4 end{gather*} Ответ: (A=fracpi 4=rho gR^4)
Пример 5*. Какую работу выполняют при запуске ракеты массой m кг с поверхности планеты на высоту h м, если радиус планеты равен R м и масса планеты равна M кг?
Сравните работу при запуске ракеты с Земли и Луны на высоту одного радиуса небесного тела, если ускорение свободного падения на поверхности Луны (g_M=1,62) м/с2, радиус Луны (R_M=1737) км; для Земли соответственно (g_E=9,81) м/с2 (R_E=6371) км.
Ускорение свободного падения на поверхности планеты: (g_0=Gfrac{M}{R^2})
Ускорение свободного падения при подъеме на высоту x: begin{gather*} g(x)=Gfrac{M}{(R+x)^2} end{gather*} Работа по преодолению силы тяжести (F(x)=mg(x)) при подъеме ракеты на высоту h: begin{gather*} A=int_{0}^{h}mg(x)dx=mint_{0}^{h}Gfrac{M}{(R+x)^2}dx=GmMint_{0}^{h}frac{dx}{(R+x^2)}=\ =GmMcdotleft(-frac{1}{R+x}right)|_{0}^{h}=GmMcdotleft(-frac{1}{R+h}+frac1Rright)=GmMleft(frac1R-frac{1}{R+g}right)=\ =GmMfrac{R+h-R}{R(R+h)}=GmMfrac{h}{R(R+h)} end{gather*} Также, если выразить работу через ускорение свободного падения на поверхности планеты: $$ A=frac{GM}{R^2}frac{mhR^2}{R(R+h)}=mg_0frac{hR}{R+h} $$ Работа по запуску на высоту одного радиуса небесного тела (h=R): $$ A(R)=mg_0frac{R^2}{2R}=frac{mg_0R}{2} $$ Отношение работ по запуску на один радиус на Земле и Луне: $$ frac{A_E(R_E)}{A_M(R_M)}=frac{mg_ER_E}{mg_MR_M}=frac{g_ER_E}{g_MR_M}, frac{A_E(R_E)}{A_M(R_M)}=frac{9,81cdot 6371}{1,62cdot 1737}approx 22,2 $$ На Земле работа в 22,2 раза больше.
Ответ: (A=GmMfrac{h}{R(R+h)}; frac{A_E(R_E)}{A_M(R_M)}approx 22,2)
Содержание:
- Определение и формула работы
- Элементарная работа
- Работа силы на конечном участке траектории
- Единицы измерения работы
- Примеры решения задач
Определение и формула работы
Определение
В том случае, если под воздействием силы происходит изменение модуля скорости движения тела, то говорят о том, что сила
совершает работу. Считают, что если скорость увеличивается, то работа является положительной, если скорость уменьшается,
то работа, которую совершает сила – отрицательна. Изменение кинетической энергии материальной точки в ходе ее движения
между двумя положениями равно работе, которую совершает сила:
$$A=Delta E_{k}=frac{m v_{2}^{2}}{2}-frac{m v_{1}^{2}}{2}(1)$$
Действие силы на материальную точку можно охарактеризовать не только с помощью изменения скорости движения тела, но при помощи
величины перемещения, которое совершает рассматриваемое тело под действием силы
($bar{F}$).
Элементарная работа
Элментарная реабота $(delta A)$ некоторой силы
$bar{F}$ определяется как скалярное произведение:
$$delta A=bar{F} cdot d bar{r}=F cdot d s cdot cos alpha(2)$$
$bar{r}$ радиус – вектор точки, к которой приложена сила,
$bar{r}$ –
элементарное перемещение точки по траектории,
$alpha$ – угол между векторами
$d s=|d bar{r}|$ и $d bar{r}$. Если
$alpha$ является тупым углом работа меньше нуля, если угол
$alpha$ острый, то работа положительная, при
$alpha=frac{pi}{2} delta A=0$
В декартовых координатах формула (2) имеет вид:
$$delta A=F_{x} d x+F_{y} d y+F_{z} d z(3)$$
где Fx,Fy,Fz – проекции вектора
$bar{F}$ на декартовы оси.
При рассмотрении работы силы, приложенной к материальной точке можно использовать формулу:
$$delta A=bar{F} bar{v} d t=bar{v} d bar{p}(4)$$
где $bar{v}$ – скорость материальной точки,
$bar{p}$ – импульс материальной точки.
Если на тело (механическую систему) действуют несколько сил одновременно, то элементарная работа, которую совершают эти силы над системой, равна:
$$delta A=sum_{i=1}^{n} delta A_{i}=sum_{i=1}^{n} bar{F}_{i} d bar{r}_{i}=sum_{i=1}^{n} bar{F}_{i} bar{v}_{i} d t(5)$$
где проводится суммирование элементарных работ всех сил, dt – малый промежуток времени, за который совершается элементарная работа
$delta$ над системой.
Результирующая работа внутренних сил, даже если твердое тело движется, равна нулю.
Пусть твердое тело вращается около неподвижной точки – начала координат (или неподвижной оси, которая проходит через эту точку).
В таком случае, элементарная работа всех внешних сил (допустим, что их число равно n), которые действуют на тело, равна:
$$delta A=bar{M} bar{omega} d t=bar{M} d bar{varphi}(6)$$
где $bar{M}$ – результирующий момент сил относительно точки вращения,
$d bar{varphi}$ – вектор элементарного поворота,
$bar{w}$ – мгновенная угловая скорость.
Работа силы на конечном участке траектории
Если сила выполняет работу по перемещению тела на конечном участке траектории его движения, то работа может быть найдена как:
$$A=int_{0}^{s} bar{F} cdot d bar{r}(7)$$
В том случае, если вектор силы – величина постоянная на всем отрезке перемещения, то:
$$A=F_{tau} cdot s$$
где $F_{tau}=F cos alpha$ – проекция силы на касательную к траектории.
Единицы измерения работы
Основной единицей измерения момента работы в системе СИ является: [A]=Дж=Н•м
В СГС: [A]=эрг=дин•см
1Дж=107 эрг
Примеры решения задач
Пример
Задание. Материальная точка движется прямолинейно (рис.1) под воздействием силы, которая задана
уравнением: $F=C sqrt{s}(C=$ const $)$ . Сила направлена по движению материальной точки.
Чему равна работа данной силы на отрезке пути от s=0 до s=s0?
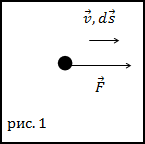
Решение. За основу решения задачи примем формулу расчёта работы вида:
$$A=int_{0}^{s_{0}} F cos alpha d s(1.1)$$
где $alpha = 0$, та как по условию задачи
$bar{F} uparrow uparrow bar{s}$ . Подставим выражение для модуля силы заданное условиями, возьмем интеграл:
$$A=int_{0}^{s_{0}} F d s=int_{0}^{s_{0}} C sqrt{s} d s=frac{2}{3} C s^{frac{3}{2}}$$
Ответ. $A=frac{2}{3} C s^{frac{3}{2}}$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
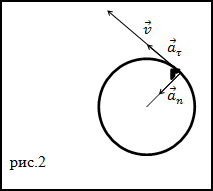
Задание. Материальная точка перемещается по окружности. Ее скорость изменяется в соответствии с
выражением: $v sim t^{2}$ . При этом работа силы, которая действует на точку,
пропорциональна времени: $A sim t^{n}$ . Каково значение n?
Решение. В качестве основы для решения задачи используем формулу:
$$delta A=bar{F} bar{v} d t=mleft(bar{a}_{n}+bar{a}_{tau}right) bar{v} d t=m bar{a}_{n} bar{v} d t+m bar{a}_{tau} bar{v} d t(2.1)$$
Зная зависимость скорости от времени найдем связь тангенциальной составляющей ускорения и времени:
$$a_{tau}=frac{d v}{d t} sim t(2.2)$$
Нормальная составляющая ускорения будет иметь вид:
$$a_{n}=frac{v^{2}}{R} sim t^{4}(2.3)$$
При движении по окружности нормальная составляющая ускорения будет всегда перпендикулярна вектору скорости, следовательно, вклад в
произведение силы на скорость будет вносить только тангенциальная составляющая, то есть выражение (2.1) преобразуется к виду:
$$delta A=m bar{a}_{tau} bar{v} d t=m a_{tau} v d t(2.5)$$
Выражение для работы найдем как:
$$A=C int_{0}^{t} t cdot t^{2} d t sim t^{4}$$
Ответ. n=4
Читать дальше: Формула силы Ампера.
Второй закон Ньютона в импульсной форме позволяет определить, как меняется скорость тела по модулю и направлению, если в течение некоторого времени на него действует определенная сила:
![]()
Работа силы
В механике также важно уметь вычислять изменение скорости по модулю, если при перемещении тела на некоторый отрезок на него действует некоторая сила. Воздействия на тела сил, приводящих к изменению модуля их скорости, характеризуется величиной, зависящей как от сил, так и от перемещений. Эту величину в механике называют работой силы.
Работа силы обозначается буквой А. Это скалярная физическая величина. Единица измерения — Джоуль (Дж).
Работа силы равна произведению модуля силы, модуля перемещения и косинусу угла между ними:
![]()

Важно!
Механическая работа совершается, если:
- На тело действует сила.
- Под действием этой силы тело перемещается.
- Угол между вектором силы и вектором перемещения не равен 90 градусам (потому что косинус прямого угла равен нулю).
Внимание! Если к телу приложена сила, но под ее действием тело не начинает движение, механическая работа равна нулю.
Пример №1. Груз массой 1 кг под действием силы 30 Н, направленной вертикально вверх, поднимается на высоту 2 м. Определить работу, совершенной этой силой.
Так как перемещение и вектор силы имеют одно направление, косинус угла между ними равен единице. Отсюда:
![]()
Работа различных сил
Любая сила, под действием которой перемещается тело, совершает работу. Рассмотрим работу основных сил в таблице.
| Работа силы тяжести |
Модуль силы тяжести: Fтяж = mg Работа силы тяжести: A = mgs cosα |
| Работа силы трения скольжения |
Модуль силы трения скольжения: Fтр = μN = μmg Работа силы трения скольжения: A = μmgs cosα |
| Работа силы упругости |
Модуль силы упругости: Fупр = kx Работа силы упругости:
|
Работа силы упругости
Работа силы упругости не может быть определена стандартной формулой, так как она может применяться только для постоянной по модулю силы. Сила же упругости меняется по мере сжатия или растяжения пружины. Поэтому берется среднее значение, равное половине суммы сил упругости в начале и в конце сжатия (растяжения):

Нужно также учесть, что перемещение тела под действием силы упругости равно разности удлинения пружины в начале и конце:
s = x1 – x2
Перемещение и направление силы упругости всегда сонаправлены, поэтому угол между ними нулевой. А косинус нулевого угла равен 1. Отсюда работа силы упругости равна:

Работы силы трения покоя
Работы силы трения покоя всегда равна 0, так как под действием этой силы тело не сдвигается с места. Исключение составляет случай, когда покоящееся тело лежит на подвижном предмете, на который действует некоторая сила. Относительно системы координат, связанной с подвижным предметом, работа силы трения покоя будет нулевой. Но относительно системы отсчета, связанной с Землей, эта сила будет совершать работу, так как тело будет двигаться, оставаясь на поверхности движущегося предмета.

Пример №2. Груз массой 100 кг волоком перетащили на 10 м по плоскости, поверхность которой имеет коэффициент трения 0,4. Найти работу, совершенной силой трения скольжения.
A = μmgs cosα = 0,4∙100∙10∙10∙(–1) = –4000 (Дж) = –4 (кДж)
Знак работы силы
Знак работы силы определяется только косинусом угла между вектором силы и вектором перемещения:
- Если α = 0о, то cosα = 1.
- Если 0о < α < 90o, то cosα > 0.
- Если α = 90о, то cosα = 0.
- Если 90о < α < 180o, то cosα < 0.
- Если α = 180о, то cosα = –1.
Работа силы трения скольжения всегда отрицательна, так как сила трения скольжения направлена противоположно перемещению тела (угол равен 180о). Но в геоцентрической системе отсчета работа силы трения покоя будет отличной от нуля и выше нуля, если оно будет покоиться на движущемся предмете (см. рис. выше). В таком случае сила трения покоя будет направлена с перемещением относительно Земли в одну сторону (угол равен 0о). Это объясняется тем, что тело по инерции будет пытаться сохранить покой относительно Земли. Это значит, что направление возможного движения противоположно движению предмета, на котором лежит это тело. А сила трения покоя направлена противоположно направлению возможного движения.
Геометрический смысл работы
Графическое определение
Механическая работа численно равна площади фигуры, ограниченной графиком с осями OF и OX.

A = Sфиг
Мощность
Определение
Мощность — физическая величина, показывающая, какую работу совершает тело в единицу времени. Мощность обозначается буквой N. Единица измерения: Ватт (Вт). Численно мощность равна отношению работы A, совершенной телом за время t:

Рассмотрим частные случаи определения мощности в таблице.
Мощность при равномерном прямолинейном движении тела |
Работа при равномерном прямолинейном движении определяется формулой: A = Fтs Fт — сила тяги, s — перемещение тела под действием этой силы. Отсюда мощность равна:
|
Мощность при равномерном подъеме груза |
Когда груз поднимается, совершается работа, по модулю равная работе силе тяжести. За перемещение в этом случае можно взять высоту. Поэтому:
|
Мгновенная мощность при неравномерном движении |
Выше мы уже получили, что мощность при постоянной скорости равна произведению этой скорости на силу тяги. Но если скорость постоянно меняется, можно вычислить мгновенную мощность. Она равна произведению силы тяги на мгновенную скорость:
|
Мощность силы трения при равномерном движении по горизонтали |
Мощность силы трения отрицательна так же, как и работа. Это связано с тем, что угол между векторами силы трения и перемещения равен 180о (косинус равен –1). Учтем, что сила трения скольжения равна произведению силы нормальной реакции опоры на коэффициент трения:
|
Пример №3. Машина равномерно поднимает груз массой 10 кг на высоту 20 м за 40 с. Чему равна ее мощность?
Коэффициент полезного действия
Не вся работа, совершаемая телами, может быть полезной. В реальном мире на тела действует несколько сил, препятствующих совершению работы другой силой. К примеру, чтобы переместить груз на некоторое расстояние, нужно совершить работу гораздо большую, чем можно получить при расчете по формулам выше.
Определения:
- Работа затраченная — полная работа силы, совершенной над телом (или телом).
- Работа полезная — часть полной работы силы, которая вызывает непосредственно перемещение тела.
- Коэффициент полезного действия (КПД) — процентное отношение полезной работы к работе затраченной. КПД обозначается буквой «эта» — η. Единицы измерения эта величина не имеет. Она показывает эффективность работы механизма или другой системы, совершающей работу, в процентах.
КПД определяется формулой:

Работа может определяться как произведение мощности на время, в течение которого совершалась работа:
A = Nt
Поэтому формулу для вычисления КПД можно записать в следующем виде:

Частые случаи определения КПД рассмотрим в таблице ниже:
Устройство |
Работа полезная и полная |
КПД |
| Неподвижный блок, рычаг |
Aполезн = mgh Асоверш. |
 |
| Наклонная плоскость |
Aполезн = mgh Асоверш. = Fl l — совершенный путь (длина наклонной плоскости). |
 |
Пример №4. Определите полезную мощность двигателя, если его КПД равен 40%, а его мощность по паспорту равна 100 кВт.
В данном случае необязательно переводить единицы измерения в СИ. Но в таком случае ответ мы тоже получим в кВт. Из этой формулы выразим полезную мощность:
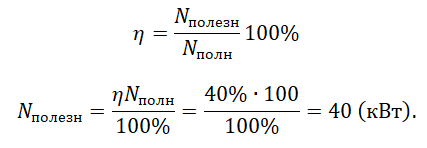
Задание EF17557
Какую мощность развивает сила тяги трактора, перемещая прицеп со скоростью 18 км/ч, если она составляет 16,5 кН?
Ответ:
а) 916 Вт
б) 3300 Вт
в) 82500 Вт
г) 297000 Вт
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Записать формулу для расчета мощности.
3.Выполнить общее решение задачи.
4.Подставить известные данные и выполнить вычисления.
Решение
Запишем исходные данные:
• Сила тяги, перемещающая прицеп, равна: Fт = 16,5 кН.
• Скорость перемещения прицепа под действием силы тяги: v = 18 км/ч.
Переведем единицы измерения в СИ:
16,5 кН = 16,5∙103 Н
18 км/ч = 18000/3600 м/с = 5 м/с
Мощность равна отношению работы ко времени, в течение которого эта работа совершалась:
N=At
Но работа равна произведению силы, перемещения и косинуса угла между векторами силы и перемещения. В данном случае будем считать, что угол равен нулю, следовательно косинус — единице. Тогда работа равна:
A = Fs
Тогда мощность равна:
N=Fst=Fv=16,5·103·5=82500 (Вт)
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17574
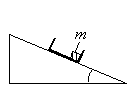 С вершины наклонной плоскости из состояния покоя скользит с ускорением лёгкая коробочка, в которой находится груз массой m (см. рисунок). Как изменятся время движения, ускорение и модуль работы силы трения, если с той же наклонной плоскости будет скользить та же коробочка с грузом массой m/2? Для каждой величины определите соответствующий характер изменения:
С вершины наклонной плоскости из состояния покоя скользит с ускорением лёгкая коробочка, в которой находится груз массой m (см. рисунок). Как изменятся время движения, ускорение и модуль работы силы трения, если с той же наклонной плоскости будет скользить та же коробочка с грузом массой m/2? Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
|
Время движения |
Ускорение |
Модуль работы силы трения |
Алгоритм решения
1.Установить наличие и характер зависимости кинематических характеристик движения от массы тела.
2.Вывести формулу для модуля работы силы трения.
3.Установить, как изменится модуль работы силы трения при уменьшении массы тела вдвое.
Решение
При скольжении с наклонной плоскости происходит равноускоренное движение. Положение тела в любой момент времени при таком движении можно определить с помощью кинематических уравнений:
x=xo+v0xt+axt22
y=yo+v0yt+ayt22
Из этих уравнений видно, что ускорение и время никак не зависят от массы тела. Следовательно, при уменьшении массы тела в 2 раза его время движения и ускорение не изменятся.
Чтобы выразить модуль работы силы трения, выберем такую систему отсчета, чтобы вектор силы трения был расположен вдоль оси Ox.Тогда сила трения будет равна:
Fтр = μmg
Известно, что работа определяется формулой:
A = Fs cosα
Тогда работа силы трения равна:
A = μmgs cosα
Вектор силы трения всегда направлен противоположно вектору перемещения. Поэтому косинус угла между ними равен –1. Но нас интересует только модуль работы. Поэтому будем считать, что он равен:
A = μmgs
Модуль работы силы трения и масса тела зависят прямо пропорционально. Следовательно, если массу тела уменьшить вдвое, то и модуль работы силы трения уменьшится вдвое.
Поэтому правильная последовательность цифр в ответе: 332.
Ответ: 332
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18646
В первой серии опытов брусок перемещают при помощи нити равномерно и прямолинейно вверх по наклонной плоскости. Во второй серии опытов на бруске закрепили груз, не меняя прочих условий.
Как изменятся при переходе от первой серии опытов ко второй сила натяжения нити и коэффициент трения между бруском и плоскостью?
Для каждой величины определите соответствующий характер её изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждого ответа. Цифры в ответе могут повторяться.
| Сила натяжения нити | Коэффициент трения |
Алгоритм решения
- Определить, какая величина изменилась во второй серии опытов.
- Определить, как зависит от этой величины сила натяжения нити.
- Определить, как зависит от этой величины коэффициент трения.
Решение
Когда к бруску подвесили груз, увеличилась масса. Когда тело на нити перемещается вверх прямолинейно и равномерно, сила натяжения нити определяется модулем силы тяжести:
T = mg
Эта формула показывает, что сила натяжения нити и масса тела зависят прямо пропорционально. Если, добавив к бруску груз, масса увеличится, то сила натяжения нити тоже увеличится.
Коэффициент трения — это величина, которая зависит только от материалов и типа поверхности. Поэтому увеличение массы тела на него никак не повлияют.
Верная последовательность цифр в ответе: 13.
Ответ: 13
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18271
Определите коэффициент полезного действия атомной электростанции, расходующей за неделю уран-235 23592U массой 1,4 кг, если её мощность равна 38 МВт. При делении одного ядра урана-235 выделяется энергия 200 МэВ.
Алгоритм решения
1.Записать исходные данные и перевести их в СИ.
2.Записать формулу для определения КПД атомной электростанции.
3.Решить задачу в общем виде.
4.Подставить известные данные и вычислить искомую величину.
5.Массовое число: A = 235.
6.Зарядовое число: Z = 92.
Решение
Запишем исходные данные:
• Энергия, выделяемая при делении одного ядра урана-235: Q0 = 200 МэВ.
• Масса урана-235: m = 1,4 кг.
• Время, в течение которого происходит деление: t = 1 неделя.
• Мощность атомной электростанции: N = 38 МВт.
Переведем все единицы измерения в СИ:
1 эВ = 1,6∙10–19 Дж
200 МэВ = 200∙106∙1,6∙10–19 Дж = 320∙10–13 Дж
1 неделя = 7∙24∙60∙60 с = 604,8∙103 с
38 МВт = 38∙106 Вт
КПД атомной электростанции есть отношение полезной работы к выделенной за это же время энергии:
η=AполезнQ100%
Полезную работу мы можем вычислить по формуле:
A=Nt
Выделенное количество теплоты мы можем рассчитать, вычислив количество атомов, содержащихся в 1,4 кг урана-235 и умножив их на энергию, выделяемую при делении одного такого атома.
Количество атомов равно произведению количество молей на постоянную Авогадро:
Nкол.атомов = νNA
Количество молей равно отношения массы вещества к его молярной массе, следовательно:
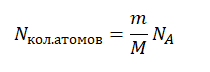
Молярная масса численно равна массовому числу в граммах на моль. Следовательно:
M = A (г/моль) = A∙10–3 (кг/моль)
Отсюда количество атомов равно:
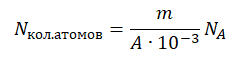
Энергия, выделенная всеми атомами, равна:
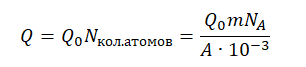
Теперь можем вычислить КПД:
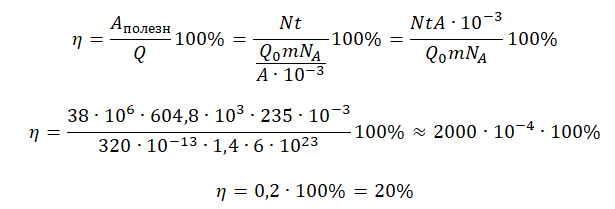
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 11.8k
Сила, перемещающая тело, совершает работу. Работа – это разность энергии тела в начале процесса и в его конце. А мощность – это работа за одну секунду. Коэффициент полезного действия (КПД) – это дробное число. Максимальный КПД равен единице, однако, часто, КПД меньше единицы.
Работы силы, формула
Сила, приложенная к телу и перемещающая его, совершает работу (рис. 1).

Рис. 1. Сила перемещает тело и совершает работу
Работа силы — это скалярное произведение вектора силы на вектор перемещения.
Работу, совершаемую силой, можно посчитать, используя векторный или скалярный вид записи такой формулы:
Векторный вид записи
[ large boxed{ A = left( vec{F} , vec{S} right) }]
Для решения задач правую часть этой формулы удобно записывать в скалярном виде:
[ large boxed{ A = left| vec{F} right| cdot left| vec{S} right| cdot cos(alpha) }]
( F left( H right) ) – сила, перемещающая тело;
( S left( text{м} right) ) – перемещение тела под действием силы;
( alpha ) – угол между вектором силы и вектором перемещения тела;
Работу обозначают символом (A) и измеряют в Джоулях. Работа – это скалярная величина.
В случае, когда сила постоянная, формула позволяет рассчитать работу, совершенную силой за полное время ее действия.
Если сила изменяется со временем, то в каждый конкретный момент времени будем получать мгновенную работу. Эти, мгновенные значения для разных моментов времени будут различаться.
Рассмотрим несколько случаев, следующих из формулы:
- Когда угол между силой и перемещением острый, работа силы положительная;
- А если угол тупой — работа отрицательная, так как косинус тупого угла отрицательный;
- Если же угол прямой – работа равна нулю. Сила, перпендикулярная перемещению, работу не совершает!
Работа — разность кинетической энергии
Работу можно рассчитать еще одним способом — измеряя кинетическую энергию тела в начале и в конце процесса движения. Рассмотрим такой пример. Пусть автомобиль, движется по горизонтальной прямой и, при этом увеличивает свою скорость (рис. 2). Масса автомобиля 1000 кг. В начале его скорость равнялась 1 м/с. После разгона скорость автомобиля равна 10 метрам в секунду. Найдем работу, которую пришлось проделать, чтобы ускорить этот автомобиль.

Рис. 2. Автомобиль движется прямолинейно и увеличивает свою скорость
Для этого посчитаем энергию движения автомобиля в начале и в конце разгона.
( E_{k1} left(text{Дж} right) ) – начальная кинетическая энергия машины;
( E_{k2} left(text{Дж} right) ) – конечная кинетическая энергия машины;
( m left( text{кг}right) ) – масса автомобиля;
( displaystyle v left( frac{text{м}}{c}right) ) – скорость, с которой машина движется.
Кинетическую энергию будем вычислять, используя формулу:
[ large E_{k} = m cdot frac{v^{2}}{2} ]
[ large E_{k1} = 1000 cdot frac{1^{2}}{2} = 500 left(text{Дж} right) ]
[ large E_{k2} = 1000 cdot frac{10^{2}}{2} = 50000 left(text{Дж} right) ]
Теперь найдем разницу кинетической энергии в конце и вначале разгона.
[ large boxed{ A = Delta E_{k} }]
[ large Delta E_{k} = E_{k2} — E_{k1} ]
[ large Delta E_{k} = 50000 – 500 = 49500 left(text{Дж} right) ]
Значит, работа, которую потребовалось совершить, чтобы разогнать машину массой 1000 кг от скорости 1 м/с до скорости 10 м/с, равняется 49500 Джоулям.
Примечание: Работа – это разность энергии в конце процесса и в его начале. Можно находить разность кинетической энергии, а можно — разность энергии потенциальной.
[ large boxed{ A = Delta E }]
Работа силы тяжести — разность потенциальной энергии
Рассмотрим теперь следующий пример. Яблоко массой 0,2 кг упало на садовый стол с ветки, находящейся на высоте 3 метра от поверхности земли. Столешница располагается на высоте 1 метр от поверхности (рис. 3). Найдем работу силы тяжести в этом процессе.

Рис. 3. На рисунке указано начальное 1 положение тела (яблока) и его конечное 2 положение, отмечены высоты для подсчета работы по вертикальному перемещению тела
Посчитаем потенциальную энергию яблока до его падения и энергию яблока на столешнице.
( E_{p1} left(text{Дж} right) ) – начальная потенциальная энергия яблока;
( E_{p2} left(text{Дж} right) ) – конечная потенциальная энергия яблока;
Примечание: Работу можно рассчитать через разность потенциальной энергии тела.
Потенциальную энергию будем вычислять, используя формулу:
[ large E_{p} = m cdot g cdot h]
( m left( text{кг}right) ) – масса яблока;
Величина ( displaystyle g approx 10 left(frac{text{м}}{c^{2}} right) ) – ускорение свободного падения.
( h left( text{м}right) ) – высота, на которой находится яблоко относительно поверхности земли.
Начальная высота яблока над поверхностью земли равна 3 метрам
[ large E_{p2} = 0,2 cdot 10 cdot 3 = 6 left(text{Дж} right) ]
Потенциальная энергия яблока на столе
[ large E_{p1} = 0,2 cdot 10 cdot 1 = 2 left(text{Дж} right) ]
Теперь найдем разницу потенциальной энергии яблока в конце падения и перед его началом.
[ large Delta E_{p} = E_{p2} — E_{p1} ]
[ large Delta E_{p} = 2 – 6 = — 4 left(text{Дж} right) ]
Важно помнить: Когда тело падает на землю, его потенциальная энергия уменьшается. Сила тяжести при этом совершает положительную работу!
Чтобы работа получилась положительной, в правой части формулы перед ( Delta E_{p}) дополнительно допишем знак «минус».
[ large boxed{ A = — Delta E_{p} }]
Значит, работа, которую потребовалось совершить силе тяжести, чтобы яблоко массой 0,2 кг упало с высоты 3 м на высоту 1 метр, равняется 4 Джоулям.
Примечания:
- Если тело падает на землю, работа силы тяжести положительна;
- Когда мы поднимаем тело над землей, мы совершаем работу против силы тяжести. Наша работа при этом положительна, а работа силы тяжести будет отрицательной;
- Сила тяжести относится к консервативным силам. Для консервативных сил перед разностью потенциальной энергии мы дописываем знак «минус»;
- Работа силы тяжести не зависит от траектории, по которой двигалось тело;
- Работа для силы (displaystyle F_{text{тяж}}) зависит только от разности высот, в которых тело находилось в конечный и начальный моменты времени.
Рисунок 4 иллюстрирует факт, что для силы (displaystyle F_{text{тяж}}) работа зависит только от разности высот и не зависит от траектории, по которой тело двигалось.

Рис. 4. Разность высот между начальным и конечным положением тела во всех случаях на рисунке одинакова, поэтому, работа силы тяжести для представленных случаев будет одинаковой
Мощность
В механике мощность часто обозначают символами N или P и измеряют в Ваттах в честь шотландского изобретателя Джеймса Уатта.
Примечание: Символ (vec{N}) используется для обозначения силы реакции опоры — она измеряется в Ньютонах и является векторной величиной. Чтобы не возникло путаницы, мощность вместо N будем обозначать символом P. Символ P – первая буква в английском слове power – мощность.
Мощность – это работа, совершенная за одну секунду (энергия, затраченная за 1 сек).
Расчет работы осуществляем, используя любую из формул:
[ large A = Delta E_{k} ]
[ large A = Delta E_{p} ]
[ large A = F cdot S cdot cos(alpha) ]
Разделив эту работу на время, в течение которого она совершалась, получим мощность.
[ large boxed{ P = frac{A}{Delta t} }]
Если работа совершалась равными частями за одинаковые интервалы времени – мощность будет постоянной величиной.
Мощность переменная, когда в некоторые интервалы времени совершалось больше работы.
Еще одна формула для расчета мощности
Есть еще один способ расчета мощности, когда сила перемещает тело и при этом скорость тела не меняется:
[ large P = left( vec{F} , vec{v} right) ]
Формулу можно записать в скалярном виде:
[ large P = left| vec{F} right| cdot left| vec{v} right| cdot cos(alpha) ]
( F left( H right) ) – сила, перемещающая тело;
( displaystyle v left( frac{text{м}}{c} right) ) – скорость тела;
( alpha ) – угол между вектором силы и вектором скорости тела;
Когда векторы (vec{F}) и (vec{v}) параллельны, запись формулы упрощается:
[ large boxed{ P = F cdot v }]
Примечание: Такую формулу для расчета мощности можно получить из выражения для работы силы, разделив обе части этого выражения на время, в течение которого работа совершалась (а если точнее, найдя производную обеих частей уравнения).
КПД
КПД – коэффициент полезного действия. Обычно обозначают греческим символом (eta) «эта». Единиц измерения не имеет, выражается либо десятичной дробью, либо в процентах.
Примечания:
- Процент – это дробь, у которой в знаменателе число 100.
- КПД — это либо правильная дробь, или дробь, равная единице.
Вычисляют коэффициент (eta) для какого-либо устройства, механизма или процесса.
[ large boxed{ eta = frac{ A_{text{полезная}}}{ A_{text{вся}}} }]
(eta) – КПД;
( large A_{text{полезная}} left(text{Дж} right)) – полезная работа;
(large A_{text{вся}} left(text{Дж} right)) – вся затраченная для выполнения работы энергия;
Примечание: КПД часто меньше единицы, так как всегда есть потери энергии. Коэффициент полезного действия не может быть больше единицы, так как это противоречит закону сохранения энергии.
[ large boxed{ eta leq 1 }]
Величина (eta) является дробной величиной. Если числитель и знаменатель дроби разделить на одно и то же число, полученная дробь будет равна исходной. Используя этот факт, можно вычислять КПД, используя мощности:
[ large boxed{ eta = frac{ P_{text{полезная}}}{ P_{text{вся затраченная}}} }]
Выводы
- Сила, приложенная к телу и перемещающая его, совершает работу;
- Когда угол между силой и перемещением острый, работа силы положительная, а если угол тупой — работа отрицательная; Если же угол прямой – работа равна нулю. Сила, перпендикулярная перемещению, работу не совершает!
- Работу можно вычислить, измеряя кинетическую энергию тела в начале и в конце его движения;
- Вычислить работу можно через разность потенциальной энергии тела в начальной и в конечной высотах над землей;
- Когда тело падает на землю, его потенциальная энергия уменьшается. Сила тяжести при этом совершает положительную работу!
- Мы совершаем работу против силы тяжести, когда поднимаем тело над землей. При этом наша работа положительная, а работа силы тяжести — отрицательная;
- Сила тяжести — это консервативная сила. Поэтому, работа силы (displaystyle F_{text{тяж}}) не зависит от траектории, по которой двигалось тело, а зависит только от разности высот, в которых тело находилось в конечный и начальный моменты времени;
- Мощность – это работа, совершенная за одну секунду, или затраченная за 1 сек. энергия;
- Коэффициент полезного действия обозначают греческим символом (eta) «эта», единиц измерения не имеет, выражается либо десятичной дробью, либо в процентах;
- КПД — это либо правильная дробь, или дробь, равная единице.
- Можно вычислять КПД, подставляя в формулу работу, или мощности