Расстояние между соседними плоскостями
с индексами (hkl) можно
вычислить в единицах длины ребра куба
с помощью уравнения:
![]()
Расстояние между плоскостями с большими
индексами малы по сравнению с расстояниями
между плоскостями, имеющими малые
индексы. У плоскостей с малыми индексами
более высокая плотность расположения
атомов (количество атомов на единицу
площади), чем у плоскостей с большими
индексами.
Расстояние между ионами (или между
атомами) в решетках можно вычислить по
плотности вещества по формуле:
![]()
Пример: Плотность поваренной соли ρ
= 2,173 г/см3,масса 1 моль NaCl
равна 58,455 г. В нем находится 2 · 6·1023
ионов, откуда
![]()
нм
Расстояние между ионами можно определить,
исходя из ионных радиусов.
Например:
![]() =0,98Å=0,098
=0,98Å=0,098
нм
![]() =1,81Å=0,181
=1,81Å=0,181
нм
Затем полученные данные сложим.
d= 0,098+0,181=0,279 нм
Этот метод менее точен. Таблица ионных
радиусов приведена в приложении.
2. Контрольные задания
2.1. Задание №1.
Определить длину ребра куба и атомный
радиус по указанным в таблице данным.
В таблице приняты следующие обозначения
решеток: простая кубическая решетка
NaCl, объемноцентрированная
– CsCl или ОЦК; гранецентрированная
решетка – ГЦК; гексагональная плотной
упаковки – ГПУ; решетки типа алмаза –
«алмаз» или ZnS (сфалерит);
решетка флюорита – CaF2.
|
№ задачи |
Металл |
Тип решетки |
Плотность, |
|
|
Pb |
ГЦК |
11,34 |
|
|
Pt |
ГЦК |
21,45 |
|
|
Cu |
ГЦК |
8,9 |
|
|
Ta |
ОЦК |
16,60 |
|
|
α |
ОЦК |
7,80 |
|
|
Na |
ОЦК |
0,97 |
|
|
Zi |
ОЦК |
0,53 |
|
|
W |
ОЦК |
19,10 |
|
|
Cr |
ОЦК |
7,00 |
|
|
V |
ОЦК |
6,10 |
|
|
γ |
ГЦК |
8,14 |
|
|
Rb |
ОЦК |
1,50 |
|
|
Au |
ГЦК |
19,32 |
|
|
Sr |
ГЦК |
2,60 |
|
|
Nb |
ОЦК |
8,58 |
|
|
Mo |
ОЦК |
10,20 |
|
|
Cs |
ОЦК |
1,90 |
|
|
Ba |
ОЦК |
3,75 |
|
|
Ag |
ГЦК |
10,50 |
|
|
Al |
ГЦК |
2,7 |
|
|
α |
ГЦК |
1,55 |
|
|
Mg |
ГПУ |
1,74 |
|
|
β |
ОЦК |
4,515 |
|
|
α |
ГПУ |
6,505 |
|
|
Tc |
ГПУ |
11,5 |
|
|
β |
ОЦК |
7,86 |
|
|
α |
ГПУ |
8,33 |
|
|
Ni |
ГЦК |
8,9 |
|
|
β |
ГЦК |
8,33 |
|
|
α |
ГПУ |
11,87 |
|
|
β |
ГЦК |
11,87 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Кристаллическую решетку характеризуют следующие основные параметры:
· период решетки;
· атомный радиус;
· энергия решетки;
· координационное число;
· базис и коэффициент компактности решетки.
Периодом решетки называется расстояние между центрами двух соседних частиц (атомов, ионов) в элементарной ячейке решетки (см. рис. 1.2, а, b). Периоды решетки выражаются в ангстремах (1 = 10-8 см). Параметры решетки металлов находятся в пределах 0,2 – 0,7 нм и определяются методом рентгеноструктурного анализа с точностью до третьего, а при необходимости и до четвертого или даже пятого знака после запятой.
Под атомным радиусом понимают половину межатомного расстояния между центрами ближайших атомов в кристаллической решетке элемента при нормальной температуре и атмосферном давлении. Однако атомный радиус не является постоянной величиной, а изменяется в зависимости от ряда факторов, важнейшими из которых являются координационное число и тип химической связи между атомами в кристалле.
Энергия кристаллической решетки определяется как энергия, выделяющаяся при образовании кристалла из ионов, атомов или других частиц, образующих кристалл, когда исходное состояние этих частиц газообразное. От величины энергии решетки зависят такие свойства вещества, как температура плавления, модуль упругости, прочность, твердость и др. Увеличение валентности атомов приводит к увеличению энергии решетки.
Координационное число (К), показывает количество атомов, находящихся на наиболее близком и равном расстоянии от любого выбранного атома в решетке.
Базисом решетки называется количество атомов, приходящихся на одну элементарную ячейку решетки.
Коэффициент компактности (?) решетки определяется отношением объема, занимаемого атомами (Va), ко всему объему решетки (Vp), т.е.
? = Va/Vp. Представленные на рис. 1.2 (сверху) типы кристаллических решеток схематично отражают взаимное расположение атомов (ионов) в кристалле. Если условно считать атомы шарами одинакового диаметра, то снизу на рис. 1.2 дано более точное представление о действительном расположении атомов в кристаллах ОЦК, ГЦК и ГПУ
Пример: Гранецентрированная кубическая решетка (рис. 1.2, б) имеет восемь атомов по вершинам и по одному атому в центре граней куба. Определим для нее такие понятия, как «координационное число» и «базис» решетки.
Оперируя с элементарной ячейкой, нельзя забывать, что в реальном кристалле такая ячейка окружена со всех сторон другими ячейками и поэтому не все атомы, отно
сящиеся к рассматриваемой ячейке, принадлежат только этой ячейке. Для того чтобы это понять, рекомендуется изобразить на клетчатой бумаге элементарную ячейку и пристроить к ней со всех сторон другие ячейки. Важность такого построения выявляется при решении конкретных задач.
Из рис. 1.2, б видно, что минимальное расстояние между атомами в решетке ГЦК равно половине диагонали грани. Пристроив около какой-либо вершины куба другие примыкающие к ней ячейки, подсчитаем координационное число: к любой вершине куба реально пристроены 8 элементарных ячеек; в каждой ячейке на расстоянии η диагонали грани находится три атома; каждая грань обслуживает две ячейки, поэтому
К = (3 · 8)/2 = 12.
А. Китайгородский Как измеряются расстояния между атомами в кристаллах
Слова «структура», «строение» – очень емкие по смыслу. Разные исследователи понимают под этими словами разные вещи. Биолог может вести речь о структуре мышечной ткани, имея в виду расположение волокон друг относительно друга; металлограф, говоря о строении сплава, обычно подразумевает форму и размеры зерен. Эти структуры наблюдаются с помощью обычного микроскопа при увеличении всего лишь в несколько сотен раз. Но те же самые слова используются и тогда, когда речь идет о частицах, входящих в состав атомного ядра, размеры которых измеряются триллионными долями сантиметра. Тут слово «структура» имеет уже условный смысл, и физики пользуются им с осторожностью, помня, что наглядные зрительные представления не годятся для столь малых кирпичиков мироздания.
В физике твердого тела слова «строение» и «структура» также могут употребляться в разных смыслах. Так, например, обсуждая электронное строение металла, имеют в виду вовсе не размещение электронов в пространстве, а характер распределения их по энергиям; говоря о структуре ферромагнитных материалов, описывают размеры, форму и расположение доменов. Есть и другие ситуации, где слово «структура» оказывается достаточно уместным.
В этой статье речь пойдет об атомной структуре кристаллов, под которой понимается узор, создаваемый центрами атомов. Атомная структура определяется рентгеноструктурным анализом, в основе которого лежит явление дифракции рентгеновских лучей. С помощью этого замечательного явления, открытого в 1912 году Максом Лауэ, удается измерить расстояния между центрами атомов твердого тела и определить их взаимное пространственное расположение. За 65 лет, которые прошли со времени открытия Лауэ, с помощью рентгеноструктурного анализа удалось установить геометрию расположения атомов примерно в десятке тысяч кристаллов.
Задача этой статьи заключается в том, чтобы познакомить читателя с основными идеями рентгеноструктурного анализа и дать представление о дороге, следуя которой, можно определить структуру кристалла: измерить расстояния между атомами, дать картину пространственного расположения атомов в молекуле и упаковку молекул в кристалле и т.п. Решая эту задачу, мы, естественно, предельно упростим ее. Наша цель – повторим еще раз – сделать ясными принципы, лежащие в основе метода.
На рисунке 1 изображена атомная структура кристалла йодистой ртути. Молекула этого вещества состоит из одного атома ртути и двух атомов йода. Атомы, образующие кристалл, расположены так, как детали рисунка обоев. Если раскрасить фигурки, соответствующие атомам разных сортов, в разные цвета, то получатся обои. Может быть, с эстетической точки зрения они оставят желать лучшего, но принцип обоев будет налицо: можно выделить элементарную ячейку, периодическим смещением которой в двух направлениях «строятся» обои. Про обои можно сказать, что они представляют двумерную решетку. Удалите мысленно все детали рисунка, кроме линий, и справедливость предыдущей фразы станет очевидной. Точки пересечения линий называют узлами.
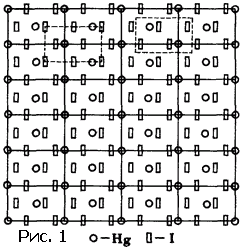
Выбор узлов и, соответственно, линий решетки, произволен. Тем не менее существуют некоторые правила выбора узлов. Дело в том, что от узла решетки отсчитываются координаты атомов, а поэтому естественно выбрать узел в симметричной точке. Из трех, указанных на рисунке 1 вариантов (из бесчисленного множества возможных), мы предпочли наиболее целесообразный.
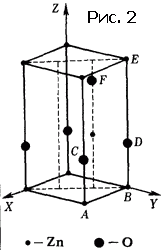
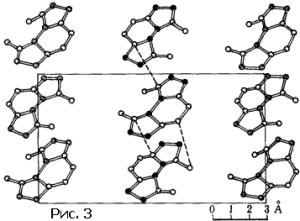
Мы погрешили против истины, сказав, что на рисунке 1 изображена структура кристалла. На самом деле показана проекция структуры на плоскость. Кристалл – трехмерные обои. Решетка кристалла не двумерная, а трехмерная. Ячейка – не параллелограмм или прямоугольник, а параллелепипед. Он может быть прямоугольным, а в некоторых случаях – выродиться в куб. Ячейка может содержать один, два атома, а в сложных случаях – сотни и тысячи. Понятно, что исследователь, желающий познакомить читателя своей статьи со структурой изученного кристалла, ограничится тем, что изобразит вид в перспективе одной ячейки. На рисунке 2 показана структура очень простого кристалла (окиси цинка), а на рисунке 3 – сложного органического соединения.
Вы познакомились с минимальными сведениями, необходимыми для того, чтобы разобраться в сущности рентгеноструктурного анализа. Принцип этого мощнейшего способа изучения вещества состоит в регистрации вторичного рентгеновского излучения, которое исходит от всех атомов кристалла, когда на него падает первичный узкий пучок рентгеновских лучей. Стараются подобрать условия опыта такими, чтобы кристалл был прозрачен для лучей. Тогда в создании рассеянного излучения (вторичного, дифрагированного – это все синонимы) будут участвовать все атомы кристалла.
Явление, о котором идет речь, далеко не простое. Но нам нет нужды входить в детали. Поэтому все проблемы будут рассмотрены на предельно простом примере. Первое упрощение – ограничимся изучением проекции структуры кристалла, второе – будем рассматривать прямоугольную решетку, третье – положим, что на ячейку приходится одна двухатомная молекула.
Сначала займемся описанием «пустой решетки», из которой атомы «удалены». Остались одни узлы. Отец и сын Брэгги показали, что дифракцию рентгеновских лучей можно рассматривать как своеобразное избирательное (то есть происходящее лишь при некоторых дискретных значениях угла) отражение лучей от систем узловых плоскостей, на которые может быть разбита решетка.
Ясно, что пространственная решетка кристалла может быть разбита на семейства узловых плоскостей самыми разными путями. На картине проекции «освобожденной» от атомов решетки легко показать следы узловых плоскостей, перпендикулярных к плоскости чертежа (рис. 4). Мы изобразили всего лишь пять семейств плоскостей. Однако эффективными для избирательного отражения, сущность которого будет описана ниже, являются несколько десятков, а то и сотен плоскостей.
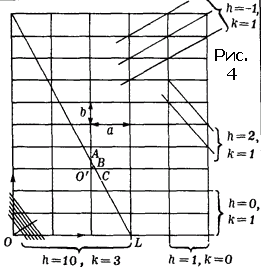
Каждая система плоскостей характеризуется индексами h и k. Их смысл иллюстрируется на примере семейства с индексами h=10 и k=3 (см. рис. 4). Чтобы не загромождать чертеж, мы построили шесть ближайших к узлу O плоскостей и провели еще одну, обозначенную L. Плоскость L является ближайшей к узлу O, отсекающей целое число периодов a и b по обеим осям решетки. Эти целые числа равны 3 по одной оси и 10 по другой. Проходя через ячейку O’, плоскость L отсекает 1/10 долю периода a и 1/3 периода b. Смысл индексов h и k становится очевидным. Предоставляем вам самим составить фразу такого типа, как любят математики: «Индексами h и k называются…».
Системы плоскостей характеризуются также межплоскостным расстоянием d. Плоскость L – ближайшая к узлу O’, поэтому |O’B|=d. Отрезки |O’A| и |O’C| можно записать, как b/k и a/h. Поскольку
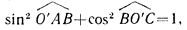
получим
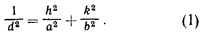
(Предлагаем вам решить превосходную задачу, которая займет у вас не один час времени – выведите аналогичную формулу для трехмерной решетки, ячейка которой является косоугольным параллелепипедом.)
Переходим к выводу основного закона селективного (избирательного) отражения рентгеновских лучей кристаллом. Пусть падающий луч, представляющий собой электромагнитную волну определенной длины ?, падает на кристалл под каким-то углом. Мы вправе полагать, что отражение рентгеновской волны будет происходить по закону: угол падения равен углу отражения, то есть по такому же закону, как и для оптического луча. Но имеется существенное различие с оптическим лучом. Луч света не проникает в глубь кристалла, а рентгеновский луч способен пройти сквозь кристалл. Это означает, что отражение рентгеновского луча будет происходить не только от внешней поверхности кристалла, а от всех его атомных плоскостей.
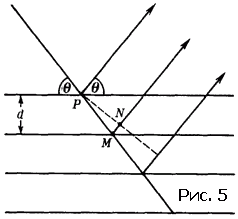
Рассмотрим одну из систем, характеризующихся межплоскостным расстоянием d (рис. 5). Каждая из плоскостей будет отражать падающий луч под одним и тем же углом ? (так называемый угол дифракции). Эти отраженные лучи когерентны, а потому долждны интерферировать между собой. Причем вторичные (отраженные) лучи будут усиливать друг друга в том случае, если после отражения от всех плоскостей семейства они будут распространяться в одной фазе. Иными словами, если разность хода между лучами равняется целому числу n длин волн. Разность хода |PM|+|MN| (см. рис. 5) между соседними отраженными лучами равна 2d sin ? (докажите!). Следовательно условие дифракции – условие усиления отраженных лучей – будет иметь вид
2d sin ? = n? (2)
Оно носит название уравнения Брэгга.
Кристалл, как мы уже сказали, можно разбить на системы плоскостей бесконечным числом способов. Но эффективной для отражения (теперь вам понятен смысл этих слова, не правда ли?) окажется лишь система плоскостей с таким межплскостным расстоянием и ориентированная так по отношению к падающему лучу, чтобы выполнялось уравнение Брэгга.
Если падающий луч монохроматический (то есть электромагнитная волна имеет одну определенную длину), то при произвольном положении кристалла по отношению к лучу отражение может и не произойти (вернее, суммарный эффект множества отражений может оказаться нулевым). Однако, поворачивая кристалл, мы можем по очереди привести в отражающее положение различные системы плоскостей. Именно такой способ работы и оказался на практике наиболее подходящим.
Из уравнения Брэгга (уравнение (2)) следует, что для заданной длины волны существует минимальное значение расстояния d между плоскостями, при котором возможно селективное отражение. Это расстояние ?/2 (поскольку синус не может быть больше единицы). С другой стороны, из приведенной выше формулы межплоскостных расстояний (формула (1)) ясно, что наибольшим значениям d соответствуют самые малые значения h и k.
Большей частью при рентгеноструктурном анализе используется одна из длин волн характеристического излучения меди, а именно 1,54 ангстрема[1]. Тогда наименьшие межплоскостным расстояния, способные принять участие в создании дифракционной картины, равны 0,77 ангстрема. Располагая этими сведениями, можно оценить, сколько систем плоскостей дадут отражения, если известны периоды решетки a и b. Попробуйте решить эту задачу геометрически для a=10 и b=20 ангстремам.
Для этой цели надо провести окружность радиуса 1/? в пространстве (в нашем двумерном случае – в плоскости) «обратной» решетки. И далее подсчитать число… (чего, догадайтесь). Но что такое «обратная» решетка и зачем нам понадобилось это новое понятие?
В нашем случае обратной решеткой называется решетка, ячейка которой есть прямоугольник со сторонами 1/a и 1/b. Как видите, прилагательное «обратная» вполне уместно. На рисунке 6 построена такая решетка. Выберем начало координат в каком-либо узле и проведем оси координат – одну перпендикулярно к оси кристалла, по которой период равен a, вторую перпендикулярно к оси с периодом b. Проведем теперь в этой решетке вектор (он так и называется: вектор обратной решетки), соединяющий начало отсчета с узлом обратной решетки, номер которого 10-й по одной оси, и 3-й по другой. Чему равна длина этого вектора? Возвратимся к уравнению (1) для межплоскостного расстояния и без труда и с интересом заметим, что длина вектора равна 1/d для системы плоскостей с h=10 и k=3.
Но этого мало. Легко доказать (докажите), что проведенный вектор обратной решетки перпендикулярен к системе плоскостей, для которых h=10, k=3. И, конечно, это справедливо для любого узла номера h, k. А как будет обстоять дело, если номер узла содержит кратный множитель n? Ответ очевиден – в этом случае длина вектора обратной решетки будет равняться n/d.
Вот теперь мы располагаем всеми неободимыми сведениями для того, чтобы вернуться к опыту. В чем же состоит эксперимент? Кристалл устанавливается на специальный держатель так, чтобы одна из его осей (одно из ребер его элементарной ячейки) была вертикальной, и поворачивается около этой оси. Таким способом мы по очереди подставляем в «отражающее» положение все системы узловых плоскостей кристалла. Для того чтобы «поймать» отраженный луч, можно прибегнуть либо к фотографическом методу, либо использовать ионизационную камеру, счетчик Гейгера или иной прибор, регистрирующий ионизирующее излучение.
Сейчас, разумеется, все это делается автоматически, а в то время, когда пишущий эти строки начинал работать, процедура была такой. Устанавливался кристалл, затем приемник вторичного луча проворачивался во всем диапазоне улов. Глаз следил при этом за показывающим ток прибором. Потом кристалл поворачивался, скажем, на один градус, и далее эти действия повторялись до тех пор, пока мы не «натыкались» на отраженный луч. При этом, как ясно из рисунка 7, фиксировались два угла – значение брэгговского угла ? и положение нормали к отражающей плоскости (по отношению к какому-либо произвольному началу отсчета).
Перед исследователем лежал лист бумаги, и он начинал строить обратную решетку. Откладывал положение нормали к отражающей плоскости и наносил на линию этой нормали значение n/d, которое однозначно определялось из уравнения Брэгга. Когда эта работа заканчивалась (в старое доброе время она занимала месяцы, а сейчас автоматический дифрактометр выполняет ее в сотни раз быстрее), физик обретал картину обратной решетки. Из ее ячейки он немедленно выяснял размеры ячейки кристалла, а каждому отражению мог приписать номер узла обратной решетки, а значит, индексы h и k и порядок отражения n.
Кроме того, исследователю известны интенсивности всех отражений. Таким образом, в его распоряжении имеются практически все сведения о структуре кристалла, всё, что касается характера строения молекулы из атомов и кристалла из молекул.
Теперь нам надо перейти от «пустой» решетки, состоящей из одних узлов, к решетке, начиненной атомами. На каких деталях дифракционной картины сказывается структура ячейки? Ответ окажется следующим: структура ячейки влияет на интенсивность отраженных лучей. Что же касается геометрии дифракционной картины, то она определяется только видом решетки. Атомы внутри ячейки не добавляют «лишних» отраженных лучей. В то же время вполне возможно, что структура ячейки заставит пропасть некоторые отражения – доведет их интенсивность до нуля.
Откуда следует такое заключение? Дело в том, что атомы внутри ячейки не создадут новых систем плоскостей. Узор атомов приведет лишь к возникновению «вставных» плоскостей. Взгляните, на рисунке 8 изображена та же решетка, что и на рисунке 4. Но теперь она не «пустая». Выберем опять предельно простой случай. Предположим, что реальная решетка построена из двухатомных молекул, а узел решетки был взят в центре такой молекулы. Реальная система плоскостей (для примера взят случай h=2 и k=1) будет выглядеть теперь, как и показано на рисунке 8. Отраженный луч пойдет в ту же сторону, брэгговский угол не изменится.
Покажем, что интенсивность отраженного луча будет зависеть от структуры ячейки – в данном случае от межатомного расстояния в молекуле и от угла, который образует ось молекулы с осью ячейки.
Интенсивность излучения пропорциональна квадрату амплитуды волны. Действительно, пусть в точке наблюдения поле, создаваемое решеткой атомов, записывается как A cos ?t. Интенсивность равна
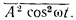
Черточка сверху означает усреднение по времени (колебания происходят быстро, и опыт фиксирует средние значения). Но
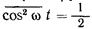
(это несложно доказать). Поэтому интенсивность оказывается пропорциональной A? – квадрату амплитуды волны.
В случае решетки двухатомных молекул результирующее поле электромагнитной волны можно рассматривать как сумму полей двух простых решеток. Эти два поля придут в точку наблюдения со сдвигом фаз, который мы обозначим 2?. Сохраняя выражение A cos ?t для решетки узлов, мы запишем теперь сумму полей двух решеток в виде
A cos (?t+?)+A cos (?t-?).
Каждый узел «расщепился» на две частицы, создающие одно поле с опережением по фазе, а другое с отставанием. Складывая, возводя в квадрат и усредняя по времени, мы получим, что интенсивность отраженного луча будет пропорциональна cos??.
По определению,
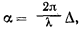
где ? – длина волны, а ? – разность хода. Хотя вывод выражения для разности хода ? ничуть не отличается от вывода формулы Брэгга, мы все же для этого случая провели аккуратное построение на рисунке 9, из которого читатель, слегка помучившись, найдет нужное выражение:
? = |OC| + |OD| = 2rn sin ?.
Где rn – проекция радиуса-вектора
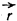
(соединяющего атомы молекулы) на направлением распространения отраженной волны (на направление нормали
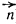
), ? – брэгговский угол рассеяния. Используем уравнение Брэгга и определение обратного вектора:
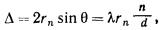
откуда разность фаз
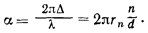
Итак, интенсивность отраженной волны, пропорциональная cos??, действительно определяется структурой элементарной ячейки кристалла. Очевидно, что если атомов в ячейке не два, а много, то все рассуждения будут аналогичными.
Что же… задача решена? Интенсивности дифрагированных лучей связаны со структурой в общем-то простой формулой: расчет интенсивностей отраженных лучей по заданной структуре не сложен. Дело сводится к тому, чтобы определить разности хода между волнами, отраженными всеми «вставными» решетками. Вы можете справиться с этой задачей и для кристалла, состоящего из сотни атомов. Вопрос лишь во времени.
Но читатель, несомненно, заметил, что расчет, о котором идет речь, не тот, который нам нужен. Задача состоит в нахождении атомного строения из данных опыта, а не в том, чтобы расчитать дифракционную картину, исходя из сведений о структуре. Прямая задача намного сложнее обратной. Интенсивность пропорциональна квадрату амплитуды результирующей волны, которая есть сумма тригонометрических функций. Не только технически сложно, но и просто невозможно определить аргументы косинусов, зная лишь квадрат их сумм. Вот если бы опыт давал значения амплитуд рассеяния, тогда дело обстояло бы совсем просто.
На первый взгляд ситуация кажется безнадежной. Долгое время исследователи действовали так называемым методом проб и ошибок. Это значит: придумывали структуру и смотрели, сочетается ли она с опытом. Но так далеко не уедешь.
Были придуманы способы обойти эту трудность. Решающую роль при этом сыграли электронно-вычислительные машины. Хотелось бы дать читателю идею о том, как эта трудность обходится, но разговор наш о рентгеноструктурном анализе затянулся. «Маленькие хитрости», к которым прибегают исследователи, это, во-первых, введение в структуру тяжелого атома (тогда в первом приближении можно считать, что кристалл состоит из одних этих атомов) и, во-вторых, очень изящная теория, которая показывает, что между разными структурными амплитудами имеются связи.
Да, хорошо было бы рассказать об этом читателю, но для «Кванта» беседа была бы слишком длинной. Посему ничего не остается, как посоветовать интересующемуся читателю обратиться к специальной литературе.
Об успехах метода судят по его результатам. То обстоятельство, что на сегодня определены структуры более 15 тысяч кристаллов, в том числе несколько десятков структуро белков, молекулы которых состоят из многих тысяч атомов, говорит само за себя. Определение структуры сложных молекул закладывает фундамент биологической химии и биолоической физики. Эти науки находятся сейчас в бурном периоде развития. От них ждут открытия секретов жизни, болезней и смерти. Рентгеноструктурный анализ, несмотря на свой солидный шестидесятипятилетний возраст, остается на передней линии фронта науки.
From Wikipedia, the free encyclopedia

(Top) Diamond crystal structure, depicting an atomic spacing of 0.154 nm. (Bottom) Graphite crystal structure, depicting an atomic spacing of 0.142 nm.
Atomic spacing refers to the distance between the nuclei of atoms in a material. This space is extremely large compared to the size of the atomic nucleus, and is related to the chemical bonds which bind atoms together.[1] In solid materials, the atomic spacing is described by the bond lengths of its atoms. In ordered solids, the atomic spacing between two bonded atoms is generally around a few ångströms (Å), which is on the order of 10−10 meters. However, in very low density gases (for example, in outer space) the average distance between atoms can be as large as a meter. In this case, the atomic spacing isn’t referring to bond length.
The atomic spacing of crystalline structures is usually determined by passing an electromagnetic wave of known frequency through the material, and using the laws of diffraction to determine its atomic spacing. The atomic spacing of amorphous materials (such as glass) varies substantially between different pairs of atoms, therefore diffraction cannot be used to accurately determine atomic spacing. In this case, the average bond length is a common way of expressing the distance between its atoms.
Example[edit]
Bond length can be determined between different elements in molecules by using the atomic radii of the atoms. Carbon bonds with itself to form two covalent network solids.[2] Diamond’s C-C bond has a distance of Sqrt[3]a/4 ≈ 0.154 nm away from each carbon since adiamond ≈ 0.357 nm, while graphite’s C-C bond has a distance of a/Sqrt[3] ≈ 0.142 nm away from each carbon since agraphite ≈ 0.246 nm. Although both bonds are between the same pair of elements they can have different bond lengths.[3]
References[edit]
- ^ Kittel, Charles (2004-11-11). Introduction to Solid State Physics (8th ed.). Wiley. ISBN 047141526X.
- ^ Rossi, Miriam. “How can graphite and diamond be so different if they are both composed of pure carbon?”. Scientific American. Scientific American. Retrieved October 9, 2007.
- ^ Brown; Lemay; Bursten (1997). Chemistry the Central Science. Upper Saddle River, NJ: Simon and Schuster. pp. 412–413.
Чтобы разобраться в вопросе, что в современной науке называется радиусом атома, вспомним, что из себя представляет сам атом. По классическим представлениям в центре атома находится ядро, состоящее из протонов и нейтронов, а вокруг ядра каждый на своей орбите вращаются электроны.
Содержание:
- Радиус атома в физике
- Атомный радиус в химии и кристаллографии
- Какие бывают виды
- Как зависит от типа химической связи
- Видео
Радиус атома в физике
Поскольку в данной модели строения атома электроны являются пространственно ограниченными частицами, т. е. корпускулами, логично считать атомным радиусом (а. р.) расстояние от его ядра до самой дальней, или внешней, орбиты, по которой вращаются так называемые валентные электроны.
Однако по современным, квантовомеханическим представлениям, определить данный параметр нельзя так однозначно, как это делается в классической модели. Здесь электроны уже не представляются в виде частиц-корпускул, а получают свойства волн, т. е. пространственно-неограниченных объектов. В такой модели точно определить положение электрона просто невозможно. Здесь эта частица уже представляется в виде электронной орбитали, плотность которой меняется, в зависимости от расстояния до ядра атома.
Итак, в современной модели строения атома его радиус нельзя определить однозначно. Поэтому в квантовой физике, общей химии, физике твердого тела и других смежных науках эту величину сегодня определяют как радиус сферы, в центре которой находится ядро, внутри которой сосредоточено 90-98% плотности электронного облака. Фактически это расстояние и определяет границы атома.
Если рассмотреть Периодическую таблицу химических элементов (таблицу Менделеева), в которой приведены атомные радиусы, можно увидеть определенные закономерности, которые выражаются в том, что в пределах периода эти числа уменьшаются слева направо, а в пределах группы они увеличиваются сверху вниз. Такие закономерности объясняются тем, что внутри периода при движении слева направо заряд атома возрастает, что увеличивает силу притяжения им электронов, а при движении внутри группы сверху вниз все больше заполняется электронных оболочек.
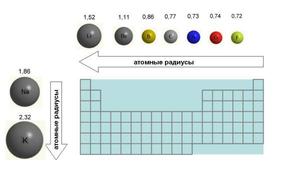
Атомный радиус в химии и кристаллографии
Какие бывают виды
Данная характеристика сильно варьируется, в зависимости от того, в какой химической связи состоит атом. Поскольку все вещества в природе в подавляющем своем большинстве состоят из молекул, понятие а. р. используют для определения межатомных расстояний в молекуле. А данная характеристика зависит от свойств входящих в молекулу атомов, т. е. их положения в Периодической системе химических элементов. Обладая разными физическими и химическими свойствами, молекулы образуют все огромное разнообразие веществ.
По сути, эта величина очерчивает сферу действия силы электрического притяжения ядра атома и его внешних электронных оболочек. За пределами этой сферы в действие вступает сила электрического притяжения соседнего атома. Существует несколько типов химической связи атомов в молекуле:
- ковалентная;
- ионная;
- металлическая;
- ван-дер-ваальсова.
Соответственно этим связям таким же будет и атомный радиус.
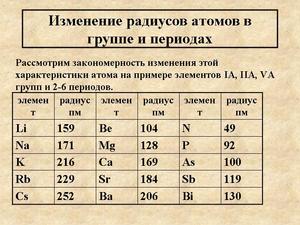
Как зависит от типа химической связи
При ковалентной связи АР определяется как половина расстояния между соседними атомами в одинарной химической связи Х—Х, причем Х — это неметалл, ибо данная связь свойственна неметаллам. Например, для галогенов ковалентный радиус будет равен половине межъядерного расстояния Х—Х в молекуле Х2, для молекул селена Se и серы S — половине расстояния Х—Х в молекуле Х8, для углерода С он будет равен половине кратчайшего расстояния С—С в кристалле алмаза.
Данная химическая связь обладает свойством аддитивности, т. е. суммирования, что позволяет определять межъядерные расстояния в многоатомных молекулах. Если связь в молекуле двойная или тройная, то ковалентный АР уменьшается, т. к. длины кратных связей меньше одинарных.
При ионной связи, образующейся в ионных кристаллах, используют значения ионного АР для определения расстояния между ближайшими анионом и катионом, находящимися в узлах кристаллической решетки. Такое расстояние определяется как сумма радиусов этих ионов.
Существует несколько способов определения ионных радиусов, при которых отличаются значения у индивидуальных ионов. Но в результате эти способы дают примерно одинаковые значения межъядерных расстояний. Эти способы или системы были названы в честь ученых, проводивших в этой области соответствующие исследования:
- Гольдшмидта;
- Полинга;
- Белова и Бокия;
- других ученых.
При металлической связи, возникающей в кристаллах металлов, АР принимаются равными половине кратчайшего расстояния между ними. Металлический радиус зависит от координационного числа К. При К=12 его значение условно принимается за единицу. Для координационных чисел 4, 6 и 8 металлические радиусы одного и того же элемента соответственно будут равны 0.88, 0.96 и 0.98.
Если взять два разных металла и сравнить металлические радиусы их элементов, то близость этих значений друг к другу будет означать необходимое, но недостаточное условие взаимной растворимости этих металлов по типу замещения. Например, жидкие калий К и литий Li в обычных условиях не смешиваются и образуют два жидких слоя, потому что их металлические радиусы сильно различаются (0.236 нм и 0.155 нм соответственно), а калий К с цезием Cs образуют твердый раствор благодаря близости их радиусов (0.236 нм и 0.268 нм).

Ван-дер-ваальсовы АР используют для определения эффективных размеров атомов благородных газов, а также расстояний между ближайшими одноименными атомами, принадлежащими разным молекулам и не связанными химической связью (пример — молекулярные кристаллы). Если такие атомы сблизятся на расстояние, меньшее суммы их ван-дер-ваальсовых радиусов, между ними возникнет сильное межатомное отталкивание. Эти радиусы определяют минимально допустимые границы контакта двух атомов, принадлежащих соседним молекулам.
Кроме того, данные АР используют для определения формы молекул, их конформаций и упаковки в молекулярных кристаллах. Известен принцип “плотной упаковки”, когда молекулы, образующие кристалл, входят друг в друга своими “выступами” и “впадинами”. На основе этого принципа интерпретируются данные кристаллографии и предсказываются структуры молекулярных кристаллов.
Видео
Это полезное видео поможет вам понять, что такое радиус атома.
