ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ ГОРОДА МОСКВЫ
Государственное бюджетное образовательное учреждение
среднего профессионального образования города Москвы
ПИЩЕВОЙ КОЛЛЕДЖ № 33
Методические рекомендации
для составления Контрольно-оценочных средств
по дисциплине/междисциплинарному курсу
ЕН.01 Математика
по дисциплине/ профессиональному модулю
15.02.06 Монтаж и техническая эксплуатация холодильно-компрессорных
машин и установок (по отраслям)
по специальности/профессии
2015
Работа с учебно-планирующей документацией
и разработка КОС
– КОС для текущего контроля знаний, умений обучающихся (могут разрабатываться разделам и темам учебных дисциплин;
– КОС для промежуточной аттестации обучающихся (могут разрабатываться по учебной дисциплине)
Формирование КОС для текущего контроля знаний, умений обучающихся, их промежуточной аттестации может осуществляться по двум направлениям:
– корректировка и адаптация имеющихся оценочных материалов с учётом компетентностного подхода к результатам обучения;
– разработка новых оценочных материалов.
Разработка оценочных материалов для включения в КОС ведётся с учётом:
– форм проведения оценочных мероприятий (устный опрос, зачёт, экзамен; письменная контрольная работа, зачёт, экзамен и т. п., тестирование, в т. ч. компьютерное).
– уровней освоения учебного материала темы (ознакомительный, репродуктивный, продуктивный);
– видов деятельности, которые будут выполнять обучающиеся в процессе оценочных мероприятий (осознанное воспроизведение информации, применение информации, анализ, синтез, оценка);
– обучающих возможностей оценочных материалов;
– возможности принятия решения об освоении обучающимися профессиональных компетенций
КОСы, собранные в единый ФОС по учебной дисциплине, рассматриваются и утверждаются на заседании предметной (цикловой) комиссии.
В состав КОС разработчики должны включать как простые, так и сложные задания.
К простым относятся задания, которые выполняются в одно или два действие. К ним можно отнести:
– тестовые задания с выбором ответа в закрытой форме, на установление соответствия в закрытой форме или на установление правильной последовательности в закрытой форме;
– простые ситуационные задачи с коротким ответом или простым действием;
– простые задания по воспроизведению текста, решения или действия и т. п.
Они предполагают выполнение обучающимися простых действий по изложению знаний понятий, определений, терминов, законов, формул и т. п. с пониманием смысла изученного материала, либо по применению информации для решения задач; применение (фактов, правил, теорий, приёмов, методов) в конкретных ситуациях, соблюдение принципов и законов.
К сложным (комплексным) заданиям могут быть отнесены задания, требующие многоходовых решений, как в стандартной, так и в нестандартной ситуациях.
К ним можно отнести:
– задания в открытой форме, требующие поэтапного решения и развернутого ответа, в т. ч. тестовые,
– задания на индивидуальное или коллективное выполнение проектов, практических действий на тренажерах, станках, манекенах и т. п.
Они предполагают выполнение обучающимися сложных действий по разделению информации на взаимозависимые части, выявлению взаимосвязей между ними, осознанию принципов организации целого и т. п.; по интерпретации результатов, творческому преобразованию информации из разных источников, созданию продукта/гипотезы, системного объяснения/решения и иной новой информации, объясняющей явление или событие, предсказывающей что-либо и т. п.; по оценке значения объекта/явления для конкретной цели, определению и высказыванию суждения о целостности идеи/метода/теории на основе проникновения в суть явлений и их сравнения, и т. п.
При формировании КОС для промежуточной аттестации обучающихся по учебной дисциплине рекомендуется включать задания, требующие от обучающихся выполнения как простых, так и сложных действий.
Для проверки комплексных умений и компетенций в ходе промежуточной аттестации, в т. ч. при проведении экзамена (квалификационного) рекомендуется применять сложные задания.
В состав КОС входят материалы обеспечивающие оценку результатов контроля. К ним относятся: критерии оценки показателей результатов обучения, эталоны решений заданий, ключи к тестам и т. п.
Критерий оценки показателей результатов обучения – признак (основание, правило) для принятия решения о соответствии результатов освоения компетенций, усвоения знаний, освоения умений предъявленным требованиям ФГОС.
Оценивание результатов должно проводиться по специально установленной шкале. Шкала определяет систему пересчёта суммы баллов (суммы веса критериев), полученных обучающимися в ходе оценочных мероприятий и правила принятия решения об итоговой оценке. Тематика курсовой работы (проекта); требования к её (его) структуре и оформлению могут быть включены в состав КОС для текущего контроля по учебной дисциплине/профессиональному модулю.
ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ ГОРОДА МОСКВЫ
Государственное бюджетное образовательное учреждение
среднего профессионального образования города Москвы
ПИЩЕВОЙ КОЛЛЕДЖ № 33
Комплект
контрольно-оценочных средств
по учебной дисциплине/междисциплинарному курсу
наименование
программа подготовки квалифицированных рабочих и служащих
код и наименование специальности (по ФГОС СПО)
(на базе …..)
для промежуточной аттестации
2015
ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ ГОРОДА МОСКВЫ
Государственное бюджетное образовательное учреждение
среднего профессионального образования города Москвы
ПИЩЕВОЙ КОЛЛЕДЖ № 33
Комплект
контрольно-оценочных средств
по учебной дисциплине
ЕН.01 Математика
наименование
программы подготовки специалистов среднего звена
15.02.06 Монтаж и техническая эксплуатация холодильно-компрессорных
машин и установок
(по отраслям)
(на базе основного полного образования)
для промежуточной аттестации
2015
|
СОГЛАСОВАНО: Предметная (цикловая) комиссия Протокол № ____ «__» _________ 20___ г. Председатель ПЦК _______________/ Л.Е.Бакулина / Подпись Ф.И.О. |
УТВЕРЖДАЮ: Зам. директора по У и УМР _______________/Т.В. Журкина/ |
Составитель(и) : ________________________________________________________________
Ф.И.О., ученая степень, должность с указанием квалификационной категории (при наличии)
________________________________________________________________
Ф.И.О., ученая степень, должность с указанием квалификационной категории (при наличии)
1. Общие положения
Контрольно-оценочные средства (КОС) являются составной частью основной профессиональной образовательной программы среднего профессионального образования по подготовке квалифицированных рабочих, служащих 15.02.06 Монтаж и техническая эксплуатация холодильно-компрессорных машин и установок (по отраслям) на базе основного полного образования и предназначены для контроля и оценки образовательных достижений обучающихся, освоивших программу учебной дисциплины ЕН.01 «Математика».
КОС включают контрольные материалы для проведения промежуточной аттестации в форме зачета.
КОС разработаны на основании:
- Положения о Фонде оценочных средств (ФОС);
- Рекомендаций по разработке контрольно-оценочных средств (КОС);
- Рабочей программы учебной дисциплины.
- Результаты освоения дисциплины, подлежащие проверке
КОС для промежуточной аттестации направлены на проверку и оценивание результатов обучения, знаний и умений:
|
Результаты обучения (освоенные умения, усвоенные знания) |
Коды формируемых профессиональных и общих компетенций |
Основные показатели оценки |
№ заданий, включенных в КОС |
|
Умение анализировать сложные функции и строить их графики |
ПК 1.4, 1.1 ОК 4 |
умеет анализировать сложные функции и строить их графики |
4 |
|
Умение выполнять действия над комплексными числами |
ПК 1.3 ОК 5 |
умеет выполнять действия над комплексными числами |
6 |
|
Умение вычислять значения геометрических величин |
ПК 1.3 ОК 8 |
умеет вычислять значения геометрических величин |
1 |
|
Умение производить операции над матрицами и определителями |
ПК 1.2,3.2 ОК 4 |
умеет производить операции над матрицами и определителями |
1, 2 |
|
Умение решать задачи на вычисление вероятности с использованием элементов комбинаторики |
ПК 3.1 ОК 8 |
умеет решать задачи на вычисление вероятности с использованием элементов комбинаторики |
11 |
|
Умение решать прикладные задачи с использованием элементов дифференциального и интегрального исчислений |
ПК 1.4, 2.2 ОК 5 |
умеет решать прикладные задачи с использованием элементов дифференциального и интегрального исчислений |
10, 12 |
|
Умение решать системы линейных уравнений различными методами |
ПК 1.3, 2.1 ОК 5 |
умеет решать системы линейных уравнений различными методами |
3 |
|
Знание основных математических методов решения прикладных задач |
ПК 3.1,3.3 ОК 5 |
знает основные математические методы решения прикладных задач |
5, 9 |
|
Знание основных понятий и методов математического анализа, линейной алгебры, теории комплексных чисел, теории вероятностей и математической статистики |
ПК 3.3 ОК 8 |
знает основные понятия и методы математического анализа, линейной алгебры, теории комплексных чисел, теории вероятностей и математической статистики |
7, 8 |
3. Распределение КОС по темам учебной дисциплины
|
Содержание учебного материала по программе |
Практические |
|
Ведение. Тема 1. Элементы линейной алгебры |
2, |
|
Тема 2. Дифференциальное и интегральное исчисление |
4, 9, 10,16, 21, 22 |
|
Тема3. Комплексные числа |
6, 7, 8, 18, 19, 20 |
|
Тема 4.Теория вероятностей |
|
|
Тема 5. Математическая статистика |
11, 23 |
4. Содержание КОС (заполняем только те виды заданий, которые присутствуют у нас)
4.1. Тестовые задания (Т).
БЛАНК ТЕСТОВОГО ЗАДАНИЯ
|
Варианты ответов |
||
|
|
Выберите один правильный ответ: Если все элементы одной строки прямоугольной матрицы А размерности n x m умножить на два то ранг матрицы А а) увеличится на 2; б) не изменится; в) увеличится в два раза. |
1 |
|
|
Выполните решение и выберите один правильный ответ: Значение определителя а) 11; б) 4; в) 5; г) 3 |
1 |
|
|
Выполните решение и выберите один правильный ответ: Пусть х и у решения системы а) 4; б) 7; в) 5; г) 6. |
1 |
|
|
Выполните решение и выберите один правильный ответ: Инте а) 5х-2+С ; б) 5х-1+С; в) 5х+С; г) 5 |
1 |
|
|
Выполните решение и выберите один правильный ответ: Вычислите: |
1 |
|
|
Выберите один правильный ответ: Что представляет собой число i: а) число, квадратный корень из которого равен -1; б) число, квадрат которого равен -1; в) число, квадратный корень из которого равен 1; г) число, квадрат которого равен 1; |
1 |
|
|
Выберите один правильный ответ: Число а) |
2 |
|
|
Выберите один правильный ответ: Говорят, что комплексное число z = r(cosφ + isinφ) записано в: а) арифметической форме; б) геометрической форме; в) векторной форме; г) тригонометрической (аргументной) форме. |
2 |
|
|
Выполните решение и выберите один правильный ответ: Применяя формулу Ньютона-Лейбница, найти чему равен данный определенный интеграл: |
2 |
|
|
Допишите предложение. Неопределенный интеграл суммы равен сумме неопределенных интегралов: а) утверждение верно; б) утверждение неверно; в) утверждение верно не всегда г) утверждение верно иногда. |
2 |
|
|
Допишите предложение: Генеральная совокупность – |
2 |
|
|
Выполните решение: Вычислите вторую производную функции |
2 |
|
|
Выберите один правильный ответ: Если все элементы одной строки прямоугольной матрицы А размерности n x m умножить на три то ранг матрицы А а) увеличится на 3; б) увеличится в три раза; в) не изменится |
1 |
|
|
Допишите предложение: Вероятность произведения независимых событий равна |
2 |
|
|
Выполните решение и выберите один правильный ответ: Значение определителя а) 1; б) 2; в) -2; г) 3 |
1 |
|
|
Выполните решение и выберите один правильный ответ: Пусть х и у решения системы а) 4; б) 0; в) 5; г) 6 |
1 |
|
|
Выполните решение и выберите один правильный ответ: Инте а) 7х-2+С ; б) 7х-1+С ; в) 7х+С ; г) |
1 |
|
|
Выполните решение и выберите один правильный ответ: Вычислите: а) 1; б) 2; в) 5; г) 3. |
1 |
|
|
Выберите один правильный ответ: Как на координатной плоскости изображается комплексное число: а) в виде отрезка; б) точкой или радиус-вектором; в) плоской геометрической фигуры; г) в виде круга. |
1 |
|
|
Выберите один правильный ответ: Число а) |
2 |
|
|
Выберите один правильный ответ: Говорят, что комплексное число z = r(cosφ + isinφ) записано в: а) тригонометрической (аргументной) форме; б) геометрической форме; в) векторной форме; г) арифметической форме. |
2 |
|
|
Выполните решение и выберите один правильный ответ: Применяя формулу Ньютона-Лейбница, найти чему равен данный определенный интеграл: |
2 |
|
|
Допишите предложение. Неопределенный интеграл разности равен разности неопределенных интегралов: а) утверждение неверно; б) утверждение верно; в) утверждение верно не всегда г) утверждение верно иногда |
2 |
|
|
Допишите предложение: Выборочная совокупность (выборка) – это |
2 |
|
|
Выполните решение: Вычислите вторую производную функции |
2 |
|
|
Допишите предложение: Вероятность суммы двух несовместных событий равна |
2 |
5. Описание процедуры проведения промежуточной аттестации
Зачет проводится за счет аудиторных часов, отведенных на дисциплину. Время проведения зачета 90 минут. Студент получает один из 2 вариантов контрольных заданий, проштампованные листы для черновика и основной работы. В черновике рекомендуют выполнять задания непоследовательно, без промежуточных вычислений, пропускать задание, которое не удается выполнить сразу, и переходить к следующему. К выполнению пропущенных заданий советуют вернуться позже, если останется время. В основной работе (чистовике) требуется выполнение решения с написанием всех применяемых формул, со всеми вычислениями и логическими пояснениями.
5.1 Время на подготовку и выполнение:
подготовка 5 мин.;
выполнение 80 мин.;
оформление и сдача 5 мин.;
всего 1 часа 30 мин.
6. Эталоны ответов
|
|
в |
|
|
а |
|
|
б |
|
|
в |
|
|
б |
|
|
б |
|
|
г |
|
|
г |
|
|
а |
|
|
в |
|
|
совокупность всех исследуемых объектов |
|
|
14 |
|
|
произведению вероятностей этих событий |
|
|
б |
|
|
б |
|
|
в |
|
|
г |
|
|
г |
|
|
б |
|
|
2 |
|
|
|
|
|
б |
|
|
г |
|
|
совокупность случайно отобранных объектов |
|
|
12 |
|
|
сумме вероятностей этих событий |
7. Критерии оценки:
Задания целесообразно сначала выполнять на черновиках, а потом оформлять всю работу на листах.
Задания 1, 2, 3, 4, 5, 6 – оценивается 1 баллом, задания 7, 8, 9, 10, 11, 12, 13– 2 балла.
В задании 1, 2, 3, 4, 5, 6 нужно выбрать один правильный ответ.
Задания 7, 8, 9, 10 выполняются с решением (или объяснением), потом записывается ответ.
Результаты:
«5» – 19-20 баллов
«4» – 16-18 баллов
«3» – 11-15 баллов
«2» – 10 баллов и меньше
7. Перечень материалов, оборудования и информационных источников, используемых при проведении промежуточной аттестации
На зачете студенту можно пользоваться ручкой, карандашом и линейкой.
8. Приложение:
варианты зачетных заданий
Приложение 1
Варианты зачетных заданий
Вариант 1
|
Выберите один правильный ответ: 1. Если все элементы одной строки прямоугольной матрицы А размерности n x m умножить на два то ранг матрицы А а) увеличится на 2; б) не изменится; в) увеличится в два раза. |
|
|
Выполните решение и выберите один правильный ответ: 2. Значение определителя а) 11; б) 4; в) 5; г) 3 |
|
|
Выполните решение и выберите один правильный ответ: 3. Пусть х и у решения системы а) 4; б) 7; в) 5; г) 6. |
|
|
Выполните решение и выберите один правильный ответ: 4. Инте а) 5х-2+С ; б) 5х-1+С; в) 5х+С; г) 5 |
|
|
Выполните решение и выберите один правильный ответ: 5. Вычислите: |
|
|
Выберите один правильный ответ: 6. Что представляет собой число i: а) число, квадратный корень из которого равен -1; б) число, квадрат которого равен -1; в) число, квадратный корень из которого равен 1; г) число, квадрат которого равен 1; |
|
|
Выберите один правильный ответ: 7.Число а) |
|
|
Выберите один правильный ответ: 8. Говорят, что комплексное число z = r(cosφ + isinφ) записано в: а) арифметической форме; б) геометрической форме; в) векторной форме; г) тригонометрической (аргументной) форме. |
|
|
Выполните решение и выберите один правильный ответ: 9. Применяя формулу Ньютона-Лейбница, найти чему равен данный определенный интеграл: |
|
|
Допишите предложение: 10. Неопределенный интеграл суммы равен сумме неопределенных интегралов: а) утверждение верно; б) утверждение неверно; в) утверждение верно не всегда г) утверждение верно иногда. |
|
|
Допишите предложение: 11. Генеральная совокупность – |
|
|
Выполните решение: 12. Вычислите вторую производную функции |
|
|
Допишите предложение: Вероятность произведения независимых событий равна. |
Вариант 2
|
Выберите один правильный ответ: 1. Если все элементы одной строки прямоугольной матрицы А размерности n x m умножить на три то ранг матрицы А а) увеличится на 3; б) увеличится в три раза; в) не изменится |
|
Выполните решение и выберите один правильный ответ: 2. Значение определителя а) 1; б) 2; в) -2; г) 3 |
|
Выполните решение и выберите один правильный ответ: 3. Пусть х и у решения системы а) 4; б) 0; в) 5; г) 6 |
|
Выполните решение и выберите один правильный ответ: 4. Инте а) 7х-2+С ; б) 7х-1+С ; в) 7х+С ; г) |
|
Выполните решение и выберите один правильный ответ: 5.Вычислите: а) 1; б) 2; в) 5; г) 3. |
|
Выберите один правильный ответ: 6. Как на координатной плоскости изображается комплексное число: а) в виде отрезка; б) точкой или радиус-вектором; в) плоской геометрической фигуры; г) в виде круга. |
|
Выберите один правильный ответ: 7. Число а) |
|
Выберите один правильный ответ: 8. Говорят, что комплексное число z = r(cosφ + isinφ) записано в: а) тригонометрической (аргументной) форме; б) геометрической форме; в) векторной форме; г) арифметической форме. |
|
Выполните решение и выберите один правильный ответ: 9.Применяя формулу Ньютона-Лейбница, найти чему равен данный определенный интеграл: |
|
Допишите предложение. 10. Неопределенный интеграл разности равен разности неопределенных интегралов: а) утверждение неверно; б) утверждение верно; в) утверждение верно не всегда г) утверждение верно иногда |
|
Допишите предложение: 11. Выборочная совокупность (выборка) – это |
|
Выполните решение: 12. Вычислите вторую производную функции |
|
Допишите предложение: Вероятность суммы двух несовместных событий равна |
Бюджетное образовательное учреждение Чувашской Республики
среднего профессионального образования
«Чебоксарский электромеханический колледж»
Министерства образования и молодежной политики Чувашской Республики
Комплект
контрольно–оценочных средств
учебной дисциплины
ЕН.01. Математика
основной образовательной программы (ОПОП)
по направлению подготовки (специальности)
151901 Технология машиностроения
Разработал:
Методист БОУ СПО ЧЭМК
Киреева Наталия Владимировна
Чебоксары, 2012
1. Общие положения
Контрольно–оценочные средства (КОС) предназначены для контроля и
оценки образовательных достижений обучающихся, освоивших программу
учебной дисциплины Математика.
КОС включают контрольные материалы для проведения текущего
контроля и промежуточной аттестации в форме экзамена (комплексного).
КОС разработаны на основании положений:
основной профессиональной образовательной программы по
направлению подготовки ВПО (специальности СПО) 151901 Технология
машиностроения;
программы учебной дисциплины Математика.
2. Результаты освоения дисциплины, подлежащие проверке
Результаты обучения
(освоенные умения, усвоенные
знания)
Основные показатели оценки результатов
Умение решать задачи
математического анализа, линейной
алгебры и аналитической геометрии
– Выполнение действий над матрицами
– Вычисление определителей
– Решение систем линейных уравнений
методом обратной матрицы
– Решение систем линейных уравнений по
формулам Крамера
– Решение систем линейных уравнений
методом Гаусса
– Выполнение действий над векторами
– Нахождение скалярного, векторного и
смешанного произведения векторов
– Построение точек и нахождение их
координат в прямоугольной декартовой и
полярной системах координат
– Вычисление предела функции в точке и в
бесконечности
– Исследование функции на непрерывность в
точке
– Нахождение производной функции
– Нахождение производных высших порядков
– Исследование функции и построение
графика
– Нахождение неопределенных интегралов
– Вычисление определенных интегралов
– Нахождение частных производных
– Исследование рядов на сходимость
Умение применять различные
методы для решения обыкновенных
дифференциальных уравнений и их
систем
– Решение дифференциальных уравнений
первого и второго порядка
Умение решать вероятностные и
статистические задачи
– Нахождение вероятности случайного
события
– Составление закона распределения
случайной величины
– Вычисление числовых характеристик
случайных величин
Знание основных методов
математического анализа,
аналитической геометрии, линейной
алгебры, элементарной теории
вероятностей
– Перечисление последовательности действий
при решении систем линейных уравнений
методом обратной матрицы, по формулам
Крамера, методом Гаусса
– Формулировка определений и перечисление
свойств скалярного, векторного и
смешанного произведения векторов
– Классификация точек разрыва
– Формулировка правил дифференцирования
и перечисление производных основных
элементарных функций
– Перечисление табличных интегралов
– Формулировка классического определения
вероятности
Знание математических моделей
простейших систем и процессов в
естествознании и технике
– Формулировка геометрического и
механического смысла производной
– Приложение определенного интеграла к
вычислению площадей плоских фигур,
объемов тел вращения, пути, пройденного
точкой
– Описание процессов в естествознании и
технике с помощью дифференциальных
уравнений
3. Распределение оценивания результатов обучения по видам контроля
Наименование элемента умений или
знаний
У 1. Умение решать задачи
математического анализа, линейной
алгебры и аналитической геометрии
У 2. Умение применять различные
методы для решения обыкновенных
дифференциальных уравнений и их
систем
У 3. Умение решать вероятностные и
статистические задачи
З 1. Знание основных методов
математического анализа,
аналитической геометрии, линейной
алгебры, элементарной теории
вероятностей
устный ответ – 3
расчетное задание – 2
З 2. Знание математических моделей
простейших систем и процессов в
естествознании и технике
устный ответ – 1
расчетное задание – 2
4. Распределение типов контрольных заданий по элементам знаний и
умений.
Содержание
учебного материала
по программе УД
Раздел 1. Элементы линейной алгебры и аналитической геометрии
Тема 1.1. Решение систем линейных
уравнений
Тема 1.2. Векторы и координаты
Раздел 2. Введение в математический анализ
Тема 2.1. Функции,
последовательности, пределы
расчетное
задание
6.4
расчетное
задание
6.5
Раздел 3. Дифференциальное исчисление функций одной переменной
Тема 3.1. Техника
дифференцирования
Тема 3.2. Применение
дифференциального исчисления для
исследования функций и
построения их графиков
Раздел 4. Интегральное исчисление функции одной переменной
Тема 4.1. Неопределенный интеграл
и его свойства
Тема 4. 2. Определенный интеграл
Раздел 5. Функции нескольких переменных
Тема 5.1. Дифференцирование
функции нескольких переменных
Раздел 6. Обыкновенные дифференциальные уравнения
Тема 6.1. Дифференциальные
уравнения 1 порядка
Тема 6.2. Дифференциальные
уравнения 2 порядка
Раздел 7. Числовые и функциональные ряды
Тема 7.2. Функциональные ряды
Раздел 8. Элементы теории вероятностей и математической статистики
Тема 8.1. Основные теоремы теории
вероятностей
Тема 8.2. Случайные величины и их
законы распределения
5. Распределение типов и количества контрольных заданий по
элементам знаний и умений, контролируемых на промежуточной
аттестации.
Содержание
учебного
материала
по программе УД
Раздел 1. Элементы линейной алгебры и аналитической геометрии
Тема 1.1. Решение
систем линейных
уравнений
экзаменационный
вопрос (устный
ответ) – 6
Тема 1.2. Векторы и
координаты
экзаменационный
вопрос (устный
ответ) – 4
Раздел 2. Введение в математический анализ
Тема 2.1. Функции,
последовательности,
пределы
экзаменационное
задание
(расчетное
задание) – 7
экзаменационный
вопрос (устный
ответ) – 3
Раздел 3. Дифференциальное исчисление функций одной переменной
Тема 3.1. Техника
дифференцирования
экзаменационное
задание
(расчетное
задание) – 5
экзаменационный
вопрос (устный
ответ) – 1
экзаменационный
вопрос (устный
ответ) – 1
Тема 3.2.
Применение
дифференциального
исчисления для
исследования
функций и
построения их
графиков
экзаменационное
задание
(расчетное
задание) – 1
экзаменационный
вопрос (устный
ответ) – 2
Раздел 4. Интегральное исчисление функции одной переменной
Тема 4.1.
Неопределенный
интеграл и его
свойства
экзаменационное
задание
(расчетное
задание) – 5
экзаменационный
вопрос (устный
ответ) – 3
Тема 4. 2.
Определенный
интеграл
экзаменационное
задание
(расчетное
задание) – 6
экзаменационный
вопрос (устный
ответ) – 2
экзаменационный
вопрос (устный
ответ) – 2
Раздел 5. Функции нескольких переменных
Тема 5.1.
Дифференцирование
функции нескольких
переменных
экзаменационный
вопрос (устный
ответ) – 1
Раздел 6. Обыкновенные дифференциальные уравнения
Тема 6.1.
Дифференциальные
уравнения 1 порядка
экзаменационное
задание
(расчетное
задание) – 2
экзаменационный
вопрос (устный
ответ) – 2
экзаменационный
вопрос (устный
ответ) – 1
Тема 6.2.
Дифференциальные
уравнения 2 порядка
экзаменационное
задание
(расчетное
задание) – 1
Раздел 7. Числовые и функциональные ряды
экзаменационный
вопрос (устный
ответ) – 4
Тема 7.2.
Функциональные
ряды
экзаменационный
вопрос (устный
ответ) – 1
Раздел 8. Элементы теории вероятностей и математической статистики
Тема 8.1. Основные
теоремы теории
вероятностей
экзаменационное
задание
(расчетное
задание) – 1
экзаменационный
вопрос (устный
ответ) – 2
Тема 8.2. Случайные
величины и их
законы
распределения
экзаменационное
задание
(расчетное
задание) – 2
экзаменационный
вопрос (устный
ответ) – 2
6. Структура контрольного задания
6.1. Расчетное задание
6.1.1. Текст задания
Вариант 1
1. Найти матрицу C=A+3B, если
.
2. Решить систему линейных уравнений методом обратной матрицы.
3. Решить систему линейных уравнений по формулам Крамера.
4. Решить систему линейных уравнений методом Гаусса.
.723
,52
,12
321
321
321
xxx
xxx
xxx
Вариант 2
1. Найти матрицу C=2A-B, если
.
2. Решить систему линейных уравнений методом обратной матрицы.
3. Решить систему линейных уравнений по формулам Крамера.
4. Решить систему линейных уравнений методом Гаусса.
.532
,72
,22
321
321
321
xxx
xxx
xxx
Вариант 3
1. Найти матрицу C=3A+B, если
.
2. Решить систему линейных уравнений методом обратной матрицы.
3. Решить систему линейных уравнений по формулам Крамера.
4. Решить систему линейных уравнений методом Гаусса.
.32
,74
,423
321
321
321
xxx
xxx
xxx
Вариант 4
1. Найти матрицу C=A-4B, если
.
2. Решить систему линейных уравнений методом обратной матрицы.
3. Решить систему линейных уравнений по формулам Крамера.
4. Решить систему линейных уравнений методом Гаусса.
.42
,63
,32
321
321
321
xxx
xxx
xxx
Вариант 5
1. Найти матрицу C=4A-B, если
.
2. Решить систему линейных уравнений методом обратной матрицы.
3. Решить систему линейных уравнений по формулам Крамера.
4. Решить систему линейных уравнений методом Гаусса.
.1073
,32
,23
321
321
321
xxx
xxx
xxx
Вариант 6
1. Найти матрицу C=A+2B, если
.
2. Решить систему линейных уравнений методом обратной матрицы.
3. Решить систему линейных уравнений по формулам Крамера.
4. Решить систему линейных уравнений методом Гаусса.
.132
,12
,3
321
321
321
xxx
xxx
xxx
6.1.2. Время на выполнение: 60 мин.
6.1.3. Перечень объектов контроля и оценки
Наименование объектов
контроля и оценки
Основные показатели
оценки результата
У 1. Умение решать задачи
математического анализа,
линейной алгебры и
аналитической геометрии
– Выполнение действий
над матрицами
– Вычисление
определителей
– Решение систем
линейных уравнений
методом обратной
матрицы
– Решение систем
линейных уравнений по
формулам Крамера
– Решение систем
линейных уравнений
методом Гаусса
З 1. Знание основных методов
математического анализа,
аналитической геометрии,
линейной алгебры, элементарной
теории вероятностей
– Перечисление
последовательности
действий при решении
систем линейных
уравнений методом
обратной матрицы, по
формулам Крамера,
методом Гаусса
За правильный ответ на вопросы или верное решение задачи
выставляется положительная оценка – 1 балл.
За неправильный ответ на вопросы или неверное решение задачи
выставляется отрицательная оценка – 0 баллов.
6.2. Устный ответ
6.2.1. Текст задания
1. Дать определение вектора.
2. Дать определение проекции вектора на ось и перечислить ее свойства.
3. Дать определение скалярного произведения векторов и перечислить его
свойства.
4. Дать определение векторного произведения векторов и перечислить его
свойства.
5. Дать определение смешанного произведения векторов и перечислить
его свойства.
6.2.2. Время на выполнение: 20 мин.
6.2.3. Перечень объектов контроля и оценки
Наименование объектов
контроля и оценки
Основные показатели
оценки результата
З 1. Знание основных методов
математического анализа,
аналитической геометрии,
линейной алгебры, элементарной
теории вероятностей
– Формулировка
определений и
перечисление свойств
скалярного, векторного и
смешанного
произведения векторов
За правильный ответ на вопросы или верное решение задачи
выставляется положительная оценка – 1 балл.
За неправильный ответ на вопросы или неверное решение задачи
выставляется отрицательная оценка – 0 баллов.
6.3. Расчетное задание
6.3.1. Текст задания
Вариант 1
Даны векторы
.
5. Найти координаты векторов
.
6. В прямоугольной декартовой системе координат построить точки A (0; 0),
B (3; -4), C (-3; 4). Определить расстояние между точками A и B, B и C, A и C.
7. Построить точки, заданные полярными координатами: A (2; /2), B (3; /4),
C (3; 3/4).
8. Даны точки в полярной системе координат A (2; /4), B (4; /2). Найти их
прямоугольные координаты.
Вариант 2
Даны векторы
.
5. Найти координаты векторов
6. В прямоугольной декартовой системе координат построить точки A (0; 0),
C (-3; 4), D (-2; 2) E (10; -3). Определить расстояние между точками C и D, A и
D, D и E.
7. Построить точки, заданные полярными координатами: A (4; 0), B (2; 3/2),
C (3; ).
8. Даны точки в прямоугольной системе координат A (0; 5), B (-3; 0), C (
; 1).
Найти их полярные координаты.
6.3.2. Время на выполнение: 70 мин.
6.3.3. Перечень объектов контроля и оценки
Наименование объектов
контроля и оценки
Основные показатели
оценки результата
У 1. Умение решать задачи
математического анализа,
линейной алгебры и
аналитической геометрии
– Выполнение действий
над векторами
– Нахождение
скалярного, векторного и
смешанного
произведения векторов
– Построение точек и
нахождение их
координат в
прямоугольной
декартовой и полярной
системах координат
За правильный ответ на вопросы или верное решение задачи
выставляется положительная оценка – 1 балл.
За неправильный ответ на вопросы или неверное решение задачи
выставляется отрицательная оценка – 0 баллов.
6.4. Расчетное задание
6.4.1. Текст задания
Вариант 1
1. Вычислить предел функции:
.
2. Вычислить предел функции:
.
3. Вычислить предел функции:
.
4. Вычислить предел функции:
.
Вариант 2
1. Вычислить предел функции:
.
2. Вычислить предел функции:
.
3. Вычислить предел функции:
.
4. Вычислить предел функции:
.
Вариант 3
1. Вычислить предел функции:
.
2. Вычислить предел функции:
.
3. Вычислить предел функции:
.
4. Вычислить предел функции:
.
Вариант 4
1. Вычислить предел функции:
.
2. Вычислить предел функции:
3. Вычислить предел функции:
.
4. Вычислить предел функции:
.
Вариант 5
1. Вычислить предел функции:
.
2. Вычислить предел функции:
.
3. Вычислить предел функции:
.
4. Вычислить предел функции:
.
Вариант 6
1. Вычислить предел функции:
.
2. Вычислить предел функции:
.
3. Вычислить предел функции:
.
4. Вычислить предел функции:
6.4.2. Время на выполнение: 40 мин.
6.4.3. Перечень объектов контроля и оценки
Наименование объектов
контроля и оценки
Основные показатели
оценки результата
У 1. Умение решать задачи
математического анализа,
линейной алгебры и
аналитической геометрии
– Вычисление предела
функции в точке и в
бесконечности
За правильный ответ на вопросы или верное решение задачи
выставляется положительная оценка – 1 балл.
За неправильный ответ на вопросы или неверное решение задачи
выставляется отрицательная оценка – 0 баллов.
6.5. Расчетное задание
6.5.1. Текст задания
Вариант 1
Исследовать функцию
.
Вариант 2
Исследовать функцию
.
Вариант 3
Исследовать функцию
.
6.5.2. Время на выполнение: 10 мин.
6.5.3. Перечень объектов контроля и оценки
Наименование объектов
контроля и оценки
Основные показатели
оценки результата
У 1. Умение решать задачи
математического анализа,
линейной алгебры и
аналитической геометрии
– Исследование функции
на непрерывность в
точке
З 1. Знание основных методов
математического анализа,
аналитической геометрии,
линейной алгебры, элементарной
теории вероятностей
– Классификация точек
разрыва
За правильный ответ на вопросы или верное решение задачи
выставляется положительная оценка – 1 балл.
За неправильный ответ на вопросы или неверное решение задачи
выставляется отрицательная оценка – 0 баллов.
6.6. Расчетное задание
6.6.1. Текст задания
Вариант 1
1. Найти производную функции
.
2. Найти производную третьего порядка функции
.
3. Написать уравнение касательной к графику функции
.
4. Материальная точка движется по закону
. Найти скорость
и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
Вариант 2
1. Найти производную функции
.
2. Найти производную третьего порядка функции
.
3. Написать уравнение касательной к графику функции
.
4. Материальная точка движется по закону
. Найти скорость и
ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
Вариант 3
1. Найти производную функции
.
2. Найти производную третьего порядка функции
.
3. Написать уравнение касательной к графику функции
.
4. Материальная точка движется по закону
. Найти скорость и
ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
Вариант 4
1. Найти производную функции
.
2. Найти производную третьего порядка функции
.
3. Написать уравнение касательной к графику функции
.
4. Материальная точка движется по закону
. Найти скорость и
ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
Вариант 5
1. Найти производную функции
.
2. Найти производную третьего порядка функции
3. Написать уравнение касательной к графику функции
.
4. Материальная точка движется по закону
. Найти скорость и
ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
Вариант 6
1. Найти производную функции
.
2. Найти производную третьего порядка функции
.
3. Написать уравнение касательной к графику функции
.
4. Материальная точка движется по закону
. Найти скорость и
ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
6.6.2. Время на выполнение: 40 мин.
6.6.3. Перечень объектов контроля и оценки
Наименование объектов
контроля и оценки
Основные показатели
оценки результата
У 1. Умение решать задачи
математического анализа,
линейной алгебры и
аналитической геометрии
– Нахождение
производной функции
– Нахождение
производных высших
порядков
З 2. Знание математических
моделей простейших систем и
процессов в естествознании и
технике
– Формулировка
геометрического и
механического смысла
производной
За правильный ответ на вопросы или верное решение задачи
выставляется положительная оценка – 1 балл.
За неправильный ответ на вопросы или неверное решение задачи
выставляется отрицательная оценка – 0 баллов.
6.7. Устный ответ
6.7.1. Текст задания
Сформулировать правила дифференцирования и записать производные основных
элементарных функций:
ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ
ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ
6.7.2. Время на выполнение: 15 мин.
6.7.3. Перечень объектов контроля и оценки
Наименование объектов
контроля и оценки
Основные показатели
оценки результата
З 1. Знание основных методов
математического анализа,
аналитической геометрии,
линейной алгебры,
элементарной теории
вероятностей
– Формулировка правил
дифференцирования и
перечисление
производных основных
элементарных функций
За правильный ответ на вопросы или верное решение задачи
выставляется положительная оценка – 1 балл.
За неправильный ответ на вопросы или неверное решение задачи
выставляется отрицательная оценка – 0 баллов.
6.8. Расчетное задание
6.8.1. Текст задания
Исследовать функцию и построить ее график.
Вариант 1
6.8.2. Время на выполнение: 20 мин.
6.8.3. Перечень объектов контроля и оценки
Наименование объектов
контроля и оценки
Основные показатели
оценки результата
У 1. Умение решать задачи
математического анализа,
линейной алгебры и
аналитической геометрии
– Исследование функции
и построение графика
За правильный ответ на вопросы или верное решение задачи
выставляется положительная оценка – 1 балл.
За неправильный ответ на вопросы или неверное решение задачи
выставляется отрицательная оценка – 0 баллов.
6.9. Расчетное задание
6.9.1. Текст задания
Вариант 1
Найти неопределенные интегралы методом непосредственного интегрирования
(для № 1-5).
1.
.
Найти неопределенные интегралы методом подстановки (для № 6-8).
6.
.
9. Найти неопределенный интеграл методом интегрирования по частям:
.
Вариант 2
Найти неопределенные интегралы методом непосредственного интегрирования
(для № 1-5).
1.
.
Найти неопределенные интегралы методом подстановки (для № 6-8).
6.
.
9. Найти неопределенный интеграл методом интегрирования по частям:
.
6.9.2. Время на выполнение: 60 мин.
6.9.3. Перечень объектов контроля и оценки
Наименование объектов
контроля и оценки
Основные показатели
оценки результата
У 1. Умение решать задачи
математического анализа,
линейной алгебры и
аналитической геометрии
– Нахождение
неопределенных
интегралов
За правильный ответ на вопросы или верное решение задачи
выставляется положительная оценка – 1 балл.
За неправильный ответ на вопросы или неверное решение задачи
выставляется отрицательная оценка – 0 баллов.
6.10. Устный ответ
6.10.1. Текст задания
Записать табличные интегралы:
1
о
.
6.10.2. Время на выполнение: 10 мин.
6.10.3. Перечень объектов контроля и оценки
Наименование объектов
контроля и оценки
Основные показатели
оценки результата
З 1. Знание основных методов
математического анализа,
аналитической геометрии,
линейной алгебры,
элементарной теории
вероятностей
– Перечисление
табличных интегралов
За правильный ответ на вопросы или верное решение задачи
выставляется положительная оценка – 1 балл.
За неправильный ответ на вопросы или неверное решение задачи
выставляется отрицательная оценка – 0 баллов.
6.11. Расчетное задание
6.11.1. Текст задания
Вариант 1
1. Вычислить определенный интеграл:
.
2. Вычислить определенный интеграл методом подстановки:
.
3. Вычислить, предварительно сделав рисунок, площадь фигуры, ограниченной
линиями:
4. Найти объем тела, полученного при вращении вокруг оси абсцисс
криволинейной трапеции, ограниченной линиями:
.
5. Скорость движения точки изменяется по закону
(м/с). Найти
путь S, пройденный точкой за 10 с от начала движения.
Вариант 2
1. Вычислить определенный интеграл:
.
2. Вычислить определенный интеграл методом подстановки:
.
3. Вычислить, предварительно сделав рисунок, площадь фигуры, ограниченной
линиями:
.
4. Найти объем тела, полученного при вращении вокруг оси абсцисс
криволинейной трапеции, ограниченной линиями:
.
5. Скорость движения точки изменяется по закону
(м/с). Найти путь S,
пройденный точкой за четвертую секунду.
6.11.2. Время на выполнение: 40 мин.
6.11.3. Перечень объектов контроля и оценки
Наименование объектов
контроля и оценки
Основные показатели
оценки результата
У 1. Умение решать задачи
математического анализа,
линейной алгебры и
аналитической геометрии
– Вычисление
определенных
интегралов
З 2. Знание математических
моделей простейших систем и
процессов в естествознании и
технике
– Приложение
определенного интеграла
к вычислению площадей
плоских фигур, объемов
тел вращения, пути,
пройденного точкой
За правильный ответ на вопросы или верное решение задачи
выставляется положительная оценка – 1 балл.
За неправильный ответ на вопросы или неверное решение задачи
выставляется отрицательная оценка – 0 баллов.
6.12. Расчетное задание
6.12.1. Текст задания
Вариант 1
Найти частные производные функций.
1.
.
Вариант 2
Найти частные производные функций.
1.
.
6.12.2. Время на выполнение: 25 мин.
6.12.3. Перечень объектов контроля и оценки
Наименование объектов
контроля и оценки
Основные показатели
оценки результата
У 1. Умение решать задачи
математического анализа,
линейной алгебры и
аналитической геометрии
– Нахождение частных
производных
За правильный ответ на вопросы или верное решение задачи
выставляется положительная оценка – 1 балл.
За неправильный ответ на вопросы или неверное решение задачи
выставляется отрицательная оценка – 0 баллов.
6.13. Расчетное задание
6.13.1. Текст задания
Вариант 1
Являются ли данные функции решениями данных дифференциальных уравнений
(для № 1-4).
1.
054,
2
5
1
yyyececy
xx
02,
21
yyyxececy
xx
.
Решить следующие дифференциальные уравнения первого и второго порядка (для
№ 6-12).
.
Вариант 2
Являются ли данные функции решениями данных дифференциальных уравнений
(для № 1-4).
1.
044,
2
2
2
1
yyyxececy
xx
06,
2
3
1
yyyececy
xx
.
Решить следующие дифференциальные уравнения первого и второго порядка (для
№ 6-12).
6.
.
6.13.2. Время на выполнение: 80 мин.
6.13.3. Перечень объектов контроля и оценки
Наименование объектов
контроля и оценки
Основные показатели
оценки результата
У 2. Умение применять
различные методы для решения
обыкновенных
дифференциальных уравнений и
их систем
– Решение
дифференциальных
уравнений первого и
второго порядка
За правильный ответ на вопросы или верное решение задачи
выставляется положительная оценка – 1 балл.
За неправильный ответ на вопросы или неверное решение задачи
выставляется отрицательная оценка – 0 баллов.
6.14. Устный ответ
6.14.1. Текст задания
1. Сформулировать общие положения при составлении дифференциального
уравнения по условию задачи.
2. Записать дифференциальное уравнение показательного роста и показательного
убывания и получить его решение. Привести примеры прикладных задач,
решаемых с его помощью.
3. Сформулировать задачу о радиоактивном распаде, записать для нее
дифференциальное уравнение.
4. Сформулировать задачу о гармонических колебаниях, записать
дифференциальное уравнение гармонических колебаний.
5. Сформулировать задачу о падении тел в атмосферной среде, записать для нее
дифференциальное уравнение.
6.14.2. Время на выполнение: 30 мин.
6.14.3. Перечень объектов контроля и оценки
Наименование объектов
контроля и оценки
Основные показатели
оценки результата
З 2. Знание математических
моделей простейших систем и
процессов в естествознании и
технике
– Описание процессов в
естествознании и
технике с помощью
дифференциальных
уравнений
За правильный ответ на вопросы или верное решение задачи
выставляется положительная оценка – 1 балл.
За неправильный ответ на вопросы или неверное решение задачи
выставляется отрицательная оценка – 0 баллов.
6.15. Расчетное задание
6.15.1. Текст задания
1. Пользуясь необходимым признаком сходимости, показать, что ряд
расходится.
2. С помощью признака Даламбера решить вопрос о сходимости ряда
3. Пользуясь признаком Лейбница, исследовать на сходимость
знакочередующийся ряд
…
1
1…
4
1
3
1
2
1
1
1
n
n
4. Пользуясь признаком сходимости знакопеременного ряда, исследовать на
сходимость ряд
…
!
1
1…
!4
1
!3
1
!2
1
1
1
n
n
6.15.2. Время на выполнение: 30 мин.
6.15.3. Перечень объектов контроля и оценки
Наименование объектов
контроля и оценки
Основные показатели
оценки результата
У 1. Умение решать задачи
математического анализа,
линейной алгебры и
аналитической геометрии
– Исследование рядов на
сходимость
За правильный ответ на вопросы или верное решение задачи
выставляется положительная оценка – 1 балл.
За неправильный ответ на вопросы или неверное решение задачи
выставляется отрицательная оценка – 0 баллов.
6.16. Расчетное задание
6.16.1. Текст задания
1. Из корзины, в которой находятся 4 белых и 7 черных шара, вынимают один шар.
Найти вероятность того, что шар окажется черным.
2. Определить вероятность появления «герба» при бросании монеты.
3. В корзине 20 шаров: 5 синих, 4 красных, остальные черные. Выбирают наудачу
один шар. Определить, с какой вероятностью он будет цветным.
4. Событие А состоит в том, что станок в течение часа потребует внимания рабочего.
Вероятность этого события составляет 0,7. Определить, с какой вероятностью
станок не потребует внимания.
5. В одной корзине находятся 4 белых и 8 черных шаров, в другой – 3 белых и 9
черных. Из каждой корзины вынули по шару. Найти вероятность того, что оба
шара окажутся белыми.
6. Бросают две монеты. Определить, с какой вероятностью появится «герб» на обеих
монетах.
7. В лотерее 100 билетов. Разыгрывается один выигрыш в 200 рублей и двадцать
выигрышей по 50 рублей. Пусть Х – величина возможного выигрыша для человека,
имеющего один билет. Составить закон распределения этой случайной величины
Х.
8. Случайная величина Х задана законом распределения:
Найти ее математическое ожидание.
9. Согласно статистике, вероятность того, что двадцатипятилетний человек проживет
еще год, равно 0,992. Компания предлагает застраховать жизнь на год на 1000 у.е. с
уплатой 10 у.е. взноса. Определить, какую прибыль ожидает компания от
страховки одного двадцатипятилетнего человека.
10. Случайная величина Х задана законом распределения:
Найти дисперсию и среднее квадратичное отклонение этой случайной величины Х.
11. Случайные величины X и Y заданы законом распределения. Найти математическое
ожидание этих случайных величин и определить по таблицам, какая из данных
величин более рассеяна. Подсчитать дисперсии D(X) и D(Y). Убедиться, что
D(X)>D(Y).
6.16.2. Время на выполнение: 45 мин.
6.16.3. Перечень объектов контроля и оценки
Наименование объектов
контроля и оценки
Основные показатели
оценки результата
У 3. Умение решать
вероятностные и статистические
задачи
– Нахождение
вероятности случайного
события
– Составление закона
распределения
случайной величины
– Вычисление числовых
характеристик
случайных величин
З 1. Знание основных методов
математического анализа,
аналитической геометрии,
линейной алгебры,
элементарной теории
вероятностей
– Формулировка
классического
определения
вероятности
За правильный ответ на вопросы или верное решение задачи
выставляется положительная оценка – 1 балл.
За неправильный ответ на вопросы или неверное решение задачи
выставляется отрицательная оценка – 0 баллов.
6.17. Экзаменационные вопросы
1. Матрицы, действия над матрицами.
2. Определители 1–го, 2–го, 3–го порядков. Правило треугольников.
3. Определители n-го порядка. Теорема Лапласа.
4. Обратная матрица. Алгоритм нахождения обратной матрицы.
5. Ранг матрицы. Алгоритм вычисления ранга матрицы с помощью элементарных
преобразований.
6. Система линейных уравнений. Метод обратной матрицы. Формулы Крамера.
Метод Гаусса.
7. Векторы и операции над ними.
8. Проекция вектора на ось и ее свойства.
9. Декартова прямоугольная система координат. Полярная система координат.
10. Скалярное, векторное и смешанное произведения векторов.
11. Предел функции в точке. Основные теоремы о пределах.
12. Предел функции при x, стремящемся к бесконечности. Замечательные пределы.
Число е.
13. Непрерывность функции в точке и на промежутке. Точка непрерывности функции.
Точка разрыва функции. Свойства непрерывных функций. Приращение аргумента.
Приращение функции.
14. Производная функции. Дифференциал функции. Геометрический смысл
производной. Механический смысл производной.
15. Таблица производных. Понятие сложной функции. Производная сложной функции.
16. Схема исследования функции. Область определения функции. Множество
значений функции. Четность и нечетность функции. Нули функции. Промежутки
знакопостоянства функции. Возрастание и убывание функции, правило
нахождения промежутков монотонности. Точки экстремума функции, правило
нахождения экстремумов функции.
17. Производные высших порядков. Физический смысл второй производной.
Исследование функции с помощью второй производной.
18. Первообразная. Неопределенный интеграл. Основные свойства неопределенного
интеграла.
19. Таблица неопределенных интегралов.
20. Методы интегрирования: метод непосредственного интегрирования; метод замены
переменной (метод подстановки); метод интегрирования по частям.
21. Определенный интеграл. Понятие интегральной суммы. Достаточное условие
существования определенного интеграла (интегрируемости функции).
22. Основные свойства определенного интеграла. Геометрический смысл
определенного интеграла.
23. Методы вычисления определенных интегралов. Формула Ньютона–Лейбница.
24. Геометрические и физические приложения определенного интеграла.
25. Функции нескольких переменных. Частные производные.
26. Понятие дифференциального уравнения. Общее и частное решение
дифференциального уравнения. Интегральные кривые. Задача Коши.
27. Задачи, приводящие к дифференциальным уравнениям.
28. Методы решения дифференциальных уравнений.
29. Понятие числового ряда. Сходимость и расходимость числовых рядов.
30. Необходимый признак сходимости ряда. Признак сравнения. Признак Даламбера.
31. Понятие знакочередующегося ряда. Признак сходимости Лейбница.
32. Абсолютная и условная сходимость знакопеременного ряда.
33. Функциональные ряды. Степенные ряды. Область сходимости степенного ряда.
Разложение элементарных функций в ряд Маклорена.
34. Понятие события. Достоверные, невозможные, совместные, несовместные,
противоположные события. Классическое определение вероятности.
35. Теорема сложения вероятностей. Теорема умножения вероятностей.
36. Случайная величина. Дискретная и непрерывная случайные величины. Закон
распределения дискретной случайной величины. Интегральная функция
распределения непрерывной случайной величины.
37. Математическое ожидание дискретной случайной величины. Отклонение
случайной величины. Дисперсия дискретной случайной величины. Среднее
квадратичное отклонение случайной величины.
6.18. Экзаменационные задания
1. Вычислить предел
.
2. Вычислить пределы:
а)
и построить ее график.
9. Вычислить значение производной следующих функций в точке
.
10. Найти производную функции
.
11. Найти производную функции
.
12. Найти производную функции
.
13. Найти производную функции
.
14. Найти неопределенный интеграл
.
15. Найти неопределенный интеграл методом замены переменной
.
16. Найти неопределенный интеграл методом замены переменной
.
17. Найти неопределенный интеграл методом замены переменной
.
18. Найти неопределенный интеграл методом замены переменной
.
19. Вычислить определенный интеграл
.
20. Вычислить определенный интеграл
.
21. Вычислить определенный интеграл
22. Скорость движения точки изменяется по закону
(м/с). Найти путь s,
пройденный точкой за 4 с от начала движения.
23. Вычислить объем тела, полученного от вращения фигуры, ограниченной линиями
, вокруг оси Ox.
24. Вычислить площадь фигуры, ограниченной линиями
.
25. Решить дифференциальное уравнение
.
26. Решить задачу Коши:
.
27. Решить дифференциальное уравнение
.
28. В одной корзине находятся 5 белых и 10 черных шаров, в другой – 4 белых и 11
черных. Из каждой корзины вынули по шару. Найти вероятность того, что оба
шара окажутся черными.
29. В лотерее 1000 билетов. Разыгрывается один выигрыш в 200 рублей и десять
выигрышей по 100 рублей. Пусть Х – величина возможного выигрыша для
человека, имеющего один билет. Составить закон распределения этой случайной
величины Х.
30. Случайная величина Х задана законом распределения:
Найти математическое ожидание, дисперсию, среднее квадратичное отклонение
этой случайной величины Х.
7. Шкала оценки образовательных достижений
Процент результативности (правильных
ответов)
8. Перечень материалов, оборудования и информационных источников,
используемых в аттестации
1. Гмурман, В.Е. Руководство по решению задач по теории
вероятностей и математической статистики. – М.: Высшее
образование, 2009.
2. Дадаян, А.А. Математика. – М.: ФОРУМ: ИНФРА, 2007.
3. Дадаян, А.А. Сборник задач по математике. – М.: ФОРУМ: ИНФРА,
2007.
Интернет ресурсы:
4. http://festival.1september.ru/
5. http://www.fepo.ru
6. www.mathematics.ru
Государственное бюджетное профессиональное образовательное учреждение
Иркутской области
«Черемховский техникум промышленной индустрии и сервиса»
|
Рассмотрены и одобрены на заседании методической комиссии преподавателей общеобразовательных дисциплин «_____»___сентября____2015 г. Протокол № ____1______ Председатель МК ___________________ Богданова В.А. |
Утверждаю Зам. директора ГБПОУ ИО ЧТПиС _______________С.Н. Дроботенко «_____»_____________2015 г |
.
КОНТРОЛЬНО-ОЦЕНОЧНЫЕ МАТЕРИАЛЫ
для проведения промежуточной и итоговой аттестации
по УД «Математика»
за период 2015-2016 учебного года
в группах 1 курса
профиля:
Разработчик:
Стефанцева Наталья Геннадьевна, преподаватель общественных дисциплин
ГБПОУ ИО ЧТПиС
Черемхово
2015
Содержание
I. Общие положения.
II. Паспорт комплекта контрольно-оценочных средств
III. Контрольно-измерительные материалы для проведения письменного экзамена в виде набора контрольных заданий
I. Общие положения
1. Пояснительная записка
1.1 Нормативная база
Комплект контрольно-оценочных средств для проведения промежуточной аттестации в форме экзамена по УД «Математика» разработан на основании нормативных документов:
-
ФГОС среднего (полного) общего образования в пределах ОПОП НПО/СПО с учетом профиля получаемого профессионального образования в соответствии с федеральными базисными учебными планами и примерными учебными планами для образовательных учреждений РФ, реализующих программы общего образования (приказ Минобразования России от 09.03.2004 г. № 1 312)
-
Рабочая программа учебной дисциплины Математика
-
Положение о текущем контроле знаний и промежуточной аттестации студентов НПО/СПО ГБПОУ ИО «Черемховский техникум промышленной индустрии и сервиса»
1.2 Общие положения
Экзамен по математике проводится за счет времени, выделяемого ФГОС НПО/СПО на промежуточную аттестацию.
Содержание экзаменационных материалов отвечает требованиям к уровню подготовки выпускников, предусмотренным государственным образовательным стандартом среднего (полного) общего образования и зафиксированным в примерной программе учебной дисциплины «Математика» для профессий НПО и специальностей СПО.
Экзамен по математике проводится с использованием экзаменационных материалов в виде набора контрольных заданий.
II. Паспорт комплекта контрольно-оценочных средств
2.1 Область применения
Комплект контрольно-оценочных средств предназначен для контроля и оценки образовательных достижений обучающихся, освоивших программу учебной дисциплины ОУД 03 Математика в рамках реализации федерального государственного образовательного стандарта по программам подготовки квалифицированных рабочих (служащих)
Профессия: Электро-газосварщик
Машинист локомотива
Технология продукции общественного питания
2.2. 2.Сводные данные об объектах оценивания, основных показателях оценки
Таблица№1
|
Результаты освоения учебных достижений (объекты оценивания) |
Основные показатели оценки результата |
|
У1. Решать рациональные, показательные, логарифмические, тригонометрические уравнения, сводящиеся к линейным и квадратным, а также аналогичные неравенства и системы; |
Выполнение:
выбор правильного ответа на числовой прямой использование свойств логарифмических функций; преобразование тригонометрических выражений |
|
У2. Умение находить производные элементарных функций; находить первообразную функции; вычислять в простейших случаях площади и объемы с использованием определенного интеграла; находить производные элементарных функций; использовать производную для изучения свойств функций и построения графиков; |
Применение
|
|
У3. Решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов); проводить доказательные рассуждения в ходе решения задач; описывать взаимное расположение прямых и плоскостей в пространстве. |
Выполнение правильного построения чертежа;
|
|
У4. Находить наименьшее и наибольшее значения функций; умение находить производную функции |
|
|
У5. Уметь решать иррациональные уравнения и логарифмические неравенства |
|
|
У6. Уметь выполнять арифметические действия над числами; находить значения корня, степени, логарифма, тригонометрических функций; находить число по проценту |
|
|
У7. Уметь выполнять преобразования выражений, применяя формулы, связанные со свойствами степеней, логарифмов, тригонометрических функций; |
|
|
У8. Уметь вычислять значение функции по заданному значению аргумента при различных способах задания функции; определять основные свойства числовых функций, строить графики функций, иллюстрировать по графику свойства элементарных функций; |
|
|
У9. Уметь описывать взаимное расположение прямых и плоскостей в пространстве, изображать основные многогранники и круглые тела; выполнять чертежи по условиям задач; |
|
|
У10. Уметь находить вероятности событий и элементы комбинаторики |
|
|
З 1.Знание свойства показательной и логарифмической функции |
– применение свойств степени, показательной функции, равносильности уравнений |
|
З 2.Знание теоретических основ начал математического анализа |
|
|
З 3. Знание формулировок аксиом и основных теорем и их следствий; понятия тела вращения: цилиндр, конус и шар; свойств перпендикуляра и наклонной; основных теорем планиметрии и стереометрии понятия объема тела |
|
|
З4. Знание понятия о числовых функциях и их основных свойствах, графиках функций. свойств и графиков степенной, показательной, логарифмической функций; |
|
|
З 5. Знание свойств иррациональных. показательных, логарифмических, тригонометрических уравнений и неравенств; Основных приемов решения уравнений и неравенств с одной и двумя переменными; |
|
|
З6. Знание обобщенного понятия о степени числа, корня n-степени из числа; преобразований степенных выражений; преобразований выражений, содержащих логарифмы; |
|
|
З7. Знание о производной функции, ее геометрическом и физическом смысле. правила вычисления производные элементарных функций;. уравнение касательной к графику функции исследования функций с помощью производной |
|
|
З8. Знание первообразной функции и определенного интеграла, формулы Ньютона – Лейбница; |
|
|
З8. Знание основ комбинаторики и теории вероятностей |
|
2.3 Содержание и структура экзаменационной работы
Письменная экзаменационная работа по учебной дисциплине ОУД 03. Математика состоит из 2-х частей: обязательной и дополнительной.
В обязательную часть включаются задания минимально обязательного уровня, в дополнительную часть – более сложные.
В обязательную часть работы включены задания базового уровня по всем основным разделам требований ФГОС – геометрия (планиметрия и стереометрия), алгебра, начала математического анализа, теория вероятностей, комбинаторика .
При выполнении заданий обязательной части обучающиеся должны продемонстрировать базовую математическую компетентность. Задания этой группы проверяют базовые вычислительные и логические умения и навыки, умение анализировать информацию, представленную в графиках и таблицах, использовать простейшие вероятностные и статистические модели, ориентироваться в простейших геометрических конструкциях, владение основными алгоритмами, знание и понимание ключевых элементов содержания (математических понятий, их свойств, приемов решения задач и пр.), умение пользоваться математической записью, а также применять математические знания в простейших практических ситуациях.
Обязательная часть содержит 19 заданий.
К каждому типу заданий прилагается инструкция по форме представления ответа.
Дополнительная часть направлена на проверку владения материалом на повышенном уровне и умение решать математические задачи, не сводящиеся к прямому применению алгоритма. Эта часть должна содержать не менее 4 заданий повышенного уровня сложности из различных разделов курса математики .
При выполнении всех заданий дополнительной части необходимо представить описание хода решения задачи и полученный ответ. Возможны различные способы решения в записи развернутого ответа. Главное требование – решение должно быть математически грамотным, из него должен быть понятен ход рассуждений автора работы. При этом оценивается продвижение обучающегося в решении задачи, а не недочеты по сравнению с «эталонным» решением. При решении задачи можно использовать любые математические факты без доказательств и ссылок, содержащиеся в учебниках и учебных пособиях, допущенных или рекомендованных Министерством образования и науки РФ.
Распределение заданий по частям экзаменационной работы с указанием первичных баллов представлено в таблице 2.
Таблица 2
|
Части работы |
Число заданий |
Максимальный первичный балл |
Тип заданий |
|
Часть 1 (обязательная) |
8 |
8 |
С выбором ответа С кратким ответом |
|
11 |
11 |
||
|
Часть 2 (дополнительная) |
7 |
14 |
С развёрнутым ответом |
|
Итого |
26 |
33 |
При подборе контрольных заданий для проведения экзамена использован перечень элементов содержания по математике.
Предлагаемый перечень элементов содержания и требований к уровню подготовки обучающихся составлен на основе Федерального компонента государственных стандартов основного общего и среднего (полного) общего образования по математике базового/профильного уровня (Приказ Минобразования России от 05.03.2004 г. № 1089 «Об утверждении федерального компонента государственных образовательных стандартов начального общего, основного общего и среднего (полного) общего образования» (в ред. Приказов Минобрнауки РФ от 03.06.2008 № 164 от 31.08.2009 № 320, от 19.10.2009 № 427).
Проверяемые элементы содержания
Таблица 3
|
Введение |
Математика в науке, технике, экономике, информационных технологиях и практической деятельности. |
|
Развитие понятия о числе |
Целые и рациональные числа. Действительные числа. |
|
Корни, степени и логарифмы |
Корни и степени. Корни натуральной степени из числа и их свойства. Степени с рациональными показателями, их свойства. Степени с действительными показателями. Логарифм. Логарифм числа. Основное логарифмическое тождество. Десятичные и натуральные логарифмы. Правила действий с логарифмами. Преобразование алгебраических, рациональных, иррациональных степенных, показательных и логарифмических выражений. |
|
Прямые и плоскости в пространстве |
Взаимное расположение двух прямых в пространстве. Параллельность прямой и плоскости. Параллельность плоскостей. Перпендикулярность прямой и плоскости. Перпендикуляр и наклонная. Угол между прямой и плоскостью. Двугранный угол. Угол между плоскостями. Перпендикулярность двух плоскостей. |
|
Элементы комбинаторики |
Основные понятия комбинаторики. Задачи на подсчет числа размещений, перестановок, сочетаний. Решение задач на перебор вариантов. Формула бинома Ньютона. Свойства биноминальных коэффициентов. Треугольник Паскаля. |
|
Координаты и векторы |
Прямоугольная (декартова) система координат в пространстве. Формула расстояния между двумя точками. Векторы. Модуль вектора. Равенство векторов. Сложение векторов. Умножение вектора на число. Разложение вектора по направлениям. Угол между двумя векторами. Проекция вектора на ось. Координаты вектора. Скалярное произведение векторов. |
|
Основы тригонометрии |
Радианная мера угла. Синус, косинус, тангенс и котангенс числа. Основные тригонометрические тождества, формулы приведения. Синус, косинус и тангенс суммы и разности двух углов. Синус и косинус двойного угла. Преобразования простейших тригонометрических выражений. Простейшие тригонометрические уравнения. Решение тригонометрических уравнений. |
|
Функции, их свойства и графики. Степенные, показательные, логарифмические и тригонометрические функции |
Функции. Область определения и множество значений; график функции, построение графиков функций, заданных различными способами. Свойства функции: монотонность, четность, нечетность, ограниченность, периодичность. Промежутки возрастания и убывания, наибольшее и наименьшее значения, точки экстремума. Графики |
|
Многогранники |
Вершины, ребра, грани многогранника. Призма. Прямая и наклонная призма. Правильная призма. Параллелепипед. Куб. Пирамида. Правильная пирамида. Тетраэдр. Симметрии в кубе, в параллелепипеде. Сечения куба, призмы и пирамиды. Представление о правильных многогранниках. |
|
Тела и поверхности вращения |
Цилиндр и конус. Основание, высота, боковая поверхность, образующая, развертка. Осевые сечения и сечения, параллельные основанию. Шар и сфера, их сечения. |
|
Начала математического анализа |
Последовательности. Способы задания и свойства числовых последовательностей. Понятие о производной функции, её геометрический и физический смысл. Уравнение касательной к графику функции. Производные суммы, разности, произведения, частного. Производные основных элементарных функций. Применение производной к исследованию функций и построению графиков. Примеры использования производной для нахождения наилучшего решения в прикладных задачах. Применение производной к исследованию функций и построению графиков. Нахождение скорости для процесса, заданного формулой и графиком. Первообразная и интеграл. Применение определенного интеграла для нахождения площади криволинейной трапеции. Формула Ньютона—Лейбница. Примеры применения интеграла в физике и геометрии. |
|
Измерения в геометрии |
Объем и его измерение. Формулы объема куба, прямоугольного параллелепипеда, призмы, цилиндра. Формулы объема пирамиды и конуса. Формулы площади поверхностей цилиндра и конуса. Формулы объема шара и площади сферы. Подобие тел. Отношения площадей поверхностей и объемов подобных тел. |
|
Элементы теории вероятностей. Элементы математической статистики |
Событие, вероятность события, сложение и умножение вероятностей. Представление данных (таблицы, диаграммы, графики), генеральная совокупность, выборка, среднее арифметическое, медиана. |
|
Уравнения и неравенства |
Равносильность уравнений, неравенств, систем. Рациональные, иррациональные, показательные и тригонометрические уравнения, неравенства и их системы. Основные приемы их решения. Использование свойств и графиков функций при решении уравнений и неравенств. Метод интервалов. |
2.3.Процедура проведения экзамена.
На выполнение письменной экзаменационной работы отводится 240 минут.
Для проведения экзамена по математике с использованием экзаменационных материалов в виде набора контрольных заданий каждому обучающемуся выдаётся:
– текст с одним из четырех вариантов письменной экзаменационной работы;
– инструкция по выполнению экзаменационной работы;
– лист для черновика.
Все задания обучающийся выполняет на листах с печатной основой
Перед началом выполнения письменной экзаменационной работы (время не входит в 4 астрономических часа) преподаватель контролирует заполнение личных данных обучающихся, знакомит обучающихся со структурой экзаменационной работы, с критериями оценивания еѐ результатов.
Обучающимся поясняется, что экзаменационная работа состоит из двух частей: обязательной и дополнительной. В обязательную часть включены задания минимально обязательного уровня, а в дополнительную часть – более сложные. Выполнение каждого из заданий оценивается в баллах. Количество баллов, которое можно получить за правильное выполнение того или иного задания, проставлено в скобках рядом с его номером. Баллы, полученные за все выполненные задания, суммируются.
Шкала перевода баллов в отметки по пятибалльной системе показывает, сколько баллов необходимо набрать, чтобы получить отметку «3», «4» или «5». Шкала остаётся открытой для обучающихся в течение всего экзамена, они могут ориентироваться на неё в ходе выполнения экзаменационной работы. Обучающиеся могут просчитать при помощи шкалы, сколько и какие задания необходимо выполнить правильно, чтобы получить определённую отметку.
Обучающиеся должны начинать выполнение экзаменационной работы с заданий обязательной части. Для получения удовлетворительной отметки необязательно выполнять минимум 15 заданий обязательной части, но только после выполнения достаточного для получения удовлетворительной отметки количества заданий обязательной части обучающийся может переходить к заданиям дополнительной части, чтобы повысить оценку до «4» или «5». Обучающийся может начинать выполнение работы с любого задания с нужным количеством баллов, учитывая при этом степень своей уверенности в ответе.
Шкала перевода баллов в отметки по пятибалльной системе
|
Отметка |
Число баллов, необходимое для получения отметки |
|
«2» (неудовлетворительно) |
Менее 15 |
|
«3» (удовлетворительно) |
15-19 |
|
«4» (хорошо) |
20-23 |
|
«5» (отлично) |
Более 23 |
III. Контрольно-измерительные материалы для проведения письменного экзамена в виде набора контрольных заданий
3.1 Краткая инструкция для обучающихся по выполнению экзаменационной работы
На письменный экзамен учащиеся приходят за 20 мин до начала экзамена. При себе иметь шариковую, гелиевую или капиллярную ручку с черными чернилами;
К экзамену по математике при себе также иметь чертежные инструменты и справочные материалы, которые можно использовать.
Во время проведения экзаменов запрещается иметь при себе и использовать средства связи и электронно-вычислительную технику, за исключением случаев, установленных нормативно-правовыми актами РФ.
Получить от преподавателя и ассистента черновики и экзаменационный комплект с вложенными в них контрольно-измерительными материалами (КИМ), бланками ответов № 1 и № 2.
Внимательно прослушать инструктаж, проводимый преподавателем, информирующий экзаменующих о порядке проведения экзамена,
правилах заполнения бланков, продолжительности экзамена
Заполнить регистрационные части бланков: бланка регистрации, бланков ответов № 1 и 2.
На выполнение экзаменационной работы дается 4 часа (240 минут).
Работа состоит из двух частей и содержит 26 заданий.
Часть 1 содержит 19 заданий с выбором ответа и с кратким ответом. Задания части 1 считаются выполненными, если экзаменующий выбрал верные ответы.
Часть 2 содержит 7 более сложных заданий ( А20-А26) по материалу курса математики. При их выполнении надо записать полное решение и ответ.
Совет: для экономии времени пропускать задание, которое не удается выполнить сразу и переходить к следующему. К выполнению пропущенных заданий можно вернуться, если у Вас останется время.
– начинать работу всем следует с выполнения заданий обязательной части;
– для получения удовлетворительной оценки не обязательно выполнять все задания обязательной части;
– правильное выполнение определенной части заданий обязательной части, во-первых, гарантирует получение отметки «3», а во-вторых, дает основу для повышения отметки до «4» или «5» при правильном выполнении нескольких заданий дополнительной части;
– при выполнении заданий дополнительной части следует проследить по шкале перевода баллов в отметки – сколько заданий достаточно правильно выполнить, чтобы получить 4 или 5; После объявления о времени начала экзамена, которое фиксируется на доске, приступить к выполнению экзаменационной работы.
Во время экзамена учащиеся должны соблюдать установленный порядок проведения экзамена и следовать указаниям организаторов.
Во время экзамена учащиеся не вправе общаться друг с другом, свободно перемещаться по кабинету, пользоваться справочными материалами, иметь при себе и использовать средства связи и электронно-вычислительной техники.
Учащиеся могут выходить из кабинета в случае необходимости (в туалет, в медицинскую комнату), предварительно сдав бланки.
По окончании экзамена необходимо:
сдать экзаменационный материал КИМ, черновики, бланки ответов № 1 и № 2;
Допускается досрочная сдача экзаменационных материалов, которая прекращается за пятнадцать минут до окончания экзамена.
Желаем успеха!
3.2. Контрольная работа по математике
По профессиям: электрогазосварщик,
машинист локомотива
ВАРИАНТ № 1
Часть 1.
1. Найдите значение выражения ![]()
2. Одна из точек, отмеченных на координатной прямой, соответствует числу ![]()
Какая это точка?
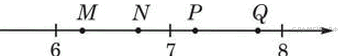
1) точка M
2) точка N
3) точка P
4) точка Q
3. Сравните числа ![]() и 10.
и 10.
В ответе укажите номер правильного варианта.
1) ![]()
2) ![]()
3) ![]()
4. Решите уравнение ![]() .
.
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
5. Установите соответствие между функциями и их графиками.
Графики
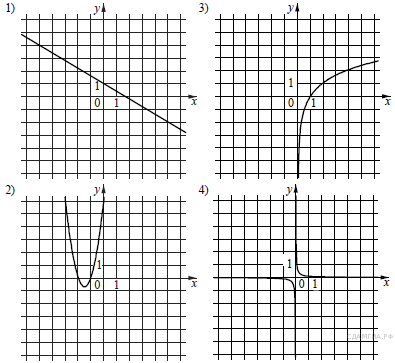
Функции
|
А) |
Б) |
В) |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
|
А |
Б |
В |
6. Выписаны первые несколько членов арифметической прогрессии: 3; 6; 9; 12;… Какое из следующих чисел есть среди членов этой прогрессии?
|
1) 83 |
2) 95 |
3) 100 |
4) 102 |
7. Найдите значение выражения ![]() при
при ![]()
8. На каком рисунке изображено множество решений неравенства ![]()
В ответе укажите номер правильного варианта.
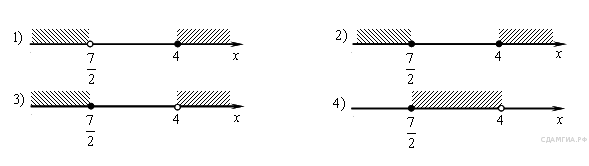
-
В выпуклом четырехугольнике ABCD
 ,
,  ,
,  ,
, 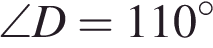 . Найдите угол A. Ответ дайте в градусах.
. Найдите угол A. Ответ дайте в градусах.
-
Найдите градусную меру ∠MON, если известно, NP — диаметр, а градусная мера ∠MNP равна 18°.
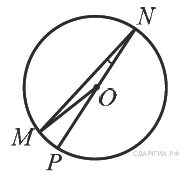
11. В прямоугольнике одна сторона равна 96, а диагональ равна 100. Найдите площадь прямоугольника.
12. На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах.
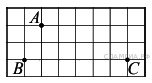
13. Укажите номера верных утверждений.
1) Любые три прямые имеют не более одной общей точки.
2) Если угол равен 120°, то смежный с ним равен 120°.
3) Если расстояние от точки до прямой больше 3, то и длина любой наклонной, проведённой из данной точки к прямой, больше 3.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
14. Куриные яйца в зависимости от их массы подразделяют на пять категорий: высшая, отборная, первая, вторая и третья. Используя данные, представленные в таблице, определите, к какой категории относится яйцо, массой 35,5 г.
|
Категория |
Масса одного яйца, г |
|
Высшая |
75,0 и выше |
|
Отборная |
65,0 − 74,9 |
|
Первая |
55,0 − 64,9 |
|
Вторая |
45,0 — 54,9 |
|
Третья |
35,0 — 44,9 |
В ответе укажите номер правильного варианта.
1) отборная
2) первая
3) вторая
4) третья
15. На рисунке показано, как изменялась температура воздуха на протяжении одних суток. По горизонтали указано время суток, по вертикали — значение температуры в градусах Цельсия. Найдите наибольшее значение температуры. Ответ дайте в градусах Цельсия.
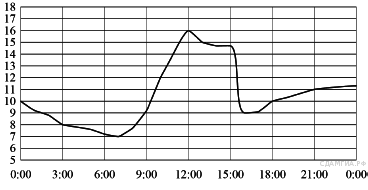
16. Расстояние от Солнца до Нептуна свет проходит примерно за 252,95 минуты. Найдите приблизительно расстояние от Солнца до Нептуна, ответ округлите до миллионов км. Скорость света равна 300 000 км/с.
17. На сколько градусов повернется Земля вокруг своей оси за 7 часов?
18. На диаграмме показано содержание питательных веществ в какао, молочном шоколаде, фасоли и сушёных белых грибах. Определите по диаграмме, в каком продукте содержание жиров находится в пределах от 15% до 25%.
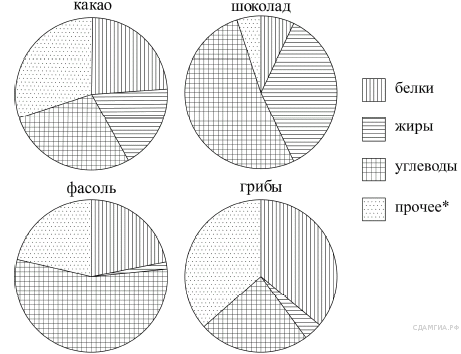
*К прочему относятся вода, витамины и минеральные вещества.
1) какао
2) шоколад
3) фасоль
4) грибы
19. Родительский комитет закупил 25 пазлов для подарков детям на окончание года, из них 15 с машинами и 10 с видами городов. Подарки распределяются случайным образом. Найдите вероятность того, что Толе достанется пазл с машиной.
Часть 2.
20. Центростремительное ускорение при движении по окружности (в м/c2) можно вычислить по формуле ![]() где
где ![]() — угловая скорость (в с−1), а R — радиус окружности. Пользуясь этой формулой, найдите расстояние R (в метрах), если угловая скорость равна 3 с−1, а центростремительное ускорение равно 45 м/c2.
— угловая скорость (в с−1), а R — радиус окружности. Пользуясь этой формулой, найдите расстояние R (в метрах), если угловая скорость равна 3 с−1, а центростремительное ускорение равно 45 м/c2.
21. Решите уравнение ![]()
22. Первую половину трассы автомобиль проехал со скоростью 55 км/ч, а вторую — со скоростью 70 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
23. Постройте график функции
![]()
и определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.
24. Основания трапеции равны 9 и 15. Найдите отрезок, соединяющий середины диагоналей трапеции.
25. Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AB и CD четырёхугольника пересекаются в точке M. Докажите, что треугольники MBC и MDA подобны.
26. В трапеции ABCD боковая сторона AB перпендикулярна основаниюBC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD = 6, BC = 5.
ВАРИАНТ № 2.
ЧАСТЬ 1.
1. Найдите значение выражения ![]()
2. На координатной прямой отмечено число ![]()
В ответе укажите номер правильного варианта.
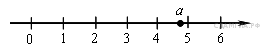
Какое из утверждений относительно этого числа является верным?
1) ![]()
2) ![]()
3) ![]()
4) ![]()
3. Найдите значение выражения (1,7 · 10− 5)(2 · 10− 2).
В ответе укажите номер правильного варианта.
1) 0,0000034
2) 34000000000
3) 0,000000034
4) 0,00000034
4. Решите уравнение (x − 9)2 = (x − 3)2.
5. На рисунке изображены графики функций вида y = kx + b. Установите соответствие между знаками коэффициентов k и b и графиками функций.
Графики
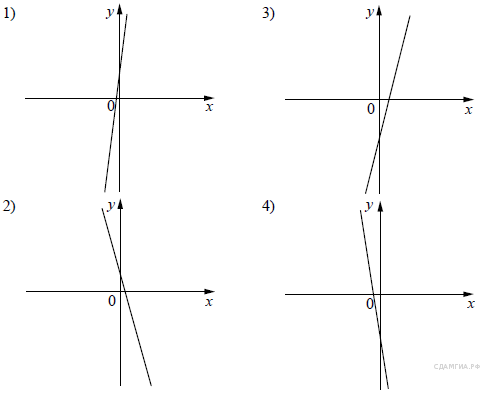
Коэффициенты
|
А) k 0, b 0 |
Б) k 0, b |
В) k 0 |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
|
А |
Б |
В |
6. Выписаны первые несколько членов геометрической прогрессии: 1; −5; 25; … Найдите сумму первых 5 её членов.
7. Упростите выражение ![]() и найдите его значение при
и найдите его значение при ![]() .
.
В ответе запишите найденное значение.
8. Решение какого из данных неравенств изображено на рисунке?
В ответе укажите номер правильного варианта.
![]()
1) ![]()
2) ![]()
3) ![]()
4) ![]()
9. В треугольнике ABC проведены медиана BM и высота BH . Известно, что AC = 15 и BC = BM. Найдите AH.
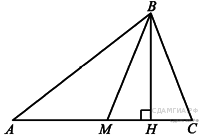
10. В окружности с центром в точке О проведены диаметры AD и BC, угол OCD равен 30°. Найдите величину угла OAB.
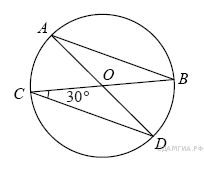
11. Периметр ромба равен 40, а один из углов равен 60°. Найдите площадь ромба, делённую на ![]() .
.
12. Найдите площадь трапеции, изображённой на рисунке.
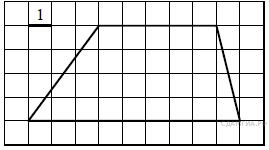
13. Укажите номера верных утверждений.
1) В любую равнобедренную трапецию можно вписать окружность.
2) Диагональ параллелограмма делит его углы пополам.
3) Площадь прямоугольного треугольника равна половине произведения его катетов.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
14. В таблице приведены расстояния от Солнца до четырёх планет Солнечной системы. Какая из этих планет ближе всех к Солнцу?
|
Планета |
Нептун |
Юпитер |
Уран |
Венера |
|
Расстояние (в км) |
4,497 · 109 |
7,781 · 108 |
2,871 · 109 |
1,082 · 108 |
В ответе укажите номер правильного варианта.
1) Нептун
2) Юпитер
3) Уран
4) Венера
15. На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите наименьшее значение атмосферного давления во вторник.
16. В начале 2010 г. в поселке было 730 жителей, а в начале 2011 г. их стало 803. На сколько процентов увеличилось число жителей поселка за год?
17. На каком расстоянии (в метрах) от фонаря стоит человек ростом 2 м, если длина его тени равна 1 м, высота фонаря 9 м?
18. На диаграмме представлены семь крупнейших по площади территории (в млн км2) стран мира. Какое из следующих утверждений неверно?
.
1) По площади территории второе место в мире занимает Канада.
2) Площадь территории Австралии составляет 7,7 млн км2.
3) Площадь Китая больше площади Канады.
4) Площадь США больше площади Бразилии на 1 млн км2.
19. В магазине канцтоваров продаётся 200 ручек, из них 31 красная, 25 зелёных, 38 фиолетовых, ещё есть синие и чёрные, их поровну. Найдите вероятность того, что при случайном выборе одной ручки будет выбрана красная или чёрная ручка.
ЧАСТЬ 2.
20. Зная длину своего шага, человек может приближённо подсчитать пройденное им расстояние s по формуле s = nl, где n — число шагов, l — длина шага. Какое расстояние прошёл человек, если l = 70 см, n =1400 ? Ответ выразите в километрах.
21. Решите неравенство
22. Из пункта А в пункт В, расстояние между которыми 13 км, вышел пешеход. Одновременно с ним из В в А выехал велосипедист. Велосипедист ехал со скоростью, на 11 км/ч большей скорости пешехода, и сделал в пути получасовую остановку. Найдите скорость пешехода, если известно, что они встретились в 8 км от пункта В.
23.. Постройте график функции и определите, при каких значениях прямая
имеет с графиком не менее одной, но не более трёх общих точек.
24. Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит её пополам. Найдите сторону АС, если сторона АВ равна 4.
25. В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AOB.
26. Основание AC равнобедренного треугольника ABC равно 8. Окружность радиуса 5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
ВАРИАНТ № 3.
ЧАСТЬ 1.
1. Вычислите:
2. Какому из данных промежутков принадлежит число
В ответе укажите номер правильного варианта.
1) [0,5;0,6]
2) [0,6;0,7]
3) [0,7;0,8]
4) [0,8;0,9]
3. Укажите наибольшее из следующих чисел.
В ответе укажите номер правильного варианта.
1)
2)
3)
4)
4. Решите уравнение
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
5. Найдите значение по графику функции , изображенному на рисунке.
|
1) |
2) |
3) |
4) |
6. Геометрическая прогрессия задана условием b1 = −7, bn + 1 = 3bn. Найдите сумму первых 5 её членов.
7. Упростите выражение и найдите его значение при . В ответ запишите полученное число.
8. На каком рисунке изображено множество решений неравенства
В ответе укажите номер правильного варианта.
1) 1
2) 2
3) 3
4) 4
9. Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 50° соответственно.
10. Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.
11. Высота BH ромба ABCD делит его сторону AD на отрезки AH = 5 и HD = 8. Найдите площадь ромба.
.
12. Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
13. Какие из следующих утверждений верны?
1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 90°, то эти две прямые параллельны.
2) Если угол равен 60°, то смежный с ним равен 120°.
3) Если при пересечении двух прямых третьей прямой внутренние односторонние углы равны 70° и 110°, то эти две прямые параллельны.
4) Через любые три точки проходит не более одной прямой.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
14. В таблице приведены размеры штрафов за превышение максимальной разрешённой скорости, зафиксированное с помощью средств автоматической фиксации, установленных на территории России на 1 января 2013 года.
|
Превышение скорости, км/ч |
11 − 20 |
21 − 40 |
41 − 60 |
61 и более |
|
Размер штрафа, руб. |
100 |
300 |
1000 |
2500 |
Какой штраф должен заплатить владелец автомобиля, зафиксированная скорость которого составила 175 км/ч на участке дороги с максимальной разрешённой скоростью 110 км/ч?
В ответе укажите номер правильного варианта.
1) 100 рублей
2) 300 рублей
3) 1000 рублей
4) 2500 рублей
15.. В таблице даны рекомендуемые суточные нормы потребления (в г/сутки) жиров, белков и углеводов детьми от 1 года до 14 лет и взрослыми.
|
Вещество |
Дети от 1 года до 14 лет |
Мужчины |
Женщины |
|
Жиры |
40—97 |
70—154 |
60—102 |
|
Белки |
36—87 |
65—117 |
58—87 |
|
Углеводы |
170—420 |
257—586 |
Какой вывод о суточном потреблении жиров, белков и углеводов 13-летним мальчиком можно сделать, если по подсчётам диетолога в среднем за сутки он потребляет 90 г жиров, 90 г белков и 359 г углеводов? В ответе укажите номера верных утверждений.
1) Потребление жиров в норме.
2) Потребление белков в норме.
3) Потребление углеводов в норме.
16. Государству принадлежит 60% акций предприятия, остальные акции принадлежат частным лицам. Общая прибыль предприятия после уплаты налогов за год составила 40 млн. р. Какая сумма из этой прибыли должна пойти на выплату частным акционерам?
17. Пол комнаты, имеющей форму прямоугольника со сторонами 4 м и 9 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 25 см. Сколько потребуется таких дощечек?
18. а диаграмме показано содержание питательных веществ в какао, молочном шоколаде, фасоли и сушёных белых грибах. Определите по диаграмме, в каком продукте содержание белков превышает 30%.
*К прочему относятся вода, витамины и минеральные вещества.
1) какао 2) шоколад 3) фасоль 4) грибы
19. Стрелок 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,5. Найдите вероятность того, что стрелок первые 3 раза попал в мишени, а последний раз промахнулся.
ЧАСТЬ 2.
20. В фирме «Родник» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле , где n — число колец, установленных при рытье колодца. Пользуясь этой формулой, рассчитайте стоимость колодца из 5 колец.
21. Решите уравнение:
22. Из пункта А в пункт В, расстояние между которыми 13 км, вышел пешеход. Через полчаса навстречу ему из В в А выехал велосипедист, который ехал со скоростью, на 11 км/ч большей скорости пешехода. Найдите скорость велосипедиста, если известно, что они встретились в 5 км от пункта А.
23. Постройте график функции и определите, при каких значениях построенный график не будет иметь общих точек с прямой
.
24. Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH = 16.
25. Окружности с центрами в точках I и J пересекаются в точках A и B, причём точки I и J лежат по одну сторону от прямой AB. Докажите, что отрезки AB и IJ перпендикулярны.
26. В равнобедренной трапеции ABCD боковые стороны равны меньшему основанию BC. К диагоналям трапеции провели перпендикуляры BH и CE. Найдите площадь четырёхугольника BCEH, если площадь трапеции ABCD равна 36 .
ВАРИАНТ № 4.
ЧАСТЬ 1.
1. Вычислите:
2. На координатной прямой отмечено число Расположите в порядке возрастания числа
и
В ответе укажите номер правильного варианта.
1)
2)
3)
4)
3. Расстояние от Земли до Солнца равно 147,1 млн км. В каком случае записана эта же величина?
В ответе укажите номер правильного варианта.
1) 1,471⋅1010 км
2) 1,471⋅108 км
3) 1,471⋅107 км
4) 1,471⋅106 км
4. Найдите корни уравнения
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
5. Задание 5 № 193101. Найдите значение по графику функции изображенному на рисунке.
6. Дана геометрическая прогрессия (bn), знаменатель которой равен 2, аb1 = 16. Найдите b4.
7. Сократите дробь
8. На каком рисунке изображено множество решений неравенства ?
В ответе укажите номер правильного варианта.
1) 1
2) 2
3) 3
4) 4
9. В треугольнике угол равен 90°, . Найдите
.
10. Центральный угол AOB опирается на хорду ABдлиной 6. При этом угол OAB равен 60°. Найдите радиус окружности.
-
Найдите площадь трапеции, изображённой на рисунке.
-
Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
13. Укажите номера верных утверждений.
1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
2) Треугольник со сторонами 1, 2, 4 существует.
3) Если в ромбе один из углов равен 90°, то такой ромб — квадрат.
4) В любом параллелограмме диагонали равны.
14. Для квартиры площадью 135 м2 заказан натяжной потолок белого цвета. Стоимость работ по установке натяжных потолков приведена в таблице.
|
Цвет потолка |
Цена в рублях за 1 м2 (в зависмости от площали помещения) |
|||
|
до 10 м2 |
от 11 до 30 м2 |
от 31 до 60 м2 |
свыше 60 м2 |
|
|
белый |
1200 |
1000 |
800 |
600 |
|
цветной |
1350 |
1150 |
950 |
750 |
Какова стоимость заказа, если действует сезонная скидка в 20%?
В ответе укажите номер правильного варианта.
1) 81 000 рублей
2) 64 800 рублей
3) 6480 рублей
4) 80 980 рублей
15. На графиках показано, как во время телевизионных дебатов между кандидатами А и Б телезрители голосовали за каждого из них. Сколько всего телезрителей проголосовало к 40-й минуте дебатов?
.
16. Площадь земель крестьянского хозяйства, отведённая под посадку сельскохозяйственных культур, составляет 24 га и распределена между зерновыми и овощными культурами в отношении 5:3. Сколько гектаров занимают овощные культуры?
17. крепостного рва равна 8 м, ширина 5 м, а высота крепостной стены от ее основания 20 м. Длина лестницы, по которой можно взобраться на стену, на 2 м больше, чем расстояние от края рва до верхней точки стены (см. рис.). Найдите длину лестницы.
18. На диаграмме показаны религиозные составы населения Германии, США, Австрии и Великобритании. Определите по диаграмме, в какой стране доля католиков превышает 50%.
1) Германия
2) США
3) Австрия
4) Великобритания
19. Стрелок 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,5. Найдите вероятность того, что стрелок первые 3 раза попал в мишени, а последний раз промахнулся.
ЧАСТЬ 2.
20. В фирме «Родник» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле C = 6000 + 4100 · n , где n — число колец, установленных при рытье колодца. Пользуясь этой формулой, рассчитайте стоимость колодца из 20 колец.
21. Решите систему уравнений
22. Расстояние между городами А и В равно 490 км. Из города А в город В со скоростью 55 км/ч выехал первый автомобиль, а через час после этого навстречу ему из города В выехал со скоростью 90 км/ч второй автомобиль. На каком расстоянии от города А автомобили встретятся?
23. Постройте график функции и определите, при каких значениях параметра прямая
имеет с графиком три общие точки.
24. Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 39°, 78° и 63°.
25. Основания BC и AD трапеции ABCD равны соответственно 5 и 20,BD = 10. Докажите, что треугольники CBD и ADB подобны.
26. В трапеции ABCD боковая сторона AB перпендикулярна основаниюBC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD = 6, BC = 5.
3.3 Критерии оценки экзаменационной работы в виде набора контрольных заданий
Оценка 5 (отлично) ставится за работу, выполненную полностью без ошибок и недочётов; в логических рассуждениях и обосновании решения нет пробелов и ошибок; в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием незнания или непонимания учебного материала).
Оценка 4 (хорошо) работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки); допущена одна ошибка или два-три недочета в выкладках, рисунках, чертежах или графиках (если эти виды работы не являлись специальным объектом проверки).
Оценка 3 (удовлетворительно) ставится, если обучающийся правильно выполнил не менее 2/3 всей работы или допустил не более одной грубой ошибки и двух недочётов, не более одной грубой и одной не грубой ошибки, не более трёх негрубых ошибок, одной негрубой ошибки и трёх недочётов, при наличии четырёх-пяти недочётов.
Оценка 2 (неудовлетворительно) ставится, если число ошибок и недочётов превысило норму для оценки 3 или правильно выполнено не менее 2/3 всей работы; допущены существенные ошибки, показавшие, что учащийся не владеет обязательными умениями по данной теме в полной мере
КЛЮЧ
|
№ |
1 вариант |
2 вариант |
3 вариант |
4 вариант |
|
|
-3786,7 |
20 |
1,03 |
1,55 |
|
|
1 |
1 |
1 |
2 |
|
|
1 |
4 |
2 |
2 |
|
|
-5;3 |
6 |
0,5;1 |
3;6 |
|
|
412 |
132 |
4 |
1 |
|
|
4 |
521 |
-847 |
128 |
|
|
31 |
1,5 |
0,4 |
84 |
|
|
4 |
3 |
1 |
2 |
|
|
95 |
11,25 |
80 |
33 |
|
|
144 |
30 |
4 |
6 |
|
|
2688 |
50 |
156 |
270 |
|
|
2 |
28 |
52 |
58 |
|
|
1;3 |
3 |
2;3;4 |
13|31|1;3|1,3 |
|
|
4 |
4 |
4 |
2 |
|
|
16 |
756 |
1;3|13|1; 3 |
50000 |
|
|
4553000000 |
10 |
16000000 |
9 |
|
|
105 |
3,5 |
1440 |
15 |
|
|
1 |
3 |
4 |
3 |
|
|
0,6 |
0,42 |
0,0625 |
0,0625 |
|
|
5 |
0,98 |
26500 |
88000 |
|
|
-8:-5 |
-1;0;5 |
(3; −4) |
|
|
|
61,6 |
5 |
16 км/ч |
220 |
|
|
2,6 |
2/3;1;2 |
(0;5) |
|
|
|
3 |
8 |
16 |
102°, 24°, 54° |
|
|
||||
|
|
3,2 |
9 |
25. 1 вариант.
Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AB и CD четырёхугольника пересекаются в точке M. Докажите, что треугольники MBC и MDA подобны.
Решение.
Поскольку четырёхугольник ABCD вписанный, сумма углов BAD и BCD равна 180°.
Следовательно,
∠MCB = 180° − ∠BCD = ∠BAD.
Получаем, что в треугольниках MBC и MDA углы MCB и MAD равны, угол M общий, следовательно, эти треугольники подобны.
25. 2 вариант.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AOB.
Решение.
Проведём высоту так, чтобы она проходила через точку
Углы и равны друг другу как вертикальные. Вспомним также, что диагонали делятся точкой пересечения пополам, следовательно, Рассмотрим треугольники и , они прямоугольные, имеют равные углы и равные гипотенузы, следовательно эти треугольники равны, а значит равны отрезки
и
. Таким образом,
Площадь параллелограмм равна а площадь треугольника
25. 3 вариант.
Окружности с центрами в точках I и J пересекаются в точках A и B, причём точки I и J лежат по одну сторону от прямой AB. Докажите, что отрезки AB и IJ перпендикулярны.
Решение.
Точка I равноудалена от A и B, поэтому она лежит на серединном перпендикуляре к отрезку AB. То же можно сказать и о J . Значит IJ — серединный перпендикуляр к AB.
25. 4 вариант.
Основания BC и AD трапеции ABCD равны соответственно 5 и 20,BD = 10. Докажите, что треугольники CBD и ADB подобны.
Решение.
Углы CBD и BDA равны, как накрест лежащие при параллельных прямых. В треугольниках и следовательно, эти треугольники подобны по двум парам подобных сторон и углу между ними.
Контрольная работа по математике
по профессии среднего профессионального образования
Технология продукции общественного питания
-
Вычислить предел:
1). Ответ:
2). Ответ:
3) Ответ
4). Ответ
5). Ответ :
6) Ответ:
7). Ответ:
8). Ответ:
9). Ответ:
10). Ответ:
11). Ответ:
12). Ответ:
13). Ответ:
2. Пользуясь определением производной, найти производную функции у, если:
-
,
-
,
-
у = 5 − 6x ,
-
у= 4 − 7x,
-
,
-
,
-
у = 2х2 – 13х +3,
-
у=-3x2-13x,
-
у=7x2+3x,
-
у =4 – 5х + 2х2,
-
у = 3х2 – 2х – 8,
-
у=х3– 9х – 4,
-
у=3х3 – 4х2 – 8х – 4,
-
у =-2х3 -4х2 -4х
-
Решить задачи по теории вероятностей.
№ 1. В кармане у Миши 4 конфеты – «Грильяж», «Маска», «Белочка», «Красная шапочка», а так же ключи от квартиры. Вынимая ключи, Миша случайно выронил из кармана одну конфету. Найдите вероятность того, что потерялась конфета «Маска»
№ 2. Оля, Денис, Витя, Артур и Рита бросали жребий – кому начать игру. Найдите
вероятность того, что начинать игру будет Рита?
№ 3. Катя, Настя, Игорь, Даша и Андрей бросали жребий – кому начать игру.
Найдите вероятность того, что начинать игру будет мальчик?
№ 4. Игральную кость бросают один раз. Найдите вероятность того, что выпало
число очков не меньше, чем 3?
№ 5. Бабушка решила дать внуку Илье на дорогу какой-нибудь случайно
выбранный фрукт. У неё было 3 зелёных яблока, 3 зеленых груши и 2 желтых
банана. Найдите вероятность того, что Илья получит фрукт зеленого цвета?
№ 6. Игральную кость бросают два раза. Найдите вероятность того, что оба раза
выпало число большее 3?
№ 7. Игральную кость бросают два раза. Найдите вероятность того, что один раз
выпало число большее 3, а другой раз – меньшее 3?
№ 8. В случайном эксперименте симметричную монету бросают дважды. Найдите
вероятность того, что орёл выпадет ровно один раз?
№ 9. В случайном эксперименте симметричную монету бросают три раза. Найдите
вероятность того, что решка выпадет ровно два раза?
№ 10. В случайном эксперименте бросают две игральные кости. Найдите
вероятность того, что в сумме выпадет 7 очков?
№ 11. В соревнованиях по керлингу выступают 20 команд из 5 стран: Швеция,
Норвегия, Финляндия, Канада, Дания. Причем каждая страна выставила по 4
команды. Порядок выступления команд определяется жеребьевкой. Найдите
вероятность того, что 17-ой по счету будет выступать одна из команд Канады?
№ 12. В соревнованиях по керлингу выступают 20 команд из 5 стран: Швеция,
Норвегия, Финляндия, Канада, Дания. Причем каждая страна выставила по 4
команды. Порядок выступления команд определяется жеребьевкой. Найдите
вероятность того, что 17-ойп по счету будет выступать одна из команд
Швеции, Норвегии или Дании?
№ 13. В коробке находятся 7 красных шаров, 13 белых шаров и 6 голубых шаров.
Определите вероятность того, что наудачу взятый из коробки шар окажется
белым.
№ 14. В копилке находятся монеты достоинством 2 рубля – 14 штук, 5 рублей – 10
штук и 10 рублей – 6 штук. Какова вероятность того, что первая монета,
выпавшая из копилки, будет достоинством 10 рублей?
№ 15. В корзине лежат 7 помидоров, 6 огурцов, 12 перцев. Найдите вероятность того,
что первый наугад взятый овощ из корзины будет перцем.
КЛЮЧ
|
№ |
№ |
ответ |
|
1 |
1 |
(-1/3) – неопределённость -раскрывать путём разложения на множители |
|
2 |
(-1/3) – неопределённость -раскрывать путём домножения на сопряжённое выражение |
|
|
3 |
:(-1/2) – неопределённость -раскрывать путём вынесения за скобки x с наибольшим показателем |
|
|
4 |
:(0) – неопределённость -раскрывать путём вынесения за скобки x с наибольшим показателем |
|
|
5 |
– неопределённость -раскрывать путём вынесения за скобки x с наибольшим показателем |
|
|
6 |
– –неопределённость – раскрывать с помощью метода приведения ко второму замечательному пределу – сначала преобразовать скобку следующим образом |
|
|
7 |
-–неопределённость – раскрывать с помощью метода приведения ко второму замечательному пределу – сначала преобразовать скобку следующим образом |
|
|
8 |
– неопределённость – раскрывать с помощью метода приведения ко второму замечательному пределу – сначала преобразовать скобку следующим образом |
|
|
9 |
– неопределённость – раскрывать с помощью метода приведения к первому замечательному пределу |
|
|
10 |
– неопределённость – раскрывать с помощью метода приведения к первому замечательному пределу=1 |
|
|
11 |
-–неопределённость – раскрывать с помощью метода приведения к первому замечательному пределу=1 |
|
|
12 |
(6). –воспользоваться свойством вычисления предела непрерывной функции |
|
|
13 |
). –воспользоваться свойством вычисления предела непрерывной функции |
|
|
2 |
1 |
-2 |
|
2 |
8 |
|
|
3 |
-6 |
|
|
4 |
-7 |
|
|
5 |
2х-1 |
|
|
6 |
2а+в |
|
|
7 |
4х-13 |
|
|
8 |
6х-13 |
|
|
9 |
14х+3 |
|
|
10 |
-5+4х |
|
|
11 |
6х-2 |
|
|
12 |
3х2-9 |
|
|
13 |
9х2-8х-8 |
|
|
14 |
-6х2-8х-4 |
|
|
3 |
1 |
0,25 |
|
2 |
0,2 |
|
|
3 |
0,4 |
|
|
4 |
2/3 |
|
|
5 |
0,75 |
|
|
6 |
0,25 |
|
|
7 |
1/3 |
|
|
8 |
0,5 |
|
|
9 |
3/8 |
|
|
10 |
1/6 |
|
|
11 |
0,2 |
|
|
12 |
0,6 |
|
|
13 |
0,5 |
|
|
14 |
0,2 |
|
|
15 |
0,48 |
Критерии оценивания заданий
|
Оценка в пятибалльной шкале |
Критерии оценки |
Количество правильно данных вопросов |
|
«2» |
Выполнено менее 50% заданий |
Даны верные ответы менее, чем на 21 вопросов |
|
«3» |
Выполнено 51-74 % заданий |
Даны верные ответы на 21-30 вопроса |
|
«4» |
Выполнено 75-89% заданий |
Даны верные ответы на 31-37 вопросов |
|
«5» |
Выполнено более 90% заданий |
Данные верные ответы на 38-42 вопросов |
Критерии оценивания заданий:
За каждое правильно выполненное тестовое задание (верный ответ) ставится 1 балл, за
Критерии оценивания выполнения практического задания
Своевременность выполнения практической работы.
Выполнение работы в полном объеме с соблюдением необходимой последовательности
вычислений.
БЮДЖЕТНОЕ УЧРЕЖДЕНИЕ
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ХАНТЫ-МАНСИЙСКОГО АВТОНОМНОГО ОКРУГА – ЮГРЫ «СОВЕТСКИЙ
ПОЛИТЕХНИЧЕСКИЙ КОЛЛЕДЖ»
УТВЕРЖДАЮ
Заместитель директора
по учебной работе
____________/Куимова Г.Р./
«___»_______2019г.
Комплект контрольно-оценочных средств
для оценки результатов освоения
ОУД.03 «Математика»
по профессии
15.01.09 Машинист лесозаготовительных
и трелевочных машин
технический
г. Советский
2019 г.
Комплект контрольно-оценочных средств
по учебной дисциплине ОУД.03 «Математика» разработан на основе Федерального
государственного образовательного стандарта среднего общего образования (утв.
приказом Министерства образования и науки РФ от «17» мая 2012 г. № 413) по профессии
15.01.09 Машинист лесозаготовительных и трелевочных машин
Организация-разработчик: бюджетное учреждение профессионального образования
Ханты -Мансийского автономного округа-Югры «Советский политехнический колледж»
Разработчик:
Невенкина
О.И., преподаватель бюджетного учреждения профессионального образования
Ханты-Мансийского автономного округа-Югры «Советский политехнический колледж»
|
РАССМОТРЕН на заседании ЦМК Протокол №____ от Председатель |
РЕКОМЕНДОВАН учебно – методическим советом Протокол №____ от Председатель _______/Горячева |
I.
ПАСПОРТ КОМПЛЕКТА ОЦЕНОЧНЫХ СРЕДСТВ
Общие положения
Учебная дисциплина ОУД.03 «Математика» изучается на 1
и 2 курсах.
Максимальное количество часов на реализацию программы
УД -427 час.
Практикоориентированность учебной дисциплины
составляет 59 %.
Учебная дисциплина ОУД.03 «Математика» состоит из 4
разделов:
Раздел 1. Алгебра
Раздел 2. Геометрия
Раздел 3. Элементы комбинаторики, теории вероятностей
и математической статистики
Раздел 4. Начала математического анализа
Профиль получаемого профессионального образования: технический.
Реализация программы учебной дисциплины способствует
формированию у обучающихся:
Личностных результатов обучения:
1) сформированность представлений о математике как
универсальном языке науки, средстве моделирования явлений и процессов, идеях и
методах математики;
2) понимание значимости математики для
научно-технического прогресса, сформированность отношения к математике как к
части общечеловеческой культуры через знакомство с историей развития
математики, эволюцией математических идей;
3) развитие логического мышления, пространственного
воображения, алгоритмической культуры, критичности мышления на уровне
необходимом для будущей профессиональной деятельности, для продолжения
образования и самообразования;
4) овладение математическими знаниями и умениями,
необходимыми в повседневной жизни, для освоения смежных естественнонаучных
дисциплин и дисциплин профессионального цикла, для получения образования в
областях, не требующих углубленной математической подготовки;
5) готовность и способность к образованию, в том числе
самообразованию, на протяжении всей жизни; сознательное отношение к
непрерывному образованию как условию успешной профессиональной и общественной
деятельности;
6) готовность и способность к самостоятельной
творческой и ответственной деятельности;
7) готовность к коллективной работе, сотрудничеству со
сверстниками в образовательной, общественно полезной, учебно-исследовательской,
проектной и других видах деятельности;
8) отношение к профессиональной деятельности как
возможности участия в решении личных, общественных, государственных,
общенациональных проблем.
Метапредметных результатов обучения:
1) умение самостоятельно определять цели деятельности
и составлять планы деятельности; самостоятельно осуществлять, контролировать и
корректировать деятельность; использовать все возможные ресурсы для достижения
поставленных целей и реализации планов деятельности; выбирать успешные
стратегии в различных ситуациях;
2) умение продуктивно общаться и взаимодействовать в
процессе совместной деятельности, учитывать позиции других участников
деятельности, эффективно разрешать конфликты;
3) владение навыками познавательной,
учебно-исследовательской и проектной деятельности, навыками разрешения проблем;
способность и готовность к самостоятельному поиску методов решения практических
задач, применению различных методов познания;
4) готовность и способность к самостоятельной
информационно-познавательной деятельности, включая умение ориентироваться в
различных источниках информации, критически оценивать и интерпретировать информацию,
получаемую из различных источников;
5) умение использовать средства информационных и
коммуникационных технологий (далее – ИКТ) в решении когнитивных,
коммуникативных и организационных задач с соблюдением требований эргономики,
техники безопасности, гигиены, ресурсосбережения, правовых и этических норм,
норм информационной безопасности;
6) умение определять назначение и функции различных
социальных институтов;
7) умение самостоятельно оценивать и принимать
решения, определяющие стратегию поведения, с учётом гражданских и нравственных
ценностей;
8) владение языковыми средствами – умение ясно,
логично и точно излагать свою точку зрения, использовать адекватные языковые
средства;
9) владение навыками познавательной рефлексии как
осознания совершаемых действий и мыслительных процессов, их результатов и
оснований, границ своего знания и незнания, новых познавательных задач и
средств их достижения.
Предметных
результатов:
1) сформированность представлений о математике как
части мировой культуры и о месте математики в современной цивилизации, о
способах описания на математическом языке явлений реального мира;
2) сформированность представлений о математических
понятиях как о важнейших математических моделях, позволяющих описывать и
изучать разные процессы и явления; понимание возможности аксиоматического
построения математических теорий;
3) владение методами доказательств и алгоритмов
решения; умение их применять, проводить доказательные рассуждения в ходе
решения задач;
4) владение стандартными приёмами решения рациональных
и иррациональных, показательных, степенных, тригонометрических уравнений и
неравенств, их систем; использование готовых компьютерных программ, в том числе
для поиска пути решения и иллюстрации решения уравнений и неравенств;
5) сформированность представлений об основных
понятиях, идеях и методах математического анализа;
6) владение основными понятиями о плоских и
пространственных геометрических фигурах, их основных свойствах;
сформированность умения распознавать на чертежах, моделях и в реальном мире
геометрические фигуры; применение изученных свойств геометрических фигур и
формул для решения геометрических задач и задач с практическим содержанием;
7) сформированность представлений о процессах и
явлениях, имеющих вероятностный характер, о статистических закономерностях в
реальном мире, об основных понятиях элементарной теории вероятностей; умений
находить и оценивать вероятности наступления событий в простейших практических
ситуациях и основные характеристики случайных величин;
8) владение навыками использования готовых
компьютерных программ при решении задач;
9) сформированность представлений о необходимости
доказательств при обосновании математических утверждений и роли аксиоматики
в проведении дедуктивных рассуждений;
10) сформированность понятийного аппарата по
основным разделам курса математики; знаний основных теорем, формул и умения их
применять; умения доказывать теоремы и находить нестандартные способы решения
задач;
11) сформированность умений моделировать реальные
ситуации, исследовать построенные модели, интерпретировать полученный
результат;
12) сформированность представлений об основных
понятиях математического анализа и их свойствах, владение умением
характеризовать поведение функций, использование полученных знаний для описания
и анализа реальных зависимостей;
13) владение умениями составления вероятностных
моделей по условию задачи и вычисления вероятности наступления событий, в том
числе с применением формул комбинаторики и основных теорем теории вероятностей;
исследования случайных величин по их распределению.
Контроль формируемых знаний и умений проводится в
процессе текущего контроля. Промежуточная аттестация предусмотрена в форме
дифференцированного зачета на первом курсе во втором семестре и экзамена на 2
курсе в 4 семестре.
Матрицы логических связей между объектами (предметами) контроля и
разделами (темами) учебной дисциплины ОУД.03 «Математика»
|
Разделы (темы) программы УД |
Объекты (предметы) контроля |
||||||||||||||||
|
Метапредметные результаты |
Предметные результаты |
||||||||||||||||
|
МР 1 |
МР 2 |
МР 3 |
МР 4 |
МР 5 |
МР 6 |
МР 7 |
МР 8 |
МР 9 |
ПР 1 |
ПР 2 |
ПР 3 |
ПР 4 |
ПР 5 |
ПР 6 |
ПР 7 |
ПР 8 |
|
|
Раздел 1. Алгебра |
|||||||||||||||||
|
Тема 1. Развитие понятия о числе |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
|||||
|
Тема Корни, |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
|||
|
Тема Основы |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
|||
|
Тема Функции, |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
|||
|
Раздел 2.Начала математического анализа |
|||||||||||||||||
|
Тема Уравнения |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
|||
|
Тема Начала |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
||
|
Раздел 3 Комбинаторика, статистика и теория |
|||||||||||||||||
|
Тема Элементы |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
|||
|
Тема Элементы |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
|||
|
Раздел 4 Геометрия |
|||||||||||||||||
|
Тема Прямые |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
||||
|
Тема |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
||||
|
Тема Тела |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
||||
|
Тема Измерения |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
||||
|
Тема Координаты |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
II. Комплект оценочных средств
2.1. Комплект материалов для
оценки сформированности личностных, метапредметных и предметных результатов по
дисциплине ОУД.03 «Математика»
2.2.2 Задания к промежуточной
аттестации по учебной дисциплине ОУД.03 «Математика» в форме дифференцированного
зачета на первом курсе во втором семестре
|
Проверяемые результаты |
Показатели |
Критерии оценки |
|
ЛР 1-10 МР 1-9 ПР 1-8 |
правильность решения рациональность |
-однозначность выбора -совпадение с |
|
Условия выполнения задания На выполнение дифференцированного зачета по Часть 1 содержит 7 заданий с кратким ответом Часть 2 содержит 3 более сложных заданий (8-10) При их выполнении заданий надо записать |
Вариант
1
Часть 1
1. Решите уравнение log2(4 – х) = 2.
2.
Используя график функции у = f(х) (см. рис. ниже), определите и запишите
ответ:
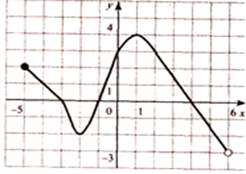
a.
Область определения функции;
b.
Область значения функции
c.
Промежутки возрастания и убывания;
d.
Нули функции;
e.
Наименьшее и наибольшее значения функции.
f.
При каких значениях х , f(х) ![]() 0.
0.
3.
Найти область определения функции ![]()
4. Решите уравнение: 9х + 2![]() 3х+1 – 7 = 0.
3х+1 – 7 = 0.
5. Решите неравенство ![]()
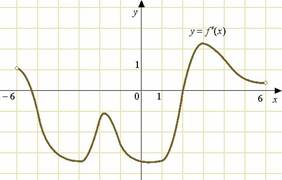 6. Из города A в город B ведут
6. Из города A в город B ведут
пять дорог, а из города B город
C – три дороги. Сколько путей, проходящих через B, ведут из A в
C?
7. На рисунке изображён график ![]() —
—
производной функции ![]() , определенной на интервале
, определенной на интервале ![]() . В какой точке отрезка
. В какой точке отрезка ![]() функция
функция ![]() принимает
принимает
наибольшее значение?
_______________________
8.Найдите промежутки возрастания и убывания функции и
определите её точки экстремума f(x)=3![]() ;
;
9. Решите систему уравнений
![]()
![]() .
.
10. Вычислить площадь фигуры, ограниченной линиями y=1-![]() , y=0.
, y=0.
Вариант II
B1. Решите уравнение ![]() = 5
= 5
B2. Используя график
функции у = g(х) (см. рис. ниже),
определите и запишите ответ:
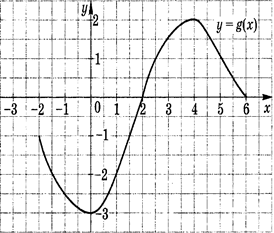
a.
Область определения функции;
b.
Область значения функции; ![]()
c.
Промежутки возрастания и убывания;
d.
Нули функции;
e.
Наименьшее и наибольшее значения функции.
f.
При каких значениях х , g(х) ![]() 0.
0.
B3. Найти область
определения функции![]()
B4. Решите уравнение 2сos2x + 7cosx
– 4 = 0
B5. Решите неравенство![]()
B 6. Сколькими способами можно
выбрать гласную и согласную буквы из слова «камзол»?
В 7. На рисунке изображен график ![]() —
—
производной функции ![]() , определенной на интервале
, определенной на интервале ![]() .
.
Найдите количество точек максимума функции ![]() , принадлежащих отрезку
, принадлежащих отрезку ![]() .
.

________________________________________
8.Найдите промежутки возрастания и убывания функции и определите
её точки экстремума f(x)=![]() ;
;
9. Решите
систему уравнений
![]()
![]() .
.
10. Вычислить площадь фигуры, ограниченной линиями y=![]() , x=-1, y=0.
, x=-1, y=0.
Эталон ответов
1 вариант
|
Часть 1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
0 |
1. [-5;6) 2. (-3;4] 3.[-2;1] –возрастает; [-5;2] 4. -3;-1;4; 5. yнаиб=4; Yнаим=-2; 6.(-3;-1) |
[-3;3] |
|
[-3;0,5] |
15 |
Наибольшее значение функции в точке x=3 |
|
|
Часть 2 |
8 |
9 |
10 |
||||
|
x max= -1 |
x= 16 , |
1 |
2 вариант
|
Часть 1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
3 |
1.[-2;6] 2.[-3;2] [0;4]-возрастает [-2;0] 4.2;6 5.Yнаим= Y 6. |
( |
n |
(-1,5;2] |
8 |
Одна точка максимума x=3 |
|
|
Часть 2 |
8 |
9 |
10 |
||||
|
x max= – |
x= 4 |
|
2.2.2 Задания к промежуточной аттестации по учебной
дисциплине ОУД.03 «Математика» в форме экзамена в четвертом семестре на
втором курсе
|
Проверяемые результаты |
Показатели оценки |
Критерии оценки |
|
ЛР 1-10 МР 1-9 ПР 1-8 |
правильность решения рациональность |
-однозначность выбора -совпадение с |
|
Условия Экзаменационная работа Ответы к заданиям 1-12 записываются в виде целого При выполнении заданий 13-19 требуется записать |
Вариант 1
Часть 1
Ответом к заданиям В1–В 12 является целое число
или конечная десятичная дробь. Единицы измерений писать не нужно.
В1. Найдите значение
выражения ![]()
В2. Найдите значение
выражения ![]() ;
;
В3. В городе 180 000 жителей, причем 30 % – это пенсионеры.
Сколько пенсионеров в этом городе?
В4. Площадь трапеции вычисляется по формуле S
=![]() , где
, где
a и b – основания
трапеции, h – её высота. Пользуясь этой
формулой, найдите S, если a=3,
b=8 и h=4.
В5. На день рождения полагается дарить букет из нечетного числа
цветов. Хризантемы стоят 50 рублей за штуку. У Вани есть 510 рублей. Из какого
наибольшего числа хризантем он может купить букет Маше на день рождения?
В6.
Найдите корень уравнения ![]() .
.
В7. На рисунке показано
изменение температуры воздуха на протяжении трех суток. По горизонтали
указывается дата и время суток, по вертикали — значение температуры в градусах
Цельсия. Определите по рисунку разность между наибольшей и наименьшей температурами
воздуха 22 января.
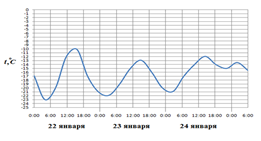
В8. Рейтинговое агентство
определяет рейтинг соотношения «цена-качество» микроволновых печей. Рейтинг
вычисляется на основе средней цены P и оценок
функциональности F, качества Q
и дизайна D . Каждый отдельный показатель оценивается
экспертами по 5-балльной шкале целыми числами от 0 до 4. Итоговый рейтинг
вычисляется по формуле
R=8(F+Q)+4D-0,01P
|
Модель печи |
Средняя цена |
Функциональность |
Качество |
Дизайн |
|
А |
1900 |
1 |
1 |
1 |
|
Б |
5900 |
4 |
1 |
2 |
|
В |
3800 |
0 |
0 |
1 |
|
Г |
4100 |
2 |
0 |
4 |
В таблице даны оценки каждого показателя для нескольких
моделей печей. Определите, какая модель имеет наивысший рейтинг. В ответ
запишите значение этого рейтинга.
В9. На экзамен вынесено 50 вопросов, Андрей не выучил
5 из них. Найдите вероятность того, что ему попадется выученный вопрос.
 В10. Объем конуса равен
В10. Объем конуса равен
9π , а его высота равна 3. Найдите радиус основания конуса.
В11. В треугольнике АВС угол С равен 90°, АС =
12,
АB
= 20, Найдите sinA.
.
В12.На рисунке изображен
график ![]() — производной функции
— производной функции ![]() , определенной на интервале
, определенной на интервале ![]() . Найдите количество точек
. Найдите количество точек
максимума функции ![]() , принадлежащих отрезку
, принадлежащих отрезку ![]() .
.

Часть II
Запишите
сначала номер выполняемого задания (С1,С2, и т. д.), а
затем полное обоснованное решение и ответ. Ответы записывайте чётко и
разборчиво.
С1. Найдите ![]() , если
, если ![]() =0,8 и
=0,8 и ![]() .
.
С2.Расстояние между городами A и B равно
150 км. Из города A в город B выехал
автомобиль, а через 30 минут следом за ним со скоростью 90 км/ч выехал мотоциклист,
догнал автомобиль в городе C и повернул обратно. Когда он
вернулся в A, автомобиль прибыл в B. Найдите расстояние от A до
C. Ответ дайте в километрах.
С3.Найдите
промежутки возрастания и убывания функции и определите её точки экстремума f(x)=![]() ;
;
С4. а) Решить уравнение 2cos2x + 4 cos
(![]() –x)+1=0;
–x)+1=0;
б) Найдите все корни этого
уравнения, принадлежащие промежутку [-![]() –
–![]() ].
].
С5. Вычислить,
предварительно сделав рисунок, площадь фигуры, ограниченной линиями: ![]() .
.
С6.Решите неравенство ![]()
С7. Сторона основания
правильной треугольной призмы ![]() равна
равна
4, а высота этой призмы равна 3.
Найдите площадь полной поверхности призмы ![]() .
.
Вариант 2
Часть 1
Ответом к заданиям В1–В 12 является целое число
или конечная десятичная дробь. Единицы измерений писать не нужно.
В1. Найдите значение выражения ![]() ;
;
В2. Найдите значение выражения ![]() ;
;
В3. Только 90% из 30 000 выпускников города правильно решили
задачу № 1. Сколько выпускников из этого города правильно решили задачу № 1?
В4. Найдите m из равенства F=m![]() , если
, если
F=84 иa=12.
В5.
На день рождения полагается дарить букет из нечетного числа цветов. Чайные розы
стоят 40 рублей за штуку. У Вани есть 190 рублей. Из какого наибольшего числа
роз он может купить букет Маше на день рождения?
В6. Найдите корень
уравнения![]()
В7. Первый посев
семян петрушки рекомендуется проводить в апреле при дневной температуре воздуха
не менее +60 С. На рисунке показан прогноз дневной температуры
воздуха в первых трех неделях апреля. Определите, в течение скольких дней за
этот период можно производить посев петрушки.
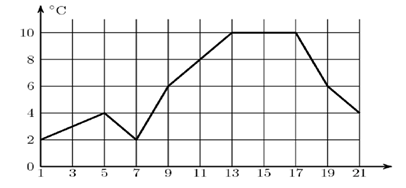
В8.
Рейтинговое агентство определяет рейтинг соотношения «цена-качество»
микроволновых печей. Рейтинг вычисляется на основе средней цены P
и оценок функциональности F,
качества Q и дизайна D
. Каждый отдельный показатель оценивается экспертами по 5-балльной шкале целыми
числами от 0 до 4. Итоговый рейтинг вычисляется по формуле
R=8(F+Q)+4D-0,01P
|
Модель печи |
Средняя цена |
Функциональность |
Качество |
Дизайн |
|
А |
4600 |
2 |
4 |
4 |
|
Б |
1600 |
2 |
2 |
0 |
|
В |
4900 |
4 |
1 |
4 |
|
Г |
5100 |
2 |
1 |
0 |
В таблице даны
оценки каждого показателя для нескольких моделей печей. Определите, какая
модель имеет наивысший рейтинг. В ответ запишите значение этого рейтинга.
В 9.На экзамен
вынесено 50 вопросов, Алексей не выучил 5 из них. Найдите вероятность того, что
ему попадется не выученный вопрос.
В10. Радиус основания цилиндра равен 3, высота равна 2. Найдите
объем цилиндра, деленный на π.
 В11. В треугольнике АВС
В11. В треугольнике АВС
угол Сравен 90°, АВ =10
АС =![]() . Найдите sin
. Найдите sin![]()
В12.На
рисунке изображён график ![]() — производной функции
— производной функции ![]() , определенной на интервале
, определенной на интервале ![]() . В какой точке отрезка
. В какой точке отрезка ![]() функция
функция ![]() принимает наибольшее
принимает наибольшее
значение?
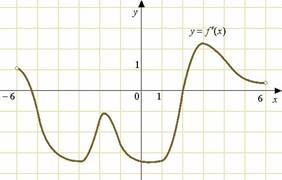
II часть
Запишите
сначала номер выполняемого задания (С1,С2, и т. д.), а
затем полное обоснованное решение и ответ. Ответы записывайте чётко и
разборчиво.
С1. Найдите ![]() ,
,
если ![]() =
=![]() ;;
;;
С2.Весной катер идёт против течения реки в 1
2/3 раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее.
Поэтому летом катер идёт против течения в 1 1/2 раза медленнее, чем по течению.
Найдите скорость течения весной (в км/ч).
С3.Найдите
промежутки возрастания и убывания функции и определите её точки экстремума f(x)=3![]() ;
;
С4. а) Решить уравнение sinx
=![]() ;
;
б) Найдите все корни этого уравнения, принадлежащие
промежутку [-![]() –
–![]() ].
].
С5.
Вычислить, предварительно сделав рисунок, площадь фигуры, ограниченной
линиями: ,осью Ох.
С6.Решите
неравенство![]()
С7. В
прямоугольном параллелепипеде![]() ребра
ребра
CD, CB и диагональ боковой
грани ![]() равны
равны
соответственно 3, 4 и 5. Найдите площадь боковой поверхности параллелепипеда ![]() .
.
Вариант
3
Часть 1
Ответом к заданиям В1–В 12 является целое число
или конечная десятичная дробь. Единицы измерений писать не нужно.
В1. Вычислите
значение выражения 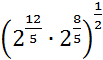
В2. Найдите значение выражения ![]()
В3.В сентябре 1 кг слив стоил 75 рублей. В октябре сливы
подорожали на 40%. Сколько рублей стоил 1 кг слив после подорожания в октябре?
В4. Площадь треугольника вычисляется по формуле S=1/2bcsinα,
где b и c — две
стороны треугольника, а α — угол между ними. Пользуясь этой формулой,
найдите площадь S, если b=18, c=16 и sinα=13.
В5. Для ремонта требуется 57 рулонов обоев. Какое наименьшее
количество пачек обойного клея нужно для такого ремонта, если 1 пачка клея
рассчитана на 5 рулонов?
В6.Решите уравнение ![]() .
.
В 7. На рисунке изображён график значений атмосферного давления
в некотором городе за три дня. По горизонтали указаны дни недели, по
вертикали — значения
атмосферного давления в миллиметрах ртутного столба.Определите по рисунку
наименьшее значение атмосферного давления
за данные три дня (в миллиметрах ртутного столба).
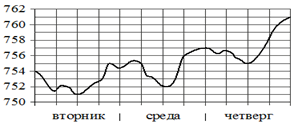
В8.Строительный подрядчик планирует купить 20 тонн
облицовочного кирпича у одного из трёх поставщиков. Один кирпич весит 5 кг.
Цена кирпича
и условия доставки всей покупки приведены в таблице.
|
Поставщик |
Цена (руб. |
Стоимость |
Специальные |
|
А |
49 |
8000 |
Нет |
|
Б |
55 |
7000 |
Доставка если превышает |
|
В |
62 |
6000 |
Доставка превышает |
Во сколько рублей
обойдётся наиболее дешёвый вариант покупки с доставкой?
В9. В среднем из 500 садовых насосов, поступивших в продажу,
25 подтекает. Найдите вероятность того, что случайно выбранный для контроля
насос подтекает.
В 10.Объём конуса
равен 25π,
а его высота равна 3. Найдите радиус основания конуса.
В 11. В треугольнике АВС угол С равен 90°, АВ =10,
ВС =6. Найдите sin![]()
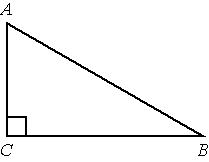
В12. На рисунке изображён график y=f′(x) — производной
функции f(x), определённой на
интервале (−9; 8). Найдите точку экстремума функции f(x) на
отрезке [−3; 3].
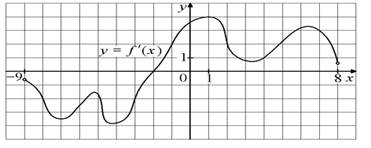
II часть
Запишите
сначала номер выполняемого задания (С1, С2, и т. д.), а
затем полное обоснованное решение и ответ. Ответы записывайте чётко и
разборчиво.
С1 Найдите значение![]() ,
,
если известно, что ![]()
![]() и
и ![]() <
<![]() <
<![]()
С2. Из пункта А в пункт В,
расстояние между которыми 75 км, одновременно выехали автомобилист и
велосипедист. Известно, что за час автомобилист проезжает на 40 км больше, чем
велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в
пункт В на 6 часов позже автомобилиста. Ответ дайте в км/ч.
С3. Напишите уравнение
касательной к графику функции ![]()
в точке с абсциссой ![]()
С4.а) Решите уравнение cos2x+![]() =0,75.
=0,75.
б) Найдите все корни этого уравнения, принадлежащие
отрезку [π; 5π/2].
С5. Найдите площадь
фигуры, ограниченной линиями у = 3х2, у = 0, х = 1 , х = 3.
С6.
Решите неравенство ![]() .
.
С7.ABCDA1B1C1D1 – прямоугольный
параллелепипед, стороны основания которого 10 см и 15 см, а его боковое ребро
равно 6 см. Найти ![]() параллелепипеда.
параллелепипеда.
Вариант
4
Часть 1
Ответом к заданиям В1–В 12 является целое число
или конечная десятичная дробь. Единицы измерений писать не нужно.
В1. Вычислите значение выражения![]() .
.
В2. Вычислите значение выражения ![]()
В3. Городской бюджет
составляет 67 млн рублей, а расходы на одну из его статей составили 15%.
Сколько миллионов рублей потрачено на эту статью бюджета?
В4.В фирме «Родник» стоимость (в рублях) колодца из
железобетонных колец рассчитывается по формуле C=6000+4100n,
где n — число колец, установленных при копании
колодца. Пользуясь этой формулой, рассчитайте стоимость колодца из 4 колец.
Ответ дайте в рублях.
В5. Шоколадка стоит 31
рубль. В воскресенье в супермаркете действует специальное предложение: заплатив
за две шоколадки, покупатель получает три (одну в подарок). Сколько шоколадок
можно получить на 170 рублей в воскресенье?
В6. Решите уравнение ![]()
.
В7. На
диаграмме показана среднемесячная температура воздуха
в Екатеринбурге (Свердловске) за каждый месяц 1973 года. По горизонтали
указываются месяцы, по вертикали —температура
в градусах Цельсия. Определите по диаграмме наибольшую среднемесячную
температуру во второй половине 1973 года. Ответ дайте в градусах Цельсия.
.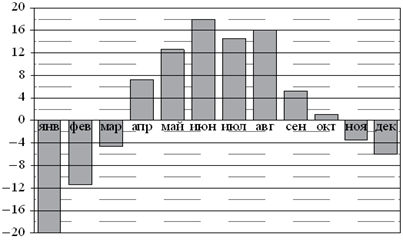
В8. Для транспортировки 40 тонн груза на 1000 км можно
воспользоваться услугами одной из трёх фирм-перевозчиков. Стоимость
перевозки и грузоподъёмность автомобилей каждого перевозчика указаны в
таблице. Во сколько рублей обойдётся наиболее дешёвый вариант перевозки?
|
Перевозчик |
Стоимость перевозки одним автомобилем |
Грузоподъёмность |
|
А |
3200 |
3,5 |
|
Б |
4100 |
5 |
|
В |
9500 |
12 |
В9. На семинар приехали 7 учёных из Норвегии, 7 из России и 6
из Испании. Каждый учёный подготовил один доклад. Порядок докладов определяется
случайным образом. Найдите вероятность того, что восьмым окажется доклад
учёного из России.
В10.
Даны два цилиндра. Радиус основания и высота первого цилиндра равны
соответственно 2 и 6, а второго — 6 и 4. Во сколько раз объём второго цилиндра больше
объёма первого?
В11.
На стороне BC прямоугольника ABCD, у которого AB=12 и AD=17, отмечена точка E так, что треугольник ABE равнобедренный. Найдите ED.
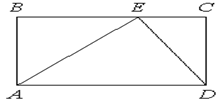
В12.
На рисунке изображён график функции y=f′(x) — производной
функции f(x), определённой на интервале (− 3 ; 8).
Найдите точку минимума функции f(x).
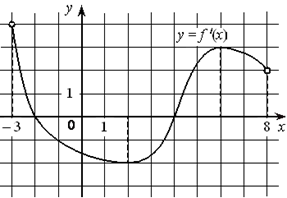
II часть
Запишите
сначала номер выполняемого задания (С1, С2, и т. д.), а
затем полное обоснованное решение и ответ. Ответы записывайте чётко и
разборчиво.
С1 Найдите значение![]() ,
,
если известно, что ![]()
![]() и 0<
и 0<![]() <π/2.
<π/2.
С2.Два велосипедиста
одновременно отправились в 88-километровый пробег. Первый ехал со скоростью, на
3 км/ч большей, чем скорость второго, и прибыл к финишу на 3 часа раньше
второго. Найти скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте
в км/ч.
С3. Найдите наименьшее значение функции y=x3−x2−8x+4 на
отрезке [1; 7].
С4.а)Решите уравнение sin2x=sinx−2cosx+1.
б) Укажите корни этого
уравнения, принадлежащие отрезку [3π/2; 3π].
С5. Найдите
площадь фигуры (предварительно сделайте рисунок), ограниченную:
а=1, b=3, f(x)=x![]() +4 и осью Ох.
+4 и осью Ох.
С6. Решите систему уравнений 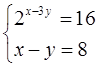
С7. Найдите объём правильной четырёхугольной пирамиды, сторона основания
которой равна 8 см, а боковое ребро равно ![]() .
.
Эталон ответов
1 вариант
|
Часть В |
В1 |
В2 |
В3 |
В4 |
В5 |
В6 |
В7 |
|
2 |
16 |
54000 |
22 |
9 |
7 |
13 |
|
|
В8 |
В9 |
В10 |
В11 |
В12 |
|||
|
А(1) |
9/10 |
3 |
4/5 |
Наибольшее значение функции в точке x=3 |
|||
|
Часть С |
С1 |
С2 |
С3 |
С4 |
C5 |
С6 |
С7 |
|
-0,6 |
90 км |
xmax= -1 |
– |
16 |
[-3;0,5] |
36+8 |
2 вариант
|
Часть В |
В1 |
В2 |
В3 |
В4 |
В5 |
В6 |
В7 |
|
2 |
4 |
27000 |
7 |
3 |
6 |
10 |
|
|
В8 |
В9 |
В10 |
В11 |
В12 |
В13 |
В14 |
|
|
A(18) |
1/10 |
18 |
1/5 |
Одна точка максимума x=3 |
Место |
||
|
Часть С |
С1 |
С2 |
С3 |
С4 |
C5 |
С6 |
С7 |
|
-12/13 |
5 км/ч |
xmax= – |
– |
6 |
(-1,5;2] |
42 |
3 вариант
|
Часть В |
В1 |
В2 |
В3 |
В4 |
В5 |
В6 |
В7 |
|
4 |
101 |
105 |
1872 |
12 |
-1 |
751 мл |
|
|
В8 |
В9 |
В10 |
В11 |
В12 |
В13 |
В14 |
|
|
124000р. |
1/20= 0,05 |
5 |
4/5=0,8 |
xmax=1 |
|||
|
Часть С |
С1 |
С2 |
С3 |
С4 |
C5 |
С6 |
С7 |
|
-7/25 |
10 км/ч |
9x+16 |
|
26 |
(5/3;4) |
600 |
4 вариант
|
Часть В |
В1 |
В2 |
В3 |
В4 |
В5 |
В6 |
В7 |
|
8 |
55 |
10.050.000 |
22400 |
7 |
725 |
16 |
|
|
В8 |
В9 |
В10 |
В11 |
В12 |
В13 |
В14 |
|
|
Б (328000) |
0,3 |
В 6 раз |
13 |
xmin=2 |
|||
|
Часть С |
С1 |
С2 |
С3 |
С4 |
C5 |
С6 |
С7 |
|
4/5 |
8 км/ч |
унаим=-8, унаиб=242 |
|
16 |
х=10, у=2 |
64 |
Шкала
оценки образовательных достижений
Каждое из
заданий В1–В12 считается выполненными верно, если экзаменуемый дал верный ответ
в виде целого числа или конечной десятичной дроби. Каждое верно выполненное
задание оценивается 1 баллом.
Количество
баллов, выставленных за выполнение заданий С1–С7, зависит от полноты решения и
правильности ответа.
Общие
требования к выполнению заданий с развёрнутым ответом: решение должно быть
математически грамотным, полным, все возможные случаи должны быть рассмотрены. Методы
решения, формы его записи иформы записи ответа могут быть разными. За решение,
в котором обоснованно получен правильный ответ, выставляется максимальное количество
баллов. Правильный ответ при отсутствии текста решения оценивается в 0 баллов.
|
Содержание |
Баллы |
|
Обоснованно получены верные ответы |
2 |
|
Обоснованно получен верный ответ в пункте а или ИЛИ получен неверный ответ из-за вычислительной ошибки, имеется верная последовательность всех шагов решения |
1 |
|
Решение |
0 |
|
Максимальный балл |
2 |
|
Процент (правильных |
Оценка уровня подготовки |
|
|
балл |
вербальный аналог |
|
|
90 ÷ 100 |
(24-26) 5 |
отлично |
|
80 ÷ 89 |
(20-23) 4 |
хорошо |
|
50 ÷ 79 |
(13-19) 3 |
удовлетворительно |
|
менее 70 |
(менее 12) 2 |
неудовлетворительно |
Перечень
материалов, оборудования и информационных источников, используемых в аттестации
Основные источники:
1. Алимов Ш.А., Колягин Ю.М.,
Ткачева М.В. и др. Алгебра и начала математического анализа (базовый уровень)
10-11 Просвещение, 2012 г.
Интернет ресурсы:
1.
www.mathematics.ru
2. http://ege.edu.ru;
3.http://www.fipi.ru.
4.http://www.itmathrepetitor.ru
Лист согласования
Дополнения и изменения к комплекту
КОС на учебный год
Дополнения
и изменения к комплекту КОСна __________ учебный год по дисциплине
_________________________________________________________________
В комплект
КОС внесены следующие изменения:
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
Дополнения
и изменения в комплекте КОС обсуждены на заседании ЦМК
_______________________________________________________
«_____» ____________ 20_____г.
(протокол № _______ ).
Председатель ЦМК ________________
/___________________/
Скачано с www.znanio.ru
Департамент охраны здоровья населения Кемеровской области
Новокузнецкий филиал
Государственное бюджетное профессиональное образовательное учреждение
«КЕМЕРОВСКИЙ ОБЛАСТНОЙ МЕДИЦИНСКИЙ КОЛЛЕДЖ»
УТВЕРЖДАЮ:
Зам. директора по УМР
_______Л.А. Лапотько
«___»_______2017г.
Комплект контрольно-оценочных средств по учебной дисциплине
Математика
программы подготовки специалистов среднего звена (ППССЗ) по специальности 34.02.01 Сестринское дело
Новокузнецк, 2017
Разработчики:
НФ ГБПОУ «КОМК», преподаватель математики первой квалификационной категории, Н. И. Шилепина
Эксперты от работодателя1:
____________________ ___________________ _________________________
(место работы, занимаемая должность, инициалы, фамилия)
____________________ ___________________ _________________________
(место работы, занимаемая должность, инициалы, фамилия)
Общие положения
Результатом освоения учебной дисциплины является освоение обучающимся знаний и умений, профессиональных компетенций, а также общих компетенций, формирующихся в процессе освоения ППССЗ в целом.
Формой аттестации по учебной дисциплине является зачет.
1. Формы аттестации по составляющим учебной дисциплины2
Таблица 1
|
Элемент учебной дисциплины |
Форма аттестации 3 |
|
Раздел 1. Связь математики с медициной |
зачет |
|
Раздел 2. Математический анализ |
зачет |
|
Раздел 3. Теория вероятности |
зачет |
|
Раздел 4. Математическая статистика |
зачет |
2. Результаты освоения учебной дисциплины, подлежащие проверке
2.1. Знания и умения
В результате контроля и оценки по учебной дисциплине осуществляется комплексная проверка следующих знаний и умений4:
Таблица 2
|
Знания |
Формы и методы контроля и оценки результата |
|
З 1. Значение математики в профессиональной деятельности и при освоении ППССЗ |
Оценка выполнения алгоритма решения задач. Оценка выступления с докладом. Оценка устного и письменного опроса. Оценка выполнения контрольной работы. |
|
З 2. Основные математические методы решения прикладных задач в области профессиональной деятельности |
Оценка выполнения алгоритма решения задач. Оценка выступления с докладом. Оценка устного и письменного опроса. Оценка выполнения контрольной работы. |
|
З 3. Основные понятия и методы теории вероятностей и математической статистики |
Оценка выполнения алгоритма решения задач. Оценка устного и письменного опроса. Оценка выполнения контрольной работы. |
|
З 4. Основы интегрального и дифференциального исчисления |
Оценка выполнения алгоритма решения задач. Оценка устного и письменного опроса. Оценка выполнения контрольной работы. |
Таблица 3
|
Умения |
Формы и методы контроля и оценки результата |
|
У 1. Решать прикладные задачи в области профессиональной деятельности. |
Оценка выполнения алгоритма решения задач. Оценка выступления с докладом. Оценка устного и письменного опроса. Оценка выполнения контрольной работы. |
2.2. Требования к портфолио
Тип портфолио не предусмотрен (портфолио документов, портфолио работ, рефлексивный портфолио, смешанный тип портфолио)
3. Оценка результатов освоения учебной дисциплины
3.1. Распределение оценивания результатов обучения по видам контроля
|
Наименование элемента умений и знаний |
Виды аттестации |
|
|
Текущий контроль |
Промежуточная аттестация |
|
|
У 1. Решать прикладные задачи в области профессиональной деятельности. |
+ |
+ |
|
З 1. Значение математики в профессиональной деятельности и при освоении ППССЗ |
+ |
+ |
|
+ |
+ |
|
+ |
+ |
|
+ |
+ |
3.2. Распределение типов контрольных заданий по элементам знаний и умений текущего контроля
|
Содержание учебного материала по программе УД |
Тип контрольного задания |
||||
|
У1 |
З1 |
З2 |
З3 |
З4 |
|
|
Раздел 1. Связь математики с медициной |
|||||
|
Тема 1.1. Применение математических методов в медицине |
З |
Зачет |
З |
||
|
Раздел 2. Математический анализ |
|||||
|
Тема 2.1. Предел функции |
Т |
||||
|
Тема 2.2. Дифференциальное исчисление |
Зачет |
И |
|||
|
Тема 2.3. Интегральное исчисление |
Зачет |
И |
|||
|
Раздел 3. Теория вероятности |
|||||
|
Тема 3.1. Основные понятия теории вероятностей |
Зачет |
Т |
|||
|
Тема 3.2. Случайные величины |
Зачет |
З |
|||
|
Раздел 4. Математическая статистика |
|||||
|
Тема 4.1. Основные понятия математической статистики |
Зачет |
Т |
Обозначения сокращений:
З – решение задач
И – индивидуальные задания
Т – тестовые задания
Зачет .
3.3. Типовые задания для оценки освоения учебной дисциплины
Тема 1.1. Применение математических методов в медицине
Вариант 1: решить предложенные задачи
Проверяемые результаты обучения4:
Оценка выполнения алгоритма решения задач
Текст задания:
1. С наступлением холодов количество больных с острыми респираторными заболеваниями (ОРЗ) увеличилось до 30 человек в день, а до этого составляло 10 человек. На сколько процентов возросло число больных с ОРЗ.
2. Имеется 60 г растворенного вещества. Сколько необходимо взять воды для приготовления 15 % раствора.
3. Сколько граммов соли и какой объем воды необходимо для приготовления 90 г 10 % раствора.
4. Больному прописано лекарство, которое нужно пить по 0,5 г 3 раза в день в течение 14 дня. В одной упаковке 8 таблеток лекарства по 0,5 г. Какого наименьшего количества упаковок хватит на весь курс лечения?
5. Одна таблетка лекарства весит 20 мг и содержит 5 % активного вещества. Ребенку в возрасте до 6 месяцев врач прописывает 1,4 мг активного вещества на каждый килограмм веса в сутки. Сколько таблеток этого лекарства следует дать ребенку весом в возрасте четырех месяцев и весом 5 кг в течение суток.
Критерии оценки:
5 правильно решенных задач оценка «5»;
4 правильно решенных задач оценка «4»;
3 правильно решенных задач оценка «3»;
Менее 3 – х правильно решенных задач оценка «2».
Вариант 2: решить предложенные задачи
Проверяемые результаты обучения4:
Оценка выполнения алгоритма решения задач
Текст задания:
1. С наступлением холодов количество больных с острыми респираторными заболеваниями (ОРЗ) увеличилось до 36 человек в день, а до этого составляло 12 человек. На сколько процентов возросло число больных с ОРЗ.
2. Имеется 90 г растворенного вещества. Сколько необходимо взять воды для приготовления 15 % раствора.
3. Сколько граммов соли и какой объем воды необходимо для приготовления 110 г 10 % раствора.
4. Больному прописано лекарство, которое нужно пить по 0,25 г 3 раза в день в течение 20 дней. В одной упаковке 8 таблеток лекарства по 0,25 г. Какого наименьшего количества упаковок хватит на весь курс лечения?
5. Одна таблетка лекарства весит 40 мг и содержит 7 % активного вещества. Ребенку в возрасте до 6 месяцев врач прописывает 1,4 мг активного вещества на каждый килограмм веса в сутки. Сколько таблеток этого лекарства следует дать ребенку весом в возрасте четырех месяцев и весом 6 кг в течение суток.
Критерии оценки:
5 правильно решенных задач оценка «5»;
4 правильно решенных задач оценка «4»;
3 правильно решенных задач оценка «3»;
Менее 3 – х правильно решенных задач оценка «2».
Вариант 3: решить предложенные задачи
Проверяемые результаты обучения4:
Оценка выполнения алгоритма решения задач
Текст задания:
1. С наступлением холодов количество больных с острыми респираторными заболеваниями (ОРЗ) увеличилось до 54 человек в день, а до этого составляло 18 человек. На сколько процентов возросло число больных с ОРЗ.
2. Имеется 44 г растворенного вещества. Сколько необходимо взять воды для приготовления 25 % раствора.
3. Сколько граммов соли и какой объем воды необходимо для приготовления 70 г 10 % раствора.
4. Больному прописано лекарство, которое нужно пить по 0,5 г 4 раза в день в течение 16 дней. В одной упаковке 10 таблеток лекарства по 0,5 г. Какого наименьшего количества упаковок хватит на весь курс лечения?
5. Одна таблетка лекарства весит 40 мг и содержит 14 % активного вещества. Ребенку в возрасте до 6 месяцев врач прописывает 0,8 мг активного вещества на каждый килограмм веса в сутки. Сколько таблеток этого лекарства следует дать ребенку весом в возрасте четырех месяцев и весом 7 кг в течение суток.
Критерии оценки:
5 правильно решенных задач оценка «5»;
4 правильно решенных задач оценка «4»;
3 правильно решенных задач оценка «3»;
Менее 3 – х правильно решенных задач оценка «2».
Вариант 4: решить предложенные задачи
Проверяемые результаты обучения4:
Оценка выполнения алгоритма решения задач
Текст задания:
1. С наступлением холодов количество больных с острыми респираторными заболеваниями (ОРЗ) увеличилось до 32 человек в день, а до этого составляло 16 человек. На сколько процентов возросло число больных с ОРЗ.
2. Имеется 80 г растворенного вещества. Сколько необходимо взять воды для приготовления 20 %
раствора.
3. Сколько граммов соли и какой объем воды необходимо для приготовления 85 г 10 % раствора.
4. Больному прописано лекарство, которое нужно пить по 0,25 г 2 раза в день в течение 16 дней. В одной упаковке 8 таблеток лекарства по 0,5 г. Какого наименьшего количества упаковок хватит на весь курс лечения?
5. Одна таблетка лекарства весит 20 мг и содержит 8 % активного вещества. Ребенку в возрасте до 6 месяцев врач прописывает 1,4 мг активного вещества на каждый килограмм веса в сутки. Сколько таблеток этого лекарства следует дать ребенку весом в возрасте пяти месяцев и весом 8 кг в течение суток.
Критерии оценки:
5 правильно решенных задач оценка «5»;
4 правильно решенных задач оценка «4»;
3 правильно решенных задач оценка «3»;
Менее 3 – х правильно решенных задач оценка «2».
Тема 2.1. Предел функции
Задание: выполните тестовые задания
Проверяемые результаты обучения4:
Оценка устного и письменного опроса
Текст задания:
-
Значение, равное 2, имеют два из приведенных ниже пределов:
-
-
Значение предела
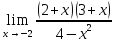 равно:
равно: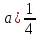
-
0
-
-
Функция
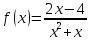 имеет разрыв в двух точках:
имеет разрыв в двух точках:-
-1
-
0
-
1
-
2
-
-
Предел
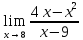 равен:
равен:-
-1
-
8
-
32
-
0
-
-
Предел
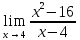 равен:
равен:-
-8
-
8
-
3
-
0
-
-
Предел
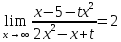 , если параметр t принимает значение, равное:
, если параметр t принимает значение, равное:-
-4
-
-0,25
4
-
-
Значение предела
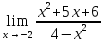 равно:
равно: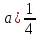
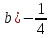
c)0
-
-
Установите соответствие между пределами и их значениями.
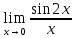
-
2
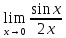
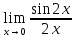
-
1
-
-
Предел
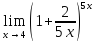 равен числу e в степени:
равен числу e в степени:-
2
-
10
-
-
Значение предела
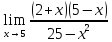 равно:
равно:
|
|
|
|
Критерии оценки:
9 – 10 правильных ответов оценка «5»;
8 – 7 правильных ответов оценка «4»;
6 правильных ответов оценка «3»;
Менее 6 – ти правильных ответов оценка «2».
Тема 2.2. Дифференциальное исчисление
Задание: найдите производную функции
Проверяемые результаты обучения4:
Оценка устного и письменного опроса
Текст задания:
|
Вариант № 1 |
Вариант № 2 |
|
|
|
|
|
|
|
|
3. |
|
|
4. |
|
|
5. |
|
|
6. |
|
|
7. |
|
Вариант № 3 |
Вариант № 4 |
|
|
1. |
|
|
|
|
|
3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант № 5 |
Вариант № 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант № 7 |
Вариант № 8 |
|
|
|
|
|
2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант № 9 |
Вариант № 10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант № 11 |
Вариант № 12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант № 13 |
Вариант № 14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Критерии оценки:
7 – 6 правильно решенных заданий оценка «5»;
5 правильно решенных заданий оценка «4»;
4 правильно решенных задания оценка «3»;
менее 4 – х правильно решенных заданий оценка «2».
Тема 2.3. Интегральное исчисление
Задание: вычислите определенные интегралы
Проверяемые результаты обучения4:
Оценка выполнения алгоритма решения задач
Текст задания:
|
Вариант № 1 |
Вариант № 2 |
|
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
|
5. |
|
Вариант № 3 |
Вариант № 4 |
|
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
|
5. |
|
Вариант № 5 |
Вариант № 6 |
|
1. |
1. |
|
2. |
2. |
|
3. |
3. |
|
4. |
4. |
|
5. |
5. |
|
Вариант № 7 |
Вариант № 8 |
|
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
|
5. |
|
Вариант № 9 |
Вариант № 10 |
|
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
|
5. |
|
Вариант № 11 |
Вариант № 12 |
|
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
|
5. |
|
Вариант № 13 |
Вариант № 14 |
|
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
|
5. |
Критерии оценки:
5 правильно решенных заданий оценка «5»;
4 правильно решенных заданий оценка «4»;
3 правильно решенных задания оценка «3»;
менее 3 – х правильно решенных заданий оценка «2».
Тема 3.1. Основные понятия теории вероятностей
Задание: выполните тест
Проверяемые результаты обучения4:
Оценка выполнения устного и письменного опроса
Текст задания:
-
В ящике 4 черных и 6 белых шара. Из урны случайным образом берут один шар. Вероятность того, что этот шар окажется черным, равна:
-
0,4
-
0,6
-
0,2
-
1
-
-
Если вероятность попадания в мишень составляет 0,3, тогда вероятность промаха равна:
-
0,3
-
0,5
-
0,7
-
1,3
-
-
Теория вероятности – это раздел математики, изучающий связи между:
-
экспериментальными данными;
-
функциями;
-
методами систематизации;
-
вероятностями случайных событий
-
-
студент сдаст экзамен на «5» с вероятностью 0,4, а второй студент с вероятностью 0,5. Вероятность сдачи этими студентами экзамена на отлично равна:
-
0
-
0,2
-
0,9
-
0,1
-
-
В ящике 3 желтых, 5 синих и 2 красных шара. Вероятность не вытащить желтый шар равна:
-
0,3
-
1
-
0,7
-
0
-
-
Из партии в 100 игрушек 2 бракованных. Относительная частота брака составляет:
-
0,2
-
0,02
-
0
-
2
-
-
Вероятность появления одного из двух несовместных событий А и В, если Р(А) = 0,4 и Р(В) = 0,3 равна:
-
0,1
-
0,12
-
0,3
-
0,7
-
-
Вероятность выпадения трех очков при бросании игрального кубика равна:
-
1/36
-
1/6
-
0
-
1
-
-
Вероятность появления двух единиц при бросании двух игральных кубиков равна:
-
1/36
-
1/6
-
0
-
1
-
-
Вероятность вытащить из колоды карт в 36 штук карту пиковой масти равна:
|
|
|
|
Критерии оценки:
10 правильных ответов оценка «5»;
9 правильных ответов оценка «4»;
8 правильных ответов оценка «3»;
менее 8 – ми правильных ответов оценка «2».
Тема 3.2. Случайные величины
Задание: решите предложенные задачи
Проверяемые результаты обучения4:
Оценка выполнения алгоритма решения задач
Текст задания:
Найдите математическое ожидание, дисперсию и среднее квадратическое отклонение дискретной случайной величины Х, если ее закон распределения задан таблицей:
Вариант № 1
|
Х |
17 |
19 |
20 |
25 |
31 |
32 |
33 |
40 |
41 |
|
Р |
0,05 |
0,1 |
0,11 |
0,15 |
0,2 |
0,15 |
0,1 |
0,09 |
0,05 |
Вариант № 2
|
Х |
5 |
9 |
10 |
12 |
15 |
18 |
20 |
23 |
24 |
|
Р |
0,01 |
0,03 |
0,05 |
0,15 |
0,43 |
0,15 |
0,1 |
0,05 |
0,03 |
Вариант № 3
|
Х |
90 |
92 |
93 |
98 |
104 |
105 |
106 |
113 |
114 |
|
Р |
0,05 |
0,1 |
0,11 |
0,15 |
0,2 |
0,15 |
0,1 |
0,09 |
0,05 |
Вариант № 4
|
Х |
18 |
19 |
21 |
25 |
28 |
32 |
34 |
39 |
40 |
|
Р |
0,05 |
0,1 |
0,11 |
0,12 |
0,24 |
0,12 |
0,11 |
0,1 |
0,05 |
Вариант № 5
|
Х |
47 |
49 |
50 |
51 |
52 |
53 |
55 |
60 |
61 |
|
Р |
0,01 |
0,03 |
0,05 |
0,15 |
0,4 |
0,18 |
0,1 |
0,05 |
0,03 |
Вариант № 6
|
Х |
1 |
5 |
10 |
11 |
15 |
19 |
25 |
30 |
35 |
|
Р |
0,02 |
0,08 |
0,13 |
0,16 |
0,3 |
0,16 |
0,1 |
0,04 |
0,01 |
Вариант № 7
|
Х |
107 |
109 |
112 |
125 |
131 |
132 |
133 |
140 |
141 |
|
Р |
0,05 |
0,1 |
0,11 |
0,15 |
0,2 |
0,15 |
0,1 |
0,09 |
0,05 |
Вариант № 8
|
Х |
67 |
68 |
71 |
74 |
76 |
78 |
81 |
84 |
88 |
|
Р |
0,05 |
0,1 |
0,11 |
0,15 |
0,17 |
0,15 |
0,12 |
0,1 |
0,05 |
Вариант № 9
|
Х |
12 |
15 |
18 |
21 |
22 |
25 |
29 |
31 |
32 |
|
Р |
0,05 |
0,1 |
0,11 |
0,15 |
0,2 |
0,15 |
0,1 |
0,09 |
0,05 |
Вариант № 10
|
Х |
1,7 |
1,9 |
2,0 |
2,5 |
3,1 |
3,2 |
3,3 |
4,0 |
4,1 |
|
Р |
0,01 |
0,04 |
0,1 |
0,15 |
0,4 |
0,15 |
0,09 |
0,04 |
0,02 |
Вариант № 11
|
Х |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
|
Р |
0,05 |
0,1 |
0,11 |
0,15 |
0,2 |
0,15 |
0,1 |
0,09 |
0,05 |
Вариант № 12
|
Х |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
32 |
33 |
|
Р |
0,01 |
0,03 |
0,05 |
0,15 |
0,43 |
0,15 |
0,1 |
0,05 |
0,03 |
Вариант № 13
|
Х |
30 |
31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
|
Р |
0,05 |
0,1 |
0,11 |
0,15 |
0,2 |
0,15 |
0,1 |
0,09 |
0,05 |
Вариант № 14
|
Х |
35 |
36 |
37 |
38 |
39 |
40 |
41 |
42 |
43 |
|
Р |
0,05 |
0,1 |
0,11 |
0,12 |
0,24 |
0,12 |
0,11 |
0,1 |
0,05 |
Критерии оценки:
0 – ошибок оценка «5»;
1 – ошибка оценка «4»;
2 – ошибки оценка «3»;
более 2 – ух ошибок оценка «2».
Тема 4.1. Основные понятия математической статистики
Задание: выполните тест
Проверяемые результаты обучения4:
Оценка выполнения устного и письменного опроса
Текст задания:
-
Количество способов составления списка из 5 человек равно:
-
120
-
5
-
1
-
2
-
-
Закон распределения вероятностей дискретной случайной величины Х имеет вид:
|
Х |
2 |
5 |
8 |
|
Р |
0,1 |
р2 |
0,6 |
Тогда вероятность р2 равна:
|
|
|
|
-
По данному распределению выборки значение выборочной средней равно:
xi
2
5
8
pi
1
4
5
-
3,9
-
3,5
-
4
-
6,2
-
-
Составьте закон распределения случайной величины Х – числа выигравших лотерейных билетов из двух купленных, если вероятность выигрыша любого лотерейного билета равна 0,1, сопоставляя значения случайной величины и их вероятности.
-
Х = 0
-
0,81
-
Х = 1
-
0,18
-
Х = 2
-
0,01
-
-
Полигон – это:
-
график функции;
-
графическое изображение интервального ряда распределения;
-
графическое изображение дискретного ряда распределения;
-
графическое изображение отношения частоты к относительной частоте.
-
-
Математическая статистика – это:
-
раздел математики, изучающий связи между случайными величинами;
-
раздел математики, посвященный методам систематизации, обработки и исследования статистических данных;
-
раздел математики, изучающий связи между методами систематизации;
-
раздел математики, изучающий связи между функциями.
-
-
Гистограмма – это
-
график функции;
-
графическое изображение интервального ряда распределения;
-
графическое изображение дискретного ряда распределения;
-
графическое изображение отношения частоты к относительной частоте.
-
-
Выборка – это:
-
множество объектов, случайно отобранных из генеральной совокупности;
-
множество объектов, однородных относительно нескольких признаков;
-
множество объектов, однородных относительно одного признака;
-
множество объектов, собранных по одному признаку.
-
-
По данному распределению выборки значение выборочной средней равно:
xi
4
7
8
pi
3
2
5
-
6,6
-
6
-
7
-
6,3
-
-
Из 400 зарегистрированных браков 50 распадаются в течение первого года. Относительная частота расторжения брака в течение первого года равна:
|
|
|
|
Критерии оценки:
0 – ошибок оценка «5»;
2 – ошибки оценка «4»;
4 – ошибки оценка «3»;
более 4 – х ошибок оценка «2».
5. Контрольно-оценочные материалы для зачета
I. ПАСПОРТ
Назначение:
КОМ предназначены для контроля и оценки результатов освоения
учебной дисциплины Математика
по специальности СПО: 34.02.01 Сестринское дело
II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ/ АТТЕСТУЕМОГО
Вариант № 1
Задание 1
Коды проверяемых знаний и умений: У1, З4
Инструкция:
Внимательно прочитайте задание.
Вы можете воспользоваться таблицей дифференцирования
Время выполнения задания – 10 минут
Текст задания:
Вычислите производную функции у = ln (+
)
Задание 2
Коды проверяемых знаний и умений: У1, З4
Инструкция:
Внимательно прочитайте задание.
Вы можете воспользоваться таблицей интегрирования
Время выполнения задания – 10 минут
Текст задания: Вычислите интеграл
Задание 3
Коды проверяемых знаний и умений: З3
Инструкция:
Внимательно прочитайте задание.
Вы можете воспользоваться (указать, чем) ____________
Время выполнения задания – ___________________
Текст задания:
Вычислите
Задание 4
Коды проверяемых знаний и умений: _______
Инструкция:
Внимательно прочитайте задание.
Вы можете воспользоваться (указать, чем) ____________
Время выполнения задания – ___________________
Текст задания:
Ребенок родился с массой 2 кг 700г. Сейчас ему 2,5 месяцев. Рассчитайте суточную и разовую потребность в питании.
Задание 5
Коды проверяемых знаний и умений: _______
Инструкция:
Внимательно прочитайте задание.
Вы можете воспользоваться (указать, чем) ____________
Время выполнения задания – ___________________
Текст задания: Имеется 80 мл 20 % раствор лекарственного препарата. Сколько мг лекарственного вещества содержится в этом препарате?
Задание 6
Коды проверяемых знаний и умений: ______
Инструкция:
Внимательно прочитайте задание.
Вы можете воспользоваться (указать, чем) ____________
Время выполнения задания – ___________________
Текст задания: Пациенту для восстановления энергетического обмена ввели за сутки 1,2 л 30% раствора глюкозы. Сколько граммов чистой глюкозы было введено больному? Сколько мл инсулина надо ввести пациенту для исключения нарушения метаболических процессов в организме (1 ЕД расщепляет 4 г сахара, 1 мл инсулина содержит 40 ЕД).
Задание 7
Коды проверяемых знаний и умений: _______
Инструкция:
Внимательно прочитайте задание.
Вы можете воспользоваться (указать, чем) ____________
Время выполнения задания – ___________________
Текст задания: В урне 4 белых и 2 черных шара. Из урны берут один шар. Вероятность того, что шар окажется белым, равна?
Задание 8
Коды проверяемых знаний и умений: _______
Инструкция:
Внимательно прочитайте задание.
Вы можете воспользоваться (указать, чем) ____________
Время выполнения задания – ___________________
Текст задания: При судорожном синдроме ребенку надо ввести в/м 30% препарат в разовой дозе 50мг/кг от массы. Масса пациента 15кг. Сколько мл препарата вы введете?
Задание 9
Коды проверяемых знаний и умений: _______
Инструкция:
Внимательно прочитайте задание.
Вы можете воспользоваться (указать, чем) ____________
Время выполнения задания – ___________________
Текст задания: Пациенту в сутки сделано 5 инъекций антибиотика. Всего введено 2 000 000 ЕД. Сколько мл надо набрать в шприц при разведении 1: 2? Сколько растворителя потребовалось для такого разведения?
Задание 10
Коды проверяемых знаний и умений: _______
Инструкция:
Внимательно прочитайте задание.
Вы можете воспользоваться (указать, чем) ____________
Время выполнения задания – ___________________
Текст задания: Вероятность распределения случайной величины Х равна:
|
Х |
6 |
2 |
8 |
|
р |
0,1 |
|
0,4 |
Вариант № 2
Задание 1
Коды проверяемых знаний и умений: У1, З4
Инструкция:
Внимательно прочитайте задание.
Вы можете воспользоваться таблицей дифференцирования
Время выполнения задания – 10 минут
Текст задания:
Найти производные функции:
Задание 2
Коды проверяемых знаний и умений: У1, З4
Инструкция:
Внимательно прочитайте задание.
Вы можете воспользоваться таблицей интегрирования
Время выполнения задания – 10 минут
Текст задания: Вычислить интеграл: .
Задание 3
Коды проверяемых знаний и умений: З3
Инструкция:
Внимательно прочитайте задание.
Вы можете воспользоваться (указать, чем) ____________
Время выполнения задания – ___________________
Текст задания:
Вычислить: .
Задание 4
Коды проверяемых знаний и умений: _______
Инструкция:
Внимательно прочитайте задание.
Вы можете воспользоваться (указать, чем) ____________
Время выполнения задания – ___________________
Текст задания:
Сколько граммов фурацилина находится в 300 мл 0,02% раствора
Задание 5
Коды проверяемых знаний и умений: _______
Инструкция:
Внимательно прочитайте задание.
Вы можете воспользоваться (указать, чем) ____________
Время выполнения задания – ___________________
Текст задания: Ребенок родился с массой 2 кг 800г. Сейчас ему 5,5 месяцев. Рассчитайте суточную и разовую потребность в питании.
Задание 6
Коды проверяемых знаний и умений: ______
Инструкция:
Внимательно прочитайте задание.
Вы можете воспользоваться (указать, чем) ____________
Время выполнения задания – ___________________
Текст задания: Имеется 50 мл 20 % раствор лекарственного препарата. Сколько мг лекарственного вещества содержится в этом препарате?
Задание 7
Коды проверяемых знаний и умений: _______
Инструкция:
Внимательно прочитайте задание.
Вы можете воспользоваться (указать, чем) ____________
Время выполнения задания – ___________________
Текст задания: В больнице 220 койко-мест. Из них заполнено 172 места. На сколько процентов заполнена больница?
Задание 8
Коды проверяемых знаний и умений: _______
Инструкция:
Внимательно прочитайте задание.
Вы можете воспользоваться (указать, чем) ____________
Время выполнения задания – ___________________
Текст задания: Каждая буква слова «РЕМЕСЛО» написана на отдельной карточке, затем карточки перемешаны. Вынимаем три карточки наугад. Какова вероятность получить слово «ЛЕС»?
Задание 9
Коды проверяемых знаний и умений: _______
Инструкция:
Внимательно прочитайте задание.
Вы можете воспользоваться (указать, чем) ____________
Время выполнения задания – ___________________
Текст задания: Сколько нужно взять 10% раствора хлорной извести и воды для приготовления 7л 0,5% раствора.
Задание 10
Коды проверяемых знаний и умений: _______
Инструкция:
Внимательно прочитайте задание.
Вы можете воспользоваться (указать, чем) ____________
Время выполнения задания – ___________________
Текст задания: Математическое ожидание дискретной случайной величины равно 6,2. Из заданного закона распределения составляет:
|
X |
2 |
|
8 |
|
p |
0,1 |
0,4 |
0,5 |
Вариант № 3
Задание 1
Коды проверяемых знаний и умений: У1, З4
Инструкция:
Внимательно прочитайте задание.
Вы можете воспользоваться таблицей дифференцирования
Время выполнения задания – 10 минут
Текст задания:
Найти производную функции:
Задание 2
Коды проверяемых знаний и умений: У1, З4
Инструкция:
Внимательно прочитайте задание.
Вы можете воспользоваться таблицей интегрирования
Время выполнения задания – 10 минут
Текст задания: Вычислить интеграл:
Задание 3
Коды проверяемых знаний и умений: З3
Инструкция:
Внимательно прочитайте задание.
Вы можете воспользоваться (указать, чем) ____________
Время выполнения задания – ___________________
Текст задания:
В штате отделения 5 медсестер. Сколькими способами можно сформировать бригаду из двух медсестер для диспансеризации?
Задание 4
Коды проверяемых знаний и умений: _______
Инструкция:
Внимательно прочитайте задание.
Вы можете воспользоваться (указать, чем) ____________
Время выполнения задания – ___________________
Текст задания:
Форма выпуска витамина Е – флаконы по 10мл 5% масляного раствора. Ребенку витамина Е дается в дозе 1мг/кг массы. В 1мл содержится 20 капель масляного раствора. Сколько капель надо назначить ребенку массой 10 кг 200г?
Задание 5
Коды проверяемых знаний и умений: _______
Инструкция:
Внимательно прочитайте задание.
Вы можете воспользоваться (указать, чем) ____________
Время выполнения задания – ___________________
Текст задания: Мышцы взрослого человека составляют 40% от общей массы тела. Какова масса мышц сорокалетнего мужчины, если его вес составляет 90 кг?
Задание 6
Коды проверяемых знаний и умений: ______
Инструкция:
Внимательно прочитайте задание.
Вы можете воспользоваться (указать, чем) ____________
Время выполнения задания – ___________________
Текст задания: На каждые 5°С свыше 25°С окружающей среды теряется дополнительно 500 мл жидкости. Рассчитать, какое количество жидкости теряет человек при t = 40°С.
Задание 7
Коды проверяемых знаний и умений: _______
Инструкция:
Внимательно прочитайте задание.
Вы можете воспользоваться (указать, чем) ____________
Время выполнения задания – ___________________
Текст задания: В больнице 250 койко-мест. Из них заполнено 150 места. На сколько процентов заполнена больница?
Задание 8
Коды проверяемых знаний и умений: _______
Инструкция:
Внимательно прочитайте задание.
Вы можете воспользоваться (указать, чем) ____________
Время выполнения задания – ___________________
Текст задания: В сборнике билетов по математике всего 20 билетов, в 7 из них встречается вопрос по производной. Найдите вероятность того, что в случайно выбранном на экзамене билете студенту не достанется вопроса по производной.
Задание 9
Коды проверяемых знаний и умений: _______
Инструкция:
Внимательно прочитайте задание.
Вы можете воспользоваться (указать, чем) ____________
Время выполнения задания – ___________________
Текст задания: Приготовить 1 литр 1% раствора хлорной извести для обработки инвентаря из 1 литра маточного 10% раствора.
Задание 10
Коды проверяемых знаний и умений: _______
Инструкция:
Внимательно прочитайте задание.
Вы можете воспользоваться (указать, чем) ____________
Время выполнения задания – ___________________
Текст задания: Математическое ожидание дискретной случайной величины заданная законом распределения равна:
|
X |
2 |
5 |
8 |
|
p |
0,1 |
0,4 |
0,5 |
III. ПАКЕТ ЭКЗАМЕНАТОРА/ ПРЕПОДАВАТЕЛЯ
III а. УСЛОВИЯ
Количество вариантов каждого задания / пакетов заданий для экзаменующегося/ аттестуемого: 3 варианта по 10 заданий
Время выполнения каждого задания: всего на выполнение 10 заданий отводиться 90 минут.
Оснащение: листы с вариантами заданий, папки с формулами, ручка с синими чернилами, карандаш, ластик, листы с печатью внесения ответов
III б. КРИТЕРИИ ОЦЕНКИ
-
Оценивание в ходе выполнения задания
Таблица 4
|
Коды проверяемых знаний и умений |
Оценка |
|
У 1. Решать прикладные задачи в области профессиональной деятельности. |
Выполнения контрольной работы. |
|
З 1. Значение математики в профессиональной деятельности и при освоении ППССЗ. |
Выполнения контрольной работы |
|
З 2. основные математические методы решения прикладных задач в области профессиональной деятельности. |
Выполнения контрольной работы |
|
З 3. Основные понятия и методы теории вероятностей и математической статистики. |
Выполнения контрольной работы |
|
З 4. Основы интегрального и дифференциального исчисления. |
Выполнения контрольной работы |
1 Рекомендуется согласовать оценочные средства с представителями профессионального сообщества (работниками и (или) специалистами по профилю получаемого образования, руководителями организаций отрасли и др.) и приложить документы, подтверждающие факт согласования
2 Формы аттестации указываются в соответствии с планом учебного процесса образовательного учреждения, в случае отсутствия аттестации по тем или иным элементам УД в соответствующей строке ставится прочерк.
3 Указывается, предусмотрена ли промежуточная аттестация по элементам УД; если предусмотрена, то в какой форме. Эти сведения указываются в соответствии с локальными нормативными актами, регламентирующими процедуру и содержание аттестации.
4 Знания и умения указываются в соответствии с разделом 2, формы и методы контроля и оценки результата – в соответствии с разделом 4 рабочей программы УД.