Как найти матрицу расстояний точек

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 23 декабря 2021 года; проверки требует 1 правка.

Матрица расстояний — это квадратная матрица типа «объект-объект» (порядка n), содержащая в качестве элементов расстояния между объектами в метрическом пространстве.

Свойства[править | править код]

Свойства матрицы являются отражением свойств самих расстояний^[1]:

1. симметричность относительно диагонали, то есть ;
2. отражение свойства тождественности расстояния в матрице расстояний проявляется в наличии 0 по диагонали матрицы, так как расстояние объекта с самим собой очевидно равно 0, а также в наличии нулевых значений для абсолютно сходных объектов;
3. значения расстояний в матрице всегда неотрицательны
4. неравенство треугольника принимает форму для всех , и .

В общем виде матрица выглядит так:

В широком смысле расстояния являются отражением такого понятия как различие, что двойственно понятию сходства, а элементы матрицы различия (в общем виде — матрицы дивергенций) двойственны элементам матрицы сходства (в общем виде — матрицы конвергенций). Связь между мерой сходства и мерой различия можно записать как , где F — мера различия; K — мера сходства. Следовательно, все свойства мер сходства можно экстраполировать на соответствующие им меры различия с помощью простого преобразования и наоборот.
Визуально отношения между объектами можно представить с помощью графовых алгоритмов кластеризации. Можно сказать, что расстояния используются намного чаще, чем меры сходства: их чаще реализуют в статистических программах (Statistica, SPSS и др.) в модуле кластерного анализа.

Расстояния[править | править код]

Известно^[2], что существует обобщённая мера расстояний, предложенная Германом Минковским:

В вышеуказанное семейство расстояний входит:

Существуют используемые расстояния и вне данного семейства. Наиболее известным является расстояние Махаланобиса.

Также интересно в качестве удачной иллюстрации связи мер сходства и различия расстояние Юрцева, двойственное мере сходства Браун-Бланке^[5]:

Пример[править | править код]

На плоскости расположено шесть различных точек (см. изображение). В качестве метрики выбрано расстояние Евклида в пикселях.

Соответствующая матрица расстояний будет равна

	a	b	c	d	e	f
a	0	184	222	177	216	231
b	184	0	45	123	128	200
c	222	45	0	129	121	203
d	177	123	129	0	46	83
e	216	128	121	46	0	83
f	231	200	203	83	83	0

Полученную матрицу можно изобразить в виде тепловой карты. Здесь более тёмный цвет соответствует меньшему расстоянию между точками.

Примечания[править | править код]

From Wikipedia, the free encyclopedia

In mathematics, a Euclidean distance matrix is an n×n matrix representing the spacing of a set of n points in Euclidean space.
For points in k-dimensional space ℝ^k, the elements of their Euclidean distance matrix A are given by squares of distances between them.
That is

where denotes the Euclidean norm on ℝ^k.

In the context of (not necessarily Euclidean) distance matrices, the entries are usually defined directly as distances, not their squares.
However, in the Euclidean case, squares of distances are used to avoid computing square roots and to simplify relevant theorems and algorithms.

Euclidean distance matrices are closely related to Gram matrices (matrices of dot products, describing norms of vectors and angles between them).
The latter are easily analyzed using methods of linear algebra.
This allows to characterize Euclidean distance matrices and recover the points that realize it.
A realization, if it exists, is unique up to rigid transformations, i.e. distance-preserving transformations of Euclidean space (rotations, reflections, translations).

In practical applications, distances are noisy measurements or come from arbitrary dissimilarity estimates (not necessarily metric).
The goal may be to visualize such data by points in Euclidean space whose distance matrix approximates a given dissimilarity matrix as well as possible — this is known as multidimensional scaling.
Alternatively, given two sets of data already represented by points in Euclidean space, one may ask how similar they are in shape, that is, how closely can they be related by a distance-preserving transformation — this is Procrustes analysis.
Some of the distances may also be missing or come unlabelled (as an unordered set or multiset instead of a matrix), leading to more complex algorithmic tasks, such as the graph realization problem or the turnpike problem (for points on a line).^[1][2]

Properties[edit]

By the fact that Euclidean distance is a metric, the matrix A has the following properties.

In dimension k, a Euclidean distance matrix has rank less than or equal to k+2. If the points are in general position, the rank is exactly min(n, k + 2).

Distances can be shrunk by any power to obtain another Euclidean distance matrix. That is, if is a Euclidean distance matrix, then is a Euclidean distance matrix for every 0<s<1.^[3]

Relation to Gram matrix[edit]

The Gram matrix of a sequence of points in k-dimensional space ℝ^k
is the n×n matrix of their dot products (here a point is thought of as a vector from 0 to that point):

, where is the angle between the vector and .

In particular

is the square of the distance of from 0.

Thus the Gram matrix describes norms and angles of vectors (from 0 to) .

Let be the k×n matrix containing as columns.
Then

, because (seeing as a column vector).

Matrices that can be decomposed as , that is, Gram matrices of some sequence of vectors (columns of ), are well understood — these are precisely positive semidefinite matrices.

To relate the Euclidean distance matrix to the Gram matrix, observe that

That is, the norms and angles determine the distances.
Note that the Gram matrix contains additional information: distances from 0.

Conversely, distances between pairs of n+1 points determine dot products between n vectors (1≤i≤n):

(this is known as the polarization identity).

Characterizations[edit]

For a n×n matrix A, a sequence of points in k-dimensional Euclidean space ℝ^k
is called a realization of A in ℝ^k if A is their Euclidean distance matrix.
One can assume without loss of generality that (because translating by preserves distances).

This follows from the previous discussion because G is positive semidefinite of rank at most k if and only if it can be decomposed as where X is an k×n matrix.^[7]
Moreover, the columns of X give a realization in ℝ^k.
Therefore, any method to decompose G allows to find a realization.
The two main approaches are variants of Cholesky decomposition or using spectral decompositions to find the principal square root of G, see Definite matrix#Decomposition.

The statement of theorem distinguishes the first point . A more symmetric variant of the same theorem is the following:

Other characterizations involve Cayley–Menger determinants.
In particular, these allow to show that a symmetric hollow n×n matrix is realizable in ℝ^k if and only if every (k+3)×(k+3) principal submatrix is.
In other words, a semimetric on finitely many points is embedabble isometrically in ℝ^k if and only if every k+3 points are.^[9]

In practice, the definiteness or rank conditions may fail due to numerical errors, noise in measurements, or due to the data not coming from actual Euclidean distances.
Points that realize optimally similar distances can then be found by semidefinite approximation (and low rank approximation, if desired) using linear algebraic tools such as singular value decomposition or semidefinite programming.
This is known as multidimensional scaling.
Variants of these methods can also deal with incomplete distance data.

Unlabeled data, that is, a set or multiset of distances not assigned to particular pairs, is much more difficult to deal with.
Such data arises, for example, in DNA sequencing (specifically, genome recovery from partial digest) or phase retrieval.
Two sets of points are called homometric if they have the same multiset of distances (but are not necessarily related by a rigid transformation).
Deciding whether a given multiset of n(n-1)/2 distances can be realized in a given dimension k is strongly NP-hard.
In one dimension this is known as the turnpike problem; it is an open question whether it can be solved in polynomial time.
When the multiset of distances is given with error bars, even the one dimensional case is NP-hard.
Nevertheless, practical algorithms exist for many cases, e.g. random points.^[10][11][12]

Uniqueness of representations[edit]

Given a Euclidean distance matrix, the sequence of points that realize it is unique up to rigid transformations – these are isometries of Euclidean space: rotations, reflections, translations, and their compositions.^[1]

Theorem — 
Let and be two sequences of points in k-dimensional Euclidean space ℝ^k.
The distances and are equal (for all 1≤i,j≤n) if and only if there is a rigid transformation of ℝ^k mapping to (for all 1≤i≤n).

In applications, when distances don’t match exactly, Procrustes analysis aims to relate two point sets as close as possible via rigid transformations, usually using singular value decomposition.
The ordinary Euclidean case is known as the orthogonal Procrustes problem or Wahba’s problem (when observations are weighted to account for varying uncertainties).
Examples of applications include determining orientations of satellites, comparing molecule structure (in cheminformatics), protein structure (structural alignment in bioinformatics), or bone structure (statistical shape analysis in biology).

See also[edit]

• Adjacency matrix
• Coplanarity
• Distance geometry
• Hollow matrix
• Distance matrix
• Euclidean random matrix
• Classical multidimensional scaling, a visualization technique that approximates an arbitrary dissimilarity matrix by a Euclidean distance matrix
• Cayley–Menger determinant
• Semidefinite embedding

Notes[edit]

References[edit]

• Dokmanic, Ivan; Parhizkar, Reza; Ranieri, Juri; Vetterli, Martin (2015). “Euclidean Distance Matrices: Essential theory, algorithms, and applications”. IEEE Signal Processing Magazine. 32 (6): 12–30. arXiv:1502.07541. doi:10.1109/MSP.2015.2398954. ISSN 1558-0792. S2CID 8603398.
• James E. Gentle (2007). Matrix Algebra: Theory, Computations, and Applications in Statistics. Springer-Verlag. p. 299. ISBN 978-0-387-70872-0.
• So, Anthony Man-Cho (2007). A Semidefinite Programming Approach to the Graph Realization Problem: Theory, Applications and Extensions (PDF) (PhD).
• Liberti, Leo; Lavor, Carlile; Maculan, Nelson; Mucherino, Antonio (2014). “Euclidean Distance Geometry and Applications”. SIAM Review. 56 (1): 3–69. arXiv:1205.0349. doi:10.1137/120875909. ISSN 0036-1445. S2CID 15472897.
• Alfakih, Abdo Y. (2018). Euclidean Distance Matrices and Their Applications in Rigidity Theory. Cham: Springer International Publishing. doi:10.1007/978-3-319-97846-8. ISBN 978-3-319-97845-1.

В математике матрица евклидовых расстояний представляет собой n × n матрица, представляющая интервал набора из n точек в евклидовом пространстве. Для точек x 1, x 2,…, xn { displaystyle x_ {1}, x_ {2}, ldots, x_ {n}}в k-мерном пространстве ℝ элементы матрицы их евклидовых расстояний A задаются квадратами расстояний между ними. То есть

A = (a i j); aij знак равно dij 2 знак равно ‖ xi – xj ‖ 2 { displaystyle { begin {align} A = (a_ {ij}); \ a_ {ij} = d_ {ij} ^ {2} ; = ; lVert x_ {i} -x_ {j} rVert ^ {2} end {align}}}

где ‖ ⋅ ‖ { displaystyle | cdot |}обозначает евклидову норму на.

A = [0 d 12 2 d 13 2… d 1 n 2 d 21 2 0 d 23 2… d 2 n 2 d 31 2 d 32 2 0… d 3 n 2 ⋮ ⋮ ⋮ ⋱ ⋮ dn 1 2 dn 2 2 dn 3 2… 0] { displaystyle A = { begin {bmatrix} 0 d_ {12} ^ {2} d_ {13} ^ {2} dots d_ {1n} ^ {2} \ d_ {21} ^ {2} 0 d_ {23} ^ {2} dots d_ {2n} ^ {2} \ d_ {31} ^ {2} d_ {32} ^ {2} 0 dots d_ {3n } ^ {2} \ vdots vdots vdots ddots vdots \ d_ {n1} ^ {2} d_ {n2} ^ {2} d_ {n3} ^ {2} точки 0 \ end {bmatrix}}}

В контексте (не обязательно евклидова) матриц расстояний элементы обычно определяются непосредственно как расстояния, а не их квадраты. Однако в евклидовом случае квадраты расстояний используются, чтобы избежать вычисления квадратных корней и упростить соответствующие теоремы и алгоритмы.

Матрицы евклидовых расстояний тесно связаны с матрицами Грама (матрицей скалярных произведений, описывающих нормы векторов и углы между ними). Последние легко анализируются методами линейной алгебры. Это позволяет охарактеризовать матрицы евклидовых расстояний и восстановить точки x 1, x 2,…, xn { displaystyle x_ {1}, x_ {2}, ldots, x_ {n}}которые это осознают. Реализация, если она существует, уникальна до жестких преобразований, т.е. сохраняющих расстояние преобразований евклидова пространства (поворотов, отражений, переводы ).

В практических приложениях расстояния являются зашумленными измерениями или происходят из произвольных оценок несходства (не обязательно метрика ). Целью может быть визуализация таких данных с помощью точек в евклидовом пространстве, матрица расстояний которых максимально приближает заданную матрицу несходства – это известно как многомерное масштабирование. В качестве альтернативы, учитывая два набора данных, уже представленных точками в евклидовом пространстве, можно спросить, насколько они похожи по форме, то есть насколько тесно они могут быть связаны посредством преобразования с сохранением расстояния – это Прокрустовый анализ. Некоторые из расстояний также могут отсутствовать или быть не помеченными (как неупорядоченный набор или мультимножество вместо матрицы), что приводит к более сложным алгоритмическим задачам, таким как проблема реализации графа или проблема магистрали (для точек на линии).

Содержание

• 1 Свойства
• 2 Отношение к матрице Грама
• 3 Характеристики
• 4 Уникальность представлений
• 5 См. Также
• 6 Примечания
• 7 Ссылки

Свойства

Поскольку евклидово расстояние является метрикой, матрица A имеет следующие свойства.

В размерности k матрица евклидова расстояния имеет ранг меньше или равна k + 2. Если точки x 1, x 2,…, xn { displaystyle x_ {1}, x_ {2}, ldots, x_ {n}}находятся в общее положение, ранг в точности равен min (n, k + 2).

Расстояния можно уменьшить любой степенью, чтобы получить другую матрицу евклидовых расстояний. То есть, если A = ( aij) { displaystyle A = (a_ {ij})}– матрица евклидовых расстояний, тогда (aijs) { displaystyle ({a_ {ij}} ^ {s})}– матрица евклидова расстояния для каждого 0

Отношение к матрице Грама

Матрица Грама последовательности точек x 1, x 2,…, хn { displaystyle x_ {1}, x_ {2}, ldo ts, x_ {n}}в k-мерном пространстве ℝ – это матрица размера n × n G = (gij) { displaystyle G = (g_ {ij})}их скалярных произведений (здесь точка xi { displaystyle x_ {i}}рассматривается как вектор от 0 до этой точки):

gij = xi ⋅ xj = ‖ xi ‖ ‖ xj ‖ cos ⁡ θ { displaystyle g_ {ij} = x_ {i} cdot x_ {j} = | x_ {i} | | x_ {j} | cos theta}, где θ { displaystyle theta}– угол между вектором xi { displaystyle x_ {i }}и xj { displaystyle x_ {j}}.

В частности,

gii = ‖ xi ‖ 2 { displaystyle g_ {ii} = | x_ {i} | ^ {2}}– это квадрат расстояния xi { displaystyle x_ {i}}от 0.

. Таким образом, матрица Грама описывает нормы и углы векторы (от 0 до) x 1, x 2,…, xn { displaystyle x_ {1}, x_ {2}, ldots, x_ {n}}.

Пусть X { displaystyle X}– матрица размера k × n, содержащая x 1, x 2,…, xn { displaystyle x_ {1}, x_ {2}, ldots, x _ {n}}в виде столбцов. Тогда

G = XTX { displaystyle G = X ^ {textf {T}} X}, потому что gij = xi T xj { displaystyle g_ {ij} = x_ {i } ^ {textf {T}} x_ {j}}(рассматривается xi { displaystyle x_ {i}}как вектор-столбец).

Матрицы которые можно разложить как XTX { displaystyle X ^ {textf {T}} X}, то есть матрицы Грама некоторой последовательности векторов (столбцы X { displaystyle X}), хорошо понятны – это в точности положительно полуопределенные матрицы.

. Чтобы связать матрицу евклидовых расстояний с матрицей Грама, заметьте, что

dij 2 = ‖ xi – xj ‖ 2 знак равно (xi – xj) T (xi – xj) = xi T xi – 2 xi T xj + xj T xj = gii – 2 gij + gjj { displaystyle d_ {ij} ^ {2} = | x_ {i } -x_ {j} | ^ {2} = (x_ {i} -x_ {j}) ^ {textf {T}} (x_ {i} -x_ {j}) = x_ {i} ^ { textf {T}} x_ {i} -2x_ {i} ^ {textf {T}} x_ {j} + x_ {j} ^ {textf {T}} x_ {j} = g_ {ii} – 2g_ {ij} + g_ {jj}}

То есть нормы и углы определяют расстояния. Обратите внимание, что матрица Грама содержит дополнительную информацию: расстояния от 0.

И наоборот, расстояния dij { displaystyle d_ {ij}}между парами из n + 1 точек x 0, x 1,…, Xn { displaystyle x_ {0}, x_ {1}, ldots, x_ {n}}определяют точечные произведения между n векторами xi – x 0 { displaystyle x_ {i } -x_ {0}}(1≤i≤n):

gij = (xi – x 0) ⋅ (xj – x 0) = 1 2 (‖ xi – x 0 ‖ 2 + ‖ Xj – x 0 ‖ 2 – ‖ xi – xj ‖ 2) = 1 2 (d 0 i 2 + d 0 j 2 – dij 2) { displaystyle g_ {ij} = (x_ {i} -x_ {0 }) cdot (x_ {j} -x_ {0}) = { frac {1} {2}} left ( | x_ {i} -x_ {0} | ^ {2} + | x_ {j} -x_ {0} | ^ {2} – | x_ {i} -x_ {j} | ^ {2} right) = { frac {1} {2}} (d_ {0i } ^ {2} + d_ {0j} ^ {2} -d_ {ij} ^ {2})}

(это известно как идентичность поляризации ).

Характеристики

Для матрицы A × n последовательность точек x 1, x 2,…, xn { displaystyle x_ {1}, x_ {2}, ldots, x_ {n}}в k-мерном евклидовом пространстве ℝ называется реализацией A в, если A – их евклидова матрица расстояний. Без ограничения общности можно предположить, что x 1 = 0 { displaystyle x_ {1} = mathbf {0}}(поскольку перевод на – x 1 { displaystyle -x_ {1}}сохраняет расстояния).

Теорема (критерий Шенберга, независимо показанный Янгом и Хаусхолдером) – Симметричная полая n × n-матрица A с действительными элементами допускает реализацию в ℝ тогда и только тогда, когда (n-1) × (n-1) матрица G = (gij) 2 ≤ i, j ≤ n { displaystyle G = (g_ {ij}) _ {2 leq i, j leq n}}определяется как

gij = 1 2 (a 1 i + a 1 j – aij) { displaystyle g_ {ij} = { frac {1} {2}} (a_ {1i} + a_ {1j } -a_ {ij})}

является положительным полуопределенным и имеет ранг не более k.

Это следует из предыдущего обсуждения, потому что G положительно полуопределенный ранг не выше k тогда и только тогда, когда он может быть разложен как G = XTX { displaystyle G = X ^ {textf {T}} X}где X – матрица размера k × n. Более того, столбцы X дают реализацию в. Следовательно, любой метод разложения G позволяет найти реализацию. Два основных подхода – это варианты разложения Холецкого или использование спектрального разложения для нахождения главного квадратного корня из G, см. Определенная матрица # Разложение.

Утверждение теоремы выделяет первую точку x 1 { displaystyle x_ {1}}. Более симметричный вариант той же теоремы следующий:

Следствие – Симметричная полая n × n-матрица A с действительными элементами допускает реализацию тогда и только тогда, когда A отрицательно полуопределено на гиперплоскость H = {v ∈ R n: e T v = 0} { displaystyle H = {v in mathbf {R} ^ {n} двоеточие e ^ {textf {T}} v = 0 }}, то есть

v TA v ≤ 0 { displaystyle v ^ {textf {T}} Av leq 0}для всех v ∈ R N { Displaystyle v in mathbf {R} ^ {n}}такой, что ∑ я = 1 nvi = 0 { displaystyle textstyle sum _ {i = 1} ^ {n} v_ {i} = 0}.

Другие характеристики включают детерминанты Кэли-Менгера. В частности, они позволяют показать, что симметричная полая n × n-матрица реализуема в тогда и только тогда, когда каждая (k + 3) × (k + 3) главная подматрица является. Другими словами, полуметрика на конечном числе точек изометрически вложима в ℝ тогда и только тогда, когда все k + 3 точки являются.

На практике определенность или условия ранжирования могут не выполняться из-за числовых ошибок, шума в измерениях или из-за того, что данные не поступают из фактических евклидовых расстояний. Точки, которые реализуют оптимально близкие расстояния, затем могут быть найдены полуопределенным приближением (и приближением низкого ранга, если требуется) с использованием линейных алгебраических инструментов, таких как разложение по сингулярным значениям или полуопределенное программирование. Это известно как многомерное масштабирование. Варианты этих методов также могут иметь дело с неполными данными о расстоянии.

Немаркированные данные, то есть набор или мультимножество расстояний, не назначенных конкретным парам, гораздо сложнее. Такие данные возникают, например, при секвенировании ДНК (в частности, восстановлении генома из частичного переваривания ) или фазовом извлечении. Два набора точек называются гомометрическими, если они имеют одно и то же мультимножество расстояний (но не обязательно связаны жестким преобразованием). Решить, может ли данный мультимножество из n (n-1) / 2 расстояний быть реализовано в данном измерении k, является сильно NP-трудным. В одном измерении это известно как проблема магистрали; остается открытым вопрос, можно ли решить эту проблему за полиномиальное время. Когда мультимножество расстояний задано с планками ошибок, даже одномерный случай NP-сложен. Тем не менее, практические алгоритмы существуют для многих случаев, например случайные точки.

Уникальность представлений

Учитывая евклидову матрицу расстояний, последовательность точек, реализующих ее, уникальна до жестких преобразований – это изометрии евклидова пространства: вращения, отражения, переводы и их композиции.

Теорема – Пусть x 1, x 2,…, xn { displaystyle x_ {1}, x_ {2}, ldots, x_ {n}}и y 1, y 2,…, yn { displaystyle y_ {1}, y_ {2}, ldots, y_ {n}}– две последовательности точек в k-мерном евклидовом пространстве ℝ. Расстояния ‖ xi – xj ‖ { displaystyle | x_ {i} -x_ {j} |}и ‖ yi – yj ‖ { displaystyle | y_ {i } -y_ {j} |}равны (для всех 1≤i, j≤n) тогда и только тогда, когда существует жесткое преобразование ℝ mapping xi { displaystyle x_ {i }}до yi { displaystyle y_ {i}}(для всех 1≤i≤n).

Доказательство

Жесткие преобразования сохраняют расстояния, поэтому одно направление остается четким. Предположим, что расстояния ‖ xi – xj ‖ { displaystyle | x_ {i} -x_ {j} |}и ‖ yi – yj ‖ { displaystyle | y_ { i} -y_ {j} |}равны. Без ограничения общности мы можем предположить x 1 = y 1 = 0 { displaystyle x_ {1} = y_ {1} = { textbf {0}}}, переведя точки на – x 1 { displaystyle -x_ {1}}и – y 1 { displaystyle -y_ {1}}соответственно. Тогда матрица Грама (n-1) × (n-1) оставшихся векторов xi = xi – x 1 { displaystyle x_ {i} = x_ {i} -x_ {1}}идентична матрице Грама векторов yi { displaystyle y_ {i}}(2≤i≤n). То есть XTX = YTY { displaystyle X ^ {textf {T}} X = Y ^ {textf {T}} Y}, где X и Y – это k × ( n-1) матриц, содержащих соответствующие векторы в виде столбцов. Это означает, что существует ортогональная k × k-матрица Q такая, что QX = Y, см. Определенная симметричная матрица # Единственность с точностью до унитарных преобразований. Q описывает ортогональное преобразование числа ℝ (композиция вращений и отражений без переводов), которое отображает xi { displaystyle x_ {i}}в yi { displaystyle y_ {i}}(и от 0 до 0 ). Окончательное жесткое преобразование описывается следующим образом: T (x) = Q (x – x 1) + y 1 { displaystyle T (x) = Q (x-x_ {1}) + y_ {1}}.

. В приложениях, когда расстояния не совпадают точно, анализ Прокруста стремится связать два набора точек как можно ближе с помощью жестких преобразований, обычно с использованием разложения по сингулярным значениям. Обычный евклидов случай известен как ортогональная проблема Прокруста или проблема Вахбы (когда наблюдения взвешиваются для учета различных неопределенностей). Примеры приложений включают определение ориентации сателлитов, сравнение структуры молекул (в хеминформатике ), структуры белка (структурное выравнивание в биоинформатике ) или структуры кости (статистический анализ формы в биологии).

См. Также

Примечания

Литература

• Докманич, Иван; Пархизкар, Реза; Раньери, Юри; Веттерли, Мартин (2015). «Матрицы евклидовых расстояний: основная теория, алгоритмы и приложения». Журнал обработки сигналов IEEE. 32 (6): 12–30. arXiv : 1502.07541. DOI : 10.1109 / MSP.2015.2398954. ISSN 1558-0792. S2CID 8603398.
• Джеймс Э. Джентл (2007). Матричная алгебра: теория, вычисления и приложения в статистике. Спрингер-Верлаг. п. 299. ISBN 978-0-387-70872-0.
• Итак, Энтони Ман-Чо (2007). Подход полуопределенного программирования к проблеме реализации графа: теория, приложения и расширения (PDF) (PhD).
• Либерти, Лео; Лавор, Карлайл; Макулан, Нельсон; Мучерино, Антонио (2014). «Евклидова дистанционная геометрия и приложения». SIAM Обзор. 56 (1): 3–69. arXiv : 1205.0349. DOI : 10.1137 / 120875909. ISSN 0036-1445. S2CID 15472897.
• Альфаких, Абдо Ю. (2018). Матрицы евклидовых расстояний и их приложения в теории жесткости. Чам: Издательство Springer International. DOI : 10.1007 / 978-3-319-97846-8. ISBN 978-3-319-97845-1.

1. Основные
   определения

Граф
– это совокупность двух множеств: вершини ребер,
между которыми определено отношениеинцидентности.

Каждое ребро e
из E
инцидентно ровно двум вершинам
и,
которые оно соединяет. При этом вершинаи реброe
называются инцидентными
друг другу, а вершины
иназываютсясмежными.

Принято обозначение
n
для числа вершин графа (мощность множества
):иm
для числа его ребер:
.
Говорят, что графG
есть (n,
m)
граф, где n
– порядок графа, m
– размер графа.

Если все ребра
графа неориентированные, т.е. пары
вершин, определяющие элементы множестваE,
неупорядочены, то такой граф называется
неориентированным графом, или неографом.
На рис. 12.1 показан пример неографа. Этот
граф имеет пять вершин и шесть ребер.

Рис. 12.1

Маршрут
– последовательность ребер, в которой
каждые два соседних ребра имеют общую
вершину. Граф связен,
если любые две вершины соединены хотя
бы одним маршрутом. Число ребер маршрута
определяет его длину.

Ребра, инцидентные
одной паре вершин, называются параллельными
или кратными.
Граф с кратными ребрами называется
мультиграфом.

Ребро
называетсяпетлей
(концевые вершины совпадают). Граф,
содержащий петли и кратные ребра,
называется псевдографом.
На рис. 12.2 показан псевдограф.

Рис. 12.2

Степень
deg(v)
вершины – это число ребер, инцидентных
v.
В неографе
сумма степеней всех вершин равна
удвоенному числу ребер
(лемма о рукопожатиях):

. (12.1)

Петля дает вклад,
равный 2, в степень вершины.

Степенная
последовательность
– последовательность степеней всех
вершин графа, записанная в определенном
порядке (по возрастанию или убыванию).

Пример
12.1. Степенная
последовательность неографа, изображенного
на рис. 12.1, записанная по возрастанию,
выглядит так:

=1,
=2,=3,=3,=3.

Сумма степеней
всех вершин графа равна:

.

Этот результат
не противоречит лемме о рукопожатиях,
поскольку граф имеет шесть ребер (m
= 6).

Матрица
смежности
графа – квадратная матрица A
порядка n,
где элемент
равен числу ребер, соединяющих вершиныi
и j.

Пример 12.2.
Граф, показанный на рис. 12.1, имеет
следующую матрицу смежности

.

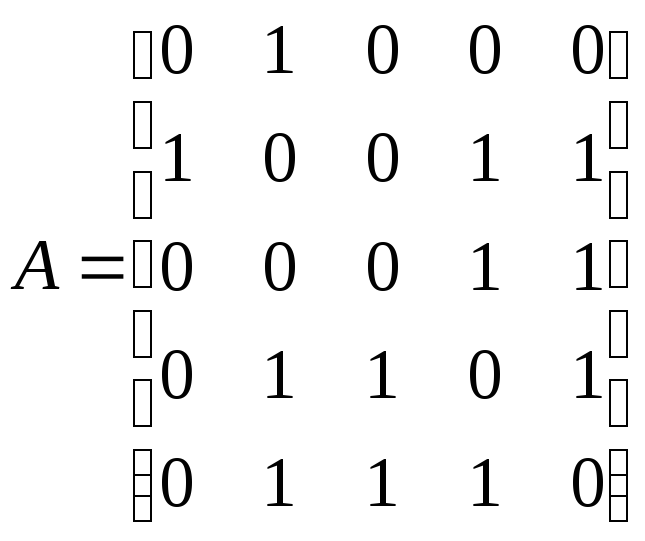Матрица
инцидентности
I
– еще один способ описания графа. Число
строк этой матрицы равно числу вершин,
число столбцов – числу ребер;
=1,
если вершинаv
инцидентна ребру e;
в противном случае
=0.
В каждом столбце матрицы инцидентности
простого графа (без петель и без кратных
ребер) содержится по две единицы. Число
единиц в строке равно степени
соответствующей вершины.

Пример 12.3.
Граф, показанный на рис. 12.1, имеет
следующую матрицу инцидентности

.

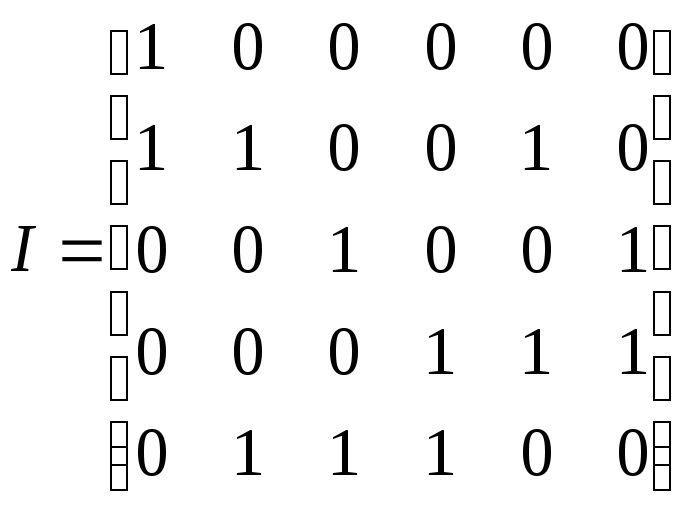Граф
называетсяподграфом
графа
,
еслии.
Если,
то подграф называетсяостовным.

Компонента
связности
графа – максимальный по включению
вершин и ребер связной подграф.

Ранг
графа
,
гдеk
– число компонент связности.

Дерево
– связной граф, содержащий n
– 1 ребро.

Пример 12.4.
На рис. 12.3 показано дерево, которое
одновременно является остовным подграфом
графа, показанного на рис. 12.1.

Рис. 12.3

1. Радиус, диаметр
   и центр графа

Вычисление
расстояний и определение маршрутов в
графе являются одной из наиболее
очевидных и практичных задач, которые
возникают в теории графов. Введем
некоторые необходимые определения.

Эксцентриситет
вершины графа – расстояние до максимально
удаленной от нее вершины. Для графа, для
которого не определен вес
его ребер, расстояние определяется в
виде числа ребер.

Радиус
графа – минимальный эксцентриситет
вершин, а диаметр
графа – максимальный эксцентриситет
вершин.

Центр
графа образуют вершины, у которых
эксцентриситет равен радиусу. Центр
графа может состоять из одной, нескольких
или всех вершин графа.

Периферийные
вершины имеют эксцентриситет, равный
диаметру.

Простая цепь с
длиной, равной диаметру графа, называется
диаметральной.

Теорема 12.1.
В связном графе диаметр не больше ранга
его матрицы смежности.

Теорема 12.2.
(Жордана) Каждое дерево имеет центр,
состоящий из одной или двух смежных
вершин.

Теорема 12.3.
Если диаметр дерева четный, то дерево
имеет единственный центр, и все
диаметральные цепи проходят через него,
если диаметр нечетный, то центров два
и все диаметральные цепи содержат ребро,
их соединяющее.

Очевидно практическое
значение центра графа. Если, например,
речь идет о графе дорог с вершинами-городами,
то в математическом центре целесообразно
размещать административный центр,
складские помещения и т.п. Этот же подход
можно применять и для взвешенного графа,
где расстояния – это веса ребер. В
качестве веса можно брать евклидовое
расстояние, время или стоимость
передвижения между пунктами.

Пример 12.5.
Найти радиус, диаметр и центр графа,
изображенного на рис. 12.1.

Решение.
В данной задаче удобно использовать
матрицу
расстояний S.
Элемент этой квадратной симметричной
матрицы
равен расстоянию между вершинойi
и вершиной j.
Для графа, показанного на рис. 12.1, матрица
расстояний имеет следующий вид:

. (12.2)

Вычислим
эксцентриситет
каждой вершины. Эту величину можно
определить как максимальный элемент
соответствующего столбца матрицы
расстояний (или строки – поскольку
матрицаS
симметрична).
Получаем

№	1	2	3	4	5
	3	2	3	2	2

Радиус графа r
– минимальный эксцентриситет вершин.
В данном случае r
= 2. Такой эксцентриситет имеют вершины
№ 2, № 4 и № 5. Эти вершины образуют центр
графа. Диаметр графа d
– максимальный эксцентриситет вершин.
В данном случае d
= 3. Такой эксцентриситет имеют вершины
№ 1 и № 3, это периферия графа. В
исследованном графе вершины оказались
либо центральными, либо периферийными.
В графах большего порядка существуют
и другие вершины.

Эксцентриситеты
вершин небольшого графа легко вычислять
непосредственным подсчетом по рисунку.
Однако не всегда граф задан своим
рисунком. Кроме того, граф может иметь
большой размер. Поэтому необходим другой
способ решения предыдущей задачи.
Известна следующая теорема.

Теорема
12.4. Пусть
– матрица смежности графаG
без петель и
,
где.
Тогдаравно числу маршрутов длиныk
от вершины
к вершине.

Решение задач
теории графов с помощью различных
преобразований матрицы смежности
называют алгебраическим
методом.

Пример 12.6.
Найти матрицу расстояний графа,
изображенного на рис. 12.1, алгебраическим
методом.

Решение.
Матрица смежности данного графа равна:

.

Будем заполнять
матрицу расстояний, рассматривая степени
матрицы смежности. Единицы матрицы
смежности показывают пары вершин,
расстояние между которыми равно единице
(т.е. они соединены одним ребром).

.

Диагональные
элементы матрицы расстояний – нули.
Умножаем матрицу смежности на себя:

.

Согласно теореме
между вершинами 2 и 3, 1 и 4 и т.д. имеется
некоторое число маршрутов длиной 2
(поскольку степень матрицы равна двум).
Число маршрутов здесь не используется,
важен сам факт наличия маршрута и его
длина, на что и указывает ненулевой
элемент степени матрицы, не совпадающий
с элементом, отмеченным при вычислении
маршрута меньшей длины. Проставляем 2
в незаполненные элементы матрицы
расстояний и получаем следующее
приближение:

.

Осталось неизвестным
расстояние между вершинами 1 и 3. Будем
умножать матрицу смежности

саму на себя до тех пор, пока в матрице


не появится ненулевой элемент
.
Тогда соответствующий элемент матрицы
расстояний равен степени матрицы
смежности:
.
На следующем шаге получаем

,

следовательно,
,
и окончательно

.

Полученная матрица
совпадает с матрицей расстояний S
(12.2), найденной непосредственными
вычислениями по рисунку.

1. Эйлерова цепь

Маршрут в неографе,
в котором все ребра разные, называется
цепью.
Цепь в графе называется эйлеровой,
если она содержит все ребра и все вершины
графа.

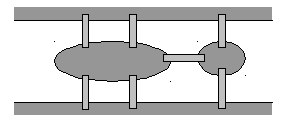
Рис. 12.4. Схема
Кенигсбергских мостов

Теория графов
многократно переоткрывалась разными
авторами при решении различных прикладных
задач. В их ряду – знаменитый математик
Леонард Эйлер (1707-1783). К созданию теории
графов его подтолкнула задача о
Кенигсберских мостах, которую он решил
в 1736 году. По условию задачи требовалось
пройти по всем семи мостам города
Кенигсберга через реку Преголь по одному
разу и вернуться к исходной точке. На
рис. 12.4 показана схема этих мостов (один
из них соединяет между собой два острова,
а остальные – острова с берегами). Этой
схеме соответствует приведенный на
следующем рисунке мультиграф с четырьмя
вершинами.

Рис. 12.5

Эйлер решил задачу
о Кенигсбергских мостах в отрицательном
смысле. Он доказал, что данная задача
не имеет решения. Для этого ему пришлось
доказать следующую теорему.

Теорема 12.5
(Эйлера).
Мультиграф обладает эйлеровой цепью
тогда и только тогда, когда он связен и
число вершин нечетной степени равно 0
или 2.

Вершины нечетной
степени в этой теореме, очевидно, являются
началом и концом цепи. Если таких вершин
нет, то эйлерова цепь становится эйлеровым
циклом.
Граф, обладающий эйлеровым циклом,
называется эйлеровым.
Если граф имеет эйлерову цепь, но не
обладает эйлеровым циклом (число вершин
нечетной степени равно 2), то он называется
полуэйлеровым
графом.

Предположим, что
граф имеет эйлеров цикл. Двигаясь по
нему, будем подсчитывать степени вершин,
полагая их до начала прохождения
нулевыми. Прохождение каждой вершины
вносит 2 в степень этой вершины. Поскольку
эйлеров цикл содержит все ребра, то
когда обход будет закончен, будут учтены
все ребра, а степени вершин – четные.

Все четыре вершины
мультиграфа, показанного на рис. 12.5,
имеют нечетные степени. Поэтому этот
граф не обладает эйлеровым циклом, а
задача о Кенигсбергских мостах не имеет
решения.

Рассмотрим для
сравнения граф, обладающий эйлеровой
цепью. В графе на рис. 12.6 только две
вершины имеют нечетную степень,
следовательно, эйлерова цепь есть.

Рис. 12.6

Цепей может быть
несколько. Например, граф на рис. 12.6
имеет две эйлеровы цепи: 1-2-3-4-1-3 и
1-2-3-1-4-3.

1. Реберный граф

Рассмотрим два
графа G
и L(G).
Граф G
имеет произвольную форму, а вершины
графа L(G)
расположены на ребрах графа G.
В этом случае граф L(G)
называется реберным
графом по
отношению к графу G.

Английское название
реберного графа – line
graph,
отсюда и обозначение графа – L(G).
На рис. 12.7 показан реберный граф (он
выделен жирными линиями), построенный
для графа с рис. 12.1.

Рис. 12.7. Реберный
граф

Теорема 12.6.
Если
– степенная последовательность (n,
m)
графа G,
то L(G)
является (m,
)-графом,
где

. (12.3)

Для графа G,
показанного на рис. 12.7 (и рис. 12.1), его
степенная последовательность: 1-3-2-3-3.
Поэтому

.

1. Раскраска графа,
   хроматический полином

Предположим, что
перед нами стоит задача: раскрасить
карту мира так, чтобы каждая страна
имела свой собственный цвет. Поскольку
на свете существует несколько сотен
государств, то, естественно, потребуется
достаточно много разных красок.

Упростим задачу.
Будем использовать меньшее количество
красок, но при этом не будем допускать,
чтобы соседние страны, имеющие общие
границы, были окрашены в один цвет.
Возникает вопрос: какое минимальное
количество красок требуется, чтобы
удовлетворить этому условию?

Ответить на этот
вопрос можно с помощью теории графов.
Для этого нужно представить карту мира
в виде графа, каждая вершина которого
соответствует отдельной стране, а ребро
между смежными вершинами соответствует
наличию между странами общей границы.

Произвольная
функция

на множестве вершин графа называется
раскраской
графа. Раскраска называется правильной,
если

для любых смежных вершин
и.
Минимальное числоk,
при котором граф G
является k-раскрашиваемым
называется хроматическим
числом
графа
.

Граф называется
пустым,
если в нем удалены все ребра и вершины
изолированы друг от друга. Граф называется
полным,
если в нем нельзя добавить новое ребро,
не добавив при этом одновременно новую
вершину.

Теорема 12.7
(Брукса).
Для любого графа G,
не являющегося полным,
,
если–максимальная
из степеней вершин графа.

Для определения
количества способов раскраски графа в
x
цветов, необходимо составить хроматический
полином
P(G,
x).
Значение полинома при некотором
конкретном
равно числу правильных раскрасок графа
вцветов.

Существует лемма,
утверждающая, что хроматический
полином графа имеет вид

,(12.4)

где
– граф, полученный изG
добавлением ребра (u,
v),
а граф
получается изG
отождествлением вершин u
и v.

Другой вариант
леммы:

, (12.5)

где
– граф, полученный изG
удалением ребра (u,
v),
а граф
получается изG
отождествлением вершин u
и v.

Операцию
отождествления вершин u
и
v
называют также стягиванием ребра (u,
v).

Оба варианта леммы
составляют основу для хроматической
редукции графа (reduction
– «сокращение» на английском).
Хроматическая редукция графа –
представление графа в виде нескольких
пустых или полных графов, сумма
хроматических полиномов которых равна
хроматическому полиному графа. Очевидно,
что хроматический полином пустого графа
равен(каждая вершина может быть раскрашена
независимо от других), а для полного
графа.
Последнее выражение называютфакториальной
степенью
переменной x:
.

Разложения по
пустым и полным графам связаны.
Факториальную степень можно представить
в виде полинома:

, (12.6)

где
– числа Стирлинга первого рода. И
наоборот, степеньможно выразить через факториальные
степени:

, (12.7)

где
– числа Стирлинга второго рода, обладающие
следующими свойствами:

при
, (12.8)

при
,при.

При получении
хроматического полинома могут быть
полезны следующие теоремы.

Теорема 12.8.
Коэффициенты хроматического полинома
составляют знакопеременную
последовательность.

Теорема 12.9.
Абсолютная величина второго коэффициента
хроматического полинома равна числу
ребер графа.

Теорема 12.10.
Наименьшее число i,
для которого отличен от нуля коэффициент
при

в хроматическом полиноме графа G,
равно числу компонент связности графа
G.

Кроме вершинной
раскраски, существует еще реберная
раскраска и раскраска граней.

Пример 12.7.
Найти хроматический полином графа,
показанного на рис. 12.8.

Рис. 12.8

Решение.
В зависимости от числа ребер графа можно
использовать разложение (12.4) или (12.5).
Если граф почти полный, то, добавив
несколько ребер по разложению (12.4),
получим хроматический полином в виде
суммы факториальных степеней. Если же
ребер мало и для получения пустого графа
требуется удалить только несколько
ребер, то следует использовать разложение
(12.5) с удалением ребер. Такие действия
называются хроматической редукцией.

1. Хроматическая
редукция по пустым графам.
Воспользуемся вначале леммой (12.5). Удаляя
ребра и отождествляя соответствующие
вершины (стягивая ребра), сведем исходный
граф к пустым графам. Сначала разложим
граф на два, убрав, а затем стянув ребро
1-3. Выполненное действие запишем в виде
условного равенства:

Здесь
операция вычитания относится не к самому
графу, а к его хроматическому полиному.
Таким образом, последнее равенство
означает, что
.
Для сокращения записи обозначениеP(…)
будем опускать. Далее разложим каждый
из графов

и
,
пользуясь той же леммой.

Приведем подобные
члены:

(12.9)

В итоге получим
искомый хроматический полином:

. (12.10)

Разложение (12.9)
называется хроматической редукцией
графа по пустым графам.

Очевидно, что
результат соответствует утверждениям
теорем 12.8-12.10. Коэффициенты в (12.10) образуют
знакопеременную последовательность,
а коэффициент при
равен четырем – числу ребер. Наименьшая
степеньx
в полиноме равна 1, т.е. числу компонент
связности графа.

2. Хроматическая
редукция по полным графам.
Добавив к изображенному на рис. 12.8 графу
ребро 1–4, получим граф с большим числом
ребер. Затем в исходном графе отождествим
вершины 1 и 4. В результате получим два
графа.

Отождествление
вершин приводит к уменьшению порядка
и иногда размера графа. Второй граф –
это полный граф
,
его преобразовывать больше не требуется.
К первому графу добавим ребро 1–2 и
отождествим вершины 1 и 2:

В итоге получим

(12.11)

Хроматический
полином примет вид

(12.12)

Разложение (12.11)
называется хроматической редукцией
графа по полным графам.

Оба способа дали
один результат, и из редукции по полным
графам легко получить редукцию по
пустым. Для этого достаточно раскрыть
скобки и привести подобные члены, как
в (12.12). Однако обратное действие не
очевидно. Для того чтобы полином
,
полученный из пустых графов, выразить
в виде суммы факториальных степеней,
необходимы числа Стирлинга 2-го рода.
Согласно рекуррентным формулам (12.8)
имеем следующие числа:

,

,

,

.

Пользуясь (12.7) и
найденными числами Стирлинга 2-го рода,
получим

,

,

.

Произведем
преобразование хроматического полинома:

Хроматическое
число
графа лучше всего получить, разложив
хроматический полином на множители:

.

Минимальное
натуральное число x,
при котором
не обращается в нуль, равно 3. Отсюда
следует.
Так как максимальная степень вершин
графа,
выполняется оценка.

1. Ранг-полином
   графа

Ранг графа
определяется как
,
гдеn
– число вершин, k
– число компонент связности графа.
Коранг графа, или цикломатический ранг,
есть
,
гдеm
– число ребер.

Ранг-полином графа
G
имеет вид

,

где
– ранг графаG
, а
– корангостовного
(т.е. включающего в себя все вершины
графа) подграфа H,
а
– его ранг. Суммирование ведется по
всем остовным подграфам графаG.

Ранг полином
служит для анализа множества остовных
подграфов. Так, например, коэффициент
при
весть число подграфов размераk,
а значение
равно числу подграфов (включая
несобственный подграф), ранг которых
равен рангу самого графа.

Пример
12.8. Найти
ранг-полином графа, изображенного на
рис. 12.8.

Решение.
Найдем все 16 остовных подграфов графа
G
(рис. 12.9). Множество представим в виде
четырех графов размера 1 (т.е. с одним
ребром), шести графов размера 2, четырех
графов размера 3 и двух несобственных
графов (пустой граф и граф G).

Рис. 12.9

Учитывая, что ранг
графа равен 3, получаем сумму:

1. Циклы

Маршрут, в котором
начало и конец совпадают, – циклический.
Циклический маршрут называется циклом,
если он – цепь.

Остовом
графа G
называется граф, не содержащий циклов
и состоящий из ребер графа G
и всех его вершин. Остов графа определяется
неоднозначно.

Ребра графа, не
входящие в остов, называются хордами.
Цикл, получающийся при добавлении к
остову графа его хорды, называется
фундаментальным
относительно
этой хорды.

Теорема 12.11.
Число ребер неографа, которые необходимо
удалить для получения остова, не зависит
от последовательности их удаления и
равно цикломатическому рангу графа.

Пример 12.8.
По заданной матрице смежности:

,

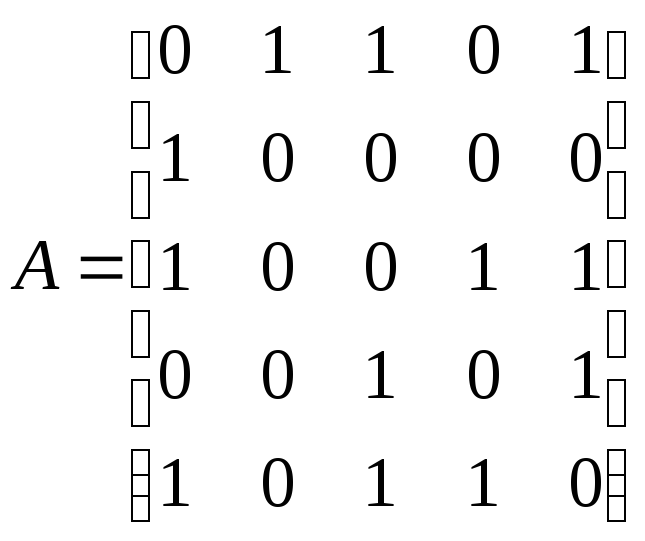определить число
циклов длины 3 ()
и длины 4 ().
Записатьматрицу
фундаментальных циклов.

Решение.
Матрица смежности данного графа
симметричная, поэтому ей соответствует
неориентированный граф. Сумма ненулевых
элементов матрицы равна 12, следовательно,
по лемме о рукопожатиях в графе 6 ребер.
Построим этот граф (рис. 12.10). Очевидно,
в нем два цикла (3–4–5 и 1–3–5) длиной 3 и
один цикл (1–3–4–5) длиной 4. В данной
задаче решение получено прямым подсчетом
по изображению графа. Для более сложных
случаев существует алгоритм решения
задачи по матрице смежности.

Известно, что след
(trace)
матрицы смежности, возведенный в k-ю
степень, равен числу циклических
маршрутов длины k
(см. теорему 12.4). Это число включает в
себя и искомое число циклов. Цикл
отличается от циклического маршрута
тем, что в нем не повторяются ребра.
Кроме того, предполагается, что искомые
циклы не помечены, а в след матрицы
входят именно помеченные маршруты.

Рис. 12.10

Непомеченных
циклов длиной 3 в 6 раз меньше, чем
помеченных, так как каждый помеченный
цикл может отличаться началом (а их в
данном случае три) и двумя направлениями
обхода (по и против часовой стрелки).
Возведем заданную матрицу смежности в
третью степень:

,

и получим

.

Поскольку
циклических маршрутов длиной 3, отличных
от циклов длиной 3, не существует,
найденное число и есть ответ в поставленной
задаче.

С циклами длиной
4 немного сложнее. В след четвертой
степени матрицы смежности графа

,

входят не только
циклы, но и циклические маршруты с
двойным и четырехкратным прохождением
ребер. Обозначим количество таких
маршрутов через
исоответственно. Очевидно, число маршрутов
с четырехкратным прохождением одного
ребра для вершиныравно степени этой вершины:.
Число маршрутов с двукратным прохождением
ребра складывается из числас висячей вершинойи числамаршрутов с вершинойв центре.

Легко заметить,
что
.
Числозависит от степеней вершин, соседних с:

,

где
– ребро, инцидентное вершинамi
и k.

Для графа на рис.
12.10 получим

,

,

,

.

С учетом того, что
непомеченных циклов длиной 4 в 8 раз
меньше, получим

.

После преобразований
формула примет вид

.

Для нахождения
матрицы фундаментальных циклов
пронумеруем ребра графа, начиная
нумерацию с хорд, как показано на рис.
12.11 (а).

Рис. 12.11

Двум хордам, 1 и 2,
соответствуют два фундаментальных
цикла: 1–4–5 и 2–4–6 (рис. 12.11 (б и в)).
Матрица фундаментальных циклов имеет
две строки (число циклов) и шесть столбцов
(число ребер).

	1	2	3	4	5	6
1	1	0	0	1	1	0
2	0	1	0	1	0	1

В первой строке
матрицы единицами отмечены столбцы с
номерами ребер, входящих в первый цикл,
а во второй строке – номера ребер из
второго цикла.

В математике , информатике и особенно теории графов , А матрица расстояний является квадратная матрица (двумерный массив) , содержащий расстояния , взятые попарно, между элементами набора. В зависимости от задействованного приложения расстояние , используемое для определения этой матрицы, может быть или не быть метрикой . Если есть N элементов, эта матрица будет иметь размер N × N . В теоретико-графических приложениях элементы чаще называют точками, узлами или вершинами.

Неметрические матрицы расстояний

В общем случае матрица расстояний – это взвешенная матрица смежности некоторого графа. В сети , ориентированном графе с весами, присвоенными дугам, расстояние между двумя узлами сети можно определить как минимум сумм весов на кратчайших путях, соединяющих два узла. Эта функция расстояния, хотя и хорошо определена, не является метрикой. Не требуется никаких ограничений на веса, кроме необходимости иметь возможность комбинировать и сравнивать их, поэтому в некоторых приложениях используются отрицательные веса. Поскольку пути являются направленными, симметрия не может быть гарантирована, и если существуют циклы, матрица расстояний не может быть пустой.

Алгебраическая формулировка сказанного выше может быть получена с помощью алгебры мин-плюс . Умножение матриц в этой системе определяется следующим образом: для двух матриц и их произведение расстояний определяется как матрица, такая что . Обратите внимание, что для недиагональных элементов, которые не связаны напрямую, необходимо установить бесконечность или подходящее большое значение для правильной работы операций min-plus. Ноль в этих местах будет неправильно интерпретирован как грань без расстояния, стоимости и т. Д.

Если – матрица, содержащая веса ребер графа , то (с использованием этого произведения расстояний) дает расстояния между вершинами, используя пути длины на большинстве ребер, и является матрицей расстояний графа.

Произвольный граф G на n вершинах можно смоделировать как взвешенный полный граф на n вершинах, присвоив вес, равный единице, каждому ребру полного графа, который соответствует ребру G, и нулю всем остальным ребрам. W для этого полного графа является матрица смежности из G . Матрица расстояний G может быть вычислена из W, как указано выше, однако W ^n, вычисленное обычным умножением матриц, кодирует только количество путей между любыми двумя вершинами длины ровно n .

Матрицы метрических расстояний

Ценность формализма матрицы расстояний во многих приложениях заключается в том, как матрица расстояний может явно кодировать аксиомы метрики и в том, как она поддается использованию методов линейной алгебры. То есть, если M = ( x _ij ) с 1 ≤ i , j ≤ N – матрица расстояний для метрического расстояния, то

1. все элементы на главной диагонали равны нулю (то есть матрица является пустой матрицей ), т.е. x _ii = 0 для всех 1 ≤ i ≤ N ,
2. все недиагональные элементы положительны ( x _ij > 0, если i ≠ j ) (то есть неотрицательная матрица ),
3. матрица является симметричной матрицей ( x _ij = x _ji ), и
4. для любых i и j , x _ij ≤ x _ik + x _kj для всех k (неравенство треугольника). Это можно сформулировать в терминах умножения тропических матриц

Когда матрица расстояний удовлетворяет первым трем аксиомам (что делает ее полуметрической), ее иногда называют матрицей предварительных расстояний. Матрица предварительных расстояний, которая может быть встроена в евклидово пространство, называется матрицей евклидовых расстояний .

Другой распространенный пример метрической матрицы расстояний возникает в теории кодирования, когда в блочном коде элементы представляют собой строки фиксированной длины по алфавиту, а расстояние между ними задается метрикой расстояния Хэмминга . Наименьший ненулевой элемент в матрице расстояний измеряет способность кода исправлять и обнаруживать ошибки.

Приложения

Иерархическая кластеризация

Матрица расстояний необходима для иерархической кластеризации .

Филогенетический анализ

Матрицы расстояний используются в филогенетическом анализе .

Другое использование

В биоинформатике матрицы расстояний используются для представления структур белков независимым от координат образом, а также попарных расстояний между двумя последовательностями в пространстве последовательностей. Они используются для структурного и последовательного выравнивания, а также для определения структур белков с помощью ЯМР или рентгеновской кристаллографии .

Иногда удобнее представить данные в виде матрицы сходства .

Он используется для определения корреляции расстояний .

Примеры

Например, предположим, что эти данные должны быть проанализированы, где евклидово расстояние пикселя является метрикой расстояния .

Матрица расстояний будет следующей:

	а	б	c	d	е	ж
а	0	184	222	177	216	231
б	184	0	45	123	128	200
c	222	45	0	129	121	203
d	177	123	129	0	46	83
е	216	128	121	46	0	83
ж	231	200	203	83	83	0

Затем эти данные можно просмотреть в графической форме в виде тепловой карты . На этом изображении черный цвет обозначает расстояние 0, а белый – максимальное расстояние.

Смотрите также

• Кластеризация данных
• Компьютерное зрение
• Умножение матриц мин-плюс

Рекомендации