Онлайн калькулятор поможет рассчитать какое будет конечное давления идеального газа от изменения температуры, при условии, что объем газа остается постоянным. Зависимость давления от температуры в этом случае описывается законом Гей-Люссака (законом Шарля).
Формула: P2 = P1×T2/T1
Где:
P1 – начальное давление;
P2 – конечное давление;
T1 – начальная температура (в Кельвинах);
T2 – конечная температура (в Кельвинах).
Например, данный калькулятор поможет приблизительно определить зависимость давления в шинах от температуры.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Смотрите также
Как определить атмосферное давление
Наверняка почти каждый день, когда вы смотрите или слушаете прогноз погоды, то обращаете внимание только на температуру воздуха и возможные осадки. Но синоптики упоминают еще несколько немаловажных параметров и атмосферное давление среди них. В общем случае атмосферное давление – это давление атмосферы на земную поверхность и все предметы на ней. На тело человека действует такое давление, которое эквивалентно давлению 15-тонного груза. Но мы его не ощущаем, так как в нашем теле тоже есть воздух.

Вам понадобится
- ртутный барометр или барометр-анероид. А если вам необходимо непрерывно снимать показания давления, то следует использовать барограф.
Инструкция
Ртутный барометр, как правило, показывает атмосферное давление в миллиметрах ртутного столба. Просто посмотрите по шкале уровень ртути в колбе – и вот уже вы знаете атмосферное давление в вашем помещении. Как правило, это значение составляет 760±20 мм.рт.ст. Если требуется узнать давление в паскалях, то воспользуйтесь простой системой перевода: 1 мм.рт.ст. = 133,3 Па. Например, 760 мм.рт.ст. = 133,3*760 Па = 101308 Па. Это давление считается нормальным на уровне моря при 15°С.
Снимать показания давления со шкалы барографа тоже очень просто. Этот прибор основан на действии анероидной коробки, которая реагирует на изменение давления воздуха. Если давление повышается – стенки этой коробки прогибаются внутрь, если давление снижается – стенки выпрямляются. Вся эта система соединена со стрелкой, и вам лишь надо посмотреть, какое значение атмосферного давления стрелка показывает на шкале прибора. Не пугайтесь, если шкала будет в таких единицах как гПа – это гектопаскаль: 1 гПа = 100 Па. А для перевода в более привычные мм.рт.ст. просто воспользуйтесь равенством из предыдущего пункта.
А найти атмосферное давление на какой-то определенной высоте можно даже без использования прибора, если вам известно давление на уровне моря. Понадобятся лишь некоторые математические навыки. Воспользуйтесь вот этой формулой:P=P0 * e^(-Mgh/RT).В этой формуле:P – искомое давление на высоте h;
P0 – это давление на уровне моря в паскалях;
M – это молярная масса воздуха, равная 0.029 кг/моль;
g – земное ускорение свободного падения, примерно равное 9.81 м/с²;
R – это универсальная газовая постоянная, принимается за 8.31 Дж/моль К;
T – температура воздуха в Кельвинах (для перевода из °C в К воспользуйтесь формулой
T = t + 273, где t – температура °C);
h – высота над уровнем моря, где находим давление, измеряется в метрах.
Полезный совет
Как видите, даже необязательно быть в конкретном месте, чтобы измерить атмосферное давление. Его можно запросто рассчитать. Посмотрите на последнюю формулу – чем выше мы поднимаемся над землей, тем будет ниже атмосферное давление. И уже на высоте 4000 метров вода будет кипеть при температуре не 100°C, как мы привыкли, а примерно при 85°C, так как давление там не 100 500 Па, а около 60 000 Па. Поэтому процесс приготовления пищи на такой высоте становится более продолжительным.
Источники:
- как найти атмосферное давление
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
| Атмосферное давление | |
|---|---|
 |
|
| Размерность | L−1MT−2 |
| Единицы измерения | |
| СИ | Па |
| СГС | дин·см-2 |
| Примечания | |
| скаляр |
Атмосфе́рное давле́ние — давление атмосферы, действующее на все находящиеся в ней предметы и на земную поверхность, равное модулю силы, действующей в атмосфере, на единицу площади поверхности по нормали к ней[1]. В покоящейся стационарной атмосфере давление равно отношению веса вышележащего столба воздуха к площади его поперечного сечения. Атмосферное давление является одним из термодинамических параметров состояния атмосферы, оно изменяется в зависимости от места и времени[2]. Давление — величина скалярная, имеющая размерность L−1MT−2, измеряется барометром.
Единицей измерения в Международной системе единиц (СИ) является паскаль (русское обозначение: Па; международное: Pa). Кроме того, в Российской Федерации в качестве внесистемных единиц давления допущены к использованию бар, миллиметр ртутного столба, миллиметр водяного столба, метр водяного столба, килограмм-сила на квадратный сантиметр и атмосфера техническая[3]. Атмосферное давление, равное давлению столба ртути высотой 760 мм при температуре 0 °C, называется нормальным атмосферным давлением (101 325 Па)[2].
История[править | править код]

Традиционно считалось, что всасывающие насосы работают из-за того, что «природа боится пустоты». Но голландец Исаак Бекман в тезисах своей докторской диссертации, защищенной им в 1618 году, утверждал: «Вода, поднимаемая всасыванием, не притягивается силою пустоты, но гонима в пустое место налегающим воздухом» (Aqua suctu sublata non attrahitur vi vacui, sed ab aere incumbentein locum vacuum impellitur).
В 1630 году генуэзский физик Балиани написал письмо Галилею о неудачной попытке устроить сифон для подъема воды на холм высотою примерно 21 метр. В другом письме Галилею (от 24 октября 1630 года) Балиани предположил, что подъем воды в трубе обусловлен давлением воздуха.
Наличие атмосферного давления привело людей в замешательство в 1638 году, когда не удалась затея герцога Тосканского украсить сады Флоренции фонтанами — вода не поднималась выше 10,3 метров. Поиски причин этого и опыты с более тяжёлым веществом — ртутью, предпринятые Эванджелистой Торричелли, привели к тому, что в 1643 году он доказал, что воздух имеет вес[5]. Совместно с В. Вивиани, Торричелли провёл первый опыт по измерению атмосферного давления, изобретя первый ртутный барометр — стеклянную трубку, в которой нет воздуха. В такой трубке ртуть поднимается на высоту около 760 мм.
Изменчивость и влияние на погоду[править | править код]
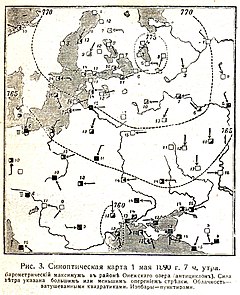
На земной поверхности атмосферное давление изменяется время от времени и от места к месту. Особенно важны определяющие погоду непериодические изменения атмосферного давления, связанные с возникновением, развитием и разрушением медленно движущихся областей высокого давления (антициклонов) и относительно быстро перемещающихся огромных вихрей (циклонов), в которых господствует пониженное давление. Отмечены колебания атмосферного давления на уровне моря в пределах 641 — 816 мм рт. ст.[6] (в центральной части смерча давление падает и может достигать значения 560 мм ртутного столба)[7].
На картах атмосферное давление изображается с помощью изобар — изолиний, соединяющих точки с одинаковым приземным атмосферным давлением, обязательно приведенным к уровню моря[8].
Атмосферное давление — очень изменчивый метеоэлемент. Из его определения следует, что оно зависит от высоты соответствующего столба воздуха, его плотности, от ускорения силы тяжести, которая меняется от широты места и высоты над уровнем моря.
-
1 Па = 0,0075 мм рт. ст., или 1 мм рт. ст. = 133,3 Па
Стандартное давление[править | править код]
В химии стандартным атмосферным давлением с 1983 года по рекомендации IUPAC считается давление, равное 100 кПа[9].
Атмосферное давление является одной из наиболее существенных характеристик состояния атмосферы. В покоящейся атмосфере давление в любой точке равно весу вышестоящего столба воздуха с единичным сечением.
В системе СГС 760 мм рт. ст. эквивалентно 1,01325 бар (1013,25 мбар) или 101 325 Па в Международной системе единиц (СИ).
Барическая ступень[править | править код]
Высота, на которую надо подняться или опуститься, чтобы давление изменилось на 1 гПа (гектопаскаль), называется «барической (барометрической) ступенью». Барической ступенью удобно пользоваться при решении задач, не требующих высокой точности, например, для оценки давления по известной разности высот. Считая, что атмосфера не испытывает существенного вертикального ускорения (то есть находится в квазистатическом состоянии), из основного закона статики получаем, что барическая ступень 
При температуре воздуха 0 °C и давлении 1000 гПа, барическая ступень равна 8 м/гПа. Следовательно, чтобы давление уменьшилось на 1 гПа, нужно подняться на 8 метров.
С ростом температуры и увеличением высоты над уровнем моря она возрастает (в частности, на 0,4 % на каждый градус нагревания), то есть она прямо пропорциональна температуре и обратно пропорциональна давлению. Величина, обратная барической ступени, — вертикальный барический градиент, то есть изменение давления при поднятии или опускании на 100 метров. При температуре 0 °C и давлении 1000 гПа он равен 12,5 гПа.
Изменения давления с высотой[править | править код]

Изменение давления с высотой.
С высотой атмосферное давление уменьшается. Например, горная болезнь начинается на высоте около 2-3 км, а атмосферное давление на вершине Эвереста составляет примерно 1/4 от показателя на уровне моря.
В стационарных условиях атмосферное давление уменьшается по мере увеличения высоты, поскольку оно создаётся лишь вышележащим слоем атмосферы. Зависимость давления от высоты описывается барометрической формулой[10].
Уравнение статики выражает закон изменения давления с высотой:
где: 





Приведение к уровню моря[править | править код]
Многие метеостанции рассылают так называемые «синоптические телеграммы», в которых указывается давление, приведённое к уровню моря (см. КН-01, METAR). Это делается для того, чтобы давление было сравнимо на станциях, расположенных на разных высотах, а также для нужд авиации. Приведённое давление используется также и на синоптических картах.
При приведении давления к уровню моря используют сокращенную формулу Лапласа:
То есть, зная давление и температуру на уровне 


Вычисление давления на высоте 


где 







На небольших высотах каждые 12 м подъёма уменьшают атмосферное давление на 1 мм рт. ст. На больших высотах эта закономерность нарушается[5].
Более простые расчёты (без учёта температуры) дают:
где 
Измерения и расчёт показывают в полном согласии, что при подъёме над уровнем моря на каждый километр давление будет падать на 0,1 долю; то же самое относится и к спуску в глубокие шахты под уровень моря — при опускании на один километр давление будет возрастать на 0,1 своего значения.
Речь идёт об изменении на 0,1 от значения на предыдущей высоте. Это значит, что при подъёме на один километр давление уменьшается до 0,9 (точнее 0,87[прим 1]) от давления на уровне моря.
В ещё более грубом приближении, двукратному изменению давления соответствует изменение высоты на каждые пять километров.
В прогнозах погоды и сводках, распространяемых для населения через интернет и по радио, используется неприведённое давление, то есть, фактическое давление на уровне местности.
См. также[править | править код]
Видеоурок: атмосферное давление
- Фактическая погода
- Атмосфера
- Разгерметизация
Примечания[править | править код]
Источники[править | править код]
- ↑ Давление Архивная копия от 20 декабря 2016 на Wayback Machine // Метеорологический словарь
- ↑ 1 2 Атмосферное давление // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
- ↑ Положение о единицах величин, допускаемых к применению в Российской Федерации Архивная копия от 2 ноября 2013 на Wayback Machine Утверждено Постановлением Правительства РФ от 31 октября 2009 г. N 879.
- ↑ Перышкин А. В. Измерение атмосферного давления. Опыт Отто Герике // Физика. 7 класс / Е. Н Тихонова. — 16-е изд. — М.: Дрофа, 2013. — С. 190. — 189 с.
- ↑ 1 2 Атмосферное давление. Класс!ная физика. Дата обращения: 9 июня 2015. Архивировано 16 марта 2015 года.
- ↑ Метеочувствительность: что это такое и как с ней бороться. РИА Новости. Дата обращения: 9 июня 2015. Архивировано 18 августа 2013 года.
- ↑ Смерч. pogoda.by. Дата обращения: 7 июня 2015. Архивировано 25 апреля 2015 года.
- ↑ Изобары (в физике) // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
- ↑ Standard pressure (англ.). IUPAC. Дата обращения: 18 августа 2013. Архивировано 18 августа 2013 года.
- ↑ Барометрическая формула // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
Сноски[править | править код]
- ↑ Формула предполагает температуру одинаковой на всех высотах. На самом же деле температура атмосферы меняется с высотой по довольно сложному закону. Тем не менее формула даёт неплохие результаты, и на высотах до 50-100 километров ею можно пользоваться. Так, нетрудно определить, что на высоте Эльбруса — около 5,6 км — давление упадёт примерно вдвое, а на высоте 22 км (рекордная высота подъёма стратостата с людьми) давление упадёт до 50 мм рт. ст.
Литература[править | править код]
- Хргиан А. Х. Физика атмосферы. — 2 изд. — М., 1958.
- Бургесс Э. К границам пространства, пер. с англ.. — М.: Изд. иностранной литературы, 1957. — 223 с.
Ссылки[править | править код]
 Медиафайлы по теме Атмосферное давление на Викискладе
Медиафайлы по теме Атмосферное давление на Викискладе- Атмосферное давление // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- График изменения атмосферного давления при изменении высоты
Атмосферное давление
Собственный вес столба воздуха создает атмосферное давление, которое уменьшается по мере удаления от поверхности Земли.
Вблизи земной поверхности: При подъеме на каждые 8 м атмосферное давление падает на 100 Па = 1 мбар.
Если предположить, что температура воздуха с высотой не меняется, то атмосферное давление уменьшается с высотой по экспоненциальному закону.
Если
| p0 | атмосферное давление у поверхности Земли, | Па |
|---|---|---|
| ph | атмосферное давление на высоте, | Па |
| h | высота над поверхностью Земли, | м |
| ρ0 | плотность воздуха у поверхности Земли, | кг.м3 |
| g | ускорение свободного падения, | м/c2 |
| e | 2.71828, |
то для высот примерно до 100 км давление (при постоянной температуре) рассчитывается по формуле
[ p_h = p_0 e^{frac{-ρ_0 gh}{p_0}} ]
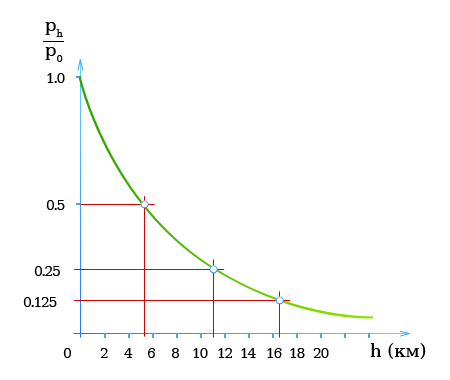
График — Атмосферное давление в зависимости от высоты
Если давление у поверхности Земли p0 = pн = 101.325 кПа (до 1980 г. — 760 мм рт. ст.)
и температура воздуха на любой высоте равна 0°С, то из формулы следует:
[ p_h = p_0 e^{frac{-h}{7.99}} ]
или
[ h = 18.4 lgbigg(frac{p_0}{p_h}bigg) ]
где высота h выражена в километрах.
Формула (1) называется барометрической формулой высоты.
При точных вычислениях атмосферного давления следует учитывать понижение температуры воздуха по мере увеличения высоты.
При pн = 101.325 кПа (среднегодовое значение атмосферного давления на уровне моря) и t = 15°С
(среднегодовое значение температуры на уровне моря) для высот до 11 000 м (тропосфера)
следует пользоваться международной формулой:
[ p_h = 101.3 bigg(1 – frac{6.5h}{288}bigg)^{5.255} ]
где давление выражено в килопаскалях, высота h — в километрах, или
[ ρ_h = 1.2255 bigg(1 – frac{6.5h}{288}bigg)^{4.255} ]
где плотность выражена в кг/м3, высота — в километрах.
Зависимость среднегодового давления от высоты.
Атмосферное давление |
стр. 509 |
|---|
Random converter
- Калькуляторы
- Термодинамика — теплота
Калькулятор закона состояния идеального газа (давление–объем–температура–количество)

Калькулятор закона состояния идеального газа определяет одну из четырех величин, входящих в уравнение состояния (давление, объем, температура или количество), если известны три другие величины.
Пример: Рассчитать давление в паскалях в 70-литровом баке работающего на метане автомобиля, если в нем хранится 800 молей метана при 30 °С.
Еще несколько примеров решения задач о состоянии идеального газа под приводится калькулятором.
Выберите неизвестную величину для решения уравнения состояния идеального газа:
PVTn
Абсолютное давление
P
Объем
V
Температура
T
ИЛИ
Поделиться ссылкой на этот калькулятор, включая входные параметры
Для расчета выберите неизвестную величину и введите три известные величины из четырех имеющихся в уравнении состояния газа (давление, объем, температура, количество). Четвертая величина будет рассчитана после нажатия на кнопку Рассчитать. Количество можно ввести в молях или указать молярную массу и массу газа. Для определения молярной массы любого газа можно использовать калькулятор молярной массы. Если нужно определить молярную массу смеси газов, например, сухого воздуха, нужно определить молярные массы каждого газа и умножить их на процентное содержание по массе каждого газа в воздухе.
Примеры решения задач по уравнению состояния идеального газа (уравнению Менделеева — Клапейрона)
Определения и формулы
Идеальный газ
Закон идеального газа
Закон Бойля — Мариотта (T=const, n=const)
Закон Авогадро (T=const, P=const)
Закон Гей-Люссака (P=const, n=const)
Закон Шарля (или второй закон Гей-Люссака) (V=const, n=const)
Примеры решения задач по уравнению состояния идеального газа (уравнению Менделеева — Клапейрона)
Задача 1: Плотность воздуха при нормальных условиях (температура 0 °С и атмосферное абсолютное давление 100 кПа) составляет 1,28 кг/м³. Определить среднюю молярную массу воздуха.
Решение: Поскольку плотность воздуха задана, это означает, что в калькулятор можно ввести массу одного кубического метра воздуха, равную 1,28 кг. Введите в калькулятор данные:
- Выберите n (Количество в молях) в селекторе Выберите неизвестную величину.
- Введите абсолютное давление P = 100 кПа.
- Введите объем V = 1 м³.
- Введите температуру T = 0 °C.
- Нажмите кнопку Рассчитать.
- Калькулятор покажет количество молей в 1 м3 воздуха.
- Введите массу воздуха m = 1,28 кг и нажмите кнопку Рассчитать.
- Калькулятор рассчитает молярную массу воздуха M = 0,029 кг/моль
Задача 2: Молярная масса газа кислорода (O₂) M = 32 г/моль. Определить абсолютную температуру 128 г. кислорода, находящегося в 10-литровом сосуде под давлением P = 3 МПа.
Решение: Нажмите кнопку Reset и введите в калькулятор данные задачи:
- Выберите T (Температура) в селекторе Выберите неизвестную величину.
- Введите молярную массу кислорода N = 32 г/моль.
- Введите массу кислорода m = 128 г.
- Калькулятор рассчитает количество кислорода в молях.
- Введите объем V = 4 л и давление P = 3 МПа.
- Нажмите кнопку Рассчитать.
- Считайте температуру в кельвинах.
Задача 3: В сосуде высокого давления находится газ под давлением P = 0.5 МПа при температуре T = 15 °С. Объем газа V = 5 л. Рассчитать объем этой массы газа при нормальных условиях (P = 100 кПа, T = 0 °С).
Решение: Нажмите кнопку Reset и введите в калькулятор данные задачи:
- Выберите T (Температура) в селекторе Выберите неизвестную величину.
- Введите давление P = 500 кПа.
- Введите температуру T = 15 °C.
- Введите объем V = 5 л.
- Нажмите кнопку Рассчитать.
- Калькулятор рассчитает количество в молях, которое будет использовано в следующем шаге.
- Выберите Объем в селекторе Выберите неизвестную величину.
- Введите температуру и давление P = 100 kPa, T = 0 °C (нормальные условия) и нажмите кнопку Рассчитать.
- Калькулятор рассчитает новый объем газа V = 23.69 л при нормальных условиях.
Задача 4: Рассчитать давление в паскалях в 70-литровом баке работающего на метане автомобиля, если в нем хранится 12,8 кг метана (молярная масса 16 г/моль) при 30 °С.
Определения и формулы
Идеальный газ
Идеальный газ — теоретическая модель, в которой газ представляется в виде множества свободно движущихся частиц бесконечно малого размера, которые взаимодействуют друг с другом абсолютно упруго, то есть при столкновении двух частиц их кинетическая энергия не изменяется и не превращается ни в какую другую форму энергию, например, в потенциальную энергию или в тепло. Считается, что суммарный размер частиц настолько мал, что занимаемый ими объем в сосуде пренебрежимо мал. Эта теоретическая модель полезна, так как она упрощает многие расчеты, а также в связи с тем, что идеальный газ подчиняется законам классической механики. Идеальный газ можно представить себе в виде множества абсолютно твердых сфер, которые только сталкиваются друг с другом и больше никак не взаимодействуют.
В обычных условиях, например, при стандартных условиях (при температуре 273,15 К и давлении в 1 стандартную атмосферу) большинство реальных газов ведут себя как идеальный газ. В общем случае, газ ведет себя как идеальный при низком давлении и высокой температуре, когда расстояния между молекулами газа относительно велики. В этих условиях потенциальная энергия вследствие действия межмолекулярных сил намного меньше кинетической энергии частиц. Размер молекул также незначителен по сравнению с расстоянием между ними. Идеальная модель не работает при низких температурах и высоких давлениях, а также для тяжелых газов. При понижении температуры и повышении давления реальный газ может стать жидкостью или даже перейти в твердое состояние, то есть может произойти фазовый переход. В то же время, модель идеального газа не допускает жидкого или твердого состояния.
Закон идеального газа
Идеальный газ, как и любой другой газ, можно охарактеризовать четырьмя переменными и одной константой, а именно:
- давление (P),
- объем (V),
- количество в молях (n),
- температура (T), and
- универсальная газовая постоянная (R)
Эти четыре переменные и одна константа объединены в приведенном ниже уравнении, которое называется уравнением состояния идеального газа:

Это уравнение также известно под названием закона идеального газа и уравнения Менделеева — Клапейрона или уравнения Клапейрона, так как уравнение было впервые выведено в 1834 г. французским инженером Эмилем Клапейроном (1799–1864). О вкладе Д. И. Менделеева — чуть ниже. В этом уравнении:
- P — абсолютное давление, измеряемое в СИ в паскалях (Па),
- V — объем, измеряемый в СИ в кубических метрах (м³),
- n — количество вещества (газа) в молях (сокращение моль). Один моль любого вещества в граммах численно равен средней массы одной молекулы в соединении, выраженной в атомных единицах массы. Например, один моль кислорода с атомной массой 16 соответствует 16 граммам. Один моль идеального газа при стандартных условиях занимает 22,4 литра.
- T — абсолютная температура.
- R — универсальная газовая постоянная, являющаяся физическим коэффициентом пропорциональности уравнения состояния идеального газа.
Приведенное выше уравнение показывает, что при нулевой абсолютной температуре получается нулевой объем. Однако это не означает, что объем реального газа действительно исчезает. При очень низких температурах все газы становятся жидкостями и уравнение идеального газа к ним неприменимо.
Универсальная газовая постоянная соответствует работе, выполненной при расширении одного моля идеального газа при нагревании на 1 К при постоянном давлении. Размерность постоянной — работа на количество вещества на температуру. Постоянная в точности равна 8,31446261815324 Дж⋅К⁻¹⋅моль⁻¹. Универсальная газовая постоянная также определяется как произведение числа Авогадро NA и постоянной Больцмана k:

Входящая в уравнение состояния идеального газа универсальная газовая постоянная была предложена и введена в уравнение Дмитрием Менделеевым в 1877 г. Поэтому уравнение состояния идеального газа в литературе на русском языке и ее переводах на другие языки, называется уравнением Менделеева — Клапейрона.
Количество газа в молях часто бывает удобно заменить массой газа. Количество газа в молях n, его масса m в граммах и молярная масса M в граммах на моль связаны формулой:

Заменяя в уравнении состояния идеального газа n на m/M, имеем:

Для определения молярной массы элемента, его относительная атомная масса умножается на коэффициент молярной массы в кг/моль

Например, молярная масса кислорода как элемента в единицах системы СИ

Если ввести в уравнение состояния идеального газа плотность ρ = m/V, мы получим:

Теперь введем понятие удельной газовой постоянной, которая представляет собой отношение универсальной газовой постоянной R к молярной массе M:

Например, удельная газовая постоянная сухого воздуха приблизительно равна 287 Дж·кг⁻¹·К⁻¹. Подставив удельную газовую постоянную в уравнение состояния идеального газа, получим:

Закон идеального газа объединяет четыре более простых эмпирических газовых закона, открытых в XVII–XIX вв. несколькими учеными, которые аккуратно измеряли свойства газа. Простые газовые законы можно также вывести из уравнения состояния идеального газа (PV=nRT). Поскольку в этом уравнении R является постоянной величиной, можно записать

Поскольку PV/NT — постоянная величина, можно записать это иначе:

Здесь индексы 1 и 2 показывают начальное и конечное состояние газа в системе. Мы будем использовать это уравнение ниже при описании четырех газовых законов.
Отметим, что исторически именно эмпирические законы поведения газа, описанные ниже, привели к открытию обобщенного закона состояния идеального газа. Эти законы были открыты несколькими учеными, которые проводили эксперименты, изменяя только две переменные состояния газа и оставляя две другие переменные постоянными.
Закон Бойля — Мариотта (T=const, n=const)

Роберт Бойль
Изменим предыдущее уравнение с учетом, что количество газа в молях n и его температура Т остаются неизменными:

или


Эдм Мариотт
Это закон Бойля — Мариотта, описывающий зависимость объема V фиксированного количества газа в молях n от давления P при постоянной температуре T. Давление фиксированной массы газа при неизменной температуре обратно пропорционально его объему. Закон был сформулирован англо-ирландским химиком и физиком Робертом Бойлем в 1662 г. В России и континентальной Европе это закон называют законом Бойля — Мариотта с учетом вклада в открытие закона французского физика и священника Эдма Мариотта.
Закон Авогадро (T=const, P=const)

Амедео Авогадро
Если температура и давление остаются неизменными, можно записать

Это закон Авогадро, указывающий, что при неизменных температуре и давлении равные объемы любых газов содержат одинаковое количество молекул. Это уравнение показывает, что, если количество газа увеличивается, объем газа пропорционально растет. Иными словами, количество атомов или молекул газа не зависит от их размеров или от молярной массы газа. Закон назван в честь итальянского ученого Амедео Авогадро, который опубликовал гипотезу об отношениях объема газа и его количества в молях в 1811 году. Число Авогадро также носит его имя.
Закон Гей-Люссака (P=const, n=const)

Жак Шарль
При постоянном давлении объем фиксированного количества газа в молях пропорционален абсолютной температуре системы с газом.

В англоязычной литературе этот закон называется законом объемов и законом Шарля. Закон описывает как расширяется любой газ при увеличении его абсолютной температуры. Закон был сформулирован в неопубликованной работе французским ученым Жаком Шарлем в 80-х гг. XVIII в. Его соотечественник Жозеф Луи Гей-Люссак опубликовал этот закон в 1803 г. и указал, что приоритет открытия принадлежит Жаку Шарлю. Поэтому этот закон в литературе не на английском языке часто называют законом Гей-Люссака. В русскоязычной литературе закон носит имя Гей-Люссака. Итальянцы называют этот закон первым законом Гей-Люссака (ит. prima legge di Gay-Lussac).
Закон Шарля (или второй закон Гей-Люссака) (V=const, n=const)

Жозеф Луи Гей-Люссак
Закон Шарля (называемый также вторым законом Гей-Люссака) гласит, что давление фиксированного количества газа в молях при его неизменном объеме прямо пропорционально абсолютной температуре газа:

Закон был сформулирован Гей-Люссаком в 1802 г. В литературе на других языках этот закон также называют законом Амонтона по имени французского ученого Гийома Амонтона, который на сто лет раньше обнаружил количественную зависимость объема газа от его температуры. Иногда закон называют вторым законом Гей-Люссака и законом Шарля, так как сам Гей-Люссак считал, что закон открыт Шарлем. Закон зависимости давления от температуры был также независимо открыт английским физиком Джоном Дальтоном в 1801 г. Итальянцы называют этот закон вторым законом Вольта–Гей-Люссака (ит. seconda legge di Volta – Gay-Lussac), потому что итальянец Алессандро Вольта независимо проводил исследования газов и получил аналогичные результаты.

При нагревании воздуха в оболочке воздушного шара его плотность уменьшается и становится меньше плотности окружающего воздуха; в результате шар приобретает положительную плавучесть
Термодинамика — теплота
На этих страницах размещены конвертеры единиц измерения, позволяющие быстро и точно перевести значения из одних единиц в другие, а также из одной системы единиц в другую. Конвертеры пригодятся инженерам, переводчикам и всем, кто работает с разными единицами измерения.
Мы работаем над обеспечением точности конвертеров и калькуляторов TranslatorsCafe.com, однако мы не можем гарантировать, что они не содержат ошибок и неточностей. Вся информация предоставляется «как есть», без каких-либо гарантий. Условия.
Если вы заметили неточность в расчётах или ошибку в тексте, или вам необходим другой конвертер для перевода из одной единицы измерения в другую, которого нет на нашем сайте — напишите нам!
Канал Конвертера единиц TranslatorsCafe.com на YouTube





