Как найти периметр трапеции по теореме пифагора

Содержание:

Формула
Примеры вычисления периметра трапеции

Формула

Чтобы найти периметр трапеции необходимо найти сумму длин её сторон.

В общем случае для произвольной трапеции
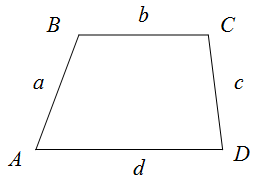
$ABCD$ со сторонами $AB=a$, $BC=b$, $CD=c$, $AD=d$ периметр вычисляется по формуле:

$$P_{Delta A B C D}=a+b+c+d$$

Если трапеция $ABCD$ равнобокая, то по определению её
боковые стороны равны $AB=CD=a$ и формула для
нахождения периметра примет вид:

$$P_{Delta A B C D}=2 a+b+d$$

Примеры вычисления периметра трапеции

Пример

Задание. Найти периметр трапеции
$ABCD$ со сторонами
$AB=1,5$ см,
$BC=2$ см,
$CD=1$ см,
$AD=3$ см.

Решение. Для нахождения периметра трапеции
$ABCD$ воспользуемся формулой

$$P_{Delta A B C D}=A B+B C+C D+A D$$

Подставляя в неё заданные в условии длины сторон, получим:

$P_{Delta A B C D}=1,5+2+1+3=7,5$ (см)

Ответ. $P_{Delta A B C D}=7,5$ (см)

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Заданна равнобокая трапеция
$ABCD$ с основаниями
$BC=3$ см,
$AD=7$ см и высотой
$BK=2 sqrt{3}$ см. Найти периметр заданной трапеции.

Решение. Сделаем рисунок.

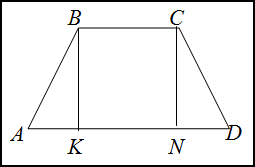
Опустим высоту $CN$. Полученный в
результате четырехугольник
$BCKN$ является прямоугольником, поэтому
$BC=KN$. Треугольники $Delta A B K quad$ и $quad Delta N C D$ – прямоугольные и равны между собой. Тогда
$AK=ND$. Найдем чему равно $AK$:

$A K=(A D-B C): 2 Rightarrow A K=(7-3): 2=2$ (см)

Из $Delta ABK$ по теореме Пифагора найдем боковую сторону
$AB$ трапеции:

$=sqrt{12+4}=sqrt{16}=4$ (см)

Тогда периметр рассматриваемой равнобокой трапеции

$P_{Delta A B C D}=2 cdot 4+3+7=18$ (см)

Ответ. $P_{Delta A B C D}=18$ (см)

Читать дальше: как найти периметр ромба.

Источник

Найти периметр равнобедренной трапеции ABCD

Для начала, задача, которая попадается в теме «теорема Пифагора». Применять только теорему совсем не обязательно. Можно попробовать что-то необычное и тогда мы точно увидим пару интересных решений.

Теорема Пифагора

Перед тем, как показать полное условие рассмотрим один простой и, самое главное, короткий способ доказательства теоремы. Чем-то подобным мы уже пользовались для короткого доказательства теоремы Косинусов, частным случаем которой и является т. Пифагора.

Нарисуем окружность, в которой на диаметре построим прямоугольный треугольник со сторонами a, b и c, при чём c – гипотенуза треугольника и радиус окружности.

Радиус окружности — c, гипотенуза — c, катеты — a и b

Дальше воспользуемся свойством пересекающихся хорд и получим выражение, результатом упрощения которого и будет теорема Пифагора:

Свойство пересекающихся хорд и следствие

Теорема доказана, ну а теперь полной условие задачи.

Условие

В равнобедренной трапеции ABCD боковая сторона в √2 раз меньше основания BC, CE — высота. Найдите периметр трапеции, если BE = √5, BD = √10.

Как всегда, ищем короткое или интересное решение (а может и решения), а не только ответ.

Пробуйте, решайте, экспериментируйте, делитесь решениями в комментариях. Удачи!

Формула вычисления периметра

Периметр (P) трапеции равняется сумме длин всех ее сторон.

P = a + b + c + d

Периметр трапеции

b и d – основания трапеции;
a и с – ее боковые стороны.

Периметр равнобедренной трапеции

В равнобедренной трапеции боковые стороны равны (a=c), из-за чего ее, также, называют равнобокой. Периметр считается так:

P = 2a + b + d или P = 2с + b + d

Периметр равнобедренной трапеции

Периметр прямоугольной трапеции

Для расчета периметра используется такая же формула, что и для разносторонней трапеции.

P = a + b + c + d

Периметр прямоугольной трапеции

Примеры задач

Задание 1
Найдите периметр трапеции, если ее основания равны 7 и 10 см, а боковые стороны – 4 и 5 см.

Решение:
Используем стандартную формулу, подставив в нее известные нам длины сторон: P = 7 см + 10 см + 4 см + 5 см = 26 см.

Задание 2
Периметр равнобедренной трапеции равняется 22 см. Найдите длину боковой стороны, если основания фигуры равны 3 см и 9 см.

Решение:
Как мы знаем, периметр равнобедренной трапеции вычисляется по формуле: P = 2a + b + d, где а – боковая сторона.
Ее длина, умноженная на два равна: 2a = P – b – d = 22 см – 3 см – 9 см = 10 см.
Следовательно, длина боковой стороны составляет: a = 10 см / 2 = 5 см.

Источник

Download Article

A trapezoid is defined as a quadrilateral with two parallel sides. As with any polygon, to find the perimeter of a trapezoid you need to add all four of its sides together. However, often you will be missing side lengths but have other information, such as the height of the trapezoid, or the angle measurements. Using this information, you can use rules of geometry and trigonometry to find the unknown lengths of sides.

1

Set up the formula for perimeter of a trapezoid. The formula is $P=T+B+L+R$ , where $P$ equals the perimeter of the trapezoid, and the variables $T$ equals the length of the top base of the trapezoid, $B$ equals the length of the bottom base, $L$ equals the length of the left side, and $R$ equals the length of the right side.^[1]
2
Plug the side lengths into the formula. If you do not know the length of all four sides of the trapezoid, you cannot use this formula.
- For example, if you have a trapezoid with a top base of 2 cm, a bottom base of 3 cm, and two side lengths of 1 cm, your formula will look like this:
  $P=2+3+1+1$
Advertisement
3

Add the side lengths together. This will give you the perimeter of your trapezoid.

1
Divide the trapezoid into a rectangle and two right triangles. To do this, draw the height from both top vertices.
- If you cannot form two right triangles because one side of the trapezoid is perpendicular to the base, just note that this side will have the same measurement as the height, and divide the trapezoid into one rectangle and one right triangle.
2
Label each height line. Since these are opposite sides of a rectangle, they will be the same length.^[2]
- For example, if you have a trapezoid with a height of 6 cm, you should draw a line from each top vertex extending down to the bottom base. Label each line 6 cm.
3
Label the length of the middle section of the bottom base. (This is the bottom side of the rectangle.) The length will equal the length of the top base (the top side of the rectangle), because opposite sides of a rectangle are of equal length.^[3] If you do not know the length of the top base, you cannot use this method.
- For example, if the top base of the trapezoid is 6 cm, then the middle section of the bottom base is also 6 cm.
4

Set up the Pythagorean Theorem formula for the first right triangle. The formula is $a^{{2}}+b^{{2}}=c^{{2}}$ , where $c$ is the length of the hypotenuse of the right triangle (the side opposite the right angle), $a$ is the height of the right triangle, and $b$ is the length of the base of the triangle.^[4]
5
6

Square the known values in the equation. Then, subtract to isolate the $b$ variable.
7

Take the square root to find the value of $b$ . (For complete instructions on how to simplify square roots, you can read Simplify a Square Root.) The result will give you the value of the missing base of your first right triangle. Label this length on the base of your triangle.
8

Find the missing length of the second right triangle. To do this, set up the Pythagorean Theorem formula for the second triangle, and follow the steps to find the length of the missing side. If you are working with an isosceles trapezoid, which is a trapezoid in which the two non-parallel sides are the same length,^[5] the two right triangles are congruent, so you can simply carry the value from the first triangle over to the second triangle.
9

Add up all the side lengths of the trapezoid. The perimeter of any polygon is the sum of all sides: $P=T+B+L+R$ . For the bottom base, you will add the bottom side of the rectangle, plus the bases of the two triangles. You will likely have square roots in your answer. For complete instructions on how to add square roots, you can read the article Add Square Roots. You can also use a calculator to convert the square roots to decimals.

1
Divide the trapezoid into a rectangle and two right triangles. To do this, draw the height from both top vertices.
- If you cannot form two right triangles because one side of the trapezoid is perpendicular to the base, just note that this side will have the same measurement as the height, and divide the trapezoid into one rectangle and one right triangle.
2
Label each height line. Since these are opposite sides of a rectangle, they will be the same length.^[6]
- For example, if you have a trapezoid with a height of 6 cm, you should draw a line from each top vertex extending down to the bottom base. Label each line 6 cm.
3
Label the length of the middle section of the bottom base. (This is the bottom side of the rectangle.) This length will be equal to the length of the top base, because opposite sides of a rectangle are of equal length.^[7]
- For example, if the top base of the trapezoid is 6 cm, then the middle section of the bottom base is also 6 cm.
4
5
Plug the known values into the sine ratio. Make sure you use the height of the triangle as the length of the opposite side in the formula. You will solve for H.
- For example, if the given interior angle is 35 degrees, and the height of the triangle is 6 cm, your formula will look like this:
  $sin(35)={frac {6}{H}}$
6
Find the sine of the angle. Do this by using the SIN button on a scientific calculator. Plug this value into the ratio.
- For example, by using a calculator you will find that the sine of a 35 degree angle is .5738 (rounded). So your formula will now be:
  $.5738={frac {6}{H}}$
7

Solve for H. To do this, multiply each side by H, then divide each side by the angle sine. Or, you can simply divide the height of the triangle by the angle sine.
8

Find the length of the hypotenuse of the second right triangle. Set up the sine ratio ( $sin theta ={frac {{text{opposite}}}{{text{hypotenuse}}}}$ ) for the second given interior angle. This will give you the length of the hypotenuse, which is also the first side of the trapezoid.
9

Set up the Pythagorean Theorem formula for the first right triangle. The Pythagorean Theorem formula is $a^{{2}}+b^{{2}}=c^{{2}}$ , where the length of the hypotenuse is $c$ , and the height of the triangle is $a$ .
10
11

Solve for $b$ . This will give you the length of base of the first right triangle, and the first missing section of the trapezoid’s bottom base.
12
13
Add up all the side lengths of the trapezoid. The perimeter of any polygon is the sum of all sides: $P=T+B+L+R$ . For the bottom base, you will add the bottom side of the rectangle, plus the bases of the two triangles.
- For example, $6+(8.5639+6+6)+10.4566+8.4854=45.5059$
  So, the approximate perimeter of your trapezoid is 45.5059 cm.

Add New Question

Question

How can I solve the hypotenuse of a right triangle with a height of 2ft?

You don’t have enough information to find the hypotenuse. You would need the lengths of both legs or the size of at least one of the acute angles or the area of the triangle.
Question

How do I find the area without knowing the length of the sides of the trapezoid?

You would have to know the height of the trapezoid (h) and the lengths of both parallel sides (a and b). The area formula is [h(a + b)] / 2.
Question

Why are there so many formulas?

It’s because there are several possible sets of known dimensions regarding a trapezoid.

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Use the laws of special triangles to find the missing lengths of special triangles without using sine or the Pythagorean Theorem. The laws apply to a 30-60-90 triangle, or a 90-45-45 triangle.
Use a scientific calculator to find the sine of an angle by entering the angle measurement, then hitting the “SIN” button. You can also use a trigonometry table.

Thanks for submitting a tip for review!

Things You’ll Need

Calculator
Pencil
Paper

References

About This Article

Article SummaryX

To find the perimeter of a trapezoid if you know the length of both sides and the bases, add together the length of all 4 sides. If you know the height, both side lengths, and the top base length, draw a straight line down from each top corner to form a square and 2 triangles. Then, use the Pythagorean Theorem to find the length of the base of each triangle. Add the length of each triangle base to the length of the top base, then add that to the top base and both sides to get the perimeter. To learn more about using the Pythagorean Theorem, keep reading!

Did this summary help you?

Thanks to all authors for creating a page that has been read 264,180 times.

Did this article help you?

Источник

Как найти площадь и периметр равнобедренной трапеции?

Как найти площадь и периметр прямоугольной трапеции?

Площадь трапеции, у которой основания a1 и a2, средняя линия m = (a1 + a2)/2, а высота h.

S = (a1 + a2)*h/2 = m*h

Периметр равнобочной трапеции, у которой боковые стороны равны b

P = a1 + a2 + 2*b

У прямоугольной трапеции одна боковая сторона перпендикулярна основаниям, то есть совпадает с высотой. Вторая равна b.

P = a1 + a2 + h + b

автор вопроса выбрал этот ответ лучшим

Stasy12
[41.4K]

5 лет назад

Геометрия интересная наука, другое дело, что не каждому она дается на изучение. Пыталась “дружить” с геометрией, конечно, не всегда все было гладко, но, если по формулам, то все удавалось. Доказывать теоремы нравилось.

Так вот трапеция, помню из курса геометрии это фигура, которая имеет разные длины сторон.Поэтому эти стороны обычно обозначают разными буквами латинского алфавита. Чтобы вычислить периметр необходимо все стороны просто сложить

Чтобы получить площадь трапеции руководствуйтесь вот этой формулой:

Вывести формулу площади трапеции можно самостоятельно, если вспомнить, что трапеция – это прямоугольник у которого одна или две стороны скошены. Площадь прямоугольника находится по формуле 1/2 ав, где а и в – стороны прямоугольника. Но точно та же формула будет справедлива и для трапеции, только если сторона В в трапеции будет равна ее высоте, то сторона А окажется равной средней линии трапеции. А средняя линия трапеции находится по формуле (А+Б)/2. Тогда получаем, что площадь трапеции следует искать по форомуле:

S = (A+B)/2*H

Ну а периметр трапеции находится как сумма всех его сторон. Если боковые стороны не известны, то пригодится теорема Пифагора как для равнобедренной трапеции, так и для прямоугольной.

Ксарфакс
[156K]

6 лет назад

Периметр трапеции

Как известно, трапеция имеет четыре стороны.

Периметр – это сумма длин всех сторон, в случае с обычной или прямоугольной трапецией он будет равен:

P = AD + CD + BC + AB.

Если трапеция равнобедренная, то AD = BC. Соответственно, P = 2AD + CD + AB.

Площадь трапеции

В общем случае она определяется по следующей формуле:

S = h*(AB + CD)/2, где h – высота, проведённая к основанию AB и (AB + CD)/2 – средняя линия трапеции.

В случае с прямоугольной трапецией её высота совпадает с одной из боковых сторон. Формула будет той же, но теперь вместо высоты трапеции будет фигурировать её сторона:

S = AD*(AB + CD)/2

Аватория
[71K]

5 лет назад

Площадь трапеции можно найти несколькими способами, все зависит от того, какие данные уже есть.

Для этого есть формулы нахождения площади трапеции.

Через основание и высоту:

Через высоту и среднюю линию:

Через все четыре стороны:

Через диагонали и угол между ними:

Через радиус вписанной окружности и угол:

Ну а периметр любой фигуры ищется сложением сумм всех сторон:

Любопытство
[135K]

5 лет назад

Что представляет собой трапеция? Прямоугольник со скошенными сторонами. Если это помнить, площадь прямоугольника со сторонами а и в можно искать по следующей формуле: 1:2 ав. А в трапеции в – ее высота, А равна средней линии трапеции (А+Б):2.

Таким образом, нам нужна вот эта формула площади:

S = (A+B)/2*H

Периметр же ищем по теореме Пифагора.

Galina7v7
[120K]

7 лет назад

Равнобедренная трапеция:

Пусть известны основания трапеции a и b (a >

b) , и боковые стороны c = d.

Периметр Р = a + b + 2c

Площадь : S= [(a+b)2]*h , где h – высота трапеции. Найдём h:

h = √[c^2 – (a – b)^2/4].

Для прямоугольной трапеции: a , b – основания , h – высота и боковая сторона ,

с – 2-я боковая сторона.

Периметр Р = a + b + c + h , но h = √ [c^2-(a-b)^2]

Площадь S = [(a + b)/2}h = [(a + b)/2]√ [c^2 – (a – b )^2].

При других исходных данных (например , углы при основании ) формулы периметра и площади будут немного другие.

Алиса в Стране
[363K]

5 лет назад

Начнем по порядку, с более простого, – с определения периметра трапеции. Допустим, у нас трапеция с вершинами А, В, С, D. Тогда периметр нашей трапеции равен длине всех ее сторон:

Р = АВ + ВС + СD + DА. Так, с периметром трапеции разобрались, ничего сложного в этом нет.

Теперь площадь трапеции. Для площади трапеции применяем специальную формулу:

Проповедник
[97.1K]

7 лет назад

Ну это смотря что известно об этой трапеции. Проще всего площадь трапеции найти так: высота умножить на длину короткой стороны прибавить отношение произведения высоты на разность длинной и короткой сторон к двум. Стороны, которые имеются ввиду- это те, которые паралленые друг другу, основания трапеции.

vksvovko
[1.6K]

6 лет назад

Чтобы найти периметр трапеции нужно сложить все его стороны. Чтобы найти площадь необходимо сложить 2 основания, поделить на два и умножить на высоту. Чтобы вычислить периметр часто в задачах нужно с начала подсчитать площадь а далее найти ребра.

Знаете ответ?

Источник

Формула

Примеры вычисления периметра трапеции

Теорема Пифагора

Условие

Читайте также:

Формула вычисления периметра

Примеры задач

Things You’ll Need

References

About This Article

Did this article help you?

Периметр Р = a + b + 2c

h = √[c^2 – (a – b)^2/4].

Периметр Р = a + b + c + h , но h = √ [c^2-(a-b)^2]

Площадь S = [(a + b)/2}h = [(a + b)/2]√ [c^2 – (a – b )^2].

Добавить комментарий Отменить ответ

Формула

Примеры вычисления периметра трапеции

Теорема Пифагора

Условие

Читайте также:

Формула вычисления периметра

Примеры задач

Things You’ll Need

References

About This Article

Did this article help you?

Периметр Р = a + b + 2c

h = √[c^2 – (a – b)^2/4].

Периметр Р = a + b + c + h , но h = √ [c^2-(a-b)^2]

Площадь S = [(a + b)/2}*h = [(a + b)/2]*√ [c^2 – (a – b )^2].

Вам также может понравиться

При сборке комода ящики встали криво как исправить

Мужчина мое мечты как найти

Как исправить замечание в дневнике

Добавить комментарий Отменить ответ

Площадь S = [(a + b)/2}h = [(a + b)/2]√ [c^2 – (a – b )^2].