Как найти закон распределения непрерывной случайной величины – Сайт, где вы сможете решить свои вопросы

Основные законы распределения непрерывных случайных величин

Определение характеристической функции и её использование в теории вероятностей. Нормальный закон распределения и его значение в теории вероятностей. Логарифмически нормальный закон. Гамма-распределение. Экспоненциальный закон и его использование в теории надёжности, теории очередей. Равномерный закон. Распределения хи-квадрат, Вейбула, Стьюдента, Фишера.

Характеристическая функция

Во многих задачах полезной характеристикой случайной величины является её характеристическая функция. Характеристической функцией случайной величины называется математическое ожидание комплексной случайной величины $e^{isX}$ , рассматриваемое как функции параметра (здесь и далее в этой части – мнимая единица). Таким образом, характеристическая функция непрерывной случайной величины задаётся формулой

$g(s)=intlimits_{-infty}^{+infty}e^{isx}f(x),dx$ , где f(x) – плотность вероятности.

Отметим следующие свойства характеристической функции:

1) при любом действительном значении характеристическая функция по модулю не превосходит единицы, то есть

|g(s)|leqslant1,~sinmathbb{R},;

2) характеристическая функция равна единицы при s=0 , то есть g(0)=1 .

Плотность вероятности случайной величины можно выразить через её характеристическую функцию:

$f(x)=frac{1}{2pi}intlimits_{-infty}^{+infty}e^{isx}g(s),ds.$

Таким образом, характеристическая функция случайной величины является её полной вероятностной характеристикой. Зная характеристическую функцию случайной величины, можно найти её плотность вероятности, а следовательно, и функцию распределения, то есть полностью определить закон распределения случайной величины. Через характеристическую функцию можно выразить также числовые характеристики случайной величины, в частности её математическое ожидание и дисперсию:

M(X)=-ig'(0);quad D[X]=g'(0)-g''(0).

Нормальный закон распределения (закон Гаусса)

Плотность вероятности нормально распределённой случайной величины выражается формулой

$f(x)=frac{1}{sigmasqrt{2pi}}exp!left(-frac{(x-a)^2}{2sigma^2}right).$

(8.1)

Кривая распределения изображена на рис. 16. Она симметрична относительно точки x=a (точка максимума). При уменьшении sigma ордината точки максимума неограниченно возрастает, при этом кривая пропорционально сплющивается вдоль оси абсцисс, так что площадь под её графиком остаётся равной единицы (рис. 17).

Кривые распределения нормального закона (закон Гаусса)

Нормальный закон распределения широко применяется в задачах практики. Объяснить причины этого впервые удалось Ляпунову. Он показал, что если случайная величина может рассматриваться как сумма большого числа малых слагаемых, то при достаточно общих условиях закон распределения этой случайной величины близок к нормальному независимо от того, каковы законы распределения отдельных слагаемых. А так как практически случайные величины в большинстве случаев бывают результатом действия множества причин, то нормальный закон оказывается наиболее распространённым законом распределения (подробнее об этом [url]см. часть 9[/url]). Укажем числовые характеристики нормально распределённой случайной величины (математическое ожидание и дисперсия):

M(X)=a;qquad D[X]=sigma^2.

Таким образом, параметры и sigma в выражении (8.1) нормального закона распределения представляют собой математическое ожидание и среднее квадратическое отклонение случайной величины. Принимая это во внимание, формулу (8.1) можно представить следующим образом:

$f(x)=frac{1}{sqrt{2pi{D[X]}}}exp!left(-frac{(x-M(X))^2}{2D[X]}right).$

Эта формула показывает, что нормальный закон распределения полностью определяется математическим ожидание и дисперсией случайной величины. Таким образом, математическое ожидание и дисперсия полностью характеризуют нормально распределённую случайную величину. Разумеется, что в общем случае, когда характер закона распределения неизвестен, знание математического ожидания и дисперсии недостаточно для определения этого закона распределения.

Характеристическая функция нормального распределения случайной величины задаётся формулой

$g(s)=exp!left(ias-frac{1}{2}sigma^2s^2right).$

Пример 1. Найти вероятность того, что нормально распределённая случайная величина удовлетворяет неравенству alpha<X<beta .

Решение. Используя свойство 3 плотности вероятности (см. раздел 4, часть 4), получаем

${P{alpha<X<beta}=intlimits_{alpha}^{beta}f(x),dx=frac{1}{sigmasqrt{2pi}}intlimits_{alpha}^{beta}exp!left(-frac{(x-a)^2}{2sigma^2}right)!dx.}$

Положим $frac{x-a}{sigma}=t$ , тогда

${P{alpha<X<beta}=frac{1}{sigmasqrt{2pi}}intlimits_{tfrac{beta-a}{sigma}}^{tfrac{alpha-a}{sigma}}sigmaexp!left(-frac{t^2}{2}right)!dt=Phi!left(frac{beta-a}{sigma}right)-Phi!left(frac{alpha-a}{sigma}right).}$

где Phi(x) — функция Лапласа.

График плотности вероятности стандартизированной нормальной величины

Выполним некоторые числовые расчёты. Если положить alpha=a-3sigma;~beta=a+3sigma в условии примера 1, то

{P{a-3sigma <X<a+3sigma}=2Phi(3)=0,!9973.}

Последний результат означает, что с вероятностью, близкой к единице (0,9973), случайная величина, подчиняющаяся нормальному закону распределения, не выходит за пределы интервала (a-3sigma;a+3sigma) . Это утверждение называют правилом трёх сигм.

Наконец, если a=0,~sigma=1 , то случайная величина, распределённая по нормальному закону с такими параметрами, называется стандартизированной нормальной величиной. На рис. 18 изображён график плотности вероятности этой величины

$f(x)=frac{1}{sqrt{2pi}}exp!left(-frac{x^2}{2}right).$

Примеры с использованием нормального закона распределения приведены также в части 9.

Логарифмически нормальное распределение

Говорят, что случайная величина имеет логарифмически нормальное распределение (сокращённо логнормальное распределение), если её логарифм ln{Y}=X распределён нормально, то есть если Y=e^X , где величина имеет нормальное распределение с параметрами a,sigma .

Плотность логнормального распределения задаётся формулой

$f(y)=frac{1}{ysigmasqrt{2pi}}exp!left(-frac{(ln{y}-a)^2}{2sigma^2}right),~~~y>0.$

Математическое ожидание и дисперсию логнормального распределения определяют по формулам

$M(Y)=exp!left(a+frac{sigma^2}{2}right); quad D[Y]=e^{2(2sigma^2+a)^2-a^2}-e^{2a+sigma^2}.$

Кривая этого распределения изображена на рис. 19.

График кривой логнормального распределения

Логарифмически нормальное распределение встречается в ряде технических задач. Оно даёт распределение размеров частиц при дроблении, содержаний элементов в минералах в извержённых горных пародах, численности рыб в море и т.д. Встречается такое распределение во всех задачах, где логарифм рассматриваемой величины можно представить в виде суммы большого количества независимых равномерно малых величин:

$ln{Y}=X=X_1+X_2+cdots+X_n=sumlimits_{k=1}^{n}X_k,$ то есть $Y=prodlimits_{k=1}^{n}e^{X_k}$ , где $e^{X_k}$ независимы.

Гамма-распределение

Говорят, что случайная величина имеет гамма-распределение с параметрами a>0 и b>0 , если её плотность распределения вероятностей имеет вид

$f(x)=begin{cases}0,&xleqslant0;\dfrac{b^a}{Gamma(a)}x^{a-1}e^{-bx},&x>0.end{cases}$ где $Gamma(a)=intlimits_{0}^{infty}t^{a-1}e^{-t},dt$ — гамма-функция Эйлера.

На рис. 20 показаны кривые распределения вероятностей при значениях параметра a>1 и a<1 (при a=1 получаем экспоненциальное распределение).

График кривых гамма-распределения вероятностей

Математическое ожидание и дисперсия, подчинённые гамма-распределению, задаются формулами

$M(X)=frac{a}{b};qquad D[X]=frac{a}{b^2}.$

Отметим, что при a>1 гамма-распределение имеет моду

$M_o=frac{a-1}{b}$

(графически это означает, что кривая распределения имеет точку максимума x=M_o , рис. 20).

Экспоненциальный закон распределения

Экспоненциальным распределением называется частный случай гамма-распределения с параметрами a=1;~b=lambda>0 , то есть то есть плотность вероятности в этом случае

$f(x)=begin{cases}0,&xleqslant0;\lambda{e^{-lambda{x}}},&x>0.end{cases}$

Используя свойства два плотности распределения ([url]см.[/url]), можно найти функцию распределения F(x) экспоненциального закона:

$F(x)=begin{cases}0,&x<0;\1-e^{-lambda{x}},&xgeqslant0.end{cases}$

Основные характеристики (математическое ожидание и дисперсия) случайной величины , распределённой по экспоненциальному, имеют вид

$M(X)=frac{1}{lambda};~~~~~D[X]=frac{1}{lambda^2}.$

Характеристическая функция экспоненциального распределения задаётся формулой

$g(s)=frac{lambda}{lambda-is}.$

Кривая экспоненциального распределения вероятностей показана на рис. 21,а, а график функции распределения F(x) — на рис. 21,б.

Графики плотности и функции экспоненциального распределения

Статистический смысл параметра lambda состоит в следующем: lambda есть среднее число событий на единицу времени, то есть 1slashlambda есть средний промежуток времени между двумя последовательными событиями.

Экспоненциальное (показательное) распределение часто встречается в теории массового обслуживания (например, — время ожидания при техническом обслуживании или — продолжительность телефонных разговоров, ежедневно регистрируемых на телефонной станции) и теории надёжности (например, — срок службы радиоэлектронной аппаратуры).

Пример 2. Случайная величина — время работы радиолампы — имеет показательное распределение. Определить вероятность того, что время работы лампы будет не меньше 600 ч, если среднее время работы радиолампы 400 ч.

Решение. По условию задачи математическое ожидание случайной величины равно 400 ч, следовательно, lambda=1slash 400 . Искомая вероятность есть

${P{Xgeqslant600}=1-P{X<600}=1-F(600)=1-Bigl(1-expfrac{-600}{400}Bigl)=e^{-1.5}approx0,!2231.}$

Распределение Вейбула

Случайная величина подчиняется закону распределения Вейбула с параметрами ninmathbb{N},~ainmathbb{R},~b>0 , если её плотность распределения вероятностей записывается в виде

График плотности распределения Вейбула

$f(x)=begin{cases}0,&xleqslant{a};\dfrac{n}{b}!left(dfrac{x-a}{b}right)^{n-1}exp!left[-!left(dfrac{x-a}{b}right)^nright],&x>a.end{cases}$

Математическое ожидание и мода случайной величины, распределённые по закону Вейбула, имеют следующий вид:

$M(X)=a+bGamma!left(1+frac{1}{n}right)!;qquad M_0=a+sqrt[LARGE{LARGE{n}}]{frac{n-1}{n}}.$

Кривая распределения Вейбула изображена на рис. 22.

Распределение Вейбула в ряде случаев характеризует срок службы радиоэлектронной аппаратуры и, кроме того, применяется для аппроксимации различных несимметричных распределений в математической статистике.

Равномерный закон распределения

Случайная величина называется распределённой равномерно на отрезке [a;b] , если её плотность распределения вероятностей постоянна на данном отрезке:

$f(x)=begin{cases}0,&xnotin[a;b],\dfrac{1}{b-a},&xin[a;b].end{cases}$

Все возможные значения равномерно распределённой случайной величины лежат в пределах некоторого интервала; кроме того. в пределах этого интервала все значения случайной величины одинаково вероятны (обладаю одной и той же плотностью вероятности). Равномерно распределение реализуется в экспериментах, где наудачу ставиться точка на отрезке [a;b] ( — абсцисса поставленной точки). Равномерно распределённая случайная величина встречается также в измерительной практике при округлении отчётов измерительных приборов до целых делений шкал. Ошибка при округлении отчёте до ближайшего целого деления является случайной величиной , которая может принимать с постоянной плотностью вероятности любое значение между двумя соседними целыми делениями.

Математическое ожидание и дисперсия равномерно распределённой случайной величины

$M(X)=frac{a+b}{2};qquad D[X]=frac{(b-a)^2}{12}.$

Характеристическая функция равномерного распределения задаётся формулой

$g(s)=frac{1}{is(b-a)}(e^{isb}-e^{isa}).$

График плотности равномерного распределения изображён на рис. 23.

Графическая иллюстрация вероятности попадания случайной величины в заданную область

Пример 3. Найти вероятность попадания случайной величины, имеющей равномерное распределение на отрезке [a;b] , на участок (alpha;beta) , представляющий собой часть отрезка [a;b] .

Решение. Используя свойство 3 плотности вероятности, получаем

$P{alpha<X<beta}=intlimits_{a}^{b}frac{dx}{b-a}=frac{beta-alpha}{b-a}.$

Графически вероятность P{alpha<X<beta} представляется в виде площади заштрихованного прямоугольника на рис. 24.

Распределение хи-квадрат

Частный случай гамма-распределения с параметрами $a=frac{n}{2},~ninmathbb{N}$ и $b=frac{1}{2}$ называется распределением хи-квадрат с степенями свободы (пишут chi^2(n) ). Если случайная величина подчиняется закону , то её плотность распределения вероятностей есть

$f(x)=begin{cases}0,&xleqslant0;\dfrac{1}{2^{n/2}Gamma!left(frac{n}{2}right)}x^{n/2-1}e^{-x/2},&x>0.end{cases}$

Основные характеристики распределение хи квадрат (математическое ожидание и дисперсия):

M(X)=n;qquad D[X]=2n.

Кривые распределения (для различных значений ) изображены на рис. 25.

График плотности распределения хи-квадрат

Случайная величина X=chi^2(n) , подчиняющаяся хи-квадрат распределению, равна сумме квадратов независимых случайных величин $U_j,~jinmathbb{N}$ , каждая из которых имеет стандартизированное нормальное распределение, то есть

chi^2(n)=U_1^2+U_2^2+cdots+U_n^2.

Пусть chi^2(n_1) и chi^2(n_2) — независимые случайные величины, имеющие хи-квадрат распределение со степенью свободы соответственно n_1 и n_2 . Сумма этих случайных величин имеет также хи-квадрат распределение с n_1+n_2 степенями свободы:

chi^2(n_1)+chi^2(n_2)=chi^2(n_1+n_2).

Заметим, что распределение chi^2(n) при больших значениях n~(n>30) с достаточной для практических расчётов точностью аппроксимируется нормальным распределением с математическим ожиданием и дисперсией . Поэтому при больших значениях вероятности рассчитываются по нормальному закону.

Распределение chi^2(n) играет большую роль в математической статистике. Подробнее об этом [url]см. часть 11[/url].

Распределение Стьюдента

Распределение хи-квадрат Случайная величина T(n) есть отношение двух независимых случайных величин и $sqrt{frac{chi^2(n)}{n}}$ , то есть

$T(n)=Ucdot!left(frac{chi^2(n)}{n}right)^{-1/2}.$

Распределение случайной величины T(n) называется распределением Стьюдента с степенями свободы. Его плотность задаётся формулой

$f(x)=frac{Gamma!left(frac{n+1}{2}right)}{sqrt{pi{n}},Gamma!left(frac{n}{2}right)}!left(1+frac{x^2}{n}right)^{-tfrac{n+1}{2}}.$

Математическое ожидание и дисперсия случайной величины, подчинённой распределению Стьюдента X=T(n) , есть

$M(X)=0;qquad D[X]=frac{n}{n-2}.$

Кривые распределения Стьюдента (для различных значений ) изображены на рис. 26.

График плотности распределения Стьюдента

Как и в случае и хи-квадрат распределением, при увеличении распределение Стьюдента стремиться к нормальному, более того, стандартизованному нормальному (то есть с нулевым математическим ожиданием и единичной дисперсией). Распределение Стьюдента, как хи-квадрат распределение, широко применяется в задачах математической обработки измерений.

Распределение Фишера

Пусть случайная величина F(n_1;n_2) равна отношению двух независимых случайных величин $frac{chi^2(n_1)}{n_1}$ и $frac{chi^2(n_2)}{n_2}$ , то есть

$F(n_1;n_2)=frac{chi^2(n_1)/n_1}{chi^2(n_2)/n_2}.$

Распределение случайной величины F(n_1;n_2) называется распределением Фишера с n_1 и n_2 степенями свободы. Оно имеет следующую плотность вероятности

$f(x)=begin{cases}0,&xleqslant0;\dfrac{Gamma!left(frac{n_1+n_2}{2}right)}{Gamma!left(frac{n_1}{2}right)!Gamma!left(frac{n_2}{2}right)}!left(dfrac{n_1}{n_2}right)^{frac{n_1}{2}}!dfrac{x^{frac{n_1}{2}-1}}{left(1+frac{n_1}{n_2}xright)^{frac{n_1+n_2}{2}}},&x>0.end{cases}$

Математическое ожидание случайной величины, подчинённой распределению Фишера, X=F(n_1;n_2) определяется по формуле

$M(X)=frac{n_2}{n_2-2},~~n_2>2.$

Графики плотностей вероятностей распределения Фишера (для различных значений n_1,n_2 ) изображены на рис. 27.

Между случайными величинами, имеющими нормальное распределение: хи-квадрат, Стьюдента и Фишера, имеют место соотношения

$T^2(n)=F(1;n),quad F(n;infty)=frac{chi^2(n)}{n},quad chi^2(1)=U^2.$

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Содержание:

Непрерывные случайные величины: функция распределения случайной величины:

Если вычислить вероятность появления непрерывной случайной величины не составляет особого труда, то решение основной задачи теории вероятностей для непрерывной случайной величины несёт большие трудности. Поэтому в материалах сегодняшней лекции мы рассмотрим методы определения вероятности попадания непрерывной случайной величины на интервал с помощью функции распределения.

Функция распределения непрерывной случайной величины

Зная функцию распределения непрерывной случайной величины, задача определения вероятности её попадания на интервал (а; b) может быть решена следующим образом.

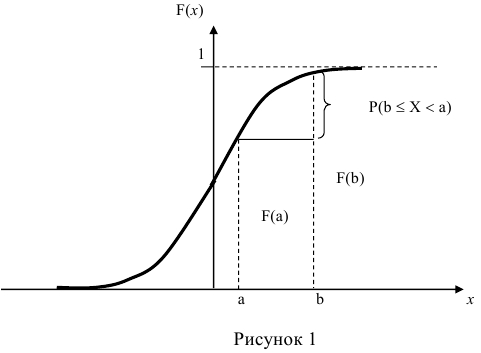
По известной функции распределения вероятность попадания непрерывной случайной величины на интервал (а; b) равна приращению функции распределения на этом участке (рис. 1).
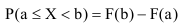
Непрерывные случайные величины - определение и вычисление с примерами решения

Непрерывные случайные величины - определение и вычисление с примерами решения

Во всех рассмотренных выше случаях случайная величина определялась путём задания значений самой величины и вероятностей этих значений.

Однако такой метод применим далеко не всегда. Например, в случае непрерывной случайной величины, её значения могут заполнять некоторый произвольный интервал. Очевидно, что в этом случае задать все значения случайной величины просто нереально.

Даже в случае, когда это сделать можно, зачастую задача решается чрезвычайно сложно. Рассмотренный только что пример даже при относительно простом условии (приборов только четыре) приводит к достаточно неудобным вычислениям, а если в задаче будет несколько сотен приборов?

Поэтому встает задача по возможности отказаться от индивидуального подхода к каждой задаче и найти по возможности наиболее общий способ задания любых типов случайных величин.

Пусть х – действительное число. Вероятность события, состоящего в том, что X примет значение, меньшее х, т.е. X

Определение. Функцией распределения называют функцию F(x), определяющую вероятность того, что случайная величина X в результате испытания примет значение, меньшее х.

F(x) = Р(Х < х)

Функцию распределения также называют интегральной функцией. Функция распределения существует как для непрерывных, так и для дискретных случайных величин. Она полностью характеризует случайную величину и является одной из форм закона распределения.

Для дискретной случайной величины функция распределения имеет
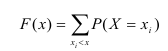
Непрерывные случайные величины - определение и вычисление с примерами решения

Знак неравенства под знаком суммы показывает, что суммирование распространяется на те возможные значения случайной величины, которые меньше аргумента х.

Функция распределения дискретной случайной величины X разрывна и возрастает скачками при переходе через каждое значение 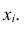Непрерывные случайные величины - определение и вычисление с примерами решения

Так для примера, который мы будем рассматривать на следующем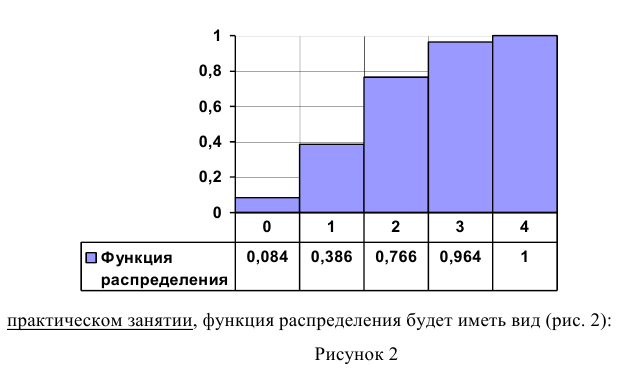 Непрерывные случайные величины - определение и вычисление с примерами решения

Свойства функции распределения

1) значения функции распределения принадлежат отрезку [0, 1].

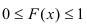
Непрерывные случайные величины - определение и вычисление с примерами решения

2) F(x) – неубывающая функция.

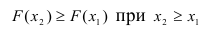
Непрерывные случайные величины - определение и вычисление с примерами решения

3) Вероятность того, что случайная величина примет значение, заключенное в интервале (а, b) , равна приращению функции распределения на этом интервале.
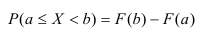
Непрерывные случайные величины - определение и вычисление с примерами решения

4) На минус бесконечности функция распределения равна нулю, на плюс бесконечности функция распределения равна единице.

5) Вероятность того, что непрерывная случайная величина X примет одно определенное значение, равна нулю.

Таким образом, не имеет смысла говорить о каком – либо конкретном значении случайной величины. Интерес представляет только вероятность попадания случайной величины в какой – либо интервал, что соответствует большинству практических задач.

Заключение по лекции:

В лекции мы рассмотрели методы решения основной задачи теории вероятностей – определения вероятности попадания непрерывной случайной величины на интервал с помощью функции распределения.

Плотность вероятности. Числовые характеристики. Моменты случайных величин

Плотность распределения

Функция распределения полностью характеризует случайную величину, однако, имеет один недостаток. По функции распределения трудно судить о характере распределения случайной величины в небольшой окрестности той или иной точки числовой оси.

Определение. Плотностью распределения вероятностей непрерывной случайной величины X называется функция f(x) – первая производная от функции распределения F(x).

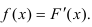
Непрерывные случайные величины - определение и вычисление с примерами решения

Плотность распределения также называют дифференциальной функцией. Для описания дискретной случайной величины плотность распределения неприемлема.

Смысл плотности распределения состоит в том, что она показывает как часто появляется случайная величина X в некоторой окрестности точки х при повторении опытов.

После введения функций распределения и плотности распределения можно дать следующее определение непрерывной случайной величины.

Определение. Случайная величина X называется непрерывной, если её функция распределения F(x) непрерывна на всей оси ОХ, а плотность распределения f(x) существует везде, за исключением (может быть, конечного числа точек).

Зная плотность распределения, можно вычислить вероятность того, что некоторая случайная величина X примет значение, принадлежащее заданному интервалу.

Теорема. Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (а, b), равна определенному интегралу от плотности распределения, взятому в пределах от а до b.

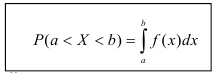
Непрерывные случайные величины - определение и вычисление с примерами решения

Доказательство этой теоремы основано на определении плотности распределения и третьем свойстве функции распределения (см. лекцию тема № 10).

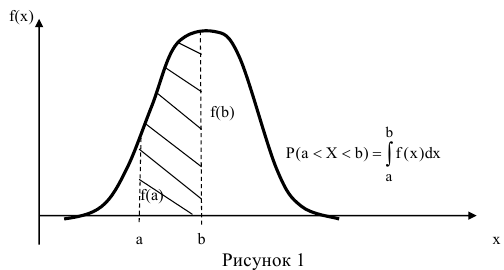
Геометрически это означает, что вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (а, b), равна площади криволинейной трапеции, ограниченной осью ОХ, кривой распределения f(x) и прямыми х=а и х=b.

Геометрически вероятность Р(а < X < b) представляется в виде заштрихованной области, ограниченной кривой распределения и осью Ох на интервале(а; b) (рис 1).

Непрерывные случайные величины - определение и вычисление с примерами решения

Функция распределения может быть легко найдена, если известна плотность распределения, по формуле:

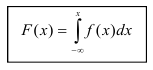
Непрерывные случайные величины - определение и вычисление с примерами решения

Свойства плотности распределения

1) Плотность распределения – неотрицательная функция.

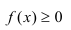
Непрерывные случайные величины - определение и вычисление с примерами решения
2) Несобственный интеграл от плотности распределения в пределах от –
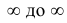равен единице.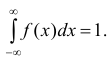 Непрерывные случайные величины - определение и вычисление с примерами решения

Плотность распределения 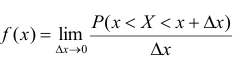Непрерывные случайные величины - определение и вычисление с примерами решения
можно представить как:

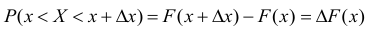
Непрерывные случайные величины - определение и вычисление с примерами решения

тогда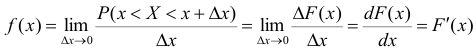 Непрерывные случайные величины - определение и вычисление с примерами решения
Поэтому иногда функцию плотности распределения f(x) называют также дифференциальной функцией распределения или дифференциальным законом распределения величины X, а функцию распределения F(x) -интегральной функцией распределения или интегральным законом распределения.

Следует заметить, что интеграл 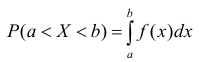Непрерывные случайные величины - определение и вычисление с примерами решения возможно трактовать как сумму бесконечно большого числа несовместных элементарных событий, каждое из которых заключается в попадании случайной величины в бесконечно малый участок (х, х + dx) и имеет вероятность:

Р(х < X < х + dx) = dF(x) = f(x)dx

Величину f(x)dx называют элементом вероятности.

По своему содержанию элемент вероятности есть вероятность попадания случайной величины X на элементарный участок dx, прилежащий к точке X.

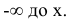
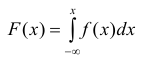
Функция распределения случайной величины X по известной плотности распределения может быть найдена, как интеграл от плотности распределения в интервале от Непрерывные случайные величины - определение и вычисление с примерами решения

Непрерывные случайные величины - определение и вычисление с примерами решения
В схеме непрерывных случайных величин можно вывести аналогии формулы полной вероятности и формулы Бейеса, рассмотренные при изучении темы 4.

Обозначим Р(А /х) условную вероятность события А при условии Х= х. Заменяя в формуле полной вероятности вероятность гипотезы элементом вероятности f(x)dx, а сумму – интегралом, получим полную вероятность события А.

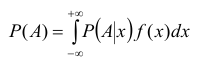
Непрерывные случайные величины - определение и вычисление с примерами решения
Данная формула называется интегральной формулой полной вероятности.

Соответствующий аналог в схеме непрерывных случайных величин имеет и формула Бейеса. Обозначив условную плотность распределения случайной величины X при условии, что в результате опыта появилось событие A через 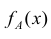Непрерывные случайные величины - определение и вычисление с примерами решения , получим:

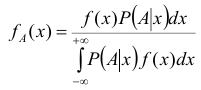
Непрерывные случайные величины - определение и вычисление с примерами решения

Данная формула называется интегральной формулой Бейеса.

Числовые характеристики непрерывных случайных величин

Пусть непрерывная случайная величина X задана функцией распределения f(x). Допустим, что все возможные значения случайной величины принадлежат отрезку [а,b].

Математическое ожидание

Определение. Математическим ожиданием непрерывной случайной величины X, возможные значения которой принадлежат отрезку [а,b], называется определенный интеграл

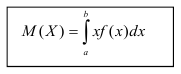
Непрерывные случайные величины - определение и вычисление с примерами решения
Если возможные значения случайной величины рассматриваются на всей числовой оси, то математическое ожидание находится по формуле:

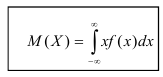
Непрерывные случайные величины - определение и вычисление с примерами решения
При этом, конечно, предполагается, что несобственный интеграл сходится.

Дисперсия

Определение. Дисперсией непрерывной случайной величины называется математическое ожидание квадрата её отклонения.

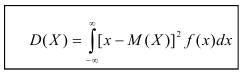
Непрерывные случайные величины - определение и вычисление с примерами решения

По аналогии с дисперсией дискретной случайной величины, для практического вычисления дисперсии используется формула:

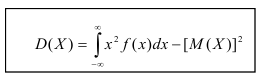
Непрерывные случайные величины - определение и вычисление с примерами решения

Среднеквадратичное отклонение

Определение. Средним квадратичным отклонением называется квадратный корень из дисперсии.

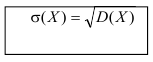
Непрерывные случайные величины - определение и вычисление с примерами решения

Мода

Определение. Модой 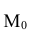Непрерывные случайные величины - определение и вычисление с примерами решения дискретной случайной величины называется её наиболее вероятное значение. Для непрерывной случайной величины мода – такое значение случайной величины, при которой плотность распределения имеет максимум.

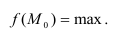
Непрерывные случайные величины - определение и вычисление с примерами решения
Если многоугольник распределения для дискретной случайной величины или кривая распределения для непрерывной случайной величины имеет два или несколько максимумов, то такое распределение называется двухмодальным или многомодальным.

Если распределение имеет минимум, но не имеет максимума, то оно
называется антимодальным.

Медиана

Определение. Медианой 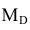Непрерывные случайные величины - определение и вычисление с примерами решения случайной величины X называется такое ее значение, относительно которого равновероятно получение большего или меньшего значения случайной величины.

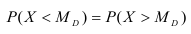
Непрерывные случайные величины - определение и вычисление с примерами решения
Геометрически медиана – абсцисса точки, в которой площадь, ограниченная кривой распределения делится пополам.

Отметим, что если распределение одномодальное, то мода и медиана совпадают с математическим ожиданием.

Начальный момент

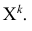
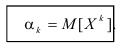
Определение. Начальным моментом порядка k случайной величины X называется математическое ожидание величины Непрерывные случайные величины - определение и вычисление с примерами решения

Непрерывные случайные величины - определение и вычисление с примерами решения

Для дискретной случайной величины: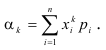 Непрерывные случайные величины - определение и вычисление с примерами решения
Для непрерывной случайной величины: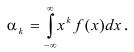

Начальный момент первого порядка равен математическому ожиданию.

Центральный момент

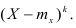
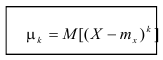
Определение. Центральным моментом порядка k случайной величины X называется математическое ожидание величины Непрерывные случайные величины - определение и вычисление с примерами решения

Непрерывные случайные величины - определение и вычисление с примерами решения

Для дискретной случайной величины: 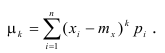Непрерывные случайные величины - определение и вычисление с примерами решения

Для непрерывной случайной величины: 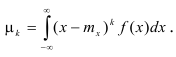Непрерывные случайные величины - определение и вычисление с примерами решения
Центральный момент первого порядка всегда равен нулю, а центральный момент второго порядка равен дисперсии. Центральный момент третьего порядка характеризует асимметрию распределения.

Коэффициент асимметрии

Определение. Отношение центрального момента третьего порядка к среднеквадратическому отклонению в третьей степени называется коэффициентом асимметрии.

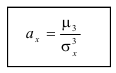
Непрерывные случайные величины - определение и вычисление с примерами решения

Эксцесс

Определение. Для характеристики островершинности и плосковершинности распределения используется величина, называемая эксцессом.

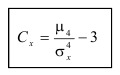
Непрерывные случайные величины - определение и вычисление с примерами решения
Кроме рассмотренных величин используются также так называемые абсолютные моменты:

Абсолютный начальный момент: 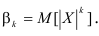Непрерывные случайные величины - определение и вычисление с примерами решения

Абсолютный центральный момент: 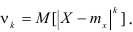Непрерывные случайные величины - определение и вычисление с примерами решения

Абсолютный центральный момент первого порядка называется средним арифметическим отклонением.

Заключение по лекции:

В лекции мы рассмотрели методы решения основной задачи теории вероятностей – определения вероятности попадания непрерывной случайной величины на интервал с помощью плотности распределения.

Законы распределения непрерывных величин: нормальное, равномерное, показательное

В материалах сегодняшней лекции мы рассмотрим законы распределения непрерывных величин.

Равномерное распределение

Определение. Непрерывная случайная величина имеет равномерное распределение на отрезке [а,b], если на этом отрезке плотность

распределения случайной величины постоянна, а вне его равна нулю.
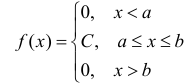
Непрерывные случайные величины - определение и вычисление с примерами решения

Постоянная величина С может быть определена из условия равенства единице площади, ограниченной кривой распределения, представленной на рис. 1
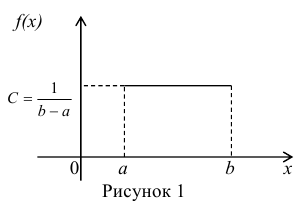
Непрерывные случайные величины - определение и вычисление с примерами решения

Получаем 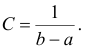Непрерывные случайные величины - определение и вычисление с примерами решения .

Найдём функцию распределения F(x) на отрезке [а,b] (рис. 2).
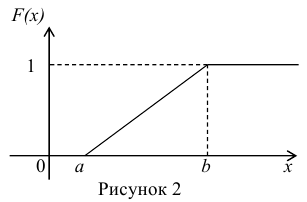
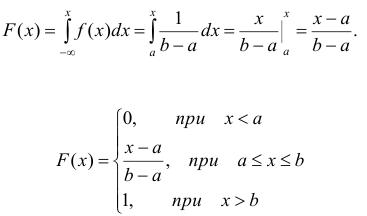
Непрерывные случайные величины - определение и вычисление с примерами решения

Для того, чтобы случайная величина подчинялась закону равномерного распределения необходимо, чтобы её значения лежали внутри некоторого определенного интервала, и внутри этого интервала значения этой случайной величины были бы равновероятны.

Определим математическое ожидание и дисперсию случайной величины, подчиненной равномерному закону распределения.
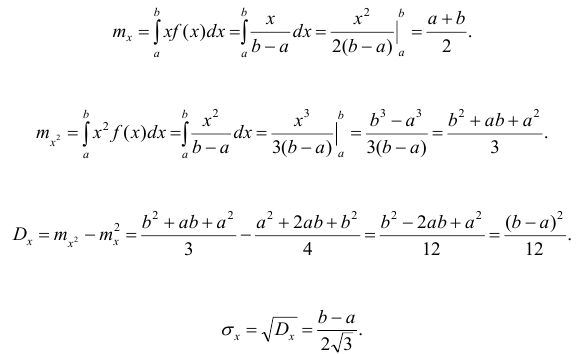
Непрерывные случайные величины - определение и вычисление с примерами решения

Вероятность попадания случайной величины в заданный интервал:
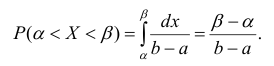
Непрерывные случайные величины - определение и вычисление с примерами решения

Показательное распределение

Определение. Показательным (экспоненциальным) называется распределение вероятностей непрерывной случайной величины X, которое описывается плотностью

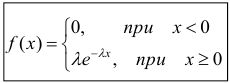
Непрерывные случайные величины - определение и вычисление с примерами решения

где 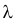Непрерывные случайные величины - определение и вычисление с примерами решения – положительное число.

Найдём закон распределения.
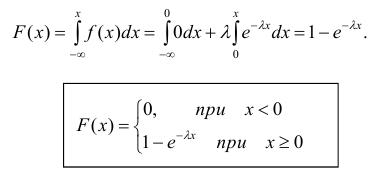
Непрерывные случайные величины - определение и вычисление с примерами решения

Графики функции распределения и плотности распределения представлены на рис. 3, 4.
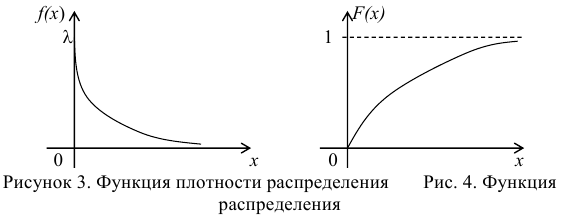
Непрерывные случайные величины - определение и вычисление с примерами решения

Найдём математическое ожидание случайной величины, подчинённой показательному распределению.
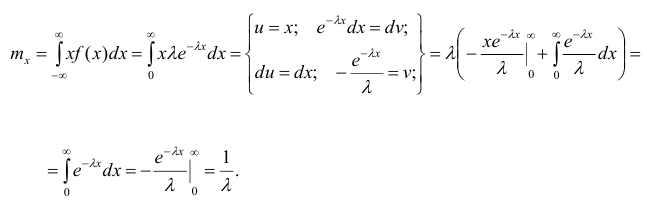
Непрерывные случайные величины - определение и вычисление с примерами решения
Результат получен с использованием того факта, что

Непрерывные случайные величины - определение и вычисление с примерами решения

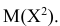
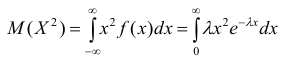
Для нахождения дисперсии найдём величину Непрерывные случайные величины - определение и вычисление с примерами решения

Дважды интегрируя по частям, аналогично рассмотренному случаю, получим:

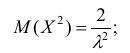
Непрерывные случайные величины - определение и вычисление с примерами решения
Тогда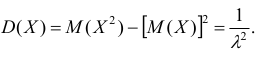
Итого: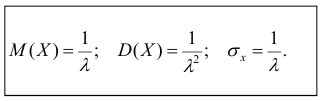

Видно, что в случае показательного распределения математическое ожидание и среднеквадратическое отклонение равны.

Также легко определить и вероятность попадания случайной величины, подчиненной показательному закону распределения, в заданный интервал.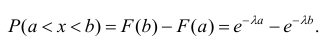 Непрерывные случайные величины - определение и вычисление с примерами решения

Показательное распределение широко используется в теории надёжности.

Допустим, некоторое устройство начинает работать в момент времени to=0, а через какое- то время t происходит отказ устройства.

Обозначим Т непрерывную случайную величину – длительность безотказной работы устройства.

Таким образом, функция распределения F(t) = P(T

Вероятность противоположного события (безотказная работа в течение времени t) равна R(t) = P(T>t) – l – F(t).

Функция надежности

Определение. Функцией надёжности R(t) называют функцию, определяющую вероятность безотказной работы устройства в течение времени t.

Часто на практике длительность безотказной работы подчиняется показательному закону распределению.

Вообще говоря, если рассматривать новое устройство, то вероятность отказа в начале его функционирования будет больше, затем количество отказов снизится и будет некоторое время иметь практически одно и то же значение. Затем (когда устройство выработает свой ресурс) количество отказов будет возрастать.

Другими словами, можно сказать, что функционирование устройства на протяжении всего существования (в смысле количества отказов) можно описать комбинацией двух показательных законов (в начале и конце функционирования) и равномерного закона распределения.

Функция надёжности для какого- либо устройства при показательном законе распределения равна:

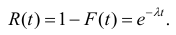
Непрерывные случайные величины - определение и вычисление с примерами решения

Данное соотношение называют показательным законом надежности.

Важным свойством, позволяющим значительно упростить решение задач теории надежности, является то, что вероятность безотказной работы устройства на интервале времени t не зависит от времени предшествующей работы до начала рассматриваемого интервала, а зависит только от длительности времени t.

Таким образом, безотказная работа устройства зависит только от интенсивности отказов 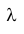Непрерывные случайные величины - определение и вычисление с примерами решения и не зависит от безотказной работы устройства в
прошлом.

Так как подобным свойством обладает только показательный закон распределения, то этот факт позволяет определить, является ли закон распределения случайной величины показательным или нет.

Нормальный закон распределения

Определение. Нормальным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности

Непрерывные случайные величины - определение и вычисление с примерами решения
Нормальный закон распределения также называется законом Гаусса.

Нормальный закон распределения занимает центральное место в теории вероятностей. Это обусловлено тем, что этот закон проявляется во всех случаях, когда случайная величина является результатом действия большого числа различных факторов. К нормальному закону приближаются все остальные законы распределения.

Можно легко показать, что параметры 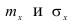Непрерывные случайные величины - определение и вычисление с примерами решения входящие в плотность распределения являются соответственно математическим ожиданием и среднеквадратическим отклонением случайной величины X.

Найдём функцию распределения F(x).

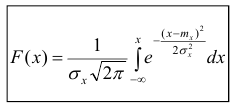
Непрерывные случайные величины - определение и вычисление с примерами решения

График плотности нормального распределения называется нормальной кривой или кривой Гаусса.

Нормальная кривая обладает следующими свойствами:

1) Функция определена на всей числовой оси.

2) При всех х функция распределения принимает только положительные значения.

3) Ось ОХ является горизонтальной асимптотой графика плотности вероятности, т.к. при неограниченном возрастании по абсолютной величине аргумента л значение функции стремится к нулю.

4) Найдём экстремум функции.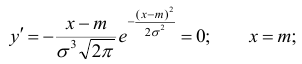 Непрерывные случайные величины - определение и вычисление с примерами решения

Т.к. при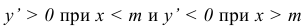 Непрерывные случайные величины - определение и вычисление с примерами решения , то в точке х = m функция имеет максимум, равный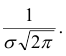

5) Функция является симметричной относительно прямой x = а, т.к. разность

(х – а) входит в функцию плотности распределения в квадрате.

6) Для нахождения точек перегиба графика найдем вторую производную функции плотности.
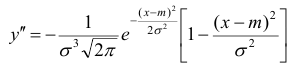
Непрерывные случайные величины - определение и вычисление с примерами решения
При 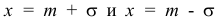вторая производная равна нулю, а при переходе через эти точки меняет знак, т.е. в этих точках функция имеет перегиб.

В этих точках значение функции равно 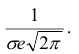Непрерывные случайные величины - определение и вычисление с примерами решения
Построим график функции плотности распределения (рис. 5).

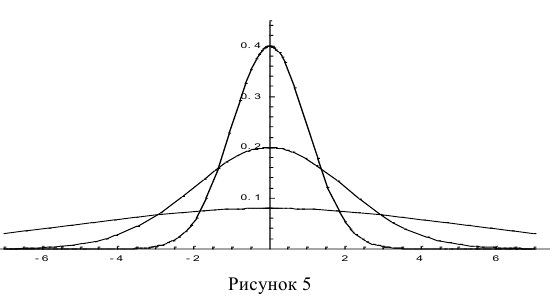
Построены графики при м =0 и трёх возможных значениях среднеквадратичного отклонения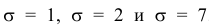 Непрерывные случайные величины - определение и вычисление с примерами решения . Как видно, при увеличении значения среднего квадратичного отклонения график становится более пологим, а максимальное значение уменьшается.

Если а > 0, то график сместится в положительном направлении, если а < 0 – в отрицательном.

При а = 0 и 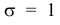Непрерывные случайные величины - определение и вычисление с примерами решения кривая называется нормированной. Уравнение нормированной кривой:

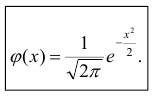
Функция Лапласа

Найдём вероятность попадания случайной величины, распределенной по нормальному закону, в заданный интервал.

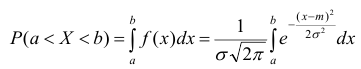
Непрерывные случайные величины - определение и вычисление с примерами решения

Обозначим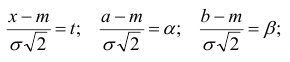 Непрерывные случайные величины - определение и вычисление с примерами решения

Тогда 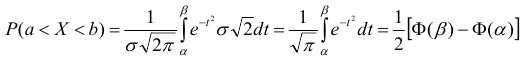Непрерывные случайные величины - определение и вычисление с примерами решения
Т.к. интеграл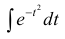 не выражается через элементарные функции, то вводится в рассмотрение функция

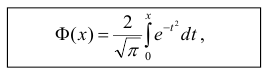
Непрерывные случайные величины - определение и вычисление с примерами решения
которая называется функцией Лапласа или интегралом вероятностей.

Значения этой функции при различных значениях х посчитаны и приводятся в специальных таблицах.

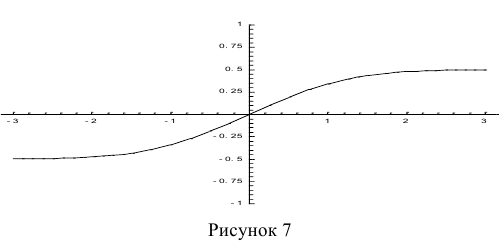
На рис. 6 показан график функции Лапласа.

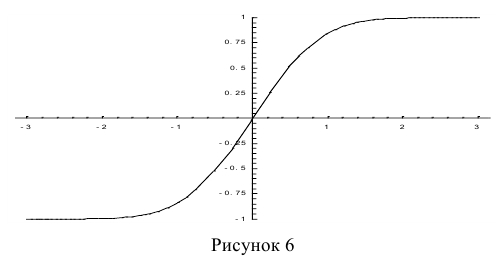
Непрерывные случайные величины - определение и вычисление с примерами решения

Функция Лапласа обладает следующими свойствами:

1) Ф(0) = 0;
2) Ф(-х) = – Ф(х);
3)

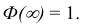
Функцию Лапласа также называют функцией ошибок и обозначают
erf х.

Ещё используется нормированная функция Лапласа, которая связана с функцией Лапласа соотношением:

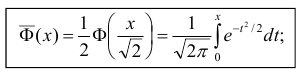
Непрерывные случайные величины - определение и вычисление с примерами решения
На рис. 7 показан график нормированной функции Лапласа.

Непрерывные случайные величины - определение и вычисление с примерами решения

Правило трёх сигм

При рассмотрении нормального закона распределения выделяется важный частный случай, известный как правило трех сигм.

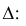
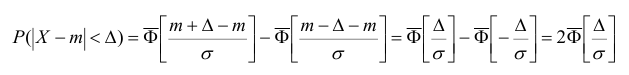
Запишем вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания меньше заданной величины Непрерывные случайные величины - определение и вычисление с примерами решения

Если принять 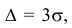, то получаем с использованием таблиц значений функции Лапласа:

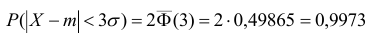
Непрерывные случайные величины - определение и вычисление с примерами решения

Т.е. вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую, чем утроенное среднее квадратичное отклонение, практически равна нулю.

Это правило называется правилом трех сигм.

Не практике считается, что если для какой-либо случайной величины выполняется правило трёх сигм, то эта случайная величина имеет нормальное распределение.

Пример:

Случайная величина Х задана плотностью распределения вероятностей:

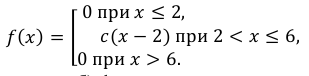
Непрерывные случайные величины - определение и вычисление с примерами решения

Найти: а) значение с; б) функцию распределения F(х) и построить ее график; в)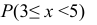 Непрерывные случайные величины - определение и вычисление с примерами решения

Решение:

а) Значение с найдем из условия нормировки: 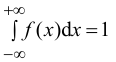Непрерывные случайные величины - определение и вычисление с примерами решения
Следовательно,

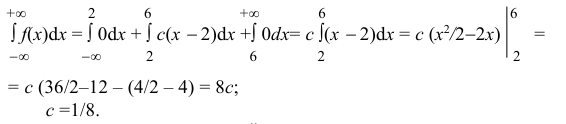
Непрерывные случайные величины - определение и вычисление с примерами решения

б) Известно, что 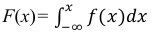Непрерывные случайные величины - определение и вычисление с примерами решения

Поэтому, если 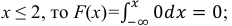Непрерывные случайные величины - определение и вычисление с примерами решения

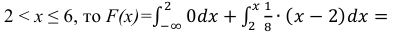
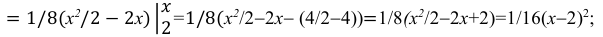
если Непрерывные случайные величины - определение и вычисление с примерами решения

Непрерывные случайные величины - определение и вычисление с примерами решения

если 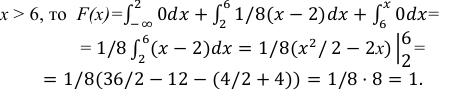Непрерывные случайные величины - определение и вычисление с примерами решения

Таким образом,

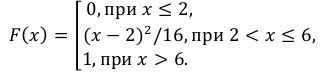
Непрерывные случайные величины - определение и вычисление с примерами решения

График функции F(х) изображен на рис. 5. 3.

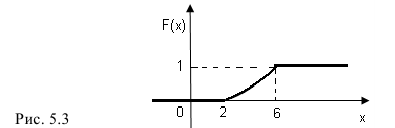
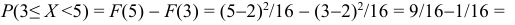
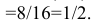
Непрерывные случайные величины - определение и вычисление с примерами решения

в) Непрерывные случайные величины - определение и вычисление с примерами решения

Непрерывные случайные величины - определение и вычисление с примерами решения

Пример:

Случайная величина Х задана функцией распределения:

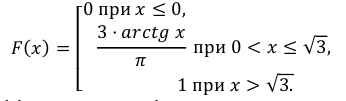
Непрерывные случайные величины - определение и вычисление с примерами решения

Найти дифференциальную функцию распределения 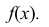Непрерывные случайные величины - определение и вычисление с примерами решения

Решение:

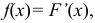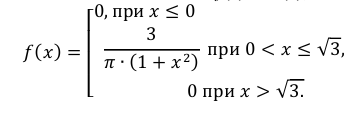
Так как Непрерывные случайные величины - определение и вычисление с примерами решения то

Непрерывные случайные величины - определение и вычисление с примерами решения

Пример:

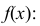
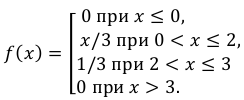
Случайная величина Х задана дифференциальной функцией Непрерывные случайные величины - определение и вычисление с примерами решения

Непрерывные случайные величины - определение и вычисление с примерами решения

Найти 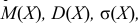Непрерывные случайные величины - определение и вычисление с примерами решения а также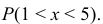

Решение:

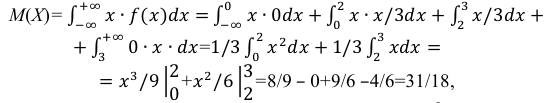
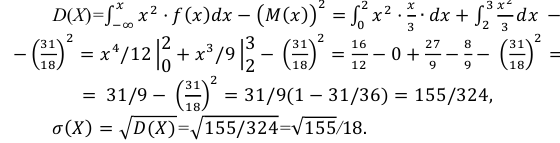
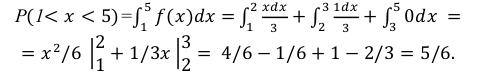
Непрерывные случайные величины - определение и вычисление с примерами решения

Некоторые законы распределения непрерывной случайной величины

Пример:

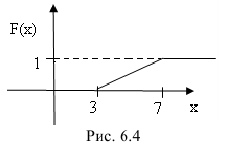
Случайная величина Х равномерно распределена на отрезке [3;7]. Найти:

а) плотность распределения вероятностей 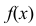Непрерывные случайные величины - определение и вычисление с примерами решения и построить ее график;

б) функцию распределения 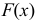Непрерывные случайные величины - определение и вычисление с примерами решения и построить ее график;

в) 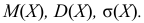Непрерывные случайные величины - определение и вычисление с примерами решения
Решение: Воспользовавшись формулами, рассмотренными выше, при а = 3, b = 7, находим:

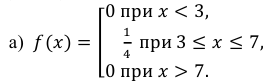
Непрерывные случайные величины - определение и вычисление с примерами решения

Построим ее график (рис. 6.3):

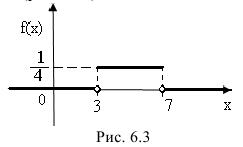
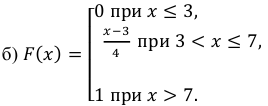
Непрерывные случайные величины - определение и вычисление с примерами решения

Построим ее график (рис. 6.4):

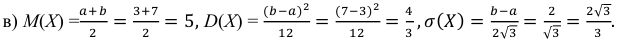
Непрерывные случайные величины - определение и вычисление с примерами решения

Пример:

Среднее время безотказной работы прибора равно 100 ч.
Полагая, что время безотказной работы прибора имеет показательный закон распределения, найти:

а) плотность распределения вероятностей;

б) функцию распределения;

в) вероятность того, что время безотказной работы прибора превысит 120 ч.

Решение.

По условию математическое ожидание 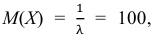Непрерывные случайные величины - определение и вычисление с примерами решения
откуда 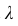= 1/100 = 0,01.
Следовательно,

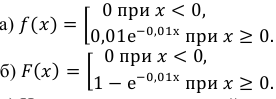
Непрерывные случайные величины - определение и вычисление с примерами решения

в) Искомую вероятность найдем, используя функцию распределения:

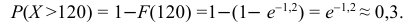
Непрерывные случайные величины - определение и вычисление с примерами решения

Пример:

Случайная величина Х распределена нормально с математическим ожиданием 32 и дисперсией 16. Найти: а) плотность распределения вероятностей 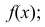Непрерывные случайные величины - определение и вычисление с примерами решения б) вероятность того, что в результате испытания Х примет значение из интервала (28;38).

Решение:

По условию m = 32, σ2 = 16, следовательно, σ = 4, тогда

а) 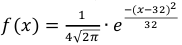Непрерывные случайные величины - определение и вычисление с примерами решения

б) Воспользуемся формулой:

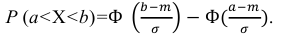
Непрерывные случайные величины - определение и вычисление с примерами решения

Подставив a = 28, b = 38, m = 32, σ = 4, получим
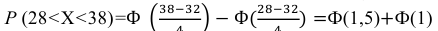
Непрерывные случайные величины - определение и вычисление с примерами решения

По таблице значений функции Ф(х) находим Ф(1,5) = 0,4332, Ф(1) = 0,3413.
Итак, искомая вероятность:

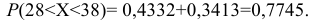
Непрерывные случайные величины - определение и вычисление с примерами решения

Заключение по лекции:

В лекции мы рассмотрели законы распределения непрерывных величин.

Закон больших чисел
Генеральная и выборочная совокупности
Интервальные оценки параметров распределения
Алгебра событий – определение и вычисление
Правило «трех сигм» в теории вероятности
Производящие функции
Теоремы теории вероятностей
Основные законы распределения дискретных случайных величин

Источник

Непрерывная
случайная величина – это переменная,
которая может принимать любое значение
в одном или нескольких заданных интервалах
или в некоторых областях плоскости.
Дадим
более строгое определение.

Определение
1.
Случайная
величина X
– непрерывная
случайная величина,
если существует функция p(x)

0, такая что, xR,
справедливо соотношение

.

Ограничимся
рассмотрением таких непрерывных
случайных величин, для которых р(х)
непрерывна всюду, кроме быть может,
конечного числа точек.

Определение
2. Функция
p(х)
называется плотностью распределения
вероятностей непрерывной случайной
величины.

Свойства непрерывной случайной величины

Доказательство
вытекает из определения.

2.
Плотность распределения p(x)
определяет закон распределения
непрерывной случайной величины

Это
свойство также следует из определения
плотности р(х).

3.
Для
любых х₁
х₂,

Доказательство.
По свойству функции распределения

.

Доказательство:

.

Вероятность
того, что непрерывная случайная величина
примет конкретное значение равна нулю,
т.е.

P(X
= a)
= 0.

Доказательство.
Событие

можно представить как

.
События
A_n=

a

Х

a
+

удовлетворят условиям аксиомы
непрерывности

A₁

A₂
…
A_n
…,

.

Тогда,
применив аксиому, получим

Из
этого свойства следует, что Р(a<X<b)
= P(a≤X<b)
= P(a<X≤b)
= P(a≤X≤b).

Если
x – точка непрерывности p(x)
и
если
Δ→0,
то

Из
этого свойства следует, что чем больше
значение плотности p(x),
тем больше вероятность попадания
случайной величины в интервал (x;
x
+ ∆).

Плотностью
распределения
может быть любая неотрицательная
функция, интеграл от которой по всей
числовой прямой равен 1, т.е.

.

Функция
распределения случайной величины любой
точке x_p
ставит в соответствие вероятность р
= F(x_p)
= P(X<x_p),
т.е. по x_p
найти F(x_p).
В иных случаях требуется решение обратной
задачи 
по значению вероятности р найти решение
уравнения F(x_p)
= р.

Определение
3.
Точка x_p,
которая является решением записанного
уравнения, называется квантилью,
отвечающей
заданному уровню вероятности р, или р
% квантилью
распределения
F(x).

Из
определения непрерывной случайной
величины следует, что функция распределения
непрерывной случайной величины
непрерывна. Поэтому для непрерывной
случайной величины для любого р,
0 < p
< 1 существует квантиль х_р.

Определение
4. Квантиль,
отвечающая вероятности р = ½, называется
медианой распределения.

Медиана
является одной из характеристик центра
распределения случайных величин.

Законы распределения непрерывных случайных величин Равномерное распределение

Определение
5.
Непрерывная
случайная величина Х, принимающая
значение на отрезке [a,b],
имеет равномерное распределение, если
плотность распределения имеет вид

.
(1)

Нетрудно
убедиться, что
,

Если
случайная величина равномерно
распределена, то вероятность того, что
она примет значение из заданного
интервала [x;
x+∆]
не зависит от положения интервала на
числовой прямой и пропорциональна длине
этого интервала