Содержание:
Формула полной вероятности:
Пусть событие А может произойти в результате появления одного и только одного события 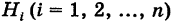
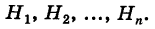
События этой группы обычно называются гипотезами.
Теорема: Вероятность события А равна сумме парных произведений вероятностей всех гипотез, образующих полную группу, на соответствующие условные вероятности данного события А, т. е.
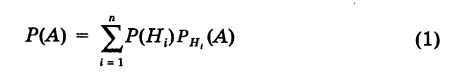
(формула полной вероятности), причем здесь

Доказательство. Так как
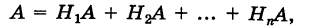
причем, ввиду несовместности событий 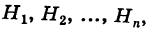 события
события 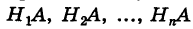 также несовместны, то на основании теорем сложения и умножения вероятностей имеем
также несовместны, то на основании теорем сложения и умножения вероятностей имеем
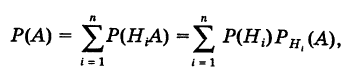
что и требовалось доказать.
Пример:
В магазин для продажи поступает продукция трех фабрик, относительные доли которых есть: I — 50%, II — 30%, III — 20%. Для продукции фабрик брак соответственно составляет: I — 2%, II — 3%, III — 5%. Какова вероятность того, что изделие этой продукции, случайно приобретенное в магазине, окажется доброкачественным (событие А)?
Решение:
Здесь возможны следующие три гипотезы: 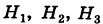 — приобретенная вещь выработана соответственно на I, II и III фабриках; очевидно, система этих гипотез полная, причем их вероятности
— приобретенная вещь выработана соответственно на I, II и III фабриках; очевидно, система этих гипотез полная, причем их вероятности
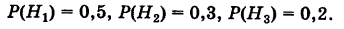
Соответствующие условные вероятности события А равны
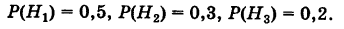
По формуле полной вероятности имеем
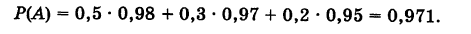
Формула Бейеса:
Пример:
Имеется полная группа несовместных гипотез
вероятности которых 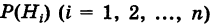 известны до опыта (вероятности априори). Производится опыт (испытание), в результате которого зарегистрировано появление события А, причем известно, что этому событию наши гипотезы приписывали определенные вероятности
известны до опыта (вероятности априори). Производится опыт (испытание), в результате которого зарегистрировано появление события А, причем известно, что этому событию наши гипотезы приписывали определенные вероятности 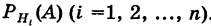 . Спрашивается, каковы будут вероятности этих гипотез после опыта (вероятности апостериори).
. Спрашивается, каковы будут вероятности этих гипотез после опыта (вероятности апостериори).
Например, очевидно, следует отбросить гипотезы, отрицающие появление события А. Вообще, проблема состоит в том, что, имея новую информацию, мы должны переоценить вероятности наших гипотез.
Иными словами, нам нужно определить условные вероятности
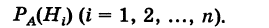
На основании теоремы умножения вероятностей имеем
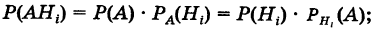
отсюда
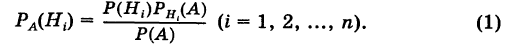
Для нахождения вероятности Р(А) можно использовать формулу полной вероятности
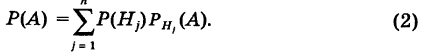
Отсюда имеем формулу вероятностей гипотез после опыта (<формулу Бейеса)
Пример:
Вероятность поражения самолета при одиночном выстреле для 1-го ракетного расчета (событие А) равна 0,2, а для 2-го (событие В) — 0,1. Каждое из орудий производит по одному выстрелу, причем зарегистрировано одно попадание в самолет (событие С). Какова вероятность, что удачный выстрел принадлежит первому расчету?
Решение:
До опыта возможны четыре гипотезы: 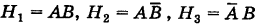
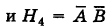 ; эти гипотезы образуют полную группу событий.
; эти гипотезы образуют полную группу событий.
Вероятности их, при независимом действии расчетов, соответственно равны
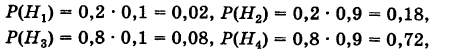
причем 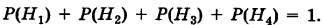
Условные вероятности для наблюдаемого события С при данных гипотезах будут
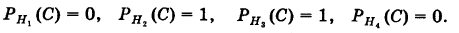
Следовательно, гипотезы 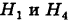 отпадают, а вероятности гипотез
отпадают, а вероятности гипотез 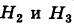 вычисляются по формуле Бейеса:
вычисляются по формуле Бейеса:
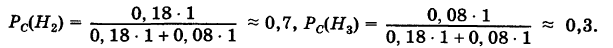
Таким образом, с вероятностью приблизительно 0,7 можно утверждать, что удачный выстрел принадлежит 1-му расчету,
Формула полной вероятности
Пусть событие А еще не произошло, но вскоре должно произойти. Событие А может протекать в различных условиях, относительно характера которых сделано  гипотез
гипотез 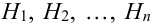 , образующих полную группу несовместных событий. Вероятности гипотез известны. Тогда вероятность события А равна сумме произведений вероятности каждой гипотезы на вероятность события при этой гипотезе:
, образующих полную группу несовместных событий. Вероятности гипотез известны. Тогда вероятность события А равна сумме произведений вероятности каждой гипотезы на вероятность события при этой гипотезе:
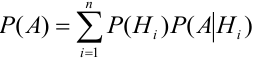 – формула полной вероятности.
– формула полной вероятности.
Доказательство.
По условию теоремы гипотезы 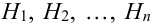 образуют полную группу несовместных событий, следовательно, событие А может произойти с одной и только с одной гипотезой:
образуют полную группу несовместных событий, следовательно, событие А может произойти с одной и только с одной гипотезой:
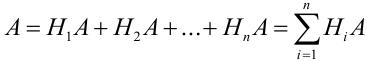 .
.
Т.к. гипотезы несовместны, то и комбинации 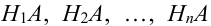 – несовместны. Применим теорему 1:
– несовместны. Применим теорему 1:
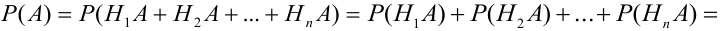
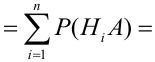 (события А и
(события А и  – зависимы, т.е. надо применить теорему 3) =
– зависимы, т.е. надо применить теорему 3) = 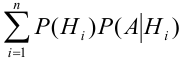 . (что и треб, доказать)
. (что и треб, доказать)
Пример:
Имеется пять урн:
2 урны состава 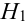 – по 2 белых шара и 1 черному,
– по 2 белых шара и 1 черному,
1 урна состава 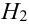 – 10 черных шаров,
– 10 черных шаров,
2 урны состава 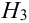 — по 3 белых и 1 черному шару.
— по 3 белых и 1 черному шару.
Наудачу выбирается урна, и из нее наудачу выбирается шар. Чему равна вероятность события А = {будет вынут белый шар}?
Решение.
Событие А еще не произошло. Шар может быть вынут из урн разных составов, следовательно, в алгебре событий событие А запишется в виде: 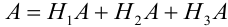 . Тогда по формуле полной вероятности:
. Тогда по формуле полной вероятности:
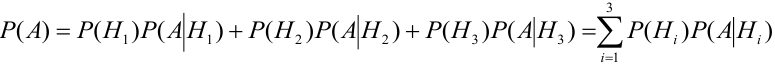 (*).
(*).
Найдем отдельно вероятности событий:
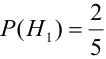 (две урны состава
(две урны состава  из пяти),
из пяти), 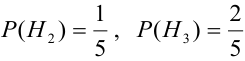 ,
,
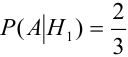 (в каждой урне состава
(в каждой урне состава 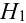 2 белых шара из трех),
2 белых шара из трех),
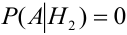 ( в урне состава
( в урне состава 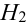 белых шаров нет),
белых шаров нет),
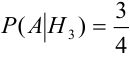 .
.
Подставим найденные вероятности в формулу (*): 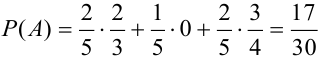 .
.
Формула полной вероятности и решение задач
Пример:
В двух одинаковых коробках имеется по 100 резисторов. В 1-й – 60 резисторов по 100 КОм, во 2-й 30 – резисторов по 100 КОм. Определить вероятность того, что взятый наугад из какой-либо коробки резистор будет 100 КОм.
Решение:
Пусть событие 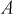 – достали резистор 100 КОм, гипотезы:
– достали резистор 100 КОм, гипотезы: 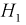 – выбрали 1-ю коробку,
– выбрали 1-ю коробку, 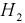 – выбрали 2-ю коробку. Так как коробки выбирали произвольно, то
– выбрали 2-ю коробку. Так как коробки выбирали произвольно, то 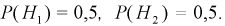 Условная вероятность того, что взяли резистор 100 КОм, при условии, что выбрана 1-я коробка –
Условная вероятность того, что взяли резистор 100 КОм, при условии, что выбрана 1-я коробка – 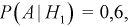 соответственно
соответственно 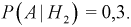 Тогда, применяя формулу (1.14) для
Тогда, применяя формулу (1.14) для 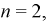 получаем
получаем 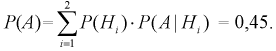
Пример №1
В первой коробке находится 20 деталей, из них 18 стандартных, во второй коробке – 10 деталей, из них 9 стандартных. Из второй коробки наудачу взята одна деталь и переложена в первую коробку.
Какова вероятность того, что деталь, наудачу извлечённая после этого из первой коробки, окажется стандартной?
Решение. Обозначим события:
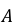 – из первой коробки извлечена стандартная деталь.
– из первой коробки извлечена стандартная деталь.
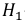 − из второй коробки в первую переложена стандартная деталь.
− из второй коробки в первую переложена стандартная деталь.
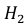 − из второй коробки в первую переложена нестандартная деталь.
− из второй коробки в первую переложена нестандартная деталь.
Событие А может наступить при условии наступления одного из событий 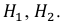 Эти события несовместны и образуют полную группу, т. е. являются гипотезами в формуле полной вероятности. Вероятность того, что из второй коробки извлечена стандартная деталь,
Эти события несовместны и образуют полную группу, т. е. являются гипотезами в формуле полной вероятности. Вероятность того, что из второй коробки извлечена стандартная деталь, 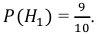
Вероятность того, что из второй коробки извлечена нестандартная деталь 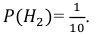
Условная вероятность того, что из первой коробки извлечена стандартная деталь, при условии, что из второй коробки в первую была переложена стандартная деталь, 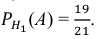
Условная вероятность того, что из первой коробки извлечена стандартная деталь, при условии, что из второй коробки в первую была переложена нестандартная деталь, 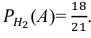
Искомая вероятность того, что из первой коробки будет извлечена стандартная деталь, по формуле полной вероятности равна:
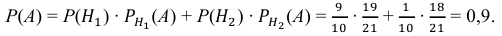 .
.
Ответ: 0,9.
Пример №2
Два станка производят одинаковые детали, которые поступают на общий конвейер. Производительность первого станка в два раза больше производительности второго станка. Первый производит 60 % деталей высшего сорта, а второй – 84 %. Наудачу взятая с конвейера деталь оказалась высшего сорта. Какова вероятность того, что эта деталь произведена на первом станке?
Решение. Обозначим события:
А – деталь, взятая с конвейера, оказалась высшего сорта.
Это событие наступит с одним из двух событий (гипотез):
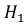 – эта деталь произведена на первом станке,
– эта деталь произведена на первом станке,
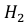 – эта деталь произведена на втором станке.
– эта деталь произведена на втором станке.
Поскольку производительность первого станка в два раза больше производительности второго станка, вероятности гипотез равны: 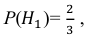
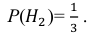
Условные вероятности события А даны: 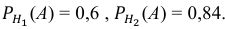
По формуле полной вероятности находим:
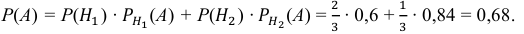
По формуле Байеса найдём условную вероятность того, что взятая наудачу деталь высшего сорта произведена на первом станке:
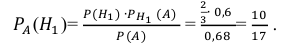
Ответ: 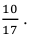
Пример №3
В ящике 20 белых и 10 чёрных шаров. Поочерёдно извлекают 4 шара, причём каждый извлечённый шар возвращают в ящик перед извлечением следующего. Какова вероятность того, что среди четырёх извлечённых шаров окажется два белых?
Решение. Вероятность извлечения белого шара одна и та же во всех четырёх испытаниях, так как каждый извлечённый шар возвращается в ящик: 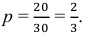
Тогда вероятность извлечения чёрного шара во всех четырёх испытаниях равна 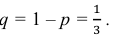
Используя формулу Бернулли, находим вероятность того, что из четырёх извлечённых шаров два шара будут белыми:
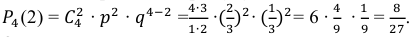
Ответ: 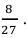
Пример №4
Вероятность поражения мишени при одном выстреле равна 0,8. Какова вероятность того, что при 100 выстрелах мишень будет поражена 75 раз?
Решение. По условию задачи 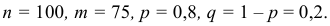
Так как n – достаточно большое число, воспользуемся локальной формулой Лапласа:
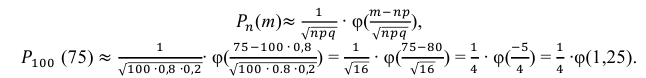
В таблице значений функции 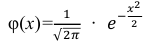 находим φ(1,25) =
находим φ(1,25) =
0,1826.
Следовательно, 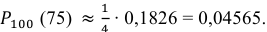
Ответ: 0,04565.
Пример №5
Вероятность поражения мишени при одном выстреле равна 0,8. Какова вероятность того, что при 100 выстрелах мишень будет поражена
а) не менее 75 раз и не более 90 раз?
б) не менее 75 раз?
в) не более 74 раз?
Решение.
Воспользуемся интегральной формулой Лапласа:
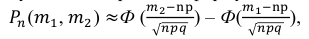
где 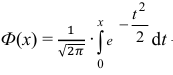 – функция Лапласа.
– функция Лапласа.
а) По условию задачи 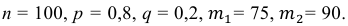 Тогда, воспользовавшись таблицей значений функции Ф(х), получаем:
Тогда, воспользовавшись таблицей значений функции Ф(х), получаем:
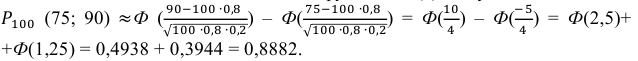
б) Требование того, чтобы событие наступило не менее 75 раз, означает следующее: число появлений события может быть равно либо 75, либо 76, … , либо 100.
Тогда следует принять 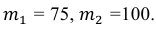 Воспользовавшись таблицей значений функции Лапласа Ф(х), получаем:
Воспользовавшись таблицей значений функции Лапласа Ф(х), получаем: 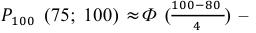
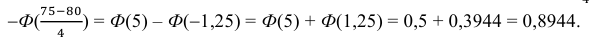
в) Событие “мишень поражена не более 74 раз” и событие “мишень поражена не менее 75 раз” являются противоположными. Поэтому сумма их вероятностей равна 1. Следовательно, искомая вероятность 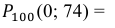
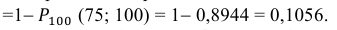
Ответ: а) 0,8882; б) 0,8944; в) 0,1056.
Пример №6
Учебник издан тиражом 100000 экземпляров.
Вероятность того, что один учебник сброшюрован неправильно, равна 0,0001. Какова вероятность того, что тираж содержит 5 бракованных книг?
Решение. По условию задачи n = 100000, p = 0,0001.
События “из n книг ровно m книг сброшюрованы неправильно”, где m = 0,1,2, … ,100000, являются независимыми. Так как число n велико, а вероятность p мала, вероятность 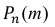 можно вычислить по формуле Пуассона:
можно вычислить по формуле Пуассона: 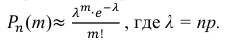
В рассматриваемой задаче 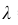 = 100000 ∙ 0,0001 = 10. Поэтому искомая вероятность
= 100000 ∙ 0,0001 = 10. Поэтому искомая вероятность 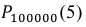 определяется равенством:
определяется равенством:
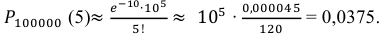
Ответ: 0,0375.
Формула Байеса (Бейеса)
Пусть событие А произошло, причем А могло протекать в различных условиях, относительно характера которых было сделано 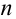 гипотез
гипотез 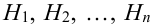 , образующих полную группу несовместных событий. Вероятности гипотез известны. Требуется узнать, как изменятся вероятности гипотез в связи с появлением события А. Т.е. надо найти условную вероятность
, образующих полную группу несовместных событий. Вероятности гипотез известны. Требуется узнать, как изменятся вероятности гипотез в связи с появлением события А. Т.е. надо найти условную вероятность 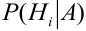 .
.
Решение:
По условию теоремы гипотезы 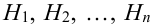 , образуют полную группу несовместных событий, следовательно событие .А произошло с одной и только с одной гипотезой:
, образуют полную группу несовместных событий, следовательно событие .А произошло с одной и только с одной гипотезой:
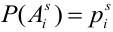 , причем события А и
, причем события А и 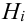 – зависимы, поэтому найдем вероятность произведения
– зависимы, поэтому найдем вероятность произведения 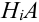 , воспользовавшись теоремой 3:
, воспользовавшись теоремой 3:
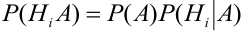 — (или, что то же самое) =
— (или, что то же самое) = 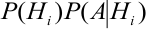 =
= 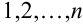 , отсюда
, отсюда
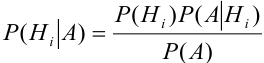 .
.
Выразим Р(А) с помощью формулы полной вероятности:
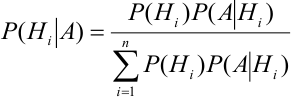 – формула Байеса.
– формула Байеса.
Пример №7
Имеется пять урн:
2 урны состава 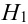 – по 2 белых шара и 3 черных шара,
– по 2 белых шара и 3 черных шара,
2 урны состава 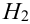 – по 1 белому и 4 черных шара,
– по 1 белому и 4 черных шара,
1 урна состава 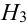 – 4 белых и 1 черный шар.
– 4 белых и 1 черный шар.
Из одной наудачу выбранной урны взят шар. Он оказался белым (событие А). Чему равна после опыта вероятность события, что шар вынут из урны третьего состава.
Решение.
Событие А произошло. Шар мог быть вынут из урн разных составов, следовательно, в алгебре событий событие А запишется в виде: 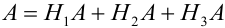 .
.
Найдем вероятности событий:
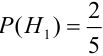 (две урны состава
(две урны состава 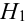 из пяти),
из пяти), 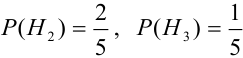 ,
,
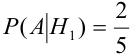 (в каждой урне состава
(в каждой урне состава 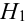 2 белых шара из пяти),
2 белых шара из пяти),
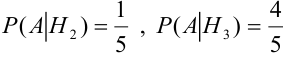 .
.
По формуле Байеса найдем условную вероятность 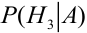 :
:
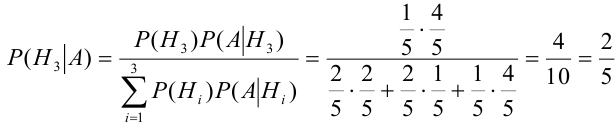 .
.
Пример №8
Вероятность дождливого дня в городе равна 0,2. Известно, что вероятность выиграть футбольный матч команде этого города в дождливый день равна 0,4, а в сухой – 0,7. Известно, что команда выиграла матч. Определить, что в этот день шел дождь.
Решение:
Событие 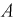 состоит в том, что команда выиграла матч. Гипотезы:
состоит в том, что команда выиграла матч. Гипотезы: 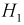 – шел дождь,
– шел дождь, 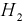 – дождя не было.
– дождя не было.
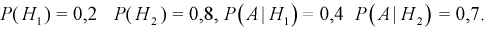
Чтобы ответить на вопрос, пересмотрим вероятность 1-й гипотезы с учетом результата опыта-появилось событие 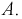 Определим апостериорную вероятность гипотезы
Определим апостериорную вероятность гипотезы 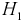 с учетом результата опыта (появилось событие
с учетом результата опыта (появилось событие 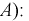
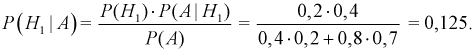
Из полученного результата видим, что с учетом события 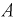 вероятность дождя в городе уменьшилась
вероятность дождя в городе уменьшилась 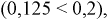 значит скорее всего дождя не было.
значит скорее всего дождя не было.
Независимые испытания
Под испытанием станем понимать осуществление определенного комплекса условий, в результате которого может произойти то или иное элементарное событие пространства 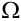 элементарных событий.
элементарных событий.
Определение 26. Если производятся испытания, при которых вероятность появления события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называются независимыми относительно события А.
В каждом испытании вероятность появления события А одинакова.
Ряд задач связан с экспериментом, в котором проводятся последовательные независимые испытания, и наблюдается результат совместного осуществления тех или иных исходов каждого испытания.
Рассматривается последовательность п независимых испытаний, под которой будем понимать дискретное новое пространство 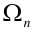 элементарных исходов, состоящее из точек
элементарных исходов, состоящее из точек 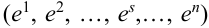 , где
, где 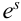 – произвольная точка пространства, отвечающая испытанию с номером s. В каждом испытании может произойти один из
– произвольная точка пространства, отвечающая испытанию с номером s. В каждом испытании может произойти один из  исходов:
исходов: 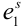 или
или 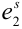 или ….
или …. 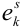 .
.
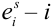 -тый исход в s-том испытании, где
-тый исход в s-том испытании, где  = 1, 2,…,
= 1, 2,…,  ; s = 1,2,…,
; s = 1,2,…,  .
.
Пример №9
Пусть испытание состоит в подбрасывании игральной кости. Пространство элементарных событий 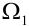 состоит из шести точек:
состоит из шести точек: 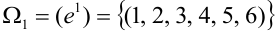 , т.е. шесть исходов. Если провести три испытания, то пространство
, т.е. шесть исходов. Если провести три испытания, то пространство 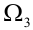 состоит из 216 точек.
состоит из 216 точек.
Обычно исходы обозначали большими заглавными буквами. Переобозначим! Пусть происходит  независимых испытаний: 1, 2,…, s,…,
независимых испытаний: 1, 2,…, s,…,  . В каждом испытании может произойти к исходов: 1-ый, 2, 3,…,
. В каждом испытании может произойти к исходов: 1-ый, 2, 3,…,  ,…,
,…,  -ый.
-ый.
Обозначим событие 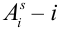 -тый исход в s-том испытании, где
-тый исход в s-том испытании, где  = 1,2,…,
= 1,2,…, ; s = 1,2,…,
; s = 1,2,…, . Эти к исходов – несовместные случайные события. Тогда для s-ого испытания можем записать:
. Эти к исходов – несовместные случайные события. Тогда для s-ого испытания можем записать:
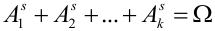 , причем
, причем 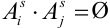 .
.
Обозначим вероятность  -ого исхода при s-том испытании через
-ого исхода при s-том испытании через 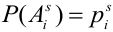 .
.
Пусть при первом испытании произошло событие под номером 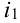 , при 2-ом – событие под номером
, при 2-ом – событие под номером 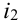 , …, при
, …, при  -ом – событие под номером
-ом – событие под номером 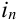 . Результат сразу
. Результат сразу  испытаний – событие, которое обозначим через произведение событий
испытаний – событие, которое обозначим через произведение событий 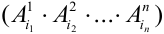 – цепочка результатов отдельных испытаний.
– цепочка результатов отдельных испытаний.
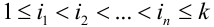 . Данное событие – цепочка состоит из всех точек
. Данное событие – цепочка состоит из всех точек 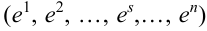 пространства
пространства 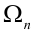 , для которых
, для которых 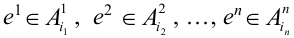 .
.
Испытания – независимые, следовательно, по теореме 4, имеет место равенство:
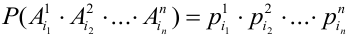
В случае, когда вероятности событий 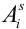 не зависят от номера испытаний,
не зависят от номера испытаний, 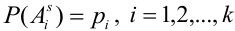 .
.
В силу несовместности и единственной возможности исходов, очевидно, что 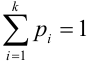 , так как
, так как 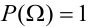 .
.
Теорема. Если данные 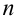 испытаний независимы, то любые
испытаний независимы, то любые 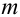 из них также независимы.
из них также независимы.
Теорема. Для того, чтобы 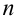 испытаний были независимы, необходимо и достаточно выполнения условия:
испытаний были независимы, необходимо и достаточно выполнения условия:
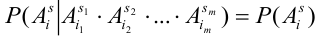 ,
,
для любой группы чисел 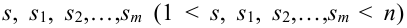 и
и 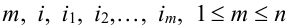 ,
, 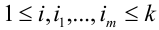 .
.
Формулы Бернулли
Пусть проводятся последовательные независимые испытания, и наблюдается результат совместного осуществления тех или иных исходов каждого испытания.
Схема независимых испытаний является математической моделью серии испытаний, повторяющихся при неизменных условиях. Такая схема называется полиномиальной.
Простейшим классом повторяющихся независимых испытаний является последовательность независимых испытаний с двумя исходами (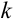 = 2): «успех», «неудача» и с неизменными вероятностями успеха – р и неудачи – q, где q = 1 – р, в каждом испытании. Такая схема называется биномиальной.
= 2): «успех», «неудача» и с неизменными вероятностями успеха – р и неудачи – q, где q = 1 – р, в каждом испытании. Такая схема называется биномиальной.
Определение 27. Независимые испытания при двух исходах называются испытаниями Бернулли.
Пример №10
Определить вероятность того, что в результате проведения 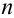 независимых испытаний некоторое событие А – успех (У) наступит ровно
независимых испытаний некоторое событие А – успех (У) наступит ровно  раз, если в каждом из этих испытаний данное событие наступает с постоянной вероятностью
раз, если в каждом из этих испытаний данное событие наступает с постоянной вероятностью 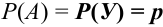 .
.
Решение.
Искомую вероятность обозначим 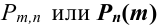 .
.
Событие А в данных испытаниях может появиться ровно  раз, причем, в разных последовательностях или комбинациях. Следовательно, остальные
раз, причем, в разных последовательностях или комбинациях. Следовательно, остальные 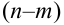 раз наступает противоположное событие
раз наступает противоположное событие 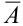 — неудача (Н), вероятность которого
— неудача (Н), вероятность которого 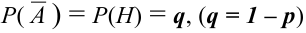 .
.
Сначала найдем вероятность того, что события У наступают при определенных  испытаниях. Элементарные события в этом случае естественно обозначать цепочками вида: УУУННУНН…УН (где У-
испытаниях. Элементарные события в этом случае естественно обозначать цепочками вида: УУУННУНН…УН (где У- штук, Н –
штук, Н – 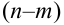 штук).
штук).
По условию данные события – независимые, следовательно, по теореме 4 для произведения независимых событий можем записать, что
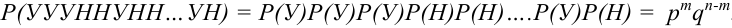 .
.
Число успехов и неудач задано. Можно менять только их расположения в цепочках, которое однозначно определяется выбором из  мест
мест  мест для успехов. Это можно сделать
мест для успехов. Это можно сделать 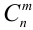 способами. Следовательно,
способами. Следовательно,
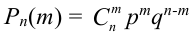 .
.
В данной задаче мы доказали теорему Бернулли.
Теорема Бернулли. Если  – число успехов в
– число успехов в  независимых испытаниях Бернулли, то вероятность того, что в результате проведения этих испытаний некоторое событие А наступит ровно
независимых испытаниях Бернулли, то вероятность того, что в результате проведения этих испытаний некоторое событие А наступит ровно  раз, находится по формуле:
раз, находится по формуле: 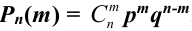 , которая называется формулой Бернулли.
, которая называется формулой Бернулли.
Следствие. 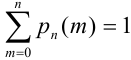 -так как события, состоящие в различном числе появления события А в серии
-так как события, состоящие в различном числе появления события А в серии  испытаний несовместны и образуют полную группу. Или можно было данное равенство объяснить так:
испытаний несовместны и образуют полную группу. Или можно было данное равенство объяснить так: 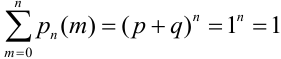 .
.
Пример №11
Пусть монета брошена 5 раз. Требуется найти вероятность того, что выпало ровно 3 орла.
Решение.
В каждом из 5 независимых испытаниях ( = 5) – бросании монеты – два исхода (
= 5) – бросании монеты – два исхода (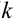 = 2: орел, решка), следовательно, это схема Бернулли с вероятностью успеха (выпал орел) и неудачи (выпала решка)
= 2: орел, решка), следовательно, это схема Бернулли с вероятностью успеха (выпал орел) и неудачи (выпала решка) 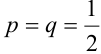 . Количество успехов:
. Количество успехов:  = 3.
= 3.
По формуле Бернулли 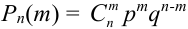 найдем искомую вероятность:
найдем искомую вероятность: 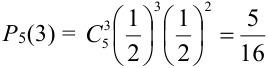 .
.
Замечания.
Замечание 1. Вероятность 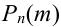 равна коэффициенту при
равна коэффициенту при 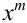 в разложении бинома
в разложении бинома 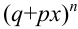 по степеням
по степеням 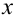 . В силу этого свойства совокупность вероятностей
. В силу этого свойства совокупность вероятностей 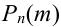 называют биномиальным законом распределения вероятностей, (будем изучать позднее)
называют биномиальным законом распределения вероятностей, (будем изучать позднее)
Замечание 2. Рассмотрим схему испытаний с произвольным количеством исходов. Пусть каждое из  независимых испытаний имеет
независимых испытаний имеет 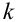 взаимно исключающих друг друга исходов, т.е. в каждом испытании может появиться одно из
взаимно исключающих друг друга исходов, т.е. в каждом испытании может появиться одно из 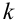 несовместных событий:
несовместных событий: 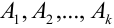 с вероятностями
с вероятностями 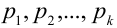 , не меняющимися от испытания к испытанию. Найдем вероятность появления в течении этих
, не меняющимися от испытания к испытанию. Найдем вероятность появления в течении этих  испытаний
испытаний 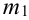 раз события
раз события 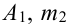 раза события
раза события 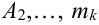 раз события
раз события 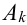 .
.  . Данная вероятность находится по формуле:
. Данная вероятность находится по формуле:
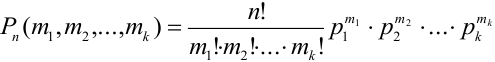 .
.
Эта совокупность вероятностей является коэффициентом при 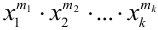 в разложении полинома
в разложении полинома 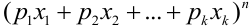 по степеням
по степеням 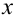 . Поэтому эту схему называют полиномиальной.
. Поэтому эту схему называют полиномиальной.
Например. При  подбрасываниях игральной кости получается полиномиальная схема с шестью исходами (
подбрасываниях игральной кости получается полиномиальная схема с шестью исходами (  = 6) и вероятностями
= 6) и вероятностями 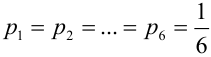 .
.
Если различать только «6» и «не 6», то получим схему Бернулли с двумя исходами ( = 2) и вероятностями успеха
= 2) и вероятностями успеха 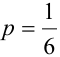 и неудачи
и неудачи 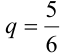 .
.
Замечание 3. При вычислении вероятности события, состоящего в том, что число успехов m лежит, например, между а и b, приходится находить числовые значения сумм вероятностей вида: 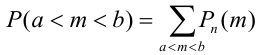 .
.
Например, вероятность того, что событие наступит а) менее  раз, b) более
раз, b) более  раз, с) не менее
раз, с) не менее  раз, d) не более
раз, d) не более  раз находятся соответственно по формулам:
раз находятся соответственно по формулам:
a) 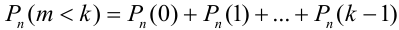 .
.
b) 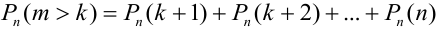 .
.
c) 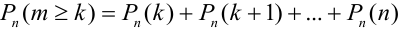 .
.
d) 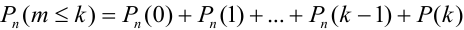 .
.
В некоторых случаях удобнее перейти к противоположному событию, например, 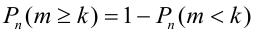 .
.
Пример №12
Пусть монета брошена 5 раз. Требуется найти вероятность того, что 1) менее двух раз выпал орел, 2) не менее двух раз выпал орел.
Решение.
Два исхода ( = 2: орел, решка) при 5 независимых испытаниях (n = 5) – схема Бернулли с вероятностью успеха и неудачи
= 2: орел, решка) при 5 независимых испытаниях (n = 5) – схема Бернулли с вероятностью успеха и неудачи 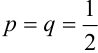 .
.
1) Орел выпал менее двух раз, значит, не выпал или выпал раз.
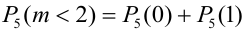 = (вероятности найдем по формуле Бернулли) =
= (вероятности найдем по формуле Бернулли) =
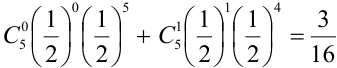
2) Орел выпал не менее двух раз, т.е. выпал два раза или три или четыре или пять:
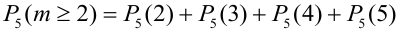 =(удобнее перейти к противоположному событию, т.е. «не менее двух», значит, противоположное событие: меньше двух, т.е. орел не выпал совсем или выпал один раз) =
=(удобнее перейти к противоположному событию, т.е. «не менее двух», значит, противоположное событие: меньше двух, т.е. орел не выпал совсем или выпал один раз) = 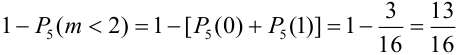 .
.
Замечание 4. В примере на формулу Бернулли вычисления проводятся очень легко, однако часто приходится вычислять вероятности при очень больших значениях n и m, например, при n = 1000, m = 500. Также затруднения при вычислении возникают при малых значениях р или q.
В этих случаях удается заменить формулу Бернулли какой-нибудь приближенной асимптотической формулой. Существуют три предельные теоремы, содержащие такие формулы.
Предельные теоремы в схеме Бернулли
Теорема Пуассона (асимптотическая формула для случая малых значений р)
Если вероятность наступления некоторого события А в n независимых испытаниях постоянна и равна р, причем  при
при  так, что
так, что 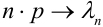 , где
, где 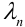 – среднее число появления события А в n испытаниях,
– среднее число появления события А в n испытаниях, 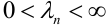 , то вероятность
, то вероятность 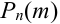 того, что в этих испытаниях событие А наступит ровно m раз, удовлетворяет при
того, что в этих испытаниях событие А наступит ровно m раз, удовлетворяет при  соотношению (или приближенно равна):
соотношению (или приближенно равна):
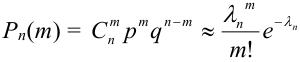
Замечания.
1. Часто формула Пуассона записывается в виде равенства, но надо помнить при этом, что оно верно при  :
:
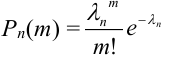 , при этом
, при этом 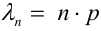 .
.
2. Формулой пользуются при больших n и малых р. Например, при n > 100, 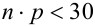 .
.
3. Теорема имеет место и в том случае, когда вероятность события А в каждом испытании равна нулю. В этом случае 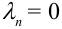 .
.
4. Существуют таблицы значений данной вероятности (стр. 410, 411 в задачнике Ефимова -Демидовича).
Пример №13
Вероятность попадания в цель при каждом выстреле равна 0,001. Найти вероятность попадания в цель двумя и более пулями, если число выстрелов равно 5000.
Решение.
Считаем каждый выстрел за испытание и попадание в цель за событие. Количество испытаний n = 5000 (велико), р = 0,001 (мало). По формуле Бернулли считать сложно. Поэтому применим формулу Пуассона.
Найдем среднее число попаданий: 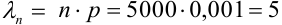 . Найдем заданную вероятность:
. Найдем заданную вероятность:
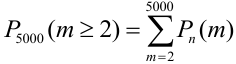 = (перейдем к противоположному событию: m < 2) =
= (перейдем к противоположному событию: m < 2) = 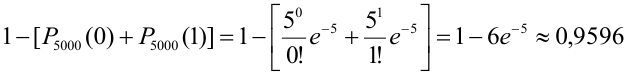 .
.
По точной формуле (формуле Бернулли) 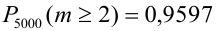 , т.е. ошибка невелика.
, т.е. ошибка невелика.
Локальная предельная теорема Муавра – Лапласа (асимптотическая формула для случая больших значений n и m)
Если вероятность наступления некоторого события А в n независимых испытаниях постоянна и равна р, (0 < р < 1), то вероятность 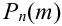 того, что в этих испытаниях событие А наступит ровно m раз, удовлетворяет при
того, что в этих испытаниях событие А наступит ровно m раз, удовлетворяет при  соотношению (или приближенно равна):
соотношению (или приближенно равна):
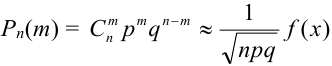 ,
,
где 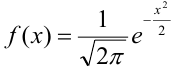 ,
, 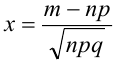 .
.
Замечания.
1. Часто формула Пуассона записывается в виде равенства, но надо помнить при этом, что оно верно при  :
:
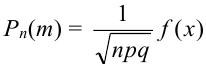
2. Формулой пользуются при больших n и m. Например, при п > 100, 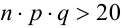 .
.
3. Из того, что  следует, что
следует, что 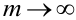 . Это означает, что n и m должны отличаться друг от друга не очень сильно. Например, для случая m = 0, теорема дает плохое приближение.
. Это означает, что n и m должны отличаться друг от друга не очень сильно. Например, для случая m = 0, теорема дает плохое приближение.
4. Существуют таблицы значений функции 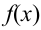 для положительных значений х (стр. 408 в задачнике Ефимова – Дсмидовича). Для отрицательных значений х используется та же таблица, так как
для положительных значений х (стр. 408 в задачнике Ефимова – Дсмидовича). Для отрицательных значений х используется та же таблица, так как 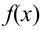 – четная функция:
– четная функция: 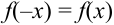 . Функцию
. Функцию 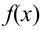 называют плотностью нормального распределения.
называют плотностью нормального распределения.
Пример №14
Найти вероятность того, что событие А наступит ровно 70 раз в 243 испытаниях, если вероятность появления этого события в каждом испытании равна 0,25.
Решение.
Количество испытаний n = 243, количество успехов m = 70, вероятность успеха р = 0,25, вероятность неудачи q = 1 – 0,25 = 0,75.
По формуле Бернулли считать сложно. Так как n и m велики, поэтому применим формулу Муавра – Лапласа.
Найдем сначала х и 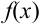 :
:
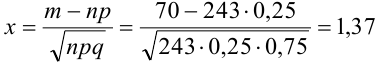 , тогда
, тогда 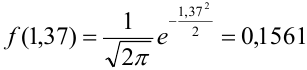 .
.
Можно было не считать значение 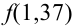 напрямую, а обратиться к таблице в учебнике.
напрямую, а обратиться к таблице в учебнике.
Подставим найденное значение 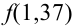 в формулу:
в формулу:
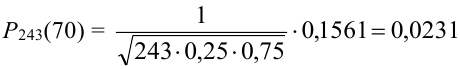 .
.
Предельная интегральная теорема Муавра – Лапласа (асимптотическая формула для случая, когда число успехов m лежит в некоторых пределах)
Теорема 1. Если m – число наступлений события А в n независимых испытаниях, в каждом из которых вероятность этого события равна р (0 < р < 1), то равномерно относительно а и b 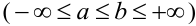 при
при 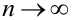 имеет место соотношение:
имеет место соотношение:
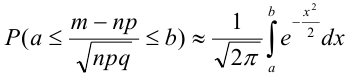 .
.
В некоторых источниках 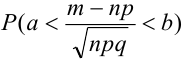 или
или 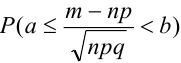 .
.
Ранее вывели, что 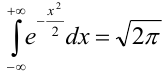 . Численное значение нашего интеграла можно найти с помощью таблиц (стр. 406 в задачнике Ефимова – Демидовича) для функции Лапласа Ф(х):
. Численное значение нашего интеграла можно найти с помощью таблиц (стр. 406 в задачнике Ефимова – Демидовича) для функции Лапласа Ф(х):
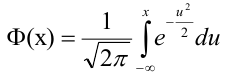 , где
, где 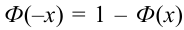 . Для тех значений х, которых нет в таблице, т.е для
. Для тех значений х, которых нет в таблице, т.е для 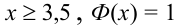
Либо, функция Лапласа может быть в виде: 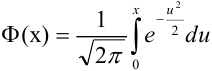 , где
, где 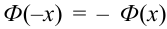 , для тех значений х, которых нет в таблице, т.е. для
, для тех значений х, которых нет в таблице, т.е. для 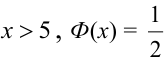 .
.
Теорема 2. (Теорема Муавра-Лапласа) Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < р < 1), событие А наступит не менее 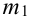 раза и не более
раза и не более 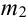 раз приближенно равна:
раз приближенно равна: 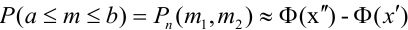 ,
,
где Ф(х) – функция Лапласа, значения 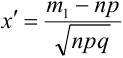 ,
, 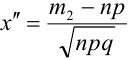 .
.
Теорема 3. (Закон больших чисел или теорема Бернулли).
При неограниченном увеличении числа однородных независимых опытов частота события будет сколь угодно мало отличаться от вероятности события в отдельном опыте.
Иначе, вероятность того, что отклонение относительной частоты наступления события 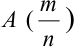 от постоянной вероятности события А (p) очень мало при
от постоянной вероятности события А (p) очень мало при 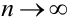 п —> оо стремится к 1.
п —> оо стремится к 1.
Доказательство.
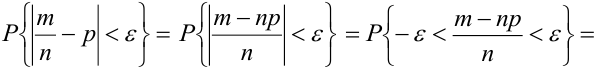
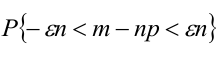 = (разделим все части неравенства на положительное число
= (разделим все части неравенства на положительное число 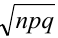 )
)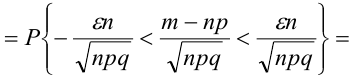
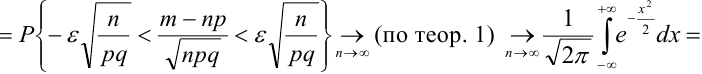
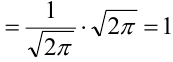 .
.
Пример №15
Вероятность появления события А в каждом из 100 независимых испытаний постоянна и равна 0,8. Найти вероятность того, что событие появиться не менее 75 раз и не более 90 раз.
Решение.
Количество испытаний n = 100, вероятность успеха р = 0,8, вероятность неудачи q = 1 – 0,8 = 0,2 , 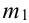 = 75,
= 75, 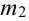 – 90.
– 90.
Найдем 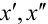 :
:
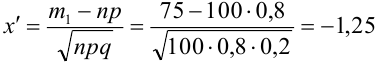 ,
, 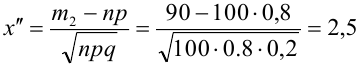 .
.
По теореме 2:
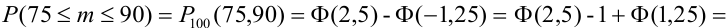 (по таблице для функции Лапласа) =
(по таблице для функции Лапласа) = 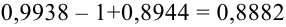 .
.
Наивероятнейшее число появления события в независимых испытаниях
Определение 28. Число 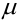 наступления события в независимых испытаниях, в каждом из которых вероятность появления события А равна р, называется наивероятнейшим, если вероятность того, что событие наступит в этих испытаниях
наступления события в независимых испытаниях, в каждом из которых вероятность появления события А равна р, называется наивероятнейшим, если вероятность того, что событие наступит в этих испытаниях 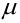 раз превышает или, по крайней мере, не меньше вероятности остальных возможных исходов испытаний.
раз превышает или, по крайней мере, не меньше вероятности остальных возможных исходов испытаний.
Наивероятнейшее число  определяется из двойного неравенства:
определяется из двойного неравенства:
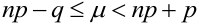 ,
,
причем 1) если (np – q) -дробное, то существует одно  , 2) если (nр- q) – целое, то существует два наивероятнейших числа, 3) если nр – целое, то
, 2) если (nр- q) – целое, то существует два наивероятнейших числа, 3) если nр – целое, то  = nр.
= nр.
Пример №16
Испытывается каждый из 15 элементов некоторого устройства. Вероятность того, что элемент выдержит испытание, равна 0,9. Найти наивероятнейшее число элементов, которые выдержат испытание и вероятность этого числа.
Решение.
Количество испытаний n = 15, вероятность успеха р = 0,9, вероятность неудачи q = 0,1.
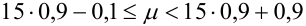 ,
, 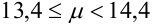 .
.
Т.к.  — целое число, то
— целое число, то  = 14— наивероятнейшее число элементов, выдержавших испытание. Вероятность этого числа найдем по формуле Бернулли:
= 14— наивероятнейшее число элементов, выдержавших испытание. Вероятность этого числа найдем по формуле Бернулли:
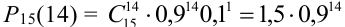 . (Удобнее было по локальной формуле Муавра – Лапласа).
. (Удобнее было по локальной формуле Муавра – Лапласа).
Всё о формуле полной вероятности
Пусть событие 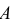 может произойти с одним и только с одним из несовместимых событий
может произойти с одним и только с одним из несовместимых событий 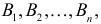 образующих полную группу. Иными словами, событие
образующих полную группу. Иными словами, событие 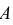 появится, если произойдет событие B1 и при этом появится событие
появится, если произойдет событие B1 и при этом появится событие 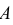 , или произойдет событие B2 и при этом появится событие
, или произойдет событие B2 и при этом появится событие 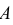 и т.д. Символическая запись этой фразы имеет вид
и т.д. Символическая запись этой фразы имеет вид
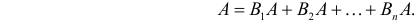
В силу несовместимости событий можно записать 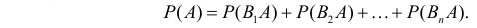
Используя теорему умножения вероятностей, получаем формулу 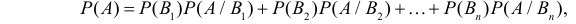
которая и называется формулой полной вероятности.
Обычно ее записывают кратко:
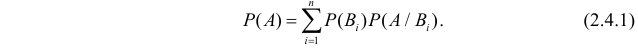
Пример №17
Имеется две коробки деталей, в каждой из которых по 10 деталей. В первой коробке среди деталей две низкого сорта, а во второй четыре низкосортных детали. Из первой коробки для нужд производства взяли наугад половину деталей, а оставшиеся высыпали во вторую коробку. Через некоторое время из второй коробки взяли наугад деталь. Какова вероятность того, что это деталь низкого сорта?
Решение. Обозначим через A событие, состоящее в выборе из второй коробки детали низкого сорта. Возможность этого выбора зависит от того, какие именно детали были добавлены во вторую коробку. На этот счет можно выдвинуть следующие предположения: B1 – во вторую коробку добавили пять годных деталей; B2 – добавили одну деталь низкого сорта и четыре доброкачественные; B3 – добавили две детали низкого сорта и три доброкачественные. Пять деталей во вторую коробку можно переложить 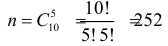 способами. Из них событию B1 благоприятствует
способами. Из них событию B1 благоприятствует 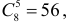 событию B2 —
событию B2 — 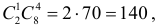 а событию B3 —
а событию B3 — 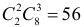 способов. Событие A произойдет, если появится событие B1 и после этого произойдет событие A или появится событие B2 и после этого произойдет событие A или появится B3 и после этого произойдет A. Символически:
способов. Событие A произойдет, если появится событие B1 и после этого произойдет событие A или появится событие B2 и после этого произойдет событие A или появится B3 и после этого произойдет A. Символически: 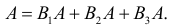 Учитывая несовместность событий
Учитывая несовместность событий  , имеем
, имеем 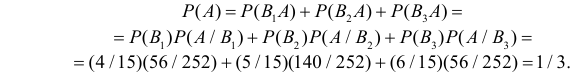
Ответ. 1/ 3.
Всё о Формуле Байеса
Пусть событие A может наступить только при появлении одного из несовместных событий 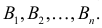 В этих условиях вероятность события A можно вычислить по формуле полной вероятности (2.4.1). События
В этих условиях вероятность события A можно вычислить по формуле полной вероятности (2.4.1). События  иногда называют «гипотезами», поскольку можно лишь предполагать какое именно из них произойдет. Предположим, что известны вероятности
иногда называют «гипотезами», поскольку можно лишь предполагать какое именно из них произойдет. Предположим, что известны вероятности 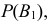
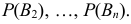
Проделан опыт, в результате которого событие A произошло. Тогда вероятности событий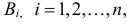 при условии появления события A определяются по формулам Байеса
при условии появления события A определяются по формулам Байеса
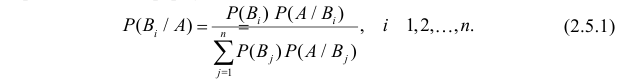
Формулы Байеса позволяют переоценивать вероятности гипотез (событий  ) с учетом информации, которую содержит в себе факт появления события A.
) с учетом информации, которую содержит в себе факт появления события A.
Пример №18
По каналу связи передается одна из последовательностей букв 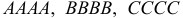 с вероятностями соответственно 0,5; 0,4; 0,1. Каждая передаваемая буква принимается правильно с вероятностью 0,8 и с вероятностями 0,1 и 0,1 за любую из двух других букв. Предполагается, что искажаются буквы при передаче независимо друг от друга. Найти вероятность того, что передано
с вероятностями соответственно 0,5; 0,4; 0,1. Каждая передаваемая буква принимается правильно с вероятностью 0,8 и с вероятностями 0,1 и 0,1 за любую из двух других букв. Предполагается, что искажаются буквы при передаче независимо друг от друга. Найти вероятность того, что передано 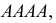 если принято
если принято 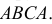
Решение. Для краткости записи формулы обозначим 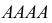 через
через 
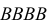 через
через  через
через 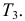 Тогда по формулам Байеса (2.5.1)
Тогда по формулам Байеса (2.5.1)

Ответ. 8/9.
Пример №19
Три стрелка производят по одному выстрелу в одну и ту же мишень. Вероятности попадания в мишень при одном выстреле для этих стрелков соответственно равны 0,8; 0,7; 0,6. Какова вероятность того, что третий стрелок промахнулся, если в мишени оказалось две пробоины?
Решение. Обозначим через А событие, состоящее в появлении двух пробоин в мишени. В отношении двух пробоин могут быть три предположения: В1 – попали первый и второй стрелки, а третий не попал, вероятность чего равна 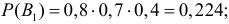 В2 – попали первый и третий, а второй не попал, вероятность чего равна
В2 – попали первый и третий, а второй не попал, вероятность чего равна 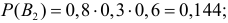 В3 – попали второй и третий, а первый не попал, вероятность чего равна
В3 – попали второй и третий, а первый не попал, вероятность чего равна 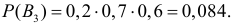
Заметим, что 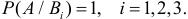 Тогда по формулам Байеса (2.5.1)
Тогда по формулам Байеса (2.5.1)
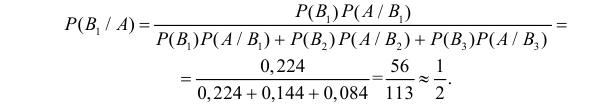
Ответ. 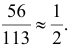
Пример №20
В партии из 10 изделий с равными шансами может оказаться от нуля до трех бракованных. Наугад взяли и проверили три изделия. Они оказались годными. Какова вероятность того, что остальные изделия в партии тоже годные?
Решение. Насчет содержания в партии бракованных изделий по условиям задачи может быть четыре предположения 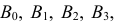 где
где 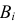 означает, что в партии
означает, что в партии 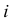 бракованных изделий. По условиям задачи все эти предположения равновозможны и поэтому имеют вероятности
бракованных изделий. По условиям задачи все эти предположения равновозможны и поэтому имеют вероятности 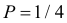 каждое. Обозначим через A факт проверки трех годных изделий. Требуется найти
каждое. Обозначим через A факт проверки трех годных изделий. Требуется найти 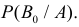
Заметим, что 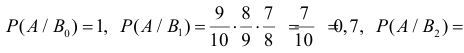
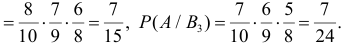 Поэтому по формулам Байеса (2.5.1)
Поэтому по формулам Байеса (2.5.1)
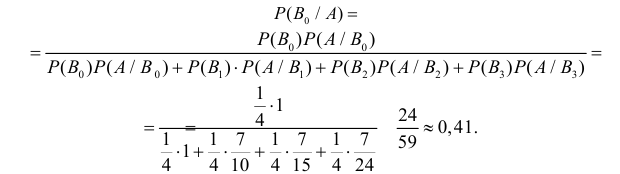
Ответ. 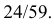
Пример №21
Вероятность того, событие B произойдет в течение часа, равна 0,9. Оказалось, что в течение первых 40 мин. событие B не произошло. Какова вероятность того, что это событие появится в оставшиеся 20 мин. времени?
Решение. В отношении события 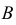 могут быть два предположения: либо оно появится
могут быть два предположения: либо оно появится 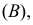 либо оно не появится
либо оно не появится 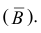 Обозначим через
Обозначим через 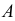 тот факт, что событие
тот факт, что событие 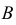 не появилось в течение первых 40 мин. Нас интересует вероятность
не появилось в течение первых 40 мин. Нас интересует вероятность 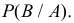 По формулам Байеса (2.5.1) получим
По формулам Байеса (2.5.1) получим
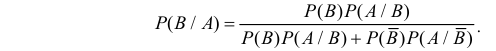
В задаче по умолчанию предполагается, что событие 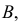 если оно происходит, то равновозможно его появление в любой момент данного часа. Поэтому по геометрическому определению вероятности
если оно происходит, то равновозможно его появление в любой момент данного часа. Поэтому по геометрическому определению вероятности 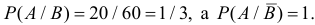 В итоге получаем, что
В итоге получаем, что
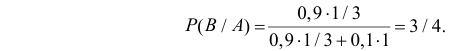
Ответ. 3/4.
Пример №22
В кошельке лежат четыре монеты. Три монеты обычных, а у четвертой на той и другой стороне изображен герб. Наугад взяли монету и подбросили три раза. Все три раза выпал герб. Какова вероятность того, что и при четвертом подбрасывании выпадет герб?
Решение. Обозначим через B1 – выбор монеты с одним гербом, через B2 – выбор монеты с двумя гербами. Априорные вероятности этих событий равны: 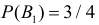 и
и 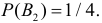
Обозначим через A – выпадение трех гербов подряд. Апостериорные вероятности по формулам Байеса равны: 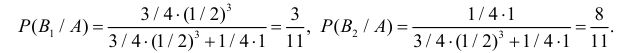
Тогда по формуле полной вероятности (2.4.1):
P(выпадения герба в четвертый раз)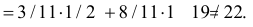
Ответ. 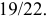
Подробное объяснение формулы полной вероятности
Постановка задачи: Пусть 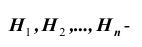 – полная система (группа) попарно несовместных событий (в дальнейшем эти события
– полная система (группа) попарно несовместных событий (в дальнейшем эти события 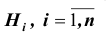 будем называть гипотезами) т. е.
будем называть гипотезами) т. е.  или что то же самое
или что то же самое  и пусть событие A может произойти лишь совместно с каким-либо одним из этих событий (гипотез).
и пусть событие A может произойти лишь совместно с каким-либо одним из этих событий (гипотез).
Требуется найти вероятность события A.
Выведем формулу решения этой задачи. Имеем
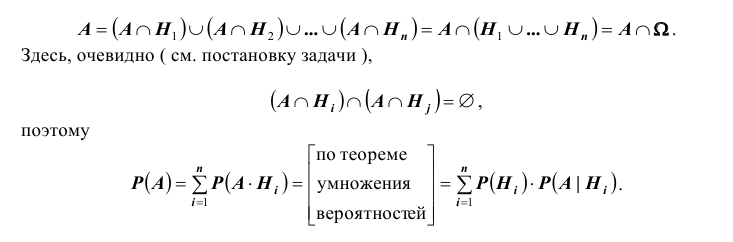
маршрутов (схема дорог). Какова вероятность того, что он попадет в пункт А ?
Решение. Как видим из схемы дорог, путь туриста обязательно проходит через один из пунктов 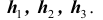 Тогда
Тогда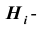 – гипотеза (предположение) которая состоит в том, что турист попал в пункт
– гипотеза (предположение) которая состоит в том, что турист попал в пункт  .
.
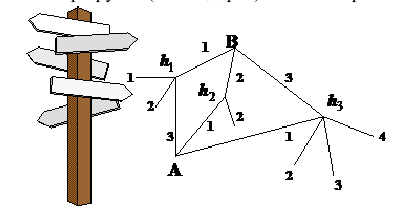
Заметим, что события (гипотезы) попарно несовместны и равновероятны, т.е., очевидно, образуют полную группу событий: во-первых,
попарно несовместны и равновероятны, т.е., очевидно, образуют полную группу событий: во-первых, , во-вторых
, во-вторых 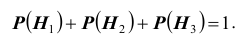 Событие A- турист попал в пункт А. Тогда, нетрудно
Событие A- турист попал в пункт А. Тогда, нетрудно
видеть (см. схему), что 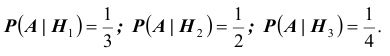 Значит, по формуле полной вероятности, получаем:
Значит, по формуле полной вероятности, получаем: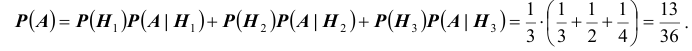

Пример №23 (о мудреце и властелине).
Властелин, разгневавшись на мудреца, приказал отрубить ему голову. Но затем, смягчившись, дал мудрецу возможность попытаться спастись. Итак, властелин взял 2 белых и 2 черных шара и предложил мудрецу распределить их по своему усмотрению по двум одинаковым урнам. После чего, палач сначала наугад выберет одну из урн, а затем также наугад, не глядя, вытащит из неё один шар. Мудрец будет помилован, если вытянутый шар оказался белым. Какую стратегию распределения шаров по урнам должен
выбрать мудрец, чтобы быть помилованным? Какова максимальная вероятность спастись мудрецу? Какая стратегия наименее выгодна для него?
Решение. Выдвинем гипотезы (предположения) 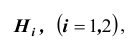 которые состоят в том, что палач вытащит шар из i – ой урны
которые состоят в том, что палач вытащит шар из i – ой урны 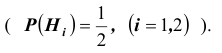 Очевидно, что эти события
Очевидно, что эти события 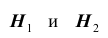 несовместны и их сумма является достоверным событием
несовместны и их сумма является достоверным событием 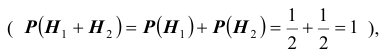 т.е. образуют полную группу (систему) событий. И пусть A- это событие состоящее в том, что
т.е. образуют полную группу (систему) событий. И пусть A- это событие состоящее в том, что
палачом вытянут белый шар. Далее, рассмотрим следующие варианты распределения мудрецом шаров по
урнам:
1). В первой урне 2 белых, а во второй 2 черных шара. Тогда 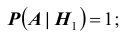
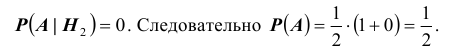
2 Хотим заметить, что далеко не всегда властелины были глупыми людьми, не знающими математики. Так, например, Наполеон был немного математиком, интересовался, в частности, геометрией. Он вёл дискуссии с Лагранжем и Лапласом, когда ещё не был правителем Франции.
Как-то в одной из таких дискуссий Лаплас резко оборвал Бонапарта: «Менее всего мы хотим от Вас, генерал, урока геометрии». В дальнейшем Лаплас стал его главным военным инженером. Наполеону приписывают теорему: «Если на сторонах произвольного треугольника во внешнюю сторону построены равносторонние треугольники, то их центры образуют равносторонний треугольник» – это так называемый вешний треугольник Наполеона.Так же ему приписывают один из знаменитых палиндромов (читается в обе стороны одинаково): «ABLE WAS I ERE I SAW ELBA» – я был силён, пока не увидел Эльбу.
2). В первой и во второй урнах по 1 белому и 1 черному шару. Тогда 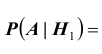
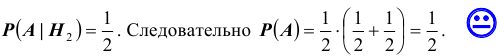
3). В первой урне 1 белый, а во второй 1 белый и 2 черных шара. Тогда 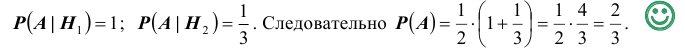
4). В первой урне 1 черный, а во второй 2 белых и 1 черный шары. Тогда 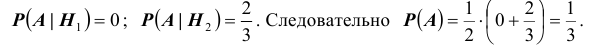
5). Первая урна оказалась пустой, т.е. все шары во второй урне. Тогда 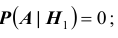
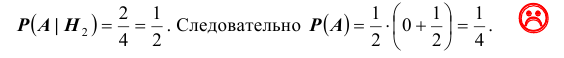
Как видим, наиболее предпочтительной является 3-я стратегия, ей соответствует вероятность быть помилованным равная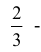 – действительно мудрое решение; наименее выгодна – последняя, 5 – я стратегия, где вероятность спастись равна
– действительно мудрое решение; наименее выгодна – последняя, 5 – я стратегия, где вероятность спастись равна 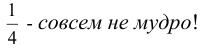
Вероятность гипотез. Формула Байеса
Постановка задачи: Пусть 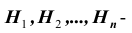 – полная система (группа) попарно несовместных событий (гипотез) т. е.
– полная система (группа) попарно несовместных событий (гипотез) т. е.
и пусть событие A может произойти лишь совместно с каким – либо одним из этих событий (гипотез) – ситуация аналогичная той, которая была ранее. И пусть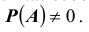 Требуется найти условную вероятность k – ой гипотезы при условии, что событие A произошло, т.е.
Требуется найти условную вероятность k – ой гипотезы при условии, что событие A произошло, т.е.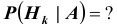 – переоценка гипотез.
– переоценка гипотез.
По теореме об умножении вероятностей
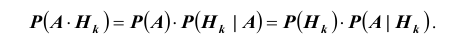 Следовательно
Следовательно 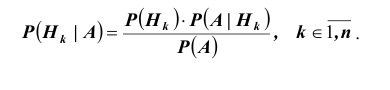
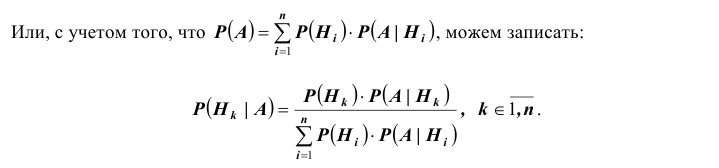
Полученная формула называется формулой Байеса (Бейеса) для переоценки гипотез. Другими словами: вероятность 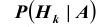 гипотезы после испытания равна произведению вероятности
гипотезы после испытания равна произведению вероятности 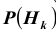 гипотезы до испытания на соответствующую ей условную вероятность
гипотезы до испытания на соответствующую ей условную вероятность 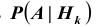 события, происшедшего при испытании, деленному на полную вероятность
события, происшедшего при испытании, деленному на полную вероятность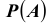 этого события.
этого события.
Пример №24
При обследовании больного имеется подозрение (т.е. делаются предположения или, что то же самое, выдвигаются гипотезы)
на одно из двух заболеваний 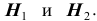 . Их вероятности в данных условиях равны
. Их вероятности в данных условиях равны 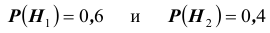 соответственно. Для уточнения диагноза назначается обследование, результатом которого будет отрицательная или положительная реакция. В случае болезни вероятность положительной реакции равна 0,9 , а в случае болезни
соответственно. Для уточнения диагноза назначается обследование, результатом которого будет отрицательная или положительная реакция. В случае болезни вероятность положительной реакции равна 0,9 , а в случае болезни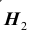 эта вероятность равна 0,5. Обследования проведены дважды и оба раза реакция оказалась отрицательной. Найти вероятность каждого заболевания.
эта вероятность равна 0,5. Обследования проведены дважды и оба раза реакция оказалась отрицательной. Найти вероятность каждого заболевания.

Решение. Во – первых, очевидно, что события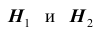 образуют полную группу событий. Действительно, эти события несовместны, так как у больного имеется подозрение только лишь на одно из двух заболеваний и сумма событий – есть достоверное событие (обследуемый болен):
образуют полную группу событий. Действительно, эти события несовместны, так как у больного имеется подозрение только лишь на одно из двух заболеваний и сумма событий – есть достоверное событие (обследуемый болен): 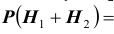 .
.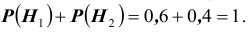 Во – вторых, если обозначить через A событие, которое состоит в том, что оба обследования дали отрицательный результат, то
Во – вторых, если обозначить через A событие, которое состоит в том, что оба обследования дали отрицательный результат, то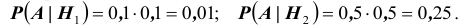 Таким образом, нетрудно видеть, что
Таким образом, нетрудно видеть, что
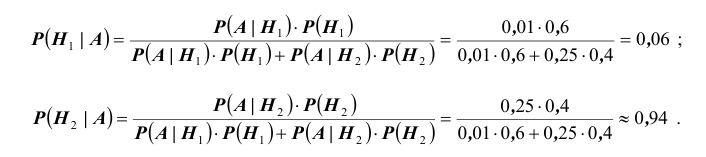
Как видим, при данных результатах обследования следует предполагать болезнь 
Повторение испытаний
Формула Бернулли (схема повторения опытов)
Опыты называются независимыми , если вероятность того или иного исхода каждого опыта не зависит от того, какие исходы имели другие опыты. Независимые опыты могут проводиться как в одинаковых условиях, так и в различных. В первом случае вероятность появления какого – либо события A во всех опытах одна и та же, во втором случае – она меняется от опыта к опыту. Ниже мы воспользуемся понятием сложного события, понимая под ним совмещение нескольких отдельных событий, которые называют простыми. Итак, пусть производится n независимых опытов в одинаковых условиях, в каждом из которых некоторое событие A может произойти с одной и той же вероятностью 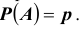 . Причём, каждый опыт (испытание) имеет лишь два исхода: событие A может появиться (произойти), либо не появиться. Условно, появление события A будем рассматривать как успех, а его не наступление (т.е. событие
. Причём, каждый опыт (испытание) имеет лишь два исхода: событие A может появиться (произойти), либо не появиться. Условно, появление события A будем рассматривать как успех, а его не наступление (т.е. событие 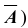 – как неудачу. Следовательно, вероятность не наступления события A в каждом испытании также постоянна и равна
– как неудачу. Следовательно, вероятность не наступления события A в каждом испытании также постоянна и равна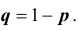 . Данная ситуация, или данная схема проведения опытов называется схемой Бернулли.
. Данная ситуация, или данная схема проведения опытов называется схемой Бернулли.
Итак, еще раз: схемой Бернулли называется последовательность n независимых испытаний, проводимых при одних и тех же условиях, в каждом из которых событие A либо происходит с постоянной вероятностью p , не зависящей от номера испытания, либо не происходит с вероятностью 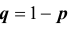
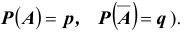
Ставятся задачи:
Задача №1. Найти вероятность  того, что в схеме Бернулли из n испытаний событие A произойдет ровно k раз
того, что в схеме Бернулли из n испытаний событие A произойдет ровно k раз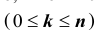 и, следовательно, не осуществится
и, следовательно, не осуществится 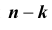 раз.
раз.
Задача № 2. Найти вероятность 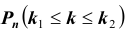 того, что в схеме Бернулли из n испытаний событие A произойдет не менее
того, что в схеме Бернулли из n испытаний событие A произойдет не менее 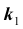 и не более
и не более 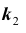 раз
раз
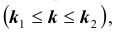 где
где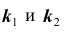 заданы.
заданы.
Задача № 3. Найти наивероятнейшее число 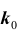 появления события A в схеме Бернулли из n испытаний, при котором
появления события A в схеме Бернулли из n испытаний, при котором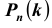 достигает наибольшего значения.
достигает наибольшего значения.
Решение №1.
Вероятность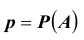 не зависит от номера испытания и, что также важно, не требуется чтобы событие A повторилось ровно k раз в определенной последовательности. Предположим, для определенности, что событие A произойдет подряд k раз, а в остальных
не зависит от номера испытания и, что также важно, не требуется чтобы событие A повторилось ровно k раз в определенной последовательности. Предположим, для определенности, что событие A произойдет подряд k раз, а в остальных 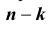 испытаниях – не произойдет. Используя теорему об умножении вероятностей, можем в этом случае записать:
испытаниях – не произойдет. Используя теорему об умножении вероятностей, можем в этом случае записать:
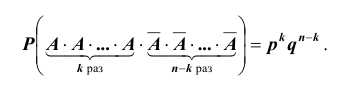
Таких несовместных событий столько, сколько сочетаний из n элементов по k элементов в каждом. Поэтому по теореме о вероятности суммы несовместных событий получим формулу, называемую формулой Бернулли:
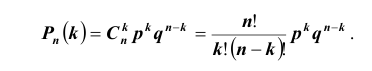
 Легко видеть, что вероятность
Легко видеть, что вероятность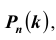 , вычисленная по формуле Бернулли, является коэффициентом при
, вычисленная по формуле Бернулли, является коэффициентом при 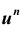 в разложении бинома
в разложении бинома 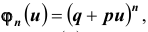 поэтому вероятность
поэтому вероятность 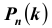 называется биномиальной, а функция
называется биномиальной, а функция 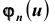 – производящей функцией для распределения вероятностей в схеме Бернулли из n испытаний. Разложение бинома Ньютона
– производящей функцией для распределения вероятностей в схеме Бернулли из n испытаний. Разложение бинома Ньютона 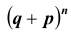 имеет вид:
имеет вид:

которую называют биномиальным законом распределения вероятностей события A в n испытаниях схемы Бернулли.
Заметим, что вероятность хотя бы одного появления события A в n испытаниях схемы Бернулли равна: 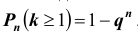 . Кстати, подумайте над
. Кстати, подумайте над
следующим вопросом: честное ли пари вам предлагают, если вы выиграете в том случае, когда при 24-х кратном бросании двух игральных костей хотя бы один раз одновременно появятся две шестёрки? Ответ дайте в конце пары.

(РЕШЕНИЕ. Вероятность одновременного выпадения двух шестерок при одном подбрасывании равна 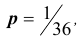 , следовательно – не выпадения равна
, следовательно – не выпадения равна 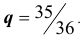 . Нетрудно видеть, что испытания, т.е. подбрасывания двух игральных костей 24 раза, удовлетворяют схеме Бернулли, следовательно вероятность одновременного появления двух шестерок хотя бы один раз равна
. Нетрудно видеть, что испытания, т.е. подбрасывания двух игральных костей 24 раза, удовлетворяют схеме Бернулли, следовательно вероятность одновременного появления двух шестерок хотя бы один раз равна 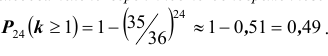 .То есть, пари нечестное.)
.То есть, пари нечестное.)
Другие примеры на применение формулы Бернулли, рассмотрим немного позднее, а именно после того, как решим задачи № 2 и № 3
Решение № 2.
Нетрудно показать, что вероятность 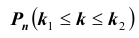 того, что в схеме Бернулли из n испытаний событие A произойдет не менее
того, что в схеме Бернулли из n испытаний событие A произойдет не менее 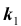 и не более
и не более 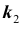 раз
раз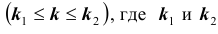 заданы, может быть вычислена по формуле:
заданы, может быть вычислена по формуле: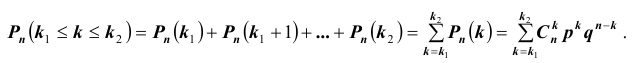
Решение № 3
Важной является задача № 3 о наивероятнейшем числе 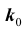 появления события A в схеме Бернулли из n испытаний.
появления события A в схеме Бернулли из n испытаний.
Рассмотрим отношение:
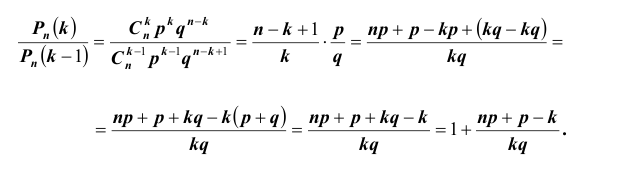
Из полученного следует, что:
1) если 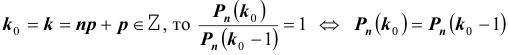 т.е. существует
т.е. существует
два максимума;
2) если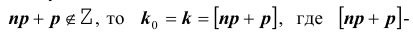 целая часть числа
целая часть числа тогда
тогда 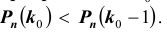

Пример №25
При некоторых условиях стрельбы вероятность p попадания в цель при одном выстреле равна
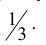 Произведено
Произведено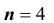 выстрела.
выстрела.
- а). Каково наивероятнейшее число попаданий в цель?
- б). Какова его вероятность?
- в). Какова вероятность двух попаданий?
- г). Какова вероятность хотя бы одного попадания?
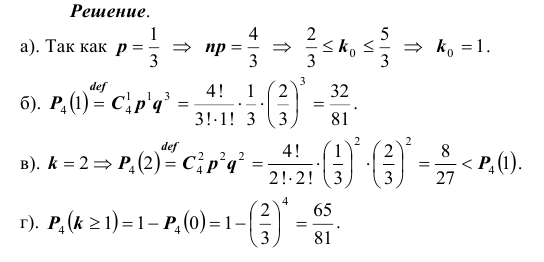
Пример №26
Некто Сэмюэль Пепайс обратился к Исааку Ньютону с вопросом: какое из событий наиболее вероятно –
- появление по крайней мере одной «шестерки» при подбрасывании 6-ти игральных костей;
- хотя бы двух «шестерок» при подбрасывании 12-ти;
- хотя бы трех «шестерок» при подбрасывании 18-ти?
Решение.
Вероятность q непоявления «шестерки» при одном подбрасывании, как известно, равна 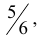 , следовательно, при шести подбрасываниях равна
, следовательно, при шести подбрасываниях равна 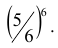
5 . Таким образом, вероятность появления по крайней мере одной «шестерки» при подбрасывании 6-ти игральных костей может быть найдена по формуле:
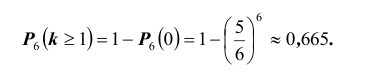
Событие «хотя бы две» противоположно событию «либо ни разу, либо один раз», т.е. 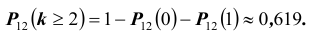
Событие «хотя бы три» противоположно событию «либо ни разу, либо один раз, либо два раза», т.е.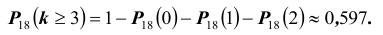
Таким образом, как видим, предпочтительнее первая стратегия – таким и был ответ Ньютона.
Замечу, что при больших значениях числа n испытаний в схеме Бернулли формула для подсчета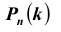 становится громоздкой для вычислений. В этих случаях пользуются асимптотическими формулами. Рассмотрим асимптотическую формулу Пуассона, которая справедлива при малых p и больших n (распределение редких событий в схеме Бернулли). Другими словами
становится громоздкой для вычислений. В этих случаях пользуются асимптотическими формулами. Рассмотрим асимптотическую формулу Пуассона, которая справедлива при малых p и больших n (распределение редких событий в схеме Бернулли). Другими словами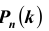 рассматривается как функция трех переменных n,k , p , при условии, что k – фиксировано, а n и p меняются
рассматривается как функция трех переменных n,k , p , при условии, что k – фиксировано, а n и p меняются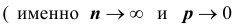
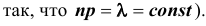
ТЕОРЕМА Пуассона 3. Пусть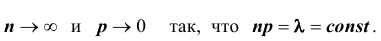 Тогда в схеме Бернулли
Тогда в схеме Бернулли 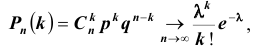 или то же самое
или то же самое 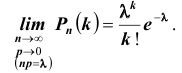
Доказательство

Что и требовалось доказать.
При доказательстве можно воспользоваться приближенной формулой Стирлинга.
Следствие: при указанных выше условиях, т.е. при 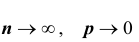 и
и 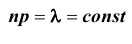 справедлива приближенная формула Пуассона:
справедлива приближенная формула Пуассона:
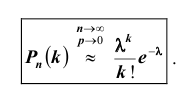
Пример №27
Телефонная станция обслуживает 800 абонентов. Для каждого абонента вероятность того, что в течении часа он позвонит на станцию равна p =0,01. Найти вероятность того, что четыре абонента позвонят на станцию в течении часа.
Решение 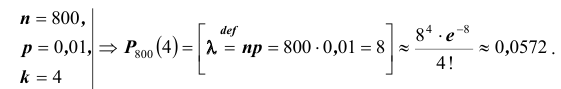
Теорема Муавра – Лапласа (локальная)
Остановлюсь еще на двух предельных теоремах в схеме Бернулли – локальной теореме Муавра – Лапласа (её доказательство получим как частный случай закона больших чисел – предельной теоремы Ляпунова, доказательство которой нам ещё предстоит провести) и интегральной теореме Муавра – Лапласа. Итак:

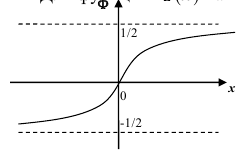
причем, во-первых, погрешность этой формулы есть величина порядка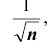 во-вторых, для функции
во-вторых, для функции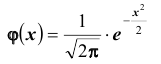 составлена таблица её значений. Для отрицательных значений аргумента пользуются той же таблицей, так как, очевидно,
составлена таблица её значений. Для отрицательных значений аргумента пользуются той же таблицей, так как, очевидно, 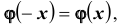 , то есть функция
, то есть функция 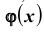 четная. Заметим также, что график функции
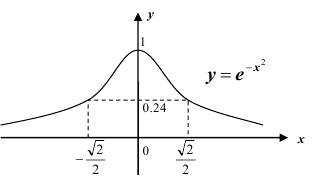
четная. Заметим также, что график функции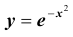 называется кривой Гаусса (см. рис.).
называется кривой Гаусса (см. рис.).
интегральная приближенная формула Лапласа ( при больших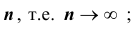
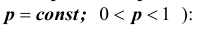

Для функции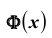 также есть табличные значения, когда
также есть табличные значения, когда 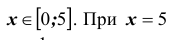 справедливо неравенство
справедливо неравенство 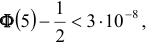
равносильно условию 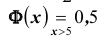 (график функции
(график функции 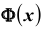 см. на рис.). Отметим, что точность растет с ростом произведения npq, и, обычно, пользуются этими формулами в случае, когда
см. на рис.). Отметим, что точность растет с ростом произведения npq, и, обычно, пользуются этими формулами в случае, когда 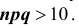
Замечание: если функция Лапласа записана в виде 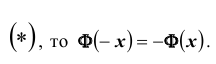 Иногда функция Лапласа может быть записана в виде
Иногда функция Лапласа может быть записана в виде
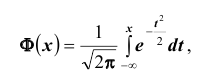
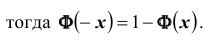 Отметим, что в схеме Бернулли рассматривались независимые испытания. Если же вероятность наступления события в k -ом опыте зависит от результата только предыдущего,
Отметим, что в схеме Бернулли рассматривались независимые испытания. Если же вероятность наступления события в k -ом опыте зависит от результата только предыдущего, 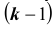 – ого опыта, то такая схема называется цепью Маркова.
– ого опыта, то такая схема называется цепью Маркова.
Формула полной вероятности и сложные задачи
В данном разделе мы рассмотрим более сложные задачи, имеющие большое практическое значение. Эти задачи встречается на практике в случае, если имеются несколько возможных сценариев развития событий (несколько вероятных гипотез). Известны как величины вероятности реализации каждого из сценариев, так и вероятность наступления интересующего нас события для любого из этих сценариев, а нас интересует, какова полная (совокупная) вероятность наступления интересующего нас события.
Предположим, что в результате опыта может произойти одно из n несовместных событий (гипотез) 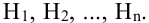 Пусть также имеется некоторое событие А и известны
Пусть также имеется некоторое событие А и известны 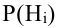 – вероятность гипотезы,
– вероятность гипотезы, 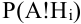 – условная вероятность события А при этой гипотезе). Тогда вероятность события А вычисляется по формуле полной вероятности:
– условная вероятность события А при этой гипотезе). Тогда вероятность события А вычисляется по формуле полной вероятности: 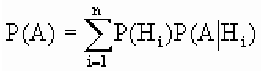
Пример №28
Из 40 деталей 10 изготовлены в первом цехе, 25 – во втором, а остальные – в третьем. Первый и третий цехи дают продукцию отличного качества с вероятностью 0,9, второй цех – с вероятностью 0,7. Какова вероятность того, что взятая наудачу деталь будет отличного качества?
Решение:
Обозначим событие А = {выбрана деталь отличного качества}, Hi= {выбранная деталь изготовлена в i цехе}, i = 1, 2, 3. Тогда 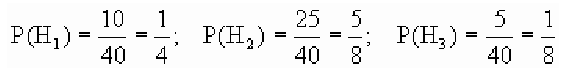
По условию задачи 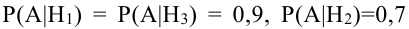 . По формуле полной вероятности находим искомую вероятность:
. По формуле полной вероятности находим искомую вероятность: 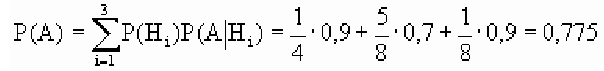
Пример №29
На рисунке изображена схема дорог. Найти вероятность того, что турист, вышедший из пункта А, попадет в пункт В, если на развилке он наугад выбирает любую дорогу (кроме обратной).
Решение:
Обозначим Нi = {приход туриста в пункт Hi}, i = 1, 2, 3, 4. Поскольку, выйдя из пункта А, он выбирает любую дорогу наугад, то 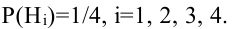
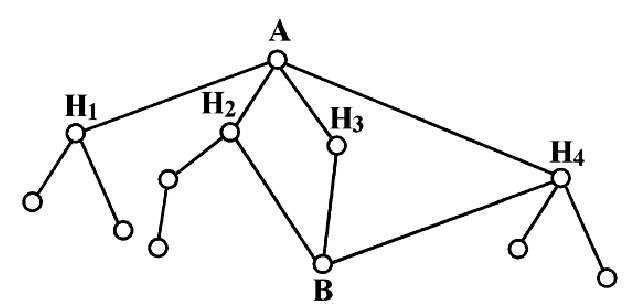
Исходя из схемы дорог, определяем, что 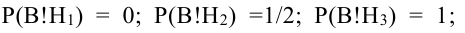
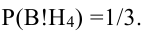
Таким образом, по формуле полной вероятности 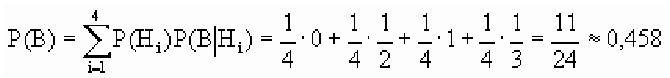
Пример №30
Из двенадцати лотерейных билетов пять выигрышных. Билеты вытягиваются по одному без возвращения. Какова вероятность того, что во второй раз вытянут выигрышный билет?
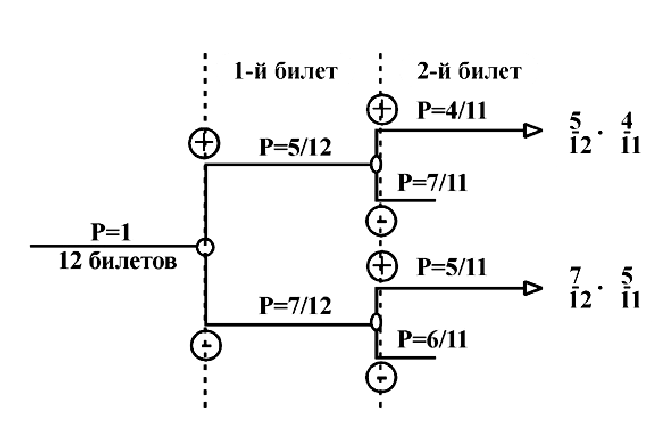
Решение:
Как обычно, вдоль каждой ветви “дерева вероятностей” значения вероятностей перемножаются, а затем значения на концах нужных веток между собой складываются. В результате получаем ответ: 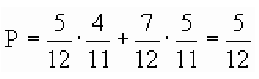
Случайные события независимые в совокупности
Следует различать попарно независимые случайные события и случайные события независимые в совокупности.
Определение: События называются попарно независимыми событиями, если любые два из них независимы.
Определение: События 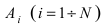 называются независимыми в совокупности, если каждое из них независимо от произведения любого числа остальных событий.
называются независимыми в совокупности, если каждое из них независимо от произведения любого числа остальных событий.
Замечание: Из определений видно, что из попарной независимости еще не следует, что эти события независимы в совокупности. Это означает, что условие независимости в совокупности является более сильным, чем условие попарной независимости случайных событий.
Теорема: Вероятность наступления хотя бы одного из событий 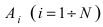 независимых в совокупности выражается формулой:
независимых в совокупности выражается формулой:
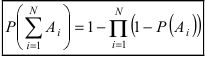 .
.
Доказательство: Обозначим через А событие, состоящее в том, что наступит хотя бы одно из событий 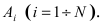 Очевидно, что противоположные события
Очевидно, что противоположные события 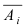 к событиям
к событиям 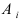 также будут независимы в совокупности. При этом событие
также будут независимы в совокупности. При этом событие 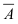 состоит в том, что в результате опыта не наступает ни одно из случайных событий
состоит в том, что в результате опыта не наступает ни одно из случайных событий 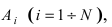 следовательно,
следовательно, 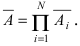 Так как события
Так как события 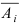 независимы в совокупности, то
независимы в совокупности, то 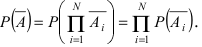 В силу того, что
В силу того, что 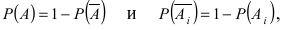 то
то 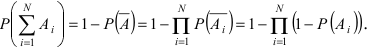
Пример №31
Пусть прибор содержит N последовательно соединенных блоков. Определить вероятность того, что цепь будет разорвана, если вероятность работы каждого блока равна р и она не зависит от работы других блоков.
Решение:
Пусть А – событие, которое состоит в том, что данная цепь разорвана. Это событие происходит, если выходит из строя хотя бы один из блоков, так как блоки включены последовательно. Противоположное событие состоит в том, что все блоки работают, т.е. 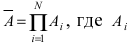 – событие, заключающееся в работе блока i. По условию задачи
– событие, заключающееся в работе блока i. По условию задачи 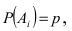 следовательно,
следовательно, 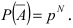 Таким образом, вероятность того, что цепь будет разорвана, равна
Таким образом, вероятность того, что цепь будет разорвана, равна 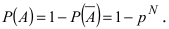
Теорема сложения вероятностей для совместных событий
Если случайные события одновременно появляются в условиях опыта, то имеет место следующая теорема.
Теорема: Вероятность суммы двух совместных событий равна сумме вероятностей этих событий минус вероятность их произведения:
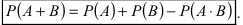
Доказательство: Пусть в результате опыта возможно n равно возможных, несовместных, элементарных исходов. При этом в 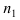 случаях наступает событие А, в
случаях наступает событие А, в 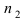 случаях – событие В, а в m случаях наступает и событие А, и событие B, т.е. событие
случаях – событие В, а в m случаях наступает и событие А, и событие B, т.е. событие 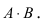 Таким образом, число исходов, в которых наступает или событие А , или событие В (т.е. событие А + В), равно
Таким образом, число исходов, в которых наступает или событие А , или событие В (т.е. событие А + В), равно 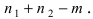 Согласно классическому определению вероятности вероятность суммы случайных, совместных событий А и В равна
Согласно классическому определению вероятности вероятность суммы случайных, совместных событий А и В равна
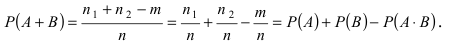
Замечание: Методом математической индукции вышеприведенная теорема может быть обобщена на любое число совместных событий, например, в случае 3 совместных событий А, В и С теорема принимает вид:
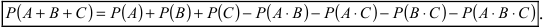
Пример №32
Найти вероятность того, что взятое наугад число из чисел от 10 до 20 делится или на 2, или на 3.
Решение:
Всего равновозможных, элементарных исходов 11 (числа от 10 включительно до 20 включительно). В 6 случаях (10, 12, 14, 16, 18, 20) число кратно 2; в 3 случаях (12, 15, 18) число кратно 3; в 2 случаях (12, 18) число кратно и 2, и 3. Пусть событие А состоит в том, что наугад взятое число кратно 2, а событие В состоит в том, что наугад взятое число кратно 3. Сложное событие С состоит в том, что наугад взятое число делится или на 2, или на 3, т.е. С = А + В. Следовательно, вероятность этого события равна:
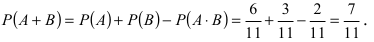
Все вышерассмотренные теоремы объединяются в теории вероятностей общим названием “основные теоремы теории вероятностей”.
Формула полной вероятности и события
Формула полной вероятности является следствием основных теорем теории вероятностей: теорем сложения и умножения вероятностей событий.
Пусть некоторое случайное событие А наступает с одним и только с одним из несовместных событий 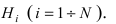
Определение: События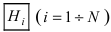 называются гипотезами, так как заранее неизвестно, какое из этих событий произойдет.
называются гипотезами, так как заранее неизвестно, какое из этих событий произойдет.
Теорема: Формула полной вероятности определяет вероятность случайного
события л, как сумму произведений вероятности каждой гипотезы 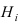 на условную вероятность события А при условии реализации гипотезы
на условную вероятность события А при условии реализации гипотезы 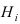 , т.е.
, т.е. 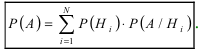
Доказательство: Событие А наступает с одним и только с одним из несовместных событий 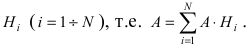 В силу того, что события
В силу того, что события 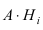 несовместны, то по теореме сложения вероятностей для несовместных событий имеем:
несовместны, то по теореме сложения вероятностей для несовместных событий имеем: 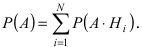 Используя теорему об умножении вероятностей зависимых событий, получаем искомую формулу:
Используя теорему об умножении вероятностей зависимых событий, получаем искомую формулу: 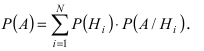
Пример №33
Пусть на сборку поступают детали с двух автоматических станков. Первый станок дает в среднем 0.3 % брака, а второй – 0.15 % брака. Производительность второго станка в два раза выше, чем первого станка. Найти вероятность того, что наугад взятая деталь окажется бракованной.
Решение:
Пусть событие А состоит в том, что наугад взятая деталь окажется бракованной. Тогда гипотеза 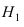 заключается в том, что эта деталь изготовлена на первом станке, а гипотеза
заключается в том, что эта деталь изготовлена на первом станке, а гипотеза 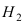 заключается в том, что эта деталь изготовлена на втором станке. Очевидно, что эти гипотезы являются несовместными событиями. В виду различной производительности станков обозначим через х количество деталей, изготовленных на первом станке, тогда на втором станке изготавливается 2х деталей. Общее число деталей, которые были изготовлены на обоих станках равна Зх. Следовательно, вероятности гипотез равны:
заключается в том, что эта деталь изготовлена на втором станке. Очевидно, что эти гипотезы являются несовместными событиями. В виду различной производительности станков обозначим через х количество деталей, изготовленных на первом станке, тогда на втором станке изготавливается 2х деталей. Общее число деталей, которые были изготовлены на обоих станках равна Зх. Следовательно, вероятности гипотез равны: 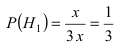 — для первой гипотезы и
— для первой гипотезы и 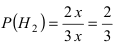 – для второй гипотезы.
– для второй гипотезы.
Вероятности события А при условии реализации первой и второй гипотез равны: 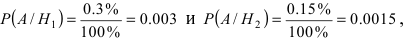 соответственно. Согласно формуле полной вероятности вероятность того, что наугад взятая деталь окажется бракованной, равна:
соответственно. Согласно формуле полной вероятности вероятность того, что наугад взятая деталь окажется бракованной, равна:
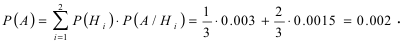
Формула вероятностей гипотез (формула Байеса)
Ниже будет получена формула, которая является следствием основных теорем теории вероятностей и формулы полной вероятности. Эта формула применяется для решения задач следующего типа. Пусть проводится эксперимент, в результате которого может появиться или не появиться событие л, которое наступает с одним и только с одним из несовместных событий 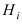 (
(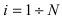 ). Предположим, что события
). Предположим, что события 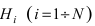 образуют полную группу и вероятности их появления
образуют полную группу и вероятности их появления 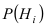 известны до проведения опыта. В результате проведения эксперимента событие А произошло. Используя этот факт, необходимо определить, какая из гипотез была ближе к истине, т.е. определить вероятность каждой гипотезы при условии реализации события А. Ответ на поставленный вопрос дает следующая теорема.
известны до проведения опыта. В результате проведения эксперимента событие А произошло. Используя этот факт, необходимо определить, какая из гипотез была ближе к истине, т.е. определить вероятность каждой гипотезы при условии реализации события А. Ответ на поставленный вопрос дает следующая теорема.
Теорема: Вероятность гипотезы 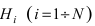 при условии реализации события А равна отношению произведения вероятности гипотезы на условную вероятность события А к паз ной вероятности события А:
при условии реализации события А равна отношению произведения вероятности гипотезы на условную вероятность события А к паз ной вероятности события А:
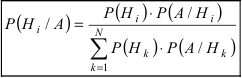
Доказательство: Событие А наступает с одним и только с одним из несовместных событий 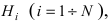 т.е. в каждом опыте происходит событие
т.е. в каждом опыте происходит событие 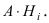 По теореме умножения вероятностей для зависимых событий:
По теореме умножения вероятностей для зависимых событий: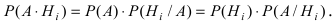
Следовательно, 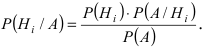 Воспользовавшись формулой полной вероятности, получим формулу Байеса:
Воспользовавшись формулой полной вероятности, получим формулу Байеса: 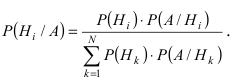
Пример №34
Однотипные пластмассовые детали изготавливаются на 3 прессах. Первый пресс выпускает 50 % всех деталей, второй – 40 %, третий – 10 % . При этом с первого пресса сходит в среднем 0.025 нестандартных деталей, со второго – 0.02 и с третьего – 0.015. Все детали поступают на сборку. Взятая наудачу деталь оказалась нестандартной. Какова вероятность того, что она изготовлена на первом прессе.
Решение:
Событие А состоит в том, что наудачу взятая деталь изготовлена на первом прессе. Гипотеза 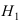 заключается в том, что эта деталь изготовлена на первом прессе, гипотеза
заключается в том, что эта деталь изготовлена на первом прессе, гипотеза 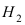 – на втором прессе, а гипотеза
– на втором прессе, а гипотеза 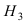 – на третьем прессе.
– на третьем прессе.
По условию задачи 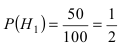 – для первой гипотезы,
– для первой гипотезы, 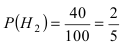 – для второй гипотезы и
– для второй гипотезы и 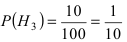 – для третьей гипотезы. Вероятности события А при условии реализации первой, второй и третьей гипотез, соответственно, равны:
– для третьей гипотезы. Вероятности события А при условии реализации первой, второй и третьей гипотез, соответственно, равны: 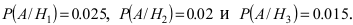 Согласно фор- муле пал ной вероятности вероятность того, что наугад взятая деталь окажется нестандартной, равна:
Согласно фор- муле пал ной вероятности вероятность того, что наугад взятая деталь окажется нестандартной, равна: 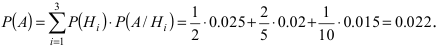
Используя формулу Байеса, получим 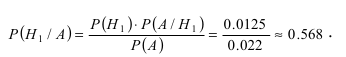
Независимые испытания и формула Бернулли
Пусть испытания повторяются n раз, причем событие А появляется в каждом опыте с одной и той же вероятностью р или не появляется с одной и той же вероятностью 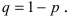
Определение: Испытания называются независимыми, если вероятность события А не зависит от того, какие события появились в предыдущих опытах, или появятся в последующих экспериментах.
Пример:
Независимы ли следующие испытания: а) многократное бросание кубика; б) извлечение карты из колоды без ее возвращения в колоду (выяснить самостоятельно).
Формула Бернулли
Теорема: Пусть проводится серия из n независимых испытаний, в каждом из которых событие А появляется с постоянной вероятностью 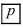 или не появляется с постоянной вероятностью
или не появляется с постоянной вероятностью 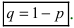 Тогда вероятность появления со- бытия А ровно m раз в серии из n независимых испытаний равна:
Тогда вероятность появления со- бытия А ровно m раз в серии из n независимых испытаний равна: 
Доказательство: Пусть 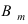 событие, состоящее в том, что в серии из n независимых испытаний событие А появится ровно m раз. Пусть
событие, состоящее в том, что в серии из n независимых испытаний событие А появится ровно m раз. Пусть 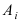 событие, описывающее появление события А в опыте i, а ему противоположное событие обозначим через
событие, описывающее появление события А в опыте i, а ему противоположное событие обозначим через 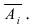 Так как вероятность появления события А в опыте i равна
Так как вероятность появления события А в опыте i равна 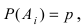 то вероятность появления противоположного события
то вероятность появления противоположного события 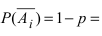
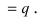 Для наступления события
Для наступления события 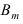 безразлично, в каких опытах произойдет событие A, а в каких – событие
безразлично, в каких опытах произойдет событие A, а в каких – событие 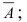 важно, чтобы число появлений события A в данной серии равнялось числу m. В качестве одного из вариантов чередования событий
важно, чтобы число появлений события A в данной серии равнялось числу m. В качестве одного из вариантов чередования событий 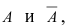 благоприятствующих появлению события
благоприятствующих появлению события 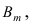 рассмотрим такое событие
рассмотрим такое событие 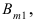 для которого событие А появится в m первых опытах и не появится в (n-m) последующих экспериментах, т.е.
для которого событие А появится в m первых опытах и не появится в (n-m) последующих экспериментах, т.е.
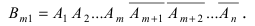
Воспользуемся теоремой умножения вероятностей для независимых событий, получим: 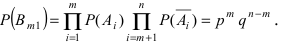 Аналогичные к
Аналогичные к 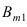 события отличаются от него только чередованием событий
события отличаются от него только чередованием событий  Все эти события равновероятны и их число равно количеству сочетаний из n элементов по m элементов, т.е.
Все эти события равновероятны и их число равно количеству сочетаний из n элементов по m элементов, т.е. 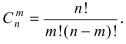 Таким образом, интересующее нас событие можно записать в виде
Таким образом, интересующее нас событие можно записать в виде 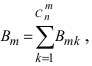 причем события
причем события  несовместны. По теореме сложения вероятностей несовместных событий вероятность изучаемого события равна
несовместны. По теореме сложения вероятностей несовместных событий вероятность изучаемого события равна 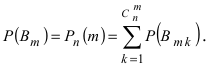 В правой части равенства суммируется
В правой части равенства суммируется 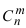 одинаковых слагаемых, следовательно,
одинаковых слагаемых, следовательно, 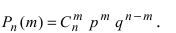 O5. Формула
O5. Формула  называется биномиальной или формулой Бернулли.
называется биномиальной или формулой Бернулли.
Пример №35
Монета подбрасывается 6 раз. Определить вероятность того, что герб выпадет а) 5 раз; б) от 2 до 4 раз.
Решение:
Вероятность выпадения герба не изменяется от опыта к опыту и равна 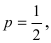 а, следовательно, вероятность выпадения решки равна
а, следовательно, вероятность выпадения решки равна 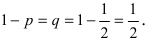 Для определения вероятности выпадения герба 5 раз в серии из 6 испытаний воспользуемся формулой Бернулли:
Для определения вероятности выпадения герба 5 раз в серии из 6 испытаний воспользуемся формулой Бернулли: 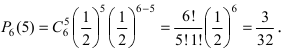 Событие, состоящее в том, что герб выпадет от 2 до 4 раз, соответствует события, которое состоит в том, что герб выпадет или 2 раза, или 3 раза, или 4 раза. Следовательно, вероятность
Событие, состоящее в том, что герб выпадет от 2 до 4 раз, соответствует события, которое состоит в том, что герб выпадет или 2 раза, или 3 раза, или 4 раза. Следовательно, вероятность 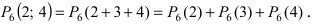 Вычислим соответствующие вероятности:
Вычислим соответствующие вероятности: 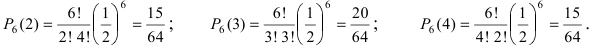 Таким образом, искомая вероятность равна
Таким образом, искомая вероятность равна 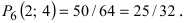
При больших значениях чисел m и n применение формулы Бернулли затруднительно, так как вычисление коэффициентов 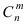 становится достаточно сложным. Поэтому при фиксированном значении т и в случае, когда вероятность появления события р<0.1, применяется формула Пуассона, а при р>0.1 – дифференциальная формула Муавра-Лапласа. Если
становится достаточно сложным. Поэтому при фиксированном значении т и в случае, когда вероятность появления события р<0.1, применяется формула Пуассона, а при р>0.1 – дифференциальная формула Муавра-Лапласа. Если  , то применяют интегральную формулу Муавра-Лапласа.
, то применяют интегральную формулу Муавра-Лапласа.
Формула Пуассона
Если при проведении серии испытаний по схеме Бернулли вероятность появления события А мала ( ), то при больших значениях чисел m и n применяют приближенную формулу Пуассона:
), то при больших значениях чисел m и n применяют приближенную формулу Пуассона: 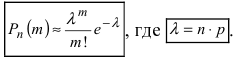
Формулы Муавра-Лапласа
Если при проведении серии испытаний по схеме Бернулли вероятность появления события А р>0.1, то при больших значениях чисел m и n применяют дифференциальную формулу Муавра-Лапласа: 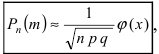 дифференциальная функция Муавра-Лапласа
дифференциальная функция Муавра-Лапласа 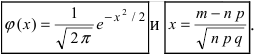
Замечание: В общем случае дифференциальная формула Муавра-Лапласа применяется при выполнении неравенств 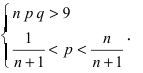
Если при проведении серии испытаний по схеме Бернулли числа m и n принимают большие значения, причем число m принимает значения от 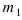 до
до 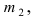 то применяют интегральную формулу Муавра-Лапласа:
то применяют интегральную формулу Муавра-Лапласа:
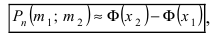 где
где 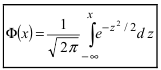 – интегральная функция Муавра-Лапласа и
– интегральная функция Муавра-Лапласа и 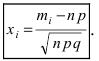
- Повторные независимые испытания
- Простейший (пуассоновский) поток событий
- Случайные величины
- Числовые характеристики случайных величин
- Комбинаторика – правила, формулы и примеры
- Классическое определение вероятности
- Геометрические вероятности
- Теоремы сложения и умножения вероятностей
Если
событие А
может произойти только при выполнении
одного из событий ![]() ,
,
которые образуютполную
группу несовместных событий,
то вероятность события А
вычисляется по формуле
![]() .
.
Эта
формула называется формулой
полной вероятности.
Вновь
рассмотрим полную группу несовместных
событий ![]() ,
,
вероятности появления которых![]() .
.
СобытиеА
может произойти только вместе с каким-либо
из событий ![]() ,
,
которые будем называтьгипотезами.
Тогда по формуле полной вероятности
![]()
Если
событие А
произошло, то это может изменить
вероятности гипотез ![]() .
.
По
теореме умножения вероятностей
![]() ,
,
откуда
![]() .
.
Аналогично,
для остальных гипотез
![]()
Полученная
формула называется формулой
Байеса
(формулой
Бейеса).
Вероятности гипотез ![]() называютсяапостериорными
называютсяапостериорными
вероятностями,
тогда как ![]() –априорными
–априорными
вероятностями.
Пример.
В магазин поступила новая продукция с
трех предприятий. Процентный состав
этой продукции следующий: 20% – продукция
первого предприятия, 30% – продукция
второго предприятия, 50% – продукция
третьего предприятия; далее, 10% продукции
первого предприятия высшего сорта, на
втором предприятии – 5% и на третьем – 20%
продукции высшего сорта. Найти вероятность
того, что случайно купленная новая
продукция окажется высшего сорта.
Решение.
Обозначим через В
событие, заключающееся в том, что будет
куплена продукция высшего сорта, через
![]() обозначим
обозначим
события, заключающиеся в покупке
продукции, принадлежащей соответственно
первому, второму и третьему предприятиям.
Можно
применить формулу полной вероятности,
причем в наших обозначениях:

Подставляя
эти значения в формулу полной вероятности,
получим искомую вероятность:
![]()
Пример.
Один из трех стрелков вызывается на
линию огня и производит два выстрела.
Вероятность попадания в мишень при
одном выстреле для первого стрелка
равна 0,3, для второго – 0,5; для третьего
– 0,8. Мишень не поражена. Найти вероятность
того, что выстрелы произведены первым
стрелком.
Решение.
Возможны три гипотезы:
![]() –
–
на линию огня вызван первый стрелок,
![]() –
–
на линию огня вызван второй стрелок,
![]() –
–
на линию огня вызван третий стрелок.
Так
как вызов на линию огня любого стрелка
равновозможен, то ![]()
В
результате опыта наблюдалось событие
В – после произведенных выстрелов мишень
не поражена. Условные вероятности этого
события при сделанных гипотезах равны:
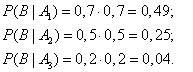
по
формуле Байеса находим вероятность
гипотезы ![]() после
после
опыта:
![]()
Пример.
На трех станках-автоматах обрабатываются
однотипные детали, поступающие после
обработки на общий конвейер. Первый
станок дает 2% брака, второй – 7%, третий
– 10%. Производительность первого станка
в 3 раза больше производительности
второго, а третьего – в 2 раза меньше,
чем второго.
а)
Каков процент брака на конвейере?
б)
Каковы доли деталей каждого станка
среди бракованных деталей на конвейере?
Решение.
Возьмем с конвейера наудачу одну деталь
и рассмотрим событие А – деталь
бракованная. Оно связано с гипотезами
относительно того, где была обработана
эта деталь: ![]() –
–
взятая наудачу деталь обработана на![]() -ом
-ом
станке,![]() .
.
Условные
вероятности (в условии задачи они даны
в форме процентов):
![]()
Зависимости
между производительностями станков
означают следующее:
![]() .
.
А
так как гипотезы образуют полную группу,
то ![]() .
.
Решив
полученную систему уравнений, найдем:
![]() .
.
а)
Полная вероятность того, что взятая
наудачу с конвейера деталь – бракованная:
![]() .
.
Другими
словами, в массе деталей, сходящих с
конвейера, брак составляет 4%.
б)
Пусть известно, что взятая наудачу
деталь – бракованная. Пользуясь формулой
Байеса, найдем условные вероятности
гипотез:
![]() ,
,
![]() ,
,
![]() .
.
Таким
образом, в общей массе бракованных
деталей на конвейере доля первого станка
составляет 33%, второго – 39%, третьего –
28%.
Практические
задания
Задание
1
Решение
задач по основным разделам теории
вероятности
Цель
– получение практических навыков в
решении задач по
разделам
теории вероятностей
Подготовка
к выполнению практического задания
Ознакомиться
с теоретическим материалом по данной
тематике, изучить содержание
теоретического, а также соответствующие
разделы в литературных источниках
Порядок
выполнения задания
Решить
5 задач согласно номеру варианта задания,
приведенного в таблице 1.
Варианты
исходных данных
Таблица
1
|
Вар-нт |
номер |
||||
|
1 |
1 |
48 |
49 |
96 |
97 |
|
2 |
2 |
47 |
50 |
95 |
98 |
|
3 |
3 |
46 |
51 |
94 |
99 |
|
4 |
4 |
45 |
52 |
93 |
100 |
|
5 |
5 |
44 |
53 |
92 |
101 |
|
6 |
6 |
43 |
54 |
91 |
102 |
|
7 |
7 |
42 |
55 |
90 |
103 |
|
8 |
8 |
41 |
56 |
89 |
104 |
|
9 |
10 |
40 |
57 |
88 |
105 |
|
10 |
11 |
39 |
58 |
87 |
106 |
|
11 |
12 |
38 |
59 |
86 |
107 |
|
12 |
13 |
37 |
60 |
85 |
108 |
|
13 |
14 |
36 |
61 |
84 |
109 |
|
14 |
15 |
35 |
62 |
83 |
110 |
|
15 |
16 |
34 |
63 |
82 |
111 |
|
16 |
17 |
33 |
64 |
81 |
112 |
|
17 |
18 |
32 |
65 |
80 |
113 |
|
18 |
19 |
31 |
66 |
79 |
114 |
|
19 |
9 |
30 |
67 |
78 |
115 |
|
20 |
20 |
29 |
68 |
77 |
116 |
|
21 |
21 |
28 |
69 |
76 |
117 |
|
22 |
22 |
27 |
70 |
75 |
118 |
|
23 |
23 |
26 |
71 |
74 |
119 |
|
24 |
24 |
25 |
72 |
73 |
120 |
Состав
отчета по заданию 1
5
решенных задач согласно номеру варианта.
Задачи
для самостоятельного решения
1..
Являются ли случаями следующие группы
событий: а) опыт — бросание монеты;
события: А1
—
появление герба; А2
—
появление цифры; б) опыт — бросание двух
монет; события: В1
—
появление двух гербов; В2
— появление
двух цифр; В3
—
появление одного герба и одной цифры;
в) опыт — бросание игральной кости;
события: С1
— появление
не более двух очков; С2
— появление
трех или четырех очков; С3
—появление
не менее пяти очков; г) опыт — выстрел
по мишени; события: D1
—
попадание; D2
—промах;
д) опыт — два выстрела по мишени; события:
Е0
—
ни одного попадания; Е1
—
одно попадание; Е2
—
два попадания; е) опыт — вынимание двух
карт из колоды; события: F1
— появление
двух красных карт; F2
—
появление двух черных карт?
2.
В урне A
белых и B
черных
шаров. Из урны вынимают наугад один шар.
Найти вероятность того, что этот шар —
белый.
3.
В урне A
белых
и B
черных
шаров. Из урны вынимают один шар и
откладывают в сторону. Этот шар оказался
белым. После этого из урны берут еще
один шар. Найти вероятность того, что
этот шар тоже будет белым.
4.
В урне A
белых
и B
черных
шаров. Из урны вынули один шар и, не
глядя, отложили в сторону. После этого
из урны взяли еще один шар. Он оказался
белым. Найти вероятность того, что первый
шар, отложенный в сторону, — тоже белый.
5.
Из урны, содержащей A
белых
и B
черных
шаров, вынимают один за другим все шары,
кроме одного. Найти вероятность того,
что последний оставшийся в урне шар
будет белым.
6.
Из
урны, в которой A
белых
шаров и B
черных, вынимают подряд все находящиеся
в ней шары. Найти вероятность того, что
вторым по порядку будет вынут белый
шар.
7.
В
урне A
белых и B
черных шаров (A
> 2).
Из урны вынимают сразу два шара. Найти
вероятность того, что оба шара будут
белыми.
8.
В урне A
белых и B
черных
шаров (A
> 2, B
> 3). Из урны вынимают сразу пять шаров.
Найти вероятность р
того,
что два из них будут белыми, а три черными.
9.
В партии, состоящей из X
изделий,
имеется I
дефектных.
Из партии выбирается для контроля I
изделий.
Найти вероятность р
того,
что из них ровно J
изделий
будут дефектными.
10.
Игральная кость бросается один раз.
Найти вероятность следующих событий:
А
— появление
четного числа очков; В
—
появление не менее 5 очков; С—
появление
не более 5 очков.
11.
Игральная кость бросается два раза.
Найти вероятность р
того,
что оба раза появится одинаковое число
очков.
12.
Бросаются одновременно две игральные
кости. Найти вероятности следующих
событий: А
—
сумма выпавших очков равна 8; В
—
произведение выпавших очков равно 8;С—
сумма
выпавших очков больше, чем их произведение.
13.
Бросаются две монеты. Какое из событий
является более вероятным: А
— монеты
лягут одинаковыми сторонами; В
— монеты
лягут разными сторонами?
14.
В урне A
белых
и B
черных
шаров (A
> 2;
B
> 2).
Из урны вынимают одновременно два шара.
Какое событие более вероятно: А
—
шары одного цвета; В
— шары
разных цветов?
15.
Трое игроков играют в карты. Каждому из
них сдано по 10 карт и две карты оставлены
в прикупе. Один из игроков видит, что у
него на руках 6 карт бубновой масти и 4
— не бубновой. Он сбрасывает две карты
из этих четырех и берет себе прикуп.
Найти вероятность того, что он прикупит
две бубновые карты.
16.
Из урны, содержащей п
перенумерованных
шаров, наугад вынимают один за другим
все находящиеся в ней шары. Найти
вероятность того, что номера вынутых
шаров будут идти по порядку: 1, 2,…, п.
17.
Та же урна, что и в предыдущей задаче,
но каждый шар после вынимания вкладывается
обратно и перемешивается с другими, а
его номер записывается. Найти вероятность
того, что будет записана естественная
последовательность номеров: 1, 2,…, п.
18.
Полная колода карт (52 листа) делится
наугад на две равные пачки по 26 листов.
Найти вероятности следующих событий:
А
— в
каждой из пачек окажется по два туза; В
—
в одной из пачек не будет ни одного туза,
а в другой — все четыре; С—в
одной
из пачек будет один туз, а в другой —
три.
19.
В
розыгрыше первенства по баскетболу
участвуют 18 команд, из которых случайным
образом формируются две группы по 9
команд в каждой. Среди участников
соревнований имеется 5 команд
экстра-класса.
Найти вероятности следующих событий:
А
—все
команды экстра-класса попадут в одну и
ту же группу; В
—
две команды экстра-класса попадут в
одну из групп, а три — в другую.
20.
На
девяти карточках написаны цифры: 0, 1, 2,
3, 4, 5, 6, 7, 8. Две из них вынимаются наугад
и укладываются на стол в порядке
появления, затем читается полученное
число, например 07(семь), 14 (четырнадцать)
и т. п. Найти вероятность того, что число
будет четным.
21.
На
пяти карточках написаны цифры: 1, 2, 3, 4,
5. Две из них, одна за другой, вынимаются.
Найти вероятность того, что число на
второй карточке будет больше, чем на
первой.
22.
Тот
же вопрос, что в задаче 21, но первая
карточка после вынимания кладется
обратно и перемешивается с остальными,
а стоящее на ней число записывается.
23.
В урне A
белых,
B
черных
и C
красных шаров. Из урны вынимают один за
другим все находящиеся в ней шары и
записывают их цвета. Найти вероятность
того, что в этом списке белый цвет
появится раньше черного.
24.
Имеется две урны: в первой A
белых
и B
черных
шаров; во второй C
белых
и D
черных.
Из каждой урны вынимается по шару. Найти
вероятность того, что оба шара будут
белыми.
25.
В условиях задачи 24 найти вероятность
того, что вынутые шары будут разных
цветов.
26.
В барабане револьвера семь гнезд, из
них в пяти заложены патроны, а два
оставлены пустыми. Барабан приводится
во вращение, в результате чего против
ствола случайным образом оказывается
одно из гнезд. После этого нажимается
спусковой крючок; если ячейка была
пустая, выстрела не происходит. Найти
вероятность р
того,
что, повторив такой опыт два раза подряд,
мы оба раза не выстрелим.
27.
В тех же условиях (см. задачу 26)найти
вероятность того, что оба раза выстрел
произойдет.
28.
В
урне имеется А; шаров, помеченных номерами
1, 2, …, к
Из
урны I
раз
вынимается по одному шару (I
<к), номер
шара записывается и шар кладется обратно
в урну. Найти вероятность р
того,
что все записанные номера будут различны.
29.
Из
пяти букв разрезной азбуки составлено
слово «книга». Ребенок, не умеющий
читать, рассыпал эти буквы и затем собрал
в произвольном порядке. Найти вероятность
р
того,
что у него снова получилось слово
«книга».
30.
Из букв разрезной азбуки составлено
слово «ананас». Ребенок, не умеющий
читать, рассыпал эти буквы и затем собрал
в произвольном порядке. Найти вероятность
р
того,
что у него снова слово «ананас
31.
Из
полной колоды карт (52 листа, 4 масти)
вынимается сразу несколько карт. Сколько
карт нужно вынуть для того, чтобы с
вероятностью, большей чем 0,50, утверждать,
что среди них будут карты одной и той
же масти?
32.
N
человек
случайным образом рассаживаются за
круглым столом (N
> 2).
Найти вероятность р
того,
что два фиксированных лица А
и
В
окажутся
рядом.
33.
Та же задача (см 32), но стол прямоугольный,
и N
человек
рассаживаются случайно вдоль одной из
его сторон.
34.
На бочонках лото написаны числа от 1 до
N.
Из
этих N
бочонков
случайно выбираются два. Найти вероятность
того что на обоих бочонках написаны
числа, меньшие чем k
(2<k<N)-
35.
На
бочонках лото написаны числа от 1 до N.
Из
этих N
бочонков
случайно выбираются два. Найти вероятность
того что на одном из бочонков написано
число, большее чем k,
а
на другом — меньшее чем k.
(2<k<N)
36.
Батарея из М
орудий
ведет огонь по группе, состоящей из N
целей
(М
< N). Орудия
выбирают себе цели последовательно,
случайным образом, при условии, что
никакие два орудия стрелять по одной
цели не могут. Найти вероятность р
того,
что будут обстреляны цели с номерами
1, 2,…, М.
37..
Батарея, состоящая из к
орудий,
ведет огонь по группе, состоящей из I
самолетов
(к
< 2).
Каждое орудие выбирает себе цель случайно
и независимо от других. Найти вероятность
того, что все к
орудий
будут стрелять по одной и той же цели.
38.
В условиях предыдущей задачи найти
вероятность того, что все орудия будут
стрелять по разным целям.
39.
Четыре шарика случайным образом
разбрасываются по четырем лункам; каждый
шарик попадает в ту или другую лунку с
одинаковой вероятностью и независимо
от других (препятствий к попаданию в
одну и ту же лунку нескольких шариков
нет). Найти вероятность того, что в одной
из лунок окажется три шарика, в другой
— один, а в двух остальных лунках шариков
не будет.
40.
Маша поссорилась с Петей и не хочет
ехать с ним в одном автобусе. От общежития
до института с 7 до 8 отправляется 5
автобусов. Не успевший на эти автобусы
опаздывает на лекцию. Сколькими способами
Маша и Петя могут доехать до института
на разных автобусах и не опоздать на
лекцию?
41.
В информационно-технологическом
управлении банка работает 3 аналитика,
10 программистов и 20 инженеров. Для
сверхурочной в праздничный день начальник
управления должен выделить одного
сотрудника. Сколькими способами это
можно сделать?
42.
Начальник службы безопасности банка
должен ежедневно расставлять 10 охранников
по 10 постам. Сколькими способами это
можно сделать?
43.
Новый президент банка должен назначить
2 новых вице президентов из числа 10
директоров. Сколькими способами это
можно сделать?
44.
Одна из воюющих сторон захватил 12, а
другая – 15 пленных. Сколькими способами
можно обменять 7 военнопленных?
45.
Петя и Маша коллекционируют видеодиски.
У Пети есть 30 комедий, 80 боевиков и 7
мелодрам, у Маши – 20 комедий, 5 боевиков
и 90 мелодрам. Сколькими способами Петя
и Маша могут обменяться 3 комедиями, 2
боевиками и 1 мелодрамой?
46.
В условиях задачи 45 сколькими способами
Петя и Маша могут обменяться 3 мелодрамами
и 5 комедиями?
47.
В условиях задачи 45 сколькими способами
Петя и Маша могут обменяться 2 боевиками
и 7 комедиями.
48.
Одна из воюющих сторон захватил 15, а
другая – 16 пленных. Сколькими способами
можно обменять 5 военнопленных?
49.
Сколько автомобилей можно зарегистрировать
в 1 городе, если номер имеет 3 цифры и 3
буквы (только те чьё написание совпадает
с латинскими – А,В,Е,К,М,Н,О,Р,С,Т,У,Х)?
50.
Одна из воюющих сторон захватил 14, а
другая – 17 пленных. Сколькими способами
можно обменять 6 военнопленных?
51.
Сколько различных слов можно составить
переставляя буквы в слове «мама»?
52.
В корзине 3 красных и 7 зеленых яблок. Из
нее вынимают одно яблоко. Найти вероятность
того, что оно будет красным.
53.
В корзине 3 красных и 7 зеленых яблок. Из
нее вынули и отложили в сторону одно
зеленое яблоко. После чего из корзины
вынимают еще 1 яблоко. Какова вероятность
того, что это яблоко будет зеленым?
54.
В партии, состоящей из 1000 изделий, 4 имеют
дефекты. Для контроля выбирают партию
из 100 изделий. Какова вероятность ТОО,
что в контрольной партии не окажется
бракованных?
56.В
80-е годы в СССР была популярна игра
«спортлото 5 из 36». Играющий отмечал на
карточке 5 чисел от 1 до 36 и получал призы
различного достоинства если он угадывал
разное число чисел, объявленных тиражной
комиссией. Найти вероятность того, что
игрок не угадал ни одного числа.
57.В
80-е годы в СССР была популярна игра
«спортлото 5 из 36». Играющий отмечал на
карточке 5 чисел от 1 до 36 и получал призы
различного достоинства если он угадывал
разное число чисел, объявленных тиражной
комиссией. Найти вероятность того, что
игрок угадал одно число.
58.В
80-е годы в СССР была популярна игра
«спортлото 5 из 36». Играющий отмечал на
карточке 5 чисел от 1 до 36 и получал призы
различного достоинства если он угадывал
разное число чисел, объявленных тиражной
комиссией. Найти вероятность того, что
игрок угадал 3 числа.
59.В
80-е годы в СССР была популярна игра
«спортлото 5 из 36». Играющий отмечал на
карточке 5 чисел от 1 до 36 и получал призы
различного достоинства если он угадывал
разное число чисел, объявленных тиражной
комиссией. Найти вероятность того, что
игрок не угадал все 5 чисел.
60.В
80-е годы в СССР была популярна игра
«спортлото 6 из 49». Играющий отмечал на
карточке 6 чисел от 1 до 49 и получал призы
различного достоинства если он угадывал
разное число чисел, объявленных тиражной
комиссией. Найти вероятность того, что
игрок угадал 2 числа.
61.
В 80-е годы в СССР была популярна игра
«спортлото 6 из 49». Играющий отмечал на
карточке 6 чисел от 1 до 49 и получал призы
различного достоинства если он угадывал
разное число чисел, объявленных тиражной
комиссией. Найти вероятность того, что
игрок не угадал ни одного числа.
62.В
80-е годы в СССР была популярна игра
«спортлото 6 из 49». Играющий отмечал на
карточке 6 чисел от 1 до 49 и получал призы
различного достоинства если он угадывал
разное число чисел, объявленных тиражной
комиссией. Найти вероятность того, что
игрок угадал все 6 чисел.
63.
В партии, состоящей из 1000 изделий, 4 имеют
дефекты. Для контроля выбирают партию
из 100 изделий. Какова вероятность ТОО,
что в контрольной партии окажется
только 1 бракованная?
64.
Сколько различных слов можно составить
переставляя буквы в слове «книга»?
65.
Сколько различных слов можно составить
переставляя буквы в слове «ананас»?
66.
В лифт вошло 6 человек, а общежитие имеет
7 этажей. Какова вероятность того что
все 6 человек выйдут на одном этаже?
67.
В лифт вошло 6 человек, здание имеет 7
этажей. Какова вероятность того что все
6 человек выйдут на разных этажах?
68.
Во время грозы на участке между 40 и 79 км
линии электропередачи произошел обрыв
провода. Считая что обрыв одинаково
возможен в любой точке, найти вероятность
того что обрыв произошел между 40-м и
45-м километрами.
69.
На 200 километровом участке газопровода
происходит утечка газа между компрессорными
станциями А и В, которая одинаково
возможна в любой точке трубопровода.
какова вероятность того что утечка
происходит не далее 20 км от А
70.
На 200 километровом участке газопровода
происходит утечка газа между компрессорными
станциями А и В, которая одинаково
возможна в любой точке трубопровода.
какова вероятность того что утечка
происходит ближе к А, чем к В
71.
Радар инспектора ДПС имеет точность 10
кмчас и округляет в ближайшую сторону.
Что происходит чаще – округление в
пользу водителя или инспектора?
72.
Маша тратит на дорогу в институт от 40
до 50 минут, причем любое время в этом
промежутке является равновероятным.
Какова вероятность того что она потратит
на дорогу от 45 до 50 минут.
73.
Петя и Маша договорились встретиться
у памятника Пушкину с 12 до 13 часов, однако
никто не смог указать точно время
прихода. Они договорились ждать друг
друга 15 минут. Какова вероятность их
встречи?
74.
Рыбаки поймали в пруду 120 рыб, из них 10
оказались окольцованными. Какова
вероятность поймать окольцованную
рыбу?
75.
Из корзины содержащей 3 красных и 7
зеленых яблок вынимают все яблоки по
очереди. какова вероятность того что
2-е яблоко окажется красным?
76.
Из корзины содержащей 3 красных и 7
зеленых яблок вынимают все яблоки по
очереди. какова вероятность того что
последнее яблоко окажется зеленым?
77.
Студенты считают что из 50 билетов 10
являются «хорошими». Петя и Маша по
очереди тянут по одному билету. Какова
вероятность того, что Маше достался
«хороший» билет?
78.
Студенты считают что из 50 билетов 10
являются «хорошими». Петя и Маша по
очереди тянут по одному билету. Какова
вероятность того, что им обоим достался
«хороший» билет?
79.
Маша пришла на экзамен зная ответы на
20 вопросов программы из 25. Профессор
задает 3 вопроса. Какова вероятность
того что Маша ответит на 3 вопроса?
80.
Маша пришла на экзамен зная ответы на
20 вопросов программы из 25. Профессор
задает 3 вопроса. Какова вероятность
того что Маша не ответит ни на один
вопрос?
81.
Маша пришла на экзамен зная ответы на
20 вопросов программы из 25. Профессор
задает 3 вопроса. Какова вероятность
того что Маша ответит на 1 вопрос?
82.
Статистика запросов кредитов в банке
такова: 10% – гос. органы, 20% – другие банки,
остальное – физические лица. Вероятность
невозвращения кредитов соответственно
0.01, 0.05 и 0.2. Какая доля кредитов не
возвращается?
83.
вероятность того что недельный оборот
торговца мороженым превысит 2000 руб.
составляет 80% при ясной погоде, 50 % при
переменной облачности и 10% при дождливой
погоде. Какова вероятность что оборот
превысит 2000 руб. если вероятность ясной
погоды – 20%, а переменной облачности и
дождей – по 40%.
84.
В урне А белых (б) и В
черных
(ч) шаров. Из урны вынимают (одновременно
или последовательно) два шара. Найти
вероятность того, что оба шара будут
белыми.
85.
В урне А
белых
и В
черных
шаров. Из урны вынимается один шар,
отмечается его цвет и шар возвращается
в урну. После этого из урны берется еще
один шар. Найти вероятность того, что
оба вынутые шара будут белыми.
86.
В
урне А
белых
и В
черных
шаров. Из урны вынимаются сразу два
шара. Найти вероятность того, что эти
шары будут разных цветов.
87.
В
урне А
белых
и В
черных
шаров. Из урны вынимается один шар,
отмечается его цвет и шар возвращается
в урну. После этого из урны берется еще
один шар. Найти вероятность того, что
эти шары будут разных цветов.
88.
Имеется
коробка с девятью новыми теннисными
мячами. Для игры берут три мяча; после
игры их кладут обратно. При выборе мячей
игранные от неигранных не отличают.
Какова вероятность того, что после трех
игр в коробке не останется неигранных
мячей?
89.
Уходя из квартиры, N
гостей,
имеющих одинаковые размеры обуви,
надевают калоши в темноте. Каждый из
них может отличить правую калошу от
левой, но не может отличить свою от
чужой. Найти вероятность того что
каждый
гость наденет свои калоши;
90.
Уходя из квартиры, N
гостей,
имеющих одинаковые размеры обуви,
надевают калоши в темноте. Каждый из
них может отличить правую калошу от
левой, но не может отличить свою от
чужой. Найти вероятность того что
каждый
гость, наденет калоши, относящиеся к
одной паре (может быть и не свои).
91.
В условиях задачи 90найти вероятность
того что каждый уйдет в своих калошах
если
гости не могут отличить правой калоши
от левой и просто берут первые попавшиеся
две калоши.
92.
Ведется стрельба по самолету, уязвимыми
частями которого являются два двигателя
и кабина пилота. Для того чтобы поразить
(вывести из строя) самолет, достаточно
поразить оба двигателя вместе или кабину
пилота. При данных условиях стрельбы
вероятность поражения первого двигателя
равна p1
второго
двигателя р2,
кабины
пилота р3.
Части
самолета поражаются независимо друг
от друга. Найти вероятность того, что
самолет будет поражен.
93.
Два стрелка, независимо один от другого,
делают по два выстрела (каждый по своей
мишени). Вероятность попадания в мишень
при одном выстреле для первого стрелка
p1
для
второго р2.
Выигравшим
соревнование считается тот стрелок, в
мишени которого будет больше пробоин.
Найти вероятность Рх
того,
что выиграет первый стрелок.
94.
за космическим объектом, объект
обнаруживается с вероятностью р.
Обнаружение
объекта в каждом цикле происходит
независимо от других. Найти вероятность
того, что при п
циклах
объект будет обнаружен.
95.
32 буквы русского алфавита написаны на
карточках разрезной азбуки. Пять карточек
вынимаются наугад одна за другой и
укладываются на стол в порядке появления.
Найти вероятность того, что получится
слово «конец».
96.
Два шарика разбрасываются случайно и
независимо друг от друга по четырем
ячейкам, расположенным одна за другой
по прямой линии. Каждый шарик с одинаковой
вероятностью 1/4 попадает в каждую ячейку.
Найти вероятность того, что шарики
попадут в соседние ячейки.
97.
Производится стрельба по самолету
зажигательными снарядами. Горючее на
самолете сосредоточено в четырех баках,
расположенных в фюзеляже один за другим.
Площади баков одинаковы. Для того чтобы
зажечь самолет, достаточно попасть
двумя снарядами либо в один и тот же
бак, либо в соседние баки. Известно, что
в область баков попало два снаряда.
Найти вероятность того, что самолет
загорится.
98.
Из
полной колоды карт (52 листа) вынимаются
сразу четыре карты. Найти вероятность
того, что все эти четыре карты будут
разных мастей.
99.
Из
полной колоды карт (52 листа) вынимаются
сразу четыре карты, но каждая карта
после вынимания возвращается в колоду.
Найти вероятность того, что все эти
четыре карты будут разных мастей..
100.
При
включении зажигания двигатель начинает
работать с вероятностью р.
Найти вероятность того, что двигатель
начнет работать при втором включении
зажигания;
101.
Прибор может работать в двух режимах:
1) нормальном и 2) ненормальном. Нормальный
режим наблюдается в 80 % всех случаев
работы прибора; ненормальный — в 20 %.
Вероятность выхода прибора из строя за
время t
в
нормальном режиме равна 0,1; в ненормальном
— 0,7. Найти полную вероятность р
выхода
прибора из строя.
102.
Магазин получает товар от 3 поставщиков:
55% от 1-го, 20 от 2-го и 25% от 3-го. Доля брака
составляет 5, 6 и 8 процентов соответственно.
Какова вероятность того что купленный
бракованный товар поступил от второго
поставщика.
103.Поток
автомобилей мимо АЗС состоит на 60% из
грузовых и на 40% из легковых автомобилей.
Какова вероятность нахождения на АЗС
грузового автомобиля, если вероятность
его заправки 0.1, а легкового – 0.3
104.
Поток автомобилей мимо АЗС состоит на
60% из грузовых и на 40% из легковых
автомобилей. Какова вероятность
нахождения на АЗС грузового автомобиля,
если вероятность его заправки 0.1, а
легкового – 0.3
105.
Магазин получает товар от 3 поставщиков:
55% от 1-го, 20 от 2-го и 25% от 3-го. Доля брака
составляет 5, 6 и 8 процентов соответственно.
Какова вероятность того что купленный
бракованный товар поступил от 1-го
поставщика.
106.
32 буквы русского алфавита написаны на
карточках разрезной азбуки. Пять карточек
вынимаются наугад одна за другой и
укладываются на стол в порядке появления.
Найти вероятность того, что получится
слово «книга».
107.
Магазин получает товар от 3 поставщиков:
55% от 1-го, 20 от 2-го и 25% от 3-го. Доля брака
составляет 5, 6 и 8 процентов соответственно.
Какова вероятность того что купленный
бракованный товар поступил от 1-го
поставщика.
108.
Два шарика разбрасываются случайно и
независимо друг от друга по четырем
ячейкам, расположенным одна за другой
по прямой линии. Каждый шарик с одинаковой
вероятностью 1/4 попадает в каждую ячейку.
Найти вероятность того, что 2 шарика
попадут в одну ячейку
109.
При включении зажигания двигатель
начинает работать с вероятностью р.
Найти вероятность того, что двигатель
начнет работать при втором включении
зажигания;
110.
Производится стрельба по самолету
зажигательными снарядами. Горючее на
самолете сосредоточено в четырех баках,
расположенных в фюзеляже один за другим.
Площади баков одинаковы. Для того чтобы
зажечь самолет, достаточно попасть
двумя снарядами в один и тот же бак.
Известно, что в область баков попало
два снаряда. Найти вероятность того,
что самолет загорится
111.
Производится стрельба по самолету
зажигательными снарядами. Горючее на
самолете сосредоточено в четырех баках,
расположенных в фюзеляже один за другим.
Площади баков одинаковы. Для того чтобы
зажечь самолет, достаточно попасть
двумя снарядами в соседние баки. Известно,
что в область баков попало два снаряда.
Найти вероятность того, что самолет
загорится
112.В
урне А
белых
и В
черных
шаров. Из урны вынимается один шар,
отмечается его цвет и шар возвращается
в урну. После этого из урны берется еще
один шар. Найти вероятность того, что
оба вынутые шара будут белыми.
113.
В
урне А
белых
и В
черных
шаров. Из урны вынимаются сразу два
шара. Найти вероятность того, что эти
шары будут разных цветов.
114.
Два шарика разбрасываются случайно и
независимо друг от друга по четырем
ячейкам, расположенным одна за другой
по прямой линии. Каждый шарик с одинаковой
вероятностью 1/4 попадает в каждую ячейку.
Найти вероятность того, что шарики
попадут в соседние ячейки.
115.
Маша пришла на экзамен зная ответы на
20 вопросов программы из 25. Профессор
задает 3 вопроса. Какова вероятность
того что Маша ответит на 2 вопроса?
116.
Студенты считают что из 50 билетов 10
являются «хорошими». Петя и Маша по
очереди тянут по одному билету. Какова
вероятность того, что им обоим достался
«хороший» билет?
117.
Статистика запросов кредитов в банке
такова: 10% – гос. органы, 20% – другие банки,
остальное – физические лица. Вероятность
невозвращения кредитов соответственно
0.01, 0.05 и 0.2. Какая доля кредитов не
возвращается?
118.
32 буквы русского алфавита написаны на
карточках разрезной азбуки. Пять карточек
вынимаются наугад одна за другой и
укладываются на стол в порядке появления.
Найти вероятность того, что получится
слово «конец».
119
Статистика запросов кредитов в банке
такова: 10% – гос. органы, 20% – другие банки,
остальное – физические лица. Вероятность
невозвращения кредитов соответственно
0.01, 0.05 и 0.2. Какая доля кредитов не
возвращается?
120.
вероятность того что недельный оборот
торговца мороженым превысит 2000 руб.
составляет 80% при ясной погоде, 50 % при
переменной облачности и 10% при дождливой
погоде. Какова вероятность что оборот
превысит 2000 руб. если вероятность ясной
погоды – 20%, а переменной облачности и
дождей – по 40%.

Теорема Байеса (или формула Байеса) — одна из основных теорем элементарной теории вероятностей, которая позволяет определить вероятность события при условии, что произошло другое статистически взаимозависимое с ним событие. Другими словами, по формуле Байеса можно уточнить вероятность какого-либо события, взяв в расчёт как ранее известную информацию, так и данные новых наблюдений. Формула Байеса может быть выведена из основных аксиом теории вероятностей, в частности из условной вероятности. Особенность теоремы Байеса заключается в том, что для её практического применения требуется большое количество расчётов, вычислений, поэтому байесовские оценки стали активно использовать только после революции в компьютерных и сетевых технологиях. На сегодняшний день активно применяется в машинном обучении и технологиях искусственного интеллекта.
При возникновении теоремы Байеса вероятности, используемые в теореме, подвергались целому ряду вероятностных интерпретаций. В одной из таких интерпретаций говорилось, что вывод формулы напрямую связан с применением особого подхода к статистическому анализу. Если использовать байесовскую интерпретацию вероятности, то теорема показывает, как личный уровень доверия может кардинально измениться вследствие количества наступивших событий. В этом заключаются выводы Байеса, которые стали основополагающими для байесовской статистики. Однако теорема не только используется в байесовском анализе, но и активно применяется для большого ряда других расчётов.
Психологические эксперименты[1] показали, что люди часто неверно оценивают реальную (математически верную) вероятность события, основываясь на некоем личном полученном опыте (апостериорная вероятность), поскольку игнорируют саму вероятность предположения (априорная вероятность). Поэтому правильный результат по формуле Байеса может сильно отличаться от интуитивно ожидаемого.
Теорема Байеса названа в честь её автора Томаса Байеса (1702—1761) — английского математика и священника, который первым предложил использование теоремы для корректировки убеждений, основываясь на обновлённых данных. Его работа «An Essay towards solving a Problem in the Doctrine of Chances» впервые опубликована в 1763 году[2], через 2 года после смерти автора. До того, как посмертная работа Байеса была принята и прочитана в Королевском обществе, она была значительно отредактирована и обновлена Ричардом Прайсом. Однако эти идеи не предавались публичной огласке до тех пор, пока не были вновь открыты и развиты Пьером-Симоном Лапласом, впервые опубликовавшим современную формулировку теоремы в своей книге 1812 года «Аналитическая теория вероятностей».
Сэр Гарольд Джеффрис писал, что теорема Байеса «для теории вероятности то же, что теорема Пифагора для геометрии»[3].
Формулировка[править | править код]
Доказательство[править | править код]
Формула Байеса вытекает из определения условной вероятности. Вероятность совместного события 
Следовательно 
Вычисление P(B)[править | править код]
В задачах и статистических приложениях 
,
где вероятности под знаком суммы известны или допускают экспериментальную оценку.
В этом случае формула Байеса записывается так:
«Физический смысл» и терминология[править | править код]
Формула Байеса позволяет «переставить причину и следствие»: по известному факту события вычислить вероятность того, что оно было вызвано данной причиной. При этом необходимо понимать, для применения теоремы причинно-следственная связь между 

События, отражающие действие «причин», в данном случае называют гипотезами, так как они — предполагаемые события, повлёкшие данное. Безусловную вероятность справедливости гипотезы называют априорной (насколько вероятна причина вообще), а условную — с учётом факта произошедшего события — апостериорной (насколько вероятна причина оказалась с учётом данных о событии).
Примеры[править | править код]
Пример 1[править | править код]
Пусть событие 

Очевидно, что вероятность 
Как следствие, апостериорная вероятность, что в баке нет топлива, если машина не заводится, то есть 

Пример 2[править | править код]
Пусть вероятность брака у первого рабочего 





Событие 





По формуле полной вероятности
По формуле Байеса получим:
Пример 3[править | править код]

Древовидная диаграмма демонстрирует частотный пример. R, C, P и P c чёрточкой — это события, обозначающие, что жук является редким, обычным, с узором и без узора. Проценты в скобках вычисляются. Отметим, что значения трёх независимых событий даны, поэтому возможно вычислить обратное дерево (смотрите на график выше).
Энтомолог предполагает, что жук может относиться к редкому подвиду жуков, так как у него на корпусе есть узор. В редком подвиде 98 % жуков имеют узор, или P(узор | редкий) = 0,98. Среди обычных жуков только 5 % имеют узор: P(узор | обычный) = 0,05. Редкого вида жуков насчитывается лишь 0,1 % среди всей популяции: P(редкий) = 0,001. Какова вероятность того, что жук, имеющий узор, относится к редкому подвиду, то есть, чему равно P(редкий | узор)?
Из расширенной теоремы Байеса получаем (любой жук может относиться либо к редким, либо к обычным):
![{displaystyle {begin{aligned}P({text{редкий}}mid {text{узор}})&={frac {P({text{узор}}mid {text{редкий}})times P({text{редкий}})}{P({text{узор}}mid {text{редкий}})times P({text{редкий}}),+,P({text{узор}}mid {text{обычный}})times P({text{обычный}})}}\[8pt]&={frac {0{,}98times 0{,}001}{0{,}98times 0{,}001+0{,}05times 0{,}999}}\[8pt]&approx 0{,}019.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99f473425064214488140f990a52c6a32b78e9a2)
Пример 4 — парадокс теоремы Байеса[править | править код]
Пусть существует заболевание с частотой распространения среди населения 0,001 и метод диагностического обследования, который с вероятностью 0,9 выявляет больного, но при этом имеет вероятность 0,01 ложноположительного результата — ошибочного выявления заболевания у здорового человека (подробнее…). Найти вероятность того, что человек здоров, если он был признан больным при обследовании.
Обозначим событие что обследование показало, человек болен как «болен» с кавычками, болен — событие, что человек действительно больной, здоров — событие, что человек действительно здоров. Тогда заданные условия переписываются следующим образом:





Вероятность того, что человек здоров, если он был признан больным равна условной вероятности:

Чтобы её найти, вычислим сначала полную вероятность признания больным:

Вероятность, что человек здоров при результате «болен»:

Таким образом, 91,7 % людей, у которых обследование показало результат «болен», на самом деле здоровые люди. Причина этого в том, что по условию задачи вероятность ложноположительного результата хоть и мала, но на порядок больше доли больных в обследуемой группе людей.
Если ошибочные результаты обследования можно считать случайными, то повторное обследование того же человека будет давать независимый от первого результат. В этом случае для уменьшения доли ложноположительных результатов имеет смысл провести повторное обследование людей, получивших результат «болен». Вероятность того, что человек здоров после получения повторного результата «болен», также можно вычислить по формуле Байеса:

Варианты интерпретации вероятностей в теореме Байеса[править | править код]
Математически теорема Байеса показывает взаимоотношения между вероятностью события A и вероятностью события B, P(A) и P(B), условной вероятности наступления события А при существующем B и наступлении события B при существующем A, P(A | B) и P(B | A).
В общей форме формула Байеса выглядит следующим образом:

Значение выражения зависит от того, как интерпретируются вероятности в данной формуле.
Интерпретация Байеса[править | править код]
В интерпретации Байеса вероятность измеряет уровень доверия. Теорема Байеса связывает воедино доверие предположению до и после принятия во внимание очевидных доказательств. Например, кто-то предположил, что при подкидывании монетки она будет приземляться в 2 раза чаще решкой вверх, а орлом вниз. Первоначально степень доверия, что такое событие случится, монета упадёт именно так — 50 %. Уровень доверия может увеличиться до 70 %, если предположение будет подтверждено доказательством.[прояснить]
Для предположения (гипотезы) A и доказательства B
- P(A) — априорная вероятность гипотезы A, первоначальный уровень доверия предположению A;
- P(A | B) — апостериорная вероятность гипотезы A при наступлении события B;
- отношение P(B | A)/P(B) показывает, как событие B помогает изменить уровень доверия предположению A.
Частотная интерпретация[править | править код]

Иллюстрация частотной интерпретации
В частотной интерпретации теорема Байеса исчисляет доли определённых результатов события. Предположим, что некий эксперимент проводился много раз и в некоторых случаях приводил к результатам А и/или B. Тогда:
- P(A) — доля случаев, когда эксперимент привёл к результату A.
- P(B) — доля случаев, когда эксперимент привёл к результату B.
- P(B | A) — доля случаев с результатом B среди случаев с результатом А.
- P(A | B) — доля случаев с результатом A среди случаев с результатом B.
Роль теоремы Байеса лучше всего можно понять из древовидных диаграмм, представленных справа. Диаграммы демонстрируют различный порядок распределения событий по наличию или отсутствию результатов A и B. Теорема Байеса выступает как связующее звено этих распределений.
Формы[править | править код]
События[править | править код]
Простая форма[править | править код]
Для событий A и B, при условии, что P(B) ≠ 0,
Во многих дополнениях к теореме Байеса указывается, что событие B известно и нужно понять, как знание о событии B влияет на уверенность в том, что произойдёт событие A. В таком случае знаменатель последнего выражения — вероятность наступления события B — известен; мы хотим изменить A. Теорема Байеса показывает, что апостериорные вероятности пропорциональны числителю:
(пропорциональность A для данного B).
Если говорить кратко: апостериорная вероятность пропорциональна априорной вероятности (смотри Lee, 2012, Глава 1).
Если события A1, A2, …, взаимоисключающие и исчерпывающие, то есть возможно только одно из событий, одновременно два события не могут случиться вместе, мы можем определить коэффициент пропорциональности, ориентируясь на то, что их вероятности в сумме должны составлять единицу. Например, для данного события A — само событие A и его противоположность ¬A взаимоисключающие и исчерпывающие. Обозначая коэффициент пропорциональности как C мы имеем:
и
.
Объединив эти две формулы, мы получим, что:
Расширенная форма[править | править код]
Часто пространство событий (таких как {Aj}) определённо в терминах P(Aj) и P(B | Aj). Именно в этом случае полезно определить P(B), применив формулу полной вероятности:
В частности
.
Непрерывные случайные величины[править | править код]

Диаграмма отображает смысл теоремы Байеса и применима к пространству событий, образованного непрерывными случайными величинами X и Y. Заметим, что по теореме Байеса для каждой точки в области существуют требования. На практике, эти требования могут быть представлены в параметрическом виде, с помощью обозначения плотности распределения как функция от x и y.
Рассмотрим пространство элементарных событий Ω, образованного двумя величинами X и Y. В принципе, теорема Байеса применяется к событиям A = {X = x} и B = {Y = y}. Однако выражения становятся равны 0 в точках, в которых переменная имеет конечную плотность вероятности. Для того, чтобы с пользой продолжать использовать теорему Байеса, можно её сформулировать в терминах подходящих плотностей (смотрите Вывод формул).
Простая форма[править | править код]
Если X непрерывна и Y дискретна, то
Если X дискретна и Y непрерывна,
Если как X, так и Y непрерывны,
Расширенная форма[править | править код]

Диаграмма, показывающая, как пространство событий, образованное непрерывными случайными величинами X и Y, часто определяется.
Непрерывное пространство событий часто определяется как числитель условий A. Непрерывное пространство событий часто представляют как числитель. В дальнейшем полезно избавиться от знаменателя, используя формулу общей вероятности. Для ‘fY(y), это становится интегралом:
Правило Байеса[править | править код]
Правило Байеса — это преобразованная теорема Байеса:
где
Это называется правилом Байеса или отношением правдоподобия. Разница в вероятности наступления двух событий — это просто отношение вероятностей этих двух событий. Таким образом,
,
,
Вывод формул[править | править код]
Для событий[править | править код]
Теорема Байеса может быть получена из определения вероятности:
Для случайных переменных[править | править код]
Для двух непрерывных случайных величин X и Y теорема Байеса может быть аналогично выведена из определения условного распределения:
См. также[править | править код]
- Байесовская фильтрация спама
- Байесовское программирование
- Байесовская сеть доверия
- Байесовская вероятность
- Некорректное априорное распределение
- Парадокс Монти Холла
Примечания[править | править код]
- ↑ Kahneman, et al, 2005, pp. 153—160.
- ↑ Bayes, Thomas, and Price, Richard (1763). «An Essay towards solving a Problem in the Doctrine of Chance. By the late Rev. Mr. Bayes, communicated by Mr. Price, in a letter to John Canton, M. A. and F. R. S.». Philosophical Transactions of the Royal Society of London 53: 370—418. Дата обращения: 21 апреля 2010. Архивировано из оригинала 10 апреля 2011 года.
- ↑ Jeffreys, Harold (1973), Scientific Inference (3rd ed.), Cambridge University Press, p. 31, ISBN 978-0-521-18078-8
Литература[править | править код]
- Гмурман В. Е. Теория вероятностей и математическая статистика, — М.: Высшее образование. 2005
- Judgment under Uncertainty: Heuristics and Biases / Daniel Kahneman, et al. — 21st. — Cambridge University Press, 2005. — 555 p. — ISBN 978-0-521-28414-1.
- Элиезер Юдковски. Наглядное объяснение теоремы Байеса
Для дальнейшего изучения[править | править код]
- McGrayne, Sharon Bertsch. The Theory That Would Not Die: How Bayes’ Rule Cracked the Enigma Code, Hunted Down Russian Submarines & Emerged Triumphant from Two Centuries of Controversy (англ.). — Yale University Press, 2011. — ISBN 978-0-300-18822-6.
- Andrew Gelman, John B. Carlin, Hal S. Stern, and Donald B. Rubin (2003), «Bayesian Data Analysis», Second Edition, CRC Press.
- Charles M. Grinstead and J. Laurie Snell (1997), «Introduction to Probability (2nd edition)», American Mathematical Society (free pdf available [1].
- Pierre-Simon Laplace. (1774/1986), «Memoir on the Probability of the Causes of Events», Statistical Science 1(3):364-378.
- Peter M. Lee (2012), «Bayesian Statistics: An Introduction», Wiley.
- Rosenthal, Jeffrey S. (2005): «Struck by Lightning: the Curious World of Probabilities». Harper Collings.
- Stephen M. Stigler (1986), «Laplace’s 1774 Memoir on Inverse Probability», Statistical Science 1(3):359-363.
- Stone, JV (2013). Chapter 1 of book «Bayes’ Rule: A Tutorial Introduction», University of Sheffield, England.
Ссылки[править | править код]
- The Theory That Would Not Die by Sharon Bertsch McGrayne New York Times Book Review by John Allen Paulos on 5 August 2011
- Weisstein, Eric W. Bayes’ Theorem (англ.) на сайте Wolfram MathWorld.
- Bayes’ theorem (англ.) на сайте PlanetMath.
- Bayes Theorem and the Folly of Prediction
- A tutorial on probability and Bayes’ theorem devised for Oxford University psychology students
- An Intuitive Explanation of Bayes’ Theorem by Eliezer S. Yudkowsky
Понравилось? Добавьте в закладки
Если событие А может произойти только при выполнении одного из событий  , которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле
, которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле
 .
.
Эта формула называется формулой полной вероятности.
Вновь рассмотрим полную группу несовместных событий  , вероятности появления которых
, вероятности появления которых  . Событие А может произойти только вместе с каким-либо из событий
. Событие А может произойти только вместе с каким-либо из событий  , которые будем называть гипотезами. Тогда по формуле полной вероятности
, которые будем называть гипотезами. Тогда по формуле полной вероятности

Если событие А произошло, то это может изменить вероятности гипотез  .
.
По теореме умножения вероятностей
 ,
,
откуда
 .
.
Аналогично, для остальных гипотез

Полученная формула называется формулой Байеса (формулой Бейеса). Вероятности гипотез  называются апостериорными вероятностями, тогда как
называются апостериорными вероятностями, тогда как  – априорными вероятностями.
– априорными вероятностями.
Пример. В магазин поступила новая продукция с трех предприятий. Процентный состав этой продукции следующий: 20% – продукция первого предприятия, 30% – продукция второго предприятия, 50% – продукция третьего предприятия; далее, 10% продукции первого предприятия высшего сорта, на втором предприятии – 5% и на третьем – 20% продукции высшего сорта. Найти вероятность того, что случайно купленная новая продукция окажется высшего сорта.
Решение. Обозначим через В событие, заключающееся в том, что будет куплена продукция высшего сорта, через  обозначим события, заключающиеся в покупке продукции, принадлежащей соответственно первому, второму и третьему предприятиям.
обозначим события, заключающиеся в покупке продукции, принадлежащей соответственно первому, второму и третьему предприятиям.
Можно применить формулу полной вероятности, причем в наших обозначениях:

Подставляя эти значения в формулу полной вероятности, получим искомую вероятность:

Пример. Один из трех стрелков вызывается на линию огня и производит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго – 0,5; для третьего – 0,8. Мишень не поражена. Найти вероятность того, что выстрелы произведены первым стрелком.
Решение. Возможны три гипотезы:
 – на линию огня вызван первый стрелок,
– на линию огня вызван первый стрелок,
 – на линию огня вызван второй стрелок,
– на линию огня вызван второй стрелок,
 – на линию огня вызван третий стрелок.
– на линию огня вызван третий стрелок.
Так как вызов на линию огня любого стрелка равновозможен, то 
В результате опыта наблюдалось событие В – после произведенных выстрелов мишень не поражена. Условные вероятности этого события при сделанных гипотезах равны:

по формуле Байеса находим вероятность гипотезы  после опыта:
после опыта:

Пример. На трех станках-автоматах обрабатываются однотипные детали, поступающие после обработки на общий конвейер. Первый станок дает 2% брака, второй – 7%, третий – 10%. Производительность первого станка в 3 раза больше производительности второго, а третьего – в 2 раза меньше, чем второго.
а) Каков процент брака на конвейере?
б) Каковы доли деталей каждого станка среди бракованных деталей на конвейере?
Решение. Возьмем с конвейера наудачу одну деталь и рассмотрим событие А – деталь бракованная. Оно связано с гипотезами относительно того, где была обработана эта деталь:  – взятая наудачу деталь обработана на
– взятая наудачу деталь обработана на  -ом станке,
-ом станке,  .
.
Условные вероятности (в условии задачи они даны в форме процентов):

Зависимости между производительностями станков означают следующее:
 .
.
А так как гипотезы образуют полную группу, то  .
.
Решив полученную систему уравнений, найдем:  .
.
а) Полная вероятность того, что взятая наудачу с конвейера деталь – бракованная:
 .
.
Другими словами, в массе деталей, сходящих с конвейера, брак составляет 4%.
б) Пусть известно, что взятая наудачу деталь – бракованная. Пользуясь формулой Байеса, найдем условные вероятности гипотез:
 ,
,
 ,
,
 .
.
Таким образом, в общей массе бракованных деталей на конвейере доля первого станка составляет 33%, второго – 39%, третьего – 28%.
Видео-уроки на тему полной вероятности и формулы Байеса
В первом уроке вы можете посмотреть подробный вывод с доказательством формулы Бейеса (любителям теории):
А здесь будут разобраны несколько типовых задач и на формулу полной вероятности, и на формулу Байеса:
Пример 1
На фабрике
станки 1,2 и 3 производят соответственно 20%, 35% и 45% всех деталей. В их
продукции брак составляет соответственно 6%, 4%, 2%. Какова вероятность того,
что случайно выбранное изделие оказалось дефектным? Какова вероятность того,
что оно было произведено: а) станком 1; б) станком 2; в) станком 3?
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Обозначим через
событие, состоящее в том,
что стандартное изделие оказалось дефектным.
Событие
может произойти только
при условии наступления одного из трех событий:
-изделие произведено на
станке 1;
– изделие произведено на
станке 2;
– изделие произведено на
станке 3;
Запишем условные вероятности:
По формуле полной вероятности
находим вероятность события
:
Вероятность того, что дефектное изделие
изготовлено на станке 1 найдем по формуле Бейеса:
Вероятность того, что дефектное изделие
изготовлено на станке 2:
Вероятность того, что дефектное изделие
изготовлено на станке 3:
Ответ: а)
; б)
; в)
.
Задача 1
На
отборочное предприятие поступили однотипные комплектующие с трех заводов в
количестве: 20 с первого завода; 50 со второго завода; 30 с третьего. Вероятность качественного
изготовления изделий на первом заводе 0,8, на втором 0,9
, на третьем 0,9. 1) Какова вероятность
того, что взятое случайным образом изделие будет качественным? 2) Взятое наугад
изделие оказалось качественным. Какова вероятность того, что это изделие завода
с номером N=1.
Задача 2
В
пирамиде 15 винтовок, 12 из которых снабжены оптическим прицелом. Вероятность
того, что стрелом поразит мишень при выстреле из винтовки с оптическим прицелом
равна 12/25; для винтовки без оптического прицела эта вероятность равна 2/25.
Найти вероятность того, что мишень будет поражена, если стрелок произведет один
выстрел из наудачу взятой винтовки.
Задача 3
На
предприятии работают две бригады рабочих: первая производит в среднем 3/4
продукции с процентом брака 4%, вторая – 1/4 продукции с процентом брака 6%.
Найти вероятность того, что взятое наугад изделие:
а)
окажется бракованным;
б)
изготовлено второй бригадой при условии, что изделие оказалось бракованным.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 4
В одном
сосуде находятся 7 белых и 6
черных шаров. Во втором – 5
белых и 9
черных. Бросают два кубика. Если сумма очков,
выпавших на верхних гранях, меньше 10, берут шар из первого сосуда, если больше
или равна 10 – из второго. Вынут белый шар. Какова вероятность того, что сумма
очков была не меньше 10?
Задача 5
Вероятность
того, что во время работы цифровой электронной машины произойдет сбой в
арифметическом устройстве, в оперативной памяти, в остальных устройствах,
относятся как 3:2:5. Вероятность обнаружения сбоя в арифметическом устройстве,
в оперативной памяти и в остальных устройствах соответственно равна 0,8; 0,9;
0,9. Найти вероятность того, что возникший в машине сбой будет обнаружен.
Задача 6
Имеется
пять урн. В первой, второй и третьей урнах находится по 2 белых и 3 черных
шара, в четвертой и пятой урнах – по 1 белому и 1 черному шару. Случайно
выбирается урна и из нее извлекается шар. Какова условная вероятность того, что
выбрана четвертая или пятая урна, если извлеченный шар оказался белым?
Задача 7
В двух
пакетах находятся конфеты. В первом пакете 16 штук сорта «Белочка» и 8 штук
сорта «Жар-птица», во втором 15 сорта «Белочка» и 5 сорта «Жар-птица». Из
первого пакета во второй переложили две конфеты, взятые случайным образом,
содержимое второго пакета перемешали и вытащили оттуда одну конфету, которая
оказалась «Жар-птицей».
Какова
вероятность, что из первого пакета во второй переложили одну «Белочку» и одну
«Жар-птицу»?
Задача 8
В городе N – 600
гостиничных номеров. Из них 100 номеров – в первой гостинице, 200 – во второй,
остальные – в третьей. В турфирме известно, что наличие свободного номера
нужного класса составляет вероятность 0,7; 0,5 и 0,8 соответственно в первой,
второй и третьей гостиницах. Определить вероятность того, что клиентов поселили
во вторую гостиницу.
Задача 9
Имеются
три партии радиоламп, насчитывающих соответственно 20,30 и 50 шт. Вероятности
того, что радиолампа проработает заданное время, равны 0,7; 0,8; 0,9. Какова
вероятность того, что наудачу выбранная лампа из 100 данных проработает
заданное время?
Задача 10
В первом
ящике 2 карандаша и 4 ручки, во втором – 3 карандаша и 1 ручка. Случайным
образом выбрали ящик и из него достали один предмет. Найти вероятность того,
что им оказался карандаш.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 11
Для
участия в студенческих отборочных соревнованиях выделено из первой группы курса
4 студента, 6 из второй и 5 студентов из третьей. Вероятности того, что
отобранный студент из первой, второй, третьей группы попадает в сборную
института, соответственно равны 0.5, 0.4 и 0.2. Наудачу выбранный участник
соревнований попал в сборную. К какой из указанных групп он вероятнее всего
принадлежит?
Задача 12
Из 10
лотерейных билетов 3 выигрышных. При подготовке вечера 2 билета потеряли, и
было решено добавить один выигрышный. Какой стала вероятность того, что
случайно выбранным билет будет выигрышным?
Задача 13
В урне
находятся 5 шаров белого цвета и 4 шара
черного цвета. Три шара последовательно извлекаются из урны (без возвращения их
в урну). Найти вероятность того, что третий извлеченный шар будет белым.
Задача 14
Родион
Раскольников покупает себе топор. У первых трех торговцев по 15 топоров с
сосновыми топорищами и по 10 топоров с дубовыми. Имеются еще два торговца, у каждого из
которых по 5 топоров с сосновыми топорищами и по 5 топоров с дубовыми. Раскольников
покупает первый попавшийся топор у наугад выбранного торговца. Какова
вероятность покупки топора с дубовым топорищем?
Задача 15
На базу
поступили одинаковые по объему партии холодильников с двух разных заводов.
Вероятность того, что холодильник проработает без поломок в течение гарантийного
срока, равна 0,85, если холодильник собран на 1-ом заводе, и 0,95, если на
втором. Найти вероятность того, что наугад взятый холодильник не сломается в
течение гарантийного срока.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 16
Банки
закатывают два автомата с одинаковой производительностью. Доля банок с дефектом
укупорки для первого автомата составляет 1%, а для второго – 0,5%. Какова
вероятность того, что взятая наугад банка будет иметь дефект укупорки?
Задание 17
У рыбака
есть три излюбленных места рыбалки. Эти места он посещает с одинаковой
вероятностью. Вероятность того, что рыба клюнет в 1-м месте – 1/3, во втором –
1/2, в 3-м – 1/4. Известно, что рыбак забросил удочку 3 раза, а вытащил только
одну рыбу. Какова вероятность того, что рыбак рыбачил в первом месте?
Задача 18
В группе
из 20 пациентов имеются 4 человека с заболеванием A
, 10 – с заболеванием B
и 6 с заболеванием C
. Вероятность аллергической
реакции при приеме витаминов для первой группы больных – 0,9, для второй – 0,7,
для третьей – 0,5. Найдите вероятность того, что: а) у наудачу выбранного
больного возникнет аллергическая реакция; б) у 2 наудачу выбранных больных
возникнет аллергическая реакция.
Задача 19
В
результате исследований, проведенных в хирургическом отделении одного лечебного
учреждения, установлено, что первая группа крови встречается у 40% больных,
вторая – у 30%, третья – у 20% , четвертая – у 10%. Во время операций
переливание крови требуется пациентам с первой группой – 2%, второй – 1%,
третьей -0,5% и четвертой -0,2%. Найдите вероятность того, что во время
операции пациенту не потребуется переливание крови.
Задача 20
Покупатель
пробует шестизарядный револьвер. Найти вероятность того, что при нажатии
покупателем на курок раздастся выстрел, если равновозможны все предположения о
количестве заряженных в револьвер патронов.






















