
|
4.1.ОПРЕДЕЛЕНИЕ РАВНОВЕСИЙ И ИХ СУЩЕСТВОВАНИЕ |
161 |
|
a |
A |
II |
a |
|
3,3,0 |
|||
|
D |
d |
||
|
III |
|
L |
R |
L |
R |
|
4,4,4 |
1,1,1 |
5,5,0 |
2,2,2 |
Рис. 4.2:Ослик Зелтена
Для того чтобы анализировать динамические игры с неполной информацией,нам необходимо решить три теоретические задачи.Во-первых необходим о сформулировать концепцию равновесия,более строгую,чем совершенное по подыграм рав новесие Нэша.Это равновесие должно исключать нерациональное поведение игроков в информационных множествах,лежащих вне траектории игры(как,например, (R, r) в игре на рисунке4.1).Во-вторых необходимо выяснить вопрос существования такого равновесия для какого-то максимально широкого класса игр — например,для конечных игр.И наконец нужно получить удобный способ проверки равновесий на соответствие этому критерию.
В этом разделе мы решим все три обозначенные задачи.Сначала мы сформулируем понятие сильного и слабого секвенциального равновесия.Далее мы до кажем существование сильного секвенциального равновесия,введя еще одно — более строгое — понятие совершенного равновесия,и доказав его сущестование 1.Наконец,мы введем определение важного подкласса игр — игр с наблюдаемыми действиями — и удобного,с точки зрен ия анализа,понятия совершенного баейсового равновесия для этих игр,и сформулируем условия его эквивалентности секвенциального равновесия.
Почему нам необходимо проделать все эти действия?Очень мно гие задачи в экономике и политической науке можно свести к играм с наблюдаемыми действиями.Проделанная работа даст нам возможность анализировать эти задачи,используя у добное в работе определение совершенного байесового равновесия.При этом мы будем уверен ы,что,с одной стороны,такое равновесие всегда существует,и,с другой стороны,определ ение такого равновесия достаточно строгое для того,чтобы исключить возможность нерациональ ного поведения.
4.1.1Сильное и слабое секвенциальное равновесие
Каким формальным критериям не удовлетворяют примеры на рисунке4.1и4.2?Дадим определение.
Определение41 Пусть Γ — игра в развернутой форме, h — информационное множество в этой игре.Назовем верой µh распределение вероятностей на вершинах,входящих в h.Обозначим за µ = (µh) веру (или систему вер)в игре Γ — распределение вероятностей для каждого информационного множества.
Вера игрока в информационном множестве отражает его представление о том,в какой именно вершие множества он в данный момент находится.По возможн ости,она должна отражать
1Определение секвенциального равновесия и доказательство большинства связанных с ним утверждений принадлежит Крепсу и Уилсону(1982).Определение совершенн ого байесового равновесия в достаточно общей форме можно найти в работе Тироля и Фаденберга(1991).

|
162 |
ГЛАВА4.ДИНАМИЧЕСКИЕ ИГРЫ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ |
его представления о стратегиях других игроков.
Определение42 Пусть Γ — игра в развернутой форме, σ — профиль поведенческих стратегий в этой игре.Пусть µ — система вер.Будем говорить,что µ слабо согласована с σ если для всех информационных множеств h, таких , что приσ существует положительная вероятность попадания игры в h,для всех вершин a h,верно следующее:
|
µh(a) = |
P (a|σ) |
, |
(4.1) |
|
P (h|σ) |
где P (a|σ) — вероятность того,что траектория игры пройдет через верши ну a, P (h|σ) = &b h P (b|σ) — вероятность того,что траектория игры пройдет через инфор мационное множество h.
Если система вер согласована с поведенческой стратегией,т о для всех информационных множеств,через которые траектория игры проходит с положит ельной вероятностью,вера вычисляется по правилу Байеса.На рисунке4.3показан пример и гры в развернутой форме и поведенческой стратегии.
|
I |
||
|
1 |
1 |
1 |
|
2 |
4 |
4 |
|
II |
||
|
1 |
2 |
|
|
3 |
3 |
III 
Рис. 4.3:Пример игры и поведенческих стратегий.
|
Построим систему вер,согласованную с этой стратегией.Для |
информационного множества |
|||||||||||||||||||||||||||
|
игрокаII,вера будет |
||||||||||||||||||||||||||||
|
µII = ) |
1 |
1 |
* = ) |
3, |
3 |
*. |
(4.2) |
|||||||||||||||||||||
|
21 + 41 , |
21 + 41 |
|||||||||||||||||||||||||||
|
2 |
4 |
2 |
1 |
|||||||||||||||||||||||||
|
Для информационного множества игрокаIIIмы имеем |
||||||||||||||||||||||||||||
|
) 41 · |
1 |
41 |
1 |
+ 41 |
41 · |
1 |
41 |
2 |
41 |
41 · 31 |
+ |
1 |
· 32 |
+ 41 |
* ) |
6 3 2 |
* |
|||||||||||
|
31 + |
· 32 |
31 + |
· 32 + |
41 |
||||||||||||||||||||||||
|
µIII = |
4 |
· |
3 |
, |
4 |
· |
3 |
, |
4 |
= |
1 |
, |
1 |
, |
1 |
. |
(4.3) |
|||||||||||
В каждом информационном множестве,оптимальное действие и грока должно зависить от веры в этом информационном множестве.Пусть σ — профиль поведенческих стратегий, µ — система вер.Пусть h — информационное множество,в котором игрок i делает ход.Определим за ui,h(σ|µh) ожидаемый выигрыш игрока i при условии,что игра достигла множества h.Будем говорить,что σi секвенциально рациональна относительно µ,если для всех σi′, ui,h(σi, σ−i) ≥ ui,h(σi′, σ−i).Можно дать следующее определение равновесия:
Определение43 Пара (σ, µ) является слабо секвенциальным равновесием,если σ секвенциально рациональна относительно µ, и µ слабо согласована с σ.
|
4.1.ОПРЕДЕЛЕНИЕ РАВНОВЕСИЙ И ИХ СУЩЕСТВОВАНИЕ |
163 |
|
|
В примере на рисунке4.1,профиль стратегий |
(R, r) не согласован ни с какой системой вер: |
|
|
при любом µ,игрокIIдолжен выбрать действие |
l.Однако определение слабой согласованности |
вер ничего не говорит про те случаи,когда одно из информацио нных множеств лежит вне траектории игры.Такое может произойти только если в некоторых информационных множествах какие-то действия играются с нулевой вероятностью;соотве тственно,потребуется сформулировать более жесткий критерий в отношении системы вер,чем с лабая согласованность.
Назовем σ вполне смешанным профилем стратегий,если в каждом информационном множестве каждое действие реализуется с положительной вероятностью.Для такого σ,уравнение (4.1)определяет веру для каждого информационного множест ва.Дадим такое определение.
Определение44 Пусть σ — профиль поведенческих стратегий.Будем говорить,что сис тема вер µ является сильно согласованной c σ,если существует последовательность вполне смешанных профилей σn → σ, таких , чтоµn → µ, где µk — система вер,слабо согласованная с профилем стратегий σk.
Сильная согласованность требует,чтобы вера являлась пред елом последовательности вер, полученных из сходящихся к стратегии σ профилей стратегий.
Дадим определение,аналогичное Определению43:
Определение45 Пара (σ, µ) является сильно секвенциальным равновесием,если σ секвенци-
ально рациональна относительно µ, и µ сильно согласована с σ.
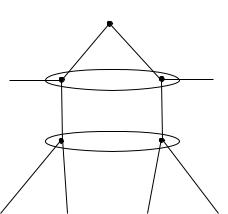
На рисунке4.4приведен пример игры,для которой существует равновесие,которое является слабо секвенциальным,однако условие сильной секвенциаль ности не выполняется.
|
III |
|||
|
l |
r |
l |
r |
|
0,0,0 |
0,0,1 |
1,2,1 |
1,0,0 |
|
Рис. 4.4:Пример игры,для которой слабо секвенциальное рав новесие не является сильно |
|||
|
секвенциальным. |
Профиль стратегий (R, u, r) является слабо секвенциальным равновесием в совокупности с системой вер µII = 0 и µIII > 12 (вера указывает вероятность оказаться в левой вершине информационного множества).Действительно,информацион ное множество игрокаIIIлежит вне траектории игры,так что мы можем придумать любую веру дл я этого множества.
Почему слабо секвенциальное равновесие в этой игре плохо соотносится с предположением о рациональности игроков?Как говорилось выше,игрокIIIвыб ерет действие r только если µIII > 12 .Если первый игрок выбирает R, а второй — u,то вероятность попадания в информационное множествоIIIравна нулю,так что по правилу Байеса в качеств е веры в этом информационном множестве мы можем выбрать любое распределение вероятностей на его вершинах.Однако какова вероятность оказаться в левой вершине множестваIII при условии,что один из игроков IиIIотклонится от заданной стратегии ?Для того,чтобы мы оказались в правой вершине
|
164 |
ГЛАВА4.ДИНАМИЧЕСКИЕ ИГРЫ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ |
|||||
|
множестваIII,достаточно,чтобы дрогнула рука у игрокаII, |
и он сыграл d вместо u. Однако для |
|||||
|
того,чтобы мы оказались в левой вершине,необходимо,чтобы |
и игрокI,и игрокIIотклонились |
|||||
|
от заданных стратегий.Если вероятности того,что каждый из |
первых двух игроков отклонится, |
|||||
|
малы,и если отклонения независимы друг от друга,то скорее в |
сего мы окажемся в правой |
|||||
|
вершине,то есть мы должны иметь |
µIII = 0. |
|||||
|
Формально,пусть (σ1k, σ2k, σ3k)k∞=1 — последовательность поведенческих стратегий,сходя- |
||||||
|
щаяся к (R, u, r).То есть σ1k → 0, |
σ2k → 0, и σ3k → 1,причем |
σik (0, 1) для i = 1, 2, 3. По |
||||
|
правилу Байеса,мы имеем |
||||||
|
σ2kσ1k |
(4.4) |
|||||
|
µIIIk = |
= σ1k → 0. |
|||||
|
σ2kσ1k + σ2k(1 − σ1k) |
||||||
|
¯ |
µIIIk |
1 |
¯ |
|||
|
Получается,что для некоторого k > 0,мы будем иметь |
< 2 |
для всех k > k,то есть |
действие r игрокаIIIне будет являться секвенциально рациональным.О днако существует равновесие (R, d, l),являющееся сильно секвенциальным:в этом равновесии,игр а проходит через все информационный множества.
4.1.2Совершенное(относительно «дрожащей руки»)равнове сие
Мы сформулировали понятие секвенциального равновесия.Он о обобщает понятие совершенства по подыграм для динамических игр с неполной информацией.Однако пока не был затронут вопрос существования такого равновесия.Для того,чтобы да ть на него ответ,нам придется ввести еще одно определение равновесия,более строгое,чем секвенциальное равновесие,и доказать его существование.
Потребуем от равновесия,чтобы стратегия каждого игрока бы ла наилучшим ответом не только на профиль стратегий остальных игроков,но и на какой -то слегка видоизмененный профиль стратегий:игрок не должен отклоняться от своей стр атегии,если у других игроков немного «задрожали руки».Вот соответствующее определени е равновесия,выдвинутое Зелте-
ном(1975):
Определение46 Пусть G — игра в нормальной форме.Пусть σ — профиль стратегий,причем существует последовательность σn вполне смешанных профилей стратегий,таких,что
1. σn → σ,
2.Для всех k,для всех i, σi является наилучшим ответом на σ−k i.
Будем называть σ совершенным (или совершенным относительно дрожащей руки)равновеси-
ем.
Верно следующее утверждение:
Теорема18 Пусть G — конечная игра в нормальной форме.Тогда в этой игре существ ует равновесие,совершенное относительно дрожащей руки.
Доказательство этого утверждения достаточно длинное;оно потребует введения альтернативных определений совершенного равновесия и доказательства эквивалентности между ними. Полностью текст доказательства приыеден в приложении на стр. 197-200.
В приеденной ниже координационной игре каждое из трех равновесий является совершенным:
|
II |
|||
|
A |
B |
||
|
I |
A |
1,1 |
0,0 |
|
B |
0,0 |
1,1 |
|
4.1.ОПРЕДЕЛЕНИЕ РАВНОВЕСИЙ И ИХ СУЩЕСТВОВАНИЕ |
165 |
||||||
|
Пусть p и q — вероятности сыграть A для игроковIиII.Возьмем равновесие |
(p, q) = (0, 0). |
||||||
|
Тогда |
последовательность σk = (ϵ |
, ϵ |
) при ϵ |
→ |
0 удовлетворяет условию Определения46. |
||
|
k |
k |
k |
условию.Для равновесия (p, q) = (1 |
, 1 ), |
|||
|
Аналогично, σ |
= (1 −ϵk, 1 −ϵk) удовлетворяет тому же |
1 |
1 |
2 |
2 |
||
|
существует единственная такая последовательность σk = (2 , |
2 ).Вовсе не обязательно,чтобы |
σ являлся бы наилучшим ответом на любую последовательность σk → σ .Если мы потребует этого,то равновесия,скоре всего,не будет существовать,т ак как это,очевидно,потребует наличия равновесия в доминирующих стратегиях.
Однако в следующем примере не все равновесия являются совершенными:
|
II |
|||
|
A |
B |
||
|
I |
|||
|
A |
10,0 |
1,1 |
|
|
B |
10,10 |
0,10 |
|
Здесь есть два равновесия: (A, B) и (B, A).Второе из них предполагает,что игрокIIреализует слабо доминируемую стратегию A.Оно не является совершенным относительно дрожащей руки,так как если игрокIреализует A с положительной вероятностью,то игрокуIIвыгодно отклониться и сыграть B.
Вообще,слабо доминируемая стратегия не может играться в со вершенном относительно дрожащей руки равновесии.Действительно,пусть Si — множество чистых стратегий игрока i, si Si — слабо доминируемая стратегия,которую мы предполагаем ра вновесной, s′i Si
слабо доминирует si,то есть для всех s−i S−i мы имеем ui(si, s−i) ≤ ui(s′i, s−i).Пусть ui(si, s′−i) < ui(s′i, s′−i) для какого-то s−i.Стратегия si может быть наилучшим ответом на какой-
то смешанный профиль стратегий σ−i только если s′−i играется с нулевой вероятностью. Рассмотрим игру Γ в развернутой форме.Пусть σ — совершенное равновесие.
Теорема19 Пусть Γ — игра в развернутой форме, G — игра в нормальной форме,соответствующая ей.Пусть σ — совершенное равновесие в G.Тогда существует вера µ,такая,что (µ,σ ) — сильно секвенциальное равновесие в Γ.
Таким образом,любое совершенное равновесие является силь но секвенциальным.Обратное неверно:существуют случаи,когда равновесие является сил ьно секвенциальным,но не совершенным.
Как следствие Теорем18и19,мы доказали еще одну:
Теорема20 Пусть Γ — игра с полной памятью.Тогда в ней существует сильно секвенциальное равновесие.
4.1.3Игры с наблюдаемыми действиями
Рассмотрим такой класс игр с несовершенной информацией.Иг роки ходят по очереди,причем все ходы всех игроков наблюдаемы;при этом частной информац ией является только тип игрока, определяющий его предпочтения относительно различных исходов игры.В такой игре порядок ходов определяется так же,как и в игре с совершенной информа цией,причем множество ходов, доступных игроку на каждом этапе игры,не зависит от его типа .Предположм также,что начальное распределение вероятностей P одинаково для всех игроков;кроме того,типы игроков независимы.
Формально,мы можем дать такое определение:
Определение47 Пусть Γ — игра в развернутой форме с совершенной информацией, T = Ti × · · · × TN — множество типов игроков, P = P1 × · · · × PN — распределение вероятностей на T , ui — функция полезностей игрока i,определяющая его выигрыш в зависимости от конечной вершины и его типа ti, u = (ui)Ni=1. Тогда Γ, T, P, u — игра с наблюдаемыми действиями.
|
166 |
ГЛАВА4.ДИНАМИЧЕСКИЕ ИГРЫ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ |
Чему соответствуют вершины в информационных множествах в такой игре?Пусть в информационном множестве h делает ход игрок i.Ему известна предыстория игры,но неизвыестны типы остальных игроков.Соответственно,каждая вершина ин формационного множества h соответствует множеству остальных игроков T−i.Вера µh в информационном множестве h — это распределение вероятностей на множестве игроков T−i.Пусть µhj — распределение вероятностей на множестве Tj типов j-го игрока в информационном множестве h.
Следуя Фаденбергу и Тиролю(1991),дадим такое определение .
Определение48 Пусть (µ,σ ) — система вер и поведенческая стратегия для игры с наблюдаемыми действиями.Назовем систему вер µ разумной относительно σ если выполняется следующее:
1. µ слабо согласована с σ.
|
2.Пусть |
h и h′ — информационные множества,такие,что в множество h′ можно попасть |
||||||
|
одним ходом из множества h.Пусть игрок k не делает ход ни в h, ни в h′. Тогда µhi = µh′i. |
|||||||
|
3. |
Пусть |
h — информационное множество,в котором делает ход игрок i. Тогда µ |
= |
1j̸=i |
µ |
. |
|
|
Если o — начальная вершина, i — игрок,делающий первых ход,то µo = P−i.h |
hj |
Третье требование означает,что в каждом информационном мн ожестве,веры игрока i относительно типов остальных игроков являются независимыми.В совокупности со вторым требованием,это означает,что пока какой-то игрок не делает хо да,остальные игроки не узнают про него ничего нового;таким образом,делая ход,игрок може т менять представления игроков только о своем типе,но не о типах остальных игроков.
Определение49 Пусть (σ, µ) — профиль поведенческих стратегий и система вер,такие,что µ является разумной относительно σ, а σ — секвенциально рациональна относительно µ. Тогде
(σ, µ) — совершенное байесово равновесие.
Байесово равновесие — намного более удобное для работы опрелеление,чем сильное секвенциальное равновесие.Доказать,что система вер µ является разумной относительно σ гораздо легче,чем доказать сильную согласованность,так как нам не требуется доказывать чтото относительно сходящихся последовательностей.С другой стороны,сильное секвенциальное равновесие отвечает довольно строгому критерию реализма: если равновесие является сильно секвенциальным,то оно не будет «паталогическим» — как,нап ример,слабо секвенциальное равновесие на (R, u, r) рисунке4.4.Поэтому представляется интересным такой вопр ос:в каком случае мы,найдя совершенное байесово равновесие,можем бы ть уверены,что это равновесие является сильно секвенциальным?
Тироль и Фаденберг(1991)доказали такой результат:
Теорема21 Пусть Γ — игра с наблюдаемыми действиями, (σ, µ) — совершенное байесово равновесие.Тогда (σ, µ) — сильно секвенциальное равновесие,если в игре Γ не более двух ходов, либо у каждого игрока есть не более двух типов.
4.2Сигнальные игры
На окраине рабочего квартала большего города есть заведение,в котором можно вкусно поесть и выпить.За столиком у окна сидит хулиган — наглый и невоспит анный молодой человек,любящий приставать к проходящим мимо него людям.В заведение з аходит человек средних лет

Совершенные
Сильно секвенциальные
Байесовы
Совершенные по подыграм
Все равновесия
Все стратегии
Рис. 4.5:Диаграмма множеств равновесий в динамических игр ах.
и направляется к барной стойке.Хулиган смотрит на него,пыт аясь понять,какой характер у пришельца,и какой жизненный опыт у него за плечами.Если он с лабак — интеллигент,выросший в центре города,в тепличных условиях — то хулиган с уд овольствием нахамит ему и попытается с ним подраться.Но что,если пришелец крутой и са м вырос на рабочих окраинах ? В таком случае хулинган знает,что лучше с ним не связываться : можно получить сдачи . Во – шедший подходит к барной стойке.Хулиган знает,что крутой п арень с рабочих окраин в такой ситуации обычно заказывает бутылку пива,а интеллигент из ц ентра города — чашку кофе. Вошедший заказал пиво.Означает ли это,что вошедший — круто й парень,с которым лучше не связываться?Или,может быть,это — интеллигент,который заказал нелюбимый напиток для того,чтобы походить на крутого и ввести хулигана в заблу ждение?
4.2.1Определение
Данная ситуация является частным случаем игры с наблюдаемыми действиями,с двумя игроками,последовательно делающими ходы.Она соответствует в от такому определению:
Определение50 Сигнальная игра это игра с наблюдаемыми действиями,в которой
1.Два игрока — ведущийSи получательR,
2.У получателя один тип,у ведущего — больше одного,
3.Первый ход делает ведущий,второй ход — получатель.
Действительно,ведущий — тип которого неизвестен — может си гнализировать свой тип второму игроку,выбирая какой-то наблюдаемое действие.Ка к,например,напиток,выбранный вошедшим в кафе посетитетем,сигнализирует хулигану его ти п,или как наличие или ответствие престижного диплома у соискателя может на самом деле давать сигнал относительно его трудолюбия.
Мы знаем,что наличие только двух ходов в игре с наблюдаемыми действиями — достаточное условие для того,чтобы совершенное байесово равновесие бы ло секвенциальным.Переформулируем понятие равновесия для сигнальной игры.Обозначим з а T все типы игрокаS.Пусть M множество действий(или сигналов)для этого игрока.Пусть m : T → M — стратегия игрокаS, предписывающее определенное действие в зависимости от типа.
У игрокаRбудет #{M} информационных множеств,по одному для каждого возможного сигнала,который может послать игрокS.Пусть µ(ti|mj) — вера игрокаRотносительно того, что игрокSимеет тип ti T при условии,что его первый ход был mj M.Обозначим за A множество действий игрока R.Пусть a : M → A — стратегия игрокаR,предписывающее действие в зависимости от сигнала,испущенного игрокомS.Обоз начим за uS(t, m, a) и uR(t, m, a) полезности двух игроков.

168 ГЛАВА4.ДИНАМИЧЕСКИЕ ИГРЫ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ
Байесово равновесие,данное в Определении49,можно перефо рмулировать следующим образом.
Определение51 Совершенное байесово равновесие в чистых стратегиях2 в сигнальной игре есть набор (m (·), a (·), µ(·|·)), такой , что
1.Для любого m M, a (m) максимизирует ожидаемый выигрыш игрокаRпри системе вер µ(·|·),то есть для всех a′ A,
|
( |
( |
||
|
µ(t|m)uR(t, m, a (m)) ≥ |
µ(t|m)uR(t, m, a′). |
(4.5) |
|
|
t T |
t T |
||
|
2.Для всех t T ,действие игрокаS |
m (t) максимизирует его выигрыш при условии,что |
||
|
игрокRбудет играть равновесную стратегию a (·): |
|||
|
uS(t, m (t), a (m (t))) ≥ uS(t, m′, a (m′)) |
(4.6) |
||
|
для всех m′ M. |
|
3.Для всех m M,таких,что если существует |
t T , такой |
||
|
после хода m определяется по правилу Байеса: |
|||
|
µ(t|m) = |
p(t) |
, |
|
|
&t′ T p(t′) |
|||
|
где p(t) — вероятность,что игрокSимеет тип |
t T . |
, чтоm (t) = m,вера игрокаR
(4.7)
Первые два требования в этом равновесии — секвенциальная рациональность игроков.Третье требование — согласованность системы вер со стратегиями игроков.
4.2.2Простой пример сигнальной игры.
Вернемся к игре,описанной в начале данного раздела.Хулига н является игрокомR,пришелец
— игрокомS.Хулиган обладает единственным типом,у пришель ца два типа — 1 (крутой,с вероятностью p) и 2 (слабак,с вероятностью 1−p).Базовая игра состоит из двух этапов:сначала пришедший решает,какой напиток ему заказать — H (пиво)или L (кофе),затем хулиган решает,драться с пришедшим,или нет( h или l).Выигрыш пришедшего(вне зависимости от его типа)равен 1 если ему удается избежеть драки и 0 если ему пришлось драться.Дополнительно, он несет издержки c > 0 если ему приходится пить нелюбимый напиток(кофе для крутог о и пиво для слабака).Хулиган получает выигрыш1если он приним ает правильное,со своей точки зрения,решение(драться со слабаком и не драться с крутым)и 0если принятое решение оказалось неправильным.Дерево этой игры изображено на рис унке4.6.
Пусть m(1), m(2) {H, L} — ходы первого игрока в зависимости от его типа.Пусть a(H), a(L) {h, l} — ходы второго игрока в зависимости от того,каким был ход пер вого игрока. Найдем совершенное байесово равновесие.
1.Для нахождения равновесия в этой игре мы должны ввести вер ы µH, µL [0, 1].Первая из этих двух величин — вероятность,с которой вошедший имеет тип 1 в том случае,если он купил кофе.Вторая величина — вероятность,с которой воше дший имеет тип 1 в том случае,если он купил пиво.Система вер является согласован ной со стратегией игрокаS, если она удовлетворяет следующим условиям:
2Определить совершенное байесово равновесие в смешанных стратегиях почти так же просто;потребуется только немного по-другому определить понятие согласованности системы вер,что мы и сделаем в одном из последующих примеров.

|
4.2.СИГНАЛЬНЫЕ ИГРЫ |
169 |
||||||
|
Тип 1 |
|||||||
|
−c, 0 |
h |
L |
H |
h |
0, 0 |
||
|
l |
p |
l |
|||||
|
1 − c, 1 |
1, 1 |
||||||
|
0, 1 |
h |
1 |
− |
p |
h |
−c, 1 |
|
|
1, 0 |
1 − c, 0 |
||||||
|
l |
L |
H |
l |
||||
Тип 2
Рис. 4.6:Игра «пиво или кофе?»
(a)µH = p, µL [0, 1] если m(1) = H, m(2) = H,
(b)µH = 1, µL = 0 если m(1) = H, m(2) = L
(c)µH = 0, µL = 1 если m(1) = L, m(2) = H,
(d)µH [0, 1], µL = p если m(1) = L, m(2) = L.
2.Найдем,каким условиям удовлетворяет стратегия игрокаR, если она рациональна относительно системы вер (µH , µL).Ожидаемый выигрыш хулигана в информационном множестве H — то есть если ход игрокаSбыл H — при собственном ходе h равен
E(uR(·, H, h)) = µH · uR(1, H, h) + (1 − µH ) · uR(2, H, h) = 1 − µH ,
а при собственном ходе l —
E(uR(·, H, l)) = µH · uR(1, H, l) + (1 − µH) · uR(2, H, l) = µH.
Аналогично получим выигрыши в информационном множестве L. Следовательно,для m {H, L} мы должны иметь
|
h, |
µm < 21 |
||
|
{ } |
µm > |
1 |
|
|
l, |
2 |
(4.8) |
|
|
a(m) = |
h, l , |
µm = |
21 |
3.Каким должна быть стратегия игрокаS,в зависимости от стр атегии игрокаR?При мы получим
(H, L), a(H) = h, a(L) = h
(m(1), m(2)) =
(L, L), a(H) = h, a(L) = l
(H, H), a(H) = l, a(L) = h
(H, L), a(H) = l, a(L) = l
При c > 1 мы будем иметь (m(1), m(2)) = (H, L) вне зависимости от a(H) и a(L).
Равновесием в этой игре является набор (m (1), m (2), a (H), a (L), µH , µL),удовлетворяющий всем трем перечисленным выше условиям.Число и тип равно весий зависят от значения переметра c:

|
170 |
ГЛАВА4.ДИНАМИЧЕСКИЕ ИГРЫ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ |
1.Если c < 1 и p ≥ 12 ,то равновесия два:
(a)m (1) = m (2) = H, a (H) = l, a (L) = h, µH = p, µL [0, 12 ].
(b)m (1) = m (2) = L, a (H) = h, a (L) = l, µL = p, µH [0, 12 ].
2.Если c < 1 и p < 12 ,то равновесия в чистых стратегиях нет.
3.Если c > 1,то равновесие в чистых стратегиях одно: m (1) = H, m (2) = L, a (H) = l, a (L) = h, µH = 1, µL = 0.
Мы видим,что возможны два типа равновесий.Первые два равно весия являются смешивающими,в которых игрокиSразных типов выбирают одно и то же действи е.То есть,в нашей истории,это означает,что и крутой,и слабак будут заказыва ть один и тот же напиток.В каком случае это возможно?Во-первых,необходимо,чтобы число кр утых было достаточно большим (p ≥ 12 ).В таком случае хулиган,видя,что вошедший заказывает «то же,что и все»,поостережется нападать,так как вероятность нарваться на «крутого» будет слишком велика.Во-вторых необходимо,чтобы издержки от употребления нелюбимого нап итка были ниже,чем издержки от драки.Если оба типа игроков заказывают один и тот же напит ок,то обязательно получится так,что для одного из них этот напиток будет нелюбимым.Если издержки от употребления нелюбимого напитка слишком высоки,то он сможет увеличить с вой выигрыш,выбрав свой любимый напиток — даже если ему придется после этого подраться.
Второй тип равновесий — разделяющие,в которых игроки S разных типов выбирают разные
|
действия.В нашем случае,такое равновесие одно,в котором к |
рутой будет выбирать пиво,а |
|
слабак — кофе.Такое равновесие будет возсожно,если издерж |
ки от употребления нелюбимого |
|
напитка более высоки,чем издержки от драки. |
Что же происходит в том случае,если c < 1 и p < 12 ?Равновесия в чистых стратегиях нет, однако согласно теореме должно существовать совершенное равновесие,которое обязательно будет предполагать наличие у хотя бы одного из игроков смешанных стратегий.Попробуем найти равновесие в смешанных стратегиях в этой игре.Пусть q1, q2 [0, 1] — вероятности,с которыми игрок S выбирает действие H в том случае,когда его тип равен 1 или 2,соответственно. По правилу Байеса,вера игрока R в информационном множестве H будет равна
|
µH = |
pq1 |
(4.10) |
|||
|
pq1 + (1 − p)q2 |
|||||
|
при условии того,что |
pqH > 0 или (1 − p)qL > 0, и µH [0, 1] в обратном случае.Аналогично, |
||||
|
получим |
|||||
|
µL = |
p(1 − q1) |
(4.11) |
|||
|
p(1 |
− q1) + (1 − p)(1 − q2) |
||||
|
при условии того,что |
pqH > 0 или (1 − p)qL > 0, и µL [0, 1] в обратном случае. |
Пусть vH , vL — вероятности,с которыми игрок R выберет действие h в информационных
|
множествах H и L,соответственно.Найдем функцию реакции игрока |
R.Эта функция будет |
||||
|
определена относительно вер µH , µL: |
|||||
|
1, |
µH < 21 |
||||
|
0, |
µH > |
1 |
, |
||
|
2 |
(4.12) |
||||
|
vH = |
[0,1], |
µH = |
21 |
||
|
1, |
µL < 21 |
||||
|
0, |
µL > |
1 |
|||
|
2 . |
(4.13) |
||||
|
vL = |
[0,1], |
µL = |
21 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Сильное секвенциальное равновесие.
Секвенциальные равновесия и равновесия Нэша.
Интуитивно ясно, что понятие секвенциального равновесия является усилением понятия равновесия по Нэшу. Во всяком случае, мы видели в примере, что не всякое равновесие Нэша может быть поддержано системой вер до секвенциального.
Скажем точнее. Пусть а – профиль поведенческих стратегий, образующий равновесие Нэша. Тогда правило Байеса однозначно определяет веры fi(h) в тех информационных множествах, которые достижимы (при стратегиях а) с положительной вероятностью (лежат на пути игры). Тогда стратегии, а секвенциально рациональны в таких информационных множествах и при таких верах. В самом деле, в противном случае игрок, делающий ход в h7 мог бы получить больший (условный, в ’’подыгре”, начинающейся в К) выигрыш, изменив стратегии в этой подыгре.
Обратно, пусть а – профиль поведенческих стратегий, секвенциально рациональных в информационных множествах, лежащих на пути игры. Мы утверждаем, что а – равновесие Нэша. В самом деле, представим, что некоторый игрок / может улучшить результат, применив альтернативную стратегию е’. Но тогда он должен сыграть лучше сг* в некотором своем информационном множестве h. Нужно взять самое первое такое множество; так как до него стратегии не менялись, то не менялись и веры. Но в таком случае стратегия Oi была не секвенциально рациональной в этом h.
Теорема. Профиль поведенческих стратегии, а является равновесием Нэша тогда и только тогда., когда найдется такая система вер fi, что:
(1) система fi слабо согласована с профилем а;
(2) профиль а секвенциально рационален (при верах n) во всех информационных множествах, лежащих на пути игры.
Отсюда можно сделать два важных вывода. Первый – вдоль пути игры (где веры однозначно определяются правилом Байеса) равновесные стратегии секвенциально рациональны. Второй – секвенциальная рациональность усиливает равновесность (по Нэшу) тем, что требует секвенциальную рациональность не только вдоль равновесного пути, но и во всех остальных информационных множествах. Этим она сближается с требованием совершенства относительно подыгр. И действительно, из приведенного выше предложения легко получить, что любое секвенциальное равновесие совершенно к подыграм.
В сильном секвенциальном равновесии мы более строго подходим к формированию вер в информационных множествах, лежащих вне пути игры. Рассмотрим пример, апеллирующий к структурной состоятельности. Пусть игра имеет вил
 И пусть первый играет и. Каковы могут быть веры у 2-го? Так как 1-й не различает эти состояния (правое и левое), он и отклоняться в них должен одинаково. Поэтому естественно считать, что веры 2-го – это .2 и .8.
И пусть первый играет и. Каковы могут быть веры у 2-го? Так как 1-й не различает эти состояния (правое и левое), он и отклоняться в них должен одинаково. Поэтому естественно считать, что веры 2-го – это .2 и .8.
Дадим теперь общее определение сильной согласованности вер со стратегиями. Поведенческий профиль о называется вполне смешанным, если любая позиция достигается с положительной вероятностью. В этом случае правило Байеса однозначно определяет согласованную с а систему вер ц(а).
Определение. Система вер ц называется сильно согласованной с профилем стратегий а, если существует последовательность вполне смешанных стратегических профилей ап, такая что оп сходится к а, а. соответствующие веры ц,п = ц,{оп) сходятся к ц„
Секвенциальное равновесие – это пара (а, ц), что ц сильно согласована с а, а, а секвенциально рациональна относительно ц„
 Следующий пример демонстрирует слабое секвенциальное равновесие, которое не сильное секвенциальное. Пусть третий игрок верит, что реализуется левая вершина в его информационном множестве. Такая вера вместе со стратегиями (R, А, г) является слабым секвенциальным равновесием. Однако оно не является сильным секвенциальным равновесием, потому что вера третьего, сильно согласованная со стратегиями R и А, указывает на правую вершину в информационном множестве 3. Сильным секвенциальным равновесием (единственным?) здесь будет (И. I). /).
Следующий пример демонстрирует слабое секвенциальное равновесие, которое не сильное секвенциальное. Пусть третий игрок верит, что реализуется левая вершина в его информационном множестве. Такая вера вместе со стратегиями (R, А, г) является слабым секвенциальным равновесием. Однако оно не является сильным секвенциальным равновесием, потому что вера третьего, сильно согласованная со стратегиями R и А, указывает на правую вершину в информационном множестве 3. Сильным секвенциальным равновесием (единственным?) здесь будет (И. I). /).
Теорема.Любая конечная игра имеет сильное секвенциальное равновесия.
Отметим также, что даже сильные секвенциальное равновесия не всегда исключают слабо доминирующие стратегии.
Вопросы для самоконтроля:
1. Дайте определение секвенциального равновесия? Приведите примеры.
2. Дайте определение слабого секвенциального равновесия? Приведите примеры.
3. Дайте определение сильного секвенциального равновесия? Приведите примеры.
Список литературы
Основная:
- Оуэн Г. Теория игр. Учебное пособие. Санкт-Петербург: ЛКИ, 2008 – 229 с.
- Мазалов В.В. Математическая теория игр и приложения: Учебное пособие. М.: Лань, 2010
- Губко М.В., Новиков Д.А Теория игр в управлении организационными процессами [Электронный ресурс]: Учебное пособие. М.: Наука, 2005 – 138 с.
- Даниловцева Е.Р., Теория игр: основные понятия: текст лекций [Электронный ресурс]. Санкт-Петербург: СПбГУАП, 2003 – 36 с.
- Коковин С.Г., Лекции по теории игр [Электронный ресурс]. Новосибирск: Типография НГУ, 2010 г. – 91 с.
Дополнительная:
- Самаров К.Л. Элементы теории игр [Электронный ресурс]. Учебное пособие. Новосибирск: Типография НГУ, 2010 г. – 91 с.
- Волков Ю.И., Волков А.Ю. Теория игр [Электронный ресурс]. Тюмень, ТГИМЭУП, 2002.
- Захаров С.Д. Курс теории игр [Электронный ресурс]. Тюмень, ТГИМЭУП, 2002.
4. Данилов В.И. Лекции по теории игр [Электронный ресурс]. КЛ/2002/001. М.: РЭШ, 2002.-192 с.
- Курсы
- Лекции
- Лекторы
- Коллекции

Определение сильного и слабого секвенциальных равновесий
ДЛЯ ЭТОЙ ЛЕКЦИИ
ПОКА НЕТ СЕКЦИЙ
Но вы можете ускорить
процесс их появления:
непосредственно помогая
с с составлением описаний
(напишите нам на dev.liot@mipt.ru)
или поддержав работу
активистов пожертвованиями.
ПОЖЕРТВОВАТЬ
3 024 просмотра
21 августа 2015
- О лекции
Лекторы

доктор физико-математических наук
Комментарий:
Осталось 512 из 512 символов.
Осталось 0 из 512 символов.
Комментарий не может быть пустым.
Следующая лекция

МАТЕМАТИКА 00:18:14
27-я лекция из курса:
Предыдущая лекция

МАТЕМАТИКА 00:08:38
25-я лекция из курса:
Отзыв о лекции
Определение сильного и слабого секвенциальных равновесий
Пожалуйста, заполните поле комментария или поставьте хотя бы одну оценку.
Ваш отзыв отправлен. Спасибо за помощь в улучшении Лектория!
Ошибка при отправке отзыва. Попробуйте ещё раз позже.
