Когда мы имеем дело со смесями газов, важно знать, что они имеют такие характеристики, как парциальный объем и парциальное давление. Для начала определим, что такое смесь идеальных газов.
Смесь идеальных газов – это смесь нескольких газообразных веществ, которые при заданных условиях не будут вступать в определенные химические реакции.
При смене условий (например, повышении температуры, понижении давления) газовая смесь все же может вступать во взаимодействие. Важный параметр любой такой смеси – так называемая весовая концентрация gi i-ного газа-компонента.
Здесь:
- N – количество газов, из которых состоит смесь;
- xi i-го газа – молярная концентрация указанного газа в составе смеси;
- νi – количество молей i-го газа, присутствующего в смеси.
Понятие парциального давления
Парциальное давление – это особая характеристика, описывающая состояние компонентов смеси идеальных газов. Сформулируем основное определение:
Парциальным называется давление pi, которое могло бы создаваться i-ым газом в смеси при условии отсутствия остальных газов и сохранения исходного объема и температуры.
Формула парциального давления будет выглядеть так:
pi=miμiRTV=μiRTV
Объем смеси здесь обозначен буквой V, ее температура – T.
Следует подчеркнуть, что поскольку средние кинетические энергии молекул смеси равны, то существует и равенство температур всех компонентов газовой смеси, находящейся в состоянии термодинамического равновесия.
Для нахождения давления смеси идеальных газов нужно воспользоваться законом Дальтона в следующей формулировке:
p=∑i=1Npi=RTV∑i=1Nνi
Исходя из него, мы можем выразить парциальное давление так:
pi=xip.
Понятие парциального объема
У газовой смеси также есть такая характеристика, как парциальный объем.
Парциальный объем Vi i-газа в газовой смеси – это такой объем, который мог бы иметь газ при условии отсутствия всех остальных газов и сохранении исходной температуры и объема.
Если речь идет о смеси идеальных газов, то к ней применим закон Амага:
V=∑i=1NVi
В самом деле, при выражении νi из формулы выше у нас получится следующее:
νi=pViRT; p=RTVpRT∑i=1NVi→V=∑i=1NVi
Для расчета парциального объема газа используется следующая формула:
Vi=xiV.
Нам известно, что параметры, определяющие состояние смеси идеальных газов, будут подчиняться уравнению Менделеева-Клайперона. Формула будет выглядеть так:
pV=mμsmRT.
Все параметры данного уравнения будут относиться ко всей смеси. Это же уравнение удобнее записать так:
pV=mRsmT.
Здесь параметры Rsm=Rμsm=R∑i=1Nqiμi означают удельную газовую постоянную смеси.
Условие: имеется сосуд объемом 1 м3, в котором находится 0,10·10-3 кг гелия и 0,5·10-3 кг водорода. Постоянная температура равна 290 К. Вычислите давление смеси и парциальное давление гелия в нем.
Решение
Начнем с вычисления количества молей каждого компонента смеси. Для этого можно использовать формулу:
νi=miμi
Зная, что молярная масса водорода, согласно таблице Менделеева, составляет μH2=2·10-3 кгмоль, мы можем найти количество его молей в смеси по формуле:
νH2=mH2μH2
Считаем, что получится:
νH2=0,5·10-32·10-3=0,25 (моль).
Точно такие же расчеты проводим и для гелия, зная, что μHe=4·10-3 кгмоль:
Теперь с помощью уравнения Менделеева-Клайперона можно найти парциальное давление каждого компонента:
piV=νiRT.
Сначала рассчитаем давление водорода:
pH2V=νH2RT→pH2=νH2RTV
Парциальное давление будет равно:
pH2=0,25·8,31·2901=602,5 (Па).
Теперь то же самое подсчитываем для гелия:
pHe=0,025·8,31·2901=60,25 (Па).
Чтобы найти общее давление смеси газов, сложим сумму давлений ее составляющих:
p=pH2+pHe
Подставляем полученные ранее значения и находим нужный результат:
p=602,5+60,25=662,75 (Па).
Ответ: общее давление смеси составляет 662,75 Па, а парциальное давление гелия в смеси равно 60,25 Па.
Условие: дана смесь газов, состоящая из 1 кг углекислого газа и 0,5 кг O2. Если считать их идеальными, какой объем они будут занимать при давлении в 1 атм? Температура смеси равна 300К.
Решение
Начнем с вычисления общей массы газовой смеси.
m=mO2+mCO2
Значит, m=1+0,5=1,5.
Переходим к вычислению массовых компонентов смеси:
gO2=0,51,5=0,33;gCO2=11,5=0,67.
Тогда газовая постоянная смеси будет равна:
Rsm=R∑i=1Ngiμi
Rsm=8,310,3332·10-3+0,6746·10-3=200 ДжкгК.
Объем смеси вычисляем с помощью уравнения Менделеева-Клайперона:
Vsm=msmRsmTsmpsm
Вспомнив, что по условию давление равно 1 атм, что равно105 Па, вычислим объем:
Vsm=1,5·200·300105=0,9 м3.
Ответ: при указанных условиях смесь займет объем, равный 0,9 м3.
Смесям идеальных газов характерно свойство аддитивности двух показателей: парциального давления и объёма. Другими словами, любому включённому в смесь инертному газу характерно такое поведение, какое было бы, если б он в единственном числе заполнял предлагаемый объём. Для лучшего понимания разумно разобраться, что выражают указанные величины.
Определения
Давление – действующая на единицу поверхности сила, прямопропорциональная числу и скоростью сталкивающихся с этой поверхностью молекул, зависящей от температуры.
Парциальное давление – давление, оказываемое компонентом газовой смеси, при условии удаления других компонентов из занимаемого объёма, сохраняя этот объём и текущую температуру.
Объём – ограниченное чертой трёхмерное пространство, вмещающее вещество и отображающее его форму.
Парциальный объём – объём, занимаемый компонентом газовой смеси, при условии удаления других компонентов из занимаемого объёма, сохраняя первоначальное давление и температуру.
Идеальный газ – научная модель для познания газов, не учитывающая силу молекулярного взаимодействия.
Смесь идеальных газов – это совокупность газов, каждый из которого, находясь в смеси, при сохранении заданных условий, не вступает в химическую реакцию с остальными компонентами.
Говоря об идеальных газах и их смеси, следует понимать, что изменение условий, например температуры или давления, всё же может спровоцировать химическую реакцию. Важным параметром такой смеси является молярная (весовая) концентрация газового компонента. Данная величина измеряется в мг/м3 и показывает количество конкретного компонента в единице объёма газовой смеси.
Парциальное давление
Описывая характеристику состояния компонентов идеальной смеси газообразных веществ, парциальное давление, создаваемое i-ым газом в случае удаления других компонентов из сохраняемых условий, является показателем pi.
Формула
Формула парционального давления:
[p i=frac{m_{i}}{mu_{i}} frac{R T}{V}=mu_{i} frac{R T}{V}]
Где V– объём смеси, R = 8,31
Дж/моль*K– универсальная газовая постоянная, а T –
температура.
Следует отметить, что равность средней кинетической энергии находящихся в смеси молекул определяет равенство температур всех компонентов термодинамически уравновешенной газовой смеси. Найти общее давление смеси идеальных газов представляется возможным через закон Дальтона, отражаемый аддитивность парциальных давлений, а именно [p=sum p_{i}].
Пользуясь данным законом, найдём давление смеси идеальных газов через следующую формулировку: [p=sum_{i}^{N}=1 rightarrow p_{i}=frac{R T}{V} sum_{i}^{N}=1^{v_{i}}], где N – количество вошедших в смесь газов, vi– количественный показатель молей i-го газа. Отсюда парциальное давление можно выразить формулой [p_{i}=x_{i} p], где xi – молярная концентрация i-го газа.
Понятие парциального объёма
Описывая характеристику состояния компонентов идеальной смеси газообразных веществ, парциальный объём, занимаемый i-ым газом в случае удаления других компонентов из сохраняемых условий, является показателем Vi. Аддитивность парциального объёма определяет закон Амага, выраженный формулой [V=sum_{i}^{N}=1 V_{i}].
Формула
Пользуясь данным законом, можно вывести формулу нахождения парциального объёма через следующую формулировку:
[v_{i}=frac{p^{V_{i}}}{R T}]; [p=frac{R T}{V} frac{p}{R T} sum_{i}^{N}=mathbf{1}^{V}_{i}] , отсюда
следует, что — [boldsymbol{V=sum_{i}^{N}=1^{V_{i}}}, text{ а } boldsymbol{V_{i}=x_{i} V}].
Зная, что характеризующие состояние смеси инертных газов показатели подчиняются уравнению Менделеева-Клапейрона, выведем формулу:
[p V=frac{m}{mu_{s m}} R T] данное уравнение свои параметры относит ко всей газовой смеси.
[pV=mR_{s m} T] такой вариант уравнения содержит показатель Rsm, обозначающий удельную газовую составляющую смеси.
Уравнение Менделеева-Клапейрона показывает возможность изменения трёх характеризующих состояние идеального газа параметров.
Нет времени решать самому?
Наши эксперты помогут!
Примеры вычисления парциального давления и объёма
Задача №1
Условие: в сосуде объёмом 2 м3, при постоянной температуре 290 К находится 0,20*10-3 кг гелия и 1*10-3 кг водорода. Необходимо вычислить давление смеси и парциальное давление гелия.
Решение.
Сначала вычислим количество молей каждого компонента, используя следующую формулу:
[mathrm{v}{mathrm{i}}=frac{mathrm{m}{mathrm{i}}}{mu_{mathrm{i}}}]
Для расчёта количество молей водорода в смеси нам понадобится его молярная масса, которую возьмём из таблицы Менделеева:
[mu_{mathrm{H}_{2}}=2 * 10^{-3} frac{mathrm{кг}}{text { моль }}]
Теперь можно найти количество молей водорода в смеси:
[mathrm{v}_{mathrm{H}_{2}}=frac{mathrm{m}_{mathrm{H}_{2}}}{mu_{mathrm{H}_{2}}}=frac{1 * 10^{-3}}{2 * 10^{-3}}=0,5 text { (моль) }]
Зная молярную массу гелия из таблицы Менделеева, рассчитаем количество молей гелия в смеси:
[mathrm{v}_{mathrm{He}}=frac{mathrm{m}_{mathrm{He}}}{mu_{mathrm{He}}}=frac{4 * 10^{-3}}{20 * 10^{-3}}=0,2 text { (моль) }]
Теперь можно найти парциальное давление каждого из компонентов с помощью уравнения Менделеева-Клапейрона:
[mathrm{p}_{mathrm{i}} mathrm{V}=mathrm{v}_{mathrm{i}} mathrm{RT}]
Сначала нужно рассчитать давление водорода:
[mathrm{p}_{mathrm{H}_{2}} mathrm{~V}=mathrm{v}_{mathrm{H}_{2}} mathrm{RT} rightarrow mathrm{p}_{mathrm{H}_{2}}=frac{mathrm{v}_{mathrm{H}_{2}} mathrm{RT}}{mathrm{V}}=frac{0,5 * 8,31 * 290}{1}=1205 text { (Па) }]
Рассчитаем парциальное давление гелия:
[mathrm{p}_{mathrm{He}}=frac{mathrm{v}_{mathrm{He}} mathrm{RT}}{mathrm{V}}=frac{0,2 * 8,31 * 290}{1}=482 text { (Па) }]
Теперь найдём полное давление газовой смеси, сложив значения компонентов:
[mathrm{p}=mathrm{p}_{mathrm{H}_{2+}} mathrm{p}_{mathrm{H}}=1205+482=1687 text { Па }]
Ответ: парциальное давление гелия равно 482 Па, а общее давление 1205 Па.
Задача №2
Условие: идеальная газовая смесь состоит из 0,5 кг углекислого газа и 0,25 кг кислорода, какой объём они займут, если давление равно 1 атм, а температура смеси равна 300 К?
Решение.
Найдём суммарную массу газовой смеси:
[mathrm{m}=mathrm{m}_{mathrm{O}_{2}}+mathrm{m}_{mathrm{CO}_{2}}=0,5+0,25=0,75 text { (кг) }]
Вычислим массовые компоненты смеси:
[g_{mathrm{O}_{2}}=frac{0,25}{0,75}=0,33] [mathrm{g}_{mathrm{CO}_{2}}=frac{0,5}{0,75}=0,67]
Тогда газовая постоянная смеси равняется:
[mathrm{R}_{mathrm{sm}}=mathrm{R} sum_{mathrm{i}=1}^{mathrm{N}} frac{mathrm{g}_{mathrm{i}}}{mu_{mathrm{i}}}=8,31left(frac{0,33}{32 * 10^{-3}}+frac{0,67}{46 * 10^{-3}}right)=200left(frac{text { Дж }}{text { кгК }}right)]
Пользуясь уравнением Менделеева-Клапейрона, и, зная, что 1 атм равна 105 Па,вычислим объём смеси:
[mathrm{V}_{mathrm{sm}}=frac{mathrm{m}_{mathrm{sm}} mathrm{R}_{mathrm{sm}} mathrm{T}_{mathrm{sm}}}{mathrm{P}_{mathrm{sm}}}=frac{0,75 * 200 * 300}{10^{5}}=0,45left(mathrm{м}^{3}right)]
Ответ: при заданных условиях смесь займёт 0,45 м3.
Навык определения парциальных давлений и объёма актуален в машиностроении, энергетике и других промышленностях, связанных с использованием тепловых двигателей, приводимых в действие парами высокой температуры.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 мая 2021 года; проверки требуют 4 правки.

Прибор Рамзая для обнаружения парциального давления.
Во внутреннем сосуде Р из палладия находится смесь азота и водорода под общим давлением в 1 атм. Сосуд Р соединён с дифференциальным манометром и помещён в сосуд большего размера. При высоких температурах водород легко диффундирует через палладиевую оболочку, и стенки сосуда Р становятся полупроницаемыми — они проницаемы для водорода, но непроницаемы для азота. Пропуская нагретый водород с давлением в 1 атм через больший сосуд, исследователь обнаружит, что давление смеси газов в сосуде Р превысит 1 атм на величину парциального давления азота при данной температуре.
Парциа́льное давление (лат. partialis «частичный» от pars «часть») — давление, которое имел бы газ, входящий в состав газовой смеси, если бы он один занимал объём, равный объёму смеси при той же температуре[1][2][3]. Общее давление газовой смеси является суммой парциальных давлений её компонентов.
В химии парциальное давление газа в смеси газов определяется как указано выше. Парциальное давление газа, растворённого в жидкости, является парциальным давлением того газа, который образовался бы в фазе газообразования в состоянии равновесия с жидкостью при той же температуре. Парциальное давление газа измеряется как термодинамическая активность молекул газа. Газы всегда будут вытекать из области с высоким парциальным давлением в область с более низким давлением; и чем больше разница, тем быстрее будет поток. Газы растворяются, диффундируют и реагируют соответственно их парциальному давлению и не обязательно зависимы от концентрации в газовой смеси.
Законы Дальтона парциального давления[править | править код]
Для идеального газа парциальное давление в смеси равно давлению, которое будет оказываться, если бы он занимал тот же объём, что и вся смесь газов, при той же температуре. Причина этого в том, что между молекулами идеального газа по определению не действуют силы притяжения или отталкивания, их соударения между собой и со стенками сосуда абсолютно упруги, а время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями. Насколько условия реально существующей смеси газов близки этому идеалу, настолько общее давление смеси равно сумме парциальных давлений каждого газа смеси, как это формулирует закон Дальтона[4]. Например, дана смесь идеального газа из азота (N2), водорода (H2) и аммиака (NH3):
, где:




Смеси идеальных газов[править | править код]
Мольная доля отдельных компонентов газа в идеальной газовой смеси может быть выражена в пределах парциальных давлений компонентов или молей компонентов:
и парциальное давление отдельных компонентов газов в идеальном газе может быть получено при использовании следующего выражения:
, где:





Мольная доля отдельного компонента в газовой смеси равна объёмной доле этого компонента в газовой смеси[5].
См. также[править | править код]
- Пар
- Газ, Идеальный газ и Уравнение состояния идеального газа
- Мольная доля и Моль
- Законы Дальтона
- Объёмный процент
- Закон Генри
Примечания[править | править код]
- ↑ Парциальное давление. Статья в физической энциклопедии. Дата обращения: 6 июля 2012. Архивировано 5 июля 2012 года.
- ↑ Charles Henrickson. Chemistry (неопр.). — Cliffs Notes, 2005. — ISBN 0-764-57419-1.
- ↑ Парциальное давление. Большая советская энциклопедия. www.booksite.ru. Дата обращения: 11 января 2021. Архивировано 13 января 2021 года.
- ↑ Dalton’s Law of Partial Pressures. Дата обращения: 29 января 2010. Архивировано из оригинала 22 декабря 2008 года.
- ↑ Pittsburgh University chemical engineering class notes. Дата обращения: 29 января 2010. Архивировано из оригинала 23 апреля 2009 года.
Загрузить PDF
Загрузить PDF
В химии «парциальным давлением» называют давление, которое оказывает отдельно взятый компонент из газовой смеси внешней среды, например, на колбу, баллон или границу атмосферы. Вы можете подсчитать давление каждого газа, если знаете его количество, какой объем он занимает и какова его температура. Затем вы можете сложить парциальные давления и найти общее парциальное давление смеси газов, или найдите вначале общее давление, а затем — парциальное.
-

1
Примите каждый газ как «идеальный». В химии «идеальный газ» — тот, который взаимодействует с другими веществами, не вступая с ними в соединение. Отдельные молекулы могут сталкиваться друг с другом и отталкиваться, как шары для бильярда, не деформируясь при этом.[1]
- Давление идеального газа возрастает, если его поместить в меньший объем, и уменьшается, если газ находится в большем объеме. Это отношение называется законом Бойля-Мариотта, по имени ученых Роберта Бойля и Эдма Мариотта. Математическая запись закона: k = P x V или, упрощенно, k = PV, где k представляет константу соотношения, P — давление, а V — объем.[2]
- Давление может быть указано в нескольких различных единицах. Одна из них, Паскаль (Па), определяется как сила в 1 ньютон, приложенная к площади в 1 квадратный метр. Другой вариант представления давления — в атмосферах (атм). Эта единица определяется как давление земной атмосферы на уровне моря. Давление в 1 атмосферу равно 101,325 Па.[3]
- Температура идеального газа возрастает при увеличении его объема и снижается при уменьшении объема. Это отношение называют законом Чарльза, по имени Жака Чарльза. Математическая запись закона: k = V / T, где k — константа соотношения между объемом и температурой, V вновь представляет объем газа, а T — его температуру.[4]
[5]
- Температура газов в этих уравнениях приведена в градусах Кельвина, ее можно найти, прибавив 273 к числу градусов Цельсия в температуре газа.
- Эти два отношения можно объединить в одно уравнение: k = PV / T, которое также можно записать как PV = kT.
- Давление идеального газа возрастает, если его поместить в меньший объем, и уменьшается, если газ находится в большем объеме. Это отношение называется законом Бойля-Мариотта, по имени ученых Роберта Бойля и Эдма Мариотта. Математическая запись закона: k = P x V или, упрощенно, k = PV, где k представляет константу соотношения, P — давление, а V — объем.[2]
-

2
Определите количество газов. У газов есть и масса, и объем. Объем обычно измеряют в литрах (л), но есть два варианта подсчета массы.
- Обычно массу измеряют в граммах или, если она достаточно велика, в килограммах.
- Поскольку газы обычно весят очень мало, их масса также вычисляется в отдельной единице измерения, называемой молекулярной массой, или молярной массой. Молярная масса определяется как сумма атомарных весов всех атомов в газообразном веществе, каждый атом сравнивается с массой карбона (12)[6]
- Поскольку атомы и молекулы слишком малы, чтобы работать с ними непосредственно, количество газа определяется в молях. Количество молей в данном газе можно найти, разделив массу на молярную массу, значение отмечается буквой n.
- Мы можем заменить постоянную k константу в уравнении газа числом n, количеством молей (mol), и ввести новую константу R. Тогда уравнение будет записано в виде nR = PV/T или PV = nRT.[7]
- Значение R зависит от единиц, в которых измеряются давление газа, объемы и температура. Для объема в литрах, температуры в Кельвинах и давления в атмосферах, значение равно 0,0821 л атм/K мол. Это можно записать в виде 0,0821 л атм K-1 мол -1, чтобы избежать использования разделительной черты при указании единиц измерения.[8]
-

3
Понимание закона Дальтона о парциальном давлении. Закон, открытый химиком и физиком Джоном Дальтоном, который первым предположил, что химические элементы состоят из отдельных атомов,[9]
гласит: общее давление смеси газов равняется сумме давлений каждого газа в смеси.- Закон Дальтона можно записать в таком виде: Pобщее = P1 + P2 + P3 … с таким количеством слагаемых после знака равенства, каково количество газов в смеси.
- Уравнение закона Дальтона можно расширить при работе с газами, чье индивидуальное давление неизвестно, но для которых известны температура и объем. Парциальное давление газа — такое же, как и для равного объема газа, полностью занимающего отведенный объем.
- Для каждого парциального давления мы можем переписать уравнение идеального газа. Вместо PV = nRT мы может оставить только P в левой части перед знаком равенства. Чтобы сделать это, обе части уравнения нужно разделить на V: PV/V = nRT/V. Две V слева сокращаются, остается P = nRT/V.
- Затем для каждого P справа мы можем выполнить замену, вписав уравнение парциального давления: Pобщее =(nRT/V) 1 + (nRT/V) 2 + (nRT/V) 3 …
Реклама
-

1
Определите уравнение парциального давления для газов, с которыми вы работаете. Для вычислительных целей возьмем пример: в колбе объемом 2 литра содержится 2 газа, нитроген (N2), оксиген (O2) и карбон диоксид, углекислый газ (CO2). Каждого газа — по 10 г, температура каждого газа в колбе равна 37 градусам Цельсия. Нужно найти парциальное давление каждого газа и общее давление смеси газов на емкость.
- Наше уравнение парциального давления будет выглядеть следующим образом: Ptotal = Pнитроген + Pоксиген + Pкарбон диоксид.
- Поскольку мы пытаемся найти давление, которое оказывает каждый из газов, знаем объем и температуру и можем найти количество молей каждого газа, основываясь на массе вещества, мы можем переписать уравнение в следующей форме: Pобщее =(nRT/V) нитроген + (nRT/V) оксиген + (nRT/V) карбон диоксид
-

2
Переведите температуру в градусы Кельвина. Температура по Цельсию равна 37 градусам, потому мы добавим 273 к 37 и получим 310 градусов K.
-

3
Найдите количество молей каждого газа в образце. Число молей газа равно массе газа, деленной на его молярную массу,[10]
которая, как уже говорилось, равна сумме весов всех атомов в составе.- Для нашего первого газа, нитрогена (N2), каждый атом обладает атомарной массой 14. Поскольку нитроген содержит два атома (состоит из двухатомных молекул), мы должны умножить 14 на 2, чтобы найти молярную массу нитрогена, она равна 28. Затем мы делим массу в граммах, 10 г, на 28, чтобы получить количество молей, которое приблизительно равно 0,4 моль.
- У второго газа, оксигена (O2), масса каждого атома равна 16. Оксиген также двухатомный газ, потому мы умножаем 16 на 2 и получаем молярную массу, равную 32. Разделив 10 г на 32, мы получим примерно 0,3 моль оксигена в составе образца смеси газов.
- Третий газ, карбон диоксид (CO2), состоит из 3 атомов: одного атома карбона с атомарной массой 12 и двух атомов оксигена, каждый с атомарной массой 16. Мы складываем все три веса: 12 + 16 + 16 = 44 составляет молярную массу. Разделив 10 г на 44, мы получим примерно 0,2 моля карбон диоксида.
-

4
Подставьте значения для молей, объема и температуры. Наше уравнение будет выглядеть так: Pобщее =(0,4 * R * 310/2) нитроген + (0,3 *R * 310/2) оксиген + (0,2 * R *310/2) карбон диоксид.
- Для простоты мы оставили текущие значения единиц измерения. Эти единицы уйдут после математических вычислений, и останутся только те, которые участвуют в определении давления.
-

5
Подставьте значение константы R. Мы будем указывать парциальное и общее давление в атмосферах, потому используем значение R, равное 0,0821 л атм/K моль. Подстановка этого значения в уравнение дает нам Pобщее =(0,4 * 0,0821 * 310/2) нитроген + (0,3 *0,0821 * 310/2) оксиген + (0,2 * 0,0821 * 310/2) карбон диоксид.
-

6
Подсчитайте парциальное давление каждого газа. Сейчас все значения на месте, пора перейти к математическим вычислениям.
- Чтобы найти парциальное давление нитрогена, умножим 0,4 моль на нашу константу 0,0821 и температуру 310 градусов K, затем разделим на 2 литра: 0,4 * 0,0821 * 310/2 = 5,09 атм, приблизительно.
- Для получения парциального давления оксигена умножим 0,3 моль на константу 0,0821 и температуру 310 градусов K, затем разделим на 2 литра: 0,3 *0,0821 * 310/2 = 3,82 атм, приблизительно.
- Чтобы найти парциальное давление карбон диоксида, умножаем 0,2 моль на константу 0,0821 и температуру 310 градусов K, затем делим на 2 литра: 0,2 * 0,0821 * 310/2 = 2,54 атм, приблизительно.
- Теперь сложим полученные значения давлений и найдем общее давление: Pобщее = 5,09 + 3,82 + 2,54, или 11,45 атм, приблизительно.
Реклама
-

1
Определите парциальное давление, как и раньше. Вновь, возьмем в пример колбу на 2 литра с тремя газами: нитрогеном (N2), оксигеном (O2) и карбон диоксидом (CO2). У нас по 10 г каждого газа, температура каждого газа в колбе равна 37 °C.
- Температура по Кельвину будет такой же, 310 градусов, как и раньше, у нас будет примерно 0,4 моль нитрогена, 0,3 моль оксигена и 0,2 моль карбон диоксида.
- Мы также будем указывать давление в атмосферах, потому будем использовать значение 0,0821 л атм/K моль для константы R.
- Таким образом, наше уравнение парциального давления на текущий момент выглядит так же, как раньше: Pобщее =(0,4 * 0,0821 * 310/2) нитроген + (0,3 *0,0821 * 310/2) оксиген + (0,2 * 0,0821 * 310/2) карбон диоксид.
-

2
Сложите количество молей каждого газа в образце, чтобы найти общее количество молей в смеси газов. Поскольку объем и температура одинаковы для всех газов, не говоря о том, что каждая молярная масса умножается на одну и ту же константу, мы можем использовать распределительное свойство умножения и переписать уравнение в следующем виде: Pобщее = (0,4 + 0,3 + 0,2) * 0,0821 * 310/2.
- Складываем 0,4 + 0,3 + 0,2 = 0,9 моль смеси газов. Это упростит наше выражение до Pобщее = 0,9 * 0,0821 * 310/2.
-

3
Найдите общее давление смеси газов. Умножаем 0,9 * 0,0821 * 310/2 = 11,45 моль, приблизительно.
-

4
Найдите пропорцию каждого газа в смеси. Для этого разделите количество молей каждого газа на общее количество молей в смеси.
- У нас 0,4 моль нитрогена, потому 0,4/0,9 = 0,44 (44 процента) в образце, приблизительно.
- У нас 0,3 моль оксигена, потому 0,3/0,9 = 0,33 (33 процента) в образце, приблизительно.
- У нас 0,2 моль карбон диоксида, потому 0,2/0,9 = 0,22 (22 процента) в образце, приблизительно.
- Хотя в вычислениях выше сумма приблизительных значений в процентах дает всего 0,99, точные значения являются периодическими, так что сумма на самом деле будет равна повторяющимся девяткам после запятой. По определению это то же самое, что 1 или 100 процентов.
-

5
Умножим пропорциональное количество каждого газа на общее давление, чтобы найти парциальное давление.
- Умножаем 0,44 * 11,45 = 5,04 атм, приблизительно.
- Умножаем 0,33 * 11,45 = 3,78 атм, приблизительно.
- Умножаем 0,22 * 11,45 = 2,52 атм, приблизительно.
Реклама
Советы
- Вы заметите небольшую разницу в значениях при вычислении сначала парциального давления, а затем общего, и при подсчете вначале общего, а затем парциального давления. Помните, что приведенные значения даны приблизительно, поскольку они округлены до 1 или 2 знаков после запятой для простоты подсчетов и понимания. Если вы выполняете вычисления самостоятельно без округления, вы заметите или меньшую разницу между значениями или не заметите ее вовсе.
Реклама
Предупреждения
- Знание парциального давления газов может стать вопросом жизни и смерти для дайверов. Слишком низкое парциальное давление кислорода может привести к бессознательному состоянию или смерти, но слишком высокое парциальное давление азота или кислорода также может привести к отравлению.[11]
[12]
Реклама
Вам потребуются
- Калькулятор
- Справочник атомарных весов / молярных масс
Об этой статье
Эту страницу просматривали 82 598 раз.
Была ли эта статья полезной?
From Wikipedia, the free encyclopedia
In a mixture of gases, each constituent gas has a partial pressure which is the notional pressure of that constituent gas as if it alone occupied the entire volume of the original mixture at the same temperature.[1] The total pressure of an ideal gas mixture is the sum of the partial pressures of the gases in the mixture (Dalton’s Law).
The partial pressure of a gas is a measure of thermodynamic activity of the gas’s molecules. Gases dissolve, diffuse, and react according to their partial pressures but not according to their concentrations in gas mixtures or liquids. This general property of gases is also true in chemical reactions of gases in biology. For example, the necessary amount of oxygen for human respiration, and the amount that is toxic, is set by the partial pressure of oxygen alone. This is true across a very wide range of different concentrations of oxygen present in various inhaled breathing gases or dissolved in blood;[2] consequently, mixture ratios, like that of breathable 20% oxygen and 80% Nitrogen, are determined by volume instead of by weight or mass.[3] Furthermore, the partial pressures of oxygen and carbon dioxide are important parameters in tests of arterial blood gases. That said, these pressures can also be measured in, for example, cerebrospinal fluid.
Symbol[edit]
The symbol for pressure is usually P or p which may use a subscript to identify the pressure, and gas species are also referred to by subscript. When combined, these subscripts are applied recursively.[4][5]
Examples:
Dalton’s law of partial pressures[edit]

Schematic showing the concept of Dalton’s Law.
Dalton’s law expresses the fact that the total pressure of a mixture of ideal gases is equal to the sum of the partial pressures of the individual gases in the mixture.[6] This equality arises from the fact that in an ideal gas, the molecules are so far apart that they do not interact with each other. Most actual real-world gases come very close to this ideal. For example, given an ideal gas mixture of nitrogen (N2), hydrogen (H2) and ammonia (NH3):
where:
Ideal gas mixtures[edit]
Ideally the ratio of partial pressures equals the ratio of the number of molecules. That is, the mole fraction 
and the partial pressure of an individual gas component in an ideal gas can be obtained using this expression:
| where: | |

|
= mole fraction of any individual gas component in a gas mixture |
|---|---|

|
= partial pressure of any individual gas component in a gas mixture |

|
= moles of any individual gas component in a gas mixture |

|
= total moles of the gas mixture |

|
= total pressure of the gas mixture |
The mole fraction of a gas component in a gas mixture is equal to the volumetric fraction of that component in a gas mixture.[7]
The ratio of partial pressures relies on the following isotherm relation:
- VX is the partial volume of any individual gas component (X)
- Vtot is the total volume of the gas mixture
- pX is the partial pressure of gas X
- ptot is the total pressure of the gas mixture
- nX is the amount of substance of gas (X)
- ntot is the total amount of substance in gas mixture
Partial volume (Amagat’s law of additive volume)[edit]
The partial volume of a particular gas in a mixture is the volume of one component of the gas mixture. It is useful in gas mixtures, e.g. air, to focus on one particular gas component, e.g. oxygen.
It can be approximated both from partial pressure and molar fraction:[8]
- VX is the partial volume of an individual gas component X in the mixture
- Vtot is the total volume of the gas mixture
- pX is the partial pressure of gas X
- ptot is the total pressure of the gas mixture
- nX is the amount of substance of gas X
- ntot is the total amount of substance in the gas mixture
Vapor pressure[edit]
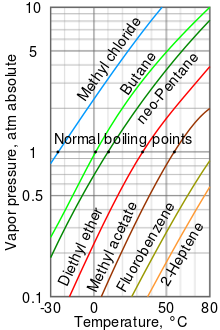
A log-lin vapor pressure chart for various liquids
Vapor pressure is the pressure of a vapor in equilibrium with its non-vapor phases (i.e., liquid or solid). Most often the term is used to describe a liquid’s tendency to evaporate. It is a measure of the tendency of molecules and atoms to escape from a liquid or a solid. A liquid’s atmospheric pressure boiling point corresponds to the temperature at which its vapor pressure is equal to the surrounding atmospheric pressure and it is often called the normal boiling point.
The higher the vapor pressure of a liquid at a given temperature, the lower the normal boiling point of the liquid.
The vapor pressure chart displayed has graphs of the vapor pressures versus temperatures for a variety of liquids.[9] As can be seen in the chart, the liquids with the highest vapor pressures have the lowest normal boiling points.
For example, at any given temperature, methyl chloride has the highest vapor pressure of any of the liquids in the chart. It also has the lowest normal boiling point (−24.2 °C), which is where the vapor pressure curve of methyl chloride (the blue line) intersects the horizontal pressure line of one atmosphere (atm) of absolute vapor pressure. Note that at higher altitudes, the atmospheric pressure is less than that at sea level, so boiling points of liquids are reduced. At the top of Mount Everest, the atmospheric pressure is approximately 0.333 atm, so by using the graph, the boiling point of diethyl ether would be approximately 7.5 °C versus 34.6 °C at sea level (1 atm).
Equilibrium constants of reactions involving gas mixtures[edit]
It is possible to work out the equilibrium constant for a chemical reaction involving a mixture of gases given the partial pressure of each gas and the overall reaction formula. For a reversible reaction involving gas reactants and gas products, such as:
the equilibrium constant of the reaction would be:
| where: | |

|
= the equilibrium constant of the reaction |
|---|---|

|
= coefficient of reactant 
|

|
= coefficient of reactant 
|

|
= coefficient of product 
|

|
= coefficient of product 
|

|
= the partial pressure of  raised to the power of raised to the power of 
|

|
= the partial pressure of  raised to the power of raised to the power of 
|

|
= the partial pressure of  raised to the power of raised to the power of 
|

|
= the partial pressure of  raised to the power of raised to the power of 
|
For reversible reactions, changes in the total pressure, temperature or reactant concentrations will shift the equilibrium so as to favor either the right or left side of the reaction in accordance with Le Chatelier’s Principle. However, the reaction kinetics may either oppose or enhance the equilibrium shift. In some cases, the reaction kinetics may be the overriding factor to consider.
Henry’s law and the solubility of gases[edit]
Gases will dissolve in liquids to an extent that is determined by the equilibrium between the undissolved gas and the gas that has dissolved in the liquid (called the solvent).[10] The equilibrium constant for that equilibrium is:
|
|
(1) |
where:
The form of the equilibrium constant shows that the concentration of a solute gas in a solution is directly proportional to the partial pressure of that gas above the solution. This statement is known as Henry’s law and the equilibrium constant 
Henry’s law is sometimes written as:[13]
|
|
(2) |
where 


Henry’s law is an approximation that only applies for dilute, ideal solutions and for solutions where the liquid solvent does not react chemically with the gas being dissolved.
In diving breathing gases[edit]
In underwater diving the physiological effects of individual component gases of breathing gases are a function of partial pressure.[14]
Using diving terms, partial pressure is calculated as:
- partial pressure = (total absolute pressure) × (volume fraction of gas component)[14]
For the component gas “i”:
- pi = P × Fi[14]
For example, at 50 metres (164 ft) underwater, the total absolute pressure is 6 bar (600 kPa) (i.e., 1 bar of atmospheric pressure + 5 bar of water pressure) and the partial pressures of the main components of air, oxygen 21% by volume and nitrogen approximately 79% by volume are:
- pN2 = 6 bar × 0.79 = 4.7 bar absolute
- pO2 = 6 bar × 0.21 = 1.3 bar absolute
| where: | |
| pi | = partial pressure of gas component i =  in the terms used in this article in the terms used in this article
|
|---|---|
| P | = total pressure =  in the terms used in this article in the terms used in this article
|
| Fi | = volume fraction of gas component i = mole fraction,  , in the terms used in this article , in the terms used in this article
|
| pN2 | = partial pressure of nitrogen =  in the terms used in this article in the terms used in this article
|
| pO2 | = partial pressure of oxygen =  in the terms used in this article in the terms used in this article
|
The minimum safe lower limit for the partial pressures of oxygen in a breathing gas mixture for diving is 0.16 bars (16 kPa) absolute. Hypoxia and sudden unconsciousness can become a problem with an oxygen partial pressure of less than 0.16 bar absolute.[15] Oxygen toxicity, involving convulsions, becomes a problem when oxygen partial pressure is too high. The NOAA Diving Manual recommends a maximum single exposure of 45 minutes at 1.6 bar absolute, of 120 minutes at 1.5 bar absolute, of 150 minutes at 1.4 bar absolute, of 180 minutes at 1.3 bar absolute and of 210 minutes at 1.2 bar absolute. Oxygen toxicity becomes a risk when these oxygen partial pressures and exposures are exceeded. The partial pressure of oxygen also determines the maximum operating depth of a gas mixture.[14]
Narcosis is a problem when breathing gases at high pressure. Typically, the maximum total partial pressure of narcotic gases used when planning for technical diving may be around 4.5 bar absolute, based on an equivalent narcotic depth of 35 metres (115 ft).
The effect of a toxic contaminant such as carbon monoxide in breathing gas is also related to the partial pressure when breathed. A mixture which may be relatively safe at the surface could be dangerously toxic at the maximum depth of a dive, or a tolerable level of carbon dioxide in the breathing loop of a diving rebreather may become intolerable within seconds during descent when the partial pressure rapidly increases, and could lead to panic or incapacitation of the diver.[14]
In medicine[edit]
The partial pressures of particularly oxygen (

| Unit | Arterial blood gas | Venous blood gas | Cerebrospinal fluid | Alveolar pulmonary gas pressures |
|
|---|---|---|---|---|---|
 |
kPa | 11–13[16] | 4.0–5.3[16] | 5.3–5.9[16] | 14.2 |
| mmHg | 75–100[17] | 30–40[18] | 40–44[19] | 107 | |
 |
kPa | 4.7–6.0[16] | 5.5–6.8[16] | 5.9–6.7[16] | 4.8 |
| mmHg | 35–45[17] | 41–51[18] | 44–50[19] | 36 |
See also[edit]
- Breathing gas – Gas used for human respiration
- Henry’s law – Gas law regarding proportionality of dissolved gas
- Ideal gas – Mathematical model which approximates the behavior of real gases
- Ideal gas law – Equation of the state of a hypothetical ideal gas
- Mole fraction – Proportion of a constituent in a mixture
- Mole (unit) – SI unit of amount of substance
- Vapor – Substances in the gas phase at a temperature lower than its critical point
References[edit]
- ^ Charles Henrickson (2005). Chemistry. Cliffs Notes. ISBN 978-0-7645-7419-1.
- ^ “Gas Pressure and Respiration”. Lumen Learning.
- ^ Gas blending
- ^ Staff. “Symbols and Units” (PDF). Respiratory Physiology & Neurobiology : Guide for Authors. Elsevier. p. 1. Archived (PDF) from the original on 2015-07-23. Retrieved 3 June 2017.
All symbols referring to gas species are in subscript,
- ^ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the “Gold Book”) (1997). Online corrected version: (2006–) “pressure, p“. doi:10.1351/goldbook.P04819
- ^ Dalton’s Law of Partial Pressures
- ^ Frostberg State University’s “General Chemistry Online”
- ^ Page 200 in: Medical biophysics. Flemming Cornelius. 6th Edition, 2008.
- ^ Perry, R.H.; Green, D.W., eds. (1997). Perry’s Chemical Engineers’ Handbook (7th ed.). McGraw-Hill. ISBN 978-0-07-049841-9.
- ^ a b An extensive list of Henry’s law constants, and a conversion tool
- ^ Francis L. Smith & Allan H. Harvey (September 2007). “Avoid Common Pitfalls When Using Henry’s Law”. CEP (Chemical Engineering Progress). ISSN 0360-7275.
- ^ Introductory University Chemistry, Henry’s Law and the Solubility of Gases Archived 2012-05-04 at the Wayback Machine
- ^ a b “University of Arizona chemistry class notes”. Archived from the original on 2012-03-07. Retrieved 2006-05-26.
- ^ a b c d e NOAA Diving Program (U.S.) (December 1979). Miller, James W. (ed.). NOAA Diving Manual, Diving for Science and Technology (2nd ed.). Silver Spring, Maryland: US Department of Commerce: National Oceanic and Atmospheric Administration, Office of Ocean Engineering.
- ^ Sawatzky, David (August 2008). “3: Oxygen and its affect on the diver”. In Mount, Tom; Dituri, Joseph (eds.). Exploration and Mixed Gas Diving Encyclopedia (1st ed.). Miami Shores, Florida: International Association of Nitrox Divers. pp. 41–50. ISBN 978-0-915539-10-9.
- ^ a b c d e f Derived from mmHg values using 0.133322 kPa/mmHg
- ^ a b Normal Reference Range Table Archived 2011-12-25 at the Wayback Machine from The University of Texas Southwestern Medical Center at Dallas. Used in Interactive Case Study Companion to Pathologic basis of disease.
- ^ a b The Medical Education Division of the Brookside Associates–> ABG (Arterial Blood Gas) Retrieved on Dec 6, 2009
- ^ a b Pathology 425 Cerebrospinal Fluid [CSF] Archived 2012-02-22 at the Wayback Machine at the Department of Pathology and Laboratory Medicine at the University of British Columbia. By Dr. G.P. Bondy. Retrieved November 2011











