Два
подпространства
называются ортогональными,
если каждый вектор одного подпространства
ортогонален каждому вектору другого
подпространства . Ортогональность
подпространств ![]()
и ![]()
обозначается ![]()
Для
того чтобы вектор ![]()
был ортогонален к подпространству ![]()
необходимо и достаточно, чтобы он был
ортогонален ко всем векторам какого-либо
базиса подпространства ![]()
Для
того чтобы два подпространства были
ортогональными, необходимо и достаточно
, чтобы каждый вектор какого-либо базиса
одного подпространства был ортогонален
ко всем векторам какого-либо базиса
другого подпространства.
Сумма
![]()
подпространств ![]()
называется ортогональной
и обозначается ![]()
если подпространства попарно ортогональны.
Ортогональная
сумма ненулевых подпространств всегда
является прямой суммой.
Совокупность
всех векторов, ортогональных к линейному
подпространству ![]()
евклидова пространства ![]()
называется ортогональным
дополнением подпространства
![]()
и обозначается ![]()
Евклидово
пространство ![]()
есть ортогональная сумма любого своего
линейного подпространства ![]()
и его ортогонального дополнения ![]()
т.е.
![]()
![]()
Любой
вектор ![]()
из евклидова пространства ![]()
всегда можно представить, причём
единственным образом, в виде
![]()
![]()
где
![]()
принадлежит некоторому подпространству
![]() ,
,
![]()
ортогонален к ![]()
Вектор ![]()
называется ортогональной
проекцией
вектора
![]()
на
подпространство
![]()
а ![]() –
–
перпендикуляром,
опущенным из ![]()
на ![]()
Пример
1.
Докажите, что 
Доказательство.
Пусть ![]()
Тогда ![]()
В силу того, что ![]()
где ![]() ,
,
а ![]() .
.
Следовательно, ![]()
Если в последнем равенстве выбрать ![]()
то из условия ![]()
заключаем, что ![]()
Полагая ![]()
получаем, что ![]()
или ![]()
Другими словами, из условия ![]()
вытекает, что ![]() Пусть
Пусть
теперь ![]() .
.
Тогда ![]() ,
,
т.к. ![]()
и ![]() .
.
Значит, ![]() .
.
Таким образом, мы получили, что если ![]() ,
,
то ![]() .
.
И, наоборот, если ![]() ,
,
то ![]() .
.
Сказанное равносильно равенству  .
.
Пример
2.
Линейное подпространство ![]()
задано системой уравнений:

Найдите
базис ортогонального дополнения ![]() .
.
Решение.
Найдем базис ![]() .
.
Для этого решим данную однородную
систему уравнений:

![]()
![]() –
–
свободные переменные;
![]()
Таким
образом, общее решение имеет вид:
![]() .
.
Выбирая значения свободных переменных
в соответствии с таблицей
|
|
|
|
|
|
|
|
|
|
|
|
получаем
базисные векторы подпространства ![]() :
:
![]() .
.
Поскольку
![]() ,
,
а ортогональная сумма есть прямая сумма,
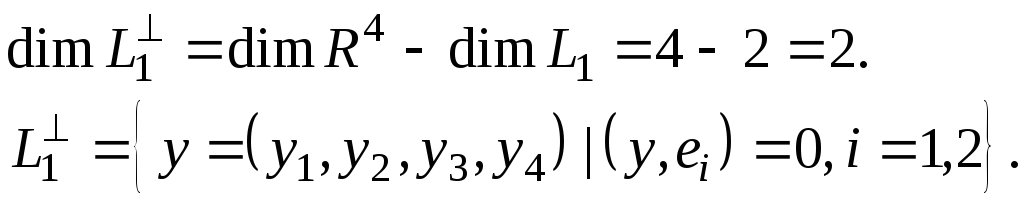
Таким
образом, ![]()
определяется системой уравнений
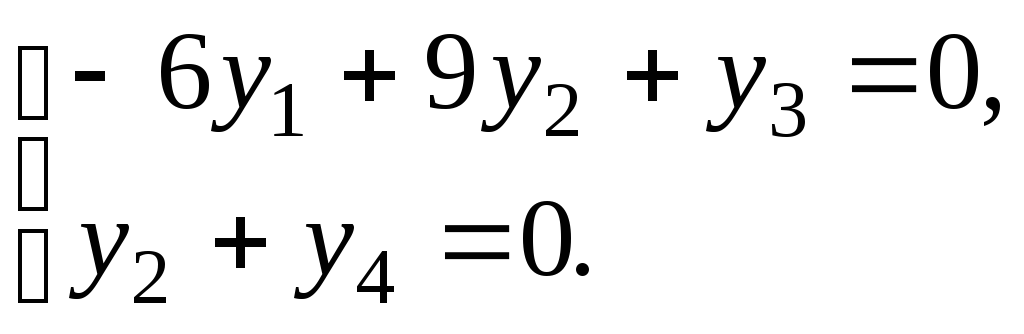
Найдя
фундаментальную систему решений этой
однородной системы уравнений, получим
базис ![]() .
.
![]() .
.
![]() –
–
свободные переменные;
![]()
![]() .
.
Общее
решение имеет вид:
![]() .
.
Выбирая
значения свободных переменных в
соответствии с таблицей
|
|
|
|
|
|
|
|
|
|
|
|
получаем
базис ортогонального дополнения ![]() :
:
![]() .
.
Пример
3.
Найдите ортогональную проекцию ![]()
и перпендикуляр ![]() ,
,
опущенный из вектора ![]()
на подпространство ![]() ,
,
порожденное векторами ![]()
и ![]() .
.
Решение.
Система векторов ![]()
образует базис подпространства ![]() .
.
Т.к. ![]()
такие, что ![]() .
.
Кроме того, справедливо (причем
единственное) представление ![]() ,
,
в котором ![]() .
.
Последнее означает, что ![]() .
.
Отсюда
![]()
т.е.
получили неоднородную систему уравнений
относительно ![]()
и ![]() ,
,
которая в матричном виде выглядит так:
 .
.
![]()
Поскольку

система
![]()
эквивалентна следующей:
![]() .
.
Отсюда
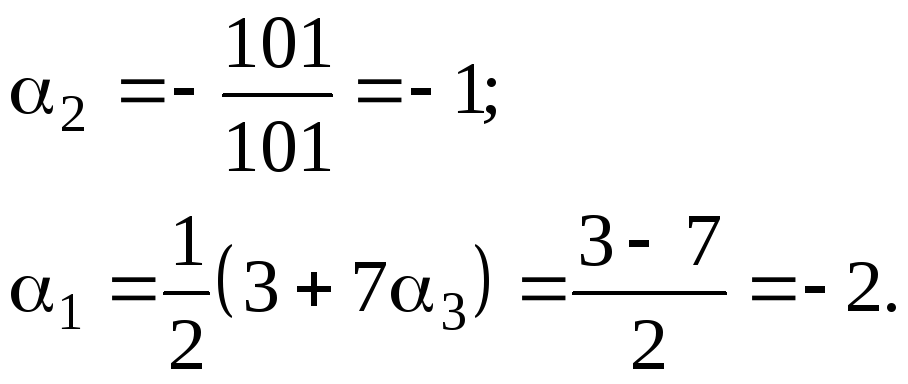
Следовательно,
![]()
5.3.1.
Докажите, что ортогональное дополнение
к линейному подпространству евклидова
пространства ![]()
обладает свойствами:
![]()
![]() если
если
![]() ,
,
то ![]()


Здесь
![]() –
–
нулевое подпространство, содержащее
лишь нулевой вектор.
5.3.2.
Найдите базис ортогонального дополнения
![]()
линейной оболочки ![]()
следующей системы векторов пространства
![]() :
:
![]()
5.3.3.
Найдите ортогональный базис ортогонального
дополнения ![]() ,
,
если
![]() и
и
![]()
5.3.4.
В пространстве ![]()
многочленов степени ![]()
с действительными коэффициентами
скалярное произведение многочленов ![]()
и ![]()
определяется формулой
![]() .
.
![]()
Найдите
ортогональное дополнение подпространства
всех многочленов, удовлетворяющих
условию ![]()
5.3.5.
Найдите ортогональную проекцию и
перпендикуляр, опущенный из вектора ![]()
на подпространство ![]() :
:
![]() натянуто
натянуто
на векторы ![]()
![]()
![]() натянуто
натянуто
на векторы ![]()
![]()
![]() задано
задано
системой уравнений:

![]() натянуто
натянуто
на векторы ![]()
![]()
Соседние файлы в папке Задачник-1
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Оглавление — Линейная алгебра
Ортогональные дополнения евклидова пространства
Ортогональным дополнением непустого подмножества [math]M[/math] евклидова пространства [math]mathbb{E}[/math] называется множество векторов, ортогональных каждому вектору из [math]M[/math]. Ортогональное дополнение обозначается
[math]M^{perp}= Bigl{ mathbf{v}colon, langle mathbf{v},mathbf{w}rangle=0,~ forall mathbf{w}in M Bigr}.[/math]
Рассмотрим примеры ортогональных дополнений евклидова пространства.
1. Ортогональным дополнением нулевого подпространства [math]{mathbf{o} } triangleleft mathbb{E}[/math] служит все пространство [math]mathbb{E} colon, {mathbf{o} }^{perp}= mathbb{E}[/math]. Ортогональным дополнением всего пространства является его нулевое подпространство [math]mathbb{E}^{perp}= {mathbf{o} }[/math].
2. Пусть в пространстве [math]{V_3 }[/math] радиус-векторов (с началом в точке [math]O[/math]) за даны три взаимно перпендикулярных радиус-вектора [math]overrightarrow{OA}[/math], [math]overrightarrow{OB}[/math] и [math]overrightarrow{ OC }[/math]. Тогда ортогональным дополнением вектора [math]overrightarrow{OA}[/math] является множество радиус- векторов на плоскости, содержащей векторы [math]overrightarrow{ OB }[/math] и [math]overrightarrow{ OC }[/math], точнее, [math]{overrightarrow{OA}}^{perp}= operatorname{Lin}(overrightarrow{OB},overrightarrow{OC})[/math]. Ортогональным дополнением векторов [math]overrightarrow{OA}[/math] и [math]overrightarrow{OB}[/math] служит множество радиус-векторов на прямой, содержащей вектор [math]overrightarrow{OC}colon {overrightarrow{OA},overrightarrow{OB}}^{perp}= operatorname{Lin} (overrightarrow{OC})[/math]. Ортогональным дополнение трех заданных векторов служит нулевой радиус-вектор: [math]{overrightarrow{OA}, overrightarrow{OB}, overrightarrow{OC}}^{perp}= {overrightarrow{OO}}[/math].
3. В пространстве [math]P_2(mathbb{R})[/math] многочленов степени не выше второй со скалярным произведением (8.29) задано подмножество [math]P_0(mathbb{R})[/math] – многочленов нулевой степени. Найдем ортогональное дополнение этого подмножества. Для этого приравняем нулю скалярное произведение многочлена [math]p_2(x)=ax^2+bx+c[/math] на постоянный многочлен [math]p_0(x)=dcolon[/math] [math]langle p_2(x),p_0(x)rangle= acdot0+bcdot0+ccdot d=0[/math]. Поскольку величина [math]d[/math] произвольная, то [math]c=0[/math]. Следовательно, ортогональным дополнением подмножества [math]P_0(mathbb{R})[/math] является множество многочленов из [math]P_0(mathbb{R})[/math] с нулевым свободным членом.
Свойства ортогонального дополнения
Рассмотрим свойства ортогональных дополнений подмножеств n-мерного евклидова пространства [math]mathbb{E}[/math].
1. Ортогональное дополнение [math]M^{perp}[/math] непустого подмножества [math]Msubset mathbb{E}[/math] является линейным подпространством, т.е. [math]M^{perp} triangleleft mathbb{E}[/math], и справедливо включение [math]Msubset (M^{perp})^{perp}[/math].
В самом деле, множество [math]M^{perp}[/math] замкнуто по отношению к операциям сложения векторов и умножения вектора на число, так как сумма двух век торов, ортогональных [math]M[/math], ортогональна [math]M[/math], и произведение вектора, ортогонального [math]M[/math], на любое число является вектором, ортогональным [math]M[/math]. До кажем включение [math]Msubset (M^{perp})^{perp}[/math]. Пусть [math]mathbf{w}in M[/math], тогда [math]langle mathbf{w},mathbf{v}rangle=0[/math] для любого вектора [math]mathbf{v}in M^{perp}[/math]. Но это означает, что [math]mathbf{w}subset (M^{perp})^{perp}[/math].
2. Пересечение любого непустого подмножества [math]Msubset mathbb{E}[/math] со своим ортогональным дополнением есть нулевой вектор: [math]Mcap M^{perp}= {mathbf{o}}[/math].
Действительно, только нулевой вектор ортогонален самому себе.
3. Если [math]L[/math] – подпространство [math]mathbb{E}~ (Ltriangleleft mathbb{E})[/math], то [math]mathbb{E}=Loplus L^{perp}[/math].
Действительно, возьмем в [math]L[/math] ортогональный базис [math](mathbf{e})= (mathbf{e}_1, ldots,mathbf{e}_k)[/math]. До полним его векторами [math](mathbf{f})= (mathbf{f}_{k+1},ldots, mathbf{f}_n)[/math] до ортогонального базиса [math](mathbf{e}),,(mathbf{f})[/math] всего пространства [math]mathbb{E}[/math]. Тогда произвольный вектор [math]mathbf{w}in mathbb{E}[/math] можно представить в виде суммы
[math]mathbf{w}= underbrace{sum_{i=1}^{k}mathbf{w}_i mathbf{e}_i}_{mathbf{u}}+ underbrace{sum_{j=k+1}^{n}mathbf{w}_j mathbf{f}_j}_{mathbf{v}} =mathbf{u}+ mathbf{v},[/math]
где [math]mathbf{u}in L[/math], а [math]mathbf{v}in L^{perp}[/math], так как [math]langle mathbf{v},mathbf{e}_irangle= sum_{j=k+1}^{n}mathbf{w}langle mathbf{f}_j, mathbf{e}_i rangle_{{}_{=0}}=0[/math] для [math]i=1,ldots,k[/math]. Следовательно, любой вектор пространства [math]mathbb{E}[/math] раскладывается по подпространствам [math]L[/math] и [math]L^{perp}[/math], т.е. [math]mathbb{E}= L+L^{perp}[/math]. Эта алгебраическая сумма является прямой суммой по свойству 2, поскольку [math]Lcap L^{perp}={mathbf{o}}[/math]. Следовательно, [math]mathbb{E}=Loplus L^{perp}[/math].
4. Если [math]Ltriangleleft mathbb{E}[/math], то [math]dim{L^{perp}}= dimmathbb{E}-dim{L}[/math].
5. Если [math]L[/math] – подпространство [math]mathbb{E}[/math], то [math]L=(L^{perp})^{perp}[/math].
Из первого свойства следует включение [math]Lsubset(L^{perp})^{perp}[/math]. Докажем, что [math](L^{perp})^{perp}subset L[/math]. Действительно, пусть [math]mathbf{w}in (L^{perp})^{perp}[/math]. По свойству 3: [math]mathbf{w}=mathbf{u}+mathbf{v}[/math], где [math]mathbf{u}in L,~ mathbf{v}in L^{perp}[/math]. Найдем скалярное произведение
[math]underbrace{langle mathbf{w},mathbf{v}rangle}_{0}= langle mathbf{w}+ mathbf{v}, mathbf{v}rangle= underbrace{langle mathbf{u},mathbf{v}rangle }_{0}+langle mathbf{v}, mathbf{v}rangle= langle mathbf{v},mathbf{v}rangle.[/math]
Следовательно, [math]langle mathbf{v},mathbf{v}rangle=0[/math], и согласно аксиоме 4 скалярного произведения [math]mathbf{v}=mathbf{o}[/math], поэтому [math]mathbf{w}=mathbf{u}+ mathbf{v}= mathbf{u}+mathbf{0}=mathbf{u}in L[/math]. Значит, [math](L^{perp})^{perp}subset L[/math]. Из двух включений [math]Lsubset (L^{perp})^{perp}[/math] и [math](L^{perp})^{perp} subset L[/math] следует равенство [math]L=(L^{perp})^{perp}[/math].
6. Если [math]L_1triangleleft mathbb{E}[/math] и [math]L_2triangleleft mathbb{E}[/math], то [math](L_1+L_2)^{perp}=L_1^{perp}cap L_2^{perp}[/math] и [math](L_1cap L_2)^{perp}= L_1^{perp}+ L_2^{perp}[/math].
Последние свойства аналогичны свойствам алгебраических дополнений.
Нахождение ортогонального дополнения подпространства
Ранее для описания подпространств линейных пространств использовались два способа описания (внешний и внутренний). Рассмотрим применение этих способов описания для нахождения ортогональных дополнений подпространств. Учитывая изоморфизм евклидовых пространств, будем рассматривать арифметическое пространство [math]mathbb{R}^n[/math] со скалярным произведением (8.27).
Для заданного подпространства [math]Ltriangleleft mathbb{R}^n[/math] требуется найти его ортогональное дополнение [math]L^{perp}[/math]. В зависимости от способа описания подпространства [math]L[/math] используем одно из следующих двух утверждений.
1. Если подпространство [math]Ltriangleleft mathbb{R}^n[/math] задано как линейная оболочка [math]L=operatorname{Lin}(a_1,ldots,a_k)[/math] столбцов матрицы [math]A= begin{pmatrix}a_1&cdots&a_kend{pmatrix}[/math], то множество решений однородной системы [math]Ax=o[/math] является его ортогональным дополнением [math]L^{perp}triangleleft mathbb{R}^n[/math], т.е.
[math]L=operatorname{Lin}(a_1,ldots,a_k)quad Rightarrowquad L^{perp}= {Ax=o}.[/math]
(8.34)
2. Если подпространство [math]Ltriangleleft mathbb{R}^n[/math] задано как множество решений однородной системы [math]Ax=o[/math] [math]m[/math] уравнений с [math]n[/math] неизвестными, то линейная оболочка столбцов [math]a_1^T,ldots,a_m^T[/math] транспонированной матрицы [math]A^T=begin{pmatrix}a_1^T&cdots&a_m^Tend{pmatrix}[/math] является его ортогональным дополнением [math]L^{perp}triangleleft mathbb{R}^n[/math], т.е.
[math]L={Ax=o}quad Rightarrowquad L^{perp}= operatorname{Lin}(a_1^T&cdots& a_m^T).[/math]
(8.35)
где [math]a_i^T[/math] – i-й столбец матрицы [math]A^T[/math].
Докажем, например, первое утверждение. Линейное однородное уравнение
[math]a_{i,1}cdot x_1+a_{i,2}cdot x_2+ldots+a_{i,n}cdot x_n=0[/math]
можно записать при помощи скалярной произведения [math]langle mathbf{a}_{i},mathbf{x} rangle=0[/math], так как [math]langle mathbf{a}_{i},mathbf{x} rangle=(a_{i})^Tx[/math] по формуле (8.27). Тогда множество [math]{langle mathbf{a}_{i},mathbf{x} rangle=o}[/math] решений одного уравнения совпадает с множеством векторов, ортогональных [math]mathbf{i}_i[/math]. Поэтому множество [math]{A^Tx=o}[/math] совпадает с множеством векторов, ортогональных каждому из векторов [math]mathbf{a}_1,ldots,mathbf{a}_k[/math], значит, и их линейной оболочке [math]L= operatorname{Lin}(mathbf{a}_1,ldots,mathbf{a}_k)[/math]. Таким образом, [math]L^{perp}={A^Tx=o}[/math].
Замечания 8.13
1. В отличие от алгебраического дополнения [math]L^{+}[/math] подпространстве [math]Ltriangleleft mathbb{E}[/math] ортогональное дополнение [math]L^{perp}[/math] находится однозначно.
2. Ортогональное дополнение [math]L^{perp}[/math] подпространства [math]Ltriangleleft mathbb{E}[/math] в силу свойства 3 является также и алгебраическим дополнением. Это обстоятельстве учитывалось при нахождении алгебраических дополнений при помощи утверждений (8.16) и (8.17), которые по существу совпадают с утверждениями (8.34) и (8.35).
Пример 8.19. В примере 8.10 для линейного подпространства [math]L= operatorname{Lin}[(t-1)^2,(t+1)^3][/math] пространства [math]P_3(mathbb{R})[/math] многочленов не более, чем 3-й степени, было найдено алгебраическое дополнение
[math]L^{+}= operatorname{Lin}!left[left(-dfrac{9}{5}-dfrac{2}{5},t+t^2right)!, left(-dfrac{2}{5}-dfrac{1}{5},t+t^3right)right].[/math]
Доказать, что это алгебраическое дополнение является ортогональным дополнением подпространства [math]L[/math] евклидова пространства [math]P_3(mathbb{R})[/math] со скалярным произведением (8.29).
Решение. Для решения задачи достаточно показать, что образующие подпространства [math]L:[/math]
[math]p_1(t)=(t-1)^2= 0cdot t^3+1cdot t^2+(-2)cdot t+1;quad p_2(t)=(t+1)^3= 1cdot t^3+3cdot t^2+3cdot t+1[/math]
ортогональны образующим алгебраического дополнения [math]L^{+}:[/math]
[math]q_1(t)=0cdot t^3+1cdot t^2+frac{-2}{5}cdot t+frac{-9}{5},quad q_2(t)= 1cdot t^3+0cdot t^2+frac{-1}{5}cdot t+frac{-2}{5},.[/math]
По формуле (8.29) находим
[math]begin{aligned}langle p_1(t),q_1(t)rangle&= 0cdot0+1cdot1+(-2)cdot!left(-dfrac{2}{5}right)+1cdot!left(-frac{9}{5}right)=0;\[2pt] langle p_1(t),q_2(t)rangle&= 0cdot1+1cdot0+(-2)cdot!left(-dfrac{1}{5}right)+1cdot!left(-frac{2}{5}right)=0;\[2pt] langle p_2(t),q_1(t)rangle&= 1cdot0+3cdot1+3cdot!left(-dfrac{2}{5}right)+1cdot!left(-frac{9}{5}right)=0;\[2pt] langle p_2(t),q_2(t)rangle&= 1cdot1+3cdot0+3cdot!left(-dfrac{1}{5}right)+1cdot!left(-frac{2}{5}right)=0. end{aligned}[/math]
Следовательно, [math]L=L^{+}[/math].
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Как следует из теоремы 2.7, в произвольном линейном пространстве L любое линейное подпространство H имеет прямое дополнение, т.е. такое линейное подпространство H’, что H ⊕ H’ = L. Такое линейное подпространство H’ не является единственным. Однако в случае евклидова пространства
среди всех возможных прямых дополнений к данному линейному подпространству одно выделяется.
Определение 3.8. Ортогональным дополнением линейного подпространства H в евклидовом пространстве Ε называют множество H⊥ всех векторов х ∈ Ε, ортогональных каждому вектору линейного подпространства H.
Пример 3.15. В евклидовом пространстве V3 свободных векторов рассмотрим линейное подпространство H векторов, параллельных данной плоскости (см. пример 2.1). Тогда ортогональным дополнением H⊥ будет множество векторов, перпендикулярных к этой плоскости (рис. 3.6, а), в то время как в качестве прямого дополнения H1 можно взять подпространство векторов, коллинеарных произвольной прямой, пересекающей плоскость в единственной точке, т.е. не параллельной плоскости и не лежащей в этой плоскости (рис. 3.6,6). Отметим, что в данном случае H⊥ является линейным подпространством в V3.
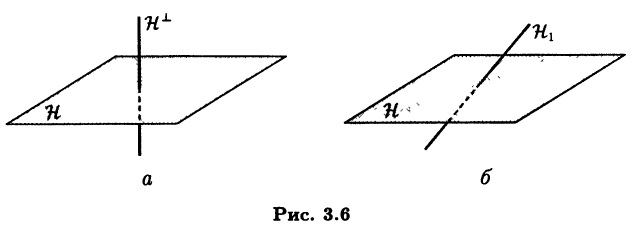
Теорема 3.6. Ортогональное дополнение H⊥ линейного подпространства Н в евклидовом подпространстве Ε является линейным подпространством в Ε, причем Ε = Н ⊕ H⊥ и dimH + dimH⊥ = dimΕ.
◄ Чтобы доказать, что H⊥ является линейным подпространством в Ε, нужно проверить условия 1) и 2) определения 2.1. Взяв два произвольных вектора x и у, принадлежащих H⊥, умножим скалярно их сумму на произвольный вектор h ∈ Н. Получим:
(x + у, h) – (x, h) + (у, h) = 0 + 0 = 0,
т.е. для любых векторов x и у из множества H⊥ их сумма x + у принадлежит тому же множеству.
Теперь рассмотрим произведение вектора x ∈ H⊥ на про-извольное действительное число λ. Для произвольного вектора h ∈ H
(λx, h) = λ (x, h) = λ • 0 = 0,
и поэтому λx ∈ H⊥ если x ∈ H⊥. Следовательно, H⊥ является линейным подпространством в Ε.
Отметим, что любой вектор x, принадлежащий пересечению Н ∩ H⊥, ортогонален самому себе: (x, x) = 0, так как любой вектор из H⊥ ортогонален любому вектору подпространства H. Но вектор ортогонален самому себе лишь в том случае, когда он нулевой (аксиома г) скалярного умножения). Поэтому Н ∩ H⊥ = {0}, а сумма Н + H⊥ рассматриваемых линейных
подпространств является прямой (см. теорему 2.3). Докажем, что эта прямая сумма совпадает со всем евклидовым пространством Ε.
Выберем некоторый ортонормированный базис f1, … , fm в линейном подпространстве H и дополним его до базиса f1, …, fm, fm+1, … , fn во всем евклидовом пространстве Ε, dimΕ = n. Исходя из этого базиса построим при помощи процесса Грама – Шмидта ортонормированный базис е = (e1 … еm em+1 … еn) в Ε. Так как первые m векторов f1, … , fm исходного базиса попарно ортогональны и имеют единичную длину, процесс ортогонализации оставит их без изменения, т.е. е1 = f1, i = 1,m. Векторы em+1, …, еn ортогональны каждому из векторов e1, …, еm базиса линейного подпространства Н и, следовательно, ортогональны Н, так как H = span{e1,… ,еm}. Поэтому все они попадают в ортогональное дополнение H⊥.
Рассмотрим произвольный вектор х ∈ Ε и запишем его разложение по базису е:
x = x1e1+ … + xnen.
Легко увидеть, что х1 = x1e1 + … + хmеm есть вектор из Н, x2 = xm+1em+1 + … + хnеn есть вектор из H⊥, при этом x = x1 + x2. Следовательно, x ∈ H ⊕ H⊥, и так как вектор х выбирался произвольно, то H ⊕ H⊥ = Ε.
Согласно следствию из теоремы 2.5, из соотношения H ⊕ H⊥ = Ε вытекает следующее равенство для размерностей: dimΕ = dimH + dimH⊥ . ►
Следствие 3.1. Каково бы ни было линейное подпространство Н в евклидовом пространстве Ε, любой вектор x ∈ Ε можно однозначно представить в виде
x = h + h⊥ (3.11)
где h ∈ H, h⊥ ∈ H⊥.
◄ Действительно, это утверждение означает, что Ε = H ⊕ H⊥. ►
Вектор h в разложении (3.11) называют ортогональной проекцией вектора х на линейное подпространство H, а вектор h⊥ – ортогональной составляющей вектора х относительно линейного подпространства H.
Как построить ортогональное дополнение к данному линейному подпространству? Пусть линейное подпространство H определено наиболее распространенным способом – как линейная оболочка некоторой системы векторов a1,… , аm. Согласно определению 3.8 ортогонального дополнения, любой вектор х ∈ H⊥ должен быть ортогонален каждому из векторов аi:
(ai,x)=0, i = l,m. (3.12)
Наоборот, если вектор х удовлетворяет системе равенств (3.12), т.е. он ортогонален каждому из векторов аi, то этот вектор ортогонален и любой линейной комбинации системы векторов a1, …, am (см. 3.5). Значит, х ортогонален каждому вектору линейного подпространства H = span{a1,… ,am} и принадлежит линейному подпространству H⊥.
Итак, система уравнений (3.12) описывает ортогональное дополнение линейного подпространства Н. Запишем эту систему в координатах в некотором ортонормированием базисе е = (e1 … еn). Пусть векторы аi в этом базисе имеют разложения
a1 = a11e1 + … + a1nen,
………………………….
ai = ai1e1 + … + ainen,
………………………….
am = am1e1 + … + amnen.
Координаты произвольного вектора х в том же базисе обозначим х1, …, хn т.е. полагаем, что
х = х1e1 + … + хnеn.
Тогда в ортонормированном базисе е
(a1,x) = (ai1e1 + … + ainen, x1e1 + … + xnen) = ai1x1 + … + ainxn, i = 1,m.
Таким образом, система (3.12), записанная в координатах относительно ортонормированного базиса е, имеет вид
a11x1 + … + a1nxn = 0,
……………….. (3.13)
am1x1 + … + amnxn = 0,
т.е. представляет собой однородную систему из m линейных алгебраических уравнений с п неизвестными. Строки матрицы А этой системы совпадают с наборами координат векторов a1, …, аm. Поэтому матрица А имеет ранг, равный рангу системы векторов a1, …, am, т.е. этот ранг совпадает с размерностью линейного подпространства Н.
Каждое решение системы (3.13) представляет собой набор координат некоторого вектора из H⊥ и наоборот, любой вектор из H⊥ описывает решение системы (3.13). Поэтому можно сказать, что множество всех решений этой системы есть линейное подпространство H⊥. Согласно теореме 3.6, это подпространство имеет размерность n – dimH = n – RgА. Множество решений однородной системы линейных алгебраических уравнений (СЛАУ) описывается при помощи фундаментальной системы решений. Напомним, что столбцы фундаментальной системы решений линейно независимы, а любое решение однородной СЛАУ представляется в виде линейной комбинации столбцов фундаментальной системы решений. Другими словами, фундаментальная система решений – это базис в подпространстве всех решений данной однородной СЛАУ. Каждый столбец фундаментальной системы решений представляет собой координатную запись вектора линейного подпространства Н⊥ в выбранном базисе е евклидова пространства Ε, при этом такие векторы в совокупности образуют базис подпространства H⊥. Мы здесь можем не различать фундаментальную систему решений системы (3.13) и соответствующий ей базис ортогонального дополнения H⊥.
Пример 3.16. Пусть линейное подпространство Н представляет собой линейную оболочку системы векторов, заданных координатами в некотором фиксированном ортонормированием базисе е четырехмерного евклидова пространства Ε:
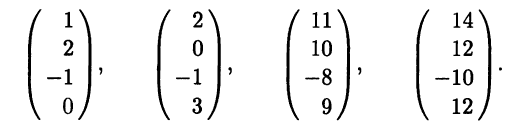
Найдем какой-либо базис ортогонального дополнения H⊥.
Записываем систему вида (3.13), используя координаты векторов ai.
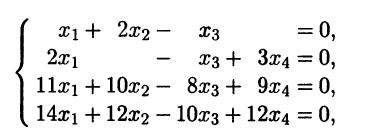
и находим ее фундаментальную систему решений. Это можно сделать, например, с помощью приведения матрицы системы к ступенчатому виду методом элементарных преобразований [III]. В качестве базисных переменных выберем x1 и x2. Тогда фундаментальная система решений будет содержать два решения, например:
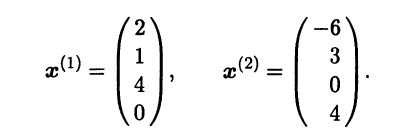
Cтолбцы найденной фундаментальной системы решений представляют собой координаты двух векторов f1, f2 из Ε, образующих базис линейного подпространства H⊥, но этот базис не является ортонормированным. Чтобы получить ор-онормированный базис H⊥, достаточно применить процесс ортогонализации Грама – Шмидта. Сделав это, находим векторы g1 = f1,
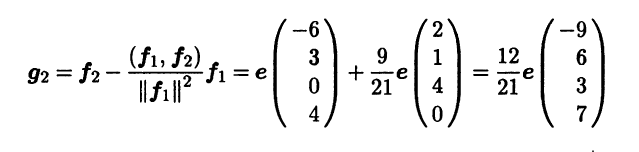
и ортонормированный базис в линейном пространстве H⊥:
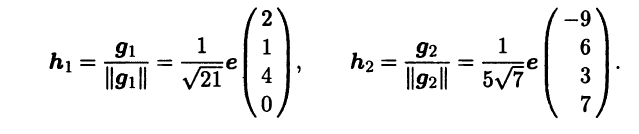
Дополнение 3.1. Нормы матриц
В линейном пространстве Мn(R) квадратных матриц порядка n норму можно задавать различными способами. Например, это линейное пространство можно трактовать как n2–мерное линейное арифметическое пространство со стандартным скалярным умножением, которому соответствует евклидова норма. Для матрицы А = (aij) ∈ Мn(R) эта норма имеет вид
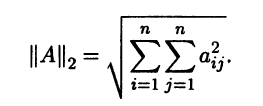
Ее называют евклидовой нормой или l2-нормой.
Евклидова норма матрицы никак не связана с расположением элементов матрицы по строкам и столбцам. Это обычно нежелательно, и поэтому она используется редко. Больший интерес представляют нормы матриц, использующие специфику записи матриц. Такая норма может быть связана с некоторой нормой, заданной для столбцов матрицы. Важно также и то, как норма связала с операцией умножения матриц. В этом разделе векторы линейных арифметических пространств удобно записывать как матрицы-столбцы, отождествляя векторы со столбцами их координат в стандартном базисе (см. замечание 1.4).
Определение 3.9. Пусть в линейном арифметическом пространстве Rn задана норма ||•||*. Норму ||•||m в линейном пространстве Мn(R) называют согласованной с нормой ||•||*, если для любой матрицы А ∈ Мn(R) и любого столбца x ∈ Rn выполняется соотношение
||Ax||* ≤ ||Ax||m||x||* (3.14)
Каждая ли норма в Rn имеет согласованную с ней норму в Мn(R)? Ответ на этот вопрос утвердительный. Приведем пример такой нормы. Пусть в Rn задана норма ||•||*. На линейном пространстве матриц Мn(R) рассмотрим функцию
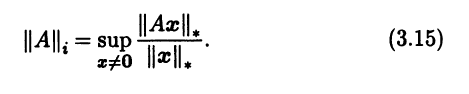
Из формулы не ясно, всегда ли определена указанная функция, т.е. всегда ли точная верхняя грань имеет конечное значение. Отметим, что, согласно аксиомам нормы и свойствам матричного умножения,
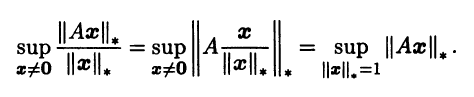
Следовательно, значение ||А||i равно точной верхней грани функции ||Ax||*, на множестве {x ∈ Rn: ||x||* = 1}. Можно покаказать, что это множество замкнутое и ограниченное (в частных случаях это показывает пример 3.8), а функция ||Ax||*
непрерывна на нем. На замкнутом ограниченном множестве непрерывная функция ограничена и достигает точной верхней грани [V]. Значит, величина ||Ax||i конечна, причем существует такой вектор у ∈ Rn единичной нормы, что ||А||i = ||Ау||*.
Итак, соотношение (3.15) корректно задает функцию на линейном пространстве Мn(R). Покажем, что эта функция является нормой, т.е. верны три аксиомы нормы. Выполнение аксиомы а) очевидно. Проверим аксиому б):
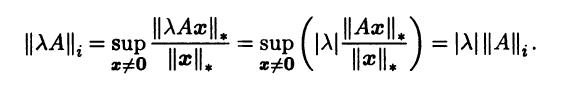
Аксиома в) нормы также верна:
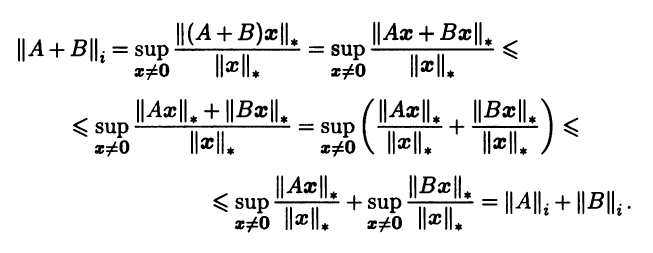
Норму, определенную соотношением (3.15), называют индуцированной (или подчиненной, операторной) и используют для нее то же обозначение, что и для порождающей ее исходной нормы в Rn:
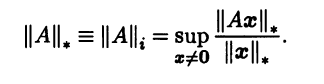
Индуцированная норма всегда согласована с исходной нормой в Rn, так как для любой матрицы А и любого x ≠ 0
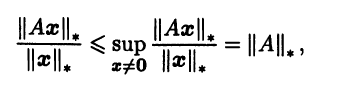
что эквивалентно (3.14) при ||А||m = ||A||*. Индуцированная норма является наименьшей из всех норм, согласованных с данной нормой в Rn. Действительно, пусть задана норма ||•|| в линейном пространстве матриц Мn(R), согласованная с нормой ||•||* в Rn. Выберем произвольную матрицу А, а в качестве вектора х выберем тот, на котором функция ||Аx||* достигает наибольшего значения на множестве {||x|| = 1} всех векторов единичной нормы. Тогда
||A||* = ||Ax||* ≤ ||A||||x||* = ||A||,
так как норма ||•||согласована с нормой ||•||*.
Говорят, что норма ||•|| в линейном пространстве матриц Mn(R) является матричной, или кольцевой, если
||AB||≤||A||||B||.
Первый термин не совсем удачен, так как более естественно назвать матричной любую норму, заданную в линейном пространстве матриц. Отметим, что любая индуцированная норма является кольцевой, так как
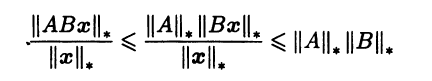
для любого ненулевого столбца x в силу согласованности индуцированной нормы. Поэтому
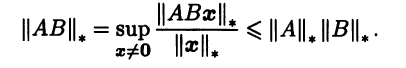
Задавая различные нормы в Rn, мы получаем индуцированные нормы в линейном пространстве матриц Мn(R). Выберем в Rn евклидову норму ||•||2:
||x||2 = √(x21 + … + x2n)
где х = (x1, … , хn). Индуцированную ею норму в линейном пространстве матриц Мn(R) называют спектральной нормой. Это название вызвано тем, что спектральная норма ||A||2 матрицы А равна √λ, где λ – максимальное собственное значение матрицы АTА.
Задав в Rn l1 – норму
||x||1 = |x1| + … + |xn|,
в качестве индуцированной получим следующую норму:
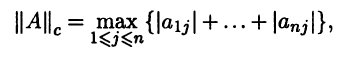
т.е. нормой матрицы А = (аij) ∈ Мn(R) является максимальная из l1 – норм столбцов этой матрицы. Поэтому ее называют максимальной столбцевой или октаэдрической.
В качестве нормы в Rn выберем l∞-норму
||x||∞ = max{|x1|,…,|xn|}.
Тогда индуцированной нормой будет функция
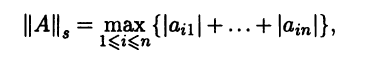
т.е. нормой матрицы А = (aij) ∈ Мn(R) будет максимальная из l1-норм строк этой матрицы. Поэтому ее называют максимальной строчной или кубической.
Особо стоит евклидова норма матриц ||A||2, которая не является индуцированной. Действительно, непосредственно из определения (3.15) индуцированной нормы следует, что, какова бы ни была норма в Rn, индуцированная норма единичной матрицы всегда равна единице. Однако нетрудно убедиться, что евклидова норма единичной матрицы Е ∈ Мn(R) равна √n > 1 (при n > 1).
Евклидова норма матриц является кольцевой. Действительно, пусть даны квадратные матрицы А = (aij) и В = (bjk) порядка n. Их произведением будет матрица С = (сikx) с элементами
cik = аi1b1k + аi2b2k + … +аinbnk. Так как, согласно неравенству Коши,
c2ik ≤ (а2i1+ … + а2in)(b21k+ … + b2nk),
заключаем, что
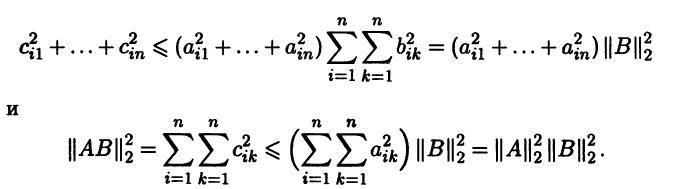
В линейном пространстве матриц Мn(R), интерпретируя его как линейное арифметическое пространство Rn , можно задать l1-норму
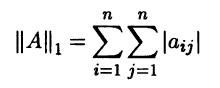
и l∞ -норму
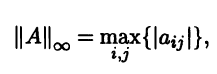
где А = (aij) ∈ Mn(R). В приложениях теории матриц первая норма заметного интереса не представляет. Вторая норма оце-нивает величину матрицы по максимальному из абсолютных значений ее элементов и необходима при изучении свойств различных методов вычислений. Можно показать, что l∞-норма в Мn(R) не является кольцевой, а потому она не согласована ни с какой нормой в Rn. Этот недостаток можно нейтрализовать, модифицировав эту норму. Новая норма
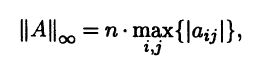
отличающаяся от старой корректирующим множителем n, равным порядку матрицы, уже является кольцевой и согласована с тремя основными нормами в Rn: евклидовой, l1-нормой и l∞-нормой.
Дополнение 3.2. Метод наименьших квадратов
Постановка задачи. Рассмотрим систему из n линейных алгебраических уравнений (СЛАУ) относительно к неизвестных
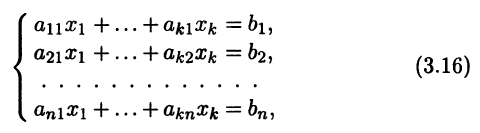
или в матричной записи
Ax = b. (3.17)
Каждому набору значений неизвестных сопоставим числа
di = bi – (a1ix1 + … + akixk), i = 1,n,
которые называют невязками уравнений системы для задан-ного набора значений неизвестных. Очевидно, что набор зна-чений неизвестных является решением системы тогда и только тогда, когда соответствующие ему невязки всех уравнений си-стемы равны нулю.
Отметим, что функция
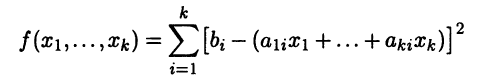
на решениях системы равна нулю и положительна в остальных случаях. Поэтому ее можно рассматривать как оценку отклоне-ния набора значений неизвестных от точного решения системы. Если система несовместна, то часто возникает задача найти вместо отсутствующих решений такой набор значений неизвестных, который приводит к наименьшему значению функции f. Такой подход в решении некорректной (т.е. не имеющей решений) задачи называют методом наименьших квадратов, поскольку ищется минимум функции, являющейся суммой квадратов.
Сформулированная задача по своему типу относится к классу задач минимизации функций многих переменных [V] и мо-жет быть решена общими методами поиска минимума. Однако ей можно придать алгебро-геометрическую интерпретацию и полностью решить методами линейной алгебры. Для придания задаче такой интерпретации будем трактовать столбцы коэф-фициентов при неизвестных, столбец правых частей уравнений (3.16) как столбцы координат векторов a1, …, аk;, b евклидова арифметического пространства Rn в стандартном базисе, отождествляя при этом векторы с их столбцами координат (см. замечание 1.4). Тогда и набор невязок уравнений системы мож-но рассматривать как вектор d = (d1, …, dn) ∈ Rn, который, согласно определению невязок, определяется соотношением
d = b – (x1a1 + … + xkak).
Число ||d|| назовем невязкой СЛАУ (3.17). Вычислив скалярный квадрат вектора d, находим
||d||2 = f (x1, … , xk)
Следовательно, задача сводится к определению таких действи-тельных коэффициентов х1, …, xk при которых величина ||d|| имеет наименьшее значение.
Решение задачи. Введем линейное подпространство H = span{a1,…,ak} и его ортогональное дополнение H⊥. Разложим вектор b на его ортогональную проекцию на линейное подпространство Н и соответствующую ортогональную составляющую:
b = h + h⊥, h ∈ H, h⊥ ∈ H⊥.
Тогда
d = h + h⊥ – (x1a1 + … + xkak) = h⊥ + (h – x1a1 – … – xkak) = h⊥ + d0,
где
d0 = h – x1a1 – … – xkak ∈ H.
Так как d0 ⊥ h⊥,то по теореме Пифагора заключаем, что
||d||2 = ||d0||2 + ||h⊥||2
Ортогональная составляющая h⊥ вектора невязок постоянна и от выбора коэффициентов хi не зависит. Поэтому минимизация величины ||d||2 сводится к поиску минимума величины ||d0||2. Эта величина является неотрицательной и достигает минимума, если обращается в нуль, т.е. при условии, что d0 = 0. А это равносильно тому, что d = h⊥, т.е. вектор невязок принадлежит ортогональному дополнению H⊥ и поэтому является решением системы
(aj, d) = 0, j = 1,k, (3.18)
или
(аj, b – x1a1 – … – хkаk) = 0, j = 1,k,
(см. 3.9). После преобразований получаем СЛАУ
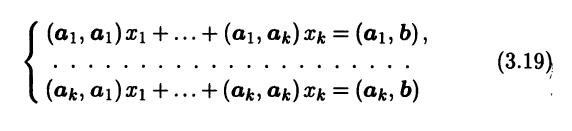
относительно неизвестных х1, …, хk. Матрица этой системы Г = ((аi,аj)) – это квадратная матрица порядка k, представляющая собой матрицу Грама для системы векторов a1, …, ak.
Теорема 3.7. Если система векторов а1, …, аk линейно независима, то ее матрица Грама является невырожденной.
◄ Докажем равносильное утверждение, что если матрица Грама системы векторов а1, …, аk вырождена, то эта система векторов линейно зависима. Вырожденность матрицы Грама означает, что ее столбцы линейно зависимы и один из них, например первый, является линейной комбинацией остальных [III]:
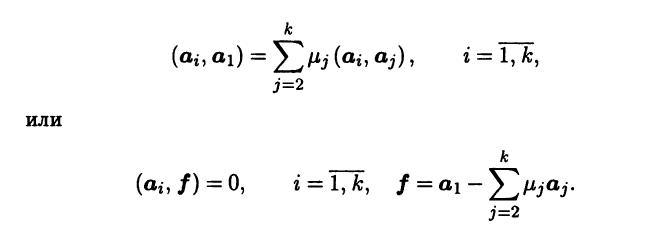
Следовательно, вектор f принадлежит ортогональному дополнению линейного подпространства span{a1,…,ak}, а поскольку f ∈ span{a1,…,ak}, то f = 0, т.е.
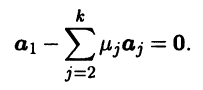
Это равенство означает, что векторы a1, … , ak линейно зависимы, так как коэффициент при a1 не равен нулю. ►
Отметим, что система линейных алгебраических уравнений (3.19) всегда совместна: ее решениями являются коэффициенты разложения вектора h ∈ H = span{a1,… ,ak} по системе векторов a1, …, аk, так как в этом случае вектор d = b – h = h⊥ – решение системы (3.18). Если система векторов a1, …, аk линейно независима, то, согласно доказанной теореме, матрица СЛАУ (3.19) невырождена и эта система имеет единственное решение, которое дает решение исходной задачи. Если же указанная система векторов линейно зависима, то матрица СЛАУ
(3.19) вырождена. В этом случае квадратная СЛАУ (3.19), будучи совместной, имеет бесконечно много решений и каждое из них дает решение исходной задачи. Среди этих решений можно выбирать те, которые удовлетворяют каким-то дополнительным условиям.
Дополнение 3.3. Псевдорешения и псевдообратная матрица
Рассмотрим систему линейных алгебраических уравнений (СЛАУ) Ах = b, вообще говоря, несовместную, с матрицей А типа n × k. Мы остановимся на тех столбцах x, которые для рассматриваемой системы дают минимальную невязку. Если СЛАУ Ах = b совместна, то такие столбцы представляют собой ее решения. Если же СЛАУ несовместна, то столбцы, дающие минимальную невязку, можно находить при помощи метода наименьших квадратов. В этом разделе изложим другой метод их нахождения, используя отождествление векторов евклидова арифметического пространства Rn с матрицами-столбцами их координат в стандартном базисе.
СЛАУ Ах = b соответствует СЛАУ АTАх = АTb, которую называют нормальной.
Пусть a1, …, ak ∈ Rn – столбцы матрицы А. СЛАУ Ах = b может быть записана в векторной форме:
x1a1 + … + xkаk = b.
Совместность СЛАУ Ах = b означает, что вектор b ∈ Rn попадает в линейную оболочку H системы векторов a1, …, аk. Пусть b ∉ Н. Разложим вектор b в сумму b = h + h⊥, где h – ортогональная проекция вектора b на линейное подпространство
H, a h⊥ – ортогональная составляющая этого вектора. Введенные обозначения используем в формулировках и доказательстве следующих трех теорем.
Теорема 3.8. Для любой СЛАУ Ах = b следующие множества совпадают:
– множество столбцов, дающих минимальную невязку для этой СЛАУ;
– множество решений СЛАУ Ах = h;
– множество решений нормальной СЛАУ АTАх = АTb.
◄ Норма вектора h⊥ представляет собой минимальную невязку СЛАУ Ах = b (см. Д.3.2), а множество векторов, дающих такую невязку, представляют собой решения СЛАУ Ах = h.
Условие h⊥ ∈ Н⊥ равносильно тому, что вектор h⊥ ортогонален каждому из векторов a1, …, ak, т.е.
(ai,h⊥) = 0, i = 1,k.
Мы имеем СЛАУ относительно компонент столбца h⊥, которая в матричной форме имеет вид ATh⊥ = 0.
Умножим СЛАУ Ах = h, решения которой дают для си-стемы Ах = b минимальную невязку, на матрицу АT слева. Учитывая, что АTА = 0, получим
АTАх = ATh = ATh + ATh⊥ = А⊥b.
Значит, все векторы х, дающие для СЛАУ Ах = b минимальную невязку, являются решениями СЛАУ АTАх = АTb. Верно и обратное: если вектор х является решением системы ATАх = АTb, то для СЛАУ Ах = b он дает минимальную невязку. Действительно, если АTАх = АTb, то АT(b – Ах) = 0, а это означает, что вектор b’ = b – Ах ортогонален векторам a1, …, аk и, следовательно, принадлежит линейному пространству, НT. Поскольку b” = Ах ∈ Н, то b = b” + b’. Согласно следствию 3.1, последнее равенство совпадает с разложением b = h + h⊥. Поэтому b’ = h⊥, а норма вектора b’, представляющая собой невязку, будет минимальной. ►
Теорема 3.9. Нормальная система линейных алгебраических уравнений всегда совместна.
◄ СЛАУ Ах = b соответствует нормальная СЛАУ АTАх = АTb. Решениями нормальной СЛАУ являются векторы х, дающие минимальную невязку для исходной СЛАУ Ах = b и являющиеся решениями СЛАУ Ах = h. Последняя же система всегда имеет решения, так как в векторной форме она имеет вид x1a1 + … + xkak = h, где h ∈ H = span{a1,… ,ak}. ►
Теорема 3.10. Для того чтобы нормальная СЛАУ АTАх = АTb имела единственное решение, необходимо и достаточно, чтобы:
– однородная СЛАУ Ах = 0 была определенной;
– ранг матрицы А совпадал с количеством ее столбцов;
– векторы a1, …, аk были линейно независимы.
◄ Так как множества решений систем Ах = h и АTАх = АTb совпадают, то из теоремы о структуре общего решения СЛАУ [III] следует, что тогда совпадают и множества решений соответствующих однородных систем Ах = 0 и АT Ах = 0. Если эти однородные системы определенны, т.е. имеют единственное решение, то СЛАУ Ах = b имеет единственный вектор с минимальной невязкой и наоборот. Для того чтобы однородная система Ах = 0 имела единственное решение, необходимо и достаточно, чтобы ранг матрицы А был равен количеству столбцов в ней, или, другими словами, чтобы столбцы матрицы были линейно независимы [III]. ►
Псевдорешения и их свойства. Если для системы Ах = b бесконечное количество векторов х дает минимальную невязку, то обычно выбор останавливают на том из них, который имеет минимальную норму. Такой вектор называют нормальным псевдорешением (или просто псевдорешением) СЛАУ Ах = b. Таким образом, псевдорешение системы линейных ал-гебраических уравнений – это такой вектор, который дает минимальную невязку в этой системе и среди таких векторов имеет минимальную норму.
Теорема 3.11. Любая СЛАУ имеет псевдорешение, и притом единственное.
◄ Множество всех векторов х, дающих минимальную невязку для СЛАУ Ах = b, описывается формулой
x = xx + xо, (3.20)
где хч – некоторое частное решение соответствующей нормальной СЛАУ; хо – общее решение однородной СЛАУ АTАх = 0, которое является общим решением и однородной СЛАУ Ах = 0 (см. доказательство теоремы 3.10).
Обозначим через K линейное подпространство всех решений однородной СЛАУ Ах = 0. Тогда имеет место представление хч = х⊥ч + х°ч, где х°ч ∈ K, х⊥ч ∈ K⊥, и поскольку х°ч + хо ∈ K, то для любого x вида (3.20), согласно теореме Пифагора, имеем
||x||2 = ||xч + xо||2 = ||x⊥ч + (xоч + xо)||2 + ||x⊥ч||2 + ||xоч + xо||2 ≥ ||x⊥ч||2
Равенство ||x|| = ||x⊥ч||2 возможно и притом лишь в единственном
случае, когда x°ч + хo = 0, или х = х 1/ч. Следовательно, среди векторов, дающих минимальную невязку СЛАУ Ах = b, минимальную норму будет иметь вектор и только он. Этот вектор является ортогональной составляющей (любого) частного решения нормальной СЛАУ относительно линейного подпространства K всех решений соответствующей однородной СЛАУ Ах = 0. ►
Оказывается, что для любой СЛАУ можно построить такую другую СЛАУ, единственным решением которой является псевдорешение исходной СЛАУ. Для нахождения такой СЛАУ воспользуемся тем, что, согласно доказательству теоремы 3.11, условие минимальности нормы псевдорешения СЛАУ Ах = b означает его ортогональность всем векторам линейного подпространства K решений соответствующей однородной системы Ах = 0. Ортогональность линейному подпространству K равносильна тому, что псевдорешение ортогонально каждому из векторов произвольно выбранной фундаментальной системы решений СЛАУ Ах = 0. Условия ортогональности представляют собой линейные уравнения, добавив которые к нормальной СЛАУ, мы и получим такую СЛАУ, единственным решением которой будет псевдорешение системы Ах = b.
Пример 3.17. Если матрица А нулевая, то псевдорешением СЛАУ Ах = b является нулевой вектор. Действительно,в этом случае невязка не зависит от выбора вектора х и равна ||b||. Минимальную же норму среди всех векторов линейного арифметического пространства имеет нулевой вектор.
Пример 3.18. Если матрица А является квадратной и невырожденной, то псевдорешение СЛАУ Ах = b совпадает с ее обычным решением, так как минимальная невязка, равная нулю, будет достигаться на единственном векторе, являющемся решением этой системы. Псевдорешение совпадет с решением и в случае, когда матрица А не является квадратной, но имеет ранг, совпадающий с количеством столбцов. Это возможно в том случае, когда число строк превышает число столбцов. Такую систему можно заменить эквивалентной ей квадратной, отбрасывая лишние уравнения.
Пример 3.19. Рассмотрим простейшую систему
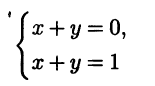
двух уравнений с двумя неизвестными. Видно, что эта система несовместна. Последовательно вычисляем
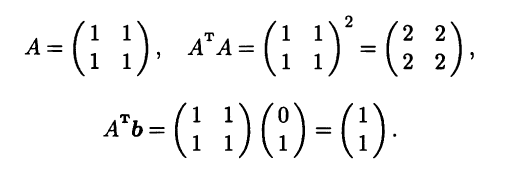
Таким образом, нормальная СЛАУ в этом случае состоит из двух одинаковых уравнений:
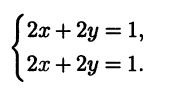
Множество решений нормальной системы, т.е. множество пар х, у, дающих минимальную невязку в исходной системе, на плоскости изображается прямой х + у = 0,5 (рис. 3.7), а псевдорешением будет точка этой прямой, ближайшая к началу координат, т.е. точка с координатами х = 0,25, у = 0,25. Этой точке соответствует радиус-вектор с наименьшей нормой среди всех радиус-векторов точек прямой х + у = 0,5.
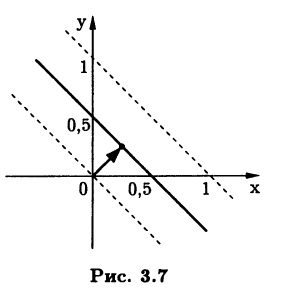
Если одно из уравнений исходной системы умножить на ко-эффициент, то и множество решений нормальной системы, и псевдорешение данной системы изменятся. Это достаточно очевидно, так как умножение уравнения на коэффициент изме-няет, вообще говоря, его невязку. Например, умножив второе уравнение рассматриваемой системы на 2:
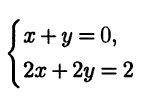
и вычислив
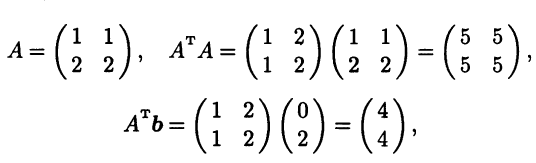
находим, что нормальная СЛАУ и в этом случае будет состоять из двух идентичных уравнений 5х + 5у = 4, но они уже другие. Псевдорешением рассматриваемой системы будет х = 0,4, y = 0,4.
Пример 3.20. Рассмотрим на плоскости треугольник с вершинами (1; 1), (2;2), (3;1) (рис. 3.8). Прямые, на которых лежат стороны этого треугольника, опишем при помощи нормальных уравнений и составим из них систему
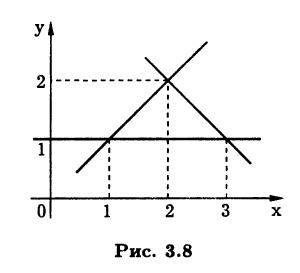
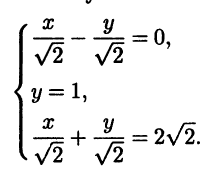
Полученная система несовместна, так как три прямых не имеют общей точки.
Определим для полученной системы нормальную СЛАУ. Для этого последовательно находим:
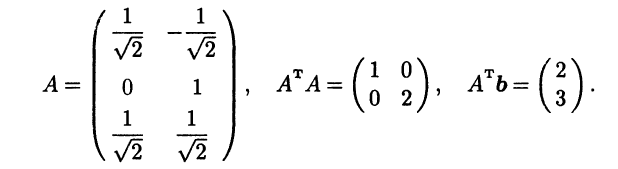
Нормальная СЛАУ AT Ax = ATb имеет единственное решение х = 2, у = 1,5, являющееся (в силу единственности) псевдорешением исходной системы.
Так как прямые плоскости заданы нормальными уравнени-ями, квадрат невязки системы для вектора (х0, у0) будет равен сумме квадратов расстояний от точки (x0;y0) до трех прямых. Найденному псевдорешению на плоскости соответствует точка (2;1,5), сумма квадратов расстояний от которой до трех сторон треугольника является минимальной. #
Псевдорешения сохраняют линейные свойства решений ли-нейных систем.
Теорема 3.12. Если х1 – псевдорешение системы Ах = b1, x2 – псевдорешение системы Ах = b1, то λ1x1 + λ2x2 – псевдорешение системы Ах = λ1b1 + λ2b2.
◄ Из условий теоремы вытекает, что xi является решением нормальной СЛАУ АTАх = ATbi, i = 1,2. Значит, λ1x1 + λ2x2 является решением нормальной СЛАУ АTАх = АTλ1b1 + АTλ2b2, и нам остается показать, что при этом λ1x1 + λ2x2 имеет минимальную норму или, что то же самое, λ1x1 + λ2x2 и любое решение у однородной СЛАУ Ау = 0 ортогональны.
Отметим, что псевдорешения xi ортогональны всем решениям СЛАУ Ау = 0 как псевдорешения систем, различающихся лишь правыми частями. Это значит, что (у, xi) = 0, если Ау = 0. Поэтому
(у, λ1x1 + λ2x2) = λ1(у, x1) + λ2 (у, x2) = 0,
если Ау = 0. ►
Псевдообратная матрица. Решение СЛАУ Ах = b с квадратной невырожденной матрицей А может быть записано с помощью обратной матрицы в виде x = А-1b [III]. Обратная матрица А-1 является решением матричного уравнения АХ = Е, где Е – единичная матрица, а столбцы сi обратной матрицы являются решениями систем Agi = еi, i = 1,n, где е1, …, еn – стандартный базис в линейном пространстве Rn (столбец еi является также i-м столбцом единичной матрицы). Для b = (b1 … bn)T справедливо разложение b = b1e1 + … + bnen, и поэтому формула x = А-1b в векторной форме записывается в виде x = b1g1 + … + bngn т.е. в виде линейной комбинации решений gi, коэффициентами в которой служат правые части bi уравнений системы.
Этот подход позволяет обобщить понятие обратной матрицы и использовать это обобщение для нахождения псевдорешений примерно так же, как обратную матрицу для построения обычных решений.
Рассмотрим СЛАУ Ах = b с произвольной матрицей А типа n × k. Пусть gi – псевдорешение системы Ах = еi, где е1, …, еn – стандартный базис в Rn. Матрицу А+ = (g1 … gn), составленную из столбцов gi, называют псевдообратной к матрице А. Отметим, что матрица А+ имеет тип k×n, т.е. тот же, что и транспонированная матрица АT.
Теорема 3.13. Псевдорешением СЛАУ Ах = b является вектор х = А+b.
◄ Действительно, если gi – псевдорешение системы Ах = еi, i = 1,n, то, согласно теореме 3.12, х = b1g1 +… + bngn является псевдорешением системы с той же матрицей и правой частью b1e1 +… + bnеn = b , т.е. рассматриваемой системы Аx = b. ►
Как вытекает из изложенного, любая матрица имеет псевдообратную. Если матрица А квадратная невырожденная, то ее псевдообратная матрица А+ совпадает с обратной А-1, так как в этом случае псевдорешения gi систем Аx = еi будут совпадать с обычными решениями и, следовательно, будут столбцами обратной матрицы.
Пример 3.21. Если А – нулевая матрица типа n × k, то А+ – также нулевая, но типа k × n. В этом случае псевдорешением системы Аx = еi, i = 1,n, будет нулевой столбец высоты k (см. пример 3.17).
Пример 3.22. Рассмотрим матрицу
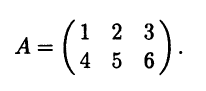
Эта матрица имеет ранг 2, а соответствующая СЛАУ при любой правой части, согласно теореме Кронекера – Капелли, будет совместна, так как ранг расширенной матрицы не может превышать двух и потому совпадает с рангом матрицы системы. Поэтому псевдорешение СЛАУ Аx = b является одним и
-
Линейные операции над векторами
-
Базис. Cкалярное произведение
-
Векторное и смешанное произведения векторов
-
Декартова система координат. прямая на плоскости
-
Плоскость в пространстве
-
Прямая в пространстве
-
Кривые второго порядка — I
-
Кривые второго порядка — II
-
Поверхности второго порядка
-
Матрицы и операции с ними
-
Обратная матрица
-
Ранг матрицы
-
Системы линейных алгебраических уравнений
-
Свойства решений однородных и неоднородных СЛАУ
mathbfin L^<perp>[/math] . Найдем скалярное произведение
Следовательно, [math]langle mathbf,mathbfrangle=0[/math] , и согласно аксиоме 4 скалярного произведения [math]mathbf=mathbf[/math] , поэтому [math]mathbf=mathbf+ mathbf= mathbf+mathbf<0>=mathbfin L[/math] . Значит, [math](L^<perp>)^<perp>subset L[/math] . Из двух включений [math]Lsubset (L^<perp>)^<perp>[/math] и [math](L^<perp>)^ <perp>subset L[/math] следует равенство [math]L=(L^<perp>)^<perp>[/math] .
6. Если [math]L_1triangleleft mathbb[/math] и [math]L_2triangleleft mathbb[/math] , то [math](L_1+L_2)^<perp>=L_1^<perp>cap L_2^<perp>[/math] и [math](L_1cap L_2)^<perp>= L_1^<perp>+ L_2^<perp>[/math] .
Последние свойства аналогичны свойствам алгебраических дополнений.
Нахождение ортогонального дополнения подпространства
Ранее для описания подпространств линейных пространств использовались два способа описания (внешний и внутренний). Рассмотрим применение этих способов описания для нахождения ортогональных дополнений подпространств. Учитывая изоморфизм евклидовых пространств, будем рассматривать арифметическое пространство [math]mathbb^n[/math] со скалярным произведением (8.27).
Для заданного подпространства [math]Ltriangleleft mathbb^n[/math] требуется найти его ортогональное дополнение [math]L^<perp>[/math] . В зависимости от способа описания подпространства [math]L[/math] используем одно из следующих двух утверждений.
1. Если подпространство [math]Ltriangleleft mathbb^n[/math] задано как линейная оболочка [math]L=operatorname(a_1,ldots,a_k)[/math] столбцов матрицы [math]A= begina_1&cdots&a_kend[/math] , то множество решений однородной системы [math]Ax=o[/math] является его ортогональным дополнением [math]L^<perp>triangleleft mathbb^n[/math] , т.е.
2. Если подпространство [math]Ltriangleleft mathbb^n[/math] задано как множество решений однородной системы [math]Ax=o[/math] [math]m[/math] уравнений с [math]n[/math] неизвестными, то линейная оболочка столбцов [math]a_1^T,ldots,a_m^T[/math] транспонированной матрицы [math]A^T=begina_1^T&cdots&a_m^Tend[/math] является его ортогональным дополнением [math]L^<perp>triangleleft mathbb^n[/math] , т.е.
где [math]a_i^T[/math] – i-й столбец матрицы [math]A^T[/math] .
Докажем, например, первое утверждение. Линейное однородное уравнение
1. В отличие от алгебраического дополнения [math]L^<+>[/math] подпространстве [math]Ltriangleleft mathbb[/math] ортогональное дополнение [math]L^<perp>[/math] находится однозначно.
2. Ортогональное дополнение [math]L^<perp>[/math] подпространства [math]Ltriangleleft mathbb[/math] в силу свойства 3 является также и алгебраическим дополнением. Это обстоятельстве учитывалось при нахождении алгебраических дополнений при помощи утверждений (8.16) и (8.17), которые по существу совпадают с утверждениями (8.34) и (8.35).
Пример 8.19. В примере 8.10 для линейного подпространства [math]L= operatorname[(t-1)^2,(t+1)^3][/math] пространства [math]P_3(mathbb)[/math] многочленов не более, чем 3-й степени, было найдено алгебраическое дополнение
Доказать, что это алгебраическое дополнение является ортогональным дополнением подпространства [math]L[/math] евклидова пространства [math]P_3(mathbb)[/math] со скалярным произведением (8.29).
Решение. Для решения задачи достаточно показать, что образующие подпространства [math]L:[/math]
ортогональны образующим алгебраического дополнения [math]L^<+>:[/math]
Найти базис в ортогональном дополнении к линейной оболочке векторов
Задачи по алгебре. Выпуск 2.
Задача 1. Найти 5А, если
.
Задача 2. Найти А +В, если
.
.
Задача 3. Найти АВ , если
.
Задача 4. Найти транспонированную матрицу относительно матрицы
.
.
Задача 5. Найти , если
.
Задача 6. Найти , если
.
Задача 7. Вычислить определитель
Решение: Разложим определитель по первой строке:
Задача 8. Найти обратную матрицу для матрицы
Определитель нулю не равен, следовательно, обратная матрица существует. Найдем алгебраические дополнения (знаки их учтем сразу), т. е.
Мы сами можем проверить результат, Известно, что . Так ли это?
Получилась единичная матрица. Значит, обратная матрица найдена верно.
Задача 9. Решить систему матричным способом:
Не является ли матрица А вырожденной? Найдем ее определитель: det А =1•[-1•4 – 1•2] – 1•[2•4 – 2•4] + 2•[2•1 – 4•(-1)] = -6 + 12 = 6
Определитель не равен нулю, то есть матрица не вырожденная. Значит, существует обратная матрица
Можно убедиться проверкой в правильности решения: подставим вектор Х в первоначальное матричное уравнение.
Действительно вектор Х удовлетворяет заданной системе.
Задача 10. Решить систему с помощью формул Крамера :
.
Задача 11. Вычислить :
Раскроем скобки и получим:
Так как , то получаем:
Задача 12. Вычислить, пользуясь формулой Муавра:
Представим число z в тригонометрической форме.
, следовательно, а=1, b =1 и .
.
.
Применим формулу Муавра:
,
Задача 13. Выполнить деление с остатком f ( x )= x 3 – x 2 – x на x -1+2 i .
Решение: Составим таблицу, в которой над чертой расположены коэффициенты многочлена f ( x ), под чертой соответствующие коэффициенты частного и остаток, последовательно вычисляемые, а слева сбоку – значение c = 1-2 i в данном примере.
Таким образом: f ( x )= x 3 – x 2 – x =( x -1+2 i ) ( x 2 -2 ix -5-2 i )-9+8 i .
Ответ : f(x)=x 3 -x 2 -x=(x-1+2i) (x 2 -2ix-5-2i)-9+8i.
Задача 14. Применяя процесс ортогонализации, построить ортогональный базис подпространства, натянутого на данную систему векторов.
, ,
;
Задача 15. Проверить, что векторы х = (1, -2, 2, -3), у = (2, -3, 2, 4) ортогональны, и дополнить их до ортогональных базисов.
Решение: Найдем скалярное произведение данных векторов: ( х , у) = 2+6+4-12 = 0 х , у – ортогональны .
Найдем векторы, дополняющие данную систему векторов до ортогонального базиса.
Пусть z = (z1, z2, z 3, z 4) попарно ортогонален с данными векторами, т.е. ( x , z ) = 0 и ( y , z ) = 0. Получаем следующую систему:
Эта система имеет множество решений, например,
Пусть теперь k = ( k 1, k 2, k 3, k 4) попарно ортогонален с векторами x , y , z . Получаем следующую систему:
Эта система имеет множество решений, например,
Таким образом, можно добавить векторы
(2, 2, 1, 0), (-5, 2, 6, 1).
Задача 16. Найти векторы, дополняющие следующую систему векторов и до ортонормированного базиса.
,
,
Пусть z = (z1, z2, z 3) попарно ортогонален с данными векторами, т.е. ( x , z ) = 0 и ( y , z ) = 0. Получаем следующую систему:
Эта система имеет множество решений, например,
Нормируя этот вектор, получим вектор, дополняющий данную систему векторов до ортонормированного базиса:
Задача 17. Доказать, что проектирование трехмерного пространства на координатную плоскость натянутую на вектора e 1, e 2 параллельно оси координат вектора e 3, является линейным преобразованием, и найти его матрицу в базисе e 1, e 2, e 3..
Решение: Пусть L – трёхмерное пространство, e 1, e 2, e 3 – базис L , преобразование – проектирование L на координатную плоскость векторов e 1, e 2 параллельно оси координат вектора e 3.
Пусть х – произвольный вектор L , т.е. x Î L .
Пусть x =( x 1, x 2, x 3) – координаты вектора x в базисе e 1, e 2, e 3, т.е. x = x 1 e 1+ x 2 e 2+ x 3 e 3. Тогда при преобразовании j имеем:
Докажем, что для любых x Î L , y Î L и числа l
1) j ( x+y )= j (x)+ j (y),
2) j ( l x )= l j (x).
j ( l x ) = ( l x 1, l x 2, 0) = l ( x 1, x 2, 0) = l j ( x ) .
Следовательно, j – линейное преобразование.
Найдем матрицу преобразования j в базисе e 1, e 2, e 3. Известно, что координаты образа j ( x ) вектора x при линейном преобразовании выражаются через координаты вектора x в том же базисе при помощи матрицы преобразования A j следующим образом:
.
Откуда следует, что
.
Задача 18. Линейное преобразование φ в базисе е 1 , е2, е3, е4 имеет матрицу
.
Выпишем матрицу перехода от базиса е 1 ,е2,е3,е4 к новому базису:
.
.
Теперь найдем матрицу преобразования В j в новом базисе по формуле В j =Т -1 А j Т.
Задача 19. Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей:
Решение: Собственные значения являются корнями характеристического уравнения преобразования j .
Составим характеристическую матрицу:
Найдем определитель матрицы и вычислим корни характеристического уравнения:
= (2 – )(3+ )(2+ )+3-2(3+ )-5(2+ ) =
= +3-6-2 -10-5 =
= 12+4 -3 -7 -13 = ,
Получим собственные значения: или .
Для каждого собственного значения найдем собственный вектор.
По определению имеем: .
Но, в тоже время,
Беря значением = -1, получаем с.л.а .у . :
Собственными векторами будут являться вектора, входящие в фундаментальную систему решений (ф.с.р.) этой с.л.а .у . Найдем ф.с.р. это с.л.а .у .
Таким образом, собственным вектором, отвечающим собственному значению = -1, является вектор .
Задача 20. Найти нормальный вид и невырожденное линейное преобразование, приводящее к этому виду, для следующей квадратичной формы: .
Решение: Ввиду отсутствия в этой форме квадратов неизвестных мы выполним сначала невырожденное линейное преобразование:
,
после чего получим .
, получим, что .
Найдем невырожденное линейное преобразование.
, , .
Задача 21. Следующую квадратичную форму привести к каноническому виду с целыми коэффициентами посредством невырожденного линейного преобразования с рациональными коэффициентами и найти выражение новых неизвестных через старые.
.
Решение: Приведем данную форму к каноническому виду:
= =2 =
= .
,
получим канонический вид квадратичной формы:
.
Учебное пособие: Методические указания для студентов 1 курса Одесса 2008
Одесский национальный университет им. И. И. Мечникова
Институт математики, экономики и механики
( решение типовых задач)
Методические указания для студентов 1 курса
Составители: д-р ф-м н., проф. Варбанец П.Д.,
к-т ф-м н., доц. Савастру О.В.
Рецензенты: д-р ф-м н., проф. Евтухов В.М.,
к-т ф-м н., доц. Белозеров Г.С.
Рекомендовано к печати
Ученым советом ИМЭМ Одесского национального университета им. И. И. Мечникова
протокол № 1 от 5 февраля 2008 г.
1. Линейные пространства …………………………………. 5
1.1. Линейные пространства и подпространства………….5
1.2. Базис пространства, его размерность…………………6
1.3. Координаты вектора в данном базисе…………….…11
1.4. Сумма и пересечение подпространств………………12
2. Евклидовы и унитарные пространства ………….…. 17
2.1. Процесс ортогонализации Шмидта………………….17
2.3. Ортогональная проекция и перпендикуляр на подпространство……………………………………………………..20
3. Операторы в линейных пространствах……………. 23
3.1. Образ, ядро линейного оператора……………………28
3.2. Матрица линейного оператора в данных базисах…..29
3.3. Собственные векторы и собственные значения..…. 31
3.4. Канонический корневой базис и жорданова нормальная форма…………………………………………………….34
4. Операторы в евклидовых и унитарных пространствах..40
5. Приведение двух квадратичных форм к каноническому виду…………………………………………………………. 45
Линейные пространства и линейные операторы представляют собой начало абстрактной части математики, с которой студенту в дальнейшем неоднократно придется иметь дело.
Эти методические указания по самостоятельной работе студентов предполагают использование следующего задачника:
И.В.Проскуряков. Сборник задач по линейной алгебре. М., Наука, 1974.
В дальнейшем мы будем придерживаться следующих обозначений (если в тексте нет специальной оговорки):
¾ – произвольные пространства над некоторым полем ;
¾ – пространство – мерных строк (столбцов) с элементами из поля над полем (арифметическое пространство).
¾ – действительное – мерное арифметическое пространство;
¾ – комплексное – мерное арифметическое пространство;
¾ – пространства геометрических векторов (прямой, плоскости, пространства);
¾ – евклидовы пространства (с указанием размерности или без него);
¾ – подпространства данного пространства (- индекс, не связанный с размерностью);
¾ векторы рассматриваемого пространства; – нулевой вектор;
¾ скаляры из данного поля, – нуль этого поля;
¾ линейные операторы, в отдельных случаях – матрицы;
¾ матрицы линейных операторов в базисах соответственно ;
¾ размерности пространств ;
¾ ранги операторов (матриц) ;
¾ скалярное произведение в данном пространстве;
¾ векторное произведение в данном пространстве .
Основными типами задач этого параграфа являются следующие:
А) выяснение вопроса, будет ли данное множество с указанными операциями линейным пространством, подпространством;
В) выделение базиса пространства, определение его размерности;
С) вычисление координат вектора в данном базисе;
D) нахождение суммы, пересечения подпространств, их размерностей и базисов.
1.1. Линейные пространства и подпространства.
Для решения задач первой группы необходимо знание аксиом линейного пространства (вообще, не следует приниматься за решение задач любого раздела, не ознакомившись предварительно с основными понятиями и теоремами данного раздела). Заметим, что в группе аксиом линейного пространства содержатся требования неограниченной применимости, однозначности и замкнутости линейных операций, которые не выделены под отдельными номерами. Распространенная ошибка: забывают проверить выполнение этих условий.
В тех условиях, когда данное множество состоит из векторов некоторого известного пространства, полезной является следующая теорема (критерий подпространства):
Теорема. Подмножество векторов пространства над полем является подпространством тогда и только тогда, когда
1. замкнуто относительно сложения, т.е. ,
2. замкнуто относительно умножения векторов на любые скаляры из основного поля : .
Некоторые из задач требуют хорошего знания других разделов курса (элементарной теории матриц, квадратичных форм, систем линейных уравнений). Ниже мы подробнее остановимся на одной из этих задач.
1.2. Базис пространства, его размерность.
Построение базиса пространства, подпространства несколько упрощается, если мы располагаем некоторыми представлениями о размерности пространства, подпространства. Одним из наводящих соображений здесь может быть следующее. Подмножество векторов пространства выделяется из с помощью дополнительных условий, накладываемых на векторы. При этом, чем больше таких условий, тем меньшей, вообще говоря, будет размерность подпространства . Если , а выделено с помощью условий специального вида, то есть основания ожидать, что .
Задача 1.1. (№1297[4]) Доказать, что множество п -мерных векторов, у которых первая и последняя координаты равны между собой, образует линейное подпространство пространства .
Решение. Множество образует линейное подпространство пространства , так как удовлетворяет критерию подпространства. Действительно, выделяется из с помощью одного условия , поэтому
1.
,
2.
.
Кроме того, нетрудно показать, что . Для этого рассмотрим векторы стандартного базиса . Векторы не принадлежат . Но построение базиса подпространства в ряде случаев удобно выполнить, исходя из стандартного базиса самого пространства, изменяя его векторы так, чтобы они «попали» в подпространство. Поэтому преобразуем векторы так, чтобы у них первая и последняя координаты были равны. Например, пусть . Рассмотрим систему векторов . Она образует базис , так как нетрудно проверить, что она является линейно независимой и каждый вектор из подпространства линейно выражается через вектора этой системы. А так как количество векторов системы равно , то и . Итак, наше предположение оказалось верным.
Линейные подпространства, размерности которых на 1 меньше размерности самого пространства называются гиперплоскостями .
В следующей задаче условий больше.
Задача 1.2. (№1298[4]) Доказать, что множество п -мерных векторов, у которых координаты с четными номерами равны нулю, образует линейное подпространство пространства .
Решение. Для доказательства того, что является подпространством, нужно также воспользоваться критерием подпространства. Так как поэтому следует ожидать, что , где – наибольшее четное число, не превышающее (, если – четное, и , если – нечетное). Базисом является подсистема стандартного базиса пространства , содержащая векторы только с нечетными номерами.
Задача 1.3. Проверить, является ли множество многочленов степени 3 с вещественными коэффициентами подпространством пространства многочленов степени ().
Решение. Воспользуемся критерием подпространства. Проверим условие .
Пусть , тогда
,
так как степень суммы этих двух многочленов равна двум. Итак, множество не является подпространством.
Задача 1.4. (№№1291, 1308[4]) Найти какой-нибудь базис и размерность линейного подпространства пространства , если составляют все векторы из , у которых сумма координат .
Решение. Очевидно векторы стандартного базиса
(1 на – ой позиции ) множеству не принадлежат ни при каком . Однако, замена на векторах последнего нуля числом (-1) дает нам векторы из . Таким образом мы получаем систему векторов
из , которая линейно независима (почему?) и обязана быть базисом , ибо из условия задачи явно следует, что из и, следовательно, .
Попутно решен вопрос (и подтвердилась гипотеза) о размерности ( выделено из одним условием).
Задача 1.4. (№1306[4]) Пусть – неотрицательная квадратичная форма от неизвестных ранга . Доказать, что все решения уравнения =0 образуют мерное линейное подпространство пространства .
Поиск решения. Вспоминаем основные понятия теории квадратичных форм (матрица формы, ранг формы, определение формы). Очевидно, что более подробные записи данного уравнения в виде
, никак не указывают на способ решения задачи.
В процессе дальнейших размышлений начинаем понимать, что мы должны исходить из неотрицательной определенности формы . Нормальный вид такой формы
(1)
а множество решений уравнения =0 в этом случае состоит из векторов вида
, (2)
Где – произвольные числа из . Имеющийся опыт (задача 1.2) подсказывает, что множество векторов такого вида есть ()-мерное подпространство пространства . Но данная нам форма не обязательно нормальная. И здесь мы вспоминаем, что каждая неотрицательно определенная форма ранга невырожденным линейным преобразованием приводится к виду (1). Создается план решения: преобразовать форму к виду (1) , найти решения (2) уравнения =0 для преобразованной формы, а затем с помощью обратного преобразования построить решения уравнения =0 для данной формы .
Решение. По теореме о приведении квадратичной формы к нормальному виду существует невырожденное линейное преобразование
, приводящее форму к виду
Множество решений уравнения состоит из векторов где , то есть из векторов
.
Обозначим (1 на – ой позиции) и докажем, что множество решений уравнения =0 есть линейная оболочка системы векторов
.
Пусть . Тогда
Очевидно и другое:
Кроме того, система линейно независима (проверяется непосредственно). Составляем линейную комбинацию . Получаем . Мы пришли к матричному уравнению, которое имеет единственное решение, так как матрица является невырожденной.
.
Отсюда . Тем самым мы показали, что система является линейно независимой. Следовательно, – линейное пространство (по построению) и его размерность
1.3. Координаты вектора в данном базисе.
Решение вопроса о ранге системы векторов, заданных координатами в некотором базисе, выделение из системы ее максимальной линейно независимой подсистемы, выражение остальных векторов в виде линейных комбинаций векторов этой подсистемы сводится к решению этих же задач для системы строк (столбцов) координатной матрицы, которые подробно обсуждались в соответствующем параграфе первой части.
1.4.Сумма и пересечение подпространств.
Пусть – данные подпространства пространства. Обычно их задают в виде линейных оболочек систем векторов или как множества решений некоторых однородных систем линейных уравнений, а сами векторы- координатными строками в некотором базисе. Вычисление не составляет особого труда: это ранг объединения базисов или порождающих систем подпространств и . находится по формуле
. (3)
Несколько сложнее обстоит дело с поиском базиса пересечения . В общем виде этот вопрос рассматривается в задаче №1319 [4]. Здесь же мы укажем, как найти решения конкретных задач (№№ 1320-1322 [4]). Задачу 1.6 мы решим двумя способами, второй – с помощью схемы Штифеля (предполагаем, что №1319 вы уже разобрали).
Задача 1.6. Найти базис суммы и пересечения подпространств, натянутых на системы векторов
и
Решение. Обозначим , . Будем считать, что координаты векторов заданы в единичном базисе .
1 способ. Как известно, базисом суммы служит любая база системы векторов , . Его построение сводится к вычислению ранга матрицы, строками которой являются координаты векторов последней системы. Кроме того, базис суммы можно получить, добавляя к базису первого подпространства некоторые из векторов базиса второго подпространства.
Итак, . Базис составляют .
. Базис составляют .
.
Базис составляют . По формуле (3) получаем . Базис пересечения будем искать из условия . Значит, представим в виде и . Приравниваем правые части . Это равенство эквивалентно системе трех линейных однородных уравнений с четырьмя неизвестными. Нужно решить эту систему и построить ФСР. Тогда будет образовывать базис пересечения.
Решив систему, строим ФСР.
Вектор образует базис .
2 способ. 1) Составим таблицу Штифеля для объединенной системы векторов , и перебрасываем наверх сначала векторы , пока это возможно (квадратиками выделены разрешающие элементы). Векторы , переходящие налево, не пишем и их координаты не вычисляем.
[spoiler title=”источники:”]
http://assorti-1.narod.ru/algebra_tasks2.html
http://www.bestreferat.ru/referat-405168.html
[/spoiler]
| Название: Методические указания для студентов 1 курса Одесса 2008 Раздел: Остальные рефераты Тип: учебное пособие Добавлен 17:40:19 17 сентября 2011 Похожие работы Просмотров: 2273 Комментариев: 8 Оценило: 1 человек Средний балл: 2 Оценка: неизвестно Скачать |
Помогаю со студенческими работами здесь
Найти ортогональный базис подпространства
Посредством процесса ортогонализации найти ортогональный базис подпространства, натянутого на…
Дополнить базис подпространства до базиса всего пространства
Доказать, что векторы вида (3a+2b, -a-b, 2a+4b) образуют линейное подпространство в пространстве…
Найдите какой-нибудь базис и определите размерность подпространства
Найдите какой-нибудь базис и определите размерность подпространства 6-мерного пространства векторов…
Найти любые два вектора, образующие базис подпространства
Рассмотрим плоскость в трехмерном пространстве R3, задаваемую уравнением вида x−2y+3z=0.
Все…
Искать еще темы с ответами
Или воспользуйтесь поиском по форуму:
